1 Introduction

Atmospheric turbulence, which perturbs the information carrying laser beam, affects the performance of free-space optical (FSO) communication systems critically. The effects of atmospheric turbulence in FSO communication have been modeled and analytically treated in the literature as turbulence induced fading, similar to the multipath fading in conventional radio-frequency (RF) communication systems [1, 2]. Owing to the efficiency of multiple-input multiple-output (MIMO) techniques in mitigating the adverse effects of multipath fading in RF communication, the multiple aperture-based optical nodes have been widely used in FSO communication systems [2,3,4]. The MIMO FSO communication offers better diversity, higher bandwidth and improved capacity [2]. A major limitation of FSO communication systems is the requirement of line-of-sight (LoS) between transmitter and receiver which limits the range of communication. The relay-assisted multi-hop communication, however, provides a viable solution for achieving a long-range communication [4,5,6].

The performance of MIMO FSO systems has been analyzed in several works [2,3,4, 7,8,9]. The concept of diversity and combining has been extended to FSO communication system with Gamma–Gamma distributed turbulence in [2], and error performance for binary modulation scheme is derived. The performance of Alamouti code is analyzed and compared with that of repetition coding in [7], and it has been found that repetition coding outperforms the Alamouti-based FSO system. Further, the error performance analysis of an FSO MIMO system with generalized OSTBC and M-PSK constellation has been given in [10]. In [9], the asymptotic bit error rate (BER) for FSO systems with transmit laser selection scheme has been analyzed over Gamma–Gamma atmospheric turbulence and pointing errors. The derived results were utilized to obtain the optimum beamwidth that minimizes the BER in different turbulence conditions.

In [3], the BER for an FSO multiple-input single-output (MISO) system with arbitrary beamforming scheme is derived in identical Gamma–Gamma faded FSO links without considering the effect of misalignment. A decode-and-forward (DF) relay-assisted dual-hop system has been analyzed with Gamma–Gamma turbulence, misalignment errors and transmit laser selection scheme in [4]. It was observed that misalignment errors significantly affect the diversity performance of the system. The analysis in [4] utilized the approximated Taylor’s series expansion for the probability density function (PDF) of the channel coefficients.

To the best of authors’ knowledge, the performance of an arbitrary beamforming scheme in a DF-based \(2\times 1\) dual-hop MISO FSO system with atmospheric turbulence and misalignment errors has not been analyzed utilizing M-ary phase shift keying (M-PSK) and M-ary quadrature amplitude modulation (M-QAM) constellations. With this motivation, an arbitrary beamforming scheme for a \(2\times 1\) dual-hop MISO system with Gamma–Gamma distributed FSO links is analyzed in this paper. The zero-boresight misalignment errors are considered in the receive apertures of relay and destination. The PDF of the received signal-to-noise ratio (SNR) over each hop of the considered system is obtained. Further, we derive the moment generating function (MGF) of the instantaneous SNR in the receiver of a \(2 \times 1\) MISO system. The expressions are obtained for the average symbol error rate (SER) for subcarrier intensity modulated (SIM) M-PSK and M-QAM signaling.

2 System model

2.1 Dual-hop MISO system

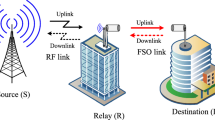
A dual-hop FSO communication system is considered with a source (S), a DF relay (R), and a destination (D). The transmission from S to D takes place via two hops (S–R and R–D) in two time slots. In first time slot, S transmits its information to the R, and in second time slot, R forwards the decoded version of the received information to D. We consider a \(2\times 1\) MISO setup in both the hops. It means, the S has two collocated transmit apertures, and destination possesses one receive aperture. The R is equipped with one receive aperture and two collocated transmit apertures.

We use \(h_{i,j}\) to represent the coefficient of FSO link from i-th transmit aperture to receive aperture in j-th hop. Here \(j=1,2\) represents the S–R and R–D hops, respectively. We assume that the two links of a hop are independent and identically distributed (i.i.d.); however, the links from two different hops are assumed to be independent and nonidentically distributed (i.n.i.d.). The channel coefficient \(h_{i,j}\) incorporates the real-valued irradiance in atmospheric turbulence \(I_{i,j}\) and the misalignment fading represented by \(m_j\). Thus, the composite channel coefficient is \(h_{i,j} = m_jI_{i,j}\). The irradiance \(I_{i,j}\) follows the Gamma–Gamma distribution with PDF given as [3],

$$\begin{aligned} f_{I_{i,j}}(I) =\frac{2(a_{j}b_{j})^{\frac{a_{j}+b_{j}}{2}}}{\varGamma (a_{j})\varGamma (b_{j})}I^{\frac{a_{j}+b_{j}}{2}-1} K_{a_{j}-b_{j}}\left( 2\sqrt{a_{j}b_{j}I}\right) , \end{aligned}$$
(1)

where \(K_v(\cdot )\) is modified Bessel function of second kind with order v. The parameters \(a_{j}\) and \(b_{j}\) characterize the irradiance fluctuations in j-th hop and can be expressed as in [3, eq. 4]. The zero-boresight misalignment coefficients \(m_j\) can be represented by the PDF given in [7] as,

$$\begin{aligned} f_{m_j}(m)=\frac{\zeta _j^{2}}{A_{0,j}^{\zeta _j^{2}}}{m}^{\zeta _j^{2}-1}, \,\,\,\,\,\,\,\,\,\,\,\, 0\le {m} \le A_{0,j} , \end{aligned}$$
(2)

where \(A_{0,j}=[\text {erf}(\nu _j)]^2\) represents the fraction of the collected optical power, \(\nu _j = \sqrt{\pi R_j^2/2w_{b_j}^2}\), \(R_j\) denotes the radius of receiver aperture, \(w_{b_j}\) is normalized beam waist, and \(\zeta _j=\frac{\omega _{e_j}}{2\sigma _{s_j}}\). \(\omega _{e_j} = [\sqrt{A_{0,j}\pi }w_{b_j}^2/(2\nu _j\text {exp}(-\nu _j^2))]^{1/2}\) is the equivalent beam width at the receiver, and \(\sigma _{s_j}^{2}\) is the variance of the pointing error displacement characterized by Gaussian distributed horizontal sway and elevation.

2.2 Transmission protocol

We assume a SIM [11]-based FSO system in order to utilize the higher RF modulation techniques in FSO environment. In first time slot, the symbol \(x \in \mathscr {A}\), where \(\mathscr {A}\) is an M-PSK or M-QAM alphabet, is multiplied by a beamforming vector \(\mathbf w = [w_1,w_2]'\), where \([\cdot ]'\) denotes the transpose of a matrix, and scaled by a factor 1 / 2 before transmission from S. Here \(w_1\) and \(w_2\) are arbitrary beamforming weights such that \(w_1+w_2\le 2\). Thus both the transmitting apertures transmit the differently weighted symbol x. The signal received at the receive aperture in relay node is given by

$$\begin{aligned} y_r =\frac{\eta }{2}\left[ w_1h_{1,1}+w_2h_{2,1}\right] x+n_r, \end{aligned}$$
(3)

where \(\eta \) is the optical-to-electrical conversion coefficient,Footnote 1 \(n_r\) represents the additive white Gaussian noise (AWGN) with zero mean and \(N_0\) variance in the relay. Similarly, the received signal in the destination is given by,

$$\begin{aligned} y_d =\frac{\eta }{2}\left[ u_1h_{1,2}+u_2h_{2,2}\right] \hat{x}+n_d, \end{aligned}$$
(4)

where \(u_1\) and \(u_2\) are arbitrary beamforming weights for the second hop such that \(u_1+u_2\le 2\), \(\hat{x} \in \mathscr {A}\) represents the decoded version of x by R, and \(n_d\) represents the AWGN with zero mean and \(N_0\) variance in the destination. If \(E_s\) be the symbol energy of M-ary data, we can write \(\mathbb {E}[|x|^2] = \mathbb {E}[|\hat{x}|^2]= E_s\), where \(\mathbb {E}[\cdot ]\) represents the expectation operator.

3 Statistics of received SNR

3.1 PDF of \(\gamma _1\) and \(\gamma _2\)

The instantaneous SNR at the relay can be given, using (3), as \(\gamma _1 = \bar{\gamma }_1\left| w_1h_{1,1}+w_2h_{2,1}\right| ^2\), where \(\bar{\gamma }_1\) is the average SNR per diversity branch for first hop, and is defined as \(\bar{\gamma }_1 = \frac{\eta ^2E_s}{4N_0}\).

Theorem 1

The PDF of \(\gamma _1 =\bar{\gamma }_1\left| w_1h_{1,1}+w_2h_{2,1}\right| ^2\) can be expressed as,

$$\begin{aligned} f_{\gamma _1}(\gamma )= & {} \sum _{n=0}^{\infty }\frac{\varPsi _{n_1}}{2\bar{\gamma }_1^{q_1}}\gamma ^{q_1-1}+\sum _{n=0}^{\infty }\frac{\varPsi _{n_2}}{2\bar{\gamma }_1^{q_2}}\gamma ^{q_2-1}\nonumber \\&+\sum _{n=0}^{\infty }\frac{\varPsi _{n_3}}{2\bar{\gamma }_1^{q_3}}\gamma ^{q_3-1} \end{aligned}$$
(5)

where

$$\begin{aligned} q_1= & {} \frac{n+2b_1}{2}, q_2 = \frac{n+b_1+a_1}{2}, q_3 = \frac{n+2a_1}{2},\nonumber \\ \varPsi _{n_1}= & {} \frac{A_{0,1}^{\zeta _1^2-(n+2b_1)}\tilde{A}_{n_1}}{\zeta _1^2-(n+2b_1)}, \varPsi _{n_2} = \frac{A_{0,1}^{\zeta _1^2-(n+a_1+b_1)}\tilde{A}_{n_2}}{\zeta _1^2-(n+a_1+b_1)},\nonumber \\ \varPsi _{n_3}= & {} \frac{A_{0,1}^{\zeta _1^2-(n+2a_1)}\tilde{A}_{n_2}}{\zeta _1^2-(n+2a_1)}\nonumber \\ \tilde{A}_{n_1}= & {} \frac{\tilde{d}_{n_1}(a_1,b_1)\star \tilde{d}_{n_2}(a_1,b_1)}{\varGamma (n+2b_1)},\nonumber \\ \tilde{A}_{n_3}= & {} \frac{\tilde{d}_{n_1}(b_1,a_1)\star \tilde{d}_{n_2}(b_1,a_1)}{\varGamma (n+2a_1)},\nonumber \\ \tilde{A}_{n_2}= & {} \frac{\left( \tilde{d}_{n_1}(a_1,b_1) \star \tilde{d}_{n_2}(b_1,a_1)\!+\!\tilde{d}_{n_1}(b_1,a_1)\star \tilde{d}_{n_2}(a_1,b_1)\right) }{\varGamma (n\!+\!a_1\!+\!b_1)}.\nonumber \\ \end{aligned}$$
(6)

Further, \(\tilde{d}_{n_i}(a,b)\), \(i \in \{1,2\}\) can be given as,

$$\begin{aligned} \tilde{d}_{n_i}(a,b) = \frac{\varGamma (n+b_1)(a_1b_1)^{b_1+n}\varGamma (a_1-b_1)}{n!w_i^{n+b_1}\varGamma (a_1)\varGamma (b_1)(1+b_1-a_1)_n} \end{aligned}$$
(7)

where \((\ell )_k = \frac{\varGamma (\ell +k)}{\varGamma (\ell )}\) represents the Pochammer’s symbol [12].

Proof

The PDF of \(Z \triangleq w_1h_{1,1}m_1+w_2h_{2,1}m_1\) conditioned over \(m_1\) can be given using [3, eq.21] as,

$$\begin{aligned} f_{Z|m_1}(z)= & {} \sum _{n=0}^{\infty }\tilde{A}_{n_1} z^{n+2b_1-1}m_1^{-n-2b_1}\nonumber \\&+\sum _{n=0}^{\infty }\tilde{A}_{n_2}z^{n+a_1 +b_1-1}m_1^{-n-b_1-a_1}\nonumber \\&+\sum _{n=0}^{\infty }\tilde{A}_{n_3} z^{n+2a_1-1}m_1^{-n-2a_1}. \end{aligned}$$
(8)

On normalizing (8) over the PDF of \(m_1\) given in (2), followed by transformation \(\gamma _1 = \bar{\gamma }_1|Z|^2\), we obtain (5). Similarly, the PDF of instantaneous SNR \(\gamma _2 = \bar{\gamma }_2\left| u_1h_{1,2}+u_2h_{2,2}\right| ^2\) in D can be expressed as,

$$\begin{aligned} f_{\gamma _2}(\gamma )= & {} \sum _{n=0}^{\infty }\frac{\varXi _{n_1}}{2\bar{\gamma }_2^{p_1}} \gamma ^{p_1-1}+\sum _{n=0}^{\infty }\frac{\varXi _{n_2}}{2\bar{\gamma }_2^{p_2}}\gamma ^{p_2-1}\nonumber \\&+\sum _{n=0}^{\infty }\frac{\varXi _{n_3}}{2\bar{\gamma }_2^{p_3}}\gamma ^{p_3-1} \end{aligned}$$
(9)

where

$$\begin{aligned} p_1= & {} \frac{n+2b_2}{2}, p_2 = \frac{n+b_2+a_2}{2}, p_3 = \frac{n+2a_2}{2},\nonumber \\ \varXi _{n_1}= & {} \frac{A_{0,2}^{\zeta _2^2-(n+2b_2)}\tilde{B}_{n_1}}{\zeta _2^2-(n+2b_2)}, \varXi _{n_2} = \frac{A_{0,2}^{\zeta _2^2-(n+a_2+b_2)}\tilde{B}_{n_2}}{\zeta _2^2-(n+a_2+b_2)},\nonumber \\ \varXi _{n_3}= & {} \frac{A_{0,2}^{\zeta _2^2-(n+2a_2)}\tilde{B}_{n_3}}{\zeta _2^2-(n+2a_2)},\nonumber \\ \tilde{B}_{n_1}= & {} \frac{\tilde{g}_{n_1}(a_2,b_2)\star \tilde{g}_{n_2}(a_2,b_2)}{\varGamma (n+2b_2)},\nonumber \\ \tilde{B}_{n_3}= & {} \frac{\tilde{g}_{n_1}(b_2,a_2)\star \tilde{g}_{n_2}(b_2,a_2)}{\varGamma (n+2a_2)},\nonumber \\ \tilde{B}_{n_2}= & {} \frac{\left( \tilde{g}_{n_1}(a_2,b_2)\star \tilde{g}_{n_2}(b_2,a_2)+\tilde{g}_{n_1}(b_2,a_2)\star \tilde{g}_{n_2}(a_2,b_2)\right) }{\varGamma (n+a_2+b_2)},\nonumber \\ \end{aligned}$$
(10)

and \(\tilde{g}_{n_i}(a_2,b_2)\), \(i \in \{1,2\}\) can be given as,

$$\begin{aligned} \tilde{g}_{n_i}(a_2,b_2) = \frac{\varGamma (n+b_2)(a_2b_2)^{b_2+n}\varGamma (a_2-b_2)}{n!u_i^{n+b_2}\varGamma (a_2)\varGamma (b_2)(1+b_2-a_2)_n}. \end{aligned}$$
(11)

3.2 MGF of \(\gamma _1\) and \(\gamma _2\)

The MGF of instantaneous SNR \(\gamma _1\) is defined as \(\mathscr {M}_{\gamma _1}(s)=\int _{0}^{\infty }{} \textit{e}^{-s\gamma }f_{\gamma _1}(\gamma )d\gamma \). Using (5) and [13, eq. 3.351.3] we get,

$$\begin{aligned} \mathscr {M}_{\gamma _1}(s)= & {} \sum _{n=0}^{\infty }\frac{\varPsi _{n_1}(q_1-1)!}{2\bar{\gamma }_1^{q_1}}s^{-q_1}+\sum _{n=0}^{\infty }\frac{\varPsi _{n_2}(q_2-1)!}{2\bar{\gamma }_1^{q_2}}s^{-q_2} \nonumber \\&+\sum _{n=0}^{\infty }\frac{\varPsi _{n_3}(q_3-1)!}{2\bar{\gamma }_1^{q_3}}s^{-q_3}\,. \end{aligned}$$
(12)

Similarly, for SNR \(\gamma _2\) the MGF can be expressed as,

$$\begin{aligned} \mathscr {M}_{\gamma _2}(s)= & {} \sum _{n=0}^{\infty }\frac{\varXi _{n_1}(p_1-1)!}{2\bar{\gamma }_2^{p_1}}s^{-p_1}+\sum _{n=0}^{\infty }\!\frac{\varXi _{n_2}(p_2-1)!}{2\bar{\gamma }_2^{p_2}}s^{-p_2} \nonumber \\&+\sum _{n=0}^{\infty }\frac{\varXi _{n_3}(p_3-1)!}{2\bar{\gamma }_2^{p_3}}s^{-p_3}\,. \end{aligned}$$
(13)

It can be seen in the subsequent section that how these MGFs are used to derive the SER for M-ary signaling scheme.

4 Error rate analysis

4.1 SER for M-QAM signaling

The average BER of a dual-hop DF FSO system for M-QAM can be written as \(P(e)= P_1(e)[1-2P_2(e)]\), where \(P_1(e)\) and \(P_2(e)\) are average BERs for first and second hop, respectively. The average BER \(P_{\ell }(e)\), \(\ell =1,2\), can be written as [14],

$$\begin{aligned} P_{\ell }(e)= \int _{0}^{\infty } \text {BER}_{\ell }(\gamma )f_{\gamma _{\ell }}(\gamma )\mathrm{{d}}\gamma , \end{aligned}$$
(14)

where \(\text {BER}_{\ell }(\gamma )\) represents the conditional BER of the \(\ell \)-th hop and can be obtained from [15] as

$$\begin{aligned} \text {BER}_{\ell }(\gamma )=\frac{1}{\sqrt{M}\text {log}_2\sqrt{M}}\sum _{j=1}^{\text {log}_2\sqrt{M}}\sum _{k=0}^{\upsilon _j}\varPhi _{kj}\text {erfc}(\sqrt{\omega _k\gamma }),\nonumber \\ \end{aligned}$$
(15)

where \(\text {erfc}(\cdot )\) is the complimentary error function [12, Eq. (06.27.02.0001.01)], \(\upsilon _j=(1-2^{-j})\sqrt{M}-1\), \(\omega _k=\) \( \frac{3(2k+1)^2\text {log}_2M}{2(M-1)}\), and \(\varPhi _{kj}=(-1)^{\lfloor \mu \rfloor }\left( 2^{j-1}-\lfloor \mu +\frac{1}{2} \rfloor \right) \) with \(\mu = \frac{k2^{j-1}}{\sqrt{M}}\). Using (15) in (14) and after some algebra, we get the expression for \(P_1(e)\) and \(P_2(e)\) as,

$$\begin{aligned}&P_1(e)=\frac{1}{\sqrt{M}\text {log}_2\sqrt{M}}\sum _{j=1}^{\text {log}_2\sqrt{M}}\sum _{k=0}^{\upsilon _j}\varPhi _{kj}\nonumber \\&\quad \times \left[ \sum _{n=0}^{\infty }\frac{\varPsi _{n_1}w_k^{-q_1}\varGamma (q_1+1/2)}{2q_1\sqrt{\pi }\bar{\gamma }_1^{q_1}}\right. +\sum _{n=0}^{\infty }\frac{\varPsi _{n_2}w_k^{-q_2}\varGamma (q_2+1/2)}{2q_2\sqrt{\pi }\bar{\gamma }_1^{q_2}}\nonumber \\&\quad +\left. \sum _{n=0}^{\infty }\frac{\varPsi _{n_3}w_k^{-q_3}\varGamma (q_3+1/2)}{2q_3\sqrt{\pi }\bar{\gamma }_1^{q_3}}\right] .\end{aligned}$$
(16)
$$\begin{aligned}&P_2(e)\!=\!\frac{1}{\sqrt{M}\text {log}_2\sqrt{M}}\sum _{j=1}^{\text {log}_2 \sqrt{M}}\sum _{k=0}^{\upsilon _j}\varPhi _{kj}\left[ \sum _{n=0}^{\infty }\frac{\varXi _{n_1}w_k^{-p_1} \varGamma (p_1\!+\!1/2)}{2p_1\sqrt{\pi }\bar{\gamma }_2^{p_1}}\right. \nonumber \\&\quad +\left. \sum _{n=0}^{\infty }\frac{\varXi _{n_2}w_k^{-p_2}\varGamma (p_2+1/2)}{2p_2\sqrt{\pi }\bar{\gamma }_2^{p_2}} +\sum _{n=0}^{\infty }\frac{\varXi _{n_3}w_k^{-p_3}\varGamma (p_3+1/2)}{2p_3\sqrt{\pi }\bar{\gamma }_2^{p_3}}\right] .\nonumber \\ \end{aligned}$$
(17)

The average BER for M-QAM signaling can be obtained by using (16) and (17) in \(P(e)= P_1(e)[1-2P_2(e)]\). Further, the average SER for an M-QAM constellation can be evaluated by multiplying the average BER with \(\log _2M\).

4.2 SER for M-PSK signaling

For a symmetric M-PSK constellation with equidimensional decision regions, the probability of error P(e) can be given, as in [6], as

$$\begin{aligned} P(e)=1-\sum _{k=1}^{M} P_k(\gamma _{1})P_k(\gamma _{2}), \end{aligned}$$
(18)

where \(P_k(\gamma _{1})\) is the probability that the source transmits \(x_j\) and the relay receives it as \(x_k\), \(k\ne j\), and \(P_k(\gamma _{2})\) is the probability that the relay transmits \(x_k\) and it is received at the destination as \(x_j\). The probabilities \(P_k(\gamma _{1})\) and \(P_k(\gamma _{2})\) can be given as [16]

$$\begin{aligned} P_k(\gamma _{i})= {\left\{ \begin{array}{ll} 1-\frac{1}{\pi } \int _{0}^{\frac{(M-1) \pi }{M}} \mathscr {M}_{\gamma _{i}}\left( \frac{\sin ^2(\frac{\pi }{M})}{\sin ^2(\phi )}\right) \mathrm{{d}}\phi , &{}k=1 \\ \frac{1}{\pi } \int _{0}^{\frac{(M-1) \pi }{M}} \mathscr {M}_{\gamma _{i}}\left( \frac{\sin ^2(\frac{\pi }{M})}{\sin ^2(\phi )}\right) \mathrm{{d}}\phi , &{}k=\frac{M}{2}+1 \\ \frac{1}{2\pi } \Bigg [\int _{0}^{\pi -a_{k-1}} \mathscr {M}_{\gamma _{i}}\left( \frac{\sin ^2(a_{k-1})}{\sin ^2(\phi )}\right) \mathrm{{d}}\phi - \int _{0}^{\pi -a_{k}} \mathscr {M}_{\gamma _{i}}\left( \frac{\sin ^2(a_{k})}{\sin ^2(\phi )}\right) \mathrm{{d}}\phi \Bigg ], &{}\text {otherwise}, \end{array}\right. } \end{aligned}$$
(19)

where \(i \in \{1,2\}\) and \(a_k = (2k-1)\frac{\pi }{M}\). The probability term \(P_k(\gamma _1)\) in (19) consists the integral of the form \(\mathscr {I}_1 = \int _{0}^{\varTheta } \mathscr {M}_{\gamma _{1}}\left( \frac{\theta }{\sin ^2(\phi )}\right) \mathrm{{d}}\phi \), where \(\varTheta \in \left\{ \frac{(M-1) \pi }{M}, \pi \!-\!a_{k-1}, \pi \!-\!a_{k}\!\right\} \) and \(\theta \in \left\{ \sin ^2(\frac{\pi }{M}), \sin ^2(a_{k-1}), \sin ^2(a_{k}) \right\} \).

On solving these integrals using MATHEMATICA, we get

$$\begin{aligned} \mathscr {I}_1= & {} \sum _{n=0}^{\infty }\frac{\varPsi _{n_1}(q_1-1)!}{2\bar{\gamma }_1^{q_1}}\varOmega (\varTheta , q_1)\nonumber \\&+\sum _{n=0}^{\infty }\frac{\varPsi _{n_2}(q_2-1)!}{2\bar{\gamma }_1^{q_2}}\varOmega (\varTheta , q_2) \nonumber \\&+\sum _{n=0}^{\infty }\frac{\varPsi _{n_3}(q_3-1)!}{2\bar{\gamma }_1^{q_3}}\varOmega (\varTheta , q_3)\,, \end{aligned}$$
(20)

where \(\varOmega (\ell _1, \ell _2) = \theta ^{-\ell _2}\left[ \lambda _1(\ell _2)-\lambda _2(\ell _1){}_2F_1[\frac{1}{2},\frac{1}{2}-\ell _2;\frac{3}{2};\right. \left. \cos ^2\ell _1]\right] \), \(\lambda _1(\ell _2)=\frac{\sqrt{\pi }\varGamma (1/2+\ell _2)}{2\varGamma (1+\ell _2)}\), and \(\lambda _2(\ell _1) = \frac{|\sin \ell _1|}{\tan \ell _1}\).

In a similar way, \(\mathscr {I}_2 = \int _{0}^{\varTheta } \mathscr {M}_{\gamma _{2}}\left( \frac{\theta }{\sin ^2(\phi )}\right) \mathrm{{d}}\phi \) for \(P_k(\gamma _2)\) can be given as,

$$\begin{aligned} \mathscr {I}_2= & {} \sum _{n=0}^{\infty }\frac{\varXi _{n_1}(p_1-1)!}{2\bar{\gamma }_2^{p_1}}\varOmega (\varTheta , p_1)\nonumber \\&+\sum _{n=0}^{\infty }\frac{\varXi _{n_2}(p_2-1)!}{2\bar{\gamma }_2^{p_2}}\varOmega (\varTheta ,p_2) \nonumber \\&+\sum _{n=0}^{\infty }\frac{\varXi _{n_3}(p_3-1)!}{2\bar{\gamma }_2^{p_3}}\varOmega (\varTheta , p_3)\,. \end{aligned}$$
(21)

Hence, the expression for the average SER for M-PSK signaling can be obtained using (18), (19), (20) and (21).

5 Results and discussions

In this section, we present the analytically obtained and simulated results for average error rate performance of the considered DF-based dual-hop MISO FSO communication system. For numerical results, we assume strong turbulence conditions \((a_1 = 4.2\) and \(b_1 = 1.4)\) for first hop, and weak turbulence conditions \((a_2 = 11.6\) and \(b_2 = 10.1)\) for second hop. Further, for misalignment errors, we consider \(R_1 = R_2 = 0.1\) and \(w_{b_1}=w_{b_2}= 0.1\). We also assume that the average SNRs of the two hops are equal.

In Fig. 1, the average SER is plotted for various M-PSK constellations and 16-QAM signaling considering equal weights, i.e., \(w_1 = w_2 = 1\) and \(u_1 = u_2 = 1\). We have assumed equal pointing error variances at two receivers, i.e., \(\sigma ^2_{s1} = \sigma ^2_{s2} = \sigma ^2_{s} = 0.01\) in Fig. 1. It can be observed from Fig. 1 that analytical results derived in this paper closely follow the exact simulations for all the modulation schemes considered here. Moreover, as the M increases, the error probability increases. Further, it can be noticed from Fig. 1 that beyond 8-PSK, the QAM signaling provides better error performance than the same sized PSK scheme.

The average BER for BPSK is plotted in Fig. 2 for different weights and different values of pointing error variance. We assume \(w_1 = w_2 = 1\) and various combinations of beamforming weights in second hop. It can be seen from Fig. 2 that equal weight beamforming \((u_1=1, u_2=1)\) performs slightly better than unequal weight beamforming \((u_1=1.9, u_2=0.1\) and \(u_1=1.5, u_2=0.5\)). Further, it can also be observed from Fig. 2 that increasing the variance parameter associated with misalignment (i.e., \(\sigma _s\)) deteriorates the error performance of the considered system.

Fig. 1
figure 1

Average SER versus average SNR performance of dual-hop \(2\times 1\) DF FSO system for M-PSK and M-QAM constellations, assuming unit weights beamforming for both hops and \(\sigma _{s1} = \sigma _{s2} = \sigma _{s} = 0.1\)

Full size image
Fig. 2
figure 2

Error performance of dual-hop MISO FSO system showing the effect of different misalignment and beamforming conditions

Full size image

6 Conclusion

We have successfully derived the average SER expressions for a dual-hop DF-based FSO MISO system using M-PSK and M-QAM signaling. It can be concluded from this paper that in a dual-hop DF system with nonidentically distributed hops, equal weight beamforming is more efficient than unequal weight beamforming.