Pointing Error Effects on Performance of Amplify-and-Forward Relaying MIMO/FSO Systems Using SC-QAM Signals Over Log-Normal Atmospheric Turbulence Channels

Abstract

In this work, we analyze pointing error effects on performance of Amplify-and-Forward (AF) relaying multiple-input multiple-output (MIMO) free space optical (FSO) communication system employing subcarrier quadrature amplitude modulation (SC-QAM) signal over log-normal distributed atmospheric turbulence channels. We study the pointing error effect by taking into account the influence of beam-width, aperture size and jitter variance on the average symbol error rate (ASER), which is derived in closed-form expressions of MIMO/FSO and SISO/FSO systems. In addition, the number of relaying stations is taken into account in the statistical model of the combined channel including atmospheric loss, atmospheric turbulence and pointing error. The numerical results show that by combining AF relaying stations and MIMO/FSO configurations, the link length can be extended due to the transmitted power is reduced accordingly to the amplifier gain. Moreover, performance of AF relaying MIMO/FSO systems is better than that of AF relaying SISO/FSO systems at the same link length.

1 Introduction

Free-space optics (FSO) is known as a line-of-sight (LOS) green communication technology, which can be used for a variety of applications ranging from high date-rate links of inter-building connections within a campus, high quality video surveillance and monitoring of a city, back-haul for next wireless mobile networks, disaster recovery links and ground to satellites [1]. The FSO’s special characteristics are unlimited bandwidth, licensing-free requirements, high security, reduced interference, cost-effectiveness and simplicity of communication system design and deployment [2]. However, there are numerous challenging issues when deploying FSO systems including the harmful effects of scattering, absorption, turbulence and the presence of pointing errors caused by misalignment between transmitter and receiver. They therefore severely impair the system performance in the link error probability [3–8]. To mitigate the impact of turbulence, multi-hop relaying FSO systems have been proposed as a promising solution to extend the transmission links and the turbulence-induced fading. Recently, performance of multi-hop relaying FSO systems over atmospheric turbulence channels has been studied in [9–11]. Moreover, recent studies have shown that, similar to wireless communications, the effect of turbulence fading with pointing errors can be significantly relaxed by using multiple-input multiple-output (MIMO) technique with multiple lasers at the transmitter and multiple photo-detectors at the receiver [12–18].

Previous works focus on MIMO FSO systems using On-Off keying (OOK) with intensity modulation and direct detection (IM/DD) and Pulse-position modulation (PPM) techniques. OOK is its simplicity and low-cost, widely used for FSO systems. However, OOK modulation needs an adaptive threshold to achieve its optimal performance, while PPM has poor bandwidth efficiency. To overcome the limitation of OOK and PPM modulation, FSO systems using sub-carrier (SC) intensity modulation schemes, such as sub-carrier quadrature amplitude modulation (SC-QAM), have been studied as the alternative modulation scheme for FSO systems [19–25]. All above studies, however, to the best of our knowledge, the pointing error effects on performance of AF relaying MIMO FSO using SC-QAM signals over log-normal atmospheric turbulence channels has not been clarified.

In this work, the ASER expressions of AF MIMO FSO systems in the log-normal atmospheric turbulence channel are analytically obtained taking into account the influence of pointing errors represented by beam-width, aperture size and jitter variance. The SC-QAM scheme is adopted for the performance analysis. Moreover, the number of relaying stations is included in the statistical model of the combined channel together with atmospheric loss, atmospheric turbulence and pointing error.

The remainder of the paper is organized into 6 sections: Sect. 2 introduces the system models, Sect. 3 discusses the atmospheric turbulence model of AF MIMO/FSO/SC-QAM systems with pointing error. Section 4 is devoted to ASER derivation of AF MIMO/FSO links. Section 5 presents the numerical results and discussion. The conclusion is reported in Sect. 6.

2 System Models

2.1 The AF Relaying SISO/FSO System Model

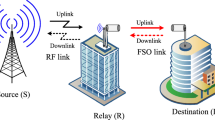
We start by investigating a typical serial multi-hop FSO system depicted in Fig. 1, which operates over independent and not identically distributed fading channels. The source node S can transmit data to the destination node D via multiple LOS free-space links arranged in an end-to-end configuration such that the source S communicates with the destination D through c relay stations R₁, R₂, . . ., R_c-1, R_c.

Fig. 1.

An illustration of a serial multi-hop relaying SISO/FSO system

It is assumed that all relay nodes concurrently receive and transmit signals in the same frequency band. In the Fig. 2, at the source node (Fig. 2 (a)), input data is first modulated into SC-QAM symbols at a subcarrier frequency $f_{c}$. The electrical SC-QAM signal at the output of electrical QAM modulator can be written as

$$ e(t) = s_{\text{I}} (t)cos(2\pi f_{c} t) - s_{\text{Q}} (t)sin(2\pi f_{c} t). $$

(1)

Fig. 2.

A SISO/FSO system model: the source node, relay node and destination node

In Eq. (1), $s_{\rm I} (t) = \sum\nolimits_{i = - \infty }^{i = + \infty } {a_{i} (t)g(t - iT_{s} )}$ and $s_{Q} (t) = \sum\nolimits_{j = - \infty }^{j = + \infty } {b_{j} (t)g(t - jT_{s} )}$ are the in-phase signal and the quadrature signal, respectively. $a_{i} (t)$, $b_{j} (t)$ are the in-phase amplitude and the quadrature information amplitude of the transmitted data symbol, respectively, $g(t)$ denotes the shaping pulse and $T_{s}$ is the symbol interval. The QAM signal is then used to modulate the intensity of an electrical-to-optical (E/O) laser before pointing laser beam through a telescope of the transmitter to the relaying node, the transmitted signal can be expressed as

$$ s\left( t \right) = P_{s} \left\{ {1 + \kappa [s_{I} (t)\cos (2\pi f_{c} t - s_{Q} (t)\sin (2\pi f_{c} t)]} \right\} , $$

(2)

where $P_{s}$ denotes the average transmitted optical power per symbol at each hop and $\kappa$ $(0 \le \kappa \le 1)$ is the modulation index. At the first relay node, the received optical signal can be written as

$$ s_{1} \left( t \right) = XP_{s} \left\{ {1 + \kappa [s_{I} (t)\cos (2\pi f_{c} t - s_{Q} (t)\sin (2\pi f_{c} t)]} \right\} . $$

(3)

In Eq. (3), X is the signal scintillation caused by log-normal atmospheric turbulence and pointing error. At each relay node, an AF module is used for signal amplification as illustrated in Fig. 2(b). The electrical signal output of the AF module at the first relay node will be

$$ e_{1} \left( t \right) = \Re P_{1} XP_{s} \kappa e(t) + \upsilon_{1} (t), $$

(4)

where $\Re$ is the photodiode (PD) responsivity, $P_{1}$ is the amplification power of the first AF module, $\upsilon_{1} (t)$ is the receiver noise that can be modeled as an additive white Gaussian noise (AWGN) process with power spectral density $N_{0}$.

Repeating such steps above through the number of relay stations, c, the electrical signal at the PD’s output of the destination node can be obtained as

$$ r_{e} \left( t \right) = P_{s} e(t)\left[ {\prod\nolimits_{i = 0}^{c} {X_{i + 1} (t)} \Re^{2i + 1} P_{i} } \right] + \sum\nolimits_{i = 0}^{c} {\upsilon_{i} (t)} , $$

(5)

where $\sum\nolimits_{i = 0}^{c} {\upsilon_{i} (t)}$ is the total receiver noise. $X_{i + 1}$ and $P_{i}$ are the stationary random process for the turbulence channel and the average transmitted optical power per symbol at the i^th relay station, respectively.

2.2 The AF Relaying MIMO/FSO System Model

Next, we consider a general AF relaying M × N MIMO/FSO system using SC-QAM signals with M-lasers pointing toward an N-aperture receiver as depicted. The source node, relaying node and destination node diagrams are presented in Fig. 3. The channel model of MIMO/FSO systems can be expressed by M × N matrix, which are denoted by $X = \left[ {{\mathbf{X}}_{mn} } \right]_{m,n = 1}^{M,N}$. The electrical signal at the input of QAM demodulator of the destination node can be expressed as

$$ r_{e} \left( t \right) = P_{s} e(t)\left[ {\sum\limits_{m = 1}^{M} {\sum\limits_{n = 1}^{N} {\prod\limits_{i = 0}^{c} {\left( {X_{i + 1} } \right)_{mn} } } } \Re^{2i + 1} P_{i} } \right] + \sum\limits_{i = 0}^{c} {\left( {\sum\limits_{m = 1}^{M} {\sum\limits_{n = 1}^{N} {v_{mn} } } } \right)_{i} (t)} , $$

(6)

Fig. 3.

An AF relaying MIMO/FSO system model

where $X_{mn}$ denotes the stationary random process of the turbulence channel from the m^th laser to the n^th PD. In this system model, we use an equal gain combining (EGC) scheme at the destination node to the estimate the received signal from sub-channels, the instantaneous electrical SNR will be

$$ \gamma = \left( {\sum\limits_{m = 1}^{M} {\sum\limits_{n = 1}^{N} {\prod\limits_{i = 0}^{c} {\left( {\sqrt {\gamma_{{i_{mn} }} } } \right)} } } } \right)^{2} , $$

(7)

where $\gamma_{{i_{mn} }}$ is the random variable (r.v.) defined as the instantaneous electrical SNR component of the sub-channel from the m^th laser to the n^th PD, it can be described by

$$ \gamma = \left( {\frac{1}{MN}\kappa \Re^{2i + 1} P_{s} \prod\limits_{i = 1}^{c} {X_{i + 1} P_{i} } } \right)^{2} /N_{0} = \overline{\text{SNR}} \left( {\prod\limits_{i = 0}^{c} {X_{i + 1} } } \right)^{2} = \bar{\gamma }\left( {\prod\limits_{i = 0}^{c} {X_{i + 1} } } \right)^{2} . $$

(8)

3 Log-Normal Atmospheric Turbulence with Pointing Error

In Eqs. (7) and (8), X represents the channel state, which models the optical intensity fluctuations caused by atmospheric loss X _l , atmospheric turbulence induced fading X _a and pointing error X _p . They can be described as

$$ X = X_{l} X_{a} X_{p} . $$

(9)

3.1 Atmospheric Loss

Firstly, atmospheric loss X _l is no randomness and a deterministic component. Therefore, it acts as a fixed scaling factor over a long time period and modeling in [2] as

$$ X_{l} = e^{{ - \sigma {\text{L}}}} , $$

(10)

where $\sigma$ denotes a attenuation coefficient and L is the link length.

3.2 Log-Normal Atmospheric Turbulence

Secondly, the most widely used model for the case of weak atmospheric turbulence regime is the log-normal distribution that has been validated by studies [2, 3]. The pdf of the irradiance intensity of log-normal channel is given as

$$ f_{{X_{a} }} (X_{a} ) = \frac{1}{{X_{a} \sigma_{I} \sqrt {2\pi } }}\exp \left( { - \frac{{[\ln (X_{a} ) + 0.5\sigma_{I}^{2} ]^{2} }}{{2\sigma_{I}^{2} }}} \right), $$

(11)

where $\sigma_{I}^{2} = \left( {\exp (\omega_{1} + \omega_{2} ) - 1} \right)$ is the log intensity, $\omega_{1}$ and $\omega_{2}$ are defined as

$$ \omega_{1} = \frac{{0.49\sigma_{2}^{2} }}{{\left( {1 + 0.18d^{2} + 0.56\sigma_{2}^{12/5} } \right)^{7/6} }}\,\,\,\,{\text{and}}\,\,\,\,\omega_{2} = \frac{{0.51\sigma_{2}^{2} (1 + 0.69\sigma_{2}^{12/5} )^{ - 5/6} }}{{1 + 0.9d^{2} + 0.62\sigma_{2}^{12/5} }} . $$

(12)

In Eq. (12), $d = \sqrt {kD^{2} /4L}$, $k = 2\pi /\lambda$ is the wave number, $\lambda$ is the wavelength, D is the receiver aperture diameter, and $\sigma_{2}$ is the Rytov variance, which is defined as

$$ \sigma_{2} = 0.492C_{n}^{2} k^{7/6} L^{11/6} , $$

(13)

where $C_{n}^{2}$ is the refractive-index structure parameter.

The pdf of (c + 1) turbulence channels, $X^{c + 1}$, for AF relaying MIMO/FSO systems will be

$$ f_{{{\mathbf{X}}_{mn} }} \left( {X_{{}}^{c + 1} } \right) = \frac{1}{{(c + 1)X_{{}}^{c + 1} \sigma_{I} \sqrt {2\pi } }}{ \exp }\left( { - \frac{{ [ {\text{ln(}}X){ + 0} . 5\sigma_{I}^{2} ]^{2} }}{{2\sigma_{I}^{2} }}} \right). $$

(14)

3.3 Pointing Error

Thirdly, a statistical model of pointing error induced fading channel is developed in [7, 8], the pdf of X _p is given as [7]

$$ f_{{X_{p} }} (X_{p} ) = X_{p}^{{\xi^{2} - 1}} \left( {{{\xi^{2} } \mathord{\left/ {\vphantom {{\xi^{2} } {A_{0}^{{\xi^{2} }} }}} \right. \kern-0pt} {A_{0}^{{\xi^{2} }} }}} \right),\,\,\,\,\,\,\,\,\,\,\,\,0 \le X_{p} \le A_{0} , $$

(15)

where $A_{0} = \left[ {{\text{erf}}(v)} \right]^{2}$ is the fraction of the collected power at radial distance 0, the parameter $v$ is given by $v = \sqrt \pi r/(\sqrt 2 \omega_{z} )$ with r and $\omega_{z}$ respectively denote the aperture radius and the beam waist at the distance z, and $\xi = \omega_{zeq} /2\sigma_{s}$, where the equivalent beam radius can be represented by [7]

$$ \omega_{zeq} = \omega_{z} \left( {\sqrt \pi \text{erf} (\nu )/2\nu \exp ( - \nu^{2} )} \right)^{1/2} . $$

(16)

In Eq. (16), $\omega_{z} = W_{0} \left( {1 + \varepsilon (\lambda L/\pi W_{0}^{2} )^{2} } \right)^{1/2} ,$ where $W_{0}$ is the transmitter beam waist radius at z = 0, $\varepsilon = (1 + 2W_{0}^{2} )/\rho_{0}^{2}$ and $\rho_{0} = (0.55C_{n}^{2} k^{2} L)^{ - 3/5}$ is the coherence length [8].

3.4 Combined Channel Model

Finally, we derive a completed statistical model of the channel considering the combined effect of atmospheric lost, atmospheric turbulence and pointing error. The unconditional pdf of the combined channel state is expressed as [8]

$$ f_{X} \left( X \right) = \mathop \smallint \nolimits f_{{\left. X \right|X_{a} }} \left( {\left. X \right|X_{a} } \right)f_{{X_{a} }} \left( {X_{a} } \right)dX_{a} , $$

(17)

where $f_{{\left. X \right|X_{a} }} \left( {\left. X \right|X_{a} } \right)$ denotes the conditional probability of given atmospheric turbulence state, which can be defined by [8]

$$ f_{{\left. X \right|X_{a} }} \left( {\left. X \right|X_{a} } \right) = \frac{1}{{X_{a} X_{l} }}f_{{X_{p} }} \left( {\frac{X}{{X_{a} X_{l} }}} \right). $$

(18)

As a result, we can derive the unconditional pdf of X can be derived as

$$ f_{X} (X) = \frac{{\xi^{2} }}{{(c + 1)(A_{0} X_{l} )^{{\xi^{2} }} }}X^{{\xi^{2} - 1}} \int_{{(X/X_{l} A_{0} )}}^{\infty } {\frac{1}{{X_{a}^{{\xi^{2} + c + 1}} \sigma_{I} \sqrt {2\pi } }}} \exp \left\{ {\frac{{ [\ln (X_{a} ) + 0.5\sigma_{I}^{2} ]^{2} }}{{2\sigma_{I}^{2} }}} \right\}dX_{a} . $$

(19)

To simplify, we can let $t = \left( {\ln (X_{a} ) + a} \right)/\left( {\sqrt 2 \sigma_{I} } \right)$, as the result Eq. (19) can be obtain in the closed-form expression as

$$ f_{X} (X) = \frac{{\xi^{2} }}{{(c + 1)(A_{0} X_{l} )^{{\xi^{2} }} }}X^{{\xi^{2} - 1}} \frac{1}{2}e^{b} \times \text{erfc} \left( {\frac{{\ln (X/X_{l} A_{0} ) + a}}{{\sqrt 2 \sigma_{I} }}} \right), $$

(20)

where $a = 0.5\sigma_{I}^{2} + \sigma_{I}^{2} (\xi^{2} + c)$ and $b = \sigma_{I}^{2} (\xi^{2} + c)\{ 1 + (\xi^{2} + c)\} /2$.

4 Average Symbol Error Rate

Now we can derive the average symbol error rate of the MIMO/FSO systems using SC-QAM signals under the effect of atmospheric turbulence and pointing error. The system’s ASER, $\overline{P}_{se}^{MIMO}$, can be generally expressed as

$$ \overline{P}_{se}^{MIMO} = \int\limits_{\Gamma } {P_{e} (\gamma ) \times f_{\Gamma } (\Gamma )d\Gamma } , $$

(21)

where $P_{e} (\gamma )$ is the conditional error probability (CEP), $\Gamma = \left\{ {\Gamma_{nm} ,\,n = 1, \ldots ,N,\,\,m = 1, \ldots ,M} \right\}$ is the matrix of the MIMO FSO channels. When using SC-QAM signals for modulating the data symbol, the CEP can be given as [21]

$$ P_{e} (\gamma ) = 2q(M_{I} )Q(A_{I} \sqrt \gamma ) + 2q(M_{Q} )Q(A_{Q} \sqrt \gamma ) - 4q(M_{I} )q(M_{Q} )Q(A_{I} \sqrt \gamma )Q(A_{Q} \sqrt \gamma ), $$

(22)

where M _I and M _Q are in-phase and quadrature signal amplitudes, respectively; $q(x) = 1 - x^{ - 1}$, Q(x) is the Gaussian Q-function, $A_{I}$ and $A_{Q}$ are defined as

$$ A_{I} = \left( {\frac{6}{{\left[ {(M_{I}^{2} - 1) + r^{2} (M_{Q}^{2} - 1)} \right]}}} \right)^{1/2} \,\,{\text{and}}\,\,A_{Q} = \left( {\frac{{6r^{2} }}{{\left[ {(M_{I}^{2} - 1) + r^{2} (M_{Q}^{2} - 1)} \right]}}} \right)^{1/2} , $$

(23)

where $r = d_{Q} /d_{I}$ is the quadrature to in-phase decision distance ratio.

Let us assume that MIMO/FSO sub-channels’ turbulence processes are uncorrelated, independent and identically distributed (iid). According to Eqs. (8) and (20), we obtain the pdfs of AF relaying MIMO/FSO systems over log-normal channel as

$$ f_{{\Gamma_{mn} }} \left( {\gamma_{mn}^{{^{{\frac{c + 1}{2}}} }} } \right) = \frac{{\xi^{2} }}{{2(c + 1)(A_{0} X_{l} )^{{\xi^{2} }} }}\frac{{\gamma_{mn}^{{^{{0.5\xi^{2} - 1}} }} }}{{\gamma_{mn}^{{0.5\xi^{2} }} }}\frac{1}{\sqrt \pi }e^{b} \times \text{erfc} \left( {\frac{{0.5\ln \left( {\frac{{\gamma_{mn} }}{{X_{l}^{2} A_{0}^{2} \bar{\gamma }_{mn} }}} \right) + a}}{{\sqrt 2 \sigma_{I} }}} \right). $$

(24)

Substituting Eqs. (22) and (24) into Eq. (21), we obtain the systems’ ASER as

$$ \begin{aligned} & \overline{P}_{se}^{MIMO} = 2q(M_{I} )\int_{\Gamma }^{{}} {Q(A_{I} \sqrt \gamma )f_{\Gamma } (\Gamma )d\Gamma } + 2q(M_{Q} )\int_{\Gamma }^{{}} {Q(A_{Q} \sqrt \gamma )f_{\Gamma } (\Gamma )d\Gamma } \\ & \quad\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,- 4q(M_{I} )q(M_{Q} )\int_{\Gamma }^{{}} {Q(A_{I} \sqrt \gamma )Q(A_{Q} \sqrt \gamma )f_{\Gamma } (\Gamma )d\Gamma } . \\ \end{aligned} $$

(25)

5 Numerical Results and Discussion

As mentioned above, using the derived expressions, Eqs. (24) and (25), we present numerical results of ASER performance of the MIMO/FSO systems. The ASER can be calculated via multi-dimensional numerical integration with the help of the Matlab^TM software. Systems’ parameters are provided in Table 1.

Table 1. Systems’ parameters

In Figs. 4 and 5, the system’s ASER is presented as a function of transmitter beam waist radius for various values of relay stations. Figure 4 illustrates the ASER against $W_{0}$ for various values of the pointing error displacement standard deviation $\sigma_{s} = 0.18\,{\text{m}},$ 0.02 m and 0.22 m. Whereas, Fig. 5 shows the ASER versus $W_{0}$ for various values of aperture radius $r = 0.074\,{\text{m,}}$ 0.075 m and 0.076 m. From these figures it can be seen that for a given condition including specific values of the number relay stations, aperture radius and average SNR, the best ASER performance can be obtained at a specific value of $W_{0}$, ranging from 0.02 to 0.025 m. This optimal value of $W_{0}$ is the optimal transmitter beam waist radius, the more the value of transmitter beam waist radius comes close to the optimal one, the lower the value of system’s ASER achieved.

Fig. 4.

ASER versus transmitter beam waist radius under various values of $\sigma_{s} .$

Fig. 5.

ASER versus transmitter beam waist radius under various values of aperture radius with $\sigma_{s} = 0.35\,\,{\text{m}}.$

Figures 6 and 7 illustrate the ASER performance versus the pointing error displacement standard deviation of the different AF relaying MIMO/FSO systems. More specifically, we compare the ASER performance of 2 × 2 and 4 × 4 MIMO/FSO configurations with SISO/FSO system, for various values of transmitter beam waist and aperture radius, the link distance L = 1000 m and SNR = 25 dB. It is also noted that the amplifier gain at each relay station is set by 3.5 dB. The system’s ASER is significantly decreases when the pointing error displacement standard deviation decreases with the same MIMO/FSO configuration and the number of relay station. The impact of the aperture radius and the transmitter beam waist radius on the system’s performance is more significant in low $\sigma_{s}$ values than in high $\sigma_{s}$ values. We thus can more easily adjust the system performance when the pointing error displacement standard deviation is low by appropriately changing the values of the aperture radius and the transmitter beam waist radius.

Fig. 6.

ASER versus the pointing error displacement standard deviation under various values of transmitter beam waist radius, $r = 0.055\,\,{\text{m,}}$ and ${\text{SNR}}\,{ = }\, 2 5\,\,{\text{dB}} .$

Fig. 7.

ASER versus the pointing error displacement standard deviation under various values of aperture radius, $W_{0} = 0.022\,\,{\text{m,}}$ ${\text{SNR}}\,{ = }\, 2 5\,\,{\text{dB}} .$

Figures 8 and 9 illustrate the ASER performance versus the aperture radius under various the numbers of relay stations and MIMO/FSO configurations. As the result, the system’s ASER is significantly decreases when the values of aperture radius and number relay stations increase. It can be found that, in the low-value region when aperture radius increases, system’s ASER is not much change. However, when aperture radius exceeded the threshold value ASER plummeted when aperture radius increases. More clearly, we could not control the pointing error displacement standard deviation but we could control the aperture radius, number relay stations, the transmitter beam waist radius and MIMO/FSO systems.

Fig. 8.

ASER versus the aperture radius under various values of transmitter beam waist radius with $\sigma_{s} = 0.16\,{\text{m,}}$ ${\text{SNR = 25}}\,{\text{dB}} .$

Fig. 9.

ASER versus the aperture radius under various values of $\sigma_{s} ,$ $W_{0} = 0.022\,\,{\text{m}},$ ${\text{SNR = 25}}\,{\text{dB}} .$

In Fig. 10, the system’s ASER is presented as a function of average SNR under various values of the transmitter beam waist radius, the number relay station c = 1 and the aperture radius $r = 0.055\,{\text{m}} .$ Besides, comparison between 2 × 2 and 4 × 4 MIMO/FSO systems and SISO/FSO system, is performed. It can be observed from Fig. 10 that the ASER decreases with the increase of the SNR, number of relay stations and MIMO/FSO configuration. The best ASER performance is achieved when the optimal beam waist radius of 0.022 m is applied. It can be confirmed that simulation results are closed agreement with analytical results. Finally, Fig. 11 depicts the ASER performance as function of the transmission link distance L for various number of relay stations c = 0, c = 1, and c = 2. It can be seen from the figure that the ASER increases when the transmission link distance is longer. In addition, when using relay stations combined MIMO/FSO systems, ASER will get better performance.

Fig. 10.

ASER versus average SNR with pointing error under various values of $W_{0}$, $\sigma_{s} = 0.16\,{\text{m}}$, the number of relay stations c = 1 and $r = 0.055\,{\text{m}}.$

Fig. 11.

The ASER versus transmission link distance under various number of relay stations with the aperture radius $r = 0.055\,{\text{m}},$$\sigma_{s} = 0.16\,{\text{m}} .$

6 Conclusion

We have studied the AF relaying MIMO/FSO scheme using SC-QAM signals over log-normal atmospheric turbulence channels with pointing error. We have derived theoretical expressions for ASER performance of SISO and MIMO systems taking into account the number of AF relay stations, MIMO configurations, and the pointing error effect. The numerical results showed the impact of pointing error on the system’s performance. By analyzing ASER performance, we can conclude that using proper values of aperture radius, transmitter beam waist radius, be partially surmounted pointing error and number relay stations combined with MIMO/FSO configurations could greatly benefit the performance of the such systems.