Shiver (2015) has argued that the standard way of characterizing mereological atomicity fails to do justice to the thesis that it is meant to capture, namely, that everything is ultimately composed of entities lacking proper parts. The standard characterizationFootnote 1 says:

(1):

Everything has atomic parts

i.e., formally,

(2):

∀x∃y(Ay & Pyx),

where ‘P’ stands for the (proper or improper) parthood relation and ‘A’ for the property of being a mereological atom:

(3):

Ay = df ∀z(Pzy → z = y)

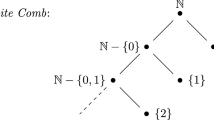
This, Shiver says, is inadequate. To see why, he calls on models with the following structure (henceforth model M), where \({\mathbb{N}}\) is the set of natural numbers and ‘P’ is interpreted as the subset relationFootnote 2:

figure a

In this model, the sequence of infinite subsets of \({\mathbb{N}}\) in the leftmost branch of the diagram is a non-terminating maximal chain. Thus, while it is true that everything has (proper or improper) atomic parts, validating (1), it is also true that every composite has a composite proper part. And “if every composite has a composite proper part, then it is false that everything is ultimately composed of atoms; it is, at least partly, composites all the way down” (pp. 608–609).

It is worth stressing, as Shiver does, that the issue would not arise if (1) were conjoined with the other axioms of classical mereology. These include, besides the basic partial-order axioms for ‘P’ (all of which are satisfied in M, along with extensionality), also an axiom schema to the effect that every specifiable non-empty set has a mereological sum:

(4):

∃xϕx → ∃z∀y(Ozy ↔ ∃x(ϕx & Oyx)),

where ‘O’ stands for the relation of mereological overlap:

(5):

Oxy = df ∃z(Pzx & Pzy)

And that schema—so-called “unrestricted composition”—fails in M, as it fails in other problematic models of (1) considered by Shiver. Still, (4) expresses a thesis that is controversial, and the friends of atomism may not be willing to endorse it. This, Shiver concludes, confirms the inadequacy of (1) as an independent characterization of atomism, leading to the interesting alternative offered in his paper.

In the following, I argue that Shiver’s conclusion can and ought to be resisted. I do so by defending two claims: (i) model M is in fact atomistic in the intended sense: everything is ultimately composed of atoms; and (ii) even though (1) does not say that everything is ultimately composed of atoms, it implies so, at least under certain plausible assumptions on the parthood relation. Thus, the standard characterization of atomism offered by (1) is perfectly fine even in the absence of (4). If there is a sense in which model M is problematic, it lies elsewhere.

1 Composites all the way down, but atomistic

Concerning claim (i), it is true, of course, that in M every composite is, at least partly, “composites all the way down”. However, that does not mean that it is not composed of atoms. For, in M an atom is just a singleton, and obviously every set is the union of the singletons of its own members. Since the singleton of each \(n \in {\mathbb{N}}\) is in the domain of M (at depth n + 1), that means every composite element in the domain is the union of its atomic parts. And in the present context this is precisely what it means to be composed of them.

Shiver does consider this objection, but rebuts it on the grounds that it rests on slippery intuitions stemming from the set-theoretic structure of M. After all, M is not a model of set theory, for it lacks a null element and is not closed under union, intersection, and so on, so “it would be a mistake to take set-theoretic intuitions about the structure very seriously” (p. 609). I agree that that would be a mistake. But it still does not follow that the infinite sets in the model are not composed of the singletons of their members. They are, at least insofar as we take “composed of” to mean what it is usually taken to mean.

To see this, consider the standard definition, as familiar from van Inwagen (1990, p. 29)Footnote 3:

(6):

x is composed of the ϕs = df x is a sum of the ϕs and the ϕs are pairwise disjoint (i.e., non-overlapping)

When each of the ϕs is mereologically atomic, the second conjunct in the definiens can be dropped, since all atoms are pairwise disjoint. Thus, to say that something, x, is composed of atoms amounts to saying that there are such and such atoms, the αs, such that

(7):

x is a sum of the αs

Now, strictly speaking the import of (7) depends on how exactly one understands “sum of”.Footnote 4 One understanding, implicit in Shiver’s formulation of Unrestricted Composition as (4), corresponds to the following general definition:

(81):

x is a sum1 of the ϕs = df x overlaps all and only those things that overlap at least one of the ϕs

Another understanding, more commonly used in connection with (6), corresponds to the following:

(82):

x is a sum2 of the ϕs = df the ϕs are all parts of x and every part of x overlaps at least one of the ϕs

Yet another understanding corresponds to the identification of “sum” with “minimal upper bound”:

(83):

x is a sum3 of the ϕs = df the ϕs are all parts of x and x is part of all those things whose parts include all the ϕs

These definitions are not equivalent. In particular, it is clear that in M any finite collection of atoms has a sum3 (their least upper bound with respect to set inclusion) but not a sum1 or a sum2. However, the question at issue is not which collections of atoms in M have a sum. The question is whether everything in M is a sum of atoms, i.e., whether (7) is true for every x and a corresponding choice of αs. And in this regard the non-equivalence of (81)–(83) is immaterial. For, corresponding to each definition, we can express (7) formally as follows:

(71):

∀y(Oxy ↔ ∃z(αz & Oyz))

(72):

∀y(αy → Pyx) & ∀y(Pyx → ∃z(αz & Oyz))

(73):

∀y(αy → Pyx) & ∀y(∀z(αz → Pzy) → Pxy)

And it is easy to verify that, for any x, each of these theses is true in M precisely when the αs are the atomic parts of x, i.e., when α is the condition given byFootnote 5:

(9):

∀z(αz ↔ (Az & Pzx))

Thus, regardless of our set-theoretic intuitions, and regardless of how exactly we define the notion of a mereological sum, on the standard understanding of “composed of” the model in question satisfies the claim that everything is ultimately composed of atoms. Hence M is not a counterexample to the adequacy of (1).

Of course, there remains something disturbing about M. For it is a fact that in M the proper parthood relation is infinitely descending: the pattern of decomposition that goes down the left branch never “bottoms out”, looking awfully similar to a gunky precipice. Thus, although M does not violate the idea that everything is ultimately composed of atoms, it violates the idea that everything can be decomposed into its ultimate constituents. As Cotnoir (2013, p. 68) points out, this is especially disturbing if atomism is meant to carry the weight of metaphysical grounding. For there can be no infinite regress of metaphysical priority. Grounding calls for well-foundedness, and in M the parthood relation is not well-founded. This is precisely why philosophers throughout history have been struggling with the thought that lines, planes, and solids are “made up” of points, and it may well be that precisely here the atomist is in trouble. For as Jonathan Schaffer would put it, in a model like M the atomist’s ontology seems to “drain away down a bottomless pit” (2007, p. 184); being is “infinitely deferred, never achieved” (2009, p. 62). Still, such concerns go beyond what is at issue here, which is whether the standard characterization of atomicity in (1) is shown to be inadequate by a model like M. And the answer is that it is not. Mereologically speaking, atomism is a thesis about composition, not decomposition.Footnote 6

It is worth noting that exactly the same sort of consideration applies to the following model, M π, which is obtained from M by adding an arbitrary element (in this case, π) to each infinite set, but leaving out the corresponding singleton.

figure b

This model, too, satisfies (1), but as Shiver points out, the intuition that M π is not atomistic is even stronger than in M, for here the elements along the infinitely descending branch on the left are not the unions of atoms (singletons) available in the domain: each such element contains π, and {π} is missing. Since M π is isomorphic to M, Shiver takes this to be further evidence that M itself is not atomistic. But M is atomistic. Thus, contrary to appearances, M π must be atomistic as well (as can be verified independently by checking that M π satisfies each of (71)–(73).Footnote 7) Yet Shiver is right: there is an obvious intuitive sense in which the infinite elements of M π are not entirely composed of atoms. So how can this be a model in which it is true—literally—that they are?

The answer, in my opinion, does not lie in the inadequacy of (1), the atomicity axiom satisfied in M π. It lies in the intrinsic limits of (6), the standard characterization of “composed of” in terms of “sum of”. This characterization has played a central role in much recent work in part-whole theories, beginning with the debate spawned by van Inwagen’s (1990) “special composition question”, and it’s fair to say that for the most part it has proved both useful and reliable. What else could it mean to say that something is composed of a number of things, if not that it is a mereological sum of those things? Yet the notion of a sum is itself less clear than one might initially think, witness the multiplicity of definitions with which mereologists have been working; and while these definitions tend to agree and work well in ordinary circumstances, abstract unintended models are always possible. Indeed, one need not go so far as to consider exotic structures such as M π to run into troubles. The simple model below is just as problematic. Here the top element counts as a sum of the bottom atoms in each sense of “sum” defined in (81)–(83), hence it fully qualifies as composed of those atoms according to definition (6). Yet there is also a clear sense in which {0, 1, 2} is not composed of {0} and {1}, i.e., it is not entirely composed of {0} and {1}.

figure c

Of course, in describing the situation we should be careful not to fall prey to the temptation mentioned by Shiver in connection with M and M π: the model looks strange because we tend to read it set-theoretically. Really, the sets are just stand-ins for nodes in a mereological structure, and a model in which the top node is represented by the set {0, 1} would be perfectly isomorphic (and unproblematic). It is also true, however, that there is nothing intrinsically set-theoretic in our intuitions about such cases. We could replace {0} and {1} with my head and my torso and {0, 1, 2} with my whole body (cum limbs). Surely this model would be isomorphic to one in which the top node is my limbless body instead. Yet again the isomorphism is not enough to obliterate the intuitive difference between the two: while it makes perfect sense to say that a limbless body is composed of a head and a torso, we normally wouldn’t say the same of a whole body (cum limbs). But we wouldn’t say so even if heads and torsos were treated as mereologically non-atomic, or as pieces of gunk. If there is a problem, here, it has nothing to do with the atomistic assumption of the models; the problem lies entirely in the fact that in one of the models the limbs seem to come from nowhere. Mutatis mutandis for the model with {0, 1, 2}, where {2} is missing from the domain, and for Shiver’s model M π, where {π} is missing. These models transgress our intuitive assumptions about what there is. The intuitive notion of composition is sensitive to the transgression—and the models seem wrong; its formal definition in (6), based on “sum”, is not—and the models are fine.

2 Hidden virtues

Let us now consider the second claim advertised above: even though the atomicity axiom (1) does not say that everything is ultimately composed of atoms, it implies so. At least, it implies so insofar as “composed of” is understood via (6). What I mean by this is that (1) implies the universal closure of (7) when the αs are precisely the atomic parts of x, as in (9), and it does so on each understanding of “sum of”. Formally:

(71′):

∀x∀y(Oxy ↔ ∃z((Az & Pzx) & Oyz))

(72′):

∀x(∀y((Ay & Pyx) → Pyx) & ∀y(Pyx → ∃z((Az & Pzx) & Oyz)))

(73′):

∀x(∀y((Ay & Pyx) → Pyx) & ∀y(∀z((Az & Pzx) → Pzy) → Pxy)).

Of course, the implication doesn’t hold merely as a matter of logic, as if ‘P’ were an arbitrary binary predicate. Nonetheless, it holds in each case under some plausible assumptions on the mereological relation that the predicate is meant to express.

To begin with (71′), all that is required in this case is that parthood be at least reflexive and transitive, two properties that are normally regarded as constitutive of the very meaning of “part” (in the inclusive sense)Footnote 8:

(10):

∀xPxx

(11):

∀x∀y∀z((Pxy & Pyz) → Pxz)

Given these minimal assumptions, it is easy to see that (71′) is implied by the atomicity axiom (1), or rather by its formal counterpart (2). Here is a simple proofFootnote 9:

figure d

The argument from (2) to (72′) rests on the same assumptions and is even simpler. In fact, the first quantified conjunct in (72′) is a generalized tautology, so we only need to show that (2) implies the closure of the second conjunct:

figure e

In the case of (73′), the proof requires an additional assumption. Specifically, we need to assume that the parthood relation satisfies the so-called “strong supplementation principle”:

(12):

∀x∀y(~Pxy → ∃z(Pzx & ~Ozy)).

This may seem unwarranted in the present context, for (12) is no less controversial than the principle of unrestricted composition (4). In particular, (12) rules out non-extensional models in which two or more composite things have exactly the same proper parts, as with c and d in the example below, and this is a consequence that an atomist may want to resist.

figure f

However, non-extensional models of this sort are in fact at odds with the idea that a sum is just a “minimal upper bound”, which is the understanding corresponding to (73′). For example, in the four-element model above it seems natural to say that c is composed of the two atoms a and b, and likewise for b; yet neither c nor d qualifies as a sum3 of those atoms, since c is not part of d (which includes all of c’s atomic parts) and d is not part of c (which includes all of d’s atomic parts). Thus, when “composed of” is understood in terms of sum3, models of this sort should be ruled out.Footnote 10 And if things are so, then (73′) is most naturally read against the assumption that ‘P’ obeys the strong supplementation principle (12). On this assumption, and given transitivity, the proof that also (73′) is entailed by (2) is easy. In fact, the first conjunct of (73′) is, again, a generalized tautology, so we only need to prove the closure of the second conjunct:

figure g

This completes the argument. No matter how we understand the notion of sum, the thesis that everything has atomic parts turns out to imply the thesis that everything is a sum of atoms. Insofar as being composed of atoms amounts to being a sum of atoms, at least according to the customary definition in (6), it follows therefore that the standard way of characterizing mereological atomicity implies precisely the thesis that it is meant to capture: everything is ultimately composed of atoms. That is, it implies that thesis as long as parthood is reflexive and transitive and, in the third case, strongly supplemented.

At this point it is only instructive to go back to our infinitely descending model M. In that model, parthood is the subset relation, hence it satisfies the reflexivity and transitivity principles (10) and (11) as well as the strong supplementation principle (12). Thus, since the whole point of considering M was that it satisfies the atomicity axiom (1), we have another proof of the claim established in the previous Section: appearances notwithstanding, M also satisfies each of (71′)–(73′), hence it is atomistic in every sense of the term. If this sounds unacceptable, the culprit is not the inadequacy of (1); it is, again, the notion of composition involved in the broader atomistic theses expressed by (71′)–(73′). Everything is composed of atoms, that is, ultimately composed; it’s just that the infinite elements of the model cannot be decomposed accordingly.