How do you say ‘everything is ultimately composed of atoms’?

Abstract

The standard definition of atomicity—the thesis that everything is ultimately composed of entities that lack proper parts—is satisfied by a model that is not atomistic. The standard definition is therefore an incorrect characterization of atomicity. I show that the model satisfies the axioms of all but the strongest mereology and therefore that the standard definition of atomicity is only adequate given some controversial metaphysical assumptions. I end by proposing a new definition of atomicity that does not require extensionality or unrestricted summation.

There seem to be exactly three options with respect to the number and compositional role of mereological atoms in the world: either (i) everything is ultimately composed of mereological atoms, (ii) nothing is ultimately composed of atoms, or (iii) some things are ultimately composed of atoms and some are not. Simons (1987), Casati and Varzi (1999), and Varzi (2012) formulate definitions for these theses as follows.^{1 , 2}

• (1) Atomicity: $\forall x\exists y (Ay\, \& \,Pyx)$

• (2) Atomlessness: $\forall x\exists yPPyx$

• (3) Mixed: $\exists xAx \, \& \, \exists x \forall y(Pyx\,\rightarrow \,\exists zPPzy)$

These definitions are inadequate. To see why, consider the following model.

Let ${\mathbb {N}}$ be the set of natural numbers and ${\mathcal {P}}({\mathbb {N}})$ be its powerset. Construct a set ${\mathbb {N}}{_{\mathfrak {M}}}$ as follows.

${\mathbb {N}}{_{\mathfrak {M}}}=\left\{ S\;|\;{\text {either}}\,{^{\ulcorner }}S\in {\mathcal {P}} ({\mathbb {N}})\,\text {and}\, |S|=|\{\emptyset \}|{^\urcorner }\; {\text {or}}\; {^{\ulcorner }} S\in {\mathcal {P}} ({\mathbb {N}})\, {\text {and}}\, |S|=|{\mathbb {N}}\,|\, {\text {and for any}}\, x\in {\mathbb {N}},\, {\text {if}} \, x\in S, \, {\text {then}} \, s(x)\in S{^{\urcorner }}\right\} .$ ³

Interpret the partially ordered set (poset) $\langle {\mathbb {N}}{_{\mathfrak {M}}},\,\subseteq \rangle$ as a model of mereology in which the singletons are atoms and the subset relation is the relation of parthood. Call this model ${\mathfrak {M}}.$

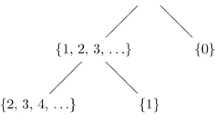
For the visually-oriented reader (and for ease of discussion), here is ${\mathfrak {M}}$ represented as an infinitely-descending Hasse-diagram.

Read the diagram as displaying the set of natural numbers as a composite object being decomposed, one by one, into its atomic parts.

It is easy to verify that ${\mathfrak {M}}$ satisfies (1)—every set in ${\mathbb {N}}{_{\mathfrak {M}}}$ is either an atom or has an atom as a proper part. However, the sequence of gapless infinite subsets of ${\mathbb {N}}$ (the leftmost branch of the diagram) is a non-terminating maximal chain in ${\mathfrak {M}}.$ ⁴ And if a poset has a non-terminating maximal chain, it follows that the poset is not atomistic.⁵

To put the point another way, even though it is true that everything in ${\mathfrak {M}}$ is either an atom or has an atom as a proper part, it is also true that every composite has a composite as a proper part. But if every composite has a composite proper part, then it is false that everything is ultimately composed of atoms; it is, at least partly, composites all the way down. Hence, ${\mathfrak {M}}$ is not atomistic even though it satisfies (1).

It is tempting to interpret the model as atomistic because of our familiarity with set theory. One might object, for example, that ${\mathfrak {M}}$ is atomistic because each infinite set in the model is a union of the singletons of its members and the singleton of every $n\in {\mathbb {N}}$ is in the model. But this reasoning fails. ${\mathfrak {M}}$ is not a model of set theory—it doesn’t have a null object, not every two sets have a union or intersection, and so on. The sets of the model are merely representations of nodes in a structure, and it would be a mistake to take set-theoretic intuitions about the structure very seriously.

If you are still unconvinced, consider the model ${\mathfrak {M}}{_{\pi }}$ that adds an arbitrary element (in this case, ${\pi }$) to each infinite set in ${\mathfrak {M}}$ but leaves out the corresponding singleton.

${\mathbb {N}}{_{\mathfrak {M}}{_{\pi }}}\; =\;\left\{ S\;|\;{\text {either}}\,{^{\ulcorner }}S\in {\mathcal {P}} ({\mathbb {N}}\cup \{\pi \})\, {\text {and}}\,|S|=|\{\emptyset \}|\;{\text {and }}\;S\ne \{\pi \}{^{\urcorner }}\; {\text {or}}\; {^{\ulcorner }} S\in {\mathcal {P}} ({\mathbb {N}}\cup \{\pi \})\, {\text {and}}\, |S|=|{\mathbb {N}} | \, {\text {and\, for\,any}}\, x\in {\mathbb {N}}, \, {\text {if}} \, x\in S, \, {\text {then}} \, s(x)\in S\,{\text {and}}\,\pi \in S{^{\urcorner }}\right\} .$

Interpret the poset $\langle {\mathbb {N}}{_{\mathfrak {M}_{\pi }}},\,\subseteq \rangle$ as a model of mereology in which the singletons are atoms and the subset relation is the relation of parthood. Call this model ${\mathfrak {M}}{_{\pi }}.$

It is more obvious that this model is not atomistic, since $\{\pi \}$ is not in ${\mathfrak {M}}{_{\pi }}.$ Yet ${\mathfrak {M}}{_{\pi }}$ is isomorphic to ${\mathfrak {M}}.$ So one of these models is atomistic just in case the other is.⁶ Hence, ${\mathfrak {M}}$ is not atomistic.

Intuitively, ${\mathfrak {M}}$ is a mixed case. In it, some things are ultimately composed of atoms (namely, the atoms represented by the singletons) and some are not (namely, all of the composites represented by the infinite sets). It is easily verified, though, that this model does not satisfy (3), since there is no object in the model such that all of its parts have proper parts.

So, neither (1) nor (3) expresses its target thesis. (1) does not rule out our mixed model and (3) does not rule it in. This isn’t too surprising. All (1) really says is that everything has at least one atom as a part. All (3) says is that there are some atoms and there are some atomless things. Since neither says anything about what things are ‘ultimately composed of’, the definitions guarantee much less than intended.⁷

A natural thought is that even though (1) fails to capture its intended thesis alone, it should nevertheless exclude the troublesome model in conjunction with the other axioms of a suitable mereological system. This was likely the thinking of the authors of the definition, since it is only ever presented in a text after the strongest mereological system has been developed.

In fact, (1) is adequate given the axioms of the strongest mereological system. It fails to exclude nonatomistic models in any weaker system, however, and is therefore not a definition of the thesis. I show this systematically in what follows and end by proposing a general statement of atomicity that is adequate for all mereological systems.⁸

The simplest mereological system, Ground Mereology (M), consists in the deductive closure of axioms (4)–(6).

• (4) (Irreflexivity): $\forall x\lnot PPxx$

• (5) (Asymmetry): $\forall x\forall y (PPxy\rightarrow \lnot PPyx)$

• (6) (Transitivity): $\forall x\forall y\forall z((PPxy\, \& \, PPyz)\,\rightarrow \,PPxz)$

Since ${\mathfrak {M}}$ is ordered by the subset relation and the proper-subset relation is irreflexive, asymmetric, and transitive, ${\mathfrak {M}}$ is a model of M. Since (1) is consistent with (4)–(6), ${\mathfrak {M}}$ is also a model of AM, which is the system obtained by adding (1) to M. Since AM countenances ${\mathfrak {M}},$ it is not an atomistic mereology.

The axioms of M are quite lax—they allow counterintuitive models of parthood such as (i) composite objects with exactly one proper part, and (ii) numerically distinct objects composed of exactly the same proper parts. If we want to rule out such objects we can add (4) and (5), respectively, to M.

• (7) (Weak Supplementation): $\forall x\forall y (PPxy\,\rightarrow \,\exists z (Pzy\, \& \,\lnot Ozx))$

• (8) (Strong Supplementation): $\forall x\forall y (\lnot Pyx\,\rightarrow \,\exists z (Pzy\, \& \,\lnot Ozx))$

Call AM together with (7) Atomistic Minimal Mereology (AMM) and AM together with (8) Atomistic Extensional Mereology (AEM). These systems are much more powerful than AM. Yet neither is strong enough to exclude ${\mathfrak {M}}.$ ${\mathfrak {M}}$ satisfies (7) since every non-singleton has at least two disjoint proper subsets. ${\mathfrak {M}}$ also satisfies (8), though this is easier to see when (8) is contraposed to (8${^{\prime }}$).

(8${^{\prime }}$)::

$\forall x\forall y(\forall z(Pzy\,\rightarrow \,Ozx)\,\rightarrow \,Pyx)$

(8${^{\prime }}$) says that if every part of y overlaps x, then y is part of x. But this is clearly satisfied by ${\mathfrak {M}}.$ Every numerically distinct composite in ${\mathfrak {M}}$ is composed of a unique set of parts. So, AMM and AEM are not atomistic mereologies.

In addition to supplementation, one can strengthen the theories of mereology by adding closure principles that guarantee the existence of arbitrary binary sums and products.

• (9) (Sum): ${\forall } x{\forall } y(Uxy\,\rightarrow \,\exists z\forall w(Owz \,\leftrightarrow \, (Owx \,\vee \, Owy)))$

• (10) (Product): ${\forall } x{\forall } y(Oxy\,\rightarrow \,\exists z\forall w(Pwz \,\leftrightarrow \, (Pwx \, \& \, Pwy)))$

Call the result of adding both (9) and (10) to AM Atomistic Closure Mereology (ACM) and the result of adding them to either AMM or AEM Atomistic Extensional Closure Mereology, or (ACEM).⁹

${\mathfrak {M}}$ clearly satisfies (10), since every two things that overlap have a product.¹⁰ However, ${\mathfrak {M}}$ does not satisfy (9). Consider any two atoms, say $\{0\}$ and $\{1\}.$ These atoms underlap, since they are both part of ${\mathbb {N}}.$ Yet there is nothing in the model such that everything it overlaps also overlaps either of the atoms. That is, there is nothing that has just the atoms, and nothing else, as its proper parts. So, adding (9) is sufficient to exclude ${\mathfrak {M}}.$ So far so good for (ACM) and (ACEM).

It is possible to add more structure to ${\mathfrak {M}}$ and generate a new model in which every underlapping pair of objects has a least upper bound. In the context of our set-theoretic representation, this would amount to adding every finite subset of ${\mathbb {N}}$ to the domain of ${\mathfrak {M}}$ in order to account for arbitrary sums of singleton pairs, and also adding the sum of every nonempty finite subset and gapless infinite subset of ${\mathbb {N}}.$ Construct the new model as follows.

Let ${\mathbb {N}}{_{\mathfrak {M}{^{\prime }}}}\; = \; \left\{ S\cup T\, |\, S,\,T\in {\mathbb {N}}{_{\mathfrak {M}}}\right\} .$

Interpret the poset $\langle {\mathbb {N}}{_{\mathfrak {M}{^{\prime }}}},\,\subseteq \rangle$ as a model of mereology in which the singletons are atoms and the subset relation is the relation of parthood. Call this model ${\mathfrak {M}}{^{\prime }}.$

When all arbitrary binary sums are added to the model, we can pick any two disjoint objects and find an object that completely overlaps both of them (and nothing else). So, (9) is satisfied by ${\mathfrak {M}}{^{\prime }}.$

The important question, though, is whether (1) is adequate on ${\mathfrak {M}}{^{\prime }}.$ Since the new sums are all binary sums formed from pairs of elements of ${\mathfrak {M}},$ a new sum will violate (1) only if a pair of elements of ${\mathfrak {M}}$ violates (1). But, as we saw above, none of them do. So ${\mathfrak {M}}{^{\prime }}$ satisfies (1).

Is ${\mathfrak {M}}{^{\prime }}$ atomistic? Clearly not. If the addition of new sums ensured that the model were atomistic, it would be because every maximal chain would be made to terminate. But because only the binary sums of members of ${\mathbb {N}}{_{\mathfrak {M}}}$ were added, and not all sums in general, there are still maximal chains in ${\mathfrak {M}}{^{\prime }}$ that do not terminate.

Let T be the maximal non-terminating chain of ${\mathfrak {M}}.$ $T\subseteq {\mathbb {N}}{_{\mathfrak {M}{^{\prime }}}},$ but T is not maximal in ${\mathfrak {M}}{^{\prime }}$ because $T\subset S$ where $S \; = \; \{X\, | \, X\in {\mathbb {N}}{_{\mathfrak {M}{^{\prime }}}}\,{\text {and}}\,|X|\, =\, |{\mathbb {N}}|\}.$ But S is both maximal and non-terminating in ${\mathfrak {M}}{^{\prime }}.$ S is clearly non-terminating (it has no minimal element), but suppose for reductio that it is not maximal. Then there is a chain Y in ${\mathfrak {M}}{^{\prime }}$ such that $S\subset Y.$ Since S contains all of the infinite subsets of ${\mathbb {N}}{_{\mathfrak {M}{^{\prime }}}},\,Y$ must contain finite sets.

All maximal chains of ${\mathbb {N}}{_{\mathfrak {M}{^{\prime }}}}$ that contain finite sets terminate. Hence, Y terminates. However, supposing that Y contains a finite set implies that some member of S is a binary sum of finite subsets (since general summation is not defined in closure mereologies). But this is not so for the members of T. None of them are binary sums of any finite sets, since, in general, no infinite set is the binary sum of any finite sets. So, since $S-T$ is just the set of sums produced by binary unions of finite sets with members of S, no member of S is a binary sum of finite sets. So, Y does not contain finite subsets. So, contrary to hypothesis, Y does not exist. So, S is maximal in ${\mathfrak {M}}{^{\prime }}.$ So, finally, ${\mathfrak {M}}{^{\prime }}$ is not atomistic.

Let us add the axiom that generates the full strength of classical mereology.

• (11) (Infinitary Sum): $\exists x\phi \,\rightarrow \,\exists z\forall y(Oyz\,\leftrightarrow \,\exists x(\phi \, \& \,Oyx))$

(11) is an axiom schema, not a single axiom. It stands in for a countable infinity of axioms (since there are only countably many formulas that can be substituted for ${\phi }$). The result of adding every instance of (11) to AEM is called Atomistic General Extensional Mereology (AGEM).

${\mathfrak {M}}{^{\prime }}$ is not a model of AGEM. General summation demands more structure of its models. Once we add the necessary structure to satisfy AGEM we finally have an atomistic model. Here’s why. The presence of infinitary summation and extensionality guarantees that there is a unique sum of all of the atoms (if there are any atoms). Suppose that there is a unique sum of the atoms and everything has an atom as a part (i.e., (1) is satisfied). Then everything overlaps the sum of the atoms. Suppose some x is not a part of the sum of the atoms. Then, contrary to (1), there is an x that doesn’t have an atom as a part. So, by reductio, everything is part of the sum of the atoms.¹¹

When ‘the sum of atoms’ is defined,¹² (1) secures atomicity. Hence, we might express the target thesis more perspicuously as follows:

• (12) (Atomicity${^{*}}$): ${\exists } x\, x={\sigma } yAy \; \& \;\forall x Px{\sigma } yAy$

This principle literally says that there is a sum of all atoms and everything is a part of it. So, given (12), if something exists at all then it is either an atom or part of something made exclusively of atoms (and is therefore ultimately made of atoms).

We can confirm the adequacy of (12) by noting that it rules out the models considered earlier. When (12) is satisfied, a composite can only be a node in a (maximal) parthood chain if that chain terminates at an atom. Since every composite is a part of the sum of the atoms, none of the chains of which it is a node will consist in composites all the way down.

We now have an adequate definition of atomicity, but the cost of expressing it is quite high. (12) is strictly nonsense without extensionality, and unmotivated without a commitment to the existence of every arbitrary sum. Without extensionality, definite descriptions like ‘${\sigma } yAy$’ may fail to denote; there will be no guarantee that there aren’t several numerically distinct objects satisfying the same description (i.e., composed of the very same atoms). Without a commitment to there always being a sum of the atoms, there is nothing for the definite descriptor in our definition to denote. But why should we think that there is always a single thing composed of all and only atoms unless we already accept unrestricted summation?

It almost goes without saying that extensionality and unrestricted summation are controversial theses. Extensionality is inconsistent, for example, with the popular idea that a statue and the material from which it is constructed are numerically distinct. Unrestricted summation, either binary (as in (9)) or general (as in (11)), is inconsistent with the popular idea that there are restrictions on composition, either because composition is a causal phenomenon occurring in some circumstances but not others, or a mere fiction that never actually occurs. There are those who happily accept both extensionality and unrestricted summation, yet surely one need not be among them to say that everything is ultimately composed of atoms!

Suppose that you, like most metaphysicians, accept a mereological system weaker than GEM, but also, like most metaphysicians, think that everything is ultimately composed of atoms. How, exactly, do you express your view?

The way to do it, I think, is to say that there is a class of sums of atoms (which may only be the atoms themselves, or may include some composites made of the atoms) and everything is a part of one of its members. This doesn’t presuppose anything about how many sums of atoms there are, whether there is a sum of all of them, whether the sums are extensionally individuated, or anything of the like. The proposal can be formalized easily using sets, but since part of the appeal of mereology is the promise of eschewing sets entirely, it is good practice to express mereological theses without invoking sets. Accordingly, the following proposal uses the resources of plural logic to denote the members of any relevant class.

Let doubled variables and constants (e.g., xx) be understood as plural variables or constants, and let ‘${\prec }$’ be the variably polyadic predicate ‘is among’. Following Oliver and Smiley (2013, pp. 123–124), use the exhaustive descriptor ‘:’ (a notational variant of the more familiar ‘such that’ operator used to define sets by abstraction) to plurally denote the individuals satisfying some predicate distributively (e.g., ‘$x:{\phi } x$’ means ‘the things that individually ${\phi }$’). Now, consider the following definitions.

‘aa’ (the atoms) $={_{df}}$ ‘$x:Ax$’

‘Sx’ (x is a sum of atoms) $={_{df}}$ ‘$\exists yy(yy\prec aa\, \& \, \forall z (Ozx\,\leftrightarrow \,\exists w(w\prec yy\, \& \,Owz)))$’

The definition of aa is clear enough; $aa$ is a name that refers plurally to all of the atoms and does the work that ‘the set of all atoms’ would usually do. Sx is designed to mimic the notion of being a sum of the members of a set of atoms. Informally, its definition says that there are some atoms such that everything overlapping x overlaps at least one of them. The idea is that Sx is satisfied by any sum of atoms, no matter how many atoms the sum includes. Given these definitions, we can state a perfectly general version of atomicity.

• (13) (General Atomicity): $\forall x\exists y(Sy\, \& \,Pxy)$

(13) says that everything is a part of a sum of atoms. When it is satisfied every maximal parthood chain terminates, since anything that exists must be a part of a sum of atoms and every maximal parthood chain of a sum of atoms terminates. It is general in the sense that it requires neither extensionality nor arbitrary summation to work. (13) doesn’t require extensionality because, unlike (12), it is consistent with the existence of non-unique sums of the atoms. (13) doesn’t require arbitrary summation because, unlike (12), it refers to sums of atoms without presupposing how many sums there are.

So, to wrap things up, I think (13), and not (12) or (1), is how you say ‘Everything is ultimately composed of atoms’.