Physical Parameters and Chemical Composition of a Nitrogen DC Discharge with Water Cathode

Abstract

This paper reports the results of the experimental study and chemical composition modeling for a DC nitrogen discharge burning above water cathode in the pressure range of 0.1–1 bar and at discharge current of 40 mA. The gas temperature, vibrational temperatures, reduced electric field strength, cathode voltage drop, and emission intensities of some nitrogen bands were obtained from experiment. The modeling chemical composition of plasma was carried out on the basis of these data. At modeling, the combined solution of Boltzmann equation for electrons, equations of vibrational kinetics for ground states of N₂, O₂, H₂O and NO molecules, equations of chemical kinetics and plasma conductivity equation were used. The calculations agree with the measured bands intensities for the second positive system of N₂ and vibrational temperatures of ${\text{N}}_{2} ( {\text{C}}^{3}\Pi _{\text{u}} )$. In the frame of the model proposed, the data of other studies were explained. The second kind collision of electrons with N₂ vibration excited states was shown to affect strongly the electron gas parameters. The electron average energy and electron density are given. The difference between the properties of the discharges in N₂ and air at the same conditions are discussed as well.

Introduction

In recent years the interest in non-thermal plasmas in contact with liquids has increased significantly [1]. This is mainly due to their ability to form strongly chemically active species (OH, O, H₂O₂, nitrogen oxides etc.), UV radiation and shock waves. As a result, plasmas in contact with liquids are very effective for carrying out many oxidative and reducing processes in a liquid phase. Among these processes it is possibly to point out the numerous environmental applications [2, 3].

For estimation of possibilities of discharge action, it is necessary to know the active species concentrations in a gas phase and their change under alterations of discharge parameters. Such data are rather limited. The emission spectra show usually the radiation bands of excited states of N₂, OH and NO and lines of atomic H and O at discharge in nitrogen containing gases [4–6]. As far as the discharges in contact with water are concerned, there are some studies where the OH radical concentrations in the ground state were measured in a gas phase for the atmospheric pressure DC discharge in an ambient air, He, Ar and N₂ by a LIF method [6, 7] and applying the absorption in UV region for Ar/H₂O [8]. For nitrogen, it was discovered that OH concentration was about (2–2.3) × 10¹⁵ cm⁻³ in the current range of 15–30 mA. It is safe to say that measurements of species densities in liquid plasmas are largely an unexplored area. For this reason, modeling becomes an efficient method to study plasma composition. For these reasons, the large number of works devoted to plasma chemistry modeling was published in recent years.

Thus, in study [9], a zero-dimension Global model was proposed for the helium RF atmospheric pressure discharge with admixture of water molecules. In study [8], a zero-dimension modeling of the chemical composition was accomplished for an atmospheric pressure argon plasma jet flowing into humid air. The reaction chemistry included 84 different species and 1880 reactions. Modeling results agreed satisfactorily with ozone concentrations measured in study [10] by adsorption method. Simulation of the NO and O formation-loss mechanism in the RF atmospheric pressure needle-type plasma jet (Ar + 2 % of air) was carried out in study [11]. For the model verification, the concentrations of NO molecules and O atoms, measured experimentally were used. The simulation of plasma chemical reactions was carried out in study [12] for argon DC discharge above water cathode in the pressure range of (0.1–1) bar. Calculated line intensities of Ar atom emission agree well with experimental ones. All models mentioned above did not consider the kinetics of vibrational states. Probably, for plasmas containing noble gases presumably it is not too important. But the modeling of atmospheric pressure DC discharge in air [13] and experimental data [14, 15] showed that effective vibrational temperatures (~5000 K) of N₂ are essentially more than translation ones (~1500 K). Therefore, vibrationally excited molecules (VEM) can influence strongly the electron energy function distribution (EEDF) over super elastic collisions.

As far as we know, there is no detailed analysis of kinetics of the processes taking place in a nitrogen DC discharge burning above the water cathode. The main aim of the given work is to develop the model allowing describing the plasma composition. The model proposed will take into consideration the influence of chemical composition and VEM on EEDF and vice versa. For the model checking the emission intensities of nitrogen bands and vibrational temperatures of N₂(C³Π_u) state will be used.

Experimental

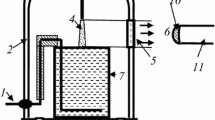
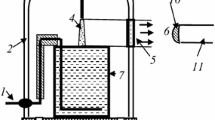
Figure 1 represents a principal scheme of the experimental set-up. The glass cell with distilled water of 80 ml volume was placed into a 5 l glass vacuum-tight bell-jar. Molecular nitrogen of the ultra high purity grade was applied as a plasma-forming gas. The gas flow rate was 300 cm³/s. At lower gas flow rate, the formation of condensed water was observed and we could not measure correctly the emission intensities. The anode was made from mechanically sharpened stainless steel wire. A high voltage (up to 4 kV) was applied between the aqueous cathode and anode, which was placed at the position 1–10 mm (typically 10 mm) above the water surface. The distance between the anode and the liquid surface was adjustable. The discharge current was 40 mA. The N₂ pressure was varied from 0.1 to 1(±0.01) bar. For the emission spectra digital registration the AvaSpec-2048FT-2 monochromator (grating of 600 line/mm) was used. The light entered the monochromator entrance slit through a quartz optical fiber. The light guide-monochromator system was calibrated by the monochromator manufacturer on a radiation power. The emission from cathode and anode discharge parts was cut off by the size of the quartz window.

Fig. 1

Schematic diagram of the experimental set-up. 1 cathode, 2 glass bell-jar, 3 anode, 4 discharge, 5 quartz window, 6 radiation output to entrance lens of light fiber, 7 glass cell with distilled water, 8, 9 gas outlet and inlet, 10 entrance lens of light fiber, 11 light fiber

The average on the discharge volume bands intensity, $\overline{I}$, was determined as follows. The quanta amount, dΦ, emitted with the discharge volume dV into solid angle Ω(r,φ,z) per unit of time is

$$d\varPhi = \frac{I}{4 \times \pi } \times \varOmega \times dV = \frac{I(r,\varphi ,z)}{4 \times \pi } \times \varOmega \times rdrd\varphi dz,$$

where I—the integral band intensity [quantum/(s × cm³)]; r,φ and z—cylindrical coordinates of emitting discharge point. Since the discharge radius (R _D  ≈ 1 mm) and discharge length (L _D  = 10 mm) are much less than the distance between the light guide entrance lens and the discharge (L = 75 mm), the Ω value is approximately the same for every discharge point and equals to

$$\varOmega = \frac{{\pi \times R_{L}^{2} }}{{L^{2} }},$$

where R _L —radius of entrance lens (2.5 mm).

Therefore, the total amount of quanta, Φ, which is registered by monochromator per second, can be written as

$$\varPhi = \frac{{R_{L}^{2} }}{{4 \times L^{2} }} \times \int\limits_{0}^{{R_{D} }} {\int\limits_{0}^{2\pi } {\int\limits_{0}^{{L_{D} }} {I \times rdrd\varphi dz = \frac{{R_{L}^{2} }}{{4 \times L^{2} }} \times \bar{I} \times V_{D} ,} } }$$

where $\overline{I}$—average on the discharge volume intensity, V _D —discharge volume.

For the determination of the electric field strength, E, and the cathode voltage drop, U _c , the voltage drop between anode and cathode was measured as a function of anode-surface water distance. The digital voltmeter Fluke 289 © (USA) was used for this purpose. Voltage drop on water layer was measured at a contact of anode with water surface. Then, this value was subtracted from the total voltage measured. The linear part of volt-distance dependence was treated with a least-squares method to obtain the electric field strength in a plasma column. The extrapolation of dependence to a zero distance gives the U _c value. This value is partly overestimated since we did not take into account the anode voltage drop. But it is well known that the anode voltage drop is essentially less than cathode one [16].

The rotational temperature was determined from non-resolved rotational structure of the band for the C³Π_u → B³Π_g (0–2) transition as it was described elsewhere [4]. In the present case, the rotational temperature is equal to the translational one. The MDR-23 spectrometer was utilized for checking possibility of this method. Its resolution (grating of 1200 line/mm) allowed to obtain the resolved structure of R₁-branch (for J′ > 15) and unresolved one depending on the split sizes. The temperatures difference obtained with both methods was not more than 40 K.

The reproducibility errors for all measured values were calculated on the base of five and more measurements using the confidence probability of 0.95. The total errors are shown in appropriate Figures as the bars.

All measurements were carried out after reaching the stationary conditions. It was controlled by temporal behavior of line intensities (actually, in 15 min of discharge burning).

Description of the Model and Calculations

The model was described with the Boltzmann equation for electrons, chemical kinetics equations, equations of vibration kinetics, and the equation of plasma conductivity. The last one was used for the determination of electron density on the base of the measured current density.

The EEDF was obtained as the solution of the homogeneous Boltzmann equation using the two-term expansion. Collision integrals include the collisions of electrons with H₂, N₂, O₂, H₂O, NO molecules in electronic ground state and with O(³P) atoms. The collisions of the second kind with vibrationally excited molecules and e–e collisions were taken into consideration as well. The cross-section sets for N₂, O₂, H₂O, NO, H₂ molecules and O(³P) atoms were taken from studies [17–22], respectively. Some details of the solution were described by us elsewhere [15, 23].

The Boltzmann equation was written as

$$\frac{d}{d\varepsilon }\left( {\beta \frac{df}{d\varepsilon }} \right) = J_{e} + J_{ine} + J_{ee} ,$$

(1)

where ε—in the electron energy, f(ε) is EEDF with the following normalization

$$\int\limits_{0}^{\infty } {f(\varepsilon )\varepsilon^{1/2} } d\varepsilon = 1.$$

In Eq. (1), β is expressed in S.I. units by:

$$\beta = \frac{{e^{2} }}{3}\left( \frac{E}{N} \right)^{2} \times \left( {\sum\limits_{i} {\sigma_{i}^{tr} } Y_{i} } \right)^{ - 1} \times \varepsilon ,$$

(2)

where E/N, e are the reduced electric field strength and the electron charge, respectively, $\sigma_{i}^{tr}$ is the momentum transfer cross-section for electron collisions with heavy particles i, Y _i is mole fraction of this type of particle.

J _e is given by:

$$J_{e} = - \frac{d}{d\varepsilon }\left( {kT \times \gamma \frac{df}{d\varepsilon } + \gamma \times f} \right),$$

(3)

where T is the gas temperature, and,

$$\gamma = 2m_{e} \times \left( {\sum\limits_{i} {\frac{{\sigma_{i}^{tr} \times Y_{i} }}{{M_{i} }}} } \right) \times \varepsilon^{2} + 6\varepsilon \times \sum\limits_{i} {hc \times (B_{i} \times \sigma_{i}^{r} \times Y_{i} )} ,$$

where M _i , B _i , and $\sigma_{i}^{tr}$ are the mass, rotational constant (cm⁻¹) and rotational excitation cross-section for heavy particles i.

The integral of inelastic collisions, J _ine , consists of two integrals, J ^I _un and J ^II _un , describing the collisions of the first and second kind, respectively:

$$\begin{aligned} J_{un}^{I} & = \sum\limits_{i} {\sum\limits_{j} {Y_{i} \left[ {\varepsilon \cdot Q_{j}^{i} \left( \varepsilon \right) \cdot f\left( \varepsilon \right) - \left( {\varepsilon + \varepsilon_{ji} } \right) \cdot Q_{j}^{i} \left( {\varepsilon + \varepsilon_{ji} } \right) \cdot f\left( {\varepsilon + \varepsilon_{ji} } \right)} \right]} } \\ J_{un}^{II} & = \sum\limits_{i} {\sum\limits_{j} {Y_{i} \left[ {\varepsilon \cdot Q_{ - j}^{i} \left( \varepsilon \right) \cdot f\left( \varepsilon \right) - \left( {\varepsilon - \varepsilon_{ji} } \right) \cdot Q_{ - j}^{i} \left( {\varepsilon - \varepsilon_{ji} } \right) \cdot f\left( {\varepsilon - \varepsilon_{ji} } \right)} \right]} } \\ \end{aligned}$$

where the summation is carried out on all j collisions for heavy particle i; ε _ji is the threshold energy of process j; Q ⁱ _j is the cross-section of collision of the first kind and Q ⁱ_−j is the cross-section of collision of the second kind. The relation between Q ⁱ _j and Q ⁱ_−j is given by the detailed balance principle:

$$Q_{ - j}^{i} = \frac{{\varepsilon - \varepsilon_{ji} }}{\varepsilon }Q_{j}^{i} \left( {\varepsilon + \varepsilon_{ji} } \right).$$

The integral of e–e collisions, J _ee , has the form:

$$J_{ee} = - \frac{1}{8\pi }\left( {\frac{{e^{2} }}{{\varepsilon_{0} }}} \right)^{2} \times Y_{e}\,\times\,\ln (\lambda ) \times \frac{d}{d\varepsilon }\left[ {f(\varepsilon )\int\limits_{0}^{\varepsilon } {\varepsilon^{1/2} } f(\varepsilon )d\varepsilon + \frac{2}{3}\frac{df}{d\varepsilon }\left( {\int\limits_{0}^{\varepsilon } {\varepsilon^{3/2} f(\varepsilon )} d\varepsilon + \varepsilon^{3/2} \int\limits_{\varepsilon }^{\infty } {f(\varepsilon )} d\varepsilon } \right)} \right],$$

(4)

where ε ₀  = 8.854 × 10⁻¹² F × m⁻¹ is the electric field constant and Y _e is the electron mole fraction. Ln(λ) is the Coulomb logarithm expressed by:

$$Ln(\lambda ) = Ln\frac{{(4\pi \varepsilon_{0} )^{3/2} (kT)^{1/2} \bar{\varepsilon }}}{{n_{e}^{1/2} e^{3} }},$$

where $\bar{\varepsilon }$ is the average electron energy and n _e —the electron concentration.

The Eq. (1) was solved by the following way. Let us take the uniform grid with the mesh point of 1.2…m…N. Integrating (1) on the one interval from ε _m to ε _m=1 (Δε = ε _m=1  − ε _m ) and calculating integrals of inelastic collisions using the method of rectangular trapeziums we obtain the system of (N − 2) difference equations:

$$a_{m} \cdot f_{m - 1} - b_{m} \cdot f_{m} + c_{m} \cdot f_{m + 1} = d_{m} .$$

(5)

The coefficients of this system are:

$$\begin{aligned} a_{m} & = \left( {\beta + \frac{kT}{e} \cdot \gamma } \right)_{m} + \frac{1}{8\pi }\left( {\frac{{e^{2} }}{{\varepsilon_{0} }}} \right)^{2} Y_{e} \cdot \ln \lambda \cdot \left[ {\frac{2}{3}\frac{1}{{\Delta \varepsilon }}\left( {\int\limits_{1}^{{\varepsilon_{m} }} {\varepsilon^{3/2} fd\varepsilon + \varepsilon^{3/2} \cdot \int\limits_{{\varepsilon_{m} }}^{{\varepsilon_{N} }} {fd\varepsilon } } } \right)} \right], \\ b_{m} & = a_{m} + a_{m + 1} + \gamma_{m} + \frac{{\Delta \varepsilon }}{2} \cdot \varepsilon_{m} \cdot \left( {\sum\limits_{i} {\sum\limits_{j} {Y_{i} \cdot Q_{j,m}^{i} + \sum\limits_{i} {\sum\limits_{j} {Y_{i} \cdot Q_{ - j,m}^{i} } } } } } \right) \\ & \quad + \frac{1}{8\pi }\left( {\frac{{e^{2} }}{{\varepsilon_{0} }}} \right)^{2} \cdot Y_{e} \ln \lambda \int\limits_{{\varepsilon_{1} }}^{{\varepsilon_{m} }} {\varepsilon^{1/2} f_{e} d\varepsilon } , \\ c_{m} & = a_{m} + \gamma_{m + 1} - \frac{{\Delta \varepsilon }}{2}\varepsilon_{m + 1} \left( {\sum\limits_{i} {\sum\limits_{j} {Y_{i} \cdot Q_{j,m + 1}^{i} + \sum\limits_{j} {\sum\limits_{i} {Y_{i} \cdot Q_{ - j,m + 1}^{i} } } } } } \right) \\ & \quad + \frac{1}{8\pi }\left( {\frac{{e^{2} }}{{\varepsilon_{0} }}} \right)^{2} \cdot Y_{e} \cdot \ln \lambda \cdot \left[ {\frac{2}{3}\frac{1}{{\Delta \varepsilon }} \cdot \left( {\int\limits_{{\varepsilon_{1} }}^{{\varepsilon_{m + 1} }} {\varepsilon^{3/2} \cdot fd\varepsilon + \varepsilon_{m + 1}^{3/2} \cdot \int\limits_{{\varepsilon_{m + 1} }}^{{\varepsilon_{N} }} {fd\varepsilon } } } \right)} \right], \\ d_{m} & = - \frac{{\Delta \varepsilon }}{2}\left[ {\sum\limits_{i} {\sum\limits_{j} {Y_{k} \left( {\varepsilon_{{m + n_{j} + 1}} \cdot f_{{m + n_{j} + 1}} \cdot Q_{{j,m + n_{j} + 1}}^{i} + \varepsilon_{{m + n_{j} }} \cdot f_{{m + n_{j} }} \cdot Q_{{j,m + n_{j} }}^{i} } \right)} } } \right. \\ & \quad + \sum\limits_{i} {\sum\limits_{j} {Y_{k} \left( {\varepsilon_{{m - n_{j} + 1}} \cdot f_{{m - n_{j} + 1}} \cdot Q_{{ - j,m - n_{j} + 1}}^{i} + \varepsilon_{{m - n_{j} }} \cdot f_{{m - n_{j} }} \cdot Q_{{ - j,m - n_{j} }}^{i} } \right)} .} \\ \end{aligned}$$

In these expressions the m, m + 1, m + 1 ± n _j , m ± n _j indexes correspond to number of grid point where appropriate value is determined. And Δε = ε _m+1−ε _m , n _j  = (ε _ij  − ε ₁ )/Δε + 1.

The boundary conditions for system (6) are

$$a_{2} \cdot f_{1} - (a_{2} + \gamma_{2} ) \cdot f_{2} = 0,$$

(6)

$$(a_{N} + \gamma_{N} ) \cdot f_{N} - a_{N} \cdot f_{N - 1} = 0.$$

(7)

The summation of all Eqs. (5–7) gives zero. Therefore, the system developed is conservative one. That is it satisfies the condition of conservation of electron amount. Due to e–e collisions the system is not linear and equation members with inelastic collisions result in the matrix sparseness (existence of large amount of zero value). For this reason the application of standard procedures for the solution requires a large volume of calculation and computer memory. To avoid this the method of iterations combined with the sweep method was used. As the zero-order approximation the maxwellian EEDF with the average energy of 1 eV was used. Using this function the coefficients a, b, c, and d of (5–7) were calculated. This procedure transformed the equation system to formally three-diagonal form with the diagonal prevalence that provided the absolute stability of solution. After that the system was fast solved with a sweep method. The EEDF obtained was used as the next approximation. The calculation was terminated when the relative error was less than 0.0001.

The electron average energy, the reduced diffusion coefficient, D _e N, the electron drift velocity, V _D , and rate coefficients, K _kj , for electron impact were calculated using obtained EEDF:

$$\begin{aligned} & \bar{\varepsilon } = \int\limits_{0}^{\infty } {\varepsilon^{3/2} \times f\left( \varepsilon \right)d\varepsilon ,\quad D_{e} N = \frac{1}{3}\left( \frac{2e}{m} \right)^{1/2} \int\limits_{0}^{\infty } {\frac{\varepsilon \times f\left( \varepsilon \right)d\varepsilon }{{\sum\limits_{i} {\sigma_{i}^{tr} \times Y_{i} } }},} } \\ & V_{D} = - \frac{1}{3}\left( \frac{2e}{m} \right)^{1/2} \left( \frac{E}{N} \right) \cdot \int\limits_{0}^{\infty } {\frac{\varepsilon }{{\sum\limits_{i} {\sigma_{i}^{tr} \times Y_{i} } }}} \cdot \frac{df}{d\varepsilon }d\varepsilon ,\quad K_{kj} = \left( \frac{2e}{m} \right)^{1/2} \cdot \int\limits_{{\varepsilon_{jk} }}^{\infty } \varepsilon \times Q_{j}^{i} \left( \varepsilon \right) \cdot f\left( \varepsilon \right)d\varepsilon . \\ \end{aligned}$$

The multiplication of (1) on ε, n _e and N, and the integration on ε from 0 to ∞ results in the equation of electron energy balance. Left side of (1) gives the power density acquired from electric field:

$$jE = n_{e} \times e \times V_{D} \times E = N \times n_{e} \times e \times V_{D} \times (E/N).$$

(8)

The power density acquired at the collisions with heavy particles having the temperature T is

$$W_{H} = - n_{e} \times N \times \sqrt {\frac{2}{{m_{e} }}} \times \int\limits_{0}^{\infty } {\left( {kT \times \gamma \times \frac{df}{d\varepsilon }} \right)d\varepsilon } .$$

(9)

The power density lost by electrons at elastic collisions with heavy particles (gas heating) is expressed:

$$W_{el} = n_{e} \times N \times \sqrt {\frac{2}{{m_{e} }}} \times \int\limits_{0}^{\infty } {\left( {2m_{e} \times \sum\limits_{i} {\frac{{Y_{i} \times \sigma_{i}^{tr} }}{{M_{i} }}} } \right) \times \varepsilon^{2} \times f(\varepsilon )d\varepsilon ,}$$

(10)

and on excitation of rotational levels is

$$W_{r} = n_{e} \times N \times \sqrt {\frac{2}{{m_{e} }}} \times \int\limits_{0}^{\infty } {6\varepsilon \times \left( {\sum\limits_{i} {B_{i} \times } Y_{i} \times \sigma_{i}^{r} } \right) \times f(\varepsilon )d\varepsilon .}$$

(11)

Every summand in (9–11) gives the input of separate component to appropriate energy loses.

The integration of J _ine gives the difference of power densities lost by electrons at all inelastic collisions of the first kind, $W_{un}^{I}$, and acquired at the collisions of the second kind, $W_{un}^{II}$,:

$$W_{un}^{I} - W_{un}^{II} = n_{e} N\sqrt {\frac{2}{{m_{e} }}} \left[ {\sum\limits_{j} {\sum\limits_{i} {Y_{i \times } \varepsilon_{ji} } } \int\limits_{{\varepsilon_{ji} }}^{\infty } {\varepsilon \times \sigma_{j}^{i} (\varepsilon )} \times f(\varepsilon )d\varepsilon - \sum\limits_{i} {\sum\limits_{j} {Y_{i} \times \varepsilon_{ij} } } \int\limits_{{\varepsilon_{ij} }}^{\infty } {\varepsilon \times \sigma_{ - j}^{i} (\varepsilon ) \times } f(\varepsilon )d\varepsilon } \right],$$

(12)

where $_{Yi} \times K_{ji} \times n_{e} \times N =_{Yi} \times \left[\sqrt {\frac{2}{{m_{e} }}} \int\limits_{{\varepsilon_{ji} }}^{\infty } {\varepsilon \times \sigma_{j}^{i} (\varepsilon ) \times f(\varepsilon )d\varepsilon } \right] \times n_{e} \times N$ is the rate of process j, and impression in a square bracket is rate constant.

The integration of J _ee gives zero.

The relations (8–12) allow calculating the energy fraction inputted to every process, δ, as the ratio of power density of appropriate process to total power density. Also, it allows checking the accuracy of EEDF calculations. In our calculation the energy balance was fulfilled with accuracy of ~0.1 %.

The population of vibrational levels of N₂, O₂, H₂O, and NO molecules in ground state was determined by solving the equations system of quasi-stationary kinetics. This system takes into consideration the single-quantum V–V, and V–T exchange between partners, e–V pumping and some other events. The kinetic equation for the concentration, [N ^(m)(V)], molecule of kind m on the vibrational level V was written as

$$\begin{aligned} \frac{{d[N^{(m)} (V)]}}{dt} & = \sum\limits_{m} {\left\{ {K_{V - !,V}^{(m)} \times \left[ {N^{(m)} (0)} \right] + \sum\limits_{W = 0}^{W* - 1} {K_{V - 1,V}^{(m)W + 1,W} \times \left[ {N^{(m)} (W + 1)} \right]} } \right\} \times [N^{(m)} (V - 1)]} \\ & \quad - \sum\limits_{m} {\left\{ {\left( {K_{V,V - 1}^{(m)} + K_{V,V + 1}^{(m)} } \right) \times \left[ {N^{m} (0)} \right] + \sum\limits_{W = 1}^{W*} {\left( {K_{V,V + 1}^{(m)W,W - 1} \times \left[ {N^{(m)} (W)} \right]} \right)} } \right.} \\ & \quad + \sum\limits_{W = 0}^{W* - 1} {\left. {\left( {K_{V,V - 1}^{(m)W,W + 1} \times \left[ {N^{(m)} (W)} \right]} \right) + n_{e} \times K_{V0}^{(m)} } \right\}} \times \left[ {N^{m} (V)} \right] + \sum\limits_{m} {\left\{ {\left( {K_{V + 1,V}^{(m)} \times \left[ {N^{m} (0)} \right]} \right)} \right.} \\ & \quad + \sum\limits_{W = 1}^{W*} {\left. {\left( {K_{V + 1,V}^{(m)W - 1,W} \times \left[ {N^{(m)} (W - 1)} \right]} \right) + K_{0V}^{(m)} \times n_{e} \times \left[ {N^{(m)} (0)} \right]} \right\} \times \left[ {N^{m} (V + 1)} \right] + Q_{V} } \\ \end{aligned}$$

(13)

where the summation on m means the summation on amount of components, K _V,V–1 and K _V–1,V are the rate constants of V–T exchange, $K_{V - 1,V}^{W + 1,W}$ and $K_{V,V + 1}^{W,W - 1}$ are the rate constants of V–V exchange, K _V0 and K _0V are the rate constants of electron pumping and deactivation of level V, V and W are the vibrational quantum numbers, [N ^(m)(W)] is the concentration of molecule m on vibrational level W, Q _V is the rates of other reactions, W* is the vibrational level corresponding to dissociation limit. W* = 14, 13, 23, 40, 36, and 46 for H₂O(001), H₂O(100), H₂O(010), NO, O₂, and N₂ molecules, respectively.

Formally, for the molecule with W* vibrational levels the systems of W* Eqs. (9) for the stationary conditions can be written as:

$$\begin{aligned} & a_{0} \cdot [N^{(m)} (1)] - b_{0} \cdot [N^{(m)} (0)] + d_{0} = 0, \\ & a_{n} \cdot [N^{(m)} (V + 1)] - b_{n} \cdot [N^{(m)} (V)] + c_{n} \cdot [N^{(m)} (V - 1)] + d_{n} = 0, \\ & - c \times [N^{(m)} (W*)] - e \times [N^{(m)} (W*)] + \sum\limits_{j} {Q_{j} } = 0, \\ \end{aligned}$$

where c, e are the frequencies of dissociation through vibrational continuum for V–V and V–T processes, respectively, the $\sum\nolimits_{j} {Q_{j} }$ is the difference of total rates of formation and the losses of vibrational excited molecules for the reactions which are not connected with V–V, V–T exchange and electron excitation-de-excitation, n is changed from 1 up to (W* − 1).

The system is not linear one since its coefficients depend on concentrations. The matrix of system has a three-diagonal form. For this reason we used the same solution method as for Boltzmann equation. As the zero-order approximation the Boltzmann distribution with vibrational temperature equals to gas one was used. The diagonal prevalence provided the absolute stability of solution. The iterations were terminated when the relative error was <0.001.

The detailed processes list is given in study [13]. The level rate constants were calculated applying SSH (Schwartz–Slawsky–Herzfeld) generalized theory [24]. For normalizing of the rate constants the experimental values of coefficients for K _1,0, $K_{0,1}^{1,0}$ of studies [25–30] were used. The molecular parameters were taken from [31, 32] and values of reverse radius in exponential repulsive potential of interaction are given in [33].

The chemical transformations included 187 reactions which describe the concentrations of the following neutral species: O₂(X), O₂(a¹Δ), O₂(b¹Σ), O₂(A³Σ), O(³P), O(¹D), O(¹S), O₃, O(3p³P), O(3s³S), H₂O, H, OH, H₂O₂, HO₂, H₂, N₂(X), N₂O, NO, NO₂, NO₃, HNO, HNO₂, HNO₃, N₂(A³Σ ⁺_u ), N₂(B³Π_g), N₂(C³Π_u), and N₂(a′¹Σ⁺). This set was already used by us for the modeling of an atmospheric pressure DC discharge in air [13]. The list of processes and data on the rate constants is given in the same study. We added to this reaction scheme the following reactions:

$$\begin{array}{*{20}l} {{\text{H}}_{2} {\text{O}} + {\text{N}}_{2} \left( {{\text{A}}^{3} \varSigma_{\text{u}}^{ + } } \right) \to {\text{OH}} + {\text{H}} + {\text{N}}_{2} \left( {\text{X}} \right),} & {{\text{K}} = 2.91 \times 10^{ - 14} \times T^{0.5} \,{\text{cm}}^{3} /{\text{s}},} & {[34]} \\ {{\text{H}}_{2} {\text{O}} + {\text{H}}_{2} {\text{O}} \to {\text{OH}} + {\text{H}} + {\text{H}}_{2} {\text{O}},} & {{\text{K}} = 6.56 \times 10^{ - 10} \times \exp \left( { - 53670/T} \right)\,{\text{cm}}^{3} /{\text{s}},} & {[35]} \\ {{\text{N}}\left( {^{4} {\text{S}}} \right) + {\text{N}}\left( {^{4} {\text{S}}} \right) + {\text{N}}_{2} \left( {\text{X}} \right) \to {\text{N}}_{2} \left( {\text{X}} \right) + {\text{N}}_{2} \left( {\text{X}} \right),} & {{\text{K}} = 1.78 \times 10^{ - 33} \times \exp \left( {485/T} \right)\,{\text{cm}}^{6} /{\text{s}},} & {[36]} \\ {{\text{N}}\left( {^{2} {\text{P}}} \right) + {\text{N}}_{2} \left( {\text{X}} \right) \to {\text{N}}_{2} \left( {\text{X}} \right) + {\text{N}}\left( {^{4} {\text{S}}} \right),} & {{\text{K}} = 5.0 \times 10^{ - 17} \,{\text{cm}}^{3} /{\text{s}},} & {[37]} \\ {{\text{N}}\left( {^{2} {\text{D}}} \right) + {\text{N}}_{2} \left( {\text{X}} \right) \to {\text{N}}_{2} \left( {\text{X}} \right) + {\text{N}}\left( {^{4} {\text{S}}} \right),} & {{\text{K}} = 1.7 \times 10^{ - 14} \,{\text{cm}}^{3} /{\text{s}},} & {[34]} \\ \end{array}$$

These reactions were not important for air plasma since in that plasma there were more fast reactions of OH formation and N(⁴S) loss, particularly, the reactions with participation of atomic oxygen.

The modeling was carried out by means of combined solution of all the equations mentioned above for the experimental values of E/N, gas temperature, and discharge current density.

The lack of data on water molecules concentrations is the main problem for the modeling. For this reason, we used these values as fitting parameters to satisfy the measured emission intensities of some N₂ bands and effective vibrational temperatures, T _v , of N₂ ground state.

The effective vibrational temperature, T _V , of the C³Πu state was obtained using measured intensities, $I_{{V^{{\prime }} ,V^{{\prime \prime }} }}$, of 0 → 3, 1 → 4, 2 → 5, 3 → 6, and 4 → 7, 0 → 2, 1 → 3, 2 → 4, 3 → 5, 4 → 6 sequences of bands of the C³Πu → B³Πg transition. According to the relation, $N_{{V^{{\prime }} }} = N_{{V^{{\prime }} = 0}} \exp ( - \varDelta E_{{V^{{\prime }} }} /kT_{V} )$, the data obtained were plotted using the coordinates of $Ln[(A_{0,1} /A_{{V^{{\prime }} ,V^{{\prime \prime }} }} )(I_{{V^{{\prime }} ,V^{{\prime \prime }} }} /I_{0,1} )] = f(\varDelta E_{{V^{{\prime }} }} )$, where $A_{{V^{{\prime }} ,V^{{\prime \prime }} }}$ is radiation probability of appropriate transition and $\varDelta E_{{V^{{\prime }} }}$ is vibrational energy for C³Πu (V′) state counted off from V′ = 0 level. After fitting the data by using the least-square method, we determined vibrational temperature, T _V , as the slope of the fitting curve. The linear dependence described the experiment with correlation coefficient greater than 0.99. Both sequences gave the same results. Molecular constants of C³Πu (V′) state were taken from Ref. [31] and $A_{{V^{{\prime }} ,V^{{\prime \prime }} }}$ values—from study [37].

For the estimation of population of vibrational levels (vibration temperature) of N₂ ground state, we used two approaches. The first was the direct solution of equation of vibrational kinetics, whereas the second was as follows. We assumed that populations of different C³Πu vibration states were reached due to electron impact with the species in vibration levels of X¹Σ ⁺_g ground states. Also, we assumed that the main process of C³Πu vibrational states destruction was not radiation decay but rather quenching via the collisions with plasma forming gas molecules. Actually, radiation probabilities for different C³Πu states are of ~2×10⁷ s⁻¹ [36], whereas quenching rate constants by O₂, H₂O and N₂ molecules are of ~10⁻¹⁰ cm³/s [38]. At the particle density of 4 × 10¹⁸ cm⁻³, the quenching frequency is ~4×10⁸ s⁻¹. Applying above assumptions, we can write the following five equations since we observed only five transitions from the C³Πu (V′ = 0-4) in irradiation spectra

$$n_{e} \times N_{{V^{{\prime }} = 0}}^{{\prime }} \cdot \sum\limits_{{V^{{\prime }} }} {\left[ {K_{{V^{{\prime }} ,0}} \exp ( - \varDelta E_{{V^{{\prime }} }} /kT_{{V^{{\prime }} }} )} \right]} = Z_{Q}^{{V^{{\prime \prime }} = 0}} \times N_{{V^{{\prime \prime }} = 0}}^{{\prime \prime }} \times \exp ( - \varDelta E_{{V^{{\prime \prime }} = 0}} /kT_{{V^{{\prime \prime }} }} ),$$

(14)

$$n_{e} \times N_{{V^{{\prime }} = 0}}^{{\prime }} \cdot \sum\limits_{{V^{{\prime }} }} {\left[ {K_{{V^{{\prime }} ,1}} \exp ( - \varDelta E_{{V^{{\prime }} }} /kT_{{V^{{\prime }} }} )} \right]} = Z_{Q}^{{V^{{\prime \prime }} = 1}} \times N_{{V^{{\prime }} = 0}}^{{\prime \prime }} \times \exp ( - \varDelta E_{{V^{{\prime }} = 1}} /kT_{{V^{{\prime }} }} ),$$

(15)

$$n_{e} \times N_{{V^{{\prime }} = 0}}^{{\prime }} \cdot \sum\limits_{{V^{{\prime }} }} {\left[ {K_{{V^{{\prime }} ,2}} \exp ( - \varDelta E_{{V^{{\prime }} }} /kT_{{V^{{\prime }} }} )} \right]} = Z_{Q}^{{V^{{\prime \prime }} = 2}} \times N_{{V{\prime \prime } = 0}}^{{\prime \prime }} \times \exp ( - \varDelta E_{{V^{{\prime \prime }} = 2}} /kT_{{V^{{\prime \prime }} }} ),$$

(16)

$$n_{e} \times N_{{V^{{\prime }} = 0}}^{{\prime }} \cdot \sum\limits_{{V^{{\prime }} }} {\left[ {K_{{V^{{\prime }} ,3}} \exp ( - \varDelta E_{{V^{{\prime }} }} /kT_{{V^{{\prime }} }} )} \right]} = Z_{Q}^{{V^{{\prime \prime }} = 3}} \times N_{{V^{{\prime \prime }} = 0}}^{{\prime \prime }} \times \exp ( - \varDelta E_{{V^{{\prime \prime }} = 3}} /kT_{{V^{{\prime \prime }} }} ),$$

(17)

$$n_{e} \times N_{{V^{{\prime }} = 0}}^{{\prime }} \cdot \sum\limits_{{V^{{\prime }} }} {\left[ {K_{{V^{{\prime }} ,4}} \exp ( - \varDelta E_{{V^{{\prime }} }} /kT_{{V^{{\prime }} }} )} \right]} = Z_{Q}^{{V^{{\prime \prime }} = 4}} \times N_{{V^{{\prime \prime }} = 0}}^{{\prime \prime }} \times \exp ( - \varDelta E_{{V^{{\prime \prime }} = 4}} /kT_{{V^{{\prime \prime }} }} ),$$

(18)

where summation has to include all the vibration levels of the X¹Σ ⁺_g state; $N_{{V^{{\prime }} }}^{{\prime }} = 0\;N_{{V^{{\prime \prime }} }}^{{\prime \prime }} = 0$ are the X¹Σ ⁺_g and C³Πu concentrations on the zero vibrational level, respectively; $K_{{V^{{\prime }} ,V^{{\prime \prime }} }}$ is rate constant for excitation of the C³Πu V″ level from X¹Σ ⁺_g V′ level by electron impact; $\varDelta E_{{V^{{\prime }} }} ,\;\varDelta E_{{V^{{\prime \prime }} }}$ are vibration energies for the X¹Σ ⁺_g and C³Π_u states counted off from zero level, respectively; $T_{{V^{{\prime }} }} ,T_{{V^{{\prime \prime }} }}$ are the “vibrational” temperatures for the X¹Σ ⁺_g and C³Πu states, respectively; n _e is electron density and $Z_{Q}^{{V^{{\prime \prime }} }}$ is quenching frequency. The $Z_{Q}^{{V^{{\prime \prime }} }}$ is equal to

$${Z_{Q}^{{V^{{\prime \prime }} }} } = \sum\limits_{i} {\left( {K_{{V^{{\prime \prime }} }}^{i} \times N^{i} } \right) + {A_{{V^{{\prime }} ,V^{{\prime \prime }} }} }}$$

where $K_{{V^{{\prime \prime }} }}^{i}$ is the quenching rate constant of C³Π_u(V″) vibrational state by O₂, H₂O and N₂ molecules, N ⁱ is the appropriate concentration.

The cross-sections were obtained using the approach described in Ref. [39]. As a result of analyzing different data, it was shown that the cross-sections for C³Π_u (V′) excitation from X¹Σ ⁺_g (V″) can be written as

$${\sigma_{{V^{{\prime }} ,V^{{\prime \prime }} }} (\varepsilon /\varepsilon (V^{{\prime }} ,V^{{\prime \prime }} )) = \left| {M_{e} } \right|^{2} \times q(V^{{\prime }} ,V^{{\prime \prime }} ) \times F(\varepsilon /\varepsilon (V^{{\prime }} ,V^{{\prime \prime }} ))},$$

where |M _e |² = 38 × 10⁻¹⁸ cm² is the square of matrix element for electronic transition and q(V′,V″) is the Frank–Condon factor of V′–V″ transition; F(ε/ε(V′,V″)) is the universal function of the ratio of electron energy to threshold energy.

The system of equations was solved for T _V′ by means of Tikhonov’s regularization method [40] using the experimental data on T _V″ .

Results and Discussion

The pressure increase results in a slight growth of cathode voltage drop, U _c , and in the increase in a cathode current density (Fig. 2). The data on U _c are close to those obtained in study [5] for atmospheric pressure.

Fig. 2

The cathode voltage drop (4) and cathode current density (5) as a pressure function at the discharge current of 40 mA. 1, 2, 3 data for Ar, N₂ and air, respectively from study [5] for the discharge current of 25 mA

The measured gas temperature (Fig. 3) depends slightly on the pressures in spite of the fact that the specific power (j × E = W, j—current density) inputted to positive column is increased with the pressure growth from 51 up to 2.2 × 10³ W/cm³. Assuming constant values of W and heat conductivity coefficient, λ, the solution of heat conductivity equation gives the following expression for the temperature averaged on discharge cross-section, $\overline{T}$.

$$\bar{T} = T(R) + 0.125 \times [(W \times \delta )/\lambda ] \times R^{2} ,$$

(19)

where R—discharge radius, T(R)—temperature on the plasma-gas interface, δ—energy part transmitting electrons into heat. The pressure growth results in the decrease of R from 0.21 to 0.072 cm (Fig. 4). The (W × R ²) value is increased by a factor of ~5.1. Therefore, the δ value has to be decreased with the pressure growth. The EEDF calculations showed that the most part of electron energy is inputted to vibration degree of freedom of N₂ and H₂O ground states. And this part depends slightly on the pressure. Thus, at the pressure of 1 bar 0.8 of total energy is inputted to N₂(X,V) and 0.16 to H₂O (X,V). At the pressure of 0.1 bar 0.81 of total energy is inputted to N₂(X,V) and 0.11 to H₂O (X,V). For the direct gas heating over elastic electron collisions with molecules the δ is ~5×10⁻³. Therefore, the main source of gas heating is V-T exchange reactions. If vibrationally excited molecules have no time to relax within discharge zone, it can be expected that the part of vibration energy transforms to heat outside the glowing part of discharge. Actually, the diffusion coefficient, D, of N₂ in N₂ is equal to D = 0.17 × (T/273)1.92 at atmospheric pressure [41]. At the discharge of radius, R, of 0.072 cm (Fig. 4) and at the temperature of 1500 K the diffusion time is equal to τ _D  = (R/2.405)²/D = 4.4 × 10⁻⁵ s. The characteristic time of V–T relaxation, τ _VT  = (K ₁₀ × [N₂])⁻¹ is equal to 1.2 × 10⁻⁴ s for the same conditions. Therefore, the part of energy which is transformed to heat in the discharge zone can be estimated as τ _D /τ _VT  = 0.36. It is necessary to point out that for the discharge in argon the all inputted energy is transformed to heat in the glowing part of discharge [12] whereas for air discharge the same behavior of temperature was observed [4]. Moreover, the gas temperatures for both discharges are practically the same. It is no wonder since for both discharges the inputted power is close, most part of energy is inputted to vibrational degree of freedom, and heat conductivity coefficients are close. The similar conclusion on the role of vibrational excited molecules in a gas heating was made in study [42] for DC discharge in air.

Fig. 3

The effective vibration (2, 3, 4) and rotational (1) temperatures. 3 were obtained from the solution of Eqs. (1)–(4) for N₂ ground state. 2 are vibration temperatures of N₂(C³П_u) state. 4 were obtained from the solution of equations of vibration kinetics for N₂ ground state

Fig. 4

The reduce electric field strength (1, 3) and radius of positive column (2) as a function of pressure. The discharge current is 40 mA. 3 was calculated by us on data from study [5]

Using the measured temperature, we calculated the total concentration of particles (P = N×kT) and values of reduced electric field strengths, E/N. The appropriate results are shown in Fig. 4. The data on vibrational temperatures for ${\text{C}}^{3}\Pi _{\text{u}}$ state are represented in Fig. 3. The gas temperatures, E and E/N values for the atmospheric pressure in air [4] and in N₂ were very close.

The OES measurements showed that molecular nitrogen (N₂) was represented by bands of second and first positive system $({\text{C}}^{3}\Pi _{\text{u}} \to {\text{B}}^{3}\Pi _{\text{g}} ,{\text{B}}^{3}\Pi _{\text{g}} , \to {\text{A}}^{3}\Sigma ^{ + }_{\text{u}} ).$ Atomic oxygen was represented by lines (777, 845 and 926.6 nm). OH radicals exhibited three bands: A²Σ → X²Π (1–0, 2–1, 3–2). Bands of NO γ-system (A²Σ → X²Π) were revealed as well. The irradiation of atomic hydrogen was represented by H_α and H_β lines.

It is difficult to compare correctly the obtained results with data of other studies. An atmospheric pressure DC discharge in N₂ was studied in works [5, 6]. In spite of close values of the most part of external discharge parameters the internal parameters determining a plasma state are essentially differ. Thus, the N₂ rotational temperature measured in study [5] was (2900 ± 200) K at atmospheric pressure and current of 25 mA. In study [6] the value of (3250 ± 150) K is given for discharge current of 30 mA. The radius of positive column was about 0.6 mm (0.7 mm in our study) [6]. The vibrational temperatures for C³Π_u state were (3500 ± 200) K [5] rather than (5000 ± 200) K as in our study (Fig. 3). The bands of N₂ first positive system were not presented in the emission spectrum. At the same time, the values of cathode voltage drop (Fig. 2) and electric field strength in positive column (~1 kV) were practically the same. We assume that such differences are conditioned with the effect of gas flow. The gas residence time in study [5] was 6 min, whereas in our study it was ~17 s. Undoubtedly, the increase in gas flow rate can lead to a gas cooling and to water molecules concentration and other neutral species dropping. The passing OH concentration through the maximum under the increase in a gas flow rate was observed in study [43].

The calculations showed that the best agreement between the experimental intensities (Fig. 5), vibrational temperatures (Fig. 3) and the calculation results is achieved at the water content represented in Fig. 6. The calculation was rather sensitive to water content. At experimental values of E/N even several tenths of percent of water influence strongly on EEDF leading to sharp drop of bands intensities. This is due to a large value of momentum transfer cross section of water (~10⁻¹³ cm²) with respect to appropriate cross section of N₂ (~10⁻¹⁵ cm²). Also, the vibrational temperatures were decreased. The calculation shows that the water content at the pressure of 1 bar is ~1 %. At the same time, the water content was estimated in study [6] as 10 % for 30 mA. The water molecules concentration depends on the balance of water rate evaporation and its pumping. We can suppose that the evaporation rate in the given study and in study [6] must be close, since the cathode current density and the cathode voltage drop are the same. Probably, faster pumping in our case provides lower density of water molecules in the discharge. Therefore, it can be expected that the concentrations of species formed from water have to be lower than in studies [5, 6].

Fig. 5

Bands intensities of N₂ second positive system (C³Π_u → B³Π_g). 1, 2, 3, 4 0 → 2, 2 → 4, 1 → 3, 3 → 5 transitions, respectively. Lines—calculation, points—experiment

Fig. 6

Concentrations of particles as a function of pressure. 1 NO, 2 ${\text{O}}_{2} \left( {{\text{a}}^{1}\Delta _{\text{g}} } \right)$, 3 ${\text{N}}_{2} \left( {{\text{A}}^{3}\Sigma ^{ + }_{\text{u}} } \right)$, 4 HNO, 5 H₂O

The results of calculations of main discharge species are shown in Figs. 6,7. The main species forming in a discharge were OH, H₂O₂, NO, and ${\text{N}}_{2} \left( {{\text{A}}^{3}\Sigma ^{ + }_{\text{u}} } \right)$ molecules. For the same discharge current the concentrations of these species in air were essentially more [13]. Thus, OH, H₂O₂, NO concentrations for N₂ discharge were ~1×10¹⁴, 8.9 × 10¹², and 1.8 × 10¹² cm⁻³, respectively, whereas for air discharge −3 × 10¹⁴, 2.7 × 10¹⁴, and 7 × 10¹⁶ cm⁻³, respectively. This fact is conditioned not only difference in O₂ content but the different EEDF. In air discharge the EEDF is “richer” with fast electrons. And rate coefficients of electron impact are more. The electron average energy for air discharge is 1.1 eV whereas for N₂ one is 0.96 eV.

Fig. 7

Concentrations of particles as a function of pressure. 1 HO₂, 2 H₂O₂, 3 H₂, 4 OH

In fact, at atmospheric pressure the OH density was ~1×10¹⁴ cm⁻³, whereas the value of 2 × 10¹⁵ cm⁻³ was obtained in study [6]. To understand the difference, we carried out the calculations using experimental results of [5, 6] as input data for our model. These data were the following: E − 1 kV, gas temperature—3000, discharge current—30 mA, discharge radius—0.6 mm, gas temperature—3000 K, water molecules content—10 %, pressure—1 bar. It gives the E/N of 4.1 × 10⁻¹⁶ V × cm². The calculation gives the values close to experimental data: OH concentration—1.1 × 10¹⁵ cm⁻³, vibrational temperature of N₂(X)—3100 K. The higher temperature in [5, 6] results in the lower (~2 times) concentration of plasma-forming gas molecules and in the higher E/N value (1.6 × 10⁻¹⁶ V × cm² in our experiment). It leads to the electron drift velocity increase and higher values of rate coefficients of electron impact. The increase degree depended on the process threshold energy. Thus, the rate constant for excitation of N₂(X,V = 1) was increased by a factor of 2 only, whereas the rate constant of ${\text{N}}_{2} \left( {{\text{A}}^{3}\Sigma ^{ + }_{\text{u}} } \right)$ excitation was increased by a factor of ~10². Due to the increase in drift velocity the electron density was decreased by a factor of ~2 in comparison with our data represented in Fig. 8. The average electron energy was 1.22 eV (0.96 eV in our study, Fig. 8) and electron density was 3.1 × 10¹² cm⁻³ (7 × 10¹² cm⁻³ in our study). Estimations made in study [6] give the close value of T_e ≈ 1 eV, but electron density was essentially more (2–6) × 10¹⁴ cm⁻³. As the result of action of factors mentioned above, the rates of main processes of water dissociation were increased essentially (see below). Calculations show that the following reactions are the main ones for the water dissociation and OH losses at any pressures:

$$\begin{aligned} & {\text{H}}_{2} {\text{O}} + {\text{e}} \to {\text{H}}\left( {^{1} {\text{S}}} \right) + {\text{OH}}^{ \cdot } + {\text{e}}\quad \left( {{\text{rate is }}3.2 \times 10^{16} \,{\text{cm}}^{ - 3} \,s^{ - 1} {\text{at 1 bar}}} \right), \\ & {\text{N}}_{2} \left( {\text{A}} \right) + {\text{H}}_{2} {\text{O}} \to {\text{N}}_{2} \left( {\text{X}} \right) + {\text{OH}}^{ \cdot } + {\text{H}}\left( {^{1} {\text{S}}} \right)\quad \left( {2.4 \times 10^{17} \,{\text{cm}}^{ - 3} \,{\text{s}}^{ - 1} } \right), \\ & {\text{OH}}^{ \cdot } + {\text{OH}}^{ \cdot } \to {\text{H}}_{2} {\text{O}} + {\text{O}}\left( {^{3} {\text{P}}} \right)\quad \left( {2.3 \times 10^{17} \,{\text{cm}}^{ - 3} \,{\text{s}}^{ - 1} } \right), \\ & {\text{OH}}^{ \cdot } + {\text{OH}}^{ \cdot } \to {\text{H}}_{2} {\text{O}}_{2} \quad \left( {3.4 \times 10^{16} \,{\text{cm}}^{ - 3} \,{\text{s}}^{ - 1} } \right), \\ & {\text{OH}}^{ \cdot } + {\text{H}}_{2} {\text{O}}_{2} \to {\text{H}}_{2} {\text{O}} + {\text{HO}}_{2}^{ \cdot } \quad \left( {1.1 \times 10^{16} \,{\text{cm}}^{ - 3} \,{\text{s}}^{ - 1} } \right), \\ & {\text{OH}}^{ \cdot } + {\text{HO}}_{2}^{ \cdot } \to {\text{H}}_{2} {\text{O}} + {\text{O}}_{2} \left( {\text{X}} \right)\quad \left( {1.1 \times 10^{16} \,{\text{cm}}^{ - 3} \,{\text{s}}^{ - 1} } \right). \\ \end{aligned}$$

Fig. 8

The electron density (1) and average electron energy (2) as a pressure function

At the conditions of study [5, 6] the dissociation rates by electron impact and via N₂(A) collisions were 8.8 × 10¹⁸ and 8.6 × 10¹⁹ cm⁻³ s⁻¹, respectively. In spite of high value of temperature the rate of thermal dissociation was negligible (6.6 × 10¹⁷ cm⁻³ s⁻¹).

The difference in vibrational temperatures is conditioned with the following reasons. The excitation frequencies of vibrational levels with the electron impact change slightly. But higher temperatures result in the increase in both the rate constants of V–T and V–V exchange. However, V–T rate constants are increased essentially more than V–V ones. According to [24] the V–V rate constant is $K_{10}^{01} = 4.54 \cdot 10^{ - 10} \exp \left( { - 23.99 \times T^{ - 0.14} } \right)$ and V–T rate constant is K ₁₀ = 4.15 × 10⁻²⁹exp(2.303 × T ^0.357). It gives K ₁₀ = 1.7 × 10⁻¹⁵ cm⁻³ s⁻¹ at 1500 K and K ₁₀ = 1.1 × 10⁻¹¹ cm⁻³ s⁻¹ at 3000 K. For the $K_{10}^{01}$ values, we obtain 8.2 × 10⁻¹⁴ and 1.8 × 10⁻¹³ cm⁻³ s⁻¹ for the same temperature. The predominance of V–T exchange over V–V one leads to equalizing the gas temperature and the vibrational one. Vibrational degrees of freedoms are practically in equilibrium with translation ones.

The results of vibrational distributions calculations are shown in Fig. 9. It is clearly seen that the distributions are not equilibrium ones. But for lower levels, distributions can be approximated by Boltzmann’s equation. Therefore, the suppositions, which were used for the derivation of Eqs. (14)–(18) are valid. The sharp bend at V = 12 reflects the action of the reaction N₂(X,V > 12) + O(³P) → NO + N [44]. At low V values the V–V exchange is predominant. It provides the decrease in population of vibrational levels with V increase. But V–T rate constants rise with V faster than V–V ones. And at V > 12 the V–T processes start to dominate forming the characteristic “|plateau”. It is necessary to point out that the data on vibrational temperatures obtained by two different methods (from the solution of vibrational kinetic equations and from the bands intensities using Eqs. (1)–(5) agree quite well. And the vibrational temperatures of N₂ (C³П_u) state can be used for estimation of vibrational temperatures of N₂ ground state. Such simple measurements of bands intensities will allow taking into account the second kind collisions of electrons with N₂(X) vibrational excited molecules at EEDF calculations. Our data represented in Fig. 10 show that it is necessary to do. The super-elastic collisions influence very strongly the high energy part of EEDF and, as the result, the rate constants of electron excitation processes with the high threshold energies.

Fig. 9

The normalized distribution of N₂(X) molecules on vibration levels, 1 1 bar; 2 0.1 bar

Fig. 10

Calculated EEDF. 1, 3 at the pressure of 1 bar. 2, 4 at the pressure of 0.1 bar. 1, 2 second kind collisions with vibration excited N₂(X) did not take into account. 3, 4 second kind collisions with vibration excited N₂(X) were taken into account

The N₂ vibrational temperatures obtained in [4, 13] for air plasma of atmospheric pressure were 1000 K less than in given study. Calculations showed that the temperature decrease is not connected with the presence of O₂ molecules because the rate constants of V–T exchange for N₂–N₂ and N₂–O₂ collisions are close. The main reason is the decrease in the excitation frequency by electron impact due to the difference in electron drift velocities. For N₂ discharge the electron density was 7.6 × 10¹² cm⁻³ whereas for air discharge—2.5 × 10¹² cm⁻³.

The calculation was very sensitive to water content. The increase in water mole fraction leads to the decrease in calculated band intensities and to the dropping effective vibrational temperatures of N₂(X). The momentum transfer cross-section for H₂O is higher than for N₂ by a two order of magnitude. It provides the decrease in the EEDF “tail” and, as the result, in the essential dropping rate constants of electron impact processes with the high threshold energy. Such influence of water content on electron kinetic parameters is not specific feature of N₂ plasma. The same situation takes place for oxygen plasma as well [45]. The vibrational quantum of N₂(X), 2359 cm⁻¹, is less than for H₂O (010) mode (1595 cm⁻¹). The rate constant of N₂ V–T exchange on H₂O is higher than for N₂–N₂ exchange by a factor of 34 at 1500 K. The rate constant for V–V process N₂(X,V = 1) + H₂O(000) → N₂(X,V = 0) + H₂O(010) is higher than for N₂(X,V = 1) + N₂(X,V = 0) → N₂(X,V = 0) + (X,V = 1) by a factor of 25. It gives the decrease in the population of N₂(X) vibrational levels under water molecule content growth. In turn, this decrease leads to the decrease in the EEDF “tail” over the collisions of the second kind.

Conclusion

In the present study, the DC discharge in N₂ was examined in a pressure range of 0.1–1 bar at the discharge current of 40 mA. The changes in the gas temperatures, electric field strengths, cathode voltage drop, intensities of some N₂ bands, and vibrational temperatures of N₂(C³Π_u) were measured. On the base of these data, the model of discharge was developed. The model included the joint solution of Boltzmann equation, equations of vibrational kinetics and equations of chemical kinetics. Calculations on that model agree with the measured bands intensities and vibrational temperatures. In addition, the proposed model explains the results of other studies. The N₂(X) vibrational molecules were shown to influence strongly the EEDF over the super elastic collision. The main species of plasma were H₂O, OH, H₂O₂, O(³P) and HO₂.