1 Introduction

The analysis of nonlinear events that arise in a range of models across many domains has made nonlinear partial differential equations (\(\textrm{NLPDEs}\)) an indispensable tool. In a wide range of scientific domains, such as dynamics, physics, geochemistry, fluid mechanics, geophysics, plasma physics, optical fibers, and many more, the \(\textrm{NLPDEs}\) are crucial in characterizing the physical behavior of actual objects and dynamical processes. In today’s cutting-edge scientific period, nonlinear phenomena are one of the most exciting subjects for analysts, because of their significant role in the knowledge of the actual aspects of the systems, finding the exact or analytical solutions has been a research area of interest Rehman et al. (2021, 2022). It has become increasingly vital for academics to find exact answers to challenging algebraic computations using efficient computing methods. Wave theory in mathematical physics has a special place for determining the precise answers Xu and Pruess (2001). These \(\textrm{NLPDEs}\) solutions provide improved support for the physical structures. To acquire the precise solution for nonlinear physical models, several robust and efficient techniques Rehman et al. (2023); Zulfiqar et al. (2022), were established, and these techniques are the Hirota bilinear technique Li et al. (2023), the F-expansion technique Sumantha and Suresha (2023), the sinh-Gordon function technique Wang (2023), the Darboux transformation technique Almusawa et al. (2021), new \(\phi ^{6}\)-model expansion approach Shahzad et al. (2023), the modified extended tanh-function technique Ghanbari and Kuo (2019), Boulaaras et al. (2023), the sin-cosine technique Fahad et al. (2023) and several others. More recently, several approaches have also been considered for various lump solutions Ghanbari (2019), Rehman et al. (2023). The modified Sardar sub-equation approach Ghanbari and Gómez-Aguilar (2019); Rehman et al. (2022) is a relatively new mathematical method, that has been applied to a range of \(\textrm{NLPDEs}\). Below is a summary of some of the most significant works that have used this approach: Using the modified Sardar sub-equation technique, wave solutions for the doubly dispersive equation are found by Rashida et al. Rasool et al. (2023), exploration of novel solitons in photonic media with more complex dispersive and nonlinear properties. This work investigates the innovative soliton solution and dynamical phase portrait analysis of (1+1)-dimensional \(\textrm{NLPSM}\) using the modified Sardar sub-equation approach and bifurcation analysis Rehman et al. (2022, 2023), respectively. The authors in Maghsoudi-Khouzani and Kurt (2024), discuss the numerical techniques. The authors in Kurt and Bektas (2023); Yalçnkaya et al. (2022); Özkan and Ali (2022); Durur et al. (2020); Tasbozan et al. (2019), study the analytical and numerical techniques and employed these techniques to NLPDEs to acquire multiple types of soliton solutions. Extensive research on the \(\textrm{NLPSM}\) has yielded important theoretical and experimental insights into the behavior of nonlinear waves in a variety of physical systems. Among other applications, the \(\textrm{NLPSM}\) has been used to study the behavior of plasma waves in fusion reactors and the dynamics of optical pulses in fiber optic communications. Investigations have also been conducted on soliton in the \(\textrm{NLPSM}\), which has important applications in optical fiber communications and other fields. In a nonlocal \(\textrm{NLPSM}\), the dynamics of dark solitons were investigated by Ozisik (2022); Turbiner (2016). They found that it would be possible to use the dark solitons to create long-lasting oscillations in the wave field, which might be useful for information processing and storage.

The main objective of the article is to find the novel soliton solutions of the given below (1+1)-dimensional nonlinear perturbed Schrödinger model Tariq et al. (2022), by using a modified Sardar sub-equation approach.

$$\begin{aligned} \psi _4 \frac{\partial ^2\mathcal {B}}{\partial x\, \partial x}+i \frac{\partial \mathcal {B}}{\partial t}-{i \left( \psi _3 \frac{\partial \mathcal {B}}{\partial x}-\psi _2 \left( \mathcal {B} \frac{\partial |\mathcal {B}|^2}{\partial x}\right) -\psi _1 \mathcal {B}\frac{\partial |\mathcal {B}|^2}{\partial x}\right) +\psi \mathcal {B}|\mathcal {B}|^2=0}, \end{aligned}$$
(1)

where i represents the imaginary unit, \(\mathcal {B}\) represents the amplitude envelope, (x) is spatial terms and t is temporal term, \(\psi ,~\psi _1,~\psi _2,~\psi _3\) and \(\psi _4\) are real constant. In many physical systems, such as optics, plasma physics, Bose-Einstein condensates, and water waves, the dynamics of nonlinear waves are represented by the (1+1)-dimensional \(\textrm{NLPSM}\). The (1+1)-dimensional \(\textrm{NLPSM}\) is used to describe nonlinear wave propagation among other scientific phenomena. A few particular uses are as follows. The model is applied to the study of light behavior in planar waveguides and nonlinear optical fibers, where nonlinear effects are important. It behaves nonlinearly in the domain of ultracold atomic gases, represented by \(\textrm{NLPSM}\), including perturbed versions such as the \(\textrm{NLPSM}\). The model aids in the comprehension of soliton dynamics, in which solitons are self-reinforcing lone waves that continue to propagate at the same speed and form. It can be used to examine how wave functions behave under perturbations in a single spatial dimension in quantum systems. Based on the observation that many physical systems exhibit nonlinear behavior, which results in complex and frequently unanticipated events emerging from interactions among system components, Eq. (1) is included. This paper, supported by earlier studies, seeks to provide common, practical, and widely compatible solutions for the model, advancing a better comprehension of the fundamental ideas. The paper’s following sections are arranged as follows: Presented is the mathematical analysis in Sect. 2. In Sect. 3, the model described in Eq. (1) is applied, and figures and solutions are produced using the \(\textrm{MSSEA}\) approach. Section 4 provides a full explanation of the bifurcation analysis, and Sec. 5 includes the results and comments. A summary of the study’s conclusions and next steps is provided in Sect. 6.

2 General description of modified Sardar sub-equation approach

This approach has been successfully used for the solution of \(\textrm{NLPDEs}\) in mathematics and science several times. Let’s assume the general form of \(\textrm{NLPDEs}\):

$$\begin{aligned} \mathcal {K}(\mathcal {B},~\mathcal {B}_x,~\mathcal {B}_t,~\mathcal {B}_{xx},~\mathcal {B}_{xt},...)=0. \end{aligned}$$
(2)

Step-1. Apply the wave transformation

$$\begin{aligned} \mathcal {B}={\mathcal {R}(\xi )e^{i \phi }}, \quad \quad \xi =x-\gamma t \quad \quad \phi =\mu _2 t-\mu _1 x, \end{aligned}$$
(3)

into Eq. (2), the nonlinear ordinary differential equations \((\textrm{NLODEs})\) is obtained as,

$$\begin{aligned} \mathcal {K}(\mathcal {R},~\mathcal {R}^{'},~\mathcal {R}^{''},...)=0. \end{aligned}$$
(4)

Step 2. The given assertion, using the given technique, clarifies the general solution for Eq. (4).

$$\begin{aligned} \mathcal {R} (\xi )=\ell _{0}+\sum _{i=1}^{J}\ell _{i}U^{i}(\xi ),~~~~~~~~~\ell _{i} \ne ~0, \end{aligned}$$
(5)

where \(\mathcal {R}=\mathcal {R}(\xi )\), and \(\ell _i\) is constant which assures

$$\begin{aligned} U(\xi )'=\sqrt{\delta _0+\delta _2 U(\xi )^4+\delta _1 U(\xi )^2}, \end{aligned}$$
(6)

where \(\delta _0\ne 1\), \(\delta _1\) and \(\delta _2\ne 0\) are integers. Calculating the constants \(\ell _{0}\) and \(\ell _{1}\) and additionally, it is invertible for \(\ell _{i}\) to be zero. Determined the value of J using the balance principle. Following are the Clusters to Eq. (6) satisfying the Eq. (6) with q is integration constant. Cluster-1: If \(\delta _0=0,~\delta _1>0~ \text {and}~ \delta _2 ~\ne 0\), we get

$$\begin{aligned} U_1(\xi )=\sqrt{-\frac{\delta _1}{\delta _2}} \text {sech}\Bigg (\sqrt{\delta _1} (\xi +q)\Bigg ),\end{aligned}$$
(7)
$$\begin{aligned} U_2(\xi )=\sqrt{{{\frac{\delta _1}{\delta _2}}}} \text {csch}\Bigg (\sqrt{\delta _1} (\xi +q)\Bigg ). \end{aligned}$$
(8)

Cluster-2:

For constants \(k_{1}~\text {and}~k_{2}\), If \(\delta _0=0,~\delta _1>0\) and \(\delta _2=+4 k_1 k_2\), we get

$$\begin{aligned} U_3(\xi )=\frac{4 k_1 \sqrt{\delta _1}}{\Bigg (4 k_1^2-\delta _2\Bigg ) \sinh \Bigg (\sqrt{\delta _1} (\xi +q)\Bigg )+\Bigg (4 k_1^2-\delta _2\Bigg ) \cosh \Bigg (\sqrt{\delta _1} (\xi +q)\Bigg )}. \end{aligned}$$
(9)

Cluster-3:

For constants \(E_{1}~\text {and}~E_{2}\), If \(\delta _0=\frac{\delta _1^2}{4 \delta _2},\delta _1<0 ~\text {and}~ \delta _2>0\), we get

$$\begin{aligned} U_4(\xi )=\sqrt{-\frac{\delta _1}{2 \delta _2}} \tanh \Bigg (\sqrt{-\frac{\delta _1}{2}} (\xi +q)\Bigg ), \end{aligned}$$
(10)
$$\begin{aligned} U_5(\xi )=\sqrt{-\frac{\delta _1}{2 \delta _2}} \coth \Bigg (\sqrt{-\frac{\delta _1}{2}} (\xi +q)\Bigg ),\end{aligned}$$
(11)
$$\begin{aligned} U_6(\xi )=\sqrt{-\frac{\delta _1}{2 \delta _2}} \Bigg (\tanh \Bigg (\sqrt{-\frac{\delta _1}{2}} (\xi +q)\Bigg )+i \text {sech}\Bigg (\sqrt{-2 \delta _1} (\xi +q)\Bigg )\Bigg ),\end{aligned}$$
(12)
$$\begin{aligned} U_7(\xi )=\sqrt{-\frac{\delta _1}{8 \delta _2}} \Bigg (\tanh \Bigg (\sqrt{-\frac{\delta _1}{8}} (\xi +q)\Bigg )+\coth \Bigg (\sqrt{-\frac{\delta _1}{8}} (\xi +q)\Bigg )\Bigg ),\end{aligned}$$
(13)
$$\begin{aligned} U_8(\xi )=\frac{\sqrt{-\frac{\delta _1}{2 \delta _2}} \Bigg (\sqrt{{E}_1^2+{E}_2^2}-{E}_1 \cosh \Bigg (\sqrt{-2 \delta _1} (\xi +q)\Bigg )\Bigg )}{{E}_1 \sinh \Bigg (\sqrt{-2 \delta _1} (\xi +q)\Bigg )+{E}_2},\end{aligned}$$
(14)
$$\begin{aligned} U_9(\xi )=\frac{\sqrt{-\frac{\delta _1}{2 \delta _2}} \cosh \Bigg (\sqrt{-2 \delta _1} (\xi +q)\Bigg )}{\sinh \Bigg (\sqrt{-2 \delta _1} (\xi +q)\Bigg )+i}. \end{aligned}$$
(15)

Cluster-4:

If \(\delta _0=0,~\delta _1<0~\text {and}~\delta _2\ne 0\), we get

$$\begin{aligned} U_{10}(\xi )=\sqrt{-\frac{\delta _1}{\delta _2}} \sec \Bigg (\sqrt{-\delta _1} (\xi +q)\Bigg ),\end{aligned}$$
(16)
$$\begin{aligned} U_{11}(\xi )=\sqrt{-\frac{\delta _1}{\delta _2}} \csc \Bigg (\sqrt{-\delta _1} (\xi +q)\Bigg ). \end{aligned}$$
(17)

Cluster-5:

If \(\delta _0=\frac{\delta _1^2}{4 \delta _2},~\delta _1>0\) and \(\delta _2>0\) and  \(E_1^2-E_2^2>0\), we get

$$\begin{aligned} U_{12}(\xi )=\sqrt{\frac{\delta _1}{2 \delta _2}} \tan \Bigg (\sqrt{\frac{\delta _1}{2}} (\xi +q)\Bigg ),\end{aligned}$$
(18)
$$\begin{aligned} U_{13}(\xi )=-\sqrt{\frac{\delta _1}{2 \delta _2}} \cot \Bigg (\sqrt{\frac{\delta _1}{2}} (\xi +q)\Bigg ),\end{aligned}$$
(19)
$$\begin{aligned} U_{14}(\xi )=-\sqrt{\frac{\delta _1}{2\delta _2}} \Bigg (\tan \Bigg (\sqrt{2 \delta _1} (\xi +q)\Bigg )-\sec \Bigg (\sqrt{2 \delta _1} (\xi +q)\Bigg )\Bigg ),\end{aligned}$$
(20)
$$\begin{aligned} U_{15}(\xi )=\sqrt{\frac{\delta _1}{8 \delta _2}} \Bigg (\tan \Bigg (\sqrt{\frac{\delta _1}{8}} (\xi +q)\Bigg )-\cot \Bigg (\sqrt{\frac{\delta _1}{8}} (\xi +q)\Bigg )\Bigg ),\end{aligned}$$
(21)
$$\begin{aligned} U_{16}(\xi )=\frac{\sqrt{\frac{\delta _1}{2 \delta _2}} \Bigg (\sqrt{E_1^2-E_2^2}-E_1 \cos \Bigg (\sqrt{2 \delta _1} (\xi +q)\Bigg )\Bigg )}{E_2+E_1 \sin \Bigg (\sqrt{2 \delta _1} (\xi +q)\Bigg )},\end{aligned}$$
(22)
$$\begin{aligned} U_{17}(\xi )=\frac{\sqrt{\frac{\delta _1}{2 \delta _2}} \cos \Bigg (\sqrt{2 \delta _1} (\xi +q)\Bigg )}{\sin \Bigg (\sqrt{2 \delta _1} (\xi +q)\Bigg )-1}. \end{aligned}$$
(23)

Cluster-6:

If \(\delta _0=0,~\delta _1>0,\) we get

$$\begin{aligned} U_{18}(\xi )=\frac{4 \delta _1 e^{\sqrt{\delta _1} (\xi +q)}}{e^{2 \sqrt{\delta _1} (\xi +q)}-4 \delta _1 \delta _2},\end{aligned}$$
(24)
$$\begin{aligned} U_{19}(\xi )=\frac{4 \delta _1 e^{\sqrt{\delta _1} (\xi +q)}}{1-4 \delta _1 \delta _2 e^{2 \sqrt{\delta _1} (\xi +q)}}. \end{aligned}$$
(25)

Cluster-7:

If \(\delta _0=0,~\delta _1=0~\text {and}~\delta _2>0\), we get

$$\begin{aligned} U_{20}(\xi )=\frac{1}{\sqrt{\delta _2} (\xi +q)},\end{aligned}$$
(26)
$$\begin{aligned} U_{21}(\xi )=\frac{i}{\sqrt{\delta _2} (\xi +q)}. \end{aligned}$$
(27)

Step 3. A polynomial written in terms of the power of \(U(\xi )\) is obtained by combining Eq. (5) with Eq. (1), using Eq. (6), and the second-order derivatives needed for Eq. (4).

Step 4. Using the same powers, collect all of the \(U(\xi )\) coefficients, then set them all to zero. After this procedure, the algebraic system for \(\ell _{0},~ \ell _{n}\)     (\(n=1,2,3,...\)) is obtained.

Step 5. Lastly, use Wolfram Mathematica to solve the algebraic equation systems and get the values of the parameters. The solutions for Eq. (1) are obtained by substituting these values into Eq. (4). Accurate solutions to \(\textrm{NLPDEs}\), such as the (1+1)-dimensional \(\textrm{NLPSM}\), may be obtained with efficiency using the \(\textrm{MSSEA}\).

3 Implementation

For an exact solution, take into consideration using Eq. (1). The corresponding \(\textrm{NLODEs}\) is obtained by replacing an wave transformation Eq. (3) with Eq. (1).

$$\begin{aligned} \mathcal {R}^3(\xi ) \left( \psi -\mu _1 \psi _2\right) +\psi _4 \mathcal {R}''(\xi )-\mathcal {R}(\xi ) \bigg (\mu _1^2 \psi _4+{\mu _2 \psi _1+\mu _1}\bigg )=0, \end{aligned}$$
(28)

where \(\mathcal {R}(\xi )\) is complex valued function, \(\psi ,~\psi _1,~\psi _2,~\psi _3,~\psi _3,~\psi _4,~\mu _1\) are all constants and \(\mu _2\) is wave speed. Using Eq. (5) and the homogeneous balance principle, we determine that \(J=1\) by finding a balance between the terms \(\mathcal {R}^{3}(\xi )\) and \(\mathcal {R}''(\xi )\).

$$\begin{aligned} \mathcal {R}(\xi )=\ell _1 U(\xi )+\ell _0. \end{aligned}$$
(29)

Calculate the derivative Eq. (9). After doubling over and taking into account Eq. (6), we obtain

$$\begin{aligned} \mathcal {R}''(\xi )=\ell _1 U(\xi ) \left( \delta _1+2 \delta _2 U(\xi )^2\right) . \end{aligned}$$
(30)

A polynomial to the power of \(U (\xi )\) may be obtained by inserting Eqs. (9) and (10) into Eq. (7). After gathering all the coefficients with identical powers of the \(U (\xi )\), set all of the coefficients to zero. The resulting algebraic equation system is as follows for \(\ell _0, ~\ell \delta _1, ~\ell \delta _1 ~ \text {and}~\mu _1\).

$$\begin{aligned} -\mu _1 \psi _2 \ell _0^3-\mu _1 \psi _1 \ell _0-\mu _1^2 \psi _4 \ell _0-\mu _2 \ell _0+\psi \ell _0^3=0\nonumber \\ +\left( \delta _1 \psi _4 \ell _1-3 \mu _1 \psi _2 \ell _1 \ell _0^2-\mu _1 \psi _1 \ell _1-\mu _1^2 \psi _4 \ell _1-\mu _2 \ell _1+3 \psi \ell _1 \ell _0^2\right) =0\nonumber \\ +\left( 3 \psi \ell _0 \ell _1^2-3 \mu _1 \psi _2 \ell _0 \ell _1^2\right) =0\nonumber \\ +\left( 2 \delta _2 \psi _4 \ell _1-\mu _1 \psi _2 \ell _1^3+\psi \ell _1^3\right) =0. \end{aligned}$$
(31)

Following the algebraic system of equations solution, we determined that family 1 is

$$\begin{aligned} \Bigg \{{\delta _0\rightarrow 0},\quad{} & {} {\delta _1}\rightarrow \frac{\sqrt{-\delta _2 \psi _4 \left( \psi _2 \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}+\psi _1\right) +2 \psi \psi _4\right) }}{\sqrt{\psi _2^2 \left( \mu _2-\delta _1 \psi _4\right) +\psi _4 \psi ^2+\psi _1 \psi _2 \psi }}, \nonumber \\{} & {} \quad \mu _1\rightarrow \frac{\sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}-\psi _1}{2 \psi _4}\Bigg \}. \end{aligned}$$
(32)

Use the above family-1 and find the following novel soliton solutions of Eq. (1).

$$\begin{aligned} \mathcal {B}_{1,1}(x,~t)= & {} \frac{\sqrt{\frac{\delta _1}{\delta _2}} \sqrt{-\delta _2 \psi _4 \left( \psi _2 \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}+\psi _1\right) +2 \psi \psi _4\right) } \text {sech}\left( \sqrt{\delta _1} (q-\gamma t+x)\right) }{\sqrt{\psi _2^2 \left( \mu _2-\delta _1 \psi _4\right) +\psi _4 \psi ^2+\psi _1 \psi _2 \psi }}\nonumber \\{} & {} \times \exp \left( i \left( \mu _2 t-\frac{x \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}-\psi _1\right) }{2 \psi _4}\right) \right) , \end{aligned}$$
(33)
$$\begin{aligned} \mathcal {B}_{1,2}(x,~t)= & {} \frac{\sqrt{\frac{\delta _1}{\delta _2}} \sqrt{-\delta _2 \psi _4 \left( \psi _2 \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}+\psi _1\right) +2 \psi \psi _4\right) } \text {csch}\left( \sqrt{\delta _1} (q-\gamma t+x)\right) }{\sqrt{\psi _2^2 \left( \mu _2-\delta _1 \psi _4\right) +\psi _4 \psi ^2+\psi _1 \psi _2 \psi }}\nonumber \\{} & {} \times \exp \left( i \left( \mu _2 t-\frac{x \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}-\psi _1\right) }{2 \psi _4}\right) \right) , \end{aligned}$$
(34)
$$\begin{aligned} \mathcal {B}_{1,3}(x,~t)= & {} \frac{4 \sqrt{\delta _1} k_1 \sqrt{-\delta _2 \psi _4 \left( \psi _2 \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}+\psi _1\right) +2 \psi \psi _4\right) } }{\sqrt{\psi _2^2 \left( \mu _2-\delta _1 \psi _4\right) +\psi _4 \psi ^2+\psi _1 \psi _2 \psi } \left( \left( 4 k_1^2-\delta _2\right) \sinh \left( \sqrt{\delta _1} (q-\gamma t+x)\right) \right) } \nonumber \\{} & {} \times \frac{\exp \left( i \left( \mu _2 t-\frac{x \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}-\psi _1\right) }{2 \psi _4}\right) \right) }{+\left( 4 k_1^2-\delta _2\right) \cosh \left( \sqrt{\delta _1} (q-\gamma t+x)\right) }, \end{aligned}$$
(35)
$$\begin{aligned} \mathcal {B}_{1,4}(x,~t)= & {} \frac{\sqrt{-\frac{\delta _1}{\delta _2}} \sqrt{-\delta _2 \psi _4 \left( \psi _2 \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}+\psi _1\right) +2 \psi \psi _4\right) } \tanh \left( \frac{\sqrt{-\delta _1} (q-\gamma t+x)}{\sqrt{2}}\right) }{\sqrt{2} \sqrt{\psi _2^2 \left( \mu _2-\delta _1 \psi _4\right) +\psi _4 \psi ^2+\psi _1 \psi _2 \psi }} \nonumber \\{} & {} \times \exp \left( i \left( \mu _2 t-\frac{x \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}-\psi _1\right) }{2 \psi _4}\right) \right) , \end{aligned}$$
(36)
$$\begin{aligned} \mathcal {B}_{1,5}(x,~t)= & {} \frac{\sqrt{-\frac{\delta _1}{\delta _2}} \sqrt{-\delta _2 \psi _4 \left( \psi _2 \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}+\psi _1\right) +2 \psi \psi _4\right) } \coth \left( \frac{\sqrt{-\delta _1} (q-\gamma t+x)}{\sqrt{2}}\right) }{\sqrt{2} \sqrt{\psi _2^2 \left( \mu _2-\delta _1 \psi _4\right) +\psi _4 \psi ^2+\psi _1 \psi _2 \psi }} \nonumber \\{} & {} \times \exp \left( i \left( \mu _2 t-\frac{x \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}-\psi _1\right) }{2 \psi _4}\right) \right) , \end{aligned}$$
(37)
$$\begin{aligned} \mathcal {B}_{1,6}(x,~t)= & {} \frac{\sqrt{-\frac{\delta _1}{\delta _2}} \sqrt{-\delta _2 \psi _4 \left( \psi _2 \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}+\psi _1\right) +2 \psi \psi _4\right) } \Bigg (\left( \tanh \left( \sqrt{2} \sqrt{-\delta _1} (q-\gamma t+x)\right) \right) }{\sqrt{2} \sqrt{\psi _2^2 \left( \mu _2-\delta _1 \psi _4\right) +\psi _4 \psi ^2+\psi _1 \psi _2 \psi }} \nonumber \\{} & {} +i \text {sech}\left( \sqrt{2} \sqrt{-\delta _1} (q-\gamma t+x)\right) \Bigg )\times \exp \left( i \left( \mu _2 t-\frac{x \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}-\psi _1\right) }{2 \psi _4}\right) \right) , \end{aligned}$$
(38)
$$\begin{aligned} \mathcal {B}_{1,7}(x,~t)= & {} \frac{\exp \left( i \left( \mu _2 t-\frac{x \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}-\psi _1\right) }{2 \psi _4}\right) \right) \left( \tanh \left( \frac{\sqrt{-\delta _1} (q-\gamma t+x)}{2 \sqrt{2}}\right) +i \coth \left( \frac{\sqrt{-\delta _1} (q-\gamma t+x)}{2 \sqrt{2}}\right) \right) }{2 \sqrt{2} \sqrt{\psi _2^2 \left( \mu _2-\delta _1 \psi _4\right) +\psi _4 \psi ^2+\psi _1 \psi _2 \psi }} \nonumber \\{} & {} \times \sqrt{-\frac{\delta _1}{\delta _2}} \sqrt{-\delta _2 \psi _4 \left( \psi _2 \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}+\psi _1\right) +2 \psi \psi _4\right) }, \end{aligned}$$
(39)
$$\begin{aligned} \mathcal {B}_{1,8}(x,~t)= & {} \frac{ \exp \left( i \left( \mu _2 t-\frac{x \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}-\psi _1\right) }{2 \psi _4}\right) \right) \left( \sqrt{{E}_1^2+{E}_2^2}-{E}_1 \cosh \left( \sqrt{2} \sqrt{-\delta _1} (q-\gamma t+x)\right) \right) }{\sqrt{2} \sqrt{\psi _2^2 \left( \mu _2-\delta _1 \psi _4\right) +\psi _4 \psi ^2+\psi _1 \psi _2 \psi } \left( {E}_1 \sinh \left( \sqrt{2} \sqrt{-\delta _1} (q-\gamma t+x)\right) +{E}_2\right) } \nonumber \\{} & {} \times \sqrt{-\frac{\delta _1}{\delta _2}} \sqrt{-\delta _2 \psi _4 \left( \psi _2 \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}+\psi _1\right) +2 \psi \psi _4\right) }, \end{aligned}$$
(40)
$$\begin{aligned} \mathcal {B}_{1,9}(x,~t)= & {} \frac{\exp \left( i \left( \mu _2 t-\frac{x \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}-\psi _1\right) }{2 \psi _4}\right) \right) \cosh \left( \sqrt{2} \sqrt{-\delta _1} (q-\gamma t+x)\right) }{\sqrt{2} \sqrt{\psi _2^2 \left( \mu _2-\delta _1 \psi _4\right) +\psi _4 \psi ^2+\psi _1 \psi _2 \psi } \left( \sinh \left( \sqrt{2} \sqrt{-\delta _1} (q-\gamma t+x)\right) +i\right) } \nonumber \\{} & {} \times \sqrt{-\frac{\delta _1}{\delta _2}} \sqrt{-\delta _2 \psi _4 \left( \psi _2 \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}+\psi _1\right) +2 \psi \psi _4\right) }, \end{aligned}$$
(41)
$$\begin{aligned} \mathcal {B}_{1,10}(x,~t)= & {} \frac{\exp \left( i \left( \mu _2 t-\frac{x \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}-\psi _1\right) }{2 \psi _4}\right) \right) \sec \left( \sqrt{-\delta _1} (q-\gamma t+x)\right) }{\sqrt{\psi _2^2 \left( \mu _2-\delta _1 \psi _4\right) +\psi _4 \psi ^2+\psi _1 \psi _2 \psi }} \nonumber \\{} & {} \times \sqrt{-\frac{\delta _1}{\delta _2}} \sqrt{-\delta _2 \psi _4 \left( \psi _2 \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}+\psi _1\right) +2 \psi \psi _4\right) }, \end{aligned}$$
(42)
$$\begin{aligned} \mathcal {B}_{1,11}(x,~t)= & {} \frac{ \exp \left( i \left( \mu _2 t-\frac{x \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}-\psi _1\right) }{2 \psi _4}\right) \right) \csc \left( \sqrt{-\delta _1} (q-\gamma t+x)\right) }{\sqrt{\psi _2^2 \left( \mu _2-\delta _1 \psi _4\right) +\psi _4 \psi ^2+\psi _1 \psi _2 \psi }} \nonumber \\{} & {} \times \sqrt{-\frac{\delta _1}{\delta _2}} \sqrt{-\delta _2 \psi _4 \left( \psi _2 \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}+\psi _1\right) +2 \psi \psi _4\right) }, \end{aligned}$$
(43)
$$\begin{aligned} \mathcal {B}_{1,12}(x,~t)= & {} \frac{ \exp \left( i \left( \mu _2 t-\frac{x \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}-\psi _1\right) }{2 \psi _4}\right) \right) \tan \left( \frac{\sqrt{\delta _1} (q-\gamma t+x)}{\sqrt{2}}\right) }{\sqrt{2} \sqrt{\psi _2^2 \left( \mu _2-\delta _1 \psi _4\right) +\psi _4 \psi ^2+\psi _1 \psi _2 \psi }} \nonumber \\{} & {} \times \sqrt{\frac{\delta _1}{\delta _2}} \sqrt{-\delta _2 \psi _4 \left( \psi _2 \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}+\psi _1\right) +2 \psi \psi _4\right) }, \end{aligned}$$
(44)
$$\begin{aligned} \mathcal {B}_{1,13}(x,~t)= & {} \frac{ \exp \left( i \left( \mu _2 t-\frac{x \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}-\psi _1\right) }{2 \psi _4}\right) \right) \cot \left( \frac{\sqrt{\delta _1} (q-\gamma t+x)}{\sqrt{2}}\right) }{\sqrt{2} \sqrt{\psi _2^2 \left( \mu _2-\delta _1 \psi _4\right) +\psi _4 \psi ^2+\psi _1 \psi _2 \psi }} \nonumber \\{} & {} \times \sqrt{\frac{\delta _1}{\delta _2}} \sqrt{-\delta _2 \psi _4 \left( \psi _2 \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}+\psi _1\right) +2 \psi \psi _4\right) }, \end{aligned}$$
(45)
$$\begin{aligned} \mathcal {B}_{1,14}(x,~t)= & {} -\frac{\exp \left( i \left( \mu _2 t-\frac{x \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}-\psi _1\right) }{2 \psi _4}\right) \right) \Bigg (\tan \left( \sqrt{2} \sqrt{\delta _1} (q-\gamma t+x)\right) \Bigg )}{\sqrt{2} \sqrt{\psi _2^2 \left( \mu _2-\delta _1 \psi _4\right) +\psi _4 \psi ^2+\psi _1 \psi _2 \psi }} \nonumber \\{} & {} -\sec \left( \sqrt{2} \sqrt{\delta _1} (q-\gamma t+x)\right) \nonumber \\{} & {} \times \sqrt{\frac{\delta _1}{\delta _2}} \sqrt{-\delta _2 \psi _4 \left( \psi _2 \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}+\psi _1\right) +2 \psi \psi _4\right) }, \end{aligned}$$
(46)
$$\begin{aligned} \mathcal {B}_{1,15}(x,~t)= & {} \frac{\exp \left( i \left( \mu _2 t-\frac{x \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}-\psi _1\right) }{2 \psi _4}\right) \right) \Bigg (\tan \left( \frac{\sqrt{\delta _1} (q-\gamma t+x)}{2 \sqrt{2}}\right) \Bigg )}{2 \sqrt{2} \sqrt{\psi _2^2 \left( \mu _2-\delta _1 \psi _4\right) +\psi _4 \psi ^2+\psi _1 \psi _2 \psi }} \nonumber \\{} & {} -\cot \left( \frac{\sqrt{\delta _1} (q-\gamma t+x)}{2 \sqrt{2}}\right) \nonumber \\{} & {} \times \sqrt{\frac{\delta _1}{\delta _2}} \sqrt{-\delta _2 \psi _4 \left( \psi _2 \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}+\psi _1\right) +2 \psi \psi _4\right) }, \end{aligned}$$
(47)
$$\begin{aligned} \mathcal {B}_{1,16}(x,~t)= & {} \frac{\exp \left( i \left( \mu _2 t-\frac{x \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}-\psi _1\right) }{2 \psi _4}\right) \right) \left( \sqrt{{E}_1^2-{E}_2^2}-{E}_1 \cos \left( \sqrt{2} \sqrt{\delta _1} (q-\gamma t+x)\right) \right) }{\sqrt{2} \sqrt{\psi _2^2 \left( \mu _2-\delta _1 \psi _4\right) +\psi _4 \psi ^2+\psi _1 \psi _2 \psi } \left( {E}_1 \sin \left( \sqrt{2} \sqrt{\delta _1} (q-\gamma t+x)\right) +{E}_2\right) } \nonumber \\{} & {} \times \sqrt{\frac{\delta _1}{\delta _2}} \sqrt{-\delta _2 \psi _4 \left( \psi _2 \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}+\psi _1\right) +2 \psi \psi _4\right) }, \end{aligned}$$
(48)
$$\begin{aligned} \mathcal {B}_{1,17}(x,~t)= & {} \frac{ \exp \left( i \left( \mu _2 t-\frac{x \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}-\psi _1\right) }{2 \psi _4}\right) \right) \cot \left( \sqrt{2} \sqrt{\delta _1} (q-\gamma t+x)\right) }{\sqrt{2} \sqrt{\psi _2^2 \left( \mu _2-\delta _1 \psi _4\right) +\psi _4 \psi ^2+\psi _1 \psi _2 \psi }} \nonumber \\{} & {} \times \sqrt{\frac{\delta _1}{\delta _2}} \sqrt{-\delta _2 \psi _4 \left( \psi _2 \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}+\psi _1\right) +2 \psi \psi _4\right) }, \end{aligned}$$
(49)
$$\begin{aligned} \mathcal {B}_{1,18}(x,~t)= & {} \frac{\exp \left( \sqrt{\delta _1} (q-\gamma t+x)+i \left( \mu _2 t-\frac{x \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}-\psi _1\right) }{2 \psi _4}\right) \right) }{\sqrt{\psi _2^2 \left( \mu _2-\delta _1 \psi _4\right) +\psi _4 \psi ^2+\psi _1 \psi _2 \psi } \left( e^{2 \sqrt{\delta _1} (q-\gamma t+x)}-4 \delta _1 \delta _2\right) } \nonumber \\{} & {} \times 4 \delta _1 \sqrt{-\delta _2 \psi _4 \left( \psi _2 \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}+\psi _1\right) +2 \psi \psi _4\right) }, \end{aligned}$$
(50)
$$\begin{aligned} \mathcal {B}_{1,19}(x,~t)= & {} \frac{ \exp \left( \sqrt{\delta _1} (q-\gamma t+x)+i \left( \mu _2 t-\frac{x \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}-\psi _1\right) }{2 \psi _4}\right) \right) }{\sqrt{\psi _2^2 \left( \mu _2-\delta _1 \psi _4\right) +\psi _4 \psi ^2+\psi _1 \psi _2 \psi } \left( 1-4 \delta _1 \delta _2 e^{2 \sqrt{\delta _1} (q-\gamma t+x)}\right) } \nonumber \\{} & {} \times 4 \delta _1 \sqrt{-\delta _2 \psi _4 \left( \psi _2 \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}+\psi _1\right) +2 \psi \psi _4\right) }, \end{aligned}$$
(51)
$$\begin{aligned} \mathcal {B}_{1,20}(x,~t)= & {} \frac{\sqrt{-\delta _2 \psi _4 \left( \psi _2 \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}+\psi _1\right) +2 \psi \psi _4\right) }}{\sqrt{\delta _2} \sqrt{\psi _2^2 \left( \mu _2-\delta _1 \psi _4\right) +\psi _4 \psi ^2+\psi _1 \psi _2 \psi } (q-\gamma t+x)} \nonumber \\{} & {} \times \exp \left( i \left( \mu _2 t-\frac{x \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}-\psi _1\right) }{2 \psi _4}\right) \right) , \end{aligned}$$
(52)
$$\begin{aligned} \mathcal {B}_{1,21}(x,~t)= & {} \frac{i \sqrt{-\delta _2 \psi _4 \left( \psi _2 \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}+\psi _1\right) +2 \psi \psi _4\right) } }{\sqrt{-\delta _2} \sqrt{\psi _2^2 \left( \mu _2-\delta _1 \psi _4\right) +\psi _4 \psi ^2+\psi _1 \psi _2 \psi } (q-\gamma t+x)} \nonumber \\{} & {} \times \exp \left( i \left( \mu _2 t-\frac{x \left( \sqrt{4 \psi _4 \left( \delta _1 \psi _4-\mu _2\right) +\psi _1^2}-\psi _1\right) }{2 \psi _4}\right) \right) . \end{aligned}$$
(53)

4 Bifurcation analysis

We shall now analyze the phase portraits of bifurcation analysis using Eq. (28). Equation (28) yields the first-order differential equations, from which the dynamical system is obtained as below:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{d \mathcal {R}}{d \xi }=W =C_1, &{}\\ \frac{dW}{d \xi }=H_1 \mathcal {R}-H_2 \mathcal {R}^3=C_2, \end{array}\right. } \end{aligned}$$
(54)

where \(H_1=\frac{\psi _4 \mu _1^2 +\mu _1 \psi _1 +\mu _2}{\psi _4}\) and \(H_2=\frac{\psi -\psi _2 \mu _1}{\psi _4}\).

Case (i): \(H_1<0\) and \(H_2<0\). By using \(\psi _4~=2, \psi _1~~=-0.7,~ \psi _2~=0.7\) and \(\mu _1~=0.7\), the equilibrium points \(q_{1}=(0, 0),~q_{2} = (\sqrt{2}, 0),~q_{3} =(-\sqrt{2}, 0)\) have been retrieved from system (54) shown in Fig. 7. It is observed, by the phase portrait, that \(H_{2}\) shows center points, whereas \(H_{1}\) is a cuspidal point.

Case (ii): \(H_1>0\) and \(H_2<0\). By using \(\psi _4~=1.4,~\psi _1 ~=0.7, \psi _2~~=0.7\) and \(\mu _1~=0.7\), there exists only one real equilibrium point \(H_{1}=(0, 0)\), which has been obtained from system (54) and shown in Fig. 7. It is observed that \(H_{1}\) is a cuspidal point.

Case (iii): \(H_1>0\) and \(H_2>0\). By using \(\psi _4~=1.2,~\psi _2 ~=-0.7,~\psi _1 ~=-0.7\) and \(\mu _1~=0.7\), there exists only one real equilibrium point \(H_{1}=(0, 0)\), which has been obtained from system (54) and shown in Fig. 7. It is observed that \(H_{1}\) is a saddle point.

Case (iv): \(H_1<0\) and \(H_2>0\). By using \(\psi _4~=1.2,~\psi _2 ~=-0.7,~\psi _1 ~=-0.7\) and \(\mu _1~=0.7\), there exists only one complex equilibrium point \(H_{1}=(0, 0)\), which has been obtained from system (54) and shown in Fig. 7. It is observed that \(H_{1}\) is a center point.

5 Results and discussions

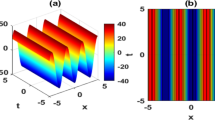
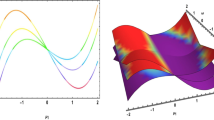
The thorough comparison of the obtained results with the previously appraised result in this section demonstrates the originality of this work. The governing model’s solutions were obtained by utilizing GREFT. This study was modified by our research to examine other techniques. This part’s unique contribution to the research is demonstrated by a detailed contrast of the assessed findings with the previously calculated results. The authors in Tariq et al. (2022), study the (1+1)-dimensional \(\textrm{NLPSM}\), by using different analytical techniques to find exact solutions. Our inquiry synthesized this research to apply more effective techniques. The modified Sardar sub-equation approach and bifurcation analysis to a wide range of fields in mathematics, physics, and engineering. It may provide solutions with physical interpretations and analytic properties. This makes it a helpful tool for understanding the behavior of complex nonlinear systems as well as for drawing new theoretical conclusions and experimental predictions. Comparing our achievements to their findings reveals the uniqueness of our calculated results, which have never been obtained in published literature previously. The evaluation’s findings are fresh and original, and they have the potential to greatly further the field of applied mathematics research. We just wanted to let you know that the obtained solutions may be of tremendous use for future studies of higher-order \(\textrm{NLPDEs}\). This research analyses solutions of the rational type, periodic solutions, dark solutions, and singular solitons. In mathematics, a non-singular solution is one in which there are no singularities anywhere in its domain. This is important because mathematical equations may break down due to singularities. Contour plots represent a 3-dimensional surface by plotting constant z slices, known as contours, on a 2-dimensional plane. These plots display relationships between two independent variables (X and Y) and an outcome (Z), with each contour line representing points of equal value to the outcome variable Z. In contrast, density plots show the distribution of data in a 2-dimensional space, often representing the probability density function of the data. While contour plots focus on displaying contours of equal values, density plots emphasize the distribution of data points and their relative concentrations. Contour plots are particularly useful when drawing in three dimensions is inconvenient, providing a clear visualization of relationships between variables in a 2-dimensional format. In mathematical physics, \(\textrm{NLPSM}\) is used to model and comprehend complicated processes like soliton dynamics. It is essential for simulating the behavior of stable, localized wave packets known as optical solitons. For fiber-optic communication systems to preserve signal integrity over extended distances, these solitons are crucial. \(\textrm{NLPSM}\) plays a role in improving our comprehension of the dynamics of nonlinear wave propagation phenomena in a variety of physical systems, including nonlinear optical fibers and Bose-Einstein condensates. These phenomena include solitary waves and soliton solutions. Applications of the model can be found in quantum physics, namely in the investigation of the behavior of quantum systems under nonlinear interactions and disturbances. On the other hand, density plots are valuable for understanding the density of data points across different regions of the plot. Non-singular solutions are favored since they are precisely specified and allow for accurate computations and forecasts. Non-singular solutions are often associated with wave equations because, in physics, differential equations with non-singular solutions may be used to explain waves. Exact solutions to nonlinear equations can be efficiently found using the modified Sardar-sub equation approach. It offers answers to many different kinds of nonlinear equations, including ones with different nonlinearities. The modified Sardar-sub equation strategy performs competitively when compared to other recent methods, such the Sardar sub-equation approach. The modified Sardar-sub equation method is effective, although it may need intricate mathematical derivations. The Schrödinger equation’s non-singular solution can be utilized to simulate the behavior of particles or wave packets in quantum physics. The (1+1)-dimensional \(\textrm{NLPSM}\) solutions found by the \(\textrm{MSSEA}\) approach may find use in optical fiber communication and plasma physics, among other areas. The paper also draws attention to several problems and unanswered issues in the area, such as the impact of higher-order nonlinear factors, stability analysis, and generalization to different equations. The dynamics of several reported solutions are shown in Figs by selecting the proper parametric values Figs. 1, 2, 3, 4, 5 and 6 as 3-D, 2-D and density plots.

Fig. 1
figure 1

Graphical illustration of bright soliton solution of Eq. (33), by using appropriate parameter values are \(\delta _1=0.7,~\delta _2=0.8,~\delta _0=0,~\psi _1=0.1,~\psi =0.9,~\psi _2=0.3,~\psi _3=0.6,~\psi _4=0.5,~q=0.1,~\mu _1=0.54~\text {and}~\mu _2=0.65\)

Full size image
Fig. 2
figure 2

Graphical illustration of singular soliton solution of Eq. (34), by using appropriate parameter values are \(\delta _1=0.7,~\delta _2=1,~\delta _0=0,~\psi _1=0.1,~\psi =0.9,~\psi _2=0.3,~\psi _3=0.6,~\psi _4=0.5,~q=0.1,~\mu _1=0.54~\text {and}~\mu _2=0.65\)

Full size image
Fig. 3
figure 3

Graphical illustration of hyperbolic soliton solution of Eq. (35), by using appropriate parameter values are \(\delta _1=0.7,~\delta _2=1,~\delta _0=0,~\psi _1=0.1,~\psi =0.9,~\psi _2=0.3,~\psi _3=0.6,~\psi _4=0.5,~q=0.1,~\mu _1=0.54~\text {and}~\mu _2=0.65\)

Full size image
Fig. 4
figure 4

Graphical illustration of dark soliton solution of Eq. (36), by using appropriate parameter values are \(\delta _1=-0.7,~\delta _2=0.8,~\delta _0=0.3,~\psi _1=0.1,~\psi =0.9,~\psi _2=0.3,~\psi _3=0.6,~\psi _4=0.5,~q=0.1,~\mu _1=0.54~\text {and}~\mu _2=0.65\)

Full size image
Fig. 5
figure 5

Graphical illustration of periodic solution of Eq. (42), by using appropriate parameter values are \(\delta _1=0.7,~\delta _2=0.8,~\delta _0=0,~\psi _1=0.1,~\psi =0.9,~\psi _2=0.3,~\psi _3=0.6,~\psi _4=0.5,~q=0.1,~\mu _1=0.54~\text {and}~\mu _2=0.65\)

Full size image
Fig. 6
figure 6

Graphical illustration of rational soliton solution of Eq. (53), by using appropriate parameter values are \(\delta _1=0,~\delta _2=0.8,~\delta _0=0,~\psi _1=0.1,~\psi =0.9,~\psi _2=0.3,~\psi _3=0.6,~\psi _4=0.5,~q=0.1,~\mu _1=0.54~\text {and}~\mu _2=0.65\)

Full size image
Fig. 7
figure 7

Graphical illustration of phase portrait analysis by using appropriate parameter values

Full size image

6 Conclusions

This study discusses optical physical phenomena and emphasizes the value and usefulness of the (1+1)-dimensional \(\textrm{NLPSM}\). Even though the model’s characteristics and behavior have already been thoroughly examined in the literature, our approach offers fresh perspectives. Effective evolution of soliton solutions is achievable. Bifurcation analysis is carried out by the transformation of the governing model into a dynamical system. Numerous diverse industries may benefit from the novel ideas presented in this study. We verified our findings by using Mathematica software to analyze and visually represent several wave patterns with various system properties. Our solutions offer distinctiveness in contrast to traditional methods. The results of this work should spark more conversations in the nonlinear physical sciences. The approach is computationally efficient in finding exact wave solutions. Our suggested approaches might be extended in the future to handle other nonlinear models. The distinct and fascinating solutions found may aid in the understanding of mathematical models of various domains. In the future, these findings will be improved and refined by further study. The soliton’s mean free velocity will be obtained by using soliton perturbation theory, which incorporates perturbation terms and takes into account stochastic perturbation components. The (1+1)-dimensional \(\textrm{NLPSM}\) will also be integrated using a variety of integration methods.