1 Introduction

Nonlinear complex models stand at the forefront of scientific inquiry, providing powerful tools to unravel intricacies in various domains. Nonlinear complex models, characterized by intricate mathematical relationships and nonlinearity, represent a class of mathematical frameworks that capture the complexities inherent in real-world phenomena. Unlike their linear counterparts, these models can describe and simulate intricate behaviors, offering a more nuanced understanding of complex systems. Nonlinear complex models find profound applications in mathematical physics, especially in studying chaotic systems and quantum phenomena [1,2,3,4,5,6,7,8,9,10]. Chaos theory utilizes these models to analyze deterministic systems with chaotic behavior, while in quantum mechanics, nonlinear Schrödinger equations with complex variables model quantum phenomena like entanglement and tunneling. The optical soliton solution of nonlinear complex models holds significant importance in nonlinear optics and communication systems. Optical solitons are stable, localized wave packets that maintain their shape and amplitude while propagating through a nonlinear medium. Considering nonlinear complex models, often described by equations like the nonlinear Schrödinger equation (NLSE), plays a crucial role in defining the balance between dispersive and nonlinear effects, enabling the formation and maintenance of solitons over long distances. This stability is crucial for signal integrity in optical communication systems. The investigation of optical soliton solutions from nonlinear complex models is complicated. Recently there are some method are developed to integrate optical soliton solution of NLCE such as Modified extended tanh-function method [11], Extended MSE technique [12, 13], novel approach [14], transformed rational function [15], two versatile integration architectures [16], \({\varphi }^{6}\)-expansion method and modified generalized exponential rational function method [17], modified extended tanh expansion method[18], New extended direct algebraic method [19], modified Sardar sub-equation method (MSSEM) [20], refined invariant subspace method [21], NMSE technique [22], simplest equation method and NMK method [23], exponential expansion method [24], Sardar subequation method, new Kudryashov's method, and \((1/G,G^{\prime}/G)\) method [25] \(exp (-\phi (\xi ))\)-expansion and NMK schemes [26], improved collocation technique [27], a single- step implicit block method [28], extended tanh expansion method [29], generalized exponential rational function method (GERFM), \((G^{\prime}/G2)-\) expansion function method [30], \((G^{\prime}/G2)\)—expansion function method, the modified direct algebraic method (MDAM), and the generalized Kudryashov method [31, 32], and so on.

Fractional calculus, which deals with derivatives and integrals of non-integer order, holds significance across various fields including physics, engineering, economics, and biology. Its history dates back to the seventeenth century, with mathematicians like Leibniz, Euler, and Laplace pondering over non-integer order differentials. However, it wasn't until the twentieth century that the subject gained momentum, notably through the works of Liouville, Riemann, and Hadamard. Fractional derivatives offer a more nuanced understanding of systems with memory, long-range dependence, and complex dynamics, which classical calculus fails to capture. They find applications in modeling phenomena such as anomalous diffusion, viscoelasticity, and fractional-order control systems. Furthermore, fractional calculus enables a deeper insight into fractals and chaotic systems. Its burgeoning relevance in modern research underscores the necessity of understanding and leveraging its principles to tackle contemporary challenges across diverse scientific disciplines. Recently there are some fractional form are developed such as conformable fraction [33,34,35], Atangana-Baleanu fractional [36], Caputo fractional derivative [37], beta fractional form [37,38,39], truncated M fractional form [40,41,42], and so on.

The nonlinear Schrödinger equation (NLSE) carries over the basic ideas of quantum mechanics to include nonlinear phenomena, which are important in many areas of science and engineering, through condensed matter physics, plasma physics, and optics, A nonlinear partial differential equation describes complex wave functions in nonlinear mediums. Zhakarov and Shabat initially presented NLSE in the 1970 s. It displays intricate dynamics, such as wave collapse and soliton propagation. Bose–Einstein condensates, ultrafast laser dynamics, and optical fiber modeling are among the applications. NLSE's transdisciplinary significance stems from its capacity to elucidate nonlinear wave behavior, hence promoting progress in several scientific and technological domains. It is well known that two forms of the variable coefficient cubic nonlinear equation Schrödinger equation are the most traditionally used. For the anomalous dispersion regime, the variable coefficient cubic nonlinear equation Schrödinger equation [43,44,45,46,47,48] read as:

$$ iD_{M,t}^{g, n} {\text{Q}} + Q_{xx} + \varepsilon \left( t \right)Q|Q|^{2} = 0, $$
(1)

It is well known that the anomalous group velocity dispersion (GVD) gives bright solitons, whereas the normal GVD gives rise to dark solitons, where both models are of wide interest in many applications, particularly in optical communications. The complex function \(Q(x, t)\), with \(x\) as the longitudinal variable parameter and \(t\) acting as the co-moving instant of time. The first term is the evolution term, the second term represents the group velocity dispersion (GVD) term, and the third term accounts for the nonlinearity, which is cubic for the Eq. (1).

The main motivation of this research work is to explain the bifurcation analysis with phase portrait and also explain the stable and unstable conditions. Secondly, in this article, we also integrate NLSE with the help of a unified solver technique and unified techniques (UT). By applying these techniques, the obtained solutions are expressed as, trigonometric, hyperbolic, and rational functions, etc. by using this technique we get 29 analytic solutions. Additionally, the modulation instability spectrum can be expressed utilizing a linear analysis technique, and the modulation instability bands are shown to be influenced by the third-order and group velocity dispersion.

The piece of work has been arranged in the following order: In Sect. 2, we elaborate on the features and properties of the truncated M fractional derivative, unified solver technique, and generalized unified technique. In Sect. 3, Mathematical Analysis of the governing model. In Sect. 4, deals with the application of analytic techniques. In Sect. 5, In Sect. 6, the description of graphs is discussed, and also observed the effect of fractional parameters. In Sect. 7, we analyze the modulation instability of the governing model. Lastly in Sect. 8, summarize the conclusion.

2 Methodology

2.1 Truncated M-fractional derivative

Definition: consider \(\Xi :\left( {0,~\infty } \right) \to \mathbb{R}\) the TMD of \(\upchi \) with order \(\text{n}\) exhibit as:

$${D}_{M,\tau }^{g, n}\Xi \left(\tau \right)=\underset{h\to 0}{\mathit{lim}}\frac{\Xi \left(\tau {H}_{n}\left(h{\tau }^{1-g}\right)\right)-\Xi \left(\tau \right)}{h0S}.; 0<g<1, n>0.$$

Here \({\text{H}}_{\text{n}}\left(.\right)\) is a truncated Mittag–Leffler function of one parameter that defined as [40, 41]:

$${H}_{n}\left(z\right)=\sum_{j=0}^{i}\frac{ {z}^{j}}{\Gamma \left(nj+1\right)}.$$

Characteristics

Suppose \(0<g<1, n>0, l,m\in \mathfrak{R}\) and \(\Xi ,\Theta , g-\) differentiable at a point \(\uptau >0,\), then

  1. (1)

    \({D}_{M,\tau }^{g, n}\left(l\Xi \left(\tau \right)+m\Theta \left(\tau \right)\right)=l{D}_{M,\tau }^{g, n}\Xi \left(\tau \right)+m{D}_{M,\tau }^{g, n}\Theta \left(\tau \right).\)

  2. (2)

    \({D}_{M,\tau }^{g, n}\left(\Xi \left(\tau \right)\Theta \left(\tau \right)\right)=\Xi \left(\tau \right){D}_{M,\tau }^{g, n}\Theta \left(\tau \right)+\Theta \left(\tau \right){D}_{M,\tau }^{g, n}\Xi \left(\tau \right).\)

  3. (3)

    \({D}_{M,\tau }^{g, n}\left(\frac{\Xi \left(\tau \right)}{\Theta \left(\tau \right)}\right)=\frac{\Xi \left(\tau \right){D}_{M,\tau }^{g, n}\Theta \left(\tau \right)+\Theta \left(\tau \right){D}_{M,\tau }^{g, n}\Xi \left(\tau \right)}{{\Theta \left(t\right)}^{2}}.\)

  4. (4)

    \({D}_{M,\tau }^{g, n}\left(\Xi \left(\tau \right)\right)=0\) where \(\Xi \left(\tau \right)=a.\)

  5. (5)

    \({D}_{M,\tau }^{g, n}\Xi \left(\tau \right)=\frac{{\tau }^{1-g}}{\Gamma \left(n+1\right)}\frac{d\Xi \left(\tau \right)}{d\tau }.\)

2.2 Unified solver method

In this subsection, we explored the unified solver technique [38, 39]. For the ordinary differential equations

$$\mathcal{B}{u}^{{\prime}{\prime}}+\mathcal{H}{u}^{3}+\mathfrak{R}u=0.$$
(2)

Here \(\mathcal{B},\mathcal{H},\mathfrak{R}\) are real numbers. The closed-form solution of the model in Eq. (2) are given below:

  1. (1)

    For \(\mathfrak{R}=0\) and \(\frac{\mathcal{H}}{\mathcal{B}}<0\), we get a rational solution

    $$u\left(\varsigma \right)=\pm \sqrt{\frac{-\mathcal{H}}{2\mathcal{B}}}\frac{1}{\varsigma },$$
  2. (2)

    For \(\frac{\mathfrak{R}}{\mathcal{B}}<0\) and \(\frac{\mathfrak{R}}{\mathcal{H}}>0\), we get trigonometric solution

    $$u\left(\varsigma \right)=\pm \sqrt{\frac{\mathfrak{R}}{\mathcal{H}}}tan\left(\sqrt{\frac{-\mathfrak{R}}{2\mathcal{B}}}\varsigma \right),$$
    $$u\left(\varsigma \right)=\pm \sqrt{\frac{\mathfrak{R}}{\mathcal{H}}}cot\left(\sqrt{\frac{-\mathfrak{R}}{2\mathcal{B}}}\varsigma \right),$$
  3. (3)

    For \(\frac{\mathfrak{R}}{\mathcal{B}}>0\) and \(\frac{\mathfrak{R}}{\mathcal{H}}<0\), we get hyperbolic solution

    $$u\left(\varsigma \right)=\pm \sqrt{\frac{-\mathfrak{R}}{\mathcal{H}}}tanh\left(\sqrt{\frac{\mathfrak{R}}{2\mathcal{B}}}\varsigma \right),$$
    $$u\left(\varsigma \right)=\pm \sqrt{-\frac{\mathfrak{R}}{\mathcal{H}}}coth\left(\sqrt{\frac{\mathfrak{R}}{2\mathcal{B}}}\varsigma \right),$$

Remark 01

The unified solver method directly executed analytic solutions of the nonlinear models. Using the unified solver method we can 5 analytic solutions that are trigonometric, hyperbolic, and rational. But this method works only for the nonlinear models Eq. (2).

2.3 Unified method

In this section, we elaborate on the procedure of a unified method to time M-fractional NLEEs. For this purpose, the fractional NLEEs are considered in the following form:

$$\text{H}\left({\mathcal{W}}_{xx},\mathcal{W}{\text{D}}_{\text{M},t}^{\text{g},\text{ n}}\mathcal{W},\varrho {\mathcal{W}}_{x},{\mathcal{W}}_{xxx},{\mathcal{W}}^{\mathcal{o}},.............\right)=0,$$
(3)

where \(\mathcal{W}(\text{x},\text{t})\) is an unaccustomed function.

Now we instigate \( \varsigma = \aleph x - \omega (n + 1)/gt^{g} . \) where \(\mathcal{W}(\text{x},\text{t})=\text{u}(\varsigma ),\) for getting an ODE form of the given nonlinear model. Then we integrate it if it’s possible.

$$ H_{1} \left( {\aleph ^{2} u_{{\varsigma \varsigma }} ,\omega u_{\varsigma } ,\omega uu_{\varsigma } ,u^{\sigma } ,K^{3} u_{{\varsigma \varsigma \varsigma }} ,........} \right) = 0. $$
(4)

Let's attempt to determine the solutions to problem (4) in the following manner:

$$\text{u}(\varsigma )={\mu }_{0}+\sum_{l=-M}^{M}{\mu }_{l}{\left(F\left(\varsigma \right)\right)}^{l},$$
(5)

where \(M\) is a free positive integer and \({\theta }_{i}\) and \({\vartheta }_{i}\) for \((0\le i\le N)\) are discovered afterward.

the solution in Eq. (5) satisfied the following auxiliary differential equation:

$$\frac{d\left(F\left(\varsigma \right)\right)}{d\varsigma }=\chi +{F\left(\varsigma \right)}^{2}.$$
(6)

If we insert the Eq. (5) into the dynamic Eq. (4) with the help of Eq. (6), then the following polynomial of \(F\left(\varsigma \right)\).

$$P\left(F\left(\varsigma \right)\right)={C}_{0}+{C}_{1}{F\left(\varsigma \right)}^{1}+{C}_{2}{F\left(\varsigma \right)}^{2}+{C}_{3}{F\left(\varsigma \right)}^{3}\dots +{C}_{-1}{F\left(\varsigma \right)}^{-1}+{C}_{-2}{F\left(\varsigma \right)}^{-2}+{C}_{-3}{F\left(\varsigma \right)}^{-3}+\dots =0,$$

where \({C}_{i}(-\text{n}\le i\le n)\) are constant coefficient of \({F\left(\varsigma \right)}^{\pm \text{n}}\). Now we set \({C}_{i}=0,i=0,\dots ,n\) and solved these equations to get the non-trivial solutions.

The solutions of Eq. (6) are:

For \(\chi >0,\)

$$ F\left( \varsigma \right) = \left. {\begin{array}{*{20}c} {\frac{{\sqrt {\left( {\Lambda ^{2} - \wp ^{2} } \right)\chi } - \Lambda \sqrt \chi \cos \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right)}}{{\Lambda \sin \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right) + \wp }}} \\ {\frac{{ - \sqrt {\left( {\Lambda ^{2} - \wp ^{2} } \right)\chi } - \Lambda \sqrt \chi \cos \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right)}}{{\Lambda \sin \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right) + \wp }}} \\ {I\sqrt \chi - \frac{{2I\Lambda \sqrt \chi }}{{\Lambda + \cos \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right) - I\sin \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right)}}} \\ { - I\sqrt \chi + \frac{{2\lambda \sqrt \chi }}{{\Lambda + \cos \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right) + I\sin \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right)}}} \\ \end{array} } \right\}. $$

For \(\chi <0,\)

$$ F\left( \xi \right) = \left. {\begin{array}{*{20}c} {\frac{{\sqrt { - \left( {\Lambda ^{2} + \wp ^{2} } \right)\chi } - \Lambda \sqrt { - \chi } \cosh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right)}}{{\Lambda \sinh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right) + \wp }}} \\ {\frac{{ - \sqrt { - \left( {\Lambda ^{2} + \wp ^{2} } \right)\chi } + \Lambda \sqrt { - \chi } \cosh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right)}}{{\Lambda \sinh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right) + \wp }}} \\ { - \sqrt { - \chi } + \frac{{2\Lambda \sqrt { - \chi } }}{{\Lambda + \cosh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right) - \sinh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right)}}} \\ {\sqrt { - \chi } - \frac{{2\Lambda \sqrt { - \chi } }}{{\Lambda + \cosh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right) - \sinh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right)}}} \\ \end{array} } \right\}. $$

For \(\chi =0,\)

$$F\left(\varsigma \right)=\frac{1}{\varsigma +h}.$$

Remark 02

The unified method is the modified version of the modified extended tanh method (METM). In the METM technique, only five solutions are generated, but using the unified method we can 9 analytic solutions, that are trigonometric, hyperbolic, and rational. We can solve any integral or non-integral models. But the rational solution most of the time is rejected.

3 Mathematical analysis of the governing model

In this section, we study the variable coefficient nonlinear Schrödinger equation [43] in the succeeding form:

$$i{Q}_{t}+{Q}_{xx}+\varepsilon \left(t\right)Q|Q{|}^{2}=0,$$

here \(\lambda (t)\) is the function of time.

According to the method we consider a transformation:

$$Q\left(x,t\right)={e}^{\text{i}\left(\theta x+\lambda \frac{\Gamma \left(\text{n}+1\right)}{g}{t}^{g}\right)}F\left(\varsigma \right), \varsigma =iK\left(x-2\theta \frac{\Gamma \left(\text{n}+1\right)}{g}{t}^{g}\right),$$

here \(K,\theta \), and \(\beta \) are constants.

Substituting the transformation into (1), we obtain an ordinary differential equation:

$$-{K}^{2}{F}_{2\zeta }-\left(\lambda +{\theta }^{2}\right)F+\varepsilon \left(t\right){F}^{3}=0.$$
(7)

4 Bifurcation analysis

According to the Galilean transformation, Eq. (7) is the following form:

$$\left\{\begin{array}{l}\frac{dF}{d\varsigma }=\wp \\ \frac{d\wp }{d\varsigma }=-{\lambda }_{1}{F}^{3}+{\lambda }_{2}F.\end{array}\right.$$
(8)

where \({\lambda }_{1}=-\frac{\varepsilon \left(t\right)}{{K}^{2}}, {\lambda }_{2}=-\frac{\left(\lambda +{\theta }^{2}\right)}{{K}^{2}}.\)

$$\mathcal{H}\left(\wp ,F\right)=\frac{{\wp }^{2}}{2}+\frac{{\lambda }_{1}{F}^{4}}{4}-\frac{{\lambda }_{2}{F}^{2}}{2}=\text{h}.$$

here \(h\) is the Hamiltonian constant. We solve the system

$$\left\{\begin{array}{l}\wp =0,\\ -{\lambda }_{1}{F}^{3}+{\lambda }_{2}F=0\end{array}.\right.$$
(9)

Now we derive the equilibrium points of (9). The derived points are:

$${E}_{1}=\left(\text{0,0}\right), {E}_{2}=\left(\sqrt{\frac{{\lambda }_{2}}{{\lambda }_{1}}},0\right), {E}_{2}=\left(-\sqrt{\frac{{\lambda }_{2}}{{\lambda }_{1}}},0\right).$$

The Jacobian matrix determinant of the system (9) is

$$j\left(F, \wp \right)=\left|\begin{array}{cc}0& 1\\ -3{\lambda }_{1}{F}^{3}+{\lambda }_{2}F& 0\end{array}\right|=-\left(-3{\lambda }_{1}{F}^{3}+{\lambda }_{2}F\right).$$

We know that:

  1. (1)

    \((F, \wp )\) is a saddle point if \(j\left(F, \wp \right)<0;\)

  2. (2)

    \((F, \wp )\) is a center point if \(j\left(F, \wp \right)>0;\)

  3. (3)

    \((F, \wp )\) is a cuspidor point if \(j\left(F, \wp \right)=0;\)

The outcomes that may be attained by altering the pertinent parameter are listed below:


Case 1: \({\lambda }_{1}>0\) and \({\lambda }_{2}>0.\)

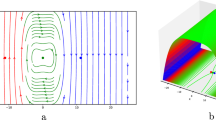
For particular values of the free parameters \(K=1, \lambda =-1.75, \theta =1, \varepsilon =-1\), there are three equilibrium points exist of the required system as \((\text{0,0}),(-\text{0.866025,0})\), and \((\text{0.866025,0})\). In Fig. 1a the point \(\left(\text{0,0}\right)\) performances as the saddle point and \((-\text{0.866025,0})\), and \((\text{0.866025,0})\) performances as the central point.

Fig. 1
figure 1

The phase portrait of the Eq. (8). a when \({\lambda }_{1}>0\) and \({\lambda }_{2}>0\); b \({\lambda }_{1}<0\) and \({\lambda }_{2}>0\); c \({\lambda }_{1}>0\) and \({\lambda }_{2}<0\); d \({\lambda }_{1}<0\) and \({\lambda }_{2}<0\)

Full size image

Case 2: \({\lambda }_{1}<0\) and \({\lambda }_{2}>0.\)

For particular values of the free parameters \(K=1, \lambda =-1.5, \theta =1, \varepsilon =1\), we find that the only real point \(\left(\text{0,0}\right)\) is the saddle point present in Fig. 1b.


Case 3: \({\lambda }_{1}>0\) and \({\lambda }_{2}<0.\)


For particular values of the free parameters \(K=1, \lambda =\theta =0.5, \varepsilon =-1\), we find that the only real point \(\left(\text{0,0}\right)\) (central point) is present in Fig. 1c.


Case 4: \({\lambda }_{1}<0\) and \({\lambda }_{2}<0.\)


For particular values of the free parameters \(K=2, \lambda =0.206, \theta =1, \varepsilon =1\), three equilibrium points exist of the required system as \((\text{0,0}),(-\text{1.0382,0})\), and \((\text{1.0382,0})\). In Fig. 1a the point \(\left(\text{0,0}\right)\) performances as the saddle point and \((-\text{1.0382,0})\), and \((\text{1.0382,0})\). performances as the central point.

5 Analytical form of optical wave pattern

In the existing section, there are several optical soliton solutions are integrated into the variable coefficient NLSE model by using the unified solver technique and generalized unified technique.

5.1 Unified solver method

In this subsection, we explored the unified solver technique [39, 50]. For the ordinary differential equations

$$-{K}^{2}{F}_{2\zeta }-\left(\beta +{\theta }^{2}\right)F+\varepsilon \left(t\right){F}^{3}=0.$$
(10)

Here \(\mathcal{B}=-{K}^{2},\mathcal{H}=\lambda \left(t\right),\mathfrak{R}=-\left(\beta +{\theta }^{2}\right)\) are real number. The closed form solution of the model in Eq. (7) are given below:

For \(\mathfrak{R}=0\) and \(\frac{\lambda \left(t\right)}{-{K}^{2}}<0\), we get rational solution:

$$Q\left(x,t\right)=\pm \sqrt{\frac{-\lambda \left(t\right)}{-2{K}^{2}}}\frac{1}{\varsigma }{e}^{\text{i}\left(\theta x+\beta \frac{\Gamma \left(\text{n}+1\right)}{g}{t}^{g}\right)},$$
(11)

For \(\frac{-\left(\beta +{\theta }^{2}\right)}{-{K}^{2}}<0\) and \(\frac{-\left(\beta +{\theta }^{2}\right)}{\lambda \left(t\right)}>0\), we get trigonometric solution:

$$Q\left(x,t\right)=\pm \sqrt{\frac{-\left(\beta +{\theta }^{2}\right)}{\lambda \left(t\right)}}tan\left(\sqrt{\frac{\left(\beta +{\theta }^{2}\right)}{-2{K}^{2}}}\varsigma \right){e}^{\text{i}\left(\theta x+\beta \frac{\Gamma \left(\text{n}+1\right)}{g}{t}^{g}\right)},$$
(12)
$$Q\left(x,t\right)=\pm \sqrt{\frac{-\left(\beta +{\theta }^{2}\right)}{\lambda \left(t\right)}}cot\left(\sqrt{\frac{\left(\beta +{\theta }^{2}\right)}{-2{K}^{2}}}\varsigma \right){e}^{\text{i}\left(\theta x+\beta \frac{\Gamma \left(\text{n}+1\right)}{g}{t}^{g}\right)},$$
(13)

For \(\frac{-\left(\beta +{\theta }^{2}\right)}{-{K}^{2}}>0\) and \(\frac{-\left(\beta +{\theta }^{2}\right)}{\lambda \left(t\right)}<0\), we get hyperbolic solution:

$$Q\left(x,t\right)=\pm \sqrt{\frac{--\left(\beta +{\theta }^{2}\right)}{\lambda \left(t\right)}}tanh\left(\sqrt{\frac{-\left(\beta +{\theta }^{2}\right)}{-2{K}^{2}}}\varsigma \right){e}^{\text{i}\left(\theta x+\beta \frac{\Gamma \left(\text{n}+1\right)}{g}{t}^{g}\right)},$$
(14)
$$Q\left(x,t\right)=\pm \sqrt{-\frac{-\left(\beta +{\theta }^{2}\right)}{\lambda \left(t\right)}}coth\left(\sqrt{\frac{-\left(\beta +{\theta }^{2}\right)}{-2{K}^{2}}}\varsigma \right){e}^{\text{i}\left(\theta x+\beta \frac{\Gamma \left(\text{n}+1\right)}{g}{t}^{g}\right)},$$
(15)

where \(\varsigma =iK\left(x-2\theta \frac{\Gamma \left(\text{n}+1\right)}{g}{t}^{g}\right).\)

5.2 Unified technique

According to the generalized unified technique [51,52,53], the trial solution of Eq. (7) is

$$\text{F}\left(\varsigma \right)={\upmu }_{0}+{\upmu }_{1}\uppsi \left(\varsigma \right)+\frac{{\upmu }_{2}}{\uppsi \left(\varsigma \right)},$$
(16)

Make the use of Eq. (16) into Eq. (7) with the help of Eq. (5). Then we get the following system of equations:

$$\left(\varepsilon \left(t\right){\mu }_{1}^{3}-2{K}^{2}{\mu }_{1}\right)=0,$$
$$3\varepsilon {\mu }_{0}{\mu }_{1}^{2}=0,$$
$$-2{K}^{2}\chi {\mu }_{1}+3\varepsilon \left(t\right){\mu }_{0}^{2}{\mu }_{1}+3\varepsilon \left(t\right){\mu }_{1}^{2}{\mu }_{2}-{\theta }^{2}{\mu }_{1}-\lambda {\mu }_{1}=0,$$
$$\varepsilon \left(t\right){\mu }_{0}^{3}+6\varepsilon \left(t\right){\mu }_{0}{\mu }_{1}{\mu }_{2}-{\mu }_{0}{\theta }^{2}-{\mu }_{0}\lambda =0,$$
$$-2{K}^{2}\chi {\mu }_{2}+3\varepsilon \left(t\right){\mu }_{0}^{2}{\mu }_{2}+3\varepsilon \left(t\right){\mu }_{1}{\mu }_{2}^{2}-{\theta }^{2}{\mu }_{2}-\lambda {\mu }_{2}=0,$$
$$3\varepsilon \left(t\right){\mu }_{0}{\mu }_{2}^{2}=0,$$
$$-2{K}^{2}{\chi }^{2}{\mu }_{2}+\varepsilon \left(t\right){\mu }_{2}^{3}=0,$$

Case 01: \(K=\sqrt{\frac{\varepsilon }{2}}{\mu }_{1},\lambda =\lambda ,\theta =\sqrt{-\left(\chi \varepsilon {\mu }_{1}^{2}+\lambda \right)},{\mu }_{0}=0,{\mu }_{1}={\mu }_{1},{\mu }_{2}=0.\)

The trigonometric solution is executed for \(\chi >0.\)

$$ Q\left( {x,t} \right) = \mu _{1} \left( {\frac{{\sqrt {\left( {\Lambda ^{2} - \wp ^{2} } \right)\chi } - \Lambda \sqrt \chi \cos \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right)}}{{\Lambda \sin \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right) + \wp }}} \right)e^{{i\left( {\theta x + \lambda \frac{{\Gamma \left( {n + 1} \right)}}{g}t^{g} } \right)}}, $$
(17)
$$ Q\left( {x,t} \right) = \mu _{1} \left( {\frac{{ - \sqrt {\left( {\Lambda ^{2} - \wp ^{2} } \right)\chi } - \Lambda \sqrt \chi \cos \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right)}}{{\Lambda \sin \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right) + \wp }}} \right)e^{{i\left( {\theta x + \lambda \frac{{\Gamma \left( {n + 1} \right)}}{g}t^{g} } \right)}} , $$
(18)
$$ Q\left( {x,t} \right) = \mu _{1} \left( {I\sqrt \chi - \frac{{2I\Lambda \sqrt \chi }}{{\Lambda + \cos \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right) - I\sin \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right)}}} \right)e^{{i\left( {\theta x + \lambda \frac{{\Gamma \left( {n + 1} \right)}}{g}t^{g} } \right)}} , $$
(19)
$$ Q\left( {x,t} \right) = \mu _{1} \left( { - I\sqrt \chi + \frac{{2\Lambda \sqrt \chi }}{{\Lambda + \cos \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right) + I\sin \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right)}}} \right)e^{{i\left( {\theta x + \lambda \frac{{\Gamma \left( {n + 1} \right)}}{g}t^{g} } \right)}} , $$
(20)

The Hyperbolic solution are executed for \(\chi <0\).

$$ Q\left( {x,t} \right) = \mu _{1} \left( {\frac{{\sqrt { - \left( {\Lambda ^{2} + \wp ^{2} } \right)\chi } - \Lambda \sqrt { - \chi } \cosh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right)}}{{\Lambda \sinh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right) + \wp }}} \right)e^{{i\left( {\theta x + \lambda \frac{{\Gamma \left( {n + 1} \right)}}{g}t^{g} } \right)}} , $$
(21)
$$ Q\left( {x,t} \right) = \mu _{1} \left( {\frac{{ - \sqrt { - \left( {\Lambda ^{2} + \wp ^{2} } \right)\chi } + \Lambda \sqrt { - \chi } \cosh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right)}}{{\Lambda \sinh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right) + \wp }}} \right)e^{{i\left( {\theta x + \lambda \frac{{\Gamma \left( {n + 1} \right)}}{g}t^{g} } \right)}} , $$
(22)
$$ Q\left( {x,t} \right) = \mu _{1} \left( { - \sqrt { - \chi } + \frac{{2\Lambda \sqrt { - \chi } }}{{\Lambda + \cosh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right) - \sinh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right)}}} \right)e^{{i\left( {\theta x + \lambda \frac{{\Gamma \left( {n + 1} \right)}}{g}t^{g} } \right)}} , $$
(23)
$$ Q\left( {x,t} \right) = \mu _{1} \left( {\sqrt { - \chi } - \frac{{2\Lambda \sqrt { - \chi } }}{{\Lambda + \cosh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right) - \sinh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right)}}} \right)e^{{i\left( {\theta x + \lambda \frac{{\Gamma \left( {n + 1} \right)}}{g}t^{g} } \right)}} , $$
(24)

where \( \varsigma = i\sqrt {\frac{\varepsilon }{2}} \mu _{1} \left( {x - 2\sqrt { - \left( {\chi \varepsilon \mu _{1}^{2} + \lambda } \right)} \frac{{\Gamma \left( {n + 1} \right)}}{g}t^{g} } \right). \)

Case 02: \( \theta = \sqrt { - \left( {\chi \varepsilon \mu _{1}^{2} + \lambda } \right)} ,\mu _{0} = 0,\mu _{1} = 0,\mu _{2} = \chi K\sqrt {\frac{2}{\varepsilon }.} \)

The trigonometric solution is executed for \(\chi >0\).

$$ Q\left( {x,t} \right) = \chi K\sqrt {\frac{2}{\varepsilon }} \left( {\frac{{\sqrt {\left( {\Lambda ^{2} - \wp ^{2} } \right)\chi } - \Lambda \sqrt \chi \cos \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right)}}{{\Lambda \sin \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right) + \wp }}} \right)^{{ - 1}} e^{{i\left( {\theta x + \lambda \frac{{\Gamma \left( {n + 1} \right)}}{g}t^{g} } \right)}} , $$
(25)
$$ Q\left( {x,t} \right) = \chi K\sqrt {\frac{2}{\varepsilon }} \left( {\frac{{ - \sqrt {\left( {\Lambda ^{2} - \wp ^{2} } \right)\chi } - \Lambda \sqrt \chi \cos \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right)}}{{\Lambda \sin \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right) + \wp }}} \right)^{{ - 1}} e^{{i\left( {\theta x + \lambda \frac{{\Gamma \left( {n + 1} \right)}}{g}t^{g} } \right)}} , $$
(26)
$$ Q\left( {x,t} \right) = \chi K\sqrt {\frac{2}{\varepsilon }} \left( {I\sqrt \chi - \frac{{2I\Lambda \sqrt \chi }}{{\Lambda + \cos \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right) - I\sin \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right)}}} \right)^{{ - 1}} e^{{i\left( {\theta x + \lambda \frac{{\Gamma \left( {n + 1} \right)}}{g}t^{g} } \right)}} , $$
(27)
$$ Q\left( {x,t} \right) = \chi K\sqrt {\frac{2}{\varepsilon }} \left( { - I\sqrt \chi + \frac{{2\Lambda \sqrt \chi }}{{\Lambda + \cos \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right) + I\sin \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right)}}} \right)^{{ - 1}} e^{{i\left( {\theta x + \lambda \frac{{\Gamma \left( {n + 1} \right)}}{g}t^{g} } \right)}} , $$
(28)

The Hyperbolic solution are executed for \(\chi <0\).

$$ Q\left( {x,t} \right) = \chi K\sqrt {\frac{2}{\varepsilon }} \left( {\frac{{\sqrt { - \left( {\Lambda ^{2} + \wp ^{2} } \right)\chi } - \Lambda \sqrt { - \chi } \cosh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right)}}{{\Lambda \sinh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right) + \wp }}} \right)^{{ - 1}} e^{{i\left( {\theta x + \lambda \frac{{\Gamma \left( {n + 1} \right)}}{g}t^{g} } \right)}} , $$
(29)
$$ Q\left( {x,t} \right) = \chi K\sqrt {\frac{2}{\varepsilon }} \left( {\frac{{ - \sqrt { - \left( {\Lambda ^{2} + \wp ^{2} } \right)\chi } + \Lambda \sqrt { - \chi } \cosh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right)}}{{\Lambda \sinh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right) + \wp }}} \right)^{{ - 1}} e^{{i\left( {\theta x + \lambda \frac{{\Gamma \left( {n + 1} \right)}}{g}t^{g} } \right)}} , $$
(30)
$$ Q\left( {x,t} \right) = \chi K\sqrt {\frac{2}{\varepsilon }} \left( { - \sqrt { - \chi } + \frac{{2\Lambda \sqrt { - \chi } }}{{\Lambda + \cosh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right) - \sinh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right)}}} \right)^{{ - 1}} e^{{i\left( {\theta x + \lambda \frac{{\Gamma \left( {n + 1} \right)}}{g}t^{g} } \right)}} , $$
(31)
$$ Q\left( {x,t} \right) = \chi K\sqrt {\frac{2}{\varepsilon }} \left( {\sqrt { - \chi } - \frac{{2\Lambda \sqrt { - \chi } }}{{\Lambda + \cosh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right) - \sinh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right)}}} \right)^{{ - 1}} e^{{i\left( {\theta x + \lambda \frac{{\Gamma \left( {n + 1} \right)}}{g}t^{g} } \right)}} , $$
(32)

where \( \varsigma = iK\left( {x - 2\sqrt { - \left( {\chi \varepsilon \mu _{1}^{2} + \lambda } \right)} \frac{{\Gamma \left( {n + 1} \right)}}{g}t^{g} } \right). \)

Case 03: \( \lambda = 4K^{2} \chi - \theta ^{2} ,\mu _{0} = 0,\mu _{1} = K\sqrt {\frac{2}{\varepsilon }} ,\mu _{2} = \chi K\sqrt {\frac{2}{\varepsilon }} . \)

The trigonometric solution is executed for \(\chi >0\).

$$ Q\left( {x,t} \right) = K\sqrt {\frac{2}{\varepsilon }} \left( {\frac{{\left( {\frac{{\sqrt {\left( {\Lambda ^{2} - \wp ^{2} } \right)\chi } - \Lambda \sqrt \chi \cos \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right)}}{{\Lambda \sin \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right) + \wp }}} \right)^{2} + \chi }}{{\frac{{\sqrt {\left( {\Lambda ^{2} - \wp ^{2} } \right)\chi } - \Lambda \sqrt \chi \cos \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right)}}{{\Lambda \sin \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right) + \wp }}}}} \right)e^{{i\left( {\theta x + \lambda \frac{{\Gamma \left( {n + 1} \right)}}{g}t^{g} } \right)}} , $$
(33)
$$ Q\left( {x,t} \right) = K\sqrt {\frac{2}{\varepsilon }} \left( {\frac{{\left( {\frac{{ - \sqrt {\left( {\Lambda ^{2} - \wp ^{2} } \right)\chi } - \Lambda \sqrt \chi \cos \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right)}}{{\Lambda \sin \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right) + \wp }}} \right)^{2} + \chi }}{{\frac{{ - \sqrt {\left( {\Lambda ^{2} - \wp ^{2} } \right)\chi } - \Lambda \sqrt \chi \cos \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right)}}{{\Lambda \sin \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right) + \wp }}}}} \right)e^{{i\left( {\theta x + \lambda \frac{{\Gamma \left( {n + 1} \right)}}{g}t^{g} } \right)}} , $$
(34)
$$ Q\left( {x,t} \right) = K\sqrt {\frac{2}{\varepsilon }} \left( {\frac{{\left( {I\sqrt \chi - \frac{{2I\Lambda \sqrt \chi }}{{\Lambda + \cos \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right) - I\sin \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right)}}} \right)^{2} + \chi }}{{I\sqrt \chi - \frac{{2I\Lambda \sqrt \chi }}{{\Lambda + \cos \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right) - I\sin \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right)}}}}} \right)e^{{i\left( {\theta x + \lambda \frac{{\Gamma \left( {n + 1} \right)}}{g}t^{g} } \right)}} , $$
(35)
$$ Q\left( {x,t} \right) = K\sqrt {\frac{2}{\varepsilon }} \left( {\frac{{\left( { - I\sqrt \chi + \frac{{2\Lambda \sqrt \chi }}{{\Lambda + \cos \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right) + I\sin \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right)}}} \right)^{2} + \chi }}{{ - I\sqrt \chi + \frac{{2\lambda \sqrt \chi }}{{\Lambda + \cos \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right) + I\sin \left( {2\sqrt \chi \left( {\varsigma + h} \right)} \right)}}}}} \right)e^{{i\left( {\theta x + \lambda \frac{{\Gamma \left( {n + 1} \right)}}{g}t^{g} } \right)}} , $$
(36)

The Hyperbolic solution is executed for \(\chi <0\).

$$ Q\left( {x,t} \right) = K\sqrt {\frac{2}{\varepsilon }} \left( {\frac{{\left( {\frac{{\sqrt { - \left( {\Lambda ^{2} + \wp ^{2} } \right)\chi } - \Lambda \sqrt { - \chi } \cosh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right)}}{{\Lambda \sinh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right) + \wp }}} \right)^{2} + \chi }}{{\frac{{\sqrt { - \left( {\Lambda ^{2} + \wp ^{2} } \right)\chi } - \Lambda \sqrt { - \chi } \cosh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right)}}{{\Lambda \sinh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right) + \wp }}}}} \right)e^{{i\left( {\theta x + \lambda \frac{{\Gamma \left( {n + 1} \right)}}{g}t^{g} } \right)}} , $$
(37)
$$ Q\left( {x,t} \right) = K\sqrt {\frac{2}{\varepsilon }} \left( {\frac{{\left( {\frac{{ - \sqrt { - \left( {\Lambda ^{2} + \wp ^{2} } \right)\chi } + \Lambda \sqrt { - \chi } \cosh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right)}}{{\Lambda \sinh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right) + \wp }}} \right)^{2} + \chi }}{{\frac{{ - \sqrt { - \left( {\Lambda ^{2} + \wp ^{2} } \right)\chi } + \Lambda \sqrt { - \chi } \cosh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right)}}{{\Lambda \sinh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right) + \wp }}}}} \right)e^{{i\left( {\theta x + \lambda \frac{{\Gamma \left( {n + 1} \right)}}{g}t^{g} } \right)}} , $$
(38)
$$ Q\left( {x,t} \right) = K\sqrt {\frac{2}{\varepsilon }} \left( {\frac{{\left( { - \sqrt { - \chi } + \frac{{2\Lambda \sqrt { - \chi } }}{{\Lambda + \cosh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right) - \sinh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right)}}} \right)^{2} + \chi }}{{ - \sqrt { - \chi } + \frac{{2\Lambda \sqrt { - \chi } }}{{\Lambda + \cosh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right) - \sinh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right)}}}}} \right)e^{{i\left( {\theta x + \lambda \frac{{\Gamma \left( {n + 1} \right)}}{g}t^{g} } \right)}} , $$
(39)
$$ Q\left( {x,t} \right) = K\sqrt {\frac{2}{\varepsilon }} \left( {\frac{{\left( {\sqrt { - \chi } - \frac{{2\Lambda \sqrt { - \chi } }}{{\Lambda + \cosh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right) - \sinh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right)}}} \right)^{2} + \chi }}{{\sqrt { - \chi } - \frac{{2\Lambda \sqrt { - \chi } }}{{\Lambda + \cosh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right) - \sinh \left( {2\sqrt { - \chi } \left( {\varsigma + h} \right)} \right)}}}}} \right)e^{{i\left( {\theta x + \lambda \frac{{\Gamma \left( {n + 1} \right)}}{g}t^{g} } \right)}} , $$
(40)

where \( \varsigma = iK\left( {x - 2\theta \frac{{\Gamma \left( {n + 1} \right)}}{g}t^{g} } \right). \)

6 Numerical discussion

The nonlinear Schrödinger equation (NLSE) carries over the basic ideas of quantum mechanics to include nonlinear phenomena, which are important in many areas of science and engineering, through condensed matter physics, plasma physics, and optics, A nonlinear partial differential equation describes complex wave functions in nonlinear mediums. Zhakarov and Shabat initially presented NLSE in the 1970s. It displays intricate dynamics, such as wave collapse and soliton propagation. Bose–Einstein condensates, ultrafast laser dynamics, and optical fiber modeling are among the applications. NLSE's transdisciplinary significance stems from its capacity to elucidate nonlinear wave behavior, hence promoting progress in several scientific and technological domains. In this division, we discuss the numerical form of the obtained solutions of NLSE with the Kerr law nonlinearity model with a wide range of significance in the applied science. The NLS equation advocates the nonlinear optical wave propagations in nonlinear optical fibers which exhibits a Kerr law nonlinearity. The optical wave pattern has a vital significance to explore the soliton propagation through fiber communications. The attained solutions for the studied equation were achieved in explicit form. These solutions establish enjoyable wave profiles and characterize fabulous phenomena in optical fiber communications. The profiles that were acquired could help clarify the capillary profiles, femtosecond impulses, laser unpredictable pulses, telecommunication demonstrations, and space observations.

6.1 Unified solver technique

To understand the dynamics inherent in the results, it is necessary to grasp the physical elucidation of the obtained solutions. In this portion, we determine the visual illustrations of the solutions we have evolved, operating the three-dimensional with density plots and two-dimensional plots to reveal our obvious solutions. Since the cNLS equation is equivalent to the Schrödinger equation, we focus on three essential components: the real, imaginary, and absolute values of the derived solutions. By using the unified solver technique, we plot some profiles of periodic wave soliton, the interaction of kink and bell shape soliton, periodic breather wave soliton, double periodic soliton, etc. These profiles find extensive applications in fields like as nonlinear optics, plasma physics, and fuzzy dynamics. For example, periodic singular soliton structures can be used in nonlinear optics to regulate and modulate light propagation. Similar to this, these structures may help understand and control periodic disturbances in furious flocks in the field of furious dynamics.

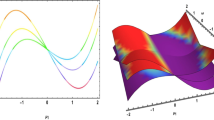
Figure 2 displays the 3D with density and 2D view of the solution Eq. (12) which is the periodic wave soliton for the parametric values \(\theta =1, \lambda =-2, K=0.5, \varepsilon =-t, n=1.5\). The effect of truncated M fractional parameters is provided by 3D and 2D plots with density plots. For the parametric values \(\theta =1, \lambda =-2, K=0.5, \varepsilon =-t, n=1.5\), the solution of Eq. (12) represents the interaction of kink and bell shape soliton solutions in Fig. 3. Figure 4, displays the 3D with density and 2D view of the solution Eq. (12) which is the periodic breather wave soliton for the parametric values \(\theta =1, \lambda =2, K=-0.5i, \varepsilon =-tanh\left(t\right), n=1.5\). The effect of truncated M fractional parameters is provided by 3D and 2D plots with density. For the parametric values \(\theta =1, \lambda =-3, K=2, \varepsilon =sec\left(t\right), n=1.5\), the solution of Eq. (12) represents the double periodic soliton solutions in Fig. 5. Figure 6 displays the 3D with density and 2D view of the solution Eq. (14) which is the periodic wave soliton for the parametric values \(\theta =1, \lambda =-0.5, K=0.5, \varepsilon =sec\left(t\right)+tan\left(t\right), n=1.5\).

Fig. 2
figure 2

3D and 2D plots are graphically numerical simulations related to the complex term of Eq. (12) for the parametric values \(\theta =1, \lambda =-2, K=0.5, \varepsilon =-t, n=1.5\)

Full size image
Fig. 3
figure 3

3D and 2D plots are graphically numerical simulations related to the complex term of Eq. (12) for the parametric values \(\theta =1, \lambda =-2, K=0.5, \varepsilon =-t, n=1.5\)

Full size image
Fig. 4
figure 4

3D and 2D plots are graphically numerical simulations related to the complex term of Eq. (12) for the parametric values \(\theta =1, \lambda =2, K=-0.5i, \varepsilon =-tanh\left(t\right), n=1.5\)

Full size image
Fig. 5
figure 5

3D and 2D plots are graphically numerical simulations related to the complex term of Eq. (12) for the parametric values \(\theta =1, \lambda =-3, K=2, \varepsilon =sec\left(t\right), n=1.5\)

Full size image
Fig. 6
figure 6

3D and 2D plots are graphically numerical simulations related to the complex term of Eq. (14) for the parametric values \(\theta =1, \lambda =-0.5, K=0.5, \varepsilon =sec\left(t\right)+tan\left(t\right), n=1.5\)

Full size image

6.2 Unified technique

In this portion, we determine the visual illustrations of the obtained solutions of the cNLSE by using a generalized unified technique. For the appropriate values of the parameters, we plot some profile of interaction of kink and periodic lump wave soliton and also with the periodic soliton, double periodic wave soliton, periodic wave soliton with lump soliton, multi periodic wave with kink shape soliton, periodic wave soliton, periodic breather wave soliton, periodic wave soliton, multi periodic wave soliton, periodic lump wave soliton, breather wave soliton multi periodic wave, etc. These profiles find extensive applications in fields like as nonlinear optics, plasma physics, and fuzzy dynamics. For example, periodic singular soliton structures can be used in nonlinear optics to regulate and modulate light propagation. Similar to this, these structures may help understand and control periodic disturbances in furious flocks in the field of furious dynamics.

Figure 7 shows 3D and 2D with a density view of the solutions in Eq. (17) which is the interaction of kink and periodic lump wave soliton and also with the periodic soliton solution for the parametric values \(\Lambda =2, K=0.1, h=-1, \wp =-2, \varepsilon =tanh\left(t\right),\chi =2,\lambda =-0.5,{\mu }_{1}=1, n=1.5.\)

Fig. 7
figure 7

3D and 2D plots are graphically numerical simulations related to the complex term of Eq. (17) for the parametric values \(\Lambda =2, K=0.1, h=-1, \wp =-2, \varepsilon =tanh\left(t\right),\chi =2,\lambda =-0.5,{\mu }_{1}=1, n=1.5\)

Full size image

Figure 8 demonstrates the 3D with density and 2D view of the solutions of Eq. (18) which is a double periodic wave soliton profile for the parametric values \(\Lambda =-0.5, K=-1, h=0.01, \wp =-6, \varepsilon =cos\left(t\right)+tanh\left(t\right),\chi =0.1,\lambda =-0.1,{\mu }_{1}=1, n=1.5.\)

Fig. 8
figure 8

3D and 2D plots are graphically numerical simulations related to the complex term of Eq. (18) for the parametric values \(\Lambda =-0.5, K=-1, h=0.01, \wp =-6, \varepsilon =cos\left(t\right)+tanh\left(t\right),\chi =0.1,\lambda =-0.1,{\mu }_{1}=1, n=1.5\)

Full size image

Figure 9 displays the 3D with density and 2D plots of the solution in Eq. (18) which is the periodic wave soliton with lump soliton solutions for the parametric values \(\Lambda =1, h=0.1, \wp =2, \varepsilon ={t}^{2},\chi =2,\lambda =5,{\mu }_{1}=1, n=1.5.\)

Fig. 9
figure 9

3D and 2D plots are graphically numerical simulations related to the complex term of Eq. (18) for the parametric values \(\Lambda =1, h=0.1, \wp =2, \varepsilon ={t}^{2},\chi =2,\lambda =5,{\mu }_{1}=1, n=1.5\)

Full size image

Figure 10 displays the 3D with density and 2D plots of the solution of Eq. (21) which is the multi-periodic wave with kink shape soliton solution for the parametric values \(\Lambda =0.4, h=-0.1, \wp =-1, \varepsilon =tanh\left(t\right),\chi =-2,\lambda =-0.5,{\mu }_{1}=1, n=1.5.\)

Fig. 10
figure 10

3D and 2D plots are graphically numerical simulations related to the complex term of Eq. (21). For the parametric values \(\Lambda =0.4, h=-0.1, \wp =-1, \varepsilon =tanh\left(t\right),\chi =-2,\lambda =-0.5,{\mu }_{1}=1, n=1.5\)

Full size image

Figure 11 represents 3D with density and 2D plots of the solution of Eq. (21) which is the periodic wave soliton for the parametric values \(\Lambda =2, h=-0.1, \wp =1, \varepsilon =sin\left(t\right),\chi =-2,\lambda =-0.5,{\mu }_{1}=1, n=1.5.\)

Fig. 11
figure 11

3D and 2D plots are graphically numerical simulations related to the complex term of Eq. (21) for the parametric values \(\Lambda =2, h=-0.1, \wp =1, \varepsilon =sin\left(t\right),\chi =-2,\lambda =-0.5,{\mu }_{1}=1, n=1.5\)

Full size image

Figure 12 shows the 3D with density and 2D plots of the solution of Eq. (25) which is a periodic breather wave soliton for the parametric values \(\Lambda =2, h=-1, \wp =1, \varepsilon =tanh\left(t\right),\chi =2,\lambda =-0.5,{\mu }_{1}=1, n=1.5.\)

Fig. 12
figure 12

3D and 2D plots are graphically numerical simulations related to the complex term of Eq. (25) for the parametric values \(\Lambda =2, h=-1, \wp =1, \varepsilon =tanh\left(t\right),\chi =2,\lambda =-0.5,{\mu }_{1}=1, n=1.5\)

Full size image

Figure 13 displays the 3D with density and 2D plots of the solution of Eq. (25) which is periodic wave soliton for the parametric values \(\Lambda =0.5, K=1, h=-1, \wp =1, \varepsilon =t,\chi =2,\lambda =5, n=1.5.\)

Fig. 13
figure 13

3D and 2D plots are graphically numerical simulations related to the complex term of Eq. (25) for the parametric values \(\Lambda =0.5, K=1, h=-1, \wp =1, \varepsilon =t,\chi =2,\lambda =5, n=1.5\)

Full size image

Figure 14 displays the 3D with density and 2D views of the solution of Eq. (30) which is the multi-periodic wave soliton for the parametric values \(\Lambda =0.5, K=-1, h=-1, \wp =0.1, \varepsilon =\text{sech}(t),\chi =-1,\lambda =0.5, n=1.5.\)

Fig. 14
figure 14

3D and 2D plots are graphically numerical simulations related to the complex term of Eq. (30) for the parametric values \(\Lambda =0.5, K=-1, h=-1, \wp =0.1, \varepsilon =\text{sech}(t),\chi =-1,\lambda =0.5, n=1.5\)

Full size image

Figure 15 displays the 3D with density and 2D plots of the solution of Eq. (30) which is the multi-periodic wave soliton for the parametric values \(\Lambda =-0.5, K=1, h=-1, \wp =4, \varepsilon =\text{sin}(t),\chi =-2,\lambda =1, n=1.5.\)

Fig. 15
figure 15

3D and 2D plots are graphically numerical simulations related to the complex term of Eq. (30) for the parametric values \(\Lambda =-0.5, K=1, h=-1, \wp =4, \varepsilon =\text{sin}(t),\chi =-2,\lambda =1, n=1.5\)

Full size image

Figure 16 represents the 3D with density and 2D plots of the solution of Eq. (38) which is periodic lump wave soliton for the parametric values \(\Lambda =-2, K=0.5, h=0.01, \wp =1, \varepsilon =\text{sec}(t),\chi =-1,\theta =-0.5, n=1.5\)

Fig. 16
figure 16

3D and 2D plots are graphically numerical simulations related to the complex term of Eq. (38) for the parametric values \(\Lambda =-2, K=0.5, h=0.01, \wp =1, \varepsilon =\text{sec}(t),\chi =-1,\theta =-0.5, n=1.5\)

Full size image

Figure 17 represents 3D with density and 2D plots of the solution of Eq. (38) which is breather wave soliton for the parametric values \(\Lambda =0.5, K=-0.5, h=0.01, \wp =1, \varepsilon =\text{tanh}(t)+\text{cos}(t),\chi =-1,\theta =0.5, n=1.5.\)

Fig. 17
figure 17

3D and 2D plots are graphically numerical simulations related to the complex term of Eq. (38) for the parametric values \(\Lambda =0.5, K=-0.5, h=0.01, \wp =1, \varepsilon =\text{tanh}(t)+\text{cos}(t),\chi =-1,\theta =0.5, n=1.5\)

Full size image

7 Modulation instability

Several higher-order non-linear complex PDEs show an instability that leads to an analysis of how the interaction between the dispersive and non-linear effects modulates the steady state. Using the conventional linear instability examination, one may determine the modulation instability of NLSE in Eq. (1). The NLSE study state solution is in the subsequent format [54]:

$$Q\left(x,t\right)=\left(\sqrt{P}+\Psi \left(x,t\right)\right){e}^{\varphi \left(t\right)},\varphi \left(t\right)=P\epsilon \delta t.$$
(41)

where \(P\) is normalized power. The perturbation \(\Psi (x,t)\) is explored by utilizing linear stability examination. Setting Eq. (41) into Eq. (1) and linearizing, we get

$$i\frac{\partial\Psi }{\partial t}+\frac{{\partial }^{2}\Psi }{\partial {x}^{2}}+P(4\lambda -\delta \epsilon )\Psi +2\lambda P{\Psi }^{*}=0.$$
(42)

where the character \({\Psi }^{*}\) designates complex conjugate. Consider the solution of Eq. (42) in the form

$$\Psi \left(x,t\right)={\alpha }_{1}{e}^{i\left(kx-\omega t\right)}+{\alpha }_{2}{e}^{-i\left(kx-\omega t\right)}.$$
(43)

where \(k\) and \(\omega \) are the standardized wave number and frequency of perturbation. The relationship between time oscillations and spatial oscillations \({e}^{i\omega t}\) of wave number \(k\) is determined by the dispersion relation \(k=k(\omega )\) of a constant coefficient linear PDE. By substituting Eq. (43) into Eq. (42), the dispersion relation that follows is derived as

$$\omega =\pm \sqrt{-\left({k}^{4}-4\lambda {k}^{2}P-{\delta }^{2}{P}^{2}{\varepsilon }^{2}+8\delta \lambda {P}^{2}\varepsilon -12{\lambda }^{2}{P}^{2}\right),}$$
(44)

The dispersion relation's Eq. (44) demonstrates that the self-phase modulation stimulated Raman scattering, wave number, and group velocity dispersion all influence the steady-state stability. If

$$\left({k}^{4}+-4\lambda {k}^{2}P-{\delta }^{2}{P}^{2}{\varepsilon }^{2}+8\delta \lambda {P}^{2}\varepsilon -12{\lambda }^{2}{P}^{2}\right)<0.$$

However, the stable solution turns into an unstable one.

$$\left({k}^{4}+-4\lambda {k}^{2}P-{\delta }^{2}{P}^{2}{\varepsilon }^{2}+8\delta \lambda {P}^{2}\varepsilon -12{\lambda }^{2}{P}^{2}\right)>0.$$

The \(\omega \) is the imaginary part since the perturbation grows exponentially. One can easily see that, for the occurrence of modulation stability when \({\gamma }^{2}{k}^{2}\ne 1\). if (Fig. 18).

Fig. 18
figure 18

Gain spectrum of MI for different values of \(k=\left[\text{3,5},7\right],\epsilon =\left[\text{0.7,0.8,0.9}\right],p=\left[-0.01,-0.03,-0.05\right],\delta =\left[\text{1,2},3\right]\)

Full size image

8 Comparison

The nonlinear Schrödinger equation (NLSE) carries over the basic ideas of quantum mechanics to include nonlinear phenomena, which are important in many areas of science and engineering, through condensed matter physics, plasma physics, and optics, A nonlinear partial differential equation describes complex wave functions in nonlinear mediums. It displays intricate dynamics, such as wave collapse and soliton propagation. Bose–Einstein condensates, ultrafast laser dynamics, and optical fiber modeling are among the applications. NLSE's transdisciplinary significance stems from its capacity to elucidate nonlinear wave behavior, hence promoting progress in several scientific and technological domains. Different researchers integrated NLSE by using different techniques [43,44,45,46,47,48] such as Taghizadeh used the simplest equation technique [43] to study NLSE with Kerr law nonlinearity, W.X. Ma applied direct algebraic technique [44] to find exact solutions to NLSE, N.H. Sweilam, Variational iteration scheme [45] for solving cNLSE, Taghizadeh found exact solutions of the NLSE by the first integral method [46] and also [47, 48]. In this division, we compare our study with existing work in [43] and also describe the novelty of our outcomes.

9 Compare with simplest equation method [36]

Simplest equation method, Taghizadeh [43]

Our study

If we set \(\mu =2, \alpha =2, K=1, a=1,{a}_{1}=-1\), \({\xi }_{0}=0\), then the solution Eq. (24) is:

\(u\left(x,t\right)=\sqrt{\frac{3}{2}} coth\left(i\left(x-4t\right)\right){e}^{i\left(2x-\frac{7}{2}t\right)}\)

If we set \(\theta =2, K=1,\beta =-\frac{7}{2} \varepsilon \left(t\right)=-1\), then the solution Eq. (15) is:

\(Q\left(x,t\right)=\sqrt{\frac{3}{2}} coth\left(i\left(x-4t\right)\right){e}^{i\left(2x-\frac{7}{2}t\right)}\)

If we set \(\mu =2, \alpha =1, K=1,\beta =1\), then the solution Eq. (27) is:

\(u\left(x,t\right)=tanh\left(i\left(x-2t\right)\right){e}^{i\left(x+t\right)}\)

If we set \(\theta =1, K=1,\beta =1,\varepsilon \left(t\right)=1\), then the solution Eq. (14) is:

\(Q\left(x,t\right)=tanh\left(i\left(x-2t\right)\right){e}^{i\left(x+t\right)}\)

9.1 Our novelty

Taghizadeh used the simplest equation (SE) technique [43] to study NLSE with Kerr law nonlinearity. Using the SE technique, they got two soliton solutions such as one exponential and one hyperbolic solution. In this work, we got 24 solutions by unified technique and 5 solutions using the unified solver technique. For numerical observation, we discuss some solutions graphically such as periodic wave soliton, the interaction of kink and bell shape soliton, periodic breather wave soliton, double periodic soliton through unified solver method, and interaction of kink and periodic lump wave soliton and also with the periodic soliton, double periodic wave soliton, periodic wave soliton with lump soliton, multi periodic wave with kink shape soliton, periodic wave soliton, periodic breather wave soliton, periodic wave soliton, multi periodic wave soliton, periodic lump wave soliton, breather wave soliton multi periodic wave through generalized unified technique, providing an insightful visualization of the discovered solutions. We also analyzed the bifurcation analytical and graphical study of the observed mechanism of static soliton through a saddle-node bifurcation in the nonlinear Schrödinger problem using a matching technique. Additionally, the modulation instability spectrum can be expressed utilizing a linear analysis technique, and the modulation instability bands are shown to be influenced by the third-order and group velocity dispersion. For the first time, we investigate a lot of phenomena from the cNLSE.

10 Conclusion

In this work, we have successfully executed the bifurcation analysis, modulation instability, and optical soliton solutions of variable coefficient third-order nonlinear Schrödinger's equation (PNLSE) with truncated time \(M\)-fractional derivative. We also discuss a few assets that the derivative satisfies. Using the bifurcation analysis, we observed the mechanism of static soliton through a saddle-node bifurcation in the nonlinear Schrödinger problem. In Fig. 1, we explain the phase portrait to check it graphically. By implementing novel two analytic techniques such as unified solver and generalized unified techniques to offer insights into wave propagation and closed form optical soliton of NLS equation. By picking suitable parameter values, the graphical profiles in 3D, density, and 2D are engendered to visually contemporary the attained solutions, including periodic wave soliton, interaction of kink and bell shape soliton, periodic breather wave soliton, double periodic soliton through unified solver method and interaction of kink and periodic lump wave soliton and also with the periodic soliton, double periodic wave soliton, periodic wave soliton with lump soliton, multi periodic wave with kink shape soliton, periodic wave soliton, periodic breather wave soliton, periodic wave soliton, multi periodic wave soliton, periodic lump wave soliton, breather wave soliton multi periodic wave through generalized unified technique, providing an insightful visualization of the discovered solutions. The collected outcomes have the potential to facilitate an understanding and elucidation of the physical characteristics of waves moving within a dispersive substance. In a two-dimensional graph, we show the effect of truncated \(M\)-fractional parameters for [\(g=0.1, 0.5, 0.9\)]. Additionally, the modulation instability spectrum can be expressed utilizing a linear analysis technique, and the modulation instability bands are shown to be influenced by the third-order and group velocity dispersion. The findings indicate that the modulation instability disappears for negative values of the fourth order in a typical dispersion regime. The performance of the obtained solutions demonstrates the efficiency, conciseness, and effectiveness of the applied techniques, leading to fewer computations and wide applicability. The results of the examined wave are reliable for the researchers and have significant implications for mathematics and optical physics. In the future, we will study the chaotic behavior and sensitivity analysis of variable coefficient nonlinear variable coefficient third order nonlinear Schrödinger’s equation (PNLSE) with truncated space–time \(M\)-fractional derivative.