1 Introduction

Graphene is a material made of pure carbon and created from graphite. It is a 2D material with fascinating electrical, thermal, mechanical, chemical, and optical properties, so it is called “material of the future”. As a 2D material in optics, graphene shows many extraordinary properties such as a broadband ultrafast optical response, strong material anisotropy and large optical nonlinearities. These have empowered a lot of new photonic devices that are basically different from those based on traditional bulk materials. Therefore, it has a wide range of uses in manufacture of smartphones, batteries, electronic circuits to the construction of solar panels (Cui et al. 2021; Fan et al. 2019; Grigorenko et al. 2012; Wu et al. 2021).

Thermophoretic motion is the movement of microscopic particles due to a temperature gradient. In the context of graphene, thermophoretic motion refers to the movement of graphene sheets or particles adsorbed on graphene due to a temperature gradient (Luo et al. 2023; Usman et al. 2023).

There are two main mechanisms of thermophoretic motion in graphene. The first is the Conventional thermophoresis which based on the interaction between the graphene and the surrounding fluid molecules. When there is a temperature gradient, the fluid molecules near the hot side move faster than those near the cold side. This difference in velocity creates a drag force on the graphene, which causes it to move towards the cold side(Ramachandran et al. 2020). Where the second type is the ballistic thermophoresis which is specific to graphene and other two-dimensional (2D) materials. It is caused by the ballistic transport of heat through the graphene sheet. Ballistic heat transport refers to the propagation of heat waves without collisions. In graphene, heat waves are carried by flexural phonons, which are vibrations of the graphene sheet. When a flexural phonon scatters off an adsorbed particle, it can transfer momentum to the particle, causing it to move (Bae et al. 2013; Han et al. 2016).

Solitons are localized wave packets that can propagate through a medium without losing their shape. They can be found in various systems, including graphene wrinkles. So it was found that the KdV-type equations can be adapted to model the thermophoretic motion of single wrinkles (Guo and Guo 2012). Recently, Abdel-Gawad et al. (2021) have driven a new (2 + 1)-dimensional nonlinear equation using the kp operator on the KdV model which could be used to describe the thermophoretic motion in graphene sheets (GS) as a 2D material

$$\begin{aligned} v_{xt}+(vv_{x}+v_{xxx}+\left( a(t)+b\right) v_{x})_{x}+\delta \left( t\right) v_{yy}=0, \end{aligned}$$
(1)

where \(v=v(t,x,y)\) is the thermophoretic moving variable and t, x,y are time, longitudinal displacement, lateral displacement respectively with \( a\left( t\right) ,b\) as the thermal conductivity coefficients where \(\delta \left( t\right) \) is the coefficient of the lateral dispersion. When \(\delta \left( t\right) =0\), Eq. (1) reduces to the one dimensional thermophoretic equation with a variable heat transmission which was solved by many authors (Gaballah and El-Shiekh 2024; Guo and Guo 2012; Javid et al. 2019) where different structure of wave solutions like lump and solitary waves were found. Equation (1) is called the variable coefficients (2 + 1)-dimensional graphene sheets (2D-vGS) equation and it used to describe the thermophoretic waves transmission in (2 + 1)-dimentional graphene sheets, as wrinkles in graphene when heated, the hotter regions of the wrinkle experience a force pushing them towards the colder regions, causing the wrinkle move. However, in graphene, this motion occurs within the solid material itself, not in a surrounding fluid. Equation (1) was solved by the extended unified method and many types of polynomial and rational solutions were obtained (Abdel-Gawad et al. 2021).

From the previous background about thermophoretic motion in graphene and with Eq. (1) which can be considered as a model to describe that motion with a wide range of possible applications in nanodevices, purifying water, developing new lab-on-a-chip devices and studying the behavior of biological systems. Therefore, we have decided to study the 2D-vGS Eq. (1) to find new n-soliton wave solutions for it using the direct bilinear method.

This paper contains five sections, the first one is the introduction which reflects the importance of the 2D-vGS equation, and the second section gives a brief description for the direct technique presented by Hereman and Nuseir (1997) to find both the Hirota bilinear form and n-soliton wave solutions for nonlinear partial differential equations (Hereman and Nuseir 1997; Wazwaz 2007). Where in the third section, we have generalized the direct bilinear method by using suitable variable coefficient transformation to find the bilinear form of the 2D-vGS equation and the n-soliton wave solutions of that equation. In section four, a discussion of the two and three solitons behavior affected with different choices of the thermal conductivity is given with the physical importance of the obtained solutions in the 2D optics and the dynamic interactions. Finally, the fifth section contains the important conclusion remarks obtained from our study with future possible applications.

2 Simplified direct Hirota’s method

Recently, many different new techniques were developed and investigated to solve variable coefficients nonlinear partial differential equations like B äcklund transformation, Lie group analysis, symmetry techniques, Jacobi expansion method, trial equation method...etc (Abdel-Gawad and Osman 2013; Baskonus et al. 2021; Boakye et al. 2024; El-Shiekh et al. 2022; El-Shiekh 2021; El-Shiekh and Al-Nowehy 2022; El-Shiekh and Gaballah 2020a, b, 2021a, b, c, 2022, 2023a, b, 2024; El-Shiekh and Hamdy 2023; Fahim et al. 2022; Gaballah et al. 2023, 2022; Gaballah and El-Shiekh 2023; Ganie et al. 2024; Khater 2022a, b, c, d, e, f, 2023a, b, c, d, e, f, g, h, i, j, k, l, m; Kumar et al. 2020; Osman et al. 2018; Rehman et al. 2024; Tarla et al. 2022; Tarla et al. 2022). Hirota bilinear method still considered as the most attractive method for finding soliton wave solutions (Fan and Bao 2024; Yuan and Ghanbari 2024).

Since Hirota’s bilinear method is so complicated with higher order nonlinear partial differential equations. In Hereman and Nuseir (1997) presented a simple and direct algorithm of the Hirota’s method as follows:

For a nonlinear partial differential equation

$$\begin{aligned} P(v_{x},v_{y},v_{t},v_{xt},v_{xy},...)=0, \end{aligned}$$
(2)

assume that v takes a solution in the form

$$\begin{aligned} v\left( x,y,t\right) =R\sum _{i=1}^{k}\frac{\partial ^{i}\hbar }{\partial x^{i}}, \end{aligned}$$
(3)

where R is a constant can be determined by finishing the linear and nonlinear terms and k is a positive integer can be found from the balance procedure between linear and nonlinear coefficients in Eq. (2). \(\hbar =\hbar \left( x,y,t\right) \) arbitrary function. After find the form of the solution (3), we can use the Hirota bilinear differential operator

$$\begin{aligned} D_{t}^{m}D_{x}^{n}\left( fg\right) =\left. \left( \frac{\partial }{\partial t }-\frac{\partial }{\partial t^{\prime }}\right) ^{m}\left( \frac{\partial }{ \partial x}-\frac{\partial }{\partial x^{\prime }}\right) ^{n}f\left( x,t\right) g\left( x^{\prime },t^{\prime }\right) \right| _{x=x^{\prime },t=t^{\prime }}. \end{aligned}$$
(4)

where f and g two differentiable functions. Than we can rewrite Eq. (2) in the bilinear form but not all integrable equations can be written in this form, so Hereman and Nuseir find another way to rewrite Eq. (2) after substituting with Eq. (3) as a combination of both linear \( \mathcal {L}\) and nonlinear N terms in \(\hbar \)

$$\begin{aligned} \hbar \mathcal {L}(\hbar )+N(\hbar ,\hbar )=0, \end{aligned}$$
(5)

Then to fined soliton wave solution assume that

$$\begin{aligned} \hbar \left( x,y,t\right) =1+\sum _{n=1}^{\infty }\varepsilon ^{n}\hbar ^{\left( n\right) }\left( x,y,t\right) , \end{aligned}$$
(6)

where \(\varepsilon \) is not a small parameter it is a book-keeping parameter. Substitute from Eq. (6) into Eq. (5) and equate the coefficients of \(\varepsilon \) to zero, we get:

$$\begin{aligned} O(\varepsilon ^{1})&:&\mathcal {L}\hbar ^{(1)}=0, \end{aligned}$$
(7)
$$\begin{aligned} O(\varepsilon ^{2})&:&\mathcal {L}\hbar ^{(2)}=-N(\hbar ^{(1)},\hbar ^{(1)}), \end{aligned}$$
(8)
$$\begin{aligned} O(\varepsilon ^{3})&:&\mathcal {L}\hbar ^{(3)}=-\hbar ^{(1)}\mathcal {L}\hbar ^{(2)}-N(\hbar ^{(1)},\hbar ^{(2)})-N(\hbar ^{(2)},\hbar ^{(1)}), \end{aligned}$$
(9)
$$\begin{aligned}{} & {} . \nonumber \\{} & {} . \nonumber \\ O(\varepsilon ^{n})&:&\mathcal {L}\hbar ^{(n)}=-\sum _{j=1}^{n-1}[\hbar ^{j}\mathcal {L}\hbar ^{(n-j)}+N(\hbar ^{(j)},\hbar ^{(n-j)})]. \end{aligned}$$
(10)

For the one soliton solution

$$\begin{aligned} \hbar \left( x,y,t\right) =1+\epsilon \hbar ^{(1)}, \end{aligned}$$
(11)

and for the two solitons

$$\begin{aligned} \hbar \left( x,y,t\right) =1+\epsilon \hbar ^{(1)}+\epsilon ^{2}\hbar ^{(2)}. \end{aligned}$$
(12)

and so on.

3 N-soliton for the 2D-vGS equation

In order to find the Hirota’s bilinear form of the 2D-vGS equation, we use assumption (3) with the balance technique between the terms \(\left( vv_{x}\right) _{x}\) and \(v_{xxxx}.\) Therefore, \(k=2\) and \(R=12.\) So, Eq. (3) can be rewritten as:

$$\begin{aligned} v=12\left( \ln (\hbar \left( x,y,t\right) )\right) _{xx}. \end{aligned}$$
(13)

Now, substitute from Eq. (13) into Eq. (1):

$$\begin{aligned} \left( \ln \hbar \right) _{xxxt}+\left( 12\left( \ln \hbar \right) _{xx}\left( \ln \hbar \right) _{xxx}+\left( \ln \hbar \right) _{xxxxx}+\left( a(t)+b\right) \left( \ln \hbar \right) _{xxx}\right) _{x}+\delta \left( t\right) \left( \ln \hbar \right) _{xxyy}=0. \end{aligned}$$
(14)

By integration twice for Eq. (14) with respect to x we get:

$$\begin{aligned} \left( \ln \hbar \right) _{xt}+\left( 6(\left( \ln \hbar \right) _{xx})^{2}+\left( \ln \hbar \right) _{xxxx}+\left( a(t)+b\right) \left( \ln \hbar \right) _{xx}\right) +\delta \left( t\right) \left( \ln \hbar \right) _{yy}=0, \end{aligned}$$
(15)

where

$$\begin{aligned} \left( \ln \hbar \right) _{xt}= & {} \frac{\hbar _{xt}\hbar -\hbar _{x}\hbar _{t}}{h^{2}},\text { \ \ }\left( \ln \hbar \right) _{xx}=\frac{\hbar _{xx}\hbar -\hbar _{x}^{2}}{\hbar ^{2}},\text { \ \ }\left( \ln \hbar \right) _{yy}=\frac{\hbar _{yy}\hbar -\hbar _{y}^{2}}{\hbar ^{2}}, \nonumber \\ \text {\ }\left( \ln \hbar \right) _{xxxx}= & {} \frac{\hbar _{xxxx}\hbar -4\hbar _{xxx}\hbar _{x}+3\hbar _{xx}^{2}}{\hbar ^{2}}-\frac{6\left( \hbar _{xx}\hbar -\hbar _{x}^{2}\right) ^{2}}{\hbar ^{4}}. \end{aligned}$$
(16)

Substitute from Eq. (16) in Eq. (15), yields

$$\begin{aligned} \left( \hbar _{xt}\hbar -\hbar _{x}\hbar _{t}\right) +\left( a(t)+b\right) \left( \hbar _{xx}\hbar -\hbar _{x}^{2}\right) +\delta \left( t\right) \left( \hbar _{yy}\hbar -\hbar _{y}^{2}\right) +\left( \hbar _{xxxx}\hbar -4\hbar _{xxx}\hbar _{x}+3\hbar _{xx}^{2}\right) =0. \end{aligned}$$
(17)

From the Hirota’s D-operator defined by Eq. (4), we get

$$\begin{aligned} D_{x}D_{t}\hbar= & {} 2(\hbar \hbar _{xt}-\hbar _{x}\hbar _{t}),\text { } D_{x}^{2}\hbar =2\left( \hbar _{xx}\hbar -\hbar _{x}^{2}\right) ,\text { } D_{y}^{2}\hbar =2\left( \hbar _{yy}\hbar -\hbar _{y}^{2}\right) , \nonumber \\ D_{x}^{4}\hbar= & {} 2\left( \hbar _{xxxx}\hbar -4\hbar _{xxx}\hbar _{x}+3\hbar _{xx}^{2}\right) . \end{aligned}$$
(18)

So, Eq. (17) has the following bilinear form

$$\begin{aligned}{}[D_{x}D_{t}+\left( a(t)+b\right) D_{x}^{2}+\delta \left( t\right) D_{y}^{2}+D_{x}^{4}]\hbar .\hbar =0. \end{aligned}$$
(19)

Also, Eq. (17) is equivalent to

$$\begin{aligned} \hbar \left( \hbar _{xt}+\left( a(t)+b\right) \hbar _{xx}+\delta \left( t\right) \hbar _{yy}+\hbar _{xxxx}\right) -\left( \hbar _{x}\hbar _{t}+\left( a(t)+b\right) \hbar _{x}^{2}+\delta \left( t\right) \hbar _{y}^{2}+4\hbar _{xxx}\hbar _{x}-3\hbar _{xx}^{2}\right) =0. \end{aligned}$$
(20)

Comparing Eq. (20) with Eq. (7), the linear operator \(\pounds \) and the nonlinear operator N can be defined as:

$$\begin{aligned} \mathcal {L}(\hbar )= & {} \left( \frac{\partial ^{2}}{\partial x\partial t}+\left( a(t)+b\right) \frac{\partial ^{2}}{\partial x^{2}}+\delta \left( t\right) \frac{\partial ^{2}}{\partial y^{2}}+\frac{\partial ^{4}}{\partial x^{4}} \right) \hbar , \end{aligned}$$
(21)
$$\begin{aligned} N(\hbar ,\hbar )= & {} -\left( \hbar _{x}\hbar _{t}+\left( a(t)+b\right) \hbar _{x}^{2}+\delta \left( t\right) \hbar _{y}^{2}+4\hbar _{xxx}\hbar _{x}-3\hbar _{xx}^{2}\right) . \end{aligned}$$
(22)

The n-soliton solutions can be considered in the form

$$\begin{aligned} \hbar ^{(1)}=\sum _{i=1}^{N}\exp (\theta _{i}), \end{aligned}$$
(23)

where \(\theta _{i}=k_{i}x+l_{i}y-\lambda _{i}\left( t\right) -m_{i}t,\) \( k_{i},l_{i},m_{i}\) are arbitrary constants this suggestion of the \(\theta _{i}\) is used to make us able to find n-solitons for variable coefficient equations, where i is an integer number and \(\lambda _{i}\left( t\right) \) are arbitrary functions of t. By substitution in (20), we get the following dispersion relation

$$\begin{aligned} \lambda _{i}\left( t\right) =\frac{1}{k_{i}}\int \left( k_{i}^{2}\left( a\left( t\right) +b\right) +l_{i}^{2}\delta \left( t\right) \right) dt,m_{i}=k_{i}^{3}. \end{aligned}$$
(24)

Therefore,

$$\begin{aligned} \theta _{i}=k_{i}x+l_{i}y-\frac{1}{k_{i}}\int \left( k_{i}^{2}\left( a\left( t\right) +b\right) +l_{i}^{2}\delta \left( t\right) \right) dt-k_{i}^{3}t+c, \end{aligned}$$
(25)

where c is an integration constant. Now, the one soliton solution when \( N=1 \) and \(\varepsilon =1\) from Eqs. (11) and (13) is

$$\begin{aligned} v_{1}=\frac{12k_{1}^{2}e^{k_{1}x+l_{1}y-\frac{1}{k1}\int \left( k_{1}^{2}\left( a\left( t\right) +b\right) +l_{1}^{2}\delta \left( t\right) \right) dt-k_{1}^{3}t+c}}{\left( 1+e^{k_{1}x+l_{1}y-\frac{1}{k_{1}}\int \left( k_{1}^{2}\left( a\left( t\right) +b\right) +l_{1}^{2}\delta \left( t\right) \right) dt-k_{1}^{3}t+c}\right) ^{2}}. \end{aligned}$$
(26)

which is equivalent to

$$\begin{aligned} v_{1}=12k_{1}^{2}sech^{2}\left( \frac{1}{2}\left( k_{1}x+l_{1}y-\frac{1}{ k_{1}}\int \left( k_{1}^{2}\left( a\left( t\right) +b\right) +l_{1}^{2}\delta \left( t\right) \right) dt-k_{1}^{3}t+c\right) \right) . \end{aligned}$$
(27)

For two solitons assume that \(N=2\) and \(\varepsilon =1\), then \(\hbar ^{\left( 1\right) }=e^{\theta _{1}}+e^{\theta _{2}},\) and \(\hbar =1+e^{\theta _{1}}+e^{\theta _{2}}+\hbar ^{(2)}\left( x,y,t\right) \) by back substitution in (8), we get \(\hbar ^{(2)}=e^{\theta _{1}+\theta _{2}+\alpha _{12}}\) and \(e^{\alpha _{12}}=\frac{\left( k_{1}-k_{2}\right) ^{2}}{\left( k_{1}+k_{2}\right) ^{2}}\) with condition that \(l_{1}=k_{1},l_{2}=k_{2}\), hence the two soliton solution for the 2D-vGS equation is given by

$$\begin{aligned} v_{2}=12\left[ \frac{(k_{1}^{2}e^{\theta _{1}}+k_{2}^{2}e^{\theta _{2}}+\left( k_{1}-k_{2}\right) ^{2}e^{\theta _{1}+\theta _{2}})}{\left( 1+1+e^{\theta _{1}}+e^{\theta _{2}}+\frac{\left( k_{1}-k_{2}\right) ^{2}}{ \left( k_{1}+k_{2}\right) ^{2}}e^{\theta _{1}+\theta _{2}}\right) }-\frac{ (k_{1}e^{\theta _{1}}+k_{2}e^{\theta _{2}}+\frac{\left( k_{1}-k_{2}\right) ^{2}}{\left( k_{1}+k_{2}\right) }e^{\theta _{1}+\theta _{2}})^{2}}{\left( 1+1+e^{\theta _{1}}+e^{\theta _{2}}+\frac{\left( k_{1}-k_{2}\right) ^{2}}{ \left( k_{1}+k_{2}\right) ^{2}}e^{\theta _{1}+\theta _{2}}\right) ^{2}} \right] , \end{aligned}$$
(28)

where

$$\begin{aligned} \theta _{i}=k_{i}(x+y)-k_{i}\int \left( \left( a\left( t\right) +b\right) +\delta \left( t\right) \right) dt-k_{i}^{3}t+c_{i},i=1,2 \end{aligned}$$
(29)

Accordingly, to find the 3-soliton wave solution we consider \(N=3\) in Eq. (23), \(\hbar ^{\left( 1\right) }=e^{\theta _{1}}+e^{\theta _{2}}+e^{\theta _{3}},\) and \(\hbar ^{(2)}=e^{(\theta _{1}+\theta _{2})+\alpha _{12}}+e^{(\theta _{1}+\theta _{3})+\alpha _{13}}+e^{(\theta _{2}+\theta _{3})+\alpha _{23}}+\hbar ^{(3)}\left( x,y,t\right) \), then we get \(\hbar ^{(3)}=e^{(\theta _{1}+\theta _{2}+\theta _{3})+\alpha _{123}},e^{\alpha _{ij}}=\frac{\left( k_{i}-k_{j}\right) ^{2}}{\left( k_{i}+k_{j}\right) ^{2}}\) where \(e^{\alpha _{123}}=\frac{(k_{1}-k_{2})^{2} \left( k_{1}-k_{3}\right) ^{2}\left( k_{2}-k_{3}\right) ^{2}}{\left( k_{1}+k_{2}\right) ^{2}\left( k_{1}+k_{2}\right) ^{2}\left( k_{1}+k_{3}\right) ^{2}}.\)Therefore, the 2D-vGS equation has the following three soliton solution

$$\begin{aligned} v_{3}=12\left( \ln \left( 1+\sum _{i=1}^{3}e^{\theta _{i}}+\sum _{1\le i\le j}^{3}\frac{\left( k_{i}-k_{j}\right) ^{2}}{\left( k_{i}+k_{j}\right) ^{2}} e^{(\theta _{i}+\theta _{j})}+\frac{(k_{1}-k_{2})^{2}\left( k_{1}-k_{3}\right) ^{2}\left( k_{2}-k_{3}\right) ^{2}}{\left( k_{1}+k_{2}\right) ^{2}\left( k_{1}+k_{2}\right) ^{2}\left( k_{1}+k_{3}\right) ^{2}}e^{(\theta _{1}+\theta _{2}+\theta _{3})}\right) \right) _{xx} \end{aligned}$$
(30)

In the same way we can determine the soliton solutions for \(n\succeq 4.\) So this emphasis that the 2D-vGS equation is completely integrable and have any n soliton solutions.

4 Application in 2D optics

Graphene, a single layer of carbon atoms arranged in a honeycomb lattice, holds immense potential in the field of 2D optics and thermophonic due to its unique electronic and thermal properties. In this paper, we have found n-soliton wave solutions for the variable coefficient’s Eq. (1) which describes the thermophoretic motion of single wrinkles in graphene sheets which consider as an intriguing area of research with potential applications in manipulating light at the nanoscale in 2D optics. Wrinkles can modify the optical properties of graphene where their presence can affect how light interacts with the material also wrinkles can influence the propagation and localization of surface plasmons, which are collective oscillations of electrons on the graphene surface. Plasmons play a crucial role in various 2D photonic devices (Deng and Berry 2016; Ogawa et al. 2020).

From the previous description of the importance of the studied equation and its possible applications in 2D optics we are interested in this section to focus on the interactions of solitary waves specially on the second and third order solitons because those solutions are characterized by a rich spectrum of collision dynamics encompassing phenomena such as fusion and fission (Yuan and Ghanbari 2024). Moreover, the one soliton solution which was investigated before (Abdel-Gawad et al. 2021), we have plotted 3D plots and density plots corresponding to three different choices for the variable coefficients a(t) and \(\delta (t)\) as constant functions \(a(t)=\delta (t)=1 \) in figures (a), linear function of t like \(a(t)=\delta (t)=t\) in figures (b) and periodic function \(a(t)=\delta (t)=\sin (0.5t)\) in figures (c) as follows (Figs. 1, 2, 3, 4).

Fig. 1
figure 1

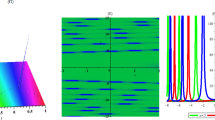
The 3D plot of the two soliton solution \(v_{2}\) given by Eq. (28) where parameters are taken as: \(k_{1}=2,k_{2}=b=c=1,y=0\)

Full size image
Fig. 2
figure 2

The density plot corresponding to the two soliton solution \(v_{2}\) for the three cases plotted in Fig. 3. The two solitons are taken the Y-shape soliton in (a) it is like a lines but in (b) and (c) take a curve shape in the second branch of the Y-shape affected with values of the variable coefficients

Full size image
Fig. 3
figure 3

The 3D plot of the three solitons solution \(v_{3}\) given by Eq. (30) where parameters are taken as: \( k_{1}=1,k_{2}=2,k_{3}=3,b=c_{1}=c_{2}=1,y=0\)

Full size image
Fig. 4
figure 4

The density plot of the three solitons solution \(v_{3}\) given by Eq. (30) and plotted in 3Dn Fig. 3, it is clear that the three solitons take a fork shape with three lines in (a) and takes three carves in (b) and (c)

Full size image
Fig. 5
figure 5

The three soliton solution taken Y-shape when we assumes \( k_{1}=k_{2}=1,k_{3}=2\) with \(b=c_{1}=c_{2}=1,y=0\)

Full size image
Fig. 6
figure 6

The density plot of the three soliton solution when \( k_{1}=k_{2}=1,k_{3}=2\) with \(b=c_{1}=c_{2}=1,y=0\), the Y-shape is so clear

Full size image

From the previous figures, we see that the two soliton waves make a Y-shape and the three soliton waves show a fork-shape when \(k_{1},k_{2},k_{3}\) take different values but it return to the Y-shape if any two k’s become equal and this means that one of the \(e^{\alpha _{ij}}=\frac{\left( k_{i}-k_{j}\right) ^{2}}{\left( k_{i}+k_{j}\right) ^{2}}=0\), and to prove this we have chosen \(k_{1}=k_{2}=0,e^{\alpha _{i2}}=0\) and plotted it in Figs. 5 and 6. The dynamic behavior and the nonlinearity properties of the obtained two and three solutions of the 2D-vGS equation could be important in 2D optic like modulation of light, surface plasmon resonance and thermal imaging.

5 Conclusion

The (2 + 1)-dimensional graphene sheets equation is a significant nonlinear model of 2D optics that broad relevance across various domains in science and engineering. In this study, we have generalized the direct Hirota bilinear method given by Hereman and Nuseir (1997), Wazwaz (2007) to find the bilinear form of the 2D-vGS model which describes the thermophoric wave motion of wrinkles in graphene sheets. According to that, one, two and three soliton solutions were obtained which yielded the n-soliton solutions for the 2D-vGS. So, we can concluded that this equation is fully integrable. In the following some important concluding remarks about the results obtained in this study:

  1. 1.

    The obtained soliton solutions specially the two and three solitons are new and didn’t obtained before for the 2D-vGS equation (Abdel-Gawad et al. 2021).

  2. 2.

    The fascinating dynamic behavior of the two solitons and three solitons as Y-shape and fork-shape solitons which could shed light on the fission and fusion dynamics of these solitary waves is illustrated.

  3. 3.

    The three solitons can give both fork shape solitary wave if the \( k^{\prime }s\) have different values but it returns to Y-shape if any two \( k^{\prime }s\) are equals.

  4. 4.

    From the 3D plots and density plots we can see the effect of both variable heat transmission function a(t) and the coefficient of the lateral dispersion \(\delta \left( t\right) \) on the propagation of the two and three solitons propagation.

Finally, we hope our work would have an impact in the manufacturer applications of the graphene sheets as a 2D material with fascinating properties specially in 2D optics.