1 Introduction

The nature of world is full of nonlinear phenomena which has become a matter of content of interest to the researchers. These complex phenomena have mostly been modeled through partial differential equations for better analyzing the behavior of nature (Miller and Ross 1993; Xu et al. 2021; Waqas et al. 2021a). Scholars and specialists on mathematical science, chemical science, biological science, atomic science, nuclear science, engineering etc. have been exploring the new-general appropriate and approximate solutions of nonlinear fractional partial differential equations on their respective area during the last few decades (Hu et al. 2008; Zhou et al. 2021; Shuaib et al. 2020a, b; Waqas et al. 2021b,c; Li et al. 2021; Ahmadian et al. 2020a, b; Gepreel 2011; Ma and Lee 2009; Guner and Eser 2014).

Firstly, we are interested to pay attention to some fractional nonlinear Schrodinger equations occurred in ample physical systems of nonlinear science. Mathematicians and physicists have taken into account various nonlinear Schrodinger types equations for wave solutions adopting several methods. Instantly, Li et al. (2019) have studied the (2 + 1)-dimensional time-fractional Schrodinger equation by using the \(\left( {G^{\prime}/G} \right)\)-expansion method, Wazwaz and Kaur (2019) has constructed optical solitons for nonlinear Schrodinger equation in normal dispersive regimes, the modified \(\left( {1/G^{\prime } } \right)\)-expansion method and the modified Kudryashov method were applied by Yokus et al. (2021) to introduce the plasma and optical fiber related complex hyperbolic type solitary waves, Cheema and Younis (2016) have used the extended Fan sub-equation method to study nonlinear Schrodinger equation for new and general wave solutions, cubic-quartic and resonant nonlinear Schrodinger equation has been considered by Gao et al. (2020) for optical soliton solutions via \(\left( {m + G^{\prime}/G} \right)\)-expansion method and exp-\(\varphi \left( \xi \right)\)-expansion method, Kaplan et al. (2016) have employed the \(\left( {G^{\prime}/G,1/G} \right)\)-expansion method and the \(\left( {1/G^{\prime}} \right)\)-expansion method to (1 + 1)-dimensional nonlinear Schrodinger equation for exact solutions, the (2 + 1)-dimensional hyperbolic nonlinear Schrodinger equation has been studied by Durur et al. (2020) by means of the \(\left( {m + 1/G^{\prime}} \right)\)-expansion method for novel complex wave solutions and many others (Younis et al. 2018; Liu et al. 2017; Chowdhury et al. 2021; Ismael et al. 2021; Zayed et al. 2021; Rizvi et al. 2017,2021; Salam et al. 2016; Pandir and Duzgun 2019; Lu et al. 2017; Akinyemi et al. 2021).

In this study, we hunt further new and general appropriate traveling wave solutions to the space and time fractional quadratic-cubic nonlinear Schrodinger equation. This equation has been considered for wave solutions by Biswas et al. (2017) by applying the semi-inverse variational principle. Pal et al. (2017) have investigated the same equation of integer order via similarity transformation method for analytical self-similar wave solutions. The most recent, Attia et al. (2021) have employed modified Khater method, generalized exp-\(\left( { - \phi \left( \xi \right)} \right)\)-expansion method and Adomian decomposition method and found analytical and semi-analytical solutions. We unravel the mentioned equation by making use of improved tanh method and rational \(\left( {G^{\prime}/G} \right)\)-expansion method and construct numerous different and novel huge analytic solutions successfully which might be significant to analyze the underlying behavior relating to optical and quantum mechanics.

A conversion of wave variable with the aid of conformable fractional derivative is used to convert the considered equations into the ordinary differential equations. Khalil et al. (2014) have proclaimed fractional derivative as follows:

The conformable derivative of a function \(u\left( x \right)\) is

$$D_{x}^{\alpha } \left( {u\left( x \right)} \right) = \mathop {lim}\limits_{\varepsilon \to 0} \frac{{u\left( {x + \varepsilon x^{1 - \alpha } } \right) - u\left( x \right)}}{\varepsilon },$$

where \(x > 0\) and \(\alpha\) denotes the order of derivative such as \(0 < \alpha \le 1\). The properties of this definition are brought out by the following theorems:

Theorem 1

If the functions \(g\left( x \right)\) and \(h\left( x \right)\) are \(\alpha\)-differentiable at any point \(x > 0\) for \(\alpha \in \left( {0,1} \right]\), then.

  1. (a)

    \(D_{x}^{\alpha } \left( {x^{n} } \right) = nx^{n - \alpha }\) \(\forall n \in {\varvec{R}}\).

  2. (b)

    \(D_{x}^{\alpha } \left( \lambda \right) = 0\), where \(\lambda\) is any constant.

  3. (c)

    \(D_{x}^{\alpha } \left( {ag\left( x \right) + bh\left( x \right)} \right) = aD_{x}^{\alpha } \left( {g\left( x \right)} \right) + bD_{x}^{\alpha } \left( {h\left( x \right)} \right)\) \(\forall a,b \in {\varvec{R}}\).

  4. (d)

    \(D_{x}^{\alpha } \left( {g\left( x \right)h\left( x \right)} \right) = g\left( x \right)D_{x}^{\alpha } \left( {h\left( x \right)} \right) + h\left( x \right)D_{x}^{\alpha } \left( {g\left( x \right)} \right)\).

  5. (e)

    \(D_{x}^{\alpha } \left( {g\left( x \right)/h\left( x \right)} \right) = \frac{{h\left( x \right)D_{x}^{\alpha } \left( {g\left( x \right)} \right) - g\left( x \right)D_{x}^{\alpha } \left( {h\left( x \right)} \right)}}{{h^{2} \left( x \right)}}\).

    if \(u\) is differentiable, then \(D_{x}^{\alpha } \left( g \right)\left( x \right) = x^{1 - \alpha } \frac{dg\left( x \right)}{{dx}}\).

Theorem 2

Suppose \(g\left( x \right)\) is differentiable and also \(\alpha\)-differentiable with \(\alpha \in \left( {0,1} \right]\). Let \(h\left( x \right)\) be a function defined in the same range of \(g\left( x \right)\) and also differentiable, then.

$$D_{x}^{\alpha } \left( {g\left( x \right).h\left( x \right)} \right) = x^{1 - \alpha } h^{\prime}\left( t \right)g^{\prime}\left( {h\left( t \right)} \right)$$

2 Explication of the method

Consider the following nonlinear partial differential equation involving \(u\left( {t, x_{1} , x_{2} , \ldots ,x_{n} } \right)\) and its different partial derivatives:

$$F\left( {u, D_{t}^{\alpha } u, D_{tt}^{2\alpha } u, \ldots ,D_{{x_{1} }}^{\alpha } u,D_{{x_{1} }}^{2\alpha } u, \ldots , D_{{x_{2} }}^{\alpha } u,D_{{x_{2} }}^{2\alpha } u, \ldots , D_{{x_{n} }}^{\alpha } u, D_{{x_{n} }}^{2\alpha } u, \ldots , D_{{x_{1} t}}^{\alpha } u, \ldots } \right) = 0$$
(1)

where \(0 < \alpha \le 1\). This equation with the assistance of wave variable transformation.

$$u = u\left( {t,x_{1} ,x_{2} , \ldots ,x_{n} } \right) = U\left( \xi \right),\;\xi = \xi \left( {t,x_{1} ,x_{2} , \ldots ,x_{n} } \right)$$
(2)

become the following ordinary differential equation due to \(\xi\):

$$R\left( {U, U^{\prime } , U^{\prime \prime } , U^{\prime \prime \prime } , \ldots \ldots \ldots } \right) = 0,$$
(3)

Differentiate Eq. (3) as many times possible. We might ignore the constant of integration for investigating soliton solutions. The main procedures of the suggested techniques are as follows:

2.1 The improved tanh method

Equation (1) is supposed to be satisfied by

$$u\left( \phi \right) = \frac{{a_{0} + \sum\nolimits_{{i = 1}}^{n} {\left( {a_{i} \varphi ^{i} \left( \phi \right) + b_{i} \varphi ^{{ - i}} \left( \phi \right)} \right)} }}{{c_{0} + \sum\nolimits_{{i = 1}}^{n} {\left( {c_{i} \varphi ^{i} \left( \phi \right) + d_{i} \varphi ^{{ - i}} \left( \phi \right)} \right)} }},$$
(4)

whose free parameters are calculated hereafter (Islam and Akter 2021). The value of \(n\) is fixed by considering the homogeneous balance principle for Eq. (3). The function \(\varphi = \varphi \left( \phi \right)\) satisfies the Riccati differential equation

$$\varphi^{\prime}\left( \phi \right) = \delta + \varphi^{2} \left( \phi \right),$$
(5)

where \(\delta\) is a constant. Eq. (5) has the following solutions:

  1. (1)

    \(\varphi \left( \phi \right) = - \sqrt { - \delta } {\text{tanh}}\left( {\sqrt { - \delta } \phi } \right)\) or \(\varphi \left( \phi \right) = - \sqrt { - \delta } {\text{coth}}\left( {\sqrt { - \delta } \phi } \right)\), \(\delta < 0\)

  2. (2)

    \(\varphi \left( \phi \right) = - 1/\phi\), \(\delta = 0\)

  3. (3)

    \(\varphi \left( \phi \right) = \sqrt \delta {\text{tan}}\left( {\sqrt \delta \phi } \right)\) or \(\varphi \left( \phi \right) = - \sqrt \delta {\text{cot}}\left( {\sqrt \delta \phi } \right)\), \(\delta > 0\).

Equation (3) adopting Eqs. (4) and (5) creates a polynomial in \(\varphi \left( \phi \right)\) whose coefficients are equated to zero and solved by any computational software for the values of the unknown constants involved in Eq. (4). Insert these values in Eq. (4) which alongside the solutions of Eq. (5) yield the solutions of Eq. (1).

2.2 The rational \(\left( {G^{\prime } /G} \right)\)-expansion method

The solution is supposed to be

$$u\left( \phi \right) = \frac{{\mathop \sum \nolimits_{i = 0}^{n} a_{i} \left( {G^{\prime } \left( \phi \right)/G\left( \phi \right)} \right)^{i} }}{{\mathop \sum \nolimits_{i = 0}^{n} b_{i} \left( {G^{\prime } \left( \phi \right)/G\left( \phi \right)} \right)^{i} }},$$
(6)

where \(n\) is determined by homogeneous balance principle to Eq. (3) and unknown parameters \(a_{i} ^{\prime}s\) and \(b_{i} ^{\prime}s\) are calculated later (Islam et al. 2015). The function \(\left( {G^{\prime}\left( \phi \right)/G\left( \phi \right)} \right)\) satisfies

$$AGG^{\prime \prime } - BGG^{\prime } - EG^{2} - CG^{\prime 2} = 0,$$
(7)

where primes denote the order of derivatives due to \(\phi\). Eq. (7) has the following solutions:

  1. (a)

    When \(B \ne 0\), \({\Psi } = A - C\) and \({\Phi } = B^{2} + 4E{\Psi } > 0\),

    $$\left( {G^{\prime } \left( \phi \right)/G\left( \phi \right)} \right) = \frac{B}{2\Psi } + \frac{\sqrt \Phi }{{2\Psi }}\frac{{C_{1} \sinh \left( {\left( {\sqrt \Phi /2A} \right)\phi } \right) + C_{2} \cosh \left( {\left( {\sqrt \Phi /2A} \right)\phi } \right)}}{{C_{1} \cosh \left( {\left( {\sqrt \Phi /2A} \right)\phi } \right) + C_{2} \sinh \left( {\left( {\sqrt \Phi /2A} \right)\phi } \right)}}$$
    (8)
  2. (b)

    For \(B \ne 0\), \({\Psi } = A - C\) and \({\Phi } = B^{2} + 4E{\Psi } < 0\),

    $$\left( {G^{\prime } \left( \phi \right)/G\left( \phi \right)} \right) = \frac{B}{2\Psi } + \frac{{\sqrt { - \Phi } }}{2\Psi }\frac{{ - C_{1} \sin \left( {\left( {\sqrt { - \Phi } /2A} \right)\phi } \right) + C_{2} \cos \left( {\left( {\sqrt { - \Phi } /2A} \right)\phi } \right)}}{{C_{1} \cos \left( {\left( {\sqrt { - \Phi } /2A} \right)\phi } \right) + C_{2} \sin \left( {\left( {\sqrt { - \Phi } /2A} \right)\phi } \right)}}$$
    (9)
  3. (c)

    If \(B \ne 0\), \({\Psi } = A - C\) and \({\Phi } = B^{2} + 4E{\Psi } = 0\),

    $$\left( {G^{\prime } \left( \phi \right)/G\left( \phi \right)} \right) = \frac{B}{2\Psi } + \frac{{C_{2} }}{{C_{1} + C_{2} \phi }}$$
    (10)
  4. (d)

    Once \(B = 0\), \({\Psi } = A - C\) and \(\Delta = {\Psi }E > 0\),

    $$\left( {G^{\prime } \left( \phi \right)/G\left( \phi \right)} \right) = \frac{\sqrt \Delta }{\Psi }\frac{{C_{1} \sinh \left( {\left( {\sqrt \Delta /A} \right)\phi } \right) + C_{2} \cosh \left( {\left( {\sqrt \Delta /A} \right)\phi } \right)}}{{C_{1} \cosh \left( {\left( {\sqrt \Delta /A} \right)\phi } \right) + C_{2} \sinh \left( {\left( {\sqrt \Delta /A} \right)\phi } \right)}}$$
    (11)
  5. (e)

    After \(B = 0\), \({\Psi } = A - C\) and \(\Delta = {\Psi }E < 0\),

    $$\left( {G^{\prime } \left( \phi \right)/G\left( \phi \right)} \right) = \frac{{\sqrt { - \Delta } }}{\Psi }\frac{{ - C_{1} \sin \left( {\left( {\sqrt { - \Delta } /A} \right)\phi } \right) + C_{2} \cos \left( {\left( {\sqrt { - \Delta } /A} \right)\phi } \right)}}{{C_{1} \cos \left( {\left( {\sqrt { - \Delta } /A} \right)\phi } \right) + C_{2} \sin \left( {\left( {\sqrt { - \Delta } /A} \right)\phi } \right)}}$$
    (12)

Equation (3) with the assistance of Eqs. (6) and (7) creates a polynomial in \(\left( {G^{\prime } \left( \phi \right)/G\left( \phi \right)} \right)\) whose coefficients assigning to zero give a set of algebraic equations. Solve the system by Maple and find the values of the constants involved in Eq. (6). Inserting these values in Eq. (6) and using the solutions of Eq. (7) yields the solutions of Eq. (1).

3 Formulation of solutions

Consider the space–time fractional quadratic-cubic fractional nonlinear Schrodinger equation.

$$iD_{t}^{\alpha } v + \iota D_{x}^{2\alpha } v - \epsilon v\left| v \right| + \epsilon v\left| v \right|^{2} = 0$$
(13)

where \(i = \sqrt { - 1}\), \(0 < \alpha < 1\); \(\iota\), \(\epsilon\) and \(\varepsilon\) are free parameters with \(\iota\) standing for the dispersion of group velocity. The variable \(v\) depends on the time variable \(t\) and space variable \(x\). Introducing the change of wave variable as

$$v\left( {x,t} \right) = e^{i\psi } u\left( \phi \right),\;\phi \left( {x,t} \right) = \left( {x^{\alpha } + \varrho t^{\alpha } } \right)/\alpha ,\;\psi \left( {x,t} \right) = \left( { - \rho x^{\alpha } + \omega t^{\alpha } } \right)/\alpha$$
(14)

confirm imaginary part to serve \(\varrho = 2\iota \rho\) and real part to be.

$$\iota u^{\prime \prime } - \left( {\omega + \iota \rho^{2} } \right)u - \epsilon u^{2} + \varepsilon u^{3} = 0.$$
(15)

In the transformation (14), \(u\left( {x,t} \right)\) is the wave amplitude component, \(\varrho\) is the wave velocity, \(\rho\) stands for soliton frequency and \(\omega\) is the wave number. Balancing principle to Eq. (3.3) gives the value \(n = 1\).

3.1 Construction of solutions by improved tanh method

Due to the balance number calculated above, the solution of Eq. (15) is appeared from Eq. (4) as

$$u\left( \phi \right) = \frac{{a_{0} + a_{1} \varphi \left( \phi \right) + b_{1} \varphi^{ - 1} \left( \phi \right)}}{{c_{0} + c_{1} \varphi \left( \phi \right) + d_{1} \varphi^{ - 1} \left( \phi \right)}}.$$
(16)

Equation (15) becomes a polynomial in \(\varphi \left( \phi \right)\) with the aid of Eq. (16) and Eq. (2.5). Set like terms to zero and solve for the parameters involved in Eq. (3.1.1) by Maple 20. We obtain the outcomes.

  • Case 1: \(a_{0} = \pm \frac{{\sqrt { - 2\iota \varepsilon } \left( {a_{1} \epsilon - 6d_{1} \iota } \right)}}{{6\iota \varepsilon }}\), \(b_{1} = \frac{{d_{1} \epsilon }}{3\varepsilon }\), \(c_{0} = \pm \frac{{a_{1} \sqrt { - 2\iota \varepsilon } }}{2\iota }\), \(c_{1} = 0\), \(\delta = \frac{{\epsilon^{2} }}{18\iota \varepsilon }\), \(\omega = - \frac{{9\iota \varepsilon \rho^{2} + 2\epsilon^{2} }}{9\varepsilon }\).

  • Case 2: \(a_{1} = 0\), \(b_{1} = \pm \frac{{a_{0} \epsilon }}{{3\sqrt { - 2\iota \varepsilon } }}\), \(c_{1} = 0\), \(d_{1} = \pm \frac{{3\varepsilon a_{0} - \varepsilon c_{0} }}{{3\sqrt { - 2\iota \varepsilon } }}\), \(\delta = \frac{{\epsilon ^{2} }}{{18\iota \varepsilon }}\), \(\omega = - \frac{{9\iota \varepsilon \rho ^{2} + 2\epsilon ^{2} }}{{9\varepsilon }}\).

  • Case 3: \(a_{0} = \frac{{c_{0} \epsilon }}{{3\varepsilon }}\), \(a_{1} = \pm \frac{{c_{0} \sqrt { - 2\iota \varepsilon } }}{\varepsilon }\), \(b_{1} = \pm \frac{{c_{0} \epsilon ^{2} }}{{18\varepsilon \sqrt { - 2\iota \varepsilon } }}\), \(c_{1} = d_{1} = 0\), \(\delta = - \frac{{\epsilon ^{2} }}{{36\iota \varepsilon }}\), \(\omega = - \frac{{9\iota \varepsilon \rho ^{2} + 2\epsilon ^{2} }}{{9\varepsilon }}\).

  • Case 4: \(a_{0} = 0\), \(a_{1} = \frac{{6\iota d_{1} }}{\epsilon }\), \(b_{1} = - \frac{{3d_{1} \left( {\epsilon + \iota \rho ^{2} } \right)}}{{2\epsilon }}\), \(c_{0} = \pm \frac{{3d_{1} \sqrt { - 2\iota \varepsilon } }}{\epsilon }\), \(c_{1} = 0\), \(\delta = - \frac{{\omega + \iota \rho^{2} }}{4\iota }\),

  • Case 5: \(a_{0} = \pm \frac{{\sqrt { - 2\iota \epsilon } \left( {a_{1} \varepsilon - 6d_{1} \iota } \right)}}{{6\iota \varepsilon }}\), \(b_{1} = - \frac{{\left( \epsilon {a_{1} \epsilon- 6d_{1} \iota } \right)}}{36\varepsilon \iota }\), \(c_{0} = \pm \frac{{a_{1} \sqrt { - 2\iota \varepsilon } }}{2\iota }\), \(c_{1} = 0\), \(\delta = - \frac{{a_{1}^{2} \epsilon ^{2} + 6\epsilon \iota a_{1} d_{1} - 72\iota ^{2} d_{1}^{2} }}{{36a_{1}^{2} \iota \varepsilon }}\), \(\omega = - \frac{{2\epsilon ^{2} a_{1}^{2} + 9a_{1}^{2} \iota \varepsilon \rho ^{2} - 6\epsilon \iota a_{1} d_{1} - 36\iota ^{2} d_{1}^{2} }}{{9a_{1}^{2} \varepsilon }}\).

  • Case 6: \(a_{0} = \frac{{c_{0}\epsilon }}{3\varepsilon }\), \(a_{1} = \pm \frac{{c_{0} \sqrt { - 2\iota \varepsilon } }}{\varepsilon }\), \(b_{1} = \pm \frac{{c_{0} \epsilon ^{2} }}{{36\varepsilon \sqrt { - 2\iota \varepsilon } }}\), \(c_{1} = d_{1} = 0\), \(\delta = \frac{{\epsilon ^{2} }}{{72\iota \varepsilon }}\), \(\omega = - \frac{{9\iota \varepsilon \rho ^{2} + 2\epsilon ^{2} }}{{9\varepsilon }}\).

  • Case 7: \(a_{0} = \frac{{c_{0} \epsilon }}{{3\varepsilon }}\), \(a_{1} = \pm \frac{{c_{0} \sqrt { - 2\iota \varepsilon } }}{\varepsilon }\), \(b_{1} = c_{1} = d_{1} = 0\), \(\delta = {\text{ }}\frac{{\epsilon ^{2} }}{{18\iota \varepsilon }}\), \(\omega = - \frac{{9\iota \varepsilon \rho ^{2} + 2\epsilon ^{2} }}{{9\varepsilon }}\).

  • Case 8: \(a_{0} = \pm \frac{{3b_{1} \sqrt { - 2\iota \varepsilon } }}{\epsilon }\), \(a_{1} = 0\), \(c_{0} = \pm {\text{ }}\frac{{9\varepsilon b_{1} \sqrt { - 2\iota \varepsilon } }}{{\epsilon ^{2} }}\), \(c_{1} = d_{1} = 0\), \(\delta = \frac{{\epsilon ^{2} }}{{18\iota \varepsilon }}\), \(\omega = - \frac{{9\iota \varepsilon \rho ^{2} + 2\epsilon ^{2} }}{{9\varepsilon }}\).

  • Case 9: \(a_{0} = \pm \frac{{d_{1} \sqrt { - 2\iota \varepsilon } }}{\varepsilon }\), \(a_{1} = 0\), \(b_{1} = \frac{{d_{1} \epsilon }}{{3\varepsilon }}\), \(c_{0} = c_{1} = 0\), \(\delta = \frac{{\epsilon ^{2} }}{{18\iota \varepsilon }}\), \(\omega = - \frac{{9\iota \varepsilon \rho ^{2} + 2\epsilon ^{2} }}{{9\varepsilon }}\).

Considering all cases abundant wave solutions might be found. For simplicity, we construct the solutions only for first three cases as follows:

  • Solution family 1: Inclusion case 1 in Eq. (16) and hence in Eq. (14) provides

    $$v_{1,2} \left( {x,t} \right) = e^{i\psi } \times \frac{{ \pm \sqrt {2\iota \epsilon \delta } \left( {a_{1} - 6d_{1} \iota } \right)\tanh \left( {\sqrt { - \delta } \phi } \right) + 6a_{1} \iota \varepsilon \delta \tanh^{2} \left( {\sqrt { - \delta } \phi } \right) - 2d_{1} \iota }}{{3\varepsilon \left\{ { \pm a_{1} \sqrt {2\iota \epsilon \delta } \tanh \left( {\sqrt { - \delta } \phi } \right) - 2d_{1} \epsilon \iota } \right\}}},\;\delta < 0$$
    (17)
    $$v_{3,4} \left( {x,t} \right) = e^{i\psi } \times \frac{{ \pm \sqrt {2\iota \epsilon \delta } \left( {a_{1} - 6d_{1} \iota } \right)\coth \left( {\sqrt { - \delta } \phi } \right) + 6a_{1} \iota \varepsilon \delta \coth^{2} \left( {\sqrt { - \delta } \phi } \right) - 2d_{1} \iota }}{{3\varepsilon \left\{ { \pm a_{1} \sqrt {2\iota \epsilon \delta } \coth \left( {\sqrt { - \delta } \phi } \right) - 2d_{1} \epsilon \iota } \right\}}},\;\delta < 0$$
    (18)
    $$v_{5,6} \left( {x,t} \right) = e^{i\psi } \times \frac{{ \pm \sqrt { - 2\iota \epsilon } \left( {a_{1} - 6d_{1} \iota } \right) - 6a_{1} \iota \varepsilon - 2d_{1} \iota \phi^{2} }}{{3\varepsilon \phi \left\{ { \pm a_{1} \sqrt { - 2\iota \varepsilon } - 2d_{1} \epsilon \iota \phi } \right\}}},\;\delta = 0$$
    (19)
    $$v_{7,8} \left( {x,t} \right) = e^{i\psi } \times \frac{{ \pm \sqrt { - 2\iota \varepsilon \delta } \left( {a_{1} - 6d_{1} \iota } \right)\tan \left( {\sqrt \delta \phi } \right) + 6a_{1} \iota \varepsilon \delta \tan^{2} \left( {\sqrt \delta \phi } \right) + 2d_{1} \iota }}{{3\varepsilon \left\{ { \pm a_{1} \sqrt { - 2\iota \varepsilon \delta } \tan \left( {\sqrt \delta \phi } \right) + 2d_{1} \epsilon \iota } \right\}}},\;\delta > 0$$
    (20)
    $$v_{9,10} \left( {x,t} \right) = e^{i\psi } \times \frac{{ \pm \sqrt { - 2\iota \varepsilon \delta } \left( {a_{1} - 6d_{1} \iota } \right)\cot \left( {\sqrt \delta \phi } \right) + 6a_{1} \iota \varepsilon \delta \cot^{2} \left( {\sqrt \delta \phi } \right) + 2d_{1} \iota }}{{3\varepsilon \left\{ { \pm a_{1} \sqrt { - 2\iota \varepsilon \delta } \cot \left( {\sqrt \delta \phi } \right) + 2d_{1} \epsilon \iota } \right\}}},\;\delta > 0$$
    (21)

    where \(\phi \left( {x,t} \right) = \left( {x^{\alpha } + 2\iota \rho t^{\alpha } } \right)/\alpha\), \(\psi \left( {x,t} \right) = - \left( {\rho x^{\alpha } + \frac{{9\iota \varepsilon \rho^{2} + 2^{2} }}{9\varepsilon }t^{\alpha } } \right)/\alpha\).

  • Solution family 2: Attachment case 2 in Eq. (16) and hereafter Eq. (14), we found the following exact solutions:

    $$v_{11,12} \left( {x,t} \right) = e^{i\psi } \times \frac{{ \pm a_{0} - 3a_{0} \sqrt {2\iota \varepsilon \delta } \tanh \left( {\sqrt { - \delta } \phi } \right)}}{{ \pm \left( {3\varepsilon a_{0} - \varepsilon c_{0} } \right) - 3c_{0} \sqrt {2\iota \varepsilon \delta } \tanh \left( {\sqrt { - \delta } \phi } \right)}},\;\delta < 0$$
    (22)
    $$v_{13,14} \left( {x,t} \right) = e^{i\psi } \times \frac{{ \pm a_{0} - 3a_{0} \sqrt {2\iota \varepsilon \delta } \coth \left( {\sqrt { - \delta } \phi } \right)}}{{ \pm \left( {3\varepsilon a_{0} - \varepsilon c_{0} } \right) - 3c_{0} \sqrt {2\iota \varepsilon \delta } \coth \left( {\sqrt { - \delta } \phi } \right)}},\;\delta < 0$$
    (23)
    $$v_{15,16} \left( {x,t} \right) = e^{i\psi } \times \frac{{ \pm a_{0} \phi - 3a_{0} \sqrt { - 2\iota \varepsilon } }}{{ \pm \left( {3\varepsilon a_{0} - \varepsilon c_{0} } \right)\phi - 3c_{0} \sqrt { - 2\iota \varepsilon } }},\;\delta = 0$$
    (24)
    $$v_{17,18} \left( {x,t} \right) = e^{i\psi } \times \frac{{3a_{0} \sqrt { - 2\iota \varepsilon \delta } \tan \left( {\sqrt \delta \phi } \right) \pm a_{0} }}{{3c_{0} \sqrt { - 2\iota \epsilon \delta } \tan \left( {\sqrt \delta \phi } \right) \pm \left( {3\varepsilon a_{0} - \varepsilon c_{0} } \right)}},\;\delta > 0$$
    (25)
    $$v_{19,20} \left( {x,t} \right) = e^{i\psi } \times \frac{{3a_{0} \sqrt { - 2\iota \varepsilon \delta } \cot \left( {\sqrt \delta \phi } \right) \pm a_{0} }}{{3c_{0} \sqrt { - 2\iota \epsilon \delta } \cot \left( {\sqrt \delta \phi } \right) \pm \left( {3\varepsilon a_{0} - \varepsilon c_{0} } \right)}},\;\delta > 0$$
    (26)

    where \(\phi \left( {x,t} \right) = \left( {x^{\alpha } + 2\iota \rho t^{\alpha } } \right)/\alpha\), \(\psi \left( {x,t} \right) = - \left( {\rho x^{\alpha } + \frac{{9\iota \varepsilon \rho^{2} + 2^{2} }}{9\varepsilon }t^{\alpha } } \right)/\alpha\).

  • Solution family 3: Merging case 3 with Eq. (16) and hence Eq. (14) carries the traveling wave solutions as follows:

    $$v_{21,22} \left( {x,t} \right) = e^{i\psi } \times \frac{{6 \epsilon \sqrt { - 2\iota \varepsilon } \pm 36\iota \varepsilon \sqrt { - \delta } \tanh \left( {\sqrt { - \delta } \phi } \right) \mp \frac{{^{2} }}{{\sqrt { - \delta } }}coth\left( {\sqrt { - \delta } \phi } \right)}}{{18\varepsilon \sqrt { - 2\iota \varepsilon } }},\;\delta < 0$$
    (27)
    $$v_{23,24} \left( {x,t} \right) = e^{i\psi } \times \frac{{6 \epsilon \sqrt { - 2\iota \varepsilon } \pm 36\iota \varepsilon \sqrt { - \delta } \coth \left( {\sqrt { - \delta } \phi } \right) \mp \frac{{^{2} }}{{\sqrt { - \delta } }}tanh\left( {\sqrt { - \delta } \phi } \right)}}{{18\varepsilon \sqrt { - 2\iota \varepsilon } }},\;\delta < 0$$
    (28)
    $$v_{25,26} \left( {x,t} \right) = e^{i\psi } \times \frac{{6 \epsilon \sqrt { - 2\iota \varepsilon } \pm 36\iota \varepsilon /\phi \mp^{2} \phi }}{{18\varepsilon \sqrt { - 2\iota \varepsilon } }},\;\delta = 0$$
    (29)
    $$v_{27,28} \left( {x,t} \right) = e^{i\psi } \times \frac{{6 \epsilon \sqrt { - 2\iota \varepsilon } \mp 36\iota \varepsilon \sqrt \delta \tan \left( {\sqrt \delta \phi } \right) \pm \frac{{^{2} }}{\sqrt \delta }cot\left( {\sqrt \delta \phi } \right)}}{{18\varepsilon \sqrt { - 2\iota \varepsilon } }},\;\delta > 0$$
    (30)
    $$v_{29,30} \left( {x,t} \right) = e^{i\psi } \times \frac{{6 \epsilon \sqrt { - 2\iota \varepsilon } \mp 36\iota \varepsilon \sqrt \delta \cot \left( {\sqrt \delta \phi } \right) \pm \frac{{^{2} }}{\sqrt \delta }tan\left( {\sqrt \delta \phi } \right)}}{{18\varepsilon \sqrt { - 2\iota \varepsilon } }},\;\delta > 0$$
    (31)

where \(\phi \left( {x,t} \right) = \left( {x^{\alpha } + 2\iota \rho t^{\alpha } } \right)/\alpha\), \(\psi \left( {x,t} \right) = - \left( {\rho x^{\alpha } + \frac{{9\iota \varepsilon \rho ^{2} + 2\epsilon ^{2} }}{{9\varepsilon }}t^{\alpha } } \right)/\alpha\).

3.2 Formulation of solutions by rational \(\left( {G^{\prime } /G} \right)\)-expansion method

Balancing number from Eq. (15) forces Eq. (4) to be

$$u\left( \phi \right) = \frac{{a_{0} + a_{1} \left( {G^{\prime}\left( \phi \right)/G\left( \phi \right)} \right)}}{{b_{0} + b_{1} \left( {G^{\prime}\left( \phi \right)/G\left( \phi \right)} \right)}}$$
(32)

Equation (15) along with the aid of Eq. (3.1.4) and Eq. (2.5) forms a polynomial in \(\left( {G^{\prime}\left( \phi \right)/G\left( \phi \right)} \right)\). Setting like terms to zero and solving by Maple provides the following outcomes:

  • Case 1: \(a_{1} = \frac{{a_{0} \left\{ {B \mp \sqrt {B^{2} + 4E\left( {A - C} \right)} } \right\}}}{2E}\), \(b_{1} = \frac{{Bb_{0} \epsilon \pm \left( {b_{0} \epsilon - 3a_{0} \varepsilon } \right)\sqrt {B^{2} + 4E\left( {A - C} \right)} }}{{2E\epsilon }}\), \(\iota = - \frac{{2A^{2} \epsilon ^{2} }}{{9\varepsilon \left\{ {B^{2} + 4E\left( {A - C} \right)} \right\}}}\), \(\omega = \frac{{2\epsilon ^{2} \left[ {A^{2} \rho ^{2} - \left\{ {B^{2} + 4E\left( {A - C} \right)} \right\}} \right]}}{{9\varepsilon \left\{ {B^{2} + 4E\left( {A - C} \right)} \right\}}}\).

  • Case 2: \(a_{1} = \frac{{a_{0} \left\{ {B \pm \sqrt {B^{2} + 4E\left( {A - C} \right)} } \right\}}}{2E}\), \(b_{0} = \frac{{3a_{0} \varepsilon }}{\epsilon }\), \(b_{1} = \frac{{3Ba_{0} \varepsilon }}{{2E\epsilon }}\), \(\iota = - \frac{{2A^{2} \epsilon ^{2} }}{{9\varepsilon \left\{ {B^{2} + 4E\left( {A - C} \right)} \right\}}}\), \(\omega = \frac{{2\epsilon^{2} \left[ {A^{2} \rho^{2} - \left\{ {B^{2} + 4E\left( {A - C} \right)} \right\}} \right]}}{{9\varepsilon \left\{ {B^{2} + 4E\left( {A - C} \right)} \right\}}}\).

  • Case 3: \(a_{0} = \frac{{b_{0} }}{2\varepsilon }\), \(a_{1} = \pm \frac{{b_{0} \left\{ {4E\left( {A - C} \right) + B^{2} \pm \sqrt {B^{2} + 4E\left( {A - C} \right)} } \right\}}}{{4E\varepsilon \sqrt {B^{2} + 4E\left( {A - C} \right)} }}\), \(b_{1} = \pm \frac{{b_{0} \left\{ {2B \pm \sqrt {B^{2} + 4E\left( {A - C} \right)} } \right\}}}{4E}\), \(\iota = - \frac{{2A^{2} \epsilon 2}}{{9\varepsilon \left\{ {B^{2} + 4E\left( {A - C} \right)} \right\}}}\), \(\omega = \frac{{2\epsilon ^{2} \left[ {A^{2} \rho ^{2} - \left\{ {B^{2} + 4E\left( {A - C} \right)} \right\}} \right]}}{{9\varepsilon \left\{ {B^{2} + 4E\left( {A - C} \right)} \right\}}}\).

  • Case 4: \(a_{0} = \frac{{b_{0} \epsilon}}{3\varepsilon }\), \(a_{1} = \pm \frac{{b_{0} \epsilon [9\varepsilon \iota \left\{ { - 4E\left( {A - C} \right) - B^{2} \pm B\sqrt {B^{2} + 4E\left( {A - C} \right)} } \right\} + 2A^{{2^{2} }} }}{{54E\varepsilon ^{2} \iota \sqrt {B^{2} + 4E\left( {A - C} \right)} }}\) \(b_{1} = \frac{{b_{0} \left\{ {B \pm \sqrt {B^{2} + 4E\left( {A - C} \right)} } \right\}}}{2E}\), \(\omega = - \frac{{A^{2}\epsilon^{2} + 3A^{2} \rho^{2} \iota \varepsilon - 3B^{2} \varepsilon \iota - 12E\iota \varepsilon \left( {A - C} \right)}}{{3A^{2} \varepsilon }}\).

  • Case 5: \(a_{0} = \pm \frac{{2b_{1} E\epsilon}}{{3\varepsilon \sqrt {B^{2} + 4E\left( {A - C} \right)} }}\), \(a_{1} = \pm \frac{{4b_{1}\epsilon \left\{ {4E\left( {A - C} \right) + B^{2} \pm \sqrt {B^{2} + 4E\left( {A - C} \right)} } \right\}}}{{12\varepsilon \left\{ {B^{2} + 4E\left( {A - C} \right)} \right\}}}\), \(b_{0} = 0\), \(\iota = - \frac{{2A^{2} \epsilon ^{2} }}{{9\varepsilon \left\{ {B^{2} + 4E\left( {A - C} \right)} \right\}}}\), \(\omega = \frac{{2^{2} \left[ {A^{2} \rho^{2} - \left\{ {B^{2} + 4E\left( {A - C} \right)} \right\}} \right]}}{{9\varepsilon \left\{ {B^{2} + 4E\left( {A - C} \right)} \right\}}}\).

These cases provide abundant traveling wave solutions. Avoiding the similar tasks, we record the solutions only for first three cases. Combining case 1, case2 and solutions of Eq. (7) Eq. (32) makes available the following results:

  • Solution family 1: Utilizing the values appeared in case 1 in Eq. (32) and combining with Eqs. (8)–(12), we gain the following exact solutions:

When \(B \ne 0\), \({\Psi } = A - C\) and \({\Phi } = B^{2} + 4E{\Psi } > 0\), (\(C_{1} \ne 0, C_{2} = 0;C_{1} = 0, C_{2} \ne 0\)):

$$v_{1,2} \left( {x,t} \right) = e^{i\psi } \times \frac{{4{\Psi } \epsilon Ea_{0} + \epsilon a_{0} \left\{ {B \mp \sqrt {\Phi } } \right\}\left( {B + \sqrt {\Phi } \tan h\left( {\left( {\sqrt {\Phi } /2A} \right)\phi } \right)} \right)}}{{4{\Psi }Eb_{0} \epsilon + 2{\Psi }Bb_{0} \epsilon \pm \left( {b_{0} \epsilon - 3a_{0} \varepsilon } \right)\sqrt {\Phi } \left( {B + \sqrt {\Phi } \tan h\left( {\left( {\sqrt {\Phi } /2A} \right)\phi } \right)} \right)}},$$
(33)
$$v_{3,4} \left( {x,t} \right) = e^{i\psi } \times \frac{{4{\Psi }E \epsilon a_{0} + a_{0} \left\{ {B \mp \sqrt {\Phi } } \right\}\left( {B + \sqrt {\Phi } \cot h\left( {\left( {\sqrt {\Phi } /2A} \right)\phi } \right)} \right)}}{{4{\Psi }Eb_{0} \epsilon + 2{\Psi }Bb_{0} \epsilon \pm \left( {b_{0} \epsilon - 3a_{0} \varepsilon } \right)\sqrt {\Phi } \left( {B + \sqrt {\Phi } \cot h\left( {\left( {\sqrt {\Phi } /2A} \right)\phi } \right)} \right)}},$$
(34)

where \(\phi \left( {x,t} \right) = \left( {x^{\alpha } + 2\iota \rho t^{\alpha } } \right)/\alpha\), \(\psi \left( {x,t} \right) = \left( { - \rho x^{\alpha } + \frac{{2 \epsilon ^{2} \left( {A^{2} \rho^{2} - {\Phi }} \right)}}{{9\varepsilon {\Phi }}}t^{\alpha } } \right)/\alpha\).

For \(B \ne 0\), \({\Psi } = A - C\) and \({\Phi } = B^{2} + 4E{\Psi } < 0\), (\(C_{1} \ne 0, C_{2} = 0;C_{1} = 0, C_{2} \ne 0\)):

$$v_{5,6} \left( {x,t} \right) = e^{i\psi } \times \frac{{4{\Psi }Ea_{0} + a_{0} \left\{ {B \mp \sqrt {\Phi } } \right\}\left( {B - \sqrt { - {\Phi }} \tan \left( {\left( {\sqrt { - {\Phi }} /2A} \right)\phi } \right)} \right)}}{{4{\Psi }Eb_{0} + 2{\Psi }Bb_{0} \pm \left( {b_{0} - 3a_{0} \varepsilon } \right)\sqrt {\Phi } \left( {B - \sqrt { - {\Phi }} \tan \left( {\left( {\sqrt { - {\Phi }} /2A} \right)\phi } \right)} \right)}},$$
(35)
$$v_{7,8} \left( {x,t} \right) = e^{i\psi } \times \frac{{4{\Psi }E \epsilon a_{0} + \epsilon a_{0} \left\{ {B \mp \sqrt {\Phi } } \right\}\left( {B + \sqrt { - {\Phi }} \cot \left( {\left( {\sqrt { - {\Phi }} /2A} \right)\phi } \right)} \right)}}{{4{\Psi }Eb_{0} \epsilon + 2{\Psi }Bb_{0} \epsilon \pm \left( {b_{0} - 3a_{0} \varepsilon } \right)\sqrt {\Phi } \left( {B + \sqrt { - {\Phi }} \cot \left( {\left( {\sqrt { - {\Phi }} /2A} \right)\phi } \right)} \right)}},$$
(36)

where \(\phi \left( {x,t} \right) = \left( {x^{\alpha } + 2\iota \rho t^{\alpha } } \right)/\alpha\), \(\psi \left( {x,t} \right) = \left( { - \rho x^{\alpha } + \frac{{2 \epsilon ^{2} \left( {A^{2} \rho^{2} - {\Phi }} \right)}}{{9\varepsilon {\Phi }}}t^{\alpha } } \right)/\alpha\).

If \(B \ne 0\), \({\Psi } = A - C\) and \({\Phi } = B^{2} + 4E{\Psi } = 0\), the solution is inconsistent.

Once \(B = 0\), \({\Psi } = A - C\) and \({\Delta } = {\Psi }E > 0\), (\(C_{1} \ne 0, C_{2} = 0;C_{1} = 0, C_{2} \ne 0\)):

$$v_{9,10} \left( {x,t} \right) = e^{i\psi } \times \frac{{E \epsilon a_{0} {\Psi } \mp \epsilon a_{0} {\Delta }\tan h\left( {\left( {\sqrt {\Delta } /A} \right)\phi } \right)}}{{Eb_{0} \epsilon {\Psi } \pm \left( {b_{0} \epsilon - 3a_{0} \varepsilon } \right){\Delta }\tan h\left( {\left( {\sqrt {\Delta } /A} \right)\phi } \right)}},$$
(37)
$$v_{11,12} \left( {x,t} \right) = e^{i\psi } \times \frac{{Ea_{0} {\Psi } \mp a_{0} {\Delta }\cot h\left( {\left( {\sqrt {\Delta } /A} \right)\phi } \right)}}{{Eb_{0} {\Psi } \pm \left( {b_{0} - 3a_{0} \varepsilon } \right){\Delta }\cot h\left( {\left( {\sqrt {\Delta } /A} \right)\phi } \right)}},$$
(38)

where \(\phi \left( {x,t} \right) = \left( {x^{\alpha } + 2\iota \rho t^{\alpha } } \right)/\alpha\), \(\psi \left( {x,t} \right) = \left( { - \rho x^{\alpha } + \frac{{2 \epsilon ^{2} \left( {A^{2} \rho^{2} - 4{\Delta }} \right)}}{{36\varepsilon {\Delta }}}t^{\alpha } } \right)/\alpha\).

After \(B = 0\), \({\Psi } = A - C\) and \(\Delta = {\Psi }E < 0\), (\(C_{1} \ne 0, C_{2} = 0;C_{1} = 0, C_{2} \ne 0\)):

$$v_{13,14} \left( {x,t} \right) = e^{i\psi } \times \frac{{Ea_{0} {\Psi } \mp a_{0} {\Delta }\tan \left( {\left( {\sqrt { - {\Delta }} /A} \right)\phi } \right)}}{{Eb_{0} {\Psi } \pm \left( {b_{0} - 3a_{0} \varepsilon } \right){\Delta } \tan \left( {\left( {\sqrt { - {\Delta }} /A} \right)\phi } \right)}},$$
(39)
$$v_{15,16} \left( {x,t} \right) = e^{i\psi } \times \frac{{E \epsilon a_{0} {\Psi } \pm \epsilon a_{0} {\Delta }\tan \left( {\left( {\sqrt { - {\Delta }} /A} \right)\phi } \right)}}{{Eb_{0} \epsilon {\Psi } \mp \left( {b_{0} \epsilon - 3a_{0} \varepsilon } \right){\Delta } \tan \left( {\left( {\sqrt { - {\Delta }} /A} \right)\phi } \right)}},$$
(40)

where \(\phi \left( {x,t} \right) = \left( {x^{\alpha } + 2\iota \rho t^{\alpha } } \right)/\alpha\), \(\psi \left( {x,t} \right) = \left( { - \rho x^{\alpha } + \frac{{2 \epsilon ^{2} \left( {A^{2} \rho^{2} - 4{\Delta }} \right)}}{{36\varepsilon {\Delta }}}t^{\alpha } } \right)/\alpha\).

Solution family 2: Employing the values involved in case 2 in Eq. (32) and combining with Eqs. (8)–(12) the following wave solutions are achieved:

For \(B \ne 0\), \({\Psi } = A - C\) and \({\Phi } = B^{2} + 4E{\Psi } > 0\), (\(C_{1} \ne 0, C_{2} = 0;C_{1} = 0, C_{2} \ne 0\)):

$$v_{17,18} \left( {x,t} \right) = e^{i\psi } \times \frac{{4{\Psi }E \epsilon + \epsilon \left( {B \pm \sqrt {\Phi } } \right)\left( {B + \sqrt {\Phi } \tan h\left( {\left( {\sqrt {\Phi } /2A} \right)\phi } \right)} \right)}}{{12{\Psi }E\varepsilon + 3B\varepsilon \left( {B + \sqrt {\Phi } \tan h\left( {\left( {\sqrt {\Phi } /2A} \right)\phi } \right)} \right)}},$$
(41)
$$v_{19,20} \left( {x,t} \right) = e^{i\psi } \times \frac{{4{\Psi }E + \left( {B \pm \sqrt {\Phi } } \right)\left( {B + \sqrt {\Phi } \cot h\left( {\left( {\sqrt {\Phi } /2A} \right)\phi } \right)} \right)}}{{12{\Psi }E\varepsilon + 3B\varepsilon \left( {B + \sqrt {\Phi } \cot h\left( {\left( {\sqrt {\Phi } /2A} \right)\phi } \right)} \right)}},$$
(42)

where \(\phi \left( {x,t} \right) = \left( {x^{\alpha } + 2\iota \rho t^{\alpha } } \right)/\alpha\), \(\psi \left( {x,t} \right) = \left( { - \rho x^{\alpha } + \frac{{2 \epsilon ^{2} \left( {A^{2} \rho^{2} - {\Phi }} \right)}}{{9\varepsilon {\Phi }}}t^{\alpha } } \right)/\alpha\).

Utilizing \(B \ne 0\), \({\Psi } = A - C\) and \({\Phi } = B^{2} + 4E{\Psi } < 0\), (\(C_{1} \ne 0, C_{2} = 0;C_{1} = 0, C_{2} \ne 0\)):

$$v_{21,22} \left( {x,t} \right) = e^{i\psi } \times \frac{{4{\Psi }E \epsilon + \epsilon \left( {B \pm \sqrt {\Phi } } \right)\left( {B - \sqrt { - {\Phi }} \tan \left( {\left( {\sqrt { - {\Phi }} /2A} \right)\phi } \right)} \right)}}{{12{\Psi }E\varepsilon + 3B\varepsilon \left( {B - \sqrt { - {\Phi }} \tan \left( {\left( {\sqrt { - {\Phi }} /2A} \right)\phi } \right)} \right)}},$$
(43)
$$v_{23,24} \left( {x,t} \right) = e^{i\psi } \times \frac{{4{\Psi }E \epsilon + \epsilon \left( {B \pm \sqrt {\Phi } } \right)\left( {B + \sqrt { - {\Phi }} \cot \left( {\left( {\sqrt { - {\Phi }} /2A} \right)\phi } \right)} \right)}}{{12{\Psi }E\varepsilon + 3B\varepsilon \left( {B + \sqrt { - {\Phi }} \cot \left( {\left( {\sqrt { - {\Phi }} /2A} \right)\phi } \right)} \right)}},$$
(44)

where \(\phi \left( {x,t} \right) = \left( {x^{\alpha } + 2\iota \rho t^{\alpha } } \right)/\alpha\), \(\psi \left( {x,t} \right) = \left( { - \rho x^{\alpha } + \frac{{2 \epsilon ^{2} \left( {A^{2} \rho^{2} - {\Phi }} \right)}}{{9\varepsilon {\Phi }}}t^{\alpha } } \right)/\alpha\).

When \(B \ne 0\), \({\Psi } = A - C\) and \({\Phi } = B^{2} + 4E{\Psi } = 0\), the solution is inconsistent.

Once \(B = 0\), \({\Psi } = A - C\) and \({\Delta } = {\Psi }E > 0\), (\(C_{1} \ne 0, C_{2} = 0;C_{1} = 0, C_{2} \ne 0\)):

$$v_{25,26} \left( {x,t} \right) = e^{i\psi } \times \frac{{2{\Delta } \epsilon \pm 2 \epsilon {\Delta }\tan h\left( {\left( {\sqrt {\Delta } /A} \right)\phi } \right)}}{{6{\Delta }\varepsilon + 3B\varepsilon \sqrt {\Delta } \tan h\left( {\left( {\sqrt {\Delta } /A} \right)\phi } \right)}},$$
(45)
$$v_{27,28} \left( {x,t} \right) = e^{i\psi } \times \frac{{2{\Delta } \epsilon \pm 2 \epsilon {\Delta }\cot h\left( {\left( {\sqrt {\Delta } /A} \right)\phi } \right)}}{{6{\Delta }\varepsilon + 3B\varepsilon \sqrt {\Delta } \cot h\left( {\left( {\sqrt {\Delta } /A} \right)\phi } \right)}},$$
(46)

where \(\phi \left( {x,t} \right) = \left( {x^{\alpha } + 2\iota \rho t^{\alpha } } \right)/\alpha\), \(\psi \left( {x,t} \right) = \left( { - \rho x^{\alpha } + \frac{{2 \epsilon ^{2} \left( {A^{2} \rho^{2} - 4{\Delta }} \right)}}{{36\varepsilon {\Delta }}}t^{\alpha } } \right)/\alpha\).

If we consider \(B = 0\), \({\Psi } = A - C\) and \(\Delta = {\Psi }E < 0\), (\(C_{1} \ne 0, C_{2} = 0;C_{1} = 0, C_{2} \ne 0\)):

$$v_{29,30} \left( {x,t} \right) = e^{i\psi } \times \frac{{2{\Delta } \epsilon \mp 2 \epsilon {\Delta }\tan \left( {\left( {\sqrt { - {\Delta }} /A} \right)\phi } \right)}}{{6{\Delta }\varepsilon - 3B\varepsilon \sqrt { - {\Delta }} \tan \left( {\left( {\sqrt { - {\Delta }} /A} \right)\phi } \right)}},$$
(47)
$$v_{31,32} \left( {x,t} \right) = e^{i\psi } \times \frac{{2{\Delta } \epsilon \pm 2 \epsilon {\Delta }\cot \left( {\left( {\sqrt { - {\Delta }} /A} \right)\phi } \right)}}{{6{\Delta }\varepsilon + 3B\varepsilon \sqrt { - {\Delta }} \cot \left( {\left( {\sqrt { - {\Delta }} /A} \right)\phi } \right)}},$$
(48)

where \(\phi \left( {x,t} \right) = \left( {x^{\alpha } + 2\iota \rho t^{\alpha } } \right)/\alpha\), \(\psi \left( {x,t} \right) = \left( { - \rho x^{\alpha } + \frac{{2 \epsilon ^{2} \left( {A^{2} \rho^{2} - 4{\Delta }} \right)}}{{36\varepsilon {\Delta }}}t^{\alpha } } \right)/\alpha\).

Solution family 3: Engaging the values from case 2 in Eq. (32) and merging with Eqs. (8)–(12) the analytic wave solutions are found as follows:

Under the conditions \(B \ne 0\), \({\Psi } = A - C\) and \({\Phi } = B^{2} + 4E{\Psi } > 0\), (\(C_{1} \ne 0, C_{2} = 0;C_{1} = 0, C_{2} \ne 0\)):

$$v_{33,34} \left( {x,t} \right) = e^{i\psi } \times \frac{{4{\Psi }E \epsilon \sqrt {\Phi } \pm \epsilon \left( {4E{\Psi } + B^{2} \pm \sqrt {\Phi } } \right)\left( {B + \sqrt {\Phi } \tan h\left( {\left( {\sqrt {\Phi } /2A} \right)\phi } \right)} \right)}}{{\varepsilon \sqrt {\Phi } \left\{ {8E{\Psi } \pm \left\{ {2B \pm \sqrt {\Phi } } \right\}\left( {B + \sqrt {\Phi } \tan h\left( {\left( {\sqrt {\Phi } /2A} \right)\phi } \right)} \right)} \right\}}},$$
(49)
$$v_{35,36} \left( {x,t} \right) = e^{i\psi } \times \frac{{4{\Psi }E \epsilon \sqrt {\Phi } \pm \epsilon \left( {4E{\Psi } + B^{2} \pm \sqrt {\Phi } } \right)\left( {B + \sqrt {\Phi } \cot h\left( {\left( {\sqrt {\Phi } /2A} \right)\phi } \right)} \right)}}{{\varepsilon \sqrt {\Phi } \left\{ {8E{\Psi } \pm \left\{ {2B \pm \sqrt {\Phi } } \right\}\left( {B + \sqrt {\Phi } \cot h\left( {\left( {\sqrt {\Phi } /2A} \right)\phi } \right)} \right)} \right\}}},$$
(50)

where \(\phi \left( {x,t} \right) = \left( {x^{\alpha } + 2\iota \rho t^{\alpha } } \right)/\alpha\), \(\psi \left( {x,t} \right) = \left( { - \rho x^{\alpha } + \frac{{2 \epsilon ^{2} \left( {A^{2} \rho^{2} - {\Phi }} \right)}}{{9\varepsilon {\Phi }}}t^{\alpha } } \right)/\alpha\).

If \(B \ne 0\), \({\Psi } = A - C\) and \({\Phi } = B^{2} + 4E{\Psi } < 0\), (\(C_{1} \ne 0, C_{2} = 0;C_{1} = 0, C_{2} \ne 0\)):

$$v_{37,38} \left( {x,t} \right) = e^{i\psi } \times \frac{{4{\Psi }E \epsilon \sqrt {\Phi } \pm \epsilon \left( {4E{\Psi } + B^{2} \pm \sqrt {\Phi } } \right)\left( {B - \sqrt { - {\Phi }} \tan \left( {\left( {\sqrt { - {\Phi }} /2A} \right)\phi } \right)} \right)}}{{\varepsilon \sqrt {\Phi } \left\{ {8E{\Psi } \pm \left\{ {2B \pm \sqrt {\Phi } } \right\}\left( {B - \sqrt { - {\Phi }} \tan \left( {\left( {\sqrt { - {\Phi }} /2A} \right)\phi } \right)} \right)} \right\}}},$$
(51)
$$v_{39,40} \left( {x,t} \right) = e^{i\psi } \times \frac{{4{\Psi }E \epsilon \sqrt {\Phi } \pm \epsilon \left( {4E{\Psi } + B^{2} \pm \sqrt {\Phi } } \right)\left( {B + \sqrt { - {\Phi }} \cot \left( {\left( {\sqrt { - {\Phi }} /2A} \right)\phi } \right)} \right)}}{{\varepsilon \sqrt {\Phi } \left\{ {8E{\Psi } \pm \left\{ {2B \pm \sqrt {\Phi } } \right\}\left( {B + \sqrt { - {\Phi }} \cot \left( {\left( {\sqrt { - {\Phi }} /2A} \right)\phi } \right)} \right)} \right\}}},$$
(52)

where \(\phi \left( {x,t} \right) = \left( {x^{\alpha } + 2\iota \rho t^{\alpha } } \right)/\alpha\), \(\psi \left( {x,t} \right) = \left( { - \rho x^{\alpha } + \frac{{2 \epsilon ^{2} \left( {A^{2} \rho^{2} - {\Phi }} \right)}}{{9\varepsilon {\Phi }}}t^{\alpha } } \right)/\alpha\).

When \(B \ne 0\), \({\Psi } = A - C\) and \({\Phi } = B^{2} + 4E{\Psi } = 0\), the solution is inconsistent.

For the usage of \(B = 0\), \({\Psi } = A - C\) and \({\Delta } = {\Psi }E > 0\), (\(C_{1} \ne 0, C_{2} = 0;C_{1} = 0, C_{2} \ne 0\)):

$$v_{41,42} \left( {x,t} \right) = e^{i\psi } \times \frac{{2 \epsilon {\Delta } \pm \epsilon \left\{ {2{\Delta } \pm \sqrt {\Delta } } \right\}\tan h\left( {\left( {\sqrt {\Delta } /A} \right)\phi } \right)}}{{2\varepsilon \left\{ {2{\Delta } \pm {\Delta }\tan h\left( {\left( {\sqrt {\Delta } /A} \right)\phi } \right)} \right\}}},$$
(53)
$$v_{43,44} \left( {x,t} \right) = e^{i\psi } \times \frac{{2 \epsilon {\Delta } \pm \epsilon \left\{ {2{\Delta } \pm \sqrt {\Delta } } \right\}\cot h\left( {\left( {\sqrt {\Delta } /A} \right)\phi } \right)}}{{2\varepsilon \left\{ {2{\Delta } \pm {\Delta }\cot h\left( {\left( {\sqrt {\Delta } /A} \right)\phi } \right)} \right\}}},$$
(54)

where \(\phi \left( {x,t} \right) = \left( {x^{\alpha } + 2\iota \rho t^{\alpha } } \right)/\alpha\), \(\psi \left( {x,t} \right) = \left( { - \rho x^{\alpha } + \frac{{2 \epsilon ^{2} \left( {A^{2} \rho^{2} - 4{\Delta }} \right)}}{{36\varepsilon {\Delta }}}t^{\alpha } } \right)/\alpha\).

If we assign \(B = 0\), \({\Psi } = A - C\) and \(\Delta = {\Psi }E < 0\), (\(C_{1} \ne 0, C_{2} = 0;C_{1} = 0, C_{2} \ne 0\)):

$$v_{45,46} \left( {x,t} \right) = e^{i\psi } \times \frac{{2 \epsilon {\Delta } \mp i \epsilon \left\{ {2{\Delta } \pm \sqrt {\Delta } } \right\}\tan \left( {\left( {\sqrt { - {\Delta }} /A} \right)\phi } \right)}}{{2\varepsilon \left\{ {2{\Delta } \mp i{\Delta }\tan \left( {\left( {\sqrt { - {\Delta }} /A} \right)\phi } \right)} \right\}}},$$
(55)
$$v_{47,48} \left( {x,t} \right) = e^{i\psi } \times \frac{{2 \epsilon {\Delta } \pm i \epsilon \left\{ {2{\Delta } \pm \sqrt {\Delta } } \right\}\cot \left( {\left( {\sqrt { - {\Delta }} /A} \right)\phi } \right)}}{{2\varepsilon \left\{ {2{\Delta } \pm i{\Delta }\cot \left( {\left( {\sqrt { - {\Delta }} /A} \right)\phi } \right)} \right\}}},$$
(56)

where \(\phi \left( {x,t} \right) = \left( {x^{\alpha } + 2\iota \rho t^{\alpha } } \right)/\alpha\), \(\psi \left( {x,t} \right) = \left( { - \rho x^{\alpha } + \frac{{2 \epsilon ^{2} \left( {A^{2} \rho^{2} - 4{\Delta }} \right)}}{{36\varepsilon {\Delta }}}t^{\alpha } } \right)/\alpha\).

Remarks

The employed schemes are provided ample exact analytic solutions of the space and time fractional quadratic-cubic nonlinear Schrodinger equation stands for optical solitons and other solutions successfully. The found results are compared with those available in the earlier study. Instantaneously, Attia et al. (2021) have discussed the analytical and semi-analytical solutions to the fractional order quadratic-cubic nonlinear Schrodinger equation by using modified Khater method, the generalized exp-\(\left( { - \phi \left( \xi \right)} \right)\)-expansion method and Adomian decomposition method (Attia et al. 2021). Biswas et al. 2017 have studied the same equation of integer order by semi-inverse variational principle. Pal et al. 2017 obtained chirped self-similar wave solutions for the same equation of integer order. It is worth-mentioning that the found solutions in this exploration beers the newness and generality than the earlier recorded results. As this research article have made available much more solutions, they might be useful to illustrate the concerned theme in wide range.

4 Graphical representations of found solutions

The wave solutions of the space and time fractional quadratic-cubic nonlinear Schrodinger equation stands for optical solitons and other solutions are successfully achieved by employing the improved tanh method and the rational \(\left( {G^{\prime}/G} \right)\)-expansion method. The solutions are figured out in 3D and 2D regions to depict their physical appearances in the shape of kink type, anti-kink type, singular kink type, bell shape, anti-bell shape, singular bell shape, periodic, singular periodic etc. We portray some of figures as follows:

5 Conclusions

In this paper, we unravel the space and time fractional Schrodinger equation with the quadratic-cubic nonlinearity by making use of the improved tanh method and the rational \(\left( {G^{\prime}/G} \right)\)-expansion method. This effort accumulates a heap of closed form traveling wave solutions in different forms such as rational function, trigonometric function and hyperbolic function. The well-furnished solutions are portrayed in two- and three-dimensional spaces for illustrating their physical phenomena which brings out different shape solitons and other solutions like kink type, anti-kink type, singular kink type, bell shape, anti-bell shape, singular bell shape, periodic, singular periodic etc. A comparable study of the acquired results is made with those of literature and claimed the newness, novelty and generality of our found outcomes. The attained solutions might be advantageous for better comprehending the mechanisms of the intricate nonlinear anatomical phenomena alongside further applications in real-world life. The whole inspection ensures that the adopted techniques are efficient, productive and concise tools which will be considered to unravel any other nonlinear partial differential equations arising in applied mathematics, mathematical physics and engineering. (Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10).

Fig. 1
figure 1

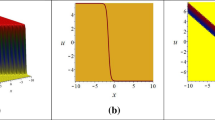
a 3D plot of (3.1.7) for \(\alpha = \epsilon = \iota = d_{1} = 1\), \(a_{1} = \varepsilon = - 1\), \(\rho = 0.5\) within the range \(- 0.1 \le x,t \le 0.1\). b 2D plot of (19) for \(\alpha = \epsilon = \iota = d_{1} = 1\), \(a_{1} = \varepsilon = - 1\), \(\rho = 0.5\), \(t = 2\) within the interval \(- 5 \le x \le 5\)

Full size image
Fig. 2
figure 2

a 3D shape of (3.1.10) for \(\alpha = \rho = \varepsilon = c_{0} = 1\), \(= - 1.75\), \(\epsilon = 3\), \(a_{0} = - 4\) within the range \(- 10 \le x,t \le 10\). b 2D profile of (22) for \(\alpha = \rho = \varepsilon = c_{0} = 1\), \(= - 1.75\), \(\epsilon = 3\), \(a_{0} = - 4\), \(t = 0.5\) in the interval \(- 10 \le x \le 10\)

Full size image
Fig. 3
figure 3

a 3D outline of (24) for \(\alpha = \rho = \iota = 1\), \(\varepsilon = - 1\), \(\epsilon = 3\), \(a_{0} = - 3\), \(c_{0} = 0.5\) within the interval \(- 5 \le x,t \le 5\). b 2D sketch of (24) for \(\alpha = \rho = \iota = 1\), \(\varepsilon = - 1\), \(\epsilon = 3\), \(a_{0} = - 3\), \(c_{0} = 0.5\), \(t = 2\) in the interval \(- 15 \le x \le 15\)

Full size image
Fig. 4
figure 4

a 3D plot of (44) for \(\alpha = c_{0} = 1\), \(\rho = 0.5\), \(\iota = - 0.5\), \(\varepsilon = - 1\), \(\epsilon = 3\), \(a_{0} = - 2\) in the range \(- 10 \le x,t \le 10\). b 2D shape of (44) for \(\alpha = c_{0} = 1\), \(\rho = 0.5\), \(\iota = - 0.5\), \(\varepsilon = - 1\), \(\epsilon = 3\), \(a_{0} = - 2\), \(t = 1\) in the interval \(- 10 \le x \le 10\)

Full size image
Fig. 5
figure 5

a 3D shape of (40) for \(\alpha = \rho = \iota = 1\), \(\epsilon = 6\), \(\varepsilon = - 1\) within the interval \(- 15 \le x,t \le 15\).b 2D figure of (50) for \(\alpha = \rho = \iota = 1\), \(\epsilon = 6\), \(\varepsilon = - 1\), \(t = 2\) within \(- 10 \le x \le 10\)

Full size image
Fig. 6
figure 6

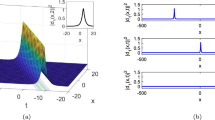
a. 3D outline of (40) for \(\alpha = \varepsilon = a_{0} = b_{0} = A = E = 1\), \(\rho = \epsilon = 0.001\), \(C = 2\) within the interval \(- 15 \le x,t \le 15\). b. 2D shape of (40) for \(\alpha = \varepsilon = a_{0} = b_{0} = A = E = 1\), \(\rho = \epsilon = 0.001\), \(C = 2\), \(t = 2\) in the range \(- 15 \le x \le 15\)

Full size image
Fig. 7
figure 7

a 3D sketch of (41) for \(\alpha = \varepsilon = A = 1\), \(\rho = 1.75\), \(\epsilon = - 0.3\), \(B = 1.5\), \(C = 2\), \(E = - 1\) in the interval \(- 5 \le x,t \le 4\). b 2D drawing of (41) for \(\alpha = \varepsilon = A = 1\), \(\rho = 1.75\), \(\epsilon = - 0.3\), \(B = 1.5\), \(C = 2\), \(E = - 1\), \(t = 0.5\) in \(- 5 \le x \le 2\)

Full size image
Fig. 8
figure 8

a 3D shape of (45) for \(\alpha = C = E = 1\), \(\rho = \varepsilon = 0.5\), \(\epsilon = 0.1\), \(A = 2\) within the interval \(- 15 \le x,t \le 15\). b 2D outline of (45) for \(\alpha = C = E = t = 1\), \(\rho = \varepsilon = 0.5\), \(\epsilon = 0.1\), \(A = 2\) in the range \(- 15 \le x \le 15\)

Full size image
Fig. 9
figure 9

a. 3D plot of (53) for \(\alpha = A = 1\), \(\epsilon = \rho = 0.01\), \(\varepsilon = - 5\), \(C = 3\)., \(E = - 1\) within the interval \(- 5 \le x,t \le 5\). b 2D sketch of (53) for \(\alpha = A = t = 1\), \(\epsilon = \rho = 0.01\), \(\varepsilon = - 5\), \(C = 3\), \(E = - 1\) within the range \(- 3 \le x \le 3\)

Full size image
Fig. 10
figure 10

a. 3D outline of (56) for \(\alpha = A = E = 1\), \(\rho = \epsilon = 0.01\), \(\varepsilon = - 5\), \(C = 3\) within the range \(- 10 \le x,t \le 10\). b 2D shape of (56) for \(\alpha = A = E = t = 1\), \(\rho = \epsilon = 0.01\), \(\varepsilon = - 5\), \(C = 3\) in the interval \(- 13 \le x \le 13\)

Full size image