1 Introduction

In end-pumped lasers, the input face is under a high thermal loading and the upper limit on the critical input power density is determined by the fracture strength of the medium. Therefore, the temperature distribution inside the medium due to power and a spot diameter of the pump light usually dominate the system design considerations for the high average power laser. Both theoretical models and experimental settings were carried out by many researchers to reduce thermal effects generated due to high pumping power (AbdulRazzaq et al. 2019; Ahmed et al. 2018; Cini and Mackenzie 2017; El-Agmy and Al-Hosiny 2017; Ghadban et al. 2020; Kim et al. 2019; Liu et al. 2016; Mojahedi and Shekoohinejad 2018; Shen et al. 2015; Shibib et al. 2017). In this work, a modified thermal model was presented by considering two different beams, namely, effective and the Gaussian beam radii. Accordingly, the maximum temperature difference on each face was obtained taking into account the dependence of thermal conductivity on temperature, and the maximum hoop stress was obtained on each incident face of the medium by considering the dependence of thermal expansion coefficient on the temperature. A small discrepancy was obtained between our analysis and the experimental work in the literature.

2 Temperature distribution analysis

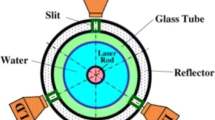
The configuration illustrated in Fig. 1, concerns a cylindrical Nd:YAG laser rod with unequally absorbed pump power density from two end faces. The nonlinear heat equation was solved to estimate the temperature distribution and the maximum hoop stress with the help of Kirchhoff’s transformation.

Fig. 1
figure 1

Proposed end-pumped geometry. The two incident powers lies at r = 0 and z = 0, L

Full size image

By considering the dependency on the temperature of the active medium thermal conductivity, the nonlinear heat equation is written as:

$$\frac{1}{r}\frac{d}{dr}\left[ {rk\left( T \right)\frac{{dT\left( {r,z} \right)}}{dr}} \right] + Q\left( {r,z} \right)$$
(1)

where \(Q\left( {r,z} \right)\), is the dissipation thermal power-per-unit rod volume and \(k\left( T \right)\) is the dependence of thermal conductivity on temperature, given by (Cini and Mackenzie 2017):

$${\text{k}}\left( {\text{T}} \right) = {\text{k}}_{\text{o}} \left( {\frac{\text{T}}{{{\text{T}}_{\text{o}} }}} \right)^{\text{m}}$$
(2)

where \({\text{k}}_{\text{o}}\), is the laser material thermal conductivity at temperature To. In this equation, m is unknown value and selected to be an agreement with the experimental work presented by Shen et al. (2015). In this study (i.e. double–Gaussian-distribution), \(Q\left( {r,z} \right)\) can be written as:

$${\text{Q}}\left( {{\text{r}},{\text{z}}} \right) = {\text{Q}}_{0,1} {\text{e}}^{{ - 2\frac{{{\text{r}}^{2} }}{{{\text{w}}_{1}^{2} }}}} {\text{e}}^{{ - {\upalpha \text{z}}}} + {\text{Q}}_{0,2} {\text{e}}^{{ - 2\frac{{{\text{r}}^{2} }}{{{\text{w}}_{2}^{2} }}}} {\text{e}}^{{ - {{\upalpha }}\left( {{\text{L}} - {\text{z}}} \right)}}$$
(3)

\(w_{1,2}\) are the effective and the waist radius of the left and right pump beams intensity profile, α and L are the absorption coefficient and the length of the laser medium respectively. In the following, two unequal spot radii are assumed i.e. \(\left( {w_{1} \ne w_{2} } \right)\). The two normalization constants \(\left( {Q_{0,1,2} } \right)\) can separately be calculated according to:

$${\text{Q}}_{0,1,2} = \frac{{{{\upeta }}_{\mathrm{h}}\,{\text{P}}_{1,2} }}{{{\mathrm{V}}_{1,2} }}$$
(4)

where \({{\upeta }}_{\text{h}}\,{\mathrm{P}}_{1,2}\) are the two absorbed incident powers, and (ηh is the rate of heat-loading). \({\text{V}}_{1,2}\) are the volumetric heating of the distributed-pump in the laser rod, i.e.

$${\text{V}}_{1} = \frac{{{\uppi \text{w}}_{1}^{2} {{\upeta }}_{\text{abs}} }}{{2\sqrt 2 {{\upalpha }}}}$$
(5a)
$${\text{V}}_{2} = \frac{{{\uppi \text{w}}_{1}^{2} {{\upeta }}_{\text{abs}} }}{{2{{\upalpha }}}}$$
(5b)

Given that the absorption efficiency is \((1 - {\text{e}}^{{ - {\upalpha \text{z}}}}\)). Defining Pin,1 and Pin,2 the incident pump powers at the faces of the laser medium, and substituting the expression of the two normalization constants into Eq. (3), With the help of Eq. (2), Eq. (1) has the form of:

$$\nabla^{2} {\text{U}}\left( {{\text{r}},{\text{z}}} \right) = - {\text{Q}}\left( {{\text{r}},{\text{z}}} \right) = \frac{{\partial^{2} {\text{U}}\left( {{\text{r}},{\text{z}}} \right)}}{{\partial {\text{r}}^{2} }} + \frac{1}{\text{r}}\frac{{\partial {\text{U}}\left( {{\text{r}},{\text{z}}} \right)}}{{\partial {\text{r}}}}$$
(6)

where

$${\text{U}} = \frac{{{\text{K}}_{0} }}{{\left( {{\text{m}} + 1} \right){\text{T}}_{0}^{\text{m}} }}{\text{T}}^{{{\text{m}} + 1}} + {\text{C}}$$
(7)

C, is the integration constant (an arbitrary).

According to Fig. 1, the boundary conditions are:

$$\left. { - \frac{{{\text{dU}}_{\text{pump}} }}{\text{dr}}} \right|_{{{\text{r}} = 0}} = 0$$
(8)

and

$$\left. { - \frac{{{\text{dU}}_{\text{unpump}} }}{\text{dr}}} \right|_{{{\text{r}} = {\text{b}}}} = {\text{h}}[{\text{T}}_{2} ({\text{r}} = {\text{b}}) - {\text{T}}_{\text{c}} ]$$
(9)

h is the coefficient of heat transfer, and Tc is the temperature of the coolant. Finally, by imposing the temperature continuity and its derivative, such that,

$$\left. {\frac{{{\text{dT}}_{\text{pump}} }}{\text{dr}}} \right|_{{{\text{r}} = 2{\text{w}}}} = \left. {\frac{{{\text{dT}}_{\text{unpump}} }}{\text{dr}}} \right|_{{{\text{r}} = 2{\text{w}}}}$$
(10)

One obtained two solutions of Eq. (6), (i.e. Tpump(r,z) in the region \((0 \le {\text{r}} \le {\text{w}}\))

$$T_{pump1} \left( {{\text{r}},{\text{z}}} \right) = \left\{ {\frac{{{{\upeta }}_{\text{h}} {{\upalpha }}\left( {{\text{m}} + 1} \right){\text{T}}_{0}^{\text{m}} }}{{4{\uppi \text{K}}_{0} }}\left( {{\text{P}}_{{{\text{in}},1}} {\text{e}}^{{ - {\upalpha \text{z}}}} } \right)\left[ {{ \ln }\left( {\frac{{{\text{b}}^{2} }}{{{\text{r}}^{2} }}} \right) + {\text{E}}_{1} \left( {\frac{{2{\text{b}}^{2} }}{{w_{1}^{2} }}} \right) - {\text{E}}_{1} \left( {\frac{{2{\text{r}}^{2} }}{{w_{1}^{2} }}} \right)} \right] + \left[ {{\text{T}}_{\text{c}} + \frac{{{{\upeta }}_{\text{h}} {{\upalpha }}}}{{4{\uppi \text{bh}}}}\left( {{\text{P}}_{{{\text{in}},1}} {\text{e}}^{{ - {\upalpha \text{z}}}} } \right)} \right]^{{{\text{m}} + 1}} } \right\}^{{\frac{1}{{{\text{m}} + 1}}}}$$
(11a)

and

$$T_{pump2} \left( {{\text{r}},{\text{z}}} \right) = \left\{ {\frac{{{{\upeta }}_{\text{h}} {{\upalpha }}\left( {{\text{m}} + 1} \right){\text{T}}_{0}^{\text{m}} }}{{4{\uppi \text{K}}_{0} }}\left( {{\text{P}}_{{{\text{in}},2}} {\text{e}}^{{ - {{\upalpha }}\left( {{\text{L}} - {\text{z}}} \right)}} } \right)\left[ {{ \ln }\left( {\frac{{{\text{b}}^{2} }}{{{\text{r}}^{2} }}} \right) + {\text{E}}_{1} \left( {\frac{{2{\text{b}}^{2} }}{{w_{2}^{2} }}} \right) - {\text{E}}_{1} \left( {\frac{{2{\text{r}}^{2} }}{{w_{2}^{2} }}} \right)} \right] + \left[ {{\text{T}}_{\text{c}} + \frac{{{{\upeta }}_{\text{h}} {{\upalpha }}}}{{4{\uppi \text{bh}}}}\left( {{\text{P}}_{{{\text{in}},2}} {\text{e}}^{{ - {{\upalpha }}\left( {{\text{L}} - {\text{z}}} \right)}} } \right)} \right]^{{{\text{m}} + 1}} } \right\}^{{\frac{1}{{{\text{m}} + 1}}}}$$
(11b)

and outside the pump region, Tunpump(r,z) in \(({\text{w}} \le {\text{r}} \le {\text{b}})\)) as follows:

$${\text{T}}_{{{\text{unpump}}1}} \left( {{\text{r}},{\text{z}}} \right) = \left\{ {\frac{{{{\upeta }}_{\text{h}} {{\upalpha }}\left( {{\text{m}} + 1} \right){\text{T}}_{0}^{\text{m}} }}{{4{\uppi \text{K}}_{0} }}\left( {{\text{P}}_{{{\text{in}},1}} {\text{e}}^{{ - {\upalpha \text{z}}}} } \right){ \ln }\left( {\frac{{{\text{b}}^{2} }}{{{\text{r}}^{2} }}} \right) + \left[ {{\text{T}}_{\text{c}} + \frac{{{{\upeta }}_{\text{h}} {{\upalpha }}}}{{4{\uppi \text{bh}}}}\left( {{\text{P}}_{{{\text{in}},1}} {\text{e}}^{{ - {\upalpha \text{z}}}} } \right)} \right]^{{{\text{m}} + 1}} } \right\}^{{\frac{1}{{{\text{m}} + 1}}}}$$
(12a)

and

$${\text{T}}_{{{\text{unpump}}2}} \left( {{\text{r}},{\text{z}}} \right) = \left\{ {\frac{{{{\upeta }}_{\text{h}} {{\upalpha }}\left( {{\text{m}} + 1} \right){\text{T}}_{0}^{\text{m}} }}{{4{\uppi \text{K}}_{0} }}\left( {{\text{P}}_{{{\text{in}},2}} {\text{e}}^{{ - {{\upalpha }}\left( {{\text{L}} - {\text{z}}} \right)}} } \right){ \ln }\left( {\frac{{{\text{b}}^{2} }}{{{\text{r}}^{2} }}} \right) + \left[ {{\text{T}}_{\text{c}} + \frac{{{{\upeta }}_{\text{h}} {{\upalpha }}}}{{4{\uppi \text{bh}}}}\left( {{\text{P}}_{{{\text{in}},2}} {\text{e}}^{{ - {{\upalpha }}\left( {{\text{L}} - {\text{z}}} \right)}} } \right)} \right]^{{{\text{m}} + 1}} } \right\}^{{\frac{1}{{{\text{m}} + 1}}}}$$
(12b)

where E1, is the exponential integral function.

Therefore, the temperature difference between the rod center and its edge, is given as

$$\Delta {\text{T}}\left( {{\text{r}},{\text{z}}} \right) = {\text{T}}_{\text{pump}} \left( {{\text{r}},{\text{z}}} \right) - {\text{T}}_{\text{unpump}} \left( {{\text{b}},{\text{z}}} \right).$$

3 Thermal stress analysis

The generation of heat in solid-state lasers is correlated with the optical pumping process. As a consequence of the nonuniform absorbed pumping, the heat generation is nonuniform which leads to the temperature gradient along the cross-section of the laser medium where the center is hotter than the outer surface of the medium and consequently internal thermal stress was induced. As the pumping power increased the induced thermal stress may exceed the maximum tensile hoop stress of the laser material and leading to fracture. The maximum hoop stress is defined and related as (Xie et al. 2003):

$$\sigma_{\theta } \left( r \right) = \frac{{\alpha_{T} E}}{{\left( {1 - \upsilon } \right)}}\left[ {\frac{1}{{b^{2} }}\mathop \int \nolimits_{0}^{b} {{\Delta }}Trdr + \frac{1}{{w^{2} }}\mathop \int \nolimits_{0}^{w} {{\Delta }}Trdr - {{\Delta }}T} \right]$$
(13)

Where \({\text{E}}\), \({{\upalpha }}_{\text{T}}\), and \({{\upupsilon }}\) are the medium parameters i.e. modulus of elasticity, thermal coefficient of expansion, and the Poisson’s ratio, respectively. In this model, the dependence of thermal expansion on the temperature was considered and given as (Cini and Mackenzie 2017):

$$\alpha_{T} \left( T \right) = 4.2 \times 10^{ - 6} + 0.62 \times 10^{ - 8} \left( {T_{c} } \right)$$
(14)

Therefore, Eq. (13) was solved at the two incident medium faces in the location where z equal to zero to estimate the maximum hoop stress.

4 Results and discussions

To evaluate our proposed model, we made a comparison with the earlier experimental work by Shen et al. (2015). The heat loading and the radial temperature distribution were simulated for the proposed model considering Nd:YAG as a gain medium. The parameters used in this analysis are listed in Table 1.

Table 1 Nd:YAG laser material parameters
Full size table

Figure 2 shows the heat loading generated on each face of the rod (i.e. z = 0, L). According to an unequal spot radius imposed on each medium-end face, the dissipated heat per unit volume was different. Furthermore, the heat loading increased as the pump radius become smaller.

Fig. 2
figure 2

Heat load distribution on each rod’s faces

Full size image

The combination of the volumetric absorbed power and the surface cooling leads to a non-uniform temperature difference in the medium as shown in Fig. 3.

Fig. 3
figure 3

The temperature difference on each rod faces

Full size image

Due to an unequal spot radius i.e. \(w_{1} = \frac{{w_{2} }}{\sqrt 2 }\)) on the right face where \(w_{2} = 0.6\;{\text{mm}}\) on left face), the radial temperature difference (i.e. z = 0, L) was different on each rod’s faces. In other words, at a pump power of 46.4 W imposed on each rod faces, the maximum critical temperature difference according to an effective Gaussian spot of 0.4 mm radius was found to be 276.36 K as compared to 274 K listed in Shen et al. (2015). While the maximum radial critical temperature difference of 213.23 K was estimated according to a spot of 0.6 mm radius. Figure 4 shows how the Gaussian beam spot radius variation affects the axial medium steady-state temperature distribution. It can be seen that on each face of the local absorption region, the temperature has a perfectly Gaussian due to the Gaussian profile of the input power and gradually declined outside the pump region. Along the z-axis, the temperature decays exponentially as a consequence of the exponential absorption of the incident power.

Fig. 4
figure 4

Temperature distribution along the medium

Full size image

The characteristics of the medium fracture stress were analyzed by calculating the temperature distribution at a maximum critical pump power as shown in Fig. 5.

Fig. 5
figure 5

Fracture stress on each face of the medium

Full size image

According to Fig. 5, as the pump power increased, the thermal stress increased too and reaching its ultimate value (i.e. fracture point) of 235.2 MPa corresponding to 0.4 mm spot radius and 186.4 MPa according to 0.6 mm pump radius at a maximum critical power of 46.4 W. It’s clear that, due to an effective spot of 0.4 mm radius, the medium is more compressed as compared to 0.6 mm spot radius imposed on the other end face. Also, the calculations show that the incident power has no effect on the location of the maximum hoop stress and the two end faces of the medium are subject to fracture at a spot of \(\sqrt 2 w_{o}\) imposed on the right face and at \(2w_{o}\) spot incident on the left face. Table 2 summarized how the obtained results are in agreement with previous works presented by Shen et al. (2015).

Table 2 Comparison between theoretical results and experimental work by Shen et al. (2015)
Full size table

The maximum hoop stress was also calculated were the Nd:YAG laser medium under lasing and non-lasing situations as illustrated in Fig. 6. At the same input power of 46.4 W, the maximum hoop stress can be varied from a theoretical lower limit where the rate of heating equal to 24% to the practical value of 32% under lasing and 43% under non-lasing situations (Koechner 2006). Generally, the theoretical value of the rate of the heat of 24% for Nd:YAG laser pumped by 810 nm laser diode and lasing at 1064 nm wavelength was admitted by Koechner (2006) which corresponds to a quantum efficiency of unity, while 32% corresponds to 90% quantum efficiency under lasing action. The value of 43% rating heat was recorded due to the absence of stimulated emission. Therefore, these variations have their signature on the maximum hoop stress.

Fig. 6
figure 6

Maximum hoop stress on both sides faces at different heating rates. Redline for 50% rating heat, blue line for 24%, dot blue line for 43%, and dot red line for 32%

Full size image

Figure 6a, b shows the maximum hoop stress variations as a function of rod radius on both sides of the medium-end faces at an input power of 46.4 W. it can be observed that at a rate of 50% heating, the maximum hoop stress of 235.2 MPa was located on the position of 0.4 mm spot radius while a 186.4 MPa was obtained at 0.6 mm radius.

5 Conclusions

In conclusion, a modified thermal model was presented to predict the temperature distribution and the maximum hoop stress within the end-pumped cylindrical laser medium. To work laser safely, the effective spot radius has been suggested as a spot pump imposed on one side face in comparison to the Gaussian spot radius was incident on the other medium side face. The radial temperature difference due to an effective beam radius was found to be 23% higher than that for a Gaussian beam radius. The results also show that the location of the maximum hoop stress is independent of the pump power and each face of the medium reaches its ultimate fracture according to the value of the spot radius. A minimum discrepancy (1%) was obtained by making a comparison with earlier works of literature. The model presented in this work can open the way for the laser designers to evaluate a different laser crystal under different environmental conditions and one of the main challenges for implementing the model will be to replace the Gaussian pumping profile by another profile like super-Gaussian or Donut shape.