1 Introduction

Diode-pumped solid-state lasers (DPSSL) cover a wide range of applications such as communications, remote sensing and detection, high-resolution spectroscopy, and precision measurements. Two main configurations such as end-pumping and side-pumping configurations are used to pump these lasers. The former can provide efficient energy transfer because almost all pump radiation can be absorbed [1–3]. Because of the end damage, the end-pumping configuration cannot be used for the realization of a high-powered DPSSL [4,5]. By using the latter structure, the high-powered DPSSLs are realized because many diode arrays can be applied along the length of the laser rod in several directions (three, four, and five-fold configuration). Moreover, a direct coupling of the pumping radiation to the laser without any complex optics yields good absorption efficiency [6–8]. As we know, only part of the pump power is converted into output laser energy, while most of the energy is eventually turned into heat consumption [9–17]. The temperature distribution in the laser rod is determined by the non-uniform distribution of the absorbed pump and the cooling arrangement. The radial heat dissipation creates thermal effects such as thermal induced birefringence and thermal lensing, which directly affect the stability of the output power and beam quality [10,11]. Therefore, precise knowledge of temperature distribution in the laser rod is necessary. The temperature distribution is dependent on the heat loading of the laser rod, which depends on the pump energy distribution that is complicated in a diode side-pumped laser [18]. Usually, the side-pumping heads are three-, four-, and five-fold configurations (several directions for pumping) [19,20]. A detailed ray trace has been carried out to evaluate the route of the pump LD-rays propagating inside the diffusing chamber [21]. To achieve high absorption efficiency and a homogeneous pump-beam distribution simultaneously, a systemic algorithm has been established to optimize the pump structure [22]. In [20–23], efforts have been made to realize the homogeneous and uniformly absorbed pump distribution, but it cannot be expected that quite uniform distribution is obtained. A near-Gaussian pump energy deposition in a diode side-pumped laser rod was observed [24], and the absorbed pump distribution was considered to have a parabolic profile [16]. Indeed, the absorbed pump distribution and heat loading in a diode side-pumped solid-state laser are an overlap of propagating Gaussian beams. Therefore, it can be said that the absorbed pump distribution in the laser rod (for side-pumped) can be approximated as nearly super-Gaussian with different super-Gaussian (SG) exponents.

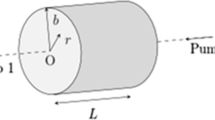
In this paper, the temperature distribution of side-pumped laser rod is investigated (with three-fold configuration as shown in figure 1). First, it is assumed that the absorbed pump distribution is a Gaussian profile and a precise analytical model is provided for the temperature distribution of the laser rod. Then, the effect of width of the Gaussian profile on the temperature distribution is investigated. In the following section, the analytical results are validated by numerical results, and a good agreement will be shown. Finally, the super-Gaussian and top-hat profiles are considered for the absorbed pump distribution. After that, the heat equation is numerically solved and temperature distributions are obtained for each profile. In this way, the absorbed pump distribution on the temperature distribution is studied.

Figure 1
figure 1

Schematic design of the cross-section of pump cavity in the three-side pump configuration.

Full size image

2 Analytical solution of heat equation

2.1 Side-pumped laser rod

Considering the fact that three lines of diode lasers pump the laser rod, a laser rod is placed in a glass tube with coolant water between the rod and the inner surface of the tube. The rod and the tube are inside a reflector and laser diode arrays are put in front of the three slits on the reflective surface. A schematic cross-section of the pump cavity for this case is shown in figure 1.

2.2 Heat equation

Analysis of the steady-state thermal problem begins by defining the governing equations and boundary conditions. The governing Poisson equation is expressed as follows:

$$ K\nabla^{2}T(r)+Q(r)=0, $$
(1)

where K is the thermal conductivity and Q(r) is the heat source (heat density in the rod) defined as the deposited power per unit volume. This equation is for a laser rod in the cylindrical coordinate. It is assumed that the absorbed pump distribution has a Gaussian profile. Since heat generated inside the laser rod is proportional to the absorbed pump inside it, we can consider a Gaussian profile for heat source as follows:

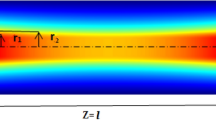
$$ Q(r)=\frac{2\eta P_{\text{abs}} }{\pi \omega^{2}L}\exp\!\left[ {-2\!\left( {\frac{r}{\omega }} \right)^{2}} \right], $$
(2)

where P abs is the absorbed power in the laser rod, η is the fraction of absorbed power converted to heat, L is the pump length and ω is the width of the Gaussian distribution.

2.3 Boundary conditions

With the assumption that the laser rod is located inside the cavity and is cooled with a fluid, the boundary conditions are:

$$ \left. {\frac{\mathrm{d}T}{\mathrm{d}r}} \right|_{r=0} =0 $$
(3)
$$ \left. {\frac{\mathrm{d}T}{\mathrm{d}r}} \right|_{r=R} =\frac{h}{K}(T_{\mathrm{w}} -T(R)). $$
(4)

Here, h is the heat transfer coefficient, T w is the temperature of the coolant, K is the thermal conductivity of the rod, and T(R) is the temperature on the surface of the rod. The convective heat transfer coefficient (h) is a function of the flow rate of the coolant, the physical properties of the coolant and laser rod, and the geometry of the pumping cavity [25].

2.4 Temperature distribution

According to eqs (1)–(4), the heat equation can be solved. Then, we reach

$$\begin{array}{@{}rcl@{}} T(r)&=&T_{\mathrm{w}} +\frac{1}{8}S\left[ {Ei\left( {1,\frac{2R^{2}}{\omega^{2}}} \right)-Ei\left( {1,\frac{2r^{2}}{\omega^{2}}} \right)} \right]\\ &&-\frac{1}{4}S\ln \left( {\frac{r}{R}} \right)+\frac{SK}{4hR}\left( {\kern-2.5pt}{1\,-\,\exp\! \left( \! {\frac{-2R^{2}}{\omega^{2}}} \right)}{\kern-2.5pt}\right)\!. \end{array} $$
(5)

The terms inside the bracket are the exponential integral functions that can be expanded as follows:

$$ Ei(1,x)=-{\Upsilon} -\ln (x)+x-\frac{x^{2}}{4}+\frac{x^{3}}{18}-\cdot \cdot \cdot , $$
(6)

where Υ=0.577456 is a constant. According to eq. (6), expansion of exponential function, eq. (5) is simplified as follows:

$$\begin{array}{@{}rcl@{}} T(r)&=&T_{\mathrm{w}} +\left( {\frac{S}{8}\sum\limits_{n=1}^{n=\infty } {\frac{(-1)^{n+1}2^{n}(R^{2n}-r^{2n})}{n\omega^{2n}n!}} } \right)\\ &&-\left( {\frac{S}{4hR}\sum\limits_{n=1}^{n=\infty } {\frac{(-2)^{n}R^{2n}}{\omega^{2n}n!}} } \right), \end{array} $$
(7)

where

$$S=\frac{\eta P_{\text{abs}} }{\pi KL}. $$

3 Effect of Gaussian-absorbed pump profile width on temperature distribution

Now, as an example, we obtain the temperature distribution of the laser rod for different Gaussian-absorbed pump profile widths. Indeed, this width indicates non-uniformity of the absorbed pump and heat loading in the laser rod. The greater the width is, the more the uniformity will be. Numerical values of all parameters are listed in table 1.

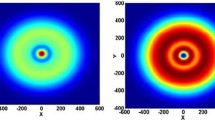
Table 1 Numerical values of parameters.
Full size table

According to table 1 and eq. (5), we plot the curve of temperature distribution for widths 0.9, 1.2, and 1.5 mm. The analytical results are compared with numerical results so that they are validated. Figure 2 shows the analytical and numerical results of temperature distribution for different Gaussian widths.

Figure 2
figure 2

Analytical (solid line) and numerical (dots) results of temperature distribution for different Gaussian widths.

Full size image

The curves of figure 2 show that if the Gaussian profile width of the absorbed pump is increased, the temperature of the laser rod will be decreased and its distribution will be more uniform. This figure also shows the effect of uniformity of the absorbed pump on the decrease in temperature in the laser rod. For various Gaussian profile widths, the temperature difference on the centre of the rod is greater than that on the surface of the rod, which can be due to the cooling of the surface of the rod as water flowing on the surface of the rod tries to prevent the surface temperature from rising. For example, by changing the width from 0.9 to 1.5, decrease in temperature for the surface and the centre of the laser rod is 1.8 and 20.7, respectively. Moreover, figure 2 shows a good agreement between the analytical and numerical results, which can prove the validity of eq. (5).

4 Effect of absorbed pump profile on temperature distribution

As absorbed pump distribution in the laser rod can have super-Gaussian and top-hat profiles, the heat equation can be numerically solved for many of these profiles. In this way, the effect of the absorbed pump profile on the temperature distribution can be investigated. Generally, the equation defined for super-Gaussian and top-hat profiles is as follows:

$$ Q(r)=\frac{\eta P_{\text{abs}} }{C\pi \omega^{2}L}\exp\!\left[ {-2\left( {\frac{r}{\omega }} \right)^{\text{SG}}} \right]\!, $$
(8)

where

$$C=2^{{-2}/{\text{SG}}}{\Gamma} \left( {1+\frac{2}{\text{SG}}} \right) $$

and Γ is the gamma function. SG is the super-Gaussian exponent which can be varied from 2 (for normal Gaussian profile) to ∞ (for top-hat profile). Values of 2, 3, 4, 5, 6, 7, 8, 12, and 16 for SG are considered to solve the heat equation numerically. The curves of the numerical solution are shown in figures 3–5. For these curves, the temperature difference, the temperature of the centre of the rod, and the temperature of the surface of the rod have been listed in table 2.

Figure 3
figure 3

Temperature distribution of the laser rod for ω=0.9 mm.

Full size image
Figure 4
figure 4

Temperature distribution of the laser rod for ω=1.2 mm.

Full size image
Figure 5
figure 5

Temperature distribution of the laser rod for ω=1.5 mm.

Full size image
Table 2 Temperature of the rod surface (T s), temperature of the rod centre (T c) and temperature difference (ΔT) for the curves shown in figures 3–5.
Full size table

As is clear in figures 3–5, if the absorbed pump distribution in the laser rod is a Gaussian profile (SG=2), the temperature distribution will be more non-uniform (this is clearer in figure 5). For super-Gaussian profiles with SG = 3, 4, and 5, the temperature of the centre of the rod is increased in comparison to the case of SG = 2. For larger widths (especially when ω=1.5), it is clear that the temperature of the surface of the rod is slightly increased; however, for SG = 6, 7, the temperature of the centre of the rod is nearly equal to the case of SG = 2. Finally, for SG≥8, the temperature of the centre of the rod is decreased and that of the surface of the rod is slightly increased so that the decrease in temperature in the centre of the rod is greater than the increase in temperature on the surface of the rod. Especially for SG = 16, which can be approximated as top-hat profile, the temperature in the centre of the rod is decreased by 3 or 4 degrees and more uniform temperature distribution is obtained.

By comparing figures 3–5, where both the width (ω) and the super-Gaussian exponent (SG) are varied, it is clear that the effect of ω on the uniformity of temperature distribution is greater than the effect of SG. Therefore, to achieve a lower temperature in the centre of the rod and uniform temperature distribution, the absorbed pump profile has to be optimized; and for this end, the laser head and the cooling must be optimized [21–23].

5 Conclusion

An analytical model for temperature distribution of diode side-pumped laser rod was derived. This model can be applied in the side-pumped laser rod whose absorbed pump profile is a Gaussian profile. Then, it was validated by numerical results, which exhibited a good agreement. By considering a general expression for super-Gaussian and top-hat profiles, and by solving the heat equation, we managed to investigate the effect of width and super-Gaussian exponent of the profile on temperature distribution. Finally, it was determined that the effect of the width profile on the uniformity of temperature distribution is greater than the effect of the super-Gaussian exponent. Therefore, to achieve a uniform temperature distribution, we must provide a uniform absorbed pump profile by optimizing laser head and the cooling.