1 Introduction

Free Space Optical Communication (FSO) is a demanding technology for next-generation communication because of its vast bandwidth, license-free spectrum, and easy installation. However, the FSO link suffers from atmospheric effects like atmospheric absorption, atmospheric turbulence, rain, and snow. Due to narrow beam divergence, FSO requires a perfect line of sight for reliable communication. Building motion due to micro-earthquakes and wind creates the misalignment or pointing errors and reduces the link availability. The above factors also limit the link distance up to a few kilometers (Bayaki et al. 2009; Ansari et al. 2015).

The use of a relay can increase the link distance and capacity. The fronthaul RF link can serve multiple users and high bandwidth FSO link can be used as a backhaul link. This configuration saves the cost of optical fiber installation for backhaul links, specifically for urban, sub-urban, and difficult terrains like hilly areas. Popular relaying techniques like Amplify and Forward (AF) (Ansari et al. 2013; Anees and Bhatnagar 2015a), Decode and Forward (Anees and Bhatnagar 2015b) are widely examined for different applications. The AF relay receives the signal, amplifies it with fixed or CSI-assisted gain (variable gain), and forward it to the destination. DF relay receives the signal, decodes it, and forwards it to the destination. The AF relay is less complex compared to the DF relay. However, it also amplifies the noise, resulting in lower SNR at the destination. DF relay seems complex but ensures better performance. In Zedini et al. (2014), Kong et al. (2015), Soleimani-Nasab and Uysal (2015) Bit Error Rate (BER), Outage Probability (OP) and Ergodic capacity is derived for dual-hop Amplify and Forward RF-FSO link, the FSO link is modeled by Gamma-Gamma, Malaga, and Double Generalized Gamma channel respectively and Nakagami-m distribution is used to model the RF link. In Al-Ebraheemy et al. (2019), Palliyembil et al. (2021) the Nakagami-m and Malaga channel models are used for dual-hop DF RF-FSO links. Further Dual hop RF-FSO link considering MIMO systems (Goel and Bhatia 2020a, b), multiple users (Goel and Bhatia 2020a; Upadhya et al. 2019a, b), and interference (Goel and Bhatia 2021; Upadhya et al. 2019a, b, 2020) are also available in the literature.

The RF and FSO link has complementary behavior against fog, snow, atmospheric turbulence, rain, and multi-path fading. An additional RF link can be used as a backup link to the FSO link or as a secondary link to increase reliability. The secondary RF link gets active when the FSO link is suffering an outage. The switching from the FSO link to the RF link requires a CSI knowledge at the transmitter side and suffers from data losses (Usman et al. 2014). The other option is using both the RF and FSO link simultaneously and applying some diversity and combining techniques like Selection Combining (SC) and adaptive combining. In Krishnan (2018), and Vishwakarma and Swaminathan (2021) Gamma-Gamma/Racian, and Malaga/\(\alpha -\eta -\kappa -\mu\) hybrid link is considered respectively, where the threshold SNR based link switching is used. Shakir (2019), Odeyemi and Owolawi (2019) and Illi et al. (2017) article, authors evaluated the BER and Outage performance of Gamma-Gamma/Nakagami-m, Malaga/\(\eta -\mu\), and Malaga-Weibull hybrid RF/FSO links with both RF and FSO links are transmitting simultaneously. The selection combining techniques is used to combine RF and FSO signal in Shakir (2019), Odeyemi and Owolawi (2019), and Maximal Ratio Combining is used in Illi et al. (2017).

Recently performance of the RF-(RF/FSO) link has been explored in various literature where the source to relay \((S \rightarrow R)\) RF link is used as a fronthaul and the relay to destination \((R \rightarrow D)\) hybrid RF/FSO link is used as a Backhaul link. This kind of link is proposed for mobile communication applications in Ali Amirabadi and Tabataba Vakili (2020). In Ali Amirabadi and Tabataba Vakili (2020) The RF and FSO links are modeled using Rayleigh and Gamma-Gamma distribution respectively. Further, the authors have analyzed the performance of the fixed-gain AF and DF relay configurations. In Torabi and Effatpanahi (2019), performance analysis is carried out for the variable gain AF scheme. In Jamali et al. (2015), Nguyen et al. (2021), Authors have utilized Gamma-Gamma and Racian channel models to model RF-(RF/FSO) link proposed for terrestrial and satellite communication. In Kumar and Borah (2014), the quantize and Encode relaying technique is analyzed for RF-(RF/FSO) link with direct RF link present between source to relay. Rayleigh and Gamma-Gamma distributions are used to model RF and FSO links, respectively. Full duplex Gamma-Gamma-Nakagami-m RF-(RF/FSO) link performance analyzed in Wang et al. (2020). Physical layer security performance is analyzed for Rayleigh-Malaga RF-(RF/FSO) and Nakagami-m-Gamma-Gamma link in Pattanayak et al. (2020) and Odeyemi et al. (2020).

Looking at prior analysis work about RF-(RF/FSO) link, In many cases, the Rayleigh distribution is used to model the RF link (Ali Amirabadi and Tabataba Vakili 2020; Torabi and Effatpanahi 2019; Ansari et al. 2013) which is suitable only when there is no Line of Sight (LOS) path available between the transmitter and receiver. However, Due to the considerable beam divergence and fixed position of the Relay and destination node, the LOS is always available for the \((R \rightarrow D)\) RF link. Unlike Lognormal, Gamma-Gamma, K, IK, and Negative exponential FSO channel models, The Malaga channel model proposed in Jurado-Navas et al. (2011), is a unified channel model which is suitable for weak to strong and saturated atmospheric turbulence. Further, Malaga distribution can be approximated to lognormal, gamma-gamma, K, and negative exponential distribution (Jurado-Navas et al. 2011, Table 1). Furthermore, to investigate the effect of the strength of both RF link fading on overall performance is one of the aim of authors. To the best of our knowledge, the performance analysis is not available for Nakagami-m-Malaga RF-(RF/FSO) link in the literature.

So in this article, performance analysis of the Decode and Forward RF-(RF/FSO) link is carried out, where the source to relay and relay to destination RF link is modeled using Nakagami-m channel model. The relay to destination FSO link is modeled using Malaga channel model with pointing errors. At the destination, selection combining technique is used to select the best SNR signal. This kind of link can be useful for mobile communication or disaster recovery link (Ali Amirabadi and Tabataba Vakili 2020). The major contributions of this article are as follow.

  • The Cumulative Distribution Function (CDF), Probability Density Function (PDF), and Moment Generating Functions (MGF) are derived for decode and forward RF-(RF/FSO) link, considering the Nakagami-m fading model for RF channels and Malaga channel model with consideration of pointing errors to model the FSO link.

  • Capitalizing on the above results, The Outage Probability, BER, and Ergodic Channel Capacity are evaluated for both Intensity Modulation & Direct Detection (IM/DD) and heterodyne detection scheme. The results are derived in terms of Meijer’s G functions considering integer values of \(m_{1}\), and \(m_{2}\).

  • In the end, the Monte-Carlo simulation is performed to validate the results.

The rest of the paper is organized as follows. System model and channel model is described in Sect. 2. Section 3 deals with the statistical characteristics of the end-to-end SNR of the link. The expressions BER, Outage, and Ergodic capacity are derived in Sect. 4. Numerical results are discussed in Sect. 5 followed by the conclusion.

2 System model and channel model

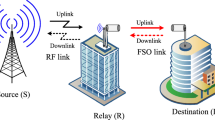
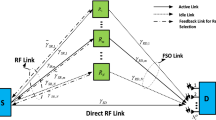
As shown in Fig. 1, a dual-hop mixed RF-(RF/FSO) link consists of a Source (S), which communicates to the Destination (D) through Relay (R). Communication happens in two phases. In the first phase, the source transmits the RF signal to the relay. Relay receives the RF signal and demodulates and decodes it. The transmitter of the relay consists of both FSO and RF transmitters. The detected signal is modulated and forwarded to the destination through parallel RF and FSO link in the second phase. To avoid clipping of signal, The FSO transmitter module applies a sufficient bias to the RF signal before converting it into an optical signal.

Fig. 1
figure 1

RF-(RF/FSO) Link

Full size image

At the destination, selection combining scheme is employed to pick-out the highest SNR signal among RF and FSO signals. Denoting the SNR of \(S \rightarrow R\) RF link by \(\gamma _{RF_{1}}\) SNR of \(R \rightarrow D\) RF link by \(\gamma _{RF_{2}}\) and \(R \rightarrow D\)n FSO link SNR by \(\gamma _{FSO}\). After selection combining, the overall SNR of the \(R \rightarrow D\) link is given by

$$\begin{aligned} \gamma _{RD} = max(\gamma _{RF_{2}}, \gamma _{FSO}) \end{aligned}$$
(1)

The end-to-end SNR of the decode and forward RF-(RF/FSO) link is given by

$$\begin{aligned} \gamma _{e2e} = min(\gamma _{RF_{1}}, \gamma _{RD}) \end{aligned}$$
(2)

The \((S \rightarrow R)\) and \((R \rightarrow D)\) RF links are modeled using the Nakagami-m distribution. The PDF and CDF of SNR of the \((S \rightarrow R)\) RF link are given by

$$\begin{aligned} f_{\gamma _{RF_{1}}}(\gamma ) = \left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}}\right) ^{m_{1}} \frac{\gamma ^{m_{1}-1}}{\Gamma (m_{1})} \; e^{-\frac{m_{1}\gamma }{\bar{\gamma }_{RF_{1}}}} \end{aligned}$$
(3)
$$\begin{aligned} F_{\gamma _{RF_{1}}}(\gamma )&= \frac{1}{\Gamma (m_{1})} \gamma \left( m_{1},\frac{m_{1}\gamma }{\bar{\gamma }_{RF_{1}}}\right) , \end{aligned}$$
(4a)
$$\begin{aligned}&= 1- e^{-\frac{m_{1}\gamma }{\bar{\gamma }_{RF_{1}}}}\sum _{l=0}^{m_{1}-1}\frac{1}{l!} \left( \frac{m_{1} \gamma }{\bar{\gamma }_{RF_{1}}}\right) ^{l} \end{aligned}$$
(4b)

Where, \(m_{1} > 0.5\) is Nakagami-m fading parameter and \(\bar{\gamma }_{RF_{1}}\) is average SNR of source to relay RF link. \(\Gamma (.)\) is the Gamma function (Gradshteyn and Ryzhik 2007, Eq. (8.310.1)). \(\gamma ( \;, \; )\) is a lower incomplete gamma function (Gradshteyn and Ryzhik 2007, Eq. (8.350.1)). Considering \(m_{1}\) is an integer, Eq. (4b) is obtained using the series form of the lower incomplete gamma function presented in (Gradshteyn and Ryzhik 2007, Eq. (8.352.1)). Putting \(m_{1}=1\) in Eq. (3), it becomes PDF of SNR of the Rayleigh channel, which fits best for the scenario where no LOS component is present. Using (Gradshteyn and Ryzhik 2007, Eq. (8.356.3) and Eq. (8.352.2)) Complimentary Cumulative Distribution Function (CCDF) of the SNR of an RF link can be expressed as Simon and Alouini (2005)

$$\begin{aligned} \begin{aligned} F^{c}_{\gamma _{RF_{1}}}(\gamma )&= 1 - F_{\gamma _{RF_{1}}}(\gamma )\\ F^{c}_{\gamma _{RF_{1}}}(\gamma )&= \frac{1}{\Gamma (m_{1})} \Gamma \left( m_{1},\frac{m_{1}\gamma }{\bar{\gamma }_{RF_{1}}}\right) ,\\&= e^{-\frac{m_{1}\gamma }{\bar{\gamma }_{RF_{1}}}}\sum _{l_{1}=0}^{m_{1}-1}\frac{1}{l_{1}!} \left( \frac{m_{1} \gamma }{\bar{\gamma }_{RF_{1}}}\right) ^{l} \end{aligned} \end{aligned}$$
(5)

Where \(\Gamma (,\;)\) is upper incomplete gamma function (Gradshteyn and Ryzhik 2007, Eq. (8.350.2), and Eq. (8.352.2)). Same way, the PDF and CDF of the relay to destination link are given by

$$\begin{aligned}{} & {} f_{\gamma _{RF_{2}}}(\gamma ) = \left( \frac{m_{2}}{\bar{\gamma }_{RF_{2}}}\right) ^{m_{2}} \frac{\gamma ^{m_{2}-1}}{\Gamma (m_{2})} \; e^{-\frac{m_{2}\gamma }{\bar{\gamma }_{RF_{2}}}} \end{aligned}$$
(6)
$$\begin{aligned} F_{\gamma _{RF_{2}}}(\gamma ){} & {} = \frac{1}{\Gamma (m_{2})} \gamma \left( m_{2},\frac{m_{2}\gamma }{\bar{\gamma }_{RF_{2}}}\right) ,\nonumber \\{} & {} \quad = 1- e^{-\frac{m_{2}\gamma }{\bar{\gamma }_{RF_{2}}}}\sum _{l_{2}=0}^{m_{2}-1}\frac{1}{l_{2}!} \left( \frac{m_{2} \gamma }{\bar{\gamma }_{RF_{2}}}\right) ^{l_{2}} \end{aligned}$$
(7)

where, \(\bar{\gamma }_{RF_{2}}\) is an avarage SNR of \(R \rightarrow D\) RF link and an integer value of \(m_{2}\) is considered for eq. (7).

For the FSO link, the irradiance fluctuation due to atmospheric turbulence by is modeled using Malaga distribution. The irradiance fluctuation due to misalignment errors caused by building sway, wind, and small earthquakes is also considered in this work. The PDF of SNR of Malaga link in the presence of pointing error is given by (Ansari et al. 2015, Eq. (9))

$$\begin{aligned} f_{\gamma _{FSO}}(\gamma )=\frac{\xi ^{2}A}{2^{r}\;\gamma }\sum _{m=1}^{\beta }b_{m}\;{\text {G}}^{3,0}_{1,3}\left[ \left. B\left( \frac{\gamma }{\mu _{r}}\right) ^{\frac{1}{r}}\right| \begin{array}{c}{{\xi ^2+1}}\\ {{\xi ^2,\alpha ,m}}\end{array}\right] ; \beta \in \mathbb {N} \end{aligned}$$
(8)

Where,

$$\begin{aligned} \begin{aligned} A&\triangleq \frac{2 \; \alpha ^{\alpha /2}}{g^{1+\alpha /2}\Gamma (\alpha )} \left( \frac{g\;\beta }{g\;\beta +\Omega ^{\prime }}\right) ^{\beta +\alpha /2},\\ b_{m}&\triangleq \left( \begin{array}{c}{\beta -1}\\ {m-1}\end{array}\right) \frac{\left( g\;\beta +\Omega ^{\prime }\right) ^{1-m/2}}{\left( m-1\right) !}\left( \frac{\Omega ^{\prime }}{g}\right) ^{m-1}\\&\times \left( \frac{\alpha }{\beta }\right) ^{m/2} \left( \frac{\alpha \;\beta }{g\;\beta +\Omega ^{\prime }}\right) ^{-(\alpha +m)/2},\\ B&= \xi ^{2}\alpha \beta \frac{(g+\Omega ^{\prime })}{(\xi ^{2}+1)\left( g\;\beta +\Omega ^{\prime }\right) }. \end{aligned} \end{aligned}$$
(9)

Where, \(\alpha\) and \(\beta ,\) are related to the large and small scale scattering process respectively. \(2b_{0}\) indicates average power of scattering components. \(\rho\) represents the amount of scattering power coupled to the LOS component. While \(g = 2b_{0}(1-\rho )\) and \(\Omega ^{\prime } = \Omega + 2b_{0} + 2 \sqrt{2b_{0}\Omega \rho } cos(\phi _{A}-\phi _{B})\). \(\Omega\) represents the average power of the LOS component. \(\phi _{A}\) and \(\phi _{B}\) are phase of LOS component and scattered component coupled to LOS component (Jurado-Navas et al. 2011; Ansari et al. 2015). Furthermore, \(\xi\) is a ratio of the equivalent beam waist of the receiver to the standard deviation of pointing error displacement (Gappmair 2011). \(\xi \rightarrow \infty\) indicates no pointing errors. \(\text {G}[.]\) is Meijer’s G function defined in (Gradshteyn and Ryzhik 2007, Eq. (9.301)), \(\mu _{r}\) is average SNR of FSO link. \(r=1\), \(\mu _{1}\) indicates SNR if heterodyne detection is used and when \(r=2\), \(\mu _{2}\) indicates average SNR for IM/DD. CDF of SNR of the relay to destination FSO link is given by (Ansari et al. 2015, Eq. (11))

$$\begin{aligned} F_{\gamma _{FSO}}(\gamma )=D\sum _{m=1}^{\beta }c_{m}\;{\text {G}}^{3r,1}_{r+1,3r+1}\left[ \left. E\frac{\gamma }{\mu _{r}}\right| \begin{array}{c}{{1,\kappa _{1}}}\\ {{\kappa _{2},0}}\end{array}\right] , \end{aligned}$$
(10)

Where, \(D= \frac{\xi ^2 A}{2^{r} (2 \pi )^{r-1}}\), \(c_{m} = b_{m} r^{\alpha +m-1}\), \(E= B^{r}/r^{2r}\), \(\kappa _{1}= \frac{\xi ^{2}+1}{r},...,\frac{\xi ^{2}+r}{r}\); contains r elements and \(\kappa _{2}= \frac{\xi ^{2}}{r},..., \frac{\xi ^{2}+r-1}{r}, \frac{\alpha }{r}... \frac{\alpha +r-1}{r}, \frac{m}{r},..., \frac{m+r-1}{r}\), contains 3r elements.

3 Statistical characteristics

3.1 Cummulative distribution function

Using Eq. (2), we can express the CDF of end-to-end SNR of dual-hop decode and forward link as,

$$\begin{aligned} \begin{aligned} F_{\gamma _{e2e}}(\gamma )&= F_{\gamma _{SR}}(\gamma ) + F_{\gamma _{RD}}(\gamma )- F_{\gamma _{SR}}(\gamma )F_{\gamma _{RD}}(\gamma )\\&= F_{\gamma _{SR}}(\gamma ) + F^{c}_{\gamma _{SR}}(\gamma )F_{\gamma _{RD}}(\gamma )\\ \end{aligned} \end{aligned}$$
(11)

From Eq. (1), The CDF of SNR of relay to destination link is written as \(F_{\gamma _{RD}} = F_{\gamma _{FSO}}(\gamma )F_{\gamma _{RF2}}(\gamma )\). substituting in Eq. (11)

$$\begin{aligned} F_{\gamma _{e2e}}(\gamma )= F_{\gamma _{RF1}}(\gamma ) + F^{c}_{\gamma _{RF1}}(\gamma )F_{\gamma _{FSO}}(\gamma )F_{\gamma _{RF2}}(\gamma ) \end{aligned}$$
(12)

From Eqs. (5), (7), (10) and (12), the CDF of end-to-end SNR can be expressed as

$$\begin{aligned} \begin{aligned} F_{\gamma _{e2e}}(\gamma ) =&\frac{1}{\Gamma (m_{1})} \gamma \left( m_{1},\frac{m_{1}\gamma }{\bar{\gamma }_{RF_{1}}}\right) \ + \ \frac{1}{\Gamma (m_{1})\Gamma (m_{2})} \Gamma \left( m_{1},\frac{m_{1}\gamma }{\bar{\gamma }_{RF_{1}}}\right) \gamma \left( m_{2},\frac{m_{2}\gamma }{\bar{\gamma }_{RF_{1}}}\right) \\&\times D\sum _{m=1}^{\beta }c_{m}\;{\text {G}}^{3r,1}_{r+1,3r+1}\left[ \left. E\frac{\gamma }{\mu _{r}}\right| \begin{array}{c}{{1,\kappa _{1}}}\\ {{\kappa _{2},0}}\end{array}\right] , \end{aligned} \end{aligned}$$
(13)
$$\begin{aligned} \begin{aligned} F_{\gamma _{e2e}}(\gamma ) = 1- e^{-\frac{m_{1}\gamma }{\bar{\gamma }_{RF_{1}}}}\sum _{l_{1}=0}^{m_{1}-1}\frac{1}{l_{1}!} \left( \frac{m_{1} \gamma }{\bar{\gamma }_{RF_{1}}}\right) ^{l_{1}} + \left[ \left( e^{-\frac{m_{1}\gamma }{\bar{\gamma }_{RF_{1}}}}\sum _{l_{1}=0}^{m_{1}-1}\frac{1}{l_{1}!} \left( \frac{m_{1} \gamma }{\bar{\gamma }_{RF_{1}}}\right) ^{l_{1}}\right) \right. \\ \left. \left( 1- e^{-\frac{m_{2}\gamma }{\bar{\gamma }_{RF_{2}}}} \sum _{l_{2}=0}^{m_{2}-1}\frac{1}{l_{2}!} \left( \frac{m_{2} \gamma }{\bar{\gamma }_{RF_{2}}}\right) ^{l_{2}}\right) \left( D\sum _{m=1}^{\beta }c_{m}\;{\text {G}}^{3r,1}_{r+1,3r+1}\left[ \left. E\frac{\gamma }{\mu _{r}}\right| \begin{array}{c}{{1,\kappa _{1}}}\\ {{\kappa _{2},0}}\end{array}\right] \right) \right] \end{aligned} \end{aligned}$$
(14)

Replacing \(m_{1}=m_{2}=1\), \(\rho =1\), \(\Omega ^{'} =1\) in the Eq. (14), it will reduced to CDF of SNR of RF-(RF/FSO) link modeled using Rayleigh and Gamma-Gamma distribution expressed in (Ali Amirabadi and Tabataba Vakili 2020, Eq. (25)) for single user.

3.2 Probability distribution function

Differentiating eq. (13) we can get PDF of end-to-end SNR.

$$\begin{aligned} f_{\gamma _{e2e}}(\gamma _{e2e}) = \frac{d}{d\gamma } F_{\gamma _{e2e}}(\gamma _{e2e}) \end{aligned}$$
(15)

Substituting Eq. (13) and differentiating using (Gradshteyn and Ryzhik 2007, Eq. (8.356.4)), [http://functions.wolfram.com, Eq. (07.34.20.0002.01)] and applying property of Meijer’s G function from (Gradshteyn and Ryzhik 2007, Eq. (9.31.1)) we can get

$$\begin{aligned} \begin{aligned}&f_{\gamma _{e2e}}(\gamma _{e2e}) = \left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}}\right) ^{m_{1}} \frac{\gamma ^{m_{1}-1}}{\Gamma (m_{1})} \; e^{-\frac{m_{1}\gamma }{\bar{\gamma }_{RF_{1}}}} + \frac{D}{\Gamma (m_{2})\Gamma (m_{1})} \sum _{m=1}^{\beta }c_{m}\;{\text {G}}^{3r,1}_{r+1,3r+1}\left[ \left. E\frac{\gamma }{\mu _{r}}\right| \begin{array}{c}{{1,\kappa _{1}}}\\ {{\kappa _{2},0}}\end{array}\right] \\ {}&\left[ \Gamma \left( m_{1},\frac{m_{1}\gamma }{\bar{\gamma }_{RF_{1}}}\right) \left( \frac{m_{2}}{\bar{\gamma }_{RF_{2}}}\right) ^{m_{2}} \gamma ^{m_{2}-1} e^{-\frac{m_{2}\gamma }{\bar{\gamma }_{RF_{2}}}} - \gamma \left( m_{2},\frac{m_{2}\gamma }{\bar{\gamma }_{RF_{2}}}\right) \left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}}\right) ^{m_{1}} \gamma ^{m_{1}-1} e^{-\frac{m_{1}\gamma }{\bar{\gamma }_{RF_{1}}}} \right] \\&+ \frac{D}{\gamma \Gamma (m_{2})\Gamma (m_{1})} \sum _{m=1}^{\beta }c_{m}\;{\text {G}}^{3r,0}_{r,3r}\left[ \left. E\frac{\gamma }{\mu _{r}}\right| \begin{array}{c}{{\kappa _{1}}}\\ {{\kappa _{2}}}\end{array}\right] \Gamma \left( m_{1},\frac{m_{1}\gamma }{\bar{\gamma }_{RF_{1}}}\right) \gamma \left( m_{2},\frac{m_{2}\gamma }{\bar{\gamma }_{RF_{2}}}\right) \end{aligned} \end{aligned}$$
(16)

3.3 Moment generating function

The MGF is defined as \(\text {M}_{\gamma } = \text {E}(e^{-\gamma s})\). It can be expressed in terms of CDF by applying integration by parts as

$$\begin{aligned} \text {M}_{\gamma _{e2e}} = s\int _{0}^{\infty } e^{-\gamma s} F_{\gamma _{e2e}}(\gamma )d\gamma . \end{aligned}$$
(17)

Substituting eq. (13) we can express eq. (17) as

$$\begin{aligned} \mathcal {M}_{\gamma _{e2e}} = s[M_{1} - M_{2} + M_{3} - M_{4}]. \end{aligned}$$
(18)

Where, \(M_{1} = \int _{0}^{\infty } e^{-\gamma s} d\gamma = \frac{1}{\gamma }\).

$$\begin{aligned} M_{2} = \int _{0}^{\infty } e^{-\gamma s} e^{-\frac{m_{1}\gamma }{\bar{\gamma }_{RF_{1}}}}\sum _{l_{1}=0}^{m_{1}-1}\frac{1}{l_{1}!} \left( \frac{m_{1} \gamma }{\bar{\gamma }_{RF_{1}}}\right) ^{l_{1}} d\gamma \end{aligned}$$
(19)

Which can be solved using (Gradshteyn and Ryzhik 2007, Eq. (3.351.3))

$$\begin{aligned}{} & {} M_{2} = \sum _{l_{1}=0}^{m_{1}-1} \left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}}\right) ^{l_{1}} \left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}} + s\right) ^{-l_{1}-1} \end{aligned}$$
(20)
$$\begin{aligned}{} & {} M_{3} = \int _{0}^{\infty } e^{-\gamma s} e^{-\frac{m_{1}\gamma }{\bar{\gamma }_{RF_{1}}}}\sum _{l_{1}=0}^{m_{1}-1}\frac{1}{l_{1}!} \left( \frac{m_{1} \gamma }{\bar{\gamma }_{RF_{1}}}\right) ^{l_{1}} D\sum _{m=1}^{\beta }c_{m}\;{\text {G}}^{3r,1}_{r+1,3r+1}\left[ \left. E\frac{\gamma }{\mu _{r}}\right| \begin{array}{c}{{1,\kappa _{1}}}\\ {{\kappa _{2},0}}\end{array}\right] d\gamma \end{aligned}$$
(21)

After re arranging the above equation and applying (Gradshteyn and Ryzhik 2007, Eq. (7.813.1)) the integration can be solved as

$$\begin{aligned} \begin{aligned} M_{3}&= D \sum _{l_{1}=0}^{m_{1}-1} \frac{1}{l_{1}!} \frac{\left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}}\right) ^{l_{1}} }{\left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}} + s\right) ^{l_{1}+1}} \sum _{m=1}^{\beta }c_{m}\ {\text {G}}^{3r,2}_{r+2,3r+1}\left[ \left. \frac{\frac{E}{\mu _{r}}}{ \left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}} + s\right) }\right| \begin{array}{c}{{-l_{1},1,\kappa _{1}}}\\ {{\kappa _{2},0}}\end{array}\right] \end{aligned} \end{aligned}$$
(22)
$$\begin{aligned} \begin{aligned} M_{4}&= \int _{0}^{\infty } e^{-\gamma s} e^{-\frac{m_{1}\gamma }{\bar{\gamma }_{RF_{1}}}}\sum _{l_{1}=0}^{m_{1}-1}\frac{1}{l_{1}!} \left( \frac{m_{1} \gamma }{\bar{\gamma }_{RF_{1}}}\right) ^{l_{1}} e^{-\frac{m_{2}\gamma }{\bar{\gamma }_{RF_{2}}}} \sum _{l_{2}=0}^{m_{2}-1}\frac{1}{l_{2}!} \left( \frac{m_{2} \gamma }{\bar{\gamma }_{RF_{2}}}\right) ^{l_{2}} \\ {}&\times D\sum _{m=1}^{\beta }c_{m}\;{\text {G}}^{3r,1}_{r+1,3r+1}\left[ \left. E\frac{\gamma }{\mu _{r}}\right| \begin{array}{c}{{1,\kappa _{1}}}\\ {{\kappa _{2},0}}\end{array}\right] d\gamma \end{aligned} \end{aligned}$$
(23)

After rearranging the above equation, we can solve the integration same was as \(M_{3}\).

$$\begin{aligned} \begin{aligned} M_{4}&= D \sum _{l_{1}=0}^{m_{1}-1} \frac{1}{l_{1}!} \left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}}\right) ^{l_{1}} \sum _{l_{2}=0}^{m_{2}-1}\frac{1}{l_{2}!} \frac{\left( \frac{m_{2}}{\bar{\gamma }_{RF_{2}}}\right) ^{l_{2}}}{\left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}} + \frac{m_{2}}{\bar{\gamma }_{RF_{2}}} + s\right) ^{l_{1}+l_{2}+1}} \times \\ {}&\sum _{m=1}^{\beta }c_{m}\;{\text {G}}^{3r,2}_{r+2,3r+1}\left[ \left. \frac{\frac{E}{\mu _{r}}}{ \left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}} + \frac{m_{2}}{\bar{\gamma }_{RF_{2}}} + s\right) }\right| \begin{array}{c}{{-l_{1}-l_{2},1,\kappa _{1}}}\\ {{\kappa _{2},0}}\end{array}\right] \end{aligned} \end{aligned}$$
(24)
$$\begin{aligned} \begin{aligned} \mathcal {M}_{\gamma _{e2e}}&= s\left[ \frac{1}{\gamma } - \sum _{l_{1}=0}^{m_{1}-1} \frac{\left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}}\right) ^{l_{1}} }{\left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}} + s\right) ^{l_{1}+1}} + D \sum _{l_{1}=0}^{m_{1}-1} \frac{1}{l_{1}!} \frac{\left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}}\right) ^{l_{1}} }{\left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}} + s\right) ^{l_{1}+1}} \sum _{m=1}^{\beta }c_{m} \right. \\&\left. {\text {G}}^{3r,2}_{r+2,3r+1}\left[ \left. \frac{\frac{E}{\mu _{r}}}{ \left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}} + s\right) }\right| \begin{array}{c}{{-l_{1},1,\kappa _{1}}}\\ {{\kappa _{2},0}}\end{array}\right] d\gamma - D \sum _{l_{1}=0}^{m_{1}-1} \frac{1}{l_{1}!} \left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}}\right) ^{l_{1}} \sum _{l_{2}=0}^{m_{2}-1}\frac{1}{l_{2}!} \right. \\&\left. \frac{\left( \frac{m_{2}}{\bar{\gamma }_{RF_{2}}}\right) ^{l_{2}}}{\left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}} + \frac{m_{2}}{\bar{\gamma }_{RF_{2}}} + s\right) ^{l_{1}+l_{2}+1}} \sum _{m=1}^{\beta }c_{m}\;{\text {G}}^{3r,2}_{r+2,3r+1}\left[ \left. \frac{\frac{E}{\mu _{r}}}{ \left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}} + \frac{m_{2}}{\bar{\gamma }_{RF_{2}}} + s\right) }\right| \begin{array}{c}{{-l_{1}-l_{2},1,\kappa _{1}}}\\ {{\kappa _{2},0}}\end{array}\right] \right] . \end{aligned} \end{aligned}$$
(25)

4 Performance analysis

4.1 Outage probablity

The availability of the overall link is given by outage probability. It is a probability that the SNR falls below the threshold level.

$$\begin{aligned} P_{out} = P(\gamma _{e2e} \le \gamma _{Th}) = F_{\gamma _{e2e}}(\gamma _{Th}) \end{aligned}$$
(26)

By changing the argument in Eq. (13) we can write the expression of outage probability as

$$\begin{aligned} \begin{aligned} P_{out}=&\frac{1}{\Gamma (m_{1})} \gamma \left( m_{1},\frac{m_{1}\gamma _{Th}}{\bar{\gamma }_{RF_{1}}}\right) \ + \ \frac{1}{\Gamma (m_{1})\Gamma (m_{2})} \Gamma \left( m_{1},\frac{m_{1}\gamma _{Th}}{\bar{\gamma }_{RF_{1}}}\right) \gamma \left( m_{2},\frac{m_{2}\gamma _{Th}}{\bar{\gamma }_{RF_{1}}}\right) \\&\times D\sum _{m=1}^{\beta }c_{m}\;{\text {G}}^{3r,1}_{r+1,3r+1}\left[ \left. E\frac{\gamma _{Th}}{\mu _{r}}\right| \begin{array}{c}{{1,\kappa _{1}}}\\ {{\kappa _{2},0}}\end{array}\right] , \end{aligned} \end{aligned}$$
(27)

4.2 Bit error rate

Formula of average BER for various binary modulations as presented in (Ansari et al. 2011, Eq. (12)) is,

$$\begin{aligned} p_{e} =\frac{q^{p}}{2 \Gamma (p)} \int _{0}^{\infty } e^{-q\gamma } \gamma ^{p-1} F(\gamma )d\gamma \end{aligned}$$
(28)

Different values of p and q for different binary modulation schemes are presented in (Ansari et al. 2015, Table 1). After substituting Eq. (14), the Eq. (28) can be written as

$$\begin{aligned} p_{e} =\frac{q^{p}}{2 \Gamma (p)} \left( I_{1} - I_{2} + I_{3} - I_{4}\right) \end{aligned}$$
(29)

Where,

$$\begin{aligned} I_{1} = \int _{0}^{\infty } e^{-q\gamma } \gamma ^{p-1} d\gamma = \frac{\Gamma (p)}{q^{p}} \end{aligned}$$
(30)

which is solved using (Gradshteyn and Ryzhik 2007, Eq. (3.351.3))

$$\begin{aligned} I_{2} = \int _{0}^{\infty } e^{-q\gamma } \gamma ^{p-1} e^{-\frac{m_{1}\gamma }{\bar{\gamma }_{RF_{1}}}}\sum _{l_{1}=0}^{m-1}\frac{1}{l_{1}!} \left( \frac{m_{1} \gamma }{\bar{\gamma }_{RF_{1}}}\right) ^{l_{1}}d\gamma \end{aligned}$$
(31)

Applying (Gradshteyn and Ryzhik 2007, Eq. (3.351.3)), the \(I_{2}\) can be solved as

$$\begin{aligned}{} & {} I_{2}= \sum _{l_{1}=0}^{m_{1}-1} \frac{\left( \frac{m_{1}}{\bar{\gamma _{RF_{1}}}}\right) ^{l_{1}}\Gamma (l_{1}+p)}{l_{1}!\;\left( \frac{m_{1}}{\bar{\gamma _{RF_{1}}}}+q\right) ^{l_{1}+p}} \end{aligned}$$
(32)
$$\begin{aligned}{} & {} I_{3} = D \sum _{l_{1}=0}^{m_{1}-1}\frac{1}{l_{1}!} \sum _{m=1}^{\beta }c_{m}\;\int _{0}^{\infty } e^{-q\gamma } \gamma ^{p-1} e^{-\frac{m_{1}\gamma }{\bar{\gamma }_{RF_{1}}}} \left( \frac{m_{1}\gamma }{\bar{\gamma }_{RF_{1}}}\right) ^{l_{1}} {\text {G}}^{3r,1}_{r+1,3r+1}\left[ \left. E\frac{\gamma }{\mu _{r}}\right| \begin{array}{c}{{1,\kappa _{1}}}\\ {{\kappa _{2},0}}\end{array}\right] d\gamma \end{aligned}$$
(33)

the integration part in \(I_{3}\) can be solved using (Gradshteyn and Ryzhik 2007, Eq. (7.813.1)),

$$\begin{aligned}{} & {} I_{3} = D \sum _{l_{1}=0}^{m_{1}-1} \sum _{m=1}^{\beta } c_{m} \frac{\left( \frac{m_{1}}{\bar{\gamma _{RF_{1}}}}\right) ^{l_{1}}}{l_{1}!\;\left( \frac{m_{1}}{\bar{\gamma _{RF_{1}}}}+q\right) ^{l_{1}+p}} {\text {G}}^{3r,2}_{r+2,3r+1}\left[ \left. \frac{E}{\mu _{r}\left( \frac{m_{1}}{\bar{\gamma _{RF_{1}}}}+q\right) }\right| \begin{array}{c}{{1-p-l_{1},1,\kappa _{1}}}\\ {{\kappa _{2},0}}\end{array}\right] \end{aligned}$$
(34)
$$\begin{aligned}{} & {} I_{4} = D \sum _{l_{1}=0}^{m_{1}-1}\frac{1}{l_{1}!} \sum _{l_{2}=0}^{m_{2}-1}\frac{1}{l_{2}!} \sum _{m=1}^{\beta }c_{m}\; \int _{0}^{\infty } e^{-q\gamma } \gamma ^{p-1} e^{-\frac{m_{1}\gamma }{\bar{\gamma }_{RF_{1}}}} \left( \frac{m_{1}\gamma }{\bar{\gamma }_{RF_{1}}}\right) ^{l_{1}} e^{-\frac{m_{2}\gamma }{\bar{\gamma }_{RF_{2}}}} \left( \frac{m_{2}\gamma }{\bar{\gamma }_{RF_{2}}}\right) ^{l_{2}} \nonumber \\{} & {} \quad \times {\text {G}}^{3r,1}_{r+1,3r+1}\left[ \left. E\frac{\gamma }{\mu _{r}}\right| \begin{array}{c}{{1,\kappa _{1}}}\\ {{\kappa _{2},0}}\end{array}\right] d\gamma \end{aligned}$$
(35)

After re-arranging the equation, The integration part in \(I_{4}\) can also be solved the same way as \(I_{3}\)

$$\begin{aligned} \begin{aligned} I4&= D \sum _{l_{1}=0}^{m_{1}-1} \sum _{l_{2}=0}^{m_{2}-1} \sum _{m=1}^{\beta } c_{m} \frac{\left( \frac{m_{1}}{\bar{\gamma _{RF_{1}}}}\right) ^{l_{1}} \left( \frac{m_{2}}{\bar{\gamma }_{RF_{2}}}\right) ^{l_{2}}}{l_{1}!\;l_{2}!\;\left( \frac{m_{1}}{\bar{\gamma _{RF_{1}}}}+\frac{m_{2}}{\bar{\gamma }_{RF_{2}}}+q\right) ^{l_{1}+l_{2}+p}} \times \\&{\text {G}}^{3r,2}_{r+2,3r+1}\left[ \left. \frac{E}{\mu _{r}\left( \frac{m_{1}}{\bar{\gamma _{RF_{1}}}}+\frac{m_{2}}{\bar{\gamma }_{RF_{2}}}+q\right) }\right| \begin{array}{c}{{1-p-l_{1}-l_{2}, 1, \kappa _{1}}}\\ {{\kappa _{2}, 0}}\end{array}\right] \end{aligned} \end{aligned}$$
(36)

using Eqs. (29), (30), (32), (34), (36)

$$\begin{aligned} \begin{aligned} p_{e}&= \frac{q^{p}}{2 \Gamma (p)} \left( \frac{\Gamma (p)}{q^{p}} - \sum _{l_{1}=0}^{m_{1}-1} \frac{\left( \frac{m_{1}}{\bar{\gamma _{RF_{1}}}}\right) ^{l_{1}} \Gamma (l_{1}+p)}{l_{1}!\;\left( \frac{m_{1}}{\bar{\gamma _{RF_{1}}}}+q\right) ^{l_{1}+p}} + D \sum _{l_{1}=0}^{m_{1}-1} \sum _{m=1}^{\beta } \frac{c_{m} \left( \frac{m_{1}}{\bar{\gamma _{RF_{1}}}}\right) ^{l_{1}}}{l_{1}!\;\left( \frac{m_{1}}{\bar{\gamma _{RF_{1}}}}+q\right) ^{l_{1}+p}} \right. \\ {}&\left. {\text {G}}^{3r,2}_{r+2,3r+1}\left[ \left. \frac{\frac{E}{\mu _{r}}}{\left( \frac{m_{1}}{\bar{\gamma _{RF_{1}}}}+q\right) }\right| \begin{array}{c}{{1-p-l_{1},1,\kappa _{1}}}\\ {{\kappa _{2},0}}\end{array}\right] - D \sum _{l_{1}=0}^{m_{1}-1} \frac{\left( \frac{m_{1}}{\bar{\gamma _{RF_{1}}}}\right) ^{l_{1}}}{l_{1}!} \sum _{l_{2}=0}^{m_{2}-1}\frac{\left( \frac{m_{2}}{\bar{\gamma }_{RF_{2}}}\right) ^{l_{2}}}{l_{2}!} \sum _{m=1}^{\beta } \right. \\ {}&\left. \frac{c_{m}}{\;\;\left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}}+\frac{m_{2}}{\bar{\gamma }_{RF_{2}}}+q\right) ^{l_{1}+l_{2}+p}} \times {\text {G}}^{3r,2}_{r+2,3r+1}\left[ \left. \frac{\frac{E}{\mu _{r}}}{\left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}}+\frac{m_{2}}{\bar{\gamma }_{RF_{2}}}+q\right) }\right| \begin{array}{c}{{1-p-l_{1}-l_{2}, 1, \kappa _{1}}}\\ {{\kappa _{2}, 0}}\end{array}\right] \right) \end{aligned} \end{aligned}$$
(37)

Making \(\rho =1\) \(\Omega ^{'} =1\), the Malaga distribution becomes equivalent to Gamma-Gamma distribution (Jurado-Navas et al. 2011). So Replacing \(m_{1}=m_{2}=1\), \(\rho =1\), and \(\Omega ^{'} =1\),in eq.  (37), it is reduced to BER expression for RF-(RF/FSO) link modeled using Rayleigh and Gamma-Gamma distribution.

4.3 Average capacity

The average capacity can be expressed in terms of CCDF as Zedini et al. (2014), Trinh et al. (2016).

$$\begin{aligned} \bar{C} = \frac{1}{ln2} \int _{0}^{\infty } \frac{F^{c}_{\gamma _{e2e}}(\gamma )}{1 + w\gamma } d\gamma \end{aligned}$$
(38)

Where \(F^{c}_{\gamma _{e2e}}(\gamma ) = 1 - F_{\gamma _{e2e}}(\gamma )\) is CCDF of end to end SNR which can be easily figured out from Eq. (14). \(\omega = 1\) for heterodyne detection (Lapidoth et al. 2009, Eq. (26)) and \(\omega = \frac{e}{2 \pi }\) for IMDD detection (Arnon et al. 2012, Eq. (7.43)).

Using identity in [http://functions.wolfram.com, Eq. (07.34.03.0271.01)], \((1+\omega \gamma )^{-1}\) can be expressed using Meijer’s G function as \((1+\omega \gamma )^{-1} = {\text {G}}^{1,1}_{1,1} \left[ \left. \omega \gamma \right| \begin{array}{c}{{0}}\\ {{0}}\end{array} \right]\). With the help of Eq. (14), we can rewrite Eq. (38) as

$$\begin{aligned} \bar{C} = \frac{1}{ln2} \left( J1 - J2 + J3 \right) \end{aligned}$$
(39)

Where,

$$\begin{aligned}{} & {} J1 = \int _{0}^{\infty } {\text {G}}^{1,1}_{1,1} \left[ \left. \omega \gamma \right| \begin{array}{c}{{0}}\\ {{0}}\end{array} \right] e^{-\frac{m_{1}\gamma }{\bar{\gamma }_{RF_{1}}}}\sum _{l_{1}=0}^{m_{1}-1}\frac{1}{l_{1}!} \left( \frac{m_{1} \gamma }{\bar{\gamma }_{RF_{1}}}\right) ^{l_{1}} d\gamma \end{aligned}$$
(40)
$$\begin{aligned}{} & {} J1 = \sum _{l_{1}=0}^{m_{1}-1} \frac{ {\text {G}}^{1,2}_{2,1}\left[ \left. \frac{\omega }{\left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}}\right) }\right| \begin{array}{c}{{-l_{1},0}}\\ {{0}}\end{array} \right] }{l_{1}!\;\left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}}\right) } \end{aligned}$$
(41)
$$\begin{aligned}{} & {} J2 = D\sum _{m=1}^{\beta }c_{m} \sum _{l_{1}=0}^{m_{1}-1}\frac{1}{l_{1}!} \int _{0}^{\infty } e^{-\frac{m_{1}\gamma }{\bar{\gamma }_{RF_{1}}}} \left( \frac{m_{1} \gamma }{\bar{\gamma }_{RF_{1}}}\right) ^{l_{1}} {\text {G}}^{3r,1}_{r+1,3r+1}\left[ \left. E\frac{\gamma }{\mu _{r}}\right| \begin{array}{c}{{1,\kappa _{1}}}\\ {{\kappa _{2},0}}\end{array}\right] \; \nonumber \\{} & {} \quad \times {\text {G}}^{1,1}_{1,1} \left[ \left. \omega \gamma \right| \begin{array}{c}{{0}}\\ {{0}}\end{array} \right] d\gamma \end{aligned}$$
(42)

The multiplication of two Meijer’s G functions in Eq. (42) can be represented as Extended Generalized Bivariant Meijer’s G function using (Sharma 1968, Eq. (6)). After some mathematical manipulation, the integral part of Eq. (42) can be solved using (Shah 1973, Eq. (2.1)).

$$\begin{aligned} J2 = D \sum _{l_{1}=0}^{m_{1}-1} \sum _{k=1}^{\beta } \frac{c_{m}}{l_{1}!} \left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}}\right) ^{-1} \; {\text {S}}\left[ \begin{array}{c} \begin{bmatrix} 1 &{} 0 \\ 0 &{} 0 \end{bmatrix}\\ \begin{bmatrix} 1 &{} 1 \\ 0 &{} 0 \end{bmatrix}\\ \begin{bmatrix} 1 &{} 3r \\ r &{} 1 \end{bmatrix}\\ \end{array} \right| \begin{array}{c}{{l_{1}+1;\; -}}\\ \\ {{0;\; 0}}\\ \\ {{1, \kappa _{1};\; \kappa _{2}, 0}}\end{array} \left| \begin{array}{c}{{\frac{\omega }{\left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}}\right) }}}\\ \\ \\ {{\frac{E}{\left( \mu _{r} \frac{m_{1}}{\bar{\gamma }_{RF_{1}}}\right) }}}\end{array} \right] \end{aligned}$$
(43)

Where S[.] is the Extended Generalized Biverent Meijer’s G Function (EBVMGF) defined in (Shah 1973, Eq. (1)). The Mathematica and Matlab implementation of EBVMGF is available in Ansari et al. (2011) and Khanna et al. (2019) respectively.

$$\begin{aligned} \begin{aligned} J3 = D\sum _{m=1}^{\beta }c_{m}&\sum _{l_{1}=0}^{m_{1}-1}\frac{1}{l_{1}!} \sum _{l_{2}=0}^{m_{2}-1}\frac{1}{l_{2}!} \; \int _{0}^{\infty } e^{-\frac{m_{1}\gamma }{\bar{\gamma }_{RF_{1}}}} \left( \frac{m_{1} \gamma }{\bar{\gamma }_{RF_{1}}}\right) ^{l_{1}} e^{-\frac{m_{2}\gamma }{\bar{\gamma }_{RF_{2}}}} \left( \frac{m_{2} \gamma }{\bar{\gamma }_{RF_{2}}}\right) ^{l_{2}} \times \\ {}&{\text {G}}^{3r,1}_{r+1,3r+1}\left[ \left. E\frac{\gamma }{\mu _{r}}\right| \begin{array}{c}{{1,\kappa _{1}}}\\ {{\kappa _{2},0}}\end{array}\right] \; {\text {G}}^{1,1}_{1,1} \left[ \left. \omega \gamma \right| \begin{array}{c}{{0}}\\ {{0}}\end{array} \right] d\gamma \end{aligned} \end{aligned}$$
(44)

J3 can be solved using the same mathematical approach used to derive the Eq. (42).

$$\begin{aligned} \begin{aligned} J3&= D \sum _{l_{1}=0}^{m_{1}-1} \sum _{l_{2}=0}^{m_{2}-1} \sum _{k=1}^{\beta } \frac{c_{m}}{l_{1}!\; l_{2}!} \frac{\left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}}\right) ^{l_{1}} \left( \frac{m_{2}}{\bar{\gamma }_{RF_{2}}}\right) ^{l_{2}}}{\left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}} + \frac{m_{2}}{\bar{\gamma }_{RF_{2}}}\right) ^{l_{1}+l_{2}+1} } \times \\ {}&{\text {S}}\left[ \begin{array}{c} \begin{bmatrix} 1 &{} 0 \\ 1 &{} 0 \end{bmatrix}\\ \begin{bmatrix} 1 &{} 1 \\ 0 &{} 0 \end{bmatrix}\\ \begin{bmatrix} 1 &{} 3r \\ r &{} 1 \end{bmatrix}\\ \end{array} \right| \begin{array}{c}{{l_{1}+l_{2}+1;\; -}}\\ \\ {{0;\; 0}}\\ \\ {{1, \kappa _{1};\; \kappa _{2}, 0}}\end{array} \left| \begin{array}{c}{{}} \\ {{\frac{\omega }{\left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}}+ \frac{m_{2}}{\bar{\gamma }_{RF_{2}}}\right) }}}\\ \\ {{\frac{E}{\mu _{r}\left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}}+ \frac{m_{2}}{\bar{\gamma }_{RF_{2}}}\right) } }}\\ {{}} \end{array} \right] \end{aligned} \end{aligned}$$
(45)

Replacing \(m_{1}=m_{2}=1\), \(\rho =1\) \(\Omega ^{'} =1\) in equation of \(J_{1}, J_{2}, J_{3}\) the Eq. (46) will reduce to Ergodic Capacity expression for RF-(RF/FSO) link modeled using Rayleigh and Gamma-Gamma distribution.

$$\begin{aligned} \begin{aligned} \bar{C}&= \frac{1}{ln2} \left[ \sum _{l_{1}=0}^{m_{1}-1} \frac{ {\text {G}}^{1,2}_{2,1}\left[ \left. \frac{\omega }{\left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}}\right) }\right| \begin{array}{c}{{-l_{1},0}}\\ {{0}}\end{array} \right] }{l_{1}!\;\left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}}\right) } - D \sum _{l_{1}=0}^{m_{1}-1} \sum _{k=1}^{\beta } \frac{c_{m}}{l_{1}!} \left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}}\right) ^{-1} \; \right. \\&\left. {\text {S}}\left[ \begin{array}{c} \begin{bmatrix} 1 &{} 0 \\ 0 &{} 0 \end{bmatrix}\\ \begin{bmatrix} 1 &{} 1 \\ 0 &{} 0 \end{bmatrix}\\ \begin{bmatrix} 1 &{} 3r \\ r &{} 1 \end{bmatrix}\\ \end{array} \right| \begin{array}{c}{{l_{1}+1;\; -}}\\ \\ {{0;\; 0}}\\ \\ {{1, \kappa _{1};\; \kappa _{2}, 0}}\end{array} \left| \begin{array}{c}{{\frac{\omega }{\left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}}\right) }}}\\ \\ \\ {{\frac{E}{\left( \mu _{r} \frac{m_{1}}{\bar{\gamma }_{RF_{1}}}\right) }}}\end{array} \right] + D \sum _{l_{1}=0}^{m_{1}-1} \frac{\left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}}\right) ^{l_{1}}}{l_{1}!} \sum _{l_{2}=0}^{m_{2}-1} \frac{\left( \frac{m_{2}}{\bar{\gamma }_{RF_{2}}}\right) ^{l_{2}}}{l_{2}!} \right. \\ {}&\left. \sum _{k=1}^{\beta } \frac{c_{m} }{\left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}} + \frac{m_{2}}{\bar{\gamma }_{RF_{2}}}\right) ^{l_{1}+l_{2}+1} } \; {\text {S}}\left[ \begin{array}{c} \begin{bmatrix} 1 &{} 0 \\ 1 &{} 0 \end{bmatrix}\\ \begin{bmatrix} 1 &{} 1 \\ 0 &{} 0 \end{bmatrix}\\ \begin{bmatrix} 1 &{} 3r \\ r &{} 1 \end{bmatrix}\\ \end{array} \right| \begin{array}{c}{{l_{1}+l_{2}+1;\; -}}\\ \\ {{0;\; 0}}\\ \\ {{1, \kappa _{1};\; \kappa _{2}, 0}}\end{array} \left| \begin{array}{c}{{}} \\ {{\frac{\omega }{\left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}}+ \frac{m_{2}}{\bar{\gamma }_{RF_{2}}}\right) }}}\\ \\ {{\frac{E}{\mu _{r}\left( \frac{m_{1}}{\bar{\gamma }_{RF_{1}}}+ \frac{m_{2}}{\bar{\gamma }_{RF_{2}}}\right) } }}\\ {{}} \end{array} \right] \right] \end{aligned} \end{aligned}$$
(46)

5 Numerical results

This section describes the results of numerical analysis and Monte-Carlo simulation of the Decode and Forward RF-(RF/FSO) link. We have considered Differential-BPSK modulation scheme \((p=1, q=1)\). For weak turbulence, \((\alpha =8, \beta =4)\), and for strong turbulence \((\alpha =2.296, \beta =2)\) have been considered. Subsequently, \(\Omega = 1.3265, \ b_{0}=0.1079, \ \rho =0.596, \ \phi _{A}-\phi _{B} =\pi /2\) has been taken Ansari et al. (2015). We have considered \(\xi =1.1\) for severe pointing errors and \(\xi =6\) for weak pointing errors. For all the results, where ever not mentioned, The average SNR of all links is considered equal, i.e \((\bar{\gamma )}_{RF_{1}} = \bar{\gamma )}_{RF_{2}} = \bar{\gamma )}_{FSO}\). To avoid multiple overlapping plots, we have considered two extreme cases. One is the best condition for FSO link, i.e., weak atmospheric turbulence, less severity of pointing errors \((\xi =6)\), and heterodyne detection. Another is the worse condition for the FSO link: strong atmospheric turbulence, high severity of pointing errors \(\xi =1.1\), and IM/DD detection. For the RF link fading parameters, different integer values of \(m_{1}\), and \(m_{2}\) are considered.

In Fig. 2, Outage probability vs. average SNR per hop for RF-(RF/FSO) link is demonstrated. The RF fading parameter for both RF link are considered equal \((m_{1} = m_{2})\). The performance is compared with dual-hop decode and forward RF-FSO link with \(m_{1}=2\). The results of Monte-Carlo simulation provide a good match with analytical results. The performance of RF-(RF/FSO) is better than the equivalent RF-FSO link. Better link performance is observed for a higher value of the RF fading parameter. It is also observed that, for \((m_{1} = m_{2})\), the outage probability of the RF-(RF/FSO) link is independent of the strength of atmospheric turbulence, the severity of pointing errors and the detection scheme.

Fig. 2
figure 2

Outage Probability of RF-(RF/FSO) link for different strengths of atmospheric turbulence and Pointing errors. Both RF links’ fading parameter is considered equal \(m_{1}=m_{2}\)

Full size image
Fig. 3
figure 3

Outage Probability of RF-(RF/FSO) link for different fading and turbulence parameters

Full size image

In Figs. 3, and 4, outage probability vs. average SNR is demonstrated for the different RF link fading strengths. From Fig. 3, it is clearly shown that the outage probability is independent of atmospheric turbulence, pointing error, and detection scheme for \(m_{1} < m_{2}\). Another interesting thing observed from Figs. 2 and 3 that the outage probability is the same for \((m_{1},m_{2}) = (1,4)\) and \((m_{1},m_{2})=(1,1)\) for a given SNR. For the case \(m_{1}=2\) and \(m_{2}=4\), the outage probability is different for the considered two extreme cases of FSO link parameters.

Fig. 4
figure 4

Comparision of Outage Probability vs SNR performance for \((m_{1},m_{2}) = (4,1)\; and\; (m_{1},m_{2}) = (4,2)\)

Full size image

The same thing is also conveyed in Fig. 4 Where, Outage probability for \((m_{1},m_{2}) = (4,1) \;and\; (4,2)\)is considered. It is observed that the outage performance is improved by changing strong turbulence to weak turbulence, \(\xi \ from \ 1.1 \ to \ 6\), and changing the detection scheme from IM/DD to heterodyne detection. Unlike other cases, when \(m_{1} > m_{2}\), the outage performance depends on atmospheric turbulence, pointing errors, and detection scheme. The explanation can be found by interpreting Eq. (2). The overall link SNR is dominated by the link with lower SNR i.e. the link experiencing a stronger fading. For the cases of \(m_{1} > m_{2}\), the source to relay link is a stronger link compared to the relay to destination link. So, overall, link performance is dominated by relay to destination link. Another interesting thing observed is the outage results for \((m_{1},m_{2})=(1,2), WT, \xi =6\) and heterodyne detection scheme is the same as the outage for \((m_{1},m_{2})=(2,2)\) plotted in Fig. 2. which can also be explained by Eq. (2).

Fig. 5
figure 5

BER vs. SNR performance of RF-(RF/FSO) link for two extreme conditions of FSO link. Fading parameters of both the RF link are taken equally (\(m_{1}=m_{2}\))

Full size image
Fig. 6
figure 6

Comparison of BER vs SNR performance for \((m_{1},m_{2}) = (4,1) \;and\; (m_{1},m_{2}) = (4,2)\) for different state of FSO link

Full size image

Figure 5 compares the average bit error rate vs. the average SNR per hop. The RF fading parameters of both RF links are considered the same \((m_{1}=m_{2})\). The link performance is also compared with the RF-FSO link with \(m_{1}=2\). It is observed that the BER performance of the link is not affected by atmospheric turbulence, pointing error, and detection scheme. Increasing the value of RF fading parameters improves the BER performance. BER performance for \((m_{1},m_{2}) = (4,1)\) all cases, \((m_{1},m_{2}) = (4,2)\) for WT, \(\xi =6\), heterodyne detection, and \((m_{1},m_{2}) = (4,4)\) for all FSO link configurations is closely matches, which can also be comprehended from Eq. (2) and (1).

Fig. 7
figure 7

Outage Probability of RF-(RF/FSO) link for weak and strong turbulence. The fading parameter for source to relay and relay to destination RF links are \(m_{1}=m_{2}=2\)

Full size image

Figure 6 presents the BER performance of RF-(RF/FSO) link for \((m_{1},m_{2}) = (1,4), (2,1) \ and \ (2,4)\). The for \(m_{1} < m_{2}\) i.e \((m_{1},m_{2}) = (1,4)\) and (2, 4) , the BER performance is not dependent on the atmospheric turbulence, pointing errors, and detection scheme. However, for the case of \((m_{1},m_{2}) = (2,4)\), the BER performance depends on the FSO link parameters. The BER performance is better in case of weak turbulence, weak severity of pointing errors \((\xi =6)\), and heterodyne detection. The performance for the \((m_{1},m_{2}) = (2,1)\) WT, \(\xi =6\), heterodyne case, \((m_{1},m_{2}) = (2,2)\) (Fig. 5) and, \((m_{1},m_{2}) = (2,4)\) and are the same. This behavior agrees with Eqs. (2) and (1).

The case of \((m_{1} > m_{2})\), where overall link performance depends upon FSO link parameters, is demonstrated in more detail in Fig. 7. The BER performance improves by changing atmospheric turbulence from weak to strong, \(\xi =1.1 \ to \ \xi =6\), and changing the detection scheme from IM/DD to heterodyne detection. The performance for \((m_{1},m_{2}) = (4,1)\) WT, \(\xi =6\), heterodyne detection, \((m_{1},m_{2}) = (4,2)\) WT, \(\xi =6\), heterodyne detection and \((m_{1},m_{2}) = (4,4)\) all cases of FSO link parameters are the same, which is again in agreement with Eqs. (2) and (1).

Fig. 8
figure 8

Ergodic channel capacity of RF-(RF/FSO) link for weak turbulence. The fading parameter for source to relay and relay to destination RF links are \(m_{1}=m_{2}=2\) and 4

Full size image

Figure 8 demonstrates the ergodic channel capacity vs. average SNR per hop. It is considered that the source to relay and relay to destination RF links experience equal strength of fading. The FSO link is experiencing weak turbulence and less severe pointing errors. The simulation results provide a good match to the analytical results. Moreover, for a given SNR, channel capacity is higher if both the RF links experience a strong LOS component, i.e. \(m_{1} = m_{2} =4\).

6 Conclusion

In this work, we have investigated a performance analysis of RF-(RF/FSO) communication systems considering the Nakagami-m fading channel, Malaga atmospheric turbulence with pointing errors and different detection schemes for FSO link. First, we presented the PDF, CDF, and MGF of end-to-end SNR of decode and forward RF-(RF/FSO) communication systems. We have investigated the Outage Probability, BER, and Ergodic Capacity of the RF-(RF/FSO) link.

The overall performance of the link is independent of FSO link parameters, i.e., atmospheric turbulence, pointing errors, and selection of detection techniques; if the source to relay RF link is experiencing a stronger fading than the relay to destination RF link \((m_{1} \le m_{2})\),

The performance depends on FSO link parameters if the relay to destination RF link is experiencing a stronger fading than the source to relay link \((m_{1} \ge m_{2})\). In summary, the overall link performance is dominated by the hop experiencing a stronger fading.