1 Introduction

Recently, there is tremendous increase in the need of high data and multimedia services such as high speed internet, video conferencing, live streaming which has led to the congestion in radio frequency (RF) spectrum. This has led to the need of changing from RF carrier to optical carrier [1]. Consequently, Free Space Optical (FSO) communication system has been proposed as alternative solution to this problem in recent times due to its various advantages. These include power consumption, cheap installation and operational cost, license-free spectrum, large bandwidth in the capacity of order of gigabytes, high level of security compare to RF systems counterpart [2, 3]. However, with these great attributes, the performance of FSO communication system highly suffers from many challenges. These challenges include atmospheric turbulence induced fading due to fluctuation in the refraction index as a result of inhomogeneous variation in temperature and pressure along the FSO link [4]. Hence, various statistical distributions have been proposed to model the atmospheric turbulence along the FSO link. One of such is lognormal distribution which is proposed for weak turbulence over a distance of less than 1 km [5]. Also, the K-distribution and negative exponential distribution have been studied to fit and offer accurate result for saturated turbulence strength over a long distance of several kilometers [6, 7]. Furthermore, Andrew et al. [8] proposed Gamma–Gamma distribution as the best distribution that agrees well with experimental data to model atmospheric turbulent from weak to strong levels. In addition to atmospheric turbulence, pointing error effect can also degrade the performance of FSO system as a result of building sway caused by dynamic wind loads, thermal expansion and weak earthquake. These cause vibrations in the transmitted beam leading to misalignment between the transmitter and receiver and limit the system performance [9]. Beside the building sway, as the link distance between the transmitter and receiver increases, the more the misalignment effect becomes pronounced, especially over a distance of 1 km or more [10]. The combined effect of these impairments on FSO link has been studied in literatures [11,12,13] and different techniques have been suggested to improve the system performance and availability over a long distance.

Studies have shown that the atmospheric turbulence induced fading and pointing error issues along the FSO link can be mitigated by using relay transmission technique [14]. This technique involves scaling down the distance between the transmitter and receiver through the use of relay hops in order to reduce the problem of a single transmitter to reach its intended target with necessary Signal to Noise Ratio (SNR). This concept was first explored by Acampora, and Krishnamurthy in [15], and few years later, the effectiveness of the relay system over a large coverage area was later studied in [16, 17]. The scheme has advantage of increasing the wireless systems coverage area to several kilometers without the needs of large power at the transmitter and relay units. It can also provide high data rate with low bit error at the end-to-end communication [18]. In this case, relay protocol can be classified into two and these include Decode-and-Forward (DF) relay that decodes any received signal from the source, re-encodes and then re-transmits the decoded information to the destination. This relay system is called regenerative relay system. The other type is Amplified–and-Forward (AF) relay which amplifies any incoming signal from the source and retransmits it to the destination without performing any sort of decoding and this is called non-regenerative relay system [19, 20].

Dual-hop relay transmission with AF protocol has been recently proposed for FSO links. For instance, in [21], On/Off Key (OOK) modulation was used to study the capacity performance of FSO dual-hops AF relay system with direct detection at the receiving end. However, OOK modulation scheme requires selecting adaptive thresholds appropriately in order to achieve optimal performance, but it also suffers from poor power efficiency [22]. Moreover, Aggarwal et al. [23] investigate the performance of Subcarrier Intensity Modulation (SIM) dual-hops CSI-assisted AF relay with direct detection over turbulence channel with pointing error. However, the SIM modulation technique employed in this study offers a significantly higher transceiver complexity as the number of subcarrier increases. It also causes poor optical average power efficiency due to the increase in the number of required DC biases [24]. Moreover, a coherent FSO AF relaying system was considered by Pack et al. [25] in which the outage probability performance of the system was studied. Nevertheless, the proposed system is a single input singe output (SISO) which is usually prone to pointing errors.

The concept of Spatial Modulation (SM) has been proposed as migration technique in FSO communication systems as it was found useful in [26,27,28] to improve the system error performance. Thus, based on our study, it shows that this type of modulation scheme has been investigated with relay technology mostly in RF wireless systems [29,30,31,32] but has not been taken into consideration in FSO systems. SM has been known to be an efficient low complex Multiple Input Multiple Output (MIMO) technique compared with other conventional MIMO schemes. At a specific instance, it allows transmission of signal from the activated antenna while other antennas remain idle [33]. This scheme has advantages of avoiding inter-channel interference, eliminating the needs of inter-antenna synchronization, and provides a robust system against channel estimation errors [34, 35]. Moreover, in many FSO research studies, Spatial Diversity (SD) combiner has been extensively considered to combat turbulence fading and pointing errors in order to improve the signal strength over a long distance [36]. The most common employed combiner includes maximum ratio combiner (MRC), equal gain combiner (EGC) and selection combiner (SC) [37]. Arguably, the combination of SM with diversity combiner as a powerful mitigation tool against fading impairments has not been investigated in FSO relaying systems. Motivated by this fact, we present the analysis of average BER and effective capacity of a dual-hop spatial modulation CSI-assisted AF relay system with diversity combiner over atmospheric turbulence and/or pointing error. In this case, the close form expression for the end-to-end SNR MGF, PDF and CDF are derived. Utilizing these results, the APEP for each combiner is determined and generic close form expression for the proposed system ABER is then obtained using union bounding technique. In consequence, the effective capacity for the system is determined through the derived ABER.

The rest of this paper is organized as follows: Sect. 2 presents the system model and the channel statistical model is discussed in Sect. 3. In Sect. 4, the statistical characteristics of end-to-end SNR are presented, while Sect. 5 presents the performance analysis of the system. Numerical and simulation results for the system performance, with their interpretation are presented in Sect. 6. Finally, the concluding remarks are outlined in Sect. 7.

2 System Model

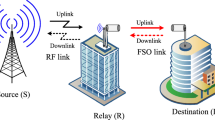
Figure 1 illustrates a dual-hop SM-based relay FSO system with the source (S) as transmitter, destination (D) as receiver and Relay (R). We assume that the S-to-R and R-to-D links are independent, non-identical channel and heterodyne detection is used at R and D. The Source and the Destination are respectively equipped with \(N_{t}^{S}\) transmit lasers and \(N_{r}^{D}\) photo-detectors. The relay (R) in the system operates as Channel State Information (CSI)-assisted AF protocol and the destination employed spatial diversity combiner such as MRC and EGC. The system conducts transmission in two time slots. In the first phase, at the source, random sequence of bits stream to be transmitted are mapped into block of q-bits that is \(q = log_{2} \left( {N_{t} M} \right)\) of \(X = \left[ {x_{1} ,x_{2} ,x_{3} \ldots x_{{N_{t} }} } \right]^{T}\). The first group of these bits \(log_{2} \left( {N_{t} } \right)\) are used to represent the transmit laser index \(j{\text{th}}\) with the laser array while the remaining \(log_{2} \left( M \right)\) bits identify the BPSK modulation symbol \(x_{p}\) in the signal constellation. During this phase, the information bits are modulated on the electric field of an optical beam as \(x_{p} = x_{p} { \exp }\left( {j\phi_{{x_{p} }} } \right)\) and are then emitted from the active transmit-laser index \(j\) at an instance over the optical atmospheric channel as:

$$X_{jp} = \left[ {0 0 \cdots \overbrace {{x_{p} e^{{j\phi_{{x_{p} }} }} }}^{{j^{th} laser\;position}} \cdots 0 0} \right]^{T}$$
(1)
Fig. 1
figure 1

Dual-hops SM-SD amplify-and-forward relay FSO system where PD photo-detector, BC beam combiner, DC down converter, PC phase compensator, BPF bandpass filter

Full size image

At any instance of time, the received electric field at the aperture plane of the relay is sum of the optical field from the transmitter and the Local oscillator at the relay which can be expressed as [28, 38]:

$$E_{R} \left( t \right) = \sqrt {2P_{t} Z_{o} } \left| {X_{jp} H_{SR} } \right|\cos \left( {\omega_{O,S} t + \phi_{h,S} + \phi_{{x_{p} }} } \right) + \sqrt {2P_{LO} Z_{o} } \cos \left( {\omega_{LO,R} t} \right)$$
(2)

where \(E_{s} \left( t \right) = \sqrt {2P_{t,S} Z_{o} } \left| {X_{jp} H_{SR} } \right|\cos \left( {\omega_{O,S} t + \phi_{h,S} + \phi_{{x_{p} }} } \right)\) and \(E_{L} \left( t \right) = \sqrt {2P_{LO,R} Z_{o} } \cos \left( {\omega_{LO,R} t} \right)\) are respectively the optical field from the transmitter and the LO field with \(Z_{o}\) denotes the free space impedance. \(P_{t,S}\) is the transmit laser power from the source, while \(P_{LO,R}\) is the relay LO power, and \(\omega_{IF}\) is the intermediate frequency given as \(\omega_{IF} = \omega_{o} - \omega_{LO,R}\) where \(\omega_{o,S}\) and \(\omega_{LO,R}\) denote the carrier frequency and relay LO frequency respectively. \(H_{SR} = \left| {h_{SR} } \right|e^{{j\phi_{h,S} }}\) denotes the fading factor where the \(h_{SR}\) and \(\phi_{h,S}\) are the fading gain and the link phase between the source and the relay.

The photocurrent at the relay photo-detector output can be obtained as [39]:

$$i_{R} \left( t \right) = \frac{R}{{Z_{o} }}\left[ {E_{S} \left( t \right) + E_{L} \left( t \right)} \right]^{2}$$
(3)

where \(R = \eta q_{e} /\left( {hv_{o} } \right)\) is the responsivity of the photo-detector with electron charge \(q_{e} = 1.6 \times 10^{ - 19} C\), and plank constant \(h = 6.6 \times 10^{ - 34} \,{\text{Js}}\), \(\eta\) denotes the photo-detector efficiency and the optical central frequency \(v_{o} = \omega_{o} /2\pi\).

$$i_{R} \left( t \right) = RP_{t,S} \left| {X_{jp} H_{SR} } \right|^{2} + RP_{L} + 2R\sqrt {P_{t} P_{LO,R} } \left| {X_{jp} H_{SR} } \right|\cos \left( {\omega_{IF,R} t - \phi_{h,S} - \phi_{{x_{p} }} } \right)$$
(4)

where \(I_{DC,S} \,\triangleq\, RP_{t,S} \left| {X_{jp} H_{SR} } \right|^{2}\) and \(I_{DC,L} \,\triangleq\, RP_{L,R}\) is the DC current generated due to signal and LO electric field respectively. \(I_{AC} \,\triangleq\, 2R\sqrt {P_{t,S} P_{L,R} } \left| {X_{jp} H_{SR} } \right|cos\left( {\omega_{IF,R} t - \phi_{h,S} - \phi_{{x_{p} }} } \right)\) is the AC current which contains the useful information about the frequency and the phase of the received signal at the relay. The total output DC current at the photo-detector can be approximately equal to \(RP_{L,R}\) [40]. Therefore, the short noise impaired during photo-detection process at this stage is dominated by LO short noise with variance of \(\sigma_{short, L,R}^{2} = 2q_{e} RP_{LO} B_{e}\), where \(B_{e}\) is the electrical bandwidth of the photo-detector. In other words, the instantaneous signal-to-noise ratio (SNR) of the optical receiver can be defined as the time-average AC photocurrent and the total noise [40]. The SNR for the heterodyne relay receiver can be expressed as:

$$SNR_{{\left( {Het} \right),SR}} = \frac{{\left\langle {i_{AC}^{2} \left( t \right)} \right\rangle }}{{2q_{e} RP_{L,R} B_{e} }} \,\triangleq\, \frac{{RP_{t} \left| {X_{jp} H_{SR} } \right|^{2} }}{{q_{e} B_{e} }}$$
(5)

Based on the \(SNR_{{\left( {Het} \right),SR}}\), the sufficient statistics at the relay can be modeled as [28, 38]:

$$y_{R} \left( t \right) = \sqrt {\overline{\gamma }_{SR} } H_{SR} X_{jp} + w_{R} \left( t \right)$$
(6)

where \(\overline{\gamma }_{SR} = RP_{t} /\left( {q_{e} \Delta f} \right)\) is the average received SNR at the relay system and \(w_{R} \left( t \right)\) is the noise term at the relay dominated by LO short noise model as Additive White Gaussian Noise (AWGN) with zero-mean and \(\sigma_{short, L,R}^{2}\).

During the second phase, the photocurrent \(i_{R} \left( t \right)\) at the relay photo-detector output is then amplified by the relay gain G, converted to optical signal and retransmitted to the destination. At the destination, using the same approach at the relay, the received optical signal at the nth heterodyne receiver at the destination can be expressed as:

$$E_{D,n} \left( t \right) = \sqrt {2P_{t,R} Z_{o} } \left| {y_{R} \left( t \right)GH_{RD} } \right|\cos \left( {\omega_{O,R} t + \phi_{h,R} } \right) + \sqrt {2P_{L,D} } \cos \left( {\omega_{LO,D} t} \right)$$
(7)

where \(E_{s} \left( t \right) \,\triangleq\, \sqrt {2P_{t} Z_{o} } \left| {y_{R} \left( t \right)GH_{RD} } \right|cos\left( {\omega_{LO} t + \phi_{h,R} } \right)\) and \(E_{L,D} \left( t \right) \,\triangleq\, \sqrt {2P_{L,D} Z_{o} } cos\left( {\omega_{LO,D} t} \right)\) are the signal electric field transmitted by relay and LO electric field at the destination respectively. \(H_{RD} \,\triangleq\, \left| {h_{RD} } \right|e^{{j\phi_{h,R} }}\) is the fading factor while the \(h_{RD}\) and \(\phi_{h,R}\) are the fading gain and the link phase between the relay and the destination.

The photocurrent at the \(n{\text{th}}\) photo-detector at the destination can be similarly obtained as:

$$\begin{aligned} i_{D,n} \left( t \right) & = \frac{R}{{Z_{o} }}\left[ {E_{s} \left( t \right) + E_{L} \left( t \right)} \right]^{2} \\ & \triangleq\, RP_{t,R} \left| {y_{R} \left( t \right)GH_{RD} } \right|^{2} + RP_{L,R} GH_{RD} + 2R\sqrt {P_{t,R} P_{L,R} } \left| {y_{R} \left( t \right)GH_{RD} } \right|\cos \left( {\omega_{IF} t - \phi_{h,R} } \right) \\ \end{aligned}$$
(8)

where \(I_{DC,s} \,\triangleq\, RP_{t,R} \left| {y_{R} \left( t \right)GH_{RD} } \right|^{2}\) and \(I_{DC,L} \,\triangleq\, RP_{L,R} GH_{RD}\) is the DC current generated due to signal and LO electric field respectively at the \(n{\text{th}}\) heterodyne receiver at the destination while \(I_{AC,D} \,\triangleq\, 2R\sqrt {P_{t} P_{L,R} } \left| {y_{R} \left( t \right)GH_{RD} } \right|cos\left( {\omega_{IF} t - \phi_{h,R} } \right)\) is the AC current which contains the useful information about the frequency and the phase of the received signal at the destination. The short noise impaired during photo-detection process at this stage is also dominated by destination LO short noise with variance of \(\sigma_{short, L,D}^{2} = 2q_{e} RP_{L,D} B_{e}\). The SNR on the R-to-D link for the \(n{\text{th}}\) heterodyne receiver can therefore be expressed as:

$$SNR_{{\left( {Het} \right),RD}} = \frac{{\left\langle {i_{AC,n}^{2} \left( t \right)} \right\rangle }}{{2q_{e} RP_{L,D} B_{e} }} \,\triangleq\, \frac{{RP_{t} \left| {y_{R} \left( t \right)GH_{RD} } \right|^{2} }}{{q_{e} B_{e} }}$$
(9)

The received signal at the \(n{\text{th}}\) heterodyne receiver can be statistically obtained as:

$$\begin{aligned} y_{D} \left( t \right) = \sqrt {\overline{\gamma }_{RD} } GH_{RD} y_{R} \left( t \right) + w_{D} \left( t \right) & \triangleq\, \sqrt {\overline{\gamma }_{RD} } GH_{RD} \left( {\sqrt {\overline{\gamma }_{SR} } H_{SR} X_{jp} + w_{R} \left( t \right)} \right) + w_{D} \left( t \right) \\ & \triangleq\, \underbrace {{\sqrt {\overline{\gamma }_{RD} \overline{\gamma }_{SR} } GH_{RD} H_{SR} X_{jp} }}_{signal\;part} + \underbrace {{\sqrt {\overline{\gamma }_{RD} } GH_{RD} w_{R} \left( t \right) + w_{D} \left( t \right)}}_{Noise\;part} \\ \end{aligned}$$
(10)

In this paper, we assume that the receiver has full CSI and therefore after the normalization of the noise, the received signal at the \(n{\text{th}}\) heterodyne receiver at the destination can be further simplified as:

$$y_{D} \left( t \right) = \sqrt K H_{RD} X_{jp} + \hat{w}\left( t \right)$$
(11)

where \(K = \frac{{G^{2} H_{RD}^{2} \overline{\gamma }_{RD} \overline{\gamma }_{SR} }}{{\overline{\gamma }_{RD} G^{2} H_{RD}^{2} + 1}}\) with G denoting the amplification factor at the relay and \(\hat{w}\left( t \right)\) is the complex additive with Gaussian noise (AWGN) at the input of the destination having similar statistical characteristic as \(w_{R} \left( t \right)\).

At destination, we assume optimum detection (OD) to detect the transmitted SM signal vector \(X_{jp}\) from the Source after the signal is combined by spatial diversity combiner. When the OD is applied, the estimated laser index \(\hat{J}\) and the transmitted constellation symbol index \(\hat{p}\) at a specific time instance can be expressed as [41]:

$$\begin{aligned} \left[ { \hat{J},\hat{p}} \right] & = \mathop {argmax}\limits_{{ \hat{J},\hat{p}}} p_{Y} \left( {y_{D} \left| {X_{jp} , H_{RD} } \right.} \right) \\ & \triangleq\, \mathop {argmin}\limits_{{\hat{J},\hat{p}}} \sqrt K \left\| {h_{l}^{D} x_{p} } \right\|_{F}^{2}\, - \,2\text{Re} \left\{ {y_{D}^{H} h_{RD} x_{p} } \right\} \\ \end{aligned}$$
(12)

The equivalent end-to-end SNR, which is the instantaneous received SNR at the destination, can be obtained as [19, 23, 42]:

$$\gamma_{eq} = \frac{{\gamma_{1} \gamma_{2} }}{{\gamma_{1} + \gamma_{2} }} \triangleq \left( {\mathop \sum \limits_{i = 1}^{2} \frac{1}{{\gamma_{i} }}} \right)^{ - 1} , i\in \left( {1,2} \right)$$
(13)

where \(\gamma_{1}\) and \(\gamma_{2}\) are the instantaneous SNR at S-to-R and R-to-S links respectively which are defined in Eqs. (5) and (9). It is assumed that both link has equal average SNR obtained as \(\overline{\gamma }_{1} = \overline{\gamma }_{2} = RP_{t} /\left( {q_{e} \Delta f} \right)\). Thus, the upper bound for the end-to-end SNR \(\gamma_{eq}\) can be derived by using the well-known inequality between geometric and harmonic means for the random variable \(\overline{\gamma }_{1}\) and \(\overline{\gamma }_{2}\) which is given as [19, 23]:

$$\gamma_{eq} \le \gamma_{a} = \frac{1}{2}\mathop \prod \limits_{i = 1}^{2} \gamma_{i}$$
(14)

3 Channel Statistical Model

The Gamma–Gamma was proposed by Andrew et al. for modeling FSO link with the conditions from weak to strong turbulence. This model probability distribution function (PDF) can be expressed as [43]:

$$f_{{H_{mk} }} \left( h \right) = \frac{{2\left( {\alpha \beta } \right)^{{\frac{\alpha + \beta }{2}}} }}{\Gamma \left( \alpha \right)\Gamma \left( \beta \right)}h^{{\frac{\alpha + \beta }{2} - 1}} K_{\alpha - \beta } \left( {2\sqrt {\alpha \beta h} } \right), \quad h > 0$$
(15)

where \(\Gamma \left( . \right)\) and \(K_{\left( . \right)}\) are defined as gamma function and \(v{\text{th}}\) order modified Bessel function of the 2nd kind respectively, \(\alpha\) and \(\beta\) are the scintillation parameters which are specified as [44]:

$$\begin{aligned} \alpha & = \left[ {\exp \left( {\frac{{0.49\sigma_{R}^{2} }}{{\left( {1 + 1.11\sigma_{R}^{12/5} } \right)^{5/6} }}} \right) - 1} \right]^{ - 1} \\ \beta & = \left[ {exp\left( {\frac{{0.51\sigma_{R}^{2} }}{{\left( {1 + 0.69\sigma_{R}^{12/5} } \right)^{5/6} }}} \right) - 1} \right]^{ - 1} \\ \end{aligned}$$
(16)

where \(\sigma_{R}^{2} = 0.49C_{n}^{2} \left( {2\pi /\lambda } \right)^{7/6} L^{11/6}\) is the Rytov Variation which is assumed to be spherical wave with λ stated as the optical wavelength, while L is the link range and \(C_{n}^{2}\) is the refractive structure parameter that defines the turbulence strength [44].

Expressing \(K_{v} \left( x \right)\) in terms of Meijer-G function [45], Eq. (14)]:

$$K_{v} \left( x \right) = \frac{1}{2}G_{0,2}^{2,0} \left({\frac{{x^{2} }}{4}}\left |\begin{array}{*{20}c} { - , - } \\ {\frac{v}{2},\frac{-v}{2}} \\ \end{array} \right. \right)$$
(17)

So, we can express the PDF of the Gamma–Gamma channel define in (15) as:

$$f_{{H_{mk} }} \left( h \right) = \frac{{\left( {\alpha \beta } \right)^{{\frac{\alpha + \beta }{2}}} }}{\Gamma \left( \alpha \right)\Gamma \left( \beta \right)}h^{{\frac{\alpha + \beta }{2} - 1}} G_{0,2}^{2,0} \left( {\alpha \beta h} \left|\begin{array}{*{20}c} { - , - } \\ {\frac{{\alpha - \beta }}{2},\frac{{\beta - \alpha }}{2}} \\ \end{array} \right.\right),\quad h > 0$$
(18)

Also, the Gamma–Gamma channel PDF can be defined in terms of generalized power series representation method of the modified Bessel function of the second kind as [44, 46]:

$$K_{v} \left( x \right) = \frac{\pi }{{2\sin \left( {\pi v} \right)}}\mathop \sum \limits_{l = 0}^{\infty } \left[ {\frac{1}{{\Gamma \left( {l - v + 1} \right)l!}}\left( {\frac{x}{2}} \right)^{2l - v} - \frac{1}{{\Gamma \left( {l + v + 1} \right)l!}}\left( {\frac{x}{2}} \right)^{2l + v} } \right]$$
(19)

where \(v \notin {\mathbb{Z}}\) and \(\left| x \right| < \infty\)

Thus, the PDF in (5) can also be expressed as:

$$f_{{H_{mk} }} \left( h \right) = \mathop \sum \limits_{l = 0}^{\infty } \left[ {a_{k} \left( {\alpha ,\beta } \right)h^{k + \beta - 1} + a_{k} \left( {\beta ,\alpha } \right)h^{k + \alpha - 1} } \right]$$
(20)

where

$$a_{k} \left( {x,y} \right) = \frac{{\pi \left( {xy} \right)^{l + \beta } }}{{\sin \left( {\pi \left( {x - y} \right)} \right)\Gamma \left( x \right)\Gamma \left( y \right)\Gamma \left( {k - x + y} \right)k!}}$$

The misalignment fading due to pointing error \(\left( {h_{p} } \right)\) loss by considering the detector size, beam width, and jitter variance is modeled by Raleigh distribution given as [47, 48]:

$$f_{{H_{mk} }} \left( {h_{p} } \right) = \frac{{\xi^{2} }}{{A_{o}^{{\xi^{2} }} }}h_{p} \xi^{2} - 1 , 0 \le h_{p} \le A_{o}$$
(21)

where \(\xi = w_{e} /2\sigma_{s}\) and \(w_{e}\) is the equivalent beam width at the receiving end, \(\sigma_{s}\) is the standard deviation of the pointing error displacement at the receiver, is given as \(A_{o} = erf^{2} \left( v \right), v = \sqrt {\pi /2} \left( {r_{a} /w_{L} } \right)\) where \(r_{a}\) denotes the radius of the receiver aperture and \(w_{L}\) is the beam waist radius at distance L. Considering the impact of pointing error impairment, the PDF of the combined channel can be expressed as [49]:

$$f_{{H_{mk} }} \left( h \right) = \frac{{\alpha \beta \xi^{2} }}{{A_{o} \Gamma \left( \alpha \right)\Gamma \left( \beta \right)}}G_{1,3}^{3,0} \left( {\frac{\alpha \beta }{{A_{o} }}h\left| {\begin{array}{*{20}c} {\xi^{2} } \\ {\xi^{2} - 1,\alpha - 1,\beta - 1} \\ \end{array} } \right.} \right)$$
(22)

The PDF of \(\gamma_{i}\) is obtained by power transformation of (22) and is expressed as:

$$f_{{\gamma_{i} }} \left( {\gamma_{i} } \right) = \frac{{\xi_{i}^{2} }}{{2\gamma_{i} \Gamma \left( {\alpha_{i} } \right)\Gamma \left( {\beta_{i} } \right)}}G_{1,3}^{3,0} \left( {\alpha_{i} \beta_{i} \sqrt {\frac{{\gamma_{i} }}{{\overline{\gamma }_{i} }}} \left| {\begin{array}{*{20}c} {\xi_{i}^{2} + 1} \\ {\xi_{i}^{2} ,\alpha_{i} ,\beta_{i} } \\ \end{array} } \right.} \right)$$
(23)

4 Statistical Characteristics of End-to-End SNR

4.1 Under the Influence of Atmospheric Turbulence Without Pointing Error

In this section, we derive the MGF, PDF and CDF of the end-to-end SNR \(\gamma_{a}\) defined in (14), with the assumption that the channel is independent non-identical distribution Gamma–Gamma turbulence channel.

4.1.1 MGF of the End-to-End SNR \(\gamma_{a}\)

The MGF of the end-to-end SNR \(\gamma_{a}\) can be derived in closed form as:

$$\begin{aligned} M_{{\gamma_{a} }} \left( { - S} \right) & = \mathop \int \limits_{0}^{\infty } \mathop \int \limits_{0}^{\infty } \left[ {\exp - \left( {S\mathop \prod \limits_{i = 1}^{2} \gamma_{i}^{1/2} } \right)} \right]\left[ {\mathop \prod \limits_{i = 1}^{2} f_{{\gamma_{i} }} \left( {\gamma_{i} } \right)} \right]d\gamma_{i} \\ & \triangleq \mathop \int \limits_{0}^{\infty } \mathop \int \limits_{0}^{\infty } \exp \left( { - S\gamma_{1}^{{\frac{1}{2}}} \gamma_{2}^{{\frac{1}{2}}} } \right)f_{{\gamma_{1} }} \left( {\gamma_{1} } \right)f_{{\gamma_{2} }} \left( {\gamma_{2} } \right)d\gamma_{1} d\gamma_{2} \\ \end{aligned}$$
(24)

It should be noted that we can use the Gamma–Gamma PDF define in (18) and (20) to evaluate the MGF defined in (24). However, the integrals of the equation will yield infinite result and will be untraceable if we apply (20) to compute these integrals. Therefore we cannot obtain the exact close form expression for the end-to-end SNR. As a result of this, we thus applied the defined PDF in (18) to determine the MGF as follows:

If the PDF in terms of end-to-end SNR for the Gamma–Gamma can be expressed as:

$$f_{{\gamma_{i} }} \left( {\gamma_{i} } \right) = \frac{{\left( {\alpha_{i} \beta_{i} } \right)^{{\frac{{\alpha_{i + } \beta_{i} }}{2}}} \gamma_{i}^{{\frac{{\alpha_{i + } \beta_{i} }}{4} - 1}} }}{{2\Gamma \left( {\alpha_{i} } \right)\Gamma \left( {\beta_{i} } \right)\overline{\gamma }_{i}^{{\frac{{\alpha_{i + } \beta_{i} }}{4}}} }}G_{0,2}^{2,0} \left( {\frac{{\alpha \beta }}{{\sqrt {\bar{\gamma }_{i} } }}\sqrt {\gamma _{i} } } \left|\begin{array}{*{20}c} { - , - } \\ {\frac{{\alpha _{i} - \beta _{i} }}{2},\frac{{\beta _{i} - \alpha _{i} }}{2}} \\ \end{array} \right.\right)$$
(25)

If we let the \(\Xi_{i} = \frac{\alpha \beta }{{\sqrt {\overline{\gamma }_{i} } }}\) and apply the Meijer-G identity defined in [50], Eq. (9.31.5)], then the PDF can be expressed as:

$$\begin{aligned} f_{{\gamma_{i} }} \left( {\gamma_{i} } \right) & = \frac{{\left( {\Xi_{i} \sqrt {\gamma_{i} } } \right)^{{\frac{{\alpha_{i + } \beta_{i} }}{2}}} }}{{2\Gamma \left( {\alpha_{i} } \right)\Gamma \left( {\beta_{i} } \right)}}\gamma_{i}^{ - 1} G_{0,2}^{2,0} \left({\Xi _{i} \sqrt {\gamma _{i} } } \left.|\begin{array}{*{20}c} { - , - } \\ {\frac{{\alpha _{i} - \beta _{i} }}{2},\frac{{\beta _{i} - \alpha _{i} }}{2}} \\ \end{array} \right. \right) \\ & \triangleq \frac{1}{{2\Gamma \left( {\alpha_{i} } \right)\Gamma \left( {\beta_{i} } \right)}}\gamma_{i}^{ - 1} G_{0,2}^{2,0} \left({\Xi _{i} \sqrt {\gamma _{i} } } \left|\begin{array}{*{20}c} { - , - } \\ {\frac{{\alpha _{i} }}{2},\frac{{\beta _{i} }}{2}} \\ \end{array} \right.\right) \\ \end{aligned}$$
(26)

The first integration in (24) on \(\gamma_{1}\) is of the form:

$${\mathfrak{T}}_{1} \left( S \right) = \frac{1}{{2\Gamma \left( {\alpha_{1} } \right)\Gamma \left( {\beta_{1} } \right)}}\mathop \int \limits_{0}^{\infty } \gamma_{1}^{ - 1} G_{0,2}^{2,0} \left({\Xi _{1} \sqrt {\gamma _{1} } } \left|\begin{array}{*{20}c} { - , - } \\ {\frac{{\alpha _{1} }}{2},\frac{{\beta _{1} }}{2}} \\ \end{array} \right.\right) \exp \left( { - SV\gamma_{1}^{1/2} } \right)d\gamma_{1}$$
(27)

where \(V = \frac{{\sqrt {\gamma_{2} } }}{2}\)

Using the Meijer-G identity of the exponential function in [45], Eq. (11)] to (27), then,

$${\mathfrak{T}}_{1} \left( S \right) = \frac{1}{{2\Gamma \left( {\alpha_{1} } \right)\Gamma \left( {\beta_{1} } \right)}}\mathop \int \limits_{0}^{\infty } \gamma_{1}^{ - 1} G_{0,2}^{2,0} \left({\Xi _{1} \sqrt {\gamma _{1} } } \left|\begin{array}{*{20}c} { - , - } \\ {\frac{{\alpha _{1} }}{2},\frac{{\beta _{1} }}{2}} \\ \end{array} \right.\right) G_{0,1}^{1,0} \left( {SV\gamma_{1}^{1/2} \left| _{\overline{0}} \right.} \right)d\gamma_{1}$$
(28)

let \(Z = \gamma_{1}^{1/2} ,Z^{2} = \gamma_{1} ,\frac{{d\gamma_{1} }}{dZ} = 2Z\;{\text{and}}\;d\gamma_{1} = 2ZdZ\), then apply the Meijer-G identity in [45], Eq. (21)]

$${\mathfrak{T}}_{1} \left( S \right) = \frac{1}{{\Gamma \left( {\alpha_{1} } \right)\Gamma \left( {\beta_{1} } \right)}}G_{2,1}^{1,2} \left( {\frac{SV}{{\Xi_{1} }}\left| {\begin{array}{*{20}c} {1 - \alpha_{1} , 1 - \beta_{1} } \\ 0 \\ \end{array} } \right.} \right)$$
(29)

Using the similar method, the integration on γ 2 can be obtained by substituting (29) for (24):

$$\begin{aligned} {\mathfrak{T}}_{2} \left( S \right) = \frac{1}{{\Gamma \left( {\alpha_{1} } \right)\Gamma \left( {\beta_{1} } \right)}}\frac{1}{{2\Gamma \left( {\alpha_{2} } \right)\Gamma \left( {\beta_{2} } \right)}}\mathop \int \limits_{0}^{\infty } \gamma_{1}^{ - 1} G_{0,2}^{2,0}\left({\Xi _{2} \sqrt {\gamma _{2} } } \left|\begin{array}{*{20}c} { - , - } \\ {\frac{{\alpha _{2} }}{2},\frac{{\beta _{2} }}{2}} \\ \end{array} \right.\right) G_{2,1}^{1,2} \left( {\frac{SV}{{\Xi_{1} }}\sqrt {\gamma_{2} } \left| {\begin{array}{*{20}c} {1 - \alpha_{1} , 1 - \beta_{1} } \\ 0 \\ \end{array} } \right.} \right)d\gamma_{1} \\ \triangleq \frac{1}{{\Gamma \left( {\alpha_{1} } \right)\Gamma \left( {\beta_{1} } \right)}}\frac{1}{{\Gamma \left( {\alpha_{2} } \right)\Gamma \left( {\beta_{2} } \right)}}G_{4,1}^{1,4} \left( {\frac{SV}{{\Xi_{1} \Xi_{2} }}\left| {\begin{array}{*{20}c} {1 - \alpha_{1} , 1 - \beta_{1} ,1 - \alpha_{2} , 1 - \beta_{2} } \\ 0 \\ \end{array} } \right.} \right) \\ \end{aligned}$$
(30)

Thus, substitute (29) and (30) for (24), then the MGF can be obtained as:

$$M_{{\gamma_{b} }} \left( S \right) = \mathop \prod \limits_{i = 1}^{2} \frac{1}{{\Gamma \left( {\alpha_{i} } \right)\Gamma \left( {\beta_{i} } \right)}}G_{4,1}^{1,4} \left( {\frac{S}{{2\Xi_{1} \Xi_{2} }}\left| {\begin{array}{*{20}c} {1 - \alpha_{1} , 1 - \beta_{1} ,1 - \alpha_{2} , 1 - \beta_{2} } \\ 0 \\ \end{array} } \right.} \right)$$
(31)

4.1.2 PDF of End-to-End SNR \(\gamma_{a}\)

The PDF of \(\gamma_{b}\) can be determined by applying the inversed Laplace Transform \({\mathcal{L}}^{ - 1}\) to the MGF in (31) and this can be expressed as \(f_{{\gamma_{a} }} \left( \gamma \right) = {\mathcal{L}}^{ - 1} \left\{ {M_{{\gamma_{a} }} \left( S \right),\gamma } \right\}\). Applying the identity [51], Eq. (3.40.1.1)] for the inverse Laplace transform of the Meijer-G function, we obtained the PDF of \(\gamma_{b}\) in closed form as:

$$f_{{\gamma_{a} }} \left( \gamma \right) = \gamma^{ - 1} \mathop \prod \limits_{i = 1}^{2} \frac{1}{{\Gamma \left( {\alpha_{i} } \right)\Gamma \left( {\beta_{i} } \right)}}G_{4,1}^{1,4} \left( {2\gamma \mathop \prod \limits_{i = 1}^{2} \Xi_{i} \left| {\begin{array}{*{20}c} - \\ {\alpha_{1} , \beta_{1} ,\alpha_{2} , \beta_{2} } \\ \end{array} } \right.} \right)$$
(32)

4.1.3 CDF of End-to-End SNR \(\gamma_{a}\)

The CDF of the \(\gamma_{a}\) can be defined as \(F_{{\gamma_{a} }} \left( \gamma \right) = \mathop \int \limits_{0}^{\gamma } f_{{\gamma_{a} }} \left( \gamma \right)d\gamma\). Applying the integral identity stated in [45], Eq. (26)], the CDF can therefore be obtained as follows:

$$\begin{aligned} F_{{\gamma_{b} }} \left( \gamma \right) & = \mathop \prod \limits_{i = 1}^{2} \frac{1}{{\Gamma \left( {\alpha_{i} } \right)\Gamma \left( {\beta_{i} } \right)}}\mathop \int \limits_{0}^{\gamma } \gamma^{ - 1} \mathop \prod \limits_{i = 1}^{2} \frac{1}{{\Gamma \left( {\alpha_{i} } \right)\Gamma \left( {\beta_{i} } \right)}}G_{4,1}^{1,4} \left( {2\gamma \mathop \prod \limits_{i = 1}^{2} \Xi_{i} \left| {\begin{array}{*{20}c} - \\ {\alpha_{1} , \beta_{1} ,\alpha_{2} , \beta_{2} } \\ \end{array} } \right.} \right) \\ & \triangleq \mathop \prod \limits_{i = 1}^{2} \frac{1}{{\Gamma \left( {\alpha_{i} } \right)\Gamma \left( {\beta_{i} } \right)}}G_{1,5}^{4,1} \left( {2\gamma \mathop \prod \limits_{i = 1}^{2} \Xi_{i} \left| {\begin{array}{*{20}c} 1 \\ {\alpha_{1} , \beta_{1} ,\alpha_{2} , \beta_{2} ,0} \\ \end{array} } \right.} \right) \\ \end{aligned}$$
(33)

4.2 Under the Influence of Atmospheric Turbulence and Pointing Error

4.2.1 MGF of End-to-End SNR \(\gamma_{a}\) for the Pointing Error

Following the same approach used in obtaining the MGG of end-to-end SNR without pointing error, the MGF of end-to-end SNR with pointing error can thus be obtained by using (24), and the first integral on \(\gamma_{1}\) is expressed as:

$${\mathfrak{T}}_{1} \left( S \right) = \mathop \int \limits_{0}^{\infty } \gamma_{1}^{ - 1} G_{1,3}^{3,0} \left( {\alpha_{1} \beta_{1} \sqrt {\frac{{\gamma_{1} }}{{\overline{\gamma }_{1} }}} \left| {\begin{array}{*{20}c} {\xi_{1}^{2} + 1} \\ {\xi_{1}^{2} ,\alpha_{1} ,\beta_{1} } \\ \end{array} } \right.} \right)G_{0,1}^{1,0} \left( {SV\gamma_{1}^{1/2} \left| {\begin{array}{*{20}c} - \\ 0 \\ \end{array} } \right.} \right)d\gamma_{1}$$
(34)

By expressing the exponential function in form of Meijer-G function [50], Eq. (8.2.2)] and the integration of \({\mathfrak{T}}_{1} \left( S \right)\) can be solved using [45], Eq. (21)] as:

$${\mathfrak{T}}_{1} \left( S \right) = 2G_{2,3}^{3,1} \left( {\frac{{\alpha_{1} \beta_{1} }}{{SV\sqrt {\overline{\gamma }_{1} } }}\left| {\begin{array}{*{20}c} {1, \xi_{1}^{2} + 1} \\ {\xi_{1}^{2} ,\alpha_{1} ,\beta_{1} } \\ \end{array} } \right.} \right)$$
(35)

To solve the second integral in (24), substitute for \({\mathfrak{T}}_{1} \left( S \right)\) and apply the Meijer-G identity given in [50], Eq. (8.2.2)] and [45], Eq. (21)], then the MGF is therefore obtained as:

$$M_{{\gamma_{a} }} \left( S \right) = \mathop \prod \limits_{i = 1}^{2} \left[ {\frac{{\xi_{i}^{2} }}{{\Gamma \left( {\alpha_{i} } \right)\Gamma \left( {\beta_{i} } \right)}}} \right]G_{3,6}^{6,1} \left( {\frac{2}{S}\mathop \prod \limits_{i = 1}^{2} \Xi_{i} \left| {\begin{array}{*{20}c} {1, \psi_{3} } \\ {\psi_{1} ,\psi_{2} } \\ \end{array} } \right.} \right)$$
(36)

where \(\psi_{1} = \alpha_{1} ,\beta_{1} \alpha_{2} ,\beta_{2}\), \(\psi_{2} = \xi_{1}^{2} ,\xi_{2}^{2}\) and \(\psi_{3} = \xi_{1}^{2} + 1, \xi_{2}^{2} + 1\)

4.2.2 PDF of End-to-End SNR \(\gamma_{a}\) for the Pointing Error

To determine the PDF of the end-to-end SNR,\(f_{{\gamma_{a} }} \left( \gamma \right)\), apply inverse Laplace transform to (36) using the identity given in [51], Eq. (30.40.1.1)] as:

$$f_{{\gamma_{a} }} \left( \gamma \right) = \gamma^{ - 1} \mathop \prod \limits_{i = 1}^{2} \left[ {\frac{{\xi_{i}^{2} }}{{\Gamma \left( {\alpha_{i} } \right)\Gamma \left( {\beta_{i} } \right)}}} \right]G_{3,6}^{6,1} \left( {2\gamma \mathop \prod \limits_{i = 1}^{2} \Xi_{i} \left| {\begin{array}{*{20}c} { \psi_{3} } \\ {\psi_{1} ,\psi_{2} } \\ \end{array} } \right.} \right)$$
(37)

4.2.3 CDF of End-to-End SNR \(\gamma_{a}\) for the Pointing Error

The CDF for the end-to-end SNR can be obtained as \(F_{{\gamma_{a} }} \left( \gamma \right) = \mathop \int \limits_{0}^{\gamma } f_{{\gamma_{a} }} \left( \gamma \right)d\gamma\). Applying the integral identity stated in [45], Eq. (26)], the CDF can therefore be obtained as follows:

$$\begin{aligned} F_{{\gamma_{a} }} \left( \gamma \right) & = \mathop \int \limits_{0}^{\gamma } \gamma^{ - 1} \mathop \prod \limits_{i = 1}^{2} \left[ {\frac{{\xi_{i}^{2} }}{{\Gamma \left( {\alpha_{i} } \right)\Gamma \left( {\beta_{i} } \right)}}} \right]G_{2,6}^{6,0} \left( {2\gamma \mathop \prod \limits_{i = 1}^{2} \Xi_{i} \left| {\begin{array}{*{20}c} { \psi_{3} } \\ {\psi_{1} ,\psi_{2} } \\ \end{array} } \right.} \right)d\gamma \\ & \triangleq \mathop \prod \limits_{i = 1}^{2} \left[ {\frac{{\xi_{i}^{2} }}{{\Gamma \left( {\alpha_{i} } \right)\Gamma \left( {\beta_{i} } \right)}}} \right]G_{3,6}^{6,1} \left( {2\gamma \mathop \prod \limits_{i = 1}^{2} \Xi_{i} \left| {\begin{array}{*{20}c} {1, \psi_{3} } \\ {\psi_{1} ,\psi_{2} } \\ \end{array} } \right.} \right) \\ \end{aligned}$$
(38)

5 Performance Analysis

At the destination, the receiver combines transmit amplified SM signal from the relay through the use of MRC and EGC. Thus, to determine the ABER for the proposed SM-SD dual-hop AF relay system, a well-known boundary technique is adopted to evaluate the BER under the fading condition. The average BER can be bounded as given in [41] by:

$$ABER_{SM - SD} \le \frac{{\left( {N_{t} M} \right)^{ - 1} }}{{\log_{2} \left( {N_{t} M} \right)}}\mathop \sum \limits_{j = 1}^{{N_{t} }} \mathop \sum \limits_{p = 1}^{M} \mathop \sum \limits_{{\hat{J} = j + 1}}^{{N_{t} }} \mathop \sum \limits_{{\hat{p} = p + 1}}^{M} N\left( {p,\hat{p}} \right)APEP\left( {x_{j, p} \to x_{{\hat{J},\hat{p}}} } \right)$$
(39)

where \(N\left( {p,\hat{p}} \right)\) is the number of bit error when selecting \(p\) instead of \(\hat{p}\) as the transmit unit index, \(APEP\left( {x_{j, p} \to x_{{\hat{J},\hat{p}}} } \right)\) dotes the Average Pairwise Error Probability (APEP) of deciding on the constellation vector \(x_{j, p}\) given that \(x_{{\hat{J},\hat{p}}}\) is transmitted.

5.1 Average Pairwise Error Probability for MRC Combiner

The instantaneous SNR at the output of MRC is defined as [52]:

$$\gamma_{t}^{MRC} = \mathop \sum \limits_{n = 1}^{{N_{r}^{D} }} \gamma_{{a_{n} }}$$
(40)

where \(\gamma_{{a_{n} }}\) is the end-to-end SNR received at the \(n{\text{th}}\) heterodyne receiver. Thus, the PEP can be expressed as:

$$\begin{aligned} PEP_{MRC} \left( {x_{j, p} \to x_{{\hat{J},\hat{p}}} } \right) & = Q\left( {\sqrt {2\gamma_{t}^{MRC} } } \right) \\ & \triangleq\, Q\left( {\sqrt {2\mathop \sum \limits_{n = 1}^{{N_{r}^{D} }} \gamma_{{a_{n} }} } } \right) \\ \end{aligned}$$
(41)

Thus, by averaging (41), the average PEP for the MRC can be obtained as:

$$APEP_{MRC} \left( {x_{j, p} \to x_{{\hat{J},\hat{p}}} } \right) = \int\limits_{0}^{\infty } {\left( {\sqrt {2\sum\limits_{n = 1}^{{N_{r}^{D} }} {\gamma_{{a_{n} }} } } } \right)} f_{{\gamma_{a} }} \left( \gamma \right)d\gamma$$
(42)

Using the upper bound of Crag’s Q-function defined as \(Q\left( x \right) \le 1/2\exp \left( { - x^{2} /2} \right)\) [53], then the average PEP can be expressed as:

$$\begin{aligned} APEP_{MRC} \left( {x_{j, p} \to x_{{\hat{J},\hat{p}}} } \right) & = \frac{1}{2}\mathop \int \limits_{0}^{\infty } \exp \left( { - \mathop \sum \limits_{n = 1}^{{N_{r}^{D} }} \gamma_{{a_{n} }} } \right)f_{{\gamma_{a} }} \left( \gamma \right)d\gamma \\ & \triangleq \frac{1}{2}\mathop \prod \limits_{n = 1}^{{N_{r}^{D} }} M_{{\gamma_{{a_{n} }} }} \left( S \right) \\ \end{aligned}$$
(43)

To determine the average PEP for the MRC-SM under the influence of atmospheric turbulence without pointing error, substitute (31) for (43) as:

$$APEP_{MRC} \left( {x_{j, p} \to x_{{\hat{J},\hat{p}}} } \right) = \frac{1}{2}\left[ {\mathop \prod \limits_{i = 1}^{2} \frac{1}{{\Gamma \left( {\alpha_{i} } \right)\Gamma \left( {\beta_{i} } \right)}}G_{4,1}^{1,4} \left( {\frac{1}{{2\Xi_{1} \Xi_{2} }}\left| {\begin{array}{*{20}c} {1 - \alpha_{1} , 1 - \beta_{1} ,1 - \alpha_{2} , 1 - \beta_{2} } \\ 0 \\ \end{array} } \right.} \right)} \right]^{{N_{r}^{D} }}$$
(44)

Similarly, the average PEP for the MRC-SM under the influence of atmospheric turbulence with pointing error, substitute (36) for (43) as:

$$APEP_{MRC} \left( {x_{j, p} \to x_{{\hat{J},\hat{p}}} } \right) = \frac{1}{2}\left[ {\mathop \prod \limits_{i = 1}^{2} \left[ {\frac{{\xi_{i}^{2} }}{{\Gamma \left( {\alpha_{i} } \right)\Gamma \left( {\beta_{i} } \right)}}} \right]G_{3,6}^{6,1} \left( {2\mathop \prod \limits_{i = 1}^{2} \Xi_{i} \left| {\begin{array}{*{20}c} {1, \psi_{3} } \\ {\psi_{1} ,\psi_{2} } \\ \end{array} } \right.} \right)} \right]^{{N_{r}^{D} }}$$
(45)

Thus, the average BER for the MRC dual-hop relay system without and with pointing error can therefore be respectively obtained by substituting (44) and (45) for (39):

$$ABER_{{MRC\left( {without\;pointing\;error} \right)}} \le \frac{{\left( {N_{t} M} \right)^{ - 1} }}{{2\log_{2} \left( {N_{t} M} \right)}}\mathop \sum \limits_{j = 1}^{{N_{t} }} \mathop \sum \limits_{p = 1}^{M} \mathop \sum \limits_{{\hat{J} = j + 1}}^{{N_{t} }} \mathop \sum \limits_{{\hat{p} = p + 1}}^{M} N\left( {p,\hat{p}} \right)\left[ {\mathop \prod \limits_{i = 1}^{2} \frac{1}{{\Gamma \left( {\alpha_{i} } \right)\Gamma \left( {\beta_{i} } \right)}}G_{4,1}^{1,4} \left( {\frac{1}{{2\Xi_{1} \Xi_{2} }}\left| {\begin{array}{*{20}c} {1 - \alpha_{1} , 1 - \beta_{1} ,1 - \alpha_{2} , 1 - \beta_{2} } \\ 0 \\ \end{array} } \right.} \right)} \right]^{{N_{r}^{D} }}$$
(46)
$$ABER_{{MRC\left( {with\;pointing\;error} \right)}} \le \frac{{\left( {N_{t} M} \right)^{ - 1} }}{{2\log_{2} \left( {N_{t} M} \right)}}\mathop \sum \limits_{j = 1}^{{N_{t} }} \mathop \sum \limits_{p = 1}^{M} \mathop \sum \limits_{{\hat{J} = j + 1}}^{{N_{t} }} \mathop \sum \limits_{{\hat{p} = p + 1}}^{M} N\left( {p,\hat{p}} \right)\left[ {\mathop \prod \limits_{i = 1}^{2} \left[ {\frac{{\xi_{i}^{2} }}{{\Gamma \left( {\alpha_{i} } \right)\Gamma \left( {\beta_{i} } \right)}}} \right]G_{3,6}^{6,1} \left( {2\mathop \prod \limits_{i = 1}^{2} \Xi_{i} \left| {\begin{array}{*{20}c} {1, \psi_{3} } \\ {\psi_{1} ,\psi_{2} } \\ \end{array} } \right.} \right)} \right]^{{N_{r}^{D} }}$$
(47)

5.2 Average Pairwise Error Probability for EGC Combiner

The instantaneous SNR at the output of MRC is defined as [52]:

$$\gamma_{t}^{EGC} = \frac{1}{{N_{r}^{D} }}\left( {\mathop \sum \limits_{n = 1}^{{N_{r}^{D} }} \sqrt {\gamma_{{a_{n} }} } } \right)^{2}$$
(48)

The approach detailed in [54, 55], \(\gamma_{T} = \left( {\mathop \sum \limits_{n = 1}^{{N_{r}^{D} }} \sqrt {\gamma_{{a_{n} }} } } \right)^{2}\) with \(\overline{\gamma }_{T} = N_{r}^{D} \overline{\gamma }\),\(\alpha_{{\gamma_{T} }} = N_{r}^{D} \alpha + \varepsilon_{\gamma }\), \(\beta_{{\gamma_{T} }} = N_{r}^{D} \beta ,\) denoting the adjustment parameter in order to improve the accuracy of proposed approximation [55] is defined as:

$$\varepsilon_{\gamma } = \left( {\frac{1}{{N_{r}^{D} }} - 1} \right)\frac{ - 0.127 - 0.95\alpha - 0.0058\beta }{1 + 0.00124\alpha + 0.98\beta }$$
(49)

The average PEP for the EGC can be expressed as:

$$\begin{aligned} APEP_{EGC} \left( {x_{j, p} \to x_{{\hat{J},\hat{p}}} } \right) & = \mathop \int \limits_{0}^{\infty } \left( {\sqrt {2\gamma_{t}^{EGC} } } \right)f_{{\gamma_{a} }} \left( \gamma \right)d\gamma \\ & \triangleq - \mathop \int \limits_{0}^{\infty } Q/\left( {\sqrt {2\gamma_{t}^{EGC} } } \right)F_{{\gamma_{a} }} \left( \gamma \right)d\gamma \\ \end{aligned}$$
(50)

where \(Q/\left( . \right)\) is the derivative of Q-function which is defined in [57] as \(Q/\left( x \right) = \frac{1}{2\sqrt \pi }\exp \left( { - x^{2} /2} \right)\)

$$APEP_{EGC} \left( {x_{j, p} \to x_{{\hat{J},\hat{p}}} } \right) = \frac{1}{2\sqrt \pi }\mathop \int \limits_{0}^{\infty } \frac{1}{{\sqrt {\gamma_{T} } }}\exp \left( { - \frac{{\gamma_{T} }}{{N_{r}^{D} }}} \right)F_{{\gamma_{a} }} \left( {\gamma_{T} } \right)d\gamma_{T}$$
(51)

To determine the APER for the EGC dual-hop AF system under the influence of atmospheric turbulence without pointing error, substitute the CDF defined in (33) for (50)

$$APEP_{EGC} \left( {x_{j, p} \to x_{{\hat{J},\hat{p}}} } \right) \triangleq \frac{1}{2\sqrt \pi }\mathop \prod \limits_{i = 1}^{2} \left[ {\frac{1}{{\Gamma \left( {\alpha_{{\gamma T_{i} }} } \right)\Gamma \left( {\beta_{{\gamma T_{i} }} } \right)}}} \right]\mathop \int \limits_{0}^{\infty } \gamma_{T}^{ - 1/2} \exp \left( { - \frac{{\gamma_{T} }}{{N_{r}^{D} }}} \right)G_{4,1}^{1,4} \times\left( {2\gamma_{T} \mathop \prod \limits_{i = 1}^{2} \Xi_{i} \left| {\begin{array}{*{20}c} 1 \\ {\alpha_{{\gamma T_{1} }} , \beta_{{\gamma T_{1} }} ,\alpha_{{\gamma T_{2} }} , \beta_{{\gamma T_{2} }} ,0} \\ \end{array} } \right.} \right)d\gamma_{T}$$
(52)

Applying the integral indent defined in [50], Eq. (7.813.1)], the APER for the EGC dual-hop AF system under the influence of atmospheric turbulence without pointing error can be expressed as:

$$APEP_{EGC} \left( {x_{j, p} \to x_{{\hat{J},\hat{p}}} } \right) \triangleq \frac{1}{2}\sqrt {\frac{{N_{r}^{D} }}{\pi }} \mathop \prod \limits_{i = 1}^{2} \left[ {\frac{1}{{\Gamma \left( {\alpha_{{\gamma T_{i} }} } \right)\Gamma \left( {\beta_{{\gamma T_{i} }} } \right)}}} \right]G_{2,5}^{4,2} \left( {2N_{r}^{D} \mathop \prod \limits_{i = 1}^{2} \Xi_{i} \left| {\begin{array}{*{20}c} {\frac{1}{2},1} \\ {\alpha_{{\gamma T_{1} }} , \beta_{{\gamma T_{1} }} ,\alpha_{{\gamma T_{2} }} , \beta_{{\gamma T_{2} }} ,0} \\ \end{array} } \right.} \right)$$
(53)

Under the influence of pointing error, using (38) in (51), the average PEP can be expressed as:

$$APEP_{EGC} \left( {x_{j, p} \to x_{{\hat{J},\hat{p}}} } \right) = \frac{1}{2\sqrt \pi }\mathop \prod \limits_{i = 1}^{2} \left[ {\frac{{\xi_{i}^{2} }}{{\Gamma \left( {\alpha_{{\gamma T_{i} }} } \right)\Gamma \left( {\beta_{{\gamma T_{i} }} } \right)}}} \right]\mathop \int \limits_{0}^{\infty } \gamma_{T}^{ - 1/2} \exp \left( { - \frac{{\gamma_{T} }}{{N_{r}^{D} }}} \right)G_{3,6}^{6,1} \times \left( {2\gamma_{T} \mathop \prod \limits_{i = 1}^{2} \Xi_{i} \left| {\begin{array}{*{20}c} {1, \psi_{3} } \\ {\psi_{1} ,\psi_{2} } \\ \end{array} } \right.} \right)d\gamma_{T}$$
(54)

Applying the integral indent defined in [50], Eq. (7.813.1)], the APER for the EGC dual-hop AF system under the influence of atmospheric turbulence without pointing error can be expressed as:

$$APEP_{EGC} \left( {x_{j,p} \to x_{{\hat{J},\hat{p}}} } \right) = \frac{1}{2}\sqrt {\frac{{N_{r}^{D} }}{\pi }} \mathop \prod \limits_{i = 1}^{2} \left[ {\frac{{\xi_{i}^{2} }}{{\Gamma \left( {\alpha_{{\gamma T_{i} }} } \right)\Gamma \left( {\beta_{{\gamma T_{i} }} } \right)}}} \right]G_{4,6}^{6,2} \left( {2N_{r}^{D} \mathop \prod \limits_{i = 1}^{2} \Xi_{i} \left| {\begin{array}{*{20}c} {\frac{1}{2},1, \psi_{3} } \\ {\psi_{1} ,\psi_{2} } \\ \end{array} } \right.} \right)$$
(55)

Thus, the average BER for the MRC dual hop relay system can therefore be obtained by substituting (53) and (55) for (39):

$$\begin{aligned} ABER_{{EGC\left( {with \;pointing\;error} \right)}} & \le \frac{{\left( {N_{t} M} \right)^{ - 1} }}{{2\log_{2} \left( {N_{t} M} \right)}}\sqrt {\frac{{N_{r}^{D} }}{\pi }} \mathop \prod \limits_{i = 1}^{2} \left[ {\frac{{\xi_{i}^{2} }}{{\Gamma \left( {\alpha_{{\gamma T_{i} }} } \right)\Gamma \left( {\beta_{{\gamma T_{i} }} } \right)}}} \right]\mathop \sum \limits_{j = 1}^{{N_{t} }} \mathop \sum \limits_{p = 1}^{M} \mathop \sum \limits_{{\hat{J} = j + 1}}^{{N_{t} }} \mathop \sum \limits_{{\hat{p} = p + 1}}^{M} N\left( {p,\hat{p}} \right) \\ & \quad \times G_{2,5}^{4,2} \left( {2N_{r}^{D} \mathop \prod \limits_{i = 1}^{2} \Xi_{i} \left| {\begin{array}{*{20}c} {\frac{1}{2},1} \\ {\alpha_{{\gamma T_{1} }} , \beta_{{\gamma T_{1} }} ,\alpha_{{\gamma T_{2} }} , \beta_{{\gamma T_{2} }} ,0} \\ \end{array} } \right.} \right) \\ \end{aligned}$$
(56)
$$ABER_{{EGC\left( {with\;pointing\;error} \right)}} \le \frac{{\left( {N_{t} M} \right)^{ - 1} }}{{2\log_{2} \left( {N_{t} M} \right)}}\sqrt {\frac{{N_{r}^{D} }}{\pi }} \mathop \prod \limits_{i = 1}^{2} \left[ {\frac{{\xi_{i}^{2} }}{{\Gamma \left( {\alpha_{{\gamma T_{i} }} } \right)\Gamma \left( {\beta_{{\gamma T_{i} }} } \right)}}} \right]\mathop \sum \limits_{j = 1}^{{N_{t} }} \mathop \sum \limits_{p = 1}^{M} \mathop \sum \limits_{{\hat{J} = j + 1}}^{{N_{t} }} \mathop \sum \limits_{{\hat{p} = p + 1}}^{M} N\left( {p,\hat{p}} \right)G_{4,6}^{6,2} \left( {2N_{r}^{D} \mathop \prod \limits_{i = 1}^{2} \Xi_{i} \left| {\begin{array}{*{20}c} {\frac{1}{2},1, \psi_{3} } \\ {\psi_{1} ,\psi_{2} } \\ \end{array} } \right.} \right)$$
(57)

5.3 Effective Capacity for the Systems

The capacity of spatial modulation systems as stated in [56,57,58,59] cannot be determined in the same way it is done in MIMO communication systems. This is because, the number of transmit antenna represents the added information, and antenna index signifies the spatial constellation not as the information source as in other MIMO systems. Therefore, using the convectional approach stated in [59], the capacity for the dual-hap spatial modulation with combiner can be expressed as:

$$C_{SM} = \log_{2} \left( {N_{t}^{s} M} \right)\left[ {1 + P_{e} \log_{2} \left( {P_{e} } \right) + P_{c} \log_{2} \left( {P_{c} } \right)} \right]$$
(58)

where, \(P_{e}\) is the overall probability of error defined in Eq. (39), and \(P_{c} = 1 - P_{e}\) represents the probability of correct detection and \(log_{2} \left( {N_{t}^{s} M} \right)\) defines the total bits convey by the system.

6 Numerical Results and Discussions

In this section, using the derived expression of Eqs. (46), (47), (56), (57) and (58), we present the effect of atmospheric turbulence and pointing error on the average BER and the effective capacity performance of optical SM-SD dual-hops CSI-assisted relay. Generally, we assume that the link between the S-R and R-D are symmetric atmospheric turbulence channel with weak \(\left( {\alpha = 3.78,\beta = 3.74} \right)\), moderate \(\left( {\alpha = 2.50,\beta = 2.06} \right)\) and strong \(\left( {\alpha = 2.04,\beta = 1.10} \right)\).

Figure 2 shows the effect of atmospheric turbulence conditions on the average BER on the system performance under different MIMO schemes when MRC is considered at the receiver. This result confirmed that the change in turbulence condition from weak to strong level significantly degrades the system performance. For instance, at average SNR of 25 dB when considering two PD at the receiver, it is discovered that atmospheric turbulence greatly degraded the system error by 99.76% between the weak and strong turbulence condition. However, this performance can be improved by increasing the number of PD. Thus, at average BER of \(10^{ - 4}\), it is shown that the MRC system with four PD offers a gain of 5 dB when compared with two PD system under the same weak turbulence.

Fig. 2
figure 2

Performance of dual-hops AF SM-MRC-FSO system under different atmospheric turbulence without pointing error When the \(N_{r}^{D} = 2\) and \(N_{r}^{D} = 4\)

Full size image

The performance comparison between the MRC and EGC is presented in Fig. 3. It is clearly shown that the MRC yields an optimal performance than EGC under the same conditions. For instance, at average SNR of 20 dB under moderate turbulence condition, MRC offers an error rate of \(1.32 \times 10^{ - 5}\) compared with EGC of \(6.20 \times 10^{ - 4}\).

Fig. 3
figure 3

Performance comparison between the EGC and MRC Dual-hop AF system under different atmospheric turbulence without pointing error when \(N_{r}^{D} = 4\)

Full size image

We also illustrate the impact of beam width on the system error rate in Fig. 4. It is depicted in Fig. 4a that as the beam width increases the better the system error performance for the MRC system over a strong atmospheric turbulence for both MIMO schemes and is least with no pointing error. It can be deduced that with four PD, there is less error compared with two PD. For instance, when considering four PD at the MRC system, at average SNR of 20 dB, the system offers an error improvement of 97% by producing an error of \(3.03 \times 10^{ - 5}\) compared to \(0.0015\) average errors produced when using two PD. Moreover, the performance of the MRC dual-hops AF relay system is also compared with the EGC in Fig. 4b when using two PD at the receiving end. Under the strong turbulence condition, it is clearly shown that MRC offers a 2 dB diversity gain compared to EGC at the average BER of \(10^{ - 2}\).

Fig. 4
figure 4

a Impart of normalized beam width on the SM-MRC dual-hop AF system with different received photo-detector at the destination. b Performance comparison between the MRC and EGC dual-hop AF system under the influence of normalized beam width at \(N_{r}^{D} = 2\)

Full size image

The impart of pointing error on the dual-hop MRC AF relay system is demonstrated in Fig. 5a under different turbulence conditions. It clearly shows that as the pointing error increases from values 2 to 5, the more the system error rate deteriorates. For instance, under the strong turbulence condition, the pointing error value of 5 causes the MRC system to offer an average error of \(0.0095\) compared to when no pointing error is considered with error \(2.25 \times 10^{ - 4}\). Under the same turbulence condition and pointing error, we compared the performance between the MRC with EGC in Fig. 5b. As expected, the MRC system offers the best performance compared to the EGC system for various values of pointing error. For instance, to achieve an average BER of \(10^{ - 3}\) when pointing error value is set to 2, the MRC system requires only a power of 21 dB compare with EGC of 24 dB when the receiver is equipped with two PD.

Fig. 5
figure 5

a Impart of pointing error on the SM-MRC dual-hop AF system with different received photo-detector at the destination. b Performance comparison between the MRC and EGC dual-hop AF system under the influence of strong turbulence and pointing error at \(N_{r}^{D} = 2\)

Full size image

In addition, the average error performance of the dual-hop MRC AF relay system is presented in Fig. 6a under different values of \(\xi\) and atmospheric turbulence ranging from weak to strong levels. It can be clearly depicted that the higher the value of \(\xi\), the lower the system error rate and also the system performance deteriorates as the atmospheric turbulence condition gets worst. For instance, at average SNR of 20 dB under weak turbulence, there is a margin error of \(3.93 \times 10^{ - 4}\) between the two \(\xi\) values, and this shows that there is 74% error improvement when \(\xi = 6.5\) under the same average SNR. Comparing the MRC with EGC as it is demonstrated in Fig. 6a at a high value of \(\xi = 6.5\), it is found that at average BER of 10−3, the MRC required a power of 20 dB compared to 25 dB for EGC.

Fig. 6
figure 6

a Average Error Performance of MRC SM dual-hops AF system under different values \(\xi\) and atmospheric turbulence. b Performance Comparison between MRC and EGC SM dual-hops AF system at \(\xi = 6.5\)

Full size image

The capacity performance of the dual-hop AF relay system is illustrated in Fig. 7 under different turbulence conditions without pointing error when considering both the MRC and EGC at the receiver. It is clearly confirmed that as the turbulence get sever, the more the capacity of the system deteriorates. It is also indicated in the result that the number of laser at the transmitter significantly improved the system capacity. For instance, at the average SNR of 14 dB, it is shown that MRC offers an effective capacity of 1.72 bit/s/Hz compared to 1.60 bits/s/Hz offered by EGC and the use of four lasers caused 32% increment in capacity for MRC under the same conditions.

Fig. 7
figure 7

Comparison between the Capacity of MRC and EGC under various turbulence conditions without pointing error

Full size image

Figure 8 illustrates the influence of both pointing error and turbulence on the MRC dual-hop AF system capacity. It is clearly shown that as the pointing error increases, the system capacity performance deteriorates for both when the laser is four and two at the transmitter as against when there is no pointing error. It is also confirmed that for a given turbulence condition and pointing error, the capacity of MRC with four lasers is higher compared to when the transmitter is equipped with two lasers. This proved that the higher the laser at the transmitter, the more the system capacity which is advantage of MIMO scheme specially SM with lower system complexity.

Fig. 8
figure 8

Influence of pointing error on Capacity of the MRC SM dual hop AF system under different atmospheric turbulence conditions

Full size image

The impact of beam width on the system capacity is presented in Fig. 9. The transmitter is equipped with two lasers and the receiver makes use of MRC and EGC under a strong turbulence condition. It can be deduced that the system capacity increases with the increase in the beam width. Thus, the MRC offers the best performance. For example, at beam width of 8, the MRC system offers capacity of 1.87 bit/s/Hz compared with 1.85 bit/s/Hz at the same average SNR of 18 dB.

Fig. 9
figure 9

Impact of normalized beam width on the MRC and EGC SM dual-hop AF system under strong turbulence with pointing error for \(N_{t}^{S} = 2\;{\text{and}}\;N_{r}^{D} = 2\)

Full size image

7 Conclusion

In this work, we analyze and evaluate the performance of optical spatial modulation heterodyne dual-hop CSI-assisted relay system with MRC and EGC combiners at the destination over Gamma–Gamma turbulence induced fading with and without pointing error. The statistical characteristics of the equivalent end-to-end SNR were derived and utilized to determine the average PEP for each combiner. The average BER close form expression for the system is then determined. The results illustrated in this paper show the significant effect of atmospheric turbulence and/or pointing error conditions on the SM-SD dual hop system. It is therefore proved that as atmospheric turbulence varies from weak to strong levels, the more the average BER and the effective system capacity degraded. Also, the result confirmed that as the pointing error increases the worst the system error and capacity become. However, large beam width at the transmitter offers the system better performance with MRC yields the best performance compared with EGC.