A novel global optimization algorithm and data-mining methods for turbomachinery design

Abstract

A new multi-objective, multi-disciplinary global optimization strategy is proposed to address the high-dimensional, computationally expensive black box problem (HEB) in turbomachinery design. The strategy consists of an adaptive sampling hybrid optimization algorithm (ASHOA), two data-mining techniques, a 3D blade parameterization method, and the aerodynamic/mechanical codes. Firstly, the ASHOA is established by integrating a novel adaptive sampling Kriging metamodel and a new hybrid optimization method. Secondly, two data-mining methods (analysis of variance (ANOVA) and self-organizing map (SOM)) are applied to set the initial design space and optimization objectives of the transonic centrifugal compressor. A refined design space and objective parameters of the optimization problem are eventually obtained. Finally, the optimization process of a transonic centrifugal compressor is carried out based on the refined design space and objectives using ASHOA. The results show that the search efficiency of the optimization strategy is 2–10 times higher when compared to other excellent optimization algorithms. For the optimized compressor, both isentropic efficiency and total pressure ratio at design condition are improved by 1.61% and 4.13%, respectively, and the maximum stress decreases by 9.68%.

1 Introduction

The auto-optimization methods have been widely applied in the design of high-performance turbomachinery (Song et al. 2016; Javed et al. 2013) and could yield better designs which are usually experience independent. Ma et al. (2018) optimized a ring cavity shape to improve the operating stability of a centrifugal compressor based on a comparative analysis of optimization algorithm. Hehn et al. (2018) conducted an aerodynamic optimization of a transonic centrifugal compressor using arbitrary blade surfaces. Elfert et al. (2017) carried out the optimization of a fast rotating high-performance centrifugal compressor impeller and implemented the experimental verification. More related literatures can be found in Li et al. 2016 for single-point and in Li et al. 2017 for multi-point multi-objective aerodynamic performance optimization, respectively. Recently, researchers paid increasing attention to multi-disciplinary optimization of turbomachinery. It includes the optimizations of aerodynamic, mechanical, and vibration performances and manufacturing requirements (Barsi et al. 2015; Deshmukh and Allison 2016). Salnikov and Danilov (2017) conducted a multi-disciplinary optimization to improve the mass, strength, and aerodynamic performances of a centrifugal compressor impeller. Barsi et al. (2018) applied a complete tool for the aero-mechanical design of a radial inflow turbine and centrifugal compressor. Verstraete et al. (2017) presented a multi-disciplinary design optimization of turbocharger radial turbine for automotive applications. Unfortunately, all previous studies showed that the optimization of turbomachinery is computationally intensive and time consuming, mainly due to the repeated CFD/FEA (computational fluid dynamics/finite element analysis) simulations in the process of optimization. The alternative methods to speed up the optimization are (1) simplifying the optimization problem based on data-mining, (2) using metamodels to replace the repeated engineering simulations, and (3) developing a high-efficiency global optimization algorithm. The three aspects are discussed in the following three paragraphs respectively.

For the turbomachinery optimization problem, there are no analytical expressions between design variables and performances. Furthermore, the interactions between the design variables and performances are complex. Thus, many design variables and several objectives are selected in multi-disciplinary optimization, which leads to unsatisfied accuracy of the metamodel and a low efficiency of the optimization algorithm. In this regard, data-mining techniques such as analysis of variance (ANOVA) provide an effective way to extract information from the design space. They make the optimization problems much more accessible by ignoring the design variables with non-significant impacts on objectives (Song et al. 2016). In addition, data mining is a useful post-processing tool, for instance the self-organizing maps (SOMs). By detecting the features of the data set such as parameter correlations (both design variables and objectives), it can gain an insightful observation into the mechanism behind performance improvement of optimized designs (Leborgne et al. 2015; Li et al. 2017). Consequently, further investigations of data-mining are still necessary.

To alleviate the scarcity of computational resource in the optimization of turbomachinery, the metamodels are frequently adopted (Pellegrini et al. 2016). The accuracy of a specific metamodel mainly depends on the sample set. Traditional sampling strategies (one-stage sampling methods) provide a more uniform space-filling, such as the successive local enumeration algorithm (Zhu et al. 2012), the translational propagation algorithm (TPLHD) (Viana et al. 2010), and the iterated local search heuristics algorithm (Grosso et al. 2009), while they do not take into account the response values, resulting in a waste of computational resources in uninterested areas like flat function. Adaptive sampling strategies consider the response values as well as the gradient of response values. The strategies have attracted many researchers over the recent decade (Xu et al. 2014; Blondet et al. 2015). Kato and Funazaki (2014) presented a POD-driven adaptive sampling for efficient surrogate modeling to optimize a supersonic turbine. Liu et al. (2015) proposed an adaptive maximum entropy sampling approach based on the Bayesian metamodel for global optimization. Luo et al. (2017) showed a sampling-based adaptive bounding evolutionary algorithm to update the search space during the evolution process for continuous optimization problems. Among all adaptive sampling strategies, the typical example is the EGO (efficient global optimization) algorithm; the original algorithm was proposed by Jones et al. (1998). Some modified EGO algorithms (Huang et al. 2006; Viana et al. 2013; Kristensen et al. 2016; Liu et al. 2016; Hu et al. 2017) are presented in recent years. For example, Picheny et al. (2010) proposed an adaptive sampling method to increase the accuracy of the region of interest (target region). The method adds a new sample point where the uncertainty prediction variance in the metamodel is maximum near the region of interest. Since it relies on numerical integration, the method would become computationally expensive if a large number of integration points are needed to compute the criterion. Song et al. (2016) adopted a modified expected improvement (EI) sampling strategy to improve the global accuracy of the metamodel by increasing sample point in the region with maximum EI value. The strategy needs to find the current maximum (or minimum) response value and then to find the maximum EI value in an iteration (twice global optimizations in one iteration). Overall, these adaptive sampling optimization algorithms are still computationally intensive, and more efficient methods are demanded for turbomachinery optimization.

In terms of the optimization algorithms for turbomachinery, gradient-based algorithms (Chen and Chen 2015; Walther and Nadarajah 2015; Ma et al. 2017) require minimum function calls to achieve the optimum solutions. However, they are likely to be trapped in local optimums. Stochastic algorithms such as genetic algorithm (GA) are free of gradients and have excellent global search performance for high-dimensional and multi-modal problems, while the stochastic algorithms usually need massive repeated numerical simulations and have low efficiency especially near convergence (Heinrich and Schwarze 2016; Lu et al. 2016; Dinh et al. 2017). A hybrid optimization algorithm, which integrates a stochastic algorithm and a gradient-based technique, is preferable for auto-optimization of turbomachinery. The hybrid algorithm combines the advantages of above two approaches and has been proven to be a very effective method over the last few years (Wu et al. 2014; Kobrunov and Priezzhev 2016; Aslimani and Ellaia 2017; Liu et al. 2018). Sevastyanov (2010) presented a hybrid algorithm and employed the dynamically dimensioned response surface method (DDRSM) for calculating gradients. Long and Wu (2014) proposed a new global optimization method by combining the genetic algorithm and Hooke–Jeeves method to solve a class of constrained optimization problems. Wang et al. (2018) developed a gradient-based multi-objective evolution algorithm for wind turbine blade design. However, the existing methods are either computationally expensive (especially for gradient evaluation) or lack enough accuracy and robustness to meet the fast optimization requirement of engineering problems. Thus, the hybrid optimization algorithms are necessary to be further studied for turbomachinery design.

Although the adaptive sampling metamodel methods and hybrid optimization algorithms both attract attention increasingly these years, the combinations between them seem to be ignored. In this paper, we present a new global optimization algorithm called adaptive sampling hybrid optimization algorithm (ASHOA), which unites a novel adaptive sampling metamodel (based on Kriging) and a new hybrid optimization method (gradient-based mutation genetic algorithm). ASHOA aims to improve the search efficiency as well as global characteristic of the optimization algorithm and to simultaneously keep high fidelity of the metamodel. ASHOA is combined with two data-mining strategies (ANOVA and SOM), 3D blade parameterization method, and the aerodynamic/mechanical codes to form a global optimization strategy for turbomachinery. A typical transonic centrifugal impeller with a vanless diffuser is selected to demonstrate the efficiency of the strategy.

The rest of this paper is organized as follows: firstly, the ASHOA is proposed and validated by typical mathematical cases. Secondly, by using the ASHOA method with data-mining strategies, a multi-disciplinary optimization of the centrifugal compressor is carried out. Then, a detailed analysis of the optimization results is presented to investigate the mechanism of performance improvements. Finally, some conclusions are drawn.

2 Adaptive sampling hybrid optimization algorithm

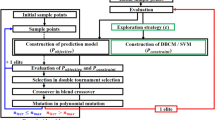
A new global optimization algorithm named ASHOA is proposed in this section. Unlike traditional method, it combines a novel adaptive sampling metamodel with a new hybrid optimization method. The adaptive sampling metamodel can decrease the required sampling set by adaptively adding new sampling points at the maximum combined expectation (CE) region near objectives, resulting in an improved efficiency and a better fidelity. The hybrid optimization method integrates a gradient mutation to a modified genetic algorithm (Li et al. 2016; Li et al. 2017) to accelerate optimization speed and to keep the global search characteristic. Therefore, the combination of the above two methods called ASHOA is expected to considerably increase the search efficiency as well as global characteristic of the optimization algorithm and simultaneously to keep the high fidelity of the metamodel. Figure 1 shows the flow chart of ASHOA; the left part shows the adaptive sampling metamodel, and the right one is showing the hybrid optimization algorithm. Both of them are introduced in the following sections respectively. In the flow chart, N₀ is the initial number of samples, N_max denotes the maximum number of samples allowed in the algorithm, R² is defined as

$$ {R}^2=1-\sum \limits_{i=1}^n{\left({y}_i-{\widehat{y}}_i\right)}^2/\sum \limits_{i=1}^n{\left({y}_i-{\overline{y}}_i\right)}^2,\kern0.6em {\overline{y}}_i=\frac{1}{n}\sum \limits_{i=1}^n{y}_i $$

(1)

where n is the total number of validation data, ${\widehat{y}}_i$ is the corresponding predicted value for the observed value y_i, and ${\overline{y}}_i$ is the mean of the observed values. From the definition, it can be found that 0 ≤ R² ≤ 1. The larger value of R² means the better accuracy of the metamodel. ${R}_0^2$ is the lower bound of R².

Fig. 1

Flow chart of ASHOA

2.1 Hybrid optimization algorithm

A new hybrid optimization algorithm is proposed by adding a gradient mutation to the modified genetic algorithm, as shown in the right part of Fig. 1. This section mainly introduces the gradient-based mutation method (highlighted in Fig. 1). The modified genetic algorithm can be found in the authors’ previous work (Li et al. 2016; Li et al. 2017).

Gradient mutation determines a direction of simultaneous improvement for all objective functions and performs a mutation step in the direction. To achieve the goal, it needs to estimate gradients of objectives versus design variables, and the Kriging metamodel is used in the gradient estimation. Therefore, the construction of the Kriging metamodel and the estimation of gradients are firstly introduced as follows (Lophaven et al. 2002):

For a set of m design sites X = [x₁⋯x_m]^T (normalized sample data) and corresponding responses Y = [y₁⋯y_m]^T, the Kriging model is generally expressed as

$$ {\widehat{y}}_i=\phi \left({\beta}_{:,i},x\right)+{z}_i(x),\kern0.48em i=1,2,...,q $$

(2)

where x is the unknown point to be predicted, ${\widehat{y}}_i$ is the ith predicted response, and q is the dimensionality of responses. ϕ and z are explained respectively as follows:

ϕ(β_{:, i}, x) denotes regression model, it can be written as

$$ {\displaystyle \begin{array}{l}\phi \left({\beta}_{:,i},x\right)=f{(x)}^T{\beta}_{;,i}\\ {}f(x)={\left[{f}_1(x)\left\Vert ...\right\Vert {f}_p(x)\right]}^T\end{array}} $$

(3)

in which β represents the regression parameter. Here the linear regression model is selected as

$$ p=n+1,{f}_1(x)=1,{f}_2(x)={x}_1,\cdots, {f}_p(x)={x}_{p-1} $$

(4)

where n is the dimensionality of design sites, p is the number of basis functions in the regression model, and x_i is the ithcomponent of x.

z_i(x) is a random function (stochastic process); it is assumed to have mean zero, and the covariance is

$$ E\left[{z}_i\left({x}_1\right){z}_i\left({x}_2\right)\right]={\sigma}_i^2\Re \left(\theta, {x}_1,{x}_2\right),\kern0.36em i=1,2,...,q $$

(5)

where E[⋅] is the expectation operator, and ${\sigma}_i^2$ is the process variance for the ith component of the response (unknown at present). ℜ(θ, x₁, x₂) is the correlation model with parameter θ. Here the Gauss correlation function is adopted

$$ \Re \left(\theta, {x}_1,{x}_2\right)=\prod \limits_{j=1}^n\exp \left[-{\theta}_j{\left({x}_1-{x}_2\right)}^2\right] $$

(6)

Further, we define the matrix R of stochastic-process correlations between x_i and x_j at design sites

$$ {R}_{ij}=\Re \left(\theta, {x}_i,{x}_j\right),\kern0.36em i,j=1,\cdots, m $$

(7)

At an untried point x, let

$$ r(x)={\left[\Re \left(\theta, {x}_1,x\right)\cdots \Re \left(\theta, {x}_m,x\right)\right]}^T $$

(8)

Now, we assume that q = 1 for convenience, which implies that β = β_{:, 1} and Y = Y_{:, 1}. Next, we consider the linear predictor

$$ {\widehat{y}}_i={c}^TY,\kern0.36em c=c(x)\in {\mathbb{R}}^m $$

(9)

where c is a coefficient matrix to be determined.

To keep the predictor unbiased, the mean squared error (MSE) φ(x) of the above predictor equals

$$ \varphi (x)=E\left[{\left(\widehat{y}(x)-y(x)\right)}^2\right]={\sigma}^2\left(1+{c}^T Rc-2{c}^Tr\right) $$

(10)

where $\widehat{y}(x)-y(x)$ is the error between the predicted response and true response, E[⋅] is the expectation operator, R is found by means of Eq. (7) and r is given by Eq. (8). σ² denotes the process variance; it is obtained through the generalized least squares fit (with respect to R)

$$ {\displaystyle \begin{array}{l}{\sigma}^2=\frac{1}{m}{\left(Y-F{\beta}^{\ast}\right)}^T{R}^{-1}\left(Y-F{\beta}^{\ast}\right)\\ {}{\beta}^{\ast }={\left({F}^T{R}^{-1}F\right)}^{-1}{F}^T{R}^{-1}Y\\ {}F={\left[f\left({x}_1\right)\cdots f\left({x}_m\right)\right]}^T\end{array}} $$

(11)

The parameters of the Kriging metamodel are estimated from the Lagrangian function L(c, λ) for the problem of minimizing φ(x) with respect to c and subject to the unbiased predictor constraint

$$ L\left(c,\lambda \right)={\sigma}^2\left(1+{c}^T Rc-2{c}^Tr\right)-{\lambda}^T\left({F}^Tc-f\right) $$

(12)

The solutions to Eq. (12) are

$$ {\displaystyle \begin{array}{l}\lambda =-2{\sigma}^2{\left({F}^T{R}^{-1}F\right)}^{-1}\left({F}^T{R}^{-1}r-f\right)\\ {}c={R}^{-1}\left(r+\frac{F\lambda}{2{\sigma}^2}\right)\end{array}} $$

(13)

The predictor is finally written as

$$ \widehat{y}(x)={r}^T{R}^{-1}Y-{\left({F}^T{R}^{-1}r-f\right)}^T{\beta}^{\ast }=f{(x)}^T{\beta}^{\ast }+r{(x)}^T{\gamma}^{\ast } $$

(14)

where γ^∗ is computed via the equation γ^∗ = R⁻¹(Y − Fβ^∗).

For multiple responses (q > 1), Eq. (14) holds for each column in Y.

The gradient is expressed as

$$ {\widehat{y}}^{\prime }={\left[\frac{\partial \widehat{y}}{\partial {x}_1}\cdots \frac{\partial \widehat{y}}{\partial {x}_n}\right]}^T={J}_f{(x)}^T{\beta}^{\ast }+{J}_r{(x)}^T{\gamma}^{\ast } $$

(15)

where J_f and J_r are the Jacobian of fand r, respectively

$$ {\left({J}_f(x)\right)}_{ij}=\frac{\partial {f}_i}{\partial {x}_j}(x),{\left({J}_r(x)\right)}_{ij}=\frac{\partial \Re }{\partial {x}_j}\left(\theta, {x}_i,x\right) $$

(16)

As soon as the Kriging metamodel is established after estimating model parameters from Eq. (12), all responses and gradients can be evaluated by Eqs. (14) and (15), respectively, for any input vector x = [x₁⋯x_m].

A new gradient mutation algorithm is proposed. The procedure of the algorithm in one evolution iteration is as follows:

Procedure I

• (1) Preprocessing: all objectives are turned into maximum problems: Max objectives, all design variables are normalized to be 0~1, i = 1, j = 1, k = 1.

• (2) For the kth individual of the genetic algorithm population, calculating the gradient of thejth objective versus the ith design variable:${G}_{i,j,k}=\frac{\partial {\widehat{y}}_j}{\partial {x}_i}$, j = j + 1.

• (3) If j < q, where q is the number of objectives, go back to step (2); otherwise, calculate the sum of the gradient of all objectives versus the ith design variable for the kth individual:${g}_{i,k}=\sum \limits_{j=1}^q{G}_{i,j,k}$; the norm of g_{i, k}is ∣g_{i, k}∣, k = k + 1, j = 1.

• (4) If k < p, where p is the number of population individuals of the genetic algorithm, go back to step (2); otherwise, rank the ∣g_{i, k}∣ for all individuals.

• (5) The top 1/q × 100% of individuals are selected to carry out gradient mutation; the normalized gradient mutation step size is λ. If g_{i, k} ≥ 0, x_{i, k} = x_{i, k} + λ; otherwise, x_{i, k} = x_{i, k} − λ. If x_{i, k}exceeds the boundary, x_{i, k}is set to be the boundary value constrainedly, i = i + 1, k = 1.

• (6) If i < n, where n is the number of design variables, go back to step (4); otherwise, end the gradient mutation.

As illustrated in step (5) of Procedure I, the parameter λ will be particularly analyzed in Section 2.3.3, and a procedure to determine the optimal λ will be given in Procedure III.

As shown above, the gradient mutation algorithm carries out mutation operation once only for a specific design variable in an iteration (the loop of design variables is outermost), which is different from the traditional algorithm. It ensures that a mutation changing must occur for a specific input, resulting in an improvement in search efficiency. The mutation direction of the algorithm is dependent on the most significant gradient of the objective versus design variable. The ranking gradient for populations is conducted, and only a part of them is chosen to mutate, which helps to recognize the most sensitive individuals for a specified input. Essentially, it recognizes the most significant design variables for each output variable (objective functions and constraints) separately. Thus, the gradient mutation can be performed reliably and efficiently in any circumstance.

2.2 Adaptive sampling metamodel

In this section, a new adaptive sampling metamodel based on the Kriging method is proposed by adding a new sampling point in the region with maximum CE. As shown in Fig. 1, the hybrid optimization algorithm (see Section 2.1) is used to search the maximum CE. The purpose of the proposed methodology in this subsection is to construct a metamodel with fewer samples. Moreover, we expect that the metamodel could approximate the response values in the design space near the target values accurately.

The space coverage of the initial sample set has a large impact on the precision of the metamodel over the entire design space; it further affects the global convergence rate of the optimization process. Thus, the initial sample set is generated by the optimum Latin hypercube sampling (OLHS) strategy (Pholdee and Bureerat 2015) to gain a better space-filling feature. For a certain metamodel such as the Kriging model, the accuracy depends on samples (sampling method, sample count) and the characteristics of the problem (problem scale, non-linearity performance). In this study, the initial sample set is generated by OLHS. Therefore, the accuracy of the metamodel is mainly dependent on the sample count and characteristics of the problem. Since engineering problems usually have various problem scales (design variable counts) and different non-linearity performances, it is hard to specify a constant initial sample count or a variable sample count as a function of problem scale. Thus, a more objective criterion (R² ≥ 0.85) is adopted to estimate the accuracy of the initial metamodel. It gradually increases the initial sample count (the step size is 10) until the accuracy of the metamodel reaches the criterion. This criterion is applied to all test cases in the following sections.

The construction of the Kriging metamodel strategy in Fig. 1 is introduced in the previous section (Section 2.1). R² is obtained from random cross-validation. Only a part of points with larger responses (the top 50%) are chosen from the cross-validation points to evaluate R², since the metamodel cares more about the accuracy near optimal objectives. Now, the combined expectation CE is discussed in detail. It is noticeable that all the objectives are turned into solving maximum problems, and the following discussion is based on the assumption.

The combined expectation CE is defined as

$$ \mathrm{CE}={\varphi}_N\mid {\widehat{y}}^{\prime}\mid {{}_{N,S}}^{-1}{\widehat{y}}_N $$

(17)

where φ_N is the normalized MSE of $\widehat{y}$; MSE in Eq. (10) is rewritten as

$$ \varphi (x)={\sigma}^2\left(1+{c}^T Rc-2{c}^Tr\right)={\sigma}^2\left(1+{u}^T{\left({F}^T{R}^{-1}F\right)}^{-1}u-{r}^T{R}^{-1}r\right) $$

(18)

in which u = F^TR⁻¹r − f. The function generalizes immediately to the multiple response cases by replacing σ by σ_i for the ith response function. φ(x)stands for the predicted error; if there is a large value of φ(x), a sampling point is more likely to be added in this region to improve the accuracy of the metamodel.

${\widehat{y}}_N$ denotes the normalized response value $\widehat{y}$. This method is mainly intended to improve the accuracy of the metamodel in the region near optimal objectives. As seen in Eq. (17), the combined expectation CE increases with ${\widehat{y}}_N$. It results in a larger probability of adding a new sampling point in this region with a larger response value. It further leads to a better accuracy near optimal objectives.

${\left|{\widehat{y}}^{\prime}\right|}_N$ represents the normalized norm of the gradient vector ${\widehat{y}}^{\prime }$. By ranking ${\left|{\widehat{y}}^{\prime}\right|}_N$ for the present design points (current population individuals in the hybrid optimization algorithm), a sorted gradient vector ${\left|{\widehat{y}}^{\prime}\right|}_{N,S}$ for the design points is obtained. $\mid {\widehat{y}}^{\prime}\mid {{}_{N,S}}^{-1}$ is a reversed order vector of ${\left|{\widehat{y}}^{\prime}\right|}_{N,S}$. It means that a design point with a smaller value of gradient has a larger value of $\mid {\widehat{y}}^{\prime}\mid {{}_{N,S}}^{-1}$. On the other hand, the penalty coefficient is introduced to the boundary of the design space to limit their gradients. A small gradient of the predicted response usually appears near local or global optimum points, and the points far away from known samples (the prediction is constant there). This criterion proposes a point near the objective (gradient is zero or at the boundary) as well as the region far away from all other points (gradient should be zero). It well balances local exploitation (the points near objectives) and global exploration (the points far away from known samples).

As analyzed above, the adaptive sampling method will consistently improve the metamodel accuracy near global optimum points and avoid sampling points gathering together near known points.

2.3 Numerical tests and parameter sensitivity analysis of ASHOA

In this section, the overall procedure of ASHOA is illustrated. Also, the numerical tests are carried out for ASHOA using five mathematical cases. Based on the test results, parameter sensitivity analysis of ASHOA is implemented.

2.3.1 Overall procedure of ASHOA

The flow chart of ASHOA is given in Fig. 1; the corresponding procedure is illustrated below:

Procedure II

• (1) A spatial uniformly distributed sample set is generated by OLHS. Real responses of the sample points are evaluated.

• (2) A Kriging metamodel is constructed with the current sample set and is validated by the cross-validation method.

• (3) The point with the maximum value of the combined expectation CE is searched using the proposed hybrid optimization algorithm. Then, the point is added to the current sample set, N=N + 1.

• (4) If the accuracy of the metamodel reaches the criterion (${R}^2>{R}_0^2$) or the total number of sample points exceeds the maximum sample set (N > N_max), the algorithm stops updating the current sample set, go next; otherwise, go back to step (2).

• (5) The final Kriging metamodel is constructed based on the final sample set. The hybrid optimization algorithm is applied to search the Pareto front solutions of the problem to be optimized.

Procedure II shows the overall process of ASHOA. In step (3) and step (5) of Procedure II, the hybrid optimization algorithm is invoked. The hybrid algorithm is discussed in Section 2.1 and shown at the right part of Fig. 1. The gradient mutation (see Fig. 1, circled in blue) of the hybrid optimization algorithm is illustrated in Section 2.1Procedure I.

2.3.2 Numerical tests

In this subsection, five well-known high-nonlinear mathematical cases ZDT1, ZDT2, ZDT3, ZDT4, and ZDT6 (Sevastyanov 2010) are considered to test ASHOA’s performance. ZDT5 is not used since its variables are discrete while the Kriging metamodel is continuous. Only ZDT3 and ZDT6 are presented in the following section; the remaining test cases are shown in Appendix 1.

ZDT3 has 30 design variables and multiple discontinuous Pareto fronts. The mathematical expression is

$$ {\displaystyle \begin{array}{l}\operatorname{Minimize}\kern0.36em {f}_1={x}_1\kern0.36em and\kern0.36em {f}_2=g\left[1-\sqrt{\frac{f_1}{g}}-\frac{f_1}{g}\sin \left(10\pi {f}_1\right)\right]\\ {}\mathrm{where},g=1+\frac{9}{n-1}\sum \limits_{i=2}^n{x}_i;\kern0.84em 0\le {x}_i\le 1,i=1,\cdots, n;n=30\end{array}} $$

(19)

The Pareto-optimal region for the case ZDT3 corresponds to x₁ ∈ [0, 1], x_i = 0, i = 2, ⋯, 30. Not all points satisfying x₁ ∈ [0, 1]are Pareto optimal since the Pareto front is discontinuous for ZDT3.

ZDT6 has 10 design variables and multiple local Pareto fronts. The mathematical formula is

$$ {\displaystyle \begin{array}{l}\operatorname{Minimize}\kern0.36em {f}_1=1-\exp \left(-4{x}_1\right){\sin}^6\left(6\pi {x}_1\right)\kern0.36em \mathrm{and}\kern0.36em {f}_2=g\left[1-{\left(\frac{f_1}{g}\right)}^2\right]\\ {}\mathrm{where},g=1+9{\left[\left(\sum \limits_{i=2}^n{x}_i\right)/\left(n-1\right)\right]}^{1/4};0\le {x}_i\le 1,i=1,\cdots, n;n=10\end{array}} $$

(20)

The global Pareto-optimal front corresponds to x₁ ∈ [0, 1], x_i = 0, i = 2, ⋯, 10. The Pareto optimal front is non-convex, and the density of solutions across the Pareto-optimal region is highly non-uniform.

The proposed method ASHOA includes two aspects: adaptive sampling and hybrid optimization. As shown in Table 1, several similar algorithms are selected to compare with ASHOA. In the table, MBOE (Song et al. 2016) is an excellent adaptive sampling multi-objective optimization algorithm and is successfully applied to the turbomachinery optimization. AME (Liu et al. 2015), CV-Voronoi (Xu et al. 2014), EGO (Jones et al. 1998), and ADE (Picheny et al. 2010) are only outstanding adaptive sampling metamodels; hence, they are coupled with high-efficiency hybrid optimization algorithms: SSG-PSO (Wu et al. 2014), MODE/D&P (Wang et al. 2018), GAHJ (Long and Wu 2014), and HMGE (Sevastyanov 2010), respectively. The combinations in Table 1 are based on their characteristics and test performances to achieve their maximum potential. Among them, ADE and MBOE are EGO-like algorithms. The same test cases (ZDT1 to ZDT6, except for ZDT5) have shown that HMGE is more efficient than NSGA-II, Pointer, and AMGA. Therefore, in the study, pure gradient algorithms and pure stochastic algorithms are not considered.

Table 1 Other similar algorithms selected to compare with ASHOA

For the algorithms in Table 1, the default parameter values recommended in the references have been used to make sure that all algorithms are in equal conditions. For convenience, AME, CV-Voronoi, EGO, and ADE are used to represent the corresponding optimization methods in the following sections.

In order to test the adaptive sampling global optimization algorithms, the analytic expressions of cases ZDT3 and ZDT6 are only utilized to evaluate responses for the sampling points. The basic optimization parameters are given in Table 2. The test is carried out on a workstation with 48-core Xeon(R) E5-2670 processor and 64 GB RAM.

Table 2 Parameters of ASHOA for ZDT3 and ZDT6

Figure 2 illustrates the comparison of optimization results using AME, CV-Voronoi, EGO, ADE, MBOE, and ASHOA for ZDT3 and ZDT6 over the same period. It can be observed that the solutions of ASHOA present an unparalleled accuracy and diversity for both ZDT3 and ZDT6 compared to the other five optimization algorithms. The test cases ZDT1, ZDT2, and ZDT4 in Appendix 1 also shows the same results. Therefore, the proposed ASHOA with proper λ seems to be a better method for solving computationally expensive problems.

Fig. 2

Results for test cases ZDT3 and ZDT6 optimized by ASHOA and five other state-of-the-art algorithms (AME, CV-Voronoi, EGO, ADE, and MBOE) at the same search time

2.3.3 Parameter sensitivity analysis

As shown in step (5) of Procedure I in Section 2.1, the normalized gradient mutation step size λ is found to be a key factor for improving the efficiency of the hybrid optimization algorithm of ASHOA. As shown in Fig. 3a, λ = 0.1 provides low efficiency and diversity while λ ≥ 0.3 shows a satisfied performance. This indicates that a larger λ for ZDT3 accelerates the optimization convergence. In terms of ZDT6 (Fig. 3b), λ = 0.1 shows the best efficiency and diversity, while a larger λ leads to poor diversity and a smaller λ causes a low convergence efficiency. Essentially, the hybrid optimization algorithm turns into the gradient descent algorithm when the value of λ is very large while it becomes a stochastic algorithm under a very small λ. Different λ contributes to different degree of acceleration, and the best value of λ varies with different problems. In this study, a simple but efficient method to search the optimal λ is presented. The methodology is that we first apply a small value of λ and then continuously increase the value with a small step until ASHOA cannot achieve the better Pareto front solutions. The procedure of the method is as follows:

Fig. 3

Effect of different values of λ on optimization efficiency and solutions diversity for ZDT3 and ZDT6

Procedure III

• (1) Let λ = 0, set the growth rate Δλ, let λ₁ = λ + Δλ.

• (2) If λ₁ ≥ 1, go to step (5); otherwise, go next.

• (3) Carry out one iteration of the optimization algorithm (ASHOA) based on λ and λ₁, respectively, and get the corresponding Pareto front solutions S_λand S_λ1. The mixed solutions are S_mixed = S_λ ∪ S_λ1; the fast non-dominated sorting approach (Deb et al. 2002) is applied to mixed solutions S_mixedto get the Pareto front solutions S.

• (4) Calculate the number of elements: N_λ = size(S ∩ S_λ) and N_λ1 = size(S ∩ S_λ1). If N_λ1 > N_λ, updateλ = λ₁, λ₁ = λ₁ + Δλ, go back to step (2); otherwise, go next.

• (5) The current λ is the optimal value, and it is used in the optimization algorithm (ASHOA); the procedure stops.

In step (4) of Procedure III, N_λ1 > N_λ usually means that the solutions based on λ₁ are better than those based on λ. Through the method, a reasonable λ is usually obtained. The relations of the above three procedures are: Procedure II is the overall procedure of ASHOA; Procedure I works in step (3) and step (5) of Procedure II; and Procedure III plays a role in step (5) of Procedure I.

The process of Procedure III is demonstrated for cases ZDT3 and ZDT6 in Appendix 2. It shows that the procedure can usually find the optimal λ within several iterations. The optimal λ found by the procedure for cases ZDT1, ZDT2, and ZDT4 are presented in Appendix 3. The results demonstrate the correctness and efficiency of the procedure.

Also, as illustrated in step (5) of Procedure I in Section 2.1, only the top 1/q × 100% of individuals are selected to carry out the mutation. This proportion may influence the global optimization performance and convergence efficiency of the optimization algorithm. Limited by the space, the detailed discussion of the proportion is given in Appendix 4. The investigation results show that the specific proportion (1/q, where q is the number of objectives) for the proposed algorithm ASHOA is reasonable and robust.

3 Data-mining techniques on initial design space

In order to potentially simplify and refine the optimization problem, data-mining analysis is applied to the initial design space of a transonic centrifugal compressor based on validated CFD/FEA data.

3.1 Numerical method validation

Before conducting the data-mining and multi-disciplinary optimization of a transonic centrifugal compressor, both aerodynamic and mechanical simulation methods are firstly validated by experimental data from the National Laboratory of Engine Turbocharging Technology, North China Engine Research Institute.

3.1.1 Aerodynamic simulation method validation

The CFD code is validated based on the testing results of a centrifugal compressor stage. The compressor stage includes an unshrouded impeller, vaneless diffuser, volute, and casing treatment. The geometrical parameters and flow boundary conditions of the stage are given in Table 3.

Table 3 Design parameters and boundary conditions of the stage

The Reynolds-averaged Navier–Stokes equations are solved using the commercial software NUMECA FINE/Turbo. The Spalart–Allmaras turbulence model, which is of high efficiency and suitable for the 3D flow with strong pressure gradient, moderate curvature, shock wave (Ning and Xu 2001), is adopted to involve the turbulence effects. The spatial discretization used for the computation is the central scheme, and the time integration scheme is an explicit four-step Runge–Kutta algorithm. A mesh independence investigation is firstly conducted by coarse, medium, and fine meshes with total mesh numbers of 0.8, 1.5, and 2.3 million, respectively (single passage of impeller and diffuser with volute as well as casing treatment). It is clear in Fig. 4 that the medium mesh seems to provide a good compromise between the accuracy and computational efficiency; hence, this mesh is used for the rest simulations (see Fig. 5). The mesh takes a structured H–O–I topology, and the size of the first cell to the wall is 5 × 10⁻⁶ m corresponding to a minimum y⁺ value less than 10.

Fig. 4

Mesh independence investigation of aerodynamic simulation

Fig. 5

Aerodynamic computational domain and mesh of compressor stage (impeller + diffuser + volute + casing treatment)

Figure 6 shows a comparison of the predicted and measured aerodynamic performance of the stage at design speed (90,000 rpm, rpm is revolutions per minute). The maximum relative error between simulated and measured performance is less than 3%. Generally, the prediction matches the measurement well, which conforms the accuracy of the numerical method.

Fig. 6

Comparison of predicted and measured aerodynamic performance of stage (impeller + diffuser + volute + casing treatment)

3.1.2 Mechanical simulation method validation

The FEA tool validation is only carried out on the impeller (the rotor part, see Fig. 7a) with 1 mm hub fillet based on the testing data. The impeller material of simulation is Aluminum Alloy 2a70, the same as the experimental impeller. The material properties are as follows: the elasticity modulus is 74,500 MPa, the mass density equals 2760 kg/m³, and Poisson’s ratio is 0.33. In addition, the yield stress of Aluminum Alloy 2a70 is 360 MPa. The coupling mechanical analysis is performed with the following loads: static pressure distribution from aerodynamic simulation (see Section 3.1.1), centrifugal force by setting a 99,000 rpm (1.1 times of design speed) rotational speed. Axial displacement is constrained while radial displacement is free. As shown in Fig. 8, the mesh check is implemented for mechanical simulations. Four types of mesh are selected, and they approximatively double versus the former one. The mesh with 1.02 million elements (see Fig. 7b) seems to provide a mesh independent solution for the stress prediction, and hence, this mesh is used for the mechanical simulation. Running the calculation on ANSYS, the von Mises stress of the impeller is evaluated.

Fig. 7

Mechanical model and mesh

Fig. 8

Maximum von Mises stress versus mesh elements for mechanical simulations

In the destruction test, the yield stress of the impeller is achieved in the location of the impeller center near the backface at 1.1 times of the design shaft speed (99,000 rpm). As shown in Fig. 9, the value of the predicted maximum von Mises stress (362.49 MPa) and the corresponding location agree well with the measurement (360 MPa, relative error is less than 0.7%), which validates the mechanical performance assessment method. Then, we could apply the aerodynamic and mechanical simulations methods in the sequel study.

Fig. 9

Predicted von Mises stress at 1.1 times of design shaft speed (99,000 rpm)

3.2 Initial design space

3.2.1 Preliminary analysis

In the aerodynamic performance validation, the centrifugal compressor stage (impeller, diffuser, volute, and casing treatment) is simulated, which is time consuming. On the other hand, the optimization of the impeller and diffuser is more challenging, and the volute as well as casing treatment are redesigned to match the impeller and diffuser. Thus, only a single passage of the centrifugal impeller with a vaneless diffuser is chosen in the optimization process.

Integrating the static pressure from aerodynamic simulation to mechanical analysis is computationally intensive. Both the reference (Barsi et al. 2015) and our simulations show that the aerodynamic force has a small effect (< 1%) on the von Mises stress of the centrifugal impeller. Therefore, the aerodynamic force is ignored in the following mechanical simulations to accelerate optimization.

The hub fillet of the centrifugal impeller is chosen as a design variable due to its importance of affecting aerodynamic and mechanical performances (Mahmood and Acharya 2006; Gowda et al. 2016).

3.2.2 Design variables

According to the preliminary analysis, only the centrifugal impeller with vaneless diffuser (aerodynamic) and impeller disk geometries (mechanical) will be optimized in this paper.

Firstly, we refer to the methods, coordinate system, and definition of variables in Li et al. (2016)) to conduct the 3D parameterization. Figure 10 shows the control points of endwalls and blade camber curves (Z and Rare axial and radial directions, respectively, and θ denotes tangential angle). In terms of the endwalls, there are in total nine control points for both hub and shroud. The blade profile is parameterized by the root and the tip sections of both full and splitter blades (four sections in total), and other camber sections are determined by a three-point Bezier curve (stacking law). Eight control points are selected for each main blade and five for each splitter blade. Meridional locations of blade leading edge (LE_{full, H/full, S/splitter, H/splitter, S}, four variables in total) and trailing edge (TE_H/S, two variables in total) are also parameterized, where LE is the leading edge, TE is the trailing edge, full is the full blade, splitter is the splitter blade, H is the hub, and S is the shroud, $dmr=\int \sqrt{d{Z}^2+d{R}^2}/R$.

Fig. 10

Control points of endwalls and blade camber curves

Figure 11 illustrates the impeller disk parameterization, in which h₁, h₂, r₁, r₂ are independent while R is constrained by the formula R = [(r₂ − r₁)²/h₂ + h₂]/2.

Fig. 11

Impeller disk parameterization

Table 4 shows all variable names and corresponding numbers of control points. Not all the variables of control points are active in the optimization process. Table 5 illustrates active variable numbers, range of variations, and constraints. To avoid the distortion of the endwalls and blade profiles, the active control points vary in a moderate range. Forty-four design variables are necessary to be selected for the initial design space according to the industrial constraints of the centrifugal compressor.

Table 4 Variable names and corresponding numbers of control points

Table 5 Active variable numbers, range of variations and constraints in initial design space

3.2.3 Objective functions

In order to ensure the feasibility of the design, the optimization of aerodynamic performance at three operating points (design point, choke point, and near surge point) is considered. The mechanical stress is only optimized at design shaft speed (multi-point and multi-disciplinary optimization). The initial objective functions at design and off-design conditions and corresponding imposed boundary conditions in CFD/FEA simulations are analyzed below.

Design point

The optimizer maximizes isentropic efficiency η_{is, design} and total pressure ratio ε_{tot, design} at design operating conditions by imposing a mass flow outlet boundary conditions (0.97 kg/s).

Choke point

The optimization strives for larger choke mass flow ${\dot{m}}_{\mathrm{choke}}$. A low backpressure (150 kPa) is assigned to ensure choking conditions.

Surge point

The CFD simulation at surge conditions is time consuming and is hard to converge. The near surge point is obtained by imposing a mass flow (0.93 kg/s) boundary condition. A positive slope of the total pressure ratio is generally associated with aerodynamic instability (Li et al. 2017). Therefore, minimizing the slope of the total pressure ratio Slope_ε is a more efficient method to extend the surge margin. The slope is estimated by ${\mathrm{Slope}}_{\varepsilon }=\varDelta \varepsilon /\varDelta {\dot{m}}_N$, where Δε is the difference of the total pressure ratio between design point and near surge point, and $\varDelta {\dot{m}}_N$ is the difference of mass flow (normalized by choke mass flow).

Mechanical stress

Maximum von Mises stress σ_{VM, max} is optimized at design shaft speed. On the other hand, the stress concentration near the blade root is dangerous; thus, the location of maximum stress must be constrained. A signal is introduced to indicate the location of maximum stress. If the maximum stress is located in the center of the impeller disk, Signal = 0; otherwise, Signal = 1.

The mathematical expression of the final optimization problem is as follows:

$$ {\displaystyle \begin{array}{l}\max :{\eta}_{\mathrm{is},\mathrm{design}},{\varepsilon}_{\mathrm{tot},\mathrm{design}},{\dot{m}}_{\mathrm{choke}}\\ {}\min :{\mathrm{Slope}}_{\varepsilon },{\sigma}_{\mathrm{VM},\max}\\ {}s.t.\kern0.36em :\mathrm{Signal}=0\end{array}} $$

(21)

3.3 Data-mining

It is important to determine a small number of key design variables from design space to simplify the design problem. Some implied information in the design space will be useful for eliminating the non-significant design variables, such as the trade-off between objective functions, the non-linear relations between design variables, and objective functions. Therefore, the efficiency and reliability of the optimization process may be improved. The process to extract information from the design space is called "data-mining". In this paper, two typical data-mining techniques, analysis of variance (ANOVA) (Song et al. 2016) and self-organizing map (SOM) (Li et al. 2017), are introduced to explore the interactions among critical aerodynamic and mechanical parameters as well as the correlations among design variables and objective functions.

3.3.1 Analysis of variance

ANOVA uses a variance of the objective functions due to design variables. It can identify not only the single effect but also the interactive effect of design variables on objective functions. ANOVA expresses the information in a quantitative way. More details can be found in the reference (Song et al. 2016).

In turbomachinery optimization, the analytical mapping relations among objective functions and design variables do not exist, while ANOVA cannot be conducted directly based on limited design samples (a set of design variables and objective functions). Thus, the response surface model should be constructed for each objective function versus design variables to carry out ANOVA. The response surface model used in the study is the Kriging model (see Eqs. (2)-(14)).

Before the data-mining process, the precision of the Kriging response surface is validated through one left cross-validation method. R² is estimated for five potential objectives (η_{is, design},ε_{tot, design}, ${\dot{m}}_{\mathrm{choke}}$,Slope_ε,σ_{VM, max}). Since the constraint variable Signal is a sign function (the response value is 0 or 1), the Kriging metamodel cannot be directly used to approximate the discrete constraint variable Signal. Therefore, the SOM-based object classification method (Wu et al. 2011) is adopted to identify the Signal. The number of samples from CFD&FEA simulation increases gradually until it provides an acceptable precision of the Kriging metamodel (R² ≥ 0.9). It is found that 500 samples could provide enough accuracy for all objectives (see Table 6); hence, they are employed in ANOVA analysis.

Table 6 Cross-validation of Kriging metamodel

After the validation of the Kriging response surface, ANOVA is performed for five objective functions and one constraint. As impeller disk design parameters (v70~v73, see Table 5) have no impact on aerodynamic performance, all design variables (44 in total) may affect mechanical stress. Therefore, 40 design variables are considered (except for v70~v73) for η_{is, design}, ε_{tot, design}, ${\dot{m}}_{\mathrm{choke}}$, andSlope_ε ANOVA-based data-mining (40 main effects of single variables and 780 joint effects of two variables), and 44 design variables for σ_{VM, max}(44 main effects of single variables and 946 joint effects of two variables). Variances of design variables and their interactions whose proportion to the total variance are larger than 2.0% are shown in Fig. 12. Since the variance proportion of each interaction effect is less than 2%, they are not listed independently. The sum of main effects of significant design variables listed in Fig. 12 (except for “others” component) accounts for more than 90% of the total variance. This means that the behavior of the objective functions as well as the constraint can be well described. The performances versus design variables for significant ones (variance proportion > 10% in Fig. 12) are shown in Fig. 13.

Fig. 12

ANOVA results of initial design space

Fig. 13

The performances versus design variables for significant design variables

As depicted in Fig. 12, the main effects of v44 account for the largest proportion for aerodynamic performances (η_{is, design},ε_{tot, design},${\dot{m}}_{choke}$, andSlope_ε); here v44 denotes the last control point of the full blade at the root section (θ_{full, root, 8}, see Tables 4 and 5 and Fig. 10b). The variable v44 determines the blade angle (related to ε_{tot, design}), and further directly or indirectly controls the sweepback (related to η_{is, design}), flow area of impeller outlet (related to ${\dot{m}}_{\mathrm{choke}}$) and the rate of diffusion imbalance (related to Slope_ε). As shown in Fig. 13a–d, the main effects of v44 generally show the largest impacts (largest range of vertical coordinates) on aerodynamic performance, corresponding to Fig. 12a–d, and they also present severe non-linear patterns. Therefore, v44 is one of the key considerations in optimization. In Fig. 12, v45 (θ_{full, tip, 1}, the first control point of the full blade at the tip section), which affects the flow angle at the leading edge, has the second largest impact on η_{is, design}.

Design variable v13 (inducer cross-section flow area) is heavily related to leading edge shock wave, and further significantly influences ε_{tot, design}. Design variable v24 determines the meridional width near the impeller outlet and is relevant to flow separation near the shroud; hence, it considerably affects flow capacity (${\dot{m}}_{\mathrm{choke}}$). Other design variables, like v53, v43, v67, and v52, also show relative large contributions to aerodynamic performance, and Figs. 13a–d presents similar results. Design variables v70 and v71 denote the thickness of the impeller disk near the outlet and near the rotating shaft, respectively (see Fig. 11). As illustrated in Fig. 12e, v70 and v71 have the most important impact on maximum stress of impeller; however, they show inverse impact trend (see Fig. 13e). It can be seen in Fig. 12f that the location of maximum stress mainly depends on v69 (Hub fillet). In Fig. 13f, Signal = 1 gathers in the small Hub fillet region while Signal = 0 is assembled in a large Hub fillet location. A larger Hub fillet is more likely to avoid stress concentration near the blade root.

ANOVA-based analysis could extract the quantitative effects of design variables on objective functions and the impact trend of objective functions versus a single design variable. The design variables with a variance proportion greater than 10% are kept in the final design space and used in the optimization. The lower bound of the variance proportion is related to the simplification degree of the initial design space. In the study, the proportion is 10%, and it could identify four or five key design variables from more than 40 initial design variables for a specific objective.

3.3.2 Self-organizing map

SOM expresses the information in a qualitative way. It visualizes not only the relation between design variables and objective functions but also the trade-off between the objective functions. SOM employs a non-linear projection algorithm from high to low dimensions and a clustering technique. The projection is based on self-organizing of a low-dimensional array of neurons. In the projection algorithm, the weights between the input vector and the array of neurons are adjusted to represent features of the high-dimensional data on the low-dimensional map. The same location on each component map corresponds to the same SOM neuron, which is colored according to its related neutron component values. By comparing the behavior of the color pattern in the same region, one can analyze the correlations of the parameters. On the other hand, the parameters are correlated if there exist similar color patterns in the same region of the corresponding component maps. More details about SOM can be found in the reference (Li et al. 2017).

Five objective functions of the initial design space are selected from the preliminary analysis and experience. The interactions between the objective functions may be not very clear, which leads to a waste of computational resource. Therefore, the data-mining technique of SOM is employed here to overcome the difficulty. The sample independence for SOM data-mining is firstly investigated by adding the sample points step by step until the SOM component maps almost remain unchanged. It is found that the 500 samples used in ANOVA-based analysis are enough to meet the independency criterion. Therefore, the samples are employed for SOM data-mining to explore the interactions among these five initial objective functions. Six hundred twenty-five SOM neurons (25 × 25) are generated for SOM training. All the employed parameters are normalized to be 0~1.

Figure 14 presents the SOM component maps of five initial objective functions. The sizes of black circles in the figures denote the winning times of the neurons. The uniformly distributed winner neurons indicate that the design space for the optimization process is well represented. Figure 14 shows non-linear correlations and severe trade-off relations among objectives, and no region exists with good performance for all the objectives. This means that it is difficult to improve all objectives without any compromise. A trade-off needs to be introduced in these objectives. For example, the cluster in the upper left-hand corner is a better choice for η_{is, design}, ε_{tot, design}, ${\dot{m}}_{\mathrm{choke}}$, andσ_{VM, max}. Yet, the corresponding performance of Slope_ε is bad. SOMs colored by η_{is, design}, ${\dot{m}}_{\mathrm{choke}}$, and Slope_ε show similar color patterns. Among them, both η_{is, design} and ${\dot{m}}_{\mathrm{choke}}$ should be maximized while Slope_ε should be minimized. This indicates that η_{is, design} and ${\dot{m}}_{\mathrm{choke}}$ are not in the trade-off relation and even present an approximate linear relation. Therefore, only one of them needs to be considered in the optimization (here η_{is, design} is chosen). However, Slope_ε shows a severe trade-off relation versus η_{is, design} and ${\dot{m}}_{\mathrm{choke}}$, indicating that Slope_ε cannot be ignored. One physical example is a high trim impeller which has a large choke flow and a good peak efficiency but tends to have a narrow speed line. The other two objective functions show complex color patterns and are kept in the optimization. After SOM data-mining, the interactions among initial objective functions are extracted. The objective function design space is simplified, and the final objective functions are determined (η_{is, design},ε_{tot, design}, Slope_ε, and Stress_von mises).

Fig. 14

SOM component maps of objective functions

Based on the above two types of data-mining results, one may derive the following conclusions: (1) the aerodynamic performance of the centrifugal compressor is most sensitive to the outlet blade angle of the full blade at the root section. Other design factors, like the inlet blade angle of full blade at the tip section, inducer cross-section flow area, and meridional width near the impeller outlet, also have significant influences on aerodynamic performance. (2) Five initial objective functions generally show a non-linear and severe trade-off relation, and compromises need to be done in optimization. η_{is, design} and ${\dot{m}}_{\mathrm{choke}}$almost present a linear relation, while Slope_ε shows a severe trade-off relation versus η_{is, design} and ${\dot{m}}_{\mathrm{choke}}$. (3) Based on two types of data-mining results (ANOVA and SOM), the insensitive design variables and superfluous performance indicators (potential objective functions) are identified. They tend to be ignored in the final design space to simplify the optimization and to improve the efficiency as well as the robustness of optimization.

3.4 Final design space

Table 7 shows the active variables and their ranges in the final design space for the optimization process. The number of active variables reduces from 44 to 17.

Table 7 Active variable numbers, range of variations and constraints in final design space

Constraints: same as Table 5.

Figure 15 illustrates active variables of endwalls and blade camber curves in the final design space, in which the arrows indicate the movement directions of the active variables in optimization.

Fig. 15

Active variables of endwalls and blade camber curves in final design space

The mathematical expression of the final optimization problem is as follows:

$$ {\displaystyle \begin{array}{l}\max :{\eta}_{\mathrm{is},\mathrm{design}},{\varepsilon}_{\mathrm{tot},\mathrm{design}}\\ {}\min :{\mathrm{Slope}}_{\varepsilon },{\sigma}_{\mathrm{VM},\max}\\ {}s.t.\kern0.36em :\mathrm{Signal}=0\end{array}} $$

(22)

4 Multi-disciplinary optimization of a transonic centrifugal compressor

4.1 Optimization method

A multi-objective and multi-disciplinary optimization method is proposed in this section. The method combines ASHOA with two data-mining techniques (ANOVA and SOM), 3D blade parameterization method, and aerodynamic/mechanical codes. A typical transonic centrifugal impeller with vanless diffuser is selected to demonstrate the performance of the proposed method. Four objectives are higher isentropic efficiency η_{is, design}, higher total pressure ratio ε_{tot, design} at design operating condition, smaller slope of total pressure ratio Slope_ε and smaller maximum von Mises stress σ_{VM, max}. The constraint is that the location of maximum stress is in the center of the impeller disk. The optimization is conducted at design shaft speed, and a Pareto-based ranking is adopted for the four objectives.

ASHOA is directly integrated to the multi-objective and multi-disciplinary optimization method. Procedures I, II, and III are the same for the compressor case. The only difference between mathematical cases and the compressor case is the “evaluate response values” (see Fig. 1 circled in red). The response values of mathematical cases are estimated from analytic expressions while those of the compressor case are from CFD/FEA simulations. The evaluating response values of the transonic centrifugal compressor are shown in Fig. 16 in detail. As shown in Fig. 16, the left-hand part is used to estimate aerodynamic performance. The grid generation and CFD simulation are automatically carried out using AutoGrid and FineTurbo of NUMECA by templates, respectively. The CFD boundary conditions imposed for different objective functions are already discussed in Section 3.2.3. The right-hand part is the prediction of maximum von Mises stress at design shaft speed on ANSYS Mechanical.

Fig. 16

Flow chart of evaluating response values in ASHOA

Table 8 shows several essential parameters of ASHOA for the transonic centrifugal compressor optimization. These parameters are estimated according to Table 2 and Table 6. The parallel computing technique is applied to the optimization process. The optimization is carried out on a workstation with the 48-core Xeon(R) E5-2670 processor, and the CPU utilization is about 86%. The total computational time (including dating mining, adaptive sampling, global optimization) required to optimize the compressor was about 142 h. Table 9 illustrates the details of parameters achieved in the actual optimization. The Kriging metamodel provides satisfying accuracy levels for all objectives (${R}^2\ge {R}_0^2=0.95$), and the adaptive sampling algorithm meets the convergence criterion before reaching the maximum samples (N = 289 < N_max = 300).

Table 8 Parameters of ASHOA for the transonic centrifugal compressor optimization

Table 9 Details of parameters achieved in the actual optimization

4.2 Results and discussions

4.2.1 Optimization efficiency

The efficiency of turbomachinery optimization based on the proposed method is analyzed. Similar to mathematical test cases in Section 2.3.2, the efficiency of ASHOA is compared with other five optimization methods (see Table 1) for compressor optimization.

As mentioned before, ASHOA achieves accuracy criterion (R² ≥ 0.95) with a total of 289 samples. Table 10 illustrates the required total sample count of different algorithms to reach the same accuracy criterion. It shows that the adaptive sampling method in ASHOA needs fewer total sample count to achieve satisfying accuracy for global optimization. For engineering optimization, response values of samples are usually obtained from experimental measurement or numerical simulation, which is time consuming. Therefore, Table 10 shows that ASHOA is more efficient for compressor optimization to some extent.

Table 10 The required total sample count of different algorithms to reach accuracy criterion (average value for 5 runs)

In this study, however, the compressor global optimization is a high-dimensional (problem scale is 17) and high-nonlinearity problem. In addition, computational complexity of those algorithms is completely different. During the adaptive sampling process, the cross-validation and the search of optimal location to add a new sample point are also time consuming. In order to evaluate the optimization efficiency more objective, two aspects are considered: (1) the Pareto front solutions obtained from ASHOA and other algorithms over the same period are compared; (2) the total optimization time of different algorithms to achieve the same Pareto front solutions is compared. The two comparisons are based on the assumption that all metamodels reach the accuracy criterion (R² ≥ 0.95).

Comparison I

Based on the metamodels that have been constructed, six sets of Pareto front solutions obtained from ASHOA and five other state-of-the-art algorithms (AME, CV-Voronoi, EGO, ADE, and MBOE) over the same period are compared. Figure 17a is the four-dimensional (four objectives, see Table 9) scatter diagram of the six sets of Pareto front solutions. Figure 17b–d are the projections of Fig. 17a on X-Y, X-Z, and Y-Z planes respectively. In the figures, −Slope_ε and −σ_{VM, max} are adopted to make all objectives be the maximization problems. As illustrated in Fig. 17, the Pareto front solutions from ASHOA spread over the edges of the diagrams, and they nearly surround the solutions obtained from AME, CV-Voronoi, EGO, ADE, and MBOE. This means that ASHOA is more efficient than the other five algorithms. On the other hand, the solutions of ASHOA seem to have a better diversity. Figure 17 shows that ASHOA has a better performance for turbomachinery optimization. To further analyze the optimization efficiency, a quantitative comparison is carried out for the different sets of Pareto front solutions. For the sake of convenience, the six sets of Pareto front solutions in Fig. 17a are marked with S_AME, S_{CV − Voronoi}, S_EGO, S_ADE, S_MBOE, and S_ASHOA, respectively. A set of mixed solutions is firstly obtained by S_mixed = S_AME ∪ S_{CV − Voronoi} ∪ S_EGO ∪ S_ADE ∪ S_MBOE ∪ S_ASHOA. Then, the fast non-dominated sorting approach (Deb et al. 2002) is applied to sort the mixed data set S_mixed. As a result, a set of new “Pareto front solutions” of the mixed data set denoted by S is obtained. S and S_ASHOA are drawn in Fig. 18. As shown in the figure, the two sets of points are completely overlapped (S = S_ASHOA). This means that the Pareto front solutions obtained from ASHOA are the new “Pareto front solutions” of the mixed data set. Clearly, the solutions of ASHOA are better than those from AME, CV-Voronoi, EGO, ADE, and MBOE, indicating that the proposed method is more efficient.

Fig. 17

Pareto front solutions obtained from ASHOA and five other state-of-the-art algorithms (AME, CV-Voronoi, EGO, ADE, and MBOE) over the same period

Fig. 18

Comparison of ASHOA’s solutions and new “Pareto front solutions” of the mixed data set (from Fig. 17a)

Comparison II

The total optimization time of different algorithms to achieve the same Pareto front solutions is compared. Considering the massive numerical simulations, the comparison tests of turbomachinery optimization are carried out on three workstations with 3×48-core Xeon(R) E5-2670 processors, and a parallel server with 120-core Xeon(R) E5-2620 processor.

The Pareto front solutions S_ASHOA obtained from ASHOA (see Fig. 17a) are set to be the reference solutions. The time consumed to get S_ASHOA is marked with t. Other optimization algorithms run in the same platform to search the Pareto front solutions. The fast non-dominated sorting approach (Deb et al. 2002) is adopted to sort the current Pareto front solutions of other algorithms and the reference solutions. When the current results of other algorithms and the reference solutions are sorted in the same class, those algorithms achieve the same Pareto front solutions, and the corresponding time is recorded. Table 11 shows the comparison of optimization time among the proposed method and other algorithms. As illustrated in the table, the proposed algorithm significantly boosts the optimization efficiency of turbomachinery design. ASHOA’s efficiency is 2–10 times higher compared to other algorithms listed in Table 11.

Table 11 Optimization time of different algorithms to achieve the same Pareto front solutions

4.2.2 Post-processing of optimization results

Though the high-dimensional scatter diagrams (Fig. 17a and Fig. 18) can provide some qualitative information of the Pareto front solutions, it is difficult to obtain the accurate values of specific solutions when the number of objective functions is larger than two. Direct projections of the high-dimensional scatter diagrams (Fig. 17b–d) are also unclear. Therefore, an insightful observation of the optimization process cannot be drawn from the high-dimensional scatter diagrams. An alternative method is to reduce the dimensionality of solutions while keeping their characteristics.

As a dimension reduction method, the self-organizing map (SOM) is able to visualize not only the relation between design variables and objective functions but also the trade-off between the objective functions. Also, as a useful post-processing tool, SOM is preferable for a designer to provide some alternative or suboptimum solutions to decide the final design. In this study, four typical Pareto front solutions and the baseline are projected on 2D maps through the SOM method based on the optimization iteration data (normalized to be 0~1, see Fig. 19). The SOM maps provide an insightful observation of the optimization process. Pareto 1~4 picked from Pareto front solutions denote the specific solutions with minimum Slope_ε, minimum σ_{VM, max}, maximum ε_{tot, design}, and maximum η_{is, design}^, respectively. SOM component maps successfully extract interactions between Pareto front solutions and the coupling optimization directions of design variables versus the baseline. For example, compared to the baseline, Pareto 3 shows better performance for ε_{tot, design},Slope_ε, and σ_{VM, max}while it deteriorates η_{is, design}. Design variable v70 decreases to reach Pareto 3 while v71 shows the inverse changing direction. An optimal solution is selected with a balanced improvement for all objective functions. Further analysis about coupling optimization directions of the optimal solution versus the baseline will be discussed in the following subsection.

Fig. 19

SOM component maps of objective functions and significant design variables with typical Pareto front solutions

The comparisons of overall performances between baseline and optimal compressor at design shaft speed are shown in Table 12. It shows an improvement of both isentropic efficiency η_{is, design} (by 1.61%) and total pressure ratio ε_{tot, design} (by 4.13%) at the design point. Meanwhile, surge mass flow ${\dot{m}}_{\mathrm{surge}}$ decreases by 0.89% while choke mass flow ${\dot{m}}_{\mathrm{choke}}$ raises by 0.39% as well, showing an improvement of the stable operating range. Besides, the maximum von Mises stress σ_{VM, max}, shows a considerable decrease by 9.68%, and the location of σ_{VM, max} is strictly constrained in the center of impeller disk.

Table 12 The comparison of overall performances between baseline and optimal compressor at 90000 rpm

Figure 20 compares the off-design aerodynamic performance of the baseline and the optimal compressors at three speeds of 90,000 rpm (design shaft speed), 86,000 rpm and 78,000 rpm. The aerodynamic performance shows an overall improvement over the whole speed lines at three shaft speeds. Particularly, the surge margins are also extended after optimization. Table 12 and Fig. 20 demonstrate the power of this multi-point, multi-objective, and multi-disciplinary optimization method. A single-point optimization is less likely to get similar results.

Fig. 20

The comparison of off-design aerodynamic performance between baseline and optimal compressor (impeller + diffuser)

The flow fields at design operating condition are further compared. Figure 21 presents a comparison of entropy distributions at 99% span (reference point is inlet total condition). A large high-entropy region at the pressure side of the full blade near the impeller outlet can be found in the baseline; it greatly decreases after optimization. The impeller exit flow is now circumferentially more uniform between two flow channels, contributing to a smaller energy loss in the vaneless diffuser. Figure 22 shows a comparison of the relative Mach number contour at 90% span. A strong inducer normal shock wave is optimized to be a weak oblique shock wave, indicating an improvement of flow field after optimization. Figure 23 gives the span performance of the impeller and diffuser outlet. For the impeller, the total pressure ratio increases almost along the whole span, while the isentropic efficiency mainly shows improvement at mid-span. It can be observed that the performance at the impeller outlet is more uniform after optimization, which is corresponding to Fig. 21.

Fig. 21

Entropy distributions at 99% span

Fig. 22

Relative Mach number contour at 90% span

Fig. 23

Spanwise performance of impeller and diffuser outlet

Figure 24 displays the comparison of von Mises stress between the baseline and optimal impeller. It generally shows similar patterns, but the stress near the backface declines, especially in the center of impeller disk (decreases by 9.68%).

Fig. 24

Comparison of von Mises stress between baseline and optimal impeller

Figure 25 compares the geometry of the baseline and the optimal impeller. The arrows indicate the changing directions of the design variables during the optimization process to achieve the optimal solution.

Fig. 25

Comparison of geometry changes between baseline and optimal impeller

As analyzed above, the optimization process achieved an improvement for both aerodynamic and mechanical performance. Thus, the new proposed method provides another better choice for the transonic centrifugal compressor optimization.

The post-processing of compressor optimization is important, since it explores the coupling optimization directions of the optimal solution versus baseline as well as the mechanism behind performance improvement of optimal design. In this study, we introduced a post-processing method by combining SOM analysis of the optimization process (Fig. 19), ANOVA data-mining of objective functions (Fig. 13), geometry changes after optimization (Fig. 25), and flow field analysis (Figs. 21, 22, and 23).

As shown in Fig. 25b, v44 (θ_{full, root, 8}, the last control point of full blade at root section) decreases after the optimization (same as Fig. 19f) to form a larger sweepback (see Fig. 10b, since θ < 0; a decrease in v44 means a larger sweepback). It helps to decrease the diffusion imbalance between the shroud and the hub, resulting in a more uniform impeller outflow and a smaller energy loss in the vaneless diffuser, which corresponds to Fig. 21. The reasonable decrease in v44 tends to improve the isentropic efficiencyη_{is, design} (see Fig. 13a). A relatively small v44 does not decline the total pressure ratio ε_{tot, design} since a smaller sweepback at the tip section (larger v52, see Fig. 25b) compensates the impeller work and pressure ratio. Since choke mass flow ${\dot{m}}_{\mathrm{choke}}$ shows an approximate linear relation versus η_{is, design}, a small v44 is more suitable for ${\dot{m}}_{\mathrm{choke}}$ (see Fig. 13c). A small rate of the diffusion imbalance resulting from a small v44 delays the stall inception and extends surge margin (Fig. 13d). The coupling optimization direction of v44 contributes to an overall aerodynamic performance improvement.

The design variable v13 (control point of hub near inducer, see Fig. 25a) decreases to form a larger inducer cross-section flow area (see Fig. 19e). Smaller v13 coupled with slightly smaller v30 (denoting smaller tip tangential velocity) reduces inducer axial velocity and relative Mach number, forming a larger inlet flow angle (axial direction). Both v45 (θ_{full, tip, 1}, the first control point of the full blade at the tip section) and v53 (θ_{splitter, root, 1}, the first control point of the splitter blade at the root section) increase the blade angles to match the larger flow angle. Also, smaller v13 transforms a strong inducer normal shock wave into a weak oblique shock wave, which is consistent with the results in Fig. 22. The coupling changing directions of v13, v30, v45, and v53 (Fig. 19) result in an improvement of aerodynamic performance, which is also validated by the results in Fig. 13a–d.

As shown in Fig. 25c, v70 (corresponding to h₁) decreases to reach the optimal solution while v71 (corresponding to h₂) shows the inverse changing direction. They try to cluster the impeller disk near the center shaft, forming a forward movement of the mass center. Under the same shaft speed, the stress near the backface is considerably decreased, particularly for the stress located in the center of the impeller disk. Meanwhile, the location of maximum stress moves forward. The analysis is validated by the results in Fig. 13e and Fig. 19i, j. The Hub fillet (v69) increases from 1.0 to 1.49 mm after optimization, which strictly constrains the Signal to be 0 (the location of σ_{VM, max} is in the center of the impeller disk).

The analysis above shows that the post-processing method can gain an insightful observation of the optimization process as well as the aerodynamic and mechanical mechanism behind performance improvement.

5 Conclusions

An adaptive sampling hybrid optimization algorithm (ASHOA) is presented in this paper. The algorithm combines with the data-mining strategies to solve the multi-objective problem. A typical transonic centrifugal impeller with a vanless diffuser is selected to demonstrate the correctness of the algorithm. The following conclusions can be drawn from the present study.

• (1) A new global optimization algorithm named ASHOA is proposed by combining a novel adaptive sampling metamodel and a new hybrid optimization method. Five high-dimensional and strong non-linear mathematical cases are introduced to test the performance of the proposed algorithm. The results show that ASHOA can increase the search efficiency and achieve a better distribution of Pareto front solutions.

• (2) The role of data-mining methods (SOM and ANOVA) is heuristic, and they are applied to the initial design space of compressor optimization. ANOVA identified both the single effect and the interactive effect of design variables on objective functions, resulting in a considerable decrease in the design variables from 44 to 17. SOM visualized and extracted trade-off relations between initial objective functions, contributing to a simplification of objective functions.

• (3) An optimization strategy is constructed by integrating ASHOA with two data-mining techniques (ANOVA and SOM), 3D blade parameterization method, and aerodynamic/mechanical codes. It is used to optimize a typical transonic centrifugal impeller with a vanless diffuser, showing 2–10 times higher efficiency when compared to other excellent optimization algorithms. Through the optimization, the isentropic efficiency and total pressure ratio at the design condition are increased by 1.61% and 4.13%, respectively. The performance of off-design conditions also shows an improvement with a larger choke mass flow (increases by 0.39%) and a better surge mass flow (decreases by 0.89%). In addition, the maximum stress is decreased by 9.68%.

• (4) The post-processing method of compressor optimization, which couples data-mining results, detailed flow analysis, and geometry changes, is an effective way to reveal the mechanism behind the performance improvement after optimization.

Appendices

Appendix 1

1.1 ZDT1

ZDT1 has 30 design variables and multiple Pareto fronts. The mathematical expression is

$$ {\displaystyle \begin{array}{l}\operatorname{Minimize}\kern0.36em {f}_1={x}_1\kern0.36em \mathrm{and}\kern0.36em {f}_2=g\left(1-\sqrt{\frac{f_1}{g}}\right)\\ {}\mathrm{where},g=1+\frac{9}{n-1}\sum \limits_{i=2}^n{x}_i;\kern0.84em 0\le {x}_i\le 1,i=1,\cdots, n;n=30\end{array}} $$

(23)

The Pareto-optimal region for the case ZDT1 corresponds to x₁ ∈ [0, 1], x_i = 0, i = 2, ⋯, 30.

1.2 ZDT2

ZDT2 has 30 design variables and multiple Pareto fronts. The mathematical expression is

$$ {\displaystyle \begin{array}{l}\operatorname{Minimize}\kern0.36em {f}_1={x}_1\kern0.36em \mathrm{and}\kern0.36em {f}_2=g\left[1-{\left(\frac{f_1}{g}\right)}^2\right]\\ {}\mathrm{where},g=1+\frac{9}{n-1}\sum \limits_{i=2}^n{x}_i;\kern0.84em 0\le {x}_i\le 1,i=1,\cdots, n;n=30\end{array}} $$

(24)

The Pareto-optimal region for the case ZDT2 corresponds to x₁ ∈ [0, 1], x_i = 0, i = 2, ⋯, 30.

1.3 ZDT4

ZDT4 has 10 design variables and multiple local Pareto fronts. The mathematical expression is

$$ {\displaystyle \begin{array}{l}\operatorname{Minimize}\kern0.36em {f}_1={x}_1\kern0.36em \mathrm{and}\kern0.36em {f}_2=g\left(1-\sqrt{\frac{f_1}{g}}\right)\\ {}\mathrm{where},g=1+10\left(n-1\right)+\sum \limits_{i=2}^n\left({x}_i^2-10\cos \left(4\pi {x}_i\right)\right);\\ {}0\le {x}_1\le 1,\kern0.48em -5\le {x}_i\le 5,i=2,\cdots, n;n=10\end{array}} $$

(25)

The Pareto-optimal region for the case ZDT4 corresponds to x₁ ∈ [0, 1], x_i = 0, i = 2, ⋯, 10. There exist 21⁹ local Pareto-optimal solutions and about 100 distinct Pareto fronts.

The basic optimization parameters of ASHOA for ZDT1, ZDT2, and ZDT4 are given in Table 13. Figure 26 shows the optimization results for test cases ZDT1, ZDT2, and ZDT4.

Table 13 Parameters of ASHOA for ZDT1, ZDT2, and ZDT4

Fig. 26

Results for test cases ZDT1, ZDT2, and ZDT4 optimized by ASHOA and five other state-of-the-art algorithms (AME, CV-Voronoi, EGO, ADE, and MBOE) at the same search time

Appendix 2

The demonstrations of the procedure (see Section 2.3.3) to search the optimal λ for test cases ZDT3 and ZDT6 (Figs. 27 and 28).

Fig. 27

The process of searching the optimal λ for ZDT3

Fig. 28

The process of searching the optimal λ for ZDT6

Fig. 29

Effect of different values of λ on optimization efficiency and solutions diversity for ZDT1, ZDT2, and ZDT4

1.1 ZDT 3

(1) λ = 0, the growth rate Δλ = 0.05, λ₁ = λ + Δλ = 0.05.

(2) λ₁ < 1, go next.

(3) & (4)

Fig. 3a, the 1st iteration,

λ = 0,λ₁ = 0.05,N_λ1 = 15 > N_λ = 1, then update λ = 0.05, λ₁ = 0.1, go next.

Fig. 3b, the 2nd iteration,

λ = 0.05,λ₁ = 0.1,N_λ1 = 6 > N_λ = 1, then update λ = 0.1,λ₁ = 0.15, go next.

Fig. 3c, the 3rd iteration,

λ = 0.1,λ₁ = 0.15,N_λ1 = 6 > N_λ = 2, then update λ = 0.15,λ₁ = 0.2, go next.

Fig. 3d, the 4th iteration,

λ = 0.15,λ₁ = 0.2,N_λ1 = 17 > N_λ = 1, then update λ = 0.2,λ₁ = 0.25, go next.

Fig. 3e, the 5th iteration,

λ = 0.2,λ₁ = 0.25,N_λ1 = 20 > N_λ = 1, then update λ = 0.25,λ₁ = 0.3, go next.

Fig. 3f, the 6th iteration,

λ = 0.25,λ₁ = 0.3,N_λ1 = 22 > N_λ = 0, then update λ = 0.3,λ₁ = 0.35, go next.

Fig. 3g, the 7th iteration,

λ = 0.3,λ₁ = 0.35,N_λ1 = 2 < N_λ = 24, end loop, go next.

(5) The current λ = 0.3 is the optimal value, and it is used in the optimization algorithm (ASHOA), and the procedure stops.

1.2 ZDT 6

(1) λ = 0, the growth rate Δλ = 0.05, λ₁ = λ + Δλ = 0.05.

(2) λ₁ < 1, go next.

(3) & (4)

Fig. 3a, the 1st iteration,

λ = 0,λ₁ = 0.05,N_λ1 = 6 > N_λ = 0, then update λ = 0.05 λ₁ = 0.1, go next.

Fig. 3b, the 2nd iteration,

λ = 0.05,λ₁ = 0.1,N_λ1 = 10 > N_λ = 1, then update λ = 0.1,λ₁ = 0.15, go next.

Fig. 3c, the 3rd iteration,

λ = 0.1,λ₁ = 0.15,N_λ1 = 1 < N_λ = 8, end loop, go next.

(5) The current λ = 0.1 is the optimal value, and it is used in the optimization algorithm (ASHOA), and the procedure stops.

Appendix 3

The optimal λ found by the procedure (see Section 2.3.3) for test cases ZDT1, ZDT2, and ZDT4 are shown in Fig. 29.

Appendix 4

In Section 2.1, the proportion of individuals to carry out gradient mutation is specified to be 1/q × 100% in step (5) of the new gradient mutation algorithm. This threshold value is an important parameter which may influence the global optimization performance and convergence efficiency of the optimization algorithm. Therefore, sensitivity analysis of the proportion is investigated with the same test cases (ZDT1 to ZDT6, except for ZDT5).

In this paper, the proportion is 1/q × 100%, where q is the number of objectives in optimization. For multi-objective optimization problems, q usually equals 2–4. In the study, the five mathematical test cases all have two objectives (1/q = 0.50). Four types of proportion (0.25, 0.50, 0.75, 1.00) are imposed for the optimization of the five test cases. The Pareto front solutions are searched over the same period with different proportions, and the results are plotted in Fig. 30. Overall, the global optimization performance and convergence efficiency are not very sensitive to the proportion between 0.25 to 1.00 for all test cases, particularly for ZDT2, ZDT3, and ZDT5. If the Pareto front solutions are compared carefully, it is found that both convergence efficiency and global optimization performance decrease slightly under small or large proportions.

Fig. 30

The comparison of Pareto front solutions searched with different individuals’ proportion over the same period

This can be explained by the following facts. When a small proportion is imposed, few individuals are selected to carry out gradient mutation, and some individuals with large gradient values are ignored. Therefore, the convergence efficiency may suffer. On the other hand, if the proportion is large, more individuals are chosen to implement gradient mutation. Those individuals which have very small gradient (near zero) are also selected to conducted gradient mutation. It will increase the computational resources and further decrease convergence efficiency. Additionally, the gradient mutation of small gradient individuals has tiny contributions to convergence. By contrast, it cannot protect excellent individuals, leading to the poorer global optimization performance and convergence efficiency.

As shown in Section 2.3.3, the normalized gradient mutation step size λ is selected adaptively during the optimization process. When the proportion of individuals for gradient mutation is specified, the ASHOA will determine a suitable λ to balance the high convergence efficiency and good global optimization performance. Taking ZDT1 as an example, when the proportion is 0.25, the optimal λ = 0.9 while when the proportion is 0.50 the optimal λ = 0.8. The effect of the varying proportion on the optimization algorithm is counteracted by adaptive λ. Therefore, the specific proportion (1/q) for the proposed algorithm ASHOA is reasonable and robust.