1 Introduction

Shipbuilding is a complex and long-term manufacturing process, which requires the coordination of a considerable number of limited resources. Traditionally, this process was carried out through a project-oriented approach. Due to a ship is generally constructed with few components, which are based on the same design but with a certain degree of customization, a modular approach began to be implemented several decades ago, taking into account the Lean principles and standardization processes. This modular approach uses an integrated modular design based on the prefabrication of blocks (or steel structures), which are then assembled in a block erection process to finally build the ship. The ship design determines the quantity of blocks to be produced and the size of each one of them. Figure 1 shows as a ship is built following the principles of the modular approach: the hull is divided into blocks and, in turn, each block is divided into sub-blocks.

Fig. 1
figure 1

Hull production—modular approach

Full size image

According to Shin and Ciccantell (2009), the production of ships and marine facilities tends to be large scale and greatly non-standardized, so the shipbuilding process requires labor-intensive and technology intensive, resulting high expensive. These authors remark that the shipbuilding industry tends to have new orders for construction of ships concentrated in short periods according to the demand, which generally fluctuates wildly following the rise and decline of this industry in the world market.

The block assembly process becomes a bottleneck for the shipbuilders due to the complexity of the production system. This process requires a high degree of coordination among several resources in order to satisfy the complex production restrictions and strict storage policies. A delay in the completion of a project increases the risk of incurring penalties in delivery. Moreover, the most shipbuilding contracts provide the buyers with the right to cancel the contract in case of delayed delivery of the vessel.

Since the block assembly process represents more than half of the whole shipbuilding process, it would be very useful to have a decision-making tool that may determine the optimal scheduling of operations, reducing at minimum the man-hours (Cho et al. 1998). Although significant developments have emerged in recent decades about this problem, few works have been focused on the scheduling problem. The main challenge is to obtain a good solution that takes into account the wide range of operational constraints. Unlike other scheduling problems published in the literature, this production problem deals with assembly operations and the processing of different types of products.

In the last years, the researchers have been tried to solve the block assembly process through heuristics, metaheuristics, and simulation-based methods with the goal of providing feasible solutions with reasonable computational effort. Some contributions have been focused on representing the production process as a constraint satisfaction problem where the precedence relationships between operations are considered constraints (Kim et al. 2002; Seo et al. 2007). In addition, some heuristic algorithms have been used to determine the best scheduling that both improves the use of the area in the long term and minimizes the processing times of the blocks (Koh et al. 2008; Shang et al. 2017). Other contributions also appear in the modeling and simulation area. Lee et al. (2009), Zhuo et al. (2012), and Cebral-Fernandez et al. (2016) have developed three discrete event simulation models in order to obtain a schedule that maximizes the productivity while minimizing the total time for completing the operations. Afterwards, Basán et al. (2017) have proposed a simulation environment to evaluate the best flow of materials that minimizes the completion time of a ship through applying different heuristic rules. Although these simulation approaches are greatly useful to represent the dynamic behavior over time of the system, the quality of solutions reported by these models are highly dependent on the heuristic rules using within them.

On the other hand, several hybrid methods have also been reported in the literature for effectively coping with large size industrial cases. For instance, a research conducted by Xiong et al. (2015) have formulated a MIP (mixed integer programming) model for the hybrid assembly-differentiation flow shop scheduling problem. Since the NP-hardness of the problem, these authors propose two fast heuristics and three hybrid meta-heuristics for treating with medium and large-size instances. Zhuo et al. (2012) have developed a hybrid planning approach using discrete-event simulation and discrete spatial optimization to take into account both the programming and the spatial arrangement. In addition, Basán et al. (2017) introduced a novel hybrid simulation-based optimization method, where a MILP mathematical model and a discrete event simulation model are incorporated together into an algorithm in order to generate complete schedules with efficient computational times for large-sized shipbuilding scheduling problems. Despite these advancements, the quality of solutions found remains the main drawback of the hybrid approaches.

Robust and reliable solutions regarding to their quality, feasibility or optimality can be achieved through exact optimization approaches. Due to the block assembly process consists of a set of products that go through different processing stages, the problem can be mathematical treated as a multi-stage system (Pinto and Grossmann 1995; Méndez et al. 2001; Kopanos et al. 2009; Castro et al. 2009), where the main objective is to find the optimal schedule that minimizes the time for completing all processing tasks. The mathematical model should consider constraints for the assignment of tasks to processing units and the sequencing of those tasks in each unit as in the classical multi-stage scheduling problem (Méndez et al. 2006; Maravelias and Sung 2009). Also, a set of new mathematical constraints should be defined for representing the assembly operations involved in the shipbuilding process. Recently, a continuous-time MILP formulation has been proposed by Basán et al. (2018) to determine the optimal schedule of a block assembly process considering up to ten blocks.

The main drawback of the MILP models is that they are characterized by high computation times. From the practical point of view, the industries prefer computational tools that report the optimal or at least, near-optimal solutions but in a quickly way. In an attempt to reduce this gap between theory and practice, the development of MILP-based hybrid approaches (Roslöf et al. 2002; Chu et al. 2014; Persson and Ölvander 2015; Tenne 2015; Fettaka et al. 2015; Larson and Wild 2016; Schweiger and Liers 2018) and techniques of decomposition-aggregation and improvement algorithms (Hasebe et al. 1991; Roslöf et al. 1999, 2001; Méndez and Cerdá 2003a; Kopanos et al. 2010; Aguirre et al. 2012; Cóccola et al. 2015; Fettaka et al. 2015) have emerged as alternative solution strategies for solving the complex scheduling problems arising in industrial environments. These techniques are generally based on rigorous mathematical programming approaches (Cerdá et al. 1997; Méndez et al. 2000, 2001, 2006; Méndez and Cerdá 2003b).

Firstly, this work proposes three new alternative continuous-time MILP formulations for the block assembly problem. The main goal is the minimization of makespan. Although these exact methods allow reaching solutions that outperform those ones achieved by evaluating alternative dispatching rules in a simulation model, such solutions are far from being the optimal ones. Moreover, the mathematical models show a high computational burden in the most examples solved. To develop a more suitable tool for industrial environments without losing the robustness exhibited by the exact optimization approaches of reaching good solutions, this paper proposes then a MILP-based decomposition algorithm that allows finding high-quality and practical solutions in few seconds of CPU time even for large-size problems.

All solution strategies proposed in this work are tested by solving several instances derived from a real-world shipbuilding problem. A detailed comparison of the computational performance of each approach is presented in order to highlight the advantages of the decomposition method.

The remainder of this paper is organized as follows. The block assembly process is described in Sect. 2. In Sect. 3, the problem statement is introduced. Afterwards, Sect. 4 presents three alternative MILP models to solve the multi-stage scheduling problem. Then, in Sect. 5, the development of the MILP-based decomposition procedure is explained in detail. Several complex problem instances of a real-world block assembly scheduling problem are presented and solved in Sect. 6. Finally, the concluding remarks follow in Sect. 7.

2 The shipbuilding process

The block assembly process may be treated as a flow shop scheduling problem, in which a set of sub-blocks and blocks must be assigned and sequenced on several processing units belonging to different processing stages. Having into account the ship design, the hull is divided into dozens of blocks of specific size (see Fig. 1). A block is the largest construction unit of a ship. In turn, each block is assembled from one or more sub-blocks, which are composed of steel plates according to the design drawn for the ship. Both blocks and sub-blocks are considered intermediate products in the modular approach used for constructing a ship, which contains other components such as pipes, supports, and electronic equipment.

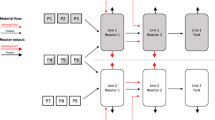
At early stages of the shipbuilding process, steel plates and profiles are processed to form the sub-blocks, which are then assembled in a dedicate workshop to obtain large blocks as an intermediate product. After that, the blocks are sequentially processed on a set of workshops and finally, they are assembled in a dry dock, operation known as Erection process. Although the blocks should arrive at the dry dock with all the necessary equipment and systems effectively installed, several elements must be usually mounted during the block erection operation. The block assembly process is depicted in Fig. 2. In this picture, the stages processing sub-blocks are referenced as \(S^{sb}\) while those ones performing operations on the blocks are classified as \(S^{b}\).

Fig. 2
figure 2

The block assembly process

Full size image

Firstly, the block assembly process begins with Construction and Assembly operation, where sheets and profiles are received, cut into small parts, and welded to form the smallest units of a ship (sub-blocks). The process continues with the Pre-outfitting operation, consisting in the installation of different components as pipes, brackets, and auxiliary elements in order to obtain the finished sub-blocks.

Once the sub-blocks are outfitted, they are assembled by welding operations to form the block structure. This stage is known as Assembly. The assembly of a block cannot begin until its sub-assemblies (sub-blocks) are ready. The next stages of the manufacturing process deal with the construction and transportation of the blocks. After assembling the sub-blocks, the Outfitting 1 operation is performed to outfit items like pipes and electrical and lighting lines inside the blocks. Then, these one are blasted and painted in the painting booths during Painting operation. During this action, the protection and design requirements of blocks are considered. After outfitting and painting stages, a second outfitting process is performed on the blocks before they will be moved to the dock (Outfitting 2 operation). All equipment that might be deteriorated in the painting stations, such as wires and electronic components, are again installed at this stage. Finally, the prefabricated and painted blocks are transported and positioned in the dry dock for assembling the ship. The Block erection operation is carried out to mount the blocks, one after another, according to a pre-predefined sequence. This assembly sequence is predefined by the company, taking into account if the unit to be assembled is a base block, a lateral block, or an upper block, as shown Fig. 3. The building of a ship always begins with a predefined base block and then, the remaining blocks are assembled and welded respecting the mentioned sequence. The processing time at Erection stage is modified taking into account the type of block to be mounted (lateral or superior block). Note that a block may be assembled just if the erection operations of its predecessor block have already been finished. Thus, if a block arrives at the dock before these operations end, it must wait.

Fig. 3
figure 3

Block erection assembly process

Full size image

3 Problem statement

According to the integrated modular design, the shipbuilding problem involves the processing of a set of product \(i \in I\) through several stages \(s \in S\), following a predefined and known production sequence. This manufacturing process is characteristic of the flexible flow shop (FFSP) environments, in which each stage \(s\) has a set \(k \in K_{s}\) of identical processing units working in parallel. In the case of shipyard, each unit represents a workshop. Hence, the block assembly process may be mathematical represented as a FFSP problem with the following features:

  • A set of products \(i \in I\) should be processed by following a predefined sequence of stages \(s \in S\).

  • The set I is partitioned in two subsets: \(I^{sb}\) and \(I^{b}\), where \(I^{sb}\) contains the products representing sub-blocks and \(I^{b}\) includes the blocks. Note that \(I = I^{b} \cup I^{sb}\).

  • Each processing stage \(s\) should be performed in a specific subset of units \(k \in K_{s}\). In addition, each unit \(k\) is able to perform just one processing stage (dedicated unit).

  • Each block \(i \in I^{b}\) is made up of one or more predefined sub-blocks \(i' \in SB_{i}\).

  • Products \(i \in I\) are not processed in all the stages \(s \in S\) because there are several assembly operations.

  • The first stages \(s \in S^{sb}\) process sub-blocks while the last stages \(s \in S^{b}\) perform operations on the blocks.

  • Sub-blocks \(i \in I^{sb}\) are assembled to form a block at intermediate stage \(s \in S^{a}\).

  • Blocks \(i \in I^{b}\) are assembled in a dock to form the hull of the ship at stage \(s \in S_{seq}^{a}.\)

  • The final assembly sequence on slipway (Erection stage), which determines the order in which the blocks must be mounted, is known a priori through the parameter \(Seq_{i}\).

  • Each workshop \(k \in K\) can process one block (or sub-block) at a time and, likewise, a product i only can be processed at most in one workshop at each stage \(s \in S\).

  • The processing times \(pt_{is}\) are known with certainty remaining invariant over time.

  • Transfer times of the blocks (or sub-blocks) between stages are considered negligible.

  • Raw material are considered unlimited.

  • Either the non-intermediate storage (NIS) policy or the unlimited intermediate storage (UIS) policy may be adopted. When a NIS strategy is used, each workshop becomes intermediate storage if its processing has finished and the next step is not available yet.

It is worth to remark that all assumptions listed above are realistic features of the block assembly process. The problem statement does not incorporate any simplification with regards to the real-data provided by the company.

4 Mathematical formulations

Having defined the block assembly process as a flexible flow shop scheduling problem, three continuous-time mathematical formulations of mixed integer linear mathematical programming (MILP) that have been published in the literature for the short-term scheduling of multistage batch plants are presented in this section (Méndez et al. 2006): (1) the first formulation is based on the concept of time-slots (Pinto and Grossmann 1995), (2) the second one is constructed following the immediate batch precedence concept (Cerdá et al. 1997), and (3) the last formulation is based on the general precedence concept (Méndez et al. 2001). These three monolithic approaches are widespread used by the communities of Operations Research and Process Systems Engineering for solving the production problems arising in the short-term scheduling area.

It is worth noticing that the MILP models presented in this paper have been modified from their original proposals in the literature in order to adapt them to the shipbuilding problem. The problem goal is to determine the optimal production schedule that minimizes the time needed to construct a ship. In this way, the mathematical model should determine: (1) the assignment of products to workshops, (2) the processing sequence for any pair of product allocated at each workshop, and (3) the completion time of each product at each processing stage.

4.1 Objective function

The shipbuilding industry aims at increasing its productive efficiency and consequently, its profit, which is directly related to the time required to build a large-scale ship. A delay in the completion of a project increases the risk of incurring penalties in delivery. Moreover, the buyers have the right to cancel the shipbuilding contract in case of delayed delivery of the vessel. Hence, the makespan criterion (MK) has been chosen as optimization goal, as shown in Eq. (1).

$$minimize\,MK$$
(1)

4.2 The slot-based continuous time formulation

In this mathematical formulation, a set of time-slots \(p \in P_{k}\) is postulated for each processing unit \(k\) in order to allocate in them the blocks or sub-blocks to be processed. A binary variable \(W_{ipk}\) is used to determine if product \(i\) is assigned to time-slot \(p\) of unit \(k\).

$$\sum\limits_{{k \in K_{s} }} {\sum\limits_{{p \in P_{k} }} {W_{ipk} = 1\quad \forall \left( {\left( {i \in I^{sb} , s \in S^{sb} } \right) \cup \left( {i \in I^{b} ,s \in S^{b} } \right)} \right)} }$$
(2)
$$\sum\limits_{\begin{subarray}{l} \left( {i \in I^{sb} , s \in S^{sb} } \right) \\ \cup \left( {i \in I^{b} ,s \in S^{b} } \right) \end{subarray} } {W_{ipk} \le 1\quad \forall s \in S,k \in K_{s} ,p \in P_{k} }$$
(3)
$$\mathop \sum \limits_{i \in I} W_{{i\left( {p + 1} \right)k}} \le \mathop \sum \limits_{i \in I} W_{ipk} \quad \forall k \in K_{s} ,p \in P_{k} , \left( {p + 1} \right) \in P_{k}$$
(4)
$$Tf_{is} \ge Ts_{is} + pt_{is} \quad \forall \left( {\left( {i \in I^{sb} , s \in S^{sb} } \right) \cup \left( {i \in I^{b} ,s \in S^{b} } \right)} \right)$$
(5)
$$Tf_{pk} \ge Ts_{pk} + \mathop \sum \limits_{{\begin{array}{*{20}c} {\left( {i \in I^{sb} , s \in S^{sb} } \right)} \\ { \cup \left( {i \in I^{b} ,s \in S^{b} } \right)} \\ \end{array} }} W_{ipk} pt_{is} \quad \forall s \in S,k \in K_{s} ,p \in P_{k}$$
(6)
$$Ts_{{i{\text{s}}}} = Tf_{{i\left( {{\text{s}} - 1} \right)}} \quad \forall \left( {\left( {i \in I^{sb} , s \in S^{sb} } \right) \cup \left( {i \in I^{b} ,s \in S^{b} } \right)} \right): s > 1$$
(7a)
$$Ts_{{i{\text{s}}}} \ge Tf_{{i\left( {{\text{s}} - 1} \right)}} \quad \forall \left( {\left( {i \in I^{sb} , s \in S^{sb} } \right) \cup \left( {i \in I^{b} ,s \in S^{b} } \right)} \right): s > 1$$
(7b)
$$Tf_{pk} \le Ts_{{\left( {p + 1} \right)k}} \quad \forall k \in K,p \in P_{k} ,\left( {p + 1} \right) \in P_{k}$$
(8)
$$\begin{aligned} & Tf_{is} - Tf_{pk} \ge -\,M\left( {1 - W_{ipk} } \right) \\ & \quad \quad \quad \quad \quad \quad \forall \left( {\left( {i \in I^{sb} , s \in S^{sb} } \right) \cup \left( {i \in I^{b} ,s \in S^{b} } \right)} \right),k \in K_{s} ,p \in P_{k} \\ \end{aligned}$$
(9a)
$$\begin{aligned} & Tf_{is} - Tf_{pk} \le M\left( {1 - W_{ipk} } \right) \\ & \quad \quad \quad \quad \quad \forall \left( {\left( {i \in I^{sb} , s \in S^{sb} } \right) \cup \left( {i \in I^{b} ,s \in S^{b} } \right)} \right),k \in K_{s} ,p \in P_{k} \\ \end{aligned}$$
(9b)
$$\begin{aligned} & Ts_{is} - Ts_{pk} \ge -\,M\left( {1 - W_{ipk} } \right) \\ & \quad \quad \quad \quad \quad \quad \forall \left( {\left( {i \in I^{sb} , s \in S^{sb} } \right) \cup \left( {i \in I^{b} ,s \in S^{b} } \right)} \right),k \in K_{s} ,p \in P_{k} \\ \end{aligned}$$
(10a)
$$\begin{aligned} & Ts_{is} - Ts_{pk} \le M\left( {1 - W_{ipk} } \right) \\ & \quad \quad \quad \quad \quad \forall \left( {\left( {i \in I^{sb} , s \in S^{sb} } \right) \cup \left( {i \in I^{b} ,s \in S^{b} } \right)} \right),k \in K_{s} ,p \in P_{k} \\ \end{aligned}$$
(10b)
$$Ts_{is} \ge Tf_{{i^{\prime}\left( {s - 1} \right)}} \quad \forall i \in I^{b} ,i^{\prime} \in SB_{i} ,s \in S^{a}$$
(11)
$$Ts_{{i^{\prime}s}} \ge Tf_{is} \quad \forall \left( {i,i^{\prime}} \right) \in I^{b} ,s \in S_{seq}^{a} :Seq_{i} < Seq_{{i^{\prime}}}$$
(12)
$$\begin{aligned} & W_{ipk} - W_{i',p + 1,k} = 0 \\ & & \quad \quad \forall \left( {i,i^{\prime}} \right) \in I^{b} ,k \in K_{s} ,s \in S_{seq}^{a} ,p \in P_{k} ,\left( {p + 1} \right) \in P_{k} : Seq_{i} < Seq_{{i^{\prime}}} \\ \end{aligned}$$
(13)
$$MK \ge Tf_{is} \quad \forall i \in I^{b} ,s \in \left| S \right|$$
(14)

Equation (2) assures that every block \(i \in I^{b}\) is processed at each stage \(s \in S^{b}\) on exactly one time-slot \(p\) of some unit \(k \in K_{s}\); in case of \(i \in I^{sb}\), the same condition must be accomplished but in this case for every stage \(s \in S^{sb}\). In turn, Eq. (3) defines that each time-slot \(p\) of unit \(k \in K_{s}\) can at most be assigned to one product \(i\) corresponding to stage \(s\). To avoid empty positions between the time slots postulated for a unit \(k\), the allocation of any product \(i\) to slot \(p + 1\) requires that at least other processing task \(i\) will be assigned to slot \(p\). This constraint is expressed through Eq. (4).

On the other hand, the timing decisions are determined by Eqs. (5)–(7). The completion time of product order \(i\) at stage \(s\), \(Tf_{is}\), and the finish time of slot \(p\) in unit \(k\), \(Tf_{pk}\), are computed by Eqs. (5) and (6), respectively, as the starting time plus the processing time \(pt_{is}\) associated to the product order \(i\) assigned to slot \(p\). The earliest time for starting the processing of product order \(i\) at stage \(s\), \(Ts_{is}\), is determined by Eq. (7). Equation (7a) is used when the non-intermediate storage policy is assumed by the scheduler; otherwise, when an UIS policy is adopted, Eq. (7b) becomes active. Since the time-slots defined for every unit \(k\) are sequentially arranged over time, the starting time of slot \(p + 1\) requires that the processing of slot \(p\) be finished, which is expressed through Eq. (8). Note that if the processing of product \(i\) at stage \(s\) is accomplished on slot \(p \in P_{k}\) with \(k \in K_{s}\), i.e. \(W_{ipk} = 1\), then it must be fulfilled that \(Tf_{is} = Tf_{pk}\) and \(Ts_{is} = Ts_{pk}\). These conditions are forced to be satisfied by Eqs. (9) and (10). For assembly stage \(s \in S^{a}\), Eq. (11) determines that a block \(i\) should not start to be constructed until their specific sub-blocks \(i^{\prime} \in SB_{i}\) have finished its processing in the above stage \(\left( {s - 1} \right)\).

For the last processing stage \(s \in S_{seq}^{a}\), in where the blocks are mounted following a predefined sequence, either Eq. (12) or Eq. (13) may be used to represent the ship assembly operation. Finally, Eq. (14) states a lower bound for the variable \(MK\) to be minimized.

4.3 The immediate precedence formulation

When the block assembly process is mathematically represented through the immediate precedence notion, three sets of binary variables are defined: \(YF_{ik}\) denoting that product \(i\) is the first being processed in unit \(k\), \(Y_{ik}\) determining that block (or sub-block) \(i\) is processed in \(k\) but not in the first place, and \(W_{{ii^{\prime}k}}\) denoting that task \(i\) is processed right before task \(i^{\prime}\) in unit \(k\). The constraints defining this continuous-time representation are follows.

$$\mathop \sum \limits_{{k \in K_{s} }} (Y_{ik} + YF_{ik} ) = 1\quad \forall \left( {\left( {i \in I^{sb} , s \in S^{sb} } \right) \cup \left( {i \in I^{b} ,s \in S^{b} } \right)} \right)$$
(15)
$$\mathop \sum \limits_{i \in I} YF_{ik} \le 1\quad \forall k \in K$$
(16)
$$W_{{ii^{\prime}k}} \le Y_{ik} + YF_{ik} \quad \forall \left( {i,i^{\prime}} \right) \in I,k \in K:i \ne i^{\prime}$$
(17)
$$W_{{ii^{\prime}k}} \le Y_{{i^{\prime}k}} \quad \forall \left( {i,i^{\prime}} \right) \in I,k \in K:i \ne i^{\prime}$$
(18)
$$YF_{ik} + \mathop \sum \limits_{{i^{\prime} \in I:i \ne i^{\prime}}} W_{{i^{\prime}ik}} \le 1 \quad \forall i \in I,k \in K$$
(19)
$$\mathop \sum \limits_{{i^{\prime} \in I:i \ne i^{\prime}}} W_{{i^{\prime}ik}} = Y_{ik} \quad \forall i \in I,k \in K$$
(20)
$$\mathop \sum \limits_{{i^{\prime} \in I:i \ne i^{\prime}}} W_{{ii^{\prime}k}} \le 1\quad \forall i \in I,k \in K$$
(21)
$$Tf_{is} \ge Ts_{is} + pt_{is} \quad \forall \left( {\left( {i \in I^{sb} , s \in S^{sb} } \right) \cup \left( {i \in I^{b} ,s \in S^{b} } \right)} \right)$$
(22)
$$Ts_{{i{\text{s}}}} = Tf_{{i\left( {{\text{s}} - 1} \right)}} \quad \forall \left( {\left( {i \in I^{sb} , s \in S^{sb} } \right) \cup \left( {i \in I^{b} ,s \in S^{b} } \right)} \right): s > 1$$
(23a)
$$Ts_{{i{\text{s}}}} \ge Tf_{{i\left( {{\text{s}} - 1} \right) }} \quad \forall \left( {\left( {i \in I^{sb} , s \in S^{sb} } \right) \cup \left( {i \in I^{b} ,s \in S^{b} } \right)} \right): s > 1$$
(23b)
$$\begin{aligned} & Ts_{{i^{\prime}s}} \ge Tf_{i,s} - M\left( {1 - W_{{ii^{\prime}k}} } \right) \\ & \quad \quad \quad \forall \left( {\left( {\left( {i, i^{\prime}} \right) \in I^{sb} , s \in S^{sb} } \right) \cup \left( {\left( {i, i^{\prime}} \right) \in I^{b} , s \in S^{b} } \right)} \right),\quad k \in K_{s} :i \ne i^{\prime} \\ \end{aligned}$$
(24)
$$Ts_{{i{\text{s}}}} \ge Tf_{{i^{\prime}\left( {{\text{s}} - 1} \right)}} \quad \forall i \in I^{b} ,i^{\prime} \in SB_{i} ,s \in S^{a}$$
(25)
$$Ts_{{i^{\prime}s}} \ge Tf_{is} \quad \forall \left( {i,i^{\prime}} \right) \in I^{b} ,s \in S_{seq}^{a} :Seq_{i} < Seq_{{i^{\prime}}}$$
(26)
$$W_{{ii^{\prime}k}} = 1\quad \forall \left( {i,i^{\prime}} \right) \in I^{b} , k \in K_{s} ,s \in S_{seq}^{a} : Seq_{i} = Seq_{{i^{\prime}}} - 1$$
(27)
$$MK \ge Tf_{is} \quad \forall i \in I^{b} ,s \in \left| S \right|$$
(28)

Equation (15) assures that every sub-block \(i \in I^{sb}\) goes through just one unit \(k \in K_{s}\) at each stage \(s \in S^{sb}\) and that every block \(i \in I^{b}\) is processed in just one unit \(k \in K_{s}\) at each stage \(s \in S^{b}\). In addition, Eq. (16) enforces the condition that at most one product \(i\) is the first processed in every unit \(k\). When a unit k is not used, \(YF_{ik} = 0 \; \forall i \in I\). For sequencing decisions, Eqs. (17) and (18) impose that the sequencing variable \(W_{{ii^{\prime}k}}\) can be active only if the pair \(\left( {i,i^{\prime}} \right)\) are processed in the same unit \(k\) (i.e., \(Y_{ik} + YF_{ik} = 1\) and \(Y_{{i^{\prime}k}} = 1\)). Moreover, Eq. (19) assures that a product \(i\) might be processed in unit \(k\) either in the first place or after another product \(i'\) while Eq. (20) states that every time a product \(i\) is not the earliest processed at the assigned unit \(k\), i.e. \(Y_{ik} = 1\), it must feature a direct predecessor \(i'\) in the processing sequence of \(k\). On the other hand, Eq. (21) states that at most a single product \(i'\) can be scheduled immediately after other product \(i\) unless \(i\) will be the last in the processing sequence of unit k.

For timing constraints, Eq. (22) computes the ending time \(Tf_{is}\) of product \(i\) at stage \(s\) as its starting time \(Ts_{is}\) plus its processing time \(pt_{is}\). The earliest time for starting the processing of product \(i\) at stage \(s\) is determined by Eqs. (23)–(25). Firstly, a product \(i\) cannot begin to be processed at stage \(s\) until its processing has finished in previous stage \(\left( {s - 1} \right)\). This condition is forced by Eq. (23a) or Eq. (23b), depending on the storage policy adopted by the scheduler. The sequencing constraint Eq. (24) determines that the starting time \(Ts_{{i^{\prime}s}}\) of a product \(i'\) at processing stage \(s\) must be greater than the ending time \(Tf_{is}\) of its immediate predecessor \(i\)\((W_{{ii^{\prime}k}} = 1 \; {\text{for any}} \; k \in K_{s} )\). Moreover, Eq. (25) determines that a block \(i \in I^{b}\) can start to be mounted at stage \(s \in S^{a}\) after their associated sub-blocks \(i^{\prime} \in SB_{i}\) have completed their processing in the previous stage. To force the assembling sequence on slipway, it may be used either the timing variables \(Tf_{is}\) or the sequencing variables \(W_{{ii^{\prime}k}}\), as is expressed through Eqs. (26) and (27), respectively. Finally, the makespan value is computed by Eq. (28).

4.4 The general precedence formulation

In contrast to the previous model, this formulation generalizes the precedence concept and reduces by more than half the number of sequencing variables used by the model. This reduction is obtained by defining the sequencing binary variable \(W_{{ii^{\prime}s}}\) just for all pair of products \(\left( {i, i'} \right)\) with \(i < i^{\prime}\), processed at stage \(s\). The variable \(W_{{ii^{\prime}s}}\) takes a meaning only when both products \(\left( {i, i^{\prime}} \right)\) are assigned to the same processing unit \(k \in K_{s}\), \(i.e. Y_{ik} = Y_{{i^{\prime}k}} = 1.\) In this case, \(W_{{ii^{\prime}s}}\) becomes equal to 1 whenever product \(i\) is processed before \(i'\) in the processing sequence of unit \(k\), otherwise it takes value 0, indicating that \(i'\) is processed before \(i\) in unit \(k\). If both product orders are not assigned to the same unit \(k \in K_{s}\), the value of \(W_{{ii^{\prime}s}}\) is negligible. On the other hand, \(Y_{ik}\) is the assignment binary variable valuing 1 if task \(i\) is processed at unit \(k\). The general precedence formulation for the problem under study includes the following sets of constraints.

$$\mathop \sum \limits_{{k \in K_{s} }} Y_{ik} = 1\quad \forall \left( {\left( {i \in I^{sb} , s \in S^{sb} } \right) \cup \left( {i \in I^{b} ,s \in S^{b} } \right)} \right) .$$
(29)
$$Tf_{is} \ge Ts_{is} + pt_{is} \quad \forall \left( {\left( {i \in I^{sb} , s \in S^{sb} } \right) \cup \left( {i \in I^{b} ,s \in S^{b} } \right)} \right)$$
(30)
$$Ts_{{i{\text{s}}}} = Tf_{{i\left( {{\text{s}} - 1} \right)}} \quad \forall \left( {\left( {i \in I^{sb} , s \in S^{sb} } \right) \cup \left( {i \in I^{b} ,s \in S^{b} } \right)} \right): s > 1$$
(31a)
$$Ts_{{i{\text{s}}}} \ge Tf_{{i\left( {{\text{s}} - 1} \right)}} \quad \forall \left( {\left( {i \in I^{sb} , s \in S^{sb} } \right) \cup \left( {i \in I^{b} ,s \in S^{b} } \right)} \right): s > 1$$
(31b)
$$\begin{aligned} & Ts_{{i^{\prime}s}} \ge Tf_{is} - M\left( {1 - W_{{ii^{\prime}s}} } \right) - M\left( {2 - Y_{ik} - Y_{{i^{\prime}k}} } \right) \\ & \quad \quad \quad \forall \left( {\left( {\left( {i, i^{\prime}} \right) \in I^{sb} , s \in S^{sb} } \right) \cup \left( {\left( {i, i^{\prime}} \right) \in I^{b} , s \in S^{b} } \right)} \right),k \in K_{s} : i < i^{\prime} \\ \end{aligned}$$
(32)
$$\begin{aligned} & Ts_{is} \ge Tf_{{i^{\prime}s}} - MW_{{ii^{\prime}s}} - M\left( {2 - Y_{ik} - Y_{{i^{\prime}k}} } \right) \\ & \quad \quad \forall \left( {\left( {\left( {i, i^{\prime}} \right) \in I^{sb} , s \in S^{sb} } \right) \cup \left( {\left( {i, i^{\prime}} \right) \in I^{b} , s \in S^{b} } \right)} \right),k \in K_{s} : i < i^{\prime} \\ \end{aligned}$$
(33)
$$Ts_{{i{\text{s}}}} \ge Tf_{{i^{\prime}\left( {{\text{s}} - 1} \right)}} \quad \forall i \in I^{b} ,i^{\prime} \in SB_{i} ,s \in S^{a}$$
(34)
$$Ts_{{i^{\prime}s}} \ge Tf_{is} \quad \forall \left( {i,i^{\prime}} \right) \in I^{b} ,s \in S_{seq}^{a} :Seq_{i} < Seq_{{i^{\prime}}}$$
(35)
$$MK \ge Tf_{is} \quad \forall i \in I^{b} ,s \in \left| S \right|$$
(36)

Equation (29) defines the allocation constraint. The timing constraints are determined by Eqs. (30) and (31), which are similar to Eqs. (22) and (23) previously explained for the immediate precedence notion. The sequencing constraints on a same processing unit \(k\) are expressed through Eqs. (32) and (33). The sub-blocks assembly operation at stage \(s \in S^{a}\) is represented by Eq. (34). On the other hand, the assembly sequence on slipway is determined by Eq. (35). This sequencing constraint forces the starting time of block \(i^{\prime}\) to be greater than the completion time of any block \(i\) that is before at erection sequence \((Seq_{i} < Seq_{{i^{\prime}}} )\). Refer to Méndez et al. (2006) and Cóccola et al. (2014) for more details about the general precedence concept.

5 The MILP-based decomposition algorithm

Although the mathematical formulations presented in above section are capable to represent and solve the block assembly process, the practice shows that realistic industrial applications are either intractable or result in poor solutions when rigorous optimization approaches are used. The computational efficiency of the rigorous MILP methods is quickly deteriorated when increasing the problem size because of the thousands of binary variables involved. To overcome this limitation, we propose a solution strategy based on a decomposition algorithm that allows finding good quality solutions with very low CPU time even for large-size problems.

The decomposition method is based on the strategy of first obtaining an initial solution (constructive stage), and then gradually enhancing it by applying several rescheduling iterations (improvement stage). Both algorithmic stages have as core the general precedence MILP model defined by Eqs. (29)–(36). Thus, the procedure exploits the benefits of combining the robustness of the MILP models with the flexibility of the heuristic rules. At this point, it is worth mentioning that any alternative mathematical formulation may be easily adapted to the proposed decomposition strategy, but in general, the general precedence representation shown the best computational performance.

The general structure of the algorithm is given in Fig. 4. Note that a feasible initial scheduling solution is obtained from inserting the blocks one by one in the scheduled and fixing the decision variables at their optimum values. A block \(i \in I^{b}\) and its sub-assemblies \(i^{\prime} \in SB_{i}\) are scheduled at each iteration of the constructive stage. Once determining a starting solution, this one is iteratively improved by executing several rescheduling actions in order to find a high-quality scheduling solution with minimal computational effort. At each improvement iteration, the assignment and sequencing decisions are left free just for the block \(i \in I^{b}\) (and its sub-assemblies) that is being rescheduled. Such decomposition strategy significantly reduces the MIP solver search space at each model execution, accelerating its resolution. When no improvements are obtained for the objective function after rescheduling all blocks, the current schedule is reported as the best solution by the procedure.

Fig. 4
figure 4

Overview of the iterative MILP-based algorithm

Full size image

5.1 Constructive step

The first phase of the decomposition algorithm aims at rapidly generating an initial full schedule for the problem under study. Here, the production problem is solved iteratively through the schedule of a subset of products at each solver execution. The constructive method is based on the insertion technique presented by Kopanos et al. (2010) for solving large-scale pharmaceutical scheduling problems: the orders are inserted (scheduled) one-by-one in an iterative mode by solving the original MILP model. The sequence in which the products are inserted may vary according to the characteristics of the problem (Roslöf et al. 2001, 2002). The insertion criterion should be always defined taking into account the features of productive system. Here, it is proposed to insert the products according to the assembly sequence on slipway, known through parameter \(Seq_{i}\). This guarantees to find a fairly good starting solution.

For programming the constructive step, the user should be also defined the number of products to be scheduling simultaneously in order to maintain a reduced search space at each solver execution. In our proposal, just one block \(i \in I^{b}\) and its sub-assemblies \(i^{\prime} \in SB_{i}\) are assigned and sequenced at each iteration, using Eqs. (29)–(36). The constructive stage ends when all blocks have been scheduled.

The pseudo-code for the constructive step is given in Fig. 5. The scalar \(iter\) identifies the number of block \(i \in I^{b}\) to be inserted in the current iteration while the boolean parameter \(active_{i}\) is true when the product \(i\) (block or sub-blocks) is selected for scheduling. Once a new block and its sub-blocks are scheduled, the MILP model (29)–(36) is solved. After solver execution, the assignment variables \(Y_{ik}\) for these new insertions are fixed at their optimal values. Note that variables \(Y_{ik}\) for the blocks (and sub-blocks) that have already been scheduled in previous iterations are also fixed and only the timing decisions can be modified for these products. In other words, the values of variable \(Y_{ik}\) for already scheduled products cannot be modified in the following iterations.

Fig. 5
figure 5

Pseudo-code for the constructive step

Full size image

It is worth to remarks that the sequencing decisions are ignored in the constructive stage and it is assumed that the production sequence at each processing stage must follow the assembly order required on slipway. This assumption is made for favoring the problem resolution. Thus, Eqs. (32) and (33) of general precedence formulation are replaced by Eq. (37).

$$\begin{aligned} & Ts_{is} \ge Tf_{{i^{\prime}s}} - M\left( {2 - Y_{ik} - Y_{{i^{\prime}k}} } \right) \\ & \quad \quad \quad \quad \quad \forall \left( {\left( {\left( {i,i^{\prime}} \right) \in I^{sb} } \right) \vee \left( {\left( {i,i^{\prime}} \right) \in I^{b} } \right)} \right),\; s \in S_{i} ,\;k \in K_{s} :Seq_{i} < Seq_{{i^{\prime}}} \\ \end{aligned}$$
(37)

The constructive step solution ends to be computed when all products (blocks and sub-blocks) have been scheduled. The best value obtaining for the makespan is saved in parameter \(CurrentSol\), while the values of binary variables \(Y_{ik}\) and \(W_{{ii^{\prime}s}}\) are copied in parameters \(sY_{ik}\) and \(sW_{{ii^{\prime}s}}\), respectively. These data become the starting point of the improvement stage.

5.2 Improvement step

Starting from the solution given by the first phase, the improvement step aims at improving iteratively the current solution though several rescheduling decisions. The procedure iterates over each element of the set \(I^{b}\) in order to perform reassignment or reordering actions on every block \(i \in I^{b}\) and its sub-blocks \(i^{\prime} \in SB_{i}\), using the MILP model (29)–(36), until no improvement can be achieved to the objective function (makespan MK). Note that a simultaneous rescheduling of all blocks results impractical because it would be equivalent to solve the full space approach. Hence, a key point for the scheduler is to determine the number of blocks to be simultaneous rescheduled at each iteration. In this case, the lowest number is adopted, i.e. one at a time, in order to reduce at minimum the resolution times of the MILP model. Thus, the number of iterations in each improvement loop is equal to the number of blocks: \(\left| {I^{b} } \right|\).

The pseudo-code for the improvement step is given in Fig. 6. Firstly, the parameter \(bestSol\) is initialized with a big value that should be greater than the makespan found in the constructive step. Then, the procedure starts to iterate over the set \(I^{b}\) following the sequence parameter \(Seq_{i }\); the parameter \(iter\) indicates the next block that will be rescheduled. When a block \(i \in I^{b}\) is chosen, the boolean parameter \(active_{i}\) is set to true for the block \(i\) and its sub-assemblies \(i^{\prime} \in SB_{i}\). The MILP model (29)–(36) can take reassignment and resequencing decisions just on products \(i \in I\) with \(active_{i} = true\). For the remaining products, those with \(active_{i} = false\), only timing variables (Tsis and Tfis) can be modified. Reassignment to other units is not allowed for blocks (and sub-blocks) with parameter \(active_{i}\) set to false. Furthermore, their relative position in the processing sequence remains unchanged. The binary variables \(Y_{ik}\) and \(W_{{ii^{\prime}s}}\) are fixed for the products with \(active_{i} = false\). This resolution strategy reduces drastically the number of binary variables with regards to the full space approach, which is equivalent to solve the MILP model (29)–(36) with \(active_{i} = true\; \forall i \in I\). Every time a rescheduling iteration terminates, the current solution is updated.

Fig. 6
figure 6

Pseudo-code for the improvement step

Full size image

Once the rescheduling step is applied for all blocks, the procedure checks the improvement reached for the objective function. If the current makespan \((CurrentSol)\) is better than the best solution found until now \((BestSol)\), the algorithm updates the makespan \((BestSol = CurrentSol)\) and goes to start the rescheduling iterations again. Otherwise, the solution procedure ends and reports the best solution found for the problem under study.

6 Computational results and discussion

In this section, several problem instances are introduced in order to evaluate and compare the computational performance of the rigorous MILP models and the decomposition procedure. These testing examples arise in the shipbuilding industry for the development of marine resources, specifically for the offshore oil and gas industry. The aim is to validate the performance of the proposed decomposition algorithm and compare its computational efficiency with regards to the exact optimization approaches when the same examples are solved.

The experimentation section is organized as follows. Firstly, ten problem instances with different features are presented. Afterwards, the inherently complexity of problems addressed and model statistics for the exact optimization approaches are shown. Finally, the MILP-based strategy is tested on all examples and a comparison between the alternative solution approaches is shown. All solution strategies are implemented in GAMS 24.9.2 with CPLEX 12.7.1.0 as MIP solver and run on a PC with four-core Intel Xeon X5650 Processor (2.6 GHz). The termination criterion imposed for each MIP solver execution was either 0% integrality gap or 3600 s of CPU time.

6.1 Real-world case study

The real-world case of study arises in a shipyard with 41 workshops and one dry dock, which are used for the construction of the vessels. The manufacturing process involves 7 processing stages \((s \in S)\), each of them with \(K_{s}\) processing units working in parallel, as shown in Fig. 7. Note that the last processing stage \(s_{7}\) has just one unit, representing the dry dock where the ship is mounted. An interesting feature of this manufacturing process is that there are two assembly stages: in the first one, stage \(s_{3}\), each block is form by welding one or more sub-blocks while in the second one, stage \(s_{7}\), the mounting of these blocks is carried out to build the ship. As depicted Fig. 7, every block can be formed by a different quantity of sub-assemblies, for instance, the block \(i_{n + 1}\) is formed by two sub-blocks (i1 and i2), the block \(i_{n + 2}\) is made from just one sub-bock (i3), while the block \(i_{n + 3}\) has three sub-assemblies (i4, i5, and i6). Other problem characteristic is that the processing times at each stage depend on the type of product that is processed. It is worth to remark that due to confidentiality issues, we cannot disclose the data of this real-world case study.

Fig. 7
figure 7

The Shipbuilding process with assembly and processing stages

Full size image

The Gantt chart of the optimal schedule for a toy example involving the processing of 8 sub-blocks and 4 blocks is given in Fig. 8. In this picture, each block \(i \in I^{b}\) and its sub-assemblies \(i' \in SB_{i}\) are depicted with the same color. In the right of Fig. 8, it is shown as the timing constraints (34) and (35) of the general precedence formulation are used for enforcing the assembly operations. Note that, for instance, the earliest starting time of block \(i_{n + 3}\) at stage \(s_{3}\) should be greater than the finishing times of its sub-assemblies \(i_{4}\), \(i_{5}\), and \(i_{6}\) at stage \(s_{2}\).

Fig. 8
figure 8

Gantt chart of a block assembly problem involving 8 sub-blocks and 4 blocks

Full size image

6.2 Problem instances

The applicability and effectiveness of the proposed solution strategy are illustrated by efficient solving a set of realistic instances derived from the original case study presented above. Since both the quality of the solution and the computational time to find it depend on the number of products (blocks and sub-blocks) involved in the scheduling problem, 10 examples are defined by varying both the amount of products to be processed and the storage policy adopted by the scheduler (NIS or UIS). All problem instances are summarized in Table 1. The expression \(N \times M\) refers to a ship constructed with \(N\) blocks and \(M\) sub-blocks. The simplest problem addressed involves 10 sub-blocks and 5 blocks, while the biggest one deals with a ship that is built from 50 sub-blocks and 25 blocks. For all examples, it is assumed that each block has two sub-assemblies. This means that twice as many products go through the processing stages \(s \in S^{sb}\) regarding to stages \(s \in S^{b}\). The amount of products \((N \times M)\) to be assigned and sequenced in the available processing units is closely related to the model complexity, which directly impacts on the resolution times. The optimization goal is the minimization of makespan for all problem instances.

Table 1 Problem instances
Full size table

6.3 Testing the exact optimization approaches

In order to underline the complexity of the problem addressed, all examples are first solved by using the three rigorous MILP model proposed in this paper. The best solution found within the predefined time limit of 1 CPU hour (3600 CPUs), the integrality gap and the CPU time requirement of each alternative are given in Table 2. In addition, Table 3 reports the problem sizes in terms of binary and continuous variables, and linear constraints. Note that the number of binary variables is strongly incremented by increasing the number of products to be processed. The information provided by Tables 2 and 3 allows making a comparative analysis between the alternative models, highlighting the resolution complexity of the instances considered when they are solved with full-space approaches.

Table 2 Computational statistics for the three alternative exact optimization approaches
Full size table
Table 3 Model sizes for the exact optimization approaches
Full size table

From Table 2, it follows that the optimal solution is reported by the MILP models just for the least size instances (P.01 and P.02). In the remaining examples, the MIP solver terminates without reaching the optimal solution because the time limit is exceeded. For these cases, feasible but poorly solutions are reported. Note that the bigger size of the model, the higher the integrality gap. Also, the worse results are obtained for examples considering NIS policy when comparing them with those ones reported for the UIS policy.

The worst computational performance is exhibited by the unit-specific direct precedence formulation. For examples P.06, P.08, and P.10, this approach is not even capable of reporting a feasible solution within the time limit. In contrast, the other two mathematical formulations are at least capable of returning a suboptimal solution with certain integrality gap within the predefined CPU time. For remaining examples, the immediate precedence formulation shows bigger integrality gaps than the other two models. This situation is directly related to the high number of binary variables used by the formulation.

On the other hand, Table 2 also shows that the general precedence formulation exhibits a slightly better computational performance than the time-slots based model, up to 3%, in all examples considered. Particularly, a solution of 319.1 days with an integrality gap of 47.4% is reported by the general precedence approach for the most complex example P.10 (25 blocks, 50 sub-blocks and NIS policy), featuring a model size of 61,376 equations, 31,700 binary variables, and 502 continuous variables (see Table 3), while the time-slots based model (140,277 equations, 17,375 binary variables, and 18,866 continuous variables) reaches a solution of 321.4 days with an integrality gap of 47.7% after 3600 s of CPU time.

Despite the high integrality gap reported by the general precedence model for problem instance P.10, it is worth to remark that the solution found (319.1 days) improves considerably the time currently employed by the shipyard for delivering a ship of size 25 × 50. A few years ago, the production schedule used by the company featured a makespan of about a year and a half. Afterwards, this total time was reduced to nearly 1 year by using the simulation models that were developed by Basán et al. (2017) and Cebral-Fernandez et al. (2016).

Taking into account that the shipbuilding is a long-term production process, involving several months, it is not strictly necessary to have a solution strategy that provides a good solution in less than 1 h of CPU time. When solving the realistic example P.10 without setting a time limit, the solution found by the time-slots formulation is 288.6 days with an integrality gap of 37.5%, while the general precedence model reaches a makespan of 284.7 days with an integrally gap of 36.6%. In both cases, the MIP solver ended after several hours of CPU time because of “out of memory” error. This solution represents a significant saving for the company because the total time required for delivering a vessel is reduced up to approximately 20%, from 1 year to 285 days. The best solution found by the general precedence model for example P.10 is shown in Fig. 9. In this picture, each block \(i \in I^{b}\) and its sub-assemblies \(i' \in SB_{i}\) are depicted with the same color and labeled according to the value of parameter \(Seq_{i}\). This helps to the reader to easily visualize the block assembly operation at stage \(s_{3}\). Moreover, the processing stages are separated through dashed lines. The Gant chart shows as the blocks are orderly processed in stage \(s_{7}\), following the assembly sequence given by parameter \(Seq_{i}\).

Fig. 9
figure 9

Gantt chart of the best solution found by the general precedence approach for example P.10 (problem structure 25 × 50 under NIS policy)

Full size image

Despite the good solutions found by the exact optimization approaches (excepting the immediate precedence formulation) with regards to other solution strategies, the computational results given in Tables 2 and 3 demonstrate that the main drawback of continuous time models is their high computation time. However, the robustness offered by these MILP models can be exploited resolving them in a decomposable way in order to find better solutions in considerably less computational time.

6.4 Testing the iterative MILP-based algorithm

For developing a comparative analysis, the ten examples proposed in Table 1 have been also solved through the MILP-based decomposition strategy. The computational results reported by the algorithm are detailed in Table 4. For every example solved, this table shows the best solution found at each algorithmic stage (MK) together with the accumulated CPU time. The number of improvement iterations and the percent of enhancement obtained from the starting solution are also given in Table 4.

Table 4 Improvement-based algorithm solutions found
Full size table

As can be seen in Table 4, the heuristic of scheduling the products one by one following the assembly sequence \(Seq_{i}\) presents a good performance and is capable of generating a good initial solution in less of 5 s of CPU time for all examples solved. Moreover, these starting solutions are always improved by the algorithm in the second stage, consuming in total less than 60 s of computational time. The constructive stage solution is always enhanced at the improvement stage, obtaining an improvement percentage of around 12%, in average. For industrial-size example P.10 dealing with 25 blocks, 50 sub-blocks, and a NIS policy, the constructive step converges to a solution of 298.3 days, which is illustrated in Fig. 10. In this starting solution, the products assigned to the same processing unit are sequenced according to the value of parameter \(Seq_{i}\) in all processing stages, not only at stage \(s_{7}\) (dry dock). When this condition is relaxed in the improvement stage and reassignment and reordering actions are iteratively applied on the schedule given in Fig. 10, the final solution depicted in Fig. 11 is reported by the procedure. The makespan is enhanced 9.3% from 298.3 to 270.5 days.

Fig. 10
figure 10

Gantt chart of the initial schedule reported by the MILP-based strategy for P.10 (problem structure 25 × 50 under NIS policy)

Full size image
Fig. 11
figure 11

Gantt chart of the best schedule reported by the MILP-based strategy for P.10 (problem structure 25 × 50 under NIS policy)

Full size image

On the other hand, a comparative table between the best results obtained through the exact optimization strategy and the decomposition algorithm for all examples considered is given in Table 5. Specifically, the results reported by the global general precedence based model are used in this table because this formulation shows the best computational performance regarding to the other two exact alternatives (see Table 2).

Table 5 Comparison between the exact MILP formulation and the decomposition method
Full size table

As can be seen in Table 5, the decomposition strategy converges to the optimal solution in examples P.01 and P.02, validating the solution approach. For the other cases, the proposed algorithm reports, in few seconds of CPU time, better solutions than those found by the MILP model after 3600 s of computational time. For realistic example P.10, the global general precedence approach reports a solution featuring a makespan of 319.1 days with an integrality gap of 37.9% after 1 h of CPU time, while the decomposition algorithm reports a makespan of 270.5 days in just 56.6 CPU seconds. Moreover, this solution outperforms that one obtained after several hours of CPU time when the MILP model is executed without setting a time limit (see Fig. 9). The schedule given in Fig. 11 represents the best solution found for `problem instance P.10; a reduction of approximately 26% is achieved in the total makespan with respect to the currently schedule used by the company.

Finally, it is worth to remark that, although the iterative approach does not assure the optimality of the solutions reported, it is capable of reaching solutions that are up to 15.2% better than those found by the exact approach with significant less computation effort. It is important to emphasize that, this improvement in the schedule allows reducing 1 month of work in the productive system and hence, a significant savings are obtained by the company, avoiding penalties for delay in the delivery of the vessels. The significant difference in the computational burden presented by both approaches is due to the iterative strategy allows decomposing the full problem into smaller sub-problems, which are solved iteratively.

7 Conclusions

This paper has presented a systematic MILP-based iterative algorithm for solving a complex scheduling problem of the shipbuilding industry. Moreover, this proposal is arisen after than three alternative rigorous MILP formulations, which are based on the notion of time-slot, global general precedence, and unit-specific direct precedence were developed for representing and solving the problem under study.

From the experimentation developed, it was demonstrated that the rigorous formulations converged to the optimal solution only when small problem instances are considered. The computational efficiency of these full-space approaches is rapidly deteriorated as the problem size increased. In order to overcome this limitation, an efficient hybrid solution strategy, which has a MILP scheduling formulation as its core, is proposed for the solution of this type of challenging real-world problem. It combines the robustness of the traditional MILP approach based on general precedence formulation with the advantages of heuristic procedures. The solution strategy is based on a systematic decomposition methodology to first obtain an initial solution (constructive stage), and then gradually enhancing it by applying several rescheduling iterations (improvement stage).

The performance of the proposed methodology has been deeply evaluated by solving several instances arising in a shipbuilding industry, comparing the results obtained with those ones found by the exact MILP models. Computational results showed that feasible and good-quality solutions can be efficiently found in short computational time by the decomposition algorithm, outperforming the pure exact optimization approaches and other solution techniques published in the literature.

It would be of great interest for us to compare the results of our proposal with other search techniques, such as genetic-algorithm-based techniques, among others. Although the data of the real-world case of study has not been provided in this paper by confidentiality issues, the problem structure is clearly explained throughout the manuscript, enabling to other authors to prove other solution techniques using data that can be generated randomly. Moreover, as the MILP formulations used in this paper can be adapted to any type of multi-stage scheduling problem, we also invite our colleagues to apply the decomposition strategy for solving other practical situations.