1 Introduction

In this paper, we explore the interpolation problem of a function f(x) within a finite interval [a, b], given its values at the nodes

$$\begin{aligned} a = x_0< x_1< \cdots< x_{n-1} < x_n=b, \qquad n\in {\mathbb N}. \end{aligned}$$
(1)

We consider arbitrary distributions of such nodes basing our estimates on the maximum and minimum distance between two consecutive nodes, namely

$$\begin{aligned} h = \max _{0\le i< n} (x_{i+1}-x_i), \qquad h^* = \min _{0\le i< n} (x_{i+1}-x_i). \end{aligned}$$
(2)

As a particular case, we consider the case of equidistant or quasi-equidistant configurations of nodes for which one has \(h=h^*\) (equidistant nodes) or \(h/h^*\le {\mathcal {C}}\) holds for all \(n\in {\mathbb N}\) with \({\mathcal {C}}>1\) an absolute constant (quasi–equidistant nodes).

In their work [9], Huybrechs and Trefethen compare various methods for approximating a function with equidistant nodes. One such method employs Floater-Hormann (FH) interpolating rational functions denoted by r(x) [6]. Such interpolants (briefly FH interpolants) generalize Berrut’s rational interpolation [1] by introducing a fixed integer parameter \(0\le d\le n\) to speed up the convergence getting, in theory, arbitrarily high approximation orders.

When \(d=0\), the FH interpolant reduces to the Berrut’s first interpolant from [1] (see also [7]). For any \(1 \le d \le n\), similarly to Berrut’s approximant, Floater and Hormann established that the approximant r(x) lacks poles on the real line, coincides with f on the set of nodes \(X_n=\{x_0,x_1,\ldots ,x_n\}\), and, for any \(x\not \in X_n\), provides a barycentric representation for efficient and stable computations [5].

Moreover, as \(h\rightarrow 0\) (and hence \(n\rightarrow \infty \)), the FH approximation error behaves, for any fixed \(d\in {\mathbb N}\), as [6, Thm. 2]:

$$\begin{aligned} \Vert r-f \Vert _\infty = \mathcal {O}(h^{d+1}), \qquad \forall f \in \mathcal {C}^{d+2}[a,b], \end{aligned}$$
(3)

For an overview of linear barycentric rational interpolation, interested readers can refer to the paper by Berrut and Klein [2].

While applicable to any node configuration, the Floater-Hormann method proves particularly effective for equidistant setups due to the logarithmic growth of the Lebesgue constants [4, 8]. In this case, (3) continues to hold but the convergence is not guaranteed for less regular functions, e.g. for functions that are only continuous on [a, b].

To overcome this problem, in [12], we extended the Floater-Hormann method by defining a new family of linear rational approximants denoted by \(\tilde{r}(x)\). These approximants depend on d and an additional parameter \(\gamma \in {\mathbb N}\). When \(\gamma = 1\), \(\tilde{r}(x)\) reduces to the original FH interpolant r(x).

Similarly to the original FH interpolants, we showed that, for all \(\gamma >1\), \(\tilde{r}(x)\) has no real poles, interpolates the data, preserves polynomials of degree \(\le d\), and has a barycentric-type representation. Moreover, in the case of equidistant or quasi-equidistant nodes, we proved the uniform boundedness of the Lebesgue constants and

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert \tilde{r} -f\Vert _\infty =0, \qquad \forall f\in \mathcal {C}[a,b]. \end{aligned}$$

Concerning the approximation rate, in [12] we established several error estimates depending on the smoothness class of f. In particular, for arbitrarily fixed \(d\in {\mathbb N}\) and equidistant or quasi-equidistant nodes, as \(n\rightarrow \infty \), we proved that

$$\begin{aligned} \Vert \tilde{r}-f \Vert _\infty = \mathcal {O}(h^{s}), \qquad \forall f \in \mathcal {C}^{s}[a,b],\qquad 1\le s\le d+1, \end{aligned}$$

holds provided that \(\gamma >s+1\), and

$$\begin{aligned} \Vert \tilde{r}-f \Vert _\infty = \mathcal {O}(h), \qquad \forall f \in \text {Lip}[a,b], \end{aligned}$$

holds provided that \(\gamma >2\).

In this paper, for the previous classes of functions, we aim to derive error estimates valid for arbitrary configurations of nodes (Theorems 3.1 and 3.4). Moreover, in the special case of equidistant or quasi-equidistant nodes, we aim to state the previous results but without any restriction on \(\gamma \) besides \(\gamma >1\) (Corollaries 3.3 and 3.5).

The outline of the paper is the following. In Section 2 we briefly recall the definition and the properties proved in [12] for generalized FH interpolants at arbitrary distribution of nodes. In Section 3 we state the new estimates. In Section 4 we show several numerical tests. Finally, in Section 5 we give conclusions.

2 Generalized Floater–Hormann interpolation

For any pair of integer parameters \(0\le d\le n\) and \(\gamma \ge 1\), the generalized FH approximation of f at the nodes (1) is given by [12]

$$\begin{aligned} \tilde{r}(f,x) = \frac{\sum _{i=0}^{n-d} \tilde{\lambda }_{i}(x) p_{i}(x)}{\sum _{i=0}^{n-d} \tilde{\lambda }_{i}(x)}, \qquad x\in [a,b], \end{aligned}$$
(4)

where

$$\begin{aligned} \tilde{\lambda }_{i}(x) = \frac{(-1)^{i \gamma }}{(x-x_i)^{\gamma }(x-x_{i+1})^{\gamma }\ldots (x-x_{i+d})^{\gamma }},\qquad i=0,\ldots , n-d, \end{aligned}$$
(5)

and \(p_i(x)\) is the unique polynomial of degree at most d interpolating f at the \((d+1)\) nodes \(x_i<x_{i+1}<\ldots <x_{i+d}\).

In the case \(\gamma =1\), \(\tilde{r}(f,x)\) coincides with the original FH interpolants introduced in [6]. In the sequel, we will also use the notation \(\tilde{r}(f)\) to represent the function \(\tilde{r}(f,x)\) as defined in (4).

For completeness, we recall below the properties already proved for the generalized FH approximants [6, 12]. Unless otherwise specified, they are valid for any distribution of nodes and for any value of the parameters \(0\le d\le n\) and \(\gamma \ge 1\).

  1. 1.

    Poles: The generalized FH rational function \(\tilde{r}(f)\) has no real poles in the interval [a, b].

  2. 2.

    Interpolation: We have \(\tilde{r}(f,x_k)=f(x_k)\), \(k=0,\ldots ,n\).

  3. 3.

    Preservation of polynomials: If f is a polynomial of degree at most d then we have \(\tilde{r}(f)=f\).

  4. 4.

    Barycentric–type form: For all \(x\notin \{x_0,\ldots , x_n\}\) we have

    $$\begin{aligned} \tilde{r}(f,x) = \frac{\sum _{k=0}^n \frac{w_k(x)}{(x-x_k)^\gamma } \ f(x_k)}{\sum _{k=0}^n \frac{ w_k(x)}{(x-x_k)^\gamma }}, \end{aligned}$$
    (6)

    where

    $$\begin{aligned} w_k(x) = \sum _{i \in J_k} (-1)^{i\gamma } \prod _{s=i,s\ne k}^{i+d} \frac{1}{(x_k-x_s)(x-x_s)^{\gamma -1}},\qquad k=0,\ldots ,n, \end{aligned}$$
    (7)

    with \(J_k=\left\{ i\in \{0,\ldots , n-d\} \, \ k-d\le i\le k\right\} \).

  5. 5.

    Lebesgue constants: They are defined as \(\Lambda _n=\sup _{f\ne 0}\frac{\Vert \tilde{r}(f)\Vert _\infty }{\Vert f\Vert _\infty }\), \(\forall n\in {\mathbb N}\). For all parameters \(\gamma > 1\) and \(1\le d\le n\), we have [12]

    $$\begin{aligned} \Lambda _n\le {\mathcal {C}}\ d 2^d \left( \frac{h}{h^*}\right) ^{\gamma +d} \end{aligned}$$
    (8)

    where \({\mathcal {C}}>0\) is a constant independent of n, h, d and \(\gamma \). For \(\gamma =1\), \(0\le d\le n\), and equidistant or quasi–equidistant distribution of nodes, we have [3, 4, 8]

    $$\begin{aligned} \Lambda _n\le {\mathcal {C}}\ 2^d \log n, \end{aligned}$$
    (9)

    where \({\mathcal {C}}>0\) is a constant independent of n, d.

3 Main results

In the space \(C^s[a,b]\) of all functions that are s–times continuously differentiable in [a, b], we state the following result.

Theorem 3.1

Let \(d,\gamma \in {\mathbb N}\) be arbitrarily fixed with \(\gamma >1\). For all \(f\in C^{s}[a,b]\) with \(1\le s\le d+1\), and any configuration of nodes \(a=x_{0}< x_{1}<\) ... \(< x_n=b\), with \(n\ge d\), the associated generalized FH interpolant \(\tilde{r}(f)\) satisfies

$$\begin{aligned} \Vert f-\tilde{r}(f)\Vert _\infty \le \mathcal {C}\left( \frac{h}{h^*}\right) ^{\gamma (d+1)}( h^*)^{s} \end{aligned}$$
(10)

where \(\mathcal {C}>0\) is a constant independent of \(n,h,h^*\).

Proof

Let \(x\in [a,b]\) be arbitrarily fixed. We shall prove that \(|f(x)-\tilde{r}(f,x)|\) is not greater than the right–hand side of (10) with \({\mathcal {C}}>0\) independent of \(n,h,h^*\), and x too. Recalling the interpolation property, we may suppose \(x\notin \{x_0,\ldots , x_n\}\), otherwise it is trivial.

By the definition of \(\tilde{r}(f,x)\) (cf. (4)) we get

$$\begin{aligned} f(x)-\tilde{r}(f,x)=\frac{\sum _{i=0}^{n-d}\tilde{\lambda }_i(x)\left[ f(x)-p_i(x)\right] }{\sum _{i=0}^{n-d}\tilde{\lambda }_i(x)} =\sum _{i=0}^{n-d}\frac{\tilde{\lambda }_i(x)}{D(x)}\left[ f(x)-p_i(x)\right] \end{aligned}$$
(11)

where, for brevity, we set

$$\begin{aligned} D(x)=\sum _{i=0}^{n-d}\tilde{\lambda }_i(x). \end{aligned}$$

Recalling that the interpolation error for \(p_i\) can be expressed by the Newton formula

$$\begin{aligned} f(x)-p_i(x)=f[x_i,\ldots ,x_{i+d},x]\prod _{s=i}^{i+d}(x-x_s), \end{aligned}$$

by (11) we obtain

$$\begin{aligned} \left| f(x)-\tilde{r}(f,x)\right| \le \sum _{i=0}^{n-d}\left| \frac{\tilde{\lambda }_i(x)}{D(x)}\right| \prod _{s=i}^{i+d}|x-x_s| \left| f[x_i,\ldots ,x_{i+d},x]\right| . \end{aligned}$$
(12)

Concerning the last factor, in the case \(f\in C^{s}[a,b]\) with \(s=d+1\), we recall that the divided differences of order \(d+1\) satisfy

$$\begin{aligned} \left| f[x_i,\ldots ,x_{i+d},x]\right| =\frac{\left| f^{(d+1)}(\xi _i)\right| }{(d+1)!} \le \frac{\Vert f^{(d+1)}\Vert _\infty }{(d+1)!}, \qquad \forall f\in C^{d+1}[a,b], \end{aligned}$$

where \(\xi _i\in [\min \{x,x_i\}, \max \{x,x_{i+d}\}]\). In the case \(s=d\) and \(f\in C^d[a,b]\), we note that

$$\begin{aligned} \left| f[x_i,\ldots ,x_{i+d},x]\right| =\left| \frac{f[x_{i+1},\ldots ,x_{i+d}, x ]-f[x_i,\ldots ,x_{i+d-1},x]}{x_{i+d}-x_i}\right| \le \frac{2\Vert f^{(d)}\Vert _\infty }{d!|x_{i+d}-x_i|}, \end{aligned}$$

and using

$$\begin{aligned} |x_i-x_j|\ge |i-j|\ h^* ,\qquad \forall i,j\in \{0,\ldots , n\}, \end{aligned}$$
(13)

we get

$$\begin{aligned} \left| f[x_i,\ldots ,x_{i+d},x]\right| \le \frac{2\Vert f^{(d)}\Vert _\infty }{d!(d h^*)},\qquad \forall f\in C^d[a,b]. \end{aligned}$$

More generally, in the case \(f\in C^s[a,b]\) with \(s=d+1-k\), reasoning by induction on \(k=0,\ldots , d\), it can be proved that

$$\begin{aligned} \left| f[x_i,\ldots ,x_{i+d},x]\right| \le \frac{c}{(h^*)^k}\Vert f^{(d+1-k)}\Vert _\infty ,\qquad \forall f\in C^{d+1-k}[a,b],\quad k=0,1,..,d, \end{aligned}$$
(14)

where \(c>0\) is a constant depending on d but not on x, f and \(i\in \{0,\ldots , n-d\}\).

Summing up, setting

$$\begin{aligned} S(x):=\sum _{i=0}^{n-d}\sigma _i(x),\qquad \sigma _i(x):=\left| \frac{\tilde{\lambda }_i(x)}{D(x)}\right| \prod _{s=i}^{i+d}|x-x_s|, \end{aligned}$$

by (12) and (14) we have

$$\begin{aligned} \left| f(x)-\tilde{r}(f,x)\right| \le c\frac{\Vert f^{(s)}\Vert _\infty }{(h^*)^{d+1-s}}\ S(x), \qquad \forall f\in C^s[a,b],\quad 1\le s\le d+1. \end{aligned}$$
(15)

In the following we estimate the summation S(x). To this aim, we recall that [12, Eq. (24)]

$$\begin{aligned} |D(x)|\ge |\tilde{\lambda }_{j}(x)|=\prod _{s=j}^{j+d}\frac{1}{|x-x_s|^{\gamma }}, \qquad \forall j\in I_\ell , \end{aligned}$$
(16)

where

$$\begin{aligned} I_\ell := \{i\in \{0,\ldots ,n-d\} \ : \ \ell -d+1\le i\le \ell \}, \end{aligned}$$

\(\ell \in \{0,\ldots ,n-1\}\) depends on x, and is defined by the condition \(x_\ell<x<x_{\ell +1}\).

Note that \(d\ge 1\) implies that \(I_\ell \ne \emptyset \) holds for any \(\ell \). Moreover, note that \(i\in I_\ell \) ensures that \(\ell \in \{i,\ldots , i+d-1\}\). Hence, for any \(i\in I_\ell \) we can write

$$\begin{aligned} \prod _{s=i}^{i+d}|x-x_s|= & \prod _{s=i}^{\ell }|x-x_s|\cdot \prod _{s=\ell +1}^{i+d}|x-x_s|\\\le & \prod _{s=i}^{\ell }(x_{\ell +1}-x_s)\cdot \prod _{s=\ell +1}^{i+d}(x_s-x_\ell ), \end{aligned}$$

and taking into account that

$$\begin{aligned} |x_i-x_j|\le h |i-j|,\qquad \forall i,j\in \{0,\ldots , n\}, \end{aligned}$$
(17)

we get

$$\begin{aligned} \prod _{s=i}^{i+d}|x-x_s|\le h^{d+1}\prod _{s=i}^{\ell }(\ell +1-s) \prod _{s=\ell +1}^{i+d}(s-\ell )= h^{d+1}(\ell +1-i)! (i+d-\ell )! \end{aligned}$$

and therefore

$$\begin{aligned} \prod _{s=i}^{i+d}|x-x_s|\le h^{d+1}d! \qquad \forall i\in I_\ell . \end{aligned}$$
(18)

Furthermore, by collecting (16) and (18), we also get

$$\begin{aligned} \frac{1}{|D(x)|}\le \left( h^{d+1}d!\right) ^\gamma . \end{aligned}$$
(19)

Given this, let us consider the following decomposition

$$\begin{aligned} S(x)= \sum _{i=0}^{\ell -d-1}\sigma _i(x)+\sum _{i=\ell -d}^{\ell +1}\sigma _i(x)+\sum _{i=\ell +2}^{n-d}\sigma _i(x) =:S_1(x)+S_2(x)+S_3(x), \end{aligned}$$

of the summation S(x) with the convention that empty summations are null (i.e., \(\sum _{i=n_1}^{n_2}a_i=0\) if \(n_1>n_2\)), and that always \(i\in \{0,\ldots , n-d\}\).

For \(\ell \ge (d+1)\) the (nonempty) summation \(S_1(x)\), can be estimated by applying (19),

$$\begin{aligned} S_1(x):=\sum _{i=0}^{\ell -d-1}\frac{\left| \tilde{\lambda }_i(x)\right| }{|D(x)|} \prod _{s=i}^{i+d}|x-x_s|\le & \left( h^{d+1}d!\right) ^\gamma \ \sum _{i=0}^{\ell -d-1}\prod _{s=i}^{i+d}\frac{1}{|x-x_s|^{\gamma -1}}\\\le & \left( h^{d+1}d!\right) ^\gamma \ \sum _{i=0}^{\ell -d-1}\prod _{s=i}^{i+d}\frac{1}{|x_\ell -x_{i+d}|^{\gamma -1}}\\= & \left( h^{d+1}d!\right) ^\gamma \ \sum _{i=0}^{\ell -d-1}\frac{1}{|x_\ell -x_{i+d}|^{(\gamma -1)(d+1)}}, \end{aligned}$$

and using (13) we get

$$\begin{aligned} S_1(x)\le & \left( h^{d+1}d!\right) ^\gamma \left[ \sum _{i=0}^{\ell -d-1}\frac{1}{|\ell -i-d|^{(\gamma -1)(d+1)}}\right] \left( \frac{1}{h^*}\right) ^{(\gamma -1)(d+1)} \\\le & \left( d!\right) ^\gamma \left( \frac{h}{h^*}\right) ^{\gamma (d+1)} \left( {h^*}\right) ^{d+1} \left[ \sum _{j=1}^{n}\frac{1}{j^{(\gamma -1)(d+1)}}\right] , \end{aligned}$$

where \((\gamma -1)(d+1)\ge 2\) implies

$$\begin{aligned} \sum _{j=1}^{n}\frac{1}{j^{(\gamma -1)(d+1)}}\le \sum _{j=1}^{n}\frac{1}{j^2}<\infty . \end{aligned}$$
(20)

Hence, we conclude that

$$\begin{aligned} S_1(x)\le {\mathcal {C}}_1 \left( \frac{h}{h^*}\right) ^{\gamma (d+1)} \left( {h^*}\right) ^{\ d+1}, \end{aligned}$$
(21)

where \({\mathcal {C}}_1= (d!)^\gamma \sum _{j=1}^\infty \frac{1}{j^2}\) is independent of x, n, h and \(h^*\).

Now, for \(\ell +2\le n-d\), let us show that (21) also holds for \(S_3(x)\) by using similar arguments. Indeed, by (19), (13), and (20), we have

$$\begin{aligned} \nonumber S_3(x):=\sum _{i=\ell +2}^{n-d}\frac{\left| \tilde{\lambda }_i(x)\right| }{|D(x)|} \prod _{s=i}^{i+d}|x-x_s|\le & \left( h^{d+1}d!\right) ^\gamma \sum _{i=\ell +2}^{n-d}\prod _{s=i}^{i+d}\frac{1}{|x-x_s|^{\gamma -1}}\\ \nonumber\le & \left( h^{d+1}d!\right) ^\gamma \sum _{i=\ell +2}^{n-d}\prod _{s=i}^{i+d}\frac{1}{(x_{i}-x_{\ell +1})^{\gamma -1}}\\ \nonumber\le & \left( h^{d+1}d!\right) ^\gamma \sum _{i=\ell +2}^{n-d}\frac{1}{(x_{i}-x_{\ell +1})^{(\gamma -1)(d+1)}}\\ \nonumber\le & \left( h^{d+1}d!\right) ^\gamma \left[ \sum _{i=\ell +2}^{n-d}\frac{1}{(i-\ell -1)^{(\gamma -1)(d+1)}}\right] \left( \frac{1}{h^*}\right) ^{(\gamma -1)(d+1)} \\\le & {\mathcal {C}}_1 \left( \frac{h}{h^*}\right) ^{\gamma (d+1)} \left( {h^*}\right) ^{\ d+1}. \end{aligned}$$
(22)

Finally, let us estimate \(S_2(x)\). To this aim, by applying (16), (17) and (13), we note that

$$\begin{aligned} \sigma _{\ell -d}(x)= & \frac{|\tilde{\lambda }_{\ell -d}(x)|}{|D(x)|}\prod _{s=\ell -d}^{\ell }|x-x_s|\\\le & \frac{|\tilde{\lambda }_{\ell -d}(x)|}{|\tilde{\lambda }_{\ell -d+1}(x)|}\prod _{s=\ell -d}^{\ell }|x-x_s|= \frac{|x-x_{\ell +1}|^\gamma }{|x-x_{\ell -d}|^\gamma }\prod _{s=\ell -d}^{\ell }|x-x_s| \\\le & \frac{|x_\ell -x_{\ell +1}|^\gamma }{|x_\ell -x_{\ell -d}|^\gamma }\prod _{s=\ell -d}^{\ell }|x_{\ell +1}-x_s|\\\le & \left( \frac{h}{d h^*}\right) ^\gamma \prod _{s=\ell -d}^{\ell }|\ell +1-s| h^{d+1} =\frac{(d+1)!}{d^\gamma }\left( \frac{h}{h^*}\right) ^\gamma h^{d+1} \end{aligned}$$

and similarly

$$\begin{aligned} \sigma _{\ell +1}(x)= & \frac{|\tilde{\lambda }_{\ell +1}(x)|}{|D(x)|}\prod _{s=\ell +1}^{\ell +1+d}|x-x_s|\\\le & \frac{|\tilde{\lambda }_{\ell +1}(x)|}{|\tilde{\lambda }_{\ell }(x)|} \prod _{s=\ell +1}^{\ell +1+d}|x-x_s|= \frac{|x-x_{\ell }|^\gamma }{|x-x_{\ell +1+d}|^\gamma }\prod _{s=\ell +1}^{\ell +1+d}|x-x_s| \\\le & \frac{|x_{\ell +1}-x_\ell |^\gamma }{|x_{\ell +1}-x_{\ell +1+d}|^\gamma } \prod _{s=\ell +1}^{\ell +1+d}|x_{\ell }-x_s|\\\le & \left( \frac{h}{d h^*}\right) ^\gamma \left( \prod _{s=\ell +1}^{\ell +1+d}|\ell -s| h^{d+1}\right) =\frac{(d+1)!}{d^\gamma }\left( \frac{h}{h^*}\right) ^\gamma h^{d+1}. \end{aligned}$$

Moreover, by (16) and (18), we get

$$\begin{aligned} \sum _{i=\ell -d+1}^\ell \sigma _i(x)=\sum _{i\in I_\ell }\frac{\left| \tilde{\lambda }_i(x)\right| }{|D(x)|} \prod _{s=i}^{i+d}|x-x_s| \le \sum _{i\in I_\ell }\prod _{s=i}^{i+d}|x-x_s|\le \sum _{i\in I_\ell }h^{d+1} d! \le h^{d+1} d! d . \end{aligned}$$

Consequently, by the above estimates, we obtain

$$\begin{aligned} S_2(x):=\sum _{i=\ell -d}^{\ell +1}\sigma _i(x)\le h^{d+1} d! d+ 2 \frac{(d+1)!}{d^\gamma }\left( \frac{h}{h^*}\right) ^\gamma h^{d+1}, \end{aligned}$$

that is \(S_2(x)\) can be estimated as

$$\begin{aligned} S_2(x)\le {\mathcal {C}}_2 \left( \frac{h}{h^*}\right) ^\gamma \ h^{d+1}, \end{aligned}$$
(23)

where \({\mathcal {C}}_2=d! d +\frac{2(d+1)!}{d^\gamma }\) is independent of x, n, h and \(h^*\).

In conclusion, from (15), (21), (22), and (23), we deduce

$$\begin{aligned} \left| f(x)-\tilde{r}(f,x)\right|\le & c\frac{\Vert f^{(s)}\Vert _\infty }{(h^*)^{d+1-s}} \left[ S_1(x)+S_3(x)+S_2(x)\right] \\\le & c \Vert f^{(s)}\Vert _\infty \left[ 2{\mathcal {C}}_1 \left( \frac{h}{h^*}\right) ^{\gamma (d+1)} \ (h^*)^{s}+{\mathcal {C}}_2 \left( \frac{h}{h^*}\right) ^{\gamma +d+1} \ (h^*)^{s}\right] , \end{aligned}$$

and the statement follows by taking into account that \(\gamma +d+1\le \gamma (d+1)\) holds for all \(\gamma ,d\in {\mathbb N}\) with \(\gamma >1\). \(\square \)

Remark 3.2

We remark that the case \(d=0\) and \(\gamma >1\), and the case \(\gamma =1\), \(0\le d\le n\), are not covered in Thm. 3.1. In the latter case, estimates can be found in [2, 6, 10, 11]. Moreover, a case close to taking \(d=0\) and \(\gamma =2\) has been considered in [13].

Concerning the bounds on s hypothesized in Thm. 3.1, we remark that if we have \(s>d+1\) then the estimate proven for \(s=d+1\) continues to hold. Indeed, looking at the proof of Thm. 3.1, in the case \(s>d+1\) we can replace (15) with

$$\begin{aligned} |f(x)-\tilde{r}(f,x)|\le c \Vert f^{(d+1)}\Vert _\infty S(x), \qquad \forall f\in C^s[a,b], \quad s>d+1, \end{aligned}$$

where \(c >0\) is a constant independent of f, x and \(n,h,h^*\). Hence, by applying the estimate proved for S(x), we conclude

$$\begin{aligned} \Vert f-\tilde{r}(f)\Vert _\infty \le {\mathcal {C}}\left( \frac{h}{h^*}\right) ^{\gamma (d+1)}( h^*)^{d+1}, \qquad \forall f\in C^s[a,b], \quad s\ge d+1, \end{aligned}$$
(24)

where \({\mathcal {C}}>0\) is a constant independent of \(n,h,h^*\).

Note that in the limit case \(\gamma =1\) the right-hand side of (24) agrees with (3).

In the special case of equidistant or quasi–equidistant distribution of nodes, by the previous theorem and remark we get the following result.

Corollary 3.3

Let \(d,\gamma \in {\mathbb N}\) be arbitrarily fixed with \(\gamma >1\). For all \(f\in C^{s}[a,b]\) with \(s\in {\mathbb N}\), and any set of \(n+1\) nodes \(a=x_0<x_1<...<x_n=b\) with \(n\ge d\) such that \(h\sim h^*\sim n^{-1}\), the associated generalized FH interpolant \(\tilde{r}(f)\) satisfies

$$\begin{aligned} \Vert f-\tilde{r}(f)\Vert _\infty \le \frac{{\mathcal {C}}}{n^r},\qquad r=\min \{s,d+1\}, \end{aligned}$$
(25)

where \({\mathcal {C}}>0\) is a constant independent of \(n,h,h^*\).

We remark that in [12, Thm. 5.3] the same estimate was proved under the additional hypothesis that \(\gamma >r+1\) holds.

Finally, we consider the case of less smooth functions f that are only Lipschitz continuous on [a, b], i.e., satisfying

$$\begin{aligned} |f(x)-f(y)|\le L |x-y|, \qquad \forall x,y\in [a,b], \end{aligned}$$
(26)

with \(L>0\) independent of x, y.

By the following theorem, we prove that in the space Lip[a, b] of such functions, we get the same error estimate proved in \(C^1[a,b]\).

Theorem 3.4

Let \(d,\gamma \in {\mathbb N}\) be arbitrarily fixed with \(\gamma >1\). For all \(f\in \text {Lip[a,b]}\) and any configuration of nodes \(a=x_0<x_1<...<x_n=b\), with \(n\ge d\), the associated generalized FH interpolant \(\tilde{r}(f)\) satisfies

$$\begin{aligned} \Vert f-\tilde{r}(f)\Vert _\infty \le {\mathcal {C}}\left( \frac{h}{h^*}\right) ^{\gamma (d+1)} h^{*}, \end{aligned}$$
(27)

where \({\mathcal {C}}>0\) is a constant independent of n,h,h\(^{*}\).

Proof

The proof is similar to the previous one. The only change regards the estimate of the factor \(|f[x_i,\ldots , x_{i+d}, x]|\) in (12), that in the case of Lipschitz continuous functions can be estimated as

$$\begin{aligned} |f[x_i,\ldots , x_{i+d}, x]|\le \frac{{\mathcal {C}}}{(h^*)^d}, \qquad \forall x\in [a,b],\quad \forall i\in \{0,\ldots , n-d\}, \end{aligned}$$
(28)

where \({\mathcal {C}}>0\) is independent of x, h and \(h^*\).

Such a bound can be easily proved reasoning by induction on \(d\in {\mathbb N}\). Indeed, for \(d=1\) it is true since by (26) we have

$$\begin{aligned} |f[x_i,x]|=\left| \frac{f(x_i)-f(x)}{x_{i}-x}\right| \le L, \qquad \forall x\in [a,b],\quad \forall i\in \{0,\ldots , n-d\}, \end{aligned}$$

and consequently

$$\begin{aligned} |f[x_i, x_{i+1}, x]|=\left| \frac{f[x_{i+1},x]-f[x_i,x]}{x_{i+1}-x_i}\right| \le \frac{2L}{h^*}. \end{aligned}$$

Moreover, assuming that (28) holds for \(d\ge 1\), we get

$$\begin{aligned} |f[x_i,\ldots x_{i+d+1}, x]|= & \left| \frac{f[x_{i+1},\ldots x_{i+d+1}, x]-f[x_i,,\ldots x_{i+d}, x]}{x_{i+d+1}-x_i}\right| \\\le & \frac{2{\mathcal {C}}}{(h^*)^d}\frac{1}{|x_{i+d+1}-x_i|}\le \frac{2{\mathcal {C}}}{(d+1)(h^*)^{d+1}} \end{aligned}$$

i.e., (28) holds for \(d+1\) too. \(\square \)

Finally, by Thm. 3.4 we get the following result concerning the case of equidistant and quasi– equidistant nodes

Corollary 3.5

Let \(d,\gamma \in {\mathbb N}\) be arbitrarily fixed with \(\gamma >1\). For all \(f\in \text {Lip}[a,b]\) and any set of \(n+1\) nodes \(a=x_0<x_1<...<x_n=b\) with \(n \ge d\) such that \(h\sim h^*\sim n^{-1}\), the associated generalized FH interpolant \(\tilde{r}(f)\) satisfies

$$\begin{aligned} \Vert f-\tilde{r}(f)\Vert _\infty \le \frac{{\mathcal {C}}}{n}, \end{aligned}$$
(29)

where \({\mathcal {C}}>0\) is a constant independent of \(n,h,h^*\).

We remark that in [12, Thm. 5.2] the same estimate was proved under the stronger hypothesis that \(\gamma >2\) holds.

4 Numerical experiments

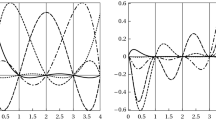
First in Fig. 1, we show the generalized FH interpolants for \(d=0,1,2,3\), with fixed \(\gamma = 2\). \(h/h^* = 5\) and \(h^* = 0.05\), approximating the Runge function \(f(x) = 1/(1+25x^2)\) in the interval \([-1,+1]\). The interpolation nodes are constructed using the procedure described below, resulting in 13 quasi-equidistant interpolation nodes.

Fig. 1
figure 1

The rational interpolant \(\tilde{r}(f,x)\) of the Runge function \(f(x) = 1/(1+25x^2)\) on the interval \([-1,+1]\), for \(\gamma =2\), \(h/h^* = 5\), \(h^* = 0.05\) and \(d=0,1,2,3\) (from left to right and top to bottom)

Full size image

Next, we investigate the behavior of the error

$$\begin{aligned} E\left( \frac{h}{h^*},h^*\right) = \Vert f-\tilde{r}(f)\Vert _\infty \end{aligned}$$

as a function of \(\frac{h}{h^*}\) and \(h^*\) for a fixed value each for the degree d and the parameter \(\gamma \). In all numerical experiments we performed it turns out that E behaves as:

$$\begin{aligned} E\left( \frac{h}{h^*},h^*\right) \approx {D}\left( \frac{h}{h^*}\right) ^{\alpha }( h^*)^{\beta }. \end{aligned}$$

This means that

$$\begin{aligned} \log E\left( \frac{h}{h^*},h^*\right) \approx \log ({D}) + \alpha \log \left( \frac{h}{h^*}\right) + \beta \log (h^*). \end{aligned}$$

To determine \(\log ({D})\), \(\alpha \) and \(\beta \), we can use linear least squares approximation when we have different measurements for the values of the function \(\log E\left( \frac{h}{h^*},h^*\right) \) for different values of \(\log \left( \frac{h}{h^*}\right) \) and \(\log (h^*)\). Consider the interval \([a,b] = [-1,+1]\). Given \(\log \left( \frac{h}{h^*}\right) \) and \(\log (h^*)\), the corresponding points \(x_i\) consist of two subsets. In the first subset there are all points \(-1, -1+h+h^*, -1+2(h+h^*), \ldots \) in the interval \([-1,+1]\). In the second subset there are all points of the first subset shifted by h to the right, i.e., \(-1+h, -1+h+(h+h^*), -1 +h+2(h+h^*),\ldots \) in the interval \([-1,+1]\). Note that the endpoint \(+1\) does not necessarily belong to the point set but it is at a maximum distance of h from the right-most point in the point set. The values taken for h and \(h^*\) are all combinations of a value of \(h^*\) chosen from

$$\begin{aligned} h^*: 2^{-13}, 2^{-12}, \ldots , 2^{-4} \end{aligned}$$

and a value of g among

$$\begin{aligned} g: 10^{0/10}, 10^{1/10}, 10^{2/10}, \ldots , 10^{10/10} \end{aligned}$$

with \(h = g h^*\). The norm \(\Vert f \Vert _\infty \) is approximated by looking at the largest value of |f| in \(10^5\) Chebyshev points in the interval \([-1,+1]\).

Let us take the function \(f(x) = x^2 |x| \in C^2[-1,+1]\), the degree \(d = 1\) and the parameter \(\gamma = 2\). A plot of the function \(E\left( \frac{h}{h^*},h^*\right) \) is given in Fig. 2. From this figure, it can be seen that the function E can be approximated very well by an affine function in \(\frac{h}{h^*}\) and \(h^*\). A similar plot was obtained for the other examples given in this section.

Solving the least squares problem gives us the values

$$\begin{aligned} D = 1.84, \qquad \alpha =1.84 ,\qquad \beta = 2.02. \end{aligned}$$
Fig. 2
figure 2

The function \(E\left( \frac{h}{h^*},h^*\right) \) for \(f(x) =x^2 |x|\) with \(\gamma = 2\) and \(d = 1\)

Full size image

In view of (10), the value \(\alpha \) should be compared to \(\gamma (d+1) = 4\) and the value \(\beta \) to \(s = 2\). Note that the value of D is small, the value of \(\alpha \) is much smaller than \(\gamma (d+1) = 4\) and the value of \(\beta \) is approximately equal to \(s=2\).

In Table 1, we give several other examples. Theorem 3.1 is illustrated by the examples with \(i=1,4,5\). Theorem 3.4 is illustrated by the example with \(i=7\). Note that for \(i = 2,3,10,11\), the value of \(\beta \) is larger than predicted by the theory of Theorem 3.1 or Theorem 3.4.

Based on these results, we give the following conjecture which we were not able to prove. Let \(C^{s,\alpha }[a,b]\) be the class of functions that are s-times continuously differentiable and whose s–th derivative is Hölder continuous with exponent \(0<\alpha \le 1\).

Table 1 The results of numerical experiments for several values of \(f, \gamma \) and d
Full size table
Fig. 3
figure 3

Pointwise absolute error when interpolating the function \(f(x) =|x|\) with \(d=1\), \(h^* =\) 1.0e-3 and \(h = 5 h^*\) for increasing values of \(\gamma = 1,2,\ldots ,7\). The error is plotted in blue for \(\gamma = 1\), in red for \(\gamma =2\) and so on

Full size image

Conjecture 4.1

Let \(d,\gamma \in {\mathbb N}\) be arbitrarily fixed with \(\gamma >1\). For all \(f\in C^{s,\alpha }[a,b]\) with \(1\le s\le (d+1)\), and any set of \(n+1\) nodes \(a=x_0<x_1<...<x_n=b\) with \(n\ge d\) such that \(h\sim h^*\sim n^{-1}\), the associated generalized FH interpolant \(\tilde{r}(f)\) satisfies

$$\begin{aligned} \Vert f-\tilde{r}(f)\Vert _\infty \le \frac{{\mathcal {C}}}{n^{s+\alpha }} \end{aligned}$$
(30)

where \({\mathcal {C}}>0\) is a constant independent of \(n,h,h^*\).

Note that in Table 1, for \(i = 6,8,9\), we also considered \(d=0\) which is not covered by the theory of Theorem 3.1 or Theorem 3.4.

When \(\gamma =1\), experimental results for \(f(x)=|x|\) are given in [6] and for \(f(x)=|x|^{0.5}\) in [1]. To illustrate the behavior of the appproximation when \(\gamma \) is varied, we consider the function \(f(x)=|x|\), \(d=1\), \(h^* =\) 1.0e-3 and \(h = 5 h^*\). For \(\gamma = 1,2,\ldots ,7\), the error function \(|f(x)-\tilde{r}(f,x)|\) is plotted in Fig. 3. When \(\gamma \) increases, the error is more and more concentrated around the x-value 0. The same behavior was also observed for equidistant points [12].

5 Conclusions

In [12], we proved several results concerning the convergence rate of generalized FH interpolants corresponding to equidistant and quasi-equidistant distributions of nodes. These results required a restriction on the value of the parameter \(\gamma \). In this paper, we proved similar convergence results without a need for a restriction on the value of \(\gamma \).

More generally, for arbitrary distributions of nodes, we stated error estimates in terms of h and \(h^*\) for continuously differentiable functions and for Lipschitz continuous functions.

Several numerical experiments confirmed the theoretical results. In the case of non–differentiable functions with isolated singularities, they show that, for fixed d and increasing values of \(\gamma \), even if the maximum absolute errors are almost comparable, we get an improvement in the pointwise approximation close to the singularities. Moreover, they indicate that even stronger results are possible in the case of continuously differentiable functions having a Hölder continuous highest derivative. The proof of this conjecture remains an open problem.