Rational interpolation operator with finite Lebesgue constant

Abstract

Classical rational interpolation usually enjoys better approximation properties than polynomial interpolation because it avoids wild oscillations and exhibits exponential convergence for approximating analytic functions. We develop a rational interpolation operator, which not only preserves the advantage of classical rational interpolation, but also has a finite Lebesgue constant. In particular, it is convergent for approximating any continuous function, and the convergence rate of the interpolants approximating a function is obtained using the modulus of continuity.

1 Introduction

Let f be a real-valued continuous function defined on some interval [a, b] of the real line, and let $x_0,x_1,\ldots ,x_n$ be $n+1$ distinct interpolation nodes in [a, b] with $a=x_0<x_1<\cdots <x_n=b$. Then, the interpolation operator $\Lambda _n$ is defined by

$$\begin{aligned} \Lambda _n(f,x)=\sum \limits _{j=0}^{n}f(x_j)\lambda _j (x), \end{aligned}$$

(1)

where $\lambda _j(x_i)=\delta _{ij}(i=0,1,\ldots ,n; j=0,1,\ldots ,n)$, and $\delta _{ij}$ is the Kronecker $\delta$, defined by $\delta _{ij}=0$ if $i\ne j$ and $\delta _{ij}=1$ if $i=j$. Evidently, we obtain

$$\begin{aligned} \Lambda _n(f,x_i)=f(x_i), \qquad i=0,1,\ldots ,n. \end{aligned}$$

When $\lambda _j (x)=l_j (x)$ with

$$\begin{aligned} l_j(x)=\prod \limits _{i=1,i\ne j}^n \frac{x-x_i}{x_j-x_i}, \qquad j=0,1,\ldots ,n, \end{aligned}$$

the interpolant operator is a well-known Lagrange interpolant operator. We define [10]

$$\begin{aligned} \Lambda _n (x)=\sum \limits _{j=0}^{n}|\lambda _j (x)|, \Vert \Lambda _n\Vert =\max \limits _{a\le x\le b} \Lambda _n (x) \end{aligned}$$

(2)

which are the Lebesgue function and Lebesgue constant of the interpolant operator $L_n$ [10], respectively. In approximation theory, the Lebesgue constant of the interpolation operator plays a significant role in estimating the approximation rate or the divergence of the operator. The Lebesgue constant of the operator depends on the node distributions. The Lebesgue constant of the Lagrange interpolant operator is bounded as (Erdös, Brutman [8]).

$$\begin{aligned} \Vert \Lambda _n\Vert >\frac{2}{\pi }\ln n+0.5212, \end{aligned}$$

However, the Lebesgue constant can achieve the optimal order of $2/{\pi } \ln n$ for Chebyshev nodes. The Lebesgue constant of the Lagrange interpolant operator is infinite as the node number $n\rightarrow \infty$. Another main problem of using high degree polynomial interpolation is Runge’s phenomenon, that is, the oscillation at the edges of an interval. Berrut [3] proposed a rational interpolant operator by replacing $\lambda _j (x)$ with $b_j (x)$ as follows:

$$\begin{aligned} b_j(x)=\frac{\omega _j}{x-x_j}/\sum \limits _{i=0}^{n} \frac{\omega _i}{x-x_i} \end{aligned}$$

for some real values $\omega _j$ to avoid this phenomenon. When considering $\omega _j=(-1)^j(j=0,1,\ldots ,n)$, Berrut used this interpolation operator to Runge’s function, and his numerical experiments suggested that it has good approximation effect. Immense literature [1,2,3,4,5,6,7, 12,13,14,15,16] deals with the practical construction of node sets such that the Lebesgue constant of this rational interpolation operator has moderate growth with the node number n. For example, the Chebyshev nodes and evenly spaced nodes have been extensively studied. For evenly spaced nodes, few studies show that the Lebesgue constants of Berrut’s interpolant are bounded as [5, 15]

$$\begin{aligned} \frac{2}{\pi }\ln n+C_1\le \Vert \Lambda _n \Vert =\max \limits _{a\le x\le b}\sum \limits _{i=0}^{n}\left| \frac{(-1)^i}{x-x_i}/\sum \limits _{j=0}^{n} \frac{(-1)^j}{x-x_j}\right| \le \frac{2}{\pi }\ln n+C_2. \end{aligned}$$

(3)

where $C_1$ and $C_2$ are positive constants. This finding implies that the associated Lebesgue constant grows logarithmically in the node number n, and it is infinite with the node number $n\rightarrow \infty$. On the basis of the Uniform Boundedness Principle, the existence of a continuous function f, whose interpolation operator $\Lambda _n(f,x)$ diverges in $n\rightarrow \infty$, can be confirmed. In 2007, Floater and Hormann [11] constructed a rational interpolation without poles and arbitrarily high approximation orders; it includes Berrut’s operator as a special case. However, the Lebesgue constants of their operator still indicate a logarithmic growth with the node number n. We will discuss this conclusion in another study. This finding shows that the interpolation operator approximation still diverges for some continuous functions.

This result motivates the construction of a new rational interpolation operator with finite Lebesgue constants for any node number n. This paper aims to report an improved rational interpolation as follows:

$$\begin{aligned} T_n (f,x)=\sum \limits _{j=0}^{n}f(x_j)\sigma _j (x), \end{aligned}$$

(4)

where $\sigma _j(x_i)=\delta _{ij}(i=0,1,\ldots ,n; \quad j=0,1,\ldots ,n)$, and $x\ne x_i$

$$\begin{aligned} \sigma _j(x)=\frac{(-1)^j}{(x-x_j)^2 sgn(x-x_j)}/\sum \limits _{i=0}^{n} \frac{(-1)^i}{(x-x_i)^2 sgn(x-x_i)} \end{aligned}$$

or written as

$$\begin{aligned} \sigma _j(x)=\frac{(-1)^j}{(x-x_j)|x-x_j|}/\sum \limits _{i=0}^{n} \frac{(-1)^i}{(x-x_i)|x-x_i|}. \end{aligned}$$

(5)

In a subsequent section of this article, we will show that the interpolation operator $T_n (f,x)$ not only preserves the advantage of classical rational interpolation, but also has finite Lebesgue constants for the evenly spaced nodes or for well-arranged nodes [13]; especially, it converges when it approximates any continuous function.

2 The interpolation with the finite Lebesgue constant

For the interpolation operator $T_n (f,x)$ in (4) the following theorem holds

Theorem 1

The Lebesgue constant $\Vert T_n\Vert$ of the rational interpolant $T_n (f,x)$ given by (4) at evenly spaced nodes is bounded by

$$\begin{aligned} \frac{21}{20}< \Vert T_n\Vert <\frac{17}{10}, \quad n\ge 10. \end{aligned}$$

(6)

Proof

For simplicity, we assume, without loss of generality, that the interpolation interval is [0,1]. Thus, the interpolation nodes are equally spaced with distance 1/n, i.e., $x_j=\frac{j}{n}, j=0,1,\ldots ,n$. If $x = x_k$ for any k, then the interpolation property of the basis functions suggests that $T_n(x) = 1$. As a result, let $x_k< x < x_{k+1}$ for some k, and the Lebesgue function according to (4) and (5) is written as

$$\begin{aligned} T_{n,k} (x):=T_n (x)=\sum \limits _{j=0}^{n}|\sigma _j(x)|=\frac{\sum \nolimits _{j=0}^{n} \frac{1}{(x-x_j)^2}}{\left| \sum \nolimits _{j=0}^{n} \frac{(-1)^j}{(x-x_j)|x-x_j|}\right| }, x_k< x < x_{k+1}. \end{aligned}$$

(7)

Multiplying the numerator and denominator in (7) by the product $(x-x_{k})^{2}(x_{k+1}-x)^2$ yields

$$\begin{aligned} T_{n,k}(x)=\frac{(x-x_{k})^{2}(x_{k+1}-x)^2\sum \nolimits _{j=0}^{n}\frac{1}{(x-x_{j})^{2}}}{\left| (x-x_{k})^{2}(x_{k+1}-x)^2\sum \nolimits _{j=0}^{n} \frac{(-1)^{j}}{(x-x_j)|x-x_j|}\right| }:=\frac{N_{k}(x)}{D_{k}(x)}. \end{aligned}$$

(8)

We initially estimate the upper bound in(6). Then, we have to bound the numerator $N_k(x)$ from above and the denominator $D_k(x)$ from below. For the numerator, we obtain

$$\begin{aligned} N_{k}(x)&=(x-x_{k})^{2}(x_{k+1}-x)^2\sum \limits _{j=0}^{n}\frac{1}{(x-x_{j})^{2}}\\&=(x-x_{k})^{2}(x_{k+1}-x)^2\left[ \sum \limits _{j=0}^{k-1}\frac{1}{(x-x_{j})^{2}}+\frac{1}{(x-x_{k})^{2}}+\frac{1}{(x_{k+1}-x)^{2}}\right. \\&\quad \left. + \sum \limits _{j=k+2}^{n}\frac{1}{(x_{j}-x)^{2}}\right] \\&=(x_{k+1}-x)^2+(x-x_{k})^{2}+(x-x_{k})^{2}(x_{k+1}-x)^2\\&\quad \left[ \sum \limits _{j=0}^{k-1}\frac{1}{(x-x_{j})^{2}} +\sum \limits _{j=k+2}^{n}\frac{1}{(x_{j}-x)^{2}}\right] . \end{aligned}$$

Let

$$\begin{aligned} x-x_{k}=t, {\text{ then }} x_{k+1}-x=\frac{1}{n}-t,~ t \in \left( 0,\frac{1}{n}\right) . \end{aligned}$$

(9)

Considering $\frac{1}{x_{i}-x_{j}}=\frac{n}{i-j}(i \ne j)$ and using some elementary inequalities

$$\begin{aligned} \sum \limits _{j=1}^{n}\frac{1}{j^2}\le \frac{\pi ^2}{6}, ~ \sum \limits _{j=1}^{n}\frac{1}{j}\le \ln (2n+1), \end{aligned}$$

we derive

$$\begin{aligned} N_{k}(x)&=(x_{k+1}-x)^2+(x-x_{k})^{2}+(x-x_{k})^{2}(x_{k+1}-x)^2\\&\quad \left( \sum \limits _{j=0}^{k-1}\frac{1}{(x-x_{j})^{2}} +\sum \limits _{j=k+2}^{n}\frac{1}{(x_{j}-x)^{2}}\right) \\&\le (x_{k+1}-x)^2+(x-x_{k})^{2}+(x-x_{k})^{2}(x_{k+1}-x)^2\\&\quad \left( \sum \limits _{j=0}^{k-1}\frac{1}{(x_{k}-x_{j})^{2}} +\sum \limits _{j=k+2}^{n}\frac{1}{(x_{j}-x_{k+1})^{2}}\right) \\&=(x_{k+1}-x)^2+(x-x_{k})^{2}+(x-x_{k})^{2}(x_{k+1}-x)^2\\&\quad \left( \sum \limits _{j=0}^{k-1}\frac{n^2}{(k-j)^{2}} +\sum \limits _{j=k+2}^{n}\frac{n^2}{(j-k-1)^{2}}\right) \\&=(x_{k+1}-x)^2+(x-x_{k})^{2}+(x-x_{k})^{2}(x_{k+1}-x)^2\\&\quad \left( \sum \limits _{j=1}^{k}\frac{n^2}{j^{2}}+\sum \limits _{j=1}^{n-k-1} \frac{n^2}{j^{2}}\right) \\&\le (x_{k+1}-x)^2+(x-x_{k})^{2}+\frac{\pi ^2}{3}n^2(x-x_{k})^{2} \left( x_{k+1}-x\right) ^2 \\&=\bar{N_{k}}(t):=\left( \frac{1}{n}-t\right) ^2+t^2+\frac{\pi ^2}{3}n^2t^2\left( \frac{1}{n}-t\right) ^2. \end{aligned}$$

Considering the denominator $D_{k}(x)$ in (8), if k and n are even, then removing the absolute value in (8) does not require changing the sign and obtaining

$$\begin{aligned} D_{k}(x)&=(x-x_{k})^{2}(x_{k+1}-x)^2\sum \limits _{j=0}^{n} \frac{(-1)^{j}}{(x-x_{j})|x-x_{j}|} \nonumber \\&=(x_{k+1}-x)^2+(x-x_{k})^{2}+(x-x_{k})^{2}(x_{k+1}-x)^2\nonumber \\&\quad \left( \sum \limits _{j=0}^{k-1}\frac{(-1)^j}{(x-x_{j})^{2}} -\sum \limits _{j=k+2}^{n}\frac{(-1)^j}{(x_{j}-x)^{2}}\right) . \end{aligned}$$

(10)

Pairing the positive and negative terms in the right most factor adequately provides

$$\begin{aligned} S_{k}(x)&:=\sum \limits _{j=0}^{k-1}\frac{(-1)^j}{(x-x_{j})^{2}} -\sum \limits _{j=k+2}^{n}\frac{(-1)^j}{(x_{j}-x)^{2}} \nonumber \\&=\frac{1}{(x-x_{0})^2}+\left( \frac{1}{(x-x_{2})^2} - \frac{1}{(x-x_{1})^2}\right) \nonumber \\&\quad +\dots +\left( \frac{1}{(x-x_{k-2})^2} - \frac{1}{(x-x_{k-3})^2}\right) - \frac{1}{(x-x_{k-1})^2} \nonumber \\&\quad -\frac{1}{(x-x_{k+2})^2}+\left( \frac{1}{(x-x_{k+3})^2}- \frac{1}{(x-x_{k+4} )^2}\right) \nonumber \\&\quad +\dots +\left( \frac{1}{(x-x_{n-1})^2}- \frac{1}{(x-x_{n})^2}\right) . \end{aligned}$$

(11)

We obtain

$$\begin{aligned} S_{k}(x)&>-\frac{1}{(x-x_{k-1})^2}-\frac{1}{(x-x_{k+2})^2} \\&= -\frac{1}{(x-x_{k}+x_{k}-x_{k-1})^2}-\frac{1}{(x-x_{k}+x_{k}-x_{k+2})^2}\\&=-\left( \frac{1}{(t+\frac{1}{n})^2}+\frac{1}{(t-\frac{2}{n})^2}\right) \end{aligned}$$

because the leading term and all paired terms are positive. By applying this estimate to (11) and considering (9), we get

$$\begin{aligned} D_{k}(x)&=(x_{k+1}-x)^2+(x-x_{k})^{2}+(x-x_{k})^{2}(x_{k+1}-x)^2S_{k}(x) \nonumber \\&>\left( \frac{1}{n}-t\right) ^2+t^2-t^2\left( \frac{1}{n}-t \right) ^2 \left( \frac{1}{(t+\frac{1}{n})^2}+\frac{1}{(t-\frac{2}{n})^2}\right) \nonumber \\&=\left( \frac{1}{n}-t\right) ^2+t^2-n^2t^2\left( \frac{1}{n}-t\right) ^2 \left( \frac{1}{(1+nt)^2}+\frac{1}{(nt-2)^2}\right) :=\bar{D_{k}}(t). \end{aligned}$$

(12)

This bound also holds if n is odd and k is even because this condition only adds a single positive term $1 /(x_{n}-x)$ to $S_{k}(x)$ in (11).

If k and n are odd numbers, removing the absolute value in (8), then we need to change the sign and obtain

$$\begin{aligned} D_{k}(x)&=-(x-x_{k})^{2}(x_{k+1}-x)^2\sum \limits _{j=0}^{n}\frac{(-1)^{j}}{(x-x_{j})|x-x_{j}|} \nonumber \\&=(x_{k+1}-x)^2+(x-x_{k})^{2}-(x-x_{k})^{2}(x_{k+1}-x)^2\nonumber \\&\quad \left( \sum \limits _{j=0}^{k-1}\frac{(-1)^j}{(x-x_{j})^{2}} -\sum \limits _{j=k+2}^{n}\frac{(-1)^j}{(x_{j}-x)^{2}}\right) . \end{aligned}$$

(13)

Similar to the front method, pairing the positive and negative terms in the rightmost factor adequately provides

$$\begin{aligned} \begin{aligned} S_{k}(x)&=\sum \limits _{j=0}^{k-1}\frac{(-1)^j}{(x-x_{j})^{2}} -\sum \limits _{j=k+2}^{n}\frac{(-1)^j}{(x_{j}-x)^{2}}\\&=\left( \frac{1}{(x-x_{0})^2}-\frac{1}{(x-x_{1})^2}\right) +\left( \frac{1}{(x-x_{2})^2}-\frac{1}{(x-x_{3})^2}\right) \\&\quad +\dots +\left( \frac{1}{(x-x_{k-3})^2}- \frac{1}{(x-x_{k-2})^2}\right) \\&\quad +\frac{1}{(x-x_{k-1})^2} +\frac{1}{(x-x_{k+2})^2}+\left( \frac{1}{(x-x_{k+4})^2}- \frac{1}{(x-x_{k+3})^2}\right) \\&\quad +\dots +\left( \frac{1}{(x-x_{n})^2}- \frac{1}{(x-x_{n-1})^2}\right) . \end{aligned} \end{aligned}$$

(14)

We obtain

$$\begin{aligned} S_{k}(x)<\frac{1}{(x-x_{k-1})^2}+\frac{1}{(x-x_{k+2})^2} = \frac{1}{(x-x_{k}+x_{k}-x_{k-1})^2}+\frac{1}{(x-x_{k}+x_{k}-x_{k+2})^2} \end{aligned}$$

and further

$$\begin{aligned} D_{k}(x)&=(x-x_{k})^{2}+(x_{k+1}-x)^2-(x-x_{k})^{2}(x_{k+1}-x)^2S_{k}(x) \nonumber \\&>\left( \frac{1}{n}-t\right) ^2+t^2-t^2\left( \frac{1}{n}-t\right) ^2 \left( \frac{1}{(t+\frac{1}{n})^2}+\frac{1}{(t-\frac{2}{n})^2}\right) \nonumber \\&=\left( \frac{1}{n}-t\right) ^2+t^2-n^2t^2\left( \frac{1}{n}-t\right) ^2 \left( \frac{1}{(1+nt)^2}+\frac{1}{(nt-2)^2}\right) :={\bar{D}}_{k}(t) \end{aligned}$$

(15)

because the leading term and all paired terms are negative. Thus (13) is still valid, as well as (15). This bound also holds if n is even and k is odd because all paired terms are negative and this condition only adds a single negative term $1 /(x_{n}-x)$ to $S_{k}(x)$ in (14). In summary, regardless of the parity of k and n, we obtain (12). Therefore,

$$\begin{aligned} T_{n,k}(x)=\frac{N_{k}(x)}{D_{k}(x)}<\frac{{\bar{N}}_{k}(t)}{{\bar{D}}_{k}(t)} =\frac{\left( \frac{1}{n}-t\right) ^2+t^2+\frac{\pi ^2}{3}n^2t^2 \left( \frac{1}{n}-t\right) ^2}{(\frac{1}{n}-t)^2+t^2-n^2t^2 \left( \frac{1}{n}-t\right) ^2\left( \frac{1}{(1+nt)^2}+\frac{1}{(nt-2)^2}\right) }. \end{aligned}$$

(16)

By applying the following expressions

$$\begin{aligned} \left( \frac{1}{n}-t\right) ^2+t^2=\frac{1}{n^2} -2t\left( \frac{1}{n}-t\right) ,\quad \frac{1}{(1+nt)^2}+\frac{1}{(nt-2)^2}\le \frac{5}{4}, \end{aligned}$$

(17)

we further get by (16)

$$\begin{aligned} \frac{{\bar{N}}_{k}(t)}{{\bar{D}}_{k}(t)}= & \, \frac{\left( \frac{1}{n}-t\right) ^2+t^2+\frac{\pi ^2}{3}n^2t^2\left( \frac{1}{n} -t\right) ^2}{(\frac{1}{n}-t)^2+t^2-n^2t^2\left( \frac{1}{n}-t\right) ^2 \left( \frac{1}{(1+nt)^2}+\frac{1}{(nt-2)^2}\right) }\nonumber \\< & \, \frac{\frac{1}{n^2} -2t\left( \frac{1}{n}-t\right) +\frac{\pi ^2}{3}n^2t^2\left( \frac{1}{n}-t\right) ^2}{\frac{1}{n^2} -2t\left( \frac{1}{n}-t\right) -\frac{5}{4}n^2t^2\left( \frac{1}{n}-t\right) ^2}:=g_1(t). \end{aligned}$$

(18)

Let $t(\frac{1}{n}-t)=u$($u \in (0,\frac{1}{4n^2})$), we obtain by (18)

$$\begin{aligned} h_1 (u)=g_1(t)=\frac{1-2n^2u+\frac{\pi ^2}{3}n^4u^2}{1-2n^2u-\frac{5}{4}n^4u^2}. \end{aligned}$$

Let $n^2u=\alpha$($\alpha \in (0,\frac{1}{4})$), and further

$$\begin{aligned} q_1(\alpha )=h_1(u)=\frac{1-2\alpha +\frac{\pi ^2}{3}\alpha ^2}{1-2\alpha -\frac{5}{4}\alpha ^2}. \end{aligned}$$

(19)

We then estimate $q_1(\alpha )$. The first derivative of $q_1(\alpha )$ is easy to compute as follows:

$$\begin{aligned} q_1^{\prime }(\alpha )=\frac{-8\alpha (15+4\pi ^2)(\alpha -1)}{3(5\alpha ^2 +8\alpha -4)^2}. \end{aligned}$$

Given that $\alpha \in (0,\frac{1}{4})$, then $q_1^{\prime }(\alpha )>0$. Thus, $q_1(\alpha )$ increases in $(0,\frac{1}{4})$. This condition leads to

$$\begin{aligned} q_1(\alpha )<q_1\left( \frac{1}{4}\right) =\frac{96+4\pi ^2}{81}<\frac{17}{10}. \end{aligned}$$

(20)

Combining (16), (18), and(19) with (20) yields

$$\begin{aligned} \Vert T_{n}\Vert =\max \limits _{k=0,1,2,\dots ,n-1}\left( \max \limits _{x_{k}< x \le x_{k+1}}\frac{N_{k}(x)}{D_{k}(x)}\right)<q_1(\alpha )<\frac{17}{10}. \end{aligned}$$

Subsequently, we estimate the lower bound in (6). Let $x=\frac{1}{2n}$, and the numerator in (8) provides

$$\begin{aligned} N\left( \frac{1}{2n}\right)&=\sum \limits _{j=0}^{n} \frac{1}{\left( \frac{1}{2n}-\frac{j}{n}\right) ^2}=4n^2\sum \limits _{j=0}^{n} \frac{1}{(2j-1)^2}=4n^2\left( 2+\sum \limits _{j=2}^{n} \frac{1}{(2j-1)^2}\right) \nonumber \\&\ge 4n^2\left( 2+\sum \limits _{j=2}^{n} \frac{1}{4j(j+1)}\right) =4n^2\left( \frac{17}{8}-\frac{1}{4(n+1)}\right) , \end{aligned}$$

(21)

and the denominator provides

$$\begin{aligned} D\left( \frac{1}{2n}\right)&=\left| \sum \limits _{j=0}^{n}\frac{(-1)^j}{\left( \frac{1}{2n} -\frac{j}{n}\right) \left| \left( \frac{1}{2n}-\frac{j}{n}\right) \right| }\right| \nonumber \\&=4n^2\left| 1-\sum \limits _{j=1}^{n}\frac{(-1)^j}{(2j-1)^2}\right| \le 8n^2. \end{aligned}$$

(22)

Thus, combining (21) with (22) yields

$$\begin{aligned} \Vert T_{n}\Vert \ge T_{n} \left( \frac{1}{2n}\right) =\frac{N\left( \frac{1}{2n}\right) }{D\left( \frac{1}{2n}\right) }\ge \frac{4n^2\left( \frac{17}{8}-\frac{1}{4(n+1)}\right) }{8n^2}=\frac{17}{16}-\frac{1}{8 (n+1)}> \frac{21}{20}, n\ge 10. \end{aligned}$$

This completes the proof of Theorem 1. $\square$

An important property of the interpolants in (4) is that they are free of poles. In fact, let $x_k<x<x_{k+1}$, the interpolants in (4) can be changed into

$$\begin{aligned} T_n (f,x)=\frac{(x-x_{k})^{2}(x_{k+1}-x)^2\sum \nolimits _{j=0}^{n}\frac{(-1)^{j}f(x_j)}{(x-x_j)|x-x_j|}}{(x-x_{k})^{2}(x_{k+1}-x)^2\sum \nolimits _{j=0}^{n} \frac{(-1)^{j}}{(x-x_j)|x-x_j|}}. \end{aligned}$$

Then, showing that the interpolant has no pole is equivalent to showing that the denominator in this expression or the denominator in (8) is not equal to zero in R. This conclusion is evident after reviewing the estimate of the denominator in the proof process of Theorem 1. Thus we obtain the following corollary:

Corollary

The interpolants defined by (4) and (5) have no poles in R.

3 Approximation error

We should review the concept about the modulus of continuity to illustrate the approximation error of the operator to continuous function. Let f(x) be a closed interval [a, b], and let

$$\begin{aligned} \omega (\delta )=\omega (f,\delta )=sup|f(x_2)-f(x_1)| {\text{ for }} x_1,x_2\in [a,b], |x_2-x_1|\le \delta . \end{aligned}$$

The function $\omega (\delta )$ is called the modulus of continuity of f(x). A well-known inequality about $\omega (\delta )$ holds for a factor $\lambda$:

$$\begin{aligned} \omega (\lambda \delta )\le (\lambda +1)\omega (\delta ), \lambda \ge 0. \end{aligned}$$

(23)

We introduce that the error bound of the rational interpolation operator (4) is approximately a continuous function f(x).

Theorem 2

Let f(x) be a continuous function, $T_n (f,x)$ is defined by (4), and $x_k$ represents evenly spaced nodes, then

$$\begin{aligned} |T_n (f,x)-f(x)| < \frac{14}{5} \omega \left( f,\frac{\ln n}{n}\right) , \quad n\ge 10. \end{aligned}$$

Proof

Assuming that x is closest to $x_{k}$, then

$$\begin{aligned} |x-x_{j}|\le |x-x_{k}|+|x_{k}-x_{j}|\le \frac{1}{2n}+\frac{|k-j|}{n} =\frac{1}{2n}(1+2|k-j|). \end{aligned}$$

(24)

Thus, we have

$$\begin{aligned} \left| f(x)-\sum \limits _{j=0}^{n}f(x_{j})\sigma _{j}(x)\right|&= \left| \sum \limits _{j=0}^{n}\left[ f(x)-f(x_{j})\right] \sigma _{j}(x)\right| \nonumber \\&\le \sum \limits _{j=0}^{n}|f(x)-f(x_{j})||\sigma _{j}(x)|\nonumber \\&\le \sum \limits _{j=0}^{n} \omega \left( f,\frac{1}{2n}(1+2|k-j|)\right) |\sigma _{j}(x)|. \end{aligned}$$

(25)

Applying (23) yields

$$\begin{aligned}&\sum \limits _{j=0}^{n} \omega \left( f,\frac{1}{2n}(1+2|k-j|)\right) |\sigma _{j}(x)| \nonumber \\&\quad =\sum \limits _{j=0}^{n} \omega \left( f,\frac{\ln n}{n}\frac{(1+2|k-j|)}{2\ln {n}}\right) |\sigma _{j}(x)| \nonumber \\&\quad \le \omega \left( f,\frac{\ln {n}}{n}\right) \sum \limits _{j=0}^{n} \left( 1+\frac{1+2|k-j|}{2\ln {n}}\right) |\sigma _{j}(x)| \nonumber \\&\quad =\omega \left( f,\frac{\ln {n}}{n}\right) \left[ \left( 1+\frac{1}{2\ln {n}}\right) \sum \limits _{j=0}^{n}|\sigma _{j}(x)|+ \frac{1}{\ln {n}} \sum \limits _{j=0}^{n}|k-j||\sigma _{j}(x)|\right] . \end{aligned}$$

(26)

We are required to bound the term $V_{n,k}(x):=\sum \limits _{j=0}^{n}|k-j| |\sigma _{j}(x)|$ in (26) because we have bounded

$$\begin{aligned} \sum \limits _{j=0}^{n}|\sigma _{j}(x)|<\frac{17}{10} \end{aligned}$$

(27)

in the proof process of Theorem 1. We obtain

$$\begin{aligned} V_{n,k}(x)= \frac{(x-x_{k})^{2}(x_{k+1}-x)^2 \sum \nolimits _{j=0}^{n}\frac{|k-j|}{(x-x_{j})^{2}}}{\left| (x-x_{k})^{2}(x_{k+1}-x)^2 \sum \nolimits _{j=0}^{n}\frac{(-1)^{j}sgn(x-x_{j})}{(x-x_{j})^{2}} \right| }=\frac{R_{k}(x)}{D_{k}(x)} \end{aligned}$$

(28)

after reviewing (4). Thus, we need to bound the numerator $R_k(x)$ and the denominator $D_k(x)$ . We obtain $D_{k}(x)>(\frac{1}{n}-t)^2+t^2-\frac{5}{4}n^2t^2(\frac{1}{n}-t)^2$ by using (12). Thus, the numerator $R_k(x)$ should be estimated and rewritten as

$$\begin{aligned} R_{k}(x)&=(x-x_{k})^{2}(x_{k+1}-x)^2\sum \limits _{j=0}^{n}\frac{|k-j|}{(x-x_{j})^{2}}\\&=(x-x_{k})^{2}(x_{k+1}-x)^2\left[ \sum \limits _{j=0}^{k-1}\frac{k-j}{(x-x_{j})^{2}}+\frac{1}{(x_{k+1}-x)^{2}}+ \sum \limits _{j=k+2}^{n}\frac{j-k}{(x_{j}-x)^{2}}\right] \\&=(x-x_{k})^{2}+(x-x_{k})^{2}(x_{k+1}-x)^2\left( \sum \limits _{j=0}^{k-1}\frac{k-j}{(x-x_{j})^{2}}+\sum \limits _{j=k+2}^{n}\frac{j-k}{(x_{j}-x)^{2}}\right) . \end{aligned}$$

Similar to the previous calculation, we get

$$\begin{aligned} R_{k}(x)&\le (x-x_{k})^{2}+n^2(x-x_{k})^{2}(x_{k+1}-x)^2 \left( \sum \limits _{j=0}^{k-1}\frac{k-j}{(k-j)^{2}}+\sum \limits _{j=k+2}^{n} \frac{(j-k-1)+1}{(j-k-1)^2}\right) \\&=(x-x_{k})^{2}+n^2(x-x_{k})^{2}(x_{k+1}-x)^2\left( \sum \limits _{j=1}^{k} \frac{1}{j}+\sum \limits _{j=1}^{n-k-1}\frac{1}{j^{2}}+\sum \limits _{j=1}^{n-k-1} \frac{1}{j}\right) \\&\le (x-x_{k})^{2}+n^2(x-x_{k})^{2}(x_{k+1}-x)^2\left( \frac{\pi ^2}{6} +\ln {((2k+1)(2n-(2k+1)))}\right) \\&\le t^2+\left( \frac{\pi ^2}{6}+2\ln {n}\right) n^2t^2\left( \frac{1}{n}-t\right) ^2\\&\le \frac{1}{2}\left[ t^2+\left( \frac{1}{n}-t\right) ^2\right] +\left( \frac{\pi ^2}{6}+2\ln {n}\right) n^2t^2\left( \frac{1}{n}-t\right) ^2, \end{aligned}$$

where we used $t^2 < \left( \frac{1}{n}-t\right) ^2$ (Note: x is closest to $x_{k}$)and further

$$\begin{aligned} V_{n,k}(x)=\frac{R_{k}(x)}{D_{k}(x)} \le \frac{\frac{1}{2}\left[ t^2+\left( \frac{1}{n}-t\right) ^2\right] +\left( \frac{\pi ^2}{6}+2\ln {n}\right) n^2t^2\left( \frac{1}{n}-t\right) ^2}{\left( \frac{1}{n}-t\right) ^2+t^2-\frac{5}{4}n^2t^2\left( \frac{1}{n}-t\right) ^2}:=g_2 (t). \end{aligned}$$

(29)

A treatment similar to (18,19) yields

$$\begin{aligned} q_2(\alpha )=g_2 (t)=\frac{\frac{1}{2}-\alpha +\left( \frac{\pi ^2}{6} +2\ln {n}\right) \alpha ^2}{1-2\alpha -\frac{5}{4}\alpha ^2},\alpha \in \left( 0,\frac{1}{4}\right) . \end{aligned}$$

(30)

We compute the first derivative of $q_2(\alpha )$ to estimate $q_2(\alpha )$, as follows:

$$\begin{aligned} q_2^{\prime }(\alpha )=\frac{4(15+4\pi ^2+48\ln {n})\alpha (1-\alpha )}{3(5\alpha ^2 +8\alpha -4)^2}. \end{aligned}$$

We get $q_2^{\prime }(\alpha )>0$, considering $\alpha \in (0,\frac{1}{4})$; thus, $q_2(\alpha )$ increases in $(0,\frac{1}{4})$. This condition yields

$$\begin{aligned} q_2(\alpha )<q_2\left( \frac{1}{4}\right) =\frac{48+2\pi ^2}{81}+\frac{8\ln {n}}{27}. \end{aligned}$$

(31)

We finally arrive at

$$\begin{aligned} |T_n (f,x)-f(x)|&\le \left( \frac{17}{10}\left( 1+\frac{1}{2\ln {n}}\right) +\frac{48+2\pi ^2}{81\ln {n}}+\frac{8}{27}\right) \omega \left( f,\frac{\ln n}{n}\right) \\&\le \left( \frac{17}{10}\left( 1+\frac{1}{2\ln {10}}\right) +\frac{48 +2\pi ^2}{81\ln {10}}+\frac{8}{27}\right) \omega \left( f,\frac{\ln n}{n}\right) \nonumber \\&<\frac{14}{5}\omega \left( f,\frac{\ln n}{n}\right) , \quad n\ge 10, \nonumber \end{aligned}$$

(32)

which completes the proof of Theorem 2 by combining (25), (26), (27), (28), (29), and (30) with (31). $\square$

$\lim \nolimits _{n\rightarrow \infty } \omega (f,\frac{\ln {n}}{n})=0$ for the continuous function f(x), the conclusion of Theorem 2 leads to

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }T_n (f,x)=f(x), \end{aligned}$$

thereby implying that the interpolant $T_n$ is convergent for any continuous function.

Note: From (32), we obtain

$$\begin{aligned} |T_n (f,x)-f(x)|\le 2 \omega \left( f,\frac{\ln n}{n}\right) \end{aligned}$$

for a sufficiently large n.

4 Numerical results

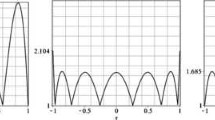
We provide few numerical experiments to further prove or analyze the behavior of the Lebesgue function and the Lebesgue constant of the proposed interpolant, as well as few approximation effect figures and approximation error figures that use the proposed interpolant and other interpolants. First, Fig. 1 shows the Lebesgue function for interpolation at $n+1$ equidistant nodes for $n = 20, 40, 80, 200$. The figures suggest that the maximum is always obtained near the center of the interpolation interval. The four subgraphs show that the Lebesgue constant of the interpolant is approximately 1.35 but not larger than 1.35 (Fig. 1). This finding further confirms the accuracy of Theorem 1. Second, we tested the behavior of oscillations by using Runge function $f(x)=\frac{1}{1+x^2}$. The results in Fig. 2 show that the approximation effect improves as the number of equidistant nodes grows, and it resists the wild oscillations. Third, we constructed a function with discontinuous derivatives at multiple points to test the approximation effect. The function is as follows:

$$\begin{aligned} g_3 (x)= {\left\{ \begin{array}{ll} \frac{3x}{2}-\frac{1}{2}, &\,\frac{2}{3} \le x \le 1 ;\\ \frac{1}{2} , &\,\frac{1}{3} \le x \le \frac{2}{3} ;\\ \frac{3x}{2}, &\, 0 \le x \le \frac{1}{3} ;\\ -\frac{3x}{2}, &\, -\frac{1}{3} \le x \le 0 ;\\ \frac{1}{2} , &\,-\frac{2}{3} \le x \le -\frac{1}{3} ;\\ -\frac{3x}{2}-\frac{1}{2}, &\,-1 \le x \le -\frac{2}{3} . \end{array}\right. } \end{aligned}$$

The results also show that the approximation effect improves as the number of equidistant nodes grows, and it resists the wild oscillations (Fig. 3). Finally, we compared the approximation errors of the classical Berrut’s interpolant with that in the present study by using the function $g_{3}(x)$. The results show that their effects are similar in general when the node number n is not very large (Fig. 4). Theoretically, the interpolant has advantages when n is very large in terms of Theorem 2. However, an experiment is difficult to conduct due to the limitation of computing power. We programmatically calculate the constants of our operator for nodes ranging from 10 to 200 and display our upper and lower bounds in Fig. 5.

Fig. 1

The Lebesgue function of the interpolant at $n + 1$ equidistant nodes for $n = 20, 40,80, 200$ from the top row to the bottom row and from the left to the right, respectively

Fig. 2

The plots of the approximation effect using the interpolant. The top left plot is of Runge function, and the plots from top right, the bottom left, and the bottom right are of the interpolant functions with equidistant node number $n =20, 40,100$

Fig. 3

The plots of the approximation effect using the interpolant. The top left plot is of the function $g_3(x)$, and the plots of the top right, the bottom left, and the bottom right are of the interpolant functions with equidistant node number $n = 20, 40, 100$

Fig. 4

The top row figures from left to right are the approximation effect graph and error graph of the function $g_3(x)$ by the interpolant. The bottom row figures from left to right are the approximation effect graph and error graph of the function $g_3(x)$ by the proposed interpolant

Fig. 5

Upper and lower bounds of the proposed Lebesgue constant are shown by the hollow dot line and the black dot line respectively, and the exact Lebesgue constants are indicated by the red dot line

5 Conclusion

We have introduced a new linear rational interpolant and provided the upper and lower bounds of the Lebesgue constant in equidistant node case. These bounds are the finite constants, which are very smaller to that of the other rational interpolant. We have also proven the convergence of using the new rational interpolant to approximate any continuous functions. Furthermore, we have obtained the approximation error of using the interpolant to approximate any continuous functions in terms of its modulus of continuity. These results are supported by numerical examples. Finally, we have made a comparison with the other interpolant. The results show that the approximation error is almost the same as Berrut’s interpolant. For a larger n, the other interpolant and functions with discontinuous derivatives are compared.