1 Introduction

The lattice Boltzmann method (LBM) [1,2,3,4,5] is based on the solution of the Boltzmann transport equation for density distribution functions in a discretized form and serves as an efficient computational method for solving evolution equations such as the Navier–Stokes equations (NSEs), advection–diffusion equations (ADEs), and others [6, 7]. However, in contrast to traditional numerical methods like the finite difference, finite elements, or finite volume methods, these macroscopic equations are not the forerunners of the LBM numerical scheme. They need to be recovered using various techniques that include the asymptotic analysis [8, 9] or the derivation of equivalent finite difference equations (EFDEs) and subsequent use of the Taylor expansion [10] to obtain the desired equivalent partial differential equations (EPDEs) or just direct Taylor expansion of the lattice Boltzmann equation [11, 12]. Alternatively, recent article [13] describes other techniques that could be used to reproduce macroscopic equations. The objective of the recovery procedure is to produce a system of equivalent partial differential equations (EPDEs) up to a given order of derivatives and, furthermore, to transform EPDEs into a system of spatial EPDEs (SEPDEs) by eliminating higher-order temporal derivatives. SEPDEs are the evolution partial differential equations for macroscopic quantities which contain spatial derivatives only, except for the first-order temporal derivatives of the quantities [10]. Consequently, these SEPDEs represent the recovered macroscopic equations (NSEs, ADEs, or others) but with additional higher-order derivatives. However, especially in 3D, the derivation of EPDEs may become extremely difficult due to the immense complexity of the equations.

We explore the approach based on EFDEs and Taylor expansion which simplifies, generalizes, and expands the method proposed in [10]. In order to derive EPDEs and SEPDEs for a general LBM, a new method and a computational tool under the name of LBMAT (Lattice Boltzmann Method Analysis Tool) is proposed and implemented. LBMAT starts with EFDEs for macroscopic quantities (raw moments), employs Taylor expansion of these quantities to obtain EPDEs, and uses sophisticated algorithms to obtain the desired SEPDEs. LBMAT is implemented as an open-source software in C++ using the GiNaC library [14] (www.ginac.de) for symbolic algebraic computations. Its applicability is demonstrated on a series of selected popular LBM variants such as the single relaxation time (SRT-LBM), multiple relaxation time (MRT-LBM), central LBM (CLBM) [15], and the cumulant LBM (CuLBM) [16, 17] for both ADE and NSE. Furthermore, by its design, LBMAT can be potentially used to improve or propose new collision operators, or even to explore possibilities of recovering SEPDEs other than ADEs or NSEs.

The paper is organized as follows. Section 2 contains the description of LBM together with the definition of raw and central moments, derivation of EFDEs, and the assessment of all assumptions required for LBMAT to work. In Section 3, detailed derivations of EPDEs and SEPDEs are presented and two algorithms, essential for the derivation, are given. In Section 4, key points of the implementation are discussed and the computational performance of LBMAT is demonstrated using computations on a common personal computer. Then, in Section 5, SEPDEs in 3D are given and briefly discussed. The resulting SEPDEs for all aforementioned LBM variants (including their mutual comparison) are given in the Supplementary Materials for popular models D1Q3, D2Q5, D2Q9, D3Q7, and D3Q27.

2 Definitions and assumptions

2.1 Lattice Boltzmann equation

The lattice Boltzmann method solves the evolution equation for the discrete density distribution functions fi, \(i=1,2,\dots ,q\), on a lattice covering a computational domain in \(\mathbb {R}^{d}\), where d denotes the dimension and q is the number of discrete velocities discretizing the velocity space [5]. For such a so-called Dd Qq model, the lattice Boltzmann equation is given by

$$ f_{i}(t+\delta_t, {\boldsymbol{x}}+\delta_t{\boldsymbol{c}}_{i}) = f_{i}(t, {\boldsymbol{x}}) + C_{i}(f_{1}(t,{\boldsymbol{x}}),f_{2}(t,{\boldsymbol{x}}),\dots,f_{q}(t,{\boldsymbol{x}})), $$
(1)

where \(i=1,2,\dots ,q\), \(t\in \mathbb {R}^{+}_{0}\) and \({\boldsymbol {x}}\in \mathbb {R}^{d}\) are the temporal and spatial coordinates, respectively, δt is the time step, ci is the discrete velocity associated with fi, and Ci denotes a discrete collision operator such as, for instance, one of the aforementioned SRT-LBM, MRT-LBM, CLBM, or CuLBM. The distance between neighboring lattice sites along each axis is considered the same and denoted by δl. Note that for those components of ci (denoted by [ci]α) that are nonzero, \(\delta _l = \lvert [\boldsymbol {c}_{i}]_{\alpha }\rvert \delta _t\), \(i=1,2,\dots ,q\) and \(\alpha =1,\dots ,d\).

In (1), for the sake of simplicity, all quantities are considered dimensionless [4, 5]. Although δt = 1 and δl = 1 are employed in practice, symbols δt and δl are used throughout the paper to underline the temporal and spatial stepping, especially in the Taylor expansion later in Section 3.

In a vector form, (1) can be considered as

$$ \sum\limits_{i=1}^{q} \mathbf{E}_{i} \boldsymbol{f} (t+\delta_t, {\boldsymbol{x}}+\delta_t{\boldsymbol{c}}_{i}) = \boldsymbol{f}(t,{\boldsymbol{x}}) + \boldsymbol{C}(\boldsymbol{f}(t,{\boldsymbol{x}})), $$
(2)

where \(\boldsymbol {f} := (f_{1},f_{2},\dots ,f_{q})^{T}\), \(\boldsymbol {C}:=(C_{1},C_{2},\dots ,C_{q})^{T}\), and Ei denotes the i-th row-selector q × q matrix, for which [Ei]i,i = 1 is the only nonzero element, \(i=1,2,\dots ,q\).

Raw moments mα, which represent the macroscopic physical quantities [5], are defined by

$$ m_{{\boldsymbol{\alpha}}} := \sum\limits_{i=1}^{q} f_{i} {\boldsymbol{c}}_{i}^{{\boldsymbol{\alpha}}}, $$
(3)

where \({\boldsymbol {\alpha }}=(\alpha _{1},\alpha _{2},\dots ,\alpha _{d})\in \mathbb {N}_{0}^{d}\) denotes a multi-index (as a row vector) and \({\boldsymbol {c}}_{i}^{{\boldsymbol {\alpha }}} := {\prod }_{j=1}^{d} [{\boldsymbol {c}}_{i}]_{j}^{\alpha _{j}}\).

Definition 1 (Conserved raw moments)

A raw moment mα is said to be conserved during the collision, if it is a collision invariant [18], i.e., for all f,

$$ \sum\limits_{i=1}^{q} C_{i}(\boldsymbol{f}) {\boldsymbol{c}}_{i}^{{\boldsymbol{\alpha}}} = \boldsymbol{0}. $$
(4)

A particular choice of a linear combination of raw moments represented by \({\boldsymbol {\mu }}=(\mu _{1},\mu _{2},\dots ,\mu _{q})^{T}\) allows to transform (2) into EFDEs for these macroscopic moments. The transformation is realized using

$$ {\boldsymbol{\mu}} = \mathbf{M}\boldsymbol{f}, $$
(5)

where M is a constant, custom-selected nonsingular transformation matrix between the discrete density distribution functions and raw moments.

2.2 Conserved and nonconserved quantities

Although M in (5) can be selected arbitrarily, additional assumptions need to be placed upon the structure (ordering) of M in order to enable deriving the desired SEPDEs.

Assumption 1

Let M be selected such that the components of μ = Mf are ordered as

$$ {\boldsymbol{\mu}} =\begin{pmatrix} \boldsymbol{\gamma} \\ \boldsymbol{\nu}\end{pmatrix} = (\gamma_{1}, \gamma_{2},\dots,\gamma_{c}, \nu_{1},\nu_{2},\dots,\nu_{n} )^{T}, $$
(6)

where c and n denote the number of conserved (denoted by \(\{\gamma _{i}:=\mu _{i}\}_{i=1}^{c}\)) and nonconserved (denoted by \(\{ \nu _{i} := \mu _{c+i} \}_{i=1}^{n}\)) quantities, respectively, with c + n = q, \({\boldsymbol {\gamma }}:=(\gamma _{1},\gamma _{2},\dots ,\gamma _{c})^{T}\), and \({\boldsymbol {\nu }}:=(\nu _{1},\nu _{2},\dots ,\nu _{n})^{T}\).

In Assumption 1, the conserved quantities (moments) γi, \(i=1,2,\dots ,c\), represent the physical macroscopic quantities that are collision invariants [18] and for which we aim to derive SEPDEs; e.g., c = 1 and c = d + 1 for ADEs and NSEs, respectively. Similar to [10], γ1 is the zeroth-order raw moment (γ1 = μ1 = m0) that corresponds to scalar quantities such as the density ρ (NSEs) or concentration (ADEs) and, in the case of NSEs, \(\gamma _{2},\dots ,\gamma _{d+1}\) correspond to the hydrodynamic momentum components (γ2 = μ2 = m(1,0,0) = ρv1, γ3 = μ3 = m(0,1,0) = ρv2, γ4 = μ4 = m(0,0,1) = ρv3, where (v1,v2,v3)T denotes the macroscopic velocity vector in 3D). Note that the definition of the conserved quantities γ can be extended to represent a general, custom-selected linear combination of conserved raw moments.

2.3 Equivalent finite difference equations

From (2), the EFDEs are obtained by substitution of f = M− 1μ (i.e., the inverse of (5)) and by multiplying (2) by M from the left. The resulting EFDEs read

$$ \Big[ \sum\limits_{i=1}^{q} \mathbf{M} \mathbf{E}_{i} \mathbf{M}^{-1} {\boldsymbol{\mu}} (t+\delta_t, {\boldsymbol{x}}+\delta_t{\boldsymbol{c}}_{i}) \Big] - {\boldsymbol{\mu}}(t,{\boldsymbol{x}}) = \mathbf{M}\boldsymbol{C}(\mathbf{M}^{-1}{\boldsymbol{\mu}}(t,{\boldsymbol{x}})). $$
(7)

In (7), the first c equations can be regarded as those defining the conserved quantities \(\{ \gamma _{i} \}_{i=1}^{c}\) and the rest of them as those associated with the nonconserved quantities \(\{ \nu _{i} \}_{i=1}^{n}\). Let the right-hand sides of (7) corresponding to c conserved and n nonconserved equations be represented by vectors Rc and Rn with components

$$ \left[ \boldsymbol{R}_{{\boldsymbol{c}}}({\boldsymbol{\gamma}},{\boldsymbol{\nu}}) \right]_{i} := \left[ \mathbf{M} \boldsymbol{C}(\mathbf{M}^{-1}{\boldsymbol{\mu}}) \right]_{i}, \quad i=1,2,\dots,c, $$
(8a)

and

$$ \left[ \boldsymbol{R}_{{\boldsymbol{n}}}({\boldsymbol{\gamma}},{\boldsymbol{\nu}}) \right]_{i} := \left[ \mathbf{M} \boldsymbol{C}(\mathbf{M}^{-1}{\boldsymbol{\mu}})) \right]_{c+i}, \quad i=1,2,\dots,n, $$
(8b)

respectively. In Assumption 1, the conserved quantities \(\{\gamma _{i}\}_{i=1}^{c}\) defined by the first c rows of M are collision invariants and as follows from Definition 1, the left multiplication by M in (7) implies Rc = 0. Assumption 2 summarizes the properties of Rn which are required for the derivation of EPDEs.

Assumption 2

Let Rn be expressed using the first-order Taylor polynomial with respect to \({\boldsymbol {\nu }}\in \mathbb {R}^{n}\) at \({\boldsymbol {\nu }}=\vec 0\) for all \({\boldsymbol {\gamma }}\in \mathbb {R}^{c}\) as

$$ \boldsymbol{R}_{{\boldsymbol{n}}}({\boldsymbol{\gamma}},{\boldsymbol{\nu}}) = \boldsymbol{Q}({\boldsymbol{\gamma}}) + \mathbf{L}({\boldsymbol{\gamma}}) {\boldsymbol{\nu}} + \boldsymbol{N}({\boldsymbol{\gamma}}, {\boldsymbol{\nu}}), $$
(9a)

where Q(γ) := Rn(γ,0), \(\mathbf {L}({\boldsymbol {\gamma }}) := \left (\mathrm {D}_{{\boldsymbol {\nu }}} \boldsymbol {R}_{{\boldsymbol {n}}} \right ) ({\boldsymbol {\gamma }}, \boldsymbol {0})\) is a n × n matrix (with Dν denoting the differential operator with respect to ν), and N(γ,ν) denotes the remainder. It is assumed that for all \({\boldsymbol {\gamma }}\in \mathbb {R}^{c}\), L(γ) is nonsingular and N(γ,ν) is polynomial in ν.

Finally, under the notation given by Assumption 2, matrix M needs to satisfy the following property given by Assumption 3.

Assumption 3

Let M be selected such that for all \({\boldsymbol {\gamma }}\in \mathbb {R}^{c}\) and \(k=1,2,\dots ,n\), [L(γ)− 1N(γ,ν)]k does not depend on νk, νk+ 1, … νn.

For any matrix-LBM (such as SRT-LBM, MRT-LBM, CLBM), Assumption 3 is always satisfied since \(\boldsymbol {N}({\boldsymbol {\gamma }},{\boldsymbol {\nu }})=\vec 0\) for all \({\boldsymbol {\gamma }}\in \mathbb {R}^{c}\) and \({\boldsymbol {\nu }}\in \mathbb {R}^{n}\), however, for nonlinear collision operators with \(\boldsymbol {N}({\boldsymbol {\gamma }},{\boldsymbol {\nu }})\neq \vec 0\), M needs to be chosen carefully. In the case of CuLBM, it was found that M can be chosen as the matrix defining the raw moments for the MRT-LBM. The definition of M for each case considered in this paper is given in Section 1.3 of each Supplementary material.

3 Equivalent partial differential equations

The derivation of equivalent partial differential equations described in this section is possible under the assumption of sufficient smoothness of μj, \(j=1,2,\dots ,q\) that allows to consider commutation of partial derivatives involved. From now on, it is assumed that μj are continuously differentiable functions of order D in time and space.

3.1 Taylor expansion

In order to transform (7) into a system of EPDEs, a Taylor expansion of μj, \(j=1,2,\dots ,q\), in time and space centered around (t,x) up to a given degree D is considered in the form

$$ \mu_{j}(t+\delta_t, {\boldsymbol{x}}+\delta_l\boldsymbol{h}) = \mu_{j}(t,{\boldsymbol{x}}) + \sum\limits_{1\leq\lvert {\boldsymbol{\sigma}} \rvert\leq D} \binom{\lvert {\boldsymbol{\sigma}} \rvert}{{\boldsymbol{\sigma}}} \delta_t^{\sigma_{1}} \delta_l^{\lvert {\boldsymbol{\sigma}} \rvert-\sigma_{1}} \Big( \prod\limits_{m=1}^{d} [\boldsymbol{h}]_{m}^{\sigma_{m+1}} \Big) \mathrm{D}_{{\boldsymbol{\sigma}}} \mu_{j}(t,{\boldsymbol{x}}), $$
(10)

where \({\boldsymbol {\sigma }}\in \mathbb {N}^{d+1}_{0}\) is a multi-index, \(\lvert {\boldsymbol {\sigma }} \rvert :={\sum }_{i=1}^{d+1}\sigma _{i}\), \(\boldsymbol {h}\in \mathbb {Z}^{d}\), and Dσ denotes the differential operator

$$ \mathrm{D}_{{\boldsymbol{\sigma}}} := \frac{\partial^{\lvert {\boldsymbol{\sigma}} \rvert}}{\partial t^{\sigma_{1}}\partial x_{1}^{\sigma_{2}}\dots\partial x_{d}^{\sigma_{d+1}}}. $$
(11)

In (10), h represents \(\frac {\delta _t}{\delta _l}{\boldsymbol {c}}_{i}\) from (7) and, to ease the notation in the following, \(\boldsymbol {h}_{i}:=\frac {\delta _t}{\delta _l}{\boldsymbol {c}}_{i}\) is used for all \(i=1,2,\dots ,q\).

After combining Taylor-expanded moments given by (10) with (7), the resulting raw EPDEs read

$$ \begin{array}{ll} \sum\limits_{i=1}^{q} \mathbf{M} \mathbf{E}_{i} \mathbf{M}^{-1} \Big[ \sum\limits_{1\leq\lvert {\boldsymbol{\sigma}} \rvert\leq D} \left( \begin{array}{c}{\lvert{\boldsymbol{\sigma}} \rvert}\\{{\boldsymbol{\sigma}}} \end{array}\right) \delta_t^{\sigma_{1}} \delta_l^{\lvert {\boldsymbol{\sigma}} \rvert-\sigma_{1}} \Big(\prod\limits_{m=1}^{d} [\boldsymbol{h}_{i}]_{m}^{\sigma_{m+1}} \Big) \mathrm{D}_{{\boldsymbol{\sigma}}} {\boldsymbol{\mu}}(t,{\boldsymbol{x}}) \Big] = \\ \mathbf{M}\boldsymbol{C}(\mathbf{M}^{-1}{\boldsymbol{\mu}}(t,{\boldsymbol{x}})), \end{array} $$
(12)

where the fact that \({\sum }_{i=1}^{q} \mathbf {E}_{i}\) gives the identity matrix is used to cancel out the zeroth-order derivatives (ZOD) of μ from the left-hand side of the equation.

Employing the notation introduced in (8a), (12) can be written as

$$ \sum\limits_{1\leq \lvert{\boldsymbol{\sigma}}\rvert\leq D}\begin{pmatrix} \mathbf{P}_{{\boldsymbol{c}},{\boldsymbol{c}}}^{({\boldsymbol{\sigma}})} & \mathbf{P}_{{\boldsymbol{c}},{\boldsymbol{n}}}^{({\boldsymbol{\sigma}})} \\ \mathbf{P}_{{\boldsymbol{n}},{\boldsymbol{c}}}^{({\boldsymbol{\sigma}})} & \mathbf{P}_{{\boldsymbol{n}},{\boldsymbol{n}}}^{({\boldsymbol{\sigma}})} \end{pmatrix} \begin{pmatrix} \mathrm{D}_{{\boldsymbol{\sigma}}}{\boldsymbol{\gamma}}(t,{\boldsymbol{x}})\\ {\mathrm{D}_{{\boldsymbol{\sigma}}}{\boldsymbol{\nu}}(t,{\boldsymbol{x}})} \end{pmatrix}= \begin{pmatrix}{\boldsymbol{0}}\\{\boldsymbol{R}_{{\boldsymbol{n}}}(t,{\boldsymbol{x}})}, \end{pmatrix} $$
(13)

where \(\{ \mathbf {P}_{\boldsymbol {\alpha },\boldsymbol {\beta }}^{({\boldsymbol {\sigma }})} \}_{\boldsymbol {\alpha },\boldsymbol {\beta } \in \{ {\boldsymbol {c}},{\boldsymbol {n}} \}}\) denote constant matrices defined by

$$ \begin{pmatrix} \mathbf{P}_{{\boldsymbol{c}},{\boldsymbol{c}}}^{({\boldsymbol{\sigma}})} & \mathbf{P}_{{\boldsymbol{c}},{\boldsymbol{n}}}^{({\boldsymbol{\sigma}})} \\ \mathbf{P}_{{\boldsymbol{n}},{\boldsymbol{c}}}^{({\boldsymbol{\sigma}})} & \mathbf{P}_{{\boldsymbol{n}},{\boldsymbol{n}}}^{({\boldsymbol{\sigma}})} \end{pmatrix} := \sum\limits_{i=1}^{q} \binom{\lvert {\boldsymbol{\sigma}} \rvert}{{\boldsymbol{\sigma}}} \delta_t^{\sigma_{1}} \delta_l^{\lvert {\boldsymbol{\sigma}} \rvert-\sigma_{1}} \Big(\prod\limits_{m=1}^{d} [\boldsymbol{h}_{i}]_{m}^{\sigma_{m+1}} \Big) \mathbf{M} \mathbf{E}_{i} \mathbf{M}^{-1}. $$
(14)

3.2 Elimination of nonconserved quantities

Assumption 2 together with (13) allows to express ν from EPDEs for the nonconserved quantities as

$$ \begin{array}{@{}rcl@{}} {\boldsymbol{\nu}} &=& \sum\limits_{1\leq\lvert {\boldsymbol{\sigma}} \rvert\leq D} \left[ \mathbf{L}({\boldsymbol{\gamma}})^{-1} \mathbf{P}_{{\boldsymbol{n}},{\boldsymbol{c}}}^{({\boldsymbol{\sigma}})} \mathrm{D}_{{\boldsymbol{\sigma}}} {\boldsymbol{\gamma}} + \mathbf{L}({\boldsymbol{\gamma}})^{-1} \mathbf{P}_{{\boldsymbol{n}},{\boldsymbol{n}}}^{({\boldsymbol{\sigma}})} \mathrm{D}_{{\boldsymbol{\sigma}}} {\boldsymbol{\nu}} \right]\\ &&- \mathbf{L}({\boldsymbol{\gamma}})^{-1}\boldsymbol{N}({\boldsymbol{\gamma}},{\boldsymbol{\nu}}) - \mathbf{L}({\boldsymbol{\gamma}})^{-1}\boldsymbol{Q}({\boldsymbol{\gamma}}). \end{array} $$
(15)

For all \(k=1,2,\dots ,n\), the ZODs of nonconservative quantities \(\{\nu _{i}\}_{i=1}^{n}\) in the right-hand side of (15) are present in the nonlinear term [L(γ)− 1N(γ,ν)]k only. Since (15) can be regarded as a recursive system of equations for \(\nu _{1}, \nu _{2},\dots , \nu _{n}\), the assumption of N being polynomial with respect to ν (Assumption 2) together with the Assumption 3 allows using a Gaussian-type recursive elimination procedure with truncation of higher order derivatives to completely eliminate all nonconservative quantities ν from the right-hand side of (15). In Definition 2, the truncation strategy used here is described and referred to as the second degree truncation since the resulting partial differential expression is assumed in a form of the second-degree polynomial in terms of derivatives of (γ,ν).

Note that in Definition 2, polynomials with higher degrees can also be used to represent the truncated expressions, however, it may not be feasible from the computational point of view because the complexity of the resulting expressions and subsequent memory demands for the derivation of EPDEs and SEPDEs will increase considerably. On the other hand, the second-degree polynomials are found to sufficiently represent the desired EPDEs and SEPDEs, therefore, only the second-degree polynomials are considered and implemented through Definition 2 in LBMAT.

The Gaussian-type elimination procedure applied to (15) is described by Algorithm 1. Note that based on Assumption 3, ZOD of νk is not present in the right-hand side of k-th (A) for all \(k=1,2,\dots ,n\).

Definition 2 (A second-degree truncation strategy of order D for a polynomial partial differential expression)

Let \(\mathcal {F}^{(A,B,C)}(y_{1}(t,{\boldsymbol {x}}), y_{2}(t,{\boldsymbol {x}}), \dots , y_{q}(t,{\boldsymbol {x}}))\) denote a partial differential expression where \(\mathcal {F}^{(A,B,C)}\) is a polynomial of degree A with respect to derivatives of \(\{y_{i}\}_{i=1}^{q}\) (of at least the first order) with general (nonlinear) coefficients, B denotes the highest order of derivatives of \(\{y_{i}\}_{i=1}^{q}\) present in the expression, and C is the highest sum of orders of derivatives present in products, i.e.,

$$ \begin{array}{@{}rcl@{}} &&\mathcal{F}^{(A,B,C)}(y_{1},y_{2},\dots,y_{q}) = a_{0}(y_{1},y_{2},\dots,y_{q}) + \end{array} $$
(16)
$$ \begin{array}{@{}rcl@{}} && \sum\limits_{i_{1}=1}^{q} \sum\limits_{1\leq\lvert {\boldsymbol{\sigma}}_{1} \rvert\leq B} a_{i_{1}}^{({\boldsymbol{\sigma}}_{1})}(y_{1},y_{2},\dots,y_{q}) \mathrm{D}_{{\boldsymbol{\sigma}}_{1}} y_{i_{1}}+ \end{array} $$
(17)
$$ \begin{array}{@{}rcl@{}} && \sum\limits_{i_{1}=1}^{q} \sum\limits_{i_{2}=i_{1}}^{q} \underset{\lvert {\boldsymbol{\sigma}}_{1} \rvert+\lvert {\boldsymbol{\sigma}}_{2} \rvert\leq C}{\underset{1\leq\lvert {\boldsymbol{\sigma}}_{2} \rvert \leq B}{\underset{1\leq\lvert {\boldsymbol{\sigma}}_{1} \rvert \leq B}{\sum}}}a_{i_{1},i_{2}}^{({\boldsymbol{\sigma}}_{1},{\boldsymbol{\sigma}}_{2})}(y_{1},y_{2},\dots,y_{q}) \mathrm{D}_{{\boldsymbol{\sigma}}_{1}} y_{i_{1}} \mathrm{D}_{{\boldsymbol{\sigma}}_{2}} y_{i_{2}} + {\dots} + \end{array} $$
(18)
$$ \begin{array}{@{}rcl@{}} && \sum\limits_{i_{1}=1}^{q} \sum\limits_{i_{2}=i_{1}}^{q} {\dots} \sum\limits_{i_{A}=i_{A-1}}^{q} \underset{{\sum}_{k=1}^{A} \lvert {\boldsymbol{\sigma}}_{k} \rvert\leq C}{\underset{1\leq \lvert {\boldsymbol{\sigma}}_{A} \rvert\leq B}{\underset{\dots}{\underset{1\leq \lvert {\boldsymbol{\sigma}}_{2} \rvert \leq B}{\underset{1 \leq \lvert {\boldsymbol{\sigma}}_{1} \rvert \leq B}{\sum}}}}} a_{i_{1},i_{2},\dots,i_{A}}^{({\boldsymbol{\sigma}}_{1},{\boldsymbol{\sigma}}_{2},\dots,{\boldsymbol{\sigma}}_{A})}(y_{1},y_{2},\dots,y_{q}) \prod\limits_{\ell=1}^{A} \mathrm{D}_{{\boldsymbol{\sigma}}_{\ell}} y_{i_{\ell}}, \end{array} $$
(19)

where the polynomial’s coefficients are represented by the symbol a. Then, the second-degree truncated partial differential expression of order D for \(\mathcal {F}^{(A,B,C)}\) is given by \(\mathcal {F}^{(2,D,D)}\).

Algorithm 1
figure a

Gaussian-type recursive elimination of ν in (15).

Full size image

After the Gaussian elimination with the second-degree truncation strategy of order D is done in (15), the nonconserved quantities can be expressed as functions of γ only:

$$ \begin{array}{@{}rcl@{}} &&\nu_{k} = {b}_{k}({\boldsymbol{\gamma}}) + \sum\limits_{j=1}^{c} \sum\limits_{1\leq\lvert {\boldsymbol{\sigma}} \rvert\leq D} b_{k,j}^{({\boldsymbol{\sigma}})}({\boldsymbol{\gamma}}) \mathrm{D}_{{\boldsymbol{\sigma}}} \gamma_{j} +\\ && \sum\limits_{j_{1}=1}^{c} \sum\limits_{j_{2}=j_{1}}^{c} \underset{\lvert{\boldsymbol{\sigma}}_{1} \rvert+\lvert {\boldsymbol{\sigma}}_{2} \rvert\leq D}{\underset{1\leq\lvert {\boldsymbol{\sigma}}_{2} \rvert\leq D}{\underset{1\leq\lvert {\boldsymbol{\sigma}}_{1} \rvert\leq D}{\sum}}}b_{k,j_{1},j_{2}}^{({\boldsymbol{\sigma}}_{1},{\boldsymbol{\sigma}}_{2})}({\boldsymbol{\gamma}}) \mathrm{D}_{{\boldsymbol{\sigma}}_{1}} \gamma_{j_{1}} \mathrm{D}_{{\boldsymbol{\sigma}}_{2}} \gamma_{j_{2}}, \end{array} $$
(20)

\(k=1,2,\dots ,n\), where all coefficients denoted by the symbol b are produced by Algorithm 1.

In the vector form, (20) can be represented by

$$ {\boldsymbol{\nu}} = {\boldsymbol{b}}({\boldsymbol{\gamma}}) + \sum\limits_{1\leq\lvert {\boldsymbol{\sigma}} \rvert\leq D} \mathbf{B}_{(2)}^{({\boldsymbol{\sigma}})}({\boldsymbol{\gamma}}) \mathrm{D}_{{\boldsymbol{\sigma}}} {\boldsymbol{\gamma}} + \underset{\lvert{\boldsymbol{\sigma}}_{1} \rvert+\lvert {\boldsymbol{\sigma}}_{2} \rvert\leq D}{\underset{1\leq\lvert {\boldsymbol{\sigma}}_{2} \rvert\leq D}{\underset{1\leq\lvert {\boldsymbol{\sigma}}_{1} \rvert\leq D}{\sum}}}\mathbf{B}_{(3)}^{({\boldsymbol{\sigma}}_{1},{\boldsymbol{\sigma}}_{2})}({\boldsymbol{\gamma}}) \mathrm{D}_{{\boldsymbol{\sigma}}_{1}} {\boldsymbol{\gamma}} \ \mathrm{D}_{{\boldsymbol{\sigma}}_{2}} {\boldsymbol{\gamma}}, $$
(21)

where \(\boldsymbol {b}=(b_{1},b_{2},\dots ,b_{n})^{T}\), and B(2) and B(3) denote the second- and third-order tensors \((b_{k,j})_{k,j=1}^{n,c}\) and \((b_{k,j_{1},j_{2}})_{k,j_{1},j_{2}=1}^{n,c,c}\), respectively.

3.3 Spatial EPDEs for conserved quantities

Combining (21) with the equations corresponding to the conserved quantities in (13), the following system of c partial differential equations for \(\{\gamma _{i}\}_{i=1}^{c}\) is obtained:

$$ \begin{array}{@{}rcl@{}} \sum\limits_{1\leq\lvert {\boldsymbol{\sigma}}_{0} \rvert\leq D} \left[ \mathbf{P}_{{\boldsymbol{c}},{\boldsymbol{c}}}^{({\boldsymbol{\sigma}}_{0})} \mathrm{D}_{{\boldsymbol{\sigma}}_{0}} {\boldsymbol{\gamma}} + \mathbf{P}_{{\boldsymbol{c}},{\boldsymbol{n}}}^{({\boldsymbol{\sigma}}_{0})} \mathrm{D}_{{\boldsymbol{\sigma}}_{0}} \boldsymbol{b}({\boldsymbol{\gamma}}) \right] + \underset{\underset{1\leq\lvert {\boldsymbol{\sigma}}_{1} \rvert\leq D}{1\leq\lvert {\boldsymbol{\sigma}}_{0} \rvert\leq D}}{\sum} \mathbf{P}_{{\boldsymbol{c}},{\boldsymbol{n}}}^{({\boldsymbol{\sigma}}_{0})} \mathrm{D}_{{\boldsymbol{\sigma}}_{0}} \left( \mathbf{B}_{(2)}^{({\boldsymbol{\sigma}}_{1})}({\boldsymbol{\gamma}}) \mathrm{D}_{{\boldsymbol{\sigma}}_{1}} {\boldsymbol{\gamma}} \right)\\ + \underset{\lvert {\boldsymbol{\sigma}}_{1} \rvert+\lvert {\boldsymbol{\sigma}}_{2} \rvert\leq D}{\underset{1\leq\lvert {\boldsymbol{\sigma}}_{2} \rvert\leq D}{\underset{1\leq\lvert {\boldsymbol{\sigma}}_{1} \rvert\leq D}{\underset{1\leq\lvert {\boldsymbol{\sigma}}_{0} \rvert\leq D}{\sum}}}} \mathbf{P}_{{\boldsymbol{c}},{\boldsymbol{n}}}^{({\boldsymbol{\sigma}}_{0})} \mathrm{D}_{{\boldsymbol{\sigma}}_{0}} \left( \mathbf{B}_{(3)}^{({\boldsymbol{\sigma}}_{1},{\boldsymbol{\sigma}}_{2})}({\boldsymbol{\gamma}}) \mathrm{D}_{{\boldsymbol{\sigma}}_{1}} {\boldsymbol{\gamma}} \mathrm{D}_{{\boldsymbol{\sigma}}_{2}} {\boldsymbol{\gamma}} \right) = \boldsymbol{0}. \end{array} $$
(22)

Expanding all derivatives together with the truncation strategy from Definition 2, (22) is transformed into

$$ \sum\limits_{1\leq\lvert {\boldsymbol{\sigma}}_{1} \rvert\leq D} \mathbf{A}_{(2)}^{({\boldsymbol{\sigma}}_{1})}({\boldsymbol{\gamma}}) \mathrm{D}_{{\boldsymbol{\sigma}}_{1}} {\boldsymbol{\gamma}} +\underset{\lvert{\boldsymbol{\sigma}}_{1} \rvert+\lvert {\boldsymbol{\sigma}}_{2} \rvert\leq D}{\underset{1\leq\lvert {\boldsymbol{\sigma}}_{2} \rvert\leq D}{\underset{1\leq\lvert {\boldsymbol{\sigma}}_{1} \rvert\leq D}{\sum}}}\mathbf{A}_{(3)}^{({\boldsymbol{\sigma}}_{1},{\boldsymbol{\sigma}}_{2})}({\boldsymbol{\gamma}}) \mathrm{D}_{{\boldsymbol{\sigma}}_{1}} {\boldsymbol{\gamma}} \mathrm{D}_{{\boldsymbol{\sigma}}_{2}} {\boldsymbol{\gamma}} = \boldsymbol{0}, $$
(23)

where A(2) and A(3) denote the resulting second- and third-order tensors, respectively.

Equation (23) is a system of partial differential equations for the conserved quantities γ with coefficients independent of ν. As such, (23) represents the sought EPDEs of (1). However, as in [10], (23) can be further processed in order to produce SEPDEs by eliminating all temporal derivatives of γ except for Dtγ (\(\mathrm {D}_{t} := \frac {\partial }{\partial t}\)). Since (23) describes the evolution of conserved quantities, it is expected that \(\mathbf {A}_{(2)}^{({\boldsymbol {\tau }})}({\boldsymbol {\gamma }})\), with \({\boldsymbol {\tau }}:=(1,\boldsymbol {0})^{T}\in \mathbb {N}_{0}^{d+1}\), is nonsingular for all γ and Dtγ can be expressed from (23) as

$$ \begin{array}{@{}rcl@{}} \mathrm{D}_{t}{\boldsymbol{\gamma}} &=& - \underset{\underset{{\boldsymbol{\sigma}}_{1}\neq{\boldsymbol{\tau}}}{1\leq\lvert {\boldsymbol{\sigma}}_{1} \rvert\leq D}}{\sum} \mathbf{A}_{(2)}^{({\boldsymbol{\tau}})}({\boldsymbol{\gamma}})^{-1} \mathbf{A}_{(2)}^{({\boldsymbol{\sigma}}_{1})}({\boldsymbol{\gamma}}) \mathrm{D}_{{\boldsymbol{\sigma}}_{1}} {\boldsymbol{\gamma}}+ \\ && \underset{\lvert {\boldsymbol{\sigma}}_{1} \rvert+\lvert {\boldsymbol{\sigma}}_{2} \rvert\leq D}{\underset{1\leq\lvert {\boldsymbol{\sigma}}_{2} \rvert\leq D}{\underset{1\leq\lvert {\boldsymbol{\sigma}}_{1} \rvert\leq D}{\sum}}}\mathbf{A}_{(2)}^{({\boldsymbol{\tau}})}({\boldsymbol{\gamma}})^{-1} \mathbf{A}_{(3)}^{({\boldsymbol{\sigma}}_{1},{\boldsymbol{\sigma}}_{2})}({\boldsymbol{\gamma}}) \mathrm{D}_{{\boldsymbol{\sigma}}_{1}} {\boldsymbol{\gamma}} \mathrm{D}_{{\boldsymbol{\sigma}}_{2}} {\boldsymbol{\gamma}}. \end{array} $$
(24)

Equation (24) forms a recursive equation for Dtγ that, as in [10], allows to eliminate all temporal derivatives of γ from its right-hand side (again with the truncation strategy described in Definition 2). This procedure is described by Algorithm 2.

Algorithm 2
figure b

Elimination of temporal derivatives from (24).

Full size image

3.4 Summary

In essence, the derivation of SEPDEs from the lattice Boltzmann equation given by (1), for which the collision operator satisfies Assumption 2, consists of the following steps:

  1. 1.

    Select matrix M that satisfies Assumptions 1 and 3.

  2. 2.

    Assemble EPDE in (13).

  3. 3.

    Use Algorithm 1 to eliminate nonconserved quantities and produce (23).

  4. 4.

    Use Algorithm 2 to eliminate temporal derivatives of γ in the right-hand side of (24) and produce SEPDEs.

4 Implementation

The computational algorithm summarized in Section 3.4 is implemented in C++ using the GiNaC library for symbolic algebraic computation [14]. The code is made available to the LBM community as open-source software LBMAT (Lattice Boltzmann Method Analysis Tool) under the terms and conditions of the GNU general public license (GPL):

Due to the extreme complexity of recurrently substituted partial differential expressions in Algorithms 1 and 2, the computational code is required to be carefully designed with respect to the computational efficiency and memory demands. In the following section, the most important implementation challenges are discussed.

4.1 Representation of truncated partial differential expressions

In the code, the truncated partial differential expressions given by Definition 2 are represented by structure TPDE which also provides all required operations on TPDE such as addition, multiplication by another TPDE, differentiation of a general order, substitution of a coefficient or a derivative for another TPDE, and simplification of the expression. By design, the second-degree truncation strategy given by Definition 2 is implemented automatically inside TPDE by storing the desired coefficients and discarding all that correspond to higher order derivatives or higher degree polynomial than D with respect to these derivatives.

Since all the aforementioned operations can become computationally expensive and substantially memory demanding, it is crucial to use an efficient storage for the coefficients. For this task, the structure std::unordered_map from the C++ Standard Template Library was found to be the best choice. Unordered map is a container in which elements are stored in buckets addressed by a hash of keys [19]. In LBMAT, these keys correspond to multi-indices α that define the derivatives of the quantities.

4.2 Symbolic substitutions

During the recurrent substitutions of partial differential expressions in Algorithms 1 and 2, the process of simplification of algebraic expressions within GiNaC is the most computationally expensive and memory demanding operation. If an algebraic expression involved in the recurrent substitutions consists of more than one summand, the number of summands in the resulting expression may increase exponentially in each iteration of the algorithms, especially for large q. Therefore, all expressions with more than one summand are replaced by a symbolic variable and the substitution is listed for later re-use.

To obtain the final EPDEs after Algorithms 1 and 2 completed, the deferred symbolic variables need to be replaced recursively by the substitutions established during the execution of the algorithms. This replacement is implemented as a post-processing step: first, the substitutions are offloaded into files stored on a disk to reduce RAM usage and outputs the EPDEs with symbolic variables, then, a separate Python script (using GiNaC internally to simplify algebraic expressions) is executed to perform recursive replacements. The dependencies between symbolic variables in the listed substitutions are analyzed and only those variables that are needed in the final EPDEs are actually substituted.

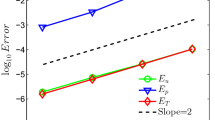
Using this approach, computational times and the amount of memory needed for both algorithms (including the post-processing step) decrease considerably and even for the most complex LBM models in 3D (CLBM or CuLBM in D3Q27), EPDEs and SEPDEs can be computed on a personal computer, see Table 1 for illustrative computational times. The execution times of the Python script are marginal with respect to the execution of LBMAT and they are not included in the computational times listed in Table 1.

Table 1 Illustrative computational times and peak memory usage for all cases computed on a personal computer equipped with a single Intel Core i9-9900KF CPU (at 3.6 GHz) and 64 GB RAM
Full size table

5 Illustrative SEPDEs in 3D

In order to demonstrate the applicability of LBMAT, SEPDEs for ADEs and NSEs in 3D using D3Q7 and D3Q27 models, respectively, are presented in this section. In the Supplementary Materials, the definitions of LBM models SRT, MRT1, MRT2, CLBM1, CLBM2, CuLBM1, and CuLBM2 are given together with the list of all SEPDEs coefficients (marked in green) that mutually differ among these models.

5.1 ADE D3Q7

In this section, for the sake of brevity, the velocity vector v is considered constant in time and space and the SEPDE for ADE is shown up to the fourth-order derivative (truncated as \(\mathcal {F}^{(2,4,4)}\) based on Definition 2). For the non-constant velocity case, the coefficients of SEPDE for ADE are listed in the Supplementary materials (ADE, model D3Q7).

$$ \frac{ \partial \rho}{\partial t} + \frac{\delta_l}{\delta_t}\boldsymbol{v}\cdot{\nabla \rho} - {\nabla} \cdot \left( \frac{\delta_l^{2}}{\delta_t} {\mathbf{D}} {\nabla \rho} \right) +\underset{\underset{3\leq \lvert \boldsymbol{\alpha} \rvert\leq4}{\boldsymbol{\alpha}\in\mathbb{N}_{0}^{3} }}{\sum} {C^{(0),\text{ADE}}_{{\mathrm{D}_{x_1}^{\alpha_{1}}\mathrm{D}_{x_2}^{\alpha_{2}}\mathrm{D}_{x_3}^{\alpha_{3}}\rho}}} \frac{\delta_l^{\lvert \boldsymbol{\alpha} \rvert}}{\delta_t} \frac{ \partial^{\lvert \boldsymbol{\alpha} \rvert} \rho}{\partial x_1^{\alpha_{1}} \partial x_2^{\alpha_{2}} \partial x_3^{\alpha_{3}}} =0, $$
(25)

where the diffusion tensor is given by

$$ {\mathbf{D}} = \left( \frac1\omega - \frac12\right) \begin{pmatrix} {c_{s}^{2}} & -v_1v_2 & -v_1v_3 \\ -v_{2} v_{1} & {c_{s}^{2}} & -v_2v_3 \\ -v_{3} v_{1} & -v_{3} v_2 & {c_{s}^{2}} \end{pmatrix} $$
(26a)

for SRT, and by

$$ {\mathbf{D}} = \begin{pmatrix} \left( \frac1{\omega_{2}} -\frac12 \right) {c_{s}^{2}} & \left( \frac12-\frac{1}{2\omega_{2}} - \frac{1}{2\omega_{3}} \right) v_1v_2 & \left( \frac12 - \frac{1}{2\omega_{2}} - \frac{1}{2\omega_{4}} \right) v_1v_3 \\ \left( \frac12 - \frac{1}{2\omega_{2}} - \frac{1}{2\omega_{3}} \right) v_{2} v_1 & \left( \frac1{\omega_{3}} -\frac12 \right) {c_{s}^{2}} & \left( \frac12 - \frac{1}{2\omega_{3}} - \frac{1}{2\omega_{4}} \right) v_2v_3 \\ \left( \frac12 - \frac{1}{2\omega_{2}} - \frac{1}{2\omega_{4}} \right) v_{3} v_1 & \left( \frac12 - \frac{1}{2\omega_{3}} - \frac{1}{2\omega_{4}} - \right) v_{3} v_2 & \left( \frac1{\omega_{4}} -\frac12 \right) {c_{s}^{2}} & \end{pmatrix} $$
(26b)

for MRT1, MRT2, CLBM1, and CLBM2. The diffusion tensor contains extra terms, which is in accordance with [20].

5.2 NSE D3Q27

The conservation of mass is recovered as

$$ \begin{array}{@{}rcl@{}} \!\!\!\!\!\!\!\!\!\!\!\!{\frac{ \partial \rho}{\partial t}} \!+ \frac{\delta_l}{\delta_t} {\nabla} \cdot \left( {\rho\boldsymbol{v}} \right) + \frac{\delta_l^{3}}{12\delta_t} \sum\limits_{k=1}^{3} \!\left[ (3 {c_{s}^{2}} - 1 + {v_{k}^{2}} )v_{k} {\frac{ \partial^{3} \rho}{\partial {x_{k}^{3}}}} + ({c_{s}^{2}} - 1+3 {v_{k}^{2}}) \rho {\frac{ \partial^{3} v_{k}}{\partial {x_{k}^{3}}}} \right] && \\ - \frac{ \rho {c_{s}^{2}}}{6}\frac{\delta_l^{3}}{\delta_t} \!\left[ {\frac{ \partial^{3} v_1}{\partial x_{1}\partial x_{2}^{2}}} + {\frac{ \partial^{3} v_1}{\partial x_1\partial x_3^{2}}} + {\frac{ \partial^{3} v_2}{\partial x_{1}^{2}\partial x_{2}}} + {\frac{ \partial^{3} v_2}{\partial x_{2}\partial x_{3}^{2}}} + {\frac{ \partial^{3} v_3}{\partial x_{1}^{2}\partial x_{3}}} + {\frac{ \partial^{3} v_3}{\partial x_{2}^{2}\partial x_{3}}} \right] &&\\ \!+ \sum\limits_{\beta \in \{ \rho, v_1, v_2, v_3 \} } \underset{ \underset{\lvert \boldsymbol{\alpha} \rvert=4}{\boldsymbol{\alpha}\in\mathbb{N}_{0}^{3}} }{\sum} {C^{(0),\text{NSE}}_{{\mathrm{D}_{x}^{\alpha_{1}}\mathrm{D}_{y}^{\alpha_{2}}\mathrm{D}_{z}^{\alpha_{3}}\beta}}} \frac{\delta_l^{4}}{\delta_t} \frac{ \partial^{\lvert \boldsymbol{\alpha} \rvert} \beta}{\partial x_{1}^{\alpha_{1}} \partial x_{2}^{\alpha_{2}} \partial x_{3}^{\alpha_{3}}} = 0,&& \end{array} $$
(27)

and for all i = 1,2,3, the conservation of momentum ρvi is given by:

$$ \begin{array}{@{}rcl@{}} {\frac{ \partial (\rho v_{i})}{\partial t}} + \frac{\delta_l}{\delta_t} {\nabla} \cdot \left( { \rho v_{i} \boldsymbol{v}} \right) + {c_{s}^{2}} \frac{\delta_l}{\delta_t}{\frac{ \partial \rho}{\partial x_{i}}} + \frac{\delta_l^{2}}{\delta_t} {\frac{ \partial \rho}{\partial x_{i}}} \left[ \sum\limits_{j=1}^{3} { C_{{\mathrm{D}_{x_{i}}\rho},{\mathrm{D}_{x_{j}}v_{j}}}^{(i)\text{NSE}}} { \frac{ \partial v_{j}}{\partial x_{j}} } \right] \\ + \frac{\delta_l^{2}}{\delta_t} \left[ \sum\limits_{\substack{j=1\\j\neq i}}^{3} {\frac{ \partial \rho}{\partial x_{j}}} \left( {{C_{{\mathrm{D}_{x_{j}}\rho},{\mathrm{D}_{x_{j}}v_{i}}}^{(i)\text{NSE}}}} {\frac{ \partial v_{i}}{\partial x_{j}}} + {{C_{{\mathrm{D}_{x_{j}}\rho},{\mathrm{D}_{x_{i}}v_{j}}}^{(i)\text{NSE}}}} {\frac{ \partial v_{j}}{\partial x_{i}}} \right) + {{C_{{\mathrm{D}_{x_{i}}\mathrm{D}_{x_{j}}v_{j}}}^{(i)\text{NSE}}}} {\frac{ \partial^{2} v_{j}}{\partial x_{i} \partial x_{j}}} \right] \\ + \frac{\delta_l^{2}}{\delta_t} \left[ \sum\limits_{j=1}^{3} {{C_{{\mathrm{D}_{x_{i}}\mathrm{D}_{x_{j}}\rho}}^{(i)\text{NSE}}}} {\frac{ \partial^{2} \rho}{\partial x_{i}\partial x_{j}}} + {{C_{{\mathrm{D}_{x_{i}}v_{j}},{\mathrm{D}_{x_{j}}v_{j}}}^{(i)\text{NSE}}}} {\frac{ \partial v_{j}}{\partial x_{i}} \frac{ \partial v_{j}}{\partial x_{j}}} + {{C_{{\mathrm{D}_{x_{j}}^{2} v_{i}}}^{(i)\text{NSE}}}} {\frac{ \partial^{2} v_{i}}{\partial {x_{j}^{2}}}} \right] \\ + \sum\limits_{\beta \in \{ \rho, v_1, v_2, v_3 \} } \underset{ \underset{3\leq\lvert \boldsymbol{\alpha} \rvert\leq4}{\boldsymbol{\alpha}\in\mathbb{N}_{0}^{3}} }{\sum} {C^{(i),\text{NSE}}_{{\mathrm{D}_{x_{1}}^{\alpha_{1}}\mathrm{D}_{x_{2}}^{\alpha_{2}}\mathrm{D}_{x_{3}}^{\alpha_{3}}\beta}}} \frac{\delta_l^{\lvert \boldsymbol{\alpha} \rvert}}{\delta_t} {\frac{ \partial^{\lvert \boldsymbol{\alpha} \rvert} \beta}{ \partial x_{1}^{\alpha_{1}} \partial x_{2}^{\alpha_{2}} \partial x_{3}^{\alpha_{3}} }} = 0. \end{array} $$
(28)

The resulting mass and momentum conservation equations (27), (28) are in accordance with macroscopic equations given in [5]. In order to match the coefficients in (28) and in the Supplementary Materials, the coefficients’ denotations in (28) need to be arranged lexicographically due to commutation of products or partial derivatives, i.e., for instance, \(C^{(i)}_{\mathrm {D}_{x_{a}}v_{b},\mathrm {D}_{x_{c}}v_{d}}=C^{(i)}_{\mathrm {D}_{x_{c}}v_{d},\mathrm {D}_{x_{a}}v_{b}}\) or \(C^{(i)}_{\mathrm {D}_{x_{a}}\mathrm {D}_{x_{b}}v_{c}}=C^{(i)}_{\mathrm {D}_{x_{b}}\mathrm {D}_{x_{a}}v_{c}}\), respectively.

6 Conclusion

A computational analysis tool LBMAT has been proposed and implemented for the derivation of equivalent partial differential equations of the lattice Boltzmann method. The applicability of LBMAT has been demonstrated using the popular velocity models Dd Qq and collision operators (SRT, MRT, CLBM, and CuLBM) for both advection–diffusion and Navier–Stokes equations. The LBMAT computer code is available to the LBM community under the GPL license and can be used to analyze existing variants of LBM. By its general design, it can be employed in the development of new variants of LBM in the future.