Abstract
This paper presents theoretical investigations of lattice Boltzmann method (LBM) to develop a completed LBM theory. Based on H-theorem with Lagrangian multiplier method, an amended theoretical equilibrium distribution function (EDF) is derived, which modifies the current Maxwell–Boltzmann distribution (MBD) to include the total internal energy as its parameter. This modification allows the three conservation laws derived directly from lattice Boltzmann equation (LBE) without additional small-parameter expansions adopted in references. From this amended theoretical EDF, an improved LBM is developed, in which the total internal energy like the mass density and mean velocity is a new macroscopic variable to be updated for different times and cells during simulations. The developed method provides a means to consider external forces and energy generation sources as generalised forces in LBM simulations. The corresponding model and implementation process of the improved LBM are presented with its performance theoretically investigated. Analytically hand-workable examples are given to illustrate its applications and to confirm its validity. The paper will excite more researchers and scientists of this area to numerically practice the new theory and method dealing with complex physical problems, from which it is expected to further advance LBM benefiting science and engineering.
Graphic abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Lattice Boltzmann method (LBM) is based on microscopic molecule dynamics [1,2,3,4,5], concerning molecule distribution in space. Boltzmann transport equation (BTE) [6,7,8,9] and H-theorem confirm that the equilibrium distribution function (EDF) is Maxwell–Boltzmann distribution (MBD) [7], contributed a way to understand macroscopic world and form a mesoscopic method dealing with macroscopic motions [10,11,12]. The solution of BTE is very difficult, and attempts have been made to simplify the collision term, for which the best-known model [13] has been implemented. LBM was developed from the lattice gas automata (LGA) [14, 15]. McNamara and Zanetti [16] contributed a historic contribution to replace the Boolean variable in LGA by a real variable, and initially created LBM. The idea of LBM is imaging gases/fluids as a finite number of particles with random motions, and their exchange of momentum and energy achieved through particle streaming and collisions. Key historic publications [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63] making LBM into new stages should be highlighted. The important review papers [39, 59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81] and the influential books [82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97] have been published. LBM is considered as an effective method to model some phenomena not easily macroscopically described by other methods [98]. It has many computer codes of LBM provided [85,86,87, 91, 99, 100].
In practical simulations based on the current LBM, it has been realized that it is probably most suitable for isothermal weakly-compressible flows. For complex flows, especially the ones involving high speed, large compressibility, and obvious energy exchanges, it has suffered from numerical problems on accuracy, efficiency, and stability. To solve these problems, when simulating multicomponent flows, Swift et al. [101, 102] added an additional term of free energy in EDF for the conservation of total energy, including the surface, kinetic, and internal energies to be satisfied [103]. Meanwhile, studying thermodynamics in incompressible limit, He et al. [104] proposed a thermal model with an internal energy density distribution expressed by a multiplication of MBD and kinetic energy, so that the evolution equations of the introduced energy distribution together with original BTE were solved to simulate temperature fields. Until now, many recent publications, such as Refs. [105,106,107,108,109,110,111,112], still tried to add some numerical techniques, such as correctly resolve energy equation, high-order lattices, double distribution functions, hybrid LBM with finite difference or finite volume approaches etc., but nobody has deeply asked if there exist some fundamental theoretical incompleteness of the current LBM model. In the history of science advances, to solve a difficult problem reported by practices, it is not only to seek some technique-modifications on it, but also, more importantly, to check the original theory and physical mechanism of the problem to find if there is its inherent theoretical incompleteness. Based on this consideration, author through carefully reading the publications of LBM concerning its original principles and basic physical mechanism has found its following theoretical problems. We know that the background of LBM is the kinetic theory and BTE developed by studying the distribution of molecules of ideal dilute gases. Theoretical EDF obtained is MBD, in which three macroscopic variables: mass density, velocity, and temperature T with Boltzmann constant K are the parameters. In this EDF, the KT reflecting the bulk energy was derived only by the state equation of gas [6], but not concerning other types of energy, such as the work done by viscous stress and the one caused by the gradient of mass density. Therefore, the momentum and energy conservation equations derived from MBD do not include the contribution from the full stress tensor in continuum mechanics, and there is not a term in the energy conservation equation concerning the contribution of external energy generation sources. Physical flows in continuum mechanics are governed by three conservation laws, of which the three variables, the mass density, velocity, and internal energy are key parameters. When we study macroscopic flows from a viewpoint of statistical mechanics, it should have a corresponding inherent theoretical EDF including these three key parameters to allow the three conservation laws to be derived from it. Therefore, this paper intends to tackle these important theoretical problems to develop an improved theory with amended LBM model, aiming for readers to follow in practical simulations to solve the mentioned difficulties of the current LBM.
The paper is a theoretical document written exactly based on the famous Boltzmann H-theorem [6] of the statistical mechanics, the laws of continuum mechanics [113,114,115], the energy flow theory [116,117,118,119,120], and the variational method in mathematical analysis. Section 1 from reading historical publications reveals the existing problems of LBM theory, that is the total internal energy is not involved in current EDF causing some theoretical and numerical problems. Sections 2.1–2.3 derive the fundamental equations from continuum mechanics, which is used in Sect. 2.4 to develop an amended theoretical EDF including internal energy as a parameter, that is new contribution of the paper, and Sect. 2 is a base of demonstrations in Sects. 3 and 4. Section 3 demonstrates three conservation laws directly from the amended EDF with no small parameter expansions adopted in references. Section 4 gives the modified LBM based on the developed EDF with mass density, mean velocity and internal energy as parameters to be updated in numerical process. The formulations on generalised forces contributed by external forces and energy generation sources are provided and the implementation process of the improved method with its performance study are given. Section 5 gives some hand-workable examples by analysis to confirm the valid of theory and to illustrate applications.
2 Internal energy and amended theoretical EDF
To develop an amended theoretical EDF based on MBD function by introducing the total internal energy density as a macroscopic parameter, the knowledge in continuum mechanics including the state equation, material derivatives, Cauchy tress tensor, stress power, internal mechanical energy and its time / space derivatives with their statistical averages are required, which are discussed in this section.
2.1 Ideal gases, state equation, and average internal thermal energy (AITE)
For ideal gases in the volume \(\Omega \) containing \(N\) molecule particles, the state pressure \(p\) is defined by the equation of state in association with the Boltzmann constant \(k\) in the form [6]
from which, we know that if the temperature \(T\) is a constant, the particle density is a function of the volume and affects the state pressure per individual particle by
Physically, the dimension of the state pressure per individual particle is the pressure over the mass density, i.e., \({\text{N m}}^{-2}/({\text{kg m}}^{-3})={(\text{m}/\text{s})}^{2}\), which is a square of the instant velocity, equaling the derivative of the pressure with respect to the mass density.
Huang [6] presented the detailed calculation of AITE based on EDF, and obtained the average thermal energy \(\widehat{e}\) of a particle
where the pressure \(p\) and the temperature \(T\) are the physically measured quantities, from which AITE of the particles per unit volume is
From Eq. (2) we may understand that the average internal energy, \(\widehat{e},\) as the square of averaged velocity of sound in the fluid.
2.2 Cauchy tress tensor, power, and average internal mechanical energy (AIME)
In the continuum mechanics, using Cartesian tensor notations, see for examples, Refs. [113,114,115], the Cauchy stress tensor of fluids is given by
where \(p\) is the pressure caused by fluid flows, \(\mu \) is the coefficient of viscosity, \({V}_{ij}\) is deformation rate tensor, and \({\stackrel{\sim }{\sigma }}_{ij}={\stackrel{\sim }{\sigma }}_{ji}\) denotes a symmetrical viscous stress tensor with \({\stackrel{\sim }{\sigma }}_{jj}=0\). If the fluid is incompressible, the fluid dilation vanishes, \(\partial {v}_{l}/\partial {x}_{l}={V}_{ll}=0,\) the stress tensor reduces to
The power of stress per unit volume is given by \({\sigma }_{ij}{V}_{ij},\) which is a measured quantity. The internal mechanical energy of the fluid per unit mass can be obtained by integration from its reference state “0” to its current state “t”
Following the discussion on AITE per unit particle above, we can obtain AIME \(\widehat{\psi }\) per unit particle in a similar form as given in Eq. (7), i.e.,
in which \(\widehat{\psi }\) has the dimension of pressure \(\widehat{p}\) per unit particle shown in Eq. (6). As a result of this, AIME of the particles per unit volume and its time derivative can be given by
from which with Eq. (7), it follows that the time change rate of AIME of the particles per unit volume is
Here \({()}_{,j} \;{\text{equals}}\;\partial ()/\partial {x}_{j},\) as used in tensor analysis [113,114,115], the \({\sigma }_{ij}{u}_{i,j}\) is understood as the averaged one, although the same stress notations are adopted.
2.3 Material derivatives and gradient of internal mechanical energy per unit volume
A material point marked by its original position coordinate \({X}_{j}\) moves in the space, and it arrives the position \({x}_{i}\) at time \(t\), so that its velocity \({v}_{i}\, {\text{equals}}\, {\left(\partial {x}_{i}/\partial t\right)}_{X}\) and acceleration \({a}_{i}\, {\text{equals}}\, {\left(\partial {v}_{i}/\partial t\right)}_{X}\), where the subscript \(X\) implies the derivatives with respect to time \(t\) are taken for the same material point. This time derivative is called as a material derivative [113,114,115]. In continuum mechanics, the Eulerian description of motion represents motion quantities in \(()({x}_{i},t)\) as functions of spatial position and time, which may be a scalar, vector, or tensor function. In the Eulerian description of motion, the material derivative is
For a set of material points in a volume \(\Omega \) with its surface \(S\) in the space at time \(t\), the total quantity \(()\) of this set of particles is
where volume \(\Omega \) is also a function of time due to the motion. The material derivative of the quantity I(t) is
where physically, on the right-hand side, the first integration denotes the time change rate of the quantity in the fixed volume, while the second one is caused by the boundary motion. Using the Green theorem [113,114,115], we can re-write above equation as
Introducing the mass density \(\rho \) and the mass conservation equation, we obtain
2.3.1 Gradient of internal mechanical energy per unit volume in equilibrium state
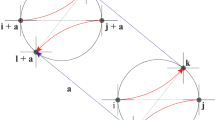
The gradient of the internal mechanical energy per unit volume in equilibrium state can be derived by using Fig. 1, in which a volume element \(\Delta \Omega \) closed by surface \(\Delta S\) of unit normal vector \({\nu }_{i}\) pointing from inside to outside of the volume is in its equilibrium state, so that it satisfies the equilibrium equation.
where \({f}_{i}\) is the body force per unit volume. When the volume tends zero, the resultant force at a point vanishes
The change of internal energy per unit volume is calculated by the work done by the stress in the gradient \(\Delta {U}_{i,j}\) of displacement field \({U}_{i}\) in the form
from which, when integrated over the volume \(\Delta \Omega \), and then using the Green theorem, it follows
Since the volume is very small, we approximate the displacement as the one at the central point, therefore, based on Eq. (17) in equilibrium state, we obtain the gradient of the internal mechanical energy per unit volume as
where we have introduced \({x}_{i}={X}_{i}+{U}_{i}\), and the particle displacement increment \(\Delta {U}_{i}=\Delta {x}_{i}.\)
2.3.2 Time change rate of AIME per unit volume in equilibrium state
The time change rate of AIME per unit volume in the equilibrium state can be derived from the principle of virtual power. Since the system is in equilibrium state, there is no power exchange with outside, so that the summation of the stress power and the time change rate of AIME per unit volume vanishes.
from which, when the Green theorem is used, it follows
Since the volume \(\Delta \Omega \) is arbitrary, we have.
where \({q}_{j}\) is defined as the component of averaged energy flow-density vector [116, 117]
2.3.3 Equation satisfied by the internal mechanical energy per unit mass
The equilibrium equation of power denoted by the internal mechanical energy per unit mass in the equilibrium state is obtained by investigating Eq. (21), which, when the material derivative Eq. (14) is used, becomes.
where “^” is to identify the quantity involving the ones for unit mass only. As a result of this, and when the Green theorem is used, it follows.
where \({\text{d}}\widehat{\Omega }\) denotes the volume element per unit mass equaling \(\frac{{{\text{d}}}{\Omega } }{\rho }.\) Therefore, from Eq. (25), we have
where the mass density is replaced by the particle density n.
2.4 Boltzmann H-theorem and amended theoretical EDF
The famous MBD function was derived for ideal gases with its AITE in the form \(\tilde{e }=3nkT/2\) [6], therefore, the momentum and energy conservation equations derived from MBD function does not include the contribution from the stress tensor in continuum mechanics. As mentioned in introduction, for simulating complex thermodynamic and multicomponent flows, etc., several technique modifications [101,102,103,104,105,106,107,108,109,110,111,112] were proposed to deal with some numerical issues met in their practices, but it has not solved the theoretical incompleteness of the current theory.
As discussed in Sect. 2.2, we have introduced an AIME per unit volume and per unit particle based on the theory of continuous mechanics and statistical average, which are summarized in the forms
where \(e\) denotes the total internal energy per unit volume, which consists of the kinetic one \(\tilde{K }\) and the thermal mechanical one \(\stackrel{\sim }{\varepsilon }\) equaling a summation of the thermal one \(\tilde{e }\) and the mechanical one \(\stackrel{\sim }{\psi }\). The hats “^” denote the corresponding variables per unit particle. These averaged internal energies are macroscopic quantities being the functions of position \({x}_{i}\) and time t.
Based on the developed AIME and the Boltzmann’s H-theorem [6], we can derive the amended theoretical EDE. We can conclude that EDF \({f}_{0}\left({\varvec{x}},{\varvec{v}},t\right)\) in a volume \(\Omega \) for a prescribed density \(n\), mean momentum \(n{\varvec{u}}\), and energy per unit volume (\(ne=0.5n({\varvec{u}}\cdot {\varvec{u}})+\stackrel{\sim }{\varepsilon }\), \(\stackrel{\sim }{\varepsilon }=1.5n\left(KT+\psi \right)=1.5n\overline{T })\) minimize the H functional
where \({\text{d}}V={\text{d}}{v}_{1}{\text{d}}{v}_{2}{\text{d}}{v}_{3}\) is the differential volume element of the velocity space. We require that the mass, momentum, and energy of this particle system in the volume \(\Omega \) are conservative, i.e.,
which are the constrains of the H functional. Using the Lagrangian multiplier method [99], introducing two scalar multipliers \({\lambda }_{1}\) and \({\lambda }_{3}\), and a vector \({{\varvec{\lambda}}}_{2}\) to release the variational constrains in Eq. (29) of the functional in Eq. (28), we obtain the new functional
The variation of the functional \(\tilde{H }\) gives
from which, when \(\delta \tilde{H }\, {\text{equals}}\, 0,\) it yields the constrain conditions in Eq. (29) and the equation
The solution of Eq. (31) is EDF satisfying the conservative constrains in Eq. (29), which is
where, we have introduced the equality
We consider a new set of Lagrangian multipliers \(d,{\varvec{\beta}},\gamma \) from which the EDF is represented in the standard form
which satisfies the conservative laws
Since the distribution is homogeneous, and it does not involve the spatial variables, the space integration gives the total volume \(\Omega \) in front of integration on velocity space. Solving Eq. (35) with Eq. (34), we can obtain the tree parameters. Here, the main contribution of this paper is that the internal mechanical energy is introduced in the energy conservation equation, based which the improved theoretical EDF derived as follows.
Using the Gaussian integrals and doing the mathematical works as deriving MBD function [6], from Eq. (35), we obtain
and especially the one for the energy conservation involving \(\psi \)
Substituting the parameters obtained by Eqs. (36) and (37) into Eq. (34) gives the new amended EDF as
Using this amended EDF and the tensor notations [113,114,115], we have the following integration formulations
Using the notation \(kT+\psi =\overline{T }\) for the mechanical energy included, it is not difficult to demonstrate that
3 Conservation laws
Here, we examine if the developed amended EDF satisfying BTE, it can be used to obtain the macroscopic conservation laws, which has not been fully addressed by using MBD function. If the answer is positive, this amended EDF will provide the basis to construct an improved LBM scheme to simulate various complex physical problems dominated by the changes of internal energy. This is because the general concepts in BTE are not only applicable for dilute gases, but also for much denser fluids.
3.1 Conservation theorem in a differential form
The EDF \(f\left({\varvec{x}},{\varvec{v}},t\right)\) satisfies a partial differential equation
Here, a new term on the change of kinetic energy energy \(\frac{{\varvec{v}}\cdot {\varvec{v}}}{2}=\widehat{K}\) introduced, since the amended should be amended EDF includes the internal energy as marcroscopic parameter, and its change effect needs to be explored, which is a new contribution of the paper.
The instant time change rate of the streaming velocity gives the instant acceleration per unit particle, i.e. the instant force \({\widehat{{\varvec{F}}}}_{v}\) per unit partice, while the time change rate of the kinetic energy per unit partice gives the insatnt energy change rate \({\widehat{\vartheta }}_{K}\). Obvously, The instnat values of the force \({\widehat{{\varvec{F}}}}_{v}\) and the energy change rate \({\widehat{\vartheta }}_{K}\) involve not only the internal motion variables, such as instant stress and streaming velcocity, but also the external quantities, such as the body force and the external energy source per unit mass. However, in the equilibirum state, the internal contributions to them are canceled each other according to the Newton’s second law, so that in the averaged equilibrium state governed by BTE, the following external force \(\widehat{{\varvec{F}}}\) and external energy gereration rate \(\widehat{\vartheta }\) are the averaged ones, i.e.,
respectively represnting the external body force and the external energy gneration rate per unit particle, which are assumed being independent of the streaming process, but the macroscopic quantities, possible functions of the time, space position and macroscopic velocity prescribed by the problems.
The right-hand side of Eq. (41) represents the un-balance part caused by collision in the system. We consider a conserved property \(\phi ({\varvec{x}},{\varvec{v}})\) with its finite value at any point of space, so that it is independent of time t. Multiplying Eq. (41) by this property, and then integrating the resultant equation over the phase space, we obtain
of which, the total collision term on the right-hand side vanishes, since the total system in the space is momentum conservative, although the collision term \({(\partial f/\partial t)}_{C}\) at a local point in the space is not zero. Equation (43) is re-written as
Using the Green theorem in the velocity space [113,114,115], we can transform the volume integration in the infinite velocity space \(V\) into a surface integration on its boundary \(S\) of unit normal vector \({\nu }_{i}\) at infinity, i.e.,
since the EDF \(f \text{tends to} 0\) when \({v}_{i} \text{tends to} \infty \) on the infinte boundary \(S\). Furthermore, the integration on the infinite volume \(V\), \({\int }_{V}\frac{\partial \left({\widehat{\vartheta }}_{K}f\phi \right)}{\partial \left(0.5{v}_{i}{v}_{i}\right)}{\text{d}}V=0,\) can be demonstrated as follows. Referring Fig. 2, on the shpere surface of radius \(r\), the kinetic energy is a constant \(\widehat{K}=0.5{v}_{i}{v}_{i}\), so that along an arbitrary radial direction \(r\), the differential element \({\text{d}}\widehat{K}={\text{d}}({0.5v}_{i}{v}_{i})\), implying the \(\widehat{K}\) is taken as a cordinate to denote the corresponding sphere. \({\text{d}}\widehat{K}={\text{d}}\left({0.5v}_{1}^{2}\right)={\text{d}}{\widehat{K}}_{1}\) can be regarded as a special case, if the direction \(r\) is chosen as the direction of velocity cordinate \({v}_{1}\) in the vellocity space. Therefore, we can use the Green theorem and the property of EDF vanishing at infinite to calculate the integration
Defining the average value of variable \(A({\varvec{x}},{\varvec{v}},t)\) as
When substituting Eq. (47) into Eq. (44), and considering Eqs. (45) and (46), it follows
where we have completed the integration in the momentum space and noticed that \(n\langle A\rangle =\langle nA\rangle \), since n is independent of \({\varvec{v}}.\)
Equation (48) is the general conservation theorem in an integration form, in which there is no restrictions on the size \(\Omega \). When we choose a small deferential volume \(\Omega \), we obtain the conservation theorem in the differential form
and furthermore
since in the equilibrium state, the external force \({\widehat{{\varvec{F}}}}_{v}\) and the external energy generation rate \({\widehat{\vartheta }}_{K}\) are independent of the streaming velocity \({\varvec{v}}\).
3.2 Conservation laws
Taking a different property \(\phi \), from Eq. (50), we can obtain its corresponding conservation law as follows.
3.2.1 Mass conservation
Letting \(\phi \, {\text{equals}}\, m\), which is the constant particle mass, we obtain the mass conservation law
where we have used the integration formulations of EDF given in Eqs. (39) and (40). Since m is a constant, we obtain
3.3 Momentum conservation
Letting \(\phi\, {\text{equals}}\; m{v}_{j}\), from Eq. (50), we obtain
of which,
due to, as mentioned, the partial derivative of velocity \({v}_{i}\) with respect to coordinate \({x}_{i}\) vanishes. Furthermore, from Eqs. (64) and (65), it follows
When substituting Eq. (54) into Eq. (53), and using the related integration formulations, we obtain
where we have used Eq. (42) to obtain \(\langle n{\widehat{F}}_{jK}\rangle +\langle n{\widehat{F}}_{iv}{\delta }_{ij}\rangle =\langle n{\widehat{F}}_{jT}\rangle =n{\widehat{F}}_{j}.\)
When the mass conservation Eq. (51) is introduced into Eq. (56), we obtain its first two terms
which gives
that is the momentum conservation law for fluids. In this equation, on the right-hand side, the first term \(\partial \left(nkT\right)/\partial {x}_{j}\) denotes the contribution from thermal pressure \(\widehat{p}=nkT\) given in Eq. (1), the second term \(\partial \left(n\psi \right)/\partial {x}_{j}\) is the contribution from the stress tensor as shown in Eq. (20). Therefore, we obtain
3.4 Energy conservation
Mechanical energy conservation When we do not interest in thermal effects, the term \(\partial \widehat{p}/\partial {x}_{j}\,{\text{equals}}\, 0\), so that we have the momentum conservation Eq. (59) for mechanical systems. Multiplying \({u}_{j}\) on both sides of the mechanical momentum equation, we obtain
that is
from which, when Eq. (10) is used for AIME of the same mass per unit volume, it yields
Here \({q}_{i}\) is the energy-flow density vector, of which the positive value implies the energy flowing from the inside to outside of the volume. Physically, Eq. (62) is the conservation law of mechanical energy, also called as the energy flow equilibrium equation, and energy flow density vector is included [116,117,118], which represents that the summation of the time change rate of kinetic and mechanic-internal energy equals a summation of the power of the body force \(n{\widehat{F}}_{j}\) per volume and the power flowing into the body from outside.
Total energy conservation To derive the total energy conservation, we take \(\phi =m{v}_{j}{v}_{j}/2\) in Eq. (50) and obtain
where due to the same reason for Eq. (54), we have
When substituting Eq. (64) into Eq. (63), and using the result obtained by Eq. (3.1.2), we have
it follows
Using Gaussian integrations [99], we obtain
by which, the first two terms on the left-hand side in Eq. (66) become
where the mass conservation Eq. (51) has been used. Furthermore, defining
and considering
obtained from Eqs. (20) and (26), we can arrange Eq. (66) as
When the conservation of mechanical energy in Eq. (62) is introduced into Eq. (71), and considering Eqs. (10) and (23) averagely give \({q}_{i,i}=\) \({\sigma }_{ij}{V}_{ij}\), we obtain the thermal energy conservation equation.
Physically, on the right-hand side of this equation, the first term denotes the thermal energy flow, the second term is the tress power, which transforms into thermal energy due to viscosity, and the third one is the energy generation from the external energy source.
It has been noted that the conservation laws derived from BTE by introducing the second order terms of partial derivatives of velocity with respect to \({x}_{i}\) [99]. Also, as reported in many references, by using the Chapman-Enskog expansions, a multi-scaling expansion [18], to express EDF and its derivatives in the forms of small parameter \(\epsilon \), the conservation laws are derived. Here, based on the amended EDF, we can directly derive the conservation laws without additional higher order derivatives of the velocities, or the Chapman-Enskog expansions. It is more important, by adding the terms of the partial derivatives of EDF with respect to the streaming velocity and the instant kinetic energy, the resultant energy conservation equation includes the external energy generation source in it, which has not found in the current publications. The introduced internal mechanical energy in EDF involves the gradient of the velocity, which was not considered in the Boltzmann’s theory for dilute ideal gases. The amended theoretical EDF provides a complete theory on LBM.
4 Improved lattice Boltzmann method
The Sects. 2 and 3 confirm the following key points: (1) the amended EDF satisfies the Boltzmann’s H-theorem and the three conservation laws in continuum mechanics, so that it is the theoretical solution of BTE; (2) in EDF, there are three macroscopic parameters, i.e., mass density, mean velocity, and internal energy, which respectively are functions of time and space point, therefore at different points in the time–space frame, the corresponding EDFs generally are different; (3) if we know the three macroscopic parameters at a point in the time–space frame, we will know the corresponding EDF at the same point, the solution at this point of BTE; (4) in a reverse case, if we obtain the solution of BTE at a point, we will know the corresponding EDF, so that the three macroscopic parameters of continuum mechanics can be derived from the moment equations.
The aim of LBM is to obtain the solution of BTE at every point in the time–space frame, then to obtain the macroscopic parameters which are the solution of the problems in continuum mechanics. To reach this aim, the discrete BTE is necessary. Here, based on the amended EDF, we develop an improved LBM, of which the main improvement is the total internal energy as a macroscopic parameter required to be updated in each time step.
4.1 Discrete lattice Boltzmann equation (LBE)
It has been shown that discrete LBE can be obtained from the continuous BTE, see for examples, Refs. [29,30,31,32]. For a single particle I, the Bhatnagar-Gross-Krook (BGK) form of the continuous BTE [13, 34, 35] can be modified as
in which, a new term involving energy as shown in Eq. (41) is added, and the amended EDF \({f}_{0}^{I}\) for 3-D case is given in Eq. (38), when using the total internal energy per unit particle \(\widehat{\varepsilon }\) defined in Eq. (27), it is
which is the function of the particle streaming velocity \({v}_{i}\) and the three macroscopic variables: mass density \(\rho \), mean velocity \({u}_{i}\), and internal energy \(\widehat{\varepsilon }\). The energy parameter including the thermal and mechanical ones is defined as
which is applied to the ideal gases/fluids, the non-thermal viscous fluids, and the thermal viscous fluids, respectively. The dimension of the internal energy per unit particle / mass is \(\text{Nm}/\text{kg}={({\text{ms}}^{-1})}^{2}\), so that the ratio of the kinetic energy over the internal energy, \(0.5{\varvec{u}}\cdot {\varvec{u}}/\widehat{\varepsilon }\), is non-dimensional parameter. For example, in the ideal gas case, we have
where we have used Eq. (1) for the definition of the gas pressure, the relationship between the dynamic pressure \(\widehat{p}\) and the sound speed \(C\) for the barotropic fluid is \(\widehat{p}=\rho {C}^{2}\) [113,114,115], and \(M\) is the Mach number.
Making a time integration of Eq. (73) from time \(t\) to \(t+\delta t=t+1\), we obtain the change of the EDF from the original equilibrium state \(({x}_{i},{v}_{i},t)\) to its state \(({x}_{i}+{e}_{I}^{i},{v}_{i},t+1)\) due to the velocity change \({e}_{I}^{i}\), therefore we have
Here, \({\dot{v}}_{I}\) denotes the particle acceleration or the particle force per unit mass, that is assumed as a constant during the small time-period \(\delta t\). The velocities \({e}_{I}^{i}\) at the nodes I are referred as the microscopic velocities. The force \({F}_{I}\) consists of the particle internal interaction force and the possible external force acted at the particle. If there is no external forces, the internal interaction forces between the two particles satisfy the third Newton’s law, so that its summation over the total particles vanishes. Also, the term \({\widehat{\Theta }}_{I}\) is the contribution from energy generation rate \({\widehat{\vartheta }}_{K}\), which vanishes if no external energy generation source in the problem.
Using Eqs. (39) and (40) divided by the summations over particle I with velocity \({v}_{Ij}\) replaced by the velocities \({e}_{I}^{j}\), and \(n=\rho ,\) as well as noting \(\partial {f}_{I}/\partial \left(0.5{\varvec{v}}\cdot {\varvec{v}}\right)=-1.5{f}_{I}/\widehat{\varepsilon }\) and \(\partial {f}_{I}/\partial {v}_{i}=-1.5{f}_{I}\left({v}_{i}-{u}_{i}\right)/\widehat{\varepsilon }=-3{f}_{I}\left({\overline{v} }_{i}-{\overline{u} }_{i}\right)/\sqrt{2\widehat{\varepsilon }}\), the following moment equations can be obtained:
It should be noticed that the force \({\tilde{F }}_{j}\) and the energy generation rate \(\stackrel{\sim }{\vartheta }\) respectively are the external force and the external energy generation rate per unit mass of the medium, since the internal interaction between the two particles are governed by the third Newton’s law, so that the summations cancel them.
The exponential function can be represented in the power series
of which, the radius of convergence is infinite. Approximating to the second order of \(u/\sqrt{2\widehat{\varepsilon }}\), we have
from which, Eq. (74) can be approximated as
in which, \(\overline{{\varvec{u}} }\) denotes the non-dimensional macroscopic velocity, \({\overline{{\varvec{v}}} }_{I}={{\varvec{v}}}_{I}/\sqrt{2\widehat{\varepsilon }}\) is a non-dimensional microscopic velocity at node I, and the non-dimensional weight \({w}_{I}\) absorbs the rest coefficient. The weight can be determined by the set of velocities of the scheme based on the moment equations. It should notice that \({\left(\sqrt{2\widehat{\varepsilon }}\right)}^{-3}\) of dimension \({\left({\text{ms}}^{-1}\right)}^{-3}\) is used for the volume element \({\text{d}}V\) of the velocity space being non-dimensional one. Therefore, we may write Eqs. (39) and (40) in the following forms by means of non-dimensional velocities:
and
It may be necessary to mention that according to the tensor rule [113,114,115], we have
so that from Eq. (40), the energy conservation equations are
In the history, the approximated form of the original EDF with the n-dimensional and b-velocities (DnQb) models was developed by Qian et al. [25, 26, 63]. Here, the number n = 1, 2, 3 denotes the dimension of problem, while b indicates the node number of the scheme. To obtain the weights \({w}_{I}\), He and Luo [30] used a third Hermite formula to approximate the integrals of the moment equation, and Abe [29] assumed \({w}_{I}\) having a simple truncated functional form based on \({{\varvec{e}}}_{I}\). More generally, the Gaussian quadrature can be adopted to determine the weights for the exact values of the moment integrals [88], which is supported by the fundamental theorem [89].
It should be noticed that the moment equations in Eqs. (86) and (87) do not include the force effect given in Eq. (76). If there are no external forces, these moment equations are valid, but if there exist some external forces, the force effect in Eq. (76) must be included.
4.2 Schemes of LBM
Using the approximate EDF in Eq. (85), i.e.,
the following schemes of LBM can be established in the DnQb forms.
4.2.1 1-D scheme D1Q3
For D1Q3, we choose three nodes (\(-1, 0, 1)\) with the corresponding velocity (\(-c,0,c)\), so that from Eq. (90), it follows
Considering the symmetry of node locations, we have no reason more favor one of them, so that to choose the same weights at the two side nodes, \({w}_{1}={w}_{-1},\) then from the first two moment equations in Eq. (15), we obtain the weights \({w}_{1}={w}_{-1}=1/6\) and \({w}_{0}=4/6\).
4.2.2 2-D scheme D2Q9
For 2-D problem, we choose 9 nodes scheme shown by Fig. 3(a), with the velocities and the weights at the nodes have been given in many publications, such as Refs. [25, 26, 29, 30, 63, 88, 99], which are
a D2Q9 scheme for 2-D problems and b D3Q19 scheme for 3-D problems [100]
4.2.3 3-D schemes D3Q19
For 3-D problems, D3Q19 scheme chooses the 19 nodes as shown by Fig. 3(b). The velocities and the weights at the nodes have been presented in the wide publications, which are
4.3 Generalised forces
In the publications, some force models have been proposed. For example, reference [48] suggested an acceleration model to denote a fore
where \({\varvec{a}}\) denotes the macroscopic acceleration of the particle, while Ref. [49] proposed a physical force model to distribute the physical force on the cell particles using distribution function in the form
where \({\varvec{F}}\) is the physical force vector defined by
Here \({\mu }_{0}\) is the chemical potential of the bulk energy of fluid, and \(\kappa \) denotes a gradient parameter relating the interface thickness of two-phase fluids.
In this developed method of the paper, the introduced terms of external force and energy generation resources are defined in Eqs. (76) and (78) and the corresponding moment equations describe by Eqs. (79)–(82). Therefore, there is no need to use any above force models proposed in the literatures. Based on the moment Eqs. (79)–(82) and using non-dimensional streaming velocities \({\overline{{\varvec{v}}} }_{I}=\frac{{{\varvec{v}}}_{{\varvec{I}}}}{\sqrt{2\widehat{\varepsilon }}}\) and \({\overline{{\varvec{u}}} }_{I}=\frac{{{\varvec{u}}}_{{\varvec{I}}}}{\sqrt{2\widehat{\varepsilon }}}\), we define the following three generalised forces contributed by the external force and energy generation source for the three conservation equations used in Sect. 4.4, which are
where superscripts m, v, and e respectively represent mass, momentum, and energy, \({\overline{F} }_{j}=\frac{{\tilde{F }}_{j}}{\sqrt{2\widehat{\varepsilon }}}\) and \(\overline{\vartheta }=\frac{\stackrel{\sim }{\vartheta }}{2\widehat{\varepsilon }}\) respectively denote the non-dimensional external force and energy generation source intensity per unit mass of the material. For the force and energy generation source at a time or space point, they can be denoted using Delta function, for example, a force applied at point \({{\varvec{x}}}_{a}\) and at time \({t}_{b}\) can be denoted as
4.4 Implementation
For programing, LBM equation with its characteristic time \(\tau \) concerning viscosity ν of the fluid to be chosen by the problems, can be generally written as
where \({F}_{I}\) and \({\widehat{\Theta }}_{I}\) denote the force and energy change rate, including the internal and external ones, per unit mass at point I. For example, the kinematic viscosity has been used in the literatures, i.e.,
In the implementation processes published in most literatures, the collision step is before the streaming one. It has been noticed that in some publications, such as Ref. [41], the streaming step is arranged before the collision step, which are: (a) streaming move \({\varvec{x}}\) to \({\varvec{x}}+{{\varvec{v}}}_{{\varvec{I}}}\) to obtain a distribution function \({\overline{f} }_{I}^{*}\), then update the macroscopic parameters and the equilibrium distribution function using the moment equations; (b) replacing \({\overline{f} }_{I}\) by \({\overline{f} }_{I}^{*}\) in Eq. (101) to collision to obtain \({\overline{f} }_{I}\left({\varvec{x}}+{{\varvec{v}}}_{{\varvec{I}}},t+1\right)\). The details of this process are described as follows.
Streaming step to obtain the distribution function by using Eq. (90), i.e.,
Macroscopic variables update calculations based on \({\overline{f} }_{I}^{(*)}\) and the following conservation laws with no external force included:
where \(\tilde{d }=1, 2, 3\) is dimension number.
Equilibrium distribution function based on macroscopic variables (*) is defined as
Collision step to obtain the distribution function
Final macroscopic variables calculations based on the distribution function \({\overline{f} }_{I}^{(\vartheta +1)}\) and the conservation laws including the generalised external force effect given in Eqs. (97)–(99), i.e.,
mass: \(\sum_{I}{\overline{f} }_{I}^{(\vartheta +1)}={\rho }^{(\vartheta +1)}-{\left({\overline{F} }^{\text{m}}\right)}^{(\vartheta )},\)
internal energy:
Here the values at the original position \(\left({\varvec{x}},t\right)\) marked by \((\vartheta )\), since generalised forces in Eqs. (97) and (98) are the ones at \((\vartheta )\), which involves the physical macroscopic quantities only.
4.5 Matrix equations for implementation process
4.5.1 Implementation steps in matrix form
To investigate the performance of a scheme, it is convenience to adopt the matrix notations to express the implementation processes. For a convenience of notations, we identify the quantities at the position \(\left({\varvec{x}},t\right),\) the middle position after streaming \(\left({\varvec{x}}+{{\varvec{v}}}_{I},t\right)\) and the last position \(\left({\varvec{x}}+{{\varvec{v}}}_{I},t+1\right)\) by the super-indexes \(\left(\vartheta \right), \left(*\right),\) and \(\left(\vartheta +1\right)\), respectively. Therefore, the implementation process in matrix form is as follows.
Streaming The distribution function vector \({\overline{{\varvec{f}}} }^{(*)}\) at the space–time position \(\left({\varvec{x}}+{{\varvec{v}}}_{I},t\right)\) is obtained, which is based on the macroscopic variable vector \({\overline{{\varvec{U}}} }^{(\vartheta )}\) consisting of the mass density, momentum, and total internal energy \(\widehat{\varepsilon }\) of the fluid at the position \(\left({\varvec{x}},t\right)\) and through the streaming operation by means of the following streaming matrix \({\varvec{S}}\),
where the streaming velocity \({{\varvec{v}}}_{{\varvec{I}}}\) is defined as
from which it follows that
Updated calculations The macroscopic displacement vector \({\overline{{\varvec{U}}} }^{(\boldsymbol{*})}\) and internal energy \({\widehat{\varepsilon }}^{(*)}\) at position \(\left({\varvec{x}}+{{\varvec{v}}}_{I},t\right)\) is calculated, which is based on the obtained distribution function vector \({\overline{{\varvec{f}}} }^{(*)}\) and through a conservation transformation by means of the following conservation matrix \(\stackrel{\sim }{{\varvec{V}}}\),
The row equations of the matrix shown in Eq. (111) can be respectively written as
which, when Eqs. (108)–(110) are substituted, respectively yields the following conservation laws of mass, momentum, and energy,
From the momentum equation, we obtain
which, when substituted into the energy equation, gives
This equation provides a transformation to obtain the internal energy \({\widehat{\varepsilon }}^{(*)}\) from the original variables before the streaming.
From the macroscopic variable vectors obtained by Eq. (111), the equilibrium distribution function \({\overline{{\varvec{f}}} }_{0}^{(*)}\) can be derived by using Eq. (108) as
Collision: From the results obtained by Eqs. (108) and (116), the distribution function \({\overline{{\varvec{f}}} }^{(\vartheta +1)}\) at position \(\left({\varvec{x}}+{{\varvec{v}}}_{I},t+1\right)\) can be obtained by the following collision calculation.
Further-updated macroscopic variables: Using Eq. (111) and replacing the distribution function \({\overline{{\varvec{f}}} }^{(*)}\) by the \({\overline{{\varvec{f}}} }^{(\vartheta +1)}\) at position \(\left({\varvec{x}}+{{\varvec{v}}}_{I},\text{ t}+1\right)\), and including the external forces given in Eqs. (97)-(99), we obtain the macroscopic variables at position \(\left(\mathbf{x}+{\mathbf{v}}_{I},\text{ t}+1\right)\) as
4.6 Integrated transformation equation
The integrated transformation equation of LBM can be derived by combining the equations of each step given in Sect. 4.5.1. Substituting Eq. (117) into Eq. (118), we obtain
from which, when Eqs. (4.5.1) and (116) are substituted, it follows
in which the \({\widehat{\varepsilon }}^{\left(*\right)}\) used in Eq. (113) can be approximated by its original values \({\widehat{\varepsilon }}^{\left(\vartheta \right)}\), so that it is updated by
After the detailed investigations on the matrices \({\overline{{\varvec{E}}} }^{\left(\vartheta \right)}\) and \({\overline{{\varvec{H}}} }^{\left(\vartheta \right)}\), we have found that the former has a factor 2 \({\widehat{\varepsilon }}^{\left(\vartheta \right)}\), but the later does not involve \({\widehat{\varepsilon }}^{\left(\vartheta \right)}\), therefore we can write
where \(\gamma \) is called as the ratio of internal energy change from the step \(\left(\vartheta \right)\) to \(\left(\vartheta +1\right).\)
4.7 Performance investigations
4.7.1 Characteristic matrix
The performance of the scheme is governed by the matrix \(\widehat{{\varvec{S}}}\), which is essentially determined by the matrix \(\widehat{{\varvec{V}}}\) combining the streaming matrix shown in Eq. (4.5.1) and the updated matrix \(\stackrel{\sim }{{\varvec{V}}}\) shown in Eq. (111) of the scheme. Therefore, this matrix is called as the characteristic matrix of the scheme. Using Eqs. (4.5.1), (111), and (121), we can obtain the matrix
of which, during the matrix multiplications, we have introduced the following definitions
As discussed before, geometrically, the weights of the schemes DnQb are center-symmetrical with the center streaming velocities \({v}_{0}^{i}=0,\) but the streaming velocities at non-central nodes are anti-center-symmetrical. As a result of this, we have \({p}^{i}=0={\overline{k} }^{rij}\), so that the characteristic matrix in Eq. (124) reduces to
For different definitions of streaming velocity, the values of above terms are given as follows:
where \({\beta }_{I}^{i}\) denotes the unit directional vector at point I. It should be noted that for case (a), the change of internal energy \(2\widehat{\varepsilon }\) is included in the matrix \(\widehat{{\varvec{V}}}\). Therefore, for the problems that involves the internal energy changes not neglected, the matrix \(\widehat{{\varvec{V}}}\) should be updated for each cell. In the case (b), the internal energy is shown in the equation, and it can be directly updated, if necessary, in simulations.
4.8 Eigenvalues of characteristic matrix
For 3-D problems, the displacement vector defined is a 10-row vector: 1 mass density, 3 velocity components, and 6 components of symmetrical tensor \({u}_{i}{u}_{j}\), so that the characteristic matrix in Eq. (126) is a \(10\times 10\) matrix, and for 1-D and 2-D problems they are respectively a \(3\times 3\) and a \(6\times 6\) matrix. Generally, the eigenvalue analysis of the matrix with higher order than \(3\times 3\) cannot be done by hand, but for the type of matrix in Eq. (126) can be analyzed as follows.
In 3-D case, the displacement vector and the characteristic matrix in Eq. (126) can be respectively written as
We can write the characteristic matrix in a block form
where each block matrix consists of the elements at the corresponding positions identified by the line and row subscripts in the matrix \(\widehat{{\varvec{V}}}\) in Eq. (129). The characteristic equation for the eigenvalues of the matrix \(\widehat{{\varvec{V}}}\) is given as
Using the Schur’s determinant identity [121], the determinant in Eq. (131) is calculated as
or
From this result, the solutions of Eq. (4.6.8) can be obtained by vanishing one of the following two lower order determinants,
This analysis provides a means to derive the eigenvalues of the characteristic matrix to analyze the performance of a scheme. However, although the two determinant equations are different orders, the derived algebraic equation with same order of eigenvalue \(\kappa ,\) so that it will not reduce the calculation tasks. It should be noted that eigenvalues of the characteristic matrix are the function of the internal energy of each simulation transformation.
4.9 Performance analysis based on eigenvalues of characteristic matrix
The matrix \(\widehat{{\varvec{V}}}\) is real matrix, of which the eigenvalues can be real or complex. If there exists a complex eigenvalue, its conjugate complex is also a complex eigenvalue of the matrix.
Eigenvalues and eigenvectors with their orthogonality The eigenvalues and the corresponding eigenvectors are governed by the following eigenvalue equation
Generally, we can represent the eigenvalue equation in the matrix form
where \({\kappa }_{I}\) and \({{\varvec{\psi}}}_{I}\) denote the Ith eigenvalues and the corresponding eigenvectors. If the eigenvalues are different, the eigenvectors are independent, so that the matrix \({\boldsymbol{\Psi }}^{-1}\) exists. As the result of this, we have
which implies the eigenvalue of matrix \({\widehat{{\varvec{V}}}}^{2}\) is the square of the eigenvalue of matrix \(\widehat{{\varvec{V}}}\) and the corresponding eigenvector is same as the one of matrix \(\widehat{{\varvec{V}}}\). Therefore, we have
Amplifying factor and numerical damping The independent eigenvectors of the characteristic matrix \(\widehat{{\varvec{V}}}\) span a complete characteristic space in which the displacement vector can be expressed as
where \({\varvec{q}}\) denotes a displacement vector in the characteristic space. From this expansion, when Eq. (139) is substituted into Eq. (120), it follows
where the external force term has been excluded because it does not affect the performance of the characteristic matrix. Substituting Eq. (138) into Eq. (140), we obtain
which, when multiplying both side by \({\boldsymbol{\Psi }}^{-1}\), gives
Physically, this result implies that the performance of the scheme is determined by the eigenvalues of the characteristic matrix of the scheme.
Generally, we may assume the eigenvalues of the scheme consist of conjugate complex numbers, since the characteristic matrix is real, therefore we have
where \({\kappa }_{J}\) is complex with its conjugate marked by *. The two complex eigenvalues can be expressed in the form
Here \({\widehat{\kappa }}_{J}\) and \({\phi }_{J}\) denote the module and phase angle of the complex eigenvalue, respectively. Using these notations, we can re-write Eq. (142) in the form
Here \(\stackrel{\sim }{{\varvec{A}}}\) is called as a complex amplifying factor matrix, which produces the amplitude amplification and the phase shift. The phase shift implies a damping effect, and the damping factor vanishes if all eigenvalues are real. For 1-D problems, its characteristic matrix is a \(3\times 3\) real matrix, so that it must have at least one real eigenvalue.
5 Examples
The key contribution of this paper is to include the internal energy parameter in the amended theoretical EDF, which allows the conservation laws to be obtained from the amended BTE. To illustrate the internal energy parameter effect, we consider the following hand-workable examples which can clearly explore the essential physical characteristics and avoid non-essential numerical treatment.
5.1 Example 1: the performance of scheme D1Q3
For this scheme, we choose three nodes (\(0,-\text{1,1})\) with the corresponding streaming velocity (\(0,-v,v)\) and the weights \({w}_{1}={w}_{-1}=1/6\) and \({w}_{0}=4/6\).
5.1.1 Streaming velocity \({v}_{I}^{i}=\sqrt{2\hat{\varepsilon }}{\beta }_{I}^{i}\)
Characteristic matrix and its eigenvalues Using the method given in Sects. 4.6.1 and 4.6.2 and considering the case with no external forces, we can obtain the following matrices for this D1Q3 scheme. For this 1D problems, we have the values
from which, when Eq. (146) is substituted into Eq. (126), it follows the characteristic matrix of the system, i.e.,
Adopting the streaming velocity form shown in Eq. (127), we obtain
The eigenvalues and eigenvectors of the matrix \(\widehat{{\varvec{V}}}\) can be obtained as
Amplifying matrix The amplifying matrix of the transformation of the scheme in Eq. (145) is
Final transformation From Eqs. (135) and (139), we have the transformation
that is
from which, when pre-multiplying the inverse matrix of the first matrix on the left-hand side, it follows
where the ratio \(\gamma \) of internal energy change is given by Eq. (123).
5.1.2 Streaming velocity \({{\varvec{v}}}_{{\varvec{I}}}^{{\varvec{i}}}={{\varvec{\beta}}}_{{\varvec{I}}}^{{\varvec{i}}}\)
Characteristic matrix and its eigenvalues In this case, from Eq. (128), we obtain
so that the characteristic matrix of the system is
with
The characteristic equation of the system is
The eigenvalues of this equation are
of which, \({\kappa }_{1}\) is real, and the last two ones are real if \(\Delta \ge 0,\) otherwise complex. Generally, as the case of complex eigenvalues, we may express these two eigenvalues as
Amplifying matrix The amplifying matrix of the transformation of this scheme in Eq. (145) is now given by
As mentioned before, in the complex eigenvalue cases, the amplifying matrices produce some damping effects causing the phase shifts in each simulation step.
5.2 1-D constant incompressible flow by D1Q3 scheme
We investigate a 1-D constant incompressible flow by the scheme D1Q3 of the weights \({w}_{1}={w}_{-1}=1/6\), \({w}_{0}=4/6\) with three nodes (\(0,-1, 1)\), and the corresponding streaming velocity (\(0,-\sqrt{2\widehat{\varepsilon }},\sqrt{2\widehat{\varepsilon }})\), of which the integrated transformation is given in Sect. 5.1.1, based on which we have
which is the theoretical solution of the problem.
5.3 1-D high pressure compressible gas flow in a tube with a unit cross-sectional area
As shown in Fig. 4, a horizontal tube of length L and unit cross-sectional area \(A=1\) locates along \(O-x\) axis. We assume that the left end of the tube connected to a very high pressed gas tank of pressure \({p}_{0}\) keeping a prescribed constant, and its right end at \(x=L\) connecting to the atmospheric pressure \({p}_{L}\), so that the difference of pressures at the two ends produces a flow in the tube. The governing equations and theoretical analysis of the problem are discussed for two cases.
5.3.1 Transient analysis before stable flow
Considering the fluid is compressible and barotropic, we respectively have its conservation equations of mass and momentum, and state equation
where \(c\) is a speed of sound, and \(\widehat{\rho }\) denotes the mass density of the gas with zero pressure. The initial and boundary conditions are
To find the internal energy per unit mass of the gas at a point, we define the specific volume \(\varphi =1/\rho \), the volume of unit mass, and use the mass conservation Eq. (161) to obtain
Using Eq. (7), we obtain the physical internal energy per unit mass
and then from Eq. (75), the statistical internal energy per unit mass is
which is a function of \(x\) and t.
The prescribed pressures at two ends of tube produce the generalised forces at the nodes of two ends for simulation used in LBM, and from Eqs. (97)–(99) they are
Here the variable \(\overline{()}\) implies its non-dimensional one by dividing with \(\sqrt{2{\widehat{\varepsilon }}_{I}}\) that involves step \(\left(\vartheta \right).\)
5.3.2 Stable flow
When the flow reaches stable, the variables of motion are independent of the time, Eqs. (161) and (162) reduces to
The integrations of Eq. (171) along the tube with respect to \(x\) yield
where C is a constant, the Mach numbers \(M\left(x\right)\,{\text{equals}}\,u(x)/c\) and \({M}_{0} \,{\text{equals}}\,{u}_{0}/c.\) Using Eq. (163), the prescribed pressures at the two tube ends are given as.
from which, it gives
which shows that the flow is supersonic, since \({p}_{0}>{p}_{L}\). Now we can obtain the speed, pressure, and mass density of the fluid at any point of tube. In this case, the internal energy in Eq. (169) will be function of x only.
5.3.3 Stable solution by LBM
Now we can use the LBM scheme D1Q3 to deal with the stable problem with the streaming velocity (\(0,-\sqrt{2\widehat{\varepsilon }},\sqrt{2\widehat{\varepsilon }})\), which is a function of cell position. We have known from the performance study of this scheme that its characteristic matrix Eq. (148) and amplifying matrix Eq. (150) are unit matrix, i.e., \(\widehat{{\varvec{V}}}={\varvec{I}}=\stackrel{\sim }{{\varvec{A}}}\), therefore the transformation \({\overline{{\varvec{U}}} }^{(\vartheta +1)}={\overline{{\varvec{U}}} }^{(\vartheta )}\) in Eq. (151) confirms the initial stable values of variables obtained by Eqs. (171)–(176) is stable solution.
The aim of the hand-workable examples given herein is mainly to show that the introduced internal energy variable into LBM equation plays an important role in dealing with problems with energy changes in the cell, which caused the difficulty of current LBM theory as mentioned in references cited in introduction of the paper. Therefore, considering page limits, we do not intend to do some numerical examples but leave it for readers to practice it for further developing the theory and proposed method.
6 Conclusion and discussion
To summary the theoretical analysis, we conclude the following contributions of the paper. (a) The short introduction on LBM provides the historically important information, which should confirm, based on the author’s check, that there have not been found any references presenting the same idea as given in the paper. (b) The amended theoretical EDF derived by the H-theorem with Lagrangian multiplier approach includes the mass density, mean velocity, and total internal energy of fluids as three macroscopic parameters, from which the three conservation laws can be directly derived from the BTE without additional small parameter expansions. (c) The improved LBM, requiring the internal energy parameter to be updated in each simulation step for general cases, and the updated non-dimensional streaming velocity provides a means to simulate more complex flow problems concerning obvious energy changes in high-speed, compressible flows. The performance study approach is formulated. (d) The modified differential BTE includes a new term concerning energy variation allowing external forces and external energy generation source to be considered in the method. (e) The hand-workable examples theoretically illustrate the essential characteristics and confirm the proposed improved LBM with the performance study.
The paper is a theoretical document, which have not given complex practical numerical examples, due to pages limited. Author wishes the interested readers may follow the proposed method numerically to tackle some engineering problems from which to further develop this new improved method benefiting to sciences and engineering advances.
References
Landau, L.D., Lifshitz, E.M.: Mechanics, 3rd edn. Butterworth-Heinenann, Oxford (1981)
Hardy, J., Pomeau, Y., De Pazzis, O.: Time evolution of a two-dimensional system, I. Invariant states and time correlation functions. J. Math. Phys. 14(2), 1746–1759 (1973)
Hardy, J., Pomeau, Y., De Pazzis, O.: Time evolution of a two-dimensional classical lattice system. Phys. Rev Lett. 31, 276–259 (1973)
Hardy, J., De Pazzis, O., Pomeau, Y.: Molecular dynamics of a lattice gas: transport properties and time correlation functions. Phys. Rev. A 13, 1949–1961 (1976)
Satoh, A.: Introduction to Practice of Molecular Simulation. Elsevier, London (2010)
Huang, K.: Statistical Mechanics, 2nd edn. Wiley, Chichester (1987)
Lerner, R.G., Trigg, G.L.: Encylopaedia of Physics, 2nd edn. VHC publishers, New York (1991)
Arkeryd, L.: On the Boltzmann equation part I: existence. Arch. Rational Mech. Anal. 45(1), 1–16 (1972)
Arkeryd, L.: On the Boltzmann equation part II: the full initial value problem. Arch. Rational Mech. Anal. 45(1), 17–34 (1972)
Crank, J., Nicolson, P.: A practical method for numerical evaluation of solution of partial differential equations of the heat conduction type. Proc. Camb. Phil. Soc. 43(1), 50–67 (1947)
Hirsch, C.: Numerical computation of internal and external flows, volume 1: fundamentals of numerical discretization. Wiley, Chichester (1988)
Inamuro, T., Sturtevant, H.: Numerical study of discrete-velocity gases. Phys. Fluids 2, 2196–2203 (1990)
Bhatnagar, P.L., Gross, E.L., Krook, M.: A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 94 (3), 511–525 (1954)
Wilson, G.: The life and times of cellular automata. New Scientist 44–47 (1988)
Chopard, B., Droz, M.: Cellular Automata Modelling of Physical Systems. Cambridge University Press, London (1998)
McNamara, G., Zanetti, G.: Use of the Boltzmann equation to simulate lattice-gas automata. Phys. Rev. Lett. 61, 2332–2335 (1988)
Broadwell, J.E.: Study of rarefied shear flow by the discrete velocity method. J. Fluid Mech. 19, 401–414 (1964)
Frisch, U., Hasslacher, B., Pomeau, Y.: Lattice-gas automata for the Navier-Stokes equation. Phys. Rev. Lett. 56(14), 1505–1508 (1986)
Frisch, U., d’Humières, D., Hasslacher, B., et al.: Lattice gas hydrodynamics in two and three dimensions. Complex Syst. 1, 649–707 (1987)
Higuera, F.J., Jimenez, J.: Boltzmann approach to lattice gas simulations. Europhys. Lett. 9, 663–668 (1989)
Higuera, F.J., Succi, S., Benzi, R.: Lattice gas dynamics with enhanced collisions. Europhys. Lett. 9, 345–349 (1989)
Qian, Y.H.: Lattice gas and lattice kinetic theory applied to the Navier-Stokes equations. PhD thesis, University Pierre et Marie Curie, Paris (1990)
Chen, S., Chen, H.D., Martinez, D., et al.: Lattice Boltzmann model for simulation on magnetohydrodynamics. Phys. Rev. Lett. 67, 3376–3379 (1991)
Chen, H., Chen, S., Matthaeus, W.H.: Recovery of the Navier-Stokes equation using a lattice-gas Boltzmann method. Phys. Rev. A 45, R5339-5342 (1992)
Qian, Y.H., d’Humières, D., Lallemand, P.: Lattice BGK models for Navier-Stokes equation. Europhys. Lett. 17, 479 (1992)
Qian, Y.H.: Simulating thermodynamics with Lattice BGK models. J. Sci. Comput. 8, 231 (1993)
Guo, Z., Shi, B., Wang, N.: Lattice BGK model for incompressible Navier-Stokes equation. J. Comput. Phys. 165, 288–306 (2000)
Guo, Z., Shi, B., Zheng, C.: A coupled lattice BGK model for the Boussinesq equations. Int. J. Numer. Meth. Fluids 39, 325–342 (2002)
Abe, T.: Derivation of the lattice Boltzmann method by means of the discrete ordinate method for the Boltzmann equation. J. Comp. Phys. 131, 241–246 (1997)
He, X., Luo, L.S.: A priori derivation of the lattice Boltzmann equation. Phys. Rev. E 55, 6333–6336 (1997)
He, X., Luo, L.S.: Theory of the lattice Boltzmann method: from the Boltzmann equation to the lattice Boltzmann equation. Phys. Rev. E 56(6), 6811–6817 (1997)
He, X., Luo, L.S.: Lattice Boltzmann for the incompressible Navier-Stokes equation. J. Stat. Phys. 88, 927–944 (1997)
Shan, X., He, X.: Discretization of the velocity space in the solution of the Boltzmann equation. Phys. Rev. Lett. 80, 65 (1998)
Chu, C.K.: Kinetic theoretic description of the formation of a shock wave. Phys. Fluids 8, 12–21 (1965)
Xu, K., Prendergast, K.H.: Numerical Navier-Stokes solutions from gas kinetic theory. J. Comput. Phys. 114, 9–17 (1994)
Wolfram, S.: Cellular automation fluids, I. Basic theory. J. Stat. Phys. 45, 471–526 (1986)
Lavallee, P., Boon, J.P., Noullez, A.: Boundaries in lattice gas flows. Physica D47, 233–240 (1991)
Chen, S., Martinez, D., Mei, R.: On boundary conditions in lattice Boltzmann methods. J. Phys. Fluids 8, 2527–2536 (1996)
Chen, S., Doolen, G.D.: Lattice Boltzmann method for fluid flows. Annual Rev. Fluid Mech. 30, 329–364 (1998)
Succi, S.: The Lattice Boltzmann Equation for Fluid Dynamics and Beyond. Oxford University Press, Oxford (2001)
Bao, Y.B., Meskas, J.: Lattice Boltzmann Method for Fluid Simulations, Courant Institute of Mathematical Sciences, New York University (2011) https://www.math.nyu.edu/~billbao/report930.pdf
Zou, Q., He, X.: Pressure and velocity boundary conditions for the lattice Boltzmann. J. Phys. Fluids 9, 1591–1598 (1997)
Guo, Z.L., Zheng, C.G., Shi, B.C.: Non-equilibrium extrapolation method for velocity and pressure boundary conditions in the lattice Boltzmann method. Chin. Phys. 11(4), 366–374 (2002)
He, X., Doolen, G.: Lattice Boltzmann method on curvilinear coordinate systems: flow around a circular cylinder. J. Comput. Phys. 134, 306 (1997)
Filippova, O., Hanel, D.: Grid refinement for lattice-BGK models. J. Comput. Phys. 147, 219–228 (1998)
Mei, R., Shyy, W.: On the finite difference-based Boltzmann method in curvilinear coordinates. J. Comput. Phys. 143, 426 (1998)
Mei, R., Shyy, W., Yu, D., et al.: Lattice Boltzmann method for 3-D flows with curved boundary. J. Comput. Phys. 161, 680–699 (2000)
He, X., Shan, X., Doolen, G.D.: Discrete Boltzmann equation model for nonideal gases. Phys. Rev. E 57, R13–R16 (1998)
Lee, T., Lin, C.L.: A stable discretization of the lattice Boltzmann equation for simulation of incompressible two-phase flows at high density ration. J. Comput. Phys. 206(1), 16–47 (2005)
Elton, B.H., Levermore, C.D., Rodrigue, H.: Convergence of convective-diffusive lattice Boltzmann methods. SIAM J. Sci. Comp. 32, 1327–1354 (1995)
Succi, S., Benzi, R., Higuera, F.: The lattice Boltzmann equation – a new tool for computational fluid dynamics. Physica D 47, 219–230 (1991)
Noble, D.R., Georgiadis, J.G., Buckius, R.O.: Comparison of accuracy and performance for lattice Boltzmann and finite difference simulation of steady viscous flow. Int. J. Numer. Meth. Fluids 23, 1–18 (1996)
Sterling, J.D., Chen, S.: Stability analysis of lattice Boltzmann methods. J. Comp. Phys. 123, 196–206 (1996)
Cao, N., Chen, S., Jin, S., et al.: Physical symmetry and lattice symmetry in lattice Boltzmann method. Phys. Rev. E 55, R21–R24 (1997)
Koelman, J.M.V.A.: A simple lattice Boltzmann scheme for Navier-Stokes fluid flow. Europhys. Lett. 15, 603–607 (1991)
Nannelli, F., Succi, S.: The lattice Boltzmann equation on irregular lattices. J. Stat. Phys. 68, 401–407 (1992)
Amati, G., Succi, S., Benzi, R.: Turbulence channel flow simulation using a coarse-grained extension of the lattice Boltzmann method. Fluid Dyn. Res. 19, 289–302 (1997)
He, X., Luo, L.S., Dembo, M.: Some progress in lattice Boltzmann method, Part I nonuniform mesh grids. J. Comp. Phys. 129, 357–363 (1996)
Benzi, R., Succi, S., Vergassola, M.: The lattice Boltzmann equation - theory and application. Phys. Rep. 222, 145–197 (1992)
Succi, S., Benzi, R., Massaioli, F.: A review of the lattice Boltzmann method. Int. J. Mod. Phys. C 4(2), 409–415 (1993)
Rothman, D.H., Zaleski, S.: Lattice gas models of phase separation: interfaces, phase transitions and multiphase flow. Rev. Mod. Phys. 66, 1417–1479 (1994)
Chen, S., Dawso, S.P., Doolen, G.D., et al.: Lattice methods and their applications to reacting systems. Comp. Chem. Eng. 19, 617–646 (1995)
Qian, Y.H., Succi, S., Orszag, S.A.: Recent advances in lattice Boltzmann computing. Annu. Rev. Comp. Phys. 3, 195–242 (1995)
Premnath, K., McCracken, M., Abraham, J.: A review of lattice Boltzmann methods for mltiphase flows relevant to engine sprays. SAE Tech. Paper, 010996 (2005)
Aidum, C.K., Clausen, J.R.: Lattice Boltzmann method for complex flows. Annu. Rev. Fluid Mech. 42, 439–472 (2010)
Seta, T.: Progress in lattice Boltzmann method. Jpn. J. Multiphase Flow 24(4), 427–434 (2010)
Yin, X., Le, G., Zhang, J.: Mass and momentum transfer across solid-fluid boundaries in the lattice-Boltzmann method. Phys. Rev. E 86(2): 026701 (2012)
Jahanshaloo, L., Pouryazdanpanah, E., Sidik, N.A.C.: A Review on the application of the lattice Boltzmann method for turbulent flow simulation. Numer. Heat Transf. A 64(11), 938–953 (2013)
Djenidi, L.: The lattice Boltzmann method and the problem of turbulence. AIP Conf. Proc. 1648, 030003 (2015)
Che Sidik, N.A., Aisyah Razali, S.: A review on lattice Boltzmann method for numerical prediction of nanofluid flow. Int. Rev Mech. Eng. 7(7), 1269–1274 (2013)
Che Sidik, N.A, Aisyah Razali, S.: Lattice Boltzmann method for convective heat transfer of nanofluids, Renew. Sustain. Energy Rev. 38(C), 864–875 (2014)
Perumal, D.A., Dass, A.K.: A Review on the development of lattice Boltzmann computation of macro fluid flows and heat transfer. Alex. Eng. J. 54(4), 955–971 (2015)
Succi, S., Moradi, N., Greiner, A., et al.: Lattice Boltzmann modeling of water-like fluids. Front. Phys. 16, 10 (2014)
Wang, J., Chen, L., Kang, Q., et al.: The lattice Boltzmann method for isothermal micro-gaseous flow and its application in shale gas flow: a review. Int. J. Heat Mass Transf. 95, 94–108 (2016)
Yoon, H., Kang, Q., Valocchi, A.J.: Lattice Boltzmann-based approaches for pore-scale reactive transport. Rev. Mineral. Geochem. 80(1), 393–431 (2015)
Liu, H., Kang, Q., Leonardi, C.R., et al.: Multiphase lattice Boltzmann simulations for porous media application: a review. Comput. Geosci. 20(4), 777–805 (2016)
Sharma, K.V., Straka, R., Tavares, F.W.: Lattice Boltzmann method for industrial applications. Ind. Eng. Chem. Res. 58, 16205–16234 (2019)
Shao, W., Li, J.: Review of lattice Boltzmann method applied to computational aeroacoustics. Arch. Acoust. 44(2), 215–238 (2019)
Carenza, L.N., Gonnella, G., Lamura, A., et al.: Lattice Boltzmann methods and active fluids. Eur. Phys. J. E 42, 1–83 (2019)
Wang, H., Yuan, X., Liang, H., et al.: A brief review of the phase-field-based lattice Boltzmann method for multiphase flows. Capillarity 2(3), 33–52 (2019)
Li, L., Lu, J., Fang, H., et al.: Lattice Boltzmann method for fluid-thermal systems: status, hotspots, trends and outlook. IEEE Access 8, 27646–27675 (2020)
Gutowitz, H.: Cellular automata: theory and experiment; proceedings of a workshop sponsored by the centre for nonlinear studies. Los Alamos National Laboratory, Los Alamos, September 9–12 (1989)
Wolf-Gladrow, D.A.: Lattice-Gas Cellular Automata and Lattice Boltzmann Models, an Introduction. Springer, Berlin (2000)
Succi, S.: Lattice Boltzmann equation for complex states of flowing matter. Oxford University Press, Oxford (2018)
Sukop, M., Thorne, D.T.: Lattice Boltzmann Modelling: An Introduction for Geoscientists and Engineers, 1st edn. Springer, Berlin (2006)
Mohamad, A.A.: Lattice Boltzmann Method: Fundamentals and Engineering Applications with Computer Codes (1st and 2nd edns). Springer, Berlin (2011/2019)
Yang, D.Y.: Lattice Boltzmann method: fundamentals and engineering applications with computer codes. Electronic Industry Press, China (2015) (in Chinese) https://www.dushu.com/book/12896397/
Guo, Z., Shu, C.: Lattice Boltzmann method and its applications in engineering. Advances in Computational Fluid Dynamics. World Scientific Publishing Company, London (2013)
Stoer, J., Bulirsch, B.: Introduction to Numerical Analysis. Springer, Berlin (1992)
Huang, H., Sukop, M., Lu, X.: Multiphase Lattice Boltzmann Methods: Theory and Application. Wiley, Chichester (2015)
Kruger, T., Kusumaatmaja, H., Kuzmin, A., et al.: The Lattice Boltzmann Method, Principles and Practice. Springer, Berlin (2017)
Montessori, A., Falcucci, G.: Lattice Boltzmann Modeling of Complex Flows in Engineering Applications. Morgan and Claypool Publishers, San Rafael (2018)
Akker, H.: Lattice Boltzmann modeling for chemical engineering. Academic Press 55(1), 2–291 (2020)
Bolton, D.C., Schwartz, B., Shreedharan, S.: Lattice Boltzmann methods (2017). https://personal.ems.psu.edu/~fkd/courses/EGEE520/2017Deliverables/LBM_2017.pdf
He, Y., Wang, Y., Li, Q.: Lattice Boltzmann method: theory and applications. Science Press, Beijing (2009). ((in Chinese))
Guo, Z., Zheng, Z.: Theory and applications of lattice Boltzmann method. Science Press, Beijing (2009). ((in Chinese))
Wang, H., Li, X.: Applications of lattice Boltzmann method in partial differential equations of soliton waves. Science Press, Beijing (2017). ((in Chinese))
Begum, R., Basit, M.A.: Lattice Boltzmann method and its applications to fluid flow problems. Eur. J. Sci. Res. 22, 216–231 (2008)
Wagner, A.J.: A practical introduction to the lattice Boltzmann method. Department of Physics, North Dakota State University, Fargo (2008)
Chen, L.: Lattice Boltzmann for flow and transport phenomena - Introduction to the lattice Boltzmann method (2018). http://nht.xjtu.edu.cn/__local/6/DD/BF/422C3B8D24E6AE4B10F619C0D2B_2C529A67_426CFE.pdf
Swift, M.R., Osborn, W.R., Yeomans, J.M.: Lattice Boltzmann simulation of nonideal fluids. Phys. Rev. Lett. 75, 830–833 (1995)
Swift, M.R., Orlandini, S.E., Osborn, W.R., et al.: Lattice Boltzmann simulation of liquid-gas and binary-fluid systems. Phys. Rev. E 54, 5041–5052 (1996)
Nadiga, B.T., Zaleski, S.: Investigations of a two-phase fluid model. Eur. J. Mech. B 15, 885–896 (1996)
He, X., Chen, S., Doolen, G.D.: A novel model for the lattice Boltzmann method in compressible limit. J. Comput. Phys. 146(1), 282–300 (1998)
Jacob, J., Malaspinas, O., Sagaut, P.: A new hybrid recursive regularized Bhatnagar-Cross-Krook collision model for lattice Boltzmann method-based large eddy simulation. J. Turbul. 19(11), 1051–1076 (2018)
Feng, Y., Boivin, P., Jacob, J., et al.: Hybrid recursive regularized thermal lattice Boltzmann model for high subsonic compressible flows. J. Comput. Phys. 394, 82–99 (2019)
Renard, F., Feng, Y., Boussuge, J.-F., et al.: Improved compressible hybrid lattice Boltzmann method on standard lattice for subsonic and supersonic flows. Comput. Fluids 219, 104867 (2021)
Shan, X.: Central-moment-based Galilean-invariant multiple-relation-time collision model. Phys. Rev. E 100(4), 043308 (2019)
Wilde, D., Krämer, A., Küllmer, K., et al.: Multistep lattice Boltzmann methods: theory and applications. Int. J. Numer. Methods Fluids 90(3), 156–169 (2019)
Saadat, M.H., Bösch, F., Karlin, I.V.: Lattice Boltzmann model for compressible flows on standard lattices: variable Prandtl number and adiabatic exponent. Phys. Rev. E 99(1), 013306 (2019)
Feng, Y.-L., Tao, W.-Q., Sagaut, P.: Regularized thermal lattice Boltzmann method for natural convection with large temperature differences. Int. J. Heat Mass Transf. 125, 1379–1391 (2018)
Wissocq, G., Sagaut, P., Boussuge, J.F.: An extended spectral analysis of the lattice Boltzmann method: model interactions and stability issues. J. Comut. Phys. 380, 311–333 (2019)
Fung, Y.C.: A first course in continuum mechanics, 3rd edn. Prentice-Hall, London (1977)
Xing, J.T.: Fluid-solid interaction dynamics, theory, variational principles, numerical methods, and applications. Academic Press, Elsevier, London (2019)
Xing, J.T.: Fluid-solid interaction dynamics, theory, variational principles, numerical methods, and applications. Higher Education Press, Beijing (2021)
Xing, J.T., Price, W.G.: A power flow analysis based on continuum dynamics. Proc. R. Soc. Lond. A 455, 401–435 (1999)
Xing, J.T., Price, W.G.: The energy flow equation of continuum dynamics. IUTAM Symposium on Statistical Energy Analysis, Kluwer academic publishers, Netherlands, 83–94 (1999)
Xing, J.T.: Energy flow theory of nonlinear dynamical systems with applications. Springer, Berlin (2015)
Xing, J.T.: Generalised energy conservation law of chaotic phenomena. Acta Mech Sin 35(6), 1257–1268 (2019)
Qin, L., Qin, H., Xing, J.T.: Energy flow characteristics of friction-induced nonlinear vibrations in a water-lubricated bearing-shat coupled system. Acta Mech Sin 37(4), 679–704 (2020)
Zhang, F.: The Schur complement and its applications. Springer, Berlin (2005)
Acknowledgements
The author acknowledges the School of Naval Architecture and Ocean Engineering, HUST, providing the finance support managed by Guoxiang Hou, enabling author to visit HUST to tackle LBM. Thanks also are given to Yuehong Qian of Soochow University for providing some references involved in the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Executive Editor: Mingjiu Ni.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Xing, J.T. Theoretical investigations on lattice Boltzmann method: an amended MBD and improved LBM. Acta Mech. Sin. 37, 1659–1682 (2021). https://doi.org/10.1007/s10409-021-01135-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10409-021-01135-6