Fitted Mesh Methods for a Class of Weakly Coupled System of Singularly Perturbed Convection–Diffusion Equations

Abstract

In this paper, a class of singularly perturbed coupled linear systems of second-order ordinary differential equations of convection–diffusion type is considered on the interval [0, 1]. Due to the presence of different perturbation parameters multiplying the diffusion terms of the coupled system, each of the solution components exhibits multiple layers in the neighbourhood of the origin. This fact is proved in the estimates of the derivatives of the solution. A numerical method composed of an upwind finite difference scheme applied on a piecewise uniform Shishkin mesh that resolves all the layers is suggested to solve the problem. The method is proved to be almost first-order convergent in the maximum norm uniformly in all the perturbation parameters. Numerical examples are provided to support the theory.

1 Introduction

Singularly perturbed differential equations of convection–diffusion type appear in several branches of applied mathematics. Roos et al. [1] describes linear convection–diffusion equations and related non-linear flow problems. Modelling real-life problems such as fluid flow problems, control problems, heat transport problems, river networks results in singularly perturbed convection–diffusion equations. Some of those models were discussed in [2]. A form of linearized Navier Stokes equations called Oseen system of equations, which models many of the physical problems, is a system of singularly perturbed convection–diffusion equations. Also systems of singularly perturbed convection–diffusion equations have applications in control problems [3].

For a broad introduction to singularly perturbed boundary value problems of convection–diffusion type and robust computational techniques to solve them, one can refer to [4,5,6]. In [7], a coupled system of two singularly perturbed convection–diffusion equations is analysed and a parameter uniform numerical method is suggested to solve the same. Here, in this paper, the following weakly coupled system of n-singularly perturbed convection–diffusion equations is considered.

$$\begin{aligned}&L \mathbf {u}(x) \equiv E\mathbf {u}^{\prime \prime }(x)+A(x)\mathbf {u}^{\prime }(x)-B(x)\mathbf {u}(x)=\mathbf {f}(x),\; x \in \varOmega =(0,1) \end{aligned}$$

(1)

$$\begin{aligned}&\mathbf {u}(0)=\mathbf {l},\;\; \mathbf {u}(1)=\mathbf {r}, \end{aligned}$$

(2)

where $\mathbf {u}(x)=\big (u_1(x),u_2(x),\ldots ,u_n(x)\big )^T$, $\mathbf {f}(x)=\big (f_1(x),f_2(x),\ldots ,f_n(x)\big )^T,$

$$E = \begin{bmatrix} \varepsilon _1 &{} 0 &{} \ldots &{}0 \\ 0 &{} \varepsilon _2 &{} \ldots &{}0\\ \vdots &{} \vdots &{} &{}\vdots \\ 0&{}0&{} \ldots &{}\varepsilon _n \end{bmatrix}, A= \begin{bmatrix} a_1 &{} 0 &{}\ldots &{}0 \\ 0 &{} a_2 &{} \ldots &{}0\\ \vdots &{} \vdots &{} &{}\vdots \\ 0&{}0&{} \ldots &{}a_n\end{bmatrix},\;B= \begin{bmatrix} b_{11} &{} b_{12} &{} \ldots &{} b_{1n} \\ b_{21}&{} b_{22}&{} \ldots &{} b_{2n}\\ \vdots &{} \vdots &{} &{}\vdots \\ b_{n1} &{} b_{n2}&{} \ldots &{} b_{nn} \end{bmatrix}. $$

Here, $\varepsilon _1, \varepsilon _2,...,\varepsilon _n$ are distinct small positive parameters and for convenience, it is assumed that $\varepsilon _i < \varepsilon _j,$ for $i<j$. The functions $a_i, b_{ij}$ and $f_i$, for all i and j, are taken to be sufficiently smooth on $\overline{\varOmega }$. It is further assumed that, $a_i(x)\ge \alpha > 0,\;b_{ij}(x) < 0,\; i\ne j$ and $\displaystyle \sum _{ j=1}^{n}b_{ij}(x) \ge \beta >0$, for all $i=1,2,\ldots ,n.$ The case $a_i(x)<0$ can be treated in a similar way with a transformation of x to $1-x.$

In [9], Linss has analysed a broader class of weakly coupled system of singularly perturbed convection–diffusion equations and presented an estimate of the derivatives of $u_i$ depending only on $\varepsilon _i,$ for $i=1,2,\ldots ,n$. He has claimed first order and almost first-order convergence if solved on Bakhvalov and Shishkin meshes, respectively, with the classical finite difference scheme.

The reduced problem corresponding to (1)–(2) is

$$\begin{aligned} \begin{aligned}&L_0 \mathbf {u}_0(x) \equiv A(x)\mathbf {u}_0^{\prime }(x)-B(x)\mathbf {u}_0(x)=\mathbf {f}(x),\; x \in \varOmega \\&\, \mathbf {u}_0 (1)=\mathbf {r}, \end{aligned} \end{aligned}$$

(3)

where $\mathbf {u}_0(x)=(u_{01}(x),u_{02}(x),...,u_{0n}(x))^T.$

If $u_k(0)\ne u_{0k}(0)$ for any k such that $0\le k\le n$, then a boundary layer of width $O(\varepsilon _k)$ is expected near $x=0$ in each of the solution component $u_i,\; 1\le i\le k$.

Notations. For any real valued function y on D, the norm of y is defined as $\Vert y\Vert _D= \displaystyle {\sup _{x \in D}}|y(x)|$. For any vector valued function $\mathbf {z}(x)=(z_1(x),z_2(x),\ldots ,z_n(x))^T$, $\Vert \mathbf {z}\Vert _D=\max \big \{\Vert z_1\Vert _D, \Vert z_2\Vert _D,\ldots ,\Vert z_n\Vert _D\big \}.$ For any mesh function Y on a mesh $D^N=\big \{x_j\big \}^N_{j=0}$, $\Vert Y\Vert _{D^N}= \displaystyle {\max _{0\le j\le N}}|Y(x_j)|$ and for any vector valued mesh function $\mathbf {Z}=(Z_1,Z_2,\ldots ,Z_n)^T$, $\Vert \mathbf {Z}\Vert _{D^N}=\max \big \{\Vert Z_1\Vert _{D^N}, \Vert Z_2\Vert _{D^N}, \ldots , \Vert Z_n\Vert _{D^N}\big \}.$

Throughout this paper, C denotes a generic positive constant which is independent of the singular perturbation and discretization parameters.

2 Analytical Results

In this section, a maximum principle, a stability result and estimates of the derivatives of the solution of the system of Eqs. (1)–(2) are presented.

Lemma 1

(Maximum Principle) Let $\mathbf {\psi }=(\psi _1, \psi _2, ..., \psi _n)^T$ be in the domain of L with $\mathbf {\psi }(0) \ge \mathbf {0}\; and\; \mathbf {\psi }(1) \ge \mathbf {0}.$ Then $L\mathbf {\psi } \le \mathbf {0}\; on\; \varOmega$ implies that $\mathbf {\psi } \ge \mathbf {0}$ on $\overline{\varOmega }.$

Lemma 2

(Stability Result) Let $\mathbf {\psi }$ be in the domain of L, then for $x \in \overline{\varOmega }$ and $1\le i\le n$

$$|\psi _i(x)|\le \max \Big \{\Vert \mathbf {\psi }(0)\Vert ,\; \Vert \mathbf {\psi }(1)\Vert ,\; \frac{1}{ \beta } \Vert L\mathbf {\psi } \Vert \Big \}.$$

Theorem 1

Let ${\mathbf {u}}$ be the solution of (1)–(2), then for x $\in \overline{\varOmega }$ and $1\le i\le n$, the following estimates hold.

$$\begin{aligned} |u_i(x)|\le & {} C\max \Big \{\Vert \mathbf {l}\Vert ,\; \Vert \mathbf {r}\Vert ,\; \frac{1}{ \beta } \Vert \mathbf {f} \Vert \Big \},\end{aligned}$$

(4)

$$\begin{aligned} |u_{i}^{(k)} (x)|\le & {} C\varepsilon _{i}^{-k}\Big (\Vert \mathbf {u}\Vert +\varepsilon _{i}\Vert \mathbf {f}\Vert \Big )\;\; for\;\; k=1,2,\;\;\;\;\end{aligned}$$

(5)

$$\begin{aligned} |u_{i}^{(3)} (x)|\le & {} C\varepsilon _{i}^{-2}\varepsilon _{1}^{-1}\Big (\Vert \mathbf {u}\Vert +\varepsilon _{i}\Vert \mathbf {f}\Vert \Big )+\varepsilon _{i}^{-1}|f_{i}^{\prime }(x)|. \end{aligned}$$

(6)

Proof

The estimate (4) follows immediately from Lemma 2 and Eq. (1). Let $x \in [0,1]$, then for each $i,\;1\le i\le n$, there exists $a\in [0,1- \varepsilon _{i}$] such that $x \in N_{a}=[a,a+\varepsilon _{i}].$ By the mean value theorem, there exists $y_{i} \in (a, a+\varepsilon _{i})$ such that

$$u_{i}^{\prime }(y_{i})=\frac{u_{i}(a+\varepsilon _{i})-u_{i}(a)}{\varepsilon _{i}}$$

and hence

$$|u_{i}^{\prime }(y_{i})|\le C\varepsilon _{i}^{-1}\Vert \mathbf {u}\Vert .$$

Also,

$$u_{i}^{\prime }(x)=u_{i}^{\prime }(y_{i})+\int _{y_{i}}^{x}u_{i}^{\prime \prime }(s)ds.$$

Substituting for $u_i^{\prime \prime }(s)$ from (1), $|u_{i}^{\prime }(x)| \le C\varepsilon _{i}^{-1}\Big (\Vert \mathbf {u}\Vert + \varepsilon _{i}\Vert \mathbf {f}\Vert \Big ).$ Again from (1), $|u_{i}^{\prime \prime }(x)|\le C\varepsilon _{i}^{-2}\Big (\Vert \mathbf {u}\Vert + \varepsilon _{i}\Vert \mathbf {f}\Vert \Big ).$ Differentiating (1) once and substituting the above bounds lead to

$$|u_{i}^{(3)} (x)|\le C\varepsilon _{i}^{-2}\varepsilon _{1}^{-1}\Big (\Vert \mathbf {u}\Vert +\varepsilon _{i}\Vert \mathbf {f}\Vert \Big )+\varepsilon _{i}^{-1}|f_{i}^{\prime }(x)|.$$

2.1 Shishkin Decomposition of the Solution

The solution $\mathbf {u}$ of the problem (1)–(2) can be decomposed into smooth $\mathbf {v}=(v_1,...,v_n)^T$ and singular $\mathbf {w}=(w_1,...,w_n)^T$ components given by $\mathbf {u}=\mathbf {v}+\mathbf {w}$, where

$$\begin{aligned} L\mathbf {v}=\mathbf {f},\;\;\mathbf {v}(0)=\mathbf {\gamma }, \;\;\mathbf {v}(1)=\mathbf {r},\end{aligned}$$

(7)

$$\begin{aligned} L\mathbf {w}=\mathbf {0},\;\; \mathbf {w}(0)=\mathbf {l}-\mathbf {v}(0),\;\; \mathbf {w}(1)=\mathbf {0}, \end{aligned}$$

(8)

where $\mathbf {\gamma }=(\gamma _1, \gamma _2, \ldots , \gamma _n)^T$ is to be chosen.

2.1.1 Estimates for the Bounds on the Smooth Components and Their Derivatives

Theorem 2

For a proper choice of $\mathbf {\gamma }$, the solution of the problem (7) satisfies for $1\le i\le n$ and $0\le k\le 3$,

$$|v_i^{(k)}(x)| \le C(1+\varepsilon _i^{2-k}),\;\; x\in \overline{\varOmega }.$$

Proof

Considering the layer pattern of the solution, first, the decomposition is done with $\varepsilon _n$, for all the components of $\mathbf {v}$. The second level decomposition with $\varepsilon _{n-1}$ is for the first $n-1$ components of $\mathbf {v}$. Then, the decomposition continues with $\varepsilon _{n-2}$ for the first $n-2$ components of $\mathbf {v}$ and so on. It is carried out in the following way.

First, the smooth component $\mathbf {v}$ is decomposed into

$$\begin{aligned} \mathbf {v}=\mathbf {y}_{n}+\varepsilon _n \mathbf {z}_{n}+\varepsilon _n^2 \mathbf {q}_{n} \end{aligned}$$

(9)

where $\mathbf {y}_{n}=\left( y_{n1},y_{n2},\ldots ,y_{nn}\right) ^T$ is the solution of

$$\begin{aligned} A(x)\mathbf {y}_{n}^{\;\prime }(x)-B(x)\mathbf {y}_{n}(x)=\mathbf {f}(x), \;\;\mathbf {y}_{n}(1)=\mathbf {r}, \end{aligned}$$

(10)

$\mathbf {z}_{n}=\left( z_{n1},z_{n2},\ldots ,z_{nn}\right) ^T$ is the solution of

$$\begin{aligned} A(x)\mathbf {z}_{n}^{\;\prime }(x)-B(x)\mathbf {z}_{n}(x)=-\varepsilon _n^{-1}E\mathbf {y}_{n}^{\;\prime \prime }(x),\;\mathbf {z}_{n}(1)=\mathbf {0} \end{aligned}$$

(11)

and $\mathbf {q}_{n}=\left( q_{n1},q_{n2},\ldots ,q_{nn}\right) ^T$ is the solution of

$$\begin{aligned} L\mathbf {q}_{n}(x)=-\varepsilon _n^{-1}E\mathbf {z}_{n}^{\;\prime \prime }(x),\;\mathbf {q}_{n}(1)=\mathbf {0}\;\text {and}\;\mathbf {q}_{n}(0)\;\text {remains to be chosen}. \end{aligned}$$

(12)

Using the fact that $\varepsilon _n^{-1}E$ is a matrix of bounded entries, and from the results in [10] for (10) and (11), it is not hard to see that

$$\begin{aligned} \Vert \mathbf {y}_{n}^{\;(k)}\Vert \le C\;\;\text {and}\; \;\Vert \mathbf {z}_{n}^{\;(k)}\Vert \le C,\;\;0\le k\le 3. \end{aligned}$$

(13)

Now, using Theorem 1 and (13), with the choice that $q_{nn}(0)=0,$

$$\begin{aligned} |q_{nn}^{\;(k)}(x)|\le C\varepsilon _n^{-k},\;\;0\le k\le 3. \end{aligned}$$

(14)

Then from (9), it is clear that $v_n(0)=\gamma _n=y_{nn}(0)+\varepsilon _nz_{nn}(0)$. Also from (13) and (14),

$$\begin{aligned} |v_n^{(k)}(x)| \le C(1+\varepsilon _n^{2-k}),\;\;0\le k\le 3. \end{aligned}$$

(15)

Now, having found the estimates of $v_n^{(k)},$ to estimate the bounds $v_i^{(k)},$ for $1\le i\le n-1$, the following notations are introduced, for $1\le l\le n,$

$$ E_l = \begin{bmatrix} \varepsilon _1 &{} 0 &{} \ldots &{}0 \\ 0 &{} \varepsilon _2 &{} \ldots &{}0\\ \vdots &{} \vdots &{} &{}\vdots \\ 0&{}0&{} \ldots &{}\varepsilon _l \end{bmatrix}, A_l= \begin{bmatrix} a_1 &{} 0 &{}\ldots &{}0 \\ 0 &{} a_2&{} \ldots &{}0\\ \vdots &{} \vdots &{} &{}\vdots \\ 0&{}0&{} \ldots &{}a_l\end{bmatrix},\;B_l= \begin{bmatrix} b_{11}&{} b_{12}&{} \ldots &{}b_{1l} \\ b_{21} &{} b_{22}&{} \ldots &{}b_{2l}\\ \vdots &{} \vdots &{} &{}\vdots \\ b_{l1} &{} b_{l2}&{} \ldots &{}b_{ll} \end{bmatrix}, $$

$\tilde{\mathbf {q}}_l=\left( q_{l1},q_{l2},\ldots ,q_{l(l-1)}\right) ^T$, $\mathbf {g}_{(l-1)}=\left( g_{(l-1)1},g_{(l-1)2},\ldots ,g_{(l-1)(l-1)}\right) ^T$, with $g_{(l-1)j}=-\dfrac{\varepsilon _j}{\varepsilon _{l}}z_{lj}^{\prime \prime }+b_{jl}q_{ll}$.

Now, considering the first ($n-1$) equations of the system (12), it follows that

$$\begin{aligned} {\tilde{L}_n}\tilde{\mathbf {q}}_n \equiv E_{n-1}\tilde{\mathbf {q}}_n^{\;\prime \prime }(x)+A_{n-1}(x)\tilde{\mathbf {q}}_n^{\;\prime }(x)-B_{n-1}(x)\tilde{\mathbf {q}}_n(x)=\mathbf {g}_{n-1}(x), \end{aligned}$$

(16)

where $\tilde{\mathbf {q}}_{n}(1)=\mathbf {0}\; \text {and}\;\tilde{\mathbf {q}}_{n}(0)$ remains to be chosen.

Furthermore, decomposing $\tilde{\mathbf {q}}_{n}$ in a similar way to (9), we obtain

$$\begin{aligned} \tilde{\mathbf {q}}_{n}=\mathbf {y}_{n-1}+\varepsilon _{n-1} \mathbf {z}_{n-1}+\varepsilon _{n-1}^2 \mathbf {q}_{n-1} \end{aligned}$$

(17)

where $\mathbf {y}_{n-1}=\left( y_{(n-1)1},y_{(n-1)2},\ldots ,y_{(n-1)(n-1)}\right) ^T$ is the solution of the problem

$$\begin{aligned} A_{n-1}(x)\mathbf {y}_{n-1}^{\;\prime }(x)-B_{n-1}(x)\mathbf {y}_{n-1}(x)=\mathbf {g}_{n-1}(x), \;\;\mathbf {y}_{n-1}(1)=\mathbf {0}, \end{aligned}$$

(18)

$\mathbf {z}_{n-1}=\left( z_{(n-1)1},z_{(n-1)2},\ldots ,z_{(n-1)(n-1)}\right) ^T$ is the solution of the problem

$$\begin{aligned} A_{n-1}(x)\mathbf {z}_{n-1}^{\;\prime }(x)-B_{n-1}(x)\mathbf {z}_{n-1}(x)=-\varepsilon _{n-1}^{-1}E_{n-1}\mathbf {y}_{n-1}^{\;\prime \prime }(x),\;\mathbf {z}_{n-1}(1)=\mathbf {0} \end{aligned}$$

(19)

and $\mathbf {q}_{n-1}=\left( q_{(n-1)1},q_{(n-1)2},\ldots ,q_{(n-1)(n-1)}\right) ^T$ is the solution of the problem

$$\begin{aligned} {\tilde{L}_n}\mathbf {q}_{n-1}(x)=-\varepsilon _{n-1}^{-1}E_{n-1}\mathbf {z}_{n-1}^{\;\prime \prime }(x),\;\mathbf {q}_{n-1}(1)=\mathbf {0}\;\text {and}\;\mathbf {q}_{n-1}(0)\;\text {remains to be chosen}. \end{aligned}$$

(20)

Now choose $\mathbf {q}_{n-1}(0)$ so that its $(n-1)\mathrm{th}$ component is zero (i.e. $q_{(n-1)(n-1)}(0)=0$).

Problem (18) is similar to the problem (11). Using the estimates (13)–(14), the solution of the problem (18) satisfies the following bound for $0\le k\le 3$.

$$\begin{aligned} \Vert \mathbf {y}_{n-1}^{(k)}\Vert \le C\left( 1+\varepsilon _n^{1-k}\right) . \end{aligned}$$

(21)

Using (21) and Lemma 2.2 in [10], the solution of the problem (19) satisfies

$$\begin{aligned} \Vert \mathbf {z}_{n-1}\Vert \le C \varepsilon _n^{-1}. \end{aligned}$$

(22)

and from (19), for $1\le k\le 3$,

$$\begin{aligned} \Vert \mathbf {z}_{n-1}^{\;(k)}\Vert \le C \varepsilon _n^{-k}. \end{aligned}$$

(23)

Now, using Theorem 1 and (23), the following estimate holds:

$$\begin{aligned} |q_{(n-1)(n-1)}^{\;(k)}(x)|\le C\varepsilon _n^{-2}\varepsilon _{n-1}^{-k},\;\;0\le k\le 3. \end{aligned}$$

(24)

By the choice of $q_{(n-1)(n-1)}(0)$, from (9) and (17), it is clear that $v_{n-1}(0)=\gamma _{n-1}=y_{n(n-1)}(0)+\varepsilon _nz_{n(n-1)}(0)+\varepsilon _n^2y_{(n-1)(n-1)}(0)+\varepsilon _n^2\varepsilon _{n-1}z_{(n-1)(n-1)}(0)$. Also, the estimates (21)–(24) imply that

$$\begin{aligned} |v_{n-1}^{(k)}(x)| \le C(1+\varepsilon _{n-1}^{2-k}). \end{aligned}$$

(25)

Proceeding in a similar way, one can derive singularly perturbed systems of l equations, $l = n-2,\; n-3,\ldots ,\; 2,\;1$,

$$\begin{aligned} {\tilde{L}_{l+1}}\tilde{\mathbf {q}}_{l+1} \equiv E_{l}\tilde{\mathbf {q}}_{l+1}^{\;\prime \prime }(x)+A_{l}(x)\tilde{\mathbf {q}}_{l+1}^{\;\prime }(x)-B_{l}(x)\tilde{\mathbf {q}}_{l+1}(x)=\mathbf {g}_{l}(x), \end{aligned}$$

(26)

with $\tilde{\mathbf {q}}_{l+1}(1)=\mathbf {0}\;\text {and}\;\tilde{\mathbf {q}}_{l+1}(0),$ to be chosen.

Now, decomposing $\tilde{\mathbf {q}}_{l+1}$ in a similar way to (9), we obtain

$$\begin{aligned} \tilde{\mathbf {q}}_{l+1}=\mathbf {y}_{l}+\varepsilon _{l} \mathbf {z}_{l}+\varepsilon _{l}^2 \mathbf {q}_{l} \end{aligned}$$

(27)

where $\mathbf {y}_{l}=\left( y_{l1},y_{l2},\ldots ,y_{ll}\right) ^T$ and $\mathbf {z}_l=\left( z_{l1},z_{l2},\ldots ,z_{ll}\right) ^T$ satisfy

$$\begin{aligned} A_l(x)\mathbf {y}_l^{\;\prime }(x)-B_l(x)\mathbf {y}_l(x)=\mathbf {g}_l(x), \;\;\mathbf {y}_l(1)=\mathbf {0},\end{aligned}$$

(28)

$$\begin{aligned} A_l(x)\mathbf {z}_l^{\;\prime }(x)-B_l(x)\mathbf {z}_l(x)=-\varepsilon _l^{-1}E_l\mathbf {y}_l^{\;\prime \prime }(x),\;\mathbf {z}_l(1)=\mathbf {0} \end{aligned}$$

(29)

respectively and $\mathbf {q}_l=\left( q_{l1},q_{l2},\ldots ,q_{ll}\right) ^T$ is the solution of the problem

$$\begin{aligned} {\tilde{L}_{l+1}}\mathbf {q}_l(x)=-\varepsilon _l^{-1}E_l\mathbf {z}_l^{\;\prime \prime }(x),\;\mathbf {q}_l(1)=\mathbf {0}\;\text {where}\;\mathbf {q}_l(0)\;\text {remains to be chosen}. \end{aligned}$$

(30)

We choose $\mathbf {q}_l(0)$ so that its $l\mathrm{th}$ component is zero (i.e. $q_{ll}(0)=0$).

From (28) it is clear that, for $0\le k\le 3$,

$$\begin{aligned} \Vert \mathbf {y}_{l}^{\;(k)}\Vert \le C\left( 1+\varepsilon _{l+1}^{1-k}\right) \prod _{i=l+2}^n\varepsilon _i^{-2} . \end{aligned}$$

(31)

Using (31) in (29), $\Vert \mathbf {z}_l\Vert \le C\left( 1+\varepsilon _{l+1}^{-1}\right) \prod _{i=l+2}^n\varepsilon _i^{-2}$ and for $1\le k\le 3$,

$$\begin{aligned} \Vert \mathbf {z}_l^{(k)}\Vert \le C\left( 1+\varepsilon _{l+1}^{-k}\right) \prod _{i=l+2}^n\varepsilon _i^{-2}. \end{aligned}$$

(32)

Now, using Theorem 1 for $\mathbf {q}_l$, we obtain

$$\begin{aligned} |q_{ll}^{\;(k)}(x)|\le C\varepsilon _{l}^{-k}\prod _{i=l+1}^n\varepsilon _i^{-2},\;\;0\le k\le 3. \end{aligned}$$

(33)

Since $q_{ll}(0)=0$, it is clear that

$$v_l(0)=\gamma _{l}=y_{nl}(0)+\varepsilon _nz_{nl}(0)+\varepsilon _n^2y_{(n-1)l}(0)+\ldots +\left( \displaystyle \prod _{j=l+1}^n\varepsilon _j^2\right) \varepsilon _lz_{ll}(0).$$

Also, the estimates (31)–(33) imply that

$$\begin{aligned} |v_l^{(k)}(x)| \le C(1+\varepsilon _l^{2-k}),\;\;\; 0\le k\le 3. \end{aligned}$$

(34)

Thus, by the choice made for $\gamma _{n},\;\gamma _{n-1},\ldots ,\gamma _{2},\;\gamma _{1}$, the solution $\mathbf {v}$ of the problem (7) satisfies the following bound for $1 \le i\le n$ and $0\le k\le 3$

$$\begin{aligned} |v_i^{(k)}(x)| \le C(1+\varepsilon _i^{2-k}),\;\; x\in \overline{\varOmega }. \end{aligned}$$

(35)

2.1.2 Estimates for the Bounds on the Singular Components and Their Derivatives

Let $\mathscr {B}_i(x),\; 1\le i\le n,$ be the layer functions defined on [0, 1] as

$$\begin{aligned} \mathscr {B}_i(x)=\exp (-\alpha x/\varepsilon _i). \end{aligned}$$

(36)

Theorem 3

Let $\mathbf {w}(x)$ be the solution of (8), then for x $\in \overline{\varOmega }$ and $1\le i\le n$ the following estimates hold.

$$\begin{aligned} |w_{i}(x)|\le & {} C \mathscr {B}_n(x),\end{aligned}$$

(37)

$$\begin{aligned} |w_{i}^{\prime }(x)|\le & {} C \Big (\varepsilon _i^{-1} \mathscr {B}_i(x)+\varepsilon _n^{-1} \mathscr {B}_n(x)\Big ), \end{aligned}$$

(38)

$$\begin{aligned} |w_{i}^{(2)}(x)|\le & {} C\displaystyle \sum _{k=i}^{n}\varepsilon _k^{-2} \mathscr {B}_k(x),\end{aligned}$$

(39)

$$\begin{aligned} |w_{i}^{(3)}(x)|\le & {} C\varepsilon _i^{-1}\Big (\displaystyle \sum _{k=1}^{i-1}\varepsilon _k^{-1} \mathscr {B}_k(x)+\displaystyle \sum _{k=i}^{n}\varepsilon _k^{-2} \mathscr {B}_k(x)\Big ). \end{aligned}$$

(40)

Proof

Consider the barrier function $\mathbf {\phi }=(\phi _1,\phi _2,\ldots ,\phi _n)^T$ defined by $\phi _i(x)=C\mathscr {B}_n(x),$ $1\le i\le n.$ Put $\mathbf {\psi }^{\pm }(x)=\mathbf {\phi }(x)\pm \mathbf {w}(x)$, then for sufficiently large C, $\mathbf {\psi }^{\pm }(0)\ge \mathbf {0},$ $\mathbf {\psi }^{\pm }(1)\ge \mathbf {0}$ and $L\mathbf {\psi }^{\pm }(x)\le \mathbf {0}$. Using Lemma 1, it follows that, $\mathbf {\psi }^{\pm }(x)\ge \mathbf {0}$. Hence, estimate (37) holds. From (8), for $1\le i\le n$

$$\begin{aligned} \varepsilon _i{(w_i^\prime )}^\prime (x)+a_i(x)(w_i^\prime )(x)=g_i(x) \end{aligned}$$

(41)

where $g_i(x) = \displaystyle \sum _{ j=1}^{n}b_{ij}(x)w_j(x)$. Let $\mathscr {A}_i(x)=\displaystyle \int _0^x a_i(s)ds$, then solving (41) leads to

$$ w_i^\prime (x)=w_i^\prime (0)\exp \big (-\mathscr {A}_i(x)/\varepsilon _i\big )+\varepsilon _i^{-1}\displaystyle \int _0^xg_i(t)\exp \big (-(\mathscr {A}_i(x)-\mathscr {A}_i(t))/\varepsilon _i\big )dt.$$

Using Theorem 1 for $\mathbf {w}$, $|w_i^\prime (0)|\le C\varepsilon _i^{-1}$. Further from the inequalities, $\exp \big (-(\mathscr {A}_i(x)$ $-\mathscr {A}_i(t))/\varepsilon _i\big ) {\le } \exp \big (-\alpha (x-t)/\varepsilon _i\big )$ for $t\le x$ and $|g_i(t)|\le C \mathscr {B}_n(t)$, it is clear that

$$\begin{aligned} |w_i^\prime (x)|\le C\varepsilon _i^{-1}\exp \big (-\alpha x/\varepsilon _i\big )+C\varepsilon _i^{-1}\displaystyle \int _0^x\exp \big (-\alpha t/\varepsilon _n\big )\exp \big (-\alpha (x-t)/\varepsilon _i\big )dt. \end{aligned}$$

Using integration by parts, it is not hard to see that

$$\begin{aligned} |w_i^\prime (x)|\le C\varepsilon _i^{-1}\exp \big (-\alpha x/\varepsilon _i\big )+C\varepsilon _n^{-1}\exp \big (-\alpha x/\varepsilon _n\big ). \end{aligned}$$

(42)

Differentiating (41) once leads to

$$\begin{aligned} \varepsilon _i{(w_i^{\prime \prime })}^\prime (x)+a_i(x)(w_i^{\prime \prime })(x)= h_i(x)\equiv g_i^\prime (x)-a_i^\prime (x)w_i^{\prime }(x). \end{aligned}$$

(43)

Then,

$$\begin{aligned} w_i^{\prime \prime }(x)=w_i^{\prime \prime }(0)\exp \big (-\mathscr {A}_i(x)/\varepsilon _i\big )+\varepsilon _i^{-1}\displaystyle \int _0^xh_i(t)\exp \big (-(\mathscr {A}_i(x)-\mathscr {A}_i(t))/\varepsilon _i\big )dt. \end{aligned}$$

Using $|w_i^{\prime \prime }(0)|\le C\varepsilon _i^{-2}, |h_i(t)|\le C \displaystyle \sum _{k=1}^{n}\varepsilon _k^{-1} \mathscr {B}_k(t)$ and hence

$$\begin{aligned} |w_i^{\prime \prime }(x)|\le C\displaystyle \sum _{k=i}^{n}\varepsilon _k^{-2} \mathscr {B}_k(x). \end{aligned}$$

(44)

Using the bounds given in (42) and (44) in (43), (40) can be derived.

As the estimates of the derivatives are to be used in the different segments of the piecewise uniform Shishkin meshes, the estimates are improved using the layer interaction points as given below.

2.1.3 Improved Estimates for the Bounds on the Singular Components and Their Derivatives

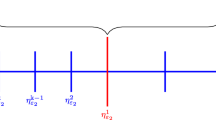
For $\;\mathscr {B}_i$, $\mathscr {B}_j,$ each $\;i,j, \;1 \le i < j \le n\;$ and each $\;s=1,2\;$ the point $\;x^{(s)}_{i,j}\;$ is defined by

$$\begin{aligned} \frac{\mathscr {B}_i(x^{(s)}_{i,j})}{\varepsilon ^s _i}= \frac{\mathscr {B}_j(x^{(s)}_{i,j})}{\varepsilon ^s _j}. \end{aligned}$$

(45)

Lemma 3

For all $\,i,j\,$ such that $\;1 \le i < j \le n\;$ and $s=1,2 \;$ the points $\;x_{i,j}^{(s)}\;$ exist, are uniquely defined and satisfy the following inequalities

$$\begin{aligned} \frac{\mathscr {B}_{i}(x)}{\varepsilon ^s_i} > \frac{\mathscr {B}_{j}(x)}{\varepsilon ^s_j},\;\; x \in [0,x^{(s)}_{i,j}),\;\; \frac{\mathscr {B}_{i}(x)}{\varepsilon ^s_i} < \frac{\mathscr {B}_{j}(x)}{\varepsilon ^s_j}, \; x \in (x^{(s)}_{i,j}, 1].\end{aligned}$$

(46)

In addition, the following ordering holds

$$\begin{aligned} x^{(s)}_{i,j}< x^{(s)}_{i+1,j}, \; \text {if} \;\; i+1<j \;\; \text {and} \;\; x^{(s)}_{i,j}< x^{(s)}_{i,j+1}, \;\; \text {if} \;\; i<j. \end{aligned}$$

(47)

Proof

Proof is similar to the Lemma 2.3.1 of [8].

Consider the following decomposition of $w_i(x)$

$$\begin{aligned} w_i=\sum _{q=1}^{n}w_{i,q},\end{aligned}$$

(48)

where the components $\;w_{i,q}\;$ are defined as follows.

$$\begin{aligned} w_{i,n}=\left\{ \begin{array}{ll} \displaystyle \sum _{k=0}^3 \dfrac{(x-x_{n-1,n}^{(2)})^k}{k!} w^{(k)}_i (x^{(2)}_{n-1,n}) &{} \text {on}\;\;[0,x^{(2)}_{n-1,n})\\ \\ w_i &{} \text {otherwise} \end{array}\right. \qquad \quad \end{aligned}$$

(49)

and, for each $\;q,\;\;n-1 \ge q \ge i$,

$$\begin{aligned} w_{i,q}=\left\{ \begin{array}{ll} \displaystyle \sum _{k=0}^3 \dfrac{(x-x_{q-1,q}^{(2)})^k}{k!}\; p^{(k)}_{i,q} (x^{(2)}_{q-1,q}) &{} \text {on} \;\; [0,x^{(2)}_{q-1,q})\\ \\ p_{i,q} &{} \text {otherwise} \end{array}\right. \qquad \quad \end{aligned}$$

(50)

and, for each $\;q,\;\;i-1 \ge q \ge 2$,

$$\begin{aligned} w_{i,q}=\left\{ \begin{array}{ll} \displaystyle \sum _{k=0}^3 \dfrac{(x-x_{q-1,q}^{(1)})^k}{k!}\; p^{(k)}_{i,q} (x^{(1)}_{q-1,q}) &{} \text {on} \;\; [0,x^{(1)}_{q-1,q})\\ \\ p_{i,q} &{} \text {otherwise} \end{array}\right. \end{aligned}$$

(51)

with $p_{i,q}=w_i-\displaystyle \sum _{k=q+1}^{n} w_{i,k}$

and

$$\begin{aligned} w_{i,1}=w_i-\sum _{k=2}^{n} w_{i,k}\;\; \text {on} \;\; [0,1]. \end{aligned}$$

(52)

Theorem 4

For each $\,q\,$ and $\;i,\;\;1 \le q \le n,\;\;1 \le i \le n\;$ and all $\;x \in \overline{\varOmega },\;$ the components in the decomposition (48) satisfy the following estimates.

$$\begin{aligned} \begin{array}{c} |w_{i,q}^{\;\prime \prime \prime }(x)| \le C\, \varepsilon _i^{-1}\varepsilon _q^{-2}\,\mathscr {B}_q(x),\;\;\text {if}\;\; i\le q,\quad |w_{i,q}^{\;\prime \prime \prime }(x)| \le C\, \varepsilon _i^{-2}\varepsilon _q^{-1}\,\mathscr {B}_q(x),\;\;\text {if}\;\; i> q,\\ \\ |w_{i,q}^{\;\prime \prime }(x)| \le C\, \varepsilon _i^{-1}\varepsilon _q^{-1}\,\mathscr {B}_q(x),\;\;\text {if}\;\; i\le q<n,\quad |w_{i,q}^{\;\prime \prime }(x)| \le C\, \varepsilon _i^{-2}\,\mathscr {B}_q(x),\;\;\text {if}\;\; i> q,\\ \\ |w_{i,q}^{\;\prime }(x)| \le C\, \varepsilon _i^{-1}\,\mathscr {B}_q(x),\;\;\text {if}\;\; q<n. \end{array} \end{aligned}$$

Proof

Differentiating (49) thrice,

$$\begin{aligned} |w_{i,n}^{\prime \prime \prime }(x)|=\left\{ \begin{array}{ll}|w_i^{\prime \prime \prime }(x^{(2)}_{n-1,n})|&{} \text {on}\;\;[0,x^{(2)}_{n-1,n})\\ \\ |w_i^{\prime \prime \prime }(x)| &{} \text {otherwise} \end{array}\right. .\qquad \quad \end{aligned}$$

Then for $x\in [0,x^{(2)}_{n-1,n})$, using Theorem 3,

$$\begin{aligned} |w_{i,n}^{\prime \prime \prime }(x)| \le C\varepsilon _i^{-1}\Big (\displaystyle \sum _{k=1}^{i-1}\varepsilon _k^{-1} \mathscr {B}_k(x^{(2)}_{n-1,n})+\displaystyle \sum _{k=i}^{n}\varepsilon _k^{-2}\mathscr {B}_k(x^{(2)}_{n-1,n})\Big ). \end{aligned}$$

Since $x_{k,n}^{(2)}\le x_{n-1,n}^{(2)}$ for $k<n$, using (46) $\varepsilon _k^{-2}\mathscr {B}_k(x^{(2)}_{n-1,n})\le \varepsilon _n^{-2}\mathscr {B}_n(x^{(2)}_{n-1,n})$ and hence

$$\begin{aligned} |w_{i,n}^{\prime \prime \prime }(x)|\le C\varepsilon _i^{-1}\varepsilon _n^{-2} \mathscr {B}_n(x^{(2)}_{n-1,n})\le C\varepsilon _i^{-1}\varepsilon _n^{-2} \mathscr {B}_n(x). \end{aligned}$$

(53)

For $x\in [x^{(2)}_{n-1,n},1]$,

$$\begin{aligned} |w_{i,n}^{\prime \prime \prime }(x)|&=|w_i^{\prime \prime \prime }(x)|\le C\varepsilon _i^{-1}\Big (\displaystyle \sum _{k=1}^{i-1}\varepsilon _k^{-1} \mathscr {B}_k(x)+\displaystyle \sum _{k=i}^{n}\varepsilon _k^{-2} \mathscr {B}_k(x)\Big ). \end{aligned}$$

As $x\ge x^{(2)}_{n-1,n}$, using (46) $\varepsilon _k^{-2}\mathscr {B}_k(x)\le \varepsilon _n^{-2}\mathscr {B}_n(x)$ and hence for $x\in [x^{(2)}_{n-1,n},1]$

$$\begin{aligned} |w_{i,n}^{\prime \prime \prime }(x)|\le C\varepsilon _i^{-1}\varepsilon _n^{-2} \mathscr {B}_n(x). \end{aligned}$$

(54)

From (49) and (50), it is not hard to see that for each $q,\;n-1 \ge q \ge i$ and $x\in [x^{(2)}_{q,q+1},1]$, $w_{i,q}(x)=p_{i,q}(x)=w_i(x)-\displaystyle \sum _{k=q+1}^{n} w_{i,k}(x)=w_i(x)-w_i(x)=0.$ Differentiating (50) thrice, on $x\in [0,x^{(2)}_{q-1,q})$

$$\begin{aligned} |w_{i,q}^{\prime \prime \prime }(x)|&=|p_{i,q}^{\prime \prime \prime }(x^{(2)}_{q-1,q})| \le C\varepsilon _i^{-1}\varepsilon _q^{-2} \mathscr {B}_q(x). \end{aligned}$$

For $x\in [x^{(2)}_{q-1,q},x^{(2)}_{q,q+1})$, using Lemma 3,

$$\begin{aligned} |w_{i,q}^{\prime \prime \prime }(x)| \le C\, \varepsilon _i^{-1}\varepsilon _q^{-2}\,\mathscr {B}_q(x). \end{aligned}$$

(55)

From (50) and (51), it is not hard to see that for each $q,\;i-1 \ge q \ge 2$ and $x\in [x^{(1)}_{q,q+1},1]$, $w_{i,q}(x)=0.$ Differentiating (51) thrice on $x\in [0,x^{(1)}_{q-1,q})$

$$\begin{aligned} |w_{i,q}^{\prime \prime \prime }(x)|&=|p_{i,q}^{\prime \prime \prime }(x^{(1)}_{q-1,q})| \le C\varepsilon _i^{-2}\varepsilon _q^{-1} \mathscr {B}_q(x). \end{aligned}$$

For $x\in [x^{(1)}_{q-1,q},x^{(1)}_{q,q+1})$, using Lemma 3,

$$\begin{aligned} |w_{i,q}^{\prime \prime \prime }(x)| \le C\varepsilon _i^{-2}\varepsilon _q^{-1} \mathscr {B}_q(x). \end{aligned}$$

(56)

From (51) and (52), it is not hard to see that $w_{i,1}(x)=0$ for $x\in [x^{(1)}_{1,2},1]$ and for $x\in [0,x^{(1)}_{1,2})$, $|w_{i,1}^{\prime \prime \prime }(x)|\le |w_i^{\prime \prime \prime }(x)| \le C\varepsilon _i^{-2}\varepsilon _1^{-1} \mathscr {B}_1(x).$ Since $w_{i,q}^{\prime \prime }(1)=0$, for $q<n$, it follows that for any $x\in [0,1]$ and $i>q$,

$$|w_{i,q}^{\prime \prime }(x)|=\Big |\int _x^1w_{i,q}^{(3)}(t)dt\Big | \le C\int _x^1\varepsilon _i^{-2}\varepsilon _q^{-1}\mathscr {B}_q(t)dt\le C\varepsilon _i^{-2}\mathscr {B}_q(x).$$

Hence,

$$\begin{aligned} |w_{i,q}^{\prime \prime }(x)| \le C\, \varepsilon _i^{-2}\,\mathscr {B}_q(x),\;\; \text {for}\;\; i>q. \end{aligned}$$

(57)

Similar arguments lead to

$$\begin{aligned} |w_{i,q}^{\prime \prime }(x)| \le C\, \varepsilon _i^{-1}\varepsilon _q^{-1}\,\mathscr {B}_q(x),\;\; \text {for}\;\; i\le q, \end{aligned}$$

(58)

and

$$\begin{aligned} |w_{i,q}^{\prime }(x)| \le C\, \varepsilon _i^{-1}\,\mathscr {B}_q(x),\; 1\le i\le n, 1\le q\le n. \end{aligned}$$

(59)

3 Numerical Method

To solve the BVP (1)–(2), a numerical method comprising of a Classical Finite Difference(CFD) Scheme and a piecewise uniform Shishkin mesh fitted on the domain [0, 1] is suggested.

3.1 Shishkin Mesh

A piecewise uniform Shishkin mesh with N mesh-intervals is now constructed. The mesh $\;\overline{\varOmega }^N\;$ is a piecewise uniform mesh on $\;[0,1]\;$ obtained by dividing [0, 1] into $n+1$ mesh-intervals as $[0,\tau _1]\cup [\tau _1,\tau _2]\cup \dots \cup [\tau _{n-1},\tau _n]\cup [\tau _n,1].$ Transition parameters $\tau _r,\;1\le r\le n$, are defined as $\tau _{n} = \min \displaystyle \left\{ \frac{1}{2},\;2\frac{\varepsilon _n}{\alpha }\ln N\right\}$ and, for $\;r=n-1,\,\dots \,1$, $\tau _{r}=\min \displaystyle \left\{ \frac{r\tau _{r+1}}{r+1},\;2\frac{\varepsilon _r}{\alpha }\ln N\right\} .$ On the sub-interval $\;[\tau _n,1], \;\frac{N}{2}+1\;$ mesh-points are placed uniformly and on each of the subintervals $\;[\tau _r,\tau _{r+1}),\;\;r=n-1,\,\dots \, 1,$ a uniform mesh of $\;\frac{N}{2n}\;$ mesh-points is placed. A uniform mesh of $\;\frac{N}{2n}\;$ mesh-points is placed on the sub-interval $[0,\tau _1).$

The Shishkin mesh is coarse in the outer region and becomes finer and finer in the inner (layer) regions. From the above construction, it is clear that the transition points $\;\tau _r,\;r=1,\dots , n,\;$are the only points at which the mesh-size can change and that it does not necessarily change at each of these points.

If each of the transition parameters $\;\tau _r,\;r=1,\dots , n,\;$ are with the left choice, the Shishkin mesh $\;\overline{\varOmega }^N\;$ becomes the classical uniform mesh with $\;\tau _r = \frac{r}{2n},\;r=1,\dots , n,\;$ and hence the step size is $\;N^{-1}\;$.

The following notations are introduced: $\;h_j = x_j-x_{j-1}$ and if $\;x_j=\tau _r,\;$ then $\;h_r^- = x_j-x_{j-1},\;\;h_r^+ = x_{j+1}-x_j,\;\;J = \{\tau _r: h_r^+ \ne h_r^-\}.$ Let $H_r=2n\,N^{-1}(\tau _r-\tau _{r-1}),\;2\le r\le n$ denote the step size in the mesh interval $(\tau _{r-1},\tau _r]$. Also, $H_1 = 2\, n N^{-1}\tau _1$ and $H_{n+1}=2\,N^{-1} (1-\tau _n)$. Thus, for $\;1 \le r \le n-1,\;$ the change in the step size at the point $\;x_j = \tau _r\;$ is

$$\begin{aligned} h^+_r-h^-_r = 2\, n N^{-1}\Big (\frac{(r+1)}{r}d_r - d_{r-1}\Big ), \end{aligned}$$

(60)

where $d_r = \frac{r\tau _{r+1}}{r+1}-\tau _r$ with the convention $\;d_n =0,$ when $\tau _n=1/2 .\;$ The mesh $\;\overline{\varOmega }^N\;$ becomes a classical uniform mesh when $\;d_r = 0\;$ for all $\;r=1,\;\dots ,\;n\;$ and $\tau _r \le C\,\varepsilon _r \ln N, \; \;\; 1 \le r \le n.$ Also $\tau _r=\frac{r}{s}\tau _{s}\;\;\mathrm {when}\;\; d_r=\dots =d_s =0, \; 1 \le r \le s \le n.$

3.2 Discrete Problem

To solve the BVP (1)–(2) numerically the following upwind classical finite difference scheme is applied on the mesh $\overline{\varOmega }^N$.

$$\begin{aligned} L^N\mathbf {U}(x_j)\equiv E\delta ^2\mathbf {U}(x_j)+A(x_j)D^+\mathbf {U}(x_j)-B(x_j)\mathbf {U}(x_j)=\mathbf {f}(x_j),\end{aligned}$$

(61)

$$\begin{aligned} \mathbf {U}(x_0)=\mathbf {l},\;\mathbf {U}(x_N)=\mathbf {r}, \end{aligned}$$

(62)

where $\mathbf {U}(x_j)=(U_1(x_j),U_2(x_j),\ldots ,U_n(x_j))^T$ and for $1\le j\le N-1,$

$$ D^+U(x_j)=\frac{U(x_{j+1})-U(x_j)}{h_{j+1}},\;\; D^-U(x_j)=\frac{U(x_j)-U(x_{j-1})}{h_j},$$

$$\delta ^2U(x_j)=\dfrac{1}{\overline{h}_j}\Big (D^+U(x_j)-D^-U(x_j)\Big ),$$

with

$$\overline{h_j}=\frac{(h_j+h_{j+1})}{2} .$$

4 Numerical Results

In this section a discrete maximum principle, a discrete stability result and the first-order convergence of the proposed numerical method are established.

Lemma 4

(Discrete Maximum Principle) Assume that the vector valued mesh function $\mathbf {\psi }(x_j)=(\psi _1(x_j),\psi _2(x_j),\ldots ,\psi _n(x_j))^T$ satisfies $\mathbf {\psi }(x_0) \ge \mathbf {0}$ and $\mathbf {\psi }(x_N)\ge \mathbf {0}$. Then $L^N\mathbf {\psi }(x_j) \le \mathbf {0}$ for $1\le j\le N-1$ implies that $\mathbf {\psi }(x_j) \ge \mathbf {0}$ for $0 \le j \le N.$

Lemma 5

(Discrete Stability Result) If $\mathbf {\psi }(x_j)=(\psi _1(x_j),\psi _2(x_j),\ldots ,\psi _n(x_j))^T$ is any vector valued mesh function defined on $\overline{\varOmega }^N,$ then for $1\le i\le n$ and $0\le j \le N$,

$$|\psi _i(x_j)| \le \max \Big \{\Vert \mathbf {\psi }(x_0)\Vert ,\;\Vert \mathbf {\psi }(x_N)\Vert ,\; \frac{1}{\beta }\;\Vert L^N\mathbf {\psi }\Vert _{\varOmega ^N}\Big \}.$$

4.1 Error Estimate

Analogous to the continuous case, the discrete solution $\mathbf {U}$ can be decomposed into $\mathbf {V}$ and $\mathbf {W}$ as defined below.

$$\begin{aligned} L^N\mathbf {V}(x_j) = \mathbf {f}(x_j), \;\text {for} \; 0< j < N,\; \mathbf {V}(x_0)=\mathbf {v}(x_0),\; \mathbf {V}(x_N)=\mathbf {v}(x_N)\end{aligned}$$

(63)

$$\begin{aligned} L^N\mathbf {W}(x_j) = \mathbf {0}, \;\text {for} \; 0< j < N,\; \mathbf {W}(x_0)=\mathbf {w}(x_0),\; \mathbf {W}(x_N)=\mathbf {w}(x_N)\; \end{aligned}$$

(64)

Lemma 6

Let $\mathbf {v}$ be the solution of (7) and $\mathbf {V}$ be the solution of (63), then

$$\Vert \mathbf {V}-\mathbf {v}\Vert _{\overline{\varOmega }^N} \le CN^{-1}.$$

Proof

For $1\le j\le N-1$,

$$\begin{aligned} L^N(\mathbf {V}-\mathbf {v})(x_j)= \begin{pmatrix} \varepsilon _1(\frac{d^2}{dx^2}-\delta ^2)v_1(x_j)+a_1(x_j)(\frac{d}{dx}-D^+)v_1(x_j)\\ \varepsilon _2(\frac{d^2}{dx^2}-\delta ^2)v_2(x_j)+a_2(x_j)(\frac{d}{dx}-D^+)v_2(x_j)\\ \vdots \\ \varepsilon _n(\frac{d^2}{dx^2}-\delta ^2)v_n(x_j)+a_n(x_j)(\frac{d}{dx}-D^+)v_n(x_j) \end{pmatrix}. \end{aligned}$$

By the standard local truncation used in the Taylor expansions,

$$|\varepsilon _i\left( \frac{d^2}{dx^2}-\delta ^2\right) v_i(x_j)+a_i(x_j)\left( \frac{d}{dx}-D^+\right) v_i(x_j)|\le C(x_{j+1}-x_{j-1})(\varepsilon _i\Vert v_i^{(3)}\Vert +\Vert v_i^{(2)}\Vert ).$$

Since $(x_{j+1}-x_{j-1}) \le CN^{-1}$, by using (35),

$$\Vert L^N(\mathbf {V}-\mathbf {v})\Vert _{\varOmega ^N} \le CN^{-1}.$$

As v and V agree at the boundary points, using Lemma 5,

$$\begin{aligned} \Vert \mathbf {V}-\mathbf {v}\Vert _{\overline{\varOmega }^N} \le CN^{-1}. \end{aligned}$$

(65)

To estimate the error in the singular component $(\mathbf {W}-\mathbf {w})$, the mesh functions $B_i^N(x_j)$ for $1\le i\le n$ on $\overline{\varOmega }^N$ are defined by

$$B_i^N(x_j)=\displaystyle \prod _{k=1}^j\left( 1+\frac{\alpha h_k}{2\varepsilon _i}\right) ^{-1}$$

with $B_i^N(x_0)=1.$ It is to be observed that $B_i^N$ are monotonically decreasing.

Lemma 7

The singular components $W_i$, $1\le i\le n$ satisfy the following bound on $\overline{\varOmega }^N$;

$$|W_i(x_j)| \le C B^N_n(x_j).$$

Proof

Consider the following vector valued mesh functions on $\overline{\varOmega }^N$,

$$\mathbf {\psi }^{\pm }(x_j)=C B^N_n(x_j)\mathbf {e} \pm \mathbf {W}(x_j)$$

where $\mathbf {e}$ is the n- vector $\mathbf {e}=(1,1,\ldots ,1)^T$.

Then for sufficiently large C, $\mathbf {\psi }^{\pm }(x_0) \ge \mathbf {0}$, $\mathbf {\psi }^{\pm }(x_N) \ge \mathbf {0}$ and $L^N \mathbf {\psi }^{\pm }(x_j) \le \mathbf {0},$ for $1\le j\le N-1$. Using Lemma 4, $\mathbf {\psi }^{\pm }(x_j)\ge \mathbf {0}$ on $\overline{\varOmega }^N,$ which implies that

$$|W_i(x_j)| \le C B^N_n(x_j).$$

Lemma 8

Assume that $d_r=0,\;\text {for}\; r=1, 2, \ldots , n.$ Let $\mathbf {w}$ be the solution of (8) and $\mathbf {W}$ be the solution of (64). Then

$$\Vert \mathbf {W}-\mathbf {w}\Vert _{\overline{\varOmega }^N} \le CN^{-1}\ln N.$$

Proof

By the standard local truncation used in the Taylor expansions,

$$\Big |\varepsilon _i(\frac{d^2}{dx^2}-\delta ^2)w_i(x_j)+a_i(x_j)(\frac{d}{dx}-D^+)w_i(x_j)\Big |\le C(x_{j+1}-x_{j-1})(\varepsilon _i\Vert w_i^{(3)}\Vert +\Vert w_i^{(2)}\Vert )$$

where the norm is taken over the interval ${[x_{j-1},x_{j+1} ]}$.

Since $d_r=0$, the mesh is uniform, $h=N^{-1}$ and $\varepsilon _k^{-1}\le C \ln N.$ Then,

$$\begin{aligned} \;|(\mathbf {L}^N(\mathbf {W}-\mathbf {w}))_i (x_j)|\le & {} C\, N^{-1} \Big (\displaystyle \sum _{k=1}^{i-1}\varepsilon _k^{-1} \mathscr {B}_k(x_{j-1})+\displaystyle \sum _{k=i}^{n}\varepsilon _k^{-2}\mathscr {B}_k(x_{j-1})\Big )\end{aligned}$$

(66)

$$\begin{aligned}\le & {} CN^{-1}\ln N+CN^{-1}\ln N\displaystyle \sum _{k=i}^{n}\varepsilon _k^{-1}\mathscr {B}_k(x_{j-1}). \end{aligned}$$

(67)

Consider the barrier function $\mathbf {\phi }=(\phi _1(x_j),\phi _2(x_j),\ldots ,\phi _n(x_j))^T$ given by

$$\phi _i(x_j)=CN^{-1} \ln N+ \frac{CN^{-1}\ln N}{\gamma (\alpha -\gamma )}\Big (\displaystyle \sum _{k=i}^{n}\exp (2\gamma h/\varepsilon _k)Y_k(x_j)\Big ),\; \text {on} \;\overline{\varOmega }^N,$$

where $\gamma$ is a constant such that $0<\gamma < \alpha$,

$$Y_k(x_j)=\dfrac{\lambda _k^{N-j}-1}{\lambda _k^N-1}\; \text {with}\; \lambda _k=1+\frac{\gamma h}{\varepsilon _k}. $$

It is not hard to see that, $0\le Y_k(x_j) \le 1,\;\;\; D^+Y_k(x_j)\le -\frac{\gamma }{\varepsilon _k}\exp (-\gamma x_{j+1}/\varepsilon _k)$ and $(\varepsilon _k\delta ^2+\gamma D^+)Y_k(x_j)=0.$ Hence,

$$\begin{aligned}\nonumber (L^N\mathbf {\phi })_i(x_j)&\le -CN^{-1}\ln N-CN^{-1}\ln N\displaystyle \sum _{k=i}^{n}\varepsilon _k^{-1}\mathscr {B}_k(x_{j-1}). \end{aligned}$$

Consider the discrete functions

$$\mathbf {\psi }^{\pm }(x_j)=\mathbf {\phi }(x_j)\pm (\mathbf {W}-\mathbf {w})(x_j), x_j \in \overline{\varOmega }^N.$$

Then for sufficiently large C, $\mathbf {\psi }^{\pm }(x_0) > \mathbf {0}$, $\mathbf {\psi }^{\pm }(x_N)\ge \mathbf {0}$ and $L^N\mathbf {\psi }^{\pm }(x_j)\le \mathbf {0}$ on $\varOmega ^N$.

Using Lemma 4, $\mathbf {\psi }^{\pm }(x_j)\ge \mathbf {0}$ on $\overline{\varOmega }^N$. Hence, $|(\mathbf {W}-\mathbf {w})_i(x_j)|\le CN^{-1}\ln N$ for $1\le i\le n$, implies that

$$\begin{aligned} \Vert (\mathbf {W}-\mathbf {w})\Vert _{\overline{\varOmega }^N} \le CN^{-1}\ln N. \end{aligned}$$

(68)

Lemma 9

Let $\mathbf {w}$ be the solution of (8) and $\mathbf {W}$ be the solution of (64); then

$$\Vert \mathbf {W}-\mathbf {w}\Vert _{\overline{\varOmega }^N} \le CN^{-1}\ln N.$$

Proof

This is proved for each mesh point $\;x_j \in (0,1)\;$ by dividing (0, 1) into $n+1$ subintervals (a) $(0,\tau _1),$ (b) $[\tau _1,\tau _2),$ (c) $[\tau _m,\tau _{m+1})$ for some $\;m,\; 2 \le m \le n-1\;$ and (d) $\;[\tau _n,1).\;$

For each of these cases, an estimate for the local truncation error is derived and a barrier function is defined. Lastly, using these barrier functions, the required estimate is established.

Case (a): $x_j \in (0,\tau _1)$.

Clearly $\;x_{j+1} - x_{j-1} \;\le \; C \varepsilon _1 N^{-1}\ln N.\;$ Then, by standard local truncation used in Taylor expansions, the following estimates hold for $x_j \in (0,\tau _1)$ and $1\le i\le n.$

$$\begin{aligned} \begin{array}{lcl} \; |(\mathbf {L}^N(\mathbf {W}-\mathbf {w}))_i (x_j)|&{}\le &{} C\,(x_{j+1}-x_{j-1})(\varepsilon _i\Vert w_i^{(3)}\Vert +\Vert w_i^{(2)}\Vert )\\ &{}\le &{} C\, N^{-1}\ln N\displaystyle \sum _{k=i}^{n}\varepsilon _k^{-1}\mathscr {B}_k(x_{j-1}).\\ \end{array} \end{aligned}$$

Consider the following barrier functions for $x_j \in (0,\tau _1)$ and $1\le i\le n.$

$$\begin{aligned} \phi _i(x_j)=CN^{-1}\ln N \sum _{k=i}^{n}\exp (2\alpha H_1/\varepsilon _k)B_k^N(x_j)+\sum _{k=1}^{n}B_k^N(\tau _k). \end{aligned}$$

(69)

Case (b): $x_j \in [\tau _1,\tau _2)$.

There are 2 possibilities: Case (b1): $\mathbf{\;d_1 = 0\;}$ and Case (b2): $\mathbf{\;d_1 > 0.\;}$

Case (b1): $\mathbf{\;d_1 = 0\;}$

Since the mesh is uniform in $\;(0,\tau _2),\;$ it follows that $x_{j+1} - x_{j-1} \;\le \; C\,\varepsilon _1 N^{-1}\ln N,$ for $x_j\in [\tau _1,\tau _2)$ . Then,

$$\begin{aligned} |(\mathbf {L}^N(\mathbf {W}-\mathbf {w}))_i (x_j)|\;\le \; C\, N^{-1}\ln N\displaystyle \sum _{k=i}^{n}\varepsilon _k^{-1}\mathscr {B}_k(x_{j-1}). \end{aligned}$$

(70)

Now for $x_j\in [\tau _1,\tau _2)\;\text {and}\;1\le i\le n$, define,

$$\begin{aligned} \phi _i(x_j)=CN^{-1}\ln N \sum _{k=i}^{n}\exp (2\alpha H_2/\varepsilon _k)B_k^N(x_j)+\sum _{k=2}^{n}B_k^N(\tau _k). \end{aligned}$$

(71)

Case (b2): ${\mathbf{d}}_{\mathbf{1}} > \mathbf{0}.\;$

For this case, $\;x_{j+1} - x_{j-1} \;\le \; C\,\varepsilon _2 N^{-1}\ln N\;$, and hence for $x_j \in [\tau _1,\tau _2)$

$$\begin{aligned} \begin{array}{lcl} \Big |(\mathbf {L}^N(\mathbf {W}-\mathbf {w}))_i (x_j)\Big |&{}\le &{} \Big |\varepsilon _i(\dfrac{d^2}{dx^2}-\delta ^2)w_i(x_j)\Big |+C\,\Big |(\dfrac{d}{dx}-D^+)w_i(x_j)\Big |\\ \\ &{}\le &{} \Big |\varepsilon _i(\dfrac{d^2}{dx^2}-\delta ^2)\displaystyle \sum _{k=1}^{n} w_{i,k}\Big |+C\,\Big |(\dfrac{d}{dx}-D^+)\displaystyle \sum _{k=1}^{n} w_{i,k}\Big |. \end{array} \end{aligned}$$

By the standard local truncation used in Taylor expansions

$$\begin{aligned} \begin{aligned} |(\mathbf {L}^N(\mathbf {W}-\mathbf {w}))_i (x_j)| \le C\, \varepsilon _i|w_{i,1}^{(2)}(x_{j-1})|+C\,(x_{j+1}-x_{j-1})\varepsilon _i \displaystyle \sum _{k=2}^{n}|w_{i,k}^{(3)}(x_{j-1})|\\+C\, |w_{i,1}^{(1)}(x_{j-1})|+C\,(x_{j+1}-x_{j-1})\displaystyle \sum _{k=2}^{n}|w_{i,k}^{(2)}(x_{j-1})|. \end{aligned} \end{aligned}$$

(72)

Now using Theorem 4, it is not hard to derive that

$$\begin{aligned} |(\mathbf {L}^N(\mathbf {W}-\mathbf {w}))_1 (x_j)| \le C\, N^{-1}\ln N\displaystyle \sum _{k=2}^{n}\varepsilon _k^{-1}\mathscr {B}_k(x_{j-1})+C\,\varepsilon _1^{-1}\mathscr {B}_1(x_{j-1}) \end{aligned}$$

(73)

and for $2\le i\le n$,

$$\begin{aligned} |(\mathbf {L}^N(\mathbf {W}-\mathbf {w}))_i (x_j)| \le C\, N^{-1}\ln N\displaystyle \sum _{k=i}^{n}\varepsilon _k^{-1}\mathscr {B}_k(x_{j-1})+C\,\varepsilon _i^{-1}\mathscr {B}_1(x_{j-1}). \end{aligned}$$

(74)

Define

$$\begin{aligned} \phi _1(x_j)=CN^{-1}\ln N \sum _{k=2}^{n}\exp (2\alpha H_2/\varepsilon _k)B_k^N(x_j)+C\,B_1^N(x_j)+C\,\sum _{k=2}^{n}B_k^N(\tau _k) \end{aligned}$$

and for $2\le i\le n$,

$$\begin{aligned} \phi _i(x_j)=CN^{-1}\ln N \sum _{k=i}^{n}\exp (2\alpha H_2/\varepsilon _k)B_k^N(x_j)+C\,B_1^N(x_j)+C\,\sum _{k=2}^{n}B_k^N(\tau _k). \end{aligned}$$

Case (c): $x_j\in (\tau _m,\tau _{m+1}]$. There are 3 possibilities:

Case (c1): $d_1=d_2=\dots =d_m=0,$

Case (c2): $d_r>0$ and $\; d_{r+1}=\;\dots \;=d_m=0$ for some $r,\; 1 \le r \le m-1$ and

Case (c3): $d_m>0$.

Case (c1): $d_1=d_2=\dots =d_m=0,$

Since $\;\tau _1=C\tau _{m+1}\;$ and the mesh is uniform in $\;(0,\tau _{m+1}),\;$ it follows that, for $x_j\in (\tau _m,\tau _{m+1}]$, $\;x_{j+1} - x_{j-1} \;\le \; C\,\varepsilon _1 N^{-1}\ln N\;$ and hence

$$\begin{aligned} |(\mathbf {L}^N(\mathbf {W}-\mathbf {w}))_i (x_j)|\;\le \; C\, N^{-1}\ln N\displaystyle \sum _{k=i}^{n}\varepsilon _k^{-1}\mathscr {B}_k(x_{j-1}). \end{aligned}$$

(75)

For $1\le i\le n$,

$$\begin{aligned} \phi _i(x_j)=CN^{-1}\ln N \sum _{k=i}^{n}\exp (2\alpha H_{m+1}/\varepsilon _k)B_k^N(x_j)+C\,\sum _{k=m+1}^{n}B_k^N(\tau _k). \end{aligned}$$

(76)

Case (c2): $d_r>0$ and $\; d_{r+1}=\;\dots \;=d_m=0$ for some $r,\; 1 \le r \le m-1$

Since, $\;\tau _{r+1} = C \tau _{m+1}$, the mesh is uniform in $\;(\tau _{r},\tau _{m+1}),\;$ it follows that $\;x_{j+1} - x_{j-1} \;\le \; C\,\varepsilon _{r+1}N^{-1}\ln N,$ for $x_j\in (\tau _m,\tau _{m+1}].\;$

By the standard local truncation used in Taylor expansions

$$\begin{aligned} \begin{aligned} |(\mathbf {L}^N(\mathbf {W}-\mathbf {w}))_i (x_j)| \le C\, \varepsilon _i\displaystyle \sum _{k=1}^{r}|w_{i,k}^{(2)}(x_{j-1})|+C\,(x_{j+1}-x_{j-1})\varepsilon _i \displaystyle \sum _{k=r+1}^{n}|w_{i,k}^{(3)}(x_{j-1})|\\+C\,\displaystyle \sum _{k=1}^{r} |w_{i,k}^{(1)}(x_{j-1})|+C\,(x_{j+1}-x_{j-1})\displaystyle \sum _{k=r+1}^{n}|w_{i,k}^{(2)}(x_{j-1})|. \end{aligned} \end{aligned}$$

(77)

Now using Theorem 4, it is not hard to derive that for $i\le r$

$$\begin{aligned} |(\mathbf {L}^N(\mathbf {W}-\mathbf {w}))_i (x_j)| \le C\, N^{-1}\ln N\displaystyle \sum _{k=r+1}^{n}\varepsilon _k^{-1} \mathscr {B}_k(x_{j-1})+C\sum _{k=i}^{r}\varepsilon _k^{-1}\mathscr {B}_k(x_{j-1}) \end{aligned}$$

and for $i > r$

$$\begin{aligned} |(\mathbf {L}^N(\mathbf {W}-\mathbf {w}))_i (x_j)| \le C\, N^{-1}\ln N\displaystyle \sum _{k=i}^{n}\varepsilon _k^{-1}\mathscr {B}_k(x_{j-1})+C\varepsilon _i^{-1}\mathscr {B}_r(x_{j-1}). \end{aligned}$$

Now define, for $i\le r$

$$\begin{aligned} \phi _i(x_j)=CN^{-1}\ln N \sum _{k=r+1}^{n}\exp \left( \frac{2\alpha H_{m+1}}{\varepsilon _k}\right) B_k^N(x_j)+C\sum _{k=i}^{r}B_k^N(x_j) +C\sum _{k=m+1}^{n}B_k^N(\tau _k) \end{aligned}$$

and for $i > r$

$$\begin{aligned} \phi _i(x_j)=CN^{-1}\ln N \sum _{k=i}^{n}\exp \left( \frac{2\alpha H_{m+1}}{\varepsilon _k}\right) B_k^N(x_j)+CB_r^N(x_j)+C\sum _{k=m+1}^{n}B_k^N(\tau _k). \end{aligned}$$

Case (c3): $d_m>0$

Replacing r by m in the arguments of the previous case Case(c2) and using $x_{j+1} - x_{j-1}\le C\varepsilon _{m+1}N^{-1}\ln N,$ the following estimates hold for $x_j\in (\tau _m,\tau _{m+1}].$

For $i\le m$,

$$\begin{aligned} |(\mathbf {L}^N(\mathbf {W}-\mathbf {w}))_i (x_j)| \le C\, N^{-1}\ln N\displaystyle \sum _{k=m+1}^{n}\varepsilon _k^{-1}\mathscr {B}_k(x_{j-1})+C\,\sum _{k=i}^{m}\varepsilon _k^{-1}\mathscr {B}_k(x_{j-1}) \end{aligned}$$

(78)

and for $i > m$

$$\begin{aligned} |(\mathbf {L}^N(\mathbf {W}-\mathbf {w}))_i (x_j)| \le C\, N^{-1}\ln N\displaystyle \sum _{k=i}^{n}\varepsilon _k^{-1}\mathscr {B}_k(x_{j-1})+C\,\varepsilon _i^{-1}\mathscr {B}_m(x_{j-1}). \end{aligned}$$

(79)

For $i\le m$, define,

$$\begin{aligned} \phi _i(x_j)=CN^{-1}\ln N \sum _{k=m+1}^{n}\exp \left( \frac{2\alpha H_{m+1}}{\varepsilon _k}\right) B_k^N(x_j)+C\sum _{k=i}^{m}B_k(x_j)+C\sum _{k=m+1}^{n}B_k^N(\tau _k) \end{aligned}$$

and for $i > m$

$$\begin{aligned} \phi _i(x_j)=CN^{-1}\ln N \sum _{k=i}^{n}\exp \left( \frac{2\alpha H_{m+1}}{\varepsilon _k}\right) B_k^N(x_j)+CB_m(x_j)+C\sum _{k=m+1}^{n}B_k^N(\tau _k). \end{aligned}$$

Case (d): There are 3 possibilities.

Case (d1): $d_1=\;\;\dots \;\;=d_n=0,$

Case (d2): $d_r>0$ and $\; d_{r+1}=\;\dots \;=d_n=0$ for some $r,\; 1 \le r \le n-1$ and

Case (d3): $d_n>0$.

Case (d1): $d_1=\;\;\dots \;\;=d_n=0,$

The mesh is uniform in [0, 1] and the result is established in the Lemma 8.

Case (d2): $d_r>0$ and $\; d_{r+1}=\;\dots \;=d_n=0$ for some $r,\; 1 \le r \le n-1$

In this case from the definition of $\tau _n$ it follows that $\;x_{j+1} - x_{j-1} \;\le \; C\,\varepsilon _{r+1}N^{-1}\ln N\;$ and arguments similar to the Case(c2) lead to the following estimates for $x_j \in (\tau _n,1]$.

For $i\le r$,

$$\begin{aligned} |(\mathbf {L}^N(\mathbf {W}-\mathbf {w}))_i (x_j)| \le C\, N^{-1}\ln N\displaystyle \sum _{k=r+1}^{n}\varepsilon _k^{-1}\mathscr {B}_k(x_{j-1})+C\,\sum _{k=i}^{r}\varepsilon _k^{-1}\mathscr {B}_k(x_{j-1}) \end{aligned}$$

(80)

and for $i > r$

$$\begin{aligned} |(\mathbf {L}^N(\mathbf {W}-\mathbf {w}))_i (x_j)| \le C\, N^{-1}\ln N\displaystyle \sum _{k=i}^{n}\varepsilon _k^{-1}\mathscr {B}_k(x_{j-1})+C\,\varepsilon _i^{-1}\mathscr {B}_r(x_{j-1}). \end{aligned}$$

(81)

Define the barrier functions $\phi _i$ for $i\le r$ by

$$\begin{aligned} \phi _i(x_j)=CN^{-1}\ln N \sum _{k=r+1}^{n}\exp (2\alpha H_{n+1}/\varepsilon _k)B_k^N(x_j)+C\,\sum _{k=i}^{r}B_k^N(x_j) \end{aligned}$$

(82)

and for $i > r$

$$\begin{aligned} \phi _i(x_j)=CN^{-1}\ln N \sum _{k=i}^{n}\exp (2\alpha H_{n+1}/\varepsilon _k)B_k^N(x_j)+CB_r^N(x_j). \end{aligned}$$

(83)

Case (d3): $d_n>0$

Now $\tau _n = 2\dfrac{\varepsilon _n}{\alpha }\ln N$. Then on $(\tau _n,1]$,

$$\begin{aligned} |(W_i-w_i)(x_j)|&\le |W_i(x_j)|+|w_i(x_j)|\\&\le C B_n^N(x_j)+C\mathscr {B}_n(x_j),\;\text {using\;\; Lemma~7\;and\;Theorem~3} \end{aligned}$$

Hence,

$$\begin{aligned} |(W_i-w_i)(x_j)|\le C N^{-1},\;\;\text {on}\; [\tau _n,1]. \end{aligned}$$

(84)

Now using the estimates derived and the barrier functions $\phi _i,\; 1\le i\le n,$ defined for all the four cases, the main proof is split into two cases

Case 1: $d_n>0$. Consider the following discrete functions for $0\le j\le N/2$,

$$\begin{aligned} \mathbf {\psi }^{\pm }(x_j)=\mathbf {\phi }(x_j)\pm (\mathbf {W} -\mathbf {w})(x_j) \end{aligned}$$

(85)

where $\mathbf {\phi }(x_j)=(\phi _1(x_j),\phi _2(x_j),\ldots ,\phi _n(x_j))^T$.

For sufficiently large C, it is not hard to see that

$$\mathbf {\psi }^{\pm }(x_0)\ge \mathbf {0},\; \mathbf {\psi }^{\pm }(x_{\frac{N}{2}})\ge \mathbf {0}\; \text {and}\; L^N\mathbf {\psi }^{\pm }(x_j)\le \mathbf {0}, \text {for}\; 0< j < N/2.$$

Then by Lemma 4, $\mathbf {\psi }^{\pm }(x_j)\ge \mathbf {0}$ for $0 \le j \le N/2.$ Consequently,

$$\begin{aligned} |(W_i-w_i)(x_j)|\le C N^{-1},\;\;\text {on}\; [0,\tau _n]. \end{aligned}$$

(86)

Hence, (84) and (86) imply that, for $d_n>0$

$$\begin{aligned} \Vert (\mathbf {W}-\mathbf {w})\Vert _{\overline{\varOmega }^N} \le CN^{-1}\ln N. \end{aligned}$$

(87)

Case 2: $d_n=0$. Consider the following discrete functions for $0\le j\le N$,

$$\begin{aligned} \mathbf {\psi }^{\pm }(x_j)=\mathbf {\phi }(x_j)\pm (\mathbf {W} -\mathbf {w})(x_j). \end{aligned}$$

(88)

For sufficiently large C, it is not hard to see that

$$\mathbf {\psi }^{\pm }(x_0)\ge \mathbf {0},\; \mathbf {\psi }^{\pm }(x_N)\ge \mathbf {0}\; \text {and}\; L^N\mathbf {\psi }^{\pm }(x_j)\le \mathbf {0}, \text {for}\; 0< j < N.$$

Then by Lemma 4, $\mathbf {\psi }^{\pm }(x_j)\ge \mathbf {0}$ for $0 \le j \le N.$ Hence, for $d_n=0$,

$$\begin{aligned} \Vert (\mathbf {W}-\mathbf {w})\Vert _{\overline{\varOmega }^N} \le CN^{-1}\ln N. \end{aligned}$$

Theorem 5

Let u be the solution of the problem (1)–(2) and U be the solution of the problem (61)–(62), then,

$$\begin{aligned} \Vert (\mathbf {u}-\mathbf {U})\Vert _{\overline{\varOmega }^N} \le CN^{-1} \ln N. \end{aligned}$$

Proof

From the Eqs. (7), (8), (63) and (64), we have

$$\begin{aligned} \Vert (\mathbf {u}-\mathbf {U})\Vert _{\overline{\varOmega }^N}&= \Vert (\mathbf {v+w}-\mathbf {V+W})\Vert _{\overline{\varOmega }^N}\\&\le \Vert (\mathbf {v}-\mathbf {V}\Vert _{\overline{\varOmega }^N}+\Vert (\mathbf {w}-\mathbf {W})\Vert _{\overline{\varOmega }^N} \end{aligned}$$

Then the result follows from Lemmas 6 and 9.

5 Numerical Illustrations

Example 1

Consider the following boundary value problem for the system of convection–diffusion equations on (0, 1)

$$\begin{aligned} \varepsilon _1 u_1^{\prime \prime }(x)+(1+x)u_1^\prime (x)-4 u_1(x)+2 u_2(x)+u_3(x)=-e^x,\\ \varepsilon _2 u_2^{\prime \prime }(x)+(2+x^2)u_2^\prime (x)+u_1(x)-6 u_2(x)+2 u_3(x)=-\sin x,\\ \varepsilon _3 u_3^{\prime \prime }(x)+(e^x)u_3^\prime (x)+3 u_1(x)+2 u_2(x)- 8 u_3(x)=-\cos x,\\ \text {with}\qquad u_1(0) =1,\;u_2(0)=1,\;u_3(0)=1\; u_1(1) =0,\;u_2(1)=0\;u_3(1)=0. \end{aligned}$$

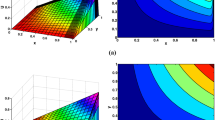
The above problem is solved using the suggested numerical method and plot of the approximate solution for $N=1536, \varepsilon _1=5^{-4}, \varepsilon _2=3^{-4}, \varepsilon _3=2^{-5}$ is shown in Fig. 1.

Fig. 1

Approximate solution of Example 1

Parameter uniform error constant and the order of convergence of the numerical method for $\varepsilon _1=\eta /625,\; \varepsilon _2=\eta /81\; \text {and}\; \varepsilon _3=\eta /32$ are computed using a variant of the two mesh algorithm suggested in [6] and are shown in Table 1.

Table 1 Maximum errors and order of convergence

It is found that the parameter $\varepsilon _i$ for any i, influences the components $u_1, u_2, \ldots ,u_{i}$ and causes multiple layers for these components, in the neighbourhood of the origin and has no significant influence on $u_{i+1},u_{i+2},\ldots ,u_n$. The following examples illustrate this.

Example 2

Consider the following boundary value problem for the system of convection–diffusion equations on (0, 1)

$$\begin{aligned} \varepsilon _1 u_1^{\prime \prime }(x)+(1+x)u_1^\prime (x)-4 u_1(x)+2 u_2(x)+u_3(x)=1-x,\\ \varepsilon _2 u_2^{\prime \prime }(x)+(2+x^2)u_2^\prime (x)+2u_1(x)-6 u_2(x)+3 u_3(x)=3-3x,\\ \varepsilon _3 u_3^{\prime \prime }(x)+u_3^\prime (x)+3 u_1(x)+3 u_2(x)- 7 u_3(x)=7x-8,\\ \text {with}\qquad u_1(0) =0,\;u_2(0)=1,\;u_3(0)=1\; u_1(1) =0,\;u_2(1)=0\;u_3(1)=0 \end{aligned}$$

The above problem is solved using the suggested numerical method. As $u_2(0)\ne u_{02}(0)$ and $u_i(0)=u_{0i}(0),\;i=1,3$ for this problem, a layer of width $O(\varepsilon _2)$ is expected to occur in the neighbourhood of the origin for $u_1$ and $u_2$ but not for $u_3$. Further $u_1$ cannot have $\varepsilon _1$ layer or $\varepsilon _3$ layer. The plot of an approximate solution of this problem for $N=384, \varepsilon _1=5^{-4}, \varepsilon _2=3^{-4}, \varepsilon _3=2^{-5}$ is shown in Fig. 2a–d.

Fig. 2

Approximation of solution components of Example 2

Example 3

Consider the following boundary value problem for the system of convection–diffusion equations on (0, 1)

$$\begin{aligned} \varepsilon _1 u_1^{\prime \prime }(x)+(1+x)u_1^\prime (x)-4 u_1(x)+2 u_2(x)+u_3(x)=x,\\ \varepsilon _2 u_2^{\prime \prime }(x)+(2+x^2)u_2^\prime (x)+2u_1(x)-6 u_2(x)+3 u_3(x)=3x,\\ \varepsilon _3 u_3^{\prime \prime }(x)+u_3^\prime (x)+3 u_1(x)+3 u_2(x)- 7 u_3(x)=1-7x,\\ \text {with}\qquad u_1(0) =0,\;u_2(0)=0,\;u_3(0)=1\; u_1(1) =0,\;u_2(1)=0\;u_3(1)=1. \end{aligned}$$

The above problem is solved using the suggested numerical method. As $u_3(0)\ne u_{03}(0)$ and $u_i(0)=u_{0i}(0),\;i=1,2$ for this problem, a layer of width $O(\varepsilon _3)$ is expected to occur in the neighbourhood of the origin for $u_1,u_2$ and $u_3$. Further $u_1$ will not have $\varepsilon _1$ layer or $\varepsilon _2$ layer. Similarly $u_2$ will not have $\varepsilon _2$ layer. The plot of an approximate solution of this problem for $N=384, \varepsilon _1=5^{-4}, \varepsilon _2=3^{-4}, \varepsilon _3=2^{-5}$ is shown in Fig. 3a–d.

Fig. 3

Approximation of solution components of Example 3

6 Conclusions

The method presented in this paper is the extension of the work done for the scalar problem in [4]. The novel estimates of derivatives of the solution help us to establish the desired error bound for the Classical Finite Difference Scheme when applied on any of the $2^n$ Shishkin meshes.

The examples given are to facilitate the reader to note the effect of coupling with the assumed order of the perturbation parameters.