Stochastic responses of nonlinear inclined cables with an attached damper and random excitations

Abstract

Flexible and lightweight cables are extensively used in engineering structures, which are prone to produce nonlinear deformation and nonlinear vibrations under random excitations. Usually, dampers are installed at certain positions of the cables to reduce the vibration response. The present paper investigates the stochastic responses of the nonlinear inclined cables with an attached damper under Gaussian white noise and wide-band noise excitations. First, the dynamical model of an inclined cable is established and the differential equations for each mode of vibration are derived by using Galerkin’s discretization method. Then, the stochastic linearization method is applied to derive the stochastic responses of the generalized displacements. The effectiveness of the truncated order, the effects of the excitation amplitude, damper installation position and damping coefficient are studied by investigating the stochastic responses. Since stochastic linearization is not applicable to systems with strong nonlinearity, stochastic averaging of energy envelope and quasi-Hamiltonian systems are adopted to study the main modal vibration of the inclined cables. The probability density functions of energy and generalized displacement are calculated. The comparisons between the results derived from the theoretical method and those derived from the numerical simulation showed the accuracy of the analytical results.

1 Introductions

Due to the lightweight and flexibility of cables, they are extensively used in many areas such as cable-stayed bridges [1], spacecraft [2] and soft robots [3]. The statics and linear dynamics of the inclined cable have been well studied in the past. Recently, the nonlinear vibrations and control of the inclined cables under external perturbations have caused many scholars’ attention. Due to the large length and the complex excitations of the cables, they are prone to nonlinear deformation under external excitations. The theoretical methods used in the analysis of the nonlinear dynamics of the inclined cables are the multi-scale method [4], equivalent linearization [5], harmonic balance method [6], etc. The stochastic linearization method was first proposed by Booton and used in electric systems [7]. Then, it is developed by many scholars and has been widely used [8, 9]. The exponential-polynomial-closure (EPC) method is another generally used approximate method for stochastically excited nonlinear systems [10,11,12], which assumes the probabilistic density function is an exponential polynomial function of state variables, and the coefficients of the polynomial are determined by minimizing the statistic errors. The state-space-split (SSS) method combining the EPC method was proposed for the probabilistic solutions of multi-degree-of-freedom nonlinear stochastic systems [13], which was further extended in [14].

Due to the nonlinearity, the nonlinear phenomena such as the vibration migration and bifurcations can exhibit. The nonlinear dynamics of an inclined cable were studied in [15] by using the multi-scale method and experimental verification, where the in-plane and out-plane displacements of the inclined cables were analyzed. The dynamics of a suspended cable with geometric nonlinearities were studied by adopting homotopy analysis in [16], and the influence of the initial conditions on the nonlinear responses are investigated. The responses of a suspended cable with time-delayed control force were calculated numerically in [17] to derive the optimal control gain and the value of time delay. To suppress the vibration of the cable, the damper is usually installed perpendicular to the cable and the dynamical analysis of damped cables has been studied and summarized in the literature [18,19,20]. The inclined cables are easy to produce random vibrations under the action of random excitations such as winds, rain [21, 22] and earthquake excitations [23], which can cause fatigue damage of the structures and hidden danger. The nonlinearity can bring great difficulties to the theoretical analysis of the dynamics of the inclined cables under random perturbations. The stochastic linearization method is a generally used method, which has been applied to various nonlinear systems under random excitations [24,25,26]. The nonlinear dynamics of a cable-mass-spring system were studied in [27] by using the equivalent linearization method and the stochastic responses of the state variables were derived and verified by the numerical simulation. By combining the SSS method and EPC method, Er et al. [28] studied the nonlinear random vibration of the inclined cables excited by uniformaly distributed Gaussian white noises. Baghaei et al. [29] combined stochastic linearization and sliding mode control methods to reduce the dynamical responses of nonlinear systems under nonstationary random excitations. It is found that the stochastic linearization method gives reliable results and agrees well with the results obtained by numerical simulation and experimental tests. The stochastic linearization method is applicable to systems with small nonlinearity.

The stochastic averaging method is another powerful tool in the analysis of nonlinear systems subject to random excitations [30,31,32]. Which is widely used in the stochastic analysis of nonlinearly mechanical and structural systems. Different from the stochastic linearization method, the stochastic averaging method divides the variables into fast-varying variables and slowly-varying variables, and the averaged diffusion equations for the slowly-varying variables are derived by using the deterministic and stochastic averaging process. The nonlinear vibrations of an axially moving laminated beam with shape memory alloy (SMA) under random loads were studied by using the stochastic averaging method in [33], and the probability density functions of the responses are derived with good agreement with the simulation results. To derive the responses of strongly nonlinear systems, the stochastic averaging method of envelope has been proposed [34] and used in various stochastic systems [35, 36]. Zhao and Zhu proposed an optimal control strategy for inclined cables based on controlling the axial support motion and the stochastic averaging method for nonintegrable Hamiltonian systems [37]. By adopting the stochastic averaging method. The dimensions of the nonlinear systems are reduced and the steady-state probability densities and response statistics are easier to solve.

The nonlinear dynamics of stochastically excited inclined cables with an attached damper are studied in the present paper. First, the nonlinear vibration model of the inclined cable is established by taking the nonlinear deformation into consideration, Then, the partial differential equation of the inclined cable is discretized by using Galerkin’s method, and the ordinary differential equations for each vibration mode are established. The derived equations for the generalized displacements are stochastically excited nonlinear equations. Then, the stochastic linearization method is adopted to derive the stochastic responses for the first Nth vibration modes. Finally, the stochastic averaging method is developed to analyze the main vibration modes and the probabilistic density functions for the energy and generalized displacement are derived. The analytical results are compared to the results obtained from the Monte-Carlo simulation to show the effectiveness of the developed methods.

2 Modeling and simplification

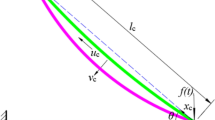
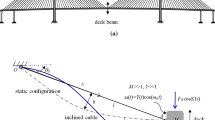
The diagrammatic sketch of the inclined cable with an attached damper is shown in Fig. 1. The inclined cable has an inclined angle $\theta$. The cable length is $l$ and the sag at the middle is $d$. The static axial tension is denoted by $T_{0}$. The mass per unit length is $m$ and the damping coefficient is $c$. The attached damper is installed perpendicular to the transverse direction at $x = x_{d}$ with a damping coefficient $c_{d}$.

Fig. 1

Configurations of the inclined cable

The static configuration can be obtained with the form of a parabolic function as

$$ y_{0} (x) = - 4d\left[ {x/l - (x/l)^{2} } \right] $$

(1)

where $d = mgl^{2} \cos \theta /8T_{0}$. The nonlinear strain is

$$ \varepsilon = \frac{{ds^{\prime } - ds}}{ds}{ = }\frac{\partial u}{{\partial x}} + \frac{{dy_{0} }}{dx}\frac{\partial v}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial v}{{\partial x}}} \right)^{2} $$

(2)

The stress in the $x$ direction can be obtained with $\tau = EA\varepsilon$, which represents the increased axial tension of the inclined cable. The dynamical equation can be established by using Newton’s second law for each micro element [38, 39] as follows

$$ \begin{aligned} m\frac{{\partial^{2} u}}{{\partial t^{2} }} & = \frac{\partial }{\partial x}\left\{ {\left. {EA\left[ {\frac{\partial u}{{\partial x}} + \frac{{dy_{0} }}{dx}\frac{\partial v}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial v}{{\partial x}}} \right)^{2} } \right]} \right\}} \right. \\ m\frac{{\partial^{2} v}}{{\partial t^{2} }} & = \frac{\partial }{\partial x}\left\{ {T_{0} \frac{\partial v}{{\partial x}} + EA\left( {\frac{{dy_{0} }}{dx} + \frac{\partial v}{{\partial x}}} \right) \times \left[ {\frac{\partial u}{{\partial x}} + \frac{{dy_{0} }}{dx}\frac{\partial v}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial v}{{\partial x}}} \right)^{2} } \right]} \right\} \\ & \quad - c\frac{\partial v}{{\partial t}} - F_{d} (t)\delta (x - x_{d} ) + f(x,t) \, \\ \end{aligned} $$

(3)

where $u$ is the longitudinal displacement and $v$ is the transverse displacement. $F_{d} (t)$ is the damping force produced by the installed damper at $x = x_{d}$. $f(x,t)$ is the random excitation, which generally has a separable form with

$$ f(x,t) = \alpha (x)w(t) $$

(4)

where $w(t)$ is the Gaussian white noise. The inclined cable is simply supported with the following boundary conditions

$$ u(0,t) = u(l,t) = 0,v(0,t) = v(l,t) = 0 $$

(5)

The inertia force in the longitudinal direction is small, which is usually neglected. Thus, the following equation is derived by using the first equation in Eq. (3)

$$ h(t) = \frac{\partial u}{{\partial x}} + \frac{{dy_{0} }}{dx}\frac{\partial v}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial v}{{\partial x}}} \right)^{2} $$

(6)

which means the tension is the same along the cable. Thus, $h = h(t)$ is only a function of time. Carrying out the integral within the interval $[0,l]$ and adopting the boundary conditions, the following equation is derived

$$ h(t) = \frac{1}{l}\left\{ {\left. {\int_{0}^{x} {\left[ {\frac{{dy_{0} }}{dx}\frac{\partial v}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial v}{{\partial x}}} \right)^{2} } \right]} dx} \right\}} \right. $$

(7)

The equation for the transverse equations $v(x,t)$ can be derived by submitting Eqs. (6) and (7) into the second equation of (3)

$$ \begin{aligned} m\frac{{\partial^{2} v}}{{\partial t^{2} }} & = \frac{\partial }{\partial x}\left\{ {\left. {T_{0} \frac{\partial v}{{\partial x}} + EA\left( {\frac{{dy_{0} }}{dx} + \frac{\partial v}{{\partial x}}} \right) \times \left\{ {\left. {\frac{1}{l}\int_{0}^{l} {\left[ {\frac{{dy_{0} }}{dx}\frac{\partial v}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial v}{{\partial x}}} \right)^{2} } \right]dx} } \right\}} \right.} \right\}} \right. \\ & \quad - F_{d} (t)\delta (x - x_{d} ) - c\frac{\partial v}{{\partial t}} + f(x,t) \\ \end{aligned} $$

(8)

which is a partial integro-differential equation. The parameters can be normalized by using the following transformation

$$ \begin{aligned} \mu & = EA/T_{0} ,\tilde{f} = f \cdot l/\pi^{2} T_{0} ,\tilde{F}_{d} = F_{d} \cdot l/\pi^{2} T_{0} ,\tilde{t} = \omega_{0} t,\omega_{0}^{2} = \pi^{2} T_{0} /ml^{2} , \\ \tilde{c} & = c/m\omega_{0} ,\tilde{x} = x/l,\tilde{y} = y/l,\tilde{v} = v/l,\tilde{d} = d/l. \\ \end{aligned} $$

(9)

Then, Eq. (8) can be rewritten with the following simplified form

$$ \begin{aligned} \frac{{\partial^{2} v}}{{\partial t^{2} }} & = \frac{1}{{\pi^{2} }}\frac{\partial }{\partial x}\left\{ {\left. {\frac{\partial v}{{\partial x}} + \mu \left( {\frac{{dy_{0} }}{dx} + \frac{\partial v}{{\partial x}}} \right) \times \left\{ {\left. {\int_{0}^{1} {\left[ {\frac{{dy_{0} }}{dx}\frac{\partial v}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial v}{{\partial x}}} \right)^{2} } \right]dx} } \right\}} \right.} \right\}} \right. \\ & \quad - F_{d} (t)\delta (x - x_{d} ) - c\frac{\partial v}{{\partial t}} + f(x,t) \\ \end{aligned} $$

(10)

where the linear damping force $F_{d} = \overline{c}_{d} \dot{v}_{d}$ is adopted with $\overline{c}_{d} = c_{d} /m\omega_{0}$ and the tilde is omitted in further analysis. The solution of Eq. (10) is expressed by the following series in order to use Galerkin’s discretization method

$$ v(x,t) = \sum\limits_{n = 1}^{\infty } {q_{n} (t)\phi_{n} (x)} $$

(11)

where $\phi_{n} (x) = \sqrt 2 sin(n\pi x)$ are the modal functions of the corresponding undamped linear equation and $q_{n} (t)$ are the corresponding generalized displacements. Multiplying Eq. (10) with $\phi_{n} (x)$ and carrying out the integral within $[0,1][0,1]$, Eq. (10) can be transformed into a series of second-order ordinary differential equations in the following form

$$ \begin{gathered} \ddot{q}_{n} + \omega_{n}^{2} q_{n} = - 2\mu_{n} \dot{q}_{n} - \sum\limits_{i = 1}^{\infty } {c_{ni} \dot{q}_{i} } - \sum\limits_{i = 1}^{\infty } {\sum\limits_{j = 1}^{\infty } {\Gamma_{nij} } } q_{i} q_{j} - \sum\limits_{i = 1}^{\infty } {\sum\limits_{j = 1}^{\infty } {\sum\limits_{h = 1}^{\infty } {\Lambda_{nijh} } q_{i} } } q_{j} q_{h} + f_{n} W(t) \hfill \\ n = 1,2,... \hfill \\ \end{gathered} $$

(12)

where the expressions for the coefficients in Eq. (12) can be derived as follows

$$ \begin{aligned} c_{ni} & = c_{d} \varphi_{n} (x_{d} )\varphi_{i} (x_{d} ),\mu_{n} = \frac{1}{2}\int_{0}^{1} {c\varphi_{n}^{2} (x)dx} ,f_{n} = \int_{0}^{1} {\alpha (x)\varphi_{n} (x)dx} , \\ \omega_{n}^{2} & = n^{2} + \frac{\mu }{{\pi^{2} }}\int_{0}^{1} {y_{0}^{\prime \prime } (x)\left[ {\int_{0}^{1} {y_{j}^{\prime } (x)\phi_{n}^{\prime } (x)dx} } \right]\phi_{n} (x)dx} , \\ \Lambda_{nijh} & = - \frac{1}{2}\frac{\mu }{{\pi^{2} }}\int_{0}^{1} {\left[ {\varphi_{j}^{\prime \prime } (x)\int_{0}^{1} {\varphi_{i}^{\prime } (x)\varphi_{h}^{\prime } (x)dx} } \right]\varphi_{n} (x)dx} , \\ \Gamma_{nij} & = - \frac{\mu }{{\pi^{2} }}\int_{0}^{1} {\left[ {\varphi_{j}^{\prime \prime } (x)\int_{0}^{1} {y_{0}^{\prime } (x)\varphi_{i}^{\prime } (x)dx} } \right]} \varphi_{n} (x)dx \\ & \quad - \frac{1}{2}\frac{\mu }{{\pi^{2} }}\int_{0}^{1} {\left[ {y_{0}^{\prime \prime } (x)\int_{0}^{1} {\varphi_{j}^{\prime } (x)\varphi_{i}^{\prime } (x)dx} } \right]\varphi_{n} (x)dx} \\ \end{aligned} $$

(13)

Usually, Eq. (12) is truncated to the $N$th order. For the convenience of the following analysis, Eq. (12) can be written in vector form by defining a new vector ${\mathbf{x}} = \left[ {q_{1} , \cdots ,q_{N} } \right]^{T}$. Then Eq. (12) can be rewritten in the following standard form

$$ {{\ddot{\mathbf{x}} + C\dot{x} + Kx + F(x) = f}}(t) $$

(14)

where ${\mathbf{C}}$ is the damping matrix, ${\mathbf{K}}$ is the linear stiffness matrix, ${\mathbf{F(x)}}$ is the nonlinear force, ${\mathbf{f}}(t) = {\mathbf{f}}w(t)$ is the stochastic excitation force with ${\mathbf{f}} = [f_{1} ,...,f_{N} ]^{T}$.

3 Stochastic linearization for stochastically excited MDOF nonlinear vibrations

3.1 Brief description of the stochastic linearization method

Equation (14) are stochastically excited nonlinear differential equations with multiple degrees of freedom (MDOF). The existing analytical methods are difficult to solve these problems. Thus, some approximate methods should be adopted to derive the dynamical responses. When the excitation amplitude is relatively small, the nonlinear forces in the vibration equation will be small. An equivalent linear system can be used to approximate the original nonlinear system. Therefore, the stochastic linearization method is adopted here to derive the stochastic responses of (14). The damping and stiffness matrix of the equivalent system can be determined by minimizing the residual error of the system.

Supposing the equivalent linear system is of the following form

$$ {{\ddot{\mathbf{X}}}} + ({\mathbf{C}} + {\mathbf{C}}^{\prime } ){\dot{\mathbf{X}}} + ({\mathbf{K}} + {\mathbf{K}}^{\prime } ){\mathbf{X}} = {\mathbf{f}}(t) $$

(15)

where ${\mathbf{C}}^{\prime }$, ${\mathbf{K}}^{\prime }$ are the equivalent damping coefficient matrix and the equivalent stiffness coefficient matrix, respectively. By comparing the original equation and the equivalent equation described in (15) and subtracting these two equations, the difference between the two equations is derived with the following expression

$$ {\mathbf{e}} = {\mathbf{F}}({\mathbf{X}}) - {\mathbf{C^{\prime}\dot{X}}} + {\mathbf{K^{\prime}X}} $$

(16)

As the original system is under random excitations, the error described in (16) should be measured in the sense of expected mean squares. The generally adopted residual error adopted is $E\left( {{\mathbf{e}}^{T} {\mathbf{e}}} \right)$. Then, ${\mathbf{C^{\prime}}}$ and ${\mathbf{K^{\prime}}}$ are selected to minimize $E\left( {{\mathbf{e}}^{T} {\mathbf{e}}} \right)$ with $E\left( \cdot \right)$ denoting the mathematical expectation. With several deductions, the expressions of ${\mathbf{C^{\prime}}}$ and ${\mathbf{K^{\prime}}}$ meet the following equations [40, 41]

$$ \begin{gathered} {\mathbf{C^{\prime}}}_{ij} = E(\partial {\mathbf{g}}_{i} /\partial {\dot{\mathbf{X}}}_{j} ) \hfill \\ {\mathbf{K^{\prime}}}_{ij} = E(\partial {\mathbf{g}}_{i} /\partial {\mathbf{X}}_{j} ) \hfill \\ \end{gathered} $$

(17)

As the nonlinear part in (14) only consists of ${\mathbf{X}}$, ${\mathbf{C^{\prime}}}{ = }{\mathbf{0}}$ can be derived.

3.1.1 Responses under Gaussian white noise excitation

When the random excitation $w(t)$ is modelled by standard Gaussian white noise, the equations in (15) can be rewritten in the form of first-order differential equations by letting ${\mathbf{Z}}(t) = [{\mathbf{q}}(t),{\dot{\mathbf{q}}}(t)]^{T}$

$$ {\dot{\mathbf{Z}}}(t) = {\mathbf{AZ}} + {\mathbf{F}}(t)w(t) $$

(18)

where

$$ {\mathbf{A}} = \left[ {\begin{array}{*{20}c} {{\mathbf{0}}_{n \times n} } & {I_{n \times n} } \\ { - {\mathbf{K}} - {\mathbf{K^{\prime}}}} & { - {\mathbf{C}}} \\ \end{array} } \right],{\mathbf{F}}(t) = \left[ {\begin{array}{*{20}c} {{\mathbf{0}}_{n \times 1} } \\ {\mathbf{f}} \\ \end{array} } \right] $$

Then, the statistical response of system (18) can be derived by the following differential Lyapunov equation

$$ {\dot{\mathbf{P}}}(t) = {\mathbf{AP}}(t) + {\mathbf{P}}(t){\mathbf{A}}^{T} + {\mathbf{FF}}^{T} $$

(19)

where

$$ {\mathbf{P}}(t) = \left[ {\begin{array}{*{20}c} {E({\mathbf{qq}}^{T} )} & {E({\mathbf{q\dot{q}}}^{T} )} \\ {E({\dot{\mathbf{q}}\mathbf{q}}^{T} )} & {E({\mathbf{\dot{q}\dot{q}}}^{T} )} \\ \end{array} } \right] $$

Omitting the differential terms on the left side of Eq. (19), the steady responses can be derived by the following algebraic Lyapunov equation

$$ {\mathbf{AP}}(t) + {\mathbf{P}}(t){\mathbf{A}}^{T} + {\mathbf{FF}}^{T} = 0 $$

(20)

As the matrix ${\mathbf{K^{\prime}}}$ in ${\mathbf{A}}$ is related to the response matrix ${\mathbf{P}}$, Eq. (20) is a nonlinear algebraic equation, which needs to be solved iteratively. The mean square of the transverse displacement of the inclined cable at any position can be derived by using its expressions described in Eq. (11)

$$ E\left[ {v^{2} (x,t)} \right] = E\left[ {\left( {\sum\limits_{n = 1}^{N} {q_{n} (t)\phi_{n} (x)} } \right)^{2} } \right] = {\varvec{\phi}}^{T} E({\mathbf{qq}}^{T} ){\varvec{\phi}} $$

where ${\varvec{\phi}} = \left[ {\phi_{1} (x), \cdots ,\phi_{N} (x)} \right]^{T}$.

The root mean square (RMS) of the transverse displacement can be derived

$$ RMS(v(x,t)) = \sqrt {E\left[ {v^{2} (x,t)} \right]} $$

(21)

3.1.2 Responses under wide-band noise excitation

Here, the wide-band noise excitation is also considered. The spectral density of the wide-band noise excitation $w(t)$ is of the following form

$$ S(\omega ) = \frac{D}{{\pi (\sigma^{2} + \omega^{2} )}} $$

(22)

where $\sigma$ is a constant characterizing the bandwidth of the excitation. The time histories of the noise excitation can be obtained by the following filtrated differential equation

$$ \dot{w}(t) + \sigma w(t) = \xi (t) $$

(23)

where $\xi (t)$ is a Gaussian white noise with intensities $2D$. By letting ${\mathbf{Z}}(t) = [{\mathbf{q}}(t),{\dot{\mathbf{q}}}(t),w(t)]^{T}$, the above equation can be combined with Eq. (15) to yield the state equations with the following form

$$ {\dot{\mathbf{Z}}}(t) = {\mathbf{AZ}} + {\mathbf{F}}(t)\xi (t) $$

(24)

where

$$ {\mathbf{A}} = \left[ {\begin{array}{*{20}c} {{\mathbf{0}}_{n \times n} } & {I_{n \times n} } & 0 \\ { - {\mathbf{K}} - {\mathbf{K^{\prime}}}} & { - {\mathbf{C}}} & {\mathbf{f}} \\ 0 & { - \sigma } & 1 \\ \end{array} } \right],\;{\mathbf{F}}(t) = \left[ {\begin{array}{*{20}c} {{\mathbf{0}}_{n \times 1} } \\ {{\mathbf{0}}_{n \times 1} } \\ 1 \\ \end{array} } \right] $$

Then, the statistical response of system (24) can be derived by the following differential Lyapunov equation

$$ {\dot{\mathbf{P}}}(t) = {\mathbf{AP}}(t) + {\mathbf{P}}(t){\mathbf{A}}^{T} + {\mathbf{D}} $$

(25)

where

$$ {\mathbf{P}}(t) = \left[ {\begin{array}{*{20}c} {E({\mathbf{qq}}^{T} )} & {E({\mathbf{q\dot{q}}}^{T} )} & {E({\mathbf{q}}w(t))} \\ {E({\dot{\mathbf{q}}\mathbf{q}}^{T} )} & {E({\mathbf{\dot{q}\dot{q}}}^{T} )} & {E({\dot{\mathbf{q}}}w(t))} \\ {E(w(t){\mathbf{q}}^{T} )} & {E(w(t){\dot{\mathbf{q}}}^{T} )} & {E(w(t)w(t))} \\ \end{array} } \right],\;{\mathbf{D}} = \left[ {\begin{array}{*{20}c} {{\mathbf{0}}_{n \times n} } & {{\mathbf{0}}_{n \times n} } & {{\mathbf{0}}_{n \times 1} } \\ {{\mathbf{0}}_{n \times n} } & {{\mathbf{0}}_{n \times n} } & {{\mathbf{0}}_{n \times 1} } \\ {{\mathbf{0}}_{1 \times n} } & {{\mathbf{0}}_{1 \times n} } & D \\ \end{array} } \right]. $$

The steady responses can be derived by the following algebraic Lyapunov equation

$$ {\mathbf{AP}}(t) + {\mathbf{P}}(t){\mathbf{A}}^{T} + {\mathbf{D}} = 0 $$

(26)

Then the statistics can be also calculated through Eq. (21).

3.2 Numerical results for Gaussian white noise excitation with constant amplitude

By solving the equations derived in the above subsection, the statistics of the vibration responses can be derived. First, the nonlinear vibrations of the inclined cable under stochastic excitations with constant amplitude are considered by adopting $\alpha (x) = f_{0}$. Through calculation, the excitation amplitude applied to the $k$th mode is

$$ f_{k} = - \sqrt 2 f_{0} \left( {\cos k\pi - 1} \right)/k\pi . $$

(27)

The parameters of the inclined cable are selected with $A = 0.25{\text{mm}}^{2} ,$$l = 1{\text{m,}}$$E = 4000{\text{Mpa}},$$T_{0} = 10{\text{N}},$$m = 1.63*10^{ - 2} {\text{kg/m,}}\theta { = }\pi {/3}$. Thus, the values of sag and the initial strain can be calculated with $d = 0.001,\mu = 100$. The other parameters adopted in the calculations are: $c = 0.02,$$c_{d} = 0.08,$$x_{d} = 0.5,f_{0} = 0.002$, otherwise mentioned. The number of the mode is selected with $N = 6$. For comparison, the Monte-Carlo simulation (MCS) results derived by using the stochastic Runge–Kutta method are also shown in the figures. The time step in simulation is $\Delta t = 0.0001s$, and the ending time is 4000 s. The program is running on a Lenovo PC with i5-6200 CPU at 2.30 GHz. The compution time for a cycle of samples is about 12 min.

Figure 2 shows the changes in the RMS values of $q_{k} (t)$ under different values of excitation amplitudes. It is seen that the results obtained by stochastic linearization method are in good agreement with the results obtained by MCS. However, the errors gradually increase with the excitation amplitudes. When the excitation amplitude increases, the vibration responses will gradually increase and the nonlinear term will have a greater impact. Generally, the equivalent linearization is applicable to the case of nonlinear vibration with small amplitudes. For the systems with large nonlinearity, the results obtained by stochastic linearization will have a certain deviation.

Fig. 2

RMS values of $q_{k} (t)$ under different values of excitation amplitude $f_{0}$

Figure 3 shows the time histories of the generalized displacement. It can be seen that the responses of the first-order modal vibration are much larger than that of other modes. Besides, the response of the even-order modal vibration is relatively small, which can be neglected. In fact, it is seen from Eq. (27) that the excitation amplitude of the even order generalized displacement is 0 for the excitations with constant amplitudes.

Fig. 3

Time histories of $q_{k} (t)$

Figure 4 shows the RMS values of the transverse vibration at each position of the inclined cable. It can be seen that its shape is similar to the shape function of the first-order modal vibration, which is mainly due to the dominant role of the first-order vibration. The theoretical results obtained by using stochastic linearization also agree well with the results obtained from MCS.

Fig. 4

The mean squares of $v(x,t)$

In Fig. 5, the RMS values of $q_{k} (t)$ are shown for different values of damping coefficients. It is seen that the amplitude of the odd order mode is larger than that of the even order mode. This is because the excitation amplitude of the even order mode is 0 from Eq. (27). Therefore, the vibration of the even order mode is mainly caused by the mutual coupling of the modes. In addition, under uniformly distributed noise excitation, the influence of the first modal vibration on the overall vibration is far greater than that of other higher-order modes. In fact, because the higher-order mode has a larger vibration frequency, its vibration energy is more easily consumed by the damping.

Fig. 5

RMS values of $q_{k} (t)$ under different values of damping coefficients $c_{d}$

In Fig. 6, the RMS values of $q_{k} (t)$ are shown under different locations of the damper $x_{d}$. It is found that for different modal vibrations, the decrease of the responses is greatly affected by the location of the damper. When the damper is installed at the extreme value of the vibration mode, the responses of the corresponding mode can be suppressed significantly. While the damper is installed at the node of the vibration mode, it has little effect on the vibration of the corresponding order. The generalized displacement $q_{k} (t)$ is the largest if the damper is located at the extreme points of the mode and it will be smallest if it is located at the nodes.

Fig. 6

RMS of $q_{k} (t)$ under different locations of the damper $x_{d}$

3.3 Numerical results for the random excitation with linear amplitude of excitation

The nonlinear vibrations of the inclined cable under stochastic excitations with linearly increasing amplitude are considered by adopting $\alpha (x) = f_{0} (1 + \alpha x)$. Through calculation, the excitation amplitude applied to the $k$th order of modal vibration is

$$ f_{n} = - \sqrt 2 f_{0} \left( {\cos n\pi - 1} \right)/n\pi - \sqrt 2 f_{0} \alpha \cos n\pi /n\pi $$

(28)

The parameters of the inclined cable are the same as selected in Sect. 3.2. Other parameters used in the calculations are: $c = 0.02,$$c_{d} = 0.08,$$x_{d} = 0.5,$$f_{0} = 0.002$,$\alpha = 1.0$, otherwise mentioned.

Figure 7 shows the changes in the RMS values of $q_{k} (t)$ under linearly distributed excitation with amplitude $f_{0}$. It can be seen that the errors between the results obtained by stochastic linearization and the results obtained by MCS increase gradually with the increasing excitation amplitudes. In addition, due to the linear distribution of excitation, the excitation amplitudes of even order modal vibration obtained from Eq. (28) are not zero. Therefore, the vibration of even order modes can have a certain impact on the overall vibration of the inclined cable.

Fig. 7

RMS values of $q_{k} (t)$ under different values of excitation amplitude $f_{0}$

Figure 8 shows the changes in RMS value of $q_{k} (t)$ under linearly distributed parameters $\alpha$. It is seen that the responses of the even order modal vibration are also affected by the slope parameter $\alpha$ of the linear distributed excitation. For example, when the value of $\alpha$ exceeds a certain critical value, the vibration responses of the second mode are greater than that of the third mode. The same situation also occurs in the fourth and fifth modal vibrations.

Fig. 8

RMS values of $q_{k} (t)$ under different values of $\alpha$

Figure 9 shows the time histories of the generalized coordinates of each mode under different values of $\alpha$. It is seen more intuitively that the vibration response of the even order mode is smaller when $\alpha$ is smaller, and the vibration response of the even order mode is larger when $\alpha$ is larger.

Fig. 9

Time histories of $q_{k} (t)$ under different values of $\alpha$, a $\alpha$ = 2.5, b $\alpha$ = 0.1

Figure 10 shows the RMS values of the transverse vibration at each position of the inclined cable under linearly distributed excitation. The theoretical results are derived from Eq. (21). Similar results can be found that the first-order modal vibration plays the dominant role.

Fig. 10

The RMS values of $v(x,t)$ under different excitation amplitude $f_{0}$

Figure 11 shows the RMS values of $q_{k} (t)$ under different damping coefficients. In calculation, the excitation amplitude is selected with $f_{0} = 0.002$ and the position of the damper is installed at the midpoint of the inclined cable. It is seen from Fig. 11 that the steady-state responses of the odd-order modal vibration will gradually decrease with the increasing damping coefficients, while the responses of the even-order modal vibration remain almost unchanged. This is due to that the position of the damper just coincides with the extreme point of the odd order mode shape function and the node of the even order mode shape function.

Fig. 11

RMS values of $q_{k} (t)$ under different values of excitation amplitude $c_{d}$

Figure 12 shows the influences of different locations of the damper on the vibration responses, which can more clearly explain the above phenomenon. When the damper is installed at the extreme value of the vibration mode, the responses of the corresponding vibration mode can be obviously suppressed. When the damper is installed at the node of the vibration mode, it has little effect on the responses of the corresponding vibration mode.

Fig. 12

RMS values of $q_{k} (t)$ under different values of location $x_{d}$

3.4 Numerical results for the wide-band random noise excitations

The responses of the inclined cable under wide-band random noise excitations can be derived from Eq. (26). Here, the wide-band random excitations with linearly increasing amplitude with $\alpha (x) = f_{0} (1 + \alpha x)$ is adopted. The random excitations with constant amplitude can be obtained by selecting $\alpha = 0$. In the calculation, The bandwidth parameter $\sigma = 2.0,D = 1.0$ is adopted and other parameters are the same as selected in Sect. 3.2.

Figure 13 shows the changes in the RMS values of $q_{k} (t)$ under different values of excitation amplitudes with $\alpha = 0,1.0$, respectively. Similar to the case for Gaussian white noises, when the amplitude of the excitation increases, the vibration responses gradually increase and the nonlinear term have a large effect. However, unlike the case under Gaussian noises, the steady state response under wideband noise excitation is smaller than the responses under Gaussian white noise excitation. This is due to that the distribution of the excitation intensity on each frequency is smaller, which can be seen from the spectral density in Eq. (22).

Fig. 13

RMS values of $q_{k} (t)$ under different values $f_{0}$, a $\alpha = 0$, b $\alpha = 1.0$

The influence of the slope parameter $\alpha$ is also shown in Fig. 14, which has a similar effect as the case of Gaussian white noise excitation. Compared to Fig. 8, the steady responses under wide-band noise excitation are much smaller than the steady response under Gaussian white noise excitation, and the results are more consistent with those obtained by MCS as the excitation increases.

Fig. 14

RMS values of $q_{k} (t)$ under different values of $\alpha$

Figure 15 shows the RMS values of $q_{k} (t)$ under different values of bandwidth parameter $\sigma$. It is seen that the responses of each order modal vibration will decrease with the increase of $\sigma$. This is because the increase in $\sigma$ can reduce the values of the excitation in each mode.

Fig. 15

RMS values of $q_{k} (t)$ under different values of $\sigma$

4 The responses of the main modes by using the stochastic averaging method

4.1 Stochastic averaging for the primary mode under wide-band noise excitation

When the responses of the system increase gradually, the nonlinear term will become larger, and the results derived from stochastic linearization will not be accurate enough. It is seen from the discussion in the previous section that the primary modal vibration has the greatest impact on the responses. The amplitudes of other vibration modes are relatively small. To obtain the responses more accurately, the stochastic averaging of the energy envelope is developed to analyze the primary modal vibration.

The vibration equation of the primary mode is

$$ \ddot{q}_{1} + \omega_{1}^{2} q_{1} = - 2\mu_{1} \dot{q}_{1} - c_{11} \dot{q}_{1} - \Gamma_{11} q_{1}^{2} - \Lambda_{111} q_{1}^{3} + F_{1} w(t) $$

(29)

where $c_{11} = c_{d} \varphi_{1} (x_{d} )\varphi_{1} (x_{d} )$ and $w(t)$ is the wide-band noise described in Eq. (23). The correlation function of $w(t)$ is

$$ R(\tau ) = R(u - v) = E[\xi (u)\xi (v)] = \frac{D}{\sigma }\exp ( - \sigma \left| \tau \right|) $$

(30)

where $\tau = u - v$.

The total energy and the potential of system (29) is

$$ H = \frac{1}{2}\dot{q}_{1}^{2} + G(q_{1} ), \, G(q_{1} ) = \int {g(q_{1} )} dq_{1} . $$

(31)

where $g(q_{1} ){ = }\omega_{1}^{2} q_{1} { + }\Gamma_{11} q_{1}^{2} { + }\Lambda_{111} q_{1}^{3}$ is the conservative force and $G(q_{1} )$ is the potential. Since the conservative force contains quadratic terms, the potential function $G(q_{1} )$ is asymmetrical. Thus, there are two values $q_{l}$ and $q_{r}$ meeting the relation $G(q_{l} ) = G(q_{r} ) = H$ for the given value of $H$. The period of system (29) is

$$ T(H) = 2\int_{{q_{l} }}^{{q_{r} }} {\frac{1}{{\sqrt {2H - 2U(q_{1} )} }}dq_{1} } $$

(32)

Let $Y = \dot{q}_{1}$. Equation (29) can be rewritten in the following form

$$ \begin{aligned} \dot{q}_{1} & = Y, \\ \dot{Y} & = - (2\mu_{1} + c_{11} )Y - g(q_{1} ) + F_{1} w(t) \\ \end{aligned} $$

(33)

By making a transformation from $(q_{1} ,Y)$ to $(q_{1} ,H)$, the equations for $(q_{1} ,H)$ are

$$ \begin{aligned} \dot{q}_{1} & = \pm \sqrt {2H - 2U(q_{1} )} \\ \dot{H} & = \mp (2\mu_{1} + c_{11} )\left( {2H - 2U(q_{1} )} \right) \pm F_{1} \sqrt {2H - 2U(q_{1} )} w(t) \\ \end{aligned} $$

(34)

To adopt the stochastic averaging method for wide-band noise excitations, the first step to derive a diffusion equation to approximate the original equation. According to the averaging procedure proposed in [42], the following equivalent diffusion equation is established

$$ \begin{aligned} dq_{1} & = \pm \sqrt {2H - 2U(q_{1} )} dt \\ dH & = \left[ { \mp (2\mu_{1} + c_{11} )\left( {2H - 2U(q_{1} )} \right) + F_{1}^{2} \Lambda } \right]dt \pm 2F_{1}^{2} \Lambda \sqrt {2H - 2U(q_{1} )} dW(t) \\ \end{aligned} $$

(35)

where $W(t)$ is the standard Wiener process and

$$ \Lambda = \int_{ - \infty }^{0} {R(\tau )d\tau } = \frac{1}{\Delta t}\int_{t}^{t + \Delta t} {du\int_{t}^{u} {E[\xi (u)\xi (v)]dv} } . $$

(36)

The above equation is accurate enough if the correlation time of the excitation is small (under wide-band noise excitation). When the damping force and excitation amplitude are small, the energy is a slowly varying variable. Thus, the stochastic averaging of the energy envelope can be applied to obtain the ItÔ equation for $H(t)$

$$ dH = m(H)dt + \sigma (H)dW(t) $$

(37)

where the drift and the diffusion coefficients are

$$ \begin{aligned} m(H) & = \frac{2}{T(H)}\int_{{q_{l} }}^{{q_{r} }} {\left[ { - (2\mu_{1} + c_{11} )\sqrt {2H - 2U(q_{1} )} + \frac{1}{2}\frac{{F_{1}^{2} \Lambda }}{{\sqrt {2H - 2U(q_{1} )} }}} \right]dq_{1} } \\ \sigma^{2} (H) & = \frac{2}{T(H)}\int_{{q_{l} }}^{{q_{r} }} {F_{1}^{2} \Lambda \sqrt {2H - 2U(q_{1} )} dq_{1} } \\ \end{aligned} $$

The probability density function (PDF) of $H(t)$ is determined by the corresponding FPK function with the following form

$$ \frac{\partial p}{{\partial t}} = - \frac{\partial }{\partial A}\left[ {m(H)p} \right] + \frac{1}{2}\frac{{\partial^{2} }}{{\partial H^{2} }}\left[ {\sigma^{2} (H)p} \right] $$

(38)

The boundary conditions for Eq. (32) are

$$ p,dp/dH \to 0,H \to \infty $$

(39)

The stationary PDF of $H(t)$ can be obtained by omitting the partial differential term with time $t$ as follows

$$ p(H) = \frac{C}{{\sigma^{2} (H)}}\exp \left( {\int_{0}^{H} {\frac{2m(u)}{{\sigma^{2} (u)}}du} } \right) $$

(40)

where $C$ is a normalized constant. The joint stationary PDF for $(q_{1} ,\dot{q}_{1} )$ can be derived from $p(H)$ with

$$ p(q_{1} ,\dot{q}_{1} ) = \left. {\frac{p(H)}{{T(H)}}} \right|_{{H = \dot{q}_{1}^{2} /2 + U(q_{1} )}} $$

(41)

and the stationary PDF of $q_{1} (t)$ can be calculated by integrating Eq. (35) with $\dot{q}_{1} (t)$

$$ p(q_{1} ) = \int {p(q_{1} ,\dot{q}_{1} )} d\dot{q}_{1} $$

(42)

Then, the RMS value of $q_{1} (t)$ can be calculated by the following equation

$$ E(q_{1}^{2} ) = \int {q_{1}^{2} \left. {\frac{p(H)}{{T(H)}}} \right|_{{H = \dot{q}_{1}^{2} /2 + U(q_{1} )}} } dq_{1} d\dot{q}_{1} $$

(43)

and the RMS of $q_{1} (t)$ can also be derived with

$$ RMS(q_{1} (t)) = \sqrt {E\left[ {q_{1}^{2} } \right]} $$

(44)

4.2 Numerical results of the primary mode under Gaussian white noise excitation

If $w(t)$ is a Gaussian white noise with intensity $2D$, $\Lambda = D$ can be derived from Eq. (36). Recalling the expressions of the stochastic excitations for the primary modal vibration, the intensity of the stochastic excitation mainly depends on its amplitude. Thus, the stochastic excitations with constant amplitude are considered by selecting $\alpha (x) = f_{0}$. Then, the amplitude of the stochastic excitation is $F_{1} = 2\sqrt 2 f_{0} /\pi$.

By using the formula derived previously, the stochastic responses of the primary modal vibration can be calculated. The parameters of the inclined cable are the same as selected in Sect. 3.2. Other parameters adopted in the calculations are: $c = 0.01,$$c_{d} = 0.005,$$x_{d} = 0.5,$$f_{0} = 0.02$,$D = 1.0$. The values of the derived parameters in Eq. (29) are $\omega_{1}^{2} = 1.0012$,$\mu_{1} = 0.005$,$c_{11} = 0.01$,$\Gamma_{11} = 1.62$,$\Lambda_{111} = 496.48$. For comparison, the stochastic responses derived by MCS are also shown in the figures.

Figure 16 shows the steady-state PDF of the energy $H$ under different values of excitation amplitude. The solid lines in the figure are the theoretical results obtained by stochastic averaging of the energy envelope and the circles are the results derived from MCS. It is seen that the PDFs of the system energy can be flatter with a larger excitation amplitude, which means the response of the primary vibration is bigger.

Fig. 16

PDFs of the energy under different values of excitation amplitude $f_{0}$

The steady PDFs of the generalized coordinates of the primary vibration can be calculated by Eq. (42). The steady PDFs of $q_{1}$ and the logarithmic plot of $p(q_{1} )$ for the right half side are shown in Fig. 17. It is seen that the theoretical solutions and the solutions obtained from MCS are also in good agreement for different values of excitation amplitude. The increasing of the excitation amplitude can increase the responses, especially in the tail of the PDFs.

Fig. 17

PDFs of the generalized displacement under different values of $f_{0}$

Figure 18 shows the RMS values of $q_{1} (t)$ of the primary modal vibration under different damping coefficients. It is seen that the responses of the primary modal vibration will decrease with bigger damping coefficients, which means the damper is effective. The theoretical results obtained by stochastic averaging of the energy envelope are in good agreement with the simulation solution, indicating the effectiveness of the stochastic averaging of the energy envelope.

Fig. 18

The RMS values of $q_{1} (t)$ under different values of $c_{d}$

Figure 19 shows the responses of the primary modal vibration under different installation positions of the damper. It is seen that the primary modal vibration is the smallest with the damper installed at the midpoint of the inclined cable. Compared with the results derived by stochastic linearization, the results obtained by stochastic averaging of energy envelope are more accurate, especially for the situation of strongly nonlinear systems.

Fig. 19

The RMS values of $q_{1} (t)$ under different values of $x_{d}$

4.3 Numerical results of the primary mode under wide-band noise excitation

Here, the responses of the primary mode under wide-band noise excitation are calculated. The parameters used in the calculation are $f_{0} = 0.02,D = 1$ and other parameters are the same values as used in the Gaussian white noise case.

Figures 20 and 21 shows the steady-state PDF of the energy $H$ and the generalized displacement $q_{1}$ under different values of band-width constant $\sigma = 1.5,2,3$, respectively. The solid lines in the figure are the theoretical results obtained by stochastic averaging of the energy envelope and the circles are the results derived from MCS. It is seen that the PDFs of the system energy is flatter with a smaller band-width constant, which means that the increasing of the band-width constant $\sigma$ can decrease the responses. This is due to that bigger value of $\sigma$ can lead to the decrease of the excitation amplitude at the primary mode. It is also seen that the theoretical solutions and the solutions obtained from MCS are in good agreement for different values of band-width constant.

Fig. 20

PDFs of the energy under different values of $\sigma$

Fig. 21

PDFs of the generalized displacement under different values of $\sigma$

4.4 Responses of the main two modes

Here, $\alpha (x) = f_{0} (1 + \alpha x)$ is adopted and the Gaussian white noise case is considered. Recalling the conclusion derived in Sect. 3, the values of $\alpha$ greatly determine the main vibration modes. Thus, two cases are discussed.

Case 1: The first-order and third-order modal responses. When $\alpha$ is relatively large, the first-order and second-order modal responses are larger. By using Eq. (12), the equations for the first-order and second-order generalized coordinates are

$$ \begin{aligned} & \ddot{q}_{1} + \omega_{1}^{2} q_{1} - a_{2} q_{1}^{2} - a_{3} q_{2}^{2} + a_{4} q_{1}^{3} + 4a_{4} q_{1} q_{2}^{2} + (2\mu_{1} + c_{11} )\dot{q}_{1} + c_{12} \dot{q}_{2} = f_{1} w(t) \\ & \ddot{q}_{2} + \omega_{2}^{2} q_{2} - 2a_{3} q_{1} q_{2} + 4a_{4} q_{2} q_{1}^{2} + 16a_{4} q_{2}^{3} + c_{21} \dot{q}_{1} + (2\mu_{2} + c_{22} )\dot{q}_{2} = f_{2} w(t) \\ \end{aligned} $$

(45)

where $w(t)$ is a Gaussian white noise with intensity $2D$. The coefficients can be obtained from Eq. (13) with

$$ \begin{aligned} a_{1} & = 24\sqrt 2 \mu d^{2} /\pi^{4} ,a_{2} = 24\sqrt 2 \mu d/\pi ,a_{3} = 32\sqrt 2 \mu d/\pi , \\ a_{4} & = \mu \pi^{2} /2,\omega_{1}^{2} = 1 + a_{1} ,\omega_{2}^{2} = 4 \\ \end{aligned} $$

(46)

It is seen from Eq. (45) that $q_{1}$ and $q_{2}$ are coupled to form a nonintegrable Hamiltonian system. The Hamiltonian and potential function of system (45) are

$$ \begin{aligned} H & = \frac{1}{2}\dot{q}_{1}^{2} + \frac{1}{2}\dot{q}_{2}^{2} + U(q_{1} ,q_{2} ), \\ U(q_{1} ,q_{2} ) & = \frac{{\omega _{1}^{2} }}{2}q_{1}^{2} + \frac{{\omega _{2}^{2} }}{2}q_{2}^{2} - \frac{{a_{2} }}{3}q_{1}^{3} - a_{3} q_{1} q_{2}^{2} + \frac{{a_{4} }}{4}q_{1}^{4} \\ & \quad + 2a_{4} q_{1}^{2} q_{2}^{2} + 4a_{4} q_{2}^{4} \\ \end{aligned} $$

(47)

Defining the generalized momentums $(p_{1} ,p_{2} ) = (\dot{q}_{1} ,\dot{q}_{2} )$, system (45) can be modelled as a quasi-nonintegrable system. Then, the stochastic averaging method for the quasi-nonintegrable system [43] can be used to yield the diffusion process for the system energy

$$ dH = m(H)dt + \sigma (H)dW(t) \, $$

(48)

where $m(H)$ and $\sigma (H)$ are the drift and diffusion coefficients with the following expressions

$$ \begin{aligned} m(H) & = \frac{1}{T(H)}\int {_{\Omega } \left[ {( - c_{11} p_{1}^{2} - c_{11} p_{2}^{2} ) + D\left( {f_{1}^{2} + f_{2}^{2} } \right)} \right]} /p_{1} dq_{1} dq_{2} dp_{2} \\ \sigma^{2} (H) & = \frac{2}{T(H)}\int {_{\Omega } \left[ {D\left( {f_{1} p_{1}^{2} + f_{2} p_{2}^{2} } \right)/p_{1} } \right]} dq_{1} dq_{2} dp_{2} \, \\ T(H) & = \int {_{\Omega } \left( {1/p_{1} } \right)} dq_{1} dq_{2} dp_{2} \, \\ \end{aligned} $$

(49)

The steady PDF for $H$ can be derived by solving the FPK equation associated with Eq. (48) with

$$ p(H) = \frac{{C_{1} }}{{\sigma^{2} (H)}}\exp \left[ {\int_{0}^{H} {\frac{2m(H)}{{\sigma^{2} (H)}}dy} } \right] \, $$

(50)

The steady PDF for $q_{1} ,q_{2} ,p_{1} ,p_{2}$ can be derived with

$$ p(q_{1} ,q_{2} ,p_{1} ,p_{2} ) = \left. {\frac{p(H)}{{T(H)}}} \right|_{{H = \dot{q}_{1}^{2} /2 + \dot{q}_{2}^{2} /2 + U(q_{1} ,q_{2} )}} $$

(51)

Thus, the PDF of $p(q_{1} )$ can be obtained from Eq. (51) by integral. For comparision, in the calculation, $\alpha (x) = 2f_{0} (1 + \alpha x)/3$ and $\alpha = 1.0$ are selected to make the excitation amplitude of the first mode equal to the value in Sect. 4.2. Other parameters are the same as those used in Sect. 4.2. The values of the derived parameters are listed in Table 1.

Table 1 Values of the derived parameters

Figures 22 and 23 shows the PDFs of the energy and the generalized displacement for the first and the second vibration mode under different values of $f_{0}$. It is seen that the PDFs of the system energy is flatter with a larger excitation amplitude, which means the response of the primary vibration is bigger. Compared with the results derived in the primary mode vibration, the PDFs of the generalized displacement $q_{1}$ is a little sharper, which means the responses are lightly reduced. This is due to the extra nonlinear stiffness of the second vibration mode. The good agreement in the figures also showed the effectiveness of the averaging method adopted in the calculation.

Fig. 22

PDFs of the energy under different values of $f_{0}$

Fig. 23

PDFs of the generalized displacement under different values of $f_{0}$

Case 2: The first-order and third-order modal responses. When $\alpha$ is relatively small, the first-order and third-order modal responses are larger. The equation for the first-order and third-order generalized coordinates is

$$ \begin{aligned} & \ddot{q}_{1} + \omega_{1}^{2} q_{1} - a_{2} q_{1}^{2} - b_{1} q_{3}^{2} - 2bq_{1} q_{3} + a_{4} q_{1}^{3} - 9a_{4} q_{1} q_{3}^{2} + (2\mu_{1} + c_{11} )\dot{q}_{1} + c_{13} \dot{q}_{3} = f_{1} w(t) \\ & \ddot{q}_{3} + \omega_{3}^{2} q_{3} - bq_{1}^{2} - b_{1} q_{3}^{2} - 2b_{1} q_{1} q_{3} + 9a_{4} q_{3} q_{1}^{2} + 81a_{4} q_{3}^{3} + c_{31} \dot{q}_{1} + (2\mu_{3} + c_{33} )\dot{q}_{3} = f_{3} w(t) \\ \end{aligned} $$

(52)

The expressions of the used coefficients are listed in Eq. (46) with $\omega_{3}^{2} = 9 + a_{1} /9$,$b_{1} = 27b,b = 8\sqrt 2 d\mu /3\pi$. The Hamiltonian and potential function of system (52) are

$$ \begin{gathered} H = \frac{1}{2}\dot{q}_{1}^{2} + \frac{1}{2}\dot{q}_{3}^{2} + U(q_{1} ,q_{3} ), \hfill \\ U = \frac{1}{2}\omega_{1}^{2} q_{1}^{2} + \frac{1}{2}\omega_{3}^{2} q_{3}^{2} - \frac{{a_{2} }}{3}q_{1}^{3} - \frac{{b_{1} }}{3}q_{1}^{3} - 27bq_{1} q_{3}^{2} - bq_{1}^{2} q_{3} + \frac{{a_{4} }}{4}q_{1}^{4} { + }\frac{{9a_{4} }}{2}q_{1}^{2} q_{3}^{2} + \frac{{81a_{4} }}{4}q_{3}^{4} \hfill \\ \end{gathered} $$

(53)

The steady probability density function for $H$ of system (52) can be derived by using a similar procedure as that in case 1 with modified potential in Eq. (53). In the calculation, $\alpha (x) = f_{0}$ is selected to make the excitation amplitude of the first mode equal with the results for primary mode vibrtion under Gaussian white noise excitation. The other parameters are the same as those calculated in Sect. 4.2. The values of the derived parameters are listed in Table 2.

Table 2 Values of the derived parameters

Figures 24 and 25 shows the PDFs of $H$ and $q_{1}$ for the first and the third vibration mode under different values of excitation amplitude. The solid lines in the figure are the theoretical results obtained by stochastic averaging of quasi-nonintegrable systems and the circles are the results derived from MCS. Similar phenomena can be derived as the results for the first and the second vibration mode. Compared with the results derived in the primary mode vibration, the PDFs of the generalized displacement $q_{1}$ is a little sharper and the responses are decreased due to the extra nonlinear stiffness of the third mode. But it is a little bigger than the responses in the first and the second vibration mode. This is due to that the excitation amplitude is smaller for the third mode under the given parameters. Thus, the extra stiffness is smaller.

Fig. 24

PDFs of the energy under different values of $f_{0}$

Fig. 25

PDFs of $q_{1}$ under different values of $f_{0}$

5 Conclusions

In this paper, the stochastic vibrations of nonlinear inclined cables under random perturbation are studied. First, the vibrational differential equations of the inclined cables are established and the equations of the generalized displacements for each vibrational mode are derived and truncated by using Galerkin’s discretization. Then, the discrete nonlinear equations under stochastic excitations are analyzed by using the stochastic linearization method and the stochastic averaging method. Through the analysis of the results, the following conclusions are obtained:

• 1. For Gaussian white noise and wide-band noise excitations with constant distribution and linear distribution, the primary modal vibration has the greatest impact on the overall vibration of the inclined cable.

• 2. For the random excitations with constant distribution, the even-order modal vibrations are very small, while they are increasing with the linear slope parameter $\alpha$ for linearly distributed random excitations.

• 3. The stochastic linearization method is applicable for nonlinear systems with small nonlinearity, while the stochastic averaging method is also accurate for strongly nonlinear systems.

• 4. The influences of excitation intensity, damping coefficient, damper installation position and other parameters on the vibrational response of the inclined cable are studied.

The results obtained are also verified by MCS simulation, which showed the effectiveness of the developed analytical methods.