An improved physics-informed neural network with adaptive weighting and mixed differentiation for solving the incompressible Navier–Stokes equations

Abstract

Physics-informed neural networks (PINNs) have been an effective tool for approximating the mapping between points in the spatio-temporal domain and solutions of partial differential equations (PDEs). However, there are still some challenges in dealing with the nonlinear characteristics and complexity of the Navier–Stokes (N–S) equations. In this paper, the improved adaptive weighting PINNs based on the Gaussian likelihood estimation are applied to solve the N–S equations. The weights of the different loss items are allocated adaptively by the maximum likelihood estimation. The improved network structure has been designed with considering both the global and local information, making it easier to capture the part of PDEs solution with drastic changes. A combinational method of the numerical differentiation (ND) and the automatic differentiation (AD) is proposed to compute the differential operators, with the improved computational efficiency. The derivative operation of the convection and pressure-gradient terms was carried out using the combined method in solving the incompressible N–S equations. The results show that the effectiveness and training efficiency of this method are better than PINNs.

1 Introduction

The incompressible Navier–Stokes (N–S) equations are fundamental for fluid flow. They are widely applied in fluid simulation, such as the applications in meteorology, aviation, and engineering. The classical numerical methods, e.g., the finite element [1], the finite volume [2], and the finite difference [3] methods are widely used in solving the N–S equations. These discretization-based methods utilize the values of grid points distributed in the space and time domains to approximate the solution of the partial differential equations (PDEs). However, the classical numerical methods present some challenges, e.g., the curse of dimensionality, the reliance on grid structures, and the numerical instabilities. Compared to traditional numerical methods, the machine learning demonstrates remarkable efficiency and accuracy in solving the incompressible Navier–Stokes equations, particularly when dealing with complex geometries, high-dimensional problems, and inverse problems. And the method without discretization can successfully address the challenges of the traditional methods in dealing with the complex problems [4,5,6,7,8,9].

The neural networks have been applied to solve PDEs, which is an important application of the machine learning. The neural networks in solving PDEs were proposed at in 1990s [10, 11]. In recent years, various types of neural networks have emerged so far, in the fields of scientific computation and deep learning. With the increase in computational power and availability of data, neural networks, show a significant impact on solving PDEs [12,13,14,15,16,17,18]. In particular, the frameworks of the physics-informed neural networks (PINNs) were developed [19,20,21], and the automatic differentiation (AD) techniques were used to compute the derivative terms in time and space. The loss function is designed based on the physical principles underlying the governing equations. The back-propagation algorithm iteratively adjusts the weights of the neural networks. Subsequently, the PINNs framework has been further developed, with various improvements and applications. Chiu et al.  [22] proposed a method that combines AD and the finite difference methods, which utilizes the neighboring points to calculate the derivatives. Patel et al. [23] proposed cvPINNs, combining the finite volume method with PINNs and utilizes the integral methods to the offset for derivative operations in equations. Other methods based on domain decomposition are also available, which divide the computational domains into a multiple of smaller subdomains [24,25,26]. Researchers have also studied some other variants of PINNs [27,28,29,30,31,32].

The continuous development of PINNs has led to widespread applications fluid mechanics [33,34,35,36]. There are two notable methods for solving the N–S equations, which deserves special attention. Jin et al. [33] proposed the NSFnets model for simulating the incompressible laminar and turbulent flows. This method directly encodes the governing equations in the deep neural networks to address the time-consuming issues of integrating multiple datasets and generating grids. Dwivedi et al. [35] developed a distributed PINNs framework for the incompressible N–S equations. It decomposes the computational domain into multiple subdomains with simple learning machines on each subdomain to solve problems, thereby reducing the burden. These methods show high accuracy and stability in solving the incompressible N–S equations.

The methods mentioned above have shown promising advantages, but they are only applicable to regular domains. Therefore, a new deep learning method is proposed in this study, which can solve the incompressible N–S equations with irregular domains. This study will focus on three aspects to reduce the errors as much as possible and improve the computational efficiency of the neural networks. Firstly, the loss function for PINNs is a combination of multiple weighted loss terms. Minimizing the loss function can be viewed as an optimization problem with multiple objectives. The issues of imbalanced each loss term can be addressed by adaptively assigning the corresponding weights to each loss term based on the maximum likelihood estimation using the Gaussian distributions. Secondly, an improved network is proposed with the global and local information. This design can transfer the input information to the hidden layers of the networks and capture the drastic parts of the PDEs solution. This enhances the expressive power of the deep neural networks with reducing the approximation errors. Thirdly, combining AD with ND can deal with the issues of computational efficiency and stability encountered in AD, thereby improving the performance of PINNs.

The paper is organized as follows. Section 2 details the incompressible N–S equations and the basic structure of the PINNs. In Sect. 3, the methods proposed in this study are presented, including the adaptive weighting, the improved neural networks, and the mixed differentiation. And the effectiveness of our method is validated through the numerical experiments in Sect. 4. Section 5 summarizes the paper and the future research prospects.

2 Preliminaries

2.1 Model equation

The non-dimensional incompressible N–S equations are considered in this study, which is expressed in a three-dimensional domain $\Omega \times (0, T]$ as follows:

$$\begin{aligned}&\frac{\partial {\textbf{u}}}{\partial t}+(\textbf{u} \cdot \nabla ) \textbf{u} =-\nabla p+\frac{1}{{\text {Re}}} \nabla ^2 \textbf{u} \quad \text{ in } \Omega \times (0, T], \end{aligned}$$

(2.1a)

$$\begin{aligned}&\nabla \cdot \textbf{u} =0 \quad \text{ in } \Omega , \end{aligned}$$

(2.1b)

$$\begin{aligned}&\textbf{u} =\textbf{u}_{\Upsilon } \quad \text{ on } \Upsilon _D, \end{aligned}$$

(2.1c)

$$\begin{aligned}&\frac{\partial \textbf{u}}{\partial n} =0 \quad \text{ on } \Upsilon _N, \end{aligned}$$

(2.1d)

$$\begin{aligned}&\textbf{u}(\textbf{x}, 0) = \textbf{s}(x) \quad \text{ in } \Omega , \end{aligned}$$

(2.1e)

where $\textbf{u}=[u(\textbf{x},t),v(\textbf{x},t),w(\textbf{x},t)]$ is the non- dimensional velocity vector, $p(\textbf{x},t)$ is the non-dimensional pressure, and ${\text {Re}}$ is the Reynolds number. The Dirichlet and Neumann boundary conditions are denoted with $\Upsilon _D$ and $\Upsilon _N$, respectively. $\textbf{s}(x)$ represents the initial velocity field.

2.2 PINNs

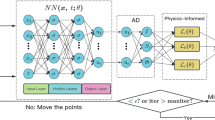
The standard PINNs (s-PINNs) approximate the mapping between the spatio–temporal domain points and the solution of PDEs using the training neural networks. In the s-PINNs framework, the core of the training model is the fully-connected neural networks. This type of neural networks typically consist of an input layer, an output layer, and n hidden layers. Figure 1 depicts the structure of the s-PINNs.

We will use the first component $\textbf{u}(\textbf{x},t)$ as an example to outline the general approach, and similar methods can be applied to the other variables. Ultimately, the construction of the network will involve all three variables simultaneously. To effectively approximate the solution $\textbf{u}(\textbf{x},t)$ of the N–S equations, the fully-connected neural networks represented as $\hat{\textbf{u}}_{N}(\textbf{x}, t; \theta )$ are applied. The input of the neural networks consists of the independent variables $\textbf{x}$ and t, while the output corresponds to the predicted solution $\hat{\textbf{u}}_{N}(\textbf{x}, t; \theta )$ at that specific points. The connections between the layers are represented as follows:

$$\begin{aligned} \begin{aligned}&Input \quad layer: \quad {\hat{u}}_{N}^{i}(\textbf{x},t)=[\textbf{x}, t]^{\textrm{T}},\\&Hidden \quad layers: \quad {\hat{u}}_{N}^{i}(\textbf{x},t)=\Phi \left( {\varvec{W}}^{i} {\mathcal {N}}^{i-1}(\textbf{x})+{\varvec{b}}^{i}\right) \\&\quad for \quad 2 \le i \le L-1,\\&Output \quad layer: \quad {\hat{u}}_{N}^{L}(\textbf{x},t)={\varvec{W}}^L {\mathcal {N}}^{L-1}(\textbf{x})+{\varvec{b}}^L,\\ \end{aligned} \nonumber \\ \end{aligned}$$

(2.2)

where ${\hat{u}}_{N}^{i}(\textbf{x},t)$ and ${\hat{u}}_{N}^{L}(\textbf{x},t)$ are the inputs and outputs of the model. $\Phi$ is the activation function, usually taken as sigmoid or tanh, sin, etc [37]. The activation function realizes the nonlinear approximation of the model by nonlinear transformation of the output values. $\theta =(\textbf{W}^i, \textbf{b}^i)$ represents a set of weight matrices and the bias vectors of the i-th layer.

Fig. 1

The architecture of the standard physics-informed neural networks

The loss functions of the s-PINNs consist of three components, including the initial and boundary conditions reflecting the spatio-temporal domains, and the residuals of the PDEs at the selected points in the domain (called collocation points). They are defined as the initial loss, the boundary loss and the residual loss, respectively. The output of the neural networks is denoted as $\hat{\textbf{u}}_{N}(\textbf{x}, t; \theta )$, the three error parts of the s-PINNs loss functions are given below [38]:

The loss of the mean squared error of the initial condition is given as:

$$\begin{aligned} \begin{aligned} {\mathcal {L}}_{ini}&={\text {MSE}}_{ini}=\frac{1}{N_{ini}} \sum _{i=1}^{N_{ini}}|\hat{\textbf{u}}_{N}\left( \textbf{x}_i^{ini}, 0\right) \\&\quad -\textbf{s}_i^{ini}|^2, \quad \textbf{x}_i^{ini} \in \Omega , \end{aligned} \nonumber \\ \end{aligned}$$

(2.3)

where $\hat{\textbf{u}}_{N}\left( \textbf{x}_i^{ini}, 0\right)$ is the output of the neural networks and $\textbf{s}_i^{ini}$ is the given initial condition at $\left( \textbf{x}_i^{ini}, 0\right)$.

The loss of the mean squared error on the boundary condition:

$$\begin{aligned} \begin{aligned} {\mathcal {L}}_{bcs}&={\text {MSE}}_{bcs}=\frac{1}{N_{bcs}} \sum _{j=1}^{N_{bcs}} \left| \hat{\textbf{u}}_{N}\left( \textbf{x}_j^{bcs}, t_j^{bcs}\right) \right. \\&\quad -\left. \textbf{h}_i^{bcs}\right| ^2,\left( \textbf{x}_j^{bcs}, t_j^{bcs}\right) \in \Upsilon \times (0, T], \end{aligned} \nonumber \\ \end{aligned}$$

(2.4)

$\textbf{h}_j^{bcs}$ stands for the boundary conditions. The point set $\left( \textbf{x}_j^{bcs}, t_j^{b cs}\right)$ represents the boundary points.

The mean squared error resulting from the residuals of the incompressible N–S equations:

$$\begin{aligned}{} & {} {R}_1(\textbf{x}, t):=\frac{\partial \textbf{u}}{\partial t}+(\textbf{u} \cdot \nabla ) \textbf{u}+\nabla p -\frac{1}{{\text {Re}}} \nabla ^2 \textbf{u}, \nonumber \\{} & {} {R}_2(\textbf{x}, t) :=\nabla \cdot \textbf{u}. \end{aligned}$$

(2.5)

$$\begin{aligned}{} & {} {\mathcal {L}}_{res}={\text {MSE}}_{res}=\frac{1}{N_{res}} \sum _{k=1}^{N_{res}}\left| {R}_1\left( \textbf{x}_k^{res}, t_k^{res}\right) \right| ^2 \nonumber \\{} & {} \qquad \quad + \left| {R}_2\left( \textbf{x}_k^{res}, t_k^{res}\right) \right| ^2, \quad \left( \textbf{x}_k^{res}, t_k^{res}\right) \in \Upsilon \times (0, T], \nonumber \\ \end{aligned}$$

(2.6)

where $\left( \textbf{x}_k^{res}, t_k^{res}\right)$ are the internal residual points that are randomly sampled and uniformly distributed. The Latin hypercube sampling method [39] is used to obtain the points within the interior domain and boundaries. Therefore, the expression for the total loss function can be written as follows:

$$\begin{aligned} \begin{aligned} {\mathcal {L}}_{s u m}={\mathcal {L}}_{ini}+{\mathcal {L}}_{bcs}+{\mathcal {L}}_{res}. \end{aligned} \end{aligned}$$

(2.7)

The loss function ${\mathcal {L}}_{s u m}$ was then minimized using the optimization techniques like Adam, LBFGS, and SGD until it is close to zero [40]. The ideal parameter is finally obtained after a specific number of iterative training.

The relative discrete $l^{2}$-error is introduced to evaluate the deviation between the approximate solution $\hat{\textbf{u}}_{N}\left( \textbf{x}^{*}_{i},t^{*}_{i}\right)$ of the neural networks and the exact solution $\textbf{u}\left( \textbf{x}^{*}_{i}, t^{*}_{i}\right)$ of the PDEs.

$$\begin{aligned} \begin{aligned} {\mathcal {E}}_{\text{ error }}: =\frac{\sqrt{\frac{1}{N}\sum _{i=1}^N\left( \hat{\textbf{u}}_{N}\left( \textbf{x}^{*}_{i}, t^{*}_{i}\right) -\textbf{u}\left( \textbf{x}^{*}_{i}, t^{*}_{i}\right) \right) ^2}}{\sqrt{\frac{1}{N}\sum _{i=1}^N\left( \textbf{u}\left( \textbf{x}^{*}_{i}, t^{*}_{i}\right) \right) ^2}}, \end{aligned} \nonumber \\ \end{aligned}$$

(2.8)

where $\hat{\textbf{u}}_{N}\left( \textbf{x}^{*}_{i},t^{*}_{i}\right)$ is the output for a series of test point networks $\left\{ \left( \textbf{x}^{*}_{i},t^{*}_{i}\right) \right\} _{i=1}^N$, and $\textbf{u}\left( \textbf{x}^{*}_{i},t^{*}_{i}\right)$ denotes the exact value.

3 Solution methodology

In this section, the maximum likelihood estimation of the Gaussian distribution is utilized to adaptively balance the weights of each loss term. According to the attention mechanism in computer vision, the s-PINNs are improved by introducing the additional spatio-temporal variable sets. Furthermore, the improved neural networks utilize the mixed differentiation to compute the differential operators, thereby enhancing the computational efficiency of the training neural networks.

3.1 Adaptive weighting method for PINNs

The schematic diagram of the adaptive weighting PINNs (aw-PINNs) is shown in Fig. 2. Following the methods in Ref [41], there are effective methods for determining the weightings of the multiple loss functions in scene geometry and semantic multi-task deep learning problems. The principle is to assign the different weights to the various losses based on their contribution to the overall performance of the model.

When solving the N–S equations, we model the output $\hat{{\textbf{u}}}_{N}(\textbf{x}, t; \theta )$ of PINNs as a Gaussian probability distribution,

$$\begin{aligned} \begin{aligned} P (u \mid \hat{\textbf{u}}_{N}(\textbf{x}, t; \theta ))=N\left( \hat{\textbf{u}}_{N}(\textbf{x}, t; \theta ), \xi ^2\right) , \end{aligned} \end{aligned}$$

(3.1)

with an uncertainty parameter $\xi$.

The uncertainty parameter for the decay of the weights is adjusted using the maximum likelihood inference. According to the probability density function of the Gaussian distribution:

$$\begin{aligned} \begin{aligned} P(\zeta \mid \theta )=\frac{1}{\sqrt{2 \pi }\xi } \exp \left( -\frac{(\zeta -\omega )^2}{2 \xi ^2}\right) , \end{aligned} \end{aligned}$$

(3.2)

where $\omega$ represents the mathematic expectation, and $\xi$ is the standard deviation. By minimizing the objective and preventing data underflow, the negative log-likelihood of the model is minimized following Eq. (3.2),

$$\begin{aligned}{} & {} -\log P(u \mid \hat{\textbf{u}}_{N}(\textbf{x}, t; \theta )) \nonumber \\{} & {} \quad = -\log N \left( \hat{\textbf{u}}_{N}(\textbf{x}, t; \theta ), \xi ^2\right) \nonumber \\{} & {} \quad \propto \frac{1}{2 \xi ^2}|u-\hat{\textbf{u}}_{N}(\textbf{x}, t; \theta )|^2 +\log \xi \nonumber \\{} & {} \quad =\frac{1}{2 \xi ^2} {\mathcal {L}}(\theta )+\log \xi , \end{aligned}$$

(3.3)

where the weighted loss functions and the uncertainty regularization terms for each task are considered. The parameter $\xi$ of each epoch is updated iteratively using the maximum likelihood estimation to adapt the weight of each loss term.

The loss of the initial and boundary conditions can be represented by the Gaussian probability models of the outputs s and h.

$$\begin{aligned}{} & {} P(u, s, h \mid \hat{\textbf{u}}_{N}(\textbf{x}, t; \theta )) \nonumber \\{} & {} \quad = P(u \mid \hat{\textbf{u}}_{N}(\textbf{x}, t; \theta )) \cdot P(s \mid \hat{\textbf{u}}_{N}(\textbf{x}, t; \theta )) \nonumber \\{} & {} \quad \cdot P(h \mid \hat{\textbf{u}}_{N}(\textbf{x}, t; \theta ))\nonumber \\{} & {} \quad =N\left( \hat{\textbf{u}}_{N}(\textbf{x}, t; \theta ), \xi _r^2\right) \cdot N\left( \hat{\textbf{u}}_{N}(\textbf{x}, t; \theta ), \xi _i^2\right) \nonumber \\{} & {} \quad \cdot N\left( \hat{\textbf{u}}_{N}(\textbf{x}, t; \theta ), \xi _b^2\right) . \end{aligned}$$

(3.4)

We aim to minimize the joint probability distribution of the multi-output model.

$$\begin{aligned} \begin{aligned}&-\log P(u, s, h \mid \hat{\textbf{u}}_{N}(\textbf{x}, t; \theta )) \propto \frac{1}{2 \xi _r^2}|u-\hat{\textbf{u}}_{N}(\textbf{x}, t; \theta )|^2\\&\quad +\frac{1}{2 \xi _i^2}|s-\hat{\textbf{u}}_{N}(\textbf{x}, t; \theta )|^2\\&\quad +\frac{1}{2 \xi _b^2}|h-\hat{\textbf{u}}_{N}(\textbf{x}, t; \theta )|^2+\log \xi _r \xi _i \xi _b \\&=\frac{1}{2 \xi _r^2} {\mathcal {L}}_{\text{ res }}(\theta )+\frac{1}{2 \xi _i^2} {\mathcal {L}}_{ini}(\theta )\\&\quad +\frac{1}{2 \xi _b^2} {\mathcal {L}}_{bcs}(\theta )+\log \xi _r \xi _i \xi _b. \\ \end{aligned} \end{aligned}$$

(3.5)

In a word, the loss functions are defined for the PINNs using a multi-output model with four vectors. The loss function of the adaptive weighting PINNs can be expressed as follows:

$$\begin{aligned} \begin{aligned} {\mathcal {L}}(\theta ; \xi )&= \frac{1}{2 \xi _r^2} {\mathcal {L}}_{res}\left( \theta \right) +\frac{1}{2 \xi _i^2} {\mathcal {L}}_{ini}\left( \theta \right) \\&\quad +\frac{1}{2 \xi _b^2} {\mathcal {L}}_{bcs}\left( \theta \right) + \log \xi _r \xi _i \xi _b, \end{aligned} \end{aligned}$$

(3.6)

where $\xi = \left\{ \xi _r, \xi _i, \xi _b \right\}$ represents the adaptive weighting coefficients assigned to each loss term. $\lambda =\left\{ \lambda _{res}, \lambda _{ini}, \lambda _{bcs}\right\}$, $\lambda :=\frac{1}{2 \xi ^2}$ denotes the overall weight of each loss term. Thus, the weight of each loss term can be adjusted automatically and systematically. During the training process, we introduce a trainable and adaptive parameter $Q=\left\{ Q_r, Q_i, Q_b\right\}$ to prevent the denominator from being zero, where $Q:=\log \xi ^2$ improves the robustness of the model. The final adaptive weighting loss function can be represented as:

$$\begin{aligned} \begin{aligned} {\mathcal {L}}(\theta ; Q)&= \frac{1}{2} \exp \left( -Q_r\right) {\mathcal {L}}_{res}\left( \theta \right) \\&\quad +\frac{1}{2} \exp \left( -Q_i\right) {\mathcal {L}}_{ini}\left( \theta \right) \\&\quad +\frac{1}{2}\exp \left( -Q_b\right) {\mathcal {L}}_{bcs}\left( \theta \right) \\&\quad +\frac{1}{2}(Q_r + Q_i + Q_b)\\&\propto \exp \left( -Q_r\right) {\mathcal {L}}_{res}\left( \theta \right) + \exp \left( -Q_i\right) {\mathcal {L}}_{ini}\left( \theta \right) \\&\quad + \exp \left( -Q_b\right) {\mathcal {L}}_{bcs}\left( \theta \right) + Q_r + Q_i + Q_b. \end{aligned} \end{aligned}$$

(3.7)

We use Eq. (3.7) as the final loss function for aw-PINNs. The loss function can be minimized through the exponential mapping without constraints. The adaptive weights converge slowly to zero because the exponential function produces only positive values, which contributes to improve numerical stability during training.

Fig. 2

The schematic diagram of the adaptive weighting physics-informed neural networks

Fig. 3

Improved neural networks: attention mechanisms are combined with neural networks, with only additional weights and biases for the transformer networks

3.2 Improved network structure for PINNs

To enhance the approximation capability of adaptive the weighting neural networks, we have devised a novel network architecture, drawing inspiration from the attention mechanisms that are prominent in transformers [42]. The neural networks with attention mechanisms are currently a hot research topic in deep learning. They enable the neural networks to selectively focus on the specific parts of the input data when processing information, rather than processing all input data equally. This selective focus can greatly improve the accuracy and efficiency of the neural networks in various tasks. The attention technique used by the neural networks is to merge the encoder–decoder framework, as described in [43]. The encoder–decoder framework encodes variable-length input sequences into fixed-length vectors, which are then processed by neural network layers to decode them into corresponding variable-length output sequences. Applying the encoder–decoder framework to PINNs, the model adds three additional transformer networks $\gamma _{1}$, $\gamma _{2}$ and $\gamma _{3}$ to enhance the performance and accuracy of the model. Finally, the neural networks will generate the output $\hat{{\textbf{u}}}_{N}(\textbf{x}, t; \theta )$ by decoding. The designed network framework connects three transformer networks to two fully connected trunk networks. The improved neural network introduces additional spatial and temporal variables as inputs, which makes the input information easier to transfer the hidden layers. Each transformer network structure is shown in Fig. 4. This design can deal with the global and local information at the same time, with maintaining the integrity of the input and enhancing the expressive capacity of the neural networks. We call the improved adaptive weighting PINNs (iaw-PINNs). The model framework of the iaw-PINNs is shown in Fig. 3. The improved adaptive weighting method is summarized as the algorithm1.

The hidden layers of the iaw-PINNs is updated based on the forward propagation rules:

$$\begin{aligned}{} & {} \gamma _{1} =\Phi \left( \mathrm {~W}_0^1 X+\textrm{b}_0^1\right) , \nonumber \\{} & {} \gamma _{2} =\Phi \left( \mathrm {~W}_0^2 X+\textrm{b}_0^2\right) , \nonumber \\{} & {} \gamma _{3} =\Phi \left( \mathrm {~W}_0^3 X+\textrm{b}_0^3\right) , \nonumber \\{} & {} Z^1 =\Phi \left( \mathrm {~W}^1 X+\textrm{b}^1\right) , \nonumber \\{} & {} Y^{k+1}_{1} =\Phi \left( \mathrm {~W}^{k+1}_{0} Z^k +\textrm{b}^{k+1}_{0}\right) , \nonumber \\{} & {} k=1,2, \cdots , L-2, \nonumber \\{} & {} Y^{k+1}_{2} =\Phi \left( \mathrm {~W}^{k+1}_{1} Z^k +\textrm{b}^{k+1}_{1}\right) , \nonumber \\{} & {} k=1,2, \cdots , L-2, \nonumber \\{} & {} H^{k+1} =\left( {I}-Y^{k+1}_{1}-Y^{k+1}_{2}\right) \odot \gamma _{1} +Y^{k+1}_{1} \odot \gamma _{2} \nonumber \\{} & {} \quad + Y^{k+1}_{2} \odot \gamma _{3}, \quad k=1,2, \cdots , L-2, \nonumber \\{} & {} \hat{{\textbf{u}}}_{N}(\textbf{x}, t; \theta ) =H^L \mathrm {~W}^L+b^L. \end{aligned}$$

(3.8)

Fig. 4

The architecture of the transformer network

where ${X}=[\textbf{x}, t]^{\textrm{T}}$ denotes the input training data-points, $\Phi$ is the activation function and $\odot$ denotes the element-wise multiplication. $\left\{ \left( \textrm{W}_0^1,\textrm{b}_0^1\right) , \left( \textrm{W}_0^1,\textrm{b}_0^1\right) \right.$, $\left. \left( \textrm{W}_0^1,\textrm{b}_0^1\right) \right\}$ are the weights and the biases used in the addition of three transformer networks. $\gamma _{1}$, $\gamma _{2}$ and $\gamma _{3}$ represent the transformer networks that incorporate the extra primitive input X. $Z^1$ is the input to the first hidden layer of an ordinary fully-connected neural network, while $Y_{1}$ and $Y_{2}$ are the two fully connected trunk networks. For example, when $k = 1$, if there are no additional $\gamma _{1}$, $\gamma _{2}$ and $\gamma _{3}$, then $Y_{1}$ and $Y_{2}$ represent the outputs produced by the first hidden layer of the two trunk fully connected networks. By introducing the extra $\gamma _{1}$, $\gamma _{2}$ and $\gamma _{3}$, the input to the second hidden layer is no longer $Y_{1}$ and $Y_{2}$, but rather $H^2$ that is transformed from $\gamma _{1}$, $\gamma _{2}$ and $\gamma _{3}$. I is a matrix whose elements are all equal to one.

Algorithm1 : Adaptive weighting method for improved the network structure.
Step1: Consider an improved fully connected neural network to define the PINNs
$\hat{\textbf{u}}_{N}(\textbf{x}, t ; \theta )$.
Step2: Compute the residuals of the PDEs with automatic differentiation and establish
terms for loss functions.(Eq.(2.3),Eq.(2.4),Eq.(2.6)).
Step3: Initialize the adaptive weights collection $\xi =\left\{ \xi _r, \xi _i, \xi _b \right\}$.
Step4: Build Gaussian probability models using the mean generated by PINNs and
the adapted collection of weights $\xi$.
Step5: Using the definition in Eq.(3.8),the hidden layers are updated.
Step6: Use L steps gradient descent algorithm iterations to update the parameters
$\xi$ and $\theta$ as:
for $k=1$ to L do
$Z^1 =\Phi \left( X\mathrm {~W}^1+\textrm{b}^1\right) ,$
$Y^{k+1}_{1} =\Phi \left( \mathrm {~W}^{k+1}Z^k+\textrm{b}^{k+1}\right) , \quad k=1,2, \cdots , L-2,$
$Y^{k+1}_{2} =\Phi \left( \mathrm {~W}^{k+1}Z^k+\textrm{b}^{k+1}\right) , \quad k=1,2, \cdots , L-2,$
$H^{k+1} =\left( {I}-Y^{k+1}_{1}-Y^{k+1}_{2}\right) \odot \gamma _{1}+Y^{k+1}_{1} \odot \gamma _{2}+Y^{k+1}_{2} \odot \gamma _{3}, \quad k=1,2, \cdots , L-2,$
(1) Create the adaptive weighting loss function ${\mathcal {L}}\left( \theta _k ; \xi _k \right)$ (Eq.(3.6)) using the maximum
likelihood estimation as the basis.
(2) Adjust the adaptive weights collection $\xi$ using the Adam+L-BFGS optimizer to maximize
the likelihood of meeting the constraints.
$\xi _{k+1} \leftarrow {\text {Adam + L-BFGS}}\left( {\mathcal {L}}\left( \theta _k ; \xi _k \right) \right)$
(3) Optimize the network parameters $\theta$ using Adam+L-BFGS optimizer.
$\theta _{k+1} \leftarrow {\text {Adam + L-BFGS}}\left( {\mathcal {L}}\left( \xi _k ;\theta _k \right) \right)$
end for
Return
The optimal values of the model parameters $\theta ^*$ and the updated adaptive weights collection
$\xi ^*$are obtained at the end.

Fig. 5

Schematic diagram of the backward propagation for derivative computation in fully connected feed-forward neural networks

3.3 Mixed differentiation for PINNs

There are significant differences between ND and AD when it comes to computing the differential operators. ND approximates the derivative term by utilizing the local support points, whereas AD precisely computes the derivatives at any given point. The AD in Tensorflow [44] is a built-in function that can be called directly. For derivative operations in the neural networks, the x-derivative of the output z concerning the input can be calculated according to the reverse chain shown in Fig. 5. The advantages of AD and ND are combined to construct a loss function coupling the neighboring support points and their derivative terms. The AD and ND are combined as the mixed differentiation in this work, which captures the physical features more accurately with greater training efficiency as compared to that of AD [22].

To estimate the first-order derivative $\frac{\partial \textbf{u}(x)}{\partial x}$, we employ the following approach.

$$\begin{aligned} \begin{aligned} \frac{\partial \textbf{u}(x)}{\partial x}&=\frac{\hat{\textbf{u}}_{Ne}-\hat{\textbf{u}}_{Nw}}{\Delta x}\\&=\frac{\hat{\textbf{u}}_{N}(x+\Delta x / 2)-\hat{\textbf{u}}_{N}(x-\Delta x / 2)}{\Delta x}, \end{aligned} \end{aligned}$$

(3.9)

The distance between the two adjacent points is represented by $\Delta x$ in Eq. (3.9). For the mixed differentiation method, $\Delta x$ is a hyper-parameter, and the $\hat{\textbf{u}}_{N}$ value at $(x+\Delta x)$ and $(x-\Delta x)$ is obtained using $\hat{\textbf{u}}_{N}(x+\Delta x; \theta )$ and $\hat{\textbf{u}}_{N}(x-\Delta x; \theta )$, as illustrated in Fig. 6.

Fig. 6

The schematic of the approximate derivative of the mixed differentiation for PINNs, the red and black points are the additional support points

3.3.1 The second-order upwind scheme for PINNs

Take the velocity component $u(\textbf{x},t)$ as an example to illustrate the scheme. As for the first-order derivative term ${\hat{u}}_{Nx}{\mid _{m}}$ of the proposed mixed differentiation, according to the multi-moment method mentioned in [45], we use ${\hat{u}}_N$ and ${\hat{u}}_{Nx}$ to approximate the first-order derivative term ${\hat{u}}_{Nx}{\mid _{m}}$, where ${\hat{u}}_{Nx}$ is obtained using AD. To couple ${\hat{u}}_N$ and ${\hat{u}}_{Nx}, {\hat{u}}_{Ne}$ is approximated as $\left. u_e\right| _{{\text {m}}(u s)}$ [22]:

$$\begin{aligned} \begin{aligned} \left. {\hat{u}}_{Ne} \cong u_e\right| _{\text{ m }(u s )}&=a{\hat{u}}_{N}(x,t; \theta )\\&\quad +b{\hat{u}}_{Nx}(x,t; \theta ). \end{aligned} \end{aligned}$$

(3.10)

We perform Taylor series expansions on ${\hat{u}}_{N}(x, t; \theta )$ and ${\hat{u}}_{Nx}(x,t; \theta )$ with respect to ${\hat{u}}_{Ne}$ and $\frac{\partial {\hat{u}}_{Ne}}{\partial x}$.

$$\begin{aligned} {\hat{u}}_{N}(x,t; \theta ){} & {} ={\hat{u}}_{Ne}-\frac{\Delta x}{2} \frac{\partial {\hat{u}}_{Ne}}{\partial x}+\left( \frac{\Delta x}{2}\right) ^2 \frac{\partial ^2 {\hat{u}}_{Ne}}{\partial x^2}\nonumber \\{} & {} \quad -\left( \frac{\Delta x}{2}\right) ^3 \frac{\partial ^3 {\hat{u}}_{Ne}}{\partial x^3}+\left( \frac{\Delta x}{2}\right) ^4 \frac{\partial ^4 {\hat{u}}_{Ne}}{\partial x^4}+\cdots ,\nonumber \\ {\hat{u}}_{Nx}(x,t; \theta ){} & {} =\frac{\partial {\hat{u}}_{Ne}}{\partial x}-\frac{\Delta x}{2} \frac{\partial ^2 {\hat{u}}_{Ne}}{\partial x^2} +\left( \frac{\Delta x}{2}\right) ^2 \frac{\partial ^3 {\hat{u}}_{Ne}}{\partial x^3}\nonumber \\{} & {} \quad -\left( \frac{\Delta x}{2}\right) ^3 \frac{\partial ^4 {\hat{u}}_{Ne}}{\partial x^4}+\left( \frac{\Delta x}{2}\right) ^4 \frac{\partial ^5 {\hat{u}}_{Ne}}{\partial x^5}+\cdots ,\nonumber \\ \end{aligned}$$

(3.11)

By eliminating the primary error terms for the above two equations, we can obtain the values of a and b:

$$\begin{aligned} \begin{aligned}&a=1, \\&b=\frac{a \Delta x}{2}=\frac{\Delta x}{2}. \end{aligned} \end{aligned}$$

(3.12)

Substituting a and b in Eq. (3.10) we get:

$$\begin{aligned} \begin{aligned} \left. u_e\right| _{{\text {m}}(us)}={\hat{u}}_{N}(x,t; \theta )+\frac{\Delta x}{2} {\hat{u}}_{Nx}(x,t;\theta ). \end{aligned} \end{aligned}$$

(3.13)

$\left. u_w\right| _{\text{ m }}$ can be obtained in the same way as:

$$\begin{aligned} \begin{aligned} \left. u_w\right| _{\text{ m }(us)}&={\hat{u}}_{N}(x-\Delta x,t; \theta )\\&\quad +\frac{\Delta x}{2} {\hat{u}}_{Nx}(x-\Delta x,t; \theta ). \end{aligned} \end{aligned}$$

(3.14)

The first-order derivative can be approximately expressed as follows:

$$\begin{aligned}{} & {} \left. \frac{\partial u(x)}{\partial x} \cong \frac{\partial u(x)}{\partial x}\right| _{{\text {m}}(us)}\nonumber \\{} & {} \quad =\frac{\left. u_e\right| _{{\text {m}}(us)}-\left. u_w\right| _{{\text {m}}(us)}}{\Delta x}\nonumber \\{} & {} \quad =\frac{{\hat{u}}_{N}(x,t; \theta )-{\hat{u}}_{N}(x-\Delta x,t; \theta )}{\Delta x}\nonumber \\{} & {} \qquad +\frac{1}{2}\left( {\hat{u}}_{Nx}(x,t; \theta ) - {\hat{u}}_{Nx}(x-\Delta x,t; \theta )\right) . \nonumber \\ \end{aligned}$$

(3.15)

The above equations have been streamlined as follows:

$$\begin{aligned} \begin{aligned}&\left. \frac{\partial u(x)}{\partial x}\right| _{\text{ m }(us)} \\&\quad ={\hat{u}}_{Nx}(x,t; \theta )\\&\qquad +\left( \frac{{\hat{u}}_{N}(x,t;\theta )-{\hat{u}}_{N}(x-\Delta x,t; \theta )}{\Delta x}\right. \\&\qquad \left. -\frac{1}{2}\left( {\hat{u}}_{Nx}(x,t; \theta )+{\hat{u}}_{Nx}(x-\Delta x,t; \theta )\right) \right) . \end{aligned} \nonumber \\ \end{aligned}$$

(3.16)

Following the Taylor series, by expanding ${\hat{u}}_{N}(x-\Delta x,t; \theta )$ and ${\hat{u}}_{Nx}(x-\Delta x,t; \theta )$ at ${\hat{u}}_{N}(x,t; \theta )$ and ${\hat{u}}_{Nx}(x,t; \theta )$, it can then be further simplified as:

$$\begin{aligned} \begin{aligned} \left. \frac{\partial u(x)}{\partial x}\right| _{\text{ m(us) } }&={\hat{u}}_{Nx}(x,t; \theta )-\left( \frac{\Delta x^2}{12}\right) {\hat{u}}_N^{(3)}(x,t; \theta )\\&\quad +\left( \frac{\Delta x^3}{24}\right) {\hat{u}}_N^{(4)}(x,t; \theta )+\cdots . \end{aligned} \end{aligned}$$

(3.17)

The second-order upwind scheme introduces the additional stabilization terms with the second-order accuracy. When $\Delta x$ approaches to zero, ${\hat{u}}_{Nx}$ is the derivative of AD.

Table 1 Relative discrete $l^{2}$-error comparison between the predicted and the exact solution obtained using different methods for the Taylor vortex problem

3.3.2 The central difference scheme for PINNs

When solving the incompressible N–S equations, the traditional central difference methods for the pressure-gradient terms may lead to decoupling between the velocity and pressure variables. To address the decoupling issue, we adopt the central difference scheme of the mixed differentiation method to approximate the pressure-gradient terms [22]. Following the same approach, we can derive the expressions for ${\hat{p}}_e$ and ${\hat{p}}_w$.

$$\begin{aligned} \begin{aligned} \left. {\hat{p}}_e \cong p_e\right| _{m(c d)}&=\frac{{\hat{p}}_{N}(x+\Delta x,t; \theta )+{\hat{p}}_{N}(x,t; \theta )}{2}\\&\quad -\frac{\Delta x}{8}\left( {\hat{p}}_{Nx}(x+\Delta x,t; \theta )\right. \\&\quad -\left. {\hat{p}}_{Nx}(x,t; \theta )\right) , \\ \end{aligned} \end{aligned}$$

(3.18)

$$\begin{aligned} \begin{aligned} \left. {\hat{p}}_w \cong p_w\right| _{m(c d)}&=\frac{{\hat{p}}_{N}(x,t; \theta )+{\hat{p}}_{N}(x-\Delta x,t; \theta )}{2}\\&\quad -\frac{\Delta x}{8}\left( {\hat{p}}_{Nx}(x,t; \theta )\right. \\&\quad -\left. {\hat{p}}_{Nx}(x-\Delta x,t; \theta )\right) , \end{aligned} \end{aligned}$$

(3.19)

The first-order derivative can be approximately expressed as follows:

$$\begin{aligned} \begin{aligned}&\left. \frac{\partial p(x)}{\partial x} \cong \frac{\partial p(x)}{\partial x}\right| _{{\text {m}}(cd)}= \frac{\left. p_e\right| _{{\text {m}}(c d)}-\left. p_w\right| _{{\text {m}}(cd)}}{\Delta x}\\&\quad =\frac{{\hat{p}}_{N}(x+\Delta x,t; \theta )-{\hat{p}}_{N}(x-\Delta x,t; \theta )}{2 \Delta x} \\&-\frac{1}{8}\left( {\hat{p}}_{Nx}(x+\Delta x,t; \theta )-2 {\hat{p}}_{Nx}(x,t; \theta )\right. \\&\quad \left. +{\hat{p}}_{Nx}(x-\Delta x,t; \theta )\right) . \end{aligned} \end{aligned}$$

(3.20)

Equation (3.20) is simplified as follows:

$$\begin{aligned} \left. \frac{\partial p(x)}{\partial x}\right| _{{\text {m}}(cd)}{} & {} ={\hat{p}}_{Nx}(x,t; \theta )\nonumber \\{} & {} \quad +\left( \frac{{\hat{p}}_{N}(x+\Delta x,t; \theta )-{\hat{p}}_{N}(x-\Delta x,t; \theta )}{2 \Delta x}\right. \nonumber \\{} & {} \quad -\frac{1}{8}\left( {\hat{p}}_{Nx}(x+\Delta x,t; \theta )+6 {\hat{p}}_{Nx}(x,t; \theta )\right. \nonumber \\{} & {} \quad \left. \left. +{\hat{p}}_{Nx}(x-\Delta x,t; \theta )\right) \right) , \end{aligned}$$

(3.21)

To further simplify into the following format:

$$\begin{aligned} \begin{aligned}&\left. \frac{\partial p(x)}{\partial x}\right| _{{\text {m}}(cd)}={\hat{p}}_{Nx}(x,t; \theta )+\left( \frac{\Delta x^2}{24}\right) {\hat{p}}_N^{(3)}(x,t; \theta )\\&\quad -\frac{\Delta x^4}{480} {\hat{p}}_N^{(5)}(x,t; \theta )+\cdots . \end{aligned} \end{aligned}$$

(3.22)

From the above Eq. (3.20), it is evident that the equation involves both the contribution of the adjacent points and the collocated contribution ${\hat{p}}_{Nx}(x; t; \theta )$. Equation (3.22) shows that the theoretical accuracy of the central difference scheme is also second-order. The fundamental analysis in [22] shows that the proposed schemes have better dispersion and dissipation performance, when compared with the baseline scheme. Furthermore, the inclusion of AD leads to more precise solutions than those of the central difference scheme.

4 Numerical experiments

In this section, the proposed method is used to simulate the two-dimensional unsteady Taylor vortex problem, the two-dimensional steady Kovasznay flow, the three-dimensional unsteady Beltrami flow, the Flow in a Lid-driven cavity and the forward and inverse problem of Cylinder wake. The convection terms are approximated using the second-order upwind scheme, whereas the pressure-gradient terms are approximated using the central difference scheme to account for the physical properties of the different derivative terms. We assessed the efficacy of the proposed approach using the relative $l^{2}$-error and compared it with that of s-PINNs.

Table 2 Relative discrete $l^{2}$-errors between the predicted and the exact solutions for the Taylor vortex problem at different numbers of residual points

4.1 Taylor vortex problem

The Taylor vortex flow [46] is simulated to verify the effectiveness of our method for solving the incompressible fluids. There is an analytical solution expressed as:

$$\begin{aligned} \begin{aligned}&u(\textbf{x},t)=-\cos (\pi x) \sin (\pi y) \exp \left( -\frac{2 \pi ^2 t}{{\text {Re}}}\right) , \\&v(\textbf{x},t)=\sin (\pi x) \cos (\pi y) \exp \left( -\frac{2 \pi ^2 t}{{\text {Re}}}\right) , \\&p(\textbf{x},t)=-\frac{1}{4}[\cos (2 \pi x)+\cos (2 \pi y)] \exp \left( -\frac{4 \pi ^2 t}{{\text {Re}}}\right) . \end{aligned} \end{aligned}$$

(4.1)

In this case, Re=1000, and the initial and boundary conditions can be derived from Eq. (4.1). The simulation was conducted within a square domain $[-1,1]^{2}$ with a circular boundary, and the radius is $r = 0.5$. For this problem, we utilized a network structure consists of 4 hidden layers, and each layer contains 50 neurons. We randomly generate a subset of samples in a size of 1000 for the initial boundary value training data. The boundary points are equidistantly spaced collocation points, as shown in Fig. 7a. The difference from the s-PINNs sampling is shown in Fig. 7b. Taking 10000 equidistantly spaced collocation points are used in the solution domain to apply to Eq. (2.1), the sampling distribution is displayed in Fig. 7c. The space-filling Latin hypercube sampling strategy is applied in the s-PlNNs to generate the randomly sampled points as shown in Fig. 7d. The equidistantly spaced collocation points can cover the entire solution region, accurately capturing the variation characteristics of the function within the region. Therefore, the evenly spaced sampling points were selected as the interpolation basis points to simplify the calculation process and improve the accuracy of the model. Figure 8 shows the downward trend of the loss functions of the s-PINNs and the improved PINNs, while the improved PINNs display a more rapid decline particularly at the initial stages. Figure 9 presents the prediction solution of velocity $u(\textbf{x},t)$, $v(\textbf{x},t)$, and pressure $p(\textbf{x},t)$ and the comparison with the exact solutions. The experimental results show that the error between the predicted and the real values is very small, and the prediction performance is excellent. The performance decline of the loss functions is compared in Fig. 10 throughout the entire iteration epoch via boxplot. The red horizontal lines refer to the usual medians, and the minimum value is marked in the form of a small circle. Observations indicate that the loss function associated with our method diminishes at a more gradual rate, which leads to the enhanced training performance. This method can accurately predict the flow behavior of Taylor vortex. It can be seen that the proposed method also achieves better prediction results than the s-PINNs. For the Taylor-vortex problem, the method adopted in this paper improves the accuracy of velocity and pressure by two orders of magnitude under the same conditions, as shown in Table 1. Table 2 presents the relative discrete $l^{2}$-error between the predicted solution and the exact solution for different numbers of sampling points.

Fig. 7

a The sampling points of the improved PINNs on the boundary. b The sampling points of s-PINNs on the boundary. c The sampling points of the improved PINNs within the region. d The sampling points of the s-PINNs within the region

Fig. 8

a The graph depicts the decreasing trend of the loss function obtained from training with s-PINNs. b The graph depicts the decreasing trend of the loss function obtained from training with improved PINNs

Fig. 9

Distribution of velocity and pressure of prediction solution, exact solution, and absolute pointwise error for Taylor vortex problem a snapshot in time $t = 1$, $Re=1000$

Fig. 10

a Training loss distribution of s-PINNs for the Taylor vortex problem. b Training loss distribution of the improved PINNs for the Taylor vortex problem

4.2 The Kovasznay flow

The two-dimensional steady Kovasznay flow is further studied. We utilize the Kovasznays analytical solution as the benchmark for comparison. For a given viscosity of $\nu =0.1$, this solution is given by

$$\begin{aligned} \begin{aligned} u^{*}(x, y)&=1-e^{\lambda x} \cos (2 \pi y), \\ v^{*}(x, y)&=\frac{\lambda e^{\lambda x}}{2 \pi }\sin (2 \pi y), \\ p^{*}(x, y)&=-\frac{1}{2} e^{\lambda x}+1/2. \end{aligned} \end{aligned}$$

(4.2)

where

$$\begin{aligned} \begin{aligned} \lambda =\frac{-8 \pi ^2}{\nu ^{-1}+\sqrt{\nu ^{-2}+64 \pi ^2}}, \end{aligned} \end{aligned}$$

(4.3)

the L-shaped domain of $\Omega =\left( -\frac{1}{2}, \frac{3}{2}\right) \times (0,2)\backslash \left( -\frac{1}{2}, \frac{1}{2}\right) \times (0,1)$ is considered. A deep neural network architecture with 4 hidden layers of 50 neurons each was used. The 500 equidistantly spaced collocation points of the boundaries, and the 2601 equidistantly spaced collocation points are distributed the region. In Table 3, the relative discrete $l^{2}$-error and the comparison between the s-PINNs and the results of this paper are shown. The $l^{2}$-error of the s-PINNs can only reach the order of $10^{-3}$, while our method can reach the order of $10^{-5}$ and predict a more accurate solution. Figure 11 shows a boxplot of the loss drops for the s-PINNs and the improved PINNs over the entire domain. It can be seen that the loss function of this method decreases fast and converges easily. Figure 12 presents a comprehensive comparison among the prediction solution, the exact solution, and the absolute pointwise error of Kovasznay flow across the entire domain. It can be seen that our method has greatly improved the accuracy of velocity and pressure, and the convergence is faster than s-PINNs.

Table 3 Relative discrete $l^{2}$-error comparison between the predicted and the exact solution obtained using different methods for the Kovasznay flow

Fig. 11

a Training loss distribution of s-PINNs for the Kovasznay flow. b Training loss distribution of the improved PINNs for the Kovasznay flow

Fig. 12

Distribution of velocity and pressure prediction solution, exact solution, and absolute pointwise error for the Kovasznay flow

Fig. 13

a Training loss distribution of s-PINNs for the Beltrami flow. b Training loss distribution of the improved PINNs for the Beltrami flow

4.3 Three-dimensional Beltrami flow

The unsteady Beltrami flow [47] is also considered, and the analytic solution is given as follows:

$$\begin{aligned} u(\textbf{x},t)={} & {} -a\left[ e^{a x} \sin (a y+d z)+e^{a z} \cos (a x+d y)\right] e^{-d^2 t}, \nonumber \\ v(\textbf{x},t)={} & {} -a\left[ e^{a y} \sin (a z+d x)+e^{a x} \cos (a y+d z)\right] e^{-d^2 t}, \nonumber \\ w(\textbf{x},t)={} & {} -a\left[ e^{a z} \sin (a x+d y)+e^{a y} \cos (a z+d x)\right] e^{-d^2 t}, \nonumber \\ p(\textbf{x},t)={} & {} -\frac{1}{2} a^2\left[ e^{2 a x}+e^{2 a y}+e^{2 a z}\right. \nonumber \\{} & {} \quad +2 \sin (a x+d y) \cos (a z+d x) e^{a(y+z)}\nonumber \\{} & {} \quad +2 \sin (a y+d z) \cos (a x+d y) e^{a(z+x)} \nonumber \\{} & {} \quad \left. +2 \sin (a z+d x) \cos (a y+d z) e^{a(x+y)}\right] e^{-2 d^2 t}. \nonumber \\ \end{aligned}$$

(4.4)

where the parameters $a=d =1$. The computational domain is $[-1,1] \times [-1,1] \times [-1,1]$, $t\in [0,1]$. The initial condition for PINNs training is the flow field at the initial moment. The unsteady Beltrami flow field is solved at a time step set of 0.05 s. In this case, we used a neural network with 5 hidden layers 50 neurons per layer to simulate the dynamic behavior of this problem. The 10000 residual training points are distributed in the spatio-temporal domain for the equation, and the 800 boundary training points, and the 1000 initial training points are also adopted. In Table 4, the relative discrete $l^{2}$-errors of the velocity and pressure predictions obtained by the different methods are shown. It is clear that the relative discrete $l^{2}$-errors of our method can reach the order of $10^{-5}$. The final adaptive error means and standard deviations are shown in Fig. 13. Figure 14 illustrates the comparison of the predicted velocity components u, v, and w on the $z = 0$ plane at $t=1$ and their exact solutions, as well as the absolute pointwise error. The absolute pointwise error of the velocity given in [33] reaches the maximum of order of $10^{-3}$, while our method is in the order of $10^{-5}$. According to the results shown in Fig. 15, our method shows a high accuracy for the prediction solution of the three-dimensional Beltrami flow pressure.

Table 4 Relative discrete $l^{2}$-error comparison between the predicted and the exact solution obtained using different methods for the Beltrami flow

Fig. 14

The distribution of exact velocities u, v, and w, as well as prediction solution for a three-dimensional Beltrami flow in the $z = 0$ plane at a snapshot in time $t = 1$

Fig. 15

The distribution of three-dimensional Beltrami flow pressure of the prediction solution, exact solution, and absolute pointwise error

4.4 Flow in a Lid-driven cavity

The classical steady flow in a two-dimensional lid-driven cavity flow in computational fluid dynamics [48] is also simulated with our method. In this case, $Re = 100$. Our goal is to train a neural network in the domain $[0,1] \times [0,1]$, and apply the no-slip boundary conditions at the left, lower, and right boundaries. The top boundary moves at a constant speed in the positive x-direction. We have constructed a neural network with 5 hidden layers, each contains 50 neurons, for predicting the potential velocity and pressure fields. We use 5000 residual points and 1000 upper bound training points to simulate fluid flow. The average relative discrete relative $l^{2}$-error for five independent runs $|\textbf{u}(\textbf{x})|=\sqrt{u^2_{1}(x)+u^2_{2}(x)}$ are summarized in Table 5. In Figs. 16, 17 and 18, the experimental results of our neural network prediction are shown. The predictions of our neural network model are consistent with the results in [48]. The predicted velocity field is in good agreement with the reference solution, whereas the s-PINNs fail to produce a reasonable prediction.

Fig. 16

s-PINNs shows the velocity prediction solution, reference solution, and absolute point error of Flow in a Lid-driven cavity

Fig. 17

Our method shows the velocity prediction solution, reference solution, and absolute point error of flow in a Lid-driven cavity

Fig. 18

Absolute pointwise error between the prediction solution and reference solution in 3D of the s-PINNs and our method for flow in a Lid-driven cavity

Table 5 Relative discrete $l^{2}$-error comparison between the predicted and the reference solution obtained using different methods for flow in a Lid-driven cavity

4.5 Cylinder wake

Fig. 19

Distribution of velocity prediction solution, reference solution, and absolute pointwise error for cylinder wake

Table 6 Relative discrete $l^{2}$-error comparison between the predicted and the reference solution obtained using different methods for cylinder wake

Cylinder wake is a classical fluid dynamics problem involving the flow and turbulence patterns of a fluid after it flows through a cylinder. This phenomenon has aroused great interest in many engineering applications, such as wind energy, ocean engineering, and aerospace. We employ the method proposed in this article to simulate the Cylinder wake, Re = 3900 [49]. The size of the simulation domain is $[0,4] \times [-\,1.5, 1.5]$. In this test case, a neural network with 7 hidden layers is utilized to predict Cylinder wake. Each hidden layer consists of 100 neurons. The training dataset for this problem contains 10000 boundary training points, 5000 initial training points, and 40000 residual training points. Table 6 summarizes the results of the average relative discrete $l^{2}$ -error for $|\textbf{u}|=\sqrt{u_{1}^2+u_{2}^2}$ across five independent runs. It is evident that our method significantly enhances the accuracy of the prediction. Figure 19 shows the distribution of the prediction solution, reference solution, and absolute pointwise error in the computational domain. It can be seen that our method produces accurate predictions with small errors, which reflects the excellent performance of the method in predicting fluid mechanics problems.

Fig. 20

Distribution of velocity prediction solution and reference solution of the wake flow of a circular cylinder for a snapshot in time t = 10

Fig. 21

Iterative training curves for the parameters $\lambda _{1}$ and $\lambda _{2}$

Fig. 22

Iterative training curves for the parameters $\lambda _{1}$ and $\lambda _{2}$

Table 7 Relative discrete $l^{2}$-error comparison between the predicted and the reference solution obtained using different methods for the wake flow of a circular cylinder

4.6 Inverse problem of the wake flow of a circular cylinder

We simulated the two-dimensional vortex shedding behind a cylinder of diameter 1 under $\textrm{Re}=100$, $\Omega =[0,8] \times [-2,-2]$ [19]. In this case, $\lambda _1=$ $1.0, \lambda _2=0.01$. We take 10000 residual points and 3000 initial boundary points as the training dataset. Our goal is to determine the values of the unknown parameters $\lambda _1, \lambda _2$, and obtain a reasonably accurate reconstruction of the velocity $u(\textbf{x}, t)$ and $v(\textbf{x},t)$ in the wake flow of a circular cylinder. We consider the unsteady incompressible N–S equations in two dimensions as follows.

$$\begin{aligned} \begin{aligned} u_t+\lambda _1\left( u u_x+v u_y\right)&=\lambda _2\left( u_{x x}+u_{y y}\right) -p_x, \\ v_t+\lambda _1\left( u v_x+v v_y\right)&=\lambda _2\left( v_{x x}+v_{y y}\right) -p_y, \\ u_x+v_y&=0. \end{aligned} \end{aligned}$$

(4.5)

The architecture of the neural network is constructed using 4 hidden layers, each consists of 50 neurons. The numerical results of the wake flow of a circular cylinder are presented in Table 7. Figure 20 shows the representative snapshots of the velocity components $u(\textbf{x},t)$, $v(\textbf{x},t)$ predicted by the training model. The results show that the error between the predicted and the true values is very small in the whole calculation domain. This method can accurately simulate the complex flow phenomena in the wake flow of a circular cylinder. The predicted $\lambda _1=1.00043, \lambda _2=0.00996$. Figure 21 shows the curves of the predicted parameters $\lambda _{1}$ and $\lambda _{2}$, and the neural network can accurately infer the unknown parameters in the equation. As shown in Fig. 22, the method can still accurately identify the unknown parameters $\lambda _{1}$ and $\lambda _{2}$ after the training data is corrupted by noise of $1\%$. This shows that the model performs well in dealing with complex problems, with a high degree of accuracy and reliability. Our adopted method accurately solves both the forward and inverse problems of circular tail traces. This method can also be applied to address corresponding challenges in other fields.

5 Conclusions

In this paper, we proposed a novel adaptive PINNs method to solve the incompressible N–S equations. The significant impact of the initial and boundary conditions on the accuracy of the problem has been studied. Secondly, the loss functions of PINNs are composed of a weighted combination of the PDEs and the initial boundary values. The weighted combination of the loss functions can easily affect the performance and convergence of the networks. Therefore, we proposed an adaptive weighting PINNs, which adaptively assigns the weights of the loss functions based on the maximum likelihood estimation of Gaussian distribution. he performance and effectiveness of the network are further enhanced, utilizing the physical equation constraints and initial boundary information to improve the accuracy of the solution. In addition, an improved neural network architecture has been designed simultaneously using the global and local information, which is good for passing the input information to the hidden layers while maintaining the integrity. As shown in the numerical experiments, this network can grasp the part of the N–S equations solution with drastic changes. The derivative term in the loss function is then approximated using the mixed differentiation, i.e., AD and the local support points. We adopt the upwind and central difference schemes to compute the derivatives of the convective and pressure-gradient terms in the N–S equations. By combining the advantages of both AD and ND, the sampling efficiency, the convergence speed, and the accuracy are improved. In future work, we will further explore how to apply the proposed model to higher dimensionality and complex geometries.