Introduction

Neural networks (NNs) have been an essential and hotspot issue thanks to the potential applications in associative memory (Shen et al. 2021), optimization (Kaviani and Sohn 2021) and deep learning (Mellit et al. 2021), etc. In recent decades, a lot of related achievements have greatly promoted the research progress of fractional calculus. Fractional calculus can availably make up for the deficiencies of integer-order NNs due to the weak heredity, weak memory and inaccurate modeling of NNs (Samko et al. 1993; Lundstrom et al. 2008; Wang et al. 2020). On account of arbitrarily selecting fractional order for fractional-order neural networks (FONNs), FONNs can exhibit more rich dynamics in comparison with integer-order NNs. By incorporating fractional calculus into NNs, it can be predicted that the research and application of FONNs will have a new leap. Some outstanding attainments and applications of FONNs have been realized, such as health assessment (Snchez et al. 2020), image encryption (Chen et al. 2020), control engineering (Lavin-Delgado et al. 2020). To better develop advantages in the applications of FONNs, it is significant to investigate the dynamic behaviors of FONNs.

Leakage delay can be regarded as a type of essential delay, occasionally it can be called as forgetting delay. It often occurs in the dynamical systems involving negative feedback terms (Gopalsamy 2007). Previous studies indicated that leakage delay cannot be neglected in handling the dynamics of nonlinear systems. Otherwise, the obtained results will be imprecise by this treatment. Gopalsamy detected that leakage delay has a significant influence in destabilizing stability performance of NNs (Gopalsamy 2007). Li et al. pointed out that dynamic NNs occurring to leakage delay can induce performance deterioration in Li et al. (2010). This is unfavorable to the design and applications of NNs if overlooking the effects of leakage delay. Lately, the effects of leakage delays on the dynamics of FONNs have been considerably concerned (Zhang et al. 2020; Ali et al. 2021; Yang et al. 2021).

It is a general consensus that researchers are capable of capturing some valuable information for a given nonlinear system in terms of active bifurcation methods (Alidousti and Ghahfarokhi 2019; Khajanchi and Nieto 2019; Cesare and Sportelli 2020; Wang et al. 2011; Nan and Wang 2013). On the basis of the bifurcations of integer-order systems, the bifurcations of fractional-order systems have been developed (Huang et al. 2019; Shi et al. 2020; Lahrouz et al. 2021). Remarkably, most of the existing bifurcations results are focused on fractional-order systems with single delay. Perceptibly, this kind of remedy cannot characterize accurately the practical dynamical behaviors of nonlinear fractional-order systems.

The outcome available of bifurcation is mainly aimed at fractional-order systems with unique delay, the important reason is that exploring the stability intervals of fractional-order systems with multiple delays is extremely inconvenient. As a matter of fact, the complexity of fractional-order systems can be induced by multiple delays. From the viewpoint of nonlinear dynamics, it is entirely reasonable to introduce multiple delays into fractional-order systems. In Rihan and Velmurugan (2020), the bifurcations of a fractional-order tumor-immune model with two delays were examined, and the bifurcation conditions were captured by regarding different delays as bifurcation parameters. In recent years, some scholars have explored the influence of multiple delays on the bifurcations of FONNs, and some eminent achievements with respect to the bifurcations of FONNs with multiple delays have been acquired (Xu et al. 2020; Huang et al. 2021a, b; Huang and Cao 2021). In Huang et al. (2021a), the issue of bifurcations of a BAM FONN with leakage and communication delays was considered, and it was detected that the stability performance of the developed FONN can be boosted if selecting a lesser leakage delay or communication delay. In Huang and Cao (2021), the problem of bifurcations for delayed FONNs with multiple neurons was studied, and the effects of self-connection delay on the stability and bifurcations was investigated. Nevertheless, there exist only a few results discussing exclusively the effects of leakage delay and communication delay on the stability performance of FONNs (Huang et al. 2021a). Evidently, this subject is worthy of further study.

Based on the previous discussions, we make a minute study of the stability and bifurcation of a FONN with different leakage delay and communication delay in this paper. The main merits of this paper can be summarized in the following: (1) The exact bifurcation points are captured by viewing leakage delay or communication delay as the bifurcation parameters. (2) The obtained results are different markedly from that of Huang et al. (2021b); Huang and Cao (2021), the issue of bifurcations for a class of FONNs with two different leakage delay and communication delay is fully studied. (3) Our results can be further viewed as an extension of Huang and Cao (2021). This largely motivates us to further explore the bifurcations of higher-order FONNs with different leakage delay and communication delay.

The remainder of the paper is constructed in the following: “Basic theoretical tool” section addresses some preliminaries consisting of fractional-order Caputo definition and the stability criteria of fractional linear systems without delays. “Mathematical modeling” section presents the basic mathematical model. “Theoretical analysis” section captures the core bifurcation results. “Numerical examples” section checks the validly of the developed results through numerical simulations. To sum up, the outcome is derived in “Conclusion” section.

Basic theoretical tool

This section includes the Caputo definition and lemma with respect to fractional calculus.

Definition 1

(Podlubny 1999) The Caputo fractional-order derivative is defined by

$$\begin{aligned} D^{q}f(t)=\frac{1}{\varGamma (k-q)}\int _0^t (t-s)^{k-q-1}f^{(k)}(s)ds, \end{aligned}$$

where \(k-1<q\le k\in Z^+\), \(\varGamma (\cdot )\) is the Gamma function.

Based on the Laplace transform, we have

$$\begin{aligned}&L\{D^{q}f(t);s\}=s^q F(s)-\sum _{k=0}^{k-1}s^{q-k-1}f^{(k)}(0),\\&\quad k-1<q\le k\in Z^+. \end{aligned}$$

If \(f^{(k)}(0)=0\), \(k=1,2,\ldots ,n\), then \(L\{D^{q}f(t);s\}=s^q F(s).\)

Lemma 1

(Deng et al. 2007) Consider the following linear fractional-order systems with no delays

$$\begin{aligned} \left\{ \begin{aligned}&D^{q_1}{\mathrm {Z}}_{1}(t)={\mathrm {m}}_{11}{\mathrm {Z}}_{1}(t)+{\mathrm {m}}_{12}{\mathrm {Z}}_{2}(t) +\cdots +{\mathrm {m}}_{1n}{\mathrm {Z}}_{n}(t),\\&D^{q_2}{\mathrm {Z}}_{2}(t)={\mathrm {m}}_{21}{\mathrm {Z}}_{1}(t)+{\mathrm {m}}_{22}{\mathrm {Z}}_{2}(t) +\cdots +{\mathrm {m}}_{2n}{\mathrm {Z}}_{n}(t),\\&\quad \vdots \\&D^{q_n}{\mathrm {Z}}_{n}(t)={\mathrm {m}}_{n1}{\mathrm {Z}}_{1}(t)+{\mathrm {m}}_{n2}{\mathrm {Z}}_{2}(t) +\cdots +{\mathrm {m}}_{nn}{\mathrm {Z}}_{n}(t), \end{aligned} \right. \end{aligned}$$
(1)

where \(q_i\in (0,1]\) \((i=1,2,\ldots ,n)\). Suppose that M is the lowest common multiple of the denominators \(\zeta _i\) of \(q_i\), where \(q_i=\frac{\sigma _i}{\zeta _i}\), \((\sigma _i,\zeta _i)=1\), \(\sigma _i,\zeta _i\in Z^+\), for \(i=1,2,\ldots ,n\), and set \(\gamma =\frac{1}{M}\). It is labeled as

$$\begin{aligned} \triangle (s)=\left[ \begin{array}{cccc} s^{Mq_1}-{\mathrm {m}}_{11} &{}\quad -{\mathrm {m}}_{12} &{}\quad \cdots &{}\quad -{\mathrm {m}}_{1n} \\ -m_{21} &{}\quad s^{Mq_2}-{\mathrm {m}}_{22} &{}\quad \cdots &{}\quad -{\mathrm {m}}_{2n}\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ -{\mathrm {m}}_{n1} &{}\quad -{\mathrm {m}}_{n2} &{}\quad \cdots &{}\quad s^{Mq_n}-{\mathrm {m}}_{nn} \end{array} \right] . \end{aligned}$$

Then the zero solution of system (1) is globally asymptotically stable in the Lyapunov sense if all roots s of the equation \(\det (\triangle (s))=0\) satisfy \(|\arg (s)|>\frac{\gamma \pi }{2}\).

Mathematical modeling

On the basis of the developed model (Hu and Huang 2009), the bifurcations of the following FONN are investigated in the present paper.

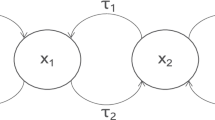
$$\begin{aligned} \left\{ \begin{aligned}&D^{q}x_1(t)=-vx_1(t-\epsilon _1)+\varphi g_1(x_1(t))+b_1g_1(x_4(t-\epsilon _2))+c_1g_1(x_2(t-\epsilon _2)),\\&D^{q}x_2(t)=-vx_2(t-\epsilon _1)+\varphi g_2(x_2(t))+b_2g_2(x_1(t-\epsilon _2))+c_2g_2(x_3(t-\epsilon _2)),\\&D^{q}x_3(t)=-vx_3(t-\epsilon _1)+\varphi g_3(x_3(t))+b_3g_3(x_2(t-\epsilon _2))+c_3g_3(x_4(t-\epsilon _2)),\\&D^{q}x_4(t)=-vx_4(t-\epsilon _1)+\varphi g_4(x_4(t))+b_4g_4(x_3(t-\epsilon _2))+c_4g_4(x_1(t-\epsilon _2)), \end{aligned} \right. \end{aligned}$$
(2)

where \(q\in (0,1]\), \(x_i(t)\) \((i=1,2,3,4)\) stand for state variables, \(v>0\) is the internal decay rate, \(\varphi \), \(b_i\), \(c_i\) stand for connection weights, \(g_i(\cdot )\) denote activation functions, \(\epsilon _1\) denote leakage delay, \(\epsilon _2\) is communication delay.

The following assumptions are addressed for establish the main results:

\(({\mathbf{H1}} )\) \(g_i\in C(R,R)\), \(g_i(0)=0\), \(xg_i(x)>0\) \((i=1,2,3,4)\) for \(x\ne 0\).

Under the condition \(({\mathbf{H1}} )\), we detect that the origin is an equilibrium point of FONN (2).

Theoretical analysis

\(\epsilon _1\) induces bifurcations in FONN (2)

Leakage delay \(\epsilon _1\) is selected as a bifurcation parameter to study the bifurcations in FONN (2) in this subsection. Firstly, the linear form of FONN (2) around the origin can be depicted as

$$\begin{aligned} \left\{ \begin{aligned}&D^{q}x_1(t)=-vx_1(t-\epsilon _1)+dx_1(t)+\kappa _1x_4(t-\epsilon _2)+\ell _1x_2(t-\epsilon _2),\\&D^{q}x_2(t)=-vx_2(t-\epsilon _1)+dx_2(t)+\kappa _2x_1(t-\epsilon _2)+\ell _2x_3(t-\epsilon _2),\\&D^{q}x_3(t)=-vx_3(t-\epsilon _1)+dx_3(t)+\kappa _3x_2(t-\epsilon _2)+\ell _3x_4(t-\epsilon _2),\\&D^{q}x_4(t)=-vx_4(t-\epsilon _1)+dx_4(t)+\kappa _4x_3(t-\epsilon _2)+\ell _4x_1(t-\epsilon _2), \end{aligned} \right. \end{aligned}$$
(3)

where \(d=\varphi g'_i(0)\), \(\kappa _i=b_ig'_i(0)\), \(\ell _i=c_ig'_i(0)\).

Noticeably, the characteristic equation for FONN (3) can be obtained as

$$\begin{aligned} \det \left( \begin{array}{cccc} s^q+ve^{-s\epsilon _1}-d &{}-\ell _1e^{-s\epsilon _2} &{} 0 &{} -\kappa _1e^{-s\epsilon _2} \\ -\kappa _2e^{-s\epsilon _2} &{} s^q+ve^{-s\epsilon _1}-d &{} -\ell _2e^{-s\epsilon _2} &{} 0\\ 0 &{} -\kappa _3e^{-s\epsilon _2} &{} s^q+ve^{-s\epsilon _1}-d &{} -\ell _3e^{-s\epsilon _2}\\ -\ell _4e^{-s\epsilon _2} &{} 0 &{} -\kappa _4e^{-s\epsilon _2} &{} s^q+ve^{-s\epsilon _1}-d \end{array} \right) =0. \end{aligned}$$
(4)

The equivalent form of Eq. (4) can be derived as

$$\begin{aligned} (s^q+ve^{-s\epsilon _1}-d)^4+\mu _1(s^q+ve^{-s\epsilon _1}-d)^2e^{-2s\epsilon _2}+\mu _2e^{-4s\epsilon _2}=0, \end{aligned}$$
(5)

where \(\mu _1=-(\kappa _4\ell _3+\kappa _3\ell _2+\kappa _2\ell _1+\kappa _1\ell _4)\), \(\mu _2=\kappa _2\ell _1\ell _3\kappa _4-\kappa _1\kappa _2\kappa _3\kappa _4-\ell _1\ell _2\ell _3\ell _4+\kappa _1\kappa _3\ell _2\ell _4.\)

By multiplying \(e^{4s\epsilon _2}\) on both sides of Eq. (5), then we clearly conclude that

$$\begin{aligned}&[(s^q+v-de^{-s\epsilon _1})e^{s\epsilon _2}]^4+\mu _1[(s^q+v-de^{-s\epsilon _1})e^{s\epsilon _2}]^2\nonumber \\&\quad +\mu _2=0. \end{aligned}$$
(6)

In Eq. (6), we label as \(\varepsilon =(s^q+v-de^{-s\epsilon _1})e^{s\epsilon_{2}}\), then

$$\begin{aligned} \varepsilon ^4+\mu _1\varepsilon ^2+\mu _2=0. \end{aligned}$$
(7)

It is clear that all the roots of Eq. (7) can be presented as

$$\begin{aligned} \varepsilon _n=\vartheta _n+i\lambda _n.\quad (i=1,2,\ldots ,4) \end{aligned}$$

where \(\vartheta _n\), \(\lambda _n\) are the real and imaginary parts of \(\varepsilon _n\), respectively.

Further, we have

$$\begin{aligned} (s^q+v-de^{-s\epsilon _1})e^{s\epsilon _2}=\varepsilon _n. \end{aligned}$$
(8)

Let \(s=w(\cos \frac{\pi }{2}+i\sin \frac{\pi }{2})\) (\(w>0\)) be a purely imaginary root of Eq. (8) if the following equations hold

$$\begin{aligned} \left\{ \begin{aligned}&\alpha _1\cos w\epsilon _1+\beta _1\sin w\epsilon _1=\gamma _1,\\&\alpha _2\cos w\epsilon _1+\beta _2\sin w\epsilon _1=\gamma _2, \end{aligned} \right. \end{aligned}$$
(9)

where \(\alpha _1=v\cos w\epsilon _2\), \(\beta _1=v\sin w\epsilon _2\), \(\gamma _1=-(w^q\cos \frac{q\pi }{2}-d)\cos w\epsilon _2+w^q\sin \frac{q\pi }{2}\sin w\epsilon _2+\vartheta _n\), \(\alpha _2=v\sin w\epsilon _2\), \(\beta _2=-v\cos w\epsilon _2\), \(\gamma _2=-w^q\sin \frac{q\pi }{2}\cos w\epsilon _2-(w^q\cos \frac{q\pi }{2}-d)\sin w\epsilon _2+\lambda _n.\)

By solving Eq. (9), it obtains as

$$\begin{aligned} \left\{ \begin{aligned} \cos w\epsilon _1&=\frac{\gamma _1\beta _2-\gamma _2\beta _1}{\alpha _1\beta _2-\alpha _2\beta _1}=\varPhi _1(w),\\ \sin w\epsilon _1&=\frac{\alpha _1\gamma _2-\alpha _2\gamma _1}{\alpha _1\beta _2-\alpha _2\beta _1}=\varPhi _2(w). \end{aligned} \right. \end{aligned}$$
(10)

It follows from Eq. (10) that

$$\begin{aligned} \varPhi ^2_1(w)+\varPhi ^2_2(w)=1. \end{aligned}$$
(11)

The following assumption is needed for establishing our main results.

\(({\mathbf{H2}} )\) There exist positive real roots \(w_k\) \((k=1,2...)\) for Eq. (11).

Based on Eq. (10), we have

$$\begin{aligned} \epsilon _{1j}^{(k)}=\frac{1}{w_k}\Big [\arccos \varPhi _1(w_k)+2j\pi \Big ],\quad j=0,1,2,\ldots . \end{aligned}$$
(12)

The bifurcation point of FONN (2) is labeled as

$$\begin{aligned} \epsilon _{10}=\epsilon _{1j}^{(0)}=\min \{\epsilon _{1j}^{(k)}\},\; w_k=w_{0}, \quad k=1,2,\ldots . \end{aligned}$$

Equation (5) can be inverted into the following form when \(\epsilon _1\) vanishes.

$$\begin{aligned}&L_1(s)+L_2(s)e^{-2s\epsilon _2}+L_3(s)e^{-4s\epsilon _2}=0, \end{aligned}$$
(13)

where \(L_1(s)=(s^q+v-d)^4\), \(L_2(s)=\mu _1(s^q+v-d)^2\), \(L_3(s)=\mu _2.\)

Multiplying \(e^{2s\epsilon _2}\) on both sides of Eq. (13), then it can be obtained as

$$\begin{aligned}&L_1(s)e^{2s\epsilon _2}+L_2(s)+L_3(s)e^{-2s\epsilon _2}=0. \end{aligned}$$
(14)

The real and imaginary parts of \(L_i(s)\) \((i=1,2,3)\) can be denoted by \(L_i^r\), \(L_i^i\), respectively. It is clear that \(L_3^i=0\).

Suppose that \(s=\bar{w}(\cos \frac{\pi }{2}+i\sin \frac{\pi }{2})\) \((\bar{w}>0)\) is a purely imaginary root of Eq. (14), then we have

$$\begin{aligned} \left\{ \begin{aligned}&(L_1^r+L_3^r)\cos 2\bar{w}\epsilon _2-L_1^i\sin 2\bar{w}\epsilon _2=-L_2^r,\\&L_1^i\cos 2\bar{w}\epsilon _2+(L_1^r-L_3^r)\sin 2\bar{w}\epsilon _2=-L_2^i. \end{aligned} \right. \end{aligned}$$
(15)

It concludes from Eq. (15) that

$$\begin{aligned} \left\{ \begin{aligned}&\cos 2\bar{w}\epsilon _2=\frac{-L_2^r(L_1^r-L_3^r)-L_1^i L_2^i}{(L_1^r)^2+(L_1^i)^2-(L_3^r)^2}=\varUpsilon _1(\bar{w}),\\&\sin 2\bar{w}\epsilon _2=\frac{-L_2^i(L_1^r+L_3^r)+L_1^i L_2^r}{(L_1^r)^2+(L_1^i)^2-(L_3^r)^2}=\varUpsilon _2(\bar{w}). \end{aligned} \right. \end{aligned}$$
(16)

By means of Eq. (16), it procures that

$$\begin{aligned} \varUpsilon _1^2(\bar{w})+\varUpsilon _2^2(\bar{w})=1. \end{aligned}$$
(17)

The following assumption is addressed.

\(({\mathbf{H3}} )\) There exists positive roots for Eq. (17).

By means of Eq. (17), the values of \(\bar{w}\) can be obtained, then the bifurcation point \(\bar{\epsilon }_{20}\) of FONN (2) with \(\epsilon _1=0\) can be derived.

If the value of \(\epsilon _2\) is zero, it follows from Eq. (13) that

$$\begin{aligned}&s^{4q}+C_1s^{3q}+C_2s^{2q}+C_3s^{q}+C_4=0, \end{aligned}$$
(18)

where \(C_1=4(v-d)\), \(C_2=6(v-d)^2+\mu _1\), \(C_3=4(v-d)^3+2\mu _1(v-d)\), \(C_4=(v-d)^4+\mu _1(v-d)^2+\mu _2.\)

Assume that all roots s of Eq. (18) obey Lemma 1, then it concludes that FONN (2) is asymptotically stable with \(\epsilon _1=\epsilon _2=0\).

To throw out the bifurcation conditions, the following assumption is addressed.

\(({\mathbf{H4}} )\) \(\frac{P_1U_1+P_2U_2}{U_1^2+U_2^2}\ne 0\),

where \(P_1\), \(P_2\), \(U_1\), \(U_2\) are described by Eq. (21).

Lemma 2

Let \(s(\epsilon _1)=\xi (\epsilon _1)+iw(\epsilon _1)\) be the root of Eq. (5) near \(\epsilon _1=\epsilon _{10}\) complying with \(\xi (\epsilon _{10})=0\), \(w(\epsilon _{10})=w_0\), then the following transversality condition holds

$$\begin{aligned} {\mathrm {Re}}\Big [\frac{ds}{d\epsilon _1}\Big ] \Big |_{(w=w_0,\epsilon _1=\epsilon _{10})}\ne 0. \end{aligned}$$

Proof

Let us adopt implicit function theorem to differentiate Eq. (5) with regard to \(\epsilon _1\), then

$$\begin{aligned}&4(s^q+ve^{-s\epsilon _1}-d)^3\Big [qs^{q-1}\frac{ds}{d\epsilon _1}\nonumber \\&\quad +ve^{-s\epsilon _1}\Big (-s-\epsilon _1\frac{ds}{d\epsilon _1}\Big )\Big ] +\mu _1\Big \{[2(s^q+ve^{-s\epsilon _1}-d)\nonumber \\&\quad \cdot \Big [qs^{q-1}\frac{ds}{d\epsilon _1}+ve^{-s\epsilon _1} \Big (-s-\epsilon _1\frac{ds}{d\epsilon _1}\Big )\Big ]\nonumber \\&\quad +(s^q+ve^{-s\epsilon _1}-d)^2\Big (-2\epsilon _2\frac{ds}{d\epsilon _1}\Big )\Big \}e^{-2s\epsilon _2}\nonumber \\&\quad +\mu _2e^{-4s\epsilon _2}\Big (-4\epsilon _2\frac{ds}{d\epsilon _1}\Big )=0. \end{aligned}$$
(19)

Simple mathematical operations from Eq. (19) deduces

$$\begin{aligned} \frac{ds}{d\epsilon _1}=\frac{P(s)}{U(s)}, \end{aligned}$$
(20)

where

$$\begin{aligned} P(s)&=vse^{-s\epsilon _1}[4(s^q+ve^{-s\epsilon _1}-d)^3\\&\quad +2\mu _1(s^q+ve^{-s\epsilon _1}-d)e^{-2s\epsilon _2}],\\ U(s)&=4(s^q+v-de^{-s\epsilon _1})^3(qs^{q-1}+d\tau _1e^{-s\epsilon _1})\\&\quad +2\mu _1[(s^q+ve^{-s\epsilon _1}-d)\cdot (qs^{q-1}-v\epsilon _1e^{-s\epsilon _1})\\&\quad -\epsilon _2(s^q+ve^{-s\epsilon _1}-d)^2]e^{-2s\epsilon _2}-4\mu _2\epsilon _2e^{-4s\epsilon _2}. \end{aligned}$$

For the sake of convenience, we label the real and imaginary parts of \(s^q+ve^{-s\epsilon _1}-d\) as a, b. The real and imaginary parts of P(s) can be labeled as \(P_1\), \(P_2\). The real and imaginary parts of U(s) can be presented as \(U_1\), \(U_2\).

It follows from Eq. (20) that

$$\begin{aligned} {\mathrm {Re}}\Big [\frac{ds}{d\epsilon _1}\Big ]\Big |_{(w=w_0,\epsilon _1=\epsilon _{10})} =\frac{P_1U_1+P_2U_2}{U_1^2+U_2^2}, \end{aligned}$$
(21)

where

$$\begin{aligned} P_1&=vw_0\{[4(a^3-3ab^2)+2\mu _1(a\cos 2w_0\epsilon _2\\&\quad +b\sin 2w_0\epsilon _2]\sin w_0\epsilon _{10} -[4(3a^2b-b^3)\\&\quad +2\mu _1(b\cos 2w_0\epsilon _2-a\sin 2w_0\epsilon _2]\cos w_0\epsilon _{10}\},\\ P_2&=vw_0\{[4(a^3-3ab^2)\\&\quad +2\phi _1(a\cos 2w_0\epsilon _2\\&\quad +b\sin 2w_0\epsilon _2]\cos w_0\epsilon _{10} +[4(3a^2b-b^3)\\&\quad +2\phi _1(b\cos 2w_0\epsilon _2-a\sin 2w_0\epsilon _2]\sin w_0\epsilon _{10}\},\\ U_1&=4(a^3-3ab^2)\\&\quad \Big [qw_0^{q-1}\cos \frac{(q-1)\pi }{2} -v\epsilon _{10}\cos w_0\epsilon _{10}\Big ]\\&\quad -4(3a^2b-b^3)\Big [qw_0^{q-1}\sin \frac{(q-1)\pi }{2}\\&\quad +v\epsilon _{10}\sin w_0\epsilon _{10}\Big ]+2\mu _1\\&\quad \Big \{ \Big [a\Big (qw_0^{q-1}\cos \frac{(q-1)\pi }{2}-v\epsilon _{10}\cos w_0\epsilon _{10}\Big )\\&\quad -b\Big (qw_0^{q-1}\sin \frac{(q-1)\pi }{2}+v\epsilon _{10}\sin w_0\epsilon _{10}\Big )-\epsilon _2(a^2-b^2)\Big ]\\&\quad \cdot \cos 2w_0\epsilon _2 +\Big [a\Big (qw_0^{q-1}\sin \frac{(q-1)\pi }{2}+v\epsilon _{10}\sin w_0\epsilon _{10}\Big )\\&\quad +b\Big (qw_0^{q-1}\cos \frac{(q-1)\pi }{2}-v\tau _{10}\sin w_0\epsilon _{10}\Big )-2\epsilon _2ab\Big ]\\&\quad \cdot \sin 2w_0\epsilon _2\Big \} -4\mu _2\epsilon _2\cos 4w_0\epsilon _2,\\ U_2&=4(a^3-3ab^2)\Big [qw_0^{q-1}\sin \frac{(q-1)\pi }{2} -v\epsilon _{10}\sin w_0\epsilon _{10}\Big ]\\&\quad +4(3a^2b-b^3)\Big [qw_0^{q-1}\cos \frac{(q-1)\pi }{2}-v\epsilon _{10}\cos w_0\epsilon _{10}\Big ]\\&\quad +2\mu _1\Big \{ -\Big [a\Big (qw_0^{q-1}\cos \frac{(q-1)\pi }{2}-v\epsilon _{10}\cos w_0\epsilon _{10}\Big ) \\&\quad -b\Big (qw_0^{q-1}\sin \frac{(q-1)\pi }{2}+v\epsilon _{10}\sin w_0\epsilon _{10}\Big )\\&\quad -\epsilon _2(a^2-b^2)\Big ]\sin 2w_0\epsilon _2 +\Big [a\Big (qw_0^{q-1}\\&\quad \sin \frac{(q-1)\pi }{2}+v\epsilon _{10}\sin w_0\epsilon _{10}\Big ) \\&\quad +b\Big (qw_0^{q-1}\cos \frac{(q-1)\pi }{2} -v\epsilon _{10}\sin w_0\epsilon _{10}\Big )\\&\quad -2\epsilon _2ab\Big ]\cos 2w_0\epsilon _2\Big \} +4\mu _2\epsilon _2\sin 4w_0\epsilon _2. \end{aligned}$$

\(({\mathbf{H4}} )\) means that transversality condition holds. The proof of Lemma 2 is finished. \(\square \)

Based on the previous investigations, we can establish the following theorem.

Theorem 1

Under \(({\mathbf{H1}} )\)–\(({\mathbf{H4}} )\), the following results can be concluded.

  1. (1)

    If \(\epsilon _2\in [0,\bar{\epsilon }_{20})\), then the origin of FONN (2) is asymptotically stable when \(\epsilon _1\in {[0,\epsilon _{10})}\).

  2. (2)

    If \(\epsilon _2\in [0,\bar{\epsilon }_{20})\), then FONN (2) experiences a Hopf bifurcation at the origin when \(\epsilon _1=\epsilon _{10}\).

\(\epsilon _2\) induces bifurcations in FONN (2)

Communication delay \(\epsilon _2\) acts as a bifurcation parameter to explore the bifurcations in FONN (2) in this subsection.

Equation (5) can be equally recast as

$$\begin{aligned} R_1(s)+R_2(s)e^{-2s\epsilon _2}+R_3(s)e^{-4s\epsilon _2}=0, \end{aligned}$$
(22)

where \(R_1(s)=(s^q+ve^{-s\epsilon _1}-d)^4\), \(R_2(s)=\mu _1(s^q+ve^{-s\epsilon _1}-d)^2\), \(R_3(s)=\mu _2\).

Denoting the real and imaginary parts of \(R_h(s)\) \((h=1,2,3)\) as \(R_h^r\), \(R_h^i\), respectively. It is clear that \(R_3^i=0\). Assume that \(s=\varpi (\cos \frac{\pi }{2}+i\sin \frac{\pi }{2})\) is a purely imaginary root of Eq. (22), \(\varpi >0\). Then it results in

$$\begin{aligned} \left\{ \begin{aligned}&(R_1^r+R_3^r)\cos 2\varpi \epsilon _2-R_1^i\sin 2\varpi \epsilon _2=-R_2^r,\\&R_1^i\cos 2\varpi \epsilon _2+(R_1^r-R_3^r)\sin 2\varpi \epsilon _2=-R_2^i. \end{aligned} \right. \end{aligned}$$
(23)

It concludes form Eq. (23) that

$$\begin{aligned} \left\{ \begin{aligned}&\cos 2\varpi \epsilon _2=\frac{-R_2^r(R_1^r-R_3^r)-R_1^i R_2^i}{(R_1^r)^2+(R_1^i)^2-(R_3^r)^2}=\varPsi _1(\varpi ),\\&\sin 2\varpi \epsilon _2=\frac{-R_2^i(R_1^r+R_3^r)+R_1^i R_2^r}{(R_1^r)^2+(R_1^i)^2-(R_3^r)^2}=\varPsi _2(\varpi ). \end{aligned} \right. \end{aligned}$$
(24)

In terms of Eq. (24), the following equation holds

$$\begin{aligned} \varPsi _1^2(\varpi )+\varPsi _2^2(\varpi )=1. \end{aligned}$$
(25)

The following assumptions is valuable for setting up our main results.

\(({\mathbf{H5}} )\) There exist positive real roots \(\varpi _k\) \((k=1,2...)\) for Eq. (25).

It follows from Eq. (24) that

$$\begin{aligned} \epsilon _{2j}^{(k)}=\frac{1}{2\varpi _k}\Big [\arccos \varPsi _1(\varpi _k)+2j\pi \Big ], j=0,1,2,\ldots . \end{aligned}$$
(26)

Label the bifurcation point of FONN (2) as

$$\begin{aligned} \epsilon _{20}=\epsilon _{2j}^{(0)}=\min \{\epsilon _{2j}^{(k)}\}, \varpi _k=\varpi _{0}, k=1,2,\ldots . \end{aligned}$$

If the value of \(\epsilon _2\) is equal to 0, then Eq. (5) can be inverted into the following form

$$\begin{aligned} (s^q+ve^{-s\epsilon_{1}}-d)^4+\mu _1(s^q+ve^{-s\epsilon _1}-d)^2+\mu _2=0. \end{aligned}$$
(27)

Assuming that \(\varTheta =s^q+ve^{-s\epsilon _1}-d\). According to Eq. (27), we have

$$\begin{aligned} \varTheta ^4+\mu _1\varTheta ^2+\mu _2=0. \end{aligned}$$
(28)

Label the four roots of Eq. (28) as

$$\begin{aligned} \varTheta _n=\eta _n+i\theta _n.\quad (i=1,2,\ldots ,4) \end{aligned}$$

where \(\eta _n\), \(\theta _n\) are the real and imaginary parts of \(\varTheta _n\), respectively.

Therefore,

$$\begin{aligned} s^q+ve^{-s\epsilon _1}-d=\varTheta _n. \end{aligned}$$
(29)

Let \(s=\bar{\varpi }(\cos \frac{\pi }{2}+i\sin \frac{\pi }{2})\)(\(\bar{\varpi }>0\)) be a purely imaginary root of Eq. (29), then we have

$$\begin{aligned} \left\{ \begin{aligned}&\bar{\varpi }^q\cos \frac{q\pi }{2}+v\cos \bar{\varpi }\epsilon _1-d=\eta _n,\\&\bar{\varpi }^q\sin \frac{q\pi }{2}-v\sin \bar{\varpi }\epsilon _1=\theta _n. \end{aligned} \right. \end{aligned}$$
(30)

It detects from Eq. (30) that

$$\begin{aligned} \left\{ \begin{aligned} \cos \bar{\varpi }\epsilon _1&=-\frac{\bar{\varpi }^q\cos \frac{q\pi }{2}-d-\eta _n}{v}=\phi _1(\bar{\varpi }),\\ \sin \bar{\varpi }\epsilon _1&=\frac{\bar{\varpi }^q\sin \frac{q\pi }{2}-\theta _n}{v}=\phi _2(\bar{\varpi }). \end{aligned} \right. \end{aligned}$$
(31)

Evidently, based on Eq. (31), we derive that

$$\begin{aligned} \phi ^2_1(\bar{\varpi })+\phi ^2_2(\bar{\varpi })=1. \end{aligned}$$
(32)

The following assumption is addressed.

\(({\mathbf{H6}} )\) Equation (32) has at least positive roots.

Based on Eq. (32), the values of \(\bar{\varpi }\) can be obtained, then the bifurcation point \(\bar{\epsilon }_{10}=0\) of FONN (2) with \(\epsilon _2=0\) can be derived.

To derive the bifurcation results, we need the following assumption

\(({\mathbf{H7}} )\) \(\frac{J_1K_1+J_2K_2}{K_1^2+K_2^2}\ne 0\),

where \(J_1\), \(J_2\), \(K_1\), \(K_2\) are described in Eq. (35).

Lemma 3

Let \(s(\epsilon _2)=\xi (\epsilon _2)+i\varpi(\epsilon _2)\) be the root of Eq. (22) near \(\epsilon _2=\epsilon _{20}\) complying with \(\xi (\epsilon _{20})=0\), \(\varpi(\epsilon _{20})=\varpi_{0}\), then the following transversality condition holds

$$\begin{aligned} {\mathrm {Re}}\Big [\frac{ds}{d\epsilon _2}\Big ] \Big |_{(\varpi =\varpi _0,\epsilon _{2}=\epsilon _{20})}\ne 0. \end{aligned}$$

Proof

By applying implicit function theorem, we differentiate Eq. (22) with respect to \(\epsilon _2\), then we have

$$\begin{aligned}&4(s^q+ve^{-s\epsilon _1}-d)^3\Big [qs^{q-1}\frac{ds}{d\epsilon _2}+ve^{-s\epsilon _1}\Big (-\epsilon _1\frac{ds}{d\epsilon _2}\Big )\Big ]\nonumber \\&\quad +\mu _1\Big \{2(s^q+ve^{-s\epsilon _1}-d)\nonumber \\&\quad \cdot \Big [qs^{q-1}\frac{ds}{d\epsilon _2}+ve^{-s\epsilon _1}\Big (-\epsilon _1\frac{ds}{d\epsilon _2}\Big )\Big ]\nonumber \\&\quad +(s^q+ve^{-s\epsilon _1}-d)^2\Big (-2s-2\epsilon _2\frac{ds}{d\epsilon _2}\Big )\Big \}e^{-2s\epsilon _2}\nonumber \\&\quad +\mu _2e^{-4s\epsilon _2}\Big (-4s-4\epsilon _2\frac{ds}{d\epsilon _2}\Big )=0. \end{aligned}$$
(33)

Direct calculation from Eq. (33) induces

$$\begin{aligned} \frac{ds}{d\epsilon _2}=\frac{J(s)}{K(s)}, \end{aligned}$$
(34)

where

$$\begin{aligned} J(s)&=s[2\mu _1(s^q+ve^{-s\epsilon _1}-d)^2e^{-2s\epsilon _2}+4\mu _2e^{-4s\epsilon _2}],\\ K(s)&=4(s^q+ve^{-s\epsilon _1}-d)^3(qs^{q-1}-v\epsilon _1e^{-s\epsilon _1})\\&\quad +2\mu _1[(s^q+ve^{-s\epsilon _1}-d) \cdot (qs^{q-1}-v\epsilon _1e^{-s\epsilon _1})\\&\quad -\epsilon _2(s^q+ve^{-s\epsilon _1}-d)^2]e^{-2s\epsilon _2}-4\mu _2\epsilon _2e^{-4s\epsilon _2}. \end{aligned}$$

It gains from Eq. (34) that

$$\begin{aligned} {\mathrm {Re}}\Big [\frac{ds}{d\epsilon _2}\Big ]\Big |_{(\varpi =\varpi _0,\epsilon _{2}=\epsilon _{20})} =\frac{J_1K_1+J_2K_2}{K_1^2+K_2^2}, \end{aligned}$$
(35)

where

$$\begin{aligned} J_1&=2\varpi _0\{\mu _1[(a^2-b^2)\sin 2\varpi _0\epsilon _{20}\\&\quad -2ab\cos 2\varpi _0\epsilon _{20}]+2\mu _2\sin 4\varpi _0\epsilon _{20}\},\\ J_2&=2\varpi _0\{\mu _1[(a^2-b^2)\cos 2\varpi _0\epsilon _{20}\\&\quad +2ab\sin 2\varpi _0\epsilon _{20}]+2\mu _2\cos 4\varpi _0\epsilon _{20}\},\\ K_1&=4\Big [(a^3-3ab^2)\Big (q\varpi _0^{q-1}\\&\quad \cos \frac{(q-1)\pi }{2}-v\epsilon _1\cos \varpi _0\epsilon _1\Big ) -(3a^2-b^3)\\&\quad \Big (q\varpi _0^{q-1}\sin \frac{(q-1)\pi }{2}+v\epsilon _1\sin \varpi _0\epsilon _1\Big )\Big ]\\&\quad +2\mu _1\Big \{\Big [a\Big (q\varpi _0^{q-1}\cos \frac{(q-1)\pi }{2}\\&\quad -v\epsilon _1\cos \varpi _0\epsilon _1\Big ) -b\Big (q\varpi _0^{q-1}\sin \frac{(q-1)\pi }{2}\\&\quad +v\epsilon _1\sin \varpi _0\epsilon _1\Big )-\epsilon _{20}(a^2-b^2)\Big ]\\&\quad \cdot \cos 2\varpi _0\epsilon _{20}+\Big [a\Big (q\varpi _0^{q-1}\sin \frac{(q-1)\pi }{2}-v\epsilon _1\sin \varpi _0 \epsilon _1\Big )\\&\quad +b\Big (q\varpi _0^{q-1}\cos \frac{(q-1)\pi }{2}+v\epsilon _1\cos \varpi _0\epsilon _1\Big )-2ab\epsilon _{20}\Big ]\\&\quad \cdot \sin 2\varpi _0\epsilon _{20}\Big \}-4\mu _2\cos 4\varpi _0\epsilon _{20},\\ K_2&=4\Big [(a^3-3ab^2)\Big (q\varpi _0^{q-1}\sin \frac{(q-1)\pi }{2}+v\epsilon _1\sin \varpi _0\epsilon _1\Big )\\&\quad +(3a^2-b^3)\Big (q\varpi _0^{q-1}\cos \frac{(q-1)\pi }{2}-v\epsilon _1\cos \varpi _0\epsilon _1\Big )\Big ]\\&\quad +2\mu _1\Big \{-\Big [a\Big (q\varpi _0^{q-1}\cos \frac{(q-1)\pi }{2}-v\epsilon _1\cos \varpi _0\epsilon _1\Big )\\&\quad -b\Big (q\varpi _0^{q-1}\sin \frac{(q-1)\pi }{2} +v\epsilon _1\sin \varpi _0\epsilon _1\Big )-\epsilon _{20}(a^2-b^2)\Big ]\\&\quad \cdot \sin 2\varpi _0\epsilon _{20}+\Big [a\Big (q\varpi _0^{q-1}\sin \frac{(q-1)\pi }{2}-v\epsilon _1\sin \varpi _0 \epsilon _1\Big ) \\&\quad +b\Big (q\varpi _0^{q-1}\cos \frac{(q-1)\pi }{2}+v\epsilon _1\cos \varpi _0\epsilon _1\Big )-2ab\epsilon _{20}\Big ]\\&\quad \cdot \cos 2\varpi _0\epsilon _{20}\Big \}+4\mu _2\sin 4\varpi _0\epsilon _{20}. \end{aligned}$$

\(({\mathbf{H7}} )\) indicates that transversality condition hold. We accomplish the proof of Lemma 3.

In view of the prevenient analysis, the following theorem can be concluded. \(\square \)

Theorem 2

Under \(({\mathbf{H1}} )\), \(({\mathbf{H5}} )\)–\(({\mathbf{H7}} )\), the following statements can be gained.

  1. (1)

    If \(\epsilon _1\in [0,\bar{\epsilon }_{10})\), then the origin of FONN (2) is asymptotically stable when \(\epsilon _2\in [0,\epsilon _{20})\).

  2. (2)

    If \(\epsilon _1\in [0,\bar{\epsilon }_{10})\), then FONN (2) undergoes a Hopf bifurcation at the origin when \(\epsilon _2=\epsilon _{20}\).

Remark 1

It should be noticed that the bifurcations of a conventional integer-order NN with two different communication delays was thoroughly discussed by taking communication delay as a bifurcation parameter in Hu and Huang (2009). In this paper, we fully consider the advantages of fractional calculus in modeling NNs and further incorporate the impact of leakage delay on the network stability performance for NNs. Therefore, the derived results overcome the defects of previous network modeling, and these results can precisely reflect the practical characteristics of dynamic networks.

Remark 2

In Xu et al. (2020); Huang et al. (2021a), the problem of bifurcations for a FONN with four communication delays was considered by taking communication delay as a bifurcation parameter. In Huang and Cao (2021), the authors explored the bifurcation mechanisation of high-order FONN with unequal delays by using self-connection delay as a bifurcation parameter. It is clear that the derived results of Xu et al. (2020); Huang et al. (2021a); Huang and Cao (2021) did not take into consideration the effects of leakage delays. In this paper, we nicely deal with this issue in FONNs.

Remark 3

There exist few references discussing the combination influence of leakage delays on the bifurcations in FONNs by viewing that leakage delay is identical with communication delay (Huang and Cao 2018). As a matter of fact, leakage delay is commonly not consistent with communication delay in FONNs. In Huang et al. (2021a), the authors pointed out that it is essential and meaningful to separately analyze the impact of leakage and communication delays on the dynamics of FONN (2) in this paper. It detects that an appropriate leakage delay or communication delay is beneficial to enhance the stability performance of FONN (2).

Numerical examples

In this section, numerical results illustrate the efficiency of the developed theory.

Example 1

Communication delay \(\epsilon _2\) is fixed and leakage delay \(\epsilon _1\) is selected as a bifurcation parameter to study the bifurcations of FONN (2). More precisely, we consider the following FONN

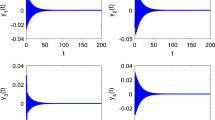
$$\begin{aligned} \left\{ \begin{aligned}&D^{0.95}x_1(t)=-0.9x_1(t-\epsilon _1)+0.8\tanh (x_1(t))+0.2\tanh (x_4(t-\epsilon _2))+0.9\tanh (x_2(t-\epsilon _2)),\\&D^{0.95}x_2(t)=-0.9x_2(t-\epsilon _1)+0.8\tanh (x_2(t))-0.5\tanh (x_1(t-\epsilon _2))-0.2\tanh (x_3(t-\epsilon _2)),\\&D^{0.95}x_3(t)=-0.9x_3(t-\epsilon _1)+0.8\tanh (x_3(t))-0.4\tanh (x_2(t-\epsilon _2))-0.6\tanh (x_4(t-\epsilon _2)),\\&D^{0.95}x_4(t)=-0.9x_4(t-\epsilon _1)+0.8\tanh (x_4(t))+1.2\tanh (x_3(t-\epsilon _2))+1.5\tanh (x_1(t-\epsilon _2)), \end{aligned} \right. \end{aligned}$$
(36)

In this example, the initial values are selected as \((x_1(0),x_2(0),x_3(0),x_4(0))=(-0.03,0.03,0.03,-0.03).\) If choosing \(\epsilon _2=0.1\), we further obtain \(w_0=1.1695\), \(\epsilon _{10}=0.4164\). It simply verifies that the conditions in Theorem 1 are met. It can be clearly seen from Figs. 1 and 2 that the zero equilibrium point of FONN (36) is locally asymptotical stable when choosing \(\epsilon _1=0.3<\epsilon _{10}\). Furthermore, Figs. 3 and 4 reflect that the instability of the zero equilibrium point FONN (36), and Hopf bifurcation takes place when \(\epsilon _1=0.5>\epsilon _{10}\).

Fig. 1
figure 1

Trajectories of FONN (36) with \(q=0.95\), \(\epsilon _2=0.1\), \(\epsilon _1=0.3<\epsilon _{10}=0.4164\)

Full size image
Fig. 2
figure 2

Phase diagrams of FONN (36) with \(q=0.95\), \(\epsilon _2=0.1\), \(\epsilon _1=0.3<\epsilon _{10}=0.4164\)

Full size image
Fig. 3
figure 3

Trajectories of FONN (36) with \(q=0.95\), \(\epsilon _2=0.1\), \(\epsilon _1=0.5>\epsilon _{10}=0.4164\)

Full size image
Fig. 4
figure 4

Phase diagrams of FONN (36) with \(q=0.95\), \(\epsilon _2=0.1\), \(\epsilon _1=0.5>\epsilon _{10}=0.4164\)

Full size image

Remark 4

Previous studies have revealed that leakage delay cannot be neglected in FONNs, and the presence of leakage delay has a negative effect on the stability and bifurcation of FONNs in Huang and Cao (2018), which can extremely demolish the stability performance and lead to the onset of bifurcation of FONNs in advance. Different from the results available in Huang and Cao (2018), we discover in this paper that leakage delay has a positive impact on network stability performance of FONNs provided that a proper size of leakage delay is selected. It can be seen from Fig. 1 that when the communication delay is fixed, the smaller the leakage delay is, the higher the system stability is.

Example 2

Leakage delay \(\epsilon _1\) is established and communication delay \(\epsilon _2\) is chosen as a bifurcation parameter to explore the bifurcations of FONN (2). We further investigate the following FONN

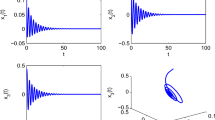
$$\begin{aligned} \left\{ \begin{aligned}&D^{0.97}x_1(t)=-1.5x_1(t-\epsilon _1)-0.6\tanh (x_1(t))-1.5\tanh (x_4(t-\epsilon _2))+1.5\tanh (x_2(t-\epsilon _2)),\\&D^{0.97}x_2(t)=-1.5x_2(t-\epsilon _1)-0.6\tanh (x_2(t))-2.5\tanh (x_1(t-\epsilon _2))-2.4\tanh (x_3(t-\epsilon _2)),\\&D^{0.97}x_3(t)=-1.5x_3(t-\epsilon _1)-0.6\tanh (x_3(t))+1.2\tanh (x_2(t-\epsilon _2))+1.5\tanh (x_4(t-\epsilon _2)),\\&D^{0.97}x_4(t)=-1.5x_4(t-\epsilon _1)-0.6\tanh (x_4(t))-0.2\tanh (x_3(t-\epsilon _2))-0.8\tanh (x_1(t-\epsilon _2)), \end{aligned} \right. \end{aligned}$$
(37)

For this example, the initial values are selected as \((x_1(0),x_2(0),x_3(0),x_4(0))=(-0.2,0.5,-0.2,0.05)\). If choosing \(\epsilon _1=0.1\), then we further procure that \(\varpi _0=3.2074\), \(\tau _{20}=0.4529\). It easily justifies that the conditions of in Theorem 2 hold. Figures 5 and 6 depict that the zero equilibrium point of FONN (37) is locally asymptotically stable when \(\epsilon _2=0.4<\epsilon _{20}\), while Figs. 7 and 8 describe that the zero equilibrium point of FONN (37) is unstable, Hopf bifurcation occurs when \(\epsilon _2=0.6>\epsilon _{20}\).

Fig. 5
figure 5

Trajectories of FONN (37) with \(q=0.97\), \(\epsilon _1=0.1\), \(\epsilon _2=0.4<\epsilon _{20}=0.4529\)

Full size image
Fig. 6
figure 6

Phase diagrams of FONN (37) with \(q=0.97\), \(\epsilon _1=0.1\), \(\epsilon _2=0.4<\epsilon _{20}=0.4529\)

Full size image
Fig. 7
figure 7

Trajectories of FONN (37) with \(q=0.97\), \(\epsilon _1=0.1\), \(\epsilon _2=0.6>\epsilon _{20}=0.4529\)

Full size image
Fig. 8
figure 8

Phase diagrams of FONN (37) with \(q=0.97\), \(\epsilon _1=0.1\), \(\epsilon _2=0.6>\epsilon _{20}=0.4529\)

Full size image

Conclusion

The issue of the bifurcations of a FONN including different leakage and communication delays has been explored. The stability domains and bifurcation results have been obtained. It has been detected that both leakage delay and communication delay have vital effects on the stability and bifurcations of the designed FONN. Once selecting a smaller leakage delay or communication delay, FONN illustrates good stability performance, if they outnumber their critical values, FONN leads to Hopf bifurcations. The excellent stability performance of FONN can be derived by modifying the size of leakage delay or communication delay. To verify the effectiveness of the derived results, two simulation examples have been provided.