The heteroclinic and codimension-4 bifurcations of a triple SD oscillator

Abstract

In this paper, the complicated heteroclinic and codimension-four bifurcations of a triple SD (smooth and discontinuous) oscillator are investigated by analyzing the bifurcation sets in three-dimensional parameter space. The structure of the transition set including the equilibrium bifurcation set and a special kind of heteroclinic orbit bifurcation set is constructed comprising of a catastrophe point of the fifth order, the catastrophe curves of third order and also the catastrophe surfaces of the first order, respectively, according to the restoring forces and also the potentials, respectively. Also, a theorem of structural stability of heteroclinic orbit in 2-dimensional Hamilton system is introduced to find the heteroclinic bifurcation set. The equilibria and the phase structures are classified and shown in details on the transition set and the enclosed structurally stable areas for smooth and discontinuous cases, respectively. The normal forms for each bifurcation surface are built up showing the complex supercritical subcritical pitchfork bifurcations and also the double saddle-node bifurcations, along with the bifurcations of homoclinic and heteroclinic orbit. Taken one of the bifurcation surfaces as an example, the complicated bifurcation is investigated by employing subharmonic Melnikov functions including Hopf, double Hopf, the closed orbit and also the homoclinic/heteroclinic bifurcations. The results presented herein this paper enriched the complex dynamic behavior for the geometrical nonlinear systems.

1 Introduction

Nonlinear oscillators [1] play an important role in both science and technology, and they have been widely applied in engineering [2,3,4], vibration control [5,6,7,8,9,10], biology [11,12,13] and electronics [14,15,16]. Some classical oscillators have been studied for over a century, such as Duffing oscillator [17] proposed in 1918, which is a traditional model to describe the hardening spring effect observed in many solid mechanical problems. Many nonlinear systems can be approximately studied with Duffing system after Taylor expansion, which is of great help in both science and engineering [18, 19]. Also, van der Pol Oscillator [20] is a classical oscillator with nonlinear damping exhibiting a limit cycle [21], which has been studied for over a long time. Chaos is first noticed by Ueda [22] in his research on Duffing oscillator with harmonic force, and a chaotic attractor is also found in a set of ordinary differential equations for fluid convection by Lorenz [23].

An archetype smooth and discontinuous oscillator comprising lumped mass and oblique springs was proposed by Cao et al. [24] in 2006 to study transition from smooth to discontinuous dynamics. This oscillator has attracted many investigations, demonstrating Hopf bifurcation under nonlinear damping [25], co-dimension two bifurcation [26], chaotic threshold [27], the transition of resonance mechanisms [28] and so on [29]. Later, the coupled SD oscillator was proposed by Han et al. [30] with two geometrical parameters exhibiting smooth and discontinuous dynamics as well, which can be regarded as a rigid coupling of two separate SD oscillators vibrating horizontally. Complicated dynamical behaviors have been demonstrated with the coupled SD oscillator, such as the chaotic phenomenon for discontinuous cases [31], buckling phenomenon and co-dimension three bifurcation [32]. In 2015, a triple SD oscillator was proposed by Han et al. [33] consisting of a horizontal spring and two oblique springs in nonlinear geometrical configuration, which exhibits multiple-well dynamics for both smooth and discontinuous cases. High-order quasi-zero stiffness [34] can be built by this triple SD oscillator due to its nonlinear geometrical configuration, which is of great value in isolation engineering [35]. However, the phase structures and dynamical behaviors of the triple SD oscillator are not classified clearly and a series of problem about the heteroclinic bifurcation and the codimension-4 bifurcation has not been studied.

The first motivation of this paper is to investigate the complicated bifurcation of the triple SD oscillator, seen from [33], with a full picture of bifurcation sets including a heteroclinic bifurcation, phase portraits and the normal forms of the codimension-4 bifurcations [36,37,38]. The second motivation is to provide a theorem of structural stability of heteroclinic orbit [39,40,41] in 2-dimensional Hamilton system to obtain the heteroclinic bifurcation set. The third motivation is to present the complicated codimension-4 bifurcations including the closed orbit bifurcation, Hopf bifurcation, double Hopf bifurcation and also the homoclinic or heteroclinic bifurcations using subharmonic Melnikov functions by taking the normal form of one of the bifurcation surfaces as an example.

This paper is organized as follows. In Sect. 2, the mathematical model is built with governing equation and the Hamiltonian. In Sect. 3, the heteroclinic bifurcation condition is obtained by introducing a theorem of structural stability of heteroclinic orbit in Hamilton system. In Sect. 4, the bifurcation sets are defined and studied, along with the complicated change of equilibria and the characteristics of restoring force, and the normal form of each bifurcation surface is built. In Sect. 5, the universal unfolding is obtained and the codimension-4 bifurcation is investigated by applying the subharmonic Melnikov function, taken one of the bifurcation surfaces as an example. Finally, the paper is closed with the summary of conclusions and the further challenges.

2 Mathematical model

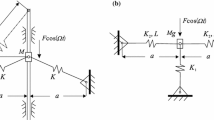
Consider a model proposed in [33] based up on the SD oscillator [24], as shown in Fig. 1, consisting of a lumped mass m, a horizontal spring and two inclined springs pinned to rigid support.

Fig. 1

Model of the triple SD oscillator [33]

Suppose the three springs are the same with stiffness k and initial length l, the horizontal distance on the left and right is c and a, respectively, and the vertical distance between the end points of the springs fixed to the rigid supports is 2b. All the springs may be pre-compressed or pre-stretched depending on the value of a, b, c and l. The governing equation of free vibration can be written as

$$\begin{aligned}&m\ddot{X}+kX\left( 1-\dfrac{l}{\sqrt{X^2+a^2}}\right) \nonumber \\&\quad +k(X+b)\left[ 1-\dfrac{l}{\sqrt{(X+b)^2+c^2}}\right] \nonumber \\&\quad +k(X-b)\left[ 1-\dfrac{l}{\sqrt{(X-b)^2+c^2}}\right] =0. \end{aligned}$$

(1)

The dimensionless form in 2-dimensional space can be obtained as shown in the following

$$\begin{aligned} {\left\{ \begin{array}{ll} x'=y, \\ y'=-f(x,\alpha ,\beta ,\gamma ), \end{array}\right. } \end{aligned}$$

(2)

where $\omega _n=\sqrt{\frac{k}{m}}$, $x=\frac{X}{l}$, $\tau =\omega _nt$, $\alpha =\frac{a}{l}$, $\beta =\frac{b}{l}$ and $\gamma =\frac{c}{l}$, and $f(x,\alpha ,\beta ,\gamma )$ is the restoring force which can be written as

$$\begin{aligned}{} & {} f(x,\alpha ,\beta ,\gamma )=3x-\dfrac{x}{\sqrt{x^2+\alpha ^2}}\nonumber \\{} & {} \quad -\dfrac{x+\beta }{\sqrt{(x+\beta )^2+\gamma ^2}}-\dfrac{x-\beta }{\sqrt{(x-\beta )^2+\gamma ^2}}, \end{aligned}$$

(3)

System (2) is a Hamilton system whose Hamiltonian is $H(x,y)=\frac{1}{2}y^2+V(x,\alpha ,\beta ,\gamma )$. $V(x,\alpha ,\beta ,\gamma )$ is the potential which can be written as

$$\begin{aligned} V(x,\alpha ,\beta ,\gamma )&=\dfrac{1}{2}\left( \sqrt{x^2+\alpha ^2}-1\right) ^2\nonumber \\&\quad +\dfrac{1}{2}\left[ \sqrt{(x+\beta )^2+\gamma ^2}-1\right] ^2\nonumber \\&\quad +\dfrac{1}{2}\left[ \sqrt{(x-\beta )^2+\gamma ^2}-1\right] ^2, \end{aligned}$$

(4)

3 Heteroclinic bifurcation of Hamilton system

The bifurcation condition of equilibriums of system (2) can be written as $f(x,\alpha ,\beta ,\gamma )=f'_x(x,\alpha ,\beta ,\gamma )=0$. Heteroclinic orbits are usually structurally unstable, but some of them remains structurally stable for special cases in Hamilton systems. A heteroclinic orbit bifurcation of this system is discovered which is independent of equilibrium change.

Consider a 2-dimensional Hamilton system

$$\begin{aligned} {\left\{ \begin{array}{ll} x'=\dfrac{\partial H}{\partial y},\\ y'=-\dfrac{\partial H}{\partial x}, \end{array}\right. } \end{aligned}$$

(5)

where the Hamiltonian $H:{\mathbb {R}}^2\times {\mathbb {R}}^k\rightarrow {\mathbb {R}}$ which can be written as $H=H(x,y,\varvec{p})$ is infinitely differentiable, which is independent of time $\tau$, and $\varvec{p}=(p_1,p_2,\cdots ,p_k)^\textrm{T}\in {\mathbb {R}}^k$ is the parameter vector. The Jacobian matrix of system (5) is

$$\begin{aligned} J=\left[ \begin{array}{ccc} \dfrac{\partial ^2H}{\partial x\partial y} &{} \dfrac{\partial ^2H}{\partial y^2} \\ -\dfrac{\partial ^2H}{\partial x^2} &{} -\dfrac{\partial ^2H}{\partial x\partial y} \end{array} \right] , \end{aligned}$$

(6)

whose eigenvalue is $\lambda _{1,2}{=}\pm \sqrt{(\dfrac{\partial ^2\,H}{\partial x\partial y})^2{-}\dfrac{\partial ^2\,H}{\partial x^2}\dfrac{\partial ^2\,H}{\partial y^2}}$.

To insure that system (5) has at least one heteroclinic orbit, it must be supposed that two saddle points with the same value of Hamiltonian exist, which indicates the condition of existence of a heteroclinic orbit as the following.

Condition 1:

$\exists (x_1,y_1), (x_2,y_2)\in {\mathbb {R}}^2$ and $\exists \varvec{p}\in {\mathbb {R}}^k$, s.t. $H(x_1,y_1,\varvec{p})-H(x_2,y_2,\varvec{p})=0$, $\dfrac{\partial H}{\partial x}\vert _{(x_l,y_l)}=\dfrac{\partial H}{\partial y}\vert _{(x_l,y_l)}=0$ and $[(\dfrac{\partial ^2\,H}{\partial x\partial y})^2-\dfrac{\partial ^2\,H}{\partial x^2}\dfrac{\partial ^2\,H}{\partial y^2}]\vert _{(x_l,y_l)}>0$, $l=1,2$.

Here, a theorem to judge the structure stability of system (5) with heteroclinic orbit is given in the following with a brief proof.

Theorem 1

Suppose condition 1 is satisfied for system (5) for a $\varvec{p}\in {\mathbb {R}}^k$, which means $(x_1,y_1)$ and $(x_2,y_2)$ are saddles connected by a heteroclinic orbit. System (5) is structurally stable if $\forall i\in \{1,2,\cdots ,k\}$, s.t. $\dfrac{\partial H}{\partial p_i}\vert _{(x_1,y_1)}-\dfrac{\partial H}{\partial p_i}\vert _{(x_2,y_2)}\equiv 0$ in a small neighborhood near $\varvec{p}$.

Proof

Assume that condition 1 is satisfied for a $\varvec{p}\in {\mathbb {R}}^k$. We take a neighborhood of $\varvec{p}$: $\varOmega _{\varvec{p}}=\{ \tilde{\varvec{p}}\vert \ \Vert \tilde{\varvec{p}}-\varvec{p}\Vert <\varepsilon , \varepsilon >0 \}$, and for simplification, it is assumed there is no equilibrium bifurcations in $\varOmega _{\varvec{p}}$. This indicates that for every $\tilde{\varvec{p}}\in \varOmega _{\varvec{p}}$, there always exists the coordinates of a pair of saddle points $x_l=x_l(\tilde{\varvec{p}})$, $y_l=y_l(\tilde{\varvec{p}})$ $(l=1,2)$ which are only dependent on parameter vector $\tilde{\varvec{p}}\in \varOmega _{\varvec{p}}$, which means

$$\begin{aligned}{} & {} \dfrac{\partial H}{\partial x}\vert _{(x_l,y_l)}=\dfrac{\partial H}{\partial y}\vert _{(x_l,y_l)}=0,\nonumber \\{} & {} \quad \left[ \left( \dfrac{\partial ^2H}{\partial x\partial y}\right) ^2-\dfrac{\partial ^2H}{\partial x^2}\dfrac{\partial ^2H}{\partial y^2}\right] \vert _{(x_l,y_l)}>0,\nonumber \\{} & {} \quad l=1,2,\ \forall \tilde{\varvec{p}}\in \varOmega _{\varvec{p}} \end{aligned}$$

(7)

Let $h(\tilde{\varvec{p}})=H(x_1(\tilde{\varvec{p}}),y_1(\tilde{\varvec{p}}),\tilde{\varvec{p}})-H(x_2(\tilde{\varvec{p}}),y_2(\tilde{\varvec{p}}),\tilde{\varvec{p}})$. Certainly we have $h(\varvec{p})=0$. System (5) with heteroclinic orbit remaining structurally stable at $\varvec{p}$ is equivalent to the fact that for every $\tilde{\varvec{p}}\in \varOmega _{\varvec{p}}$, such that $h(\tilde{\varvec{p}})=0$, which means $\nabla h(\tilde{\varvec{p}})=0$.

Considering Eq. (7), the partial derivative of $h(\tilde{\varvec{p}})$ with respect to $p_i$ can be written as

$$\begin{aligned}&\dfrac{\partial h}{\partial p_i}=\dfrac{\partial H}{\partial x}\dfrac{\partial x_1}{\partial p_i}+\dfrac{\partial H}{\partial y}\dfrac{\partial y_1}{\partial p_i}\nonumber \\&\qquad +\dfrac{\partial H}{\partial p_i}-\dfrac{\partial H}{\partial x}\dfrac{\partial x_2}{\partial p_i}-\dfrac{\partial H}{\partial y}\dfrac{\partial y_2}{\partial p_i}-\dfrac{\partial H}{\partial p_i}\nonumber \\&\quad =\dfrac{\partial H}{\partial p_i}\vert _{(x_1,y_1)}-\dfrac{\partial H}{\partial p_i}\vert _{(x_2,y_2)}\hspace{1.02cm} (i=1,2,\cdots ,k) \end{aligned}$$

(8)

Thus, Theorem 1 is proved. To understand this theorem better, two examples of heteroclinic bifurcations are shown in appendix C. $\square$

For a special kind of Hamilton system whose Hamiltonian can be written as $H(x,y,\varvec{p})=\dfrac{1}{2}y^2+V(x,\varvec{p})$, the theorem of structure stability with heteroclinic orbit can be simplified as follows:

Corollary 1

For $H(x,y,\varvec{p})=\dfrac{1}{2}y^2+V(x,\varvec{p})$, system (5) is structurally stable with heteroclinic orbit if $\exists x_1, x_2\in {\mathbb {R}}$, $\exists \varvec{p}\in {\mathbb {R}}^k$, s.t. $V(x_1,\varvec{p})-V(x_2,\varvec{p})=0$, $V'_x(x_l,\varvec{p})=0$, $V''_{xx}(x_l,\varvec{p})<0$, $l=1,2$; and $\forall i\in \{1,2,\cdots ,k\}$, s.t. $V'_{p_i}\vert _{x=x_1}-V'_{p_i}\vert _{x=x_2}\equiv 0$ in a small neighborhood near $\varvec{p}$.

For system (2), it is obvious that $V(-x,\varvec{p})=V(x,\varvec{p})$, where $\varvec{p}=(\alpha ,\beta ,\gamma )^\textrm{T}$, and there are at most three saddles.

For the case of existing two saddles $(x_l,0)$ $(l=1,2)$, considering the symmetry, we have $x_2=-x_1$ and $V'_{p_i}\vert _{x=x_1}-V'_{p_i}\vert _{x=x_2}=0$ $(p_i=\alpha ,\beta ,\gamma )$; thus, the system is structurally stable. But for the case of three saddles $(x_l,0)$ $(l=1,2,3, x_1<x_2<x_3)$, we have $x_3=-x_1$, $x_2=0$, and

$$\begin{aligned} {\left\{ \begin{array}{ll} V'_{\alpha }\vert _{x=x_l}-V'_{\alpha }\vert _{x=0}=1-\dfrac{\alpha }{\sqrt{x_l^2+\alpha ^2}},\\ V'_{\beta }\vert _{x=x_l}-V'_{\beta }\vert _{x=0}=\dfrac{2\beta }{\sqrt{\beta ^2+\gamma ^2}}-\dfrac{x_l+\beta }{\sqrt{(x_l+\beta )^2+\gamma ^2}}+\dfrac{x_l-\beta }{\sqrt{(x_l-\beta )^2+\gamma ^2}},\\ V'_{\gamma }\vert _{x=x_l}-V'_{\gamma }\vert _{x=0}=\dfrac{2\gamma }{\sqrt{\beta ^2+\gamma ^2}}-\dfrac{\gamma }{\sqrt{(x_l+\beta )^2+\gamma ^2}}-\dfrac{\gamma }{\sqrt{(x_l-\beta )^2+\gamma ^2}}, \end{array}\right. } \end{aligned}$$

(9)

where $l=1,3$. It is obvious that $V'_{\alpha }\vert _{x=x_l}-V'_{\alpha }\vert _{x=0}>0$ for every $x_l\in {\mathbb {R}}\setminus \{0\}$ and every $\alpha \in {\mathbb {R}}$. Therefore, the conclusion of heteroclinic bifurcation of system (2) can be drawn as the following.

Corollary 2

System (2) is structurally unstable with heteroclinic orbit if $\exists x_1, x_2\in {\mathbb {R}}{\setminus }\{0\}$, $\exists \varvec{p}\in {\mathbb {R}}^3$, s.t. $V(x_l,\varvec{p})-V(0,\varvec{p})=0$, $V'_x(x_l,\varvec{p})=0$, $V''_{xx}(x_l,\varvec{p})<0$, $l=1,2$, where $\varvec{p}=(\alpha ,\beta ,\gamma )^\textrm{T}$.

If the condition of Corollary 2 is satisfied, then we always have $V'_{\alpha }\vert _{x=x_l}-V'_{\alpha }\vert _{x=0}>0$, which indicates the occurring of heteroclinic bifurcation.

Fig. 2

Bifurcation sets $\varSigma$ in $(\alpha ,\beta ,\gamma )$ parameter space: a. catastrophe curves and the catastrophe point; b. bifurcation sets in front view; c. in dorsal view. (Bifurcation sets divide the $(\alpha ,\beta ,\gamma )$ plane into five persistent regions, marked $\varOmega _1$ to $\varOmega _5$, for which the corresponding phase portraits are persistent, on the boundaries $\textrm{B}_1$ to $\textrm{B}_7$, the portraits are nonpersistent)

Fig. 3

Restoring force and potential energy for $\alpha >0$ and $\gamma >0$: a. restoring force for $\textrm{P}$, $\textrm{L}_1$, $\textrm{L}_2$; b. restoring force for $\textrm{L}_3$, $\textrm{L}_4$, $\textrm{L}_5$; c. restoring force for $\textrm{B}_1$, $\textrm{B}_2$; d. restoring force for $\textrm{B}_3$, $\textrm{B}_4$; e. restoring force for $\textrm{B}_5$, $\textrm{B}_6$, $\textrm{B}_7$; (f). potential energy for $\textrm{L}_2$, $\textrm{B}_7$, $\textrm{P}$

4 Bifurcation sets and normal forms

4.1 Definition of bifurcation sets

According to Sect. 3, the bifurcation set can be obtained and written as

$$\begin{aligned} \varSigma&=\{ (\alpha ,\beta ,\gamma )\vert f(x,\alpha ,\beta ,\gamma )=f'_x(x,\alpha ,\beta ,\gamma )=0 \} \nonumber \\&\cup \{ (\alpha ,\beta ,\gamma )\vert V(x,\alpha ,\beta ,\gamma )=V(0,\alpha ,\beta ,\gamma ),\nonumber \\&\quad V'_x(x,\alpha ,\beta ,\gamma )=0, V''_{xx}(x,\alpha ,\beta ,\gamma )<0 \}, \end{aligned}$$

(10)

which can be written in the following form

$$\begin{aligned} \varSigma= & {} \textrm{B}_1\cup \textrm{B}_2\cup \textrm{B}_3\cup \textrm{B}_4\cup \textrm{B}_5\cup \textrm{B}_6\nonumber \\{} & {} \cup \textrm{B}_7\cup \textrm{L}_1\cup \textrm{L}_2 \cup \textrm{L}_3\cup \textrm{L}_4\cup \textrm{L}_5\cup \textrm{P}, \end{aligned}$$

(11)

where

$$\begin{aligned}&\textrm{B}_1=\{ (\alpha ,\beta ,\gamma )\vert C_1(\alpha ,\beta ,\gamma )>0; \exists x_1<0<x_2, \\&f(x_i)=f'(x_i)=0,i=1,2, f''(x_1)<0<f''(x_2) \},\\&\textrm{B}_2=\{ (\alpha ,\beta ,\gamma )\vert C_1(\alpha ,\beta ,\gamma )=0;\\&C_3(\alpha ,\beta ,\gamma )>0;\exists x>0, f(x)<0 \},\\&\textrm{B}_3=\{ (\alpha ,\beta ,\gamma )\vert C_1(\alpha ,\beta ,\gamma )<0; \exists x_1<0<x_2, \\&f(x_i)=f'(x_i)=0,i=1,2, f''(x_1)<0<f''(x_2) \},\\&\textrm{B}_4=\{ (\alpha ,\beta ,\gamma )\vert C_1(\alpha ,\beta ,\gamma )=0;\\&C_3(\alpha ,\beta ,\gamma )>0;\forall x>0, f(x)>0 \},\\&\textrm{B}_5=\{ (\alpha ,\beta ,\gamma )\vert C_1(\alpha ,\beta ,\gamma )<0; \exists x_1<0<x_2,\\&f(x_i)=f'(x_i)=0,i=1,2, f''(x_1)>0>f''(x_2) \},\\&\textrm{B}_6=\{ (\alpha ,\beta ,\gamma )\vert C_1(\alpha ,\beta ,\gamma )=0; C_3(\alpha ,\beta ,\gamma )<0 \},\\&\textrm{B}_7=\{ (\alpha ,\beta ,\gamma )\vert C_1(\alpha ,\beta ,\gamma )<0; \exists x_i, \\&V(x_i)=V(0), V'(x_i)=0, V''(x_i)<0,i=1,2 \}, \end{aligned}$$

are all bifurcation surfaces of the first order,

$$\begin{aligned}&\textrm{L}_1=\{ (\alpha ,\beta ,\gamma )\vert C_1(\alpha ,\beta ,\gamma )<0; \exists x_i, \\&f(x_i)=f'(x_i)=f''(x_i)=0,i=1,2 \},\\&\textrm{L}_2=\{ (\alpha ,\beta ,\gamma )\vert C_1(\alpha ,\beta ,\gamma )<0; \exists x_1<0<x_2, \\&V(x_i)=V(0), f(x_i)=f'(x_i)=0,i=1,2 \},\\&\textrm{L}_3=\{ (\alpha ,\beta ,\gamma )\vert C_1(\alpha ,\beta ,\gamma )=0;\\&C_3(\alpha ,\beta ,\gamma )=0;C_5(\alpha ,\beta ,\gamma )<0 \},\\&\textrm{L}_4=\{ (\alpha ,\beta ,\gamma )\vert C_1(\alpha ,\beta ,\gamma )=0; \exists x_1<0<x_2, \\&f(x_i)=f'(x_i)=0,i=1,2, f''(x_1)<0<f''(x_2) \},\\&\textrm{L}_5=\{ (\alpha ,\beta ,\gamma )\vert C_1(\alpha ,\beta ,\gamma )=0;\\&C_3(\alpha ,\beta ,\gamma )=0;C_5(\alpha ,\beta ,\gamma )>0 \}, \end{aligned}$$

are all catastrophe curves of the third order, and

$$\begin{aligned}&\textrm{P}=\{ (\alpha ,\beta ,\gamma )\vert C_1(\alpha ,\beta ,\gamma )=0;C_3(\alpha ,\beta ,\gamma )=0;\\&C_5(\alpha ,\beta ,\gamma )=0 \}\approx (0.69967,0.48105,0.57721), \end{aligned}$$

is the catastrophe point of the fifth order, where $C_i(\alpha ,\beta ,\gamma )=\frac{f^{(i)}_x(0,\alpha ,\beta ,\gamma )}{i!}$ ($i=1,3,5$) is the Taylor expansion coefficient of the restoring force, which can be obtained as

Table 1 Equilibriums and stability of each set and each area, $x_i, (i=1,2,3)$ has no analytical solution and $0<x_1<x_2<x_3$

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}C_1(\alpha ,\beta ,\gamma )=3-\dfrac{1}{\alpha }-\dfrac{2\gamma ^2}{(\beta ^2+\gamma ^2)^\frac{3}{2}},\\ &{}C_3(\alpha ,\beta ,\gamma )=\dfrac{1}{2\alpha ^3}-\dfrac{\gamma ^2(4\beta ^2-\gamma ^2)}{(\beta ^2+\gamma ^2)^\frac{7}{2}},\\ &{}C_5(\alpha ,\beta ,\gamma )=-\dfrac{3}{8\alpha ^5}-\dfrac{3\gamma ^2(8\beta ^4-12\beta ^2\gamma ^2+\gamma ^4)}{4(\beta ^2+\gamma ^2)^\frac{11}{2}}. \end{array}\right. }\end{aligned}$$

(12)

It is worth noticing that set $\textrm{B}_3$ is divided into $\textrm{B}_{3-1}$ and $\textrm{B}_{3-2}$ by set $\textrm{B}_7$, which is

$$\begin{aligned}&\textrm{B}_{3-1}=\{ (\alpha ,\beta ,\gamma )\vert (\alpha ,\beta ,\gamma )\in \textrm{B}_3; V(x_i)>V(0),\\&f(x_i)=f'(x_i)=0,i=1,2 \}\\&\textrm{B}_{3-2}=\{ (\alpha ,\beta ,\gamma )\vert (\alpha ,\beta ,\gamma )\in \textrm{B}_3; V(x_i)<V(0),\\&f(x_i)=f'(x_i)=0,i=1,2 \}. \end{aligned}$$

4.2 Structure of bifurcation sets

The bifurcation surfaces $\textrm{B}_i$, catastrophe curves $\textrm{L}_j$ and the catastrophe point P satisfy

$$\begin{aligned} {\left\{ \begin{array}{ll} \textrm{L}_1=\partial \textrm{B}_3\cap \partial \textrm{B}_5\setminus \textrm{P}, \textrm{L}_2=\textrm{B}_3\cap \partial \textrm{B}_7\setminus \textrm{P},\\ \textrm{L}_3=\partial \textrm{B}_2\cap \partial \textrm{B}_6\setminus \textrm{P}=\partial \textrm{B}_5\cap \partial \textrm{B}_7\setminus \textrm{P}, \\ \textrm{L}_4=\partial \textrm{B}_1\cap \partial \textrm{B}_3\setminus \textrm{P}=\partial \textrm{B}_2\cap \partial \textrm{B}_4\setminus \textrm{P},\\ \textrm{L}_5=\partial \textrm{B}_4 \cap \partial \textrm{B}_6\setminus \textrm{P}=\partial \textrm{B}_1\cap \partial \textrm{B}_4\setminus \textrm{P}, \\ \textrm{P}=\partial \textrm{L}_i\cap \partial \textrm{L}_j\quad (i\ne j). \end{array}\right. } \end{aligned}$$

(13)

where $\partial \textrm{B}_i$ and $\partial \textrm{L}_j$ represent the boundary of $\textrm{B}_i$ and $\textrm{L}_j$, respectively.

The important property shown in Eq. (13), which is proved in appendix B, indicates the structure of the bifurcation set $\varSigma$, as shown in Fig. 2 to provide a better understanding. The set $\varSigma$ bifurcates at the catastrophe point $\textrm{P}\approx (0.69967,0.48105,0.57721)$ of the fifth order into five catastrophe curves $\textrm{L}_1\sim \textrm{L}_5$ of the third order and then into seven bifurcation surfaces $\textrm{B}_1\sim \textrm{B}_7$ of the first order. The surfaces are connected by the catastrophe curves: curve $\textrm{L}_1$ connects $\textrm{B}_3$ and $\textrm{B}_5$; $\textrm{L}_2$ connects $\textrm{B}_3$ and $\textrm{B}_7$; $\textrm{L}_3$ connects $\textrm{B}_2$, $\textrm{B}_5$, $\textrm{B}_6$ and $\textrm{B}_7$; $\textrm{L}_4$ connects $\textrm{B}_1$, $\textrm{B}_2$, $\textrm{B}_3$ and $\textrm{B}_4$; also, curve $\textrm{L}_5$ connects $\textrm{B}_1$, $\textrm{B}_4$ and $\textrm{B}_6$. The system exhibits different topological structure or dynamical behavior on each bifurcation surface and each catastrophe.

For $\alpha >0$ and $\gamma >0$, the system shows continuous dynamics (discontinuous cases are shown in appendix A) and the $\alpha$-$\beta$-$\gamma$ parameter space is divided into five areas named $\varOmega _1$ to $\varOmega _5$ by the bifurcation sets, as shown in Fig. 2b and Fig. 2c from the front view and dorsal view, respectively.

The restoring force f(x) corresponding to the catastrophe point, the catastrophe curves and the bifurcation surfaces is plotted in Fig. 3. The restoring force f(x) for $\textrm{L}_2$, $\textrm{L}_4$, $\textrm{B}_1$, $\textrm{B}_3$ and $\textrm{B}_5$ is all tangent to x-axis as there exists $x_i (i=1,2)$ that $f(x_i)=f'(x_i)=0,f''(x_i)\ne 0$, and the restoring force for $\textrm{P}$, $\textrm{L}_1$, $\textrm{L}_3$, $\textrm{L}_4$, $\textrm{B}_2$ and $\textrm{B}_4$ exhibits stable quasi-zero stiffness, while the restoring force for $\textrm{L}_5$ and $\textrm{B}_6$ exhibits unstable quasi-zero stiffness. This quasi-zero stiffness characteristics is of great value in isolation engineering.

The equilibriums and their stability of this system corresponding to each set and each area are shown in Table 1, which complicatedly changes as the varying of the three parameters, and the analytical solution cannot be obtained. The phase portraits corresponding to each set and each area are plotted in appendix A for different values of the Hamiltonian $H(x,y)=E$.

Fig. 4

Bifurcation diagrams for smooth cases: a. bifurcation diagram for x versus $\beta$ for $\alpha =0.2$ and $\gamma =0.1$; b. bifurcation diagram for x versus $\alpha$ for $\beta =0.764$ and $\gamma =0.1$; c. bifurcation diagram for x versus $\gamma$ for $\alpha =0.85$ and $\beta =0.35$

It is worth noticing that some high-order degenerated points are found as the varying of the three geometrical parameters, such as a 5th-order degenerated center at point $\textrm{P}$, a 3rd-order degenerated center at curve $\textrm{L}_5$ and a 1st-order degenerated center at the bifurcation surface $\textrm{B}_4$, which can be applied in engineering isolation. A pair of 1st-order degenerated center is found at curve $\textrm{L}_1$, curve $\textrm{L}_4$ and surface $\textrm{B}_2$. Meanwhile, a 3rd-order tangent saddle and a 1st-order tangent saddle are found at curve $\textrm{L}_3$ and surface $\textrm{B}_6$, respectively.

Multiple-well dynamics is also found on this system, such as a single well around by heteroclinic at $\textrm{L}_4$ and $\textrm{B}_1$, a double well at $\textrm{L}_1$, $\textrm{L}_2$, $\textrm{L}_5$, $\textrm{B}_6$ and $\varOmega _3$, triple well at $\varOmega _2$ and quadruple well at $\textrm{B}_7$.

4.3 Normal forms of bifurcation surfaces

The bifurcation diagrams for x versus $\beta$, $\alpha$ and $\gamma$ with fixed $(\alpha ,\gamma )$, $(\beta ,\gamma )$ and $(\alpha ,\beta )$ are plotted in Fig. 4a, b and c, respectively, from which the type of bifurcation of each surface can be classified clearly. $\textrm{B}_2$ and $\textrm{B}_4$ are supercritical pitchfork bifurcation surfaces across which a stable center bifurcates into a pair of stable centers and an unstable saddle, changing through a degenerated center. But $\textrm{B}_6$ is subcritical pitchfork bifurcation surface across which an unstable saddle bifurcates into a pair of unstable saddles and a stable center, changing through a tangent saddle. $\textrm{B}_1$, $\textrm{B}_3$ and $\textrm{B}_5$ are sets of double saddle-node bifurcation across which a pair of stable centers and a pair of unstable saddles appear, changing through a pair of cuspidal saddles. $\textrm{B}_7$ is the set of heteroclinic bifurcation independent to equilibrium bifurcations.

Table 2 Normal forms corresponding to the bifurcation surfaces

The normal form of each bifurcation surface is shown in Table 2, along with the local bifurcation diagram and the changing of homoclinic or heteroclinic orbits. A pair of homoclinic orbits appears across the supercritical pitchfolk bifurcation set $\textrm{B}_2$ and $\textrm{B}_4$, and a heteroclinic orbit appears across the subcritical pitchfolk bifurcation set $\textrm{B}_6$. The saddle-node bifurcation sets $\textrm{B}_1$ and $\textrm{B}_{3-1}$ lead to a cuspidal heteroclinic orbit and the appearance of a pair of homoclinic orbits, but a cuspidal homoclinic orbit and the appearance of homoclinic orbits are led by saddle-center bifurcation set $\textrm{B}_{3-2}$ and $\textrm{B}_5$.

5 Codimension-4 bifurcations

5.1 Universal unfolding and Subharmonic Melnikov function

The system can be written in the following form after Taylor expansion

$$\begin{aligned} {\left\{ \begin{array}{ll} x'=y, \\ y'=-c_1(\alpha ,\beta ,\gamma )x-c_3(\alpha ,\beta ,\gamma )x^3\\ \qquad -c_5(\alpha ,\beta ,\gamma )x^5-c_7(\alpha ,\beta ,\gamma )x^7, \end{array}\right. } \end{aligned}$$

(14)

where $c_i(\alpha ,\beta ,\gamma )\ (i=1,3,5,7)$ is the coefficient of Taylor series of the restoring force.

We assume that the system is perturbed by a general van der Pol nonlinear damping, which leads to the forced dissipative oscillator as follows

$$\begin{aligned} {\left\{ \begin{array}{ll} x'=y, \\ y'=-(\xi +\eta x^2+\zeta x^4+\nu x^6)y-c_1(\alpha ,\beta ,\gamma )x-c_3(\alpha ,\beta ,\gamma )x^3\\ \qquad -c_5(\alpha ,\beta ,\gamma )x^5-c_7(\alpha ,\beta ,\gamma )x^7. \end{array}\right. } \end{aligned}$$

(15)

System (15) is the universal unfolding of system (14) which will be proved in another work. This system exhibits unfolded dynamics of three parameter codimension-four. Assuming $c_7(\alpha ,\beta ,\gamma )>0$ and applying the scale transformation

$$\begin{aligned} x\rightarrow \dfrac{c_7^\frac{1}{6}}{\nu ^\frac{1}{3}}x,\quad \tau \rightarrow \dfrac{\nu }{c_7}\tau , \end{aligned}$$

a system equivalent to the nonlinear damped triple SD oscillator is obtained as follows

$$\begin{aligned} {\left\{ \begin{array}{ll} x'=y, \\ y'=\mu _1x+\mu _2x^3+\mu _3x^5+\mu _4y\\ \qquad +\mu _5x^2y+\mu _6x^4y-x^7-x^6y, \end{array}\right. } \end{aligned}$$

(16)

where $\mu _1=-\nu ^2c_1c_7^{-2}$, $\mu _2=-\nu ^\frac{4}{3}c_3c_7^{-\frac{5}{3}}$, $\mu _3=-\nu ^\frac{2}{3}c_5c_7^{-\frac{4}{3}}$, $\mu _4=-\frac{\xi \nu }{c_7}$, $\mu _5=-\frac{\eta \nu ^\frac{1}{3}}{c_7^\frac{2}{3}}$ and $\mu _6=-\frac{\zeta }{\nu ^\frac{1}{3}c_7^\frac{1}{3}}$.

In order to study the global bifurcations for the corresponding homoclinic and heteroclinic orbits for three-parameter codimension-four bifurcation, a scale transformation is introduced as shown in the following

$$\begin{aligned} (x,y)\rightarrow (\delta ^{n-1}x,\delta ^ny),\quad \tau \rightarrow \dfrac{1}{\delta }\tau . \end{aligned}$$

And let $\mu _1=\textrm{sgn}\mu _1\delta ^2$, $\mu _2=-\delta ^{4-2n}\varepsilon _1$, $\mu _3=-\delta ^{6-4n}\varepsilon _2$, $\mu _4=\delta ^2\varepsilon _3$, $\mu _5=\delta ^{4-2n}\varepsilon _4$ and $\mu _6=\delta ^{6-4n}\varepsilon _5$, system (16) can be led to

$$\begin{aligned} {\left\{ \begin{array}{ll} x'=y, \\ y'=\textrm{sgn}\mu _1x-\varepsilon _1x^3-\varepsilon _2x^5-x^7\\ \qquad +\delta (\varepsilon _3+\varepsilon _4x^2+\varepsilon _5x^4-x^6)y, \end{array}\right. } \end{aligned}$$

(17)

while $n=\frac{4}{3}$.

For $\delta =0$, system (17) is a Hamilton system

$$\begin{aligned} {\left\{ \begin{array}{ll} x'=y, \\ y'=\textrm{sgn}\mu _1x-\varepsilon _1x^3-\varepsilon _2x^5-x^7, \end{array}\right. } \end{aligned}$$

(18)

whose Hamiltonian function can be obtained as

$$\begin{aligned} H(x,y)=\dfrac{1}{2}y^2-\dfrac{\textrm{sgn}\mu _1}{2}x^2+\dfrac{\varepsilon _1}{4}x^4 +\dfrac{\varepsilon _2}{6}x^6+\dfrac{1}{8}x^8.\nonumber \\ \end{aligned}$$

(19)

The number of limit cycles of system (17) is related to the number of zero points of the subharmonic Melnikov function which can be obtained as follows

$$\begin{aligned} M(h)&=\int _{0}^{T}y^2(\tau )[\varepsilon _3+\varepsilon _4x^2(\tau )+\varepsilon _5x^4(\tau )-x^6(\tau )]\textrm{d}\tau \nonumber \\&=\int _{\varGamma (h)}y(\varepsilon _3+\varepsilon _4x^2+\varepsilon _5x^4-x^6)\textrm{d}x, \end{aligned}$$

(20)

where $\varGamma (h)=\{(x,y)\vert H(x,y)=h\}$ and T is the period of curve $\varGamma (h)$.

It is clear that the above subharmonic Melnikov function can be used to deprive all the bifurcations corresponding to the normal forms in Table 1. For example, when $\varepsilon _1>0$ and $\varepsilon _2<-2\sqrt{\varepsilon _1}$, for $\textrm{B}_2$, when $\mu _1>0$, $\varepsilon _1=\epsilon _1-\lambda$ and $\varepsilon _2=\epsilon _2$, for $\textrm{B}_{3-1}$ and $\textrm{B}_{3-2}$, and also the complicated bifurcation corresponding to normal form of $\textrm{B}_5$ and $\textrm{B}_7$ can be shown if the parameters $\mu _1>0$, $\varepsilon _1=\epsilon _1+\lambda$ and $\varepsilon _2=\epsilon _2$ are taken.

Due to the limited space, only the codimension bifurcations for $\textrm{B}_2$ are presented in the following parts, that is, $\varepsilon _1>0$ and $\varepsilon _2<-2\sqrt{\varepsilon _1}$. For the convenience, $\mu _1\in {\mathbb {R}}$ is assumed and $\varepsilon _1=5.5, \varepsilon _2=-5$ is taken in the following analysis.

For $\mu _1<0$, $\varGamma (h)$ is classified to three types of periodic orbits as shown in Fig. 5a: $\varGamma _1(h)$ for $0<h<h_2$, $\varGamma _2(h)$ for $h_1<h<h_2$ and $\varGamma _3(h)$ for $h>h_2$, while $\varGamma (h_2)$ is the homo-heteroclinic orbits. $h_1\approx 1.47881$ and $h_2\approx 1.83333$ are the potential energy at the equilibriums of system (18) for $\mu _1<0$.

For $\mu _1>0$, $\varGamma (h)$ is classified to four types of periodic orbits as shown in Fig. 5c: $\varGamma _4(h)$ for $h_3<h<h_4$, $\varGamma _5(h)$ for $h_4<h<0$, $\varGamma _6(h)$ for $0<h<h_5$ and $\varGamma _7(h)$ for $h>h_5$, while $\varGamma (0)$ is the double-homoclinic orbits and $\varGamma (h_5)$ is the homo-heteroclinic orbits. $h_3\approx -1.87814$, $h_4\approx -0.05206$ and $h_5\approx 0.20104$ are the potential energy at the equilibriums of system (18) for $\mu _1>0$.

For $\mu _1=0$, $\varGamma (h)$ is classified to three types of periodic orbits as shown in Fig. 5b: $\varGamma _8(h)$ for $0<h<h_7$, $\varGamma _9(h)$ for $h_6<h<h_7$ and $\varGamma _{10}(h)$ for $h>h_7$, while $\varGamma (h_7)$ is the homo-heteroclinic orbits. $h_6\approx -0.15585$ and $h_7\approx 0.92668$ are the potential energy at the equilibriums of system (18) for $\mu _1=0$.

Let

$$\begin{aligned} I_n^i(h)=\int _{\varGamma _i(h)}x^{2n}y\textrm{d}x,\ P_n^i(h)=\frac{I_n^i(h)}{I_0^i(h)}, \end{aligned}$$

and $p_i(h)=P_3^i(h)-\varepsilon _5P_2^i(h)-\varepsilon _4P_1^i(h)$. The zero points of function M(h) can be regarded as the intersections of curve $p=p_i(h)$ and line $p=\varepsilon _3$.

Fig. 5

Different types of orbit $\varGamma (h)=\{(x,y)\vert H(x,y)=h\}$ of system (18) for $\varepsilon _1=5.5, \varepsilon _2=-5$: a. $\mu _1<0$; b. $\mu _1=0$; c. $\mu _1>0$

5.2 Jacobian matrix and eigenvalues

To classify the equilibriums, the Jacobian matrix of system (17) is obtained as follows

$$\begin{aligned} J=\begin{bmatrix} 0 &{} 1 \\ -f'(x_i) &{} \delta (\varepsilon _3+\varepsilon _4x_i^2+\varepsilon _5x_i^4-x_i^6) \end{bmatrix}, \end{aligned}$$

(21)

where $f'(x)=-\textrm{sgn}\mu _1+3\varepsilon _1x^2+5\varepsilon _2x^4+7x^6$ is the stiffness and $(x_i,0)$ is one of the equilibriums. The eigenvalues can be written as

$$\begin{aligned} \lambda _{1,2}= & {} \dfrac{1}{2}[\delta (\varepsilon _3+\varepsilon _4x_i^2+\varepsilon _5x_i^4-x_i^6)\nonumber \\{} & {} \pm \sqrt{\delta ^2(\varepsilon _3+\varepsilon _4x_i^2+\varepsilon _5x_i^4-x_i^6)^2-4f'(x_i)}]. \end{aligned}$$

(22)

For the equilibrium $(x_i,0)$ being saddle point ($f'(x_i)<0$) without perturbation ($\delta =0$), the eigenvalues $\lambda _{1,2}$ under perturbation ($\delta >0$) are a pair of real numbers being positive and negative, respectively, implying that $(x_i,0)$ for $f'(x_i)<0$ is always a saddle point for every $\varepsilon _3$, $\varepsilon _4$ and $\varepsilon _5$.

For the equilibrium $(x_i,0)$ being center point ($f'(x_i)>0$) without perturbation ($\delta =0$), the conclusion is more complicated under perturbation ($\delta >0$). $(x_i,0)$ is stable node when $\varepsilon _3<-\frac{2\sqrt{f'(x_i)}}{\delta }-\varepsilon _4x_i^2-\varepsilon _5x_i^4+x_i^6$, stable degenerated node when $\varepsilon _3=-\frac{2\sqrt{f'(x_i)}}{\delta }-\varepsilon _4x_i^2-\varepsilon _5x_i^4+x_i^6$, stable focus when $-\frac{2\sqrt{f'(x_i)}}{\delta }-\varepsilon _4x_i^2-\varepsilon _5x_i^4+x_i^6<\varepsilon _3<-\varepsilon _4x_i^2-\varepsilon _5x_i^4+x_i^6$, center point when $\varepsilon _3=-\varepsilon _4x_i^2-\varepsilon _5x_i^4+x_i^6$, unstable focus when $-\varepsilon _4x_i^2-\varepsilon _5x_i^4+x_i^6<\varepsilon _3<\frac{2\sqrt{f'(x_i)}}{\delta }-\varepsilon _4x_i^2-\varepsilon _5x_i^4+x_i^6$, unstable degenerated node $\varepsilon _3=\frac{2\sqrt{f'(x_i)}}{\delta }-\varepsilon _4x_i^2-\varepsilon _5x_i^4+x_i^6$, unstable node $\varepsilon _3>\frac{2\sqrt{f'(x_i)}}{\delta }-\varepsilon _4x_i^2-\varepsilon _5x_i^4+x_i^6$.

5.3 Codimension-4 bifurcations

For the next analysis, it is assumed that $\varepsilon _1=5.5, \varepsilon _2=-5$, $\varepsilon _4=-1$, $\varepsilon _5=3.6$ and $\delta =0.4$.

5.3.1 Equilibrium change

For $\mu _1<0$, equilibrium $(\pm 1.41421,0)$ is a pair of saddles for every $\varepsilon _3$, while equilibriums (0, 0) and $(\pm 1.77716,0)$ are listed in Table 3 for different $\varepsilon _3$. For $\mu _1>0$, equilibriums (0, 0) and $(\pm 1.12104,0)$ are saddles for every $\varepsilon _3$, while equilibriums $(\pm 0.47565,0)$ and $(\pm 1.87537,0)$ are listed in Table 4 for different $\varepsilon _3$.

Table 3 Equilibrium change for $\mu _1<0$

Table 4 Equilibrium change for $\mu _1>0$

5.3.2 Limit cycle bifurcations

Fig. 6

a. The curve of function p(h) for $\mu _1<0$; b. the curve of function p(h) for $\mu _1>0$; c. detail of the gray box in figure b; d. the curve of function p(h) for $\mu _1=0$

The curves of $p_i(h)$ for both $\mu _1>0$, $\mu _1<0$ and $\mu _1=0$ are calculated by numerical integration method and shown in Fig. 6 and the bifurcation diagram on $\mu _1-\mu _4$ plane can be obtained by using the transformation $\mu _1=\textrm{sgn}\mu _1\delta ^2,\ \mu _4=\delta ^2\varepsilon _3$. The bifurcation sets shown in Fig. 7a can be described as follows:

$$\begin{aligned}&\textrm{B}_\textrm{I}=\{\mu _4=c_1\mu _1,\mu _1<0\},\\&\textrm{H}_1=\{\mu _4=c_2\mu _1,\mu _1<0\},\\&\textrm{HL}_\textrm{I}=\{\mu _4=c_3\mu _1,\mu _1<0\},\\&\textrm{HL}_\textrm{II}=\{\mu _4=c_4\mu _1,\mu _1<0\},\\&\textrm{B}_\textrm{II}=\{\mu _4=c_5\mu _1,\mu _1<0\},\\&\textrm{H}_\textrm{2I}=\{\mu _4=c_6\mu _1,\mu _1<0\},\\&\textrm{HL}_\textrm{III}=\{\mu _4=c_7\mu _1,\mu _1<0\},\\&\textrm{H}_\textrm{2II}=\{\mu _4=c_8\mu _1,\mu _1>0\},\\&\textrm{HL}_\textrm{IV}=\{\mu _4=c_9\mu _1,\mu _1>0\}, \\&\textrm{HL}_\textrm{V}=\{\mu _4=c_{10}\mu _1,\mu _1>0\},\\&\textrm{B}_\textrm{III}=\{\mu _4=c_{11}\mu _1,\mu _1>0\},\\&\textrm{H}_\textrm{2III}=\{\mu _4=c_{12}\mu _1,\mu _1>0\},\\&\textrm{HL}_\textrm{VI}=\{\mu _4=c_{13}\mu _1,\mu _1>0\},\\&\textrm{HL}_\textrm{VII}=\{\mu _4=c_{14}\mu _1,\mu _1>0\}, \end{aligned}$$

where $c_1\approx 0.03737$, $c_2=0$, $c_3\approx -0.50463$, $c_4\approx -0.84214$, $c_5\approx -0.95882$, $c_6\approx -1.242$, $c_7\approx -1.93395$, $c_8\approx 2.5$, $c_9\approx 0.82500$, $c_{10}\approx 0.33091$,$c_{11}\approx 0.17889$, $c_{12}\approx 0.056$, $c_{13}\approx 0.01413$ and $c_{14}\approx -0.21213$. The bifurcation sets divide the $\mu _1-\mu _4$ plane into sixteen areas, named I to XVI.

Fig. 7

a. bifurcation diagram on $\mu _1-\mu _4$ plane; b. detail of the gray box in figure a, the bifurcation for $\mu _1=0$ for detail

Fig. 8

Phase portraits of system (17) for $\mu _1<0$, $\varepsilon _1=5.5$, $\varepsilon _2=-5$, $\varepsilon _4=-1$ and $\varepsilon _5=3.6$ ($\delta =0.4$, green points represent equilibrium points and red lines represent limit cycles)

It is worth noticing that the limit cycle bifurcation also happens while $\mu _1\equiv 0$, dividing line $\mu _1=0$ into eight parts, which can be described as the following:

$$\begin{aligned} \textrm{O}_\textrm{I}&=\{\mu _4>\delta ^2b_1,\mu _1=0\},\\ \textrm{L}_1&=\{\delta ^2b_2<\mu _4<\delta ^2b_1,\mu _1=0\},\\ \textrm{L}_2&=\{\delta ^2b_3<\mu _4<\delta ^2b_2,\mu _1=0\},\\ \textrm{L}_3&=\{\delta ^2b_4<\mu _4<\delta ^2b_3,\mu _1=0\},\\ \textrm{L}_4&=\{\delta ^2b_5<\mu _4<\delta ^2b_4,\mu _1=0\},\\ \textrm{L}_5&=\{\delta ^2b_6<\mu _4<\delta ^2b_5,\mu _1=0\},\\ \textrm{L}_6&=\{\delta ^2b_7<\mu _4<\delta ^2b_6,\mu _1=0\},\\ \textrm{O}_\textrm{II}&=\{\mu _4<\delta ^2b_7,\mu _1=0\}, \end{aligned}$$

where $b_1\approx 0.71441$, $b_2=0.03832$, $b_3\approx 0$, $b_4\approx -0.34552$, $b_5\approx -0.43164$, $b_6\approx -0.46325$ and $b_7\approx -0.59598$.

As shown in Fig. 5, $\varGamma _1$, $\varGamma _3$, $\varGamma _6$, $\varGamma _7$, $\varGamma _8$ and $\varGamma _{10}$ all represent a single periodic orbit for a constant h, so each intersection of $p=\varepsilon _3$ and $p=p_i(h)\ (i=1,3,6,7,8,10)$ corresponds to a single limit cycle. Similarly, each intersection of $p=\varepsilon _3$ and $p=p_i(h)\ (i=2,4,5,9)$ corresponds to a pair of limit cycles because $\varGamma _2$, $\varGamma _4$, $\varGamma _5$ and $\varGamma _9$ all represent a pair of periodic orbits. $\varGamma (h_2)$ for $\mu _1<0$, $\varGamma (0)$ and $\varGamma (h_5)$ for $\mu _1>0$, $\varGamma (h_7)$ for $\mu _1=0$ are all homoclinic or heteroclinic orbits, implying that $p_i(h_2)$ for $\mu _1<0$, $p_i(0)$, $p_i(h_5)$ for $\mu _1>0$ and $p_i(h_7)$ for $\mu _1>0$ correspond to homoclinic or heteroclinic bifurcation. Thus, the conclusion can be drawn as the following:

(1) closed orbit bifurcation set: $\textrm{B}_{I}$, $\textrm{B}_{II}$, $\textrm{B}_{III}$($\varepsilon _3=c_1,c_5,c_{11}$), where a semi-stable limit cycle bifurcates into a stable one and an unstable one;

(2) Hopf bifurcation set: $\textrm{H}_1$($\varepsilon _3=c_2$);

(3) double Hopf bifurcation set: $\textrm{H}_{2I}$, $\textrm{H}_{2II}$, $\textrm{H}_{2III}$($\varepsilon _3=c_6,c_8,c_{12}$);

(4) homoclinic or heteroclinic bifurcation set: $\textrm{HL}_{I}$, $\textrm{HL}_{II}$, $\textrm{HL}_{III}$, $\textrm{HL}_{IV}$, $\textrm{HL}_{V}$, $\textrm{HL}_{VI}$, $\textrm{HL}_{VII}$($\varepsilon _3=c_3,c_4,c_7,c_9,c_{10},c_{13},c_{14}$), where limit cycle turns into homoclinic or heteroclinic orbit;

(5) supercritical pitchfolk equilibrium bifurcation set: $\textrm{O}_I$, $\textrm{O}_{II}$.

The phase portraits are shown in Fig. 8, 9 and 10 for $\mu _1<0$, $\mu _1=0$ and $\mu _1>0$, respectively, corresponding to each area and each bifurcation set in Fig. 7.

Fig. 9

Phase portraits of system (17) for $\mu _1=0$, $\varepsilon _1=5.5$, $\varepsilon _2=-5$, $\varepsilon _4=-1$ and $\varepsilon _5=3.6$ ($\delta =0.4$, green points represent equilibrium points and red lines represent limit cycles)

Fig. 10

Phase portraits of system (17) for $\mu _1>0$, $\varepsilon _1=5.5$, $\varepsilon _2=-5$, $\varepsilon _4=-1$ and $\varepsilon _5=3.6$ ($\delta =0.4$, green points represent equilibrium points and red lines represent limit cycles)

6 Conclusion and discussions

The complicated bifurcations of a nonlinear oscillator consisting of a horizontal spring and two oblique springs in nonlinear geometrical configuration governed by three geometrical parameters have been studied in this paper. The bifurcation sets have been defined according to the characteristics of restoring force and potential, including bifurcation surfaces, catastrophe curves of the first and third order, and also a catastrophe point of the fifth order. A special kind of heteroclinic bifurcation of this oscillator is discovered by investigating the structural stability of heteroclinic orbits in Hamilton system. The phase portraits, multiple-well potential energy and force-displacement characteristics have been investigated, demonstrating high-order singulars and multiple-well dynamics. Complex bifurcations have been demonstrated in smooth region with the normal form of each bifurcation surface, classified as supercritical pitchfolk bifurcation, subcritical pitchfolk bifurcation and double saddle-center bifurcation. Subharmonic Melnikov function has been employed to detect the complicated bifurcations of limit cycles including closed orbit bifurcation, Hopf bifurcation, double Hopf bifurcation and homoclinic or heteroclinic bifurcations, taken bifurcation surface $\textrm{B}_2$ as an example. The codimension-4 bifurcation of the triple SD oscillator corresponding to other normal forms will be investigated in another paper. Also, further researches can be undertaken to analyze for the complicated behaviors of this oscillator such as resonant behaviors [42, 43] and the chaotic behaviors [44,45,46] under the external perturbations as well.

Appendices

Phase structures

1.1 Smooth cases

Phase portraits of smooth case for $\alpha >0$ and $\gamma >0$ are plotted in Fig. 11. Orange lines represent small periodic orbits, green and blue lines represent large periodic orbits which encircle heteroclinic or homoclinic orbits, and black lines represent heteroclinic or homoclinic orbits.

Fig. 11

Phase portraits for $\alpha >0$ and $\gamma >0$ with a catastrophe point, 5 catastrophe curves, 7 bifurcation surfaces and 5 areas (The value of parameters and the belonged set are shown in each figure legend)

Fig. 12

Bifurcation diagrams for $\alpha =0$: a. equilibrium bifurcation surfaces; b. bifurcation sets on $\beta$-$\gamma$ plane. (Bifurcation sets divide the $(\beta ,\gamma )$ plane into three persistent regions, marked $\varOmega _3$, $\varOmega _4$ and $\varOmega _5$, for which the corresponding phase portraits are persistent, on the boundaries $\textrm{B}_{3-1}$, $\textrm{B}_{3-2}$, $\textrm{B}_5$ $\textrm{B}_7$, the portraits are nonpersistent)

1.2 Discontinuous cases

For $\alpha =0$ and $\gamma >0$, only $x=0$ is discontinuous. The restoring force can be written as $f(x,0,\beta ,\gamma )=3x-\textrm{sgn}x-\dfrac{x+\beta }{\sqrt{(x+\beta )^2+\gamma ^2}}-\dfrac{x-\beta }{\sqrt{(x-\beta )^2+\gamma ^2}}$. The bifurcation diagram along with the bifurcation sets is shown in Fig. 12. And the phase portraits corresponding to each set and each area are shown in Fig. 13.

Fig. 13

Phase portraits for $\alpha =0$ (The value of parameters and the belonged set are shown in each figure legend)

For $\alpha >0$, $\beta >0$ and $\gamma =0$, $x=\beta$ and $x=-\beta$ are discontinuous. The restoring force can be written as $f(x,\alpha ,\beta ,0)=-\dfrac{x}{\sqrt{x^2+\alpha ^2}}-\textrm{sgn}(x+\beta )-\textrm{sgn}(x-\beta )$. The bifurcation diagram along with the bifurcation sets is shown in Fig. 14. The corresponding phase portraits are shown in Fig. 15.

For $\alpha =0$, $\beta >0$ and $\gamma =0$, $x=0$, $x=\beta$ and $x=-\beta$ are all discontinuous. The restoring force can be written as $f(0,\beta ,0)=3x-\textrm{sgn}x-\textrm{sgn}(x+\beta )-\textrm{sgn}(x-\beta )$. The bifurcation diagram is shown in Fig. 16 for x versus $\beta$. The phase portraits are plotted in Fig. 17.

Relationship between bifurcation surfaces and catastrophe curves

To prove the relationship between bifurcation surfaces and catastrophe curves shown in Eq. (8), set $\textrm{B}_1$ to $\textrm{B}_7$ are divided into a series of sets as shown in the following

Fig. 14

Bifurcation diagrams for $\gamma =0$: a. equilibrium bifurcation surfaces; b. bifurcation sets on $\alpha$-$\beta$ plane. (Bifurcation sets divide the $(\alpha ,\beta )$ plane into five persistent regions, marked $\varOmega _1$ to $\varOmega _5$, for which the corresponding phase portraits are persistent, on the boundaries $\textrm{B}_1$ to $\textrm{B}_7$, the portraits are nonpersistent)

Fig. 15

Phase portraits for $\gamma =0$ (The value of parameters and the belonged set are shown in each figure legend)

$$\begin{aligned}&{\mathcal {M}}_+=\{ (\alpha ,\beta ,\gamma )\vert \exists x_1<0<x_2,\\&f(x_i)=f'(x_i)=0,i=1,2, f''(x_1)<0<f''(x_2) \},\\&{\mathcal {M}}_-=\{ (\alpha ,\beta ,\gamma )\vert \exists x_1<0<x_2,\\&f(x_i)=f'(x_i)=0,i=1,2, f''(x_1)>0>f''(x_2) \},\\&{\mathcal {N}}_-=\{ (\alpha ,\beta ,\gamma )\vert \exists x>0, f(x)<0 \},\\&{\mathcal {N}}_+=\{ (\alpha ,\beta ,\gamma )\vert \forall x>0, f(x)>0 \},\\&{\mathcal {E}}_-^i=\{ (\alpha ,\beta ,\gamma )\vert C_i(\alpha ,\beta ,\gamma )<0 \},\\&{\mathcal {E}}_+^i=\{ (\alpha ,\beta ,\gamma )\vert C_i(\alpha ,\beta ,\gamma )>0 \},\quad (i=1,3,5)\\&{\mathcal {G}}=\{ (\alpha ,\beta ,\gamma )\vert \exists x_i,\\&V(x_i)=V(0), V'(x_i)=0, V''(x_i)<0,i=1,2 \},\\&{\mathcal {K}}=\{ (\alpha ,\beta ,\gamma )\vert \exists x_1<0<x_2,\\&f(x_i)=f'(x_i)=f''(x)=0,i=1,2 \}.\\ \end{aligned}$$

It is obvious that ${\mathcal {N}}_\pm$ and ${\mathcal {E}}_\pm ^i$ are areas, ${\mathcal {M}}_\pm$ and ${\mathcal {G}}$ are surfaces, ${\mathcal {K}}$ is curve. And we have

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {M}}_+\cap {\mathcal {M}}_-={\mathcal {N}}_+\cap {\mathcal {N}}_-={\mathcal {E}}_+^i\cap {\mathcal {E}}_-^i=\varnothing ,\quad \partial ^2{\mathcal {E}}_\pm ^i=\varnothing \\ \partial {\mathcal {E}}_-^i=\partial {\mathcal {E}}_+^i=\{ (\alpha ,\beta ,\gamma )\vert C_i(\alpha ,\beta ,\gamma )=0 \},\\ \partial {\mathcal {N}}_-=\partial {\mathcal {N}}_+={\mathcal {M}}_+, \quad \partial {\mathcal {M}}_-=\partial {\mathcal {M}}_+={\mathcal {K}}. \end{array}\right. } \end{aligned}$$

(B1)

Also, we give some lemmas about the characteristics of restoring force f(x) without proving:

Lemma 1

$f(-x)=-f(x)$, $\lim \limits _{x\rightarrow \pm \infty }f(x)=\pm \infty$ and $f^{(2n)}(0)=0, n\in {\mathbb {N}}$;

Lemma 2

f(x) has at most 3 zero points for $x\in (0,+\infty )$;

Lemma 3

f(x) has at most 3 extreme points and 2 inflection points for $x\in (0,+\infty )$;

Lemma 4

if $f'(0)=f'''(0)=0$, then $f^{(5)}(0)<0\iff (\alpha ,\beta ,\gamma )\in {\mathcal {N}}_-$;

Lemma 5

if $f'(0)=f'''(0)=0$, then $f^{(5)}(0)>0\iff (\alpha ,\beta ,\gamma )\in {\mathcal {N}}_+$;

Lemma 6

if $f'(0)=0$ and $(\alpha ,\beta ,\gamma )\in {\mathcal {M}}_+$, then $C_3(\alpha ,\beta ,\gamma )>0$.

(1)

Set $\textrm{B}_1$ can be divided into $\textrm{B}_1={\mathcal {E}}_+^1\cap {\mathcal {M}}_+$ and $\partial \textrm{B}_1$ can be divided into $\partial \textrm{B}_1=(\partial {\mathcal {E}}_\pm ^1\cap {\mathcal {M}}_+)\cup ({\mathcal {E}}_+^1\cap \partial {\mathcal {M}}_\pm )\cup (\partial {\mathcal {E}}_\pm ^1\cap \partial {\mathcal {M}}_\pm )$.

We have $\partial {\mathcal {E}}_\pm ^1\cap {\mathcal {M}}_+=\textrm{L}_4$, $\partial {\mathcal {E}}_\pm ^1\cap \partial {\mathcal {M}}_\pm =\textrm{P}$ and

$$\begin{aligned}{} & {} {\mathcal {E}}_+^1\cap \partial {\mathcal {M}}_\pm =\lim \limits _{x_i\rightarrow 0}\{ (\alpha ,\beta ,\gamma )\vert C_1(\alpha ,\beta ,\gamma )>0;\nonumber \\ {}{} & {} \exists x_1<0<x_2, f(x_i)=f'(x_i)=0,i=1,2, f''(x_1)\nonumber \\ {}{} & {} <0<f''(x_2) \}. \end{aligned}$$

(B2)

Fig. 16

Bifurcation diagrams for $\alpha =0$ and $\gamma =0$

Fig. 17

Phase portraits for $\alpha =0$ and $\gamma =0$ (The value of parameters and the belonged set are shown in each figure legend)

Assume that $f(x)=ax(x^2-x_i^2)^2+bx^3(x^2-x_i^2)^3+cx^5(x^2-x_i^2)^4+o(x^7)$, which is

$$\begin{aligned}{} & {} f(x)=ax_i^4x-(2ax_i^2+bx_i^6)x^3+(a+3bx_i^4+cx_i^8)\nonumber \\ {}{} & {} x^5+o(x^7), \end{aligned}$$

(B3)

and let Eq. (B3) be the Taylor series of the restoring force, so that $C_1(\alpha ,\beta ,\gamma )=ax_i^4$, $C_3(\alpha ,\beta ,\gamma )=-(2ax_i^2+bx_i^6)$ and $C_5(\alpha ,\beta ,\gamma )=(a+3bx_i^4+cx_i^8)$, where $x_i=x_i(\alpha ,\beta ,\gamma )$ and $a>0$. Let $x_i\rightarrow 0$ and we can obtain $\lim \limits _{x_i\rightarrow 0}C_1(\alpha ,\beta ,\gamma )=0$, $\lim \limits _{x_i\rightarrow 0}C_3(\alpha ,\beta ,\gamma )=0$ and $\lim \limits _{x_i\rightarrow 0}C_5(\alpha ,\beta ,\gamma )=a>0$.

Therefore, we have ${\mathcal {E}}_+^1\cap \partial {\mathcal {M}}_\pm =\textrm{L}_5$, and $\partial \textrm{B}_1=\textrm{L}_4\cup \textrm{L}_5\cup \textrm{P}$.

(2)

Set $\textrm{B}_2$ can be divided into $\textrm{B}_2=\partial {\mathcal {E}}_\pm ^1\cap {\mathcal {E}}_+^3\cap {\mathcal {N}}_-$ and $\partial \textrm{B}_2$ can be divided into $\partial \textrm{B}_2=(\partial {\mathcal {E}}_\pm ^1\cap \partial {\mathcal {E}}_\pm ^3\cap {\mathcal {N}}_-)\cup (\partial {\mathcal {E}}_\pm ^1\cap {\mathcal {E}}_+^3\cap \partial {\mathcal {N}}_\pm )\cup (\partial {\mathcal {E}}_\pm ^1\cap \partial {\mathcal {E}}_\pm ^3\cap \partial {\mathcal {N}}_\pm )$.

From lemma 4 we have $\partial {\mathcal {E}}_\pm ^1\cap \partial {\mathcal {E}}_\pm ^3\cap {\mathcal {N}}_-=\textrm{L}_3$, and form lemma 6 we have $\partial {\mathcal {E}}_\pm ^1\cap {\mathcal {E}}_+^3\cap \partial {\mathcal {N}}_\pm =\partial {\mathcal {E}}_\pm ^1\cap {\mathcal {M}}_+={\mathcal {L}}_4$, we also have $\partial {\mathcal {E}}_\pm ^1\cap \partial {\mathcal {E}}_\pm ^3\cap \partial {\mathcal {N}}_\pm =\textrm{P}$. Therefore, $\partial {B}_2=\textrm{L}_3\cup \textrm{L}_4\cup \textrm{P}$.

(3)

Set $\textrm{B}_3$ can be divided into $\textrm{B}_3={\mathcal {E}}_-^1\cap {\mathcal {M}}_+$ and $\partial \textrm{B}_3$ can be divided into $\partial \textrm{B}_3=(\partial {\mathcal {E}}_\pm ^1\cap {\mathcal {M}}_+)\cup ({\mathcal {E}}_-^1\cap \partial {\mathcal {M}}_\pm )\cup (\partial {\mathcal {E}}_\pm ^1\cap \partial {\mathcal {M}}_\pm )$.

It is obvious that $\partial {\mathcal {E}}_\pm ^1\cap {\mathcal {M}}_+=\textrm{L}_4$, ${\mathcal {E}}_-^1\cap \partial {\mathcal {M}}_\pm ={\mathcal {E}}_-^1\cap {\mathcal {K}}=\textrm{L}_1$ and $\partial {\mathcal {E}}_\pm ^1\cap \partial {\mathcal {M}}_\pm =\textrm{P}$. Therefore, $\partial \textrm{B}_3=\textrm{L}_1\cup \textrm{L}_4\cup \textrm{P}$.

(4)

Set $\textrm{B}_4$ can be divided into $\textrm{B}_4=\partial {\mathcal {E}}_\pm ^1\cap {\mathcal {E}}_+^3\cap {\mathcal {N}}_+$ and $\partial \textrm{B}_4$ can be divided into $\partial \textrm{B}_4=(\partial {\mathcal {E}}_\pm ^1\cap \partial {\mathcal {E}}_\pm ^3\cap {\mathcal {N}}_+)\cup (\partial {\mathcal {E}}_\pm ^1\cap {\mathcal {E}}_+^3\cap \partial {\mathcal {N}}_\pm )\cup (\partial {\mathcal {E}}_\pm ^1\cap \partial {\mathcal {E}}_\pm ^3\cap \partial {\mathcal {N}}_\pm )$.

From lemma 5 we have $\partial {\mathcal {E}}_\pm ^1\cap \partial {\mathcal {E}}_\pm ^3\cap {\mathcal {N}}_+=\textrm{L}_5$. We also have $\partial {\mathcal {E}}_\pm ^1\cap {\mathcal {E}}_+^3\cap \partial {\mathcal {N}}_\pm =\textrm{L}_4$ and $\partial {\mathcal {E}}_\pm ^1\cap \partial {\mathcal {E}}_\pm ^3\cap \partial {\mathcal {N}}_\pm =\textrm{P}$. Therefore, $\partial {B}_4=\textrm{L}_4\cup \textrm{L}_5\cup \textrm{P}$.

(5)

Set $\textrm{B}_5$ can be divided into $\textrm{B}_5={\mathcal {E}}_-^1\cap {\mathcal {M}}_-$ and $\partial \textrm{B}_5$ can be divided into $\partial \textrm{B}_5=(\partial {\mathcal {E}}_\pm ^1\cap {\mathcal {M}}_-)\cup ({\mathcal {E}}_-^1\cap \partial {\mathcal {M}}_\pm )\cup (\partial {\mathcal {E}}_\pm ^1\cap \partial {\mathcal {M}}_\pm )$.

It is obvious that ${\mathcal {E}}_\pm ^1\cap \partial {\mathcal {M}}_\pm =\textrm{L}_1$, $\partial {\mathcal {E}}_\pm ^1\cap \partial {\mathcal {M}}_\pm =\textrm{P}$ and

$$\begin{aligned}{} & {} \partial {\mathcal {E}}_\pm ^1\cap {\mathcal {M}}_-=\lim \limits _{C_1\rightarrow 0^-}\{ (\alpha ,\beta ,\gamma )\vert C_1(\alpha ,\beta ,\gamma )<0;\nonumber \\ {}{} & {} \exists x_1<0<x_2,\nonumber \\{} & {} \quad f(x_i)=f'(x_i)=0,i=1,2, f''(x_1)>0>f''(x_2) \}.\nonumber \\ \end{aligned}$$

(B4)

Considering $f(0)=f(x_i)=0$, $f'(0)<0$, $f'(x_i)=0$, $f''(0)=0$, $f''(x_i)<0$ and lemma 3, we have

• (a). there exists minimum points $x_\textrm{I}\in (0,x_i)$ and $\exists x_\textrm{II}\in (x_i,+\infty )$, $f(x_\textrm{I})<0$, $f(x_\textrm{II})<0$, $f'(x_\textrm{I})=f'(x_\textrm{II})=0$, $f''(x_\textrm{I})>0$, $f''(x_\textrm{II})>0$;

• (b). $\exists x_a\in (x_\textrm{I},x_i)$, $\exists x_b\in (x_i,x_\textrm{II})$, $f''(x_a)=0$, $f''(x_b)=0$;

• (c). $f'(x)$ monotone increases in $(0,x_a)$, monotone decreases in $(x_a,x_b)$ and monotone increases in $(x_b,+\infty )$.

So it is clear that

$$\begin{aligned} f(x_\textrm{I})=\int _0^{x_\textrm{I}}f'(x)dx>f'(0)x_\textrm{I}, \end{aligned}$$

let $f'(0)\rightarrow 0^-$ and we have $f(x_\textrm{I})\rightarrow 0^-$, then we have $f(x)\rightarrow 0^-$ for $\forall x\in (0,x_i)$ because $f(x_\textrm{I})\le f(x)<0$ in $(0,x_i)$. From lemma 2, it can be derived that

$$\begin{aligned} \lim \limits _{f'(0)\rightarrow 0^-}x_i=0. \end{aligned}$$

(B5)

Assume that $f(x)=ax(x^2-x_i^2)^2+bx^3(x^2-x_i^2)^3+cx^5(x^2-x_i^2)^4+o(x^7)$ and $a<0$, which is the same form as Eq. (B3). Then let it be the Taylor series of the restoring force, so that $C_1(\alpha ,\beta ,\gamma )=ax_i^4$, $C_3(\alpha ,\beta ,\gamma )=-(2ax_i^2+bx_i^6)$ and $C_5(\alpha ,\beta ,\gamma )=(a+3bx_i^4+cx_i^8)$, where $x_i=x_i(\alpha ,\beta ,\gamma )$ and $a>0$. Let $x_i\rightarrow 0$ and we can obtain $\lim \limits _{C_1\rightarrow 0^-}C_3(\alpha ,\beta ,\gamma )=0$ and $\lim \limits _{C_1\rightarrow 0^-}C_5(\alpha ,\beta ,\gamma )=a<0$.

Therefore, we have $\partial {\mathcal {E}}_\pm ^1\cap {\mathcal {M}}_-=\textrm{L}_3$, and $\partial \textrm{B}_5=\textrm{L}_1\cup \textrm{L}_3\cup \textrm{P}$.

(6)

Set $\textrm{B}_6$ can be divided into $\textrm{B}_6=\partial {\mathcal {E}}_\pm ^1\cap {\mathcal {E}}_-^3$ and $\partial \textrm{B}_6$ can be divided into $\partial \textrm{B}_6=\partial {\mathcal {E}}_\pm ^1\cap {\mathcal {E}}_\pm ^3$, which is

$$\begin{aligned} \partial \textrm{B}_6=\{ (\alpha ,\beta ,\gamma )\vert C_1(\alpha ,\beta ,\gamma )=0;C_3(\alpha ,\beta ,\gamma )=0 \}. \end{aligned}$$

(B6)

It is obvious that $\partial \textrm{B}_6=\textrm{L}_3\cup \textrm{L}_5\cup \textrm{P}$.

(7)

Set $\textrm{B}_7$ can be divided into $\textrm{B}_7={\mathcal {E}}_-^1\cap {\mathcal {G}}$ and $\partial \textrm{B}_7$ can be divided into $\partial \textrm{B}_7=(\partial {\mathcal {E}}_\pm ^1\cap {\mathcal {G}})\cup ({\mathcal {E}}_-^1\cap \partial {\mathcal {G}})\cup (\partial {\mathcal {E}}_\pm ^1\cap \partial {\mathcal {G}})$, where

$$\begin{aligned}&\partial {\mathcal {G}}=\{ (\alpha ,\beta ,\gamma )\vert \exists x_1<0<x_2, \\&V(x_i)=V(0), V'(x_i)=V''(x_i)=0, i=1,2 \}. \end{aligned}$$

(B6)

Fig. 18

Heteroclinic orbits for Hamilton system: a $a=0.95$, $b=-1$; b $a=1$, $b=-1$; c $a=1.05$, $b=-1$

Fig. 19

Heteroclinic orbits for Hamilton system: a $a=\frac{1}{2}$, $b=-1$, $c=-4$, $q=3.98$; b $a=\frac{1}{2}$, $b=-1$, $c=-4$, $q=4$; c $a=\frac{1}{2}$, $b=-1$, $c=-4$, $q=4.02$

It is obvious that ${\mathcal {E}}_-^1\cap \partial {\mathcal {G}}=\textrm{L}_2\subseteq \textrm{B}_3$. And

$$\begin{aligned}{} & {} \partial {\mathcal {E}}_\pm ^1\cap {\mathcal {G}}=\lim \limits _{C_1\rightarrow 0^-}\{ (\alpha ,\beta ,\gamma )\vert C_1(\alpha ,\beta ,\gamma )<0;\nonumber \\ {}{} & {} \exists x_1<0<x_2,\nonumber \\{} & {} \quad V(x_i)=V(0), V'(x_i)=0, V''(x_i)<0, i=1,2 \}.\nonumber \\ \end{aligned}$$

(B7)

Considering $\int _0^{x_i}f(x)dx=V(x_i)-V(0)=0$, $f(x_i)=0$, $f'(x_i)<0$, lemma 1, lemma 2 and lemma 3, we have

• (a). $\exists x_k\in (0,x_i), x_j\in (x_i,+\infty ), f(x_k)=f(x_i)=f(x_j)=0$;

• (b). there exists minimum $x_\textrm{I}\in (0,x_k)$, maximum $x_\textrm{II}\in (x_k,x_i)$ and minimum $x_\textrm{III}\in (x_i,x_j)$, $f'(x_\textrm{I})=f'(x_\textrm{II})=f'(x_\textrm{III})=0$;

• (c). $f'(x)$ monotone increases in $(0,x_\textrm{I})$.

So it is clear that

$$\begin{aligned} f(x_\textrm{I})=\int _0^{x_\textrm{I}}f'(x)dx>f'(0)x_\textrm{I}, \end{aligned}$$

let $f'(0)\rightarrow 0^-$ and we have $f(x_\textrm{I})\rightarrow 0^-$.

Considering $f(x_\textrm{I})x_k<\int _0^{x_k}f(x)dx<0$, we have $\int _0^{x_k}f(x)dx\rightarrow 0^-$ and $\int _{x_k}^{x_i}f(x)dx=-\int _0^{x_k}f(x)dx\rightarrow 0^+$. So it can be derived that $f(x)\rightarrow 0^-$ for $\forall x\in (0,x_k)$ and $f(x)\rightarrow 0^+$ for $\forall x\in (x_k,x_i)$.

From lemma 2, it can be derived that

$$\begin{aligned} \lim \limits _{f'(0)\rightarrow 0^-}x_i=\lim \limits _{f'(0)\rightarrow 0^-}x_k=0. \end{aligned}$$

(B8)

Assume that $V(x)=ax^2(x^2-x_i^2)^2+bx^4(x^2-x_i^2)^3+cx^6(x^2-x_i^2)^4+o(x^7)$, and $f(x)=V'(x)$, which is

$$\begin{aligned} f(x)= & {} 2ax_i^4x-4(2ax_i^2+bx_i^6)x^3\nonumber \\{} & {} +6(a+3bx_i^4+cx_i^8)x^5+o(x^7), \end{aligned}$$

(B9)

and let Eq. (B9) be the Taylor series of the restoring force, so that $C_1(\alpha ,\beta ,\gamma )=2ax_i^4$, $C_3(\alpha ,\beta ,\gamma )=-4(2ax_i^2+bx_i^6)$ and $C_5(\alpha ,\beta ,\gamma )=6(a+3bx_i^4+cx_i^8)$, where $x_i=x_i(\alpha ,\beta ,\gamma )$ and $a<0$. Let $x_i\rightarrow 0$ and we can obtain $\lim \limits _{C_1\rightarrow 0}C_3(\alpha ,\beta ,\gamma )=0$ and $\lim \limits _{C_1\rightarrow 0}C_5(\alpha ,\beta ,\gamma )=6a<0$.

Therefore, we have $\partial {\mathcal {E}}_\pm ^1\cap {\mathcal {G}}=\textrm{L}_3$, and $\partial \textrm{B}_7=\textrm{L}_2\cup \textrm{L}_3\cup \textrm{P}$.

Structural stability of Hamilton system with heteroclinic orbits

Without loss of generality, a 2-dimensional Hamilton system is considered, whose Hamilton function can be written in the following form

$$\begin{aligned} H(x,y)=\sum \limits _{i=1}^{\infty }\sum \limits _{j=1}^{\infty }a_{i,j}x^iy^j. \end{aligned}$$

(C1)

two examples are given to illustrate the condition of heteroclinic bifurcation of 2-dimensional Hamilton system, which is shown in theorem 1.

Example 1

Let $a_{2,0}=1, a_{1,1}=a, a_{1,2}=b, a_{2,3}=-1, a,b\in {\mathbb {R}}$ and $a_{i,j}\equiv 0$(else), the Hamilton function is $H(x,y,\varvec{p})=x^2+axy+bxy^2-x^2y^3$, where $\varvec{p}=(a,b)^\textrm{T}$, which leads to the following Hamilton system

$$\begin{aligned} {\left\{ \begin{array}{ll} x'=ax+2bxy-3x^2y^2, \\ y'=-2x-ay-by^2+2xy^3. \end{array}\right. } \end{aligned}$$

(C2)

Three saddles $\textrm{A}(0,0)$, $\textrm{B}(0,-\frac{a}{b})$ and $C(x_c(\varvec{p}),y_c(\varvec{p}))$ can be found. When $\varvec{p}=(1,-1)^\textrm{T}$, we have $H\vert _\textrm{A}=H\vert _\textrm{B}=H\vert _\textrm{C}=0$, thus three heteroclinic orbits can be found, as shown in Fig. 18b: $\varGamma _1$ connecting $\textrm{A}(0,0)$ and $\textrm{B}(0,1)$; $\varGamma _2$ connecting $\textrm{B}(0,1)$ and $\textrm{C}(-\frac{1}{3},1)$; $\varGamma _3$ connecting $\textrm{A}(0,0)$ and $\textrm{C}(-\frac{1}{3},1)$. Calculation shows that

$$\begin{aligned}&\frac{\partial H}{\partial a}\vert _B-\frac{\partial H}{\partial a}\vert _A=0,\\&\frac{\partial H}{\partial b}\vert _B-\frac{\partial H}{\partial b}\vert _A=0,\\&\frac{\partial H}{\partial a}\vert _C-\frac{\partial H}{\partial a}\vert _B=x_c(\varvec{p})y_c(\varvec{p})\ne 0,\\&\frac{\partial H}{\partial b}\vert _C-\frac{\partial H}{\partial b}\vert _B=x_c(\varvec{p})y_c^2(\varvec{p})\ne 0, \\&\frac{\partial H}{\partial a}\vert _C-\frac{\partial H}{\partial a}\vert _A=x_c(\varvec{p})y_c(\varvec{p})\ne 0,\\&\frac{\partial H}{\partial b}\vert _C-\frac{\partial H}{\partial b}\vert _A=x_c(\varvec{p})y_c^2(\varvec{p})\ne 0, \end{aligned}$$

which means heteroclinic orbit $\varGamma _1$ is structurally stable, but $\varGamma _2$ and $\varGamma _3$ are structurally unstable. The neighborhood systems are shown in Fig. 18a and c. Heteroclinic orbit $\varGamma _2$ splits into orbits $\varGamma _{1,0}\cup \varGamma _{1,1}$ or $\varGamma _{2,0}\cup \varGamma _{2,1}$, while heteroclinic orbit $\varGamma _3$ splits into orbits $\varGamma _{1,0}\cup \varGamma _{1,2}$ or $\varGamma _{2,0}\cup \varGamma _{2,2}$.

Example 2

Consider the Hamilton function $H(x,y,\varvec{p})=\frac{1}{2}y^2-(x-a)^2(x-b)^2(x^2+cx+q)$, where $\varvec{p}=(a,b,c,q)^\textrm{T}$, which leads to the following Hamilton system

$$\begin{aligned} {\left\{ \begin{array}{ll} x'=y, \\ y'=2(x-a)(x-b)(2x-a-b)(x^2+cx+q)\\ \qquad +(x-a)^2(x-b)^2(2x+c). \end{array}\right. } \end{aligned}$$

(C3)

Three saddles $\textrm{A}(a,0)$, $\textrm{B}(b,0)$ and $C(x_c(\varvec{p}),0)$ can be found. When $\varvec{p}=(\frac{1}{2},-1,-4,4)^\textrm{T}$, we have $H\vert _\textrm{A}=H\vert _\textrm{B}=H\vert _\textrm{C}=0$, and two heteroclinic orbits can be found, as shown in Fig. 19b: $\varGamma _1$ connecting $\textrm{A}(\frac{1}{2},0)$ and $\textrm{B}(-1,0)$; $\varGamma _2$ connecting $\textrm{A}(\frac{1}{2},0)$ and $\textrm{C}(x_c(\varvec{p}),0)$. Calculation shows that

$$\begin{aligned}&\frac{\partial H}{\partial p_i}\vert _A-\frac{\partial H}{\partial p_i}\vert _B=0\ (p_i=a,b,c,q), \\&\frac{\partial H}{\partial c}\vert _C-\frac{\partial H}{\partial c}\vert _A=-x_c(\varvec{p})(x_c(\varvec{p})-a)^2(x_c(\varvec{p})-b)^2\ne 0,\\&\frac{\partial H}{\partial q}\vert _C-\frac{\partial H}{\partial q}\vert _A=-(x_c(\varvec{p})-a)^2(x_c(\varvec{p})-b)^2\ne 0, \end{aligned}$$

which means heteroclinic orbit $\varGamma _1$ is structurally stable, but $\varGamma _2$ is structurally unstable. The neighborhood systems are shown in Fig. 19a and c. Heteroclinic orbit $\varGamma _2$ splits into orbits $\varGamma _{1,0}\cup \varGamma _{1,1}$ or $\varGamma _{2,0}\cup \varGamma _{2,1}$.