Codimension two bifurcations of discrete Bonhoeffer–van der Pol oscillator model

Abstract

The non-degeneracy is one of the conditions to check for bifurcation analysis. Therefore, we need to compute the critical normal form coefficients to verify the non-degeneracy of the listed bifurcations. Using the critical normal form coefficients method to examine the bifurcation analysis makes it avoid calculating the central manifold and converting the linear part of the map into Jordan form. This is one of the most effective methods in the bifurcation analysis that has not received much attention so far. So in this article, we turn our attention to this method. In this study, the dynamic behaviors of the discrete Bonhoeffer–van der Pol (BVP) model are discussed. It is shown that the BVP model undergoes codimension one (codim-1) bifurcations such as pitchfork, fold, flip (period doubling) and Neimark–Sacker. Besides, codimension two (codim-2) bifurcations including resonance 1:2, 1:3, 1:4 and Chenciner have been achieved. For each bifurcation, normal form coefficients along with its scenario are investigated thoroughly. Bifurcation curves of the fixed points are drawn with the aid of numerical continuation techniques. Besides, a numerical continuation not only confirms our analytical results but also reveals richer dynamics of the model especially in the higher iteration.

1 Introduction

Neurons are the basic elements in the nervous system; they depend on each other and are responsible for stimulating and directing emotions. There are approximately $10^{11}$ neurons in the human’s brain and $10^9$ in spinal nerve, and each one has nearly $10^4$ synaptic connections with other neurons. Every neuron consists of Axon, Myelin, and Dendrite as its main components. Action potential or the firing of the neuron sourcing from abrupt changes of the cell’s electrical potential has a prominent role in the connection between the neurons which gets to the other cells through Axon and synaptic relations after production.

The abrupt changes of cell’s membrane usually take place due to ions displacement including sodium $(\hbox {Na}^{+})$, calcium $(\hbox {Ca}^{2+})$ and potassium $(\hbox {K}^{+})$. These ions are present in the neuron’s cell membrane, and through sodium, calcium and potassium valves called voltage gates, they are allowed to enter and exit the cell membrane. The first neural model, Hodgkin–Huxley (H–H), was introduced in 1952 by the pioneers named Hodgkin and Huxley. This model is based on the electrophysiological experiments conducted on the Axon of a squid-like creature called the squid giant. See Izhikevich (2000a, 2000b), Wang and Wang (2011), Guchenhermer and Oliva (2002), Hodgkin and Huxley (1952) and their references.

The BVP model was developed by FitzHugh and Nagumo by simplifying the Hodgkin–Huxley (H–H) model in 1961, see FitzHugh (1961), Nagumo et al. (1962). They reduced the four-dimensional H–H model to a two-dimensional one which might be considered as a reasonable extension of van der Pol equation because the BVP model can be examined by a circuitry Rocsoreanu et al. (2000). Besides, this equation can be achieved using a nonlinear conductor in a circuitry. Nowadays, BVP equation has turned into a well-known nonlinear oscillator.

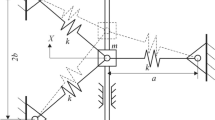
A full investigation from the BVP model with the nonlinearity of cubic order was carried out by Bautin (1975). In Kitajima et al. (1998) the bifurcation diagrams of this system were studied and a great diversity of nonlinear phenomena was observed compared to the van der Pol equation. The applications of the BVP equation with the mentioned background could be observed in Hoque and Kawakami (1995), Papy and Kawakami (1996), Tsumoto et al. (1999). More bifurcations of the model can be found in Rocsoreanu et al. (2001), Flores (1991), Freitas and Rocha (2001), Jones (1984), Jing et al. (2002). Figure 1 shows the main BVP model, and the circuit equations are as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} C\frac{\mathrm{d}V}{\mathrm{d}t}=-I-g(V),\\ L\frac{\mathrm{d}I}{\mathrm{d}t}=V-RI+E. \end{array}\right. \end{aligned}$$

(1)

We presume that g(V) is an odd function and E is skipped. Therefore, the above equation is symmetry under $(V,I)\rightarrow (-V,-I)$ permutation. Thus, E as a voltage source applies to eliminate the symmetric feature of the model.

Fig. 1

BVP oscillator

In this paper, nonlinear conductance is considered as

$$\begin{aligned} g(V)=-A\left( BV-\frac{1}{3}(BV)^3\right) , \end{aligned}$$

and the model turns into a discrete one by applying the Euler scheme. Then, we examine the dynamics of the discrete-time BVP oscillation equation and we have:

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{x}=-y+\gamma x-\frac{1}{3}(\gamma x)^3,\\ \dot{y}=x-ky+\beta , \end{array}\right. \end{aligned}$$

(2)

where

$$\begin{aligned} {\dot{x}}&=\frac{\mathrm{d}x}{\mathrm{d}\tau },\quad {\dot{y}=\frac{\mathrm{d}y}{\mathrm{d}\tau }},\quad x=\frac{V}{A}\sqrt{\frac{C}{L}},\\ y&=\frac{I}{A},\quad \tau =\frac{t}{\sqrt{LC}},\quad k=R\sqrt{\frac{C}{L}},\\ \gamma&=AB\sqrt{\frac{L}{C}},\quad \beta =\frac{E}{A}\sqrt{\frac{C}{L}}. \end{aligned}$$

In Wang and Guangqing (2010), the authors propose the following discrete-time BVP model:

$$\begin{aligned} \left\{ \begin{array}{ll} x_{n+1}=x_{n}+\epsilon (-y_{n}+\gamma x_{n}-\frac{1}{3}(\gamma x_{n})^3),\\ y_{n+1}=y_{n}+\epsilon (x_{n}-ky_{n}+\beta ), \end{array}\right. \end{aligned}$$

(3)

where $\epsilon$ is the integral step size and $k,\gamma , \epsilon$ are positive constants and $\beta \in {\mathbb {R}}$.

The existence and stability of the fixed points of model (3) as well as some bifurcations of it, through the numerical method, have been investigated in Wang and Guangqing (2010). In this paper, we study all of the codim-1 bifurcation analysis such as pitchfork, fold, flip (period doubling) and Neimark–Sacker, analytically by regarding k as bifurcation parameter; also, all of the codim-2 bifurcations of the system are extracted by regarding $\epsilon$ and k as free parameters. It will be shown that the system undergoes some bifurcations like Chenciner, resonance 1:2, resonance 1:3 and resonance 1:4 bifurcations under change of these two parameters. Moreover, all the bifurcation curves for the model will be drawn with the aid of numerical continuation methods. The numerical results prove the analytic results and reveal more complicated dynamic of the system.

The bifurcation theory allows us to identify and predict changes or metamorphoses in the dynamics of a system. Hence, bifurcation theory is one of the important branches of dynamic systems. Bifurcations in a dynamic model are examined from both analytical and numerical aspects. Many methods have proposed to study the bifurcations in each of these two aspects, among which some methods are more efficient than others. One of the most effective analytical methods in the bifurcation theory is the computation of the critical normal form coefficients. This method is more prone to be noticed in many dynamical systems. In this paper, the computation of the normal form coefficients is done analytically which is also confirmed numerically using MatContM; for more details, see Kuznetsov and Meijer (2005), Govaerts et al. (2007). Furthermore, this paper provides an efficient analytical and numerical method for extensive implementation on different discrete-time models.

The paper structure is organized as follows: In Sect. 2, the basic assumptions are introduced and the existence of the fixed points of (3) is presented. In Sect. 3, all of the codim-1 bifurcations of (3) by considering k as a free parameter are investigated. In Sect. 4, the codim-2 bifurcations are discussed by considering $\epsilon$ and k as free parameters. In Sect. 5, the numerical continuations are provided. Finally, this paper ends with some concluding remarks.

2 Existence of the fixed points and bifurcation analysis

The fixed points $(x_{*},y_{*})$ of (3), are satisfied in the following equation:

$$\begin{aligned} \left\{ \begin{array}{ll} -y_{*}+\gamma x_{*}-\frac{1}{3}(\gamma x_{*})^3=0,\\ x_{*}-ky_{*}+\beta = 0. \end{array}\right. \end{aligned}$$

The conditions of asymptotic stability of the fixed point $E_{*}= (x_{*},\frac{\beta +x_{*}}{k})$ of (3) can be found in Wang and Guangqing (2010).

First, let us consider model (3) as follows:

$$\begin{aligned} \begin{pmatrix} x\\ y \end{pmatrix} \mapsto {\mathcal {N}}(\xi ,\vartheta )= \begin{pmatrix} x+\epsilon (-y+\gamma x-\frac{1}{3}(\gamma x)^3)\\ y+\epsilon (x-ky+\beta ) \end{pmatrix}, \end{aligned}$$

(4)

where $\xi =(x,y)^T$ and $\vartheta =(\epsilon ,\gamma ,k,\beta )^T$. The Jacobian matrix of the map (3) is given by:

$$\begin{aligned} {\mathcal {J}}(\xi ,\vartheta )=\begin{pmatrix} -\epsilon \,{\gamma }^{3}{x}^{2}+\epsilon \, \gamma +1&{}-\epsilon \\ \epsilon &{}-\epsilon \,k+1 \end{pmatrix}. \end{aligned}$$

Similar to Kuznetsov and Meijer (2005), the second and third multi-linear forms of (3) can be expressed as

$$\begin{aligned} B_i(\varGamma ,\varSigma ,\vartheta )&=\sum _{j,k=1}^{2}\frac{\partial ^2{\mathcal {N}}_i(\xi ,\vartheta )}{\partial \xi _j\partial \xi _k}\gamma _j\sigma _k,\\ C_i(\varGamma ,\varSigma ,\varUpsilon ,\vartheta )&=\sum _{j,k,l=1}^{2}\frac{\partial ^3f_i(x,y,\lambda ,\mu )}{\partial \xi _j\partial \xi _k\partial \xi _l}\gamma _j\sigma _k\upsilon _l, \end{aligned}$$

where

$$\begin{aligned} \varGamma =(\gamma _1,\gamma _2)^T,\quad \varSigma =(\sigma _1,\sigma _2)^T,\quad \varUpsilon =(\upsilon _1,\upsilon _2)^T. \end{aligned}$$

Then, the multi-linear forms corresponding to the model (3) are given by

$$\begin{aligned} B(\varGamma ,\varSigma ,\vartheta )&=\begin{pmatrix} -2\,\epsilon \,{\gamma }^{3}x\gamma _{{1}}\sigma _{{1}}\\ 0 \end{pmatrix}, \\ C(\varGamma ,\varSigma ,\varUpsilon ,\vartheta )&=\begin{pmatrix} -2\,\epsilon \,{\gamma }^{3}{x\gamma _1}\,{\sigma _1 }\,{\upsilon _1}\\ 0 \end{pmatrix}. \end{aligned}$$

Since ${\mathcal {N}}$ is smooth enough, it can be written as follows:

$$\begin{aligned} {\mathcal {N}}(\xi ,\vartheta )={\mathcal {J}}(\xi ,\vartheta )\xi +\frac{1}{2!}B(\xi ,\xi ,\vartheta )+\frac{1}{3!}C(\xi ,\xi ,\xi ,\vartheta ). \end{aligned}$$

3 Codim-1 bifurcations

In this section, we consider $\gamma , \beta , \epsilon$ as fixed parameters and k as a free parameter. We have the following theorems for local codim-1 bifurcations.

Theorem 1

$E_{*}$ experiences a non-degenerate limit point bifurcation, at $k=-{\frac{1}{\gamma \, \left( {\gamma }^{2}{{x_{*}}}^{2}-1 \right) }}$, provided

$$\begin{aligned} x_{*}\ne 0, \quad {\frac{\epsilon \,{\gamma }^{6}{{x_{*}}}^{4}-2\,\epsilon \,{\gamma }^{4 }{{x_{*}}}^{2}-{\gamma }^{3}{{x_{*}}}^{2}+\epsilon \,{\gamma }^{2}- \epsilon +\gamma }{\gamma \, \left( {\gamma }^{2}{{x_{*}}}^{2}-1 \right) }}\ne \pm 1. \end{aligned}$$

Proof

There is a fixed point of (3) with multiplier $+1$ if

$$\begin{aligned} \left\{ \begin{array}{ll} {\mathcal {N}}(\xi ,\vartheta )=\xi ,\\ \det ({\mathcal {J}}(\xi ,\vartheta )-I_2)=0. \end{array} \right. \end{aligned}$$

(5)

Clearly

$$\begin{aligned} t_{LP}:~ (x,y,k)=\left( x_{*},\frac{1}{k}(x_{*}+\beta ),-{\frac{1}{\gamma \, \left( {\gamma }^{2}{{x_{*}}}^{2}-1 \right) }}\right) , \end{aligned}$$

satisfies the algebraic system (5). The Jacobian matrix at the curve $t_{LP}$ has a simple multiplier $\lambda _1=+1$ and the other multipliers are not on the unit circle provided

$$\begin{aligned} {\frac{\epsilon \,{\gamma }^{6}{{x_{*}}}^{4}-2\,\epsilon \,{\gamma }^{4 }{{x_{*}}}^{2}-{\gamma }^{3}{{x_{*}}}^{2}+\epsilon \,{\gamma }^{2}- \epsilon +\gamma }{\gamma \, \left( {\gamma }^{2}{{x_{*}}}^{2}-1 \right) }}\ne \pm 1. \end{aligned}$$

(6)

The center manifold at $k=-{\frac{1}{\gamma \, \left( {\gamma }^{2}{{x_{*}}}^{2}-1 \right) }}$ can be considered as

$$\begin{aligned} M(\nu )&=\nu v+m_2\nu ^2+{\mathcal {O}}(\nu ^3),\quad M:{\mathbb {R}}\rightarrow {\mathbb {R}}^2,\nonumber \\ m_2&=(m_{21},m_{22})^T, \end{aligned}$$

(7)

where

$$\begin{aligned} {\mathcal {J}}v=v,\quad {\mathcal {J}}^Tw=w,\quad \left\langle w,v \right\rangle =1, \end{aligned}$$

and

$$\begin{aligned} v&=\begin{pmatrix} -{\frac{1}{\gamma \, \left( {\gamma }^{2}{{ x_{*}}}^{2}-1 \right) }}\\ 1 \end{pmatrix},\\ w&=\begin{pmatrix} {\frac{\gamma \, \left( {\gamma }^{2}{{x_{*} }}^{2}-1 \right) }{{\gamma }^{6}{{x_{*}}}^{4}-2\,{\gamma }^{4}{{x_{*}} }^{2}+{\gamma }^{2}-1}}\\ {\frac{{\gamma }^{2} \left( {\gamma }^{2}{{x_{*}}}^{2}-1 \right) ^{2}}{{\gamma }^{6}{{ x_{*}}}^{4}-2\,{\gamma }^{4}{{x_{*}}}^{2}+{\gamma }^{2}-1}} \end{pmatrix}. \end{aligned}$$

The restriction of the map (3) on (7) has the following form:

$$\begin{aligned} \nu \mapsto G(\nu )=\nu +a_{LP}\nu ^2+{\mathcal {O}}\left( \nu ^3\right) . \end{aligned}$$

The center manifold invariance requires

$$\begin{aligned} {\mathcal {N}}(M(\nu ),\vartheta _{*})=M(G(\nu )). \end{aligned}$$

(8)

The following linear system is obtained by collecting the $\nu ^2-$terms in (8):

$$\begin{aligned} ({\mathcal {J}}-I_2)m_2=2a_{LP}-B(v,v,\vartheta _{*}), \end{aligned}$$

(9)

where $\vartheta _{*}=(\epsilon ,\gamma ,-{\frac{1}{\gamma \, \left( {\gamma }^{2}{{x_{*}}}^{2}-1 \right) }},\beta )^T$.

The solvability condition (9) is as follows:

$$\begin{aligned} \langle w,2a_{LP}-B(v,v,\vartheta _{*})\rangle =0; \end{aligned}$$

therefore,

$$\begin{aligned} a_{LP}=-{\frac{\epsilon \,{x_{*}}}{ \left( {\gamma }^{2}{{x_{*}}}^{2}-1 \right) ^{3}}}. \end{aligned}$$

So the fold bifurcation is non-degenerate provided $x_{*}\ne 0$. $\square$

Theorem 2

On the curve

$$\begin{aligned} t_{Pitch}:~ (x,y,k)=\left( 0,0,\frac{1}{\gamma }\right) , \end{aligned}$$

there is a pitchfork bifurcation provided $\epsilon \ne \frac{2\gamma }{1-\gamma ^{2}}, \gamma \ne 1$.

Proof

Clearly the map (3) has a fixed point with multiplier $+1$ on the curve $t_{Pitch}$. Since $a_{LP}=0$, a pitchfork bifurcation is expected on this curve.

Let us consider the center manifold at $k=\frac{1}{\gamma }$ as follows:

$$\begin{aligned} M_{P}(\iota )&=\iota v+m_2\iota ^2+m_3\iota ^3+{\mathcal {O}}(\iota ^4),\quad M_{P}:{\mathbb {R}}\rightarrow {\mathbb {R}}^2,\nonumber \\ m_i&=(m_{21},m_{22})^T,\quad i=2,3, \end{aligned}$$

(10)

where

$$\begin{aligned} {\mathcal {J}}v=v,\quad {\mathcal {J}}^Tw=w,\quad \left\langle w,v \right\rangle =1, \end{aligned}$$

and

$$\begin{aligned} v&=\begin{pmatrix} {\gamma }^{-1}\\ 1 \end{pmatrix},\\ w&=\begin{pmatrix} -{\frac{\gamma }{{\gamma }^{2}-1}} \\ {\frac{{\gamma }^{2}}{{\gamma }^{2}-1}} \end{pmatrix}. \end{aligned}$$

The map (3) can be restricted to (10) as follows:

$$\begin{aligned} \iota \mapsto G_P(\iota )=\iota +c_{\mathrm{Pitch}}\iota ^3+{\mathcal {O}}(\iota ^4). \end{aligned}$$

Due to the center manifold properties the following equation can be obtained:

$$\begin{aligned} {\mathcal {N}}\left( M_P(\iota ),\vartheta _{*}\right) =M_P\left( G_P(\iota )\right) . \end{aligned}$$

(11)

The following linear systems are obtained by collecting the power of $\iota$ terms up to the cubic order:

$$\begin{aligned} ({\mathcal {J}}-I_2)m_2&=-B(v,v,\vartheta _{*}), \end{aligned}$$

(12)

$$\begin{aligned} ({\mathcal {J}}-I_2)m_3&=6c_{\mathrm{Pitch}}-C(v,v,v,\vartheta _{*})-3B(v,m_2,\vartheta _{*}), \end{aligned}$$

(13)

where $\vartheta _{*}=(\epsilon ,\gamma ,k,\beta )^T=(\epsilon ,\gamma ,\frac{1}{\gamma },\beta )^T$.

Since

$$\begin{aligned} \langle w,B(v,v,\vartheta _{*})\rangle =0, \end{aligned}$$

the system (12) is solvable and $m_2=\left( {\begin{matrix} 0\\ 0 \end{matrix}}\right)$ is its solution obtained by the bordering technique. The system (13) is solvable if

$$\begin{aligned} \langle w,6c_{\mathrm{Pitch}}-C(v,v,v,\vartheta _{*})-3B(v,m_2,\vartheta _{*})\rangle =0; \end{aligned}$$

therefore,

$$\begin{aligned} c_{\mathrm{Pitch}}=-{\frac{\epsilon }{3\gamma }}. \end{aligned}$$

$\square$

Theorem 3

There is a non-degenerate period doubling bifurcation of $E_{*}$ at $k={\frac{2\,\epsilon \,{\gamma }^{3}{{x_{*}}}^{2}-{\epsilon }^{2}-2\, \epsilon \,\gamma -4}{\epsilon \, \left( \epsilon \,{\gamma }^{3}{{x_{*}}} ^{2}-\epsilon \,\gamma -2 \right) }}$, provided

$$\begin{aligned} {\frac{{\epsilon }^{2}{\gamma }^{6}{{x_{*}}}^{4}-2\,{\epsilon }^{2}{ \gamma }^{4}{{x_{*}}}^{2}-3\,\epsilon \,{\gamma }^{3}{{x_{*}}}^{2}+{ \epsilon }^{2}{\gamma }^{2}-{\epsilon }^{2}+3\,\epsilon \,\gamma +2}{ \epsilon \,{\gamma }^{3}{{x_{*}}}^{2}-\epsilon \,\gamma -2}} \ne \pm 1. \end{aligned}$$

Proof

There is a fixed point with multiplier $+1$ for the map (3) if

$$\begin{aligned} \left\{ \begin{array}{ll} {\mathcal {N}}(\xi ,\vartheta )-\xi =0,\\ \det ({\mathcal {J}}(\xi ,\vartheta )+I_2)=0. \end{array} \right. \end{aligned}$$

(14)

Clearly, the curve

$$\begin{aligned} t_{PD}:~\left( x,y,k\right) =\left( x_{*},\frac{1}{k}(x_{*}+\beta ),{\frac{2\,\epsilon \,{\gamma }^{3}{{x_{*}}}^{2}-{\epsilon }^{2}-2\, \epsilon \,\gamma -4}{\epsilon \, \left( \epsilon \,{\gamma }^{3}{{x_{*}}} ^{2}-\epsilon \,\gamma -2 \right) }} \right) , \end{aligned}$$

satisfies the system (14). Let us consider

$$\begin{aligned} M_{PD}(\phi )&=v\phi +m_2\phi ^2+m_3\phi ^3+{\mathcal {O}}(\phi ^4),\quad M_{PD}:{\mathbb {R}}\rightarrow {\mathbb {R}}^2,\nonumber \\ m_i&=(m_{i1},m_{i2})^T,\quad i=2,3, \end{aligned}$$

(15)

as the center manifold corresponding to the map (3) at $k={\frac{2\,\epsilon \,{\gamma }^{3}{{x_{*}}}^{2}-{\epsilon }^{2}-2\, \epsilon \,\gamma -4}{\epsilon \, \left( \epsilon \,{\gamma }^{3}{{x_{*}}} ^{2}-\epsilon \,\gamma -2 \right) }}$, where

$$\begin{aligned} {\mathcal {J}}v=-v,\quad {\mathcal {J}}^Tw=-w,\quad \left\langle w,v \right\rangle =1, \end{aligned}$$

in which

$$\begin{aligned} v&=\begin{pmatrix} -{\frac{\epsilon }{\epsilon \,{\gamma }^{3}{{ x_{*}}}^{2}-\epsilon \,\gamma -2}}\\ 1 \end{pmatrix},\\ w&=\begin{pmatrix} {\frac{ \left( \epsilon \,{\gamma }^{3}{{ x_{*}}}^{2}-\epsilon \,\gamma -2 \right) \epsilon }{{\epsilon }^{2}{\gamma }^{ 6}{{x_{*}}}^{4}-2\,{\epsilon }^{2}{\gamma }^{4}{{x_{*}}}^{2}-4\, \epsilon \,{\gamma }^{3}{{x_{*}}}^{2}+{\epsilon }^{2}{\gamma }^{2}-{ \epsilon }^{2}+4\,\epsilon \,\gamma +4}}\\ {\frac{ \left( \epsilon \,{\gamma }^{3}{{x_{*}}}^{2}-\epsilon \,\gamma -2 \right) ^{2}}{{\epsilon }^{2}{\gamma }^{6}{{x_{*}}}^{4}-2\,{\epsilon }^ {2}{\gamma }^{4}{{x_{*}}}^{2}-4\,\epsilon \,{\gamma }^{3}{{x_{*}}}^{2}+ {\epsilon }^{2}{\gamma }^{2}-{\epsilon }^{2}+4\,\epsilon \,\gamma +4}} \end{pmatrix}. \end{aligned}$$

The map (3) can be restricted to (15) as follows:

$$\begin{aligned} \phi \mapsto G_{PD}=-\phi +b_{PD}\phi ^3+{\mathcal {O}}{(\phi ^4)}, \end{aligned}$$

(16)

the center manifold property implies that

$$\begin{aligned} {\mathcal {N}}\left( M_{PD}(\phi ),\vartheta _{*}\right) =M_{PD}\left( G_{PD}(\phi )\right) . \end{aligned}$$

Collecting the power of $\phi$ terms up to the third order gives

$$\begin{aligned} ({\mathcal {J}}-I_2)m_{2}&=-B(v,v,\vartheta _{*}), \end{aligned}$$

(17)

$$\begin{aligned} ({\mathcal {J}}+I_2)m_{3}&=6b_{PD}-C(v,v,v,\vartheta _{*})-3B(v,m_2,\vartheta _{*}), \end{aligned}$$

(18)

where $\vartheta _{*}=\left( \epsilon ,\gamma ,{\frac{2\,\epsilon \,{\gamma }^{3}{{x_{*}}}^{2}-{\epsilon }^{2}-2\, \epsilon \,\gamma -4}{\epsilon \, \left( \epsilon \,{\gamma }^{3}{{x_{*}}} ^{2}-\epsilon \,\gamma -2 \right) }},\beta \right)$.

The system (17) is non-singular and

$$\begin{aligned} m_2= \begin{pmatrix} -{\frac{ \left( 2\,\epsilon \,{\gamma }^{3}{{ x_{*}}}^{2}-{\epsilon }^{2}-2\,\epsilon \,\gamma -4 \right) {\epsilon }^{ 2}{\gamma }^{3}{} { x_{*}}}{ \left( \epsilon \,{\gamma }^{6}{{ x_{*}}}^{4}-2 \,\epsilon \,{\gamma }^{4}{{ x_{*}}}^{2}-2\,{\gamma }^{3}{{ x_{*}}}^{2}+ \epsilon \,{\gamma }^{2}-\epsilon +2\,\gamma \right) \left( \epsilon \,{ \gamma }^{3}{{ x_{*}}}^{2}-\epsilon \,\gamma -2 \right) ^{2}}} \\ -{\frac{{\epsilon }^{3}{\gamma }^{3}{} { x_{*}}}{ \left( \epsilon \,{\gamma }^{6}{{ x_{*}}}^{4}-2\,\epsilon \,{\gamma }^{4} {{ x_{*}}}^{2}-2\,{\gamma }^{3}{{ x_{*}}}^{2}+\epsilon \,{\gamma }^{2}- \epsilon +2\,\gamma \right) \left( \epsilon \,{\gamma }^{3}{{ x_{*}}}^{2 }-\epsilon \,\gamma -2 \right) }} \end{pmatrix}. \end{aligned}$$

is its solution. The singular system (18) is solvable provided

$$\begin{aligned} \langle w,6b_{PD}-C(v,v,v,\vartheta _{*})-3B(v,m_2,\vartheta _{*})\rangle =0. \end{aligned}$$

Thus,

$$\begin{aligned} b_{PD}=\frac{b_1(\gamma ,\epsilon ,x_{*})}{b_2(\gamma ,\epsilon ,x_{*})}, \end{aligned}$$

where

$$\begin{aligned} b_1(\gamma ,\epsilon ,x_{*})&=- \left( 5\,\epsilon \,{\gamma }^{6}{{x_{*}}}^{4}-3\,{\epsilon }^{2}{ \gamma }^{3}{{x_{*}}}^{2}-4\,\epsilon \,{\gamma }^{4}{{x_{*}}}^{2}\right. \\&\quad \left. -10\,{\gamma }^{3}{{x_{*}}}^{2}-\epsilon \,{\gamma }^{2}+\epsilon -2\,\gamma \right) {\gamma }^{3}{\epsilon }^{5},\\ b_2(\gamma ,\epsilon ,x_{*})&=3\, \left( \epsilon \,{\gamma }^{6}{{x_{*}}}^{4}-2\,\epsilon \,{\gamma }^ {4}{{x_{*}}}^{2}-2\,{\gamma }^{3}{{x_{*}}}^{2}+\epsilon \,{\gamma }^{2}\right. \\&\quad \left. -\epsilon +2\,\gamma \right) \left( \epsilon \,{\gamma }^{3}{{x_{*}}}^{ 2}-\epsilon \,\gamma -2 \right) ^{2} \\&\quad \left( {\epsilon }^{2}{\gamma }^{6}{{ x_{*}}}^{4}-2\,{\epsilon }^{2}{\gamma }^{4}{{x_{*}}}^{2}-4\,\epsilon \, {\gamma }^{3}{{x_{*}}}^{2}+{\epsilon }^{2}{\gamma }^{2}\right. \\ {}&\quad \left. -{\epsilon }^{2}+4 \,\epsilon \,\gamma +4 \right) . \end{aligned}$$

The flip bifurcation is non-degenerate provided $b_{PD}\ne 0$. If $b_{PD}$ is positive, the bifurcation is supercritical and the double period cycle is stable. When $b_{PD}<0$, it is subcritical and unstable. $\square$

Theorem 4

On the curve

$$\begin{aligned} t_{NS}:~\left( x,y,k \right) =\left( x_{*},\frac{1}{k}(x_{*}+\beta ),-{\frac{-{\gamma }^{3}{{x_{*}}}^{2}+\epsilon +\gamma }{\epsilon \,{ \gamma }^{3}{{x_{*}}}^{2}-\epsilon \,\gamma -1}} \right) , \end{aligned}$$

there is a non-degenerate Neimark–Sacker bifurcation.

Proof

The map (3) has a fixed point with a pair complex multiplier on the unit circle if

$$\begin{aligned} \left\{ \begin{array}{ll} {\mathcal {N}}(\xi ,\vartheta )=\xi ,\\ \det ({\mathcal {J}}\odot {\mathcal {J}})=1, \end{array} \right. \end{aligned}$$

(19)

where $\odot$ is the bi-alternate matrix product. Clearly the curve $t_{NS}$ satisfies the algebraic system (19).

Along the curve $t_{NS}$ there is a pair of complex multipliers on the unit circle

$$\begin{aligned} \lambda _{1,2}=\frac{1}{2}\,{\frac{-{{\gamma }}^{6}{{x_{*}}}^{4}{{\epsilon }}^{2}+2\,{ {\gamma }}^{4}{{x_{*}}}^{2}{{\epsilon }}^{2}+2\,{{\gamma }}^{ 3}{{x_{*}}}^{2}{\epsilon }-{{\gamma }}^{2}{{\epsilon }}^{2}-2 \,{\gamma }\,{\epsilon }+{{\epsilon }}^{2}-2}{{{\gamma }}^{3 }{{x_{*}}}^{2}{\epsilon }-{\gamma }\,{\epsilon }-1}}\pm {\frac{i u}{2\,{{\gamma }}^{3}{{x_{*}}}^{2}{\epsilon }-2\,{\gamma }\,{ \epsilon }-2}}, \end{aligned}$$

that satisfy on the non-resonance conditions, where

$$\begin{aligned} u=\sqrt{- \left( {{\gamma }}^{6}{{x_{*}}}^{4}-2\,{{\gamma }}^{4} {{x_{*}}}^{2}+{{\gamma }}^{2}-1 \right) {{\epsilon }}^{2} \left( {{\gamma }}^{6}{{x_{*}}}^{4}{{\epsilon }}^{2}-2\,{{ \gamma }}^{4}{{x_{*}}}^{2}{{\epsilon }}^{2}-4\,{{\gamma }}^{3}{{ x_{*}}}^{2}{\epsilon }+{{\gamma }}^{2}{{\epsilon }}^{2}+4\,{ \gamma }\,{\epsilon }-{{\epsilon }}^{2}+4 \right) }. \end{aligned}$$

The center manifold at $k=-{\frac{-{\gamma }^{3}{{x_{*}}}^{2}+\epsilon +\gamma }{\epsilon \,{ \gamma }^{3}{{x_{*}}}^{2}-\epsilon \,\gamma -1}}$, can be considered as

$$\begin{aligned} M_{NS}(\varsigma ,{\bar{\varsigma }})&=v\varsigma +{\bar{\varsigma }}{\bar{v}}+\sum _{2\le k+l}\frac{1}{(k+l)!}m_{kl}\varsigma ^k{\bar{\varsigma }}^l,\nonumber \\ \varsigma&\in {\mathbb {C}}, \quad m_{kl}\in {\mathbb {C}}, \end{aligned}$$

(20)

where

$$\begin{aligned} {\mathcal {J}}v=e^{i\theta _0}v,\quad {\mathcal {J}}^Tw=e^{-i\theta _0}w,\quad \left\langle v,w\right\rangle =1, \end{aligned}$$

and

$$\begin{aligned}&v=\begin{pmatrix} 1\\ -\frac{1}{2}\,{\frac{{{ \gamma }}^{6}{{x_{*}}}^{4}{{\epsilon }}^{2}-2\,{{\gamma }}^{4}{{ x_{*}}}^{2}{{\epsilon }}^{2}-2\,{{\gamma }}^{3}{{x_{*}}}^{2}{ \epsilon }+{{\gamma }}^{2}{{\epsilon }}^{2}+iu+{{\epsilon }}^ {2}+2\,{\gamma }\,{\epsilon }}{{\epsilon }\, \left( {{\gamma }}^{3}{{x_{*}}}^{2}{\epsilon }-{\gamma }\,{\epsilon }-1 \right) }} \end{pmatrix},\\&w=\frac{1}{\overline{pq}}\begin{pmatrix} 1\\ -\frac{1}{2}\,{\frac{-{{\gamma }}^{6}{{x_{*}}}^{4}{{\epsilon }}^{2}+2\,{{\gamma }}^{4}{{ x_{*}}}^{2}{{\epsilon }}^{2}+2\,{{\gamma }}^{3}{{x_{*}}}^{2}{ \epsilon }-{{\gamma }}^{2}{{\epsilon }}^{2}+iu-{{\epsilon }}^ {2}-2\,{\gamma }\,{\epsilon }}{{\epsilon }\, \left( {{\gamma }}^{3}{{x_{*}}}^{2}{\epsilon }-{\gamma }\,{\epsilon }-1 \right) }} \end{pmatrix},\\&pq=\frac{(pq)_{1}(\epsilon ,\gamma ,x_{*})}{4\,{{\epsilon }}^{2} \left( {{\gamma }}^{3}{{x_{*}}}^{2}{\epsilon }-{\gamma }\,{\epsilon }-1 \right) ^{2}},\\&(pq)_{1}(\epsilon ,\gamma ,x_{*})= 2\,{{\gamma }}^{6}{{x_{*}}}^{4}{{\epsilon }}^{4}-4\,{{\gamma }}^{4}{{x_{*}}}^{2}{{\epsilon }}^{4}-4\,{{\gamma }}^{3}{{x_{*}} }^{2}{{\epsilon }}^{3}\\&\quad -{{\gamma }}^{12}{{x_{*}}}^{8}{{ \epsilon }}^{4}+4\,{{\gamma }}^{10}{{x_{*}}}^{6}{{\epsilon }}^{4}+ 4\,{{\gamma }}^{9}{{x_{*}}}^{6}{{\epsilon }}^{3}\\&\quad -6\,{{\gamma }}^{8}{{x_{*}}}^{4}{{\epsilon }}^{4}-12\,{{\gamma }}^{7}{{x_{*} }}^{4}{{\epsilon }}^{3}+4\,{{\gamma }}^{6}{{x_{*}}}^{2}{{ \epsilon }}^{4}\\&\quad +12\,{{\gamma }}^{5}{{x_{*}}}^{2}{{\epsilon }}^{3}- 2\,iu\,{{\epsilon }}^{2}-2\,i{{\gamma }}^{2}u\,{{\epsilon }}^{2 }\\&\quad -4\,i{\gamma }\,u\,{\epsilon }-{{\epsilon }}^{4}+{u}^{2}-4\,{{ \gamma }}^{6}{{x_{*}}}^{4}{{\epsilon }}^{2}\\&\quad +8\,{{\gamma }}^{4 }{{x_{*}}}^{2}{{\epsilon }}^{2}-4\,{{\gamma }}^{2}{{\epsilon } }^{2}+4\,{{\epsilon }}^{2}-2\,i{{\gamma }}^{6}u\,{{x_{*}}}^{4}{{ \epsilon }}^{2}\\&\quad +4\,i{{\gamma }}^{4}u\,{{x_{*}}}^{2}{{\epsilon }}^{2}+4\,i{{\gamma }}^{3}u\,{{x_{*}}}^{2}{\epsilon }\\&\quad +2\,{{\gamma }}^{2}{{\epsilon }}^{4}+4\,{\gamma }\,{{\epsilon }}^{3}-{ {\gamma }}^{4}{{\epsilon }}^{4}-4\,{{\gamma }}^{3}{{ \epsilon }}^{3}. \end{aligned}$$

The restriction of the map (3) on (20), at the critical value k has the form

$$\begin{aligned} \varsigma \mapsto G_{NS}=e ^{i\theta _0}\varsigma +d_{NS}\varsigma |\varsigma |^2+{\mathcal {O}}(\varsigma ^4),\quad \varsigma \in {\mathbb {C}}, \end{aligned}$$

(21)

where $d_{NS}$ is a complex number. Given the properties of the center manifold, the following equation is obtained

$$\begin{aligned} {\mathcal {N}}\left( M_{NS}(\varsigma ,\vartheta _{*}\right) =M_{NS}\left( G_{NS}(\varsigma )\right) . \end{aligned}$$

(22)

The following equations can be found by collecting the power of $\varsigma$ terms up to the third:

$$\begin{aligned} ({\mathcal {J}}-e^{2i\theta _0}I_2)m_{20}&=-B(v,v,\vartheta _{*}), \end{aligned}$$

(23)

$$\begin{aligned} ({\mathcal {J}}-I_2)m_{11}&=-B(v,{\bar{v}},\vartheta _{*}), \end{aligned}$$

(24)

$$\begin{aligned} ({\mathcal {J}}-e^{3i\theta _0}I_2)m_{30}&=-C(v,v,v,\vartheta _{*})-3B(v,m_{20},\vartheta _{*}), \end{aligned}$$

(25)

$$\begin{aligned} ({\mathcal {J}}-e^{i\theta _0}I_2)m_{21}&=2d_{NS}v-C(v,v,{\bar{v}},\vartheta _{*})\nonumber \\&\quad -B({\bar{v}},m_{20},\vartheta _{*})-2B(v,m_{11},\vartheta _{*}). \end{aligned}$$

(26)

where $,\vartheta _{*}=\left( \epsilon ,\gamma ,-{\frac{-{\gamma }^{3}{{x_{*}}}^{2}+\epsilon +\gamma }{\epsilon \,{ \gamma }^{3}{{x_{*}}}^{2}-\epsilon \,\gamma -1}},\beta \right)$. Equations (23)–(25) have a unique solution because 1, $e^{2i\theta _0}$ and $e^{3i\theta _0}$ are not eigenvalues of ${\mathcal {J}}$. To avoid the complexity of the computation, we consider

$$\begin{aligned} \gamma =1.32,\quad \beta =1,\quad \epsilon =0.7. \end{aligned}$$

The solutions of (23)–(25) can be calculated as

$$\begin{aligned} m_{20}&=-({\mathcal {J}}-e^{2i\theta _0}I_2)^{-1}B(v,v,\vartheta _{*})\\&\Rightarrow m_{20}=\begin{pmatrix} - 1.5298- 0.86186\,i\\ - 0.14670- 0.95607\,i \end{pmatrix},\\ m_{11}&=-({\mathcal {J}}-I_2)^{-1}B(v,{\bar{v}},\vartheta _{*})\\&\Rightarrow m_{11}=\begin{pmatrix} 1.0487- 0.00000021703\,i \\ 0.41699- 0.000000086299\,i \end{pmatrix},\\ m_{30}&=({\mathcal {J}}-e^{3i\theta _0}I_2)^{-1}\left( -C(v,v,v,\vartheta _{*})-3B(v,m_{20},\vartheta _{*})\right) \\&\Rightarrow m_{30}=\begin{pmatrix} 0.59123- 9.3739\,i\\ - 1.6095- 3.7344\,i \end{pmatrix}. \end{aligned}$$

The system (26) is singular; therefore, it is solvable if

$$\begin{aligned}&\langle w,2d_{NS}v-C(v,v,{\bar{v}},\vartheta _{*})-B({\bar{v}},m_{20},\vartheta _{*})\\&\quad -2B(v,m_{11},\vartheta _{*})\rangle =0. \end{aligned}$$

So we conclude that

$$\begin{aligned} d_{NS}=3.2480+ 0.86940\,i. \end{aligned}$$

The first Lyapunov coefficient of the Neimark–Sacker bifurcation is

$$\begin{aligned} c_{NS}=\mathfrak {R}\left( {e^{-i\theta _0}d_{NS}}\right) =- 1.716436045. \end{aligned}$$

Since $c_{NS}<0$, the Neimark–Sacker bifurcation is supercritical and the closed invariant curve is stable. $\square$

4 Codim-2 bifurcations

In this section we consider $\gamma , \beta$ as fixed parameters and k and $\epsilon$ as free parameters. The system (3) has the following local codim-2 bifurcations.

Theorem 5

There is a non-degenerate 1:2 resonance bifurcation of the fixed point $E_{*}$ at the parameter values $k={\gamma }^{3}{{x_{*}}}^{2}-\gamma +2$ and $\epsilon =2\, ( {\gamma }^{3}{{x_{*}}}^{2}-\gamma +1 ) ^{-1}$.

Proof

The map (3) has a fixed point with two multipliers $-1$ if

$$\begin{aligned} \left\{ \begin{array}{ll} {\mathcal {N}}(\xi ,\vartheta )=0,\\ \det \left( {\mathcal {J}}(\xi ,\vartheta )\odot {\mathcal {J}}(\xi ,\vartheta ) -I_2\right) =0,\\ \kappa +1=0, \end{array} \right. \end{aligned}$$

(27)

where $\kappa$ is the real part of the critical multipliers $e^{\pm i\theta _0}$ along the Neimark–Sacker curve. The exact solution of (27) is

$$\begin{aligned} x&=x_{*},&y&=\frac{1}{k}(x_{*}+\beta ),\\ k&={\gamma }^{3}{{x_{*}}}^{2}-\gamma +2,&\epsilon&=2\, \left( {\gamma }^{3}{{x_{*}}}^{2}-\gamma +1 \right) ^{-1}. \end{aligned}$$

The center manifold of the map (3) at $k ={\gamma }^{3}{{x_{*}}}^{2}-\gamma +2$ and $\epsilon =2\, \left( {\gamma }^{3}{{x_{*}}}^{2}-\gamma +1 \right) ^{-1}$ can be considered as follows:

$$\begin{aligned} M_{R_2}(\eta _1,\eta _2)&=\eta _1v_0+\eta _2v_1\nonumber \\&\quad +\sum _{2\le j+k \le 3}\frac{1}{j1k!}m_{jk}\eta _1^j\eta _2^k, \end{aligned}$$

(28)

where

$$\begin{aligned} {\mathcal {J}}v_0&=-v_0,&{\mathcal {J}}v_1&=-v_1+v_0\\ {\mathcal {J}}^Tw_0&=-w_0,&{\mathcal {J}}^Tw_1&=-w_1+w_0,\\ \left\langle w_0,v_1\right\rangle&=\left\langle w_1,v_0\right\rangle =1,&\left\langle w_0,v_0\right\rangle&=\left\langle w_1,v_1\right\rangle =0,\\ v_0&=\begin{pmatrix} 1\\ 1 \end{pmatrix},&v_1&=\begin{pmatrix} 0\\ \frac{1}{2} \end{pmatrix},\\ w_0&=\begin{pmatrix} -2\\ 2 \end{pmatrix},&w_1&=\begin{pmatrix} 1\\ 0 \end{pmatrix}. \end{aligned}$$

The map (3) can be restricted to (28) as follows:

$$\begin{aligned} \begin{pmatrix} \eta _1\\ \eta _2 \end{pmatrix}&\mapsto G_{R_2}(\eta )= \begin{pmatrix} -\eta _1+\eta _2\\ -\eta _2+C_{R_2}\eta _1^3+D_{R_2}\eta _1^2\eta _2 \end{pmatrix},\nonumber \\ \eta&=(\eta _1,\eta _2)\in {\mathbb {R}}^2. \end{aligned}$$

(29)

Given the invariance property of the central manifold, we concluded that

$$\begin{aligned} {\mathcal {N}}\left( M_{R_2}(\eta ),\vartheta _{*}\right) =M_{R_2}\left( G_{R_2}(\eta )\right) . \end{aligned}$$

(30)

The following equations are obtained from (30):

$$\begin{aligned} ({\mathcal {J}}-I_2)m_{20}&=-B(v_0,v_0,\vartheta _{*})\\&\Rightarrow m_{20}=\begin{pmatrix} -2\,{\frac{ \left( {\gamma }^{3}{{ x_{*}}}^ {2}-\gamma +2 \right) {\gamma }^{3}{} { x_{*}}}{ \left( {\gamma }^{3}{{ x_{*}}}^{2}-\gamma +1 \right) ^{2}}}\\ -2\,{\frac{ {\gamma }^{3}{} { x_{*}}}{ \left( {\gamma }^{3}{{ x_{*}}}^{2}-\gamma +1 \right) ^{2}}} \end{pmatrix}, \\ ({\mathcal {J}}-I_2)m_{11}&=-B(v_0,v_1,\vartheta _{*})-m_{20}\\&\Rightarrow m_{11}= \begin{pmatrix} -{\frac{{\gamma }^{3}{} { x_{*}}\, \left( 3\,{ \gamma }^{3}{{ x_{*}}}^{2}-3\,\gamma +7 \right) }{ \left( {\gamma }^{3 }{{ x_{*}}}^{2}-\gamma +1 \right) ^{2}}}\\ -4\,{ \frac{{\gamma }^{3}{} { x_{*}}}{ \left( {\gamma }^{3}{{ x_{*}}}^{2}- \gamma +1 \right) ^{2}}} \end{pmatrix}, \\ ({\mathcal {J}}-I_2)m_{02}&=-B(v_1,v_1,\vartheta _{*})-2m_{11}+m_{20}\\&\Rightarrow m_{02}=\begin{pmatrix} -{\frac{{\gamma }^{3}{} { x_{*}}\, \left( 2\,{ \gamma }^{3}{{ x_{*}}}^{2}-2\,\gamma +7 \right) }{ \left( {\gamma }^{3 }{{ x_{*}}}^{2}-\gamma +1 \right) ^{2}}}\\ -5\,{ \frac{{\gamma }^{3}{} { x_{*}}}{ \left( {\gamma }^{3}{{ x_{*}}}^{2}- \gamma +1 \right) ^{2}}} \end{pmatrix}. \end{aligned}$$

The cubic part of (30) gives

$$\begin{aligned} ({\mathcal {J}}+I_2)m_{30}&=6\,C_{R_2}v_1+C(v_0,v_0,v_0,\vartheta _{*})\nonumber \\&\quad -3B(v_0,m_{20},)\vartheta _{*}, \end{aligned}$$

(31)

$$\begin{aligned} ({\mathcal {J}}+I_2)m_{21}&=2\,D_{R_2}v_1+m_{30}-C(v_0,v_0,v_1,\vartheta _{*})\nonumber \\&\quad -2B(v_0,m_{11},\vartheta _{*})-B(v_1,m_{20},\vartheta _{*}), \end{aligned}$$

(32)

$$\begin{aligned} ({\mathcal {J}}+I_2)m_{12}&=2\,m_{21}-m_{30}-C(v_0,v_0,v_0,\vartheta _{*})\nonumber \\&\quad -2B(v_1,m_{11},\vartheta _{*})-B(v_0,m_{02},\vartheta _{*}), \end{aligned}$$

(33)

$$\begin{aligned} ({\mathcal {J}}+I_2)m_{03}&=3(m_{12}-m_{21})+m_{30}\nonumber \\&\quad -C(v_1,v_1,v_1,\vartheta _{*})-3B(v_1,m_{02},\vartheta _{*}), \end{aligned}$$

(34)

where $\vartheta _{*}=\left( 2\, \left( {\gamma }^{3}{{x_{*}}}^{2}-\gamma +1 \right) ^{-1},\gamma ,{\gamma }^{3}{{x_{*}}}^{2}-\gamma +2,\beta \right)$. The solvability condition of the singular system (31) implies that

$$\begin{aligned} \langle w_0,6\,C_{R_2}v_1+C(v_0,v_0,v_0,\vartheta _{*})-3B(v_0,m_{20},\vartheta _{*})\rangle&=0; \end{aligned}$$

thus,

$$\begin{aligned} C_{R_2}={\frac{-4{\gamma }^{3} \left( 5\,{\gamma }^{6}{{ x_{*}}}^{4}-4\,{ \gamma }^{4}{{ x_{*}}}^{2}+10\,{\gamma }^{3}{{ x_{*}}}^{2}-{\gamma }^{ 2}+2\,\gamma -1 \right) }{3 \left( {\gamma }^{3}{{ x_{*}}}^{2}-\gamma + 1 \right) ^{3}}}. \end{aligned}$$

The singular system (32) has an unique solution provided

$$\begin{aligned}&\langle w_0,2\,D_{R_2}v_1+m_{30}-C(v_0,v_0,v_1,\vartheta _{*})-2B(v_0,m_{11},\vartheta _{*})\\&\quad -B(v_1,m_{20},\vartheta _{*})\rangle =0. \end{aligned}$$

Since

$$\begin{aligned} \langle w_0,m_{30}\rangle&=-\langle w_1,3\,B(v_0,m_{20},\vartheta _{*})+C(v_0,v_0,v_0,\vartheta _{*})\rangle \\&=-4\,{\frac{{\gamma }^{3} \left( 5\,{\gamma }^{6}{{ x_{*}}}^{4}-4\,{ \gamma }^{4}{{ x_{*}}}^{2}+10\,{\gamma }^{3}{{ x_{*}}}^{2}-{\gamma }^{ 2}+2\,\gamma -1 \right) }{ \left( {\gamma }^{3}{{ x_{*}}}^{2}-\gamma + 1 \right) ^{3}}}, \end{aligned}$$

the third-order coefficient of (29) can be calculated as

$$\begin{aligned} D_{R2}&=-2\,{\frac{{\gamma }^{3} \left( 7\,{\gamma }^{6}{{x_{*}}}^{4}-8\,{ \gamma }^{4}{{x_{*}}}^{2}+18\,{\gamma }^{3}{{x_{*}}}^{2}+{\gamma }^{ 2}-2\,\gamma +1 \right) }{ \left( {\gamma }^{3}{{x_{*}}}^{2}-\gamma + 1 \right) ^{3}}}. \end{aligned}$$

The non-degeneracy conditions of this bifurcation are $C_{1}=4C_{R_2}\ne 0$ and $D_{1}=-2D_{R_2}-6C_{R_2}\ne 0$. The sign of $C_{1}$ determines the type of the critical point. The bifurcation scenario is indicated by the coefficient $D_{1}$. $\square$

Theorem 6

There is a non-degenerate 1 : 3 resonance bifurcation of the fixed point $E_{*}$ at

$$\begin{aligned} k&=-{\frac{-{{\gamma }}^{6}{{x_{*}}}^{4}+2\,{{\gamma }}^{4}{{ x_{*}}}^{2}+{{\gamma }}^{3}u\,{{x_{*}}}^{2}-{{\gamma }}^{2}- {\gamma }\,u+2}{{{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }+u}},\\ \epsilon&=\frac{1}{2}\,{\frac{{{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }+u}{{{\gamma }}^{6}{{x_{*}}}^{4}-2\,{{\gamma }}^{4}{{x_{*}}}^{2}+ {{\gamma }}^{2}-1}}, \end{aligned}$$

where

$$\begin{aligned} u=\sqrt{-3\,{\gamma }^{6}{{x_{*}}}^{4}+6\,{\gamma }^{4}{{x_{*}}}^{2}- 3\,{\gamma }^{2}+4}. \end{aligned}$$

Proof

The map (3) has a fixed point with a pair of complex conjugate multipliers $e^{\pm i \frac{2\pi }{3}}$ if

$$\begin{aligned} \left\{ \begin{array}{ll} {\mathcal {N}}(\xi ,\vartheta )-\xi =0,\\ \det \left( {\mathcal {J}}(\xi ,\vartheta )\odot {\mathcal {J}}(\xi ,\vartheta ) -I_2\right) =0,\\ \kappa +\frac{1}{2}=0, \end{array} \right. \end{aligned}$$

(35)

where $\kappa =\cos (\theta _0)$ along the Neimark–Sacker curve. The exact solution of (35) is

$$\begin{aligned} x&=x_{*},\quad y=\frac{1}{k}(x_{*}+\beta ),\\ k&=-{\frac{-{{\gamma }}^{6}{{x_{*}}}^{4}+2\,{{\gamma }}^{4}{{ x_{*}}}^{2}+{{\gamma }}^{3}u\,{{x_{*}}}^{2}-{{\gamma }}^{2}- {\gamma }\,u+2}{{{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }+u}}, \\ \epsilon&=1/2\,{\frac{{{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }+u}{{{\gamma }}^{6}{{x_{*}}}^{4}-2\,{{\gamma }}^{4}{{x_{*}}}^{2}+ {{\gamma }}^{2}-1}}. \end{aligned}$$

Let us consider

$$\begin{aligned} M_{R_3}(\zeta ,{\bar{\zeta }})&=v\zeta +{\bar{\zeta }}{\bar{v}}+\sum _{2\le k+l}\frac{1}{(k+l)!}m_{kl}\zeta ^k{\bar{\zeta }}^l, \nonumber \\ \zeta&\in {\mathbb {C}}, \quad m_{kl}\in {\mathbb {C}}, \end{aligned}$$

(36)

as the center manifold of (3) at $k=-{\frac{-{{\gamma }}^{6}{{x_{*}}}^{4}+2\,{{\gamma }}^{4}{{ x_{*}}}^{2}+{{\gamma }}^{3}u\,{{x_{*}}}^{2}-{{\gamma }}^{2}- {\gamma }\,u+2}{{{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }+u}}$ and $\epsilon =1/2\,{\frac{{{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }+u}{{{\gamma }}^{6}{{x_{*}}}^{4}-2\,{{\gamma }}^{4}{{x_{*}}}^{2}+ {{\gamma }}^{2}-1}}$, where

$$\begin{aligned} {\mathcal {J}}v=e^{\frac{2\pi }{3}i}v,\quad {\mathcal {J}}^Tw=e^{\frac{-2\pi }{3}i}w,\quad \left\langle w,v\right\rangle =1, \end{aligned}$$

and

$$\begin{aligned} v&=\begin{pmatrix} -{\frac{{{\gamma }}^{3}{{x_{*}}}^{2}-{ \gamma }+u}{i{{\gamma }}^{6}{{x_{*}}}^{4}\sqrt{3}-2\,i{{\gamma }}^{4}{{x_{*}}}^{2}\sqrt{3}+{{\gamma }}^{3}u\,{{x_{*}}}^{2 }+i{{\gamma }}^{2}\sqrt{3}-i\sqrt{3}-{\gamma }\,u+1}} \\ 1 \end{pmatrix},\\ w&=\frac{1}{\overline{wv}}\begin{pmatrix} {\frac{{{\gamma }}^{3}{{x_{*}}}^{2}-{ \gamma }+u}{-i{{\gamma }}^{6}{{x_{*}}}^{4}\sqrt{3}+2\,i{{\gamma }}^{4}{{x_{*}}}^{2}\sqrt{3}+{{\gamma }}^{3}u\,{{x_{*}}}^{2 }-i{{\gamma }}^{2}\sqrt{3}-{\gamma }\,u+i\sqrt{3}+1}} \\ 1 \end{pmatrix},\\ vw&=-{\frac{ \left( {{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }+u \right) ^{2}}{ \left( i{{\gamma }}^{6}{{x_{*}}}^{4}\sqrt{3}-2\,i {{\gamma }}^{4}{{x_{*}}}^{2}\sqrt{3}+{{\gamma }}^{3}u\,{{ x_{*}}}^{2}+i{{\gamma }}^{2}\sqrt{3}-i\sqrt{3}-{\gamma }\,u+1 \right) ^{2}}}+1. \end{aligned}$$

The restriction of the map (3) on (36) has the form

$$\begin{aligned}&\zeta \mapsto G_{R_3}(\zeta )=e ^{\frac{2\pi }{3}i}\zeta +B_{R_3}{\bar{\zeta }}^2+C_{R_3}\zeta |\zeta |^2+{\mathcal {O}}(\zeta ^{4}),\\&\quad \zeta \in {\mathbb {C}}. \end{aligned}$$

The invariance property of the center manifold cause to

$$\begin{aligned} {\mathcal {N}}\left( M_{R_3}(\zeta ),\vartheta _{*}\right) =M_{R_3}\left( G_{R_3}(\zeta )\right) , \end{aligned}$$

(37)

where $\vartheta _{*}=\left( 1/2\,{\frac{{{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }+u}{{{\gamma }}^{6}{{x_{*}}}^{4}-2\,{{\gamma }}^{4}{{x_{*}}}^{2}+ {{\gamma }}^{2}-1}}),\gamma ,\right. \left. -{\frac{-{{\gamma }}^{6}{{x_{*}}}^{4}+2\,{{\gamma }}^{4}{{ x_{*}}}^{2}+{{\gamma }}^{3}u\,{{x_{*}}}^{2}-{{\gamma }}^{2}- {\gamma }\,u+2}{{{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }+u}},\beta \right)$. The quadratic terms of (37) gives

$$\begin{aligned} ({\mathcal {J}}-e^{\frac{4\pi }{3}i}I_2)m_{20}&=2\, \overline{B_{R_3}}\overline{v}-B(v,v,\vartheta _{*}), \end{aligned}$$

(38)

$$\begin{aligned} ({\mathcal {J}}-I_2)m_{11}&=-B(v,{\bar{v}}), \end{aligned}$$

(39)

$$\begin{aligned} ({\mathcal {J}}-e^{\frac{-4\pi }{3}i}I_2)m_{02}&=2\, B_{R_3}v-B({\bar{v}},{\bar{v}},\vartheta _{*}). \end{aligned}$$

(40)

Applying the Fredholm condition to singular system (40), we have

$$\begin{aligned} \langle w,2\, B_{R_3}v-B({\bar{v}},{\bar{v}},\vartheta _{*})\rangle =0\Rightarrow B_{R_3}=\frac{B_{1R_3}(\gamma ,x_{*}) }{B_{2R_3}(\gamma ,x_{*})}, \end{aligned}$$

where

$$\begin{aligned}&B_{1R_3}(\gamma ,x_{*})=- ( {{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }+u ) ^{4} ( i{{\gamma }}^{6}{{x_{*}}}^{4}\sqrt{3}-2\,i{{\gamma }}^ {4}{{x_{*}}}^{2}\sqrt{3}\\&\quad +{{\gamma }}^{3}u\,{{x_{*}}}^{2}+i{{\gamma }}^{2}\sqrt{3}-i\sqrt{3}-{\gamma }\,u+1 ) {{\gamma }}^{3}{x_{*}},\\&B_{2R_3}(\gamma ,x_{*})=2\, ( -3\,{{\gamma }}^{12}{{x_{*}}}^{8}+2\,i\sqrt{3}{\gamma }\,u+12\,{{\gamma }}^{10}{{x_{*}}}^{6}\\&\quad +2\,i{{\gamma }}^{6 }{{x_{*}}}^{4} \sqrt{3}-6\,i\sqrt{3}{{\gamma }}^{7}u\,{{x_{*}}}^ {4}-18\,{{\gamma }}^{8}{{x_{*}}}^{4}\\&\quad +{{\gamma }}^{6}{u}^{2}{{ x_{*}}}^{4}+2\,i\sqrt{3}{{\gamma }}^{9}u\,{{x_{*}}}^{6}+5\,{{ \gamma }}^{6}{{x_{*}}}^{4}-2\,i\sqrt{3}{{\gamma }}^{3}u\,{{ x_{*}}}^{2}\\&\quad +6\,i\sqrt{3}{{\gamma }}^{5}u\,{{x_{*}}}^{2}+12\,{{ \gamma }}^{6}{{x_{*}}}^{2}\\&\quad -2\,{{\gamma }}^{4}{u}^{2}{{x_{*}}}^ {2}-2\,i\sqrt{3}{{\gamma }}^{3}u-10\,{{\gamma }}^{4}{{x_{*}}}^ {2}-4\,i{{\gamma }}^{4}{{x_{*}}}^{2}\\&\quad \sqrt{3}-2\,i\sqrt{3}-3\,{{ \gamma }}^{4}+{{\gamma }}^{2}{u}^{2}+2\,i{{\gamma }}^{2} \sqrt{3}\\&\quad +5\,{{\gamma }}^{2}-{u}^{2}-2 )( {{\gamma }}^{6}{{x_{*}}}^{4}-2\,{{\gamma }}^{4}{{x_{*}}}^{2}+{{\gamma } }^{2}-1 )\\&\quad ( i{{\gamma }}^{6}{{x_{*}}}^{4}\sqrt{3}-2\, i{{\gamma }}^{4}{{x_{*}}}^{2}\sqrt{3}-{{\gamma }}^{3}u\,{{ x_{*}}}^{2}\\&\quad +i{{\gamma }}^{2}\sqrt{3}-i\sqrt{3}+{\gamma }\,u-1 ) ^{2}. \end{aligned}$$

The unique solution of the singular system is obtained as follows:

$$\begin{aligned} m_{11}=\begin{pmatrix} \frac{2\,{x_{*}}\,{{\gamma }}^{3} \left( {{\gamma }}^{3}{{x_{*}}}^{2 }-{\gamma }+u \right) ^{2} \left( {{\gamma }}^{6}{{x_{*}}}^{4}- 2\,{{\gamma }}^{4}{{x_{*}}}^{2}-{{\gamma }}^{3}u\,{{x_{*}}}^{2 }+{{\gamma }}^{2}+{\gamma }\,u-2 \right) }{m_{11R_3}}\\ \frac{2\, \left( {{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }+u \right) ^{3 }{{\gamma }}^{3}{x_{*}} }{m_{11R_3}} \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned}&m_{11R_3}=\left( {{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }-u \right) \left( {{\gamma }}^{6}{{x_{*}}}^{4}-2\,{{\gamma }}^{4}{{x_{*} }}^{2}+{{\gamma }}^{2}-1 \right) \\&\quad \left( i{{\gamma }}^{6}{{ x0}}^{4}\sqrt{3}-2\,i{{\gamma }}^{4}{{x_{*}}}^{2}\right. \\&\left. \quad \sqrt{3}+{{\gamma }}^{3}u\,{{x_{*}}}^{2}+i{{\gamma }}^{2}\sqrt{3}-i\sqrt{3}- {\gamma }\,u+1 \right) \\&\quad \left( i{{\gamma }}^{6}{{x_{*}}}^{4} \sqrt{3}-2\,i{{\gamma }}^{4}{{x_{*}}}^{2}\sqrt{3}-{{\gamma }} ^{3}u\,{{x_{*}}}^{2}+i{{\gamma }}^{2}\right. \\&\left. \quad \sqrt{3}-i\sqrt{3}+{\gamma }\,u-1 \right) , \end{aligned}$$

The $\zeta ^2{\bar{\zeta }}-$terms in (37) gives:

$$\begin{aligned}&({\mathcal {J}}-e^{\frac{2\pi }{3}i}I_2)m_{21}=2\,C_{R_3}v+e^{-\frac{-2\pi }{3}i}\overline{B_{R_3}}m_{02}\nonumber \\&\quad -2B(v,m_{11},\vartheta _{*})-B({\bar{v}},m_{20},\vartheta _{*})-C(v,v,{\bar{v}},\vartheta _{*}). \end{aligned}$$

(41)

The singular system (41) can be solved if

$$\begin{aligned}&\langle w, 2\,C_{R_3}v+e^{-\frac{-2\pi }{3}i}\overline{B_{R_3}}m_{02}-2B(v,m_{11},\vartheta _{*})\nonumber \\&\quad -B({\bar{v}},m_{20},\vartheta _{*})-C(v,v,{\bar{v}},\vartheta _{*})\rangle =0; \end{aligned}$$

therefore, $C_{R_3}$ can be obtained as follows:

$$\begin{aligned} C_{R_3}=\frac{C_{1R_3}(\gamma ,x_{*})}{C_{2R_3}(\gamma ,x_{*})}, \end{aligned}$$

where $C_{1R_3}(\gamma ,x_{*})=\zeta _{1}+\zeta _{2}+\zeta _{3}+ \zeta _{4}+\zeta _{5}+\zeta _{6}+\zeta _{7}+\zeta _{8}+\zeta _{9}$, and

$$\begin{aligned} \zeta _{1}&= ( {{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }+u ) ^{5}{{ \gamma }}^{3} ( 2\,i\sqrt{3}{{\gamma }}^{2}{u}^{2}\\&\quad -214\,{{ \gamma }}^{9}u\,{{x_{*}}}^{6}+354\, {{\gamma }}^{7}u\,{{x_{*}}} ^{4}-66\,{{\gamma }}^{5}u\,{{x_{*}}}^{2}\\&\quad -38\,i\sqrt{3}{{\gamma }}^{21}u\,{{x_{*}}}^{14}+218\,i\sqrt{3}{{\gamma }}^{19}u\,{{x_{*}}}^{12}\\&\quad -14\,i\sqrt{3}{{\gamma }}^{18}{u}^{2}{{x_{*}}}^{12} +38\,i\sqrt{3}{{\gamma }}^{18}u\,{{x_{*}}}^{12}\\&\quad -510\,i\sqrt{3}{{\gamma }}^{17}u\,{{x_{*}}}^{10}+64\,i\sqrt{3}{{\gamma }}^{16}{ u}^{2}{{x_{*}}}^{10}\\&\quad +14\,i\sqrt{3}{{\gamma }}^{15}{u}^{3}{{x_{*} }}^{10}-180\,i\sqrt{3}{{\gamma }}^{16}u\,{{x_{*}}}^{10}\\&\quad +14\,i\sqrt{3}{{\gamma }}^{15}{u}^{2}{{x_{*}}}^{10}+30\,i\sqrt{3}{{ \gamma }}^{15}u\,{{x_{*}}}^{10}\\&\quad +610\,i\sqrt{3}{{\gamma }}^{15} u\,{{x_{*}}}^{8}-110\,i\sqrt{3}{{\gamma }}^{14}{u}^{2}{{x_{*}}}^ {8}\\&\quad -54\,i\sqrt{3}{{\gamma }}^{13}{u}^{3}{{x_{*}}}^{8}+8\,i\sqrt{ 3}{{\gamma }}^{12}{u}^{4}{{x_{*}}}^{8}\\&\quad +330\,i\sqrt{3}{{\gamma }}^{14}u\,{{x_{*}}}^{8}-50\,i\sqrt{3}{{\gamma }}^{13}{u}^{2}{{ x_{*}}}^{8}\\&\quad -14\,i\sqrt{3}{{\gamma }}^{12}{u}^{3}{{x_{*}}}^{8}-92 \,i\sqrt{3}{{\gamma }}^{13}u\,{{x_{*}}}^{8}\\&\quad +28\,i\sqrt{3}{{\gamma }}^{12}{u}^{2}{{x_{*}}}^{8}-30\,i\sqrt{3}{{\gamma }}^{12}u \,{{x_{*}}}^{8} \end{aligned}$$

$$\begin{aligned} \zeta _{2}&=-370\,i\sqrt{3}{{\gamma }}^{13}u\,{{x_{*}}}^{6}+ 80\,i\sqrt{3}{{\gamma }}^{12}{u}^{2}{{x_{*}}}^{6}\\&\quad +76\,i\sqrt{3}{ {\gamma }}^{11}{u}^{3}{{x_{*}}}^{6}-22\,i\sqrt{3}{{\gamma }}^{ 10}{u}^{4}{{x_{*}}}^{6}\\&\quad -280\,i\sqrt{3}{{\gamma }}^{12}u\,{{x_{*} }}^{6}+60\,i\sqrt{3}{{\gamma }}^{11}{u}^{2}{{x_{*}}}^{6}\\&\quad +40\,i \sqrt{3}{{\gamma }}^{10}{u}^{3}{{x_{*}}}^{6}-8\,i\sqrt{3}{{\gamma }}^{9}{u}^{4}{{x_{*}}}^{6}\\&\quad +68\,i\sqrt{3}{{\gamma }}^{11}u\, {{x_{*}}}^{6}-76\,i\sqrt{3}{{\gamma }}^{10}{u}^{2}{{x_{*}}}^{6}\\&\quad +10\,i\sqrt{3}{{\gamma }}^{9}{u}^{3}{{x_{*}}}^{6}+62\,i\sqrt{3}{{ \gamma }}^{10}u\,{{x_{*}}}^{6}\\&\quad -28\,i\sqrt{3}{{\gamma }}^{9}{u} ^{2}{{x_{*}}}^{6}+78\,i\sqrt{3}{{\gamma }}^{11}u\,{{x_{*}}}^{4}\\&\quad -10\,i\sqrt{3}{{\gamma }}^{10}{u}^{2}{{x_{*}}}^{4}-44\,i\sqrt{3}{ {\gamma }}^{9}{u}^{3}{{x_{*}}}^{4}\\&\quad -6\,i\sqrt{3}{{\gamma }}^{9} u\,{{x_{*}}}^{6}+18\,i\sqrt{3}{{\gamma }}^{8}{u}^{4}{{x_{*}}}^{4 }\\&\quad +90\,i\sqrt{3}{{\gamma }}^{10}u\,{{x_{*}}}^{4}-20\,i\sqrt{3}{{ \gamma }}^{9}{u}^{2}{{x_{*}}}^{4}\\&\quad -36\,i\sqrt{3}{{\gamma }}^{8} {u}^{3}{{x_{*}}}^{4}+14\,i\sqrt{3}{{\gamma }}^{7}{u}^{4}{{x_{*}} }^{4}\\&\quad +48\,i\sqrt{3}{{\gamma }}^{9}u\,{{x_{*}}}^{4}+60\,i\sqrt{3} {{\gamma }}^{8}{u}^{2}{{x_{*}}}^{4}\\&\quad -24\,i\sqrt{3}{{\gamma }}^{7}{u}^{3}{{x_{*}}}^{4}+3\,i\sqrt{3}{{\gamma }}^{6}{u}^{4}{{x_{*} }}^{4}\\&\quad -6\,i\sqrt{3}{{\gamma }}^{8}u\,{{x_{*}}}^{4}+48\,i\sqrt{3}{{\gamma }}^{7}{u}^{2}{{x_{*}}}^{4} \end{aligned}$$

$$\begin{aligned} \zeta _{3}&=-10\,i\sqrt{3}{{\gamma }}^{6}{u}^{3}{{x_{*}}}^{4}-3\,{{\gamma }}^{8}+30\,i\sqrt{3}{{\gamma }}^{24}{{x_{*}}}^{16}\\&\quad -198\,i\sqrt{3}{{\gamma }}^{22}{{ x_{*}}}^{14} -30\,i\sqrt{3}{{\gamma }}^{21}{{x_{*}}}^{14}+546\,i \sqrt{3}{{\gamma }}^{20}{{x_{*}}}^{12}\\&\quad +168\,i\sqrt{3}{{\gamma }}^{19}{{x_{*}}}^{12}-135\,i\sqrt{3}{{\gamma }}^{18}{{ x_{*}}}^{12}\\&\quad -798\,i\sqrt{3}{{\gamma }}^{18}{{x_{*}}}^{10}-378\,i \sqrt{3}{{\gamma }}^{17}{{x_{*}}}^{10}\\&\quad +645\,i\sqrt{3}{{\gamma }}^{16}{{x_{*}}}^{10}+135\,i\sqrt{3}{{\gamma }}^{15}{{ x_{*}}}^{10}\\&\quad +630\,i\sqrt{3}{{\gamma }}^{16}{{x_{*}}}^{8}+420\,i \sqrt{3}{{\gamma }}^{15}{{x_{*}}}^{8}\\&\quad -1200\,i\sqrt{3}{{\gamma }}^{14}{{x_{*}}}^{8}-510\,i\sqrt{3}{{\gamma }}^{13}{{x_{*}}}^{8}\\&\quad -210\,i\sqrt{3}{{\gamma }}^{14}{{x_{*}}}^{6}+150\,i\sqrt{3 }{{\gamma }}^{12}{{x_{*}}}^{8}\\&\quad -210\,i\sqrt{3}{{\gamma }}^{13}{ {x_{*}}}^{6}+1050\,i\sqrt{3}{{\gamma }}^{12}{{x_{*}}}^{6}\\&\quad +690\,i\sqrt{3}{{\gamma }}^{11}{{x_{*}}}^{6}-42\,i\sqrt{3}{{\gamma } }^{12}{{x_{*}}}^{4}\\&\quad -424\,i\sqrt{3}{{\gamma }}^{10}{{x_{*}}}^{6}- 150\,i\sqrt{3}{{\gamma }}^{9}{{x_{*}}}^{6}\\&\quad -375\,i\sqrt{3}{{\gamma }}^{10}{{x_{*}}}^{4}-360\,i\sqrt{3}{{\gamma }}^{9}{x_{*}}\\&\quad +54\,i\sqrt{3}{{\gamma }}^{10}{{x_{*}}}^{2}+372\,i\sqrt{3}{{\gamma }}^{8}{{x_{*}}}^{4^{4}} \end{aligned}$$

$$\begin{aligned} \zeta _{4}&=42\,i\sqrt{3}{{\gamma }}^{9}{{ x_{*}}}^{2}+274\,i\sqrt{3}{{\gamma }}^{7}{{x_{*}}}^{4}\\&\quad -15\,i\sqrt{3 }{{\gamma }}^{8}{{x_{*}}}^{2}-56\,i{{\gamma }}^{6}{{x_{*}}}^{4 }\sqrt{3}\\&\quad +15\,i\sqrt{3}{{\gamma }}^{7}{{x_{*}}}^{2}-10\,i\sqrt{3}{{\gamma }}^{7}u\\&\quad +6\,i\sqrt{3}{{\gamma }}^{6}{u}^{2}-72\,i{{ \gamma }}^{6}{{x_{*}}}^{2}\sqrt{3}+2\,i\sqrt{3}{{\gamma }}^{5 }{u}^{3}\\&\quad -2\,i\sqrt{3}{{\gamma }}^{4}{u}^{4} -10\,i\sqrt{3}{{\gamma }}^{6}u+6\,i\sqrt{3}{{\gamma }}^{5}{u}^{2}\\&\quad -98\,i\sqrt{3}{{ \gamma }}^{5}{{x_{*}}}^{2}+2\,i\sqrt{3}{{\gamma }}^{4}{u}^{3}\\&\quad -2\,i\sqrt{3}{{\gamma }}^{3}{u}^{4}+28\,i\sqrt{3}{{\gamma }}^{5 }u-8\,i\sqrt{3}{{\gamma }}^{4}{u}^{2}\\&\quad +48\,i{{\gamma }}^{4}{{x_{*}}}^{2}\sqrt{3}-4\,i\sqrt{3}{{\gamma }}^{3}{u}^{3}\\&\quad +2\,i\sqrt{3}{{\gamma }}^{2}{u}^{4}+28\,i\sqrt{3}{{\gamma }}^{4}u-8 \,i\sqrt{3}{{\gamma }}^{3}{u}^{2}\\&\quad +56\,i\sqrt{3}{{\gamma }}^{3} {{x_{*}}}^{2}-4\,i\sqrt{3}{{\gamma }}^{2}{u}^{3}\\&\quad +2\,i\sqrt{3}{ \gamma }\,{u}^{4}-26\,i\sqrt{3}{{\gamma }}^{3}u+2\,i\sqrt{3}{ \gamma }\,{u}^{3}\\&\quad -26\,i\sqrt{3}{{\gamma }}^{2}u+2\,i\sqrt{3}{ \gamma }\,{u}^{2}\\&\quad +8\,i\sqrt{3}{\gamma }\,u+22\,i\sqrt{3}{{\gamma }}^{9}u\,{{x_{*}}}^{2}\\&\quad -16\,i\sqrt{3}{{\gamma }}^{8}{u}^{2}{ {x_{*}}}^{2}+6\,i\sqrt{3}{{\gamma }}^{7}{u}^{3}{{x_{*}}}^{2} \end{aligned}$$

$$\begin{aligned} \zeta _{5}&=-14\,i\sqrt{3}{{\gamma }}^{7}u\,{{x_{*}}}^{4}-2\,i\sqrt{3}{{\gamma }}^{6}{u}^{4}{{x_{*}}}^{2}\\&\quad -14\,i\sqrt{3}{{\gamma }}^{6}{u}^ {2}{{x_{*}}}^{4}+12\,i\sqrt{3}{{\gamma }}^{8}u\,{{x_{*}}}^{2}\\&\quad -10\,i\sqrt{3}{{\gamma }}^{7}{u}^{2}{{x_{*}}}^{2}+8\,i\sqrt{3}{{ \gamma }}^{6}{u}^{3}{{x_{*}}}^{2}\\&\quad +6\,i\sqrt{3}{{\gamma }}^{6}u \,{{x_{*}}}^{4}-4\,i\sqrt{3}{{\gamma }}^{5}{u}^{4}{{x_{*}}}^{2}\\&\quad -82\,i\sqrt{3}{{\gamma }}^{7}u\,{{x_{*}}}^{2}-4\,i\sqrt{3}{{\gamma }}^{6}{u}^{2}{{x_{*}}}^{2}\\&\quad +18\,i\sqrt{3}{{\gamma }}^{5}{u}^ {3}{{x_{*}}}^{2}-5\,i\sqrt{3}{{\gamma }}^{4}{u}^{4}{{x_{*}}}^{2} \\&\quad -54\,i\sqrt{3}{{\gamma }}^{6}u\,{{x_{*}}}^{2}-12\,i\sqrt{3}{{ \gamma }}^{5}{u}^{2}{{x_{*}}}^{2}\\&\quad +14\,i\sqrt{3}{{\gamma }}^{4} {u}^{3}{{x_{*}}}^{2}-3\,i\sqrt{3}{{\gamma }}^{3}{u}^{4}{{x_{*}}} ^{2}\\&\quad +46\,i\sqrt{3}{{\gamma }}^{5}u\,{{x_{*}}}^{2}+12\,i\sqrt{3}{ {\gamma }}^{4}{u}^{2}{{x_{*}}}^{2}\\&\quad -2\,i\sqrt{3}{{\gamma }}^{3} {u}^{3}{{x_{*}}}^{2}+20\,i\sqrt{3}{{\gamma }}^{4}u\,{{x_{*}}}^{2 }\\&\quad +14\,i\sqrt{3}{{\gamma }}^{3}{u}^{2}{{x_{*}}}^{2}-8\,i\sqrt{3}{ {\gamma }}^{3}u\,{{x_{*}}}^{2}\\&\quad +24\,{\gamma }+24\,u+214\,{{\gamma }}^{6}u\,{{x_{*}}}^{4} \end{aligned}$$

$$\begin{aligned} \zeta _{6}&=-140\,{{\gamma }}^{4}u\,{{x_{*}}}^{2} +78\,{{\gamma }}^{6}u\,{{x_{*}}}^{2}-3\,{{\gamma }}^{7}\\&\quad -238\,{{ \gamma }}^{9}{{x_{*}}}^{6}+426\,{{\gamma }}^{7}{{x_{*}}}^{4}- 22\,{\gamma }\,{u}^{2}\\&\quad +22\,{{\gamma }}^{3}{u}^{2}{{x_{*}}}^{2}+29\,{{\gamma }}^{5}+6\,{{\gamma }}^{3}{u}^{4}{{x_{*}}}^{2}\\&\quad +75\, {{\gamma }}^{18}u\,{{x_{*}}}^{12}+20\,{{\gamma }}^{10}{u}^{3}{{ x_{*}}}^{6}+{{\gamma }}^{9}{u}^{4}{{x_{*}}}^{6}\\&\quad +1564\,{{\gamma }}^{11}u\,{{x_{*}}}^{6}+78\,{{\gamma }}^{10}{u}^{2}{{x_{*}} }^{6}+2\,{{\gamma }}^{9}{u}^{3}{{x_{*}}}^{6}\\&\quad +45\,{{\gamma }}^{ 11}u\,{{x_{*}}}^{4}+180\,{{\gamma }}^{10}{u}^{2}{{x_{*}}}^{4}\\&\quad -8\,{{\gamma }}^{9}{u}^{3}{{x_{*}}}^{4}-6\,{{\gamma }}^{8}{u}^{4}{{ x_{*}}}^{4}+9\,{{\gamma }}^{7}{u}^{5}{{x_{*}}}^{4}\\&\quad +105\,{{\gamma }}^{10}u\,{{x_{*}}}^{4} +184\,{{\gamma }}^{9}{u}^{2}{{x_{*}} }^{4}\\&\quad -12\,{{\gamma }}^{8}{u}^{3}{{x_{*}}}^{4}-3\,{{\gamma }}^{7 }{u}^{4}{{x_{*}}}^{4}+5\,{{\gamma }}^{6}{u}^{5}{{x_{*}}}^{4}\\&\quad -786 \,{{\gamma }}^{9}u\,{{x_{*}}}^{4}+6\,{{\gamma }}^{8}{u}^{2}{{ x_{*}}}^{4}\\&\quad -10\,{{\gamma }}^{7}{u}^{3}{{x_{*}}}^{4}-9\,{{\gamma }}^{6}{u}^{4}{{x_{*}}}^{4}+87\,{{\gamma }}^{9}u\,{{x_{*}}}^{2}\\&\quad +24\,{{\gamma }}^{8}{u}^{2}{{x_{*}}}^{2} -8\,{{\gamma }}^{7}{ u}^{3}{{x_{*}}}^{2} \end{aligned}$$

$$\begin{aligned} \zeta _{7}&=4\,{{\gamma }}^{6}{u}^{4}{{x_{*}}}^{2}-3\,{{ \gamma }}^{5}{u}^{5}{{x_{*}}}^{2}+60\,{{\gamma }}^{8}u\,{{ x_{*}}}^{2}\\&\quad +4\,{{\gamma }}^{7}{u}^{2}{{x_{*}}}^{2}-4\,{{\gamma }}^ {6}{u}^{3}{{x_{*}}}^{2}+3\,{{\gamma }}^{5}{u}^{4}{{x_{*}}}^{2}\\&\quad -4\,{{\gamma }}^{4}{u}^{5}{{x_{*}}}^{2}+4\,{{\gamma }}^{7}u\,{{ x_{*}}}^{2}-86\,{{\gamma }}^{6}{u}^{2}{{x_{*}}}^{2}\\&\quad +14\,{{\gamma }}^{5}{u}^{3}{{x_{*}}}^{2}+8\,{{\gamma }}^{4}{u}^{4}{{x_{*} }}^{2}-2\,{{\gamma }}^{3}{u}^{5}{{x_{*}}}^{2}\\&\quad +3\,{{\gamma }}^{ 21}{{x_{*}}}^{14}-84\,{{\gamma }}^{20}{{x_{*}}}^{12}-21\,{{\gamma }}^{19}{{x_{*}}}^{12}\\&\quad -71\,{{\gamma }}^{18}{{x_{*}}}^{12}+ 168\,{{\gamma }}^{18}{{x_{*}}}^{10}\\&\quad +63\,{{\gamma }}^{17}{{ x_{*}}}^{10}+326\,{{\gamma }}^{16}{{x_{*}}}^{10}-210\,{{\gamma }}^ {16}{{x_{*}}}^{8}\\&\quad -105\,{{\gamma }}^{15}{{x_{*}}}^{8}-565\,{{\gamma }}^{14}{{x_{*}}}^{8}\\&\quad +168\,{{\gamma }}^{14}{{x_{*}}}^{6}+105 \,{{\gamma }}^{13}{{x_{*}}}^{6}\\&\quad +420\,{{\gamma }}^{12}{{x_{*}}} ^{6}-84\,{{\gamma }}^{12}{{x_{*}}}^{4}-63\,{{\gamma }}^{11}{{ x_{*}}}^{4}\\&\quad -65\,{{\gamma }}^{10}{{x_{*}}}^{4} +24\,{{\gamma }}^ {10}{{x_{*}}}^{2}+21\,{{\gamma }}^{9}{{x_{*}}}^{2}-74\,{{\gamma }}^{8}{{x_{*}}}^{2}\\&\quad -27\,{{\gamma }}^{7}u-20\,{{\gamma }}^ {6}{u}^{2}+4\,{{\gamma }}^{5}{u}^{3}-{{\gamma }}^{4}{u}^{4}-{{ \gamma }}^{3}{u}^{5}\\&\quad -27\,{{\gamma }}^{6}u-20\,{{\gamma }}^{5} {u}^{2}+4\,{{\gamma }}^{4}{u}^{3}-{{\gamma }}^{3}{u}^{4}\\&\quad -{{\gamma }}^{2}{u}^{5}+77\,{{\gamma }}^{5}u+42\,{{\gamma }}^{4}{u}^{2}-6\,{{\gamma }}^{3}{u}^{3} \end{aligned}$$

$$\begin{aligned} \zeta _{8}&={{\gamma }}^{2}{u}^{4}+{\gamma }\,{u}^{5}+{\gamma }\,{u}^{4}-138\,{{\gamma }}^{5}{{x_{*}}}^{2} \\&\quad -3{{\gamma }}^{24}{{x_{*}}}^{16}+24\,{{\gamma }}^{22}{{x_{*} }}^{14}-75\,{{\gamma }}^{21}u\,{{x_{*}}}^{14}\\&\quad +423\,{{\gamma }}^{19}u\,{{x_{*}}}^{12}+76\,{{\gamma }}^{18}{u}^{2}{{x_{*}}}^{12}\\&\quad - 963\,{{\gamma }}^{17}u\,{{x_{*}}}^{10}-360\,{{\gamma }}^{16}{u} ^{2}{{x_{*}}}^{10}\\&\quad +8\,{{\gamma }}^{15}{u}^{3}{{x_{*}}}^{10}-348\,{{\gamma }}^{16}u\,{{x_{*}}}^{10}-76\,{{\gamma }}^{15}{u}^{2}{{ x_{*}}}^{10}\\&\quad +312\,{{\gamma }}^{15}u\,{{x_{*}}}^{10}+1095\,{{\gamma }}^{15}u\,{{x_{*}}}^{8}\\&\quad +660\,{{\gamma }}^{14}{u}^{2}{{x_{*} }}^{8}-28\,{{\gamma }}^{13}{u}^{3}{{x_{*}}}^{8}\\&\quad -{{\gamma }}^{12 }{u}^{4}{{x_{*}}}^{8}+615\,{{\gamma }}^{14}u\,{{x_{*}}}^{8}+284\, {{\gamma }}^{13}{u}^{2}{{x_{*}}}^{8}\\&\quad -8\,{{\gamma }}^{12}{u}^{3} {{x_{*}}}^{8}-1171\,{{\gamma }}^{13}u\,{{x_{*}}}^{8}-40\,{{\gamma }}^{12}{u}^{2}{{x_{*}}}^{8}\\&\quad -585\,{{\gamma }}^{13}u\,{{x_{*} }}^{6} -560\,{{\gamma }}^{12}{u}^{2}{{x_{*}}}^{6}+32\,{{\gamma } }^{11}{u}^{3}{{x_{*}}}^{6}\\&\quad +4\,{{\gamma }}^{10}{u}^{4}{{x_{*}}}^{6 } -5\,{{\gamma }}^{9}{u}^{5}{{x_{*}}}^{6}-480\,{{\gamma }}^{12}u \,{{x_{*}}}^{6}\\&\quad -376\,{{\gamma }}^{11}{u}^{2}{{x_{*}}}^{6}-2\,{{ \gamma }}^{3}{u}^{3}{{x_{*}}}^{2}+2\,{\gamma }\,{u}^{3}+2\,{u}^ {3}\\&\quad -44\,{{\gamma }}^{7}{{x_{*}}}^{2}+77\,{{\gamma }}^{4}u+42\,{ {\gamma }}^{3}{u}^{2} \end{aligned}$$

$$\begin{aligned} \zeta _{9}&=-6\,{{\gamma }}^{2}{u}^{3}+72\,{{x_{*}}}^{10}{{\gamma }}^{15}-259\, {{x_{*}}}^{8}{{\gamma }}^{13}\\&\quad +316\,{{ x_{*}}}^{6}{{\gamma }}^{11}-114\,{{x_{*}}}^{4}{{\gamma }}^{9}- 42\,{{\gamma }}^{5}{u}^{2}{{x_{*}}}^{2}\\&\quad +42\,{{\gamma }}^{9}{u}^ {2}{{x_{*}}}^{6}-42\,{{\gamma }}^{7}{u}^{2}{{x_{*}}}^{4}-696\,{{ \gamma }}^{8}u\,{{x_{*}}}^{4}\\&\quad +10\,{{\gamma }}^{4}{u}^{3}{{ x_{*}}}^{2}-4\,{{\gamma }}^{6}{u}^{3}{{x_{*}}}^{4}\\&\quad -309\,{{\gamma } }^{12}u\,{{x_{*}}}^{8}+850\,{{\gamma }}^{10}u\,{{x_{*}}}^{6}+29\, {{\gamma }}^{6}\\&\quad -50\,{{\gamma }}^{4}-50\,{{\gamma }}^{3}+24\,{\gamma }\,u\\&\quad -24\,{{\gamma }}^{3}u\,{{x_{*}}}^{2}+24\,{{\gamma }}^{2}\\&\quad +144\,{{\gamma }}^{4}{{x_{*}}}^{2}+168\,{{\gamma }} ^{3}{{x_{*}}}^{2}-168\,{{\gamma }}^{6}{{x_{*}}}^{4}\\&\quad -22\,{{\gamma }}^{6}{u}^{2}{{x_{*}}}^{4}+44\,{{\gamma }}^{4}{u}^{2}{{ x_{*}}}^{2}-74\,{{\gamma }}^{3}u\\&\quad +238\,{{\gamma }}^{12}{{x_{*}}}^{8 }-664\,{{\gamma }}^{10}{{x_{*}}}^{6}+564\,{{\gamma }}^{8}{{ x_{*}}}^{4}\\&\quad -22\,{{\gamma }}^{2}{u}^{2}-88\,{{\gamma }}^{6}{{x_{*}} }^{2}+{u}^{5}-74\,{{\gamma }}^{2}u\\&\quad -12\,i\sqrt{3}{{\gamma }}^{8} -12\,i\sqrt{3}{{\gamma }}^{7}+30\,i\sqrt{3}{{\gamma }}^{6}\\&\quad +30\,i\sqrt{3}{{\gamma }}^{5}-26\,i\sqrt{3}{{\gamma }}^{4}-26\,i \sqrt{3}{{\gamma }}^{3}\\&\quad +2\,i\sqrt{3}{u}^{3}+8\,i{{\gamma }}^{2 }\sqrt{3}+8\,i\sqrt{3}{\gamma }+8\,i\sqrt{3}u ) \end{aligned}$$

$$\begin{aligned}&C_{2R_3}(\gamma ,x_{*})=2\, ( {{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }-1 ) ( {{\gamma }}^{6}{{x_{*}}}^{4}+4\,i{{\gamma }}^{6}{{ x_{*}}}^{4}\sqrt{3}\\&\quad -2\,{{\gamma }}^{4}{{x_{*}}}^{2}-8\,i{{\gamma }}^{4}{{x_{*}}}^{2}\sqrt{3}+{{\gamma }}^{2}+4\,i{{\gamma }}^{2 }\sqrt{3}-4\,i\sqrt{3}-{u}^{2} )\\&\quad ( 3\,{{\gamma }}^{12 }{{x_{*}}}^{8}+2\,i\sqrt{3}{{\gamma }}^{9}u\,{{x_{*}}}^{6}-12\,{ {\gamma }}^{10}{{x_{*}}}^{6}\\&\quad +6\,i\sqrt{3}{{\gamma }}^{5}u\,{{ x_{*}}}^{2}-2\,i\sqrt{3}{{\gamma }}^{3}u +18\,{{\gamma }}^{8}{{ x_{*}}}^{4}-{{\gamma }}^{6}{u}^{2}{{x_{*}}}^{4}\\&\quad +2\,i\sqrt{3}{ \gamma }\,u-5\,{{\gamma }}^{6}{{x_{*}}}^{4}+2\,i{{\gamma }}^ {6}{{x_{*}}}^{4}\sqrt{3}+2\,i{{\gamma }}^{2}\sqrt{3}-12\,{{\gamma }}^{6}{{x_{*}}}^{2}\\&\quad +2\,{{\gamma }}^{4}{u}^{2}{{x_{*}}}^{2}- 2\,i\sqrt{3}{{\gamma }}^{3}u\,{{x_{*}}}^{2}+10\,{{\gamma }}^{4 }{{x_{*}}}^{2}\\&\quad -6\,i\sqrt{3}{{\gamma }}^{7}u\,{{x_{*}}}^{4}-4\,i{ {\gamma }}^{4}{{x_{*}}}^{2}\sqrt{3}+3\,{{\gamma }}^{4}\\&\quad -{{\gamma }}^{2}{u}^{2}-2\,i\sqrt{3}-5\,{{\gamma }}^{2}+{u}^{2}+2 ) \\&\quad ( {{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }-u ) ( i{{\gamma }}^{6}{{x_{*}}}^{4}\sqrt{3}-2\,i{{\gamma }}^{4}{{x_{*}}}^{2}\sqrt{3}\\&\quad -{{\gamma }}^{3}u\,{{x_{*}}}^{2 }+i{{\gamma }}^{2}\sqrt{3}-i\sqrt{3}+{\gamma }\,u-1 )\\&\quad ( i{{\gamma }}^{6}{{x_{*}}}^{4}\sqrt{3}-2\,i{{\gamma }}^ {4}{{x_{*}}}^{2}\sqrt{3}+{{\gamma }}^{3}u\,{{x_{*}}}^{2}+i{{\gamma }}^{2}\sqrt{3}\\&\quad -i\sqrt{3}-{\gamma }\,u+1 ) \\&\quad ( {{ \gamma }}^{6}{{x_{*}}}^{4}-2\,{{\gamma }}^{4}{{x_{*}}}^{2}+{{ \gamma }}^{2}-1 ) ^{2} \\&\quad ( -3\,{{\gamma }}^{6}{{x_{*}} }^{4}+2\,i\sqrt{3}{{\gamma }}^{3}u\,{{x_{*}}}^{2}+6\,{{\gamma }}^{4}{{x_{*}}}^{2}\\&\quad -2\,i\sqrt{3}{\gamma }\,u+2\,i\sqrt{3}-3\,{{ \gamma }}^{2}+{u}^{2}+2 ) \end{aligned}$$

The stability of the bifurcating closed invariant curve is determined by

$$\begin{aligned} \mathfrak {R}\left( \frac{1}{3}\left( \frac{e^{\frac{4\pi }{3}i}C_{1}}{|B_{1}|^2}-1 \right) \right) . \end{aligned}$$

$\square$

Theorem 7

There is a non-degenerate 1 : 4 resonance bifurcation of the fixed point $E_{*}$ at

$$\begin{aligned} k&={\frac{{{\gamma }}^{6}{{x_{*}}}^{4}-2\,{{\gamma }}^{4}{{x_{*} }}^{2}-u\,{{\gamma }}^{3}{{x_{*}}}^{2}+{{\gamma }}^{2}+u\,{\gamma }-2}{{{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }+u}} , \\ \epsilon&={\frac{{{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }+u}{{{\gamma } }^{6}{{x_{*}}}^{4}-2\,{{\gamma }}^{4}{{x_{*}}}^{2}+{{\gamma }} ^{2}-1}}, \end{aligned}$$

where

$$\begin{aligned} u=\sqrt{-\gamma ^6x_{*}^4+2\gamma ^4x_{*}^2-\gamma ^2+2}. \end{aligned}$$

Proof

The map (3) has a fixed point with a pair of complex conjugate multipliers $e^{\pm i \frac{\pi }{2}}$ if

$$\begin{aligned} \left\{ \begin{array}{ll} {\mathcal {N}}(\xi ,\vartheta )-\xi =0,\\ \det \left( {\mathcal {J}}(\xi ,\vartheta )\odot {\mathcal {J}}(\xi ,\vartheta ) -I_2\right) =0,\\ \kappa =0, \end{array} \right. \end{aligned}$$

(42)

where $\kappa =\cos (\theta _0)$ along the Neimark–Sacker curve. The exact solution of (35) is

$$\begin{aligned} x&=x_{*}, \quad y=\frac{1}{k}(x_{*}+\beta ), \\ k&={\frac{{{\gamma }}^{6}{{x_{*}}}^{4}-2\,{{\gamma }}^{4}{{x_{*} }}^{2}-u\,{{\gamma }}^{3}{{x_{*}}}^{2}+{{\gamma }}^{2}+u\,{\gamma }-2}{{{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }+u}},\\ \epsilon&={\frac{{{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }+u}{{{\gamma } }^{6}{{x_{*}}}^{4}-2\,{{\gamma }}^{4}{{x_{*}}}^{2}+{{\gamma }} ^{2}-1}}. \end{aligned}$$

Suppose that

$$\begin{aligned} M_{R_4}(\varrho ,{\bar{\varrho }})&=v\varrho +{\bar{\varrho }}{\bar{v}}+\sum _{2\le k+l}\frac{1}{(k+l)!}m_{kl}\varrho ^k{\bar{\varrho }}^l, \nonumber \\ \varrho&\in {\mathbb {C}}, \quad m_{kl}\in {\mathbb {C}}, \end{aligned}$$

(43)

as the center manifold of (3) at the

$$\begin{aligned} k&={\frac{{{\gamma }}^{6}{{x_{*}}}^{4}-2\,{{\gamma }}^{4}{{x_{*} }}^{2}-u\,{{\gamma }}^{3}{{x_{*}}}^{2}+{{\gamma }}^{2}+u\,{\gamma }-2}{{{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }+u}}, \\ \epsilon&={\frac{{{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }+u}{{{\gamma } }^{6}{{x_{*}}}^{4}-2\,{{\gamma }}^{4}{{x_{*}}}^{2}+{{\gamma }} ^{2}-1}}, \end{aligned}$$

where

$$\begin{aligned} {\mathcal {J}}v=e^{\frac{\pi }{2}i}v,\quad {\mathcal {J}}^Tw=e^{\frac{\pi }{2}i}w,\quad \left\langle w,v\right\rangle =1, \end{aligned}$$

Fig. 2

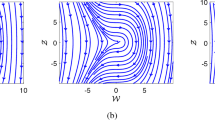
Phase portraits of (3) for $\gamma =1.32, \beta =1, \epsilon =0.7$. a Attractor before a Neimark–Sacker bifurcation for $k=2.48$. b Neimark–Sacker bifurcation for $k=2.514$. c The invariant closed curve created after Neimark–Sacker bifurcation for $k=2.9$. d The breakdown of the closed invariant curve for $k=3.1$

and

$$\begin{aligned}&v= \begin{pmatrix} -{\frac{{{\gamma }}^{3}{{x_{*}}}^{2}-{ \gamma }+u}{i{{\gamma }}^{6}{{x_{*}}}^{4}-2\,i{{\gamma }}^{4 }{{x_{*}}}^{2}+u\,{{\gamma }}^{3}{{x_{*}}}^{2}+i{{\gamma }}^{2 }-u\,{\gamma }+1-i}}\\ 1 \end{pmatrix},\\&w=\frac{1}{\overline{vw}}\begin{pmatrix} {\frac{{{\gamma }}^{3}{{x_{*}}}^{2}-{ \gamma }+u}{-i{{\gamma }}^{6}{{x_{*}}}^{4}+2\,i{{\gamma }}^{ 4}{{x_{*}}}^{2}+u\,{{\gamma }}^{3}{{x_{*}}}^{2}-i{{\gamma }}^{ 2}-u\,{\gamma }+1+i}}\\ 1 \end{pmatrix}. \end{aligned}$$

The restriction of the map (3) to (43) has the form

$$\begin{aligned} \varrho \mapsto G_{R_4}(\varrho )= i~\varrho +C_{R_4}\varrho ^2{\bar{\varrho }}+D_{R_4}{\bar{\varrho }}^3+{\mathcal {O}}(\varrho ^5),\quad \varrho \in {\mathbb {C}}. \end{aligned}$$

(44)

The invariance property of the center manifold cause to

$$\begin{aligned} {\mathcal {N}}\left( M_{R_4}(\varrho ),\vartheta _{*}\right) =M_{R_4}\left( G_{R_4}(\varrho )\right) , \end{aligned}$$

(45)

where $\vartheta _{*}=\left( {\frac{{{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }+u}{{{\gamma } }^{6}{{x_{*}}}^{4}-2\,{{\gamma }}^{4}{{x_{*}}}^{2}+{{\gamma }} ^{2}-1}},\gamma ,\right. \left. {\frac{{{\gamma }}^{6}{{x_{*}}}^{4}-2\,{{\gamma }}^{4}{{x_{*} }}^{2}-u\,{{\gamma }}^{3}{{x_{*}}}^{2}+{{\gamma }}^{2}+u\,{\gamma }-2}{{{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }+u}},\beta \right)$. The quadratic terms of (45) gives

$$\begin{aligned} ({\mathcal {J}}+I_2)m_{20}&=-B(v,v,\vartheta _{*}),\\&\Rightarrow m_{20}=\begin{pmatrix} \frac{2\, \left( {{\gamma }}^{2}{{x_{*}}}^{2}-1 \right) {{\gamma }}^{ 4} \left( {{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }+u \right) ^{3} {x_{*}} }{{m_{20}}_1}\\ \frac{-2\, \left( {{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }+u \right) ^{ 3}{{\gamma }}^{3}{x_{*}} }{{m_{20}}_1} \end{pmatrix},\\ ({\mathcal {J}}-I_2)m_{11}&=-B(v,{\bar{v}},\vartheta _{*}),\\&\Rightarrow m_{11}=\begin{pmatrix} \frac{2\,{x_{*}}\,{{\gamma }}^{3} \left( {{\gamma }}^{3}{{x_{*}}}^{2 }-{\gamma }+u \right) ^{2} \left( {{\gamma }}^{6}{{x_{*}}}^{4}- 2\,{{\gamma }}^{4}{{x_{*}}}^{2}-u\,{{\gamma }}^{3}{{x_{*}}}^{2 }+{{\gamma }}^{2}+u\,{\gamma }-2 \right) }{{m_{11}}_1}\\ \frac{2\, \left( {{\gamma }}^{3}{{ x_{*}}}^{2}-{\gamma }+u \right) ^{3 }{{\gamma }}^{3}{} { x_{*}} }{{m_{11}}_1} \end{pmatrix}, \end{aligned}$$

Fig. 3

a Continuation of fixed point in (k, x)-space. The Neimark–Sacker (ns) and period-doubling (pd) points. b pd curve of the first iterate consists of r2 point, rooted at the pd point

where

$$\begin{aligned} {m_{20}}_{1}&=\left( {\gamma }^{3}{x_{*}}^{2}-\gamma -u \right) \left( {\gamma }^{6}{x_{*}}^{4}-2\,{\gamma }^{4}{{ x0 }}^{2}+{\gamma }^{2}-1 \right) \\&\quad \left( i{\gamma }^{6}{x_{*}}^{4}-2\,i{\gamma }^{4}{x_{*}}^{2}+u\,{\gamma }^{3}{x_{*}}^{2}+i{\gamma }^{2}-u\,\gamma +1-i \right) ^{2},\\ {m_{11}}_{1}&=\left( {\gamma }^{3}{x_{*}}^{2}-\gamma -u \right) \left( {\gamma }^{6}{x_{*}}^{4}-2\,{\gamma }^{4}{x_{*}}^{2}+{\gamma }^{2}-1 \right) \\&\quad \left( i{\gamma }^{6}{x_{*}}^{4}-2\,i{\gamma }^{4}{x_{*}}^{2}+u\,{\gamma }^{3}{x_{*}}^{2}+i{\gamma }^{2}-u\,\gamma +1-i \right) \\&\quad \left( i {\gamma }^{6}{x_{*}}^{4}-2\,i{\gamma }^{4}{x_{*}}^{2}- u\,{\gamma }^{3}{x_{*}}^{2}+i{\gamma }^{2}+u\,{\gamma }-1-i \right) . \end{aligned}$$

Collecting the resonance terms of (45), we get

$$\begin{aligned} ({\mathcal {J}}-e^{\frac{\pi }{2}i}I_2)m_{21}&=2\, C_{R_4}v-C(v,v,{\bar{v}},\vartheta _{*})-2B(v,m_{11})\nonumber \\&\quad -2B(v,m_{11},\vartheta _{*})-B({\bar{v}},m_{20},\vartheta _{*}), \end{aligned}$$

(46)

$$\begin{aligned} ({\mathcal {J}}-e^{\frac{\pi }{2}i}I_2)m_{03}&=6\, D_{R_4}v-C({\bar{v}},{\bar{v}},{\bar{v}},\vartheta _{*})\nonumber \\&\quad -3B({\bar{v}},m_{02},\vartheta _{*}). \end{aligned}$$

(47)

The solvability conditions of the singular systems (46) and (47) are as follows:

$$\begin{aligned}&\langle w, 2\, C_{R_4}v-C(v,v,{\bar{v}},\vartheta _{*})-2B(v,m_{11},\vartheta _{*})\\&\quad -2B(v,m_{11},\vartheta _{*})-B({\bar{v}},m_{20},\vartheta _{*})\rangle =0,\\&\langle w, 6\, D_{R_4}v-C({\bar{v}},{\bar{v}},{\bar{v}},\vartheta _{*})-3B({\bar{v}},m_{02},\vartheta _{*})\rangle =0. \end{aligned}$$

Thus,

$$\begin{aligned} C_{R_4}=\frac{C_{1R_4}(\gamma ,x_{*})}{C_{2R_4}(\gamma ,x_{*})}, \qquad D_{R_4}=\frac{D_{1R_4}(\gamma ,x_{*})}{D_{2R_4}(\gamma ,x_{*})}, \end{aligned}$$

where

Fig. 4

Neimark–Sacker bifurcation curve consists of resonance 1:2 (r2), resonance 1:3 (r3), resonance 1:4 (r4) and Chenciner (ch) bifurcation

Fig. 5

Neimark–Sacker bifurcation curves of the first and third iterate

$$\begin{aligned}&C_{1R_4}(\gamma ,x_{*})=( {{\gamma }}^{9}{{x_{*}}}^{6}-{{\gamma }}^{7}{{x_{*}}}^ {4}-5\,{{\gamma }}^{6}u\,{{x_{*}}}^{4}-{{\gamma }}^{5}{{x_{*}} }^{2}\\&\quad +4\,{{\gamma }}^{4}u\,{{x_{*}}}^{2}-7\,{{\gamma }}^{3}{{ x_{*}}}^{2}+{{\gamma }}^{3}+{{\gamma }}^{2}u-{\gamma }-u)\\&\quad {{\gamma }}^{3}( {{\gamma }}^{3}{{x_{*}}}^{2}-{ \gamma }+u ) ^{5},\\&C_{2R_4}(\gamma ,x_{*})=( i{{\gamma }}^{6}{{x_{*}}}^{4}-2\,i{{\gamma }}^{4}{{ x_{*}}}^{2}+u\,{{\gamma }}^{3}{{x_{*}}}^{2}\\&\quad +i{{\gamma }}^{2}-u\,{ \gamma }+1-i ) ( {{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }-u ) ( i{{\gamma }}^{6}{{x_{*}}}^{4}\\&\quad -2\,i{{\gamma }}^{4}{{x_{*}}}^{2}-u\,{{\gamma }}^{3}{{x_{*}}}^{2}+i{{\gamma }}^{2}+u\,{\gamma }-1-i ) \\&\quad ( {{\gamma }}^{6}{{ x_{*}}}^{4}-2\,{{\gamma }}^{4}{{x_{*}}}^{2}+{{\gamma }}^{2}-1 ) ^{2} ( -{{\gamma }}^{12}{{x_{*}}}^{8}\\&\quad -4\,i{{\gamma }}^{4}{{x_{*}}}^{2}+4\,{{\gamma }}^{10}{{x_{*}}}^{6}+6\,i{{ \gamma }}^{5}u\,{{x_{*}}}^{2}-6\,{{\gamma }}^{8}{{x_{*}}}^{4}\\&\quad +{{\gamma }}^{6}{u}^{2}{{x_{*}}}^{4}-6\,i{{\gamma }}^{7}u\,{{ x_{*}}}^{4}+{{\gamma }}^{6}{{x_{*}}}^{4}\\&\quad -2\,i{{\gamma }}^{3}u+ 4\,{{\gamma }}^{6}{{x_{*}}}^{2}-2\,{{\gamma }}^{4}{u}^{2}{{ x_{*}}}^{2}+2\,i{{\gamma }}^{2}\\&\quad +2\,i{\gamma }\,u-2\,{{\gamma }}^ {4}{{x_{*}}}^{2}-2\,iu\,{{\gamma }}^{3}{{x_{*}}}^{2}-{{\gamma }}^{4}\\&\quad +{{\gamma }}^{2}{u}^{2}+2\,i{{\gamma }}^{6}{{x_{*}}}^{4}+ 2\,\\&\quad i{{\gamma }}^{9}u\,{{x_{*}}}^{6}+{{\gamma }}^{2}-{u}^{2}-2\, i )\\&D_{1R_4}(\gamma ,x_{*})=- ( {{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }+u ) ^{5}\\&\quad ( i{{\gamma }}^{6}{{x_{*}}}^{4}-2\,i{{\gamma }}^{4}{{ x_{*}}}^{2}+u\,{{\gamma }}^{3}{{x_{*}}}^{2}+i{{\gamma }}^{2}-u\,{ \gamma }+1-i )\\&\quad {{\gamma }}^{3} ( 7\,{{\gamma }}^{9 }{{x_{*}}}^{6} -15\,{{\gamma }}^{7}{{x_{*}}}^{4}+5\,{{\gamma }} ^{6}u\,{{x_{*}}}^{4}+9\,{{\gamma }}^{5}{{x_{*}}}^{2}\\&\quad -4\,{{\gamma }}^{4}u\,{{x_{*}}}^{2}-{{\gamma }}^{3}{{x_{*}}}^{2}-{{\gamma }}^{3}-{{\gamma }}^{2}u+{\gamma }+u )\\&D_{2R_4}(\gamma ,x_{*})=3\, ( -{{\gamma }}^{12}{{x_{*}}}^{8}-4\,i{{\gamma }}^{4}{{ x_{*}}}^{2}+4\,{{\gamma }}^{10}{{x_{*}}}^{6}+6\,i{{\gamma }}^{ 5}u\,{{x_{*}}}^{2}\\&\quad -6\,{{\gamma }}^{8}{{x_{*}}}^{4} +{{\gamma }}^{6}{u}^{2}{{x_{*}}}^{4}-6\,i{{\gamma }}^{7}u\,{{x_{*}}}^{4}\\&\quad +{{\gamma }}^{6}{{x_{*}}}^{4}-2\,i{{\gamma }}^{3}u+4\,{{\gamma }}^{6}{{x_{*}}}^{2}-2\,{{\gamma }}^{4}{u}^{2}{{x_{*}}}^{2}+2\,i{{ \gamma }}^{2}\\&\quad +2\,i{\gamma }\,u-2\,{{\gamma }}^{4}{{x_{*}}}^{ 2}-2\,iu\,{{\gamma }}^{3}{{x_{*}}}^{2}\\&\quad -{{\gamma }}^{4}+{{\gamma }}^{2}{u}^{2}+2\,i{{\gamma }}^{6}{{x_{*}}}^{4}\\&\quad +2\,i{{\gamma }}^{9}u\,{{x_{*}}}^{6}+{{\gamma }}^{2}-{u}^{2}-2\,i ) ( {{\gamma }}^{6}{{x_{*}}}^{4}-2\,{{\gamma }}^{4}{{x_{*} }}^{2}+{{\gamma }}^{2}-1 ) ^{2}\\&\quad ( i{{\gamma }}^{6}{{ x_{*}}}^{4}-2\,i{{\gamma }}^{4}{{x_{*}}}^{2}-u\,{{\gamma }}^{3 }{{x_{*}}}^{2}+i{{\gamma }}^{2}+u\,{\gamma }-1-i ) ^{3}\\&\quad ( {{\gamma }}^{3}{{x_{*}}}^{2}-{\gamma }-u ) \end{aligned}$$

The bifurcation scenario near the $R_4$ point is determined by

$$\begin{aligned} A_{0}=-\frac{iC_{R_4}}{\vert D_{R_4}\vert }. \end{aligned}$$

$\square$

5 Numerical continuation

In this section, we perform a continuation method in order to numerically illustrate the dynamical behavior of system (3) by using the matlab package matcontm.

We consider two cases:

Case 1: We fix $\gamma =1.32, \beta =1, \epsilon =0.7$ and then vary k as a free parameter. Phase portraits of system (3) for different values of k are depicted in Fig. 2. When k varies as a free parameter, the matcontm report is as follows:

Fig. 6

Continuation of fixed point in (k, x)-space. The fold point (lp), Neimark–Sacker point (ns) and period-doubling (pd) point

By Theorem 3, the fixed point $E_{*}$ has period-doubling bifurcations in which period-doubling point is detected as a pd. By Theorem 4, the fixed point $E_{*}$ has Neimark–Sacker bifurcations and Neimark–Sacker detected as ns. See Fig. 3a.

Bifurcation curves for two control parameters k and $\epsilon$ and keeping $\gamma =1.32, \beta =1$ fixed are presented in Figs. 3b and 4. pd curve of the first iterate consisting of r2 point is presented in Fig. 3b, and the matcontm report is as follows:

Continuation of the Neimark–Sacker curve is presented below, and the ns curve is plotted in Fig. 4:

Fig. 7

Neimark–Sacker bifurcation curve consists of resonance 1:2 (r2), resonance 1:3 (r3) points

Fig. 8

Phase portraits of (3) for $k=1.9, \beta =0.5, \epsilon =0.88$. a Attractor for $\gamma =2.2$. b resonance 1:3 bifurcation for $\gamma =2.31$. c Chaotic attractor for $\gamma =2.33$

See Theorems 5, 6 and 7.

By selecting r3 point to start the continuation Neimark–Sacker bifurcation curves of the third iterate are depicted in Fig. 5 and matcontm report is as follows:

Case 2: We fix $\gamma =2.2, \beta =.5, \epsilon =0.7$ and then vary k as a free parameter, the matcontm report is

By Theorem 1, the fixed point $E_{*}$ has fold bifurcations in which fold point is detected as a lp. By Theorem 3, the fixed point $E_{*}$ has period-doubling bifurcation in which period-doubling point is detected as a pd, and by Theorem 4, the fixed point $E_{*}$ has Neimark–Sacker bifurcations detected as ns. see Fig. 6.

Bifurcation curves for two control parameters k and $\epsilon$ are presented in Fig. 7, and the matcontm report is as follows:

Given that $R3=(0.588187 0.571752 1.903248 0.885721 -0.500000)$ phase portraits of system (3) for $k=1.9, \beta =0.5, \epsilon =0.88$ and different values of $\gamma$ are depicted in Fig. 8. Curve of “Neutral Saddle” of the third iterate is presented in Fig. 9.

6 Conclusion

In this work, we studied the BVP discrete model introduced in [14]. The bifurcation conditions of this model along with the computation of normal form coefficients are done through the reduction of the model to the center manifold. Then, with the aid of the numerical continuation method, all of the bifurcation curves of the model was drawn and the numerical results confirmed our analysis results.

Fig. 9

Curve of “Neutral Saddle” of the third iterate