Spatial vegetation pattern formation and transition of an extended water–plant model with nonlocal or local grazing

Abstract

In this paper, we analyze how vegetation patterns occur in arid and semi-arid ecosystems with different types of grazing, using both modelling approaches and mathematical analysis. The concepts of Tipping point and Turing point are helpful for us to understand the desertification that catastrophic and critical transitions may have on ecosystems. In the mathematical analysis, we extrapolated our analysis to local stability and Turing instability of local and nonlocal models. We found that the uniform vegetation state changes to vegetation pattern state or bare soil state, which means that there is overgrazing in this ecosystem. Therefore, we propose that vegetation patterns may be a warning signal for the onset of desertification. Some notes on numerical simulation are given, based on different diffusion coefficients, infiltration parameters and grazing rate. Numerical simulation not only verifies the validity of the theoretical results, but also obtains some results which can not be obtained in mathematical analysis.

1 Introduction

Fig. 1

The transition of different vegetation states in an ecosystem

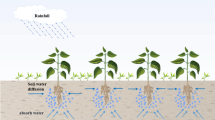
Vegetation patterns exist widely in the arid and semi-arid ecosystems [1,2,3,4,5,6,7,8,9,10]. Vegetation patterns are viewed as precursors of a catastrophic transition to a degraded state [2, 6,7,8], and important as potential indicators of climate change and desertification. Humans and climate affect ecosystems and their services, which may involve catastrophic and critical transitions from one stable state to another (see Fig. 1). Catastrophic transitions, where a system shifts abruptly between alternate steady states, are a generic feature of many nonlinear systems [3, 8]. Understanding the drivers and dynamics of catastrophic transitions in vegetation patterns is crucial for effective ecosystem management and conservation. Scientists use mathematical models and empirical studies to investigate the mechanisms behind these transitions and develop strategies to prevent or mitigate their negative impacts. For terrestrial ecosystems, it has been hypothesized that vegetation patchiness could be used as a signature of imminent transitions [2, 7]. Satellite observations and field surveys indicate that rainfall and grazing have a global control on vegetation density along the water-limited ecosystems, whereas local and nonlocal interactions influence the spatial arrangement of vegetation [11,12,13,14,15,16]. In particular, vegetation patterns that occur in a scenario of flat terrain and hill side in several models have been shown in simulations to evolve through a sequence of morphologies, “ homogeneous vegetation $\rightarrow$ vegetation patterns $\rightarrow$ bare soil (desert)” (Fig. 1), as ecosystem aridity increases [5]. In this way, vegetation patterns may serve as early-warning signs of catastrophic ecosystem transitions [1, 2, 9]. The vegetation status changes directly to the bare soil status, “ homogeneous vegetation $\rightarrow$ bare soil (desert)” (Fig. 1), which means that the ecosystem has undergone catastrophic changes [17].

Indeed much work in the last two decades has gone into mathematizing the water redistribution and plant facilitation mechanisms into idealized models that are able to qualitatively reproduce the patterns. Mathematical models play a key role in understanding formation of vegetation patterns, and a large number of mathematical models have been established about the origin of this vegetation pattern formation [4, 5, 9, 10, 17,18,19,20,21,22,23,24,25,26]. One of the first mathematical models is the Klausmerier model [4], which has a connection between plant biomass and limited water resources. In the past two decades, many extensions of water–plant model has been proposed [11, 12, 14,15,16]. Klausmerier model and many others based on feedback mechanisms of plant biomass and limited water resources have been established. One family of models captures the spatial and temporal dynamics of coarsely defined water and vegetation fields through reaction–advection–diffusion partial differential equations. The model for surface water (W) and plant biomass (B) and balance is defined on an infinite domain indexed by X as a function of time T, as follows:

$$\begin{aligned} \frac{\partial B}{\partial T}= & {} \{plant ~growth ~at ~\vec {X}~ at ~T\}\\{} & {} -\{plant ~ loss ~at ~\vec {X}~ at ~T\}\pm \{plant ~ dispersal\}.\\ \frac{\partial W}{\partial T}= & {} \{rainfall ~ rate ~at ~\vec {X}~ at ~T\}\\{} & {} -\{infiltration~ rate~at ~\vec {X}~ at ~T\}\\{} & {} -\{evaporation ~and ~drainage ~at ~\vec {X}~ at ~T\}\\{} & {} \pm \{water~ movement\}. \end{aligned}$$

An understanding of plant growth is therefore essential to understand vegetation patterns, including competition, plant–herbivore interactions, interactions between plants and their abiotic environment and local community dynamics [11]. Most mathematical models ignore many natural factors affecting vegetation growth, and only consider some factors such as infiltration rate [26], light affect [11] and carbon dioxide [12]. Mathematical formulations and parameters are taken from literature [4, 5, 10, 11, 20] and we summarized in Table 1.

Table 1 Relative growth rates and plant lost, where $K_2,p,M_0,M_1,j$ are positive constant and $I_j(B)=\frac{1}{Vol(\Omega )}\int _{X\in \Omega }B^j(X)dX$, $\Omega$: denote a connected bounded spatial domain and $Vol(\Omega )$ is volume (length or area, depending on the dimension)

Fig. 2

Flowchart for nonlinear grazing

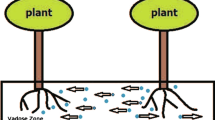
Plant biomass may be lost due to natural mortality or removal by herbivores [5]. In many previous studies [1,2,3,4,5, 9,10,11,12, 17, 20, 25,26,33], for the sake of simplicity, grazing has been ignored or the functional response of herbivores to changes in plant availability are assumed to be linear. By modeling grazing with a linear term, the grazing pressure is independent of the local availability of vegetation. Therefore, the local linear term is used to simulate grazing, assuming that the grazing pressure is constant. In real ecosystems, the demographic response and functional response most likely depend on the vegetation distribution, leading to a variable grazing pressure [14] (see Fig. 2). The grazing pressure is dependent of the local availability of vegetation, at a location which is independent of the presence of vegetation elsewhere. This type of grazing is called local grazing [15, 16]. However, the grazing pressure at a location is dependent of the presence of vegetation elsewhere, this type of grazing so called nonlocal grazing [14,15,16]. Mathematical formulations are taken from literature [14,15,16, 34,35,36] and summarized in Table 1.

It is well known that plants reproduce asexually [5], Klausmeier [4] and other biomathematics experts [5, 9,10,11,12, 17, 20, 25, 26] describe the process of vegetative propagation by diffusion. In detail, the diffusion term  $D_B\triangle B$ simulates the dispersal of seeds from the plant to the ground, where $\triangle$ represents Laplace operator.

The rainfall can change seasonally and tends to be intermittent in time [4, 5, 26], but here we view rainfall as a climatic parameter that may slowly change over time and is constant in the absence of climate change. All the types of vegetation models use linear terms to simulate water evaporation [4]. Water is regarded as surface water, and the process of infiltration and subsequent uptake of soil water are combined in the surface water uptake terms. The surface water uptake terms depend on the plant growth function. Klausmeier [4] studied vegetation patterns on flat land completely ignoring water diffusion. As we all know, plants have the ability to redistribute the water in the soil. Hardenberg [25] firstly used this idea in water–plant interaction, in which the extended model was used to describe the feedback effect between vegetation biomass and water. The main idea is to add $\triangle (W-\beta B)$. Recently, some authors propose different types of vegetation patterns model [15, 16, 31,32,33, 37,38,39,40,41,42] which includes cross-diffusion terms, this type of water–plant models have potential ecological reality and intrinsic theoretical interest.

The rest of this article is organized as follows. In Sect. 2, we present an extended water–plant model with cross-diffusion and nonlinear grazing. In Sect. 3, we explain the biological and mathematical meanings of catastrophic transition and critical transition, and we obtain some parameter conditions for linear stability and vegetation patterns formation. In Sect. 4, we compare the three type of grazing models using the critical diffusion coefficients. Section 5 gives the numerical simulations results of the extended water–plant model. Finally, some conclusions and discussions are presented in Sect. 6.

2 The extended model

Several modelling frameworks to describe the ecohydrological dynamics in vegetation patterns have been proposed over the last two decades. One system that stands out due to its simplicity is the extended Klausmeier model. The vegetation growth term of the extended Klausmeier model is $WB^2$, on the basis of mathematical simplicity rather than ecological data. Our objective is to study how model predictions change with the strength of the dependence of infiltration on vegetation biomass, and we consider specifically the one-parameter family of plant growth terms $WB^p$ with $p\ge 1$. Understanding the mechanisms and dynamics of grazing-induced vegetation transitions is important for managing grazing systems and conserving biodiversity. By considering the impacts of grazing on vegetation patterns, land managers can implement appropriate grazing strategies, such as rotational grazing or targeted grazing, to maintain desired vegetation communities and prevent undesirable shifts in ecosystem structure and function. To understand how grazing alters the desertification process, we include the different grazing terms in an extended Klausmeier model. Therefore, we propose an extended water–plant model based on the models of Klausmeier model [4, 14, 16], Shnerb model [17, 34,35,36] and Sherratt model [15, 26]:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\partial W}{\partial T}=D_w\triangle (W-K_1 B)+\tilde{R}-K_2WB^p-K_3W,\\&\frac{\partial B}{\partial T}=D_b\triangle B+K_4K_2WB^p-M(B)B,\\ \end{aligned} \right. \end{aligned}$$

(2.1)

where plant biomass death rate dependence of natural mortality rate and nonlinear grazing pressure in the following form

$$\begin{aligned} \overbrace{M(B)B}^{plant \; loss}=\overbrace{M_0 B}^{natural\; mortality}+\overbrace{{G}_{j}B^j}^{grazing}, \end{aligned}$$

where $G_{j}$ denote grazing pressure, j is a constant and represents aggregation parameter. The grazing pressure at a location is dependent of the presence of vegetation elsewhere (see Fig. 2), then $G_{j}$ represent

$$\begin{aligned} {G}_j=\left\{ \begin{array}{ll} \frac{M_{sus}}{\tilde{K}_{sus}+I_j(B)}, &{}\quad for\; sustained \; type \\ &{}\quad nonlocal \; grazing, \\ \frac{M_{nat}I_j(B)}{(\tilde{K}_{nat})^2+(I_j(B))^2}, &{}\quad for \; natural \; type \\ &{}\quad nonlocal \; grazing. \\ \end{array} \right. \end{aligned}$$

(2.2)

where sustained grazing with constant herbivore numbers and Holling type II functional response, natural grazing with constant functional response and demographic response by a type III sigmoid function [14]. $M_{sus}$, $M_{nat}$ (maximal grazing rate per unit area) and $\tilde{K}_{sus}$, $\tilde{K}_{nat}$ (half-persistence) are positive constant.

The grazing pressure is independent of the local availability of vegetation (see Fig. 2), then $G_{j}$ represent

$$\begin{aligned} {G}_j=\left\{ \begin{array}{ll} \frac{M_{sus}}{\tilde{K}_{sus}+B^j}, &{} \quad for\; sustained \; type \; local \\ {} &{} \quad grazing, \\ \frac{M_{nat}B^j}{(\tilde{K}_{nat})^2+B^{2j}}, &{}\quad for \; natural \; type \; local \\ {} &{}\quad grazing. \\ \end{array} \right. \end{aligned}$$

(2.3)

Fig. 3

Grazing as a function of plant density with $M_0=0.225$, $M_{sus}=M_{nat}=1.5$, $K_{sus}=K_{nat}=1$ and $j=2$

Remark 1

For all the types of grazing, the grazing is an increasing function of B (see Fig. 3), so that locations with relatively large biomass bear a large grazing rate and locations with small biomass bear a small grazing rate. The nonlocal natural grazing is bigger than the nonlocal sustained grazing for small B($< B^*$) and smaller than large B($> B^*$) (Fig. 3a), but the opposite is true for local grazing (Fig. 3b). Since the local sustained and local natural grazing functions (with $M_{sus} =M_{nat}$, $K_{sus}=K_{nat}$ and the same value of j) are almost equal for large B, in this regime the same dynamics are likely to occur for local sustained and local natural grazing.

In the study of vegetation patterns, bounded regions are often chosen to focus on specific ecosystems or habitats. By defining the boundaries, researchers can investigate how vegetation interacts with its surrounding environment and how it responds to external factors within the confined area. Neumann boundary conditions

$$\begin{aligned} \frac{\partial W}{\partial \nu }=\frac{\partial B}{\partial \nu }=0, \end{aligned}$$

where $\nu$ is the unit outer normal vector on smooth boundary, can be applied to the boundaries of these bounded regions to model the exchange of resources between the vegetation and its surroundings. This allows researchers to simulate and analyze how vegetation patterns evolve and respond to different environmental conditions and disturbances within the defined boundaries. To reduce the number of parameters, we introduce the dimensionless variables and parameters, which are indicated below:

$$\begin{aligned}{} & {} w=K_4K_2^{\frac{1}{p}}K_3^{-\frac{1}{p}}W, \ b=K_2^{\frac{1}{p}}K_3^{-\frac{1}{p}}B, \\{} & {} t=K_3T\,\ x=K_3^{1/2}D^{-1/2}_WX, \ r=D_BD_W^{-1},\\{} & {} \alpha =K_1K_4,\ R=\tilde{R}K_4K_3^{-1-1/p}K_2^{1/p}, \ m_0=M_0K_3^{-1}, \\{} & {} {k}_{sus}=\tilde{K}_{sus}K_2^{j/p}K_3^{-j/p},\; {k}_{nat}=\tilde{K}^2_{nat}K_2^{2j/p}K_3^{-2j/p},\\{} & {} m_{sus}=M_{sus}K_3^{-1-1/p}K_2^{1/p}\, \ m_{nat}=M_{nat}K_3^{-1/p}K_2^{1/p}. \end{aligned}$$

The dimensionless model is given by

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial w}{\partial t}=\triangle w-\alpha \triangle b+R-wb^p-w ,&{} x\in \Omega ,t>0,\\ \frac{\partial b}{\partial t}=r\triangle b+wb^p-m_0 b-\Theta _j(b), &{} x\in \Omega ,t>0,\\ \frac{\partial w}{\partial \nu }=\frac{\partial b}{\partial \nu }=0 , \quad &{} x\in \partial \Omega , t>0,\\ w(x,0)=w_0(x)\ge 0,b(x,0)\\ \quad =b_0(x)\ge 0 , &{} x\in \Omega ,\\ \end{array} \right. \end{aligned}$$

(2.4)

where $\Omega$ is a bounded domain in the Euclidean space ${\mathbb {R}}^1$ or ${\mathbb {R}}^2$ with smooth boundary, denoted as $\partial \Omega$, $\nu$ is the unit outer normal vector on $\partial \Omega$. $\Theta _{j}$ is different types of grazing are implemented by choosing either

$$\begin{aligned} {\Theta }_j=\left\{ \begin{array}{ll} \frac{m_{sus}b^j}{{k}_{sus}+I_j(b)} &{} for\; sustained \; type \\ {} &{} nonlocal \; grazing, \\ \frac{m_{nat}I_j(b)b^j}{({k}_{nat})^2+(I_j(b))^2} &{} for \; natural \; type \\ {} &{} nonlocal \; grazing, \\ \end{array} \right. \end{aligned}$$

(2.5)

or

$$\begin{aligned} \Theta _j=\left\{ \begin{array}{ll} \frac{m_{sus}b^j}{k_{sus}+b^j}, &{} for\; sustained \; type \; local \\ {} &{} grazing, \\ \frac{m_{nat}b^{2j}}{(k_{nat})^2+b^{2j}},&{} for \; natural \; type \; local \\ {} &{} grazing. \\ \end{array} \right. \end{aligned}$$

(2.6)

According to [14,15,16] and Remark 1, in order to compare the two nonlocal grazing type models and the corresponding two local type models, we choose $k_{sus}=k_{nat}=1$ and $m_1:=m_{sus}=m_{nat}$, for the sustained grazing model $j=p\ge 1$, for the natural grazing model $j=\frac{p}{2}$ ($p\ge 1$), and analyze an extended water–plant model:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial w}{\partial t}=\triangle w-\alpha \triangle b+R-wb^p-w, &{} x\in \Omega ,t>0,~\\ \frac{\partial b}{\partial t}=r\triangle b+wb^p-m_0 b-\Theta _p(b), &{} x\in \Omega ,t>0,~\\ \frac{\partial w}{\partial \nu }=\frac{\partial b}{\partial \nu }=0 , &{} x\in \partial \Omega , t>0,\\ w(x,0)=w_0(x)\ge 0,b(x,0)\\ =b_0(x)\ge 0, &{} x\in \Omega ,\\ \end{array} \right. \end{aligned}$$

(2.7)

where $p\ge 1$ and

$$\begin{aligned} {\Theta }_p(b)=\left\{ \begin{array}{ll} \frac{m_1b^p}{1+I_p(b)}, &{} for \; sustained \; \ type \\ {} &{} nonlocal \; grazing, \\ \frac{m_1I_{p/2}(b)b^{p/2}}{1+(I_{p/2}(b))^2}, &{} for \; natural \; type \\ {} &{} nonlocal \; grazing, \\ \frac{m_1b^{p}}{1+b^{p}}, &{} for \; local \; grazing. \\ \end{array} \right. \end{aligned}$$

(2.8)

Manor et al. [34], Wang et al. [35], and Lei et al. [36] considered a biomass per capita death rate $m_0+\frac{m_1}{1+b}$ with $p=1$, and showed that Turing instability can occur for system with large water diffusion or small vegetation diffusion. Siero [14] using numerical simulations method considered extended Klausmeier model $(p=2)$ without cross-diffusion. In our previous work [16], we studied extended Klausmeier model $(p=2)$ with sustained type nonlocal grazing and local grazing model, and compared the two types of extended model. From [16], we can learn that nonlocal terms promote linear stability, and the system may produce pattern under the influences of self-diffusion and cross-diffusion. Sherratt et al. [26] investigated the case that $p>1$, $d_w=0$ and $m_1=0$, and their results showed that the parameter p affects different types of solutions such that spatial patterns, homogeneous vegetation and bare ground on flat terrain. In our previous work [15], we studied an extended Sherratt model with sustained grazing $(p\ge 1)$, and proved that the model has very rich dynamics properties, including multiple stable equilibria, saddle-node bifurcation of positive equilibria, some characterizations for the non-constant positive steady state solutions, and existence of non-constant positive solutions.

3 Equilibrium state transition and spatial pattern formation

The study of equilibrium state transitions and spatial pattern formation is important in understanding the behavior of complex model (2.7). It helps us understand how systems respond and adapt to changes in their environment, and how order and structure can emerge from simple interactions and dynamics. Equilibrium state transition refers to the transition of a system from one stable equilibrium state to another. In equilibrium, a system is in a balanced state where the forces and interactions within the system are in equilibrium. However, when external conditions or internal dynamics change, the system may undergo a transition to a new equilibrium state. This transition can be triggered by various factors such as changes in parameters, fluctuations, or perturbations in the system.

In this section, for convenience of explanation, we define

$$\begin{aligned} M_1:=R-m_0, ~M_2:=R-m_0p(p-1)^{-1+\frac{1}{p}}. \end{aligned}$$

The model (2.7) has a bare-solid (desert) steady state $(w_0, b_0) = (R, 0)$. For positive equilibriums, we have the following two cases [15]:

(a) If $p=1$, $m_1<M_1$, then the model (2.7) has a unique positive equilibrium

$$\begin{aligned} (w_1,b_1)=\left( \frac{m_0R}{R-m_1},\frac{R-m_0-m_1}{m_0}\right) . \end{aligned}$$

If $m_1= M_1$, then the model (2.7) has a unique equilibrium (R, 0), and it is a so-called transcritical bifurcation point [15, 35].

(b) If $p>1$, then equilibriums must satisfy $b^{1-p}+b=\frac{R-m_1}{m_0}$, with $w=\frac{R}{1+b^p}$. Set

$$\begin{aligned} H(b)=b^{1-p}+b-\frac{R-m_1}{m_0}. \end{aligned}$$

Function H(b) has a unique minimum at

$$\begin{aligned} b_{min}=(p-1)^{\frac{1}{p}} \end{aligned}$$

(3.1)

and $H(b)\rightarrow \infty$ as $b\rightarrow 0$ and $\infty$ [15]. Therefore, function H(b) has no solution if when $m_1>M_2$ (see Fig. 4), and has two solutions $b_2$, $b_3$ if $m_1<M_2$ and

$$\begin{aligned} b_3<b_{min}<b_2. \end{aligned}$$

(3.2)

The two equilibrium solutions are called higher vegetation state $(w_2,b_2)$ and lower vegetation state $(w_3,b_3)$. Note that the two states coincide at $m_1=M_2$. In fact here a so-called saddle-node bifurcation takes place [15].

Fig. 4

Positive constant equilibrium solution of the extended water–plant model expressed in plant biomass b as function of grazing parameter $m_1$ for $R=3$ and $m_0=0.225$. a $p=1,1.5,2,4$; b Drawing of partial enlargement of (a)

We study linear stability of spatial homogeneous model in the neighborhood of each equilibrium. For the sake of simplicity, we introduce some notations

$$\begin{aligned} f(w,b):= & {} R-wb^p-w,~ g(w,b)\\:= & {} wb^p-m_0 b-\frac{m_1b^j}{1+b^j}. \end{aligned}$$

The Jacobian matrix of spatial homogeneous model evaluated at the equilibrium points $(w_i,b_i)$ are

$$\begin{aligned} J(w_i,b_i)=\left( \begin{array}{cc} f^{(i)}_{w} &{}\quad f^{(i)}_{b}\\ g^{(i)}_{w} &{}\quad g^{(i)}_{b}\\ \end{array}\ \right) , \end{aligned}$$

where $i=1,2,3$ and

$$\begin{aligned}{} & {} f^{(i)}_{w}=- b_i^p -1<0, \ f^{(i)}_{b}=-p w_i b_i^{p-1}<0, \nonumber \\{} & {} g^{(i)}_{w}=b_i^p>0, \end{aligned}$$

(3.3)

$$\begin{aligned}{} & {} g^{(i)}_{b}=p\left( wb_i^{(p-1)}-\frac{m_1b_i^{(p-1)}}{1+b_i^p}\right) \nonumber \\{} & {} \quad -m_0+\frac{pm_{1}b_i^{2p-1}}{\big (1+b_i^p\big )^2}=m_0(p-1)+\frac{pm_{1}b_i^{2p-1}}{\big (1+b_i^p\big )^2}>0.\nonumber \\ \end{aligned}$$

(3.4)

By simple calculations, we know that

$$\begin{aligned} \textrm{det}(J(w_i,b_i))= & {} -m_0(b_i^p +1)(p-1)-\frac{pm_{1}b_i^{2p-1}}{\big (1+b_i^p\big )}\nonumber \\{} & {} +p\left( m_0+\frac{m_{1}b_i^{p-1}}{\big (1+b_i^p\big )}\right) b^p\nonumber \\= & {} m_0(b_i^p-p+1). \end{aligned}$$

(3.5)

According to (3.2), we can obtain

$$\begin{aligned}{} & {} \textrm{det}(J(w_1,b_1))=m_0b_1>0, \\{} & {} \textrm{det}(J(w_2,b_2))>0,\ \textrm{det}(J(w_3,b_3))<0. \end{aligned}$$

Therefore, $(w_3,b_3)$ is always unstable when it exists. Stability of $(w_1, b_1)$ and $(w_2, b_2)$ depends on the sign of the $tr(J(w_i,b_i))$. If

$$\begin{aligned} tr(J(w_i,b_i))= & {} - b_i^p -1+m_0(p-1)\nonumber \\{} & {} +\frac{pm_{1}b_i^{2p-1}}{\big (1+b_i^p\big )^2}<0 \end{aligned}$$

(3.6)

holds, then the equilibriums $(w_1,b_1)$ and $(w_2,b_2)$ are locally asymptotically stable.

Let us address the extended model (2.7). For the sake of simplicity, we introduce some notations

$$\begin{aligned} \tilde{g}(w,b)= & {} wb^p-m_0 b-\frac{m_{1}b^p}{1+I_p(b)},\\ \hat{g}(w,b)= & {} wb^p-m_0 b-\frac{m_{1}I_{p/2}(b)b^{p/2}}{1+(I_{p/2}(b))^2}. \end{aligned}$$

Let $f^{(i)}_w$, $f^{(i)}_b$, $g^{(i)}_w$, $g^{(i)}_b$, $\tilde{g}^{(i)}_w$, $\tilde{g}^{(i)}_b$, $\hat{g}^{(i)}_w$ and $\hat{g}^{(i)}_b$ be the derivatives of f(w, b), g(w, b), $\tilde{g}(w, b)$ and $\hat{g}(w,b)$ with respect to w and b evaluated at the steady state $(w_i,b_i)$,

$$\begin{aligned}{} & {} f^{(i)}_{w}=- b_i^p -1, \ \ f^{(i)}_{b}=-p w_i b_i^{p-1}, \\{} & {} g_{w}^{(i)}=\tilde{g}_{w}^{(i)}=\hat{g}_{w}^{(i)}=b_i^p. \end{aligned}$$

However, $\tilde{g}(w,b)$ and $\hat{g}(w,b)$ contain integrals, their differentation requires a bit more attention. The $G\hat{a}teaux$ differential of $I_p$ is given by

$$\begin{aligned} dI(b)_p{} & {} = \lim \limits _{\epsilon \rightarrow 0}\frac{I_p(b_i+\epsilon \tilde{b})- I_p(b_i)}{\epsilon }\\ {}{} & {} =\frac{pb^{p-1}_i}{Vol(\Omega )}\int _{\Omega }\,\tilde{b} dx, \end{aligned}$$

where $\tilde{b}$ represents small perturbation. Now we differentiate $G_{p,sus}:=\frac{m_1}{1+I_p(b)}$:

$$\begin{aligned} dG_{p,sus}= & {} \lim \limits _{\epsilon \rightarrow 0}\frac{G_{p,sus}(b_i+\epsilon \tilde{b})- G_{p,sus}(b_i)}{\epsilon }\\= & {} \lim \limits _{\epsilon \rightarrow 0}\frac{\frac{m_1}{1+I_p(b_i+\epsilon \tilde{b})}-\frac{m_1}{1+I_p(b_i)}}{\epsilon }\\= & {} \frac{-m_1}{1+I_p(b_i)}\lim \limits _{\epsilon \rightarrow 0}\frac{1}{1+I_p(b_i+\epsilon \tilde{b})}\\{} & {} \frac{I_p(b_i+\epsilon \tilde{b})-I_p(b_i)}{\epsilon }\\= & {} \frac{-m_1}{(1+I_p(b_i))^2}dI_p(b_i,\tilde{b}). \end{aligned}$$

Through the relationship between $G\hat{a}teaux$ differential and $Fr\acute{e}chet$ differential, we can get

$$\begin{aligned} \tilde{g}^{(i)}_b=m_0(p-1)+\frac{pm_{1}b_i^{2p-1}}{Vol(\Omega )\big (1+b_i^p\big )^2}\int _{\Omega }\cdot \ \, dx, \end{aligned}$$

(3.7)

where $\int _{\Omega }\cdot \, dx$ is integral operator. Similarly, we can get

$$\begin{aligned} \hat{g}^{(i)}_b= & {} m_0(p-1)+\frac{m_1pb_i^{p-1}}{2\big (1+b_i^p\big )}\nonumber \\{} & {} +\frac{1}{Vol(\Omega )}\left( \frac{pm_{1}b_i^{2p-1}}{\big (1+b_i^p\big )^2}-\frac{m_1pb_i^{p-1}}{ 2\big (1+b_i^p\big )}\right) \int _{\Omega }\cdot \ \, dx.\nonumber \\ \end{aligned}$$

(3.8)

Substituting

$$\begin{aligned}{} & {} U=U_i+\Psi , \ (U=(w,b)^T,\ U_i=(w_i,b_i)^T,\\{} & {} \Psi =\left( \tilde{w},\tilde{b})^T\right) \end{aligned}$$

into models (2.7), on neglect higher order terms, we obtain the following linearized model, written in vector form

$$\begin{aligned} \Psi _t= & {} D\Psi _{xx}+J_1\Psi , \; for\; local\; grazing\nonumber \\ {}{} & {} model, \end{aligned}$$

(3.9)

$$\begin{aligned} \Psi _t= & {} D\Psi _{xx}+J_2\Psi +J_3, \nonumber \\{} & {} for \; sustained \; type\; nonlocal\; grazing\nonumber \\ {}{} & {} model, \end{aligned}$$

(3.10)

$$\begin{aligned} \Psi _t= & {} D\Psi _{xx}+J_4\Psi +J_5\Psi ,\nonumber \\{} & {} for \; natural \; type\; nonlocal\; grazing\nonumber \\ {}{} & {} model, \end{aligned}$$

(3.11)

with

$$\begin{aligned} D= & {} \left( \begin{array}{cc} 1 &{}\quad -\alpha \\ 0 &{}\quad r\\ \end{array}\ \right) , \ \ J_1=\left( \begin{array}{cc} f^{(i)}_{w} &{}\quad f^{(i)}_{b}\\ {g}^{(i)}_{w} &{}\quad {g}^{(i)}_{w}\\ \end{array}\ \right) , \\ J_2= & {} \left( \begin{array}{cc} f^{(i)}_{w} &{}\quad f^{(i)}_{b}\\ {g}^{(i)}_{w} &{}\quad m_0(p-1)\\ \end{array}\ \right) ,\\ J_3= & {} \left( \begin{array}{cc} 0 &{}\quad 0\\ 0 &{}\quad \frac{pm_{1}b_i^{2p-1}}{Vol(\Omega )\big (1+b_i^p\big )^2}\int _{\Omega } \ \cdot \ dx\\ \end{array}\ \right) ,\\ J_4= & {} \left( \begin{array}{cc} f^{(i)}_{w} &{}\quad f^{(i)}_{b}\\ g^{(i)}_{w} &{}\quad m_0(p-1)+\frac{m_1pb_i^{p-1}}{2\big (1+b_i^p\big )}\\ \end{array}\ \right) ,\\ J_5= & {} \left( \begin{array}{cc} 0 &{}0\\ 0 &{}\frac{1}{Vol(\Omega )}\left( \frac{pm_{2}b_i^{2p-1}}{\big (1+b_i^p\big )^2}-\frac{m_1pb_i^{p-1}}{2\big (1+b_i^p\big )}\right) \int _{\Omega } \ \cdot \ dx\\ \end{array}\ \right) . \end{aligned}$$

where $i=1,2,3$, $\Psi$ denotes the vector of solutions to the linear model of partial differential equations.

Here, we propose the corresponding characteristic equation of linear equation (3.9)–(3.11). At first, we introduce some eigenvalue problems which are useful throughout this section. Let

$$\begin{aligned} 0=\mu _{0}<\mu _{1}\le \mu _{2}\le \cdots \le \mu _{j}\le \cdots \rightarrow \infty , \end{aligned}$$

(3.12)

denote the eigenvalues of $-\Delta$ in $\Omega$ subject to the homogeneous Neumann boundary condition [38, 39, 43]. Therefore, characteristic equation of linearized system (3.9), (3.10) and (3.11) consists of the following sequences of equations

$$\begin{aligned} \lambda {\mathbb {I}} -\mathscr {L}(r,\alpha ,\mu _k)=0, \end{aligned}$$

where ${\mathbb {I}}$ is an identity matrix and

$$\begin{aligned} \mathscr {L}(r,\alpha ,\mu _k):=\left( \begin{array}{cc} -\mu _k+f^{(i)}_{w} &{}\quad \alpha \mu _k+f^{(i)}_{b}\\ g^{(i)}_{w} &{}\quad -r\mu _k+H^{(i)}\\ \end{array}\ \right) . \end{aligned}$$

(3.13)

According to the properties of the eigenvectors of the Laplace operator, we obtain

$$\begin{aligned} H^{(i)}=\left\{ \begin{array}{ll} m_0(p-1)+\frac{pm_{1}b_i^{2p-1}}{\big (1+b_i^p\big )^2},\quad k=0, \\ \left\{ \begin{array}{ll} H_{sus}^{(i)}:=m_0(p-1), \\ \quad k\ne 0,\ \ for\ \ sustained \; type \\ nonlocal \; grazing, \\ H_{nat}^{(i)}:=m_0(p-1)+\frac{m_1pb_i^{p-1}}{2\big (1+b_i^p\big )},\\ \quad k\ne 0, \; for \; natural \; type \\ nonlocal \; grazing,\\ H_{loc}^{(i)}:=m_0(p-1)+\frac{pm_{1}b_i^{2p-1}}{\big (1+b_i^p\big )^2},\\ \quad k\ne 0, \; for \; local \; type \; grazing. \end{array} \right. \end{array} \right. \end{aligned}$$

(3.14)

It is worth mentioning that when $k=0$, we have the absence of diffusion model, thus $\lambda$ satisfies the dispersion relation

$$\begin{aligned} \lambda ^2-tr(J(w_i,b_i))\lambda +det(J(w_i.b_i))=0, \end{aligned}$$

where the expression of $tr(J(w_i,b_i))$ and $det(J(w_i.b_i))$ are given by (3.5) and (3.6).

In the presence of diffusion, we have

$$\begin{aligned} \lambda ^2-{Tr}(r,\alpha ,\mu _k)\lambda +{Det}(r,\alpha ,\mu _k)=0, \end{aligned}$$

(3.15)

where $k\in \mathbb {N^+}:=\{1,2,3,\cdots \}$ and

$$\begin{aligned} {Tr}(r,\alpha ,\mu _k):= & {} {tr}(\mathscr {L}(r,\alpha ,\mu _k))\nonumber \\= & {} -(1+r)\mu _k+f^{(i)}_{w}+H^{(i)}, \end{aligned}$$

(3.16)

$$\begin{aligned} {Det}(r,\alpha ,\mu _k):= & {} {det}(\mathscr {L}(r,\alpha ,\mu _k))\nonumber \\= & {} r\mu ^2_k-\left( rf^{(i)}_{w}+H^{(i)}+\alpha g^{(i)}_{w}\right) \mu _k\nonumber \\{} & {} +H^{(i)}f^{(i)}_{w}-f^{(i)}_{b}g^{(i)}_{w}. \end{aligned}$$

(3.17)

If

$$\begin{aligned}{} & {} tr(J(w_i,b_i))<0, det(J(w_i,b_i))>0, \nonumber \\{} & {} {Tr}(r,\alpha ,\mu _k)<0~ and ~{Det}(r,\alpha ,\mu _k)>0 \end{aligned}$$

(3.18)

for all $k\in {\mathbb {N}}^+$, then $(w_i,b_i)$ is locally stable with respect to the nonlocal or local problem (2.7).

3.1 Catastrophic transition and critical transition

The concept of catastrophic transition and critical transition contributes to our understanding of desertification and ecological change [2, 3, 9]. In mathematical models, when an equilibrium state loses its attraction and disappears in response to a parameter passing a critical value, Tipping will occur. At that moment, the system underwent a catastrophic transition. The saddle-node bifurcation and transcritical bifurcation point are Tipping points (see Fig. 4). The Tipping points have one zero eigenvalue, in which the nontrivial stable uniform solution loses stability. In ecosystems, vegetated areas replace barren deserts in arid and semi-arid grazing ecosystems, because of drought or overgrazing. The classical theory of Tipping [2], predominantly based on nonspatial models, led to the creation of generic early warning signs before such Tipping occurs. In spatial systems, this idea becomes more complicated because it may now depend on critically the nature of the different spatial disturbances. Up to now, the regular spatial patterns resulting from Turing instability have been regarded as early warning signals for critical transition toward an alternative state in various ecosystems [9]. A major part of mathematical literature on vegetation pattern formation (i.e., critical transition) focuses on the onset of Turing patterns close to homogeneous equilibria [1,2,3, 9]. The homogeneous equilibria can be diffusionally driven unstable and thus create spatial patterns. As the grazing parameter moves around the Turing point we can obtain vegetation patterns. When the grazing rate reached Turing point or Tipping point (see Figs. 5 and 6), at which time this stable state disappears or loses its stability, the system undergoes a critical or catastrophic transition toward an alternative equilibrium.

Fig. 5

Transition diagram depicting the constant equilibrium points of model (2.7) when $p=1$. Solid lines describe the stability of the system state variables, while the dotted line indicates the unstable states. a Catastrophic transition; b Critical transition

In the spatially extended model, if $p=1$ and $m_1> M_1$, then the system only has desert state (0, R) and it is linearly stable. If $p=1$ and $m_1= M_1$, then the system undergoes a transcritical bifurcation at $m_1= M_1$ (Tipping point). The bifurcation diagram depicting these spatially uniform states and their stability as a function of $m_1$ is plotted in Fig. 5. If grazing parameter $m_1$ is smaller than $M_1$ and (3.18) holds, then the spatially uniform state $(w_1,b_1)$ is stable, and the system will fall into a degraded bare desert state when $m_1>M_1$ (see Fig. 5a). This is a catastrophic transition from a stable homogeneous vegetation state to a bear solid state. If grazing parameter is greater than Turing point and (3.18) does not hold, then Turing bifurcations on the uniform vegetated equilibrium will produce patterned states at the Turing point (see Fig. 5b). This is critical transition from a stable and homogeneous vegetation state to vegetation pattern state.

Fig. 6

Transition diagram depicting the constant equilibrium points of model (2.7) when $p>1$. Solid lines describe the stability of the system state variables, while the dotted line indicates the unstable states. a Catastrophic transition; b Critical transition

If $p>1$, then the desert state (R, 0) is linearly stable for all the parameters, and undergoes a saddle-node bifurcation at $m_1=M_2$ (Tipping point). The bifurcation diagram depicting these spatially uniform states and their stability as a function of $m_1$ is plotted in Fig. 6. If grazing parameter is smaller than $M_2$ and (3.18) holds, then the spatially uniform state $(w_2,b_2)$ is stable, and the system will fall into a degraded bare desert state when $m_1>M_2$ (see Fig. 6a), this is a catastrophic transition from vegetation state to a bear solid state. If grazing parameter is greater than Turing point and (3.18) does not hold, then Turing bifurcations on the uniform vegetated equilibrium $(w_2,b_2)$ will produce patterned states at the Turing point (see Fig. 6b). The critical transition from a stable and homogeneous vegetation state to a vegetation pattern state refers to a significant change in the spatial arrangement and structure of vegetation within an ecosystem. It signifies a shift from a uniform distribution of vegetation to the emergence of distinct patterns or patches. The transition from a vegetation pattern state to a desert state is a significant and concerning phenomenon known as desertification. The vegetation pattern transformation of desert only occurs in The critical transition, but not in the Catastrophic transition. Catastrophic and critical transition are ecologically represented by the transition diagram in Fig. 1.

3.2 Stability analysis

Stability analysis involves determining the stability of an equilibrium state and understanding how the system behaves in its vicinity. In stability analysis, the focus is on small perturbations or deviations from the equilibrium state. The goal is to determine whether these perturbations will grow or decay over time, indicating the stability or instability of the equilibrium. Stability analysis is crucial in understanding the behavior and dynamics of complex system (2.7). It provides insights into the long-term behavior of the system, such as whether it converges to a stable state, exhibits oscillations, or undergoes chaotic behavior. By analyzing the stability of equilibrium states, researchers can predict and control the system response to perturbations and external influences.

The bare-soil (R, 0) is always locally stable for the models (2.7) with $p>1$, and this equilibrium is locally stable for the models (2.7) when $R<m_0+m_1$ and $p=1$. For the model (2.7) with $p>1$, we have $det(J(w_3,b_3))<0$, hence $(w_3,b_3)$ is always unstable. Therefore, in the following analysis, we mainly discuss equilibrium points $(w_1,b_1)$ and $(w_2,b_2)$.

In this case, we introduce critical self-diffusion coefficients

$$\begin{aligned} \Upsilon ^{(i)}:=\frac{f^{(i)}_{w}H^{(i)} -2f^{(i)}_{b}g^{(i)}_{w}-2\sqrt{-f^{(i)}_{b}g^{(i)}_{w}\left( f^{(i)}_{w}H^{(i)} -f^{(i)}_{b}g^{(i)}_{w}\right) }}{\left( f_{w}^{(i)}\right) ^2} ,\nonumber \\ \end{aligned}$$

(3.19)

and critical cross-diffusion coefficients

$$\begin{aligned} \Lambda ^{(i)}=\frac{-f^{(i)}_{w} r+2\sqrt{H^{(i)}f^{(i)}_{w}-f^{(i)}_{b}g^{(i)}_{w}}\sqrt{r} -H^{(i)}}{g^{(i)}_{w}}.\nonumber \\ \end{aligned}$$

(3.20)

For the different types of grazing and positive equilibriums $U_i=(w_i,b_i) (i=1,2)$, we have $H^{(i)}:=H^{(i)}_{loc}, H^{(i)}_{nat}, H^{(i)}_{loc}$ [see Eq. (3.14)]. Therefore, there are different types of models corresponding to $\Upsilon ^{(i)}_{sus}, \Upsilon ^{(i)}_{nat}$, $\Upsilon ^{(i)}_{loc}$ and $\Lambda ^{(i)}_{sus}, \Lambda ^{(i)}_{nat}, \Lambda ^{(i)}_{loc}$. The main results on stability for model (2.7) are given in the following Theorem.

Theorem 3.1

Assume that $p=1$ and (3.6) holds.

• (i) For the absence of cross-diffusion model:

  • (a) If $m_1<M_1$, then equilibrium $(w_1,b_1)$ is locally stable for the sustained grazing model.

  • (b) If $m_1\le M_1-m_0$ and $r>\Upsilon ^{(1)}_{nat}$, then $(w_1,b_1)$ is locally stable for the natural grazing model.

  • (c) If $m_1<M_1$ and $r>\Upsilon ^{(1)}_{loc}$, then $(w_1,b_1)$ is locally stable for local grazing model.

• (ii) For the cross-diffusion model:

  • (a) Suppose that $m_1<M_1$ holds. If $0<\alpha <\Lambda ^{(1)}_{sus}$, then $(w_1,b_1)$ is locally stable for the sustained grazing model.

  • (b) Suppose that $m_1\le M_1-m_0$ and $r>\Upsilon ^{(1)}_{nat}$ hold. If $0<\alpha <\Lambda ^{(i)}_{nat}$, then $(w_1,b_1)$ is locally stable for the natural grazing model.

  • (c) Suppose that $m_1<M_1$ and $r>\Upsilon ^{(1)}_{loc}$ hold. If $0<\alpha <\Lambda ^{(1)}_{loc}$, then $(w_1,b_1)$ is locally stable for the local grazing model.

Proof

$\mathrm {(i)}$ $\mathrm {(a)}$ According to (3.14), we obtain $H^{(1)}_{sus}=0$ when $p=1$. If the sustained grazing model without cross-diffusion is locally stable, then we must have

$$\begin{aligned} Det(r,0,\mu _k)= & {} r\mu ^2_k-rf_{w}\mu _k-f_{b}g_{w}>0, \end{aligned}$$

(3.21)

$$\begin{aligned} Tr_{sus}(r,0,\mu _k)= & {} -r\mu ^2_k+f_w<0, \end{aligned}$$

(3.22)

for all $\mu _k$. Hence, $(w_1,b_1)$ is locally stable with respect to the sustained grazing model.

$\mathrm {(b)}$ Assume that $p=1$, $m_1<M_1-m_0$, we obtain $H_{nat}^{(1)}<H_{loc}^{(1)}$. Suppose that (3.6) holds, that is to say

$$\begin{aligned} Tr_{sus}(r,0,\mu _k)\le Tr_{loc}(r,0,\mu _k)<0. \end{aligned}$$

(3.23)

If the natural grazing model (2.7) without cross-diffusion is locally stable, then we must have

$$\begin{aligned} Det(r,0,\mu _k)= & {} r\mu ^2_k-(H_{nat}^{(1)}+rf_{w})\mu _k\nonumber \\{} & {} +H_{nat}^{(1)}f_{w}-f_{b}g_{w}>0 \end{aligned}$$

(3.24)

for all $\mu _k$. Thus we obtain the following stability conditions

$$\begin{aligned} H_{nat}^{(1)}+rf_{w}\le 0 \end{aligned}$$

(3.25)

or

$$\begin{aligned} H_{nat}^{(1)}+rf_{w}>0 \ and \ \min Det(r,0,\mu _k)>0. \end{aligned}$$

(3.26)

The inequality (3.25) is equivalent to $r\ge r_0:=\frac{H_{nat}^{(1)}}{|f_w|}$ and the first inequality in (3.26) is equivalent to $r<r_0$. Whereas, the second inequality in (3.26) is satisfied if either $\Upsilon ^{(1)}_{nat}<r<\bar{\Upsilon }^{(1)}_{nat}$, where

$$\begin{aligned}{} & {} \Upsilon ^{(1)}_{nat}:=\\{} & {} \frac{H^{(1)}_{nat}f_w-2f_bg_w-2\sqrt{f_bg_w\big (f_bg_w-H_{nat}^{(1)}f_w\big )}}{f^2_w},\\{} & {} \bar{\Upsilon }^{(1)}_{nat}:=\\{} & {} \frac{H_{nat}^{(1)}f_w-2f_bg_w+2\sqrt{f_bg_w\big (f_bg_w-H_{nat}^{(1)}f_w\big )}}{f^2_w}, \end{aligned}$$

where $\Upsilon ^{(1)}_{nat},\bar{\Upsilon }^{(1)}_{nat}$ are the two positive roots of equation

$$\begin{aligned} \big (rf_w+H_{nat}^{(1)}\big )^2-4\big (H_{nat}^{(1)}f_w-f_bg_w\big )r=0. \end{aligned}$$

By simple calculation, we obtained $0<\Upsilon ^{(1)}_{nat}<r_0<\bar{\Upsilon }^{(1)}_{nat}$. Thus stability conditions are

$$\begin{aligned} r\ge r_0 \ \ or \ \ \Upsilon ^{(1)}_{nat}<r<r_0. \end{aligned}$$

Thus, if r satisfies conditions $r>\Upsilon ^{(1)}_{nat}$, then the eigenvalues of the operator $\mathscr {L}(r,0,\mu _k)$ are with negative real part for all $k\in \mathbb {N^+}$.

The proof of $\mathrm {(c)}$ is similar with $\mathrm {(b)}$, thus we omit it.

$\mathrm {(ii)}$ $\mathrm {(a)}$ To show stability of the cross-diffusion model, we only need to verify that

$$\begin{aligned} Det(r,\alpha ,\mu _k)= & {} r\mu _k^2-\big (rf_{w}+H^{(1)}_{sus}+\alpha g_{w}\big )u_k\nonumber \\{} & {} +H^{(1)}_{sus}f_w-g_wf_b>0 \end{aligned}$$

(3.27)

for all k. Then the condition for the stability of $(w_1,b_1)$ is

$$\begin{aligned} rf_{w}+H^{(1)}_{sus}+\alpha g_{w}\le 0 \end{aligned}$$

(3.28)

or

$$\begin{aligned} rf_{w}+H^{(1)}_{sus}+\alpha g_{w}>0\ and \ \min Det_{sus}(r,\alpha ,k)>0.\nonumber \\ \end{aligned}$$

(3.29)

Since $r>\Upsilon ^{(1)}_{sus}$, we have

$$\begin{aligned} rf_{w}+m_0<2\sqrt{H^{(1)}_{sus}f_{w}-f_{b}g_{w}}\sqrt{r}. \end{aligned}$$

Therefore, the inequality (3.28) and (3.29) are equivalent to

$$\begin{aligned} \alpha \le \alpha _0=\frac{-H^{(1)}_{sus}-rf_w}{g_w} \end{aligned}$$

or

$$\begin{aligned}{} & {} rf_{w}+H^{(1)}_{sus}+\alpha g_{w}<2\sqrt{r(H^{(1)}_{sus}f_{w}-f_{b}g_{w})}\\{} & {} \quad and \ \ \alpha >\alpha _0. \end{aligned}$$

By simple calculation, we can easily get the stability conditions

$$\begin{aligned}{} & {} \alpha>\Lambda ^{(1)}_{sus}\nonumber \\{} & {} \quad :=\frac{-f_{w} r+2\sqrt{r\big (H^{(1)}_{sus}f_{w}-f_{b}g_{w}\big )}-H^{(1)}_{sus}}{g_{w}}>0.\nonumber \\ \end{aligned}$$

(3.30)

The proof of (b) and (c) are similar with (a), thus we omit them. This completes the proof. $\square$

Remark 2

If $p>1$, $m_1<M_2$, then $f^{(2)}_wH_{sus}^{(2)}-f^{(2)}_bg^{(2)}_w>det(J(w_2,b_2))>0$ is established for the sustained grazing model. Therefore, when $p > 1$, the stability of the equilibrium point $(w_2,b_2)$ to the sustained grazing model and local grazing model can be considered, but for natural grazing model, when $1< p < 2$, the sign of $H_{nat}^{(2)}f^{(2)}_w-f^{(2)}_bg^{(2)}_w$ cannot be judged. Thus, when $1<p<2$, the stability of the equilibrium point $(w_2,b_2)$ for the natural grazing model cannot be judged. However, when $p\ge 2$ and $m_1<M_2$, it can guarantee that $H_{nat}^{(2)}f^{(2)}_w-f^{(2)}_bg^{(2)}_w>det(J(w_2,b_2))>0$, so the stability of $(w_2,b_2)$ to the natural grazing model can be judged.

Theorem 3.2

Assume that $m_1<M_2$ and (3.6) holds. The following statements hold:

• (i) For the absence of cross-diffusion model:

  • (a) If $p>1$ and $r>\Upsilon ^{(2)}_{sus} ( r>\Upsilon ^{(2)}_{loc})$, then $(w_2,b_2)$ is locally stable for sustained (local) grazing model.

  • (b) If $p\ge 2$ and $r>\Upsilon ^{(2)}_{nat}$, then $(w_2,b_2)$ is locally stable for natural grazing model.

• (ii) For the cross-diffusion model:

  • (a) Suppose that $p>1$ and $r>\Upsilon ^{(2)}_{sus} ( r>\Upsilon ^{(2)}_{loc})$ hold. If $0<\alpha<\Lambda ^{(2)}_{sus} ( 0<\alpha <\Lambda ^{(2)}_{loc})$, then $(w_2,b_2)$ is locally stable for sustained (local) grazing model.

  • (b) Suppose that $p\ge 2$ and $r>\Upsilon ^{(2)}_{nat}$ hold. If $0<\alpha <\Lambda ^{(2)}_{nat}$, then $(w_2,b_2)$ is locally stable for natural grazing model.

The proof of the Theorem 3.2 is similar with Theorem 3.1, thus we omit it.

3.3 Spatial pattern formation

Spatial vegetation pattern formation refers to the emergence of organized patterns in the distribution of vegetation across a landscape. The formation of spatial vegetation patterns is influenced by a combination of ecological processes and environmental factors, studying spatial vegetation pattern formation is essential for advancing our ecological understanding, conserving biodiversity, maintaining ecosystem functioning, guiding land management practices, and adapting to climate change. It provides valuable insights into the complex interactions between plants, animals, and their environment, and helps us make informed decisions for sustainable land use and conservation. Turing instability is a simple mechanism to generate heterogeneous spatial patterns via reaction–diffusion model. Turing instability indicates that there exists a $\mu _k$ such that the root $\lambda$ of (3.15) satisfies $Re(\lambda ) >0$. In this case, we can see that

$$\begin{aligned} {Det}(r,\alpha ,\mu _k)= & {} r\mu ^2_k-\big (rf^{(i)}_{w}+H^{(i)}+\alpha g^{(i)}_{w}\big )\mu _k\nonumber \\{} & {} +H^{(i)}f^{(i)}_{w}-f^{(i)}_{b}g^{(i)}_{w}=0, \end{aligned}$$

(3.31)

have two positive roots:

$$\begin{aligned}{} & {} \mu ^\pm (r,\alpha )\nonumber \\{} & {} \quad =\frac{rf_w+\alpha g_w+H^{(i)}\pm \sqrt{\big (rf_w+\alpha g_w+H^{(i)}\big )^2-4r\big (H^{(i)}f_w-f_bg_w\big )}}{2r}. \end{aligned}$$

(3.32)

For the different types of model, we have different $\mu ^\pm _{sus}(r,\alpha )$, $\mu ^\pm _{nat}(r,\alpha )$ and $\mu ^\pm _{loc}(r,\alpha )$. It is obvious that if $\mu ^-_k(r,\alpha )< \mu _k< \mu ^+_k(r,\alpha )$ holds for some $\mu _k$, then ${Det}(r,\alpha ,\mu _k)<0$, and the positive equilibrium $(w_i,b_i)$ $(i=1,2)$ of model (2.7) is unstable. According to Theorems 3.1 and 3.2, we obtain the following result with respect to spatial Turing instability of the model (2.7).

Theorem 3.3

Suppose that $p=1$ and (3.6) holds.

• (i) For the absence of cross-diffusion model:

  • (a) If $m_1<M_1$, then equilibrium $(w_1,b_1)$ is always locally stable for the sustained grazing model. That is, the Turing instability will not occur in sustained grazing model.

  • (b) If $m_1\le M_1-m_0$ and $0<r<\Upsilon ^{(1)}_{nat}$, then the positive equilibrium $(w_1,b_1)$ of natural grazing model (2.7) is unstable and thus model experiences the Turing instability provided that $\mu ^-_{nat}(r,0)< \mu _k< \mu ^+_{nat}(r,0)$ for some $k\ge 1$.

  • (c) If $m_1<M_1$ and $0<r<\Upsilon ^{(1)}_{loc}$, then the positive equilibrium $(w_1,b_1)$ of local grazing model (2.7) is unstable and thus model experiences the Turing instability provided that $\mu ^-_{loc}(r,0)<\mu _k<\mu ^+_{loc}(r,0)$ for some $k\ge 1$.

• (ii) For the cross-diffusion model:

  • (a) Assume that $m_1<M_1$ holds. If $\alpha >\Lambda ^{(1)}_{sus}$, then the positive equilibrium $(w_1,b_1)$ of sustained grazing model (2.7) is unstable and thus model experiences the Turing instability provided that $\mu ^-_{sus}(r,\alpha )< \mu _k< \mu ^+_{sus}(r,\alpha )$ for some $k\ge 1$.

  • (b) Assume that $m_1\le M_1-m_0$ and $r>\Upsilon ^{(1)}_{nat}$ hold. If $\alpha >\Lambda ^{(1)}_{nat}$, then the positive equilibrium $(w_1,b_1)$ of natural grazing model (2.7) is unstable and thus model experiences the Turing instability provided that $\mu ^-_{nat}(r,\alpha )< \mu _k< \mu ^+_{nat}(r,\alpha )$ for some $k\ge 1$.

  • (c) Assume that $m_1<M_1$ and $r>\Upsilon ^{(1)}_{loc}$ hold. If $\alpha >\Lambda ^{(1)}_{loc}$, then the positive equilibrium $(w_1,b_1)$ of natural grazing model (2.7) is unstable and thus model experiences the Turing instability provided that $\mu ^-_{loc}(r,\alpha )< \mu _k< \mu ^+_{loc}(r,\alpha )$ for some $k\ge 1$.

Proof

$\mathrm {(i)}$ (a) In Theorem 3.1$\mathrm {(i)}$(a), we have known that sustained grazing model without cross-diffusion is unconditionally stable. Therefore, (a) is clearly true.

(b) Assume that $p=1$, $m_1<M_1-m_0$, we obtain $H_{nat}^{(1)}<H_{loc}^{(1)}$. To show Turing instability driven by the self-diffusion, we only need to verify that

$$\begin{aligned} Det_{nat}(r,\alpha ,\mu _k):= & {} r\mu _k^2-\big (rf_{w}+H_{nat}^{(1)}\big )\mu _k\nonumber \\{} & {} +H_{nat}^{(1)}f_w-g_wf_b<0, \end{aligned}$$

for some $\mu _k>0$, which is equivalent to

$$\begin{aligned} \left\{ \begin{aligned}&rf_w+H_{nat}^{(1)}>0, \\&\big (rf_w+H_{nat}^{(1)}\big )^2-4\big (H_{nat}^{(1)}f_w-f_bg_w\big )r>0 . \end{aligned} \right. \end{aligned}$$

(3.33)

Using the same argument as in the proof of Theorem 3.1, we obtain $0<r<\Upsilon ^{(1)}_{nat}$. Thus, if r satisfies conditions $0<r<\Upsilon ^{(1)}_{nat}$, then there is an eigenvalue of the operator $\mathscr {L}(r,\alpha ,k)$ with positive real part if and only if the inequality $\mu ^-_{nat}(r,0)< \mu _k< \mu ^+_{nat}(r,0)$ is satisfied for some $k\in \mathbb {N^+}$.

The proof $\mathrm {(i)} \mathrm {(c)}$ is similar with $\mathrm {(i)} \mathrm {(b)}$, thus we omit it.

$\mathrm {(ii)}$ (a) Using the same argument as $\mathrm {(i)}$, we only need to verify that

$$\begin{aligned} Det(r,\alpha ,\mu _k):= & {} r\mu _k^2-(rf_{w}+H^{(1)}_{sus}\nonumber \\{} & {} +\alpha g_{w})\mu _k+H^{(1)}_{sus}f_w-g_wf_b<0, \end{aligned}$$

for some $\mu _k>0$, which is equivalent to

$$\begin{aligned} \left\{ \begin{aligned}&rf_w+\alpha g_w+H^{(1)}_{sus}>0, \\&\big (rf_w+\alpha g_w+H^{(1)}_{sus}\big )^2-4\big (H^{(1)}_{sus}f_w-f_bg_w\big )r>0 . \end{aligned} \right. \end{aligned}$$

(3.34)

If $\alpha >\Lambda ^{(1)}$, then there is an eigenvalue of the operator $\mathscr {L}(r,\alpha ,k)$ with positive real part if and only if inequality $\mu ^-(r,\alpha )< \mu _k< \mu ^+(r,\alpha )$ is satisfied for some $k\in \mathbb {N^+}$.

The proof of the $\mathrm {(ii)} \mathrm {(b)}$ and (c) are very similar with $\mathrm {(ii)} \mathrm {(a)}$. The difference is that the self-diffusion coefficient in the natural grazing model and local grazing model have parameter restrictions, That is to say, the model without cross-diffusion should be stable, but the self-diffusion constraint is not required in the sustained grazing model (i.e., the sustained grazing model without cross-diffusion is always locally stable). This completes the proof. $\square$

Theorem 3.4

Suppose that $m_1<M_2$ and (3.6) holds.

• (i) For the absence of cross-diffusion model:

  • (b) If $p>1$ and $0<r<\Upsilon ^{(2)}_{sus}$ $(0<r<\Upsilon ^{(2)}_{loc})$, then the positive equilibrium $(w_2,b_2)$ of natural (local) grazing model (2.7) is unstable and thus model experiences the Turing instability provided that $\mu ^-_{sus}(r,0)< \mu _k< \mu ^+_{sus}(r,0)$ $(\mu ^-_{loc}(r,0)<\mu _k<\mu ^+_{loc}(r,0))$ for some $k\ge 1$.

  • (b) If $p\ge 2$ and $0<r<\Upsilon ^{(2)}_{nat}$, then the positive equilibrium $(w_2,b_2)$ of natural grazing model (2.7) is unstable and thus model experiences the Turing instability provided that $\mu ^-_{nat}(r,0)< \mu _k< \mu ^+_{nat}(r,0)$ for some $k\ge 1$.

• (ii) For the cross-diffusion model:

  • (a) Assume that $p>1$ and $r>\Upsilon ^{(2)}_{sus}$ $(r>\Upsilon ^{(2)}_{loc})$ hold. If $\alpha >\Lambda ^{(1)}_{sus}$ $(\alpha >\Lambda ^{(1)}_{loc})$, then the positive equilibrium $(w_2,b_2)$ of sustained (local) grazing model (2.7) is unstable and thus model experiences the Turing instability provided that $\mu ^-_{loc}(r,0)< \mu _k< \mu ^+_{loc}(r,0)$ $(\mu ^-_{loc}(r,0)< \mu _k< \mu ^+_{loc}(r,0))$ for some $k\ge 1$.

  • (b) Assume that $p\ge 2$ and $r>\Upsilon ^{(2)}_{nat}$ hold. If $\alpha >\Lambda ^{(1)}_{nat}$, then the positive equilibrium $(w_2,b_2)$ of natural grazing model (2.7) is unstable and thus model experiences the Turing instability provided that $\mu ^-_{nat}(r,0)< \mu _k< \mu ^+_{nat}(r,0)$ for some $k\ge 1$.

The proof of the Theorem 3.4 is similar with Theorem 3.3, thus we omit it.

Remark 3

In Theorems 3.1–3.4, we studied the influence of the diffusion coefficients $r (:=\frac{D_b}{D_w})$ and $\alpha$, and obtain the diffusion-induced instability region. In fact, to obtain pattern occurrence the water diffuses much faster than the vegetation, i.e., $D_b \ll D_w$, or the cross-diffusion is small enough.

By using separation of variables, we get eigenvalues of $\triangle$ on $\Omega$ with Neumann boundary conditions. The eigenvalue $\mu _k:=\frac{n^2}{L^2}$ (n is a integer) in the one-dimensional (i.e., $\Omega :=(0,L\pi )$) case and $\mu _k:=\frac{n^2}{L^2}+\frac{m^2}{L^2}$ (n, m are two integers) in the two-dimensional case (i.e., $\Omega :=(0,L\pi )\times (0,L\pi )$) [43].

We present detailed comparisons between the different types of grazing. In Fig. 7, we fix all parameter values and vary only the self-diffusion coefficient r. In Fig. 7, we plot ${Det}(r,0,\mu _k)$ for the cases $p=1$ at the equilibrium $(w_1,b_1)$ from stability to self-diffusion driven instability.

Fig. 7

Plots of $Det(r,0,\mu _k)$ fixed parameters $m_0=0.225$, $m_1=1.5$ and $R=3$. a and b sustained grazing model; c and d natural grazing model; e and f local grazing model

• 1. Sustained grazing model without cross-diffusion: If we take $r= 0.1,0.0001$ (black and green curve in Fig. 7a), then ${Det}(r,0,\mu _k)>0$ for all n. Similarly, for two-dimensional case, if we take $r= 0.1,0.0001$ (see Fig. 7b, c), then ${Det}(r,0,\mu _k)>0$ for all n, m in space ${Det}(r,0,\mu _k)-n-m$. That is, the Turing instability will not occur in sustained grazing model.

• 2. Natural grazing model without cross-diffusion: If we take $r=0.0012$ (black curve in Fig. 7d), which is less than the critical diffusion coefficient $\Upsilon ^{(1)}_{nat}=0.0015$ (red curve in Fig. 7d), then ${Det}(r,0,\mu _k)<0$ for some n. If we take $r= 0.0045$ (green curve in Fig. 7c, d), a value that is greater than the critical diffusion coefficient $\Upsilon ^{(1)}_{nat}=0.0015$ (red curve in Fig. 7d), then ${Det}(r,0,\mu _k)>0$ for all n. Similarly, for two-dimensional case, if we take $r= 0.0015$ (see Fig. 7e), then ${Det}(r,0,\mu _k)<0$ for some n, m in space ${Det}(r,0,\mu _k)-n-m$, and if $r= 0.0045$ (see Fig. 7f), then ${Det}(r,0,\mu _k)>0$ for all n, m in space ${Det}(r,0,\mu _k)-n-m$. It is clear that self-diffusion in natural grazing model induces diffusion-driven instability when $r<\Upsilon ^{(1)}_{nat}$.

• 3. Local grazing model without cross-diffusion: If we take $r=0.0045$ (black curve in Fig. 7g), which is less than the critical diffusion coefficient $\Upsilon ^{(1)}_{loc}=0.0049$ (red curve in Fig. 7g), then ${Det}(r,0,\mu _k)<0$ for some n. If we take $r= 0.005$ (green curve in Fig. 7g), a value that is greater than the critical diffusion coefficient $\Upsilon ^{(1)}_{loc}=0.0049$ (red curve in Fig. 7g), then ${Det}(r,0,\mu _k)>0$ for some n. Similarly, for two-dimensional case, if we take $r= 0.0045$ (see Fig. 7e), then ${Det}(r,0,\mu _k)<0$ for some n, m in space ${Det}(r,0,\mu _k)-n-m$, and if $r= 0.005$ (see Fig. 7f), then ${Det}(r,0,\mu _k)>0$ for all n, m in space ${Det}(r,0,\mu _k)-n-m$. It is clear that self-diffusion in local grazing model induces diffusion-driven instability when $r<\Upsilon ^{(1)}_{loc}$.

In Fig. 8, we fix all parameters except the cross-diffusion coefficient $\alpha$ and show ${Det}(r,\alpha ,\mu _k)$ for the cases $p=1$. If we take $r=0.006$, then it is greater than all the critical self-diffusion coefficients $\Upsilon ^{(1)}_{sus},\Upsilon ^{(1)}_{nat}$ and $\Upsilon ^{(1)}_{loc}$. By Fig. 7 the positive equilibrium $(w_1, b_1)$ of model (2.7) without cross-diffusion $(\alpha = 0)$ is stable. It is clear that self-diffusion in three types of models does not induce diffusion-driven instability. For the sustained (natural or local) grazing model with cross-diffusion, if we take $\alpha =0.29$ (0.22 or 0.2), then it is less than the critical cross-diffusion coefficient $\Lambda ^{(1)}_{sus}$ ($\Lambda ^{(1)}_{nat}$ or $\Lambda ^{(1)}_{loc}$). We observe that $Det(r, \alpha , \mu _k) > 0$ for all n in one-dimensional case (green curve in Fig. 8a, d, g). Similarly, for two-dimensional case, if we take $\alpha =0.29$ (0.22 or 0.2), then ${Det}(r,\alpha ,\mu _k)>0$ for all n, m in space ${Det}(r,0,\mu _k)-n-m$ (see Fig. 8b, e, h). Hence, the equilibrium solution $(w_1, b_1)$ is stable when $\alpha <\Lambda ^{(1)}_{sus}$ ($\Lambda ^{(1)}_{nat}$ or $\Lambda ^{(1)}_{loc}$). If we take $\alpha = 0.3$ (0.25 or 0.29), a value that is greater than the critical cross-diffusion coefficient $\Lambda ^{(1)}_{sus}=0.2963$ ($\Lambda ^{(1)}_{nat}=0.2478$ or $\Lambda ^{(1)}_{loc}=0.2101$) (red curve in Fig. 8a, d, g), then ${Det}(r,\alpha ,\mu _k)<0$ for some n. Similarly, for two-dimensional case, if we take $\alpha = 0.3$ (0.25 or 0.29), then ${Det}(r,\alpha ,\mu _k)<0$ for some n, m in space ${Det}(r,\alpha ,\mu _k)-n-m$ (see Fig. 8c, f, i). It is clear that cross-diffusion in different grazing types of models induces cross-diffusion-driven instability when $\alpha >\Lambda ^{(1)}_{sus}$($\Lambda ^{(1)}_{nat}$ or $\Lambda ^{(1)}_{loc}$).

Fig. 8

Plots of $Det(r,\alpha ,\mu _k)$ fixed parameters $m_0=0.225$, $m_1=1.5$, $R=3$ and $r=0.06$. a–c Sustained grazing model; d–f natural grazing model; g–i local grazing model

4 A comparison between local and nonlocal grazing models

There are three grazing models that have been developed to simulate and study the effects of grazing on vegetation patterns and ecosystem dynamics. Here, I will provide a brief comparison of three grazing models: local grazing model, nonlocal sustained grazing model and nonlocal natural grazing model. It is important to note that each grazing model has its own assumptions, strengths, and limitations. The choice of model depends on the specific research question and the level of complexity desired. We use a combination of models to gain a more comprehensive understanding of grazing effects on vegetation patterns and ecosystem dynamics.

Let $\Upsilon ^{(i)}_{sus}, \Upsilon ^{(i)}_{nat}, \Upsilon ^{(i)}_{loc}$ and $\Lambda ^{(i)}_{sus}, \Lambda ^{(i)}_{nat}, \Lambda ^{(i)}_{loc}$ represent critical self-diffusion coefficients and critical cross-diffusion coefficients for sustained grazing model, natural grazing model and local grazing model, respectively. Then we can obtain the following results:

Theorem 4.1

For the model (2.7) of the corresponding critical self-diffusion coefficients has the following relationship:

• (i) If $p=1$ and $m_1\le M_1-m_0$, then $0< \Upsilon ^{(1)}_{nat}<\Upsilon ^{(1)}_{loc}$.

• (ii) If $p>1$ and $m_1<M_2$, then $0<\Upsilon ^{(2)}_{sus}<\Upsilon ^{(2)}_{loc}$.

• (iii) If $p\ge 2$ and $m_1<M_2$, then $0<\Upsilon ^{(2)}_{sus}<\Upsilon ^{(2)}_{nat}<\Upsilon ^{(2)}_{loc}$.

Proof

$\mathrm {(i)}$ Since $m_1\le M_1-m_0$, it’s easy to get $H^{(1)}_{loc}> H^{(1)}_{nat}>0$. By simple calculation, we obtained

$$\begin{aligned} {Det}_{loc}(r,0,\mu _k)<{Det}_{nat}(r,0,\mu _k), \end{aligned}$$

where

$$\begin{aligned} {Det}_{loc}(r,0,\mu _k):= & {} r\mu ^2_k-\big (rf^{(1)}_{w}+H^{(1)}_{loc}\big )\mu _k\\{} & {} +H^{(1)}_{loc}f^{(1)}_{w}-f^{(1)}_{b}g^{(1)}_{w},\\ {Det}_{nat}(r,0,\mu _k):= & {} r\mu ^2_k-\big (rf^{(1)}_{w}+H^{(1)}_{nat}\big )\mu _k\\{} & {} +H^{(1)}_{nat}f^{(1)}_{w}-f^{(1)}_{b}g^{(1)}_{w}. \end{aligned}$$

If  ${Det}_{loc}(r,0,\mu _k)>0$ holds, then  ${Det}_{nat}(r,0,\mu _k)>0$ must be true. Therefore, Theorem 4.1$\mathrm {(i)}$ is true.

$\mathrm {(ii)}$ By similar way as described above, we have following results

$$\begin{aligned} {Det}_{loc}(r,0,\mu _k)<{Det}_{sus}(r,0,\mu _k), \end{aligned}$$

where

$$\begin{aligned} {Det}_{loc}(r,0,\mu _k):= & {} r\mu ^2_k-\big (rf^{(2)}_{w}+H_{loc}^{(2)}\big )\mu _k\\{} & {} +H_{loc}^{(2)}f^{(2)}_{w}-f^{(2)}_{b}g^{(2)}_{w},\\ {Det}_{sus}(r,0,\mu _k):= & {} r\mu ^2_k-\big (rf^{(2)}_{w}+H_{sus}^{(2)}\big )\mu _k\\{} & {} +H_{sus}^{(2)}f^{(2)}_{w}-f^{(2)}_{b}g^{(2)}_{w}. \end{aligned}$$

If ${Det}_{loc}(r,\alpha ,\mu _k)>0$ holds, then ${Det}_{sus}(r,0,\mu _k)>0$ must hold. Hence, Theorem 4.1$\mathrm {(ii)}$ is true.

$\mathrm {(iii)}$ According to the inequality (3.2), we obtained

$$\begin{aligned} b_2>(p-1)^{\frac{1}{p}}. \end{aligned}$$

When $p\ge 2$, it is easy to conclude from the above inequality that $b_2>1$. By (3.4), (3.7) and (3.8), we have ${g^{(2)}_{b}}> \hat{g}^{(2)}_{b}> \tilde{g}^{(2)}_{b}$ when $p\ge 2$. Therefore, it’s easy to get the following inequality

$$\begin{aligned}{} & {} f^{(2)}_{w}\tilde{g}^{(2)}_{b}-f^{(2)}_{b}{g}^{(2)}_{w}>f^{(2)}_{w}\hat{g}^{(2)}_{b} -f^{(2)}_{b}{g}^{(2)}_{w}\\{} & {} \quad>f^{(2)}_{w}{g}^{(2)}_{b}-f^{(2)}_{b}{g}^{(2)}_{w}>0. \end{aligned}$$

According to the above inequalities, we obtain

$$\begin{aligned} {Det}_{sus}(r,0,\mu _k)>{Det}_{nat}(r,0,\mu _k)>{Det}_{loc}(r,0,\mu _k). \end{aligned}$$

Hence, Theorem 4.1$\mathrm {(iii)}$ is proved. When $1<p<2$, since $b_2<1$, $g^{(2)}_{b}<\hat{g}^{(2)}_{b}$ holds. Since $f^{(2)}_{w}\hat{g}^{(2)}_{b}< f^{(2)}_{w}{g}^{(2)}_{b}<0$, the positivity of $f^{(2)}_{w}\hat{{g}}^{(2)}_{b}-f^{(2)}_{b}{g}^{(2)}_{w}$ cannot be guaranteed when $f^{(2)}_{w}{g}^{(2)}_{b}-f^{(2)}_{b}{g}^{(2)}_{w}>0$. Therefore, when $1<p<2$, we could not compare the stability between the local grazing model and the natural grazing model. $\square$

Theorem 4.2

For the model (2.7), the corresponding critical cross-diffusion coefficients has the following relationship:

• (i) If $p=1$, $m_1\le M_1-m_0$ and $r>\Upsilon ^{(1)}_{loc}$, then $\Lambda ^{(1)}_{sus}>\Lambda ^{(1)}_{nat}>\Lambda ^{(1)}_{loc}$.

• (ii) If $p>1$, $m_1<M_2$ and $r>\Upsilon ^{(2)}_{loc}$, then $\Lambda ^{(2)}_{sus}>\Lambda ^{(2)}_{loc}$.

• (iii) If $p\ge 2$, $m_1<M_2$ and $r>\Upsilon ^{(2)}_{loc}$, then $\Lambda ^{(2)}_{sus}>\Lambda ^{(2)}_{nat}>\Lambda ^{(2)}_{loc}$.

The proof of the Theorem 4.2 is similar with Theorem 4.1, thus we omit it.

Remark 4

In Theorems 4.1 and 4.2, we can see the nonlocal terms promote linear stability, which implies that if the local model is stable, then the nonlocal model is always stable. On the contrary, if the nonlocal model is stable, the local model may produce vegetation patterns. For the two non local models, the stability of the sustained grazing model is better than that of the natural grazing model. If the sustained grazing model is stable, then the natural grazing model is also stable.

Here, we use numerical simulation to compare the three grazing types models and consider the effect of grazing parameter $m_1$ on model (2.7). For the fixed other parameters, the absence of cross-diffusion model (2.7) is stable when $r> \Upsilon ^{(i)}(m_1)$, and the cross-diffusion model (2.7) is stable when $r>\Upsilon ^{(i)}(m_1)$ and $0<\alpha <\Lambda ^{(i)}(m_1)$. To describe the pattern formation, we give the following examples.

Example 1

Let $m_0=0.225,R=3,p=1$. We obtain the effect of the grazing parameter $m_1$ on pattern formation and desertification process in Fig. 9. Figure 9 simulates the desertification process with a slowly increasing grazing parameter $m_1$. It is easy to see that large values of the grazing parameter $m_1$ is grater than Tipping point, the homogeneous or vegetation pattern state becomes the bare desert state. When the grazing pressure drops below a Turing point, the model resides in a more stable homogeneously vegetated state. We present detailed analysis three types of grazing models. In Fig. 9 we summarize our results as follows:

Fig. 9

The effects of grazing rate $m_1$ on pattern formation for a different models with $p = 1$. Critical diffusion coefficient $\Upsilon ^{(1)}_{sus}, \Upsilon ^{(1)}_{nat}$, $\Upsilon ^{(1)}_{loc}$ and $\Lambda ^{(1)}_{sus}, \Lambda ^{(1)}_{nat}, \Lambda ^{(1)}_{loc}$ are given by Theorem 3.3 and 3.4. H.V. and P.F. are respectively represent homogenous vegetation region and pattern formation region. a Sustained grazing model without cross-diffusion; b Natural grazing model without cross-diffusion; c Local grazing model without cross-diffusion; d Natural grazing model with cross-diffusion; e Sustained grazing and local grazing model with cross-diffusion; f Drawing of partial enlargement of (e)

• 1. Model of absent cross-diffusion: If $m_1>R-m_0$, then the model (2.7) only has stable bare soil state. If $m_1<R-m_0$, then the model (2.7) has stable homogeneous vegetation state for sustained grazing model, homogenous vegetation state or vegetation pattern state exist for local grazing models. For the natural grazing model, when $m_1\le R-2m_0$, we can judge occur vegetation pattern or maintain homogenous vegetation, but when $m_1\le R-2m_0$, we cannot judge it. It is easy to see from Fig. 9a that vegetation patterns will not occur in sustained grazing model, there is no vegetation patterns in the sustained grazing ecosystem, which means that catastrophic changes have taken place in the ecosystem. By comparing the natural grazing and local grazing models, we can find that the vegetation pattern region of the local grazing case is larger than the natural grazing case (see Fig. 9b, c).

• 2. Model with cross-diffusion: By the analyses above, we take $r=0.06$, which guarantees that self-diffusion model is stable. If $m_1<R-m_0$ $(m_1\le R-2m_0)$, then the homogenous vegetation or vegetation pattern exists for sustained and local (natural) grazing model with cross-diffusion. Specifically, for the natural grazing model pattern formation in the magenta region, pattern does not occur in the green region, and unable to determine pattern or homogenous vegetation in the cyan region. Similarly, for the sustained grazing model patterns does not occur in the green region and cyan region, pattern formation in the magenta region. For the local grazing model patterns does not occur in the green region, pattern formation in the magenta region and cyan region. It is easy to see from Fig. 9e and f that the Turing region of the local grazing case is lager than the sustained grazing case.

Fig. 10

The effects of grazing rate $m_1$ on pattern formation for a different models with $p = 2$. a Model of different grazing types without cross-diffusion; b Drawing of partial enlargement of (a); c Model of different grazing types with cross-diffusion; d Drawing of partial enlargement of (c)

Example 2

Let $m_0=0.225,R=3,p=2$. If $m_1>M_2$, then the model (2.7) only has stable bare soil state. If $m_1<M_2$, then the model (2.7) has stable homogenous vegetation state or vegetation pattern state for all the grazing types of models. We obtain the effect of the grazing parameter $m_1$ on pattern formation and desertification process in Fig. 10. For the different grazing types models, the bare soil state, pattern state and homogenous vegetation state exist, and we have following results:

• 1. Model of absent cross-diffusion: By comparing different grazing type models, we can find that the vegetation pattern region of the local grazing case (yellow, cyan and magenta regions in Fig. 10a, b) is lager than the natural grazing case (yellow and cyan regions in Fig. 10a, b) and the sustained grazing case (magenta regions in Fig. 10a, b) is smaller than the natural grazing case. However, the homogenous vegetation region of the local grazing case (green region in Fig. 10a, b) is smaller than the natural grazing case (green and cyan regions in Fig. 10a, b) and the sustained grazing case (green, cyan and yellow regions in Fig. 10a, b) is lager than the natural grazing case.

• 2. Model with cross-diffusion: By the analyses above, we take $r=0.75$, which guarantees that self-diffusion model is stable. It is easy to see from Fig. 10c and d that the desertification process is opposite for the without cross-diffusion model (Fig. 10a, b).

For different p, the corresponding critical self-diffusion coefficients $\Upsilon ^{(i)}$ $(i=1,2)$ and cross-diffusion coefficients $\Lambda ^{(i)}$ are given in Table 2. From the Table 2, we can know when $p\in [1,1.5)$, $\Upsilon ^{(i)}$ value increases gradually, but when $p\in [1.5,+\infty )$, $\Upsilon ^{(i)}$ value decreases gradually. Through simple analysis, we know that all the critical cross-diffusion coefficients $\Lambda ^{(i)}$ increases with respect to $p\in [1,+\infty )$. According to Table 2, we further verify that $0<\Upsilon ^{(i)}_{sus}<\Upsilon ^{(i)}_{nat}<\Upsilon ^{(i)}_{loc}$ and $\Lambda ^{(i)}_{sus}>\Lambda ^{(i)}_{nat}>\Lambda ^{(i)}_{loc}$.

Table 2 The critical self-diffusion and cross-diffusion coefficients for different p. When $p = 1$, $\Upsilon ^{(i)}$ and $\Lambda ^{(i)}$ represent $\Upsilon ^{(1)}$ and $\Lambda ^{(1)}$ respectively; when $p > 1$, $\Upsilon ^{(i)}$ and $\Lambda ^{(i)}$ represent $\Upsilon ^{(2)}$ and $\Lambda ^{(2)}$ respectively

5 Numerical simulations

In this section, the results of theoretical analysis are verified by numerical simulation. We combine the finite difference method with the Gauss–Seidel iterative method to conduct numerical simulations. The finite difference method is used to approximate derivatives in system (2.7) by discretizing the domain into a grid of points. This results in a system of algebraic equations that can be solved numerically. The Gauss–Seidel iterative method is then applied to solve this system iteratively. All of our numerical simulations employ the homogeneous Neumann boundary conditions. The initial distributions of both plant and water are taken as follows:

$$\begin{aligned} w(0,x)=w_i+\varepsilon \zeta , \, b(0,x)=b_i+\varepsilon \zeta \; (i=1,2), \end{aligned}$$

where $\varepsilon =0.001$, $\zeta$ is tiny random perturbation term [44, 45]. The choice of initial condition reflects small inhomogeneous spatial perturbation from homogeneous steady-state. For models of different grazing types, the results of numerical simulation are very similar. Therefore, in this section, we only give numerical simulation related to the local grazing model.

5.1 One dimensional simulations

In this subsection, we will perform a series of numerical simulations of model (2.7) with local grazing in one-dimension space. By the Table 2, we can see that critical self-diffusion $\Upsilon ^{(1)}_{loc}=0.0049$ and critical cross-diffusion $\Lambda ^{(1)}_{loc}=0.2101$ for $r=0.06$ when $p=1$. First, we consider the effect of self-diffusion coefficient r on the stability of positive constant steady state $(w_1,b_1)$ for local model (2.7) without cross-diffusion (i.e., $\alpha = 0$). Taking $r =0.004$, we obtain simulation diagrams of positive solution b(x, t) of local model (2.7) with $\alpha = 0$ (see Fig. 11a), which shows that $(w_1,b_1)$ is unstable. Taking $r = 0.0052$, we obtain Fig. 11b and find that $(w_1,b_1)$ is locally asymptotically stable. In short, one can conclude that self-diffusion coefficient r plays an important role in determining the stability of positive constant steady state $(w_1, b_1)$ for local model (2.7) without cross-diffusion. Similarly, we consider the effect of cross-diffusion $\alpha$ on the stability of positive constant steady state $(w_1,b_1)$ for local model (2.7) with $r = 0.06$. Taking $\alpha =0.018$, we obtain simulation diagrams of positive solution b(x, t) of local model (2.7) (see Fig. 11c), which shows that $(w_1,b_1)$ is locally asymptotically stable. Taking $\alpha =0.024$, we obtain Fig. 11d and find that $(w_1,b_1)$ is unstable.

Fig. 11

Simulation diagrams of positive solution b(x, t) of local grazing model (2.7) with $p=1,R=3,m_0=0.255,m_1=1.5,L=10$ and $t=1000$. a $r=0.004, \alpha =0$; b $r=0.052, \alpha =0$; c $r=0.006, \alpha =0.018$; d $r=0.006, \alpha =0.024$

Since the influence of p on the stability of the model is difficult, we can only use the numerical methods to study the influence of p on the model (see Table 2). Then, we study the stability of equilibrium $(w_2,b_2)$ by only changing r for different p and fixing other parameters $R=3, m_0=0.225,m_1=1.5,\alpha =0$. On one hand, taking $p=1.2,1.5$, one can get simulation diagrams of positive solution b(x, t) of local model (2.7) with $r=0.006,0.0069$, respectively (see Fig. 12a–d). By comparing Fig. 12a–d, we find that parameter p can change the stability of $(w_2,b_2)$, which is indicate that the stability of local model (2.7) becomes better with the increase of p on the interval (1, 1.5]. On the other hand, On one hand, taking $p=2,21.5$, one can get simulation diagrams of positive solution b(x, t) of local model (2.7) with $r=0.0029,0.0045$, respectively (see Fig. 12e–h). By comparing Fig. 12e–h, we find that the smaller p is on the interval $(1.5,\infty ]$, the better the stability of local model (2.7). To sum up, these interesting advances indicate that parameter p is important to determine spatial pattern.

Fig. 12

Simulation diagrams of positive solution b(x, t) of local grazing model (2.7) with $R=3,m_0=0.255,m_1=1.5,L=10$ and $t=1000$. a $r=0.006, p=1.2$; b $r=0.0069, p=1.2$; c $r=0.006, p=1.5$; d $r=0.0069, p=1.5$; e $r=0.0029, p=2$; f $r=0.0045, p=2$; g $r=0.0029, p=2.5$; h $r=0.0045, p=2.5$

5.2 Two dimensional simulations

In this subsection, we take fixed values $R=3$ and $m_0=0.225$ for numerical simulations and consider r, $m_1$ and p as controlling parameters. The model (2.7) is solved numerically using the Euler method with a time step size of $\bigtriangleup t = 0.01$ and space step size $\bigtriangleup x=\bigtriangleup y = 0.0004$. As a result, we only show our results of pattern formation about vegetation distribution. It is worthy to mention that the patterns reported in this paper are independent of the choice of $\bigtriangleup x$ and $\bigtriangleup t$ as we have checked with smaller values of time and space stepping.

Now we are in a position to look at the vegetation patterns obtained from numerical simulations of (2.7) satisfying initial and boundary conditions. It is found that, when $r = 0.001$ and $p = 2$, that is to say the stationary state pattern presented such as spot-like (Fig. 13b, c) and stripe-like (Fig. 13d–f) patterns. Associated colorbar in the figure shows abrupt fluctuation in vegetation density at different time steps. In every pattern, the yellow (blue) represents the high (low) density of vegetation b. Simulation results presented in Fig. 13 of different time steps mentioned at the caption of figure, one can see that for the case $r = 0.001, p = 2$ and $m_1 = 1.5$, on increasing the time steps, the sequence “spots $\longrightarrow$ spots$\longrightarrow$stripes mixtures $\longrightarrow$ stripe” is observed, and we have checked the patterns for greater values of t and obtained patterns are same as we have presented here.

Fig. 13

Spatiotemporal pattern exhibited by vegetation density b(x, y, t) with advancement of time. Vegetation distribution at different time steps: a $t = 0$; b $t = 300$; c $t = 800$; d $t = 1500$; e $t = 3000$; f $t =5000$. Parameter values are $p = 2$, $m_0 = 0.225$, $m_1 = 1.5$ and $r = 0.002$

Numerical simulation methods are commonly used in studying grazing parameters to model and analyze the complex interactions between grazers, vegetation, and the environment. Figure 14 depicts the stationary distribution of vegetation over the spatial domain at $t = 1500$ for different grazing parameter $m_1$ and fixed $r = 0.001$ and $p = 2$. In Fig. 14, For the different values of $m_1$ located in the “vegetation pattern regions” (yellow, cyan and magenta regions in Fig. 10a, b), we show two categories of Turing patterns for the distribution of vegetation b of model (2.7). If the grazing rate $m_1 = 1$ and $p = 2$, then we obtained $\Upsilon _{loc}(m_1) = 0.0016$. When $r = 0.002$, the self-diffusion is not satisfied with the parameter conditions of the pattern formation (i.e., $r = 0.002 \in (0, \Upsilon _{loc})$). In Fig. 14a, when $m_1= 1$ and $r = 0.002$, we observed the emergence of a uniform vegetative state. If the grazing rate $m_1 = 1.8$ and $p = 2$, then we obtained $\Upsilon _{loc}(m_1) = 0.0125$, by the theoretical results, we know that the grazing rate $m_1 = 1.8$ satisfy $r = 0.002 \in (0, \Upsilon _{loc}(m_1))$, thus vegetation pattern appear in model (2.7) with local grazing (see Fig. 10b). The numerical simulation results in Fig. 10c and b also show that the numerical simulation results correspond to the theoretical results. From Figs. 13d and 14, one can see that for the cases $m_1 = 1.8, 2$, on increasing the controlled parameter $m_1$, the maximum vegetation density also increased (i.e., $5.1455\longrightarrow 6.523$).

Fig. 14

Stationary spatial pattern exhibited by the vegetation density b(x, y, t) at $t = 1500$ for fixed $R = 3, m_0 = 0.225, r = 0.002$ and three different values of $m_1$. a $m_1 =1$; b $m_1 = 1.8$

Fig. 15

Stationary spatial pattern exhibited by the vegetation density b(x, y, t) at $t = 1500$ for fixed $R = 3, m_0 = 0.225, m_1 = 1.5, r = 0.001$ and three different values of p. a $p = 3$; b $p = 4$

We continue our investigation into the effects of changing the parameter p. Figure 15 depicts the stationary distribution of vegetation over the spatial domain at $t = 1500$ for different p and fixed $r = 0.002$ and $m_1 = 1.5$. These patterns are obtained for the parameter values lying within Turing domain $r \in (0, \Upsilon _{loc}(p))$ [where $\Upsilon _{loc}(p)$ is depend on p and given by (3.19)] and the maximum vegetation density are changing with increasing magnitude of p. In Fig. 15, we found that the maximum density of vegetation decreased with the increase of infiltration rate p. The numerical simulation results in Fig. 15a and Table are consistent. By the Fig. 12e and f and Table 2, we found that the smaller p is on the interval $(1.5,+\infty )$, the better the stability of local model (2.7). To sum up, these interesting advances indicate that parameter p is important to determine spatial pattern.

6 Conclusions and discussions

These extended water–plant models provide a framework for understanding the dynamics and spatial organization of vegetation, and they can be used to guide conservation efforts, land management practices, and ecological research. It is important to note that these models are simplified representations of complex ecological processes, and they may not capture all the factors and mechanisms that influence vegetation patterns in every ecosystem. Additionally, different ecosystems may require different models or a combination of models to adequately describe their vegetation patterns.

In this paper, an extended water–plant model is proposed, which has power-exponential plant growth, cross-diffusion and three kinds of nonlocal grazing. This model is based on the well-known Klausmeier model. The nonlocal interaction is characterized by an integral term. Through the comparative study of the two nonlocal models and local model, the influence of nonlocal term on the stability of the model is further understood. We presented local stability analysis of interior equilibrium solution of the proposed local and nonlocal models. The results indicated that if the infiltration parameter is equal to 1 the unique positive equilibrium is always locally stable for sustained grazing type model without cross-diffusion. However, under certain parameter constraints, Turing instability can be observed in both natural grazing and local grazing models.

For the model with cross-diffusion, when $p=1$, the three models all have the parameter conditions for Turing instability. When $p>1$, we can obtain parameter constraints for Turing instability in the sustained grazing and local grazing models. Nevertheless, the stability cannot be judged in the natural grazing model when $p\in (1,2)$, but the parameter conditions for Turing instability can be obtained when $p \ge 2$. Understanding diffusion-induced instability in vegetation patterns is important for studying the dynamics and resilience of ecosystems. This research can assist in identifying the factors that contribute to the formation and transition of vegetation patterns. Additionally, studying diffusion-induced instability can provide insights into the mechanisms driving vegetation pattern formation and the potential impacts of disturbances or environmental changes on ecosystem dynamics.

Grazing can directly impact vegetation by removing plant biomass through herbivory. This can result in a decrease in vegetation cover and biomass, creating gaps in the vegetation. These gaps provide opportunities for different plant species to establish and grow, leading to shifts in species composition and diversity. We used numerical simulation methods considered the effect of grazing parameter $m_1$ on model (2.7). For the fixed other parameters, the absence of the cross-diffusion model (2.7) is stable when $r>\Upsilon ^{(i)}(m_1)$, and the cross-diffusion model (2.7) is stable when $r>\Upsilon ^{(i)}(m_1)$ and $\alpha <\Lambda ^{(i)}(m_1)$. Therefore, when the self-diffusion (cross-diffusion) coefficient caused by grazing rate is greater (less) than the critical self-diffusion (cross-diffusion) coefficient, Turing pattern will emerge. More interestingly, vegetation state transition from homogenous vegetation $\rightarrow$ vegetation patterns $\rightarrow$ bare soil as grazing rate increases. Vegetation Pattern formation can be recognized as desertification and early warning indicator of collapse for arid and semiarid grazing ecosystems which provides a new insight for ecological protection.

Some characterizations for the non-constant positive steady state solutions, including a priori estimate of the positive solutions, bifurcation solutions and the non-existence and existence of non-constant positive solutions of local grazing and natural grazing models are similar to the sustained grazing model studied in our previous paper [15, 16], we omit a detailed analysis of these properties in this article. It is worth mentioning that there are many uncertain factors in the natural environment, such as sand, toxicity, deforestation and natural disaster, which may cause desertification. In addition, meteorological factors, such as light, temperature and carbon dioxide, have great influence on vegetation pattern formation, which should be integrated into the vegetation model. This paper ignores these natural environment and meteorological factors in this paper, and we will further study these factors in future. The nonlocal grazing pressures of sustained and natural grazing derived in paper [14], only depend on global mean forage $I_j(B)=\frac{1}{Vol(\Omega )}\int _{X\in \Omega }B^j(X)dX$, which means that grazing at any location depends equally on alternative forage nearby and further away. An alternative modelling approach could be to assume that consumers have overlapping utilization distributions $K(x_0-x)$, which measure the use of locations for foraging as a function of distance to individual refuge sites $x_0$. The (weighted) local mean forage near $x_0$ would now be given by the convolution

$$\begin{aligned} K*B^j=\int _{X\in \Omega }K(X_0-X)B^j(X)dX. \end{aligned}$$

The dependence of the grazing pressure on $I_j(B)$ should now be replaced by a dependence on $K*B^j$: the grazing pressure also becomes variable in space. We further investigate an extended water–plant model with $K*B^j$.