1 Introduction

Vegetation, called “ecosystem engineer,” plays an important role in the ecological environment. [1]. First of all, the photosynthesis of vegetation provides the energy and power of ecosystem operation. Secondly, vegetation has the function of preventing wind and fixing sand. Last but not least, it promotes the global water cycle that soil water evaporates into the atmosphere through transpiration [2,3,4].

Vegetation pattern is used to describe the distribution of vegetation density in both time and space, and it can be used as an indicator to provide vegetation protection [5,6,7,8,9,10,11]. Regular vegetation patterns have been observed in many semi-arid areas of the world: stripes, spots and gaps, etc [12,13,14]. Many scientists have done a lot of research on the formation mechanism of vegetation pattern in semi-arid areas [15,16,17,18,19,20,21,22,23]. Klausmeier used vegetation and water as variables constructing mathematical models to describe vegetation patterns [24]. The work in Ref. [25] analyzed the vegetation–water cross diffusion model in detail and revealed the positive feedback mechanism of vegetation pattern formation. Sherratt and Synodiros use a simple reaction–diffusion–advection model to show that rain water will flow to the place with high vegetation coverage and permeate with high permeability because of the low permeability of rain water, which falls on the bare surface. This process explains the positive feedback effect of vegetation and water in local areas [26]. Hillerislambers et al. showed that the formation of vegetation pattern in semi-arid region is not only related to vegetation density and local precipitation infiltration, but also related to spatial distribution of runoff water [27].

Besides, a lot of researches have been done on the function of vegetation pattern [28,29,30,31,32,33]. The spatial exchange of water can not only enhance the resistance of vegetation to the outside world, but also enable vegetation to survive under the condition of low rainfall [34]. Kéfi et al. obtained that the change of patch number-size distribution can be used as an early warning signal for desertification by establishing cellular automata model and field investigation [35]. Vegetation ecosystems in semi-arid areas may be more adaptable to environmental changes, but their resilience depends largely on the adaptability of vegetation patterns [36].

The change of environment will affect the distribution of vegetation in space. Similarly, vegetation will also affect the change of environment [37,38,39,40,41]. Seddon et al. proposed vegetation sensitivity index to identify areas sensitive to climate change and identified which climatic factors can promote vegetation growth in each month through regression modeling [37]. Brasswell et al. showed that the response of biological communities to environmental changes had a certain time lag by analyzing the data of temperature and vegetation spatial index. Analysis shows that the relationship between climate and carbon storage may change due to changes in the distribution of ecosystems [38]. Forzieri et al. provided more evidence to prove that the formation of LAI-climate was due to the influence of vegetation on temperature [39].

In semi-arid areas, vegetation patterns will change with each other under different environments [42,43,44]. Taking rainfall as a parameter change, the transformation mode of vegetation pattern is as follows: uniform vegetation \(\rightarrow \) labyrinth pattern \(\rightarrow \) spot pattern [42]. Gowda et al. analyzed a specific model through bifurcation theory and calculated a standard sequence, which can be used as a series of parameter values in numerical simulation. Finally, they proposed a method to evaluate the robustness of the standard sequence in other models and formulas [43]. In semi-arid areas, the degree of drought will affect the change of vegetation pattern. With the increase in drought intensity, the vegetation pattern will change as follows: spot pattern\(\rightarrow \) stripe pattern \(\rightarrow \) bare land. Lejeune et al. established a model to explain this phenomenon [44]. In semi-arid regions, continuous drought is likely to lead to desertification [45, 46].

In recent years, nonlocal effects have attracted more and more attention in many fields [47,48,49]. It can depict various morphogenesis phenomena. Chen and Shi constructed a phytoplankton model with age structure and nonlocal effects. This paper classified the threshold dynamics of the model. The results showed that the dynamics of phytoplankton models were affected by mortality and maturation time. Phytoplankton may become extinct when the death rate exceeds the critical death rate. On the contrary, when the death rate was lower than the critical death rate, there would be another threshold at maturity [50]. A reaction–diffusion model with nonlocal effects and Dirichlet boundary conditions is studied by Lyapunov–Schmidt method to study the existence and stability of nonhomogeneous and periodic solutions in the model space. In addition, this model is applied in one-dimensional space to illustrate the correctness of the results [51]. Deforestation not only affected the temperature in some areas, but also in other areas. The nonlocal effect of the global average temperature dominates the local effect. The climate model is used to simulate and get the following conclusion: The influence of nonlocal effect on the global average temperature is greater than that of local effect and has no relation with the area and location of deforestation [52]. Boushaba and Ruan proposed a reaction–diffusion equation to describe the growth of plankton community. The model includes the delay of nutrient cycle and plankton growth, both of which are nonlocal. It is found that Turing pattern will appear when the diffusion coefficient changes, and spatiotemporal pattern will appear when the time delay changes [53].

Time delay is very important for research in many fields [54,55,56,57,58]. An important indicator for studying vegetation growth and productivity is vegetation index. Wu and Fu proposed a new neural network method with time delay to predict vegetation index. Using actual data detection, it was found that the new method has better prediction effect. The method has important application value in reducing overgrazing and grassland vegetation restoration [59]. In general, the study of vegetation pattern is carried out in a continuous spatial area. However, a vegetation–water model on the network is established by considering the propagation of seeds and connecting the whole scattered areas. It is used to describe the spatial dynamics of vegetation in semi-arid areas. The model established by stability analysis proves that the coexistence of vegetation and water is stable without delay. When the delay exceeds the threshold, the stability of Hopf bifurcation changes [60]. Han et al. studied the stochastic resonance phenomenon of a kind of vegetation ecosystem with delay. Firstly, it is assumed that the system vegetation dynamics is affected by internal and external noise. Then, the signal-to-noise ratio is calculated by adding weak periodic signals. Finally, the influence of time delay and correlation intensity of internal and external noise on the signal-to-noise ratio is discussed [61].

As we all know, vegetation has two ways of absorbing water. Firstly, when the vegetation leaves are wet by rain water or dew, the leaves absorb water but the quantity is very small. This is of no importance to the water supply of vegetation. Secondly, the root system of vegetation absorbs water. The root system is the main organ for vegetation to absorb soil water. It is the main source of water resources needed for vegetation growth. In fact, the roots can absorb water from the entire region, and this process will take a certain time. The traditional reaction–diffusion equation can not accurately represent its characteristics. Due to the pioneer work of Britton, spatial model with nonlocal delay was introduced to mathematical model, which can reflect the nonlocal interactions between different individuals [62]. To well reveal the mechanisms of these nonlocal effects on the vegetation pattern. In this paper, the reaction–diffusion equation with nonlocal delay is introduced to characterize this characteristic.

As far as we know, little work have been studied on the dynamics of vegetation pattern with nonlocal delay. As a result, we explained how to build the model and made a detailed analysis of this model. The structure of other parts of this paper is as follows. The second part is the derivation of the model. The third part is the stability analysis of the model. The fourth part is the pattern structure of numerical simulation. Finally, some conclusions and discussions are drawn.

2 Model derivation

The vegetation pattern in many semi-arid regions is amazing. Klausmeier firstly proposed a vegetation–water model to simulate the vegetation pattern in semi-arid regions [23]:

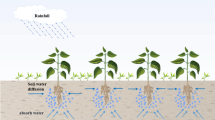
$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial N}{\partial t}=RJWN^2-MN+D_{1}\nabla ^2 N,\\ \frac{\partial W}{\partial t}=A-LW-RWN^2+V\frac{\partial W}{\partial X}.\\ \end{array}\right. } \end{aligned}$$
(1)

The model has two variables vegetation (N) and water (W), in which water is uniformly supplied at rate A and lost at LW rate due to evaporation. Vegetation absorbs water at \( RWN^2 \) rate and converts it into its own growth at conversion rate J. Vegetation density decreases at the rate MN. Water flows downhill at speed V. \(\nabla ^2=\frac{\partial ^2}{\partial X^2}+\frac{\partial ^2}{\partial Y^2}\) is the general Laplace operator. \(D_{1}\) is the diffusion rate of vegetation, which represents the rate of vegetation movement by clonal growth or seed dispersal.

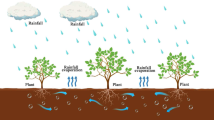
As a matter of fact, rainfall is the most important source of water in semi-arid areas. After rainfall, water permeates into the ground, and the roots of vegetation absorb water resources around them over a certain period of time. Consequently, we introduce nonlocal delays to characterize the process:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial N}{\partial T}=RJN^2\int _{\Omega }\int _{-\infty }^T Q(x,y,T-U)H(T-U)\\ \qquad \quad \times W(y,U)\mathrm{d}U\mathrm{d}y-MN+D_{1}\nabla ^2 N,\\ \frac{\partial W}{\partial T}=A-LW-RN^2\int _{\Omega }\int _{-\infty }^T Q(x,y,T-U)\\ \qquad \quad \times H(T-U)W(y,U)\mathrm{d}U\mathrm{d}y\\ \ \ \ \ \ \ \ \ \ +V\frac{\partial W}{\partial X}+D_{2}\nabla ^2 W,\\ \end{array}\right. } \end{aligned}$$
(2)

where \(\Omega =[a,b]\times [a,b]\), \(x=X\times Y\in \Omega \). \(D_{2}\) is the diffusion rate of the water in absence of the vegetation (Fig. 1).

Fig. 1
figure 1

Vegetation roots can absorb both water resources near themselves and water resources at a distance. Blue circles indicate underground water and arrows indicate the direction of water flow. (Color figure online)

Full size image

The nonlocal item \(\int _{\Omega }\int _{-\infty }^T Q(x,y,T-U)H(T-U)W(y,U)\mathrm{d}U\mathrm{d}y\) indicates that water resources at any position can be absorbed by roots to the current position, and this value represents the average amount of water resources absorbed by vegetation at the current moment. Q(x, y, T) is the solution of

$$\begin{aligned} \frac{\partial Q}{\partial T}=D\left( \frac{\partial ^2 Q}{\partial X^2}+\frac{\partial ^2 Q}{\partial Y^2}\right) \end{aligned}$$

subject to

$$\begin{aligned} \frac{\partial Q}{\partial n}=0 \hbox { and } Q(x,y,0)=\sigma (x-y), \end{aligned}$$

n is unit normal vector and \(\sigma \) is Dirac delta function. We choose Neumann boundary conditions [63,64,65,66,67]. The delay kernel \(H(T)=\frac{1}{\tau }e^{\frac{-T}{\tau }}\) [68]. The kernel function Q(x, T)H(T) represents the weight of water resources reaching the current position at any position before time T.

We rescale the model (2), then the simplified system can be given as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial n}{\partial t}=n^2\int _{\Omega }\int _{-\infty }^t Q(x,y,t-u)h(t-u)w(y,u)\mathrm{d}u\mathrm{d}y\\ \qquad \quad -mn+\nabla ^2 n,\\ \frac{\partial w}{\partial t}=a-w-n^2\int _{\Omega }\int _{-\infty }^t Q(x,y,t-u)h(t-u)\\ \quad \qquad \times w(y,u)\mathrm{d}u\mathrm{d}y+v\frac{\partial w}{\partial x}+\delta \nabla ^2 w.\\ \end{array}\right. } \end{aligned}$$
(3)

\(v\frac{\partial w}{\partial x}\) represents the surface runoff, meaning that water flows downhill (in the negative direction of x) at speed v. Hillside is not a necessary formation condition for vegetation pattern [23]. In this sense, we mainly consider the following systems:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial n}{\partial t}=n^2\int _{\Omega }\int _{-\infty }^t Q(x,y,t-u)h(t-u)w(y,u)dudy\\ \qquad \quad -mn+\nabla ^2 n,\\ \frac{\partial w}{\partial t}=a-w-n^2\int _{\Omega }\int _{-\infty }^t Q(x,y,t-u)h(t-u)\\ \qquad \quad \times w(y,u)\mathrm{d}u\mathrm{d}y+\delta \nabla ^2 w.\\ \end{array}\right. } \end{aligned}$$
(4)

As far as we know, very few work has been done to study the dynamics of vegetation patterns with nonlocal delays. Therefore, we have analyzed the vegetation–water model with nonlocal delay. First of all, we analyzed the stability of the model. Furthermore, we carried out numerical simulation to show the pattern structure with rich vegetation density. We also give some conclusions and discussions.

3 Stability analysis

Let \(v(x,t)=\int _{\Omega }\int _{-\infty }^t Q(x,y,t-u)h(t-u)w(y,u)dudy,\) and then system (4) will change as the following form:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial n}{\partial t}=\nabla ^2 n+g_1(n,w,v),\\ \frac{\partial w}{\partial t}=\delta \nabla ^2 w+g_2(n,w,v),\\ \frac{\partial v}{\partial t}=d\nabla ^2 v+g_3(n,w,v),\\ \end{array}\right. } \end{aligned}$$
(5)

where

$$\begin{aligned} \begin{aligned} g_1(n,w,v)&=wn^2-mn ,\\ g_2(n,w,v)&=a-w-wn^2 ,\\ g_3(n,w,v)&=\frac{1}{\tau }(w-v). \end{aligned} \end{aligned}$$

We are only interested in the internal positive equilibrium point. Solving system (3) to obtain three equilibrium points \(E_0=(n_0,w_0,v_0)=(0,a,a)\), \(E_1^*=(n_1^*,w_1^*,v_1^*) \) and \( E_2^*=(n_2^*,w_2^*,v_2^*)\), with

$$\begin{aligned} n_1^*= & {} \frac{a-\sqrt{a^2-4m^2}}{2 m},\\ w_1^*= & {} \frac{2m^2}{a-\sqrt{a^2-4m^2}},\\ v_1^*= & {} \frac{2m^2}{a-\sqrt{a^2-4m^2}},\\ n_2^*= & {} \frac{a+\sqrt{a^2-4m^2}}{2 m},\\ w_2^*= & {} \frac{2m^2}{a+\sqrt{a^2-4m^2}},\\ v_2^*= & {} \frac{2m^2}{a+\sqrt{a^2-4m^2}}. \end{aligned}$$

We can get the necessary condition for the existence of equilibrium point is:

$$\begin{aligned} a>2m. \end{aligned}$$

3.1 Stability analysis of equilibrium point \(E_1^*=(n_1^*,w_1^*,v_1^*)\)

Under the condition that the system (3) does not diffuse, the linearized system at the coexistence state \(E_1^*\) is expressed as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\mathrm{d} n}{\mathrm{d} t}=a_{11}^{(1)}n+a_{12}^{(1)}w+a_{13}^{(1)}v,\\ \frac{\mathrm{d} w}{\mathrm{d} t}=a_{21}^{(1)}n+a_{22}^{(1)}w+a_{23}^{(1)}v,\\ \frac{\mathrm{d} v}{\mathrm{d} t}=a_{31}^{(1)}n+a_{32}^{(1)}w+a_{33}^{(1)}v,\\ \end{array}\right. } \end{aligned}$$
(6)

where,

$$\begin{aligned}&a_{11}^{(1)}=m, a_{12}^{(1)}=0,\\&a_{13}^{(1)}=\frac{(a-\sqrt{a^2-4m^2})^2}{4 m^2}, \\&a_{21}^{(1)}=-m, a_{22}^{(1)}=-1,\\&a_{23}^{(1)}=-\frac{(a-\sqrt{a^2-4m^2})^2}{4 m^2}, \\&a_{31}^{(1)} =0, a_{32}^{(1)}=\frac{1}{\tau }v, a_{33}^{(1)}=-\frac{1}{\tau }. \end{aligned}$$

We analyzed the stability of the equilibrium point \(E_{1}^{*}\) in Table 1.

Table 1 Analysis of stability of equilibrium point \(E_{1}^{*}\) by Routh–Hurwitz criterion
Full size table

When \(a>2m\), the positive state \(E_1^*=(n_1^*, w_1^*, v_1^*)\) of system (6) is unstable, due to \(b_3^{(1)}(0)<0\).

3.2 Stability analysis of endemic state \(E_2^*=(n_2^*,w_2^*,v_2^*)\)

The system (3) linearized at \(E_2^*\) has the following form:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial n}{\partial t}=\nabla ^2 n+a_{11}^{(2)}n+a_{12}^{(2)}w+a_{13}^{(2)}v,\\ \frac{\partial w}{\partial t}=\delta \nabla ^2 w+a_{21}^{(2)}n+a_{22}^{(2)}w+a_{23}^{(2)}v,\\ \frac{\partial v}{\partial t}=d \nabla ^2 v+a_{31}^{(2)}n+a_{32}^{(2)}w+a_{33}^{(2)}v,\\ \end{array}\right. } \end{aligned}$$
(7)

where

$$\begin{aligned}&a_{11}^{(2)}=m, a_{12}^{(2)}=0,\\&a_{13}^{(2)}=\frac{(a+\sqrt{a^2-4m^2})^2}{4m^2},\\&a_{21}^{(2)}=-2m, a_{22}^{(2)}=-1,\\&a_{23}^{(2)}=-\frac{(a+\sqrt{a^2-4m^2})^2}{4m^2},\\&a_{31}^{(2)} =0, a_{32}^{(2)}=\frac{1}{\tau }, a_{33}^{(2)}=-\frac{1}{\tau }. \end{aligned}$$

We analyzed the stability of the equilibrium point \(E_{2}^{*}\) in Table 2.

Table 2 Analysis of stability of equilibrium point \(E_{2}^{*}\) by Routh–Hurwitz criterion
Full size table
Fig. 2
figure 2

Dispersion relation of system (4): for different \(\tau \), we get the relation graph between the real part of the characteristic root and \(\kappa \). The real part of the eigenvalue increases with the increase in \(\tau \). Red curve: \(\tau =0.5\); Blue curve: \(\tau = 1\); Green curve: \(\tau =1.5\). The figure illustrates that the system is stable when there is no space. When space is added, the instability of the system is related to wave number k. (We set other parameter value as: \(\sigma =10\), \(m=1.7\), \(a=4.4\), \(d=1\)). (Color figure online)

Full size image

In other words, the equilibrium point \(E_2^*\) is locally stable if \(a>2m\), and stability conditions hold.

Let

$$\begin{aligned} \begin{pmatrix} n\\ w\\ v\\ \end{pmatrix} =\begin{pmatrix} \zeta _1 \\ \zeta _2 \\ \zeta _3 \\ \end{pmatrix} \exp {(\lambda t+i\kappa r)}, \end{aligned}$$
(8)

where \(\lambda \) is the growth rate of perturbations in time t, and \(\kappa \) is wave number. Substituting (8) into (5), we can obtain characteristic equation \(\mathrm det(A)=0\), as follows:

$$\begin{aligned} det(A)= \begin{vmatrix} a_{11}^{(2)}-\kappa ^2-\lambda&a_{12}^{(2)}&a_{13}^{(2)} \\ a_{21}^{(2)}&a_{22}^{(2)}-\delta \kappa ^2-\lambda&a_{23}^{(2)} \\ a_{31}^{(2)}&a_{32}^{(2)}&a_{33}^{(2)}-d \kappa ^2-\lambda \end{vmatrix}. \end{aligned}$$

The following dispersion relation can be obtained by solving the characteristic equation:

$$\begin{aligned} \lambda ^3+b_1^{(2)}(\kappa )\lambda ^2+b_2^{(2)}(\kappa ) \lambda +b_3^{(2)}(\kappa )=0, \end{aligned}$$
(9)

with

$$\begin{aligned} b_1^{(2)}(\kappa )= & {} -\frac{(-\kappa ^2\tau -\delta \kappa ^2\tau -d \kappa ^2\tau +m\tau -\tau -1)}{\tau },\\ b_2^{(2)}(\kappa )= & {} \frac{1}{2\tau m^2}(2m^2\delta \kappa ^4\tau +2m^2 d \kappa ^4\tau \\&+\,2m^2\delta d \kappa ^4 \tau -2m^3\delta \kappa ^2\tau \\&-\,2m^3 d \kappa ^2\tau +2m^2 \kappa ^2\tau +2m^2 d \kappa ^2\tau \\&+\,2m^2 \kappa ^2+2m^2\delta \kappa ^2\\&-\,2m^3\tau -2m^3+a^2\\&+\,a\sqrt{(a-2m)(a+2m)}),\\ b_3^{(2)}(\kappa )= & {} \frac{1}{2m^2\tau }(2m^2\delta d \kappa ^6\tau -2m^3\delta d \kappa ^4\tau \\&+\,2m^2 d \kappa ^4\tau +2m^2\delta \kappa ^4+2m^3 d \kappa ^2\tau \\&-\,2m^3\delta \kappa ^2+a^2 \kappa ^2\\&+\,a\sqrt{(a-2m)(a+2m)}\kappa ^2\\&+\,a^2m+am\sqrt{(a-2m)(a+2m)}-4m^3). \end{aligned}$$

Of course, we demonstrated the dispersion relation in Fig. 2. Stability of the system (3) without diffusion is a necessary condition for the occurrence of Turing pattern, while the equilibrium is unstable with diffusion. Next, we will examine in detail the conditions under which Turing pattern occurs from the equilibrium point \(E_2^*\).

4 Analysis of Turing bifurcation

Next, we will find the conditions of Turing pattern occurring. There are three conditions.

Condition 1

\(b_1^{(2)}(\kappa )>0,\) and \(b_1^{(2)}(\kappa )=(1+\delta +d)\kappa ^2\tau +b_1^{(2)}(0).\) Since the diffusion condition is positive, the situation 1 is always established on the condition \(b_1^{(2)}(0)>0\) holds.

Condition 2

\(b_3^{(2)}(\kappa )>0.\)

Let \(b_3^{(2)}(\kappa )=F_2^{(2)}(\kappa ^2)\) and \(u=\kappa ^2.\) We can get the following expressions (Table 3):

Table 3 Expressions and coefficients of equation \(F_2^{(2)}(u)\)
Full size table

The properties of polynomial \(F_2^{(2)}(u)\) are analyzed as follows:

  1. 1.

    \(\lim _{u \rightarrow +\infty } F_2^{(2)}(u) =+\infty .\)

  2. 2.

    Calculate the first derivative of \(F_2^{(2)}(u)\):

    $$\begin{aligned} \frac{\mathrm{d}F_2^{(2)}(u)}{\mathrm{d}u}=3f_{23}^{(2)}u^2+2f_{22}^{(2)}u+f_{21}^{(2)}. \end{aligned}$$

    We can calculate the two extreme points of \(F_2^{(2)}(u)\). It follows that:

    \(u_{21}^{(2)}=\frac{-f_{22}^{(2)}+\sqrt{(f_{22}^{(2)})^2 -3f_{23}^{(2)}f_{21}^{(2)}}}{3f_{23}^{(2)}}\) and \(u_{22}^{(2)}=\frac{-f_{22}^{(2)}-\sqrt{(f_{22}^{(2)})^2 -3f_{23}^{(2)}f_{21}^{(2)}}}{3f_{23}^{(2)}}.\)

    Second derivation of \(F_2^{(2)}(u)\) has:

    $$\begin{aligned} \frac{\mathrm{d}^2F_2^{(2)}(u)}{\mathrm{d}u^2}=6f_{23}^{(2)}u+2f_{22}^{(2)}. \end{aligned}$$

    It is easy to obtain \(6f_{23}^{(2)}=6\delta d>0\), according to the concavity discrimination method, we have \(F_2^{(2)}(u)\) is a concave upward function when u is large enough.

  3. 3.

    According to the property of the cubic polynomial with positive first coefficient, we will get the following result:

    $$\begin{aligned} u_{2,\max }^{(2)}<u_{2,\min }^{(2)}=u_{21}^{(2)}. \end{aligned}$$

To meet the occurrence conditions of turing pattern, the following conditions need to be met: \(F_2^{(2)}(u_{2,\min }^{(2)})=F_2^{(2)}(u_{21}^{(2)})<0.\) Since \(u_{2,\min }^{(2)}=u_{21}^{(2)}=\frac{-f_{22}^{(2)} +\sqrt{(f_{22}^{(2)})^2-3f_{23}^{(2)}f_{21}^{(2)}}}{3f_{23}^{(2)}}\) is the wave number, therefore \(u_{2,\min }^{(2)}=u_{21}^{(2)}\) is positive. The number in the square root of \(u_{2,\min }^{(2)}\) is positive by \((f_{22}^{(2)})^2-3f_{23}^{(2)}f_{21}^{(2)}>0\).

We summarized the analysis methods and sufficient conditions for producing Turing pattern under condition 2 in Table 4.

Table 4 Methods and the sufficient conditions for Turing pattern
Full size table

Condition 3

\(b_1^{(2)}(\kappa )b_2^{(2)}(\kappa )-b_3^{(2)}(\kappa )>0\).

Let \(b_1^{(2)}(\kappa )b_2^{(2)}(\kappa )-b_3^{(2)}(\kappa )=F_3^{(2)}(\kappa ^2)\) and \(u=\kappa ^2\), then \(F_3^{(2)}(u)=f_{33}^{(2)}u^3+f_{32}^{(2)}u^2+f_{31}^{(2)}u+f_{30}^{(2)}\), where

$$\begin{aligned} f_{33}^{(2)}=(\delta +d+1)(\delta +d+\delta d)-f_{23}^{(2)}, \end{aligned}$$
$$\begin{aligned} \begin{aligned} f_{32}^{(2)}&=\frac{1}{\tau }(\tau +2\delta \tau +3d\tau \\&\quad +2\delta d\tau +d^2\tau +1+3\delta +2d+\delta ^2\\&\quad +2\delta d-2m\delta \tau -2md\tau -m\tau \delta ^2\\&\quad -3md\delta \tau -m\tau d^2)-f_{22}^{(2)},\\ f_{31}^{(2)}&=\frac{1}{2m^2\tau ^2}(2m^4d\tau ^2-4m^3\tau ^2 -4m^3\tau ^2\delta \\&\quad -6m^3d\tau ^2-4m^3\tau -6m^3\delta \tau -4m^3d\tau \\&\quad +2m^2\tau ^2+2m^2\tau ^2d+a^2\tau +a^2\tau \delta \\&\quad +a^2d\tau +a\tau \sqrt{a^2-4m^2})+a\delta \tau \sqrt{a^2-4m^2}\\&\quad +ad\tau \sqrt{a^2-4m^2}+4\tau m^2+2m^2\delta \tau \\&\quad +2m^2d\tau +2m^2 +2m^2\delta )-f_{21}^{(2)},\\ f_{30}^{(2)}&=\frac{1}{2m^2\tau ^2}(1+\tau -m\tau )\\&\quad (-2m^3\tau -2m^3 +a^2+a\sqrt{a^2-4m^2})-f_{20}^{(2)}. \end{aligned} \end{aligned}$$

The coefficient \(f_{33}^{(2)}=(d_1+1)(d_2+1)(d_1+d_2)>0\) always holds. The properties of polynomial \(F_3^{(2)}(u)\) are analyzed as follows:

  1. 1.

    \(\lim _{u \rightarrow +\infty } F_3^{(2)}(u) =+\infty .\)

  2. 2.

    Calculate the first derivative of \(F_3^{(2)}(u)\):

    $$\begin{aligned} \frac{dF_3^{(2)}(u)}{dz}=3f_{33}^{(2)}u^2+2f_{32}^{(2)}u+f_{31}^{(2)}. \end{aligned}$$

    We will get two extreme points of \(F_3^{(2)}(u)\) by calculating, as follows:

    \(u_{31}^{(2)}=\frac{-f_{32}^{(2)}+\sqrt{(f_{32}^{(2)})^2 -3f_{33}^{(2)}f_{31}^{(2)}}}{3f_{33}^{(2)}}\) and \(u_{32}^{(2)}=\frac{-f_{32}^{(2)}-\sqrt{(f_{32}^{(2)})^2 -3f_{33}^{(2)}f_{31}^{(2)}}}{3f_{33}^{(2)}}.\)

    Second derivative of \(F_3^{(2)}(u)\) has:

    $$\begin{aligned} \frac{\mathrm{d}^2F_3^{(2)}(u)}{\mathrm{d}z^2}=6f_{33}^{(2)}u+2f_{32}^{(2)}. \end{aligned}$$

    It is easy to obtain \(6f_{33}^{(2)}=6(\delta +1)(d+1)(d+\delta )>0\). According to the concavity discrimination method, we have \(F_3^{(2)}(u)\) is a concave upward function when u is large enough.

  3. 3.

    According to the property of the cubic polynomial with positive first coefficient, we will get the following result:

    $$\begin{aligned} u_{3,\max }^{(2)}<u_{3,\min }^{(2)}=u_{31}^{(2)}. \end{aligned}$$

\(F_3^{(2)}(u_{3,\min }^{(2)})=F_3^{(2)}(u_{31}^{(2)})<0\) ensures the emergence of Turing pattern. Since \(u_{3,\min }^{(2)}=u_{31}^{(2)}=\frac{-f_{32}^{(2)}+\sqrt{(f_{32}^{(2)})^2-3f_{33}^{(2)}f_{31}^{(2)}}}{3f_{33}^{(2)}}\) is the wave number, \(u_{3,\min }^{(2)}=u_{31}^{(2)}\) is positive. The number in the square root of \(u_{3,\min }^{(2)}\) is positive by \((f_{32}^{(2)})^2-3f_{33}^{(2)}f_{31}^{(2)}>0\).

We summarized the analysis methods and sufficient conditions for producing Turing pattern under condition 3 in Table 5.

In order to show the parameter space for the emergence of Turing pattern, we show the Hopf and Turing bifurcation (According to the critical condition of branching, the bifurcation curves are drawn with \(\tau \) as the independent variable and m as the dependent variable) in Fig. 3. In the spatial domain denoted by T, one can obtain the stationary patterns with rich pattern structures.

Table 5 Methods and the sufficient conditions for Turing pattern
Full size table

Hopf bifurcation occurs when the fixed point of the system switches from stable focus to unstable focus. If Hopf bifurcation occurs, it needs to satisfy the following conditions:

$$\begin{aligned} \mathrm{Im}(\lambda _{\kappa })\ne 0, \mathrm{Re}(\lambda _{\kappa })=0,\hbox { at }\kappa =0. \end{aligned}$$

According to the Routh–Hurwitz, we can obtain the critical condition for Hopf bifurcation to occur as follows:

$$\begin{aligned} b_1^{(2)}(0)b_2^{(2)}(0)-b_3^{(2)}(0)=0. \end{aligned}$$

The non-equilibrium phase transition corresponding to Turing bifurcation is the transformation of the system from the uniform stationary state to the non-uniform spatial periodic oscillation state. The condition for Turing bifurcation is that the system is stable without spatial diffusion and unstable with spatial diffusion. Therefore, we can obtain that the critical condition for Turing bifurcation to occur as follows:

$$\begin{aligned} \mathrm{Re}(\lambda _{\kappa })=0, \mathrm{Im}(\lambda _{\kappa })=0,\hbox { at }\kappa ^2=u_{2,\min }^{(2)}\ne 0. \end{aligned}$$

That is \(b_3^{(2)}(\kappa )=0\) with \(\kappa ^2=u_{2,\min }^{(2)}\).

Fig. 3
figure 3

Bifurcation diagram of system (5) with \(a = 4.4\) and \( \delta = 10\). Red curve: Turing bifurcation; Blue curve: Hopf bifurcation. The brown part of Turing region is marked by T. (Color figure online)

Full size image

5 Numerical results

In this section, based on the previous theoretical analysis of the system (4), we select appropriate parameters for numerical simulation in the conditions of branching. The program runs until the vegetation pattern reaches a stable state or its main characteristics do not seem to change any more. We use finite difference algorithm and select the Newman boundary condition. A network consisting of a finite number of discrete points is used instead of a continuous fixed solution region, and these discrete points are called nodes of the network. The derivative of each lattice point is replaced by a finite difference approximation formula. The size of space is \(100\times 100\). The space step is \(dx=h=1\), and the time step is \(dt = 0.001\). Assumed spatial region \(\Omega =(a,b)\times (a,b),b\gg a,h=(b-a)/(Z-1)\). We can get the spatial points as the follows form:

$$\begin{aligned}&{\overline{\Omega }}_{h}=(x_{p},y_{q}):x_{p}=(p-1)h+1,\\&y_{q}=(q-1)h+1, p,q=1,2, \ldots , Z. \end{aligned}$$

According to Taylor’s expansion, we can get the following form:

$$\begin{aligned}&\frac{\partial ^{2}n(x_{p},y_{q})}{\partial x^2} =\frac{n(x_{p+1},y_{q})-2n(x_{p},y_{q}) +n(x_{p-1},y_{q})}{h^2}\\&\qquad \quad \qquad \qquad +o(h^2),\\&\frac{\partial ^{2}w(x_{p},y_{q})}{\partial x^2} =\frac{w(x_{p+1},y_{q})-2w(x_{p},y_{q}) +w(x_{p-1},y_{q})}{h^2}\\&\qquad \qquad \quad \qquad +o(h^2). \end{aligned}$$

where, \(o(h^2)\) is a higher-order term.

We define \(n_{pq}\) and \(w_{pq}\) as the finite difference approximation of \(n(x_{p},y_{q})\) and \(w(x_{p},y_{q})\). For the vegetation–water model, the difference semidiscrete form of internal nodes in space, namely \((x_{p},y_{q})\in \Omega _{h}\), is as follows:

$$\begin{aligned}&\frac{\mathrm{d}n_{pq}}{\mathrm{d}t}=g_{1}(n_{pq},w_{pq})\\&\quad +\,d(n_{p-1,q}+n_{p,q-1}-4n_{pq} +n_{p,q+1}+n_{p+1,q}),\\&\frac{\mathrm{d}w_{pq}}{\mathrm{d}t}=g_{1}(n_{pq},w_{pq})\\&\quad +\,d(w_{p-1,q}+w_{p,q-1}-4w_{pq} +w_{p,q+1}+w_{p+1,q}). \end{aligned}$$

For corner nodes:

$$\begin{aligned}&\frac{\mathrm{d}n_{pq}}{\mathrm{d}t}=g_{1}(n_{pq},w_{pq})\\&\quad +\,d(n_{p,q+1}-2n_{pq}+n_{p+1,q}),\\&\frac{\mathrm{d}wn_{pq}}{\mathrm{d}t}=g_{1}(n_{pq},w_{pq})\\&\quad +\,d(w_{p,q+1}-2w_{pq}+w_{p+1,q}). \end{aligned}$$

For boundary nodes except corner nodes:

$$\begin{aligned}&\frac{\mathrm{d}n_{pq}}{\mathrm{d}t}=g_{1}(n_{pq},w_{pq})\\&\quad +\,d(n_{p,q-1}+n_{p+1,q} +n_{p,q+1}-3n_{pq}),\\&\frac{\mathrm{d}w_{pq}}{\mathrm{d}t}=g_{1}(n_{pq},w_{pq})\\&\quad +\,d(w_{p,q-1}+w_{p+1,q} +w_{p,q+1}-3w_{pq}). \end{aligned}$$
Fig. 4
figure 4

Snapshots of contour pictures of evolution of vegetation at different time. Parameters are taken as \(m=0.93\), \(a=3\), \(\tau =0.55\), \(d=1\) and \(\sigma =50\). a\(t=10\); b\(t=25\); c\(t=599\); d\(t=10000\)

Full size image
Fig. 5
figure 5

Stationary patterns of vegetation with different nonlocal delay parameter. a\(\tau =0.25\); b\(\tau =0.45\); c\(\tau =0.65\); d\(\tau =0.74\); e\(\tau =0.89\); f\(\tau =1.11\)

Full size image
Fig. 6
figure 6

Variation of vegetation average density with time. (I) \(\tau =1.11\); (II) \(\tau =0.89\); (III) \(\tau =0.74\); (IV) \(\tau =0.65\); (V) \(\tau =0.45\); (VI) \(\tau =0.25\). Parameters are taken as \(m=0.93\), \(a=3\), \(\tau =0.55\), \(d=1\) and \(\sigma =50\). This figure shows that the average density of vegetation tends to be stable with time

Full size image
Fig. 7
figure 7

Changes of vegetation average density with root water absorption intensity

Full size image

The Turing pattern we studied is that the equilibrium point of the system is stable when there is no diffusion, and it is unstable when there is diffusion. After the previous theoretical analysis, we determined the initial distribution of vegetation and water are as follows:

$$\begin{aligned} n(x,y,0)= & {} \frac{a+\sqrt{a^2-4m^2}}{2 m}+\eta _{1},\\ w(x,y,0)= & {} \frac{2m^2}{a+\sqrt{a^2-4m^2}}+\eta _{2}, \end{aligned}$$

where \(\eta _{i}(i=1,2)\) is a small random perturbation term. In the system (4), we are more concerned about the evolution of vegetation density with time in spatial location. For this purpose, the parameters are taken as \(m=0.93\), \(a=3\), \(\tau =0.55\), \(d=1\), \(\sigma =50\). The evolution process is shown in Fig. 4.

From Fig. 5, we can clearly observe that low-density gap patterns (Fig. 5a) appeared when the water absorption strength in the stagnant nucleus was relatively small. The perfect gap patterns (Fig. 5b) will appear when the water absorption intensity in the delayed effect is increased slightly. If the water absorption strength is further increased, high-density mixed patterns of stripes and spot (Fig. 5c) will appear due to the difference of water absorption capacity of vegetation. Then, there will be high density spot patterns (Fig. 5c, d). Finally, the greater the water absorption intensity, the isolated spot patterns will occupy the whole space (Fig. 5f). From the phase transformation of vegetation pattern, we can see that the vegetation isolation becomes larger, which makes the vegetation system more vulnerable to disturbance and increases the possibility of desertification. This shows that in a certain range, the greater the water absorption intensity and the higher the vegetation density, the less prone the region is to desertification. From Fig. 5, we can clearly observe that with the increase in water absorption intensity in the delay kernel, the vegetation pattern gradually transits from the initial low-density wide strip to the high-density narrow strip and then evolves into a high-density mixed pattern. When the water absorption intensity reaches a certain value, an isolated high-density spot pattern (hot spot pattern) will appear. This shows that in a certain range, the greater the water absorption intensity and the higher the vegetation density.

In fact, after rainfall in semi-arid areas, rainwater permeates the root system of vegetation, and the root system will preferentially absorb the water resources in the nearest position. The water resources in the nearest position are not enough. It will absorb water from the entire region. When the root water absorption intensity is small, the competition of water resources between vegetation is small, and vegetation distribution with low density and wide range will appear in space. Increasing the water absorption capacity of roots will increase the competition of water resources among vegetation, and there will be high-density dotted mixed vegetation distribution in space. When the water absorption capacity of root system increases to a certain extent, the competition of water resources between vegetation becomes greater, and there will be high-density isolated vegetation spot distribution in space. Reflected in the numerical simulation is the final hot spot pattern.

By changing different water absorption intensities in the delay kernel, the vegetation pattern has reached a stable state (shown in Fig. 6). The numerical simulation results show that with the passage of time, the density of vegetation tends to a certain value at any position. The density of vegetation may vary in different locations, and the chart is a Turing pattern.

In addition, we simulated the effect of water absorption intensity of vegetation roots on vegetation in nonlocal delay. As seen from Fig. 7, in a certain range, the higher the water absorption intensity, the higher the vegetation density. In other words, increasing the water absorption intensity of vegetation within a certain range can prevent desertification.

6 Conclusions

In this paper, the pattern dynamics of a vegetation–water model with nonlocal delay in semi-arid region is studied. The stability of the equilibrium point of the model without diffusion is mainly analyzed. The conditions for the generation of vegetation pattern are obtained by analyzing Turing instability in the case of diffusion. Nonlocal effect is introduced to characterize the water resources absorbed by vegetation roots in the whole region. Finally, the Turing pattern with different nonlocal delay effects is obtained by taking appropriate parameters that satisfy the conditions to carry out numerical simulation on the model.

The results in this work show that with the increase in the intensity of nonlocal delay effect, the vegetation pattern gradually changed from the initial low-density wide strip to the high-density narrow strip. Then, it evolved into a high-density dot-line mixed pattern. Finally, it evolves into an isolated high-density spot pattern, when the water absorption intensity reaches a certain value. The results well reflect the effect of nonlocal delay effect. What we are concerned about is that the vegetation pattern structure represents the actual distribution of vegetation density in semi-arid areas. The understanding of vegetation patterns can provide new theoretical guidance for the protection of vegetation and the prevention of land desertification. At the same time, the construction of this model also enriches the existing models of studying vegetation pattern.

In this work, the natural evolution of the water–vegetation model is mainly considered, and human factors are not considered. In fact, there are many factors that affect vegetation density, such as deforestation and overgrazing. When the density of vegetation decreases to a certain extent, desertification will reach a certain extent. In order to solve the problem of desertification, the most common method is probably afforestation. Of course, many scholars have also established different models to study this topic. However, the study of vegetation pattern dynamics is only at the theoretical level and there is no specific experiment to support it. Therefore, we hope to reveal its essentials characteristics through experimental research in the further study [69]. What is more, our results can be extended in other related research fields, such as spatial epidemiology [70,71,72] or predator-prey systems [73,74,75].