UDE-based adaptive dynamic surface control for attitude-constrained reusable launch vehicle

Abstract

This paper presents an adaptive dynamic surface control scheme for vertical takeoff and landing reusable launch vehicles (VTLVs) with unknown disturbances, model uncertainties, and an attitude constraint to achieve exact attitude tracking control in the aerodynamic descent phase. First, the six-degree-of-freedom dynamic model of the VTLV is established. Next, the unknown disturbances and model uncertainties in the VTLV model are considered as the total disturbances, which are estimated by employing an uncertainty and disturbance estimator to compensate the controller, thereby enhancing the control accuracy of the system. Moreover, a symmetric time-varying barrier Lyapunov function is utilized to cope with the attitude-constrained problem. Finally, the high tracking performance of the proposed adaptive dynamic surface controller is verified by numerical simulation results.

1 Introduction

Since the concept of reusable launch vehicle (RLV) was proposed in the 1950s, researches on RLVs have received extensive attention [1]. Unlike traditional expendable launch vehicles, RLVs can be partially or fully recycled after accomplishing the mission and put back into operation after maintenance and refuelling, which significantly increases the launch efficiency and lowers the launch costs [2]. According to the methods used for takeoff and landing, RLVs can be divided into several categories, with vertical takeoff and vertical landing reusable launch vehicles (VTLVs) emerging as a critical field of study in recent years [3]. Currently, VTLVs mostly use the method of two-stage-to-orbit, and the sub-stages of completed launch missions are recovered vertically, such as the “New Glenn” of Blue Origin and the “Falcon” series of SpaceX, both of which have accomplished the vertical recovery reuse of the sub-stages and reduced the cost of a single launch markedly [4]. However, it is essential to notice that many launch tests of VTLVs have failed mainly due to the lack of enough control accuracy and mechanical failures. Therefore, the key to ensure the safety and reliable flight of VTLVs lies in improving their attitude control performance under multiple constraints.

In the vertical recovery phase of VTLVs, particularly during the aerodynamic descent phase, the design of the attitude control system is critically hampered by a long non-powered time of the engine, highly dynamic flight environment, external and internal disturbances, as well as strong coupling. For solving such a complex nonlinear control problem, the attitude control system needs to be devised with nonlinear control methods because linear ones cannot be adequate for the demand of high control precision and robustness. The sliding mode control method is used to improve the stability and dynamic response of attitude control of RLV in [5,6,7]. However, owing to the internal jitter and singularity issues, it is a challenging task to design the parameters of the controller, which limits its applications. Accordingly, a robust adaptive inverse control strategy was developed to ensure the accurate attitude tracking of RLV with unknown boundaries of disturbances and uncertainties in [8, 9]. To avoid the “differential explosion” problem associated with the traditional inversion method, dynamic surface control (DSC) was proposed in [10] to design controllers with arbitrarily small tracking error for a class of nonlinear systems. Based on DSC, [11] designed the RLV attitude adaptive control strategy and achieved great control results. In the field of RLV, while DSC research on attitude control achieves positive results in a variety of aircrafts [12, 13, 33, 34], there is a lack of more in-depth research. Also, despite conventional nonlinear controllers typically apply robust approaches to reduce the effects of uncertainties, it is necessary to estimate and compensate uncertainties to realize a better control performance of the system. In recent years, many researchers have made efforts on disturbance observer (DO) to improve the performance and the adaptability of the controller, such as adaptive DO [5, 14], extended state observer (ESO) [6, 15], and uncertainty and disturbance estimator (UDE) [16]. UDE was proposed to evaluate external disturbances and uncertainties by [17]. UDE has the advantage of weakening the adverse influence of complex disturbances availably while simplifying the structure of the controller [18]. By applying UDE, [19] achieved effective disturbance rejection and reference tracking for the servo system. For the control system of aircraft, [20] extended the UDE-based disturbance observer to design the controller, whose excellent tracking performance and antijamming capability were demonstrated by simulations. In [21], a control algorithm based on UDE was applied to industrial processes with a time delay. UDE has widespread studies and applications, but basically no application to RLV.

In consideration of safety and realistic conditions, certain physical quantities of the RLV must be constrained. Ma et al. [22] employed prescribed performance control (PPC) for the control system as a feasible approach to the issue of state restriction. PPC constructs the control law by converting the existing restricted system into an equal unconstrained system to ensure that the tracking error maintains within the bound specified by the designer. At present, there exist three types of PPC schemes, which are barrier Lyapunov function (BLF)-based PPC, funnel-based control PPC and coordinated transformation-based PPC [23]. As a candidate for solving the state-constrained problem, the funnel control (FC) method has been developed to guarantee the transient performance specified throughout the process [24]. In [25], a neural funnel controller was presented for air-breathing hypersonic vehicles to maintain velocity and attitude tracking errors within desired funnels, realizing the expected transient and steady-state performance of both tracking errors. Aiming at solving the issue of attitude tracking for reusable launch vehicles with overload constraint, funnel-control was utilized in [26] to design a performance improvement-oriented control algorithm to keep tracking error within prescribed performance function throughout the reentry phase. Funnel-based PPC, however, requires that the controlled systems be S-type linear or nonlinear systems, and that the relative degree should be one or two with a known high frequency gain sign, which limits its applications. Compared to the other two methods, coordinated transformation-based PPC is more widely used in the attitude control of RLVs. In [27, 28], the attitude constraints of reusable launch vehicles were considered, and the logarithmic error transformation method was used to map the constrained attitude tracking errors into unconstrained tangent errors. Wang et al. [29] designed a novel predefined-time prescribed performance function and utilized the tangent error transformation method to maintain the tracking error within the desired range. On the basis of the PPC method, the predesigned constraint is equivalently substituted by the state-constraint dynamics to achieve the required output tracking performance, while the controller is constructed using the backstepping algorithm in [30]. Most of the existing PPC approaches do not take into account the constraint for the transformed error provided by the PPC strategy, thereby making it difficult to guarantee the boundedness of virtual control derivatives. As a result, when coordinated transformation-based PPC is employed in DSC, the virtual controller may produce a large output in order to stabilize the transformed error and cause an excessive steady-state error overshoot.

As a particular type of Lyapunov function that tends to infinity when its variables approach the intended limit, BLF is widely used in situations requiring state restriction [31]. At present, the state constraint problem can be effectively solved by using several novel forms of BLFs even when the constraint border goes to infinity, such as tangent BLFs and exponential BLFs. Flight control issues for controlled objects with attitude constraints, such as airplanes, spacecraft, and missiles, have been thoroughly investigated based on BLF and the inversion approach. Tee et al. [32] developed the inverse controller to guarantee the output bound according to the symmetric BLF, solving the control problem in the output-constrained case of strict feedback systems and lessening the restriction of the initial conditions successfully. Based on the tangent BLF, [33] used DSC to construct the velocity and attitude controllers for hypersonic vehicles, ensuring the total state constraints. In order to handle the output constraint problem for the variant aircraft, [34] suggested a composite adaptive control strategy based on the inverse approach and the exponential BLF, in combination with the minimal parameter learning technique and the first order sliding mode differentiator. The (BLF)-based PPC method has been successfully applied into hypersonic vehicles and can be further extended into the RLV. Inspired by the previous work, this paper plans to address the attitude-constrained problem of VTLV under the influence of unknown external disturbances and model uncertainties. The main contributions of this study are summarised as follows.

• 1. A UDE is employed to approximate the unknown disturbances and model uncertainties of a VTLV. Compared to the existing DO results applied in RLVs [5, 6, 36], UDE provides a more straightforward structure, fewer parameter settings and excellent estimation accuracy. Moreover, its stability is more accessible to verify.

• 2. The improved exponential BLF adopted in this paper enables the proposed attitude controller to deal with time-varying attitude constraints of each attitude angle. Compared with the PPC methods in [26,27,28], the BLF-based PPC method eliminates the need for complex error conversions, thus reducing the complexity of the control laws and getting higher reliability.

• 3. The proposed UDE-based adaptive DSC controller considers attitude constraints and complex disturbances simultaneously. In contrast to the existing studies on VTLVs [5, 28, 36], the proposed control system is chattering-free and needs fewer restrictions on control parameters to satisfy the stability and, thus, has higher practical application values.

The rest of this paper is organized as follows. Section 2 presents the control model of the VTLV with unknown disturbances and model uncertainties. In Sect. 3, based on UDE and an exponential BLF, an adaptive dynamic surface controller is designed to achieve high-precision attitude tracking for the VTLV, and the uniform boundedness of the attitude angle of the VTLV is demonstrated. The usefulness and superiority of the control method are verified by contrasting the simulation results of two cases in Sect. 4. The work of this paper is summarized in Sect. 5.

2 Problem formulation and preliminaries

2.1 Mathematical model of VTLV

In this section, the mathematical model of a VTLV is studied in detail. The mission profile of the whole flight stage for a VTLV is shown in Fig. 1 [35]. In general, the whole flight phase of a VTLV consists of seven sections: the ascent phase, the attitude adjustment phase, the boost back phase, the unpowered descent phase, the powered descent phase, the aerodynamic descent phase and the vertical landing phase. One of the most critical phases in the vertical recovery of the VTLV is the aerodynamic descent phase, characterized by substantial nonlinearity, strong coupling, and parameter uncertainties. As a result, it is the main emphasis of this study to design the appropriate attitude control law for the VTLV in the aerodynamic descent phase.

Fig. 1

Mission profile of the VTLV

During the aerodynamic descent phase, the engines of the VTLV are turned off, which means that the control torque cannot be obtained from them. Thus the aerodynamic force and aerodynamic moment are the major factors that change the speed and attitude of the VTLV. The dynamic equations of rotational motion of the VTLV are given by

$$\begin{aligned} \left\{ \begin{aligned} {\dot{\alpha }}=&-p\cos \alpha \tan \beta +q-r\sin \alpha \tan \beta +\frac{\sin \sigma }{\cos \beta }\times \\&[{\dot{\psi }}\cos \gamma -{\dot{\phi }}\sin \psi \sin \gamma +({\dot{\theta }}+{{\omega }_{e}})(\cos \phi \cos \psi \times \\&\sin \gamma -\sin \phi \cos \gamma )]-\frac{\cos \sigma }{\cos \beta }[{\dot{\gamma }}-{\dot{\phi }}\cos \psi - \\&({\dot{\theta }}+{{\omega }_{e}})\cos \phi \sin \psi ] \\ {\dot{\beta }}=&\sin \sigma [{\dot{\gamma }}-{\dot{\phi }}\cos \psi +({\dot{\theta }}+{{\omega }_{e}})\cos \phi \sin \psi ]+ \\&\cos \sigma [{\dot{\psi }}\cos \gamma -{\dot{\phi }}\sin \psi \sin \gamma -({\dot{\theta }}+{{\omega }_{e}})(\cos \phi \times \\&\cos \psi \sin \gamma -\sin \phi \cos \gamma )]+p\sin \alpha -r\cos \alpha \\ {\dot{\sigma }}=&-p\cos \alpha \cos \beta -q\sin \beta -r\sin \alpha \cos \beta + \\&{\dot{\alpha }}\sin \beta -{\dot{\psi }}\sin \gamma -{\dot{\phi }}\sin \psi \cos \gamma +({\dot{\theta }}+{{\omega }_{e}})\times \\&(\cos \phi \cos \psi \cos \gamma +\sin \phi \sin \gamma ) \\ \end{aligned} \right. \nonumber \\ \end{aligned}$$

(1)

and the kinematic equations of the VTLV are listed as follows:

$$\begin{aligned} \left\{ \begin{aligned} {\dot{p}}=&\frac{1}{{{J}'_{xx}}{{J}'_{zz}}-{J'_{xz}}^{2}}[{J'_{zz}}{{M}_{x}}+{J'_{xz}}{{M}_{z}}+({J'_{xx}}-{J'_{yy}}+ \\&{J'_{zz}}){J'_{xz}}pq+(({J'_{yy}}-{J'_{zz}}){J'_{zz}}-{J'_{xz}}^{2})qr] \\ {\dot{q}}=&\frac{1}{{J'_{yy}}}[{{M}_{y}}+{J'_{xz}}({{r}^{2}}-{{p}^{2}})+({J'_{zz}}-{J'_{xx}})pr] \\ {\dot{r}}=&\frac{1}{{J'_{xx}}{J'_{zz}}-{J'_{xz}}^{2}}[{J'_{xz}}{{M}_{x}}+{J'_{xx}}{{M}_{z}}+(({J'_{xx}}-{J'_{yy}})\times \\&{J'_{xx}}+{J'_{xz}}^{2})pq+{J'_{xz}}({J'_{yy}}-{J'_{xx}}-{J'_{zz}})qr] \\ \end{aligned} \right. \nonumber \\ \end{aligned}$$

(2)

where $\alpha ,\beta ,\sigma$ are the attack angle, sideslip angle, and bank angle, respectively. p, q, r denote the angular velocity of the roll, pitch, and yaw, respectively. $\gamma$ is the flight path angle and $\psi$ is the heading angle. $\theta ,\phi$ denote the latitude and longitude, respectively. ${{\omega }_{e}}$ is the earth angular velocity. ${J'_{ij}}={{J}_{ij}}+\Delta {{J}_{ij}}$ $(i=x,y,z,j=x,y,z)$ denotes the moment of inertia, wherein ${J}_{ij}$ and $\Delta {{J}_{ij}}$ represent the nominal moment and uncertain moment of inertia, respectively. ${{M}_{i}}$ $(i=x,y,z)$ indicates the rotational moments of the roll, pitch, and yaw, respectively. The aerodynamic moments are described as

$$\begin{aligned} \left\{ \begin{aligned} {{M}_{x}}&=[\frac{m_{x}^{p}{{L}_{r}}}{v}+m_{x}^{\beta }\beta +(\Delta {m}_{x}^{{{\delta }_{a}}}+m_{x}^{{{\delta }_{a}}}){{\delta }_{a}}]{{q}_{0}}{{S}_{r}}{{L}_{r}} \\ {{M}_{y}}&=[\frac{m_{y}^{q}{{L}_{r}}}{v}+m_{y}^{\alpha }\alpha +(\Delta {m}_{x}^{{{\delta }_{a}}}+m_{y}^{{{\delta }_{e}}}){{\delta }_{e}}]{{q}_{0}}{{S}_{r}}{{L}_{r}} \\ {{M}_{z}}&=[\frac{m_{z}^{r}{{L}_{r}}}{v}+m_{z}^{\beta }\beta +(\Delta {m}_{z}^{{{\delta }_{r}}}+m_{z}^{{{\delta }_{r}}}){{\delta }_{r}}]{{q}_{0}}{{S}_{r}}{{L}_{r}} \\ \end{aligned} \right. \end{aligned}$$

where v is the velocity. ${{S}_{r}}, {{L}_{r}}$ are the cross-sectional area and reference length of the VTLV, respectively. $m_{x}^{p}$, $m_{y}^{q}$, $m_{z}^{r}$ denote the damping moment coefficients of the roll, pitch, and yaw channels, respectively. $m_{x}^{\beta }$, $m_{y}^{\alpha }$, $m_{z}^{\beta }$ are the static stability moment coefficients. $m_{x}^{{{\delta }_{a}}},m_{y}^{{{\delta }_{e}}},m_{z}^{{{\delta }_{r}}}$ denote the nominal control moment coefficients, and $\Delta {m}_{x}^{{{\delta }_{a}}},\Delta {m}_{y}^{{{\delta }_{e}}},\Delta {m}_{z}^{{{\delta }_{r}}}$ are the uncertain control moment coefficients. ${{q}_{0}}$ is the dynamic pressure. ${{\delta }_{a}}, {{\delta }_{e}}, {{\delta }_{r}}$ denote the equivalent three-channel grid fins angles that are used to control roll channel, pitch channel, and yaw channel, respectively.

2.2 Control-oriented model of VTLV

Let $\varOmega ={{[\alpha ,\beta ,\sigma ]}^{T}}$ and $\omega ={{[p,q,r]}^{T}}$. Consider the merging of unknown disturbance terms in the model, (1) and (2) can be further simplified as

$$\begin{aligned} \left\{ \begin{aligned} {\dot{\varOmega }}&=R\omega +{{d}_{1}} \\ {\dot{\omega }}&=-{{J}^{\prime -1}}{{\omega }^{\times }}J'\omega +{{J}^{\prime -1}}(B+\Delta {B})\delta +{{d}_{2d}} \\ \end{aligned} \right. \end{aligned}$$

(3)

where ${{d}_{1}}$ represents the unknown mismatched disturbance caused by uncertain parameters and external disturbances, and ${{d}_{2d}}$ is caused by the external disturbance moment and the hard-to-measure aerodynamic moment. $\delta ={{[{{\delta }_{a}},{{\delta }_{e}},{{\delta }_{r}}]}^{T}}$ denotes the control input. $J'=J+\Delta {J}$ is the inertia matrix of the RLV, wherein J and $\Delta {J}$ denote the nominal and uncertain inertia matrix, respectively. ${{\omega }^{\times }}$ is the skew-symmetric matrix operator on vector. R is the coordinate transformation matrix. B and $\Delta$B are the nominal and uncertain control moment matrix, respectively. The following control-oriented model can be gained easily through derivation

$$\begin{aligned} \left\{ \begin{aligned} {\dot{\varOmega }}&=R\omega +{{d}_{1}} \\ {\dot{\omega }}&=-{{J}^{-1}}{{\omega }^{\times }}J\omega +{{J}^{-1}}B\delta +{{d}_{2}} \\ \end{aligned} \right. \end{aligned}$$

(4)

where $d_2=J^{-1}J'd_{2d}+d_{2m}$ is the unknown matched disturbance, wherein ${{d}_{2\,m}}=J^{-1}(-{\omega }^{\times }\Delta {J}{\omega }-\Delta {J}{\dot{\omega }}+\Delta {B}\delta )$ results from the uncertainties of the inertia matrix and the control moment coefficients. The representations of J, ${{\omega }^{\times }}$, R, and B are respectively written as

$$\begin{aligned}J= & {} \left[ \begin{matrix} {{J}_{xx}} &{} {0} &{} -{{J}_{xz}} \\ {0} &{} {{J}_{yy}} &{} {0} \\ -{{J}_{xz}} &{} {0} &{} {{J}_{zz}} \\ \end{matrix} \right] , {{\omega }^{\times }}=\left[ \begin{matrix} 0 &{} -r &{} q \\ r &{} 0 &{} -p \\ -q &{} p &{} 0 \\ \end{matrix} \right] \text {,}\\ R= & {} \left[ \begin{matrix} -\cos \alpha \tan \beta &{} 1 &{} -\sin \alpha \tan \beta \\ \sin \alpha &{} 0 &{} -\cos \alpha \\ -\cos \alpha \cos \beta &{} -\sin \beta &{} -\sin \alpha \cos \beta \\ \end{matrix} \right] ,\\ B= & {} \left[ \begin{matrix} m_{x}^{{{\delta }_{x}}}{{q}_{0}}{{S}_{r}}{{L}_{r}} &{} {0} &{} {0} \\ {0} &{} m_{y}^{{{\delta }_{y}}}{{q}_{0}}{{S}_{r}}{{L}_{r}} &{} {0} \\ {0} &{} {0} &{} m_{z}^{{{\delta }_{z}}}{{q}_{0}}{{S}_{r}}{{L}_{r}} \\ \end{matrix} \right] . \end{aligned}$$

For the VTLV attitude control model (4), a UDE-and-BLF-based adaptive dynamic surface controller is proposed in this paper to permit the VTLV attitude vector $\varOmega$ to track the control command ${{\varOmega }_{d}}={{[{{\alpha }_{d}},{{\beta }_{d}},{{\sigma }_{d}}]}^{T}}$ in the presence of unknown disturbances and model uncertainties, and it also satisfies the given constraint condition regarding the attitude error, that is, $\left| {{\varOmega }_{i}}-{{\varOmega }_{di}} \right| <{{k}_{bi}}$, $i=1,2,3$, ${{k}_{bi}}>0$.

Remark 1

The upper bounds of the VTLV attitude angle and desired attitude angle, respectively denoted as ${{k}_{c}}$ and ${{k}_{r}}$, are usually given in practical applications. Without loss of generality, consider ${{k}_{ci}}>{{k}_{ri}}>0$. Correspondingly, the upper bound of the attitude error can be gained by ${{k}_{bi}}={{k}_{ci}}-{{k}_{ri}}$, $i=1,2,3$.

3 Adaptive dynamic surface controller design based on UDE and BLF

3.1 Notations, lemmas and assumptions

In this section, for the construction of the adaptive dynamic surface attitude controller used for the VTLV control model described by (4), the following notations, lemmas and assumptions are necessary:

Notiation 1

For the vector $x={{[{{x}_{1}},\ldots ,{{x}_{n}}]}^{T}}$, there are some definitions as follows:

$$\begin{aligned}{} & {} ||x||=\sqrt{{{x}^{T}}x}\\{} & {} \tanh x={{[\tanh {{x}_{1}},\tanh {{x}_{2}},\ldots ,\tanh {{x}_{n}}]}^{T}} \end{aligned}$$

Notiation 2

[36] Assume that D is an open region containing the origin and tha the BLF function V(x) is a scalar function defined on D concerning the system states x, then there exist some properties of V(x) as below:

(i) V(x) is smooth and positive definite.

(ii) There exists one-order continuous partial derivative of V(x) at each point on D.

(iii) When x approaches the boundary of D, V(x) tends to be infinite.

(iv) For any $t>0$, when $x(0)\in D$, we have $V(x(t))\le b$, where $b\in {{R}^{+}}$.

By Notation 2, the form of general exponential BLF is selected as follows [37]:

$$\begin{aligned} F(z)=\frac{1}{2}\log \left( \frac{k_{b}^{2}}{k_{b}^{2}-{{z}^{2}}}\right) \end{aligned}$$

(5)

and the time derivative of F(z) is written as

$$\begin{aligned} F'(z)=\frac{z}{k_{b}^{2}-{{z}^{2}}}({\dot{z}}-\frac{{{{{\dot{k}}}}_{b}}}{{{k}_{b}}}z) \end{aligned}$$

(6)

where $\log (\centerdot )$ denotes the natural logarithm of $\centerdot$, and ${{k}_{b}}$ is a time-varying positive parameter satisfying $\left| z \right| <{{k}_{b}}$. It can be shown that F(z) is positive definite and continuous when $\left| z \right| <{{k}_{b}}$.

Lemma 1

[38] For any ${{k}_{b}}>0$ and $\left| z \right| <{{k}_{b}}$, the following inequality holds:

$$\begin{aligned} \log \left( \frac{k_{b}^{2}}{k_{b}^{2}-{{z}^{2}}}\right) \le \frac{{{z}^{2}}}{k_{b}^{2}-{{z}^{2}}} \end{aligned}$$

Lemma 2

[39] For any ${{\omega }_{0}}>0$ and $x\in R$, the following inequality holds:

$$\begin{aligned} 0\le \left| x \right| -x\tanh \frac{x}{{{\omega }_{0}}}\le {{\kappa }_{0}}{{\omega }_{0}} \end{aligned}$$

where ${{\kappa }_{0}}$ is a constant satisfying ${{\kappa }_{0}}={{e}^{-({{\kappa }_{0}}+1)}}$, i.e., ${\kappa }_{0}=0.2785$.

Lemma 3

[40] For a system with bounded initial condition, if there exists a continuous and positive definite Lyapunov function that satisfies ${\dot{V}}(x)\le -kV(x)+c$, where both of k and c are positive constants, the system is uniformly bounded, and the following inequality holds:

$$\begin{aligned} V(x)\le (V(0)-\frac{c}{k}){{e}^{-kt}}+\frac{c}{k} \end{aligned}$$

(7)

Assumption 1

[41] The derivative of the unknown disturbance ${{d}_{i}}$ is bounded, that is, there exists a positive constant ${{\bar{d}}_{i}}$ such that $||{{{\dot{d}}}_{i}}||\le {{\bar{d}}_{i}}<\infty$, $i=1,2$.

Assumption 2

The desired attitude ${{\varOmega }_{d}}$ and the upper bound of the attitude error ${{k}_{b}}$ are smooth, and for any $t\ge 0$, there exist positive constants ${{\bar{W}}_{1}}$ and ${{\bar{W}}_{2}}$ such that $||{{\varOmega }_{d}}|{{|}^{2}}+||{{\dot{\varOmega }}_{d}}|{{|}^{2}}+||{{\ddot{\varOmega }}_{d}}|{{|}^{2}}\le {{\bar{W}}_{1}}$ and $||{{k}_{b}}|{{|}^{2}}+||{{{\dot{k}}}_{b}}|{{|}^{2}}+||{{\ddot{k}}_{b}}|{{|}^{2}}\le {{\bar{W}}_{2}}$.

Assumption 3

For all $t>0$, the sideslip angle satisfies $\left| \beta \right|<{\bar{\beta }}<\pi /2$, where ${\bar{\beta }}$ is a positive constant, which ensures the continuous smooth function matrix R is nonsingular. Thus, there are positive constants $\bar{R}_1$ and $\bar{R}_2$ ($\bar{R}_1<\bar{R}_2$), such that $\bar{R}_1<\text {max}\{||{\dot{R}}||,||R||\}\le \bar{R}_2$.

Remark 2

The external disturbance moment as well as the aerodynamic moment in the flight environment are constantly changing and difficult to predict, but their total energy is limited. Simultaneously, note that ${{d}_{1}}$ and ${{d}_{2m}}$ vary with the motion state and grid fins angles of the RLV, which have a limited range and change rate. Therefore, ${{d}_{i}}$ and its derivative can be considered to be unknown but bounded, which explains the rationality of Assumption 2.

Remark 3

In practice, it is possible to obtain the states (Euler angle and attitude angular velocity) of RLV by means of the inertia navigation system. To prevent the heating rate, the sideslip angle should also be zero during the reentry phase [42]. Hence, Assumption 1 is reasonable.

3.2 Disturbance estimation based on UDE

In this section, UDE is utilized to estimate the composite disturbances in (4), due to its simplicity and great estimation performance. Then the disturbance estimation is compensated to the subsequent control law to improve the control accuracy. Moreover, we also analyze the uniform boundness of the estimation error of UDE.

According to (4), the unknown disturbances in the VTLV dynamics model can be expressed as

$$\begin{aligned} \left\{ \begin{aligned} {{d}_{1}}&={\dot{\varOmega }}-R\omega \\ {{d}_{2}}&={\dot{\omega }}+{{J}^{-1}}{{\omega }^{\times }}J\omega -{{J}^{-1}}B\delta \\ \end{aligned} \right. \end{aligned}$$

(8)

UDE estimates unknown interference via filters [18], and the design method is expressed as the following transfer function:

$$\begin{aligned} {{\hat{D}}_{i}}(s)={{G}_{f}}(s){{D}_{i}}(s),i=1,2 \end{aligned}$$

(9)

where ${{\hat{D}}_{i}}(s),{{D}_{i}}(s)$ respectively denote the Laplace transformation of ${{\hat{d}}_{i}},{{d}_{i}}$, and ${{\hat{d}}_{i}}$ is the estimation of ${{d}_{i}}$. ${{G}_{f}}(s)={{({{\tau }_{i}}s+I)}^{-1}}$ represents the matrix form of the one-order filter, in which ${{\mathbf {\tau }}_{i}}$ is the coefficient matrix of the filter to be designed.

Adopting the inverse Laplace transformation, (9) is transferred as

$$\begin{aligned} {{\dot{\hat{d}}}_{i}}={{\tau }_{i}}^{-1}({{d}_{i}}-{{\hat{d}}_{i}}) \end{aligned}$$

(10)

By calculating the integrals of the expressions on both sides of the equal sign simultaneously, the expression for disturbance estimation can be given by

$$\begin{aligned} {{\hat{d}}_{i}}=\int _{0}^{t}{{{\tau }_{i}}^{-1}({{d}_{i}}-{{{\hat{d}}}_{i}})dt}+{{\hat{d}}_{i}}(0) \end{aligned}$$

(11)

Define the disturbance estimation error ${{\tilde{d}}_{i}}$ as

$$\begin{aligned} \tilde{d}={{d}_{i}}-{{\hat{d}}_{i}}.\ \end{aligned}$$

(12)

Fig. 2

Block diagram of anti-interference adaptive dynamic surface control system based on BLF

Through (10) and (13), it is obtained that

$$\begin{aligned} {{\dot{\tilde{d}}}_{i}}={{{\dot{d}}}_{i}}-\tau _{i}^{-1}{{\tilde{d}}_{i}} \end{aligned}$$

(13)

To demonstrate the uniform boundedness of the estimation error of UDE, we give the Lyapunov function form of the UDE as follows:

$$\begin{aligned} {{V}_{{{U}_{d}}}}=\sum \limits _{i=1}^{2}{\frac{1}{2}\tilde{d}_{i}^{T}{{{\tilde{d}}}_{i}}} \end{aligned}$$

(14)

Then the derivative of ${{V}_{{{U}_{d}}}}$ with respect to time reads

$$\begin{aligned} {{{\dot{V}}}_{{{U}_{d}}}}=\sum \limits _{i=1}^{2}{\tilde{d}_{i}^{T}{{{\dot{\tilde{d}}}}_{i}}} \end{aligned}$$

(15)

Applying Assumption 1 and the Young inequality, we get

$$\begin{aligned} {{{{\dot{V}}}}_{{{U}_{d}}}}&=\sum \limits _{i=1}^{2}{\left( -\tilde{d}_{i}^{T}\tau _{i}^{-1}{{{\tilde{d}}}_{i}}+\tilde{d}_{i}^{T}{{{{\dot{d}}}}_{i}}\right) } \nonumber \\&\le \sum \limits _{i=1}^{2}{\left( -\tilde{d}_{i}^{T}\tau _{i}^{-1}{{{\tilde{d}}}_{i}}+{{\mu }_{i}}{{\left\| {{{\tilde{d}}}_{i}} \right\| }^{2}}+\frac{{{\left\| \dot{{d}_{i}} \right\| }^{2}}}{4{{\mu }_{i}}}\right) }\nonumber \\&\le -\sum \limits _{i=1}^{2}{\tilde{d}_{i}^{T}\left( \tau _{i}^{-1}-{{\mu }_{i}}I\right) {{{\tilde{d}}}_{i}}+\sum \limits _{i=1}^{2}{\frac{{{{{\bar{d}}}_{i}}^{2}}}{4{{\mu }_{i}}}}} \nonumber \\&= -{{a}_{0}}{{V}_{{{U}_{d}}}}+{{b}_{0}} \end{aligned}$$

(16)

where ${{\mu }_{i}}\in {{R}^{+}}$, ${{a}_{0}}=\underset{i=1,2}{\mathop {\min }}\,\{2{{\lambda }_{\min }}(\tau _{i}^{-1})-2{{\mu }_{i}}\}>0$, and ${{b}_{0}}=\sum \limits _{i=1}^{2}{{({{{\bar{d}}}_{i}}^{2}}/4{{\mu }_{i}})}$. Furthermore, the coefficient matrix of the filter satisfies ${{\lambda }_{\min }}(\tau _{i}^{-1})>{{\mu }_{i}}$.

According to Lemma 3, for $i=1,2$, we obtain

$$\begin{aligned}{} & {} {{V}_{{{U}_{d}}}}\le \left( {{V}_{{{U}_{d}}}}(0)-\frac{{{b}_{0}}}{{{a}_{0}}}\right) {{e}^{-{{a}_{0}}t}}+\frac{{{b}_{0}}}{{{a}_{0}}} \end{aligned}$$

(17)

$$\begin{aligned}{} & {} \underset{t\rightarrow \infty }{\mathop {\lim }}\,\left\| {{{\tilde{d}}}_{i}} \right\| \le \sqrt{\frac{2{{b}_{0}}}{{{a}_{0}}}} \end{aligned}$$

(18)

Therefore, it is possible to adjust the filter coefficients so that the estimation error of interference can converge to an arbitrarily small range around 0, that is, the UDE can estimate the unknown interference terms in (4) accurately.

3.3 Design of adaptive dynamic surface controller based on BLF

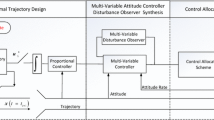
In this section, the dynamic surface control method is adopted to decompose the VTLV attitude control model (4) with model uncertainties and complex disturbances into the outer attitude loop and the inner angular rate loop, for which the control laws are designed separately to achieve accurate attitude control. Moreover, the exponential BLF and the adaptive control law are integrated to cope with the attitude-constrained problem. The detailed block diagram of the attitude control system is shown in Fig. 2.

According to (6), the exponential BLF form is selected as follows:

$$\begin{aligned} {{V}_{1}}=\frac{1}{2}\sum \limits _{i=1}^{3}{\log \left( \frac{k_{bi}^{2}}{k_{bi}^{2}-S_{1i}^{2}}\right) } \end{aligned}$$

(19)

It is clear that ${{V}_{1}}$ is positive definite and continuously differentiable in the set $\left| {{S}_{1i}} \right| <{{k}_{bi}}$.

Remark 4

During the early stage, ${{k}_{bi}}$ provides attitude constraints for the attitude control transient process, while during the later stage, it ensures attitude constraints for the steady state process, which means ${{\dot{k}}_{bi}}$ needs to converge to zero. Then we should ensure that ${{k}_{bi}}$ satisfies the differentiability conditions in Assumption 1 and the initial constrained condition$\left| {{\varOmega }_{1i}}(0)-{{\varOmega }_{di}}(0) \right| <{{k}_{bi}}(0)$. Besides, an appropriate ${{k}_{bi}}(\infty )$ should be designed to improve the effectiveness of attitude constraint and avoid the chattering problem of the control input.

Taking the derivative of ${{V}_{1}}$ yields

$$\begin{aligned} {{{{\dot{V}}}}_{1}}&=\sum \limits _{i=1}^{3} {\left( \frac{{{S}_{1i}}{{{{\dot{S}}}}_{1i}}}{k_{bi}^{2}-S_{1i}^{2}} -\frac{S_{1i}^{2}{{{{\dot{k}}}}_{bi}}}{{{k}_{bi}}(k_{bi}^{2}-S_{1i}^{2})}\right) } \nonumber \\&=\delta _{{{S}_{1}}}^{T}({{{{\dot{S}}}}_{1}}-{{K}_{b}}{{S}_{1}}) \end{aligned}$$

(20)

where $\delta _{{{S}_{1}}}^{T}={{[{{\delta }_{{{S}_{11}}}},{{\delta }_{{{S}_{12}}}},{{\delta }_{{{S}_{13}}}}]}^{T}}$, ${{\delta }_{{{S}_{1i}}}}={{S}_{1i}}/(k_{bi}^{2}-S_{1i}^{2})$, ${{k}_{bi}}$ denotes the time-varying upper bound of the attitude error, and ${{K}_{b}}$= diag (${{{\dot{k}}}_{b1}}/{{k}_{b1}}$, ${{{\dot{k}}}_{b2}}/{{k}_{b2}}$, ${{{\dot{k}}}_{b3}}/{{k}_{b3}}$), $i=1,2,3$.

In order to track the desired attitude accurately, it is necessary to design a virtual control law for the outer attitude loop.

Step 1. Define the attitude error of the VTLV as

$$\begin{aligned} {{S}_{1}}=\varOmega -{{\varOmega }_{d}} \end{aligned}$$

(21)

The time derivative of ${{{\dot{S}}}_{1}}$ is given by

$$\begin{aligned} {{{\dot{S}}}_{1}}={\dot{\varOmega }}-{{{\dot{\varOmega }}}_{d}}=R\omega +{{d}_{1}}-{{{\dot{\varOmega }}}_{d}} \end{aligned}$$

(22)

It is straightforward to show from (18) that both of ${{\tilde{d}}_{1}}$ and ${{\tilde{d}}_{2}}$ have the upper bounds, that is, $\left\| {{d}_{j}}-{{{\hat{d}}}_{j}} \right\| \le {{b}_{j}}$, $j=1,2$. Then the virtual controller ${\bar{\omega }}$ is designed as

$$\begin{aligned} {\bar{\omega }}=&{{R}^{-1}}[-({{K}_{1}}+{{{\bar{K}}}_{1}}){{S}_{1}}-{{{\hat{d}}}_{1}}+{{{\dot{\varOmega }}}_{d}}-\frac{1}{2}R{{R}^{T}}{{\delta }_{{{S}_{1}}}}- \nonumber \\&{{{\hat{b}}}_{1}}\tanh (\varepsilon _{1}^{-1}{{\delta }_{{{S}_{1}}}})] \end{aligned}$$

(23)

where ${{K}_{1}}\in {{R}^{3\times 3}}$ is the gain matrix, ${{\bar{K}}_{1}}=\text {diag}({{\bar{k}}_{1}},{{\bar{k}}_{2}},$ ${{\bar{k}}_{3}})$, ${{\bar{k}}_{i}}=\sqrt{{{({{{{\dot{k}}}}_{bi}}/{{k}_{bi}})}^{2}}+\beta _0 }$, and $\beta _0$ is a positive constant, which ensures that the time derivative of ${\bar{\omega }}$ is bounded even when ${{{\dot{k}}}_{bi}}$ are zero. ${{\varepsilon }_{1}}$ is the definite symmetric matrix to be designed. ${{\hat{b}}_{1}}$ represents the estimation of ${{b}_{1}}$, which satisfies the below adaptive control law:

$$\begin{aligned} {{\dot{\hat{b}}}_{1}}={{\gamma }_{1}}[\delta _{{{S}_{1}}}^{T}\tanh (\varepsilon _{1}^{-1}{{\delta }_{{{S}_{1}}}})-{{\sigma }_{1}}{{\hat{b}}_{1}}] \end{aligned}$$

(24)

where ${{\sigma }_{1}}$ and ${{\gamma }_{1}}$ are both positive constants.

Substituting (23) into (22), this yields

$$\begin{aligned} {{{{\dot{S}}}}_{1}}=&R(\omega -{\bar{\omega }})+R\bar{\omega }+{{d}_{1}}-{{{{\dot{\varOmega }}}}_{d}} \nonumber \\ =&R(\omega -\bar{\omega })-({{K}_{1}}+{{{\bar{K}}}_{1}}){{S}_{1}}-{{{\hat{d}}}_{1}}+ \nonumber \\&{{d}_{1}}-{{{\hat{b}}}_{1}}\tanh (\varepsilon _{1}^{-1}{{\delta }_{{{S}_{1}}}})-\frac{1}{2}R{{R}^{T}}{{\delta }_{{{S}_{1}}}} \end{aligned}$$

(25)

Substituting (25) into (11), the expression for ${{\hat{d}}_{1}}$ is written as follows:

$$\begin{aligned} {{\hat{d}}_{1}}{=}&\tau _{1}^{{-}1}\{{{S}_{1}}{-}{{S}_{1}}(0){-}\int _{0}^{t}{[R(\omega -{\bar{\omega }})}-({{K}_{1}}{+}{{\bar{K}}_{1}}){{S}_{1}}{-} \nonumber \\&{{\hat{b}}_{1}}\tanh (\varepsilon _{1}^{-1}{{\delta }_{{{S}_{1}}}})-\frac{1}{2}R{{R}^{T}}{{\delta }_{{{S}_{1}}}}]dt\}+{{\hat{d}}_{1}}(0) \end{aligned}$$

(26)

In addition, in order to avoid the “differential explosion” problem caused by direct derivation of ${\bar{\omega }}$, the tracking signal of the inner loop is given by passing the virtual control law through the one-order filter as

$$\begin{aligned} {{\tau }_{3}}{{{\dot{\omega }}}_{d}}+{{\omega }_{d}}=\bar{\omega }, {{\omega }_{d}}(0)={\bar{\omega }}(0) \end{aligned}$$

(27)

Let ${\tilde{\omega }}={\bar{\omega }}-{{\omega }_{d}}$, there is

$$\begin{aligned} {{{\dot{\omega }}}_{d}}=\tau _{3}^{-1}({\bar{\omega }}-{{\omega }_{d}})=\tau _{3}^{-1}{\tilde{\omega }} \end{aligned}$$

(28)

The time derivative of ${\tilde{\omega }}$ is written as

$$\begin{aligned} \dot{{\tilde{\omega }}}=-\tau _{3}^{-1}\tilde{\omega }+\dot{{\bar{\omega }}} \end{aligned}$$

(29)

where ${{\tau }_{3}}\in {{R}^{3\times 3}}$ is the definite symmetric matrix to be designed, and ${{\omega }_{d}}\in {{R}^{3}}$ denotes the desired signal of $\omega$.

To demonstrate the stability of the closed-loop control system, define ${{\tilde{b}}_{1}}={{b}_{1}}-{{\hat{b}}_{1}}$, and the following candidate Lyapunov function is considered:

$$\begin{aligned} {{V}_{2}}={{V}_{1}}+\frac{1}{2{{\gamma }_{1}}}\tilde{b}_{1}^{2} \end{aligned}$$

(30)

The time derivative of ${{V}_{2}}$ is given by

$$\begin{aligned} {{{\dot{V}}}_{2}}={{{\dot{V}}}_{1}}+\frac{1}{{{\gamma }_{1}}}{{\tilde{b}}_{1}}{{\dot{\tilde{b}}}_{1}} \end{aligned}$$

(31)

According to (24), we have

$$\begin{aligned} \frac{1}{{{\gamma }_{1}}}{{\tilde{b}}_{1}}{{\dot{\tilde{b}}}_{1}}={{\tilde{b}}_{1}}[-\delta _{{{S}_{1}}}^{T}\tanh (\varepsilon _{1}^{-1}{{\delta }_{{{S}_{1}}}})+{{\sigma }_{1}}{{\hat{b}}_{1}}] \end{aligned}$$

(32)

Note that

$$\begin{aligned} {{{\tilde{b}}}_{1}}{{{\hat{b}}}_{1}}=\frac{{{({{{\hat{b}}}_{1}} +{{{\tilde{b}}}_{1}})}^{2}}}{2} -\frac{\hat{b}_{1}^{2}}{2}-\frac{\tilde{b}_{1}^{2}}{2} \le \frac{b_{1}^{2}}{2}-\frac{\tilde{b}_{1}^{2}}{2} \end{aligned}$$

(33)

and $\omega -{\bar{\omega }}=\omega -{{\omega }_{d}}+{{\omega }_{d}}-{\bar{\omega }}={{S}_{2}}-{\tilde{\omega }}\$. Furthermore, it is obvious that

$$\begin{aligned} -{{{\dot{k}}}_{bi}}/{{k}_{bi}}-\sqrt{{{({{{{\dot{k}}}}_{bi}}/{{k}_{bi}})}^{2}}+\beta _0 }<0,i=1,2,3. \end{aligned}$$

Thus, we obtain

$$\begin{aligned} -\delta _{{{S}_{1}}}^{T}({{K}_{b}}+{{\bar{K}}_{1}}){{S}_{1}}<0 \end{aligned}$$

The final expression for ${{{\dot{V}}}_{2}}$ is written as

$$\begin{aligned} {{{{\dot{V}}}}_{2}}\le&-\delta _{{{S}_{1}}}^{T}{{K}_{1}}{{S}_{1}} -\frac{{{\sigma }_{1}}\tilde{b}_{1}^{2}}{2}+\frac{{{\sigma }_{1}}b_{1}^{2}}{2}+\delta _{{{S}_{1}}}^{T}{{{\tilde{d}}}_{1}}-{{b}_{1}}\delta _{{{S}_{1}}}^{T}\times \nonumber \\&\tanh (\varepsilon _{1}^{-1}{{\delta }_{{{S}_{1}}}})+\delta _{{{S}_{1}}}^{T}R{{S}_{2}}-\delta _{{{S}_{1}}}^{T}R\tilde{\omega }-\frac{1}{2}\delta _{{{S}_{1}}}^{T}R{{R}^{T}}{{\delta }_{{{S}_{1}}}} \end{aligned}$$

(34)

Step 2. Define the angular rate error of the VTLV as

$$\begin{aligned} {{S}_{2}}=\omega -{{\omega }_{d}} \end{aligned}$$

(35)

The derivative of ${S}_{2}$ is obtained as follows:

$$\begin{aligned} {{{\dot{S}}}_{2}}={\dot{\omega }}-{{\dot{\omega }}_{d}}=-{{J}^{-1}}{{\omega }^{\times }}J\omega +{{J}^{-1}}B\delta +{{d}_{2}}-\tau _{3}^{-1}{\tilde{\omega }} \end{aligned}$$

(36)

Based on UDE and adaptive control, the actual control law is designed as

$$\begin{aligned} {{\delta }_{c}}=&{{B}^{-1}}[J(-{{K}_{2}}{{S}_{2}}+\tau _{3}^{-1}{\tilde{\omega }}-{{{\hat{b}}}_{2}}\tanh (\varepsilon _{2}^{-1}{{S}_{2}})- \nonumber \\&{{R}^{T}}{{\delta }_{{{S}_{1}}}}-{{{\hat{d}}}_{2}})+{{\omega }^{\times }}J\omega ] \end{aligned}$$

(37)

where ${{K}_{2}}\in {{R}^{3\times 3}}$ is the gain matrix, ${{\varepsilon }_{2}}\in {{R}^{3\times 3}}$ denotes the definite symmetric matrix to be designed, and ${{\hat{b}}_{2}}$ is the estimation of ${{b}_{2}}$, which satisfies

$$\begin{aligned} {{\dot{\hat{b}}}_{2}}={{\gamma }_{2}}[S_{2}^{T}\tanh (\varepsilon _{2}^{-1}{{S}_{2}})-{{\sigma }_{2}}{{\hat{b}}_{2}}] \end{aligned}$$

(38)

where ${{\sigma }_{1}}$ and ${{\gamma }_{1}}$ are both positive constants.

Substituting (37) into (36), this yields

$$\begin{aligned} {{{{\dot{S}}}}_{2}}=&-{K}_{2}{S}_{2}-{{{\hat{b}}}_{2}}\tanh (\varepsilon _{2}^{-1}{{S}_{2}})-{{R}^{T}}{{\delta }_{{{S}_{1}}}}+d_2-{{\hat{d}}_{2}} \end{aligned}$$

(39)

Substituting (39) into (11), the expression for ${{\hat{d}}_{2}}$ is written as follows:

$$\begin{aligned} \hat{d}_{2}=&\tau _{2}^{-1}\{{{S}_{2}}-S_2(0)+\int _{0}^{t}{({K}_{2}{S}_{2} +{\hat{b}_{2}}\tanh (\varepsilon _{2}^{-1}{{S}_{2}})} \nonumber \\&{{R}^{T}}{{\delta }_{{{S}_{1}}}})dt\}+{{\hat{d}}_{2}}(0) \end{aligned}$$

(40)

Next, define the total Lyapunov function as

$$\begin{aligned} V={{V}_{2}}+\frac{1}{2}S_{2}^{T}{{S}_{2}}+\frac{1}{2{{\gamma }_{2}}}\tilde{b}_{2}^{2}+\frac{1}{2}{{\tilde{\omega }}^{T}}{\tilde{\omega }} \end{aligned}$$

(41)

Then we present the main conclusion of this paper and demonstrate the stability of the designed closed-loop control system as follows:

Theorem 1

Consider the VTLV control model (4) under Assumptions 1–3. Given initial condition satisfies $|{{S}_{1i}(0)}|<{{k}_{bi}},i=1,2,3$, and $V(0)<p$, where p is a positive constant. Based on the disturbance estimation from UDE, DSC laws (23), (37) and the adaptive control laws (24), (38) are employed to design the attitude controller for the VTLV, then the attitude angle $\varOmega$ is within the given constraint ${{k}_{c}}$, and the track error ${{S}_{1}}$ can converge to an arbitrarily small range.

Proof

Taking the derivative of V yields

$$\begin{aligned} {\dot{V}}={{{\dot{V}}}_{2}}+S_{2}^{T}{{{\dot{S}}}_{2}}+\frac{1}{{{\gamma }_{2}}}{{\tilde{b}}_{2}}{{\dot{\tilde{b}}}_{2}}+{{\tilde{\omega }}^{T}}\dot{{\tilde{\omega }}} \end{aligned}$$

(42)

Like (32) and (33), we derive

$$\begin{aligned} \frac{1}{{{\gamma }_{2}}}{{\tilde{b}}_{2}}{{\dot{\tilde{b}}}_{2}}\le -{{\tilde{b}}_{2}}S_{2}^{T}\tanh (\varepsilon _{2}^{-1}{{S}_{2}})-\frac{{{\sigma }_{2}}}{2}\tilde{b}_{2}^{2}+\frac{{{\sigma }_{2}}}{2}b_{2}^{2} \end{aligned}$$

(43)

Invoking (39) and (43), we have

$$\begin{aligned} S_{2}^{T}{{{{\dot{S}}}}_{2}}+\frac{1}{{{\gamma }_{2}}} {{{\tilde{b}}}_{2}}{{{\dot{\tilde{b}}}}_{2}}&\le S_{2}^{T} {{{\tilde{d}}}_{2}}-S_{2}^{T}{{K}_{2}}{{S}_{2}}-S_{2}^{T}{{R}^{T}} {{\delta }_{{{S}_{1}}}} \nonumber \\&-{{b}_{2}}S_{2}^{T}\tanh (\varepsilon _{2}^{-1}{{S}_{2}})-\frac{{{\sigma }_{2}}}{2}\tilde{b}_{2}^{2}+\frac{{{\sigma }_{2}}}{2}b_{2}^{2} \end{aligned}$$

(44)

According to Lemma 2 and the Young inequality, the following inequalities are given by

$$\begin{aligned} \left\{ \begin{aligned}&\delta _{{{S}_{1}}}^{T}{{{\tilde{d}}}_{1}}-{{b}_{1}}\delta _{{{S}_{1}}}^{T}\tanh (\varepsilon _{1}^{-1}{{\delta }_{{{S}_{1}}}})\le {{b}_{1}}\sum \limits _{i=1}^{3}{(|{{\delta }_{{{S}_{1}}i}}|}- \\&{{\delta }_{{{S}_{1}}i}}\tanh \frac{{{\delta }_{{{S}_{1}}i}}}{{{\varepsilon }_{1i}}})\le {{b}_{1}}\sum \limits _{i=1}^{3}{|{{\varepsilon }_{1i}}|}{{\kappa }_{0}}={{{{\bar{\varepsilon }}}}_{1}} \\&S_{2}^{T}{{{\tilde{d}}}_{2}}-{{b}_{2}}S_{2}^{T}\tanh (\varepsilon _{2}^{-1}{{S}_{2}})\le {{b}_{2}}\sum \limits _{i=1}^{3}{|{{\varepsilon }_{2i}}|}{{\kappa }_{0}}={{{{\bar{\varepsilon }}}}_{2}} \\ \end{aligned} \right. \end{aligned}$$

(45)

$$\begin{aligned} \left\{ \begin{aligned}&-\delta _{{{S}_{1}}}^{T}R{\tilde{\omega }}-\frac{1}{2}\delta _{{{S}_{1}}}^{T}R{{R}^{T}}{{\delta }_{{{S}_{1}}}}=-(R^{T}\delta _{{{S}_{1}}})^{T}{\tilde{\omega }}-\\&\frac{1}{2}(R^{T}\delta _{{{S}_{1}}})^{T}({{R} ^{T}}{{\delta }_{{{S}_{1}}}})\le \frac{1}{2}{{{{\tilde{\omega }}}}^{T}}\tilde{\omega } \\&{{{{\tilde{\omega }}}}^{T}}\dot{{\tilde{\omega }}}=-{{{\tilde{\omega }}}^{T}}(\tau _{3}^{-1}-{{\mu }_{3}}I)\tilde{\omega }+\frac{{{\left\| {\dot{{\bar{\omega }}}} \right\| }^{2}}}{4{{\mu }_{3}}} \\ \end{aligned} \right. \end{aligned}$$

(46)

where ${{\mu }_{3}}\in {{R}^{+}}$.

Finally, the expression for V is simplified as

$$\begin{aligned} {\dot{V}} =&{{{{\dot{V}}}}_{2}}+\delta _{{{S}_{2}}}^{T}{{{{\dot{S}}}}_{2}}+\frac{1}{{{\gamma }_{2}}}{{{\tilde{b}}}_{2}}{{{\dot{\tilde{b}}}}_{2}}+{{{\tilde{\omega }}}^{T}}\dot{{\tilde{\omega }}} \nonumber \\ {\le }&{-}\delta _{{{S}_{1}}}^{T}{{K}_{1}}{{S}_{1}}{-}\frac{{{\sigma }_{1}}\tilde{b}_{1}^{2}}{2}{-}S_{2}^{T}{{K}_{2}}{{S}_{2}}{-}\frac{{{\sigma }_{2}}}{2}\tilde{b}_{2}^{2}{-}{{{{\tilde{\omega }}}}^{T}}(\tau _{3}^{-1}- \nonumber \\&{{\mu }_{3}}I-\frac{1}{2}I){\tilde{\omega }}+\frac{{{\sigma }_{1}}b_{1}^{2}}{2}+\frac{{{\sigma }_{2}}b_{2}^{2}}{2}+{{{{\bar{\varepsilon }}}}_{1}}+{{{\bar{\varepsilon }}}_{2}}+\frac{{{\left\| {\dot{{\bar{\omega }}}} \right\| }^{2}}}{4{{\mu }_{3}}} \end{aligned}$$

(47)

By Assumption 2, the set

$$\begin{aligned} \begin{aligned} {{\varPi }_{1}}=&\left\{ (\varOmega _{d}^{T},\dot{\varOmega }_{d}^{T},\ddot{\varOmega }_{d}^{T},{{{\tilde{d}}}_{1}},{{k}_{b}},{{{{\dot{k}}}}_{b}},{{{\ddot{k}}}_{b}}):\sum \limits _{i=0}^{2}{({{\left\| \varOmega _{d}^{(i)} \right\| }^{2}})}+ \right. \\&\sum \limits _{i=0}^{2}{({{\left\| k_{b}^{(i)} \right\| }^{2}})}+\left. {{\left\| {{{\tilde{d}}}_{1}} \right\| }^{2}}\le {{{\bar{W}}}} \right\} \end{aligned} \end{aligned}$$

is compact in ${{R}^{21}}$, where ${\bar{W}}={\bar{W}}_{1}+{\bar{W}}_{2}+{b}_{1}^{2}$. Consider the set

$$\begin{aligned} {{\varPi }_{2}}=\left\{ (S_{1}^{T},S_{2}^{T},{{{\tilde{\omega }}}^{T}},{{{\tilde{b}}}_{1}},{{{\tilde{b}}}_{2}}):V\le p \right\} \end{aligned}$$

is compact in ${{R}^{11}}$. For all variables belonging to ${{\varPi }_{1}}\times {{\varPi }_{2}}$, $\dot{\bar{\omega }}=D({{S}_{1}},{{S}_{2}},\tilde{\omega },{{\tilde{b}}_{1}},{{\tilde{b}}_{2}},{{\tilde{d}}_{1}},{{\varOmega }_{d}},{{{\dot{\varOmega }}}_{d}},{{\ddot{\varOmega }}_{d}},{{k}_{b}},{{{\dot{k}}}_{b}},$ ${{\ddot{k}}_{b}})$ is a continuous vector function from Assumption 3. Therefore, $\left\| {{\dot{{\bar{\omega }}}}} \right\|$ have an upper bound ${{D}_{0}}$ on ${{\varPi }_{1}}\times {{\varPi }_{2}}$.

Let

$$\begin{aligned} {{k}_{1}}=\min \{&2{{\lambda }_{\min }}({{K}_{1}}),{{\sigma }_{1}}{{\gamma }_{1}},2{{\lambda }_{\min }}({{K}_{2}}),{{\sigma }_{2}}{{\gamma }_{2}},\nonumber \\&2{{\lambda }_{\min }}(\tau _{3}^{-1}-{{\mu }_{3}}I-\frac{1}{2}I)\}, \end{aligned}$$

(48)

$$\begin{aligned} {{c}_{1}}=\frac{{{\sigma }_{1}}b_{1}^{2}}{2}+\frac{{{\sigma }_{2}}b_{2}^{2}}{2}+{{{{\bar{\varepsilon }}}}_{1}}+{{{\bar{\varepsilon }}}_{2}}+\frac{D_{0}^{2}}{4{{\mu }_{3}}}. \end{aligned}$$

(49)

From Lemma 1, we obtain

$$\begin{aligned} \begin{aligned} -\delta _{{{S}_{1}}}^{T}{{K}_{1}}{{S}_{1}}&\le -\sum \limits _{i=1}^{3}{\frac{{{k}_{1}}}{2}\frac{S_{1i}^{2}}{k_{b1i}^{2}-S_{1i}^{2}}}\\&\le -\frac{{{k}_{1}}}{2}\sum \limits _{i=1}^{3}{\left( \log \frac{k_{b1i}^{2}}{k_{b1i}^{2}-S_{1i}^{2}}\right) } \end{aligned} \end{aligned}$$

Consequently, ${\dot{V}}\le -{{k}_{1}}V+{{c}_{1}}$. Then, according to the first lemma in [38], we have $\left| {{S}_{1i}} \right| <{{k}_{bi}}$.

Let ${{k}_{1}}>{{c}_{1}}/p$, which can be achieved by setting the controller parameters large enough, then ${\dot{V}}\le 0$ on $V=p$, which means that for any $t>0$, $V\le p$ provided that $V(0)\le p$. The controller parameters should ensure ${{\lambda }_{\min }}(\tau _{3}^{-1})-{{\mu }_{3}}>0.5$ simultaneously. From Lemma 3, the inequality is gained as follows:

$$\begin{aligned} V\le (V(0)-\frac{{{c}_{1}}}{{{k}_{1}}}){{e}^{-{{k}_{1}}t}} +\frac{{{c}_{1}}}{{{k}_{1}}} \end{aligned}$$

Therefore, for any $i=1,2,3$, we derive

$$\begin{aligned}&\frac{1}{2}\log \left( \frac{k_{b1i}^{2}}{k_{b1i}^{2}-S_{1i}^{2}}\right) \le V(0)+\frac{{{c}_{1}}}{{{k}_{1}}} \nonumber \\&\left| {{S}_{1i}} \right| \le {{k}_{bi}}\sqrt{(1-{{e}^{-2(V(0) +{{c}_{1}}/{{k}_{1}})}})}<{{k}_{bi}} \end{aligned}$$

(50)

$$\begin{aligned}&\underset{t\rightarrow \infty }{\mathop {\text {lim}}}\,\frac{1}{2}\log \left( \frac{k_{b1i}^{2}}{k_{b1i}^{2}-S_{1i}^{2}}\right) \le \frac{{{c}_{1}}}{{{k}_{1}}} \nonumber \\&\underset{t\rightarrow \infty }{\mathop {\text {lim}}}\,\left| {{S}_{1i}} \right| \le {{k}_{bi}}\sqrt{(1-{{e}^{-2{{c}_{1}}/{{k}_{1}})}})} \end{aligned}$$

(51)

By (50), $\left| {{\varOmega }_{i}} \right| -\left| {{\varOmega }_{di}} \right| \le \left| {{S}_{1i}} \right| <{{k}_{bi}}$, we have

$$\begin{aligned} \left| {{\varOmega }_{i}} \right|<{{k}_{bi}}+\left| {{\varOmega }_{di}} \right| <{{k}_{bi}}+{{k}_{ri}}={{k}_{ci}}, i=1,2,3. \end{aligned}$$

To sum up, the attitude angle of the VTLV is within the desired constraint and can converge to an arbitrarily small region around 0 by adjusting the controller parameters. This completes the proof of Theorem 1. $\square$

Remark 5

The following controller parameters should be selected when designing the developed controller. A larger ${{K}_{ji}}>0$ and a smaller ${{\tau }_{3i}}>0$ meeting ${{\lambda }_{\min }}(\tau _{3}^{-1})-{{\mu }_{3}}>0.5$ $(i=1,2,3,j=1,2)$ will be capable of decreasing the convergence time and steady-state error of the attitude tracking error. Then, select ${{\gamma }_{j}}>0$ to determine the estimation performance of ${{b}_{j}}$. In the event that the RLV system encounters undesired uncertainties, a larger ${{\gamma }_{j}}$ will improve the estimation procedure within a shorter period of time. According to (49), a smaller ${{\sigma }_{j}}>0$ and ${{\varepsilon }_{ji}}>0$ will contribute to smaller steady-state error. Note that ${{\hat{b}}_{j}}$ can be maintain within a small range around ${{b}_{j}}$ by setting a properly large ${{\sigma }_{j}}$.

4 Simulation and results

Fig. 3

Comparison of simulation results in two cases

In this section, simulation tests are designed using Matlab to verify the effectiveness of the proposed control scheme. The VTLV dynamics model parameters and aerodynamic coefficients in this study are the same as those in [35]. The uncertainties are set in consideration of 20% bias for aerodynamic coefficients and 20% bias for the moment of inertia of VTLV.

Table 1 The simulation results of three control methods

In the simulation, the initial states are set to be ${{\varOmega }_{0}}={{[174.5,-4,0.8]}^{T}}{{(}^{\circ }})$, $v=1180\text {m/s}$, $\phi =-{{47}^{\circ }}$, $\theta =-47.15{^\circ }$, $\gamma ~=~-{{41}^{\circ }}$ and $\psi ~={{0}^{\circ }}$. The desired attitude is selected to be ${{[180,0,0]}^{T}}{{(}^{\circ }})$, and the control command is generated through the first-order filter, where the time constant is set to be 1 s. Meanwhile, the simulation sampling step is set as 5ms, and the simulation time is 40 s. The parameters of the dynamic surface controller are set to be ${{K}_{1}}_{~}=\text {diag}\left( 40,40,40\right)$, ${{K}_{2}}=\text {diag}(20,20,20)$, and ${{\tau }_{3}}=\text {diag}\left( 0.05,0.05,0.05 \right)$. The parameters of adaptive control laws are set to be ${{\gamma }_{1}}={{\gamma }_{2}}=20$, ${{\varepsilon }_{1}}={{\varepsilon }_{2}}=\text {diag}\left( 0.01,0.01,0.01\right)$, ${{\sigma }_{1}}={{\sigma }_{2}}=0.1$, and $\beta _0 =0.1$. The parameters of the UDE-based disturbance observer are set to be ${{\tau }_{1}}={{\tau }_{2}}=\text {diag}\left( 0.05,0.05,0.05\right)$.

Furthermore, in order to verify the robustness of the simulation, and its expression is written as

$$\begin{aligned} {{M}_{d}}=\left\{ \begin{aligned}&[4+2\sin (0.2t)20+20\sin (0.2t) \\&10+5\cos (0.4t){{]}^{T}}(\text {N}\cdot \text {m}),\quad \\&20\,\text {s}<t<30\,\text {s}\\&0,{} & {} \text {others} \end{aligned} \right. \end{aligned}$$

Furthermore, to verify the superiority of the proposed controller, we select the robust adaptive dynamic surface control (ADSC) method in [11] to design ADSC scheme. In addition, based on the framework of UDE-based adaptive dynamic surface controller, the fix-time performance function and error transformation function from [33] are chose to design PFADSC scheme. The selected representation of ${{k}_{bi}}(t)(i=1,2,3)$ is the same as the following fixed-time prescribed performance function in [27].

$$\begin{aligned} {{\rho }_{i}}(t)=\left\{ \begin{aligned}&({{\rho }_{i0}}-{{\rho }_{i}}_{\infty }) \left[ \frac{\sin (2\pi t/{{T}})}{2\pi }-\frac{t}{{{T}_{f}}}\right] \\&\quad +{{\rho }_{i}}_{0},0\le t\le {{T}} \\&{{\rho }_{i\infty }},t>T \\ \end{aligned} \right. \end{aligned}$$

It can be easily known that the choice of meets requirements in Remark 7. Also, the parameters of ${{k}_{bi}}(t)$ and $\rho (t)$ are selected as ${{\rho }_{0i}}=1.5{}^\circ ,{{\rho }_{\infty i}}=1.5{}^\circ$, and ${{T}}=2\,\text {s}$. For the purpose of ensuring fairness in simulation comparisons, the controller parameters of ADSC scheme and PFADSC scheme are identical to the proposed scheme. The simulation results of three groups are shown in Fig. 3a–d and Table 1. Also, the comparison between the interference estimations gained by UDE and the actual value of the total interferences is shown in Fig. 3e, f.

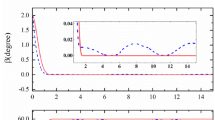
From Fig. 3a, the comparison between the desired attitude and the actual attitude of VTLV in three groups simulation results is displayed. Although there both exist interferences and model uncertainties in the VTLV model, all of designed control schemes provide sufficient convergence rate and attitude tracking accuracy for the VTLV, and the application of PPC improves tracking speed and tracking accuracy markedly. As is shown in Fig. 3b that the VTLV control input is maintained within a reasonable range in three schemes. Although both of PFADSC scheme and proposed scheme cause a degree of control input oscillation when VTLV encounters sudden disturbance, their control input curves can level off within a relatively short period of time. However, there is a greater degree of oscillation in the control input curve of PFADSC scheme.

As shown in Fig. 3c, d, in the event of existing sudden perturbation, the proposed scheme significantly reduces the overshoot of the attitude angle tracking error curve and attitude angular rate tracking error one, improving the robustness of the system and ensuring that the attitude tracking error is always within the error bounds. Table 1 clearly shows that the proposed control system has a higher transient performance and stronger robustness against the complex disturbance. In comparison with the other scheme, a clear improvement was evident in control performance when the proposed scheme was adopted. It is possible to accurately estimate the unknown disturbances in the model with the UDE in Fig. 3e, f.

In conclusion, the adaptive dynamic surface controller based on UDE and BLF exhibits an excellent attitude performance and sufficient robustness.

5 Conclusion

In this paper, an adaptive dynamic surface controller is proposed for the VTLV dynamics model in the aerodynamic descent phase using UDE and BLF. For precise tracking of VTLV attitude to attitude command, UDE and BLF are applied to handle unknown disturbances in the model and the attitude-constrained problem, respectively. Numerical simulation analysis indicates that the proposed controller achieves better performances and lower steady-state error in comparison to the case with only disturbance estimation and that the presented UDE-based disturbance observer also has great estimation performances. Then the effectiveness and superiority of the control scheme is demonstrated.