1 Introduction

Since RLV could allow for far lower per flight costs than expendable vehicle, intensive research has been investigated at NASA’s Marshall Space Flight Center in order to improve safety, reliability and affordability for RLV. To this end, the system must have capabilities of optimality, robustness and reconfiguration. As pointed in [1], reentry guidance algorithms that are not based on optimal control and high fidelity model compromise safety. Thus, the guidance technique based on optimal feedback and high fidelity model is absolute necessary for RLV. In addition, the RLV, especially in the reentry phase, suffers from severe model parameter uncertainties and unknown external disturbances which require that the system has enough robustness. The reconfiguration capability means that the system can recover from some unexpected events such as retargeted trajectory and control effector failures. From a guidance and control perspective, the optimality, robustness and reconfiguration for next generation of RLV cause enormous challenges for researchers. The reasons can be summarized as [2–4]: (1) path constraints: Heat rate, structural loads and dynamic pressure restrict the reentry flight corridor in very narrow scope; (2) high accuracy and rapid attitude tracking requirements: The attitude control with high accuracy and rapid convergence is essential but not easy to be realized due to the influence of uncertainties and external disturbances. Although the difficulties mentioned above, guidance and control technologies for RLV have been intensively studied during the last decades.

Reentry guidance is tasked to generate guidance commands which guide vehicle from its initial position to reach desired landing point with specified accuracy. In general, reentry guidance methods can be classified as trajectory following guidance and predictive guidance. In trajectory following guidance, a nominal trajectory needs to be pre-computed. Then, a linear time-varying system is obtained along the nominal trajectory. Based on the obtained linear time-varying system, many methods, such as LQR [5], indirect Legendre pseudospectral [6] and dynamic inversion [7] can be used to design reentry guidance law which controls RLV back to the nominal trajectory in the presence of uncertainties and external disturbances. The advantages of this method are that the path constraints can be dealt with carefully and it requires minimal onboard computational effort. In addition, there is no issue with respect to the convergence of solution due to the fact that the nominal trajectory can be generated prior to flight. Many reentry missions were performed using this guidance method such as Space Shuttle guidance [8] and Apollo guidance in the final phase of reentry flight [9]. Although the trajectory following guidance method is proved to be successful, it has to consider enormous pre-mission planning to account for unexpected conditions which may be difficult to be known in practice. As a result, a large deviation from nominal trajector may be observed in the presence of disturbance. Predictive guidance methods compute trajectory onboard repeatedly based on current state and expected final condition [10, 11]. The main advantage of predictive guidance is able to adapt to different conditions which may differ significantly from nominal conditions. However, an obstacle of this method in practice is the computational burden. Therefore, in order to ensure fast and reliable convergence, guidance parameters to be found must be kept at minimum. Zimmerman et al. [12] presented an effective reentry guidance method. In the method, the reentry trajectory is divided into two parts. In the first one, the vehicle flies on a constant heating-rate trajectory, and then, two parameters predictor-corrector guidance algorithm is used in the second part. The number of total guidance parameters to be solved in guidance cycle is four which reduced computational burden to some extent. A constrained predictor-corrector guidance method based on quasi-equilibrium-glide condition is proposed in [13] where the guidance is divided into longitudinal and lateral channel. In the longitudinal channel, the path constraints are converted into bank angle constraints. Then, the magnitude of bank angle is determined via solving a root-finding problem which ensures that RLV reaches the expected landing site at specified energy level. The lateral guidance determines the sign of bank angle which can be achieved via bank reversals logic. As a result, only one guidance parameters to be iteratively found online during a guidance cycle which further reduces the computational burden comparing with that provided in [12]. Recently, with the advance in onboard computational capability, the reentry guidance methods based on real-time trajectory optimization have received much attention. Combining model predictive control and approximate dynamic programming, an efficient model predictive static programming (MPSP) is proposed by Padhi et al. [14]. The method brings in the philosophy of real-time trajectory into the framework of guidance design which in turn yields an effective guidance scheme which has already many applications in aerospace engineering [15–17]. Another alternative optimization technique is pseudospectral method (PM), especially the Gauss PM (GPM) [18–20]. In comparison with MPSP, GPM provides a complete covector mapping theorem which ensures that the obtained trajectory is optimal [21]. As mentioned previously, the optimality is an important requirement for RLV. Taking into account this feature, this method is included in proposed scheme. Also, the implementation of this method under architecture of integrated guidance and control for six-degree-of-freedom (6DOF) RLV is to be discussed.

The reentry attitude control becomes the focus of integrated guidance and control system when the guidance law is obtained. The main aim of attitude control system is to achieve attitude tracking in the presence of model parameter uncertainties and unknown external disturbances. To implement the integrated system successfully, reentry attitude controller needs to have enough robustness with respect to uncertainties. During the last decades, many control methods have been applied in the design of attitude controller, such as gain scheduling [22, 23], backstepping control [24, 25], trajectory linearization control [26, 27] and dynamic inversion technique [28, 29]. Although many control methods have been proposed, the sliding mode control stays the main choice for nonlinear dynamic system with bounded uncertainties due to its inherent insensitivity to uncertainties and external disturbances [30–34].

Shtessel has done excellent work in the field of attitude control based on sliding mode technique [35–40]. In [35, 36], sliding mode control is used for RLV attitude control in ascent and reentry phase. In the method, a discontinuous bang–bang type control is used to drive system state to sliding manifold and then rapid switching control is applied to keep it on manifold. In order to reduce control chattering, the discontinuous sign function is replaced by saturation function which is a trade-off between the smoothness of control action and robustness. With the aim to improve control performance, a disturbance observer technique is investigated in satellite formation attitude control [37]. Subsequently, to improve high-gain switching control because of conservative estimation of disturbance bounds, Hall and Shtessel [38] combine gain adaptation with disturbance observer to provide the least gain needed for X-38 attitude control. The similar technique has also been applied in attitude controller design for launch vehicle [39] and quadrotor vehicle [40]. However, in all these developments, a single-input control structure is used which means multivariables attitude control problem has to be transformed into decoupled single-input problem and then is solved via single-input single-output sliding mode technique. As pointed in [41], multivariables control scheme provides a more elegant solution than trying to employ a decoupled single variable structure. In addition, only asymptotic convergence can be achieved via the methods mentioned above. It is well known that the finite time convergent property is able to provide better robustness and higher tracking accuracy. To this end, it is necessary to design reentry controller under multivariables control scheme with finite time convergence despite of uncertainties.

The main contributions of the paper are stated as follows: (I) A guidance and control architecture with online trajectory design, multivariables controller and control allocation is integrated for 6DOF RLV with the aim to improve RLV’s robustness, autonomy and safety. (II) A Lyapunov-based multivariables smooth second-order sliding mode controller and disturbance observer is proposed to achieve reentry attitude tracking in finite time. The paper is organized as follows: the problem studied in the research is formulated in Sect. 2. In Sect. 3, an integrated guidance and control scheme is provided. In Sect. 4, some representative simulation tests are carried out. The conclusions and future work are presented in Sect. 5.

2 Problem formulation

2.1 Translational equations of motion

During the entry phase, most applications assume steady, coordinated turns such that the sideslip angle is kept to zero. Thus, the equations of translational motion of the RLV in three-dimensional space over a spherical, rotating Earth are described by the following equations

$$\begin{aligned} \dot{h}&= V\sin \gamma \end{aligned}$$
(1)
$$\begin{aligned} \dot{\phi }&= \frac{V\cos \gamma \sin \chi }{\left( {R_E +h} \right) \cos \theta }\end{aligned}$$
(2)
$$\begin{aligned} \dot{\theta }&= \frac{V}{\left( {R_E +h} \right) }\cos \gamma \cos \chi \end{aligned}$$
(3)
$$\begin{aligned} \dot{V}&= -\frac{D}{m}-g\sin \gamma +\Omega ^{2}\left( {R_e +h} \right) \cos \theta \left( \sin \gamma \cos \theta \right. \nonumber \\&\quad \left. -\,\cos \gamma \sin \theta \cos \chi \right) \end{aligned}$$
(4)
$$\begin{aligned} \dot{\gamma }&= \frac{L\cos \sigma }{mv}-\left( {\frac{g}{V}-\frac{V}{\left( {R_E +h} \right) }} \right) \cos \gamma \nonumber \\&\quad +\,2\Omega \cos \theta \sin \chi +\frac{\Omega ^{2}\left( {R_E +h} \right) }{V}\cos \theta \nonumber \\&\quad \times \,\left( {\cos \gamma \cos \theta +\sin \gamma \sin \theta \cos \chi } \right) \end{aligned}$$
(5)
$$\begin{aligned} \dot{\chi }&= \frac{L\sin \sigma }{mv\cos \gamma }+\frac{V}{\left( {R_E +h} \right) }\cos \gamma \sin \chi \tan \theta \nonumber \\&\quad -\,2\Omega \left( {\tan \gamma \cos \theta \cos \chi -\sin \theta } \right) \nonumber \\&\quad +\,\frac{\Omega ^{2}\left( {R_E +h} \right) }{V\cos \gamma }\sin \theta \cos \theta \sin \chi \end{aligned}$$
(6)

where \(h\) represents the flight altitude; \(V\) is velocity; \(\phi \) is latitude; \(\theta \) is longitude; \(\gamma \) is flight path angle (FPA); \(\chi \) is heading angle; \(L\) is lift force; \(D\) is drag force; \(g\) is gravity (\(g=\mu /\left( {R_E +h} \right) ^{2}\) with \(\mu \) being the Earth gravity constant); \(\Omega \) is Earth angular speed; \(R_E \) is radius of Earth. The control input used for trajectory optimization and guidance law design are angle of attack (AOA) \(\alpha \) and the bank angle \(\sigma \) (BA).

2.2 Rotational equations of motion

The rotational motion is caused by the moments about the center of mass that acts on the vehicle and is used to design the altitude controller during the entry flight, is given as:

$$\begin{aligned} \dot{p}&= \frac{I_{zz} M_x }{I_{xx} I_{zz} -I_{xz}^2 }+\frac{I_{xz} M_z }{I_{xx} I_{zz} -I_{xz}^2 }\nonumber \\&\quad +\,\frac{\left( {I_{xx} -I_{yy} \!+\!I_{zz} } \right) I_{xz} }{I_{xx} I_{zz} -I_{xz}^2 }pq\!+\!\frac{\left( {I_{yy} \!-\!I_{zz} } \right) I_{zz} -I_{xz}^2 }{I_{xx} I_{zz} \!-\!I_{xz}^2 }qr\nonumber \\\end{aligned}$$
(7)
$$\begin{aligned} \dot{q}&= \frac{M_y }{I_{yy} }+\frac{I_{xz} }{I_{yy} }\left( {r^{2}-p^{2}} \right) +\frac{I_{zz} -I_{xx} }{I_{yy} }pr\end{aligned}$$
(8)
$$\begin{aligned} \dot{r}&= \frac{I_{xz} M_x }{I_{xx} I_{zz} -I_{xz}^2 }+\frac{I_{xx} M_z }{I_{xx} I_{zz} -I_{xz}^2 }\nonumber \\&\quad +\,\frac{\left( {I_{xx} \!-\!I_{yy} } \right) I_{xx} \!+\!I_{xz}^2 }{I_{xx} I_{zz} \!-\! I_{xz}^2 }pq\!+\!\frac{\left( {I_{yy} \!-\!I_{xx} \!-\!I_{zz} } \right) I_{xz} }{I_{xx} I_{zz} \!-\! I_{xz}^2 }qr\nonumber \\\end{aligned}$$
(9)
$$\begin{aligned} \dot{\alpha }&= -p\cos \left( \alpha \right) \tan \left( \beta \right) +q-r\sin \left( \alpha \right) \tan \left( \beta \right) \nonumber \\&\quad +\,\frac{\sin \left( \sigma \right) }{\cos \left( \beta \right) }\left[ {\dot{\chi }\cos \left( \gamma \right) -\dot{\phi }\sin \left( \chi \right) \sin \left( \gamma \right) } \right. \nonumber \\&\quad \times \,\left. \left( {\dot{\theta }\!+\!\Omega } \right) \left( {\cos \left( \phi \right) \cos \left( \chi \right) \sin \left( \gamma \right) \!-\!\sin \left( \phi \right) \cos \left( \gamma \right) } \right) \right] \nonumber \\&\quad \times \,\frac{\cos \left( \sigma \right) }{\cos \left( \beta \right) }\left[ {\dot{\gamma }-\dot{\phi }\cos \left( \chi \right) } \right. \left. -\left( {\dot{\theta }+\Omega } \right) \cos \left( \phi \right) \sin \left( \chi \right) \right] \nonumber \\\end{aligned}$$
(10)
$$\begin{aligned} \dot{\beta }&= p\sin \left( \alpha \right) -r\cos \left( \alpha \right) +\sin \left( \sigma \right) \left[ \dot{\gamma }-\dot{\phi }\cos \left( \chi \right) \right. \nonumber \\&\quad \left. +\,\left( {\dot{\theta }+\Omega } \right) \cos \left( \phi \right) \sin \left( \chi \right) \right] +\cos \left( \sigma \right) \left[ \dot{\chi }\cos \left( \gamma \right) \right. \nonumber \\&\quad \left. -\,\dot{\phi }\sin \left( \chi \right) \sin \left( \gamma \right) \!-\!\left( {\dot{\theta }\!+\!\Omega } \right) \left( \cos \left( \phi \right) \cos \left( \chi \right) \sin \left( \gamma \right) \right. \right. \nonumber \\&\quad \left. \left. -\,\sin \left( \phi \right) \cos \left( \gamma \right) \right) \right] \end{aligned}$$
(11)
$$\begin{aligned} \dot{\sigma }&= -p\cos \left( \alpha \right) \cos \left( \beta \right) -q\sin \left( \beta \right) -r\sin \left( \alpha \right) \cos \left( \beta \right) \nonumber \\&\quad +\,\dot{\alpha }\sin \left( \beta \right) -\dot{\chi }\sin \left( \gamma \right) -\dot{\phi }\sin \left( \chi \right) \cos \left( \gamma \right) \nonumber \\&\quad +\,\left( {\dot{\theta }+\Omega } \right) \left[ \cos \left( \phi \right) \cos \left( \chi \right) \cos \left( \gamma \right) \right. \nonumber \\&\left. \quad +\,\sin \left( \phi \right) \sin \left( \gamma \right) \right] \end{aligned}$$
(12)

where \(p,\,q,\,r\) denote roll, pitch and yaw angular rate, respectively; \(\beta \) denotes sideslip angle (SA); \(I_{ij} \left( {i=x,y,z;j=x,y,z} \right) \) denotes moments inertia; \(M_x,\,M_y ,\,M_z\) are roll, pitch and yaw moments.

The objective of the work is to develop an guidance and control scheme including real trajectory, multivariable attitude controller and control allocation for 6DOF RLV. Through the proposed scheme, a RLV can be guided from an initial position to terminal area energy management (TAEM) interface to be given later with minimizing final latitude and without deviating from path constraints provided in [6]. More importantly, it is able to adapt to some unexpected events, such as the retargeting of TAEM.

3 Integrated guidance and control scheme

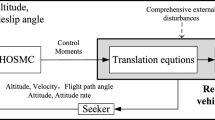
To achieve objective of the research, an integrated guidance and control architecture is proposed in Fig. 1 which is an extension of the result in [42]. It can be seen from Fig. 1 that the system consists of real-time optimal trajectory, multivariables attitude controller–disturbance observer and control allocator. The first part is used to generate reentry trajectory online and provides feasible guidance commands, including AOA and bank angle, for attitude control system. The multivariables controller and disturbance observer are designed in second part to achieve high accuracy and rapid tracking for guidance commands. The control allocator is used to convert control moments into control surface commands. Finally, the 6ODF RLV model provided in (1)–(12) is used as the simulation model. The implementations of each part are described in detail in the remainder of this section.

Fig. 1
figure 1

Integrated guidance and control architecture

Full size image

3.1 Real-time optimal trajectory design

The implementation of real-time optimal trajectory is composed of trajectory optimization algorithm and real-time feedback logic. As noted earlier, the PM has been widely used over last few years to solve a variety of trajectory optimization problems. Recently, the adaptive GPM is proposed in [43] and it is also used in our separated paper [44]. For brevity, the details for this method are omitted here. From the previous results, it has been known that the reentry trajectory can be obtained quickly if initial reentry condition, path constraints, terminal condition, cost function and initial guess are provided properly. Next, the emphasis of the section is paid on real-time feedback logic. The feedback logic is based on the recently proposed pseudospectral optimal feedback theory [45]. In this theory, the closed-loop feedback solution is formulated via real-time optimal open-loop control. Since the guidance commands need to be tracked by attitude loop, it must be smooth enough. However, it is known that open-loop optimal control generated via real-time trajectory optimization is discontinuous. In order to address the issue, the derivatives of AOA and bank angle, namely \({\mathbf {u}}=\left[ {\dot{\alpha },\dot{\sigma }} \right] ^{T}\in R^{2}\), are used as virtual control for trajectory optimization. Then, the augmented states become \({\mathbf {x}}=\left[ {h,\,\phi ,\,\theta ,\,V,\,\gamma ,\,\chi ,\,\alpha ,\,\sigma } \right] ^{T}\in R^{8}\). As a result, continuous guidance commands are generated via integrating virtual control \({\mathbf {u}}\) (see Fig. 1). Combining adaptive GPM and pseudospectral optimal feedback theory, the real-time optimal trajectory under the integrated guidance and control architecture is implemented as follows:

  • Step 1 (Before \(t_0\)) Calculate reentry trajectory based on given initial reentry condition, TAEM interface, cost function and path constraints using adaptive GPM. Then, the off-line trajectory and control, \({\mathbf {x}}_0^{*} \left( {t\!\ge \! t_0 } \right) {\mathbf {u}}_0^* \left( {t\ge t_0 } \right) \), are obtained and will be used as initial value guess for the first real-time trajectory design.

  • Step 2 (\([{t_0,t_1}])\) Track guidance commands \(\alpha _\mathrm{cmd\_0}\,\hbox {and}\,\sigma _\mathrm{cmd\_0} \) given in (13) through control input generated from attitude controller and control allocation to be developed soon. Then, the actual trajectory and attitude at \(t=t_1\) (\(t_1 =15\) which can be defined by the user) can be obtained from the output and it will be used as the initial value guess for next calculation.

  • Step 3 \(([{t_i,t_{i+1}}]({i=1,2,\ldots }))\) Two programs run simultaneously in this step. One is optimization program which is used to generate new reentry trajectory from current state \({\mathbf {x}}\left( {t=t_i } \right) \) to TAEM interface. The other is control program including attitude controller and control allocation which make the attitude track the guidance commands \(\alpha _\mathrm{cmd\_\left( {i-1} \right) }\,\hbox {and}\,\sigma _\mathrm{cmd\_\left( {i-1} \right) } \). During this phase, the program stops if landing accuracy given in (35) is satisfied; otherwise, set \(i=i+1\), repeat Step 3.

Similar to [46], the following proportional controller is included in proposed scheme to improve \(\alpha \) and \(\sigma \) tracking

$$\begin{aligned} \dot{\alpha }_\mathrm{cmd\_i} \!&= \!k_\alpha \left( {\alpha _\mathrm{des\_i} -\alpha } \right) \!,\nonumber \\ \dot{\sigma }_\mathrm{cmd\_i}\!&= \!k_\sigma \left( {\sigma _\mathrm{des\_i} \!-\!\sigma } \right) \!,\,t\!\in \! \left[ {t_i,t_{i+1} } \right] \left( {i\!=\!0,1,2,\ldots } \right) \nonumber \\ \end{aligned}$$
(13)

where \(\alpha _\mathrm{des\_i} \) and \(\sigma _\mathrm{des\_i} \) are obtained via integrating \({\mathbf {u}}_{i-1}^*\). The parameters \(\alpha \) and \(\sigma \) denote actual flight attitude obtained from the output of 6DOF RLV model.

Remark 1

In step 3, \(t_{i+1} =t_i +\Delta T_i \) where \(\Delta T_i \) is the time consumed to generate new reentry trajectory. It should be noted that the guidance commands are \(\alpha _\mathrm{des\_i-1}\,\hbox {and}\,\sigma _\mathrm{des\_i-1} \) during the time interval \(\left[ {t_i,t_{i+1} } \right] \). That is because the new guidance commands \(\alpha _\mathrm{des\_i}\,\hbox {and}\,\sigma _\mathrm{des\_i} \) are not available until time \(t_{i+1} \).

Remark 2

The TAEM interface in step 3 is alterable, and this feature is beneficial for RLV to reach any feasible landing site. As a result, it will enhance flexibility, safety and autonomy of RLV significantly.

3.2 Multivariables attitude controller–disturbance observer synthesis

3.2.1 Preliminaries

This subsection introduces some useful lemmas and theorem to be used in controller and disturbance observer design.

Lemma 1

[47] Consider a system in the form of \(\dot{\mathbf{x}}=f\left( \mathbf{x} \right) ,f\left( 0 \right) =0\) with \(\mathbf{x}\in R^{m}\). It is assumed that there exists a continuous positive definite function \(V\) such that \(\dot{V}\left( \mathbf{x} \right) +c\left[ {V\left( \mathbf{x} \right) } \right] ^{a}\le 0\) with \(c>0\,\hbox {and}\,a\in \left( {0,1} \right) \). Then, the origin is finite time stable. Moreover, the convergent time can be calculated by \(T\left( {\mathbf{x}_0 } \right) \,\le \frac{\left[ {V\left( {\mathbf{x}_0 } \right) } \right] ^{1-a}}{c\left( {1-a} \right) }\) for any initial value \(\mathbf{x}_0 \).

Lemma 2

[41] For the following multivariables system

$$\begin{aligned} \dot{\mathbf{x}}_1&= -k_1 \frac{\mathbf{x}_1 }{\left\| {\mathbf{x}_1 } \right\| ^{1/2}}-k_2 \mathbf{x}_1 +\mathbf{x}_2 +\varvec{\Delta }_\mathbf{1}, \nonumber \\ \dot{\mathbf{x}}_2&= -k_3 \frac{\mathbf{x}_1 }{\left\| {\mathbf{x}_1 } \right\| }-k_4 \mathbf{x}_1 +\varvec{\Delta }_2 \end{aligned}$$
(14)

where \(\mathbf{x}_1,\mathbf{x}_2 \in R^{m}\) and \(\varvec{\Delta }_1,\varvec{\Delta }_2 \in R^{m}\) are bounded uncertainties satisfying \(\left\| {\varvec{\Delta }_1 } \right\| \le \delta _1 \left\| {\mathbf{x}_1 } \right\| ,\,\left\| {\varvec{\Delta }_2 } \right\| \le \delta _2 \) with known constants \(\delta _1\,\hbox {and}\,\delta _2 \). Then, vectors \(\mathbf{x}_1\,\hbox {and}\,\mathbf{x}_2 \) converge to zero in finite time if the following conditions hold

$$\begin{aligned}&k_1 >\sqrt{2\delta _2 },\,k_2 >2\delta _1,\,k_3 >\max \left( {k_3^\Omega ,k_3^\Psi } \right) ,\nonumber \\&\quad k_4 >\max \left( {k_4^\Omega ,k_4^\Psi } \right) \end{aligned}$$
(15)

where \(k_3^\Omega =3\delta _2 +\frac{2\delta _2^2 }{k_1^2 },\,k_3^\Psi =\frac{9\left( {k_1 \delta _1 } \right) ^{2}}{16k_2 \left( {k_2 -2\delta _1 } \right) }+\frac{k_1^2 \delta _1 -4k_1^2 k_2 +2k_2 \delta _2 }{2\left( {k_2 -2\delta _1 } \right) },\,k_4^\Omega =\frac{\left( {1.5k_1^2 k_2 +3k_2 \delta _2 } \right) ^{2}}{k_1^2 k_3 -2\delta _2^2 -3k_1^2 \delta _2}+2k_2^2 +\frac{3}{2}k_2 \delta _1 \) and \(k_4^\Psi =\frac{\alpha _1 }{\alpha _2 \left( {k_2 -2\delta _1 } \right) }+\frac{k_2 \delta \left( {8k_2 +\delta _1 } \right) }{4\left( {k_2 -2\delta _1 } \right) }\) with \(\alpha _1=\frac{9\left( {k_1 \delta _1 } \right) ^{2}\left( {k_2 +0.5\delta _1 } \right) ^{2}}{16k_2^2 }\,\hbox {and}\,\alpha _2=k_2 \left( {k_3 +2k_1^2 -\delta _2 } \right) -\left( 2k_3 +0.5k_1^2 \right) \delta _1 -\frac{9\left( {k_1 \delta _1 } \right) ^{2}}{16k_2 }\).

In addition to Lemmas 1 and 2, the following theorem that is an extension (from single variable to multivariables) of the result in [48] is also needed in order to obtain multivariables controller–disturbance observer.

Theorem 1

Suppose that the uncertain terms \(\varvec{\Delta }_1\,\hbox {and}\,\varvec{\Delta }_2 \) in (16) are bounded with known constants \(\delta _1 \,\hbox {and}\,\delta _2 \) such that \(\left\| {\varvec{\Delta }_1} \right\| \le \delta _1 \) and \(\left\| {\varvec{\Delta }_2} \right\| \le \delta _2 \), then the solution of system (16) is globally bounded if constants \(0.5<p<1,\,k_1 >0\,\hbox {and}\,k_2 >0\). Furthermore, \(\mathbf{x}_1\,\hbox {and}\,\mathbf{x}_2\) converge to zero in finite time for any \(0.5<p<1,k_1 >0\,\hbox {and}\,k_2 >0\) if \(\varvec{\Delta }_1 =\varvec{\Delta }_2 =0\) in (16).

$$\begin{aligned} \mathbf{x}_1&= -k_1 \left\| {\mathbf{x}_1 } \right\| ^{p-1}\mathbf{x}_1 +\mathbf{x}_2 +\varvec{\Delta }_1,\nonumber \\ \mathbf{x}_2&= -k_2 p\left\| {\mathbf{x}_1 } \right\| ^{2\left( {p-1} \right) }\mathbf{x}_1 +\varvec{\Delta }_2 \end{aligned}$$
(16)

Proof

See “Appendix”. \(\square \)

3.3 Control-oriented model

Since RLV’s rotational motion is much faster than translational motion, the translational terms and angular velocity of the Earth are neglected in attitude controller design [50]. This simplified rotational equations are described by

$$\begin{aligned}&\dot{\varvec{\Theta }}=\mathbf{R}{\varvec{\upomega }}+\Delta \mathbf{F}\end{aligned}$$
(17)
$$\begin{aligned}&\mathbf{I}\dot{{\varvec{\upomega }}}=-\varvec{\Omega }\, \mathbf{I}\,{\varvec{\upomega }}+\mathbf{M}+\Delta \mathbf{D} \end{aligned}$$
(18)

where \({\varvec{\upomega }}=\left[ {p,\,q,\,r} \right] ^{T},\, \varvec{\Theta } =\left[ {a,\,\beta ,\,\sigma } \right] ^{T},\, \mathbf{M}=\left[ {M_l,\,M_m,\,M_n } \right] ^{T},\,\Delta \mathbf{F}=\left[ {\Delta f_1,\Delta f_2,\Delta f_3} \right] ^{T}\) and \(\varvec{\Delta } \mathbf{D}=\left[ {\Delta D_1,\Delta D_2,\Delta D_3} \right] ^{T}\). \(\Delta \mathbf{D}\) denotes model parameters uncertainties and unknown external disturbances. The matrices \(\mathbf{I},\,\varvec{\Omega },\,\mathbf{R}\in R^{3\times 3}\) are defined as follows:

$$\begin{aligned}&\mathbf{I}\!=\!\left[ {{\begin{array}{ccc} {I_{xx} }&{}\quad {-I_{xy} }&{}\quad {-I_{xz} } \\ {-I_{yx} }&{}\quad {I_{yy} }&{}\quad {-I_{yz} } \\ {-I_{zx} }&{}\quad {-I_{zy} }&{}\quad {I_{zz} } \\ \end{array} }} \right] \quad \! \varvec{\Omega }\!=\!\left[ {{\begin{array}{ccc} 0&{}\quad \! {-r}&{}\quad \! q \\ r&{}\quad \! 0&{}\quad \! {-p} \\ {-q}&{}\quad \! p&{}\quad \! 0 \\ \end{array}}} \!\right] \nonumber \\&\mathbf{R}\!=\!\left[ {{\begin{array}{ccc} {-\cos \alpha \tan \beta }&{}\quad 1&{}\quad {-\sin \alpha \tan \beta } \\ {\sin \alpha }&{}\quad 0&{}\quad {-\cos \alpha } \\ {-\cos \alpha \cos \beta }&{}\quad {-\sin \beta }&{}\quad {-\sin \alpha \cos \beta } \\ \end{array} }} \right] \end{aligned}$$
(19)

The controller design is based on double-loops architecture where the outer-loop generates the desired attitude angular rate and the inner-loop produces the control moments commands.

3.3.1 Attitude controller–disturbance observer design

The problem of interest can be stated to design an attitude controller such that guidance command \(\varvec{\Theta }^{*}=\left[ {\alpha _\mathrm{cmd}\,\beta _\mathrm{cmd}\,\sigma _\mathrm{cmd} } \right] ^{T}\) can be tracked by attitude angle \(\varvec{\Theta }\) in finite time in the presence of uncertainties \(\Delta \mathbf{F}\) and \(\Delta \mathbf{D}\). The system (17) and (18) can be considered as multivariables cascaded system and the proposed attitude control scheme is composed of two nested control loops. For inner-loop, \({\varvec{\upomega }}\) is chosen as the virtual control input to be designed to make \(\left( {\varvec{\Theta }-\varvec{\Theta }^{*}} \right) \rightarrow 0\) in finite time. For outer-loop, let \(\mathbf{M}\) be actual input with the aim at steering \(\left( {{\varvec{\upomega }}-{\varvec{\upomega }}^{*}} \right) \rightarrow 0\) in finite time. To this end, define tracking errors \(\varvec{\upsigma }_o =\varvec{\Theta }-\varvec{\Theta }^{*}\,\hbox {and}\,\varvec{\upsigma }_i ={\varvec{\upomega }}-{\varvec{\upomega }}^{*}\), then the error dynamics of (17) and (18) can be described as following multivariables cascade system

$$\begin{aligned} \dot{\varvec{\upsigma }}_o&= \mathbf{R}{\varvec{\upomega }} ^{*}+\mathbf{R}\,\varvec{\upsigma }_i -\dot{\varvec{\Theta }}^{*}+\Delta \mathbf{F}_1\end{aligned}$$
(20)
$$\begin{aligned} \dot{\varvec{\upsigma }}_i&= -\mathbf{I}^{-1}\varvec{\Omega }\, \mathbf{I}\,{\varvec{\upomega }}- \dot{{\varvec{\upomega }}}^{*}+\mathbf{I}^{-1}\mathbf{M}+\Delta \mathbf{F}_2 \end{aligned}$$
(21)

where \(\Delta \mathbf{F}_1 =\Delta \mathbf{F},\, \Delta \mathbf{F}_2 =\mathbf{I}^{-1}\Delta \mathbf{D}\) and \({\varvec{\upomega }}^{*}\) denotes desired attitude angular rates to be developed.

Assumption 1

For system (20) and (21), suppose that \(\Delta \mathbf{F}_1 \) and \(\Delta \mathbf{F}_2 \) are continuously differentiable and there exist known constants \(\delta _1\,\hbox {and}\,\delta _2 \) such that \(\left\| {\dot{\Delta }\mathbf{F}_1 } \right\| \le \delta _1 ,\left\| {\dot{\Delta }\mathbf{F}_{_2 } } \right\| \le \delta _2 \).

The proposed multivariables controller and disturbance observer for attitude cascade system can be summarized via the following theorem.

Theorem 2

For system (20) and (21), inner-loop and outer-loop controllers and disturbance observers are designed as follows:

  • (a1) Outer-loop disturbance observer

    $$\begin{aligned} \dot{\mathbf{z}}_1^o&= -k_1^o \frac{\mathbf{e}_1^o }{\left\| {\mathbf{e}_1^o } \right\| ^{1/2}}-k_2^o \mathbf{e}_1^o +\mathbf{z}_2^o \nonumber \\&\quad +\,\left( \mathbf{R}\,{\varvec{\upomega }}^{*}+\mathbf{R}\,\varvec{\upsigma }_i -\dot{\varvec{\Theta }}^{*} \right) ,\nonumber \\ \dot{\mathbf{z}}_2^o&= -k_3^o \frac{\mathbf{e}_1^o }{\left\| {\mathbf{e}_1^o } \right\| }-k_4^o \mathbf{e}_1^o \end{aligned}$$
    (22)

  • (a2) Outer-loop attitude controller

    $$\begin{aligned} \mathbf{R}{\varvec{\upomega }}^{*}&= \dot{\varvec{\Theta }}^{*}-K_1^o \left\| {\varvec{\upsigma }_o } \right\| ^{p-1}\varvec{\upsigma }_o +\mathbf{x}_2^o -\hat{{\Delta }}\mathbf{F}_1,\nonumber \\ \dot{\mathbf{x}}_2^o&= -K_2^o p\left\| {\varvec{\upsigma }_o } \right\| ^{2\left( {p-1} \right) }\varvec{\upsigma }_o \end{aligned}$$
    (23)

  • (b1) Inner-loop disturbance observer

    $$\begin{aligned} \dot{\mathbf{z}}_{1}^i&= -k_{1}^i \frac{\mathbf{e}_{1}^i }{\left\| {\mathbf{e}_{1}^\mathrm{I} } \right\| ^{1/2}}-k_2^i \mathbf{e}_{1}^i +\mathbf{z}_2^i\nonumber \\&\quad +\,\left( {-\mathbf{I}^{-1}\varvec{\Omega }\,\mathbf{I}\,{\varvec{\upomega }}-\dot{{\varvec{\upomega }}}^{*}+\mathbf{I}^{-1}\mathbf{M}} \right) ,\nonumber \\ \dot{\mathbf{z}}_2^i&= -k_3^i \frac{\mathbf{e}_{1}^i }{\left\| {\mathbf{e}_{1}^i } \right\| }-k_4^i \mathbf{e}_{1}^i \end{aligned}$$
    (24)

  • (b2) Inner-loop attitude controller

    $$\begin{aligned}&\mathbf{I}^{-1}\mathbf{M}=-\left( {-\mathbf{I}^{-1}\varvec{\Omega }\,\mathbf{I}\,{\varvec{\upomega }}-\dot{{\varvec{\upomega }}}^{*}} \right) -K_1^i \left\| {\varvec{\upsigma }_i } \right\| ^{p-1}\varvec{\upsigma }_i \nonumber \\&\quad +\,\mathbf{x}_{2}^\mathrm{I} -\hat{{\Delta }}\mathbf{F}_2,\quad \dot{\mathbf{x}}_{2}^\mathrm{I} =-K_2^i p\left\| {\varvec{\upsigma }_i } \right\| ^{2\left( {p-1} \right) }\varvec{\upsigma }_i \end{aligned}$$
    (25)

    where \(\hat{{\Delta }}\mathbf{F}_1 =\mathbf{z}_2^o,\hat{{\Delta }}\mathbf{F}_2 =\mathbf{z}_2^i,\,\mathbf{e}_1^j =\mathbf{z}_1^j -\varvec{\upsigma }_j\,\left( {j=i,o} \right) \). If Assumption 1 holds and the parameters are chosen as, \(K_m^j >0\left( {m=1,2;j=i,o} \right) \) and \(k_n^j \left( {n=1,2,3,4;j=i,o} \right) \) are determined according to Lemma 2, then \(\varvec{\upsigma }_o\,\hbox {and}\,\varvec{\upsigma }_i \) converge to zero in finite time.

Proof

The proof inspired from [51] can be split into three steps. In the first step, we will show that system (21) is finite time convergent with inner-loop disturbance observer (24) and controller (25). Substituting (25) into (21) yields

$$\begin{aligned}&\dot{\varvec{\upsigma }}_i =-K_1^i \left\| {\varvec{\upsigma }_i } \right\| ^{p-1}\varvec{\upsigma }_i +\mathbf{x}_2^i +\left( {\Delta \mathbf{F}_2 -\hat{{\Delta }}\mathbf{F}_2 } \right) ,\nonumber \\&\dot{\mathbf{x}}_2^i =-K_2^i p\left\| {\varvec{\upsigma }_i } \right\| ^{2\left( {p-1} \right) }\varvec{\upsigma }_i \end{aligned}$$
(26)

Define \(\mathbf{e}_2^i =\mathbf{z}_2^i -\Delta \mathbf{F}_2 \). Taking into account \(\mathbf{e}_1^i =\mathbf{z}_1^i -\varvec{\upsigma }_i\), the error dynamics for inner-loop disturbance observer (24) can be transformed into the following form

$$\begin{aligned}&\dot{\mathbf{e}}_1^i =-k_1^i \frac{\mathbf{e}_1^i }{\left\| {\mathbf{e}_1^i } \right\| ^{1/2}}-k_2^i \mathbf{e}_1^i +\mathbf{e}_2^i,\,\dot{\mathbf{e}}_2^i =-k_3^i \frac{\mathbf{e}_1^i }{\left\| {\mathbf{e}_1^i } \right\| }\nonumber \\&\quad \qquad -\,k_4^i \mathbf{e}_1^i -\dot{\Delta }\mathbf{F}_2 \end{aligned}$$
(27)

Taking into account Assumption 1 and lemma1, it can be observed that if the parameters \(k_n^i \left( {n=1,2,3,4} \right) \) are chosen properly, then \(\mathbf{e}_1^i,\mathbf{e}_2^i \rightarrow 0\) in finite time, namely \(T_1 \). Clearly, \(\mathbf{e}_2^i =\hat{{\Delta }}\mathbf{F}_2 -\Delta \mathbf{F}_2 \) is bounded for \(t\in \left[ {0,T_1 } \right] \). It follows from Theorem 1 that \(\varvec{\upsigma }_i \left( t \right) \) in (26) is bounded for \(t\in \left[ {0,T_1 } \right] \). After \(T_1 \), system (26) is reduced to \(\dot{\varvec{\upsigma }}_i =-K_1^i \left\| {\varvec{\upsigma }_i } \right\| ^{p-1}\varvec{\upsigma }_i +\mathbf{x}_2^i,\,\dot{\mathbf{x}}_2^i =-K_2^i p\left\| {\varvec{\upsigma }_i } \right\| ^{2\left( {p-1} \right) }\varvec{\upsigma }_i \) which is a special case for (16). In view of Theorem 1, \(\varvec{\upsigma }_i \left( t \right) \) converge to zero from any bounded initial value \(\varvec{\upsigma }_i \left( {T_1 } \right) \) in finite time, namely \(T_2 \). Therefore, it follows that \(\varvec{\upsigma }_i \left( t \right) \) is bounded and \(\varvec{\upsigma }_i \left( t \right) =0\) for \(t\ge T_1 +T_2\).

Next, we need to prove that \(\varvec{\upsigma }_o \left( t \right) \) is bounded. Substituting (23) into (20) results in

$$\begin{aligned}&\dot{\varvec{\upsigma }}_o =-K_1^o \left\| {\varvec{\upsigma }_o } \right\| ^{p-1}\varvec{\upsigma }_o \,{+}\,\mathbf{x}_2^o \,{+}\,\mathbf{R}\,\varvec{\upsigma }_i \,{+}\,\left( {\Delta \mathbf{F}_1 \,{-}\,\hat{{\Delta }}\mathbf{F}_1 } \right) \!,\nonumber \\&\dot{\mathbf{x}}_2^o =-K_2^o p\left\| {\varvec{\upsigma }_o } \right\| ^{2\left( {p-1} \right) }\varvec{\upsigma }_o \end{aligned}$$
(28)

Using outer-loop disturbance observer and similar analysis in the previous, it is easily found that \(\mathbf{z}_1^i \rightarrow \Delta \mathbf{F}_1 \) in finite time, namely \(T_3 \), which means \(\mathbf{z}_1^i -\Delta \mathbf{F}_1 =\hat{{\Delta }}\mathbf{F}_1 -\Delta \mathbf{F}_1 \) is bounded and converge to zero after \(T_3 \). Therefore, the item \(\mathbf{R}\,\varvec{\upsigma }_i +\left( {\Delta \mathbf{F}_1 -\hat{{\Delta }}\mathbf{F}_1 } \right) \) can be viewed as a bounded perturbation for (28). It follows from Theorem 1 that \(\varvec{\upsigma }_o \) is bounded.

Finally, the proof of finite time stability for (20) and (21) is provided. In view of the analysis in the previous, it can be seen that there exists \(T_4 =\max \left( {T_1 +T_2,T_3 } \right) \) such that \(\varvec{\upsigma }_i \rightarrow 0\,\hbox {and}\,\left( {\Delta \mathbf{F}_1 -\hat{{\Delta }}\mathbf{F}_1 } \right) \rightarrow 0\) for \(t\ge T_4 \). After that, (28) is reduced to \(\dot{\varvec{\upsigma }}_o =-K_1^o \left\| {\varvec{\upsigma }_o } \right\| ^{p-1}\varvec{\upsigma }_o +\mathbf{x}_2^o,\,\dot{\mathbf{x}}_2^o =-K_2^o p\left\| {\varvec{\upsigma }_o } \right\| ^{2\left( {p-1} \right) }\varvec{\upsigma }_o \). It follows from Theorem 1 that \(\varvec{\upsigma }_o \rightarrow 0\) from any bounded initial value \(\varvec{\upsigma }_o \left( {T_4 } \right) \) in finite time, namely \(T_5 \). As a result, both \(\varvec{\upsigma }_i \) and \(\varvec{\upsigma }_o \) converge to zero in finite time \(T_4 +T_5 \). This completes the proof.\(\square \)

Remark 3

The controller (23) and (25) can be interpreted as a smooth multivariables controller. If parameter \(p=1/2\) is used in (26) and (28), the control law is continuous but not smooth (the detailed analysis can be found in [52, 53]). However, the smoothness is necessary for multiloop system. Therefore, \(p=1/2\) is not included in proposed control scheme.

3.4 Control allocation

For completeness, control allocation algorithm provided in [54] is used here to transform control moment commands into control surface deflections. The aerodynamic moment expressions used in the research are expressed as

$$\begin{aligned} \left[ {{\begin{array}{l} {M_x } \\ {M_y } \\ {M_z } \\ \end{array} }} \right] =0.5\rho V^{2}S\left[ {{\begin{array}{l} {bC_l } \\ {cC_m } \\ {bC_n } \\ \end{array} }} \right] \end{aligned}$$
(29)

where \(C_l,\,C_m \,\hbox {and}\,C_n \) denote roll, pitch and yaw moment coefficients. In order to implement control allocator, it is assumed that the relationship between moments and control surface is linear [48]

$$\begin{aligned}&\left[ {{\begin{array}{c} {C_l } \\ {C_m } \\ {C_n } \\ \end{array} }} \right] =\left[ {{\begin{array}{c} {C_{l_\mathrm{base} } +C_{l_p } +C_{l_r } } \\ {C_{m_\mathrm{base} } +C_{m_q } } \\ {C_{n_\mathrm{base} } +C_{n_p } +C_{n_r } } \\ \end{array} }} \right] +\,\left[ {{\begin{array}{c} {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {C_{l_{\delta \mathrm{REI}} } }&{} {C_{l_{\delta \mathrm{REO}} } }&{} {C_{l_{\delta \mathrm{LEI}} } }&{} {C_{l_{\delta \mathrm{ELO}} } }&{} {C_{l_{\delta \mathrm{RF}} } }&{} {C_{l_{\delta \mathrm{LF}} }}&{} {C_{l_{\delta \mathrm{RR}} }}&{} {C_{l_{\delta \mathrm{LR}} }} \\ \end{array} }} \\ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {C_{m_{\delta \mathrm{REI}} } }&{} {C_{m_{\delta \mathrm{REO}} } }&{} {C_{m_{\delta \mathrm{LEI}} } }&{} {C_{m_{\delta \mathrm{ELO}} } }&{} {C_{m_{\delta \mathrm{RF}} } }&{} {C_{m _{\delta \mathrm{LF}}} }&{} {C_{m _{\delta \mathrm{RR}} }}&{} {C_{m _{\delta \mathrm{LR}} }} \\ \end{array} }} \\ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {C_{n_{\delta \mathrm{REI}} } }&{} {C_{l_{\delta \mathrm{REO}} } }&{} {C_{l_{\delta \mathrm{LEI}} } }&{} {C_{l_{\delta \mathrm{ELO}} } }&{} {C_{l_{\delta \mathrm{RF}} } }&{} {C_{n _{\delta \mathrm{LF}}} }&{} {C_{n _{\delta \mathrm{RR}} }}&{} {C_{n _{\delta \mathrm{LR}} }} \\ \end{array} }} \\ \end{array} }} \right] \varvec{\updelta }\nonumber \\ \end{aligned}$$
(30)

where vector \(\varvec{\updelta }=\left[ {\delta _\mathrm{REI}\,\delta _\mathrm{REO} \,\delta _\mathrm{LEI}\,\delta _\mathrm{LEO}\,\delta _\mathrm{RF} \,\delta _\mathrm{LF}\,\delta _\mathrm{RR}\,\delta _\mathrm{LF} } \right] \in R^{8}\) represents eight control surfaces, namely right elevon inboard, right elevon outboard, left elevon inboard, left elevon outboard, right body flap, left body flap, right rudder and left rudder. In addition, the control surface vector satisfies the following constraints

$$\begin{aligned} \varvec{\updelta }_{\min } \le \varvec{\updelta }\le \varvec{\updelta }_{\max } \end{aligned}$$
(31)

Substituting (30) into (29) yields

$$\begin{aligned} \underbrace{\left[ {{\begin{array}{l} {M_x } \\ {M_y } \\ {M_z } \\ \end{array} }} \right] }_\mathbf{M}&= 0.5\rho V^{2}Sb\underbrace{\left[ {{\begin{array}{c} {\left( {C_{l_\mathrm{base} } +C_{l_p } +C_{l_r } } \right) } \\ {\frac{c}{b}\left( {C_{m_\mathrm{base} } +C_{m_q } } \right) } \\ {\left( {C_{n_\mathrm{base} } +C_{n_p } +C_{n_r } } \right) } \\ \end{array} }} \right] }_{\mathbf{C}_B }\nonumber \\&\quad \,+\,0.5\rho V^{2}Sb{\underbrace{\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} C_{l_{\delta \mathrm{REI}} }&{}C_{l_{\delta \mathrm{REO}}}&{}C_{l_{\delta \mathrm{LEI}} }&{}C_{l_{\delta \mathrm{ELO}} }&{}C_{l_{\delta \mathrm{RF}}}&{}C_{l _{\delta \mathrm{LF}}}&{}C_{l _{\delta \mathrm{RR}}}&{}C_{l_{\delta \mathrm{LR}}} \\ \frac{c}{b}C_{m_{\delta \mathrm{REI}} }&{}\frac{c}{b}C_{m_{\delta \mathrm{REO}} } &{}\frac{c}{b}C_{m_{\delta \mathrm{LEI}} }&{}\frac{c}{b}C_{m_\mathrm{LEO} }&{}\frac{c}{b}C_{m_{\delta \mathrm{RF}} }&{} \frac{c}{b}C_{m_{{\delta \mathrm{LF}}}}&{} \frac{c}{b}C_{m_{{\delta \mathrm{RR}} }}&{}\frac{c}{b}C_{m_{\delta \mathrm{LR}} } \\ C_{n_{\delta \mathrm{REI}}} &{}C_{n_{\delta \mathrm{REO}} }&{}C_{n_{\delta \mathrm{LEI}} } &{}C_{n_{\delta \mathrm{ELO}}}&{}C_{n_{\delta \mathrm{RF}} }&{}C_{n_{{\delta \mathrm{LF}}}} &{}C_{n_{{\delta \mathrm{RR}} }}&{}C_{n_{{\delta \mathrm{LR}} }} \\ \end{array}\right] }_\mathbf{B}\,\varvec{\updelta }} \end{aligned}$$
(32)

The resulting mapping from control moments \(\mathbf{M}\) to control surface \(\varvec{\updelta }\) can be rewritten as matrix form

$$\begin{aligned} \mathbf{M}=\Lambda \mathbf{C}_B +\Lambda \mathbf{B}\,\varvec{\updelta } \end{aligned}$$
(33)

where \(\Lambda =0.5\rho V^{2}Sb\). Now, we hope to determine, at each sampling instant, a control command \(\varvec{\updelta }\) that is feasible with respect to the actuator constraints (31). The solution of (33) can be obtained via the following optimization problem:

$$\begin{aligned}&\varvec{\updelta }=\arg \,\mathop {\min }\limits _{\varvec{\updelta }\in \Theta } \,\varvec{\updelta }^{T}W_\updelta \varvec{\updelta }, \nonumber \\&\quad \Theta =\arg \, \mathop {\min }\limits _{\varvec{\updelta }_{\min } \le \varvec{\updelta }\le \varvec{\updelta }_{\max } } \left[ {\Lambda \mathbf{B}\,\varvec{\updelta }-\left( {\mathbf{M}-\Lambda \mathbf{C}_B } \right) } \right] ^{T}\nonumber \\&\quad \quad \times W_M \left[ {\Lambda \mathbf{B}\,\varvec{\updelta }-\left( {\mathbf{M}-\Lambda \mathbf{C}_B } \right) } \right] \end{aligned}$$
(34)

where \(W_\delta \) and \(W_M \) denote the weight matrix which allow designer to prioritize between the control surfaces. The equation (34) can be interpreted as follows: given \(\Theta \), the set of feasible control input satisfies position constraints minimizing \(\left[ {\Lambda \mathbf{B}\,\varvec{\updelta }-\left( {\mathbf{M}-\Lambda \mathbf{C}_B } \right) } \right] \) and then picks control surface that minimizes \(\varvec{\updelta }^{T}W_\delta \varvec{\updelta }\) weighted by \(W_\delta \). Finally, the resulting optimization problem can be efficiently solved using active set methods provided in [55].

4 Results and discussion

The reentry initial position is chosen as \(h_0 =183.33\,\hbox {kft},\phi _0 =60.43,\,\theta _0 =14.55^{\circ },\,V_0 =17{,}147.04\,\hbox {ft/s},\,\gamma _0 =-0.30^{\circ }\) and \(\chi _0 =57.51^{\circ }\). The aerodynamic coefficients and path constraints are same with those provided in [6]. The elements of inertia matrix are \(I_{xx} =434{,}270\,\hbox {slug-ft}^{2},\, I_{xz} =17{,}880\,\hbox {slug-ft}^{2},\, I_{yy} =961{,}200\,\hbox {slug-ft}^{2},\, I_{zz} =1{,}131{,}541\,\hbox {slug-ft}^{2}\) and \(I_{xy} =I_{yz}=0\,\hbox {slug-ft}^{2}\). In order to verify the robustness of the proposed control scheme, the disturbances \(\Delta \mathbf{D}_i =\left[ {1+\sin \left( {\pi t/125} \right) +\sin \left( {\pi t/250} \right) } \right] \times 10^{2} \quad \left( {i=1,2,3} \right) \) are added. In addition, the parameter uncertainty \(\Delta \mathbf{I}=30\,\% \mathbf{I}\) is also included in the simulation. The control surface constraints are \(\varvec{\updelta }_{\min } =\left[ {-40,-40,-40,-40,-40,-40,-40,-40} \right] \deg \) and \(\varvec{\updelta }_{\max } =-\varvec{\updelta }_{\min } \). The controller and disturbance observer parameters are set as follows: \(K_1^o =0.04,K_2^o =0.01,K_1^i =0.2,K_2^i =0.01,\, p=0.8\) and \(k_1^o =k_1^i =0.15,\,k_2^o =k_2^i =0.2,\, k_3^o =k_3^i =0.35 \quad k_4^o =k_4^i =0.01\), the weight matrixes in control allocation are given as: \(W_\delta =\hbox {diag}\left( {1,1,1,1,1,1,1,1} \right) ,\, W_M =\hbox {diag}\left( {1,1,1} \right) \). In addition, the simulation stops when landing accuracy satisfies

$$\begin{aligned} \left| {h_d -h_f } \right|&\le 30\,\hbox {ft},\left| {V_d -V_f } \right| \le 3\,\hbox {ft/s},\left| {\gamma _d -\gamma _f } \right| \nonumber \\&\le 0.1^{\circ } \end{aligned}$$
(35)

where \(h_d,\,V_d\) and \(\gamma _d \) are actual final flight altitude, velocity and FPA, respectively. The TAEM interface will be provided in the next. The sampling time of rotational motions is 5 ms. The updated cycle of guidance commands is not fixed, and it depends on the time consumed to generate the trajectory onboard which can be seen from Fig. 2a, b. Next, two representative cases are discussed.

Fig. 2
figure 2

Feedback calculation times, guidance commands and reentry trajectory curves

Full size image

Case 1 The TAEM interface is fixed and defined as \(h_f =80{,}000\,\hbox {ft},\, V_f =2{,}500\,\hbox {ft},\,\gamma _f =-5^{\circ }\) namely original TAEM interface (see Fig. 2). The performance of proposed system in guiding RLV from initial position to TAEM interface is to be evaluated in this case. The simulation results are provided in Figs. 2, 3, 4 and 5. Figure 2a shows the feedback number and time consumed to obtain new trajectory during reentry phase. From that, it can be seen that a new trajectory can be generated between 0.4 and 1.85 s. Furthermore, the feedback number during flight is 1,818. The average time used to update guidance commands is about 0.5806 s which are also provided in Table 1. The guidance commands including angle of attack and bank angle are shown in Fig. 2c, d where the continuous commands can be observed. The tracking errors for reentry attitudes and attitude angular rates are provided in Fig. 3. From the simulation results, it can be observed that both the attitudes and attitude angular rates can be tracked well with relatively small errors using the proposed control scheme. The curves for path constraints plotted in Fig. 4a–c show that they satisfy the predefined constraints in [6]. Furthermore, it follows from the results in Fig. 4b, c that the dynamic pressure and load factor increase with the decreasing altitude. In fact, the increase of dynamic pressure and load factor is caused by the increase of atmospheric density which is inversely proportional to altitude. The curves for control moments and control surface deflections are given in Figs. 4 and 5. At the end of reentry phase, control chattering can be observed from these results. Further analysis shows that it may be caused by rapid change of angle of attack which can be seen in Fig. 2c. Figure2e shows the actual reentry flight trajectory from initial position to TAEM interface. Finally, the simulation results demonstrate that the proposed integrated guidance and control scheme is able to guide RLV to the desired TAEM interface in the presence of model parameter uncertainties and unknown external disturbance. In addition, the landing accuracy is also provided in Table 1. The terminal errors for altitude, velocity and FPA with respect to predefined TAEM interface are about 12.3438 ft, 2.9226 ft/s and \(0.0985^{\circ }\), respectively.

Fig. 3
figure 3

Attitude and attitude angular rate errors

Full size image
Fig. 4
figure 4

Path constraints and control moments

Full size image
Fig. 5
figure 5

Control surface deflection

Full size image
Table 1 Simulation test results
Full size table

Case 2 In this case, the capacity of trajectory reshaping is verified. Suppose that the TAEM interface is \(h_f =80{,}000\,\hbox {ft},\,V_f =2{,}500\,\hbox {ft}\,\hbox {and}\,\gamma _f =-5^{\circ }\) prior to flight. During flight, assume that the TAEM interface is changed to \(h_f =80{,}000\,\hbox {ft},\,V_f =2{,}000\,\hbox {ft}\,\hbox {and}\,\gamma _f =-6^{\circ }\), namely updated TAEM interface. For simulation purpose, suppose that the moment when new TAEM interface is available for system is determined by \(t_r =100\left( {1+\varepsilon } \right) \) with a random number \(0<\varepsilon <1\). The same initial conditions, constraints and controller parameters with case 1 are used. The feedback calculation time over entire reentry trajectory is shown in Fig. 2b. From the simulation results, it can be seen that the maximum calculation time is about 3.1316 s. In fact, the original trajectory is still used as the initial value guess for calculation of the first reentry trajectory with updated TAEM interface being final condition. However, the original trajectory does not provide a good guess for updated trajectory. Therefore, it needs a longer time to obtain the first updated trajectory. After that, the calculation time reduced rapidly which can be seen from Fig. 2b. The attitude tracking error and corresponding control information including control moments as well as control surface deflections are also provided in Figs. 3, 4 and 5. In comparison with original trajectory in case 1, the updated trajectory in this case needs more time to reach updated TAEM interface. That is because the terminal velocity in case 2 is lower than that in case 1. Hence, RLV needs enough time to dissipate energy to ensure that RLV is able to enter updated TAEM interface. Furthermore, it follows from Fig. 2b, c the dynamic pressure and load factor decrease rapidly with the decreasing velocity. The opposite trends for dynamic pressure and load factor at the end of reentry phase in case 1 and case 2 can be explained as follows: the increase of atmospheric density is dominant in case 1, whereas the velocity decreases so quickly that it become dominant effect on dynamic pressure and load factor. The good tracking performance provided in Fig. 3 and flight trajectory in Fig. 2e demonstrate that the successful landing for RLV even in the alteration of unpredictable TAEM interface is achieved.

5 Conclusion and future work

An integrated guidance and control scheme with trajectory reshaping capacity is proposed for 6DOF RLV. Firstly, a reentry guidance law is designed based on real-time trajectory ensuring the flexibiligy and autonomy of RLV. Then, a multivariables smooth second-order sliding mode attitude controller and disturbance observer scheme is proposed to ensure that the guidance commands can be tracked in finite time. Also, the control allocation is included in the integrated guidance and control system. Finally, some representative simulations are provided for 6DOF RLV in order to verify the effectiveness of proposed integrated guidance and control scheme. If the aerodynamic moment coefficients uncertainties are included in the system, the system performance would be degraded. Therefore, the robust control allocation will be discussed in future.