Nonlinear dynamic modeling and global instability analyses of planetary gear trains considering multi-state engagement and tooth-contact temperature effects

Abstract

Gear disengaging, back-side tooth contact or poor dynamic behavior during operating leads to dynamic instability in planetary gear trains (PGTs). A novel nonlinear dynamic model of PGTs with internal and external gear pairs considering multi-state engagement induced by backlash and contact ratio is established. An improved time-varying meshing stiffness model including temperature stiffness is analytically derived. The time-varying meshing stiffness with temperature effect, friction, backlash, time-varying pressure angle, and time-varying friction arm are to be incorporated into the dynamic model of PGTs. Multi-state engaging behavior is efficiently identified by constructing different Poincaré mappings. A method to calculate dynamic instability is proposed in the time-domain trace. The intrinsic relationship between multi-state engaging and dynamic instability is investigated via multi-section bifurcation plots and phase trajectory topology. The global dynamic instability is revealed based on the bifurcation and evolution of coexistence behavior under the parameter-state synergy. The results show that the multi-state engagement is heavily depending on bifurcation and phase trajectory topology, which whereby affects the dynamic instability. Two special phenomena, complete and incomplete bifurcations, are discovered under parameter-state synergy. Complete bifurcation causes global instability and incomplete bifurcation results in local instability and yields coexistence responses. Incomplete bifurcation brings about new bifurcation branches.

1 Introduction

Because of the small size, light weight, high load capacity and large transmission ratio, planetary gear trains (PGTs) are extensively used in various mechanical systems, such as robots, aircrafts and vehicles. However, the vibration and noise problems of PGTs are also prominent due to their complex structure and operating conditions, such as including internal and external meshing gear pairs, single- and double-tooth engagements caused by the non-integer contact ratio, gear separation and back-side tooth contact induced by backlash [1,2,3]. In particular, the long-term accumulation of unhealthy meshing status or dynamic instability caused by changes in the number of meshing tooth pairs and gear disengagement restricts gear life and aggravates failure behaviors, thereby affecting equipment operating accuracy, transmission efficiency and service life [4,5,6]. Therefore, studying the global dynamic instability and healthy meshing conditions of PGTs based on multi-state engagement (MSE) and revealing the mechanisms of MSE and nonlinear dynamics on dynamic instability are essential in order to evaluate and improve the dynamic engagement, transmission quality and remaining life of PGTs.

The accuracy of the dynamic model of PGTs determines the validity and reliability of the analyzed results. Recently, many researchers have developed extensive dynamic models of PGTs and analyzed the nonlinear dynamic response characteristics taking various influencing factors into account. For instance, Kahraman [7] established a torsional dynamic model of the planetary gear set. Parker et al. have conducted meaningful research in dynamics modeling and analysis of planetary gearing systems with various conditions, such as two-dimensional dynamic model [8], tooth profile modification [9], elastic-body vibration [10], and parametric instability [11,12,13]. Li et al. [14] established an integrated drivetrain coupling analysis model of wind turbine gearbox with the effect of non-torque loads. Liu et al. [15] established a dynamic model for a double planetary gear set containing sun gear, ring gear, carrier, inner planet, outer planet, planetary bearing roller, and planetary bearing cage. In order to obtain accurate evaluation models, more significant influencing factors are analyzed and considered in the modeling of PGTs, such as friction and backlash [16,17,18], positioning errors [19,20,21], gear eccentricities [22, 23], rotational-translational dynamics [24, 25], time-varying pressure angles and contact ratios [26], random tooth profile errors [27], structural flexibility [28], load sharing characteristics [29,30,31], gyroscopic effects [32], and so on. Additionally, as one of the key internal excitations of geared systems, the calculation of time-varying meshing stiffness (TVMS) plays a pivotal role in the dynamic modeling and analysis of PGTs. There are abundant methods in existing literatures to calculate TVMS with considering multiple factors. Ma et al. have conducted extensive works on the TVMS calculation methods [33,34,35], laying the great foundation for the analysis and fault diagnosis of meshing vibration and dynamics of geared systems. Chen et al. have developed some interesting researches on TVMS modeling with tooth deformation, gear body structure coupling effect, and tooth profile deviations [36,37,38]. These models are widely used in the modeling and analysis of nonlinear dynamics of geared systems and provide theoretical guidance for dynamics prediction. Afterward, many modified TVMS models have also been proposed including wear evolution process [39, 40], addendum modification [41], tooth profile modification [42, 43], profile-shifted spur gears [44], viscoelastic behavior [45], different crack lengths [46,47,48], centrifugal effect [49], static transmission error [50], and lubrication and temperature effects [51]. Marafona et al. [52] reviewed in detail the different types of models to calculated the TVMS of parallel axis cylindrical gears including analytical, finite element, hybrid and approximated analytical models. Although numerous and effective TVMS models have been obtained, the effect of TVMS with temperature effect on the dynamic model and nonlinear dynamics of PGTs has rarely been reported. The tooth contact temperature is critical for the TVMS and the dynamic response of PGTs. Furthermore, the model mentioned above characterizes the engagement vibration of PGTs simply and equivalently in terms of springs and damping. The variation in the number of simultaneously meshed gear-tooth pairs, gear disengagement, back-side contact, and the time-varying characteristics of the meshing position are ignored, thus an accurate dynamic analysis and evaluation model for PGTs cannot be obtained effectively.

In dynamic analysis, backlash is essential to ensure the normal operation and good lubrication of the geared system and results in non-smooth nonlinear dynamic characteristics of the systems [53,54,55]. Backlash leads to multi-state mesh and is affected by various influencing factors, such as the gear wear [56], assembly/manufacturing errors [57], and temperature [58, 59]. Guo and Parker [60] investigated the bifurcation and chaos characteristics of planetary gears considering tooth separation and backlash. Liu et al. [61] observed the phenomenon of tooth separations with increasing in the rotating speed. Shi et al. [62] investigated the effects of backlash on the tooth separation and back-side tooth meshing behavior for a spur gear pair system. Tooth disengagement or back-side tooth contact induced by backlash leads to dynamic instability or unhealthy meshing situation for PGTs, which not only aggravates the vibration and noise, but also weakens the transmission smoothness and reliability. Long term accumulation of dynamic instability is prone to gear fatigue failure. Moreover, the dynamic behavior of PGTs is jointly governed by parameters and initial conditions. Thus, co-existence responses are easy to occur for PGTs and leads to complicated vibration behavior. The transitions of the dynamic response in the initial value domain may cause the global dynamic instability. Coexistence behavior has been heavily observed in geared systems, such as spur gear system [63,64,65,66], gear-rattling impact model [67], and face gear-bearing system [68]. Based on coexisting response, the safety characteristics [69] and two-parameter bifurcation [70] of a spur gear pair were discussed and some valuable research results were obtained. However, the coexistence behavior and global dynamic instability properties for PGTs have not yet been reported, which is extremely significant for vibration attenuation and dynamics improvement of PGTs.

Based on the above analysis, a nonlinear dynamic model of PGTs with internal and external meshing gear pairs considering multi-state mesh is established. The model includes the time-varying pressure angle, time-varying friction arm, and radius of the meshing point. A method to calculate the time-varying meshing stiffness taking temperature effect into account is derived. Multi-state meshing behavior of PGTs is efficiently characterized and analyzed via constructing different types of Poincaré mappings. A calculation method of dynamic instability for PGTs is proposed. The effect and intrinsic mechanism of multi-state engaging behavior and nonlinear dynamics on dynamic instability have been studied in details as the system parameters change. Subsequently, the multi-stability response of PGTs and its effect on dynamic instability are discussed with the parameter-state synergistic effect.

The rest of this paper is organized as follows: Sect. 2 presents a new dynamic model of PGTs with multi-state engaging behavior and time-varying meshing parameters. The time-varying meshing stiffness model with temperature effect is also presented in this section. An identification method of multi-state meshing behavior and a calculation method of dynamic instability are proposed in Sect. 3. Section 4 describes the impact mechanism of multi-state mesh and nonlinear dynamics on dynamic instability, as well as the generation and evolution of coexisting responses under the synergistic effect of parameter space and state space. Some conclusions are outlined in Sect. 5.

2 Modelling of planetary gear trains with multi-state engagement

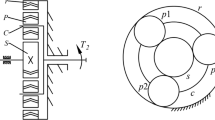
It is assumed that the planetary gear trains (PGTs) are rigidly supported without considering the lateral vibration of the gears, only its pure torsional vibration, a simplified physical model is shown in Fig. 1. PGTs is composed of sun gear, planetary gear, carrier and ring gear, wherein the gear ring is fixed on the foundation. θ_s, θ_c, and θ_pi represent the torsional displacements of the sun, carrier and the ith planet gear (i = 1,2,…,N), respectively. R_sb, R_rb, and R_pbi denote the radii of the base circle of the sun, ring, and the ith planet gear, respectively. R_c is the radius of the planet carrier. k_si(τ), c_si, μ_si(τ), e_si(τ), and 2D_si are the time-varying meshing stiffness, meshing damping, friction coefficient, dynamic transmission error, and backlash of the internal meshing gear pair (planet-ring mesh). k_ri(τ), c_ri, μ_ri(τ), e_ri(τ), and 2D_ri are the time-varying meshing stiffness, meshing damping, friction coefficient, dynamic transmission error, and backlash of the external meshing gear pair (sun-planet mesh). The nonlinear dynamics of pure torsional planetary gear trains is mainly caused by the meshing vibration of internal and external gear pairs. Thus, it is very significant to analyze the meshing vibration behavior of internal and external gear pairs.

Fig. 1

A simplified physical model of a planetary gear train

2.1 Internal mesh gear pair (planet-ring mesh)

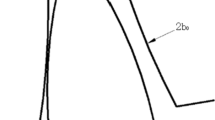
When the contact ratio, ε_r, of the planet-ring gear pair is between 1 and 2 (1 < ε_r < 2), the alternating mesh between single and double teeth is obtained during its operation. The details of the line of action (LoA_r) for the planet-ring gear pair is illustrated in Fig. 2. R_ra and R_pai are the addendum radii of the ring gear and the ith planet gear, respectively. Line segment AD is the actual line of action. A is the let in point and D is the let out point. AB and CD zones are double-tooth meshing areas, and BC is single-tooth meshing area. Let X_rpi = θ_piR_pbi-θ_cR_cb-e_ri(τ) be the relative displacement of the internal gear pair along LoA_r. Considering the drive-side tooth mesh, gear tooth disengagement and back-side tooth mesh, the contact force, F_Nri, at the meshing point along LoA_r is expressed as Eq. (1) by introducing backlash D_ri.

$$ F_{{{\text{Nr}}i}} = \left\{ {\begin{array}{*{20}l} {K_{{{\text{r}}i}} (\tau )\left[ {X_{{{\text{rp}}i}} - D_{{{\text{r}}i}} } \right] + c_{{{\text{r}}i}} \dot{X}_{{{\text{rp}}i}} } \hfill & {\left( {X_{{{\text{rp}}i}} \ge D_{{{\text{r}}i}} } \right)} \hfill \\ 0 \hfill & {\left( {|X_{{{\text{rp}}i}} | < D_{{{\text{r}}i}} } \right)} \hfill \\ {K_{{{\text{r}}i}} (\tau )\left[ {X_{{{\text{rp}}i}} + D_{{{\text{r}}i}} } \right] + c_{{{\text{r}}i}} \dot{X}_{{{\text{rp}}i}} } \hfill & {\left( {X_{{{\text{rp}}i}} \le - D_{{{\text{r}}i}} } \right)} \hfill \\ \end{array} } \right. $$

(1)

Fig. 2

The details of the line of action for the internal gear pair

The total load is unevenly distributed on two gear pairs in double-tooth area, and only acts on one gear pair in single-tooth area. Thus, in order to obtain accurate dynamic meshing force, the force analysis for the single- and the double-tooth meshes should be carried out respectively, as plotted in Figs. 3 and 4.

Fig. 3

Schematic of force analysis of planet-ring gear pair under double-tooth state

Fig. 4

Schematic of force analysis of planet-ring gear pair under single-tooth engaging state

2.1.1 Double-tooth mesh state

Figure 3 presents the force analysis at the meshing points under double-tooth engaging state, and two pairs of gear teeth engage simultaneously. F_pr1i, F_pr2i, F_rp1i and F_rp2i are the positive forces acting on the ith planet gear and ring gear along LoA_r. f_pr1i, f_pr2i, f_rp1i and f_rp2i are the friction forces acting on the ith planet gear and ring gear perpendicular to LoA_r. The positive forces can be calculated by Eq. (2), and the friction forces can be written as Eq. (3).

$$ F_{{{\text{p}} {\text{r}}1i}} = F_{rp1i} = L_{r1i} (\tau )F_{{{\text{Nr}}i}} ,\;\;F_{{{\text{pr2}}i}} = F_{{{\text{rp2}}i}} = L_{{{\text{r2}}i}} (\tau )F_{{{\text{Nr}}i}} $$

(2)

where $L_{r1i} (\tau )$ and $L_{r2i} (\tau ) = 1 - L_{r1i} (\tau )$ are the load distribution ratios of spur gear pairs, and detailed calculations can be obtained in the Ref. [8].

$$ f_{{{\text{pr1}}i}} = f_{{{\text{rp1}}i}} = \lambda_{{{\text{r1}}i}} (\tau )\mu_{{{\text{r1}}i}} (\tau )L_{{{\text{r1}}i}} (\tau )F_{{{\text{Nr}}i}} ,\;\;f_{{{\text{pr2}}i}} = f_{{{\text{rp2}}i}} = \lambda_{{{\text{r2}}i}} (\tau )\mu_{{{\text{r2}}i}} (\tau )L_{{{\text{r2}}i}} (\tau )F_{{{\text{Nr}}i}} $$

(3)

Herein, $\mu_{{{\text{r1}}i}} (\tau )$ and $\mu_{{{\text{r2}}i}} (\tau )$ are the time-varying friction coefficients at the meshing point for the planet-ring gear pair. $\lambda_{{{\text{r1}}i}} (\tau )$ and $\lambda_{{{\text{r2}}i}} (\tau )$ are the direction coefficients of the friction forces and can be obtained by Eq. (4).

$$ \lambda_{{{\text{r1}}i}} (\tau ) = sgn(v_{{{\text{r1}}i}} ),\;\;\lambda_{{{\text{r2}}i}} (\tau ) = sgn(v_{{{\text{r2}}i}} ) $$

(4)

where sgn(•) is the sign function, and $v_{{{\text{r1}}i}}$ and $v_{{{\text{r2}}i}}$ are the sliding speeds at the meshing points.

The friction moments of the planet-ring gear pair at the meshing points for the double-tooth engaging, S_pr1i(τ), S_r1i(τ), S_pr2i(τ) and S_r2i(τ), can be got from Eq. (5).

$$ \left\{ \begin{aligned} S_{{{\text{pr1}}i}} (\tau ) &= \sqrt {R_{{{\text{ra}}}}^{2} - R_{{{\text{pb}}}}^{2} } + R_{{{\text{pb}}}} \omega_{{{\text{p}}i}} \tau \hfill \\ S_{{{\text{r1}}i}} (\tau ) &= \sqrt {R_{{{\text{rp}}}}^{2} - R_{{{\text{rb}}}}^{2} } - \sqrt {R_{{{\text{pp}}}}^{2} - R_{{{\text{pb}}}}^{2} } + \sqrt {R_{{{\text{ra}}}}^{2} - R_{{{\text{pb}}}}^{2} } + R_{{{\text{pb}}}} \omega_{{{\text{p}}i}} \tau \hfill \\ \end{aligned} \right.,\;\;\left\{ \begin{aligned} S_{{{\text{pr2}}i}} (\tau ) &= S_{{{\text{p1}}i}} (\tau + T_{0} ) \hfill \\ S_{{{\text{r2}}i}} (\tau ) &= S_{{{\text{r1}}i}} (\tau + T_{0} ) \hfill \\ \end{aligned} \right. $$

(5)

where R_pp and R_rp are the pitch radii of the planet gear and ring gear. T₀ = 2π/(z_piω_pi) is a single- and double-tooth meshing cycle. ω_pi and z_pi are the tooth number and the rotational angular velocity of the ith planet gear, respectively.

2.1.2 Single-tooth mesh state

The force analysis at the meshing point under single-tooth state is plotted in Fig. 4, and only one pair of gear teeth meshes. The total load of the planet-ring gear pair acts on one pair of meshing teeth. The positive force and friction force at the meshing point for the planet-ring gear are expressed as Eq. (6).

$$ F_{{{\text{pr2}}i}} = F_{{{\text{rp2}}i}} = F_{{{\text{Nr}}i}} ,\;\;f_{{{\text{pr2}}i}} = f_{{{\text{rp2}}i}} = \lambda_{{{\text{r2}}i}} (\tau )\mu_{{{\text{r2}}i}} (\tau )F_{{{\text{Nr}}i}} $$

(6)

2.2 External mesh gear pair (sun-planet mesh)

Figure 5 presents the details of the line of action (LoA_s) for the sun-planet gear pair. R_sa and R_pai are the addendum radii of the sun gear and the ith planetary gear, respectively. ε_s is the contact ratio of the sun-planet gear pair. Single-tooth meshing (BC zone) and double-tooth meshing (AB and CD zones) occur periodically along LoA_s due to 1 < ε_s < 2. In order to have a good understanding of the dynamic characteristics of PGTs, the detailed meshing vibration behavior of the gear pair is considered in this work. Take X_spi = θ_sR_sb-θ_piR_pbi-θ_cR_cb-e_si(τ) as the relative displacement of the sun-planet gear pair along LoA_s. Introducing backlash D_si, the contact force, F_Nsi, at the meshing point along LoA_r is got by Eq. (7).

$$ F_{{{\text{Ns}} i}} = \left\{ {\begin{array}{*{20}l} {K_{{{\text{s}}i}} (\tau )\left[ {X_{{{\text{sp}}i}} - D_{{{\text{s}}i}} } \right] + c_{{{\text{s}}i}} \dot{X}_{{{\text{sp}}i}} } \hfill & {\left( {X_{{{\text{sp}}i}} \ge D_{{{\text{s}}i}} } \right)} \hfill \\ 0 \hfill & {\left( {|X_{{{\text{sp}}i}} | < D_{{{\text{s}}i}} } \right)} \hfill \\ {K_{{{\text{s}}i}} (\tau )\left[ {X_{{{\text{sp}}i}} + D_{{{\text{s}}i}} } \right] + c_{{{\text{s}}i}} \dot{X}_{{{\text{sp}}i}} } \hfill & {\left( {X_{{{\text{sp}}i}} \le - D_{{{\text{s}}i}} } \right)} \hfill \\ \end{array} } \right. $$

(7)

Fig. 5

The details of the line of action for the external gear pair

For single- and double-tooth meshes of the external meshing gear pair, the force at the meshing point is discussed in detail as follows.

2.2.1 Double-tooth mesh state for sun-planet mesh

The force analysis of sun-planet gear pair under double-tooth state is shown in Fig. 6. The total contact force F_Nsi along the line of action LoA_s is not uniformly distributed between the two meshing points. The positive forces at the engaging points along LoA_s is shown in Eq. (8).

$$ F_{{{\text{ps}} 1i}} = F_{sp1i} = L_{s1i} (\tau )F_{{{\text{Ns}}i}} ,\;\;F_{{{\text{ps2}}i}} = F_{{{\text{sp2}}i}} = L_{{{\text{s2}}i}} (\tau )F_{{{\text{Ns}}i}} $$

(8)

Fig. 6

Schematic of force analysis of sun-planet gear pair under double-tooth engaging state

The friction force at the engaging points perpendicular to LoA_s is written as Eq. (9).

$$ f_{{{\text{ps1}}i}} = f_{{{\text{sp1}}i}} = \lambda_{{{\text{s1}}i}} (\tau )\mu_{{{\text{s1}}i}} (\tau )L_{{{\text{s1}}i}} (\tau )F_{{{\text{Ns}}i}} ,\;\;f_{{{\text{ps2}}i}} = f_{{{\text{sp2}}i}} = \lambda_{{{\text{s2}}i}} (\tau )\mu_{{{\text{s2}}i}} (\tau )L_{{{\text{s2}}i}} (\tau )F_{{{\text{Ns}}i}} $$

(9)

Herein, $\mu_{{{\text{s1}}i}} (\tau )$ and $\mu_{{{\text{s2}}i}} (\tau )$ represent the time-varying friction coefficients at the meshing points for the planet-ring gear pair. $\lambda_{{{\text{s1}}i}} (\tau )$ and $\lambda_{{{\text{s2}}i}} (\tau )$ denote the direction coefficients of the friction forces and can be got by Eq. (10).

$$ \lambda_{{{\text{s1}}i}} (\tau ) = sgn(v_{{{\text{s1}}i}} ),\;\;\lambda_{{{\text{s2}}i}} (\tau ) = sgn(v_{{{\text{s2}}i}} ) $$

(10)

where sgn(•) is the sign function, and $v_{{{\text{s1}}i}}$ and $v_{{{\text{s2}}i}}$ are the sliding speeds at the meshing points for the external gear pair (sun-planet gear pair).

The friction moments from any engaging point to the sun gear and planet gear can be got by Eq. (11).

$$ \left\{ {\begin{array}{*{20}l} {S_{{{\text{s1}}i}} (\tau ) = \left( {R_{{{\text{sb}}}} + R_{{{\text{pb}}i}} } \right)\tan \alpha - \sqrt {R_{{{\text{pa}}i}}^{2} - R_{{{\text{pb}}i}}^{2} } + R_{{{\text{sb}}}} \omega_{{\text{s}}} \tau } \hfill \\ {S_{{{\text{ps1}}i}} (\tau ) = \sqrt {R_{{{\text{pa}}i}}^{2} - R_{{{\text{pb}}i}}^{2} } - R_{{{\text{sb}}}} \omega_{{\text{s}}} \tau } \hfill \\ \end{array} ,\quad \left\{ {\begin{array}{*{20}l} {S_{{{\text{s2}}i}} (\tau ) = S_{{{\text{s1}}i}} (\tau + T_{0} )} \hfill \\ {S_{{{\text{ps2}}i}} (\tau ) = S_{{{\text{ps1}}i}} (\tau + T_{0} )} \hfill \\ \end{array} } \right.} \right. $$

(11)

2.2.2 Single-tooth mesh state for sun-planet mesh

The total contact force along LoA_s acts on one engagement point, as shown in Fig. 7, and the positive forces and friction forces at the engagement point are as in Eq. (12).

$$ F_{{{\text{ps2}}i}} = F_{{{\text{sp2}}i}} = L_{{{\text{s2}}i}} (\tau )F_{{{\text{Ns}}i}} ,\;\;f_{{{\text{ps2}}i}} = f_{{{\text{sp2}}i}} = \lambda_{{{\text{s2}}i}} (\tau )\mu_{{{\text{s2}}i}} (\tau )L_{{{\text{s2}}i}} (\tau )F_{{{\text{Ns}}i}} $$

(12)

Fig. 7

Schematic of force analysis of sun-planet gear pair under single-tooth engaging state

2.3 Dynamic model of PGTs with sun-planet and planet-ring gear pairs

The torsional vibration of planetary gear trains (PGTs) is mainly caused by the meshing vibration of the sun-planet gear pairs and the planet-ring gear pairs. From Fig. 1, the sun gear and the planetary carrier are the input and output, respectively. The alternate meshing between single and double teeth, gear disengagement and back-side tooth contact are considered comprehensively herein. It is assumed that the gear impact is small when switching between different meshing states, and the gear tooth collision behavior is not considered in this work. Based on the action decomposition of engaging process of the gear pair and the force analyses at the meshing point, the purely torsional equations of the sun gear, the ith planet gear and the carrier under double-tooth mesh areas are written as Eq. (13) according to the principle of 2nd Newtonian law.

$$ \left\{ {\begin{array}{*{20}l} {I_{{\text{s}}} \ddot{\theta }_{{\text{s}}} + \sum\limits_{i = 1}^{N} {\left[ {R_{{{\text{sb}}}} + \lambda_{{{\text{s1}}i}} (\tau )\mu_{{{\text{s1}}i}} (\tau )L_{{{\text{s1}}i}} (\tau )S_{{{\text{s1}}i}} (\tau ) + \lambda_{{{\text{s2}}i}} (\tau )\mu_{{{\text{s2}}i}} (\tau )L_{{{\text{s2}}i}} (\tau )S_{{{\text{s2}}i}} (\tau )} \right]F_{{{\text{Ns}}i}} } = T_{{{\text{in}}}} } \hfill \\ {I_{{{\text{p}}i}} \ddot{\theta }_{{{\text{p}}i}} - \left[ {R_{{{\text{pb}}i}} + \lambda_{{{\text{s1}}i}} (\tau )\mu_{{{\text{s1}}i}} (\tau )L_{{{\text{s1}}i}} (\tau )S_{{{\text{ps1}}i}} (\tau ) + \lambda_{{{\text{s2}}i}} (\tau )\mu_{{{\text{s2}}i}} (\tau )L_{{{\text{s2}}i}} (\tau )S_{{{\text{ps2}}i}} (\tau )} \right]F_{{{\text{Ns}}i}} } \hfill \\ {\quad \quad + \left[ {R_{{{\text{pb}}i}} + \lambda_{{{\text{r1}}i}} (\tau )\mu_{{{\text{r1}}i}} (\tau )L_{{{\text{r1}}i}} (\tau )S_{{{\text{pr1}}i}} (\tau ) + \lambda_{{{\text{r2}}i}} (\tau )\mu_{{{\text{r2}}i}} (\tau )L_{{{\text{r2}}i}} (\tau )S_{{{\text{pr2}}i}} (\tau )} \right]F_{{{\text{Nr}}i}} = 0} \hfill \\ {I_{{{\text{cm}}}} \ddot{\theta }_{c} - \sum\limits_{i = 1}^{N} {\left[ {R_{{{\text{cb}}}} + \lambda_{{{\text{s1}}i}} (\tau )\mu_{{{\text{s1}}i}} (\tau )L_{{{\text{s1}}i}} (\tau )S_{{{\text{s1}}i}} (\tau ) + \lambda_{{{\text{s2}}i}} (\tau )\mu_{{{\text{s2}}i}} (\tau )L_{{{\text{s2}}i}} (\tau )S_{{{\text{s2}}i}} (\tau )} \right]F_{{{\text{Ns}}i}} } } \hfill \\ {\quad \quad - \left[ {R_{{{\text{cb}}}} + \lambda_{{{\text{r1}}i}} (\tau )\mu_{{{\text{r1}}i}} (\tau )L_{{{\text{r1}}i}} (\tau )S_{{{\text{r1}}i}} (\tau ) + \lambda_{{{\text{r2}}i}} (\tau )\mu_{{{\text{r2}}i}} (\tau )L_{{{\text{r2}}i}} (\tau )S_{{{\text{r2}}i}} (\tau )} \right]F_{{{\text{Nr}}i}} = - T_{{{\text{out}}}} } \hfill \\ \end{array} } \right. $$

(13)

where T_in and T_out are the input and output torques respectively. I_s, I_pi and I_cm denote the equivalent mass moment of inertia of the sun gear, the ith planet gear and the carrier, respectively, and I_cm can be obtained by Eq. (14).

$$ I_{{{\text{cm}}}} = I_{{\text{c}}} + \sum\limits_{i = 1}^{N} {m_{{{\text{p}}i}} R_{{\text{c}}}^{2} } $$

(14)

Herein, I_c is the mass moment of inertia of the carrier, m_pi the mass of the ith planet gear. The condition of double-tooth engagement can be effectively identified in the time domain, that is, nT₀ < τ ≤ nT₀(ε_s-1), n = 1,2,3,….

The purely torsional equations of the sun gear, the ith planet gear and the carrier under single-tooth mesh area can be expressed as Eq. (15). The condition of single-tooth engagement in the time domain is T₀(ε_s-1) < τ ≤ (n-1)T₀.

$$ \left\{ {\begin{array}{*{20}l} {I_{{\text{s}}} \ddot{\theta }_{{\text{s}}} + \sum\limits_{i = 1}^{N} {\left[ {R_{{{\text{sb}}}} + \lambda_{{{\text{s2}}i}} (\tau )\mu_{{{\text{s2}}i}} (\tau )S_{{{\text{s2}}i}} (\tau )} \right]F_{{{\text{Ns}}i}} } = T_{{{\text{in}}}} } \hfill \\ {I_{{{\text{p}}i}} \ddot{\theta }_{{{\text{p}}i}} - \left[ {R_{{{\text{pb}}i}} + \lambda_{{{\text{s2}}i}} (\tau )\mu_{{{\text{s2}}i}} (\tau )S_{{{\text{ps2}}i}} (\tau )} \right]F_{{{\text{Ns}}i}} + \left[ {R_{{{\text{pb}}i}} + \lambda_{{{\text{r2}}i}} (\tau )\mu_{{{\text{r2}}i}} (\tau )S_{{{\text{pr2}}i}} (\tau )} \right]F_{{{\text{Nr}}i}} = 0} \hfill \\ {I_{{{\text{cm}}}} \ddot{\theta }_{c} - \sum\limits_{i = 1}^{N} {\left[ {R_{{{\text{cb}}}} + \lambda_{{{\text{s2}}i}} (\tau )\mu_{{{\text{s2}}i}} (\tau )S_{{{\text{s2}}i}} (\tau )} \right]F_{{{\text{Ns}}i}} - } \sum\limits_{i = 1}^{N} {\left[ {R_{{{\text{cb}}}} + \lambda_{{{\text{r2}}i}} (\tau )\mu_{{{\text{r2}}i}} (\tau )S_{{{\text{r2}}i}} (\tau )} \right]F_{{{\text{Nr}}i}} } = - T_{{{\text{out}}}} } \hfill \\ \end{array} } \right. $$

(15)

To better understand the meshing vibration of the external and internal gear pairs, the relative displacements X_rpi = θ_piR_pbi-θ_cR_cb-e_ri(τ) and X_spi = θ_sR_sb-θ_piR_pbi-θ_cR_cb-e_si(τ) along the lines of action are introduced. According to Eq. (13), the nonlinear dynamic model of PGTs with external and internal gear pairs under single-tooth engaging state is expressed in Eq. (16).

$$ \left\{ {\begin{array}{*{20}l} {\ddot{X}_{{{\text{sp}}i}} + \sum\limits_{i = 1}^{N} {{{\left[ {1 + \lambda_{{{\text{s2}}i}} (\tau )\mu_{{{\text{s2}}i}} (\tau )g_{{{\text{s2}}i}} (\tau )} \right]F_{{{\text{Ns}}i}} } \mathord{\left/ {\vphantom {{\left[ {1 + \lambda_{{{\text{s2}}i}} (\tau )\mu_{{{\text{s2}}i}} (\tau )g_{{{\text{s2}}i}} (\tau )} \right]F_{{{\text{Ns}}i}} } {m_{{{\text{sc}}}} }}} \right. \kern-0pt} {m_{{{\text{sc}}}} }}} + \sum\limits_{i = 1}^{N} {{{\left[ {1 + \lambda_{{{\text{r2}}i}} (\tau )\mu_{{{\text{r2}}i}} (\tau )g_{{{\text{r2}}i}} (\tau )} \right]F_{{{\text{Nr}}i}} } \mathord{\left/ {\vphantom {{\left[ {1 + \lambda_{{{\text{r2}}i}} (\tau )\mu_{{{\text{r2}}i}} (\tau )g_{{{\text{r2}}i}} (\tau )} \right]F_{{{\text{Nr}}i}} } {m_{{{\text{cm}}}} }}} \right. \kern-0pt} {m_{{{\text{cm}}}} }}} } \hfill \\ {\quad + {{\left[ {1 + \lambda_{{{\text{s2}}i}} (\tau )\mu_{{{\text{s2}}i}} (\tau )g_{{{\text{ps2}}i}} (\tau )} \right]F_{{{\text{Ns}}i}} } \mathord{\left/ {\vphantom {{\left[ {1 + \lambda_{{{\text{s2}}i}} (\tau )\mu_{{{\text{s2}}i}} (\tau )g_{{{\text{ps2}}i}} (\tau )} \right]F_{{{\text{Ns}}i}} } {m_{{{\text{p}}i}} }}} \right. \kern-0pt} {m_{{{\text{p}}i}} }} - {{\left[ {1 + \lambda_{{{\text{r2}}i}} (\tau )\mu_{{{\text{r2}}i}} (\tau )g_{{{\text{pr2}}i}} (\tau )} \right]F_{{{\text{Nr}}i}} } \mathord{\left/ {\vphantom {{\left[ {1 + \lambda_{{{\text{r2}}i}} (\tau )\mu_{{{\text{r2}}i}} (\tau )g_{{{\text{pr2}}i}} (\tau )} \right]F_{{{\text{Nr}}i}} } {m_{{{\text{p}}i}} }}} \right. \kern-0pt} {m_{{{\text{p}}i}} }} = T_{1} - \ddot{e}_{{{\text{sp}}i}} } \hfill \\ {\ddot{X}_{{{\text{rp}}i}} - {{\left[ {1 + \lambda_{{{\text{s2}}i}} (\tau )\mu_{{{\text{s2}}i}} (\tau )g_{{{\text{ps2}}i}} (\tau )} \right]F_{{{\text{Ns}}i}} } \mathord{\left/ {\vphantom {{\left[ {1 + \lambda_{{{\text{s2}}i}} (\tau )\mu_{{{\text{s2}}i}} (\tau )g_{{{\text{ps2}}i}} (\tau )} \right]F_{{{\text{Ns}}i}} } {m_{{{\text{p}}i}} }}} \right. \kern-0pt} {m_{{{\text{p}}i}} }} + {{\left[ {1 + \lambda_{{{\text{r2}}i}} (\tau )\mu_{{{\text{r2}}i}} (\tau )g_{{{\text{pr2}}i}} (\tau )} \right]F_{{{\text{Nr}}i}} } \mathord{\left/ {\vphantom {{\left[ {1 + \lambda_{{{\text{r2}}i}} (\tau )\mu_{{{\text{r2}}i}} (\tau )g_{{{\text{pr2}}i}} (\tau )} \right]F_{{{\text{Nr}}i}} } {m_{{{\text{p}}i}} }}} \right. \kern-0pt} {m_{{{\text{p}}i}} }}} \hfill \\ {\quad + \sum\limits_{i = 1}^{N} {{{\left[ {1 + \lambda_{{{\text{s2}}i}} (\tau )\mu_{{{\text{s2}}i}} (\tau )g_{{{\text{2s}}i}} (\tau )} \right]F_{{{\text{Ns}}i}} } \mathord{\left/ {\vphantom {{\left[ {1 + \lambda_{{{\text{s2}}i}} (\tau )\mu_{{{\text{s2}}i}} (\tau )g_{{{\text{2s}}i}} (\tau )} \right]F_{{{\text{Ns}}i}} } {m_{{{\text{cm}}}} }}} \right. \kern-0pt} {m_{{{\text{cm}}}} }} - } \sum\limits_{i = 1}^{N} {{{\left[ {1 + \lambda_{{{\text{r2}}i}} (\tau )\mu_{{{\text{r2}}i}} (\tau )g_{{{\text{r2}}i}} (\tau )} \right]F_{{{\text{Nr}}i}} } \mathord{\left/ {\vphantom {{\left[ {1 + \lambda_{{{\text{r2}}i}} (\tau )\mu_{{{\text{r2}}i}} (\tau )g_{{{\text{r2}}i}} (\tau )} \right]F_{{{\text{Nr}}i}} } {m_{{{\text{cm}}}} }}} \right. \kern-0pt} {m_{{{\text{cm}}}} }}} = T_{2} - \ddot{e}_{{{\text{sp}}i}} } \hfill \\ \end{array} } \right. $$

(16)

Similarly, the nonlinear dynamic model of PGTs with external and internal gear pairs under single-tooth engaging state is written as Eq. (17).

$$ \left\{ {\begin{array}{*{20}l} {\ddot{X}_{{{\text{sp}}i}} + \sum\limits_{{i = 1}}^{N} {{{\left[ {1 + \lambda _{{{\text{s1}}i}} (\tau )\mu _{{{\text{s1}}i}} (\tau )L_{{{\text{s1}}i}} (\tau )g_{{{\text{s1}}i}} (\tau ) + \lambda _{{{\text{s2}}i}} (\tau )\mu _{{{\text{s2}}i}} (\tau )L_{{{\text{s2}}i}} (\tau )g_{{{\text{s2}}i}} (\tau )} \right]F_{{{\text{Ns}}i}} } \mathord{\left/ {\vphantom {{\left[ {1 + \lambda _{{{\text{s1}}i}} (\tau )\mu _{{{\text{s1}}i}} (\tau )L_{{{\text{s1}}i}} (\tau )g_{{{\text{s1}}i}} (\tau ) + \lambda _{{{\text{s2}}i}} (\tau )\mu _{{{\text{s2}}i}} (\tau )L_{{{\text{s2}}i}} (\tau )g_{{{\text{s2}}i}} (\tau )} \right]F_{{{\text{Ns}}i}} } {m_{{{\text{sc}}}} }}} \right. \kern-\nulldelimiterspace} {m_{{{\text{sc}}}} }}} } \hfill \\ {\qquad + \sum\limits_{{i = 1}}^{N} {{{\left[ {1 + \lambda _{{{\text{r1}}i}} (\tau )\mu _{{{\text{r1}}i}} (\tau )L_{{{\text{r1}}i}} (\tau )g_{{{\text{r1}}i}} (\tau ) + \lambda _{{{\text{r2}}i}} (\tau )\mu _{{{\text{r2}}i}} (\tau )L_{{{\text{r2}}i}} (\tau )g_{{{\text{r2}}i}} (\tau )} \right]F_{{{\text{Nr}}i}} } \mathord{\left/ {\vphantom {{\left[ {1 + \lambda _{{{\text{r1}}i}} (\tau )\mu _{{{\text{r1}}i}} (\tau )L_{{{\text{r1}}i}} (\tau )g_{{{\text{r1}}i}} (\tau ) + \lambda _{{{\text{r2}}i}} (\tau )\mu _{{{\text{r2}}i}} (\tau )L_{{{\text{r2}}i}} (\tau )g_{{{\text{r2}}i}} (\tau )} \right]F_{{{\text{Nr}}i}} } {m_{{{\text{cm}}}} }}} \right. \kern-\nulldelimiterspace} {m_{{{\text{cm}}}} }}} } \hfill \\ {\qquad + {{\left[ {1 + \lambda _{{{\text{s1}}i}} (\tau )\mu _{{{\text{s1}}i}} (\tau )L_{{{\text{s1}}i}} (\tau )g_{{{\text{ps1}}i}} (\tau ) + \lambda _{{{\text{s2}}i}} (\tau )\mu _{{{\text{s2}}i}} (\tau )L_{{{\text{s2}}i}} (\tau )g_{{{\text{ps2}}i}} (\tau )} \right]F_{{{\text{Ns}}i}} } \mathord{\left/ {\vphantom {{\left[ {1 + \lambda _{{{\text{s1}}i}} (\tau )\mu _{{{\text{s1}}i}} (\tau )L_{{{\text{s1}}i}} (\tau )g_{{{\text{ps1}}i}} (\tau ) + \lambda _{{{\text{s2}}i}} (\tau )\mu _{{{\text{s2}}i}} (\tau )L_{{{\text{s2}}i}} (\tau )g_{{{\text{ps2}}i}} (\tau )} \right]F_{{{\text{Ns}}i}} } {m_{{{\text{p}}i}} }}} \right. \kern-\nulldelimiterspace} {m_{{{\text{p}}i}} }}} \hfill \\ {\qquad - {{\left[ {1 + \lambda _{{{\text{r1}}i}} (\tau )\mu _{{{\text{r1}}i}} (\tau )L_{{{\text{r1}}i}} (\tau )g_{{{\text{pr1}}i}} (\tau ) + \lambda _{{{\text{r2}}i}} (\tau )\mu _{{{\text{r2}}i}} (\tau )L_{{{\text{r2}}i}} (\tau )g_{{{\text{pr2}}i}} (\tau )} \right]F_{{{\text{Nr}}i}} } \mathord{\left/ {\vphantom {{\left[ {1 + \lambda _{{{\text{r1}}i}} (\tau )\mu _{{{\text{r1}}i}} (\tau )L_{{{\text{r1}}i}} (\tau )g_{{{\text{pr1}}i}} (\tau ) + \lambda _{{{\text{r2}}i}} (\tau )\mu _{{{\text{r2}}i}} (\tau )L_{{{\text{r2}}i}} (\tau )g_{{{\text{pr2}}i}} (\tau )} \right]F_{{{\text{Nr}}i}} } {m_{{{\text{p}}i}} }}} \right. \kern-\nulldelimiterspace} {m_{{{\text{p}}i}} }} = T_{1} - \ddot{e}_{{{\text{sp}}i}} } \hfill \\ {\ddot{X}_{{{\text{rp}}i}} - {{\left[ {1 + \lambda _{{{\text{s1}}i}} (\tau )\mu _{{{\text{s1}}i}} (\tau )L_{{{\text{s1}}i}} (\tau )g_{{{\text{ps1}}i}} (\tau ) + \lambda _{{{\text{s2}}i}} (\tau )\mu _{{{\text{s2}}i}} (\tau )L_{{{\text{s2}}i}} (\tau )g_{{{\text{ps2}}i}} (\tau )} \right]F_{{{\text{Ns}}i}} } \mathord{\left/ {\vphantom {{\left[ {1 + \lambda _{{{\text{s1}}i}} (\tau )\mu _{{{\text{s1}}i}} (\tau )L_{{{\text{s1}}i}} (\tau )g_{{{\text{ps1}}i}} (\tau ) + \lambda _{{{\text{s2}}i}} (\tau )\mu _{{{\text{s2}}i}} (\tau )L_{{{\text{s2}}i}} (\tau )g_{{{\text{ps2}}i}} (\tau )} \right]F_{{{\text{Ns}}i}} } {m_{{{\text{p}}i}} }}} \right. \kern-\nulldelimiterspace} {m_{{{\text{p}}i}} }}} \hfill \\ {\qquad + {{\left[ {1 + \lambda _{{{\text{r1}}i}} (\tau )\mu _{{{\text{r1}}i}} (\tau )L_{{{\text{r1}}i}} (\tau )g_{{{\text{pr1}}i}} (\tau ) + \lambda _{{{\text{r2}}i}} (\tau )\mu _{{{\text{r2}}i}} (\tau )L_{{{\text{r2}}i}} (\tau )g_{{{\text{pr2}}i}} (\tau )} \right]F_{{{\text{Nr}}i}} } \mathord{\left/ {\vphantom {{\left[ {1 + \lambda _{{{\text{r1}}i}} (\tau )\mu _{{{\text{r1}}i}} (\tau )L_{{{\text{r1}}i}} (\tau )g_{{{\text{pr1}}i}} (\tau ) + \lambda _{{{\text{r2}}i}} (\tau )\mu _{{{\text{r2}}i}} (\tau )L_{{{\text{r2}}i}} (\tau )g_{{{\text{pr2}}i}} (\tau )} \right]F_{{{\text{Nr}}i}} } {m_{{{\text{p}}i}} }}} \right. \kern-\nulldelimiterspace} {m_{{{\text{p}}i}} }}} \hfill \\ {\qquad + \sum\limits_{{i = 1}}^{N} {{{\left[ {1 + \lambda _{{{\text{s1}}i}} (\tau )\mu _{{{\text{s1}}i}} (\tau )L_{{{\text{s1}}i}} (\tau )g_{{{\text{1s}}i}} (\tau ) + \lambda _{{{\text{s2}}i}} (\tau )\mu _{{{\text{s2}}i}} (\tau )L_{{{\text{s2}}i}} (\tau )g_{{{\text{2s}}i}} (\tau )} \right]F_{{{\text{Ns}}i}} } \mathord{\left/ {\vphantom {{\left[ {1 + \lambda _{{{\text{s1}}i}} (\tau )\mu _{{{\text{s1}}i}} (\tau )L_{{{\text{s1}}i}} (\tau )g_{{{\text{1s}}i}} (\tau ) + \lambda _{{{\text{s2}}i}} (\tau )\mu _{{{\text{s2}}i}} (\tau )L_{{{\text{s2}}i}} (\tau )g_{{{\text{2s}}i}} (\tau )} \right]F_{{{\text{Ns}}i}} } {m_{{{\text{cm}}}} }}} \right. \kern-\nulldelimiterspace} {m_{{{\text{cm}}}} }}} } \hfill \\ { \qquad - \sum\limits_{{i = 1}}^{N} {{{\left[ {1 + \lambda _{{{\text{r1}}i}} (\tau )\mu _{{{\text{r1}}i}} (\tau )L_{{{\text{r1}}i}} (\tau )g_{{{\text{r1}}i}} (\tau ) + \lambda _{{{\text{r2}}i}} (\tau )\mu _{{{\text{r2}}i}} (\tau )L_{{{\text{r2}}i}} (\tau )g_{{{\text{r2}}i}} (\tau )} \right]F_{{{\text{Nr}}i}} } \mathord{\left/ {\vphantom {{\left[ {1 + \lambda _{{{\text{r1}}i}} (\tau )\mu _{{{\text{r1}}i}} (\tau )L_{{{\text{r1}}i}} (\tau )g_{{{\text{r1}}i}} (\tau ) + \lambda _{{{\text{r2}}i}} (\tau )\mu _{{{\text{r2}}i}} (\tau )L_{{{\text{r2}}i}} (\tau )g_{{{\text{r2}}i}} (\tau )} \right]F_{{{\text{Nr}}i}} } {m_{{{\text{cm}}}} }}} \right. \kern-\nulldelimiterspace} {m_{{{\text{cm}}}} }}} = T_{2} - \ddot{e}_{{{\text{sp}}i}} } \hfill \\ \end{array} } \right. $$

(17)

where $m_{{{\text{sc}}}} = {{I_{{\text{s}}} I_{{{\text{cm}}}} } \mathord{\left/ {\vphantom {{I_{{\text{s}}} I_{{{\text{cm}}}} } {\left( {I_{{{\text{cm}}}} R_{{{\text{sb}}}}^{2} + I_{{\text{s}}} R_{{{\text{cb}}}}^{2} } \right)}}} \right. \kern-0pt} {\left( {I_{{{\text{cm}}}} R_{{{\text{sb}}}}^{2} + I_{{\text{s}}} R_{{{\text{cb}}}}^{2} } \right)}}$, $m_{{{\text{cm}}}} = {{I_{{{\text{cm}}}} } \mathord{\left/ {\vphantom {{I_{{{\text{cm}}}} } {R_{{{\text{cb}}}}^{2} }}} \right. \kern-0pt} {R_{{{\text{cb}}}}^{2} }}$, $m_{{{\text{p}}i}} = {{I_{{{\text{p}}i}} } \mathord{\left/ {\vphantom {{I_{{{\text{p}}i}} } {R_{{{\text{pb}}i}}^{2} }}} \right. \kern-0pt} {R_{{{\text{pb}}i}}^{2} }}$, $g_{{{\text{r1}}i}} (\tau ) = {{S_{{{\text{r1}}i}} (\tau )} \mathord{\left/ {\vphantom {{S_{{{\text{r1}}i}} (\tau )} {R_{{{\text{cb}}}} }}} \right. \kern-0pt} {R_{{{\text{cb}}}} }}$, $g_{{{\text{s1}}i}} (\tau ) = {{\left( {I_{{{\text{cm}}}} R_{{{\text{sb}}}} + I_{{\text{s}}} R_{{{\text{cb}}}} } \right)S_{{{\text{s1}}i}} (\tau )} \mathord{\left/ {\vphantom {{\left( {I_{{{\text{cm}}}} R_{{{\text{sb}}}} + I_{{\text{s}}} R_{{{\text{cb}}}} } \right)S_{{{\text{s1}}i}} (\tau )} {\left( {I_{{{\text{cm}}}} R_{{{\text{sb}}}}^{2} + I_{{\text{s}}} R_{{{\text{cb}}}}^{2} } \right)}}} \right. \kern-0pt} {\left( {I_{{{\text{cm}}}} R_{{{\text{sb}}}}^{2} + I_{{\text{s}}} R_{{{\text{cb}}}}^{2} } \right)}}$, $g_{{{\text{s2}}i}} (\tau ) = {{\left( {I_{{{\text{cm}}}} R_{{{\text{sb}}}} + I_{{\text{s}}} R_{{{\text{cb}}}} } \right)S_{{{\text{s2}}i}} (\tau )} \mathord{\left/ {\vphantom {{\left( {I_{{{\text{cm}}}} R_{{{\text{sb}}}} + I_{{\text{s}}} R_{{{\text{cb}}}} } \right)S_{{{\text{s2}}i}} (\tau )} {\left( {I_{{{\text{cm}}}} R_{{{\text{sb}}}}^{2} + I_{{\text{s}}} R_{{{\text{cb}}}}^{2} } \right)}}} \right. \kern-0pt} {\left( {I_{{{\text{cm}}}} R_{{{\text{sb}}}}^{2} + I_{{\text{s}}} R_{{{\text{cb}}}}^{2} } \right)}}$, $g_{{{\text{r2}}i}} (\tau ) = {{S_{{{\text{r2}}i}} (\tau )} \mathord{\left/ {\vphantom {{S_{{{\text{r2}}i}} (\tau )} {R_{{{\text{cb}}}} }}} \right. \kern-0pt} {R_{{{\text{cb}}}} }}$, $g_{{{\text{ps1}}i}} (\tau ) = {{S_{{{\text{ps1}}i}} (\tau )} \mathord{\left/ {\vphantom {{S_{{{\text{ps1}}i}} (\tau )} {R_{{{\text{pb}}i}} }}} \right. \kern-0pt} {R_{{{\text{pb}}i}} }}$, $g_{{{\text{ps2}}i}} (\tau ) = {{S_{{{\text{ps2}}i}} (\tau )} \mathord{\left/ {\vphantom {{S_{{{\text{ps2}}i}} (\tau )} {R_{{{\text{pb}}i}} }}} \right. \kern-0pt} {R_{{{\text{pb}}i}} }}$, $g_{{{\text{pr1}}i}} (\tau ) = {{S_{{{\text{pr1}}i}} (\tau )} \mathord{\left/ {\vphantom {{S_{{{\text{pr1}}i}} (\tau )} {R_{{{\text{pb}}i}} }}} \right. \kern-0pt} {R_{{{\text{pb}}i}} }}$, $g_{{{\text{pr2}}i}} (\tau ) = {{S_{{{\text{pr2}}i}} (\tau )} \mathord{\left/ {\vphantom {{S_{{{\text{pr2}}i}} (\tau )} {R_{{{\text{pb}}i}} }}} \right. \kern-0pt} {R_{{{\text{pb}}i}} }}$, $g_{{{\text{1s}}i}} (\tau ) = {{S_{{{\text{s1}}i}} (\tau )} \mathord{\left/ {\vphantom {{S_{{{\text{s1}}i}} (\tau )} {R_{{{\text{cb}}}} }}} \right. \kern-0pt} {R_{{{\text{cb}}}} }}$, $g_{{{\text{2s}}i}} (\tau ) = {{S_{{{\text{s2}}i}} (\tau )} \mathord{\left/ {\vphantom {{S_{{{\text{s2}}i}} (\tau )} {R_{{{\text{cb}}}} }}} \right. \kern-0pt} {R_{{{\text{cb}}}} }}$, $T_{{1}} = {{\left( {T_{{{\text{in}}}} I_{{{\text{cm}}}} R_{{{\text{sb}}}} + T_{{{\text{out}}}} I_{{\text{s}}} R_{{{\text{cb}}}}^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {T_{{{\text{in}}}} I_{{{\text{cm}}}} R_{{{\text{sb}}}} + T_{{{\text{out}}}} I_{{\text{s}}} R_{{{\text{cb}}}}^{2} } \right)} {I_{{\text{s}}} I_{{{\text{cm}}}} }}} \right. \kern-0pt} {I_{{\text{s}}} I_{{{\text{cm}}}} }}$, $T_{{2}} = {{T_{{{\text{out}}}} R_{{{\text{cb}}}} } \mathord{\left/ {\vphantom {{T_{{{\text{out}}}} R_{{{\text{cb}}}} } {I_{{{\text{cm}}}} }}} \right. \kern-0pt} {I_{{{\text{cm}}}} }}$.

2.4 Dimensionless normalized analytical model of PGTs

The established dynamic model of PGTs in Sect. 2.3 includes single- and double-tooth meshes, backlash, time-varying meshing parameters, etc., which has strong non-smooth and nonlinear time-varying characteristics. It is very difficult to solve such models directly, so it is very necessary to build its dimensionless normalized analytical model for easy solution and analysis. The dimensionless time t = ω_nτ is introduced, where ω_n² = k_sp/m_eq, k_sp the average meshing stiffness of the external gear pair, m_eq = (m_scm_pim_cm)/(m_scm_cm + m_scm_pi + m_pim_cm) the equivalent mass. Take D₀ as the displacement nominal scale, then the dimensionless backlash is D₁ = D_si/D₀ and D₂ = D_ri/D₀, and the dimensionless displacement is x_si = X_si/D₀ and x_ri = X_ri/D₀. By introducing multiple sub-functions, furthermore, the dimensionless normalized analytical model of PGTs with internal and external gear pairs considering multi-state mesh is obtained by Eq. (18).

$$ \left\{ {\begin{array}{*{20}l} {\ddot{x}_{{{\text{s}}i}} + \sum\limits_{i = 1}^{N} {o_{{{\text{s}}i}} h_{{{\text{s}}i}} (t)F_{{{\text{ns}}i}} (t)} + \sum\limits_{i = 1}^{N} {o_{{{\text{c}}i}} h_{{{\text{r}}i}} (t)F_{{{\text{nr}}i}} (t)} + o_{{{\text{p}}i}} h_{{{\text{ps}}i}} (t)F_{{{\text{ns}}i}} (t) - o_{{{\text{p}}i}} h_{{{\text{pr}}i}} (t)F_{{{\text{nr}}i}} (t)} \hfill \\ {\quad = F_{1} - \varepsilon_{1} \omega^{2} \cos (\omega t)} \hfill \\ {\ddot{x}_{{{\text{r}}i}} - o_{{{\text{p}}i}} h_{{{\text{ps}}i}} (t)F_{{{\text{ns}}i}} (t) + o_{{{\text{p}}i}} h_{{{\text{pr}}i}} (t)F_{{{\text{nr}}i}} (t) + \sum\limits_{i = 1}^{N} {o_{{{\text{c}}i}} h_{{{\text{2s}}i}} (t)F_{{{\text{ns}}i}} (t)} + \sum\limits_{i = 1}^{N} {o_{{{\text{c}}i}} h_{{{\text{r}}i}} (t)F_{{{\text{nr}}i}} (t)} } \hfill \\ {\quad = F_{2} - \varepsilon_{2} \omega^{2} \cos (\omega t)} \hfill \\ \end{array} } \right. $$

(18)

where $h_{{{\text{s}}i}} (t)$, $h_{{{\text{r}}i}} (t)$, $h_{{{\text{ps}}i}} (t)$, $h_{{{\text{pr}}i}} (t)$, and $h_{{{\text{2s}}i}} (t)$ are the engaging state functions to characterize and identify double-tooth meshing behavior, $nT_{0} < t \le nT_{0} \left( {\varepsilon_{s} - 1} \right)$, and single-tooth meshing behavior, $T_{0} \left( {\varepsilon_{s} - 1} \right) < t \le \left( {n - 1} \right)T$, and can be written as Eqs. (19)–(23).

$$ h_{{{\text{s}}i}} (t) = \left\{ {\begin{array}{*{20}l} {1 + \lambda_{{{\text{s1}}i}} (t)\mu_{{{\text{s1}}i}} (t)L_{{{\text{s1}}i}} (t)g_{{{\text{s1}}i}} (t) + \lambda_{{{\text{s2}}i}} (t)\mu_{{{\text{s2}}i}} (t)L_{{{\text{s2}}i}} (t)g_{{{\text{s2}}i}} (t),} \hfill & {nT_{0} < t \le nT_{0} \left( {\varepsilon_{s} - 1} \right)} \hfill \\ {1 + \lambda_{{{\text{s2}}i}} (t)\mu_{{{\text{s2}}i}} (t)g_{{{\text{s2}}i}} (t),} \hfill & {T_{0} \left( {\varepsilon_{s} - 1} \right) < t \le \left( {n - 1} \right)T_{0} } \hfill \\ \end{array} } \right. $$

(19)

$$ h_{{{\text{r}}i}} (t) = \left\{ {\begin{array}{*{20}l} {1 + \lambda_{{{\text{r1}}i}} (t)\mu_{{{\text{r1}}i}} (t)L_{{{\text{r1}}i}} (t)g_{{{\text{r1}}i}} (t) + \lambda_{{{\text{r2}}i}} (t)\mu_{{{\text{r2}}i}} (t)L_{{{\text{r2}}i}} (t)g_{{{\text{r2}}i}} (t),} \hfill & {nT_{0} < t \le nT_{0} \left( {\varepsilon_{s} - 1} \right)} \hfill \\ {1 + \lambda_{{{\text{r2}}i}} (t)\mu_{{{\text{r2}}i}} (t)g_{{{\text{r2}}i}} (t),} \hfill & {T_{0} \left( {\varepsilon_{s} - 1} \right) < t \le \left( {n - 1} \right)T_{0} } \hfill \\ \end{array} } \right. $$

(20)

$$ h_{{{\text{ps}}i}} (t) = \left\{ {\begin{array}{*{20}l} {1 + \lambda_{{{\text{s1}}i}} (t)\mu_{{{\text{s1}}i}} (t)L_{{{\text{s1}}i}} (t)g_{{{\text{ps1}}i}} (t) + \lambda_{{{\text{s2}}i}} (t)\mu_{{{\text{s2}}i}} (t)L_{{{\text{s2}}i}} (t)g_{{{\text{ps2}}i}} (t),} \hfill & {nT_{0} < t \le nT_{0} \left( {\varepsilon_{s} - 1} \right)} \hfill \\ {1 + \lambda_{{{\text{s2}}i}} (t)\mu_{{{\text{s2}}i}} (t)g_{{{\text{ps2}}i}} (t),} \hfill & {T_{0} \left( {\varepsilon_{s} - 1} \right) < t \le \left( {n - 1} \right)T_{0} } \hfill \\ \end{array} } \right. $$

(21)

$$ h_{{{\text{pr}}i}} (t) = \left\{ {\begin{array}{*{20}l} {1 + \lambda_{{{\text{r1}}i}} (t)\mu_{{{\text{r1}}i}} (t)L_{{{\text{r1}}i}} (t)g_{{{\text{pr1}}i}} (t) + \lambda_{{{\text{r2}}i}} (t)\mu_{{{\text{r2}}i}} (t)L_{{{\text{r2}}i}} (t)g_{{{\text{pr2}}i}} (t),} \hfill & {nT_{0} < t \le nT_{0} \left( {\varepsilon_{s} - 1} \right)} \hfill \\ {1 + \lambda_{{{\text{r2}}i}} (t)\mu_{{{\text{r2}}i}} (t)g_{{{\text{pr2}}i}} (t),} \hfill & {T_{0} \left( {\varepsilon_{s} - 1} \right) < t \le \left( {n - 1} \right)T_{0} } \hfill \\ \end{array} } \right. $$

(22)

$$ h_{{{\text{2s}}i}} (t) = \left\{ {\begin{array}{*{20}l} {1 + \lambda_{{{\text{s1}}i}} (t)\mu_{{{\text{s1}}i}} (t)L_{{{\text{s1}}i}} (t)g_{{{\text{1s}}i}} (t) + \lambda_{{{\text{s2}}i}} (t)\mu_{{{\text{s2}}i}} (t)L_{{{\text{s2}}i}} (t)g_{{{\text{2s}}i}} (t),} \hfill & {nT_{0} < t \le nT_{0} \left( {\varepsilon_{s} - 1} \right)} \hfill \\ {1 + \lambda_{{{\text{s2}}i}} (t)\mu_{{{\text{s2}}i}} (t)g_{{{\text{2s}}i}} (t),} \hfill & {T_{0} \left( {\varepsilon_{s} - 1} \right) < t \le \left( {n - 1} \right)T_{0} } \hfill \\ \end{array} } \right. $$

(23)

In Eq. (18), $F_{nsi} (t)$ and $F_{nri} (t)$ denote the meshing force functions of the external and internal gear pairs, respectively, which are used to characterize the drive-side engagement, gear disengagement and back-side contact behaviors of PGTs, and can be expressed as Eqs. (24) and (25).

$$ F_{nsi} (t) = \left\{ {\begin{array}{*{20}l} {k_{{{\text{s}}i}} (t)\left[ {x_{{{\text{s}}i}} - D_{1} } \right] + \xi_{{{\text{s}}i}} \dot{x}_{{{\text{s}}i}} } \hfill & {\left( {x_{{{\text{s}}i}} \ge D_{1} } \right)} \hfill \\ 0 \hfill & {\left( {|x_{{{\text{s}}i}} | < D_{1} } \right)} \hfill \\ {k_{{{\text{s}}i}} (t)\left[ {x_{{{\text{s}}i}} + D_{1} } \right] + \xi_{{{\text{s}}i}} \dot{x}_{{{\text{s}}i}} } \hfill & {\left( {x_{{{\text{s}}i}} \le - D_{1} } \right)} \hfill \\ \end{array} } \right. $$

(24)

$$ F_{nri} (t) = \left\{ {\begin{array}{*{20}l} {k_{{{\text{r}}i}} (t)\left[ {x_{{{\text{r}}i}} - D_{2} } \right] + \xi_{{{\text{r}}i}} \dot{x}_{{{\text{r}}i}} } \hfill & {\left( {x_{{{\text{r}}i}} \ge D_{2} } \right)} \hfill \\ 0 \hfill & {\left( {|x_{{{\text{r}}i}} | < D_{2} } \right)} \hfill \\ {k_{{{\text{r}}i}} (t)\left[ {x_{{{\text{r}}i}} + D_{2} } \right] + \xi_{{{\text{r}}i}} \dot{x}_{{{\text{r}}i}} } \hfill & {\left( {x_{{{\text{r}}i}} \le - D_{2} } \right)} \hfill \\ \end{array} } \right. $$

(25)

The remainders of the dimensionless parameters are as follows: $k_{{{\text{s}}i}} (\tau ) = {{K_{{{\text{s}}i}} (\tau )} \mathord{\left/ {\vphantom {{K_{{{\text{s}}i}} (\tau )} {(m{}_{{{\text{eq}}}}\omega_{{\text{n}}}^{2} )}}} \right. \kern-0pt} {(m{}_{{{\text{eq}}}}\omega_{{\text{n}}}^{2} )}}$, $\xi_{{{\text{s}}i}} = {{c_{{{\text{s}}i}} } \mathord{\left/ {\vphantom {{c_{{{\text{s}}i}} } {(m{}_{{{\text{eq}}}}\omega_{{\text{n}}} )}}} \right. \kern-0pt} {(m{}_{{{\text{eq}}}}\omega_{{\text{n}}} )}}$, $k_{{{\text{r}}i}} (\tau ) = {{K_{{{\text{r}}i}} (\tau )} \mathord{\left/ {\vphantom {{K_{{{\text{r}}i}} (\tau )} {(m{}_{{{\text{eq}}}}\omega_{{\text{n}}}^{2} )}}} \right. \kern-0pt} {(m{}_{{{\text{eq}}}}\omega_{{\text{n}}}^{2} )}}$, $\xi_{{{\text{r}}i}} = {{c_{{{\text{r}}i}} } \mathord{\left/ {\vphantom {{c_{{{\text{r}}i}} } {(m{}_{{{\text{eq}}}}\omega_{{\text{n}}} )}}} \right. \kern-0pt} {(m{}_{{{\text{eq}}}}\omega_{{\text{n}}} )}}$,$o_{{{\text{s}}i}} = {{m{}_{{{\text{eq}}}}} \mathord{\left/ {\vphantom {{m{}_{{{\text{eq}}}}} {m{}_{{{\text{sc}}}}}}} \right. \kern-0pt} {m{}_{{{\text{sc}}}}}}$, $o_{{{\text{c}}i}} = {{m{}_{{{\text{eq}}}}} \mathord{\left/ {\vphantom {{m{}_{{{\text{eq}}}}} {m{}_{{{\text{cm}}}}}}} \right. \kern-0pt} {m{}_{{{\text{cm}}}}}}$, $o_{{{\text{p}}i}} = {{m{}_{{{\text{eq}}}}} \mathord{\left/ {\vphantom {{m{}_{{{\text{eq}}}}} {m_{{{\text{p}}i}} }}} \right. \kern-0pt} {m_{{{\text{p}}i}} }}$, $\varepsilon_{1} \omega^{2} \cos (\omega t) = {{\ddot{e}_{{{\text{sp}}i}} } \mathord{\left/ {\vphantom {{\ddot{e}_{{{\text{sp}}i}} } {D_{0} \omega_{{\text{n}}}^{2} }}} \right. \kern-0pt} {D_{0} \omega_{{\text{n}}}^{2} }}$, $\varepsilon_{2} \omega^{2} \cos (\omega t) = {{\ddot{e}_{{{\text{rp}}i}} } \mathord{\left/ {\vphantom {{\ddot{e}_{{{\text{rp}}i}} } {D_{0} \omega_{{\text{n}}}^{2} }}} \right. \kern-0pt} {D_{0} \omega_{{\text{n}}}^{2} }}$, $F_{1} = {{T_{1} } \mathord{\left/ {\vphantom {{T_{1} } {D_{0} \omega_{n}^{2} }}} \right. \kern-0pt} {D_{0} \omega_{n}^{2} }}$, $F_{2} = {{T_{2} } \mathord{\left/ {\vphantom {{T_{2} } {D_{0} \omega_{n}^{2} }}} \right. \kern-0pt} {D_{0} \omega_{n}^{2} }}$, $\omega = {{\omega_{{\text{h}}} } \mathord{\left/ {\vphantom {{\omega_{{\text{h}}} } {\omega_{{\text{n}}} }}} \right. \kern-0pt} {\omega_{{\text{n}}} }}$.

Therefore, a nonlinear dimensionless analytical model of PGTs with sun-planet and planet-ring gear pairs including time-varying meshing stiffness with temperature effect, backlash, dynamic transmission error, friction, time-varying load distribution, and single- and double-tooth mesh is obtained. The time-varying geometric characteristics of the meshing point along the line of action or the tooth profile, such as the meshing point position, friction moments, time-varying pressure angle, sliding speed, etc., are considered in the established model. This model can better analyze and evaluate the meshing vibration and nonlinear vibration mechanism of PGTs, and provide accurate analysis model for the dynamic performance prediction and control of such systems.

2.5 Calculation of time-varying meshing stiffness with temperature effect

The temperature rise in tooth contact gives rise to thermal deformation of the gear-tooth profile, which in turn affects the meshing stiffness of the gear system. The contribution of temperature effect to TVMS is characterized by temperature stiffness. Thus, the comprehensive TVMS incorporating Hertzian contact stiffness k_h(τ), bending stiffness k_b(τ), axial compressive stiffness k_a(τ), shearing stiffness k_s(τ), fillet-foundation stiffness k_f(τ), and temperature stiffness k_t(τ) can be obtained from Eq. (26).

$$ \frac{1}{{K_{si} (\tau )}}{ = }\frac{1}{{K_{ri} (\tau )}}{ = }\frac{1}{{k_{{\text{h}}} (\tau )}} + \frac{1}{{k_{{\text{b}}} (\tau )}} + \frac{1}{{k_{{\text{a}}} (\tau )}} + \frac{1}{{k_{{\text{s}}} (\tau )}} + \frac{1}{{k_{{\text{f}}} (\tau )}} + \frac{1}{{k_{{\text{t}}} (\tau )}} $$

(26)

where k_h(τ), k_b(τ), k_a(τ), k_s(τ), and k_f(τ) can be calculated via Eqs. (27)–(31) [71, 72].

$$ k_{\text{h}} = \frac{\pi EB}{{4\left( {1 - v^{2} } \right)}} $$

(27)

$$ \frac{1}{{k_{{\text{b}ji}} }} = \int_{{ - \sigma_{ji} }}^{{\theta_{{\text{b}j}} }} {\frac{{3\left\{ {\cos \sigma_{ji} \left[ {{{l_{1} } \mathord{\left/ {\vphantom {{l_{1} } {R_{{\text{bp}}} }}} \right. \kern-0pt} {R_{{\text{bp}}} }} + \cos \theta_{{\text{b}j}} - \cos \alpha + (\theta_{{\text{b}j}} - \alpha )sin\alpha } \right] - {{h_{1} \sin \sigma_{ji} } \mathord{\left/ {\vphantom {{h_{1} \sin \sigma_{ji} } {R_{{\text{bp}}} }}} \right. \kern-0pt} {R_{{\text{bp}}} }}} \right\}^{2} (\theta_{{\text{b}j}} - \alpha )\cos \alpha }}{{2EB\left[ {\sin \alpha + (\theta_{{\text{b}j}} - \alpha )\cos \alpha } \right]^{3} }}} {\text{ d}}\alpha $$

(28)

$$ \frac{1}{{k_{{\text{a}ji}} }} = \int_{{ - \sigma_{ji} }}^{{\theta_{{\text{b}j}} }} {\frac{{(\theta_{bj} - \alpha )\cos \alpha \sin^{2} \sigma_{ji} }}{{2EB\left[ {\sin \alpha + (\theta_{bj} - \alpha )\cos \alpha } \right]}}} {\text{ d}}\alpha $$

(29)

$$ \frac{1}{{k_{{\text{s}ji}} }} = \int_{{ - \sigma_{ji} }}^{{\theta_{{\text{b}j}} }} {\frac{{1.2(1 + \nu )(\theta_{{\text{b}j}} - \alpha )\cos \alpha \cos^{2} \sigma_{ji} }}{{EB\left[ {\sin \alpha + (\theta_{{\text{b}j}} - \alpha )\cos \alpha } \right]}}} \;{\text{d}}\alpha $$

(30)

$$ \frac{1}{{k_{f} }} = \frac{{\cos^{2} \alpha }}{EB}\left[ {L^{*} \left( {\frac{{u_{f} }}{{S_{f} }}} \right)^{2} + M^{*} \left( {\frac{{u_{f} }}{{S_{f} }}} \right) + P^{*} (1 + Q^{*} \tan^{2} \alpha )} \right] $$

(31)

In Eqs. (27)–(31), E, B, $v$ denote Young’s modulus, tooth width and Poisson’s ratio, respectively. $\theta_{{\text{b}j}} \;(j = p,\;g)$ is half of the tooth angle measured on the base circle of pinion $(j = p)$ and gear $(j = g)$. The detailed calculation of relevant parameters can be found in Refs. [71, 72].

According to the thermo-elastic theory, the temperature stiffness can be calculated by Eq. (32).

$$ k_{{{\text{t}}j}} (t){ = }\frac{{\Delta F_{n} }}{{\Delta \delta_{{\text{t}}} (t)}} $$

(32)

Herein, $\Delta F_{n}$ and $\Delta \delta_{{\text{t}}} (t)$ represent the dynamic contact force increment and thermal deformation increment at the meshing point, respectively. The thermal deformation, δ_tj, of the j-th gear tooth can be expressed as Eq. (33).

$$ \delta_{{{\text{t}}j}} (t) = \left[ {\gamma \smallint_{0}^{{R_{j} (t)}} (T_{j} (r_{j} ) - T_{0} ){\text{d}}r_{j} - R_{j} (t)} \right]\sin (\alpha_{j} (t)) + \frac{1}{2}S_{j} (R_{j} )\left\{ {\gamma \left[ {T_{j} (R_{j} ) - T_{0} } \right] - 1} \right\}\cos (\alpha_{j} (t)) $$

(33)

where γ is the linear expansion coefficient of the gear material, T₀ the initial temperature, r_j the distance from any position to the gear center, T_j(R_j) and S_j(R_j) the temperature and tooth thickness at the meshing point R_j. α_j(t) is the time-varying pressure angle and can be got by Eq. (34).

$$ \alpha_{j} {(}t{\text{) = arccos(}}{{R_{bj} } \mathord{\left/ {\vphantom {{R_{bj} } {R_{j} {(}t{)}}}} \right. \kern-0pt} {R_{j} {(}t{)}}}{)} $$

(34)

where R_bj is the base circle radius of the j-th gear. R_j(t) is the distance from the meshing point to the gear center, and can be written as Eq. (35).

$$ \left\{ {\begin{array}{*{20}l} {R_{p} (t) = \sqrt {R_{{\text{bp}}}^{2} + [(R_{{\text{bp}}} + R_{{\text{bg}}} )tan\alpha - \sqrt {R_{{\text{ag}}}^{2} - R_{{\text{bg}}}^{2} } + R_{{\text{bp}}} \omega_{\text{p}} t]^{2} } } \hfill \\ {R_{g} (t) = \sqrt {R_{{\text{bg}}}^{2} + [\sqrt {R_{{\text{ag}}}^{2} - R_{{\text{bg}}}^{2} } - R_{{\text{bp}}} \omega_{\text{p}} t]^{2} } } \hfill \\ \end{array} } \right. $$

(35)

It is assumed that the gear temperature has a gradient distribution in the radial direction and an isothermal distribution in the circumferential direction. The temperature field distribution of the gear in the radial direction, T_j(r_j), can be obtained by Eq. (36) [52].

$$ T_{j} (r_{j} ) = T_{{{\text{s}}j}} (R_{{{\varvec{s}}j}} ) + \left[ {T_{{{\text{a}}j}} (R_{{{\varvec{a}}j}} ) - T_{{{\text{s}}j}} (R_{{{\varvec{s}}j}} )} \right]\frac{{\ln r_{j} - \ln R_{{{\varvec{s}}j}} }}{{\ln R_{{{\varvec{a}}j}} - \ln R_{{{\varvec{s}}j}} }}\;\;\;(j = p,g) $$

(36)

where T_sj(R_sj) is the temperature on the gear shaft, and T_aj(R_aj) is the temperature of the outer circumference of the gear.

3 Analysis methods

Backlash can induce gear separation or back-side tooth contact, leading to multi-state meshing behavior that can be effectively identified by constructing three Poincaré maps, as seen from Sect. 3.1. In addition, tooth separation or back-side tooth contact causes gear shock or bumping in the planetary gear train, resulting in a dynamic instability of the system. A method for calculating the dynamic instability rate of geared systems is proposed in the time domain based on the multi-state engagement as shown in Sect. 3.2.

3.1 Identification method of multi-state engaging behavior

Without losing generality, the differential equations of PGTs can be expressed as follows:

$$ {\dot{\mathbf{x}}} = f({\mathbf{x}},t). $$

(37)

where ${\mathbf{x}} = (x_{s1} ,x_{s2} ,x_{s3} ,x_{r1} ,x_{r2} ,x_{r3} ,)$ is a 6-dimensional state variable of PGTs, and t is a time variable. Define a 6-dimensional Poincaré mapping section Π_t in the 6 + 1-dimensional phase space ${\mathbf{R}}^{6} \times {\mathbf{R}}$, as shown in Eq. (38).

$$ \Pi_{{\text{t}}} = \left\{ {\left( {{\mathbf{x}},t} \right)|\bmod \left( {t,T} \right) = 0} \right\} $$

(38)

The system Poincaré mapping equation on the section Π_t is as Eq. (39), and the mapping schematic in Π_t is shown in Fig. 8a, where Γ represents the system phase trajectory.

$$ \Pi_{{\text{t}}} \to \Pi_{{\text{t}}} :\;{\mathbf{x}}^{n + p} = {\mathbf{x}}^{n} + \int_{0}^{pT} {f({\mathbf{x}},t)} {\text{d}} t,\left( {{\mathbf{x}}^{n + p} ,{\mathbf{x}}^{n} \in \Pi_{{\text{t}}} } \right) $$

(39)

where n = (1,2,3,…) is the number of iterations in Π_t and p is a positive integer to determine the type of system motion.

Fig. 8

a The mapping schematic in Π_t; b The mapping schematics in Π_b and Π_s

Gear separation and back-side tooth engagement can be effectively identified by defining two types of Poincaré mapping sections Π_s and Π_b, as written in Eq. (40).

$$ \begin{aligned} \Pi_{{\text{s}}} & = \left\{ {\left( {{\mathbf{x}},t} \right)|\left( {{\mathbf{x}},t} \right) \in {\mathbf{R}}^{6} \times {\mathbf{R}},x_{s1} = D_{1} } \right\}, \\ \Pi_{{\text{b}}} & = \left\{ {\left( {{\mathbf{x}},t} \right)|\left( {{\mathbf{x}},t} \right) \in {\mathbf{R}}^{6} \times {\mathbf{R}},x_{s1} = - D_{1} } \right\} \\ \end{aligned} $$

(40)

If Eq. (41) holds, it means that the phase trajectory of the system does not cross sections Π_s and Π_b. The system only exhibits a drive-side tooth meshing state, without gear separation or back-side tooth mesh occurring. If Eq. (41) does not hold, it indicates that the system phase trajectory may cross sections Π_s and Π_b, and that tooth separation or back-side tooth meshing may occur during gear operation, as shown in Fig. 8b.

$$ \Pi_{{\text{s}}} \cap \Gamma \ne \emptyset ,\;\;\Pi_{{\text{b}}} \cap \Gamma \ne \emptyset $$

(41)

where the symbol Γ denotes the phase trajectory and $\emptyset$ denotes the empty set.

It can be seen that the motion type of the system can be identified based on the Poincaré mapping Eq. (39), and the multi-state meshing behavior can be identified according to Eq. (41).

3.2 A calculation method of dynamic instability rate (DIR)

Backlash divides the phase plane, x_s1-$\dot{X}$_s1, of the system into three regions: the drive-side meshing region (x_s1 > D₁), the gear separation region (|x_s1|< D₁), and the back-side meshing region (x_s1 < −D₁), as seen from Fig. 9. The possible forms of the trajectory of the system in the phase plane x_s1-$\dot{X}$_s1 consist of three, such as Γ1, Γ2 and Γ3. Γ1 indicates that the system only drive-side tooth engages, Γ2 the drive-side tooth mesh and gear separation (disengagement), and Γ3 the drive-side tooth mesh, gear separation and back-side engagement. Assuming counterclockwise as the positive direction, G_2in and G_2out are the let in and let out points of the trajectory Γ2 through the cross section Π_s. G_3in and G_3out are the let in and let out points of Γ3 through Π_s. B_3in and B_3out are the let in and let out points of Γ3 through Π_b. Γ2 and Γ3 characterize the dynamic instability condition of the system, which is prone to poor dynamic behavior or transmission failure. In order to better predict the transmission quality of the geared system, therefore, a method for calculating the dynamic instability rate is proposed. The dynamic instability rate, DIR, in the time domain during gear operation can be calculated by Eq. (42).

$$ {\text{DIR}} = \frac{{t_{s} + t_{b} }}{{t_{\text{d}} + t_{s} + t_{b} }} $$

(42)

where t_d indicates the duration of dive-side engagement, and t_s is the duration of gear separation, and t_b is the duration of back-side engagement. T_d and t_b can be obtained by Eq. (43). T_s can be calculated by Eq. (44) for Γ2 and Γ3, respectively.

$$ t_{\text{d}} = \int_{{{\text{G}}_{{{\text{2out}}}} }}^{{{\text{G}}_{{{\text{2in}}}} }} {{\text{d}} t} = \int_{{{\text{G}}_{{{\text{3out}}}} }}^{{{\text{G}}_{{{\text{3in}}}} }} {{\text{d}} t} ,\;\;t_{b} = \int_{{{\text{G}}_{{{\text{3in}}}} }}^{{{\text{G}}_{{{\text{3out}}}} }} {{\text{d}} t} $$

(43)

$$ t_{s} = \int_{{{\text{G}}_{{{\text{2in}}}} }}^{{{\text{G}}_{{{\text{2out}}}} }} {{\text{d}} t} ,\;\;t_{s} = \int_{{{\text{G}}_{{{\text{3in}}}} }}^{{{\text{B}}_{{{\text{3in}}}} }} {{\text{d}} t} + \int_{{B_{{{\text{3out}}}} }}^{{{\text{G}}_{{{\text{3out}}}} }} {{\text{d}} t} $$

(44)

Fig. 9

Schematic diagram of system engagement reliability calculation

The dynamic stability rate, DSR, can be obtained by Eq. (45).

$$ {\text{DSR}} = 1 - {\text{DIR}} = \frac{{t_{{\text{d}}} }}{{t_{\text{d}} + t_{s} + t_{b} }} $$

(45)

The back-side meshing dynamic instability rate, BDIR, can be calculated by Eq. (46) to obtain the contribution or effect of back-side engagement.

$$ {\text{BDIR}} = \frac{{t_{b} }}{{t_{\text{d}} + t_{s} + t_{b} }} $$

(46)

4 Results and discussion

Gear separation and back-side tooth engagement break the dynamic stability meshing conditions. The type of motion and bifurcation have also a big impact on DIR. In addition, the coexisting dynamic response greatly impacts DIR due to their different topologies. In this section, the immanence between DIR and multi-state engagement (MSE) is explored as the transmission error amplitude ε and loading factor F are used as control parameters, respectively. The impact of coexisting response of the system on global dynamic instability has also been studied as the meshing frequency ω changes with parameter-state space synergy. A set of parameters for the studied PGTs is shown in Table 1.

Table 1 A set of parameters for the studied planetary gear train

4.1 The immanence between multi-state mesh and dynamic instability rate

4.1.1 The effect of ε

Let ε = ε₁ = ε₂ be the parameter variable, and the remaining parameters are shown in Table 1. Based on the methods proposed in Sects. 3.1 and 3.2, the evolution laws of the multi-state engagement (MSE) and the dynamic instability of the system is shown in Fig. 10 as the parameter ε increases. Figure 10a shows the bifurcation of the dynamic behavior in the section Π_t, characterizing the evolution of the motion type of the system. Figure 10b illustrates the tooth separation (in sea green) and back-side tooth meshing (in orange) characteristics. In Fig. 10c, DSR denotes drive-side tooth engagement, and DIR denotes unhealthy engagement conditions (gear separation and back-side tooth mesh). BDIR is the back-side mesh, which gives the effect or contribute of the back-side engagement.

Fig. 10

Evolution of dynamic instability and multi-state engagement (MSE) with the increase of transmission error amplitude ε

From Fig. 10, when ε is very small (on the left side of point A), the system exhibits a period-1 response without gear disengagement and back-side meshing behavior. The phase trajectory and Poincaré mapping in Π_t for the period-1 response are shown in Fig. 11a, where the red symbol × denotes Poincaré mapping. Increasing in ε, gear separation occurs near point A due to the expansion of the phase trajectory of period-1 response, as in Fig. 11b. The portrait traverses section Π_s and the dynamic stability rate, DSR, is destroyed. DSR starts to decrease and the dynamic instability rate, DIR, increases, as shown in Fig. 10c. Near point B, the period-1 response transitions to a period-2 response by period-doubling bifurcation and gear separation persists. DSR forms local minima at B and increases due to period-doubling bifurcation. A grazing bifurcation is observed near point C for period-2 response and the number of gear separation shocks decreases, as seen from Fig. 11c. In contrast, DSR forms a local maximum at C point and starts to decrease because of grazing bifurcation, as shown in Fig. 10c. Compared to DSR, DIR undergoes the opposite change around points B and C.

Fig. 11

Phase trajectories and Poincaré mappings of the system in the phase plane x_s1-$\dot{X}$_s1 for different values of ε. a ε = 0.005; b ε = 0.02; c ε = 0.035; d ε = 0.06; e ε = 0.16; f ε = 0.24; g ε = 0.287; h ε = 0.31; i ε = 0.37; j ε = 0.39; k ε = 0.414; l ε = 0.42; m ε = 0.435; n ε = 0.465; o ε = 0.495

Period-2 response transitions to a chaotic response near point D, where gear separation and back-side meshing are observed. DSR suddenly drops sharply at D and DIR dominates during gear operation, as in Fig. 10c. BDIR is relatively small, and gear separation is the main cause of DIR. Figure 11d gives the phase trajectory of chaotic response, and the trajectory is mainly distributed in the region of gear separation (−D₁ < x_s1 < D₁), and DSR is low. The chaotic response degenerates to a period-4 response near point E, and gear separation and back-side tooth meshing persist, as in Fig. 11e. DSR hardly changed much for the period-4 response. Subsequently, the period-4 response enters chaos again near the point F as in Fig. 11f, and the DSR has increased. DIR decreases and BDIR increases for the chaotic response. The chaotic response degenerates to a period-2 response at point G and the phase trajectory is as in Fig. 11g. DSR increases slightly and remains smooth with the increases of ε. Hopf bifurcation is observed near the point H, and the period-2 response transitions to a quasi-periodic response with two limit cycles in the Poincaré section Π_t, as shown in yellow Fig. 11h. However, DSR and DIR do not change significantly near the Hopf bifurcation point. The quasi-periodic response transitions to a period-2 response at I and DSR increases abruptly, followed by the period-2 response converts to a period-4 response at J, and enters chaos via a short period-doubling bifurcation, as in Fig. 10 and 11i–k.

The chaotic response degenerates to a period-6 response at point K and DSR suddenly decreases due to the expansion of the phase trajectory, as shown in Fig. 11l. The period-6 response changes to a period-12 response via a period-doubling bifurcation, as in Fig. 11m, and then enters chaos near the point L. Subsequently, the chaotic response degenerates to a period-8 response with the phase trajectory and the Poincaré mapping as in Fig. 11n. The period-8 response degenerates to a period-4 response near the point M, and its phase trajectory and Poincaré mapping are shown in Fig. 11o. The variation of DSR is relatively stable for larger ε.

Therefore, the transmission error amplitude ε greatly governs the multi-state engagement (MSE) behavior and dynamic instability properties of the system. Gear separation and back-side meshing occurs gradually and MSE becomes complex increasing in ε. The occurrence of MSE reduces the DSR of the system. For small ε, DSR or DIR is severely affected by bifurcation and chaotic response of the system. Two interesting phenomena are obtained: (1) period-doubling bifurcation improves DSR of the system and causes it to form local minima, as in point B in Fig. 10c; (2) grazing bifurcation reduces DSR and causes it to form local maxima, as in point C in Fig. 10c. For larger ε or back-side tooth mesh, the period-doubling and Hopf bifurcations have a small effect on DSR, but DSR is greatly influenced by chaotic response. In addition, DSR is closely related to the topology of the system dynamics response, the larger the phase trajectory the smaller the DSR.

4.1.2 The effect of F

As one of the key parameters, the load factor F has a significant influence on the multi-state mesh and dynamic instability of the system. Take ω = 1.0 and ε = 0.21, other parameters remain unchanged. The evolution of MSE and DSR of PGTs with decreasing F is depicted in Fig. 12. When F is large (to the right of point A), the system only exhibits a complete drive-side meshing state, without multi-state meshing. The system has the highest reliability of healthy meshing (DSR = 1.0), and operates in a healthy and safe state. The vibration amplitude is very small, as shown in Fig. 13a for the phase portrait and Poincaré mapping of the period-1 response. As F decreases, the phase trajectory continues to expand and the vibration amplitude increases. The trajectory passes through section Π_s at point A and gear tooth detachment occurs, as shown in Fig. 13b. DSR begins to decrease and healthy meshing state is disrupted. At point B the system undergoes a period jump, and the type of dynamic response does not change before and after the jump, but the topology of the phase trajectory changes and increases, as shown in Fig. 13c. DSR suddenly plummeted near the B point and the gear separation ratio is expanded again. Local maximum value of DSR appears near point B1, followed by a decrease in DSR and increase in DIR.

Fig. 12

Evolution of dynamic instability and MSE decreasing in load factor F

Fig. 13

Phase trajectories and Poincaré mappings of the system in the phase plane x_s1–$\dot{X}$_s1 for different values of F. a F = 0.28; b F = 0.245; c F = 0.22; d F = 0.16; e F = 0.025; f F = 0.0465; g F = 0.033; h F = 0.03

As F decreases to point C, the period-1 response transitions to a chaotic response and back-side tooth engagement occurs. DSR decreases greatly and DIR and BDIR increase suddenly, aggravating drive-side and back-side tooth impact due to chaos. Subsequently, the system exhibits a chaotic response with MES in the BC region, corresponding to a smaller DSR. The chaotic response degenerates to a periodic response at point D, and then transitions to a period-2 response after bifurcation and a short chaos. At small F conditions, although the system exhibits a stable periodic response, multi-state engagement persists and DSR decreases again due to elevated BDIR and DIR.

Consequently, as the load factor F decreases, the system gradually develops gear separation and back-side tooth meshing, exacerbating the complexity of multi-state engagement (MSE). Also, the dynamic stability rate (DSR) is decreasing, and the dynamic instability rate (DIR) and back-side meshing rate (BDIR) are increasing. Phase trajectory expansion causes gear separation and reduces DSR, and the chaotic response leads to back-side tooth meshing and greatly reduces DSR. The effect of MSE on DSR is large and the effect of dynamic response type is small under light load conditions. Under heavy load conditions, however, the impact of dynamic response type on DSR is greater than that of multi-state engagement behavior.

4.2 Global dynamic instability properties under the parameter-state space synergy

The dynamic characteristics of nonlinear systems are collectively dominated by parameters and initial values. The disturbance of parameters may induce bifurcation or chaos in the system’s dynamic response, and the disturbance of initial conditions may lead to coexisting behavior of the dynamic response (multi-stability). Taking ε₁ = ε₂ = 0.14 and F₁ = F₂ = 0.1, the remaining parameters are shown in Table 1, and let meshing frequency ω be a parameter variable to form a one-dimensional bounded parameter space, $\Phi = \{ \omega |\omega \in (0.01,5.0)\}$. Considering the impact of the initial perturbation of the relative displacement of the sun-planetary engaging gear pair on the nonlinear dynamic characteristics of PGTs, and set $\Omega = \{ x_{si} ,\dot{x}_{si} ,x_{ri} ,\dot{x}_{ri} |x_{si} \in ( - 3.0,3.0),\dot{x}_{si} \in ( - 3.0,3.0),x_{ri} = \dot{x}_{ri} = 0.0\}$ as a bounded state space. Thus, the bifurcation and evolution of the multi-stable response under the synergistic effect of parameter space Φ and state space Ω are illustrated in Fig. 14a with decreasing in ω, and the corresponding DSR are shown in Fig. 14b.

Fig. 14

The evolution law of multi-stability response and HMR with decreasing in ω under the synergistic effect of parameter-state space: a Multi-stability response; b DSR

The diversity of bifurcation branches is clearly observed under the synergistic effect of parameter space Φ and state space Ω with the decrease of ω, as shown in Fig. 14a, and there are six bifurcation branches. For example, the period-1 response (p1) transitions to a period-5 response (p5) from a partial initial value at point G1, and continues within the remaining initial value range Ω, forming a bifurcation branch (Branch #1). p5 undergoes bifurcation at points G2 and G3 before entering chaos, and then returns to p1 at point G4. At point B1, p1 transfers to a period-3 response (p3) at some initial values and persists at another initial value, forming a new bifurcation branch (Branch #2). p3 enters chaos at point B4 after bifurcation at points B2 and B3, and then degenerates into a period-2 response (q2) at point B5. p3 shifts to a period-6 response (p6) at point Q1 under some initial values and sustains under another initial values, forming a bifurcation branch (Branch #3). p6 transitions to chaos (c) at point Q2 and then degenerates into period-4 response (q4) at point Q3. q4 transfers to p3 at point Q4. The chaotic response degenerates into a period-4 response (p4) at point P1 within some initial values and persists for the remaining initial values, forming a bifurcation branch (Branch #4). p4 shifts to chaos at point P2. Correspondingly, a new branch (Branch #5) is obtained at point R1, which is generated by chaos under partial initial values. q2 degenerates into a stable period-1 response (q1) at point R2 after a very momentary chaos. At point S1, a new period-2 response (r2) is observed, which is generated by q2, forming a new branch (Branch #6).

As can be seen, the overlap of different bifurcation branches within a certain range of ω leads to the coexistence of multiple dynamic responses. The coexistence of bifurcation and dynamic response is also been obtained. Due to the differences in trajectory topology, vibration amplitude, and stability of coexisting responses, their corresponding DSR is different. For instance, the DSR of q1 is significantly greater than that of q5 for Branch #1 (between G1 and G3). As ω is small (to the left of the S1 point), the system exhibits q1 and healthy engagement behavior. DSR = 1.0 is observed for q1. However, the DSR of q1 is greatly influenced by r2 taking the initial perturbation into account between S1 and S2. Thus, when the parameters of the system are fixed, the initial conditions can be adjusted to ensure that the system operates on the expected motion trajectory. Bifurcation behavior can be purposefully avoided by revising the initial conditions. Identically, when the initial value changes within a certain range, the desired dynamic response can be obtained by regulating the parameters. The bifurcation and evolution mechanisms of multi-stable responses under the synergistic effect of parameter space Φ and state space Ω are analyzed in detail in Fig. 15.

Fig. 15

Schematic of the evolution mechanism of multi-stability response decreasing in ω under the synergistic effect of parameter-state space (corresponding to Fig. 14)

In order to have a well understand of the generation and transition mechanisms of multi-stable response, it is necessary to define some symbols and their terms. In Fig. 15, the symbol circle represents the dynamic response (periodic or chaotic response). Yellow square denotes the complete bifurcation, which means that the system dynamic response completely transitions to another dynamic response with a different phase trajectory topology at all initial values. Red square means the incomplete bifurcation, which indicates that the dynamic response transitions to a new dynamic response at some initial values, while remaining unchanged at another initial values. White square stands for the no bifurcation, which implies that the dynamic response continues at all initial values without bifurcation. → represents the direction in which parameter ω decreases. It is easy to observe that there are six branches (such as Branch #1, Branch #2, Branch #3, Branch #4, Branch #5, and Branch #6), six incomplete bifurcation points (such as G1, B1, Q1, P1, R1, and S1), sixteen complete bifurcation points, and thirteen different dynamic responses in Fig. 15. The bifurcation and transition laws of multi-stable responses under the synergistic effect of parameter space Φ and state space Ω are extremely luxuriant and sophisticated.

Combining Figs. 14 and 15, an incomplete bifurcation G1 is observed for p1 with the decrease of ω, which generates a bifurcation branch, Branch #1. It implies that p1 transmigrates to p5 at a partial initial value of Ω and persists at the remaining initial values. Thus, a multi-stable response containing p1 and p5 is obtained via incomplete bifurcation G1. The phase trajectories of p1 and p5 are shown in Fig. 16a, where the symbols × and + represent Poincaré mappings. The vibration of p5 is stronger than that of p1. With decreasing in ω, p1 undergoes incomplete bifurcation again at point B1 and yields p3 and p1. A new bifurcation branch, Branch #2, is obtained. p5 continues without bifurcation at point B1. As a result, the coexistence of p1, p3, and p5 is observed after B1, and the phase portraits is shown in Fig. 16b, where · denotes Poincaré mappings. It is obvious that the vibration of p3 is greater than that of p5. p5 goes through a complete bifurcation at G2 and transitions to q5 under all its initial values. p1 and p3 go on after passing G2. Thereby, the coexisting behavior of p1, p3, and q5 is obtained after G2, as shown in Fig. 16c for the phase portraits where the topology of q5 is different from p5. At G3, p1 and p3 persist and q5 transfers to chaos (c), thus the coexisting response including p1, p3, and chaos is found, as shown in Fig. 16d for the trajectories. Although the chaos is unstable, its vibration amplitude is still less than that of p3. At G4, p1 and p3 continue and the chaos degenerates to p1, which means that Branch #1 ends and only p1 and p3 coexist after G4. p1 shifts to p2 by the complete bifurcation T1 and then enters chaos via the complete bifurcation T2. p3 continues through T1 and T2. The coexistence of p2 and p3 between T1 and T2, and the coexistence of p3 and chaos between T2 and T3 are discovered, as shown in Fig. 16e, f for the phase portraits. The chaos degenerates into p3 through complete bifurcation at T3 and there is only p3 in Ω.

Fig. 16

Topology of phase trajectories with coexisting responses at different ω values: a ω = 4.4; b ω = 4.14; c ω = 4.08; d ω = 4.02; e ω = 3.65; f ω = 3.5; g ω = 3.2; h ω = 2.9; i ω = 2.74; j ω = 2.64; k ω = 2.4; l ω = 2.25; m ω = 2.05; n ω = 1.4; o ω = 0.82

Further decreasing in ω, an incomplete bifurcation for p3 at Q1 is observed, which gives rise to a bifurcation branch, Branch #3. The coexistence of p3 and p6 formed by p3 is obtained, and the phase portraits are plotted in Fig. 16g. p6 enters chaos by complete bifurcation at Q2, and no bifurcation for p3. Thus, the coexistence of p3 and chaos is received, as shown in Fig. 16h for the portraits. The vibration of chaos is stronger than the vibration of p1. A new bifurcation branch, Branch #4, is acquired due to an incomplete bifurcation at P1, where the chaos degenerates into p4 under partial initial values and sustains under the remaining initial values. There is no bifurcation for p3 after passing through P1. The coexistence of p3, p4, and chaos is gained, as plotted in Fig. 16i for the portraits. There is no bifurcation for p4 in Branch #4 after passing through a series of points, such as Q3, Q4, B2, B3, and B4. The chaos transfers to q4 via complete bifurcation at Q3 and then shifts to p3 by complete bifurcation at Q4. The multi-stable response including p3, p4 and q4 is got between Q3 and Q4 and shown in Fig. 16j. The coexistence of p3 and p4 after Q4 is obtained. Subsequently, p3 converts to q3 at B2 via complete bifurcation, and q3 shifts to q6 at B3 by complete bifurcation. q6 enters chaos at B4 by complete bifurcation. The multi-stable responses with p4 and q3, and with p4 and q6 are attained, and with p4 and chaos are observed, as plotted respectively in Fig. 16k–m. p4 transfers to chaos at P2 by complete bifurcation and only chaos without coexisting response.

An incomplete bifurcation occurs in response to chaos at point R1, and a bifurcation branch, Branch #5, is obtained. The chaos transfers to q2 after R1 under partial initial values and then the coexistence of q2 and chaos is observed, as shown in Fig. 16n for the phase portraits. The chaos degenerates into q2 at B5 via the complete bifurcation. q2 transitions to an extremely short chaos at point R2, and then undergoes an incomplete bifurcation at S1 and shifts to q1 and r2, forming a bifurcation branch, Branch #6. The trajectories of q1 and r2 are plotted in Fig. 16o, where the vibration amplitude of r2 is much larger than q1 and DSR is relatively small. Subsequently, r2 shifts to q1 at point S2 by the complete bifurcation and the system only exhibits a q1 response for the small ω.

The generation and evolution of the coexistence response is controlled synergistically by the parameter space and state space. The distribution and evolution of different types of coexisting responses in the one-dimensional parameter space are clearly illustrated in Figs. 14 and 15. Also, the phase trajectory topology of the coexistence response is given in Fig. 16a–o. Nevertheless, it is very interesting to effectively reveal the initial value domain or basin of attraction of the coexistence response in the state space. Figure 17 plots the basin of attraction of various types of coexistence responses in state space Ω at different values of ω. Different colors indicate the initial value domain or basin of attraction of different dynamic responses, and some symbols, such as × , + , •, represent the attractor. Figure 17a shows the basin of attraction of p1 in sea green and p5 in orange calculated for ω = 4.4, where + and × stand for the attractors of p1 and p5, respectively. The basin of attraction of p1 or p5 exhibits a sieve shaped distribution within Ω. It indicates that p1 or p5 have strong sensitivity to initial values, and slight perturbation of the initial value give rise to continuous switching behavior between p1 and p5. In this way, the global dynamical properties of p1 or p5 are unstable. The basin of attraction of p1, p3, and p5 is plotted in Fig. 17b, where • denotes the attractor of p3. The initial domain of p3 is continuous and in blue. Because of the transition of p5 to chaos, the attractive basin where p1, p3, and chaos coexist are shown in Fig. 17c. Compared to Fig. 17b, the initial domain of p3 is expanded and the global stability is enhanced. Figures 17d express the basins of attraction of p2 in sea green and p3 in blue, and Fig. 17e plots the basins of attraction of p3 in blue and chaos in sea green. The initial value domain area of p2 or chaos is greater than that of p3. The basins of attraction of p3 and p6 in pink is shown in Fig. 17f, where the initial area of p6 is greater than that of p3. The system behaves as p6 in most initial value domains. The sieve shaped attraction domain has been widely observed to respond to different coexisting responses, such as the coexistence of p3 in blue and chaos in pink, the coexistence of p3 in blue and p4 in red, the coexistence of p6 in blue and p4 in red, and the coexistence of q2 in magenta and chaos in blue, as shown in Figs. 17g–j. The continuous switching behavior between different types of dynamic responses under initial perturbation is obtained. Figure 17k shows the basins of attraction of q1 in magenta and r2 in green, where the initial domains is continuously distributed. The global dynamics of q1 and r2 are relatively stable within their respective initial domains.

Fig. 17

Basin of attraction of the coexistence response at different values of ω

Based on the above analysis and discussion, all the possible dynamic features of the system under the synergistic effect of parameter space and state space are fully revealed, and some potential dynamic behaviors (including bifurcation and dynamic response) that are easily hidden are completely discovered. Two different bifurcation phenomena have been found: incomplete bifurcation and complete bifurcation. Complete bifurcation leads to global instability of the system in the initial value domain Ω, while incomplete bifurcation results in local instability in Ω and yields coexistence of multiple responses. With changes in parameters and initial values, incomplete bifurcation generates new bifurcation branches, leading to the coexistence of multiple dynamic responses, as well as the coexistence of bifurcation and dynamic responses. With the collaboration of one-dimensional parameter space Φ and two-dimensional state space Ω, six incomplete bifurcations are observed, generating 6 bifurcation branches and inducing various two-stable and three-stable responses. By reasonably regulating the parameter, initial value and their matching relationship, the system dynamic behavior can be purposefully controlled, thus avoiding undesired dynamic response or bifurcation, improving the system transmission quality and reliability, and extending the service life.

5 Conclusions

Dynamic instability, such as gear disengagement, back-side tooth contact and poor dynamic behavior, not only reduce the transmission quality and stability of PGTs, but also accelerate gear damage and failure. In order to prevent early failure and prolong life of PGTs, multi-state engagement and dynamic stability rate (DSR) of PGTs is investigated in this work based on and nonlinear dynamics. A multi-state meshing nonlinear dynamics model of PGTs close to real engineering is developed considering the diversity of influencing factors. An effective identification method of multi-state engaging behavior and a calculation method of DSR are proposed. The intrinsic correlation between multi-state meshing behavior and DSR was analyzed. The mechanisms of generation and transition of multi-stability response or coexistence behavior under the synergistic effect of parameter-state space is studied. Some conclusions are as follows.

Firstly, multi-state engagements caused by backlash and non-integer contact ratio, such as single- and double-tooth meshes, drive-side and back-side tooth meshes, and gear separation, are considered in this work. A new nonlinear dynamic model of PGTs with internal and external meshing gear pairs containing multi-state engaging is established. A modified time-varying meshing stiffness model considering tooth profile thermal deformation due to temperature rise is derived. Some key parameters, such as backlash, transmission error, time-varying meshing stiffness with temperature effect, load factor, time-varying pressure angle, time-varying friction arm, time-varying meshing position and friction, are included in this model. The model contains multiple subfunctions that characterize the multi-state meshing, periodic switching behavior and non-smooth properties of PGTs.

Secondly, as the amplitude of transmission error increases or the load factor decreases, the unique drive-side meshing behavior gradually shifts to multi-state meshing behavior. DSR also progressively weakens with the complexity of multi-state meshing behavior. The occurrence of multi-state meshing behavior leads to dynamic instability or unhealthy meshing situations. Bifurcation, chaos, and phase trajectory topology greatly affect the DSR of PGTs. Period-double bifurcation improves dynamic stability and increases DSR, forming a local minimum, while grazing bifurcation weakens dynamic stability and decreases DSR, forming a local maximum. Expansion of phase trajectory topology reduces DSR.

Finally, some easily hidden dynamical behaviors are fully revealed under the synergy of parameter space and state space. Diversity of coexistence behavior is obtained, such as the coexistence of diversity types of dynamic responses, and the coexistence of dynamic responses and bifurcation. Two special bifurcation phenomena, complete and incomplete bifurcations, are discovered, which have not been reported in the existing literature due to the failure to consider the parameter-state space synergy effect. Complete bifurcation causes global instability in the initial value domain Ω, and incomplete bifurcation leads to local instability in Ω and yields coexistence of multiple responses. Incomplete bifurcation gives rise to new bifurcation branches, leading to the coexistence of multiple dynamic behaviors. The DSR of each response in the coexistence behavior differs due to different phase trajectory topologies. Therefore, the dynamic behavior of PGTs can be precisely controlled by reasonably regulating the parameters, initial values, and their matching relationships to avoid inferior dynamic behavior or multi-state meshing behavior, and improve the DSR. This study provides a good understanding of the healthy and unhealthy meshing conditions and therefore serve as a useful source of reference for engineering in designing and controlling such gear systems.