1 Introduction

At present, COVID-19 has become a pandemic, as it has spread worldwide. The main reason for the difficulty controlling the outbreak is due to the unique characteristics of COVID-19. These features are: (1) The virus mutates more frequently. Then, it weakens the effectiveness of the vaccine. (2) The incubation period is long, which allows the virus to survive longer in individuals. (3) Asymptomatic individuals who are not easily identified lead to the concealed transmission of the disease. The studies in [1] show that the virus is mainly transmitted by the asymptomatic individuals. This is one of the main causes of secondary infections in some recovered people. (4) The recovery period is long and the treatment cost is high. These characteristics of the virus make immunity take a long time, and several peaks of the widespread infection are occurring. It is evident that these characteristics of COVID-19 lead to the strong fluctuations and cycles of the current epidemic in many countries.

The reality is that although several highly efficacious vaccines against COVID-19 are available for mass vaccination, it is clear that vaccines alone are not sufficient to stop the widespread transmission of the virus. Some theoretical studies and simulations studies also partially supported the conclusions from different perspectives and various forms [2, 3]. This implies that non-vaccine auxiliary interventions are essential to more effectively control further spread of the virus. Therefore, it is inevitable that the vaccine and some special interventions will be coordinated and combined to prevent and control the epidemic for some time. Because of the adoption of such different interventions, different nations have shown various evolutionary patterns. In China, the government has approved the use of traditional Chinese medicine (TCM) as a method of social intervention since the outbreak to prevent people from contracting COVID-19 and to provide adjunctive treatment for the infected (e.g., asymptomatic and symptomatic) individuals due to the antiviral and analgesic effects of some TCM medicines. TCM has made remarkable positive contributions on mitigating the spreading of the epidemic [4]. China’s experience with COVID-19 strongly suggests that the combination of vaccines with auxiliary treatments rather than solely relying on vaccines is an efficient way to control the disease. However, although the importance of the combined application of the vaccination and treatment to control COVID-19 has been shown in practice and in some studies, the causality of the combined effect of the two has not yet been investigated in detail. In particular, targeting both asymptomatic and symptomatic individuals has not yet been explored theoretically. Therefore, there is an urgent need to understand the potential joint impact of both vaccination and auxiliary treatments on COVID-19 transmission through qualitative and quantitative exploration. This is also main motivation of the present work.

Here, the meaning of auxiliary treatment can be broad and takes many forms, including various measures taken for infected persons or for the general public to help reduce the spread of the virus. For example, specific pharmaceutical or non-pharmaceutical interventions (hospitalization, isolation, wearing masks, etc.), policy constraints, behavioral standards, etc., can be treatments or interventions recommended by professional authorities. Following [5], we collectively consider them as recommended treatment.

In the current study, based on the concept of the recommended treatment, we aim to study the incorporated impacts of vaccination and a recommended treatment to control the spread of COVID-19 in general. As a result, a new mathematical model of seven compartments for the spread of COVID-19 is proposed. In the model, in addition to considering the susceptible (S), vaccinated (V), exposed (E), symptomatic (P), asymptomatic (A) and recovered (R) compartments, we designed a recommended treatment compartment (C) for individuals who can be partially considered in both symptomatic and asymptomatic groups receiving a recommended treatment. This particular consideration can be more generalized to include a wide range of auxiliary interventions or treatments that contribute to the mitigation of the epidemic, and provide a way to investigate the joint effect of both the vaccination and recommended treatments on the symptomatic and asymptomatic groups.

Compared with the existing literature, this study summarizes the following highlights in addition to its own technical route within the underlying theoretical framework adopted by most literature.

1. The model has its own feature compartment network structure. The model is composed of a closed connection network, reflecting key factors, such as the repeated transmission of COVID-19 and the limited protection period of the vaccine. Particularly, while introducing the recommended treatment compartment (C) directly connecting both symptomatic and asymptomatic compartments as the final stage of disease transmission, the closer linkages between the model compartments can be built. Therefore, the close relationships among the vaccine parameters \(\alpha \) and \(\beta \) and recommended treatment parameter \(m(\tau )\) are established through the effective reproduction number \({\mathcal {R}}_0\), which are used to detect the joint effect of the two group parameters on asymptomatic and symptomatic compartments (see Sect. 4).

Remark

Here, the effective reproduction number \({\mathcal {R}}_0\) represents the average number of secondary infections generated by a single infectious individual during his entire infectious period in a totally susceptible population when vaccination and recommended treatments are implemented [6,7,8]. An application of the concept in an optimal control model can be seen in [2, 3].

2. Developing the proposed model is very pertinent, and the model also has extensive generalization. Compared with most of the literature considering some types of treatments, the treatment compartment (C) is a conceptualization that can represent more different treatments. Moreover, it specifically targets (connects) both symptomatic (P) and asymptomatic (A) compartments at the same time, with the aim of exploring the precision and concentration of the treatment measures on the two compartments. Because the infected individuals in these two groups have been identified, the recommended treatment can be easily used on them. In addition, if the connection of compartment (C) to other compartments is relaxed (removed), the model will return to the situations described in more literature where the treatment compartments were designed for a specific treatment (hospitalization, quarantine, etc.). For instance, if the compartments (P), (A) and (C) are reduced to one, then our model becomes the model proposed in [9]. The model proposed in this paper can also be considered a generalization of the model in [10, 11] if compartment (C) in our model is removed or regarded as an isolation room.

3. Our theoretical findings and numerical simulations adapt well to the real case data. The proposed SVEPACR model has valuable qualitative properties and good overall behavior for simulating real case data. Particularly, through fitting with the real data on the COVID-19 epidemic in Shanghai China in 2022, the model’s ability to simulate real cases is verified (see Sect. 3.3). Accordingly, by estimating the value of the \({\mathcal {R}}_0<1\), the model really reflects the decreasing trend of COVID-19 confirmed cases at that time.

4. New concepts, cross-infection rate and relative change number are introduced. Due to the design of the compartment (C), the cross-infection rate and relative change number are (see definition 1 and equation (8) in Sect. 4.2) introduced to account for the cross-infections among the compartments in our model, which make more clear implications of the model parameters’ roles and their corporations.

5. The established model has good extensibility. The idea and method for establishing the SVEPACR model can be generalized and applied to a wider range of areas due to the high reliability of theoretical and numerical analysis shown in the article. For example, the study can be extended to include some epidemic–logistics problems where it is necessary to consider the impact of more epidemic factors on emergency logistics optimal models of medical supplies [12].

The rest of the article is arranged as follows. Section 2 briefly reviews the relevant literature to show the current research status. Section 3 presents the proposed model and its qualitative analysis, including proving that the model is well-posed, thus demonstrating the existence and stability of the equilibrium points, and the determining effective reproduction number of the model. Fitting our model with real data from the epidemic occurring in Shanghai is also demonstrated here. Section 4 provides the dynamic analysis of the model, including the sensitivity analysis of the effective reproduction number to the model parameters. The results are represented by symbolic calculation, numerical calculation and graphical display. The discussion and conclusion are given in Sect. 5.

2 Literature review

In this section, we briefly review recent works on the application of the compartment model to COVID-19 studies relevant to this paper.

Dating the compartment mathematical modeling method for epidemiology begins with Kermack and Mckendrickand [13] and has been greatly developed as a new branch of applied mathematics [14, 15]. Recently, as extensions of traditional epidemiology modeling, there are many compartmental models that have been proposed focusing on exploring the transmission dynamics of COVID-19 according to its features and considering some related social interventions. In the following, we cite a few of them.

Diagne et al. [2] developed a seven compartmental COVID-19 model incorporating vital dynamics of the disease and two key therapeutic measures: vaccination and hospitalization for individual treatment. Simulation results suggest that despite the effectiveness of vaccination and hospitalization treatment, the additional social interventions should continue to be implemented to achieve better control of the disease. Rajapaksha, et al. [9] proposed a five compartmental SEIRV model and simulated potential vaccine strategies under a range of epidemic conditions. The results show that when the reproduction number is increased in the model along with the increase in the vaccination efficacy and vaccination rate, the vaccination population is reducing. Viana, Rozhnova et al. [16], as opposed to strengthening social intervention, investigated the relaxation scenarios of social actives using an age-structured ten compartments transmission model. The analyses suggest that the pressing need to restart socioeconomic activities that can lead to new pandemic waves. Additional waves can be prevented altogether if measures are relaxed in a stepwise manner. Oduro and Magagula [17] developed five compartment COVID-19 epidemic models to study earlier aggressive treatment strategies as a recommended treatment to control the pandemic. This shows that if the treatment works perfectly, containing the disease is possible. Additionally, the existence of a dual-rate effect is investigated. Ndaïrou et al. [18] proposed an eight compartment mathematical model for the spread of COVID-19 with special focus on the contagious of super-spreader individuals. This model is verified by the data from the outbreak of COVID-19 that occurred in Wuhan, China. Mamo [5] developed a SHEIQRD model of COVID-19 considering some health interventions. The study enhanced the perspective that the special interventions, such as the stay-at-home rate, high coverage of precise identification and isolation of exposed and infected individuals, can mitigate the COVID-19 pandemic. Huo et al. [1] developed a time-dependent seven-compartment mathematical model to describe the dynamics of the disease transmission in Wuhan, China. Based on the reported data, they estimated that around 20\(\%\) of infections were asymptomatic and their transmissibility was about 70\(\%\) of symptomatic ones. The total number of asymptomatic individuals was also estimated. Tomochi and Kono [19] constructed a six compartment mathematical model of COVID-19 to describe the spread of the infection. The model can handle asymptomatic individuals. Following the IHME COVID-19 forecasting team [20], a four compartment model to study the potential impact of the use of face masks to curtail the spread of the COVID-19 pandemic was studied. It was found that achieving universal mask use (95\(\%\) mask use in public) could be sufficient to ameliorate the worst effects of epidemic resurgences in many states in USA. They also suggested that community-wide benefits are likely to be greatest when face masks are used in conjunction with other non-pharmaceutical practices (such as social or physical distancing), and high universal adoption and compliance. Musa et al. [21] presented a nine-compartment mathematical model to study the transmission dynamics of COVID-19 in Nigeria. They introduced an awareness program in the model. The analysis of the model shows that the awareness program is an essential basic guide to take effective measure (treatment) to control and mitigate the COVID-19 pandemic in Nigeria. With an eight compartmental dynamic model, Rong et al. [22] investigated the effect of the delay in the diagnosis of the COVID-19. The model shows that by strengthening early diagnosis, the virus can be greatly limited, shortening the peak time and reducing the peak value of new confirmed cases. Mandal et al. [23] presented five compartmental mathematical models of the spread of COVID-19. The models proved that enhancing the public health interventions would mitigate the COVID-19 pandemic greatly. Lin et al. [24] proposed a model for the COVID-19 outbreak in Wuhan by incorporating individual behavioral reaction and governmental actions. The model captures the possible course of the COVID-19 outbreak and reveals the patterns of the outbreak. Song et al. [25] established a four compartment model of COVID-19 transmission. By using the data from Harbin, China, and based on the model, they estimated the outbreak size of COVID-19 in Harbin and warned people to be vigilant about the presence of asymptomatic patients to control the epidemic. Li et al. [26] provided a ten compartment mathematical model focusing on the treatment for people complaining of influenza-like symptoms, potentially at risk of contracting COVID-19. The model shows that increasing influenza vaccine uptake would facilitate the management of respiratory outbreaks coinciding with the peak flu season. Schlickeiser and Kröger [27] proposed a four compartmental epidemic model with a compartment of vaccinated individuals and a time-dependent effective vaccination rate. The influence of vaccination on the total cumulative number and the maximum rate of new infections in different countries is discussed. Ghostine et al. [10] built a seven-compartment model with a vaccination compartment to simulate the novel coronavirus disease spread in Saudi Arabia. The numerical results demonstrate the model’s capability of achieving accurate prediction of the epidemic development for up to two-week time scales. Firdos Karim et al. [28] proposed a combined epidemic-economics model that analyzes the system dynamics generated in the presence of COVID-19. The study revealed several important phenomena in the relationship between the epidemic and the economy. For example, vaccination can boost economic growth, complete vaccination can greatly reduce all infectious diseases, overexposure to the media can contribute to the spread of infectious diseases, and parameter sensitivity analysis can greatly aid policy development. Kambali et al. [29] used a nonlinear three compartmental model of susceptibility, infection and immunity incorporating dynamic transmission rates (expressed as a cosine function) and vaccination policy to model and analyze the dynamics of COVID-19 evolution. This study demonstrated the value of systematic nonlinear dynamic analysis in pandemic modeling and showed the effects of vaccination and the frequency, phase and amplitude of the transmission rate on the persistent dynamic behavior of COVID-19.

Fig. 1
figure 1

The flowchart of the proposed SVEPACR model with compartments S, V, E, P, A, C and R

Full size image

In addition, the optimal control theory has also been applied to understand the ways to control the spread of infectious diseases by devising optimal intervention strategies. Giordano et al. [3], based on the Italian case study, studied several scenarios of COVID-19 with a nine-compartment model (SIDARTHE-V) (three of which can be uncoupled). The model confirmed that implementation of strong non-pharmaceutical interventions could bring the epidemic under control without vaccines or before reaching population immunity. Acuña-Zegarra et al. [11] developed a seven-compartment model (one of which can be uncoupled) and considered the optimal control problem by introducing control variables of vaccination rates to obtain the vaccination scheduling policy. The results of the study show that response regarding vaccine-induced immunity and reinfection periods would play a dominant role in mitigating COVID-19. An eight compartment optimal control COVID-19 transmission model was presented by Moore and Okyere [30]. They examined the impact of control strategies for this disease using personal protection, treatment with diagnosis and spraying the virus in the environment as time-dependent control variables to contain the disease. Considering the dynamics of the virus in the environment, Asamoah et al. [31] presented a six compartment optimal control model, including asymptomatic and symptomatic compartments. The model proved that the safety measures adopted by the asymptomatic and symptomatic individuals are the most effective strategies among all the control intervention strategies under consideration. More literature on optimal control mathematical models for pandemic can be found in a review paper by Sharomi and Malik [32].

In addition to the compartment model method, there are other model-like approaches. For example, in contrast from the compartmental model, Moghadas et al. [33] formulated an age-structured transmission model for COVID-19 as an agent-based model. The results of the study indicate that although vaccination can have a substantial impact on mitigating COVID-19 outbreaks, even with limited protection against the infection, continued compliance with non-pharmaceutical interventions is essential to achieve this impact.

3 A COVID-19 dynamic model and qualitative analysis

3.1 Model

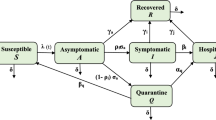
We propose a seven-compartment model considering vaccination and a recommended treatment for symptomatic and asymptomatic people to simulate the transmission epidemic of the COVID-19 outbreak. We decomposed the total human population at time t, denoted by \(N=N(t)\), into the mutually exclusive compartments of susceptible (S), exposed (E), vaccinated (V), symptomatic (denoted by P), asymptomatic (A), recommended treatment (denoted by C) and recovered (R) individuals, respectively. Thus, we have \(N(t)=S(t)+E(t)+V(t)+R(t)+I(t)\) where \(I(t)=P(t)+A(t)+C(t)\) denotes the total infected population at time t. Particularly, a vaccinated room V is designed to observe the influence of the vaccine and learn the experience of using vaccine. Moreover, for the population receiving a particular recommended treatment in compartments (P) and (A), we specifically designed the recommended treatment room (C) to investigate the combined effect of that particular treatment with the vaccination. We use \(\delta \) and \(\sigma \) to measure the proportion of people in rooms (P) and (A) who are willing to receive this particular treatment, and m represents the curative ratio of the recommended treatment. Hence, these ratios consist of a quantification of the recommended treatment. Additionally, this room can also be considered as the group of special treated people in the asymptomatic and symptomatic compartments who are more vulnerable to novel coronavirus attacks. For instance, this group of people includes elderly individuals with some chronic underlying diseases. Therefore, the recommended treatment compartment (C) is a general conceptual compartment that can contain the various treatments or interventions, including the vulnerable group in both (P) and (A). We simply call this model the SVEPACR model. Moreover, the SVEPACR model is designed to not only consider the role of vaccines, but to also consider the strategy of using various specific treatments (interventions) to control COVID-19.

The flowchart of the model is given in Fig. 1 and the state variables are governed by the following system of nonlinear ordinary differential equations:

$$\begin{aligned} \left\{ \begin{array}{ll} {\dot{S}}&{}=\Pi -\beta _s S {\tilde{I}}-\theta _7 S+{\gamma } R, \\ {\dot{V}}&{}=\alpha S-\beta _v V {\tilde{I}}-\theta _6 V, \\ {\dot{E}}&{}=\beta _s S{\tilde{I}}+\beta _v V{\tilde{I}}-\theta _3 E, \\ {\dot{P}}&{}=b_1 E-\theta _1 P, \\ {\dot{A}}&{}= b_2 E-\theta _2 A, \\ {\dot{C}}&{}=\delta P+\sigma A-\theta _4C, \\ {\dot{R}}&{}=c_1 P+c_2 A+\tau C+\beta V-\theta _5 R. \end{array} \right. \end{aligned}$$
(1)

where \({\tilde{I}}=\varepsilon _{a}A+\varepsilon _{p}P+\varepsilon _{c}C\), \(\mu _a=\mu +(1-\mu )\delta _a\), \(\mu _p=\mu +(1-\mu )\delta _p\), \(\mu _c=\mu +(1-\mu )\delta _c\) and \(\tau =r+(1-r)m\), \(\beta _s=1-\alpha , \beta _v=1-\beta \). The system admits nonnegative initial values \(S(0)=S_0, E(0)=E_0, P(0)=P_0, A(0)=A_0, C(0)=C_0, R(0)=R_0\) and \(V(0)=V_0\). Here, for simplicity we use notations of letters, \(\theta \) and \(\epsilon \), listed in Table 1 to represent some compound parameters made up of basic parameters given in Table 2. The meanings of the basic parameters used in the proposed model are explained in Table 2. We assume that all compartments admit the same natural death rate \(\mu \).

Table 1 Some compounded parameters with their notations
Full size table

In order to observe the influences of some major factors on the dynamic behavior of the model, the basic parameters used in the model are divided into two groups as mainly observed (o) and fixed (f) parameters. The main parameters are \(\alpha , \beta , \gamma , \tau , \sigma \) and \(\delta \). The joint efficiencies \(\mu _i (i=p, a, c)\) and \(\tau \) are used if there are two efficiencies in one compartment.

Table 2 State variables, fixed (f) and main observed (o) parameters
Full size table
Table 3 Baseline value ranges of the parameters used in the model (1)
Full size table

The parameters in the model can take various values according to different scenarios. In our qualitative analysis, the parameters are not assigned any specific values. To serve the numerical simulation of the dynamic behavior of the model in the next section, under reference [4, 10, 17, 19, 31, 34,35,36] and estimation, we determine a baseline value range of each parameter in the model as shown in Table 3. Referencing the research in [17, 18], we suppose the state variables take initial values, such as \(S_0=12,797,248, V_0=0, E_0=2792, P_0=19, A_0=10 (\textrm{estimated}), C_0=0, R_0=0\) and \(\Pi =10,000\). These values are approximations to the scale of COVID-19 cases in Wuhan and Pennsylvania (USA) in early 2020. There was no vaccine at that time, so we are able to compare some of the numerical results with the results in these papers and see the effects of the vaccine and the recommended treatment through the proposed model.

It is emphasized here that the recommended treatment in our numerical simulation is taken as an example of traditional Chinese medicine using a therapeutic effect m [34]. The efficiency of the vaccine is within the range of the standards required by the World Health Organization, Bernal et al. [36] provided more detailed information.

3.2 Qualitative analysis of the model

In the following, we demonstrate that the model is well-posed (1) by proving the boundedness, nonnegativity of the solutions and the local and global stability of disease-free equilibrium and the existence of endemic equilibrium. The effective reproduction number of the model (1) is also derived.

3.2.1 Nonnegativity and boundedness

In order to easily prove the nonnegativity of the solution to (1), we use the method used in [5]. To this end, we take transformation \(F(t)=f(t) N(t)\) for all \(F\in \{S, V, E, P, A, C, R\}\) and correspondingly \(f\in \{s, v, e, p, a, c, r\}\) to normalize the system (1). Here denote the recruit \(\Pi =b N\) with birth rate b. Thus, the normalized system is read as

$$\begin{aligned} \left\{ \begin{array}{ll} {\dot{s}}&{}=b-\beta _si s -(\alpha +b)s+\gamma r+i_d s,\\ {\dot{v}}&{}=\alpha s-\beta _vi v -(b+\beta )v + i_d v,\\ {\dot{e}}&{}=\beta _v i v +\beta _s i s -\left( b+b_1+b_2\right) e+i_d e,\\ {\dot{p}}&{}=b_1 e- \left( b+c_1+\delta +\mu _p-\mu \right) p+i_d p,\\ {\dot{a}}&{}=b_2 e-\left( b+c_2+\sigma +\mu _a-\mu \right) a+i_d a,\\ {\dot{c}}&{}=a \sigma +\delta p-\left( b+\mu _c-\mu +\tau \right) c+i_d c,\\ {\dot{r}}&{}=c_1 p +c_2 a +\tau c +\beta v-(b+\gamma )r +i_d r. \end{array} \right. \end{aligned}$$

where \(i=a \epsilon _A+c \epsilon _C+p \epsilon _P\) and \(i_d=a \left( \mu _a-\mu \right) +c \left( \mu _c-\mu \right) +p \left( \mu _p-\mu \right) \) by denoting \(\epsilon _A=\epsilon _aN, \epsilon _P=\epsilon _pN, \epsilon _C=\epsilon _cN\). Since \(s+v+e+p+a+c+r\equiv 1\). Removing the first equation from above system, we have a system of the following six equations with replacing s by \(1-v-e-p-a-c-r\) as

$$\begin{aligned} \left\{ \begin{array}{ll} {\dot{v}}&{}=\alpha (1-v-e-p-a-c-r)-\beta _vi v\\ &{}\quad -(b+\beta )v + i_d v,\\ {\dot{e}}&{}=\beta _v i v +\beta _s i (1-v-e-p-a-c-r) \\ &{}\quad -\left( b+b_1+b_2\right) e+i_d e,\\ {\dot{p}}&{}=b_1 e- \left( b+c_1+\delta +\mu _p-\mu \right) p+i_d p,\\ {\dot{a}}&{}=b_2 e-\left( b+c_2+\sigma +\mu _a-\mu \right) a+i_d a,\\ {\dot{c}}&{}=a \sigma +\delta p-\left( b+\mu _c-\mu +\tau \right) c+i_d c,\\ {\dot{r}}&{}=c_1 p +c_2 a +\tau c +\beta v-(b+\gamma )r +i_d r. \end{array} \right. \end{aligned}$$
(2)

Let \(X=(x_1, x_2, x_3, x_4, x_5, x_6)=(e, p, a, c, v, r)\) and h(X) be right sides of system (2). Then, the system can be written as \(\frac{dX}{dt}=h(X)\) and we have feasible domain \(\Omega =\{X\in R^6_+: \sum _{i=1}^6 x_i\le 1\}\) for the system. The domain is compact and convex with seven boundary surfaces: \(P_i=\{X\in R^6_+: x_i=0,\forall x_j\in [0,1], \sum _{j=1}^6 x_j\le 1\}(i=1,2,\ldots , 6)\) and \(P_7=\{X\in R^6_+: \sum _{j=1}^6x_j=1\}\) with corresponding outside normal vectors \(n_i=X_i\) and \(n_7=(1, 1, 1, 1, 1, 1)\) respectively. The \(X_i\) represents the vector in \(R^6\) whose ith coordinate is \(-1\), others are zeros for \(i=1, 2, \ldots , 6\). It is easily computed that the scale products \(h(X)\cdot n_i\le 0\). Hence, it is confirmed that domain \(\Omega \) is invariant, that is \(x_i\ge 0 (i=1, 2, \ldots , 6)\) from the results in [37]. This proved the nonnegativity of the solutions of the system (2). In turn, we have proved the nonnegativity of the solution to the system (1). For proving the boundedness of the solutions, we return to original system (1). Summing all equations in (1), we have

$$\begin{aligned} {\dot{N}}(t)= & {} \Pi -\mu N(t)-[(\mu _p-\mu )P(t)+(\mu _a-\mu )A\\{} & {} +(\mu _c-\mu )C]\le \Pi -\mu N(t) \end{aligned}$$

which implies that \(N(t)\le \frac{\Pi }{\mu }+(N_0-\frac{\Pi }{\mu })e^{-\mu t}\). This proved the boundedness of the solutions to system (1). Hence, we have

Theorem 1

If all initial values \(S(0)=S_0\), \(V(0)=V_0\), \(E(0)=E_0\), \(P(0)=P_0\), \(A(0)=A_0\), \(C(0)=C_0\) and \(R(0)=R_0\) are nonnegative and all parameters in the model (2) are positive, then the solutions of model (2) remain nonnegative for all \(t\ge 0\).Moreover, the total population number \(N(t)\le \frac{\Pi }{\mu }+(N_0-\frac{\Pi }{\mu })e^{-\mu t}\) for all \(t\ge 0\). Consequently, the solutions of model (1) are uniformly bounded.

3.2.2 Disease-free equilibrium and effective reproduction number

Under variable order taking in \(X=(E, P, A, C, S, V, R)\), let the right sides of (1) be zeros. Then, we get the disease-free equilibrium

$$\begin{aligned} X_0=(0, 0, 0, 0, \theta _6 T, \alpha T,\alpha \beta T/ \theta _5), \end{aligned}$$
(3)

where \(T=\Pi \theta _5(\mu \left( \alpha \beta +(\theta _7+\beta )\theta _5\right) )^{-1}.\) It is easily seen that the system (1) can be written as

$$\begin{aligned} \frac{dX}{dt}={\mathcal {F}}(X)-{\mathcal {V}}(X) \end{aligned}$$

by taking into account the new infectious where

$$\begin{aligned} {\mathcal {F}}= & {} \left( \begin{array}{c} (\beta _sS+\beta _v V){\tilde{I}}\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ \end{array}\right) ,\\ {\mathcal {V}}= & {} \left( \begin{array}{l} \theta _3E \\ \theta _1P - b_1 E \\ \theta _2A -b_2 E\\ \theta _4C-\delta P -\sigma A \\ \theta _7 S -\gamma R -\Pi +{\tilde{I}} \beta _s S \\ \theta _6 V+V{\tilde{I}} \beta _v - \alpha S \\ \theta _5 R -\beta V -\tau C -c_1 P -c_2 A \\ \end{array} \right) . \end{aligned}$$

Their Jacobins at \(X_0\) are

$$\begin{aligned} J_{\mathcal {F}}= & {} \left( \begin{array}{cc} F&{}0\\ 0&{}0 \end{array}\right) ,J_{\mathcal {V}}\\= & {} \left( \begin{array}{cc} V&{}0 \\ J_3&{}J_4 \end{array} \right) \end{aligned}$$

in which

$$\begin{aligned} F= & {} T \epsilon _3\left( \begin{array}{cccc} 0 &{} \epsilon _p &{}\epsilon _a &{} \epsilon _c \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right) ,\\ J_4= & {} \left( \begin{array}{ccc} \theta _7 &{} 0 &{} -\gamma \\ -\alpha &{} \theta _6 &{} 0 \\ 0 &{} -\beta &{} \theta _7 \\ \end{array} \right) ,\\ V= & {} \left( \begin{array}{cccc} \theta _3&{} 0 &{} 0 &{} 0 \\ -b_1 &{} \theta _1 &{} 0 &{} 0 \\ -b_2 &{} 0 &{} \theta _2&{} 0 \\ 0 &{} -\delta &{} -\sigma &{} \theta _4\\ \end{array} \right) . \end{aligned}$$

Obviously, matrix F is nonnegative, \(J_4\) and V are non-singular M-matrices. Calculating the eigenvalues of the next generation matrix \(FV^{-1}\) [6], we obtain the effective reproduction number [2, 3, 7, 8]

$$\begin{aligned} {\mathcal {R}}_0=\frac{\left( \theta _1 b_2 \epsilon _2+\theta _2 b_1 \epsilon _1\right) \epsilon _3 }{\theta _1 \theta _2 \theta _3\theta _4}T \end{aligned}$$

for system (1) with parameters given in Tables 1 and 2.

In order to see the joint impacts of parameters on various compartments in the model, \({\mathcal {R}}_0\) is broken down into three components

$$\begin{aligned} {\mathcal {R}}_0={\mathcal {R}}_{EP}+{\mathcal {R}}_{EA}+{\mathcal {R}}_{AP}, \end{aligned}$$
(4)

in which

$$\begin{aligned}{} & {} {\mathcal {R}}_{EP}=\frac{b_1\epsilon _p\epsilon _3}{\theta _1\theta _3}T,\,\,\, {\mathcal {R}}_{EA}=\frac{b_2\epsilon _a\epsilon _3}{\theta _2\theta _3}T,\,\,\, \\{} & {} \quad {\mathcal {R}}_{PA}=\frac{\epsilon _c\epsilon _3}{\theta _3\theta _4}(\frac{\delta b_1}{\theta _1}+\frac{\sigma b_2}{\theta _2})T. \end{aligned}$$

These components are the new infections induced by the susceptible individuals (E) contacts with symptomatic individuals (P), asymptomatic individuals (A) and those in treatment (C). In other words, each entry of \({\mathcal {R}}_0\) represents, respectively, the contribution of asymptomatic, symptomatic and treated individuals to the spread of COVID-19 in our SVEPACR model.

Theorem 2

The disease-free equilibrium \(X_0\) in (3) of dynamic system (1) is locally asymptotically stable for \({\mathcal {R}}_0<1\) and unstable for \({\mathcal {R}}_0>1\).

Proof of Theorem 2

The characteristic equation of the eigenvalues of Jacobin of system (1) at \(X_0\) is given by \(f_1f_2f_3=0\) where

$$\begin{aligned} \begin{array}{ll} f_1=&{}\lambda +\mu ,\\ f_2=&{}\alpha \beta +(\lambda +\theta _5 ) (\alpha +\beta +\lambda +\mu ),\\ f_3=&{}\lambda ^4+k_3\lambda ^3+k_2\lambda ^2+k_1\lambda +k_0, \end{array} \end{aligned}$$
(5)

with coefficients in \(f_3\) as

$$\begin{aligned} k_0= & {} (1-{\mathcal {R}}_0)\theta _1 \theta _2 \theta _3\theta _4,\\ k_1= & {} \theta _4(\theta ^*-\frac{(b_1\epsilon _1+b_2\epsilon _2)\theta _1\theta _2\theta _3}{(b_1\epsilon _1\theta _2+b_2\epsilon _2\theta _1)}\\{} & {} {\mathcal {R}}_0)+\theta _1 \theta _2 \theta _3(1-{\mathcal {R}}_{EA}-{\mathcal {R}}_{EP}),\\ k_2= & {} (\theta _1+\theta _2+\theta _3)\theta _4+\theta _3 \theta _2 \\{} & {} \left( 1-R_{EA}\right) +\theta _1 \theta _3\left( 1-{\mathcal {R}}_{EP}\right) +\theta _1 \theta _2,\\ k_3= & {} \theta _1+\theta _2+\theta _3+\theta _4,\,\, \theta ^*=\theta _1\theta _2+\theta _1\theta _3+\theta _2\theta _3. \end{aligned}$$

Without loss of generality, we suppose that \(\theta _1\le \theta _2\) holds, thus we have inequality \(\frac{(b_1\epsilon _1+b_2\epsilon _2)\theta _1\theta _2\theta _3}{(b_1\epsilon _1\theta _2+b_2\epsilon _2\theta _1)}\) \(\le \theta _2\theta _3\), which leads to

$$\begin{aligned}{} & {} k_1\ge \theta _1\theta _4(\theta _2+\theta _3)\\{} & {} \quad +(\theta _2\theta _3\theta _4+\theta _1\theta _2\theta _3)(1-{\mathcal {R}}_0).\end{aligned}$$

In addition, we have \(\Delta =k_2k_3-k_1=B_1+B_2+B_3\) with

$$\begin{aligned} B_1= & {} T \epsilon _3 [b_2 \left( \theta _1 \epsilon _{A}+\epsilon _2\right) +b_1 \left( \theta _2 \epsilon _{P}+\epsilon _1\right) ],\\ B_2= & {} (\theta _1+\theta _2+\theta _3+\theta _4) [(\theta _1+\theta _2+\theta _3)\theta _4 \\{} & {} +\,\theta ^*-\theta _2\theta _3{\mathcal {R}}_{EA} -\theta _1 \theta _3 {\mathcal {R}}_{EP}],\\ B_3= & {} -\theta ^* \theta _4-\theta _1 \theta _2 \theta _3. \end{aligned}$$

Since \(B_1> 0\) and \(B_2> \theta ^*\theta _4+\theta _1\theta _2\theta _3\) when \({\mathcal {R}}_0<1\), we have \(\Delta \ge 0\). Consequently, when \({\mathcal {R}}_0<1\) all coefficients \(k_i>0(i=0,1,2,3)\) and discriminant \(\Delta > 0\). This proved the eigenvalues admitted by the Jacobin system of (1) have negative real parts according to the Lienard–Chipard test [38]. This demonstrates the local stability of the disease-free equilibrium \(X_0\). \(\square \)

The global stability of disease-free equilibrium is given by using Lyapunov function method in the following theorem.

Theorem 3

The disease-free equilibrium \(X_0\) of dynamic system (1) is globally stable for \({\mathcal {R}}_0\le 1\).

Proof of Theorem 3

Suppose the Lyapunov function L for disease-free equilibrium point \(X_0\) as follows

$$\begin{aligned} L=k_0E(t)+k_1P(t)+k_2A(t)+k_3C(t), \end{aligned}$$

with positive constants \(k_i (i=0,1,2,3)\) to be determined. Differentiating L w. r. t t and substituting \({\dot{E}}, {\dot{P}}, {\dot{A}}\) and \({\dot{C}}\) from system (1), we obtain

$$\begin{aligned}{} & {} {\dot{L}}=k_0( (\beta _s S+\beta _vV){\tilde{I}}-\theta _3 E)+k_1(b_1E-\theta _1 P)\\{} & {} \quad +k_2(b_2 E-\theta _2A)+k_3(\delta P+\sigma A-\theta _4C). \end{aligned}$$

Then collecting the derivative by P, A, C, E and using \(S\le N, P\le N\) and \(C\le N\), we have

$$\begin{aligned} {\dot{L}}\le & {} ((k_0(\beta _s+\beta _v)\epsilon _a+k_3\sigma -k_1\theta _2)A \nonumber \\{} & {} +(k_0(\beta _s+\beta _v)\epsilon _p+k_3\delta -k_1\theta _1)P +k_0(\beta _s\nonumber \\{} & {} +\beta _v)\epsilon _c+k_3\theta _4)C+(k_1b_1+k_2b_2-\theta _3)E. \end{aligned}$$
(6)

Letting the coefficients of P, A and C be zero and solving the obtained system in \(k_1, k_2, k_3\), we have

$$\begin{aligned} \begin{array}{ll} &{}k_1=\frac{(\beta _s+\beta _v)}{\theta _1}\left( \epsilon _p+\frac{\delta }{\theta _4}\epsilon _c\right) k_0,\\ &{}k_2=\frac{(\beta _s+\beta _v)}{\theta _2}\left( \epsilon _a+\frac{\sigma }{\theta _4}\epsilon _c\right) k_0,\\ &{}k_3=\frac{(\beta _s+\beta _v)}{\theta _4}\epsilon _c k_0. \end{array} \end{aligned}$$

Choosing constant as \(k_0=\frac{b((\gamma +\mu )\beta _s+\alpha \beta _v)}{\mu (\alpha \beta +(\alpha +\beta +\mu )(\gamma +\mu ))}\), we have from (6)

$$\begin{aligned} {\dot{L}}\le \theta _3({\mathcal {R}}_0-1)E. \end{aligned}$$
(7)

Therefore, \({\dot{L}}\le 0\) whenever \({\mathcal {R}}_0\le 1\). Also, \({\dot{L}}=0\) if and only if \(E=0\) which results in \({\tilde{I}}=0\) from the third equation in system (1). Since the nonnegativeness of P, A, C and parameters in the system (1), we have \(E=P=A=C=0\). Consequently, the invariant set \(\{U=(E, P, A, C, S, V, R)\in {\mathbb {R}}^4: {\dot{L}}=0 \text { at } U \}\) constitutes only equilibrium \(X_0\) given in (3). Hence, by the Krasovskii–LaSalle theorem in [14], disease-free equilibrium \(X_0\) is globally stable. Thus, the theorem has been proved. \(\square \)

The effective reproduction number \({\mathcal {R}}_0\) shows the epidemic is expected to increase exponentially if \({\mathcal {R}}_0>1\), and to end if \({\mathcal {R}}_0\le 1\).

3.2.3 Existence of endemic equilibrium

Let the right sides of (1) be zeros with \(EPAC\not =0\). From the fourth, fifth and sixth equations of (1), we obtain \(E^*=n_1P^*\), \(A^*=n_2 P^*\), \(C^*=n_3 P^*\) with \(n_1={\theta _1}/{b_1}\), \(n_2={b_2 n_1}/{\theta _2}\), \(n_3=\left( \delta +n_2 \sigma \right) /\theta _4.\) Substituting the \(E^*, A^*\) and \(C^*\) into third equation of (1) and solving the equation, we obtain \(V^*=\left( {\alpha \theta _3 n_1}\right) /\left( {n_4 \left( n_4 P^* \beta _s \beta _v+\epsilon _3\right) }\right) .\) Substituting the \(E^*, A^*\) and \(C^*\) into second equation of (1) and solving the equation, we obtain

$$\begin{aligned} S^*=\left( {\left( \theta _6 +n_4 P^* \beta _v\right) }/{\alpha }\right) V^*. \end{aligned}$$

From seventh equation, we have \(R^*=(P^*(c_2 n_2+c_1+n_3 \tau )+\alpha V^*)/{\theta _5}\). Substituting these expressions of \(E^*, A^*, C^*, S^*, V^*\) and \(R^*\) into first equation of (1), we get a quadratic equation in \(P^*\):

$$\begin{aligned} \eta {P^*}^2+\xi P^*+\zeta =0 \end{aligned}$$

with \(\xi \) an expression of parameters in the model (1) and

$$\begin{aligned} \begin{array}{ll} \eta &{}=\left( (c_1+c_2 n_2+n_3 \tau )\gamma -n_1 \theta _3\theta _5\right) n_4^2\beta _s\beta _v,\\ \zeta &{}=\mu \theta _3 n_1 (\alpha \beta +(\alpha +\beta +\mu ) \theta _5)\left( {\mathcal {R}}_0-1\right) . \end{array} \end{aligned}$$

Using the expressions of \(n_1,n_2,n_3\), one easily prove that \(\eta <0\). The expression of \(\zeta \) shows that \(\zeta >0\) when \({\mathcal {R}}_0>1\). Hence, the endemic equilibrium point \(X^*=(E^*, P^*, A^*, C^*, S^*, V^*, R^*)\) of system (1) uniquely exists when \({\mathcal {R}}_0>1\). Thus, we have proved the following theorem for the endemic equilibrium \(X^*\).

Theorem 4

The system (1) has unique endemic equilibrium \(X^*\) for \({\mathcal {R}}_0>1\).

Theorems 1–3 proved the well-posedness of the model (1).

Fig. 2
figure 2

The real case data fitting. The histograms are the real data of P and A cases obtained from report [39] while the red and pink lines have been obtained by solving numerically our model SVEPACR for variables P and A

Full size image
Fig. 3
figure 3

Under the fitting parameters the population S, V, E, C, R (c) and P, A (d) obtained by solving the SVEPACR model, which show the well-posdeness properties of the model given in Theorem 1–3

Full size image

Because of the strong non-linearity of model (1), the stability of the endemic equilibrium in the general sense has not yet been obtained. The local stability of endemic equilibrium is guaranteed by the Jacobin matrix of model (1) at the point admitting negative real part eigenvalues. In the next section, we provide numerical simulations of the local and global stability of the endemic equilibrium.

3.3 Numerical simulations: the real case study of Shanghai China

In the previous section, we prove that the proposed SVEPACR model has good qualitative properties. In this section, we further demonstrate that the model also has a strong simulation capability for real case data. From late March to late May 2022, an outbreak of COVID-19 occurred in Shanghai, China, causing a large number of infections. At that time, the Shanghai government adopted many measures, such as mass vaccination, nucleic acid and antigen detection, traditional Chinese medicine intervention and a partial lockdown of the city to effectively control the spread of the virus, and the epidemic data during this period were recorded in the literature [39]. We performed numerical simulations to compare the results of our model with real epidemic data from Pudong, the largest district in Shanghai, following the reports [39]. We fitted the variables P and A. The fitting results are shown in Fig. 2a, b which shows that our SVEPACR model describes the data on daily symptomatic (P) and asymptomatic (A) cases well during the 49 days from March 21 to May 8, 2022, with initial values of \(S_0=279\), \(V_0=1.5*10^5\), \(E_0=163\), \(P_0=0\), \(A_0=0\), \(C_0=0\), \(R_0=0\). For the fitting result, we obtained the biological parameters, \(\Pi = 100\), \(\delta =0.2257\), \(\delta _a=0.01546\), \(\delta _p=0.0151\), \(\delta _c=0.0199\); \(b_1 = 0.01\), \(b_2=0.24\), \(c_1=0.0727\), \(c_2=0.1718\); \(\mu =0.0011\); \(\alpha =0.699970\), \(\beta =0.011384\), \(\beta _s=0.9886\), \(\beta _v=0.30003\); \(r=0.42\), \(m=0.8643\), \(\sigma =0.4784\), \(\gamma =0.0010\); \(\epsilon _a=7.2101546*10^{-6}\), \(\epsilon _p=5.787028*10^{-6}\), \(\epsilon _c=3.0674*10^{-5}\). Correspondingly, we obtained the estimated value \({\mathcal {R}}_0=0.011987\) of the effective reproduction number using formula (4). The value \({\mathcal {R}}_0<1\) is in line with the strict prevention and control measures adopted by the government at that time, and effectively indicates the end of the epidemic. In addition, under these fitting parameters, the overall performance of our SVEPACR model is shown in Fig. 3c, d. It shows that our theoretical findings and numerical simulation results adapt well to the real data and demonstrate the stability of the conclusions given in Theorems 1–3.

For completeness, we provide the list here of the number of symptomatic and asymptomatic cases: \(D_P=\{\)6, 0, 0, 12, 31, 1, 4, 39, 169, 249, 180, 79, 107, 140, 205, 162, 151, 307, 348, 517, 212, 493, 192, 1139, 1252, 1142, 1002, 521, 1075, 720, 756, 409, 704, 541, 874, 292, 206, 534, 1456, 131, 37, 132, 38, 49, 50, 28, 33, 28, 34\(\}\) and \(D_A=\{\)163, 237, 218, 183, 1884, 322, 1420, 2463, 2018, 1949, 2224, 2518, 1949, 3529, 6788, 7892, 8296, 8734, 6938, 10,613, 6520, 7813, 10,857, 13,888, 10,404, 9140, 9789, 7219, 7756, 4926, 3709, 4246, 7257, 7085, 5307, 3620, 2539, 2459, 2016, 1897, 1588, 1520, 1124, 834, 839, 649, 551, 647, 658\(\}\) in Pudong, Shanghai, per day, corresponding to the histogram in Fig. 3. The list \(D_P\) represents the numbers of symptomatic cases from March 21 to May 8, 2022, and analogously, \(D_A\) is the number of the asymptomatic cases during same time period.

Fig. 4
figure 4

Comparisons of the populations E, P, A, C, I and S for \({\mathcal {R}}_0<1\) and \({\mathcal {R}}_0>1\) at \(values_1\) and \(values_2\)

Full size image

It is worth mentioning that some gaps exist between the data and our model results on real data cases. Especially in late April, the Shanghai municipal government adjusted the testing strategy by expanding the coverage of nucleic acid and antigen testing, which led to the fluctuations in the actual data, showing a slightly higher fitting gap. However, even with these types of disturbances, our proposed model captures the overall trend of the epidemic relatively accurately.

4 Dynamics analysis

4.1 Numerical experiments

In order to simulate the strong behavioral dynamic characteristics of the model in a more general case, we randomly select two values in the baseline range corresponding to \({\mathcal {R}}_0<1\) and \({\mathcal {R}}_0>1\), respectively.

The first group of parameters is taken as follows:

\(value_1=\{\alpha =3.8*10^{-5}, \beta =0.7430, \beta _v= 1-\beta , \beta _s=1-\alpha , b_1=0.5582, b_2=0.3382\), \(\epsilon _p= 4.6401*10^{-8}, \epsilon _a=4.8591*10^{-8}, \epsilon _c=2.525*10^{-7}, \delta =0.5258\), \(\sigma =0.7083, r=0.4296, m=0.8635, \tau =0.9220, c_1=0.35, c_2=0.25\), \(\mu =0.003418, \delta _p=0.01658, \delta _a=0.01915, \delta _c=0.01757\), \(\mu _p=0.01994\), \(\mu _a=0.02250, \mu _c=0.0209, \gamma =0.0011428\)} with a corresponding value of the effective reproduction number, \({\mathcal {R}}_0=0.636738<1\), and the second one is taken as follows:

\(value_2=\{\alpha =3.6*10^{-5}, \beta =0.7790, \beta _v=1-\beta , \beta _s=1-\beta , b_1=0.4582, b_2=0.3382\), \(\epsilon _p= 4.5968*10^{-8}, \epsilon _a=4.5493*10^{-8}, \epsilon _c=3.0674*10^{-7}, \delta =0.8257, \sigma =0.5684, r= 0.4200, m=0.8643, \tau =0.9213, c_1=0.1543, c_2=0.4019, \mu =0.0011, \delta _p=0.0151, \delta _a=0.01546, \delta _c=0.0199\), \(\mu _p=0.016, \mu _a= 0.0165, \mu _c=0.0210, \gamma =0.0010\)} with a corresponding value of the effective reproduction number, \({\mathcal {R}}_0=2.49605>1\).

Some of the effects of these major parameters are illustrated graphically by numerical solutions of the SVEPACR model, as shown in Fig. 4a–f. These effects show that, compared with the case, \({\mathcal {R}}_0>1\), the population peaks are delayed and the population in each compartment for \({\mathcal {R}}_0<1\) is reduced considerably in the same period of time.

However, all figures in Fig. 4 show the convergences of the trajectories of model (1) to the corresponding disease-free equilibrium \(X_0=( 0, 0, 0, 0,\) \(2.90273*10^6, 146.904, 22519.9)\) for \({\mathcal {R}}_0<1\) and endemic equilibrium \(X^*=(14,000, 6431.76, 4793.38, 8517.43,\) \(3.57148*10^6, 165.165, 5.1327*10^6)\) for \({\mathcal {R}}_0>1\). This demonstrates the asymptotic stability trends of the two equilibrium, as shown in Theorems 2–3. Particularly, Fig. 4f shows the global stability of both disease-free and endemic equilibrium for the solutions (say S as example) of model (1). This implies that the spread of COVID-19 ends when \({\mathcal {R}}_0<1\) and continues in the community whenever \({\mathcal {R}}_0>1\).

4.2 Sensitivity analysis

The effective reproduction number \({\mathcal {R}}_0\) is a substantial indicator of both transmission risks and control of an infectious virus. In the following, to provide a comprehensive understanding of the influence of the different parameters, and to characterize the major parameters and their variations on the model outcomes, we compute \({\mathcal {R}}_0\) sensitivity analysis of system (1) using the normalized sensitivity index [40]

$$\begin{aligned} \Gamma =\frac{\partial {\mathcal {R}}_0}{\partial \lambda }\times \frac{\lambda }{{\mathcal {R}}_0}, \end{aligned}$$

for basic parameter representative \(\lambda \) in model (1). Thus, in Table 4, the normalized sensitivity indices formula, \(\Gamma \), and its signs and specific values at \(value_1\) and \(value_2\) are presented symbolically and numerically.

Table 4 \({\mathcal {R}}_0\) Sensitivity analysis by \(\Gamma =\frac{\partial {\mathcal {R}}_0}{\partial \lambda }\times \frac{\lambda }{{\mathcal {R}}_0}\)
Full size table

General analysis. From the calculation indices, it is clear that the main parameters to observe have strongly influenced the diffusion dynamics of the virus spreading. Particularly, parameters \(\alpha \) (the daily rate of vaccinated), \(\beta \) (the efficiency rate of vaccination), \(\tau \) (the cure rate of recommended treatment), and \(c_i(i=1,2)\) (the recovery rate from symptomatic and asymptomatic compartments) have a negative contribution on the effective reproduction number \({\mathcal {R}}_0\), that is, an increase in these parameters at some extend leads to an decrease in the \({\mathcal {R}}_0\) at same level. These are shown in Fig. 5a–d for the values of the parameters.

The parameters, \(\epsilon _i( i\in \{p, a, c\})\) (contact transmission rates) and \(\gamma \) (transmission rate of recovered people to susceptible individuals), always have positive contributions on \({\mathcal {R}}_0\); that is, an increase in these parameters to some extent leads to an increase in \({\mathcal {R}}_0\) at same level. However, it can be seen that \({\mathcal {R}}_0\) is a linear function of the transmission rates \(\epsilon _i(i=p,a,c)\). Hence, the monotonous positive influences of these parameters on \({\mathcal {R}}_0\) are clear. The rest of the parameters have a nonlinear influence on \({\mathcal {R}}_0\). Figure 5e shows the nonlinear dependence of \({\mathcal {R}}_0\) on \(\gamma \) as an example.

Fig. 5
figure 5

Dependence of \({\mathcal {R}}_0\) on parameters \(\alpha , \beta , \tau , c_1, \gamma , \sigma \) and \(\delta \)

Full size image

The influences of major parameters on \({\mathcal {R}}_0\) are discussed in the following.

Fig. 6
figure 6

Impacts of main parameters on the population in our model (1) at different parameters values with the confirmed individuals \(I=P+A+C\)

Full size image

Impact of \(\alpha \)and \(\beta \). Here, we considered five different values of \(\alpha \) (as shown in Fig. 6) to observe the effect of the vaccination for a fixed \(\beta \). Intensifying the vaccination campaign starts to considerably decrease the number of infected people. The more the vaccination rate \(\alpha \) is increasing, the more the infected population is decreasing for I and S, as shown in Fig. 6a, b; additionally, more people are vaccinated and recovered for V and R, as shown in Fig. 6c, d. Similarly, we take three different values of \(\beta \) to observe the effect of \(\beta \) for the fixed \(\alpha \). It is shown that the higher the value of \(\beta \) is, the less infected people there are, as shown in Fig. 6e for I. However, it can be seen that although the number of patients decreases when \(\beta \) increases, its magnitude does not decrease considerably. This shows that the vaccination rate, \(\alpha \), is important against the Covid-19 virus. Moreover, the vaccination rate, \(\alpha \), and efficiency rate, \(\beta \), must incorporate each other to essentially influence the reproduction number, \({\mathcal {R}}_0\). It should also be noted that the \({\mathcal {R}}_0\) is significantly decreasing when \(\alpha \) and \(\beta \) are increasing simultaneously. It can be seen that the number of infected individuals who are vaccinated is much lower than those without vaccination (\(\alpha \ll 1\) or \(\beta \ll 1\)).

Table 5 Relative changes of infected population as increasing of \(\tau \) and \(\epsilon _c\) in different time
Full size table

Impact of \(\tau \)and \(\epsilon _c\). In Table 4, it is explicitly noted that the most dominant influences are occurred on \(\tau \) and \(\epsilon _c\) rather than on the related vaccine parameters, \(\alpha \) and \(\beta \), for \(value_1\) and \(value_2\). This releases an important message that the recommended treatment on both symptomatic and asymptomatic infections and exposure transmission rate \(\epsilon _c\) have a critical impact on \({\mathcal {R}}_0\). The higher efficiency treatment rate \(\tau \) is and the less transmission rate \(\epsilon _c\) is, the higher the opportunity to control the disease from spreading. This demonstrates that the coordination between \(\alpha \), \(\beta \) and \(\tau \) is playing much more prominent roles for controlling the disease, implying that the vital role of combination between recommended treatment and vaccination in controlling a epidemic. Similarly, it is clear that the number of infections with the recommended treatment is much lower than without the recommended treatment (\(\tau \ll 1\)) as shown in Fig. 6f.

From the perspective of relative change analysis, we can also see the important roles of \(\tau \) and \(\epsilon _c\). As a result, we investigated the relative change of the number of infected individuals when \(\tau \) changes. We took five values of \(\tau \). Let \(\tau _i\) represent the ith one and \(I_i=P_i[t]+A_i[t]+C_i[t]\) be the total number of infected individuals at time t and \(\tau _i\). Then, the relative change of the population is characterized by the formula

$$\begin{aligned} R_{[l,r]}^i=\frac{\int _{t_l}^{t_r}I_i(s)ds}{\int _0^{t_r}I_i(s)ds} \end{aligned}$$
(8)

on interval \([t_l,t_r]\) at rate \(\tau _i\). The numerator of the formula is the total number of infected individuals in interval \([t_l,t_r]\) at \(\tau _i\). The denominator is the total number of infected individuals in interval \([0, t_r]\) for same \(\tau _i\). Actually, the \(R^i_{[t_l, t_r]}\) is the relative increased number of infected individuals in interval \([t_l, t_r]\) and w. r. t total number of infected people on the whole interval \([0, t_r]\).

We observed the relative change in population as \(\tau _i\) increases by \(55\%, 65\%, 75\%, 85\%\) and \(95\%\), on each interval [10, 20], [20, 30], [30, 40] (that is \(t_l=10, 20, 30\) and \(t_r=20, 30, 40\)) for two different values \(\epsilon _c=3.067*10^{-8}\) in \(value_1\) and \(\epsilon _c=3.067*10^{-7}\) in \(value_2\), which correspond to \({\mathcal {R}}_0<1\) and \({\mathcal {R}}_0>1\) respectively. The rest of the parameter values were taken as \(value_1\) and \(value_2\) correspondingly. The computation results are shown in Table 5.

It can be seen in this table that when \({\mathcal {R}}_0<1\), the proportion of infected people decreases rapidly with the increase in \(\tau \) in different time intervals. However, when \({\mathcal {R}}_0>1\), although the growth rate of infected people decreases with the increase in \(\tau \), the proportion of infected people keeps increasing at all time intervals. Again, this demonstrates the necessity of raising \(\tau \) and lowering \(\epsilon _c\), which leads to a decrease in \({\mathcal {R}}_0\).

In the time dimension, the number of infected people always decreases at different time levels. This can be interpreted as the overall impact of vaccinations and recommended treatments for mitigating outbreaks of the disease over time.

Combined impacts of \(\alpha , \beta \) and \(\tau \). Suppose the parameters that are not involved in the following limits are fixed. It can be seen that \(\lim _{\alpha \rightarrow 1} {\mathcal {R}}_0\not =0\), \(\lim _{\beta \rightarrow 1} {\mathcal {R}}_0\not =0\), \(\lim _{\tau \rightarrow 1} {\mathcal {R}}_0\not =0\), \(\lim _{(\alpha ,\tau ) \rightarrow (1, 1)} {\mathcal {R}}_0\not =0\) and \(\lim _{(\beta , \tau ) \rightarrow (1, 1)} {\mathcal {R}}_0\not =0\), while \(\lim _{(\alpha , \beta ) \rightarrow (1, 1)} {\mathcal {R}}_0=0\). These limits show important information on controlling the epidemic using vaccines and recommended treatments. That is, to mitigate the spreading of the virus (expecting \({\mathcal {R}}_0\ll 1\)), \(\alpha \approx 1\) and \(\beta \approx 1\) are needed simultaneously. However, it is difficult for humans to achieve the values of the limits. Therefore, it is not sufficient to eradicate the disease using vaccination or special treatment alone. Even if a specific medicine is found (expecting \(\tau \rightarrow 1\)), it still needs to be used in combination with a large scale of vaccinations (\(\alpha \rightarrow 1\)) to avoid repeated outbreaks of the pandemic. This demonstrates the importance of alliance among \(\alpha \), \(\beta \) and \(\tau \).

Impact of \(\sigma , \delta \). A particular situation about the impacts of \(\delta \) and \(\sigma \) on \({\mathcal {R}}_0\). In Table 4, it can be seen that their contribution signs on \({\mathcal {R}}_0\) are not deterministic. It depends on the interactions between compartments (P) and (C) ((A) and (C)). To characterize the phenomena, we introduce a concept called cross-infection rate of a compartment w.r.t another one in the following definition.

Definition 1

The product between the total rate of removal from one compartment (say (P)) to both recovery and death and the rate of transmission in the other compartment (say (C)) is called the cross-infection rate of the compartment (P) w.r.t another one (C).

By this definition, products \((c_1+\mu _p)\epsilon _c\) and \(\theta _4\epsilon _p\) are the cross-infection rates of compartment (P) w.r.t (C) and (C) w.r.t (P), respectively. Thus, according to the sensitivity analysis formula in Table 4, the difference between the two cross-infection rates decides the sensitivity contribution of \(\delta \) to \({\mathcal {R}}_0\). That is, if the cross-infection rate of (P) w.r.t (C) is less than the that of (C) w.r.t (P), i.e., \((c_1+\mu _p)\epsilon _c<\theta _4\epsilon _p\), then \(\delta \) makes a negative contribution to \({\mathcal {R}}_0\); otherwise, it makes a positive contribution to \({\mathcal {R}}_0\). Similarly, \(\sigma \) makes a negative contribution if the cross-infection rate of (A) w.r.t (C) is less than the one of (C) w.r.t (A), i.e., \((c_1+\mu _a)\epsilon _c<\theta _4\epsilon _a\); otherwise it makes a positive contribution to \({\mathcal {R}}_0\). These situations are illustrated numerically in Fig. 5f–i. Hence, in the real world, it is more desirable for the treated individuals to have a lower infectious rate and to expect \(\epsilon _c\rightarrow 0\) so that \(\delta \) and \(\sigma \) can have a negative influence on \({\mathcal {R}}_0\). This suggests that authorities should take public healthy interventions on infected compartments (P), (A) and (C) to reduce the infectious rates \((c_1+\mu _p)\epsilon _c\) and increase \(\theta _4=\tau +\mu _c\) since this contributed massively to the reduction in secondary infections from one infected compartment to another. Equivalently, the authorities should make efforts to allow the transmission rate to reduce as \(\epsilon _c\rightarrow 0\) and intensify efforts to take more effective recommended treatment (expecting \(\tau \rightarrow 1\)).

Impact of the secondary infectious rate \(\gamma \). The parameter, \(\gamma \), is the secondary infectious rate of the recovered individuals, which always has a positive influence on \({\mathcal {R}}_0\), as seen from the formula in Table 4. It can also represent the expiration of a vaccine in a sense. This means that the existence of the secondary infections (\(\gamma >0\)) may not stop spreading the disease. This proves that decreasing the value of \(\gamma \) is one essential factor for eliminating ways to spread the disease. Again, this proves the importance of authorities strongly intervening, by maintaining special social interventions. This also calls for recommending treatment, which should be advocated toward provision for long term or permanent immunity to break the path between the recovered class and reinfections. Furthermore, this also implies that the booster vaccine campaign to improve the herd immunity is necessary.

Impact of compounded parameters \(\theta _i\)and \(\epsilon _i\). At a more macroscopic level, the basic parameters given in Table 2 have comprehensive influences on the dynamic performance of the model through their compounding, as provided in Table 1. It is clear that \({\mathcal {R}}_0\) is inversely proportional to the rates \(\theta _i(I =1,2, \ldots , 7)\) of people leaving the compartments and is directly proportional to the contact rates \(\epsilon _i(i =1,2,3)\). This indicates that the sooner an individual’s virus-carrying status is confirmed, the better the chance of reducing the transmission of the virus and controlling the outbreak. Hence, screening out carriers as earlier as possible is crucial for epidemic prevention. That is why many countries (including China) have resorted to mass testing. Therefore, the proposed model has been revealed and strengthened by the basic principles of epidemic prevention.

5 Discussion and conclusion

Inspired by using of vaccination and more recommended treatments to contain the COVID-19 pandemic, a new dynamical model of COVID-19 transmission is proposed to study the dynamic behavior of the spread of COVID-19. To reflect the special nature of the virus, the model especially includes the symptomatic and asymptomatic individuals compartments. However, in addition to the compartments of susceptible groups, exposed groups and recovered groups, the model also includes vaccination and a recommended treatment compartments to reflect the effects of vaccines and special treatments. Particularly, the recommended treatment in this article is a general conceptual compartment that can contain various treatments or interventions quantified by \(\delta , \sigma \) and \(\tau \). Thus, the model is a general and strong nonlinear mathematical model composed of seven compartments and eighteen parameters.

Achievements of the study can be briefly summarized as follows.

First, the nonnegativity, boundedness of the solutions to the proposed model and local and global stability of disease-free equilibrium and unique existence of endemic equilibrium are proved using the analysis methods and symbolic computations, which demonstrate that the model is well-posed. Particularly, the model’s ability to adapt to real case data is verified by fitting the model with the real data on the epidemic that occurred in Shanghai, China in 2022. Correspondingly, the reproduction number is estimated as \({\mathcal {R}}_0<1\) by our model, which is in line with the actual policy situation at the time and the fact that the pandemic in Shanghai ended at the end of May 2022.

Second, one of most critical indices of the model’s effective reproduction number \({\mathcal {R}}_0\) is determined by the next generation method. As seen in (4), \({\mathcal {R}}_0\) is expressed by the parameters in the model and written as a summation of three terms representing the correlative influences of the compartments (E), (P), (A) and (C) on \({\mathcal {R}}_0\). This proved the compatibility among model’s the compartments.

Third, detailed analysis on the influence of major parameters on the reproduction number \({\mathcal {R}}_0\) is carried out through a sensitivity analysis of \({\mathcal {R}}_0\). For vaccination to have an appreciable impact on containment, the analysis indicates that a massive increase in vaccination rate \(\alpha \) and vaccine effectiveness \(\beta \) is needed since \(\lim _{(\alpha ,\beta ) \rightarrow (1,1)}{\mathcal {R}}_0=0\). This basic feature of the model is consistent with people’s perceptions and expectations. The analysis also shows that the therapeutic effect, \(\tau \), of the recommended treatment is a prominent element in curbing the spread of the virus. It considerably enhances the effectiveness of controlling the virus with the vaccine. Thus, an effective combination of the vaccines and recommended treatments is a necessary way to control the pandemic. The contact transmission rates \(\epsilon _j (j\in \{p, a, c\})\) have positive influences on \({\mathcal {R}}_0\) directly. Particularly, the compartment (C) as the ultimate stage of transmission is playing the last defense role for preventing the disease. Therefore, lowering the contact transmission rate \(\epsilon _c\) and increasing curative ratio \(\tau \) are the tasks that must be carried out to control the recurrence of the epidemic. Because the individuals in compartment (C) have been identified (diagnosed), it is easier to take measures to control the infections, i.e., expecting \(\epsilon _c\rightarrow 0\). As a result, parameters \(\delta \) and \(\sigma \) have negative influences on \({\mathcal {R}}_0\); otherwise, we would have the opposite result. To further show the roles of compartment (C) (through \(\epsilon _c\) and \(\tau \)), we use a concept of relative change number of infected individuals, explaining the decrease of infected people as \(\tau \) increases and time goes. In addition, to explain the impacts of \(\delta \) and \(\sigma \), we introduce the concept of cross-infection rate of a compartment w.r.t (see Definition 3.1). The concept can illustrate the cross-infections among the disease compartments in the SVEPACR model, which determines the trend of spreading COVID-19 to some extent. On this basis, the model can explain the measures and objectives taken by the Chinese government to control the epidemic, such as establishing shelter hospitals, isolating the infected individuals from the society (decreasing \(\epsilon _c\)) and using TCM treatment (increasing \(\tau \)). However, the model clearly shows that the existence of secondary infections (positive contribution of \(\gamma >0\) on \({\mathcal {R}}_0\)) means that the spread of COVID-19 potentially exist.

Fourth, similar papers with present articles are articles [2, 5, 10, 11, 17, 27]. Compared with our proposed model, although Diagne et al. [2] used their seven-compartment COVID-19 model to consider vaccination and treatment, their model was different in terms of the compartmental network structure (in which the treatment compartment was only connected with the symptomatic one) and in their research method (they used the optimal control method). The articles [5, 17] considered intensive early diagnosis and stay-at-home measurements as specific treatments without vaccination. Acuña-Zegarra et al. [11] considered the vaccination, symptomatic and asymptomatic compartments in their seven-compartment model of COVID-19, but did not consider the treatment. The articles [10, 27] only considered the use of vaccines, but treatment. These studies show the importance of considering the vaccination and treatment to control the epidemic from the different point of view. Although it is impossible to compare in detail, it can be seen from the calculation results that under approximate initial conditions, the total number of infected individuals obtained by our model is in line with the result of the articles [17]. However, our model became a considerably delayed during the peaks of infected people. This is due to the combined effect of vaccination and recommended treatments.

In summary, the proposed model has the ability to achieve features of COVID-19 dynamic transmission and provide alternative perspectives to understand the mechanism of the disease. Intensifying the combination of the vaccination campaign and recommended treatments can help reduce the number of COVID-19 infections substantially.

In addition, this paper provides a purposeful reference for management cost accounting. Generally, the recommended treatment is at a relatively lower cost, and it is safe and easily operative. As a result, it will substantially reduce the overall cost of fighting the COVID-19 pandemic. This low-cost recommended treatment can be replicated in low- and middle-income regions and countries in the long run. Hence, the proposed model can serve as a basic tool for health authorities to plan, prepare and take appropriate measures to control the spread of COVID-19 or other diseases.

Furthermore, this study has some limitations as a new model of the relatively recent elements related to COVID-19, and therefore, few real cases of data are accessible in this investigation. We did not consider the time depending rate of vaccination. In fact, time varying is more suitable to describe the real cases. In the future, we can further explore this model. Even with these shortcomings, the model can be useful due to its highly reliable abilities for theoretical and numerical analysis, as shown in the article.

Finally, we suggest new directions for further research on the model:

  1. 1.

    Fit the parameters of the model to simulate real cases with different scenarios.

  2. 2.

    Implement the corresponding optimal control model.

  3. 3.

    Study the time depending on the vaccination rate.

  4. 4.

    Based on this model, develop an optimization model of vaccine or specific medicine production, inventory and distribution logistics against a pandemic.

These new directions are under current study and will be addressed elsewhere.