Abstract
Mathematical modelling of infectious diseases has shown that combinations of isolation, quarantine, vaccine and treatment are often necessary in order to eliminate most infectious diseases. However, if they are not administered at the right time and in the right amount, the disease elimination will remain a difficult task. Optimal control theory has proven to be a successful tool in understanding ways to curtail the spread of infectious diseases by devising the optimal diseases intervention strategies. The method consists of minimizing the cost of infection or the cost of implementing the control, or both. This paper reviews the available literature on mathematical models that use optimal control theory to deduce the optimal strategies aimed at curtailing the spread of an infectious disease.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Since the late 1950s, public health officials have been focusing on the control and elimination of the organisms that cause infectious diseases. The introduction of antibiotics, sanitation and vaccinations brought a positive perspective of disease eradication Hethcote (2000). However, factors such as resistance to the medicine by the microorganisms, demographic evolution, accelerated urbanization and increased travelling, led to new infectious diseases and the reemergence of existing diseases Hethcote (2000). Newly identified diseases include Lyme disease (1975), Legionnaires disease (1976), Toxic shock syndrome (1978), Hepatitis C (1989), Hepatitis E (1990), and Hantavirus (1993) Hethcote (2000). The emergence of Human Immunodeficiency Virus (HIV) in 1981 suddenly became an important sexually transmitted disease throughout the world Hethcote (2000). Antibiotic-resistant strains of tuberculosis, pneumonia and gonorrhea have evolved and these diseases are reemerging. Malaria, dengue, and yellow fever have also reemerged and are spreading into new regions because of climate change. Diseases such as plague and cholera continue to erupt occasionally. Most recently, the reemergence of Ebola virus disease (EVD) in 2013 has perplexed the world. Reemergence remains a serious medical burden all around the world with 15 million deaths per year estimated to be directly related to reemergence of infectious diseases Hethcote (2000).
Mathematical modelling continues to play a significant role in epidemiology by providing deeper insight into the underlying mechanisms for the spread of emerging and reemerging infectious diseases and suggesting effective control strategies Hethcote (2000). The successful eradication of these emerging diseases does not depend only on the availability of medical infrastructures but also on the ability to understand the transmission dynamics of a particular disease and the application of optimal control strategies and the implementation of logistic policies Hethcote (2000). Mathematical models have been used in comparing, planning, implementing, evaluating, and optimizing various detection, prevention, therapy, and control programs. Epidemiology modelling has contributed to the design and analysis of epidemiological surveys, suggested crucial data that should be collected, identified trends, made general forecasts, and estimate the uncertainty in forecasts Hethcote (2000). Mathematical models have been used to answer the following questions
-
How many people will be infected?
-
How many infected people will require hospitalization?
-
What is the expected maximum number of people infected at any given time?
-
What is the estimated duration of the epidemic?
These questions are of interest to the public health officials, which are generally explored by identifying the mechanisms responsible for the epidemic, without adequately taking into consideration the economic constraints in analyzing the control strategies. Since economic resources are limited, epidemiological models have started taking into consideration the economic constraints imposed by limited resources when analyzing control strategies. Optimal control theory has been applied to the mathematical models of HIV models Zarei et al. (2010), Kwon et al. (2012), Karrakchou et al. (2006), Kwon (2007), Roshanfekr et al. (2014), Okosun et al. (2013), Zhou et al. (2014), Adams et al. (2005), Costanza et al. (2013), Orellana (2011), Malaria Okosun et al. (2013), Okosun et al. (2011), Okosun and Makinde (2014), Makinde and Okosun (2011), Kim (2012), Prosper et al. (2014), Tuberculosis Moualeu et al. (2015), Silva and Torres (2013), Agusto and Adekunle (2014), Bowong and Aziz Alaoui (2013), Whang et al. (2011), Vector borne diseases Lashari (2012), Graesboll et al. (2014), Sung Lee and Ali Lashari (2014) and other diseases Yan and Zou (2008), Agusto (2013), Brown and Jane White (2011), Zaman et al. (2008), Okosun and Makinde (2014), Su and Sun (2015), Buonomo et al. (2014), Lowden et al. (2014), Roshanfekr et al. (2014), Apreutesei et al. (2014), Imran et al. (2014).
Epidemiological models often split the total population into different classes called compartments with labels such as \(S\), \(V\), \(E\), \(I\), \(R\), and \(T\) to represent, respectively, the susceptible, vaccinated, exposed, infectious, recovered and treated individuals. The choice of compartments to be included in a mathematical model often depends on the following:
-
the control mechanism;
-
the type and properties of the disease being modelled;
-
the purpose of the mathematical model.
An ordinary differential equation (ODE) or a partial differential equation (PDE) with respect to time is usually formulated for each subclass. For the purpose of this survey, mathematical models will be classified based on the control mechanism and theoretical results will be given.
The paper is organized as follows. A brief description of the necessary and sufficient conditions for the existence of multi-objective optimal control is provided in Sect. 2. A detailed description and analysis of the application of the multi-objective optimal control theory applied to continuous-time mathematical models is presented in Sect. 3. Similarly, Sect. 4 gives detailed description and analysis of application of the theory to discrete-time mathematical models. Finally, Sect. 5 summaries the conclusions based on the review.
2 Multi-objective optimal control
Suppose \(x(t)\in X \subset {\mathbb {R}}^n\), represents the state variables of a system and \(u(t)\in {\mathfrak {U}} \subset {\mathbb {R}}^m\) represents the control variables at time \(t\), with \(t_0\le t\le t_f\). An optimal control problem consists of finding a piecewise continuous control \(u(t)\) and the associated state \(x(t)\) that optimizes a cost functional \(J[x(t),u(t)]\). The majority of mathematical models that uses the optimal control theory relies on the Pontryagin’s Maximum Principle, which is a first-order condition for finding the optimal solution. This is reproduced below for convenience.
Theorem 2.1
(Pontryagin’s Maximum Principle Lenhart and Workman (2007)) If \(u^*(t)\) and \(x^*(t)\) are optimal for the problem
then there exists a piecewise differentiable adjoint variable \(\lambda (t)\) such that
for all controls \(u\) at each time \(t\), where the Hamiltonian \(H\) is given by
and
While the Pontryagin’s Maximum Principle gives the necessary conditions for the existence of an optimal solution, the following theorem provides the sufficient conditions.
Theorem 2.2
(Arrow Sufficiency Theorem Chiang (1992)) For the optimal control problem (1), the conditions of the maximum principle are sufficient for the global minimization of \(J[x(t),u(t)]\), if the minimized Hamiltonian function \(H\), defined in (2), is convex in the variable \(x\) for all \(t\) in the time interval \([t_0,t_f]\), for a given \(\lambda \).
One of the major side-effects of vaccination/treatment is the creation of drug resistant virus/bacteria which eventually leads to drug failure (due to ineffectiveness of the vaccine/treatment). Optimal control has been used to curb the creation of drug resistant virus/bacteria or drug failure (at the same time reducing the cost of treatment or vaccination) by imposing a condition that monitors the global effect of the vaccination/treatment program. Hence if \(x(t)\) represents the group of individuals to be vaccinated/treated and \(u(t)\in {\mathcal {U}}\) represents the control on vaccination/treatment, where the control set \({\mathcal {U}}\) is given by
Then, the following objective functions are to be minimized simultaneously:
and the optimal solution can be represented as
In general, there does not exist a feasible solution that minimizes both objective functions simultaneously. Hence, Pareto optimality concept is used to find the optimal control \(u^*\) that minimizes both objective functions simultaneously.
Definition 1
A solution \(u^*\in {\mathcal {U}}\) is called Pareto optimal solution of the problem (3) if and only if, there exists no other solution \(u\in {\mathcal {U}}\) such that \(I_i(u^*)\le I_i(u)\) for all \(i=1,2\), and \(I_i(u^*)<I_i(u)\) for some \(i=1,2\).
The following (Scalarization and Goal Programming Model) are two of the various methods usually used for obtaining a Pareto optimal solution for a multi-objective problem.
2.1 Goal programming model
The goal programming model is a well-known aggregating methodology for solving multi-objective programming problems by taking into account simultaneously several conflicting objectives. Thus the solution obtained through the goal programming model represents the best compromise that can be achieved by the decision maker. The Goal Programming model is a distance function where the unwanted positive and negative deviations, between the achievement and aspiration levels, are to be minimized. Goal Programming model has been widely applied in several fields such as accounting, marketing, quality control, human resources, production, economics and operations management [for example, in stochastic and deterministic optimal control models Paolo et al. (2014), Forster et al. (2014), Anita et al. (2013), La Torre and Marsiglio (2010) and in stochastic and deterministic scenario-based multi-criteria decision making models Aouni et al. (2014), Belad et al. (2013), Marco and La Torre (2012)]. In epidemiology, the scalarization method is widely used and this is discussed next.
2.2 Scalarization method
A multi-objective problem is often solved by combining all multiple objectives into one single-objective scalar function, known as the weighted-sum or scalarization method. Hence, for the problem (3), a single-objective functional \(I(u)\) can be formed by summing the weighted objectives as follows
The following Theorem guarantees that the solution of the weighted sum is Pareto optimal.
Theorem 2.3
The solution of the weighted sum problem (4) is Pareto optimal if the weighting coefficients are positive, that is, \(A_i>0\) for all \(i=1,2\) and \(\displaystyle \sum _{i=0}^2{A_i}=1\).
The present survey focuses on the use of multi-criteria optimal control in deterministic mathematical models. Deterministic mathematical models can either be continuous-time or discrete-time. We consider first, the continuous-time mathematical models.
3 Continuous-time mathematical model
Continuous mathematical models have been used to study the dynamic of infectious diseases within a human host and in the population. Optimal control has been used, in the past, to find an optimal schedule for vaccine, treatment and chemotherapy for an infected individual. It has also been used to optimally manage the resources associated to quarantine and isolation programs Yan and Zou (2008).
Consider the following SIR model without control strategies, initially designed and studied by Kermack and McKendrick (1927). This model categorises individuals in a population as Susceptible \((S)\), Infected \((I)\) and Recovered \((R)\). It simulates the transmission dynamics of diseases where individuals acquire permanent immunity. Examples include mumps, typhoid fever and smallpox:
The model assumes a constant recruitment rate (by birth) \(\Pi \) into the susceptible class. Susceptible individuals acquire infection and become infected, following effective contact with infected individuals, at a rate \(\beta SI\), where \(\beta \) is the effective contact rate. Infected individuals recover and move to the Recover class \(R\) at a rate \(\gamma \). Natural death occurs in all class at a rate \(\mu \). All discussions will be based on incorporating different controls in the SIR model. This is done next.
3.1 Optimal control in SIR model with vaccination
Consider the extension of the SIR model 5 through incorporation of a vaccination class \((V)\):
with the initial conditions \(S(0)>0, I(0)\ge 0\), \(R(0)\ge 0\) and \(V(0)\ge 0\). The new class represents the group of individuals who get vaccinated when susceptible, at a continuous rate \(\alpha u(t)\). The model assumes that the vaccination is not 100 % efficient and as such, individuals in this class can be infected via contact with individuals in the infected/infectious class \(I\), but at a lower rate \(\beta \epsilon \,(0\le \epsilon <1)\). The control function \(u(t)\), with \(0\le u(t)\le 1\) represents the fraction of susceptible individuals that requires vaccination. When \(u(t)\) is close to 1, then vaccination failure is very low but with high implementation costs.
For the model (6), the single-objective cost functional to be minimized is given by
with \(a_0>0\) and \(a_1>0\), where we want to minimize the infected/infectious group \(I\) while also keeping the cost of vaccination \(u(t)\) low. It is generally assumed that the cost of control is usually nonlinear with the quadratic form as given in Eq. (7) which is a convex function. This quadratic form in Eq. (7) represents “giving too much of vaccine to an individual” which often leads to waste. The term \(a_0I(t)\) represents the cost of infection, while the term \(\displaystyle \frac{a_1}{2}u^2(t)\) represents the cost of vaccination program at the time \(t\). The goal is to find an optimal control, \(u^*\), such that
where
Applying the Pontryagins Maximum Principle, we have the following result
Theorem 3.1
There exists an optimal control \(u^*\) and the corresponding solution \((S^*, V^*, I^*, R^*)\) of the system (6), that minimizes \(J(u)\) over \(\Omega _1\). Furthermore, there exist adjoint functions, \(\lambda _1(t), \ldots , \lambda _4(t)\), such that
with the transversality conditions
and the control \(u^*\) satisfies the optimality condition
Proof
The existence of an optimal control is guaranteed by Corollary 4.1 of Fleming and Rishel (1975) due the following
-
the convexity of the integrand of \(J\) with respect to \(u\);
-
a priori boundedness of the state solutions;
-
Lipschitz property of the state system with respect to the state variables.
Thus, applying Pontryagin’s Maximum Principle, we convert (6), (7) and (8) into a problem of minimizing a Hamiltonian, \(H\), pointwise with respect to \(u\):
where \(f_i\), \(i=1,\ldots ,4\) are the right-hand sides of the system (6) and we have the adjoint equations
Evaluating the equations in (14) at the optimal control and the corresponding states will give the adjoint system (10) and (11). On the interior of the set \(\Omega \), where \(0< u<1\), we have
Solving Equation (15) for \(u^*\) gives the characterization (12). \(\square \)
It can be shown that the state \([S(t), V(t), I(t), R(t)]\) and the adjoint functions \(\lambda _1(t), \ldots , \lambda _4(t)\) are all bounded. Furthermore, based on the Lipschitz structure of the ODEs, a unique optimal control \(u^*\) is obtained for small \(t_f\). The uniqueness of the optimal control follows from the uniqueness of the optimality system, which consists of (6), (10) and (11) with the characterizations (12).
3.2 Optimal control in SIR model with treatment
Consider the SIR model with treatment, given by:
A new treatment class \((T)\) is added to the SIR model (5) which represents the group of individuals who are receiving treatment to cure an infection. The model assumes that people leave the infected class \(I\) at a rate \(\gamma \). A fraction \((1-u(t)\kappa )\) of those leaving the infected class will recover from the infection without receiving treatment while the remaining fraction \(u(t)s\) will receive treatment and move to the treatment class \((T)\). Treated individuals recover faster at a rate \(\tau \) as compared to those who do not receive treatment so that \(\tau >(1-u(t)\kappa )\gamma \). The control function \(u(t)\), with \(0\le u(t)\le 1\) represents the fraction of the infected individuals who are identified and will be treated (to reduce the number of individuals that may be infectious). When \(u(t)\) is close to 1, then the treatment failure is low but the implementation cost is high.
For the model (16), the single-objective cost functional to be minimized is given by
with \(a_0>0\) and \(a_1>0\), where we want to minimize the infectious group \(I\) while also keeping the cost of treatment \(u(t)\) low. The term \(a_0I(t)\) represents the cost of infection, while the term \(\displaystyle \frac{a_1}{2}u^2(t)\) represents the cost of treatment. The goal is to find an optimal control, \(u^*\), such that
where
Applying the Pontryagins Maximum Principle, we have the following result
Theorem 3.2
There exists an optimal control \(u^*\) and the corresponding solution \((S^*, I^*, T^*, R^*)\) of the system (16), that minimizes \(J(u)\) over \(\Omega _2\). Furthermore, there exists adjoint functions, \(\lambda _1(t),\ldots ,\lambda _4(t)\), such that
with transversality conditions
The control \(u^*\) satisfies the optimality condition
Proof
The proof is similar to that of Theorem 3.1 with the Hamiltonian, \(H\), given by
where \(f_i\), \(i=1,\ldots ,4\) are the right-hand sides of the differential Eq. (16). \(\square \)
Similarly, due to the uniqueness of the optimality system (16), (20), (21) with the characterizations (22), a unique optimal control \(u^*\) exists for small \(t_f\).
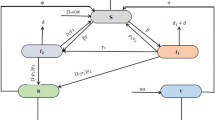
3.3 Optimal control in SIR model with quarantine and isolation
Consider the SIR model with quarantine and isolation, given by:
Here, three additional classes the exposed \((E)\), quarantine \((Q)\) and isolation \((J)\) classes have been added. The new model (24) assumes that susceptible individuals acquire new infection via contact with individuals in the Quarantine, exposed or isolation classes at a rate \(\beta S(I+\epsilon _QQ+\epsilon _JJ)\) with \(\epsilon _Q\ge 0\) representing varying levels of hygiene precautions that may or may not limit the quarantined individuals from making an effective contact with the susceptible individuals. The parameter \(\epsilon _J\ge 0\) represents level of hygiene precautions during isolation. Upon exposure to infection, exposed individuals who can be identified are quarantined at a rate \(u_1(t)\kappa \gamma \) while those who cannot be identified will become infectious at a rate \((1-u_1(t)\kappa )\gamma \), without being quarantined. Some of the individuals in the quarantined class will develop symptoms at a rate \(\eta \) and will be isolated while those who do not develop symptoms and clear infection may become susceptible again at a rate \(\rho \). Infectious individuals who have been identified are isolated at a rate \(u_2(t)\nu \alpha \) while others recover from the infection at a rate \((1-u_2(t)\nu )\alpha \). Isolated individuals eventually recover from the infection at a rate \(\sigma \) and move to the \(R\) class.
The control function \(u_1(t)\), with \(0\le u_1(t)\le 1\) represents the fraction of the quarantined individuals (people who have been in contact with an infected individual) who are identified and will be quarantined. The control function \(u_2(t)\), with \(0\le u_2(t)\le 1\) similarly represents the fraction of the isolated individuals (isolation of symptomatic individuals) who are identified and will be isolated. When \(u_1(t)\) or \(u_2(t)\) is close to 1, then the quarantined or isolation failure is low and their implementation costs are high. For the model (24), the single-objective cost functional to be minimized is given by
with \(a_i>0\), \(i=1,\ldots ,5\), where we want to minimize the infectious group \(I\) while also keeping the cost of treatment \(u(t)\) low. The term \(a_0I(t)\) represents the cost of infection, while the terms \(\displaystyle \frac{a_3}{2}u_1^2(t)\) and \(\displaystyle \frac{a_4}{2}u_2^2(t)\) represent the cost of quarantine and isolation, respectively. The goal is to find an optimal control pair, \(u_1^*\) and \(u_2^*\), such that
where
Applying the Pontryagin’s Maximum Principle, we have the following result
Theorem 3.3
There exists an optimal control pair \(u_1^*\) and \(u_2^*\) and the corresponding solution \((S^*, E^*, Q^*, I^*, J^*, R^*)\) of the system (24), that minimizes \(J(u_1,u_2)\) over \(\Omega _3\). Furthermore, there exist adjoint functions, \(\lambda _1(t),\ldots ,\lambda _6(t)\), such that
with transversality conditions
The control pair \(u_1^*\) and \(u_2^*\) satisfies the optimality condition
Proof
The proof follows with the Hamiltonian, \(H\), given by
where \(f_i\), \(i=1,\ldots ,6\) are the right-hand sides of the differential Equation (24). \(\square \)
Here, again, due to the uniqueness of the optimality system (24), (28), (29) with the characterizations (30), a unique optimal control pair \((u_1^*,u_2^*)\) exists for small \(t_f\).
3.4 Optimal control in age-structured model
Consider the SVIR model with age-structure given by:
with
for \(0\le t\le t_f\) and \(0\le a\le a_m\). The rates \(\Pi \), \(\alpha , \epsilon \) and \(\gamma \) (assumed independent of age) are the same as in the SVIR model (6) without age structure. In the model (32), it is assumed that the contact rate between people of age \(a\) and \(\check{a}\) is separable in the form \(\beta (a,\check{a})=\kappa (a)\delta (\check{a})\), while \(\mu (a)\) is the age-specific per-capita death rate. The functions \(\kappa (a)\), \(\delta (a)\) and \(\mu (a)\) are assumed continuous and will take the value zero beyond some maximum age \((a_m)\). For the model (32), the single-objective cost functional to be minimized is given by
with \(A>0\) and \(B>0\), where the goal is to minimize the infectious group \(I\) while also keeping the cost of treatment \(u(t)\) low. The term \(AI(a,t)\) represents the cost of infection for all individuals in age group \(a\) at time \(t\), while the terms \(\displaystyle \frac{B}{2}u^2(a,t)\) represents the cost of treatment for all individuals in age group \(a\) at time \(t\). The goal is to find an optimal control, \(u^*\), such that
where
The sensitivity equation (for variation \(l\)) of the model (32) is given by
which can be written in the form
with,
where, \(M\) is the matrix
and
The final term \({\mathcal {G}}\) is given by
Using the relation
where, \({\mathcal {L}}^*\) is the adjoint operator. We can find the equations of the adjoints \(\lambda _1,\ldots ,\lambda _4\). The adjoint PDE system
where \(A\) is a constant from the cost functional. The adjoint operator is given by
with
For the adjoint system, we have zero Neumann conditions and zero final-time solutions. The adjoint system is calculated at the optimal control \(u^*\) and the corresponding states \(S^*, V^*, I^*\) and \(R^*\). The transversality conditions are
The characterization of the optimal control is obtained by computing the directional derivative of the functional \(J(u)\) with respect to \(u\) in the direction \(l\) at \(u^*\). Since \(J(u^*)\) is the minimum value, we have
This implies that the optimal controls are
Thus, we have the following result.
Theorem 3.4
There exists an optimal control \(u^*\) and the corresponding solution \((S^*(a,t),V^*(a,t),I^*(a,t),R^*(a,t))\) of the system (32), that minimizes \(J(u)\) over \(\Omega _4\). Furthermore, there exists adjoint equations (PDEs), given by (42) with transversality conditions (45) and the control \(u^*\) satisfies the optimality condition
4 Optimal control in discrete-time mathematical model
Consider the discrete-time equivalent of the SIR model with vaccination given by:
For the model (47), the single-objective cost functional to be minimized is given by
with \(A_k>0\) and \(B_k>0\) for \(k=1,\ldots ,t_f\), where the parameters \(A_k>0\) and \(B_k>0\) are the cost balancing factors. The problem minimizes the number of infected individuals during the time steps \(k=0\) to \(k=t_f\) while minimizing the cost of the control at the same time. The goal is to find an optimal control \(u^*\), such that
where,
Applying the Pontryagin’s Maximum Principle, we have the following result
Theorem 4.1
There exists an optimal control \(u^*\) and the corresponding solution, \((S_k^*, V_k^*, I_k^*, R_k^*)\), that minimizes \(J(u)\) over \(\Omega _5\). Furthermore, there exist adjoint functions, \(\lambda _{1,k},\ldots ,\lambda _{4,k}\), such that
with transversality conditions
and the controls \(u^*\) satisfies the optimality condition
Proof
The Hamiltonian \(H_k\) at the time step \(k\), is given by,
where \(f_i\), \(i=1,\ldots ,4\) are the right-hand sides of the system (47). For \(k=0,\ldots ,t_f-1\), the adjoint equations and the transversality conditions are obtained by using the Pontryagin’s Maximum Principle, in discrete time, such that
and the optimality condition (51) is obtained by solving for \(u_k^*\) in the interior of \(\Omega _5\) when
\(\square \)
5 Conclusions
In this survey, we have shown how the multi-objective optimal control has been implemented in epidemiological models. Mathematical models have been useful in comparing, planning, implementing and evaluating various intervention strategies for the prevention and control of various infectious diseases. Furthermore, the original goal of optimal control is to enforce the natural restriction of economic constraints imposed by limited resources when analyzing control strategies, it has also been helpful in devising control strategies aimed at curbing creation of drug/vaccine resistant virus/bacteria. This is achieved by limiting the amount of drugs administered to an infected individual or by limiting the amount of vaccine administered to a susceptible individual (while reducing the cost of implementation at the same time). Because of Optimal control theory, the goal of eradicating infectious diseases in a community with limited resources, is now a step closer to being achieved.
References
Adams, B. M., Banks, H. T., Davidian, M., Kwon, H., Tran, H. T., Wynne, S. N., & Rosenberg, E. S. (2005). HIV dynamics: Modeling, data analysis, and optimal treatment protocols. Journal of Computational and Applied Mathematics, 184(1), 10–49. Special Issue on Mathematics Applied to Immunology Special Issue on Mathematics Applied to Immunology.
Agusto, F. B. (2013). Optimal isolation control strategies and cost-effectiveness analysis of a two-strain avian influenza model. Biosystems, 113(3), 155–164.
Agusto, F. B., & Adekunle, A. I. (2014). Optimal control of a two-strain tuberculosis-hiv/aids co-infection model. Biosystems, 119, 20–44.
Anita, S., Capasso, V., Kunze, H., & La Torre, D. (2013). Optimal control and long-run dynamics for a spatial economic growth model with physical capital accumulation and pollution diffusion. Applied Mathematics Letters, 26(8), 908–912.
Aouni, B., Colapinto, C., & La Torre, D. (2014). Financial portfolio management through the goal programming model: Current state-of-the-art. European Journal of Operational Research, 234(2), 536–545. 60 years following Harry Markowitzs contribution to portfolio theory and operations research.
Apreutesei, N., Dimitriu, G., & Strugariu, R. (2014). An optimal control problem for a two-prey and one-predator model with diffusion. Computers and Mathematics with Applications, 67(12), 2127–2143. Efficient Algorithms for Large Scale Scientific Computations.
Belad, A., Cinzia, C., & La Torre, D. (2013). A cardinality constrained stochastic goal programming model with satisfaction functions for venture capital investment decision making. Annals of Operations Research, 205(1), 77–88.
Bowong, S., & Aziz Alaoui, A. M. (2013). Optimal intervention strategies for tuberculosis. Communications in Nonlinear Science and Numerical Simulation, 18(6), 1441–1453.
Brown, V. L., & Jane White, K. A. (2011). The role of optimal control in assessing the most cost-effective implementation of a vaccination programme: {HPV} as a case study. Mathematical Biosciences, 231(2), 126–134.
Buonomo, B., Lacitignola, D., & Vargas-De-Len, C. (2014). Qualitative analysis and optimal control of an epidemic model with vaccination and treatment. Mathematics and Computers in Simulation, 100, 88–102.
Chiang, A. C. (1992). Elements of dynamic optimization. New York, NY: McGraw-Hill international editions, McGraw-Hill. [u.a.], internat. ed. edition.
Costanza, V., Rivadeneira, P. S., Biafore, F. L., & DAttellis, C. E. (2013). Optimizing thymic recovery in HIV patients through multidrug therapies. Biomedical Signal Processing and Control, 8(1), 90–97.
Fleming, W. H., & Rishel, R. W. (1975). Deterministic and stochastic optimal control. New York: Springer.
Forster, M., La Torre, D., & Lambert, P. J. (2014). Optimal control of inequality under uncertainty. Mathematical Social Sciences, 68, 53–59.
Graesboll, K., Enoe, C., Bodker, R., & Engbo Christiansen, L. (2014). Optimal vaccination strategies against vector-borne diseases. Spatial and Spatio-temporal Epidemiology, 11, 153–162.
Hethcote, Herbert W. (2000). The mathematics of infectious diseases. SIAM Review, 42(4), 599–653.
Imran, M., Rafique, H., Khan, A., & Malik, T. (2014). A model of bi-mode transmission dynamics of hepatitis c with optimal control. Theory in Biosciences, 133(2), 91–109.
Karrakchou, J., Rachik, M., & Gourari, S. (2006). Optimal control and infectiology: Application to an hiv/aids model. Applied Mathematics and Computation, 177(2), 807–818.
Kermack, W. O., & McKendrick, A. G. (1927). A contribution to the mathematical theory of epidemics. Proceedings of the Royal Society of London. Series A, 115(772), 700–721.
Kim, B. N., Nah, K., Chu, C., Ryu, S. U., Kang, Y. H., & Kim, Y. (2012). Optimal control strategy of plasmodium vivax malaria transmission in korea. Osong Public Health and Research Perspectives, 3(3), 128–136.
Kwon, H. (2007). Optimal treatment strategies derived from a {HIV} model with drug-resistant mutants. Applied Mathematics and Computation, 188(2), 1193–1204.
Kwon, H., Lee, J., & Yang, S. (2012). Optimal control of an age-structured model of {HIV} infection. Applied Mathematics and Computation, 219(5), 2766–2779.
La Torre, D., & Marsiglio, S. (2010). Endogenous technological progress in a multi-sector growth model. Economic Modelling, 27(5), 1017–1028.
Lashari, A. A., & Zaman, G. (2012). Optimal control of a vector borne disease with horizontal transmission. Nonlinear Analysis: Real World Applications, 13(1), 203–212.
Lee, K. S., & Lashari, A. A. (2014). Stability analysis and optimal control of pine wilt disease with horizontal transmission in vector population. Applied Mathematics and Computation, 226, 793–804.
Lenhart, S., & Workman, J. T. (2007). Optimal control applied to biological models. Mathematical and computational biology. Boca Raton (Fla.), London: Chapman & Hall/CRC.
Lowden, J., Miller Neilan, R., & Yahdi, M. (2014). Optimal control of vancomycin-resistant enterococci using preventive care and treatment of infections. Mathematical Biosciences, 249, 8–17.
Makinde, O. D., & Okosun, K. O. (2011). Impact of chemo-therapy on optimal control of malaria disease with infected immigrants. Biosystems, 104(1), 32–41.
Marco, M., & La Torre, D. (2012). A goal programming model with satisfaction function for risk management and optimal portfolio diversification. INFOR: Information Systems and Operational Research, 20(3), 117–126.
Moualeu, D. P., Weiser, M., Ehrig, R., & Deuflhard, P. (2015). Optimal control for a tuberculosis model with undetected cases in cameroon. Communications in Nonlinear Science and Numerical Simulation, 20(3), 986–1003.
Okosun, K. O., Ouifki, R., & Marcus, N. (2011). Optimal control analysis of a malaria disease transmission model that includes treatment and vaccination with waning immunity. Biosystems, 106(23), 136–145.
Okosun, K. O., Makinde, O. D., & Takaidza, I. (2013). Impact of optimal control on the treatment of hiv/aids and screening of unaware infectives. Applied Mathematical Modelling, 37(6), 3802–3820.
Okosun, K. O., Rachid, O., & Marcus, N. (2013). Optimal control strategies and cost-effectiveness analysis of a malaria model. Biosystems, 111(2), 83–101.
Okosun, K. O., & Makinde, O. D. (2014). A co-infection model of malaria and cholera diseases with optimal control. Mathematical Biosciences, 258, 19–32.
Orellana, J. M. (2011). Optimal drug scheduling for HIV therapy efficiency improvement. Biomedical Signal Processing and Control, 6(4), 379–386.
Paolo, P., Martin, F., & La Torre, D. (2014). Optimal bayesian sequential sampling rules for the economic evaluation of health technologies. Journal of the Royal Statistical Society: Series A (Statistics in Society), 177(2), 419–438.
Prosper, O., Ruktanonchai, N., & Martcheva, M. (2014). Optimal vaccination and bednet maintenance for the control of malaria in a region with naturally acquired immunity. Journal of Theoretical Biology, 353, 142–156.
Roshanfekr, M., Hadi Farahi, M., & Rahbarian, R. (2014). A different approach of optimal control on an {HIV} immunology model. Ain Shams Engineering Journal, 5(1), 213–219.
Silva, C. J., & Torres, D. F. M. (2013). Optimal control for a tuberculosis model with reinfection and post-exposure interventions. Mathematical Biosciences, 244(2), 154–164.
Su, Y., & Sun, D. (2015). Optimal control of anti-hbv treatment based on combination of traditional chinese medicine and western medicine. Biomedical Signal Processing and Control, 15, 41–48.
Whang, S., Choi, S., & Jung, E. (2011). A dynamic model for tuberculosis transmission and optimal treatment strategies in south korea. Journal of Theoretical Biology, 279(1), 120–131.
Yan, X., & Zou, Y. (2008). Optimal and sub-optimal quarantine and isolation control in {SARS} epidemics. Mathematical and Computer Modelling, 47(12), 235–245.
Zaman, G., Han Kang, Y., & Hyo Jung, I. (2008). Stability analysis and optimal vaccination of an {SIR} epidemic model. Biosystems, 93(3), 240–249.
Zarei, H., Vahidian Kamyad, A., & Effati, S. (2010). Multiobjective optimal control of hiv dynamics. Mathematical Problems in Engineering 2010 (Article ID 568315):1–29.
Zhou, Y., Liang, Y., & Wu, J. (2014). An optimal strategy for {HIV} multitherapy. Journal of Computational and Applied Mathematics, 263, 326–337.
Acknowledgments
The authors are grateful to the anonymous reviewers for their constructive comments, which have improved the manuscript.
Funding
This research was supported by Khalifa University Internal Research Fund (Grant No. 210032).
Conflict of Interest
The authors declare that they have no conflict of interest.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Sharomi, O., Malik, T. Optimal control in epidemiology. Ann Oper Res 251, 55–71 (2017). https://doi.org/10.1007/s10479-015-1834-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-015-1834-4