Reinforcement learning-based optimal control of unknown constrained-input nonlinear systems using simulated experience

Abstract

Reinforcement learning (RL) provides a way to approximately solve optimal control problems. Furthermore, online solutions to such problems require a method that guarantees convergence to the optimal policy while also ensuring stability during the learning process. In this study, we develop an online RL-based optimal control framework for input-constrained nonlinear systems. Its design includes two new model identifiers that learn a system’s drift dynamics: a slow identifier used to simulate experience that supports the convergence of optimal problem solutions and a fast identifier that keeps the system stable during the learning phase. This approach is a critic-only design, in which a new fast estimation law is developed for a critic network. A Lyapunov-based analysis shows that the estimated control policy converges to the optimal one. Moreover, simulation studies demonstrate the effectiveness of our developed control scheme.

1 Introduction

Optimal control is a demanding design objective of control systems, in which a cost function quantifies the system’s desired behavior with the goal of developing a control policy that minimizes the cost function under the constraints of the system dynamics. Solutions to the optimal control problem of dynamic systems generally aim to solve the underlying Hamilton-Jacobi-Bellman (HJB) equation. For nonlinear systems, an HJB equation is a nonlinear partial differential equation whose analytical solution is very difficult or even impossible to derive. Dynamic programming is the classic method used to solve HJB equations; however, since this is a backward approach, only offline solutions are possible, and it is also computationally expensive for complex systems.

Owing to the similarity of reinforcement learning (RL) and optimal control, RL has been widely implemented to solve optimal control problems. In fact, in RL, an agent interacts with its environment and improves its behavior based on the observed reward, where a complete exploration of the environment leads to the agent’s optimal behavior. Such performance resembles solutions to optimal control problems in the sense that solving HJB equations gives an evaluation of the control policy, and then the controller is updated based on this evaluation to achieve optimal performance. RL-based approaches that solve optimal control problems are also called adaptive or approximate dynamic programming (ADP), in which mainly neural networks (NNs) are used to approximately solve dynamic programming in a forward-in-time manner, thus reducing the computational complexity.

RL-based adaptive optimal controllers were first developed for discrete-time systems due to the iterative nature of the ADP approach [1, 2]. Extensions of RL-based controllers to continuous-time systems were investigated by several researchers [3,4,5]. For continuous-time systems, the problem involves several challenges, including guaranteeing convergence to optimal control policies as well as stability during the training process, dealing with the system’s model uncertainties, and ensuring that the algorithm is online. For online solutions, Vamvoudakis and Lewis [5] developed an RL-based policy iteration (PI) approach adopting the actor-critic structure, where actor and critic neural networks are simultaneously tuned. Such a method requires a model of the system. One online actor-critic approach developed for linear systems [6], called integral RL, does not require a system’s internal dynamics but rather sequentially updates the critic and actor neural networks. A previously proposed PI algorithm [7] deals with unknown system models by incorporating a model identifier in the design.

Although the main goal of RL-based controllers is to approximately solve the optimal control problem, previous works [5, 7] achieved this goal by making the system states satisfy a persistence of excitation (PE) condition, which is analogous to the exploration concept in RL. Generally, it is difficult to satisfy the PE condition in practice and impossible to guarantee it in advance. A common practice in designing RL-based controllers that satisfy the PE condition is to add a probing signal to the controller [3, 5, 7, 8]. However, this solution is problematic because the proper design of probing noise requires much trial-and-error development: The probing signal can affect the system’s stability, and when to remove the signal from the controller remains unclear. Although one approach [9] utilized the system’s recorded values to solve the online optimal control problem without a PE, other results [10, 11] showed that simulated experience using the system model can be more effective than recorded experience. Another approach [11] utilized a model identifier that estimates the system dynamics over the entire operating domain to simulate experience. However, the model identifiers that learn the system model over the whole task space are usually slow, especially for complex systems, and thus the system’s stability during the learning phase cannot be ensured.

A further issue, which is critical from a practical point of view, is the amplitude limitation on control inputs. Previous designs [5, 7, 11, 12] failed to guarantee that the control commands remain within an admissible range, which may degrade the system performance or even result in instability. Some bounded-input PI algorithms [13,14,15,16] require a dynamic model of the system. Other approaches [17, 18] guarantee convergence to the optimal problem solution by adding a probing signal, whose effect was not clarified in the stability analysis. The bounded controllers in other works [9, 19] used recorded data to deal with satisfying the PE condition; however, this approach still needs to add a finite amount of probing noise as input to the system.

In this study, we designed an RL-based approach for optimal control of input-constrained uncertain nonlinear systems. Our main motivation was to apply the simulated experience concept [11] in developing an RL controller for bounded-input systems. To achieve this goal, two novel model identifiers are incorporated in the design: a slow identifier that learns the system model over the entire operating domain of the system, which is used for experience simulation, and a fast and precise identifier that learns the model along the system trajectory, which keeps the system stable until the slow identifier provides sufficient information to solve the optimal control problem. Unlike most RL approaches that use separate networks for critics and actors as a way to maintain stability, our design is a critic-only approach, which is facilitated by exploiting a bounded feature in the components of the cost function. The update law of the critic network includes a new bounded control term that increases the learning rate. We conducted a Lyapunov-based analysis to show that the closed-loop system is uniformly ultimately bounded (UUB) and that the UUB convergence of the control policy to the optimal policy is guaranteed. Simulation studies demonstrate the effectiveness of our developed control scheme.

The main contributions of this study are as follows.

• 1. A new online RL method is developed for nonlinear systems that takes into account input constraints. Existing works addressing the same problem require an exploration signal [9, 13, 15, 18], which is difficult to design for unknown systems while ensuring that it does not threaten stability.

• 2. New model identifiers are developed that guarantee fast convergence and high precision. The identifiers are used to apply the concept of experience simulation in the solution of the RL problem for bounded-input systems.

• 3. Unlike many online RL approaches [5, 7, 11, 15], our design is a critic-only approach. In addition, a non-standard bounded adaptation term is designed for the critic network, which is shown to significantly increase the rate of convergence.

2 Optimal control problem and system definition

We studied a continuous-time nonlinear system defined as

$$\begin{aligned} \dot{{\textbf{x}}}(t)={\textbf{f}}({\textbf{x}})+{\textbf{g}}({\textbf{x}}){\textbf{u}}(t), \end{aligned}$$

(1)

where ${\textbf{x}}\in {\mathbb {R}}^{n}$ is the system state vector, ${\textbf{f}}({\textbf{x}})\in {\mathbb {R}}^{n}$ is the unknown drift dynamics of the system, ${\textbf{g}}({\textbf{x}})\in {\mathbb {R}}^{n\times m}$ is the input dynamics, which is assumed to be known in this paper, and ${\textbf{u}}=[u_1,\cdots ,u_m]^{\top }\in {\mathbb {R}}^{m}$ is the control input, which is saturated such that $|u_i|\le \lambda$ for $i=1,\cdots ,m$, where $\lambda$ is a known upper constraint of the inputs. Throughout this paper, any variable denoted with a time-dependent argument, such as ${\textbf{x}}(t)$, is used interchangeably with the corresponding variable without the argument, such as ${\textbf{x}}$.

Assumption 1

The functions ${\textbf{f}}({\textbf{x}})$ and ${\textbf{g}}({\textbf{x}})$ are second-order differentiable. In addition, ${\textbf{g}}({\textbf{x}})$ fulfills the following condition:

$$\begin{aligned} \Vert {\textbf{g}}({\textbf{x}})\Vert \le b_g \end{aligned}$$

for some $b_g\in {\mathbb {R}}^{+}$ [7, 10].

Remark 1

The boundedness of the input dynamics ${\textbf{g}}({\textbf{x}})$ that is noted in Assumption 1 is satisfied in many practical systems, including robotic systems [20] and aircraft systems [21].

For ${\textbf{u}}\in \Omega _a$, where $\Omega _a$ is the set of admissible policies [5], the following performance/value function is introduced [18]:

$$\begin{aligned} V({\textbf{x}}(t))\triangleq \int _t^{\infty }[Q({\textbf{x}}(\tau ))+U({\textbf{u}}(\tau ))]\text {d}\tau , \end{aligned}$$

(2)

where $Q({\textbf{x}})\in {\mathbb {R}}$ is a general continuous positive-definite function that penalizes states, and the positive-definite integrand function is defined as

$$\begin{aligned} U({\textbf{u}})\triangleq 2\int _{\textbf{0}}^{{\textbf{u}}}(\lambda \tanh ^{-1}({\textbf{v}}/\lambda ))^{\top }{\textbf{R}}\text {d}{\textbf{v}}, \end{aligned}$$

(3)

where ${\textbf{v}}\in {\mathbb {R}}^{m}$ is an auxiliary variable and ${\textbf{R}}=\text {diag}({\bar{r}}_1,\cdots ,{\bar{r}}_m)\in {\mathbb {R}}^{m\times m}$ is a positive-definite diagonal matrix. This nonquadratic function, which penalizes inputs, is widely adopted in the literature and practical systems to deal with input constraints [4, 13, 18].

The objective of the optimal controller is to minimize the performance function defined in Eq. (2). To develop this controller, we first differentiated V along the system trajectories (Eq. 1) using Leibniz’s rule to achieve the following Bellman equation:

$$\begin{aligned} {\dot{V}}({\textbf{x}})=-Q({\textbf{x}})-U({\textbf{u}}). \end{aligned}$$

Therefore, we can define the following Hamiltonian function:

$$\begin{aligned} H({\textbf{x}},{\textbf{u}},\nabla V)\triangleq&~Q({\textbf{x}})+U({\textbf{u}})\nonumber \\&\quad +\nabla V({\textbf{x}})\left( {\textbf{f}}({\textbf{x}})+{\textbf{g}}({\textbf{x}}){\textbf{u}}({\textbf{x}})\right) , \end{aligned}$$

(4)

where $\nabla V({\textbf{x}})\triangleq \partial V({\textbf{x}})/\partial {\textbf{x}}\in {\mathbb {R}}^{1\times n}$ is the gradient of $V({\textbf{x}})$.

Assume $V^{*}({\textbf{x}})$ is the optimal cost (value) function and that $H({\textbf{x}},{\textbf{u}}, \nabla V^{*})$ is the corresponding Hamiltonian. Consequently, the optimal controller can be obtained by employing the stationary condition on the Hamiltonian; in other words, by taking the derivative of the Hamiltonian with respect to ${\textbf{u}}$ and setting the obtained equation to zero. Then the optimal controller can be written as [13]

$$\begin{aligned} {\textbf{u}}^{*}({\textbf{x}})&=\arg \min _{{\textbf{u}}\in \Omega _a}[H({\textbf{x}},{\textbf{u}}, \nabla V^{*})]\nonumber \\&=-\lambda \tanh ({\textbf{D}}^{*}), \end{aligned}$$

(5)

where ${\textbf{D}}^{*}\triangleq \frac{1}{2\lambda }{\textbf{R}}^{-1}{\textbf{g}}({\textbf{x}})^{\top }\nabla V^{*}({\textbf{x}})^{\top }\in {\mathbb {R}}^{n}$. Substituting Eq. (5) into Eq. (3) and solving it gives [13]

$$\begin{aligned} U({\textbf{u}}^{*})\triangleq \lambda ^{2}\bar{{\textbf{R}}}\ln ({\textbf{1}}-\tanh ^{2}({\textbf{D}}^{*}))+\lambda \nabla V^{*} {\textbf{g}}\tanh ({\textbf{D}}^{*}),\nonumber \\ \end{aligned}$$

(6)

where $\bar{{\textbf{R}}}=[{\bar{r}}_1,\cdots \,{\bar{r}}_m]\in {\mathbb {R}}^{1\times n}$ and ${\textbf{1}}\in {\mathbb {R}}^{n}$ is a vector whose elements all equal 1. The optimal performance function and the associated optimal controller satisfy the following Hamilton-Jacobi-Bellman (HJB) equation:

$$\begin{aligned} H({\textbf{x}},{\textbf{u}}^{*},\nabla V^{*})&=Q({\textbf{x}})+U({\textbf{u}}^{*})+\nabla V^{*}({\textbf{f}}+{\textbf{g}}{\textbf{u}}^{*})=0. \end{aligned}$$

(7)

The optimal controller in Eq. (5) can be obtained by solving the HJB equation (Eq. 7) for the optimal value $V^{*}$ and using it in Eq. (5). However, it is generally very difficult, if not impossible, to solve this equation for nonlinear systems. The uncertainty in the dynamic model also increases the technical difficulties.

It was previously shown [13] that the above-mentioned optimal problem can be solved through offline policy iteration in a reinforcement learning-based method by estimating the value function $V({\textbf{x}})$ for a given control policy ${\textbf{u}}({\textbf{x}})$ from the Hamiltonian function (or Bellman equation) (Eq. 4) and updating the policy with the estimated value function and the structured form of the controller in Eq. (5). Thus, the algorithm converges to the solution of the HJB equation. An online policy iteration solution was proposed [5] that directly estimated the optimal value function $V^{*}({\textbf{x}})$ to solve the HJB equation expressed in Eq. (7).

This paper considers an online policy iteration-based method to solve the optimal regulation problem, and the function approximation property of neural networks (NN) estimates both optimal value function $V^{*}$ and unknown dynamic model ${\textbf{f}}$, where the estimations are denoted by ${\hat{V}}$ and $\hat{{\textbf{f}}}$, respectively. Using the estimated values, the approximate HJB equation can be written as

$$\begin{aligned} H({\textbf{x}}, \hat{{\textbf{x}}}, \hat{{\textbf{u}}},\nabla {\hat{V}}) =Q({\textbf{x}})+U(\hat{{\textbf{u}}})+\nabla {\hat{V}}(\hat{{\textbf{f}}}+{\textbf{g}}\hat{{\textbf{u}}}), \end{aligned}$$

(8)

where $\hat{{\textbf{x}}}$ is the estimate of ${\textbf{x}}$, and

$$\begin{aligned} U(\hat{{\textbf{u}}})\triangleq \lambda ^{2}\bar{{\textbf{R}}}\ln ({\textbf{1}}-\tanh ^{2}(\hat{{\textbf{D}}}))+\lambda \nabla {\hat{V}} {\textbf{g}}\tanh (\hat{{\textbf{D}}}), \end{aligned}$$

(9)

in which $\hat{{\textbf{D}}}\in {\mathbb {R}}^{n}$ is the estimate of ${\textbf{D}}^{*}$, and $\hat{{\textbf{u}}}\triangleq -\lambda \tanh (\hat{{\textbf{D}}})$.

Bellman residual error $\delta _{B}$, defined as the error between the actual and approximate HJB equations, is given by

$$\begin{aligned} \delta _{B}&\triangleq H({\textbf{x}}, \hat{{\textbf{x}}}, \hat{{\textbf{u}}},\nabla {\hat{V}})-H({\textbf{x}},{\textbf{u}}^{*},\nabla V^{*})\nonumber \\&=H({\textbf{x}}, \hat{{\textbf{x}}}, \hat{{\textbf{u}}},\nabla {\hat{V}}). \end{aligned}$$

(10)

The Bellman error is measurable and mainly used to design the tuning rule of the neural network of the value function estimator (critic network). Such a tuning approach requires the system states to satisfy the PE condition in order to guarantee convergence. However, it is difficult in practice to guarantee PE in online estimation because the system needs to visit many points in the state space. Adding probing noise is one possible solution to this problem [5, 7, 18]. The selection of probing noise requires careful attention because no analytical approach is able to compute probing noise that provides PE to nonlinear systems and, moreover, such added noise may result in instability. Although previous works [9, 22] have used the recorded past visited values of the Bellman error to solve the online optimal control problem without PE, the results of other work [11] show that the simulated experience of the Bellman error based on a system model can be more effective than using experienced data.

According to Eqs. (10) and (4), in applying a simulated experience, a uniform estimation of function ${\textbf{f}}$ is required over the entire operating domain, which allows us to estimate the value of the Bellman error in unexplored points. Online techniques for estimating ${\textbf{f}}$ over the whole task space are generally slow because they need to visit and collect sufficiently rich data. Therefore, using only this type of model identifier in the Bellman error might deteriorate the system performance and cause instability. Therefore, we use both a fast identifier that rapidly estimates the value of ${\textbf{f}}$ along the system trajectory and a slow identifier that estimates ${\textbf{f}}$ over a large space to simulate experience at the unvisited points. These estimates are denoted as $\hat{{\textbf{f}}}$ and $\hat{{\textbf{f}}}_s$, and they are used to predict the Bellman error along the trajectory and at unexplored points, respectively. These Bellman errors are used together to estimate the optimal value function. A certain amount of time is required before $\hat{{\textbf{f}}}_s$ can become accurate enough to simulate experience, so during this period, the estimated Bellman error using $\hat{{\textbf{f}}}$ provides information for stabilizing the system.

In some existing works [18, 23], a model identifier is designed to estimate the input dynamics ${\textbf{g}}({\textbf{x}})$ and drift dynamics ${\textbf{f}}({\textbf{x}})$. However, estimating them separately requires rich information, which is difficult to collect in optimal regulation problems where state and control trajectories quickly converge to zero. Therefore, similar to previous works [7, 10], in this study, we assume that the function ${\textbf{g}}({\textbf{x}})$ is known and thus only estimate the drift dynamics.

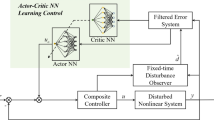
In the following sections, we first present the identifiers that estimate unknown drift dynamics ${\textbf{f}}({\textbf{x}})$, and then we present an approach to estimate the optimal value function. The critic-only optimal policy can then be extracted from the estimated value function. A block diagram of the proposed control system is shown in Fig. 1.

Fig. 1

Block diagram of proposed RL-based optimal controller

3 Identifier design

3.1 Fast model identifier along system trajectories

Our objective here is to design a fast and precise estimator for the drift dynamics ${\textbf{f}}({\textbf{x}})$ of the system (Eq. 1). To achieve this, the function approximation property of NNs is used in conjunction with a robust integral of the sign of error (RISE) term to gain continuous estimation with zero error. The prescribed performance feature is also added to satisfy the desired convergence rate.

The function ${\textbf{f}}({\textbf{x}})$ can be represented by a neural network over compact set $\Omega _N$:

$$\begin{aligned} {\textbf{f}}({\textbf{x}})={\textbf{W}}_f^{\top }\varvec{\sigma }_f({\textbf{z}})+\varvec{\epsilon }_f, \end{aligned}$$

(11)

where ${\textbf{W}}_f\in {\mathbb {R}}^{{\mathcal {L}}_f\times n}$ is a bounded constant ideal weight matrix, ${\mathcal {L}}_f$ denotes the number of neurons, $\varvec{\sigma }_f(\cdot )\in {\mathbb {R}}^{{\mathcal {L}}_f}$ is the activation matrix with vector ${\textbf{z}}$ as its input, and $\varvec{\epsilon }_f\in {\mathbb {R}}^{n}$ denotes the functional reconstruction error. Activation function $\varvec{\sigma }_f$, error $\varvec{\epsilon }_f$, and their time derivatives are assumed to be bounded [18]. Substituting Eq. (11) into Eq. (1), we obtain $\dot{{\textbf{x}}}={\textbf{W}}_f^{\top }\varvec{\sigma }_f+\varvec{\epsilon }_f+{\textbf{g}}({\textbf{x}}){\textbf{u}}$.

The identifier state is denoted by $\hat{{\textbf{x}}}\in {\mathbb {R}}^{n}$, and identification error $\tilde{{\textbf{x}}}\in {\mathbb {R}}^{n}$ is defined as $\tilde{{\textbf{x}}}\triangleq {\textbf{x}}-\hat{{\textbf{x}}}$. The objective is to design an identifier such that error $\tilde{{\textbf{x}}}$ and its time derivative converge to zero. Accordingly, the identifier can be used as an estimator of the system model. To gain a high-performance identifier, we constrain error signal $\tilde{{\textbf{x}}}=[{\tilde{x}}_1,\cdots ,{\tilde{x}}_n]^{\top }$ to converge with some desired performance conditions. According to Assumption 1, imposing a convergence rate on $\tilde{{\textbf{x}}}$ also imposes a convergence rate on the estimation of unknown function ${\textbf{f}}({\textbf{x}})$.

To constrain $\tilde{{\textbf{x}}}$, a smoothly decreasing performance function $\mu (t)\in {\mathbb {R}}^{+}$ is first introduced as [24]

$$\begin{aligned} \mu (t)\triangleq \left( \mu _{0}-\mu _{\infty }\right) \text {e}^{-\kappa _{\mu } t}+\mu _{\infty }, \end{aligned}$$

(12)

where $\kappa _{\mu }>0$ and $\mu _{0}>\mu _{\infty }>0$ are design parameters. Then, provided the error signal satisfies the condition

$$\begin{aligned} -{\bar{\delta }}_i\mu (t)<{\tilde{x}}_{i}(t)<{\bar{\delta }}_i\mu (t), \end{aligned}$$

(13)

where ${\bar{\delta }}_i\in {\mathbb {R}}^{+}$ are positive prescribed constants for $i=1,\cdots ,n$, the convergence rate of ${\tilde{x}}_{i}(t)$ is guaranteed to be faster than that of function $\mu (t)$. It can be seen from Eqs. (12) and (13) that $-{\bar{\delta }}_i\mu _0$ and ${\bar{\delta }}_i\mu _0$ respectively signify the lower bound of the undershoot and the upper bound of the overshoot of ${\tilde{x}}_{i}(t)$. In addition, the lower bound of the convergence rate of error is given by $\kappa _{\mu }$.

The following transformation is assumed to transform the constrained error $\tilde{{\textbf{x}}}$ into an unconstrained one:

$$\begin{aligned} {\tilde{x}}_{i}(t)=\mu (t)T_i(\varsigma _i), \end{aligned}$$

(14)

where $\varsigma _i\in {\mathbb {R}}$ denotes the transformed unconstrained error, and $T_i(\varsigma _i)\in {\mathbb {R}}$ is a strictly increasing function satisfying the following criteria:

$$\begin{aligned}&-{\bar{\delta }}_i<T_i(\varsigma _i)<{\bar{\delta }}_i,\quad \lim \limits _{\varsigma _i\rightarrow -\infty }T_i(\varsigma _i)=-{\bar{\delta }}_i, \end{aligned}$$

(15)

$$\begin{aligned}&\lim \limits _{\varsigma _i\rightarrow +\infty }T_i(\varsigma _i)={\bar{\delta }}_i, \end{aligned}$$

(16)

which is defined as [24]

$$\begin{aligned} T_i(\varsigma _i)\triangleq \frac{{\bar{\delta }}_i\text {e}^{\varsigma _i}-{\bar{\delta }}_i\text {e}^{-\varsigma _i}}{\text {e}^{\varsigma _i}+\text {e}^{-\varsigma _i}}. \end{aligned}$$

(17)

Considering the properties of $T_i(\varsigma _i)$ and the fact that $\mu (t)>0$, we conclude that inverse transformation $\varsigma _i(t)= T_i^{-1}[{\tilde{x}}_{i}(t)/\mu (t)]$ is properly defined provided that $\varsigma _i$ is bounded. Consequently, to achieve the prescribed performance condition (Eq. 13), we only need to guarantee the boundedness of $\varsigma _i$.

Using Eq. (17), $\varsigma _i$ can be written as

$$\begin{aligned} \varsigma _i(t)=\frac{1}{2}\ln \frac{{\bar{\delta }}_i+{\tilde{x}}_{i}(t)/\mu (t)}{{\bar{\delta }}_i-{\tilde{x}}_{i}(t)/\mu (t)}. \end{aligned}$$

(18)

Then the time derivative of $\varsigma _i$ can be obtained as ${\dot{\varsigma }}_i=r_i(\dot{{\tilde{x}}}_{i}-\frac{{\dot{\mu }}}{\mu }{\tilde{x}}_{i})$, where $r_i\triangleq \phi _i/\mu$ with $\phi _i\in {\mathbb {R}}$ is defined as $\phi _i\triangleq \frac{1}{2}(\frac{1}{{\bar{\delta }}_i+{\tilde{x}}_{i}/\mu }+\frac{1}{{\bar{\delta }}_i-{\tilde{x}}_{i}/\mu })$. Considering the properties of the transformation, it can be concluded that $r_i>0$ provided that Eq. (13) is satisfied. For an n-dimensional system, the transformed error vector can be defined as $\varvec{\varsigma }\triangleq [\varsigma _1\cdots \varsigma _n]^{\top }\in {\mathbb {R}}^{n}$, whose time derivative can be written as follows:

$$\begin{aligned} \dot{\varvec{\varsigma }}=\varvec{\Upsilon }\left( \dot{\tilde{{\textbf{x}}}}-\ell \tilde{{\textbf{x}}}\right) , \end{aligned}$$

(19)

where $\ell \triangleq {\dot{\mu }}/\mu \in {\mathbb {R}}$, and diagonal matrix $\varvec{\Upsilon }\in {\mathbb {R}}^{n\times n}$ can be defined as $\varvec{\Upsilon }\triangleq \text {diag}\{r_1,\cdots ,r_n\}$.

The following identifier is proposed to approximate the system given by Eq. (1):

$$\begin{aligned} \dot{\hat{{\textbf{x}}}}\triangleq \hat{{\textbf{W}}}_f^{\top }\hat{\varvec{\sigma }}_f+{\textbf{g}}({\textbf{x}}){\textbf{u}}-\ell \tilde{{\textbf{x}}}+\varvec{\Upsilon }^{-1}\varvec{\nu }, \end{aligned}$$

(20)

where $\hat{{\textbf{W}}}_f\in {\mathbb {R}}^{{\mathcal {L}}_f\times n}$ is the estimated weight matrix, $\hat{\varvec{\sigma }}_f\triangleq \varvec{\sigma }_f(\hat{{\textbf{x}}})$, and $\varvec{\nu }\in {\mathbb {R}}^{n}$ is the RISE term defined as [25]

$$\begin{aligned} \varvec{\nu }\triangleq k_f\varvec{\varsigma }-k_f\varvec{\varsigma }(0)+\int _0^t[\alpha k_f\varvec{\varsigma }({\bar{t}})+\beta _1\text {sgn}(\varvec{\varsigma }({\bar{t}}))]\text {d}t, \end{aligned}$$

in which $k_f,\alpha ,\beta _1\in {\mathbb {R}}^{+}$ are constant design parameters. Having $\dot{\hat{{\textbf{x}}}}$ through Eq. (20), the estimate of drift dynamics ${\textbf{f}}$ in Eq. (1) can be given as

$$\begin{aligned} \hat{{\textbf{f}}}\triangleq \dot{\hat{{\textbf{x}}}}-{\textbf{g}}({\textbf{x}}){\textbf{u}}. \end{aligned}$$

(21)

The first term in the right-hand side of Eq. (20) is a neural network-based estimate of function ${\textbf{f}}({\textbf{x}})$. The second component is a feedforward term that utilizes known information in the system dynamics (Eq. 1). The term $-\ell \tilde{{\textbf{x}}}$ is included in Eq. (20) to cancel out the effect of its counterpart in Eq. (19), and the last component in Eq. (20) includes the RISE term featured by the prescribed performance property. This term applies feedback information and compensates all residual estimation errors such that the prescribed performance condition (Eq. 13) is fulfilled and the estimation error converges to zero.

Now, utilizing Eqs. (1) and (20), the identification error dynamics can be developed as

$$\begin{aligned} \dot{\tilde{{\textbf{x}}}}={\textbf{W}}_f^{\top }\varvec{\sigma }_f-\hat{{\textbf{W}}}_f^{\top }\hat{\varvec{\sigma }}_f+\varvec{\epsilon }_f+\ell \tilde{{\textbf{x}}}-\varvec{\Upsilon }^{-1}\varvec{\nu }. \end{aligned}$$

(22)

Owing to the definition of $\varvec{\Upsilon }$ and the induced norm for matrices, when the condition set in Eq. (13) is satisfied, we can consider a lower bound for the norm of $\varvec{\Upsilon }$ as $\Vert \varvec{\Upsilon }\Vert \ge \phi _m/\mu$, where $\phi _m$ denotes the minimum value of $\phi _i$ for $i=1,\cdots ,n$. Considering this and substituting Eq. (22) into Eq. (19), $\dot{\varvec{\varsigma }}$ can be obtained as

$$\begin{aligned} \dot{\varvec{\varsigma }}=&-k_f\varvec{\varsigma }-\int _0^t[\alpha k_f\varvec{\varsigma }({\bar{t}})+\beta _1\text {sgn}(\varvec{\varsigma }({\bar{t}}))]\text {d}t+\varvec{\Upsilon }\tilde{{\textbf{W}}}_f^{\top }\varvec{\sigma }_f\nonumber \\&+{\textbf{S}}+\varvec{\epsilon }_0, \end{aligned}$$

(23)

where $\varvec{\epsilon }_0\triangleq \varvec{\Upsilon }_0\varvec{\epsilon }_f$, ${\textbf{S}}\triangleq \varvec{\Upsilon }\hat{{\textbf{W}}}_f^{\top }\tilde{\varvec{\sigma }}_f+\varvec{\Upsilon }_1\varvec{\epsilon }_f$, $\tilde{\varvec{\sigma }}_f\triangleq \varvec{\sigma }_f-\hat{\varvec{\sigma }}_f$, $\varvec{\Upsilon }_0\triangleq \phi _m/\mu {\textbf{I}}_{n}\in {\mathbb {R}}^{n\times n}$, ${\textbf{I}}_{n}$ denotes the identity matrix of dimension n, and $\varvec{\Upsilon }_1\triangleq \varvec{\Upsilon }-\varvec{\Upsilon }_0$. Now auxiliary variable ${\textbf{e}}_{\varsigma }\in {\mathbb {R}}^{n}$ is defined as

$$\begin{aligned} {\textbf{e}}_{\varsigma }\triangleq \dot{\varvec{\varsigma }}+\alpha \varvec{\varsigma }. \end{aligned}$$

(24)

Taking the time derivative of (23), $\dot{{\textbf{e}}}_{\varsigma }$ can be obtained as

$$\begin{aligned} \dot{{\textbf{e}}}_{\varsigma }=-k_f{\textbf{e}}_{\varsigma }-\beta _1\text {sgn}(\varvec{\varsigma }(t))-\varvec{\varsigma }+\tilde{{\textbf{N}}}+{\textbf{N}}_B+\dot{\varvec{\epsilon }}_0,\nonumber \\ \end{aligned}$$

(25)

where $\tilde{{\textbf{N}}},{\textbf{N}}_B\in {\mathbb {R}}^{n}$ are defined as

$$\begin{aligned} \tilde{{\textbf{N}}}\triangleq \dot{\varvec{\Upsilon }}\tilde{{\textbf{W}}}_f^{\top }\varvec{\sigma }_f-\varvec{\Upsilon }\dot{\hat{{\textbf{W}}}}_f^{\top }\varvec{\sigma }_f+\varvec{\Upsilon }_1\tilde{{\textbf{W}}}_f^{\top }\dot{\varvec{\sigma }}_f+\varvec{\varsigma }+\dot{{\textbf{S}}}+\alpha \dot{\varvec{\varsigma }}, \end{aligned}$$

and ${\textbf{N}}_B\triangleq \varvec{\Upsilon }_0\tilde{{\textbf{W}}}_f^{\top }\dot{\varvec{\sigma }}_f$. Considering Assumption 1, the results from Appendix A in a previous work [26] can be invoked to obtain the following upper bound for $\tilde{{\textbf{N}}}$:

$$\begin{aligned} \Vert \tilde{{\textbf{N}}}\Vert \le \rho (\Vert \varvec{\omega }\Vert )\Vert \varvec{\omega }\Vert , \end{aligned}$$

(26)

where $\varvec{\omega }\in {\mathbb {R}}^{2n}$ is defined as $\varvec{\omega }\triangleq [\varvec{\varsigma }^{\top }\;{\textbf{e}}_{\varsigma }^{\top }]^{\top }$ and $\rho (\Vert \varvec{\omega }\Vert )\in {\mathbb {R}}^{+}$ is a positive globally invertible non-decreasing function. Considering the definitions of $\varvec{\epsilon }_0$ and ${\textbf{N}}_B$ and the properties of their components, the following bounds can also be stated:

$$\begin{aligned}&\Vert \dot{\varvec{\epsilon }}_0\Vert \le \zeta _1, \quad \Vert \ddot{\varvec{\epsilon }}_0\Vert \le \zeta _2, \end{aligned}$$

(27)

$$\begin{aligned}&\Vert {\textbf{N}}_B\Vert \le \zeta _3, \quad \Vert \dot{{\textbf{N}}}_B\Vert \le \zeta _4+\zeta _5\Vert \varvec{\varsigma }\Vert , \end{aligned}$$

(28)

where $\zeta _1,\zeta _2,\zeta _3,\zeta _4,\zeta _5\in {\mathbb {R}}^{+}$ are positive constants.

Theorem 1

For the system defined by Eq. (1) and the adaptation rule for the NN weights given by

$$\begin{aligned} \dot{\hat{{\textbf{W}}}}_f\triangleq \text {Proj}(\gamma \dot{\varvec{\sigma }}_f\varvec{\varsigma }^{\top }\varvec{\Upsilon }_0), \end{aligned}$$

(29)

in which $\gamma \in {\mathbb {R}}^{+}$ is a positive adaptation gain and $\text {Proj}(\cdot )$ denotes the projection operator, provided Assumption 1 holds, the initial conditions satisfy Eq. (13), gain $k_f$ is selected as sufficiently large based on the initial conditions, and the following conditions are satisfied:

$$\begin{aligned}{} & {} \beta _1>\max (\zeta _1+\zeta _3,\zeta _1+\frac{\zeta _3+\zeta _4}{\alpha }), \end{aligned}$$

(30)

$$\begin{aligned}{} & {} \beta _2>\zeta _5,\; \text {and}\; \beta _2<\alpha \end{aligned}$$

(31)

in which $\beta _2$ is defined in Eq. (49), the identifier given in Eq. (20) guarantees the asymptotic identification of the state and its derivative, in the sense that $\Vert \tilde{{\textbf{x}}}\Vert ,\Vert \dot{\tilde{{\textbf{x}}}}\Vert \rightarrow 0$ as $t\rightarrow \infty$.

Proof

See the proof in Appendix A. $\square$

Remark 2

The neural network used for estimating drift dynamics ${\textbf{f}}$ employs the error between ${\textbf{x}}$ and $\hat{{\textbf{x}}}$ and thus is decoupled from the value function estimator introduced in Sect. 4.

3.2 Model identifier satisfying convergence

The identifier developed in the previous section assures the fast convergence of $\hat{{\textbf{f}}}$ to the true values along the system trajectories. However, the convergence of NN weights to true values is not guaranteed. This means that we cannot use $\hat{{\textbf{f}}}$ to estimate drift dynamics ${\textbf{f}}$ at the unvisited points. It is known from the literature that the convergence of these weights requires a PE condition, which is often difficult to achieve in practice and nearly impossible to verify online. To relax the PE condition while estimating the drift dynamics over the entire operating domain, we follow the experience replay approach [27] that uses recorded input-output data to improve the efficiency of information utilization. Although this method does not require a restrictive PE condition, the recorded data must still be rich enough to estimate the true weights; consequently, the estimation of function ${\textbf{f}}$ by this method is much slower than using the method in the previous section, despite providing an opportunity to explore the Bellman error at the unvisited points and relaxing the PE condition required for convergence of the critic weights.

Similar to the previous section, it is assumed that function ${\textbf{f}}({\textbf{x}})$ can be represented by an NN as ${{\textbf{f}}}={\textbf{W}}_s^{\top }\varvec{\sigma }_s+\varvec{\epsilon }_s$, where ${\textbf{W}}_s\in {\mathbb {R}}^{{\mathcal {L}}_s\times n}$ is an unknown weight matrix, $\varvec{\sigma }_s\in {\mathbb {R}}^{{\mathcal {L}}_s}$ is the activation function vector, $\varvec{\epsilon }_s\in {\mathbb {R}}^{n}$ is the estimation error, ${\mathcal {L}}_s$ is the number of neurons, and the following bounds are satisfied:

$$\begin{aligned} \Vert \varvec{\epsilon }_s\Vert \le b_{\epsilon s},\quad \Vert \varvec{\sigma }_s\Vert \le b_{\sigma s}, \quad \Vert \nabla \varvec{\sigma }_s\Vert \le b_{\sigma sx}, \end{aligned}$$

where $b_{\epsilon s}, b_{\sigma s},b_{\sigma sx}\in {\mathbb {R}}^{+}$ are positive constants. Hence, an estimate of ${\textbf{f}}$ can be represented as $\hat{{\textbf{f}}}_s\triangleq \hat{{\textbf{W}}}_s^{\top }\varvec{\sigma }_s$, where $\hat{{\textbf{W}}}_s\in {\mathbb {R}}^{{\mathcal {L}}_s\times n}$ is an estimate of ${\textbf{W}}_s$. Having an exact estimate of function ${\textbf{f}}$ along the system trajectory, obtained through the RISE-based approach in the previous section, function estimation error ${\textbf{e}}_s\in {\mathbb {R}}^{n}$ is considered to be¹

$$\begin{aligned} {\textbf{e}}_{s}&\triangleq {\textbf{f}}-\hat{{\textbf{f}}}_s\nonumber \\&=\tilde{{\textbf{W}}}_s^{\top }\varvec{\sigma }_s+\varvec{\epsilon }_s, \end{aligned}$$

(32)

where $\tilde{{\textbf{W}}}_s\triangleq {\textbf{W}}_s-\hat{{\textbf{W}}}_s\in {\mathbb {R}}^{{\mathcal {L}}_s\times n}$. Now assume that a history stack contains M recorded pairs of $({\textbf{f}}_{sj},\varvec{\sigma }_{sj})$ for $j=1\cdots M$, where subscript j denotes the jth sample in all variables. The function estimation error for each pair of recorded data based on the current estimated weight can be written as

$$\begin{aligned} {\textbf{e}}_{sj}&={\textbf{f}}_{sj}-\hat{{\textbf{W}}}_s^{\top }\varvec{\sigma }_{sj}\\&=\tilde{{\textbf{W}}}_s^{\top }\varvec{\sigma }_{sj}+\varvec{\epsilon }_{sj}. \end{aligned}$$

Assumption 2

The recorded data in the history stack contain sufficient linearly independent elements $\varvec{\sigma }_{sj}$ for $j=1\cdots M$ such that

$$\begin{aligned} 0< c_{\sigma _1}\triangleq \lambda _{\min }(\sum _{j=1}^{M}\varvec{\sigma }_{sj}\varvec{\sigma }_{sj}^{\top }), \end{aligned}$$

(33)

where $\lambda _{\min }$ denotes the minimum eigenvalue. This condition is satisfied when $\text {rank}(\sum _{j=1}^{M}\varvec{\sigma }_{sj}\varvec{\sigma }_{sj}^{\top })={\mathcal {L}}_s$, which can be easily verified online [10].

Assumption 2 requires the system states to be excited over a finite time interval. This is a less restrictive condition than the PE condition in traditional estimation methods. The PE condition needs the excited states to be present throughout an infinite time period, and it is very difficult or even impossible to verify online. It has been shown that condition (33) can be fulfilled in the RL control of nonlinear systems [11]. It has also been shown [10, 28] that one can use an a priori available history stack to satisfy Eq. (33).

The objective is to design an estimation law for $\hat{{\textbf{W}}}_s$ that guarantees that the estimated weight matrix converges as closely as possible to the true weight matrix ${\textbf{W}}_s$. According to the subsequent convergence analysis, the following estimation law is designed:

$$\begin{aligned} \dot{\hat{{\textbf{W}}}}_s\triangleq \varvec{\Gamma }_s\varvec{\sigma }_s{\textbf{e}}_s^{\top }+\gamma _{s1}\varvec{\Gamma }_s\varvec{\Sigma }+\gamma _{s2}\varvec{\Gamma }_s\frac{\varvec{\Sigma }}{\Vert \varvec{\Sigma }\Vert +\varepsilon _s}, \end{aligned}$$

(34)

where $\gamma _{s1},\gamma _{s2}\in {\mathbb {R}}^{+}$ are positive constants, $\varepsilon _s$ is a small positive value, $\varvec{\Sigma }\in {\mathbb {R}}^{{\mathcal {L}}_s\times n}$ is defined as $\varvec{\Sigma }\triangleq \sum _{j=1}^{M}\varvec{\sigma }_{sj}{\textbf{e}}_{sj}^{\top }$, and variable least-squares gain matrix $\varvec{\Gamma }_s\in {\mathbb {R}}^{{\mathcal {L}}_s\times {\mathcal {L}}_s}$ is defined as

$$\begin{aligned} \dot{\varvec{\Gamma }}_s\triangleq {\left\{ \begin{array}{ll} \rho _s\varvec{\Gamma }_s-\varvec{\Gamma }_s(\varvec{\sigma }_s\varvec{\sigma }_s^{\top })\varvec{\Gamma }_s,\quad \text {if}\quad \Vert \varvec{\Gamma }_s\Vert \le {\bar{\Gamma }}_s\\ {\textbf{0}},\qquad \qquad \qquad \qquad \qquad \;\; \text {otherwise} \end{array}\right. }, \end{aligned}$$

where ${\bar{\Gamma }}_s\in {\mathbb {R}}^{+}$ is a saturation constant, $\rho _s\in {\mathbb {R}}^{+}$ is a forgetting factor, and $\varvec{\Gamma }_s(0)$ is a symmetric positive-definite matrix satisfying $\Vert \varvec{\Gamma }_s(0)\Vert \le {\bar{\Gamma }}_s$. Using (32), (34) and the definition of $\tilde{{\textbf{W}}}_s$, the dynamics of $\tilde{{\textbf{W}}}_s$ can be written as

$$\begin{aligned} \dot{\tilde{{\textbf{W}}}}_s\triangleq&-\varvec{\Gamma }_s\varvec{\sigma }_s(\varvec{\sigma }_s^{\top }\tilde{{\textbf{W}}}_s+\varvec{\epsilon }_{s}^{\top })\nonumber \\&-\gamma _{s1}\varvec{\Gamma }_s\sum _{j=1}^{M}(\varvec{\sigma }_{sj}\varvec{\sigma }_{sj}^{\top }\tilde{{\textbf{W}}}_s+\varvec{\sigma }_{sj}\varvec{\epsilon }_{sj}^{\top })\nonumber \\&-\gamma _{s2}\varvec{\Gamma }_s\frac{\sum _{j=1}^{M}(\varvec{\sigma }_{sj}\varvec{\sigma }_{sj}^{\top }\tilde{{\textbf{W}}}_s+\varvec{\sigma }_{sj}\varvec{\epsilon }_{sj}^{\top })}{\Vert \varvec{\Sigma }\Vert +\varepsilon _s}. \end{aligned}$$

(35)

Remark 3

The last term in Eq. (34) was inspired by previous work [29], where a non-smooth form of it, i.e., $\varvec{\Sigma }/\Vert \varvec{\Sigma }\Vert$, is used in the estimation law; moreover, this work showed that, in the absence of function reconstruction error $\varvec{\epsilon }_s$, a finite-time convergence could be achieved. The use of this type of bounded control term (and its variations, e.g., [30]) is a common practice in the control of uncertain systems and improves stability and performance without employing a high-gain control term that may degrade system performance in the presence of noise [30]. Although the last term in Eq. (34) does not guarantee finite-time convergence due to the embedded smoothening term $\varepsilon _s$ and the existence of the function estimation error, simulation studies show that this bounded term significantly improves the convergence rate.

The convergence of $\hat{{\textbf{W}}}_s$ to the true value can be analyzed by considering the following Lyapunov function:

$$\begin{aligned} L_{W_s}\triangleq \frac{1}{2}\text {tr}(\tilde{{\textbf{W}}}_s^{\top }\varvec{\Gamma }_s^{-1}\tilde{{\textbf{W}}}_s), \end{aligned}$$

(36)

whose time derivative using (35) can be obtained as

$$\begin{aligned}&{\dot{L}}_{W_s}= -\text {tr}(\tilde{{\textbf{W}}}_s^{\top }\varvec{\sigma }_s\varvec{\sigma }_s^{\top }\tilde{{\textbf{W}}}_s)-\text {tr}(\tilde{{\textbf{W}}}_s^{\top }\varvec{\sigma }_s\varvec{\epsilon }_s^{\top })\\&\qquad \quad -\text {tr}(\gamma _{s1}\sum _{j=1}^{M}\tilde{{\textbf{W}}}_s^{\top }\varvec{\sigma }_{sj}\varvec{\sigma }_{sj}^{\top }\tilde{{\textbf{W}}}_s)\\&\qquad \quad -\text {tr}(\gamma _{s1}\sum _{j=1}^{M}\tilde{{\textbf{W}}}_s^{\top }\varvec{\sigma }_{sj}\varvec{\epsilon }_{sj}^{\top })\\&\qquad \quad -\text {tr}(\frac{\gamma _{s2}\sum _{j=1}^{M}\tilde{{\textbf{W}}}_s^{\top }\varvec{\sigma }_{sj}\varvec{\sigma }_{sj}^{\top }\tilde{{\textbf{W}}}_s}{\Vert \varvec{\Sigma }\Vert +\varepsilon _s})\\&\qquad \quad -\text {tr}(\frac{\gamma _{s2}\sum _{j=1}^{M}\tilde{{\textbf{W}}}_s^{\top }\varvec{\sigma }_{sj}\varvec{\epsilon }_{sj}^{\top }}{\Vert \varvec{\Sigma }\Vert +\varepsilon _s})\\&\qquad \quad -\frac{1}{2}\text {tr}\left( \tilde{{\textbf{W}}}_s^{\top }\varvec{\Gamma }_s^{-1}(\rho _s\varvec{\Gamma }_s-\varvec{\Gamma }_s\varvec{\sigma }_s\varvec{\sigma }_s^{\top }\varvec{\Gamma }_s)\varvec{\Gamma }_s^{-1}\tilde{{\textbf{W}}}_s\right) . \end{aligned}$$

By defining $c_{\sigma _2}\triangleq \lambda _{\max }(\sum _{j=1}^{M}\varvec{\sigma }_{sj}\varvec{\sigma }_{sj}^{\top })$, where $\lambda _{\max }$ denotes the maximum eigenvalue, we have

$$\begin{aligned} -\text {tr}(\frac{\gamma _{s2}\sum _{j=1}^{M}\tilde{{\textbf{W}}}_s^{\top }\varvec{\sigma }_{sj}\varvec{\sigma }_{sj}^{\top }\tilde{{\textbf{W}}}_s}{\Vert \varvec{\Sigma }\Vert +\varepsilon _s}) \le -\gamma _{s2}\vartheta _s\Vert \tilde{{\textbf{W}}}_s\Vert _F, \end{aligned}$$

where $\vartheta _s>0$ is defined as

$$\begin{aligned} \vartheta _s\triangleq 1-\frac{(c_{\sigma _2}-c_{\sigma _1})\Vert \tilde{{\textbf{W}}}_s\Vert _F+Mb_{\epsilon s}b_{\sigma s}+\varepsilon _s}{c_{\sigma _2}\Vert \tilde{{\textbf{W}}}_s\Vert _F+Mb_{\epsilon s}b_{\sigma s}+\varepsilon _s}. \end{aligned}$$

Furthermore, assuming that $\varepsilon _s$ is selected such that it satisfies $(\Vert \varvec{\Sigma }\Vert +\varepsilon _s)>\sum _{j=1}^{M}\sup \limits _{j=1\cdots M}(\Vert \varvec{\sigma }_{sj}\varvec{\epsilon }_{sj}^{\top }\Vert _F)$, we have

$$\begin{aligned} -\text {tr}(\frac{\gamma _{s2}\sum _{j=1}^{M}\tilde{{\textbf{W}}}_s^{\top }\varvec{\sigma }_{sj}\varvec{\epsilon }_{sj}^{\top }}{\Vert \varvec{\Sigma }\Vert +\varepsilon _s})\le \gamma _{s2}\varpi _s\Vert \tilde{{\textbf{W}}}_s\Vert _F \end{aligned}$$

for some $\varpi _s<1$ (note that $\Vert \varvec{\Sigma }\Vert <\Vert \sum _{j=1}^{M}\varvec{\sigma }_{sj}\varvec{\epsilon }_{sj}^{\top }\Vert$ happens only if $\Vert \sum _{j=1}^M\varvec{\sigma }_{sj}\varvec{\sigma }_{sj}^{\top }\tilde{{\textbf{W}}}_s\Vert {<}2\Vert \sum _{j=1}^{M}\varvec{\sigma }_{sj}\varvec{\epsilon }_{sj}^{\top }\Vert$, which means for small values of $\tilde{{\textbf{W}}}_s$). Therefore, considering Eq. (33), an upper bound of ${\dot{L}}_{W_s}$ can be written as

$$\begin{aligned} {\dot{L}}_{W_s}\le -\gamma _{s1}c_{\sigma _1}\Vert \tilde{{\textbf{W}}}_s\Vert _F^2+\epsilon _{w}\Vert \tilde{{\textbf{W}}}_s\Vert _F, \end{aligned}$$

(37)

where $\epsilon _{w}\triangleq (1+\gamma _{s1}M)b_{\epsilon s}b_{\sigma s}-\gamma _{s2}(\vartheta _s-\varpi _s)$, and $\Vert \cdot \Vert _F$ is the Frobenius norm. Then, from Eqs. (36) and (37), we can conclude that $\tilde{{\textbf{W}}}_s$ converges to a neighborhood of zero.

Remark 4

For large values of $\Vert \varvec{\Sigma }\Vert$, since $\varepsilon _s$ is bounded, the term $(\vartheta _s-\varpi _s)$ will be a positive value that results in a smaller $\epsilon _w$, and thus, according to (37), a faster convergence. In addition, one can consider $\gamma _{s2}$ a strictly increasing saturated function of $\Vert \varvec{\Sigma }\Vert$ to reduce the effect of the last term in (34) for the small values of $\Vert \varvec{\Sigma }\Vert$ (indicating the estimation error).

Remark 5

In contrast to the PE condition, the rank condition in Eq. (33) can be easily verified online. An algorithm for the selection of data points based on maximizing singular value was given previously [27]. The history stack can be updated to improve the estimation performance by replacing old data with new data if they result in larger $c_{\sigma _1}$.

4 Optimal value function approximation

The solution of the optimal control problem, according to the closed-form equation of the optimal controller (Eq. 5), requires the optimal value function $V^{*}({\textbf{x}})$. Consequently, in this section, we present an approach to estimate this function, which can then be used to derive the estimated optimal controller. Following the standard RL techniques [4, 13], the Bellman error $\delta _B$ can be employed as an indirect performance metric of the quality of the estimate of the value function. According to Eqs. (8) and (10), the Bellman error depends on the dynamics of the system. Therefore, using the estimate of the drift dynamics through the model identifiers proposed in the previous section, this section presents an online method to estimate the optimal value function using the Bellman error. Considering the function approximation property of NNs, optimal value function $V^{*}$ can be represented as

$$\begin{aligned} V^{*}({\textbf{x}})={\textbf{W}}_c^{\top }\varvec{\sigma }_c({\textbf{x}})+\epsilon _c({\textbf{x}}), \end{aligned}$$

(38)

where ${\textbf{W}}_c\in {\mathbb {R}}^{{\mathcal {L}}_c}$ is the constant ideal weight vector, $\varvec{\sigma }_c\in {\mathbb {R}}^{{\mathcal {L}}_c}$ is the basis function or activation function vector satisfying $\varvec{\sigma }_c({\textbf{0}})={\textbf{0}}$ and $\nabla \varvec{\sigma }({\textbf{0}})\triangleq \partial \varvec{\sigma }_c({\textbf{0}})/\partial {\textbf{x}}={\textbf{0}}$, $\epsilon _c$ is the functional reconstruction error, and ${\mathcal {L}}_c$ is the number of neurons. Error $\epsilon _c$ and its gradient $\nabla \epsilon _c$ are bounded over the compact set $\Omega _N$ as [31]

$$\begin{aligned} |\epsilon _c|\le b_{\epsilon c},\quad \Vert \nabla \epsilon _c\Vert \le b_{\epsilon cx} \end{aligned}$$

for some positive $b_{\epsilon c}, b_{\epsilon cx}\in {\mathbb {R}}^{+}$, and the following bounds are considered for the activation function [5, 8]:

$$\begin{aligned} \Vert \varvec{\sigma }_c\Vert \le b_{\sigma c},\quad \Vert \nabla \varvec{\sigma }_c\Vert \le b_{\sigma cx}, \end{aligned}$$

where $b_{\sigma c},b_{\sigma cx}\in {\mathbb {R}}^{+}$ are positive constants.

Using (38), the gradient of $V^{*}$ can be written as

$$\begin{aligned} \nabla V^{*}({\textbf{x}})={\textbf{W}}_c^{\top }\nabla \varvec{\sigma }_c({\textbf{x}})+\nabla \epsilon _c({\textbf{x}}). \end{aligned}$$

(39)

Substituting Eq. (39) into Eq. (7), the HJB equation can be written as

$$\begin{aligned} Q({\textbf{x}})+U({\textbf{u}}^{*})+{\textbf{W}}_c^{\top }\nabla \varvec{\sigma }_c\left( {\textbf{f}}+{\textbf{g}}{\textbf{u}}^{*}\right) =\epsilon _{hjb}, \end{aligned}$$

(40)

where $\epsilon _{hjb}\triangleq -\nabla \epsilon _c({\textbf{f}}+{\textbf{g}}{\textbf{u}}^{*})$, which is a bounded term [7, 18].

Since ideal weight vector ${\textbf{W}}_c$ is not available, the optimal value function is estimated through the following critic neural network:

$$\begin{aligned} {\hat{V}}({\textbf{x}})=\hat{{\textbf{W}}}_c^{\top }\varvec{\sigma }_c({\textbf{x}}), \end{aligned}$$

(41)

where $\hat{{\textbf{W}}}_c\in {\mathbb {R}}^{{\mathcal {L}}_c}$ is the estimation of ${\textbf{W}}_c$. Using Eq. (41), we obtain $\nabla {\hat{V}}=\hat{{\textbf{W}}}_c^{\top }\nabla \varvec{\sigma }_c$. Therefore, considering Eq. (5), the optimal controller (actor) can be estimated as

$$\begin{aligned} \hat{{\textbf{u}}}=-\lambda \tanh (\hat{{\textbf{D}}}), \end{aligned}$$

(42)

where $\hat{{\textbf{D}}}\triangleq \frac{1}{2\lambda }{\textbf{R}}^{-1}{\textbf{g}}^{\top }\nabla \varvec{\sigma }_c^{\top }\hat{{\textbf{W}}}_c$. Accordingly, the solution to the optimal control problem is converted to finding an adaptation rule for $\hat{{\textbf{W}}}_c$ such that a proper estimation is guaranteed for the optimal value function.

In reinforcement learning, the online update law for $\hat{{\textbf{W}}}_c$ is developed using the Bellman error. To guarantee that $\hat{{\textbf{W}}}_c$ converges to a true value, sufficient exploration of the state space is required. In this paper, we follow a previous approach [11] that utilizes a system’s model to simulate the Bellman error at any desired unexplored point. Since the estimate of drift dynamics ${\textbf{f}}$ is available at any desired point ${\textbf{x}}_j$ through $\hat{{\textbf{f}}}_s$, the Bellman error can be evaluated at such points as follows:

$$\begin{aligned} \delta _{Bj}\triangleq&~Q({\textbf{x}}_j)+U(\hat{{\textbf{u}}}({\textbf{x}}_j,\hat{{\textbf{W}}}_c))\\&+\nabla {\hat{V}}({\textbf{x}}_j)(\hat{{\textbf{f}}}_{s}({\textbf{x}}_j)+{\textbf{g}}\hat{{\textbf{u}}}({\textbf{x}}_j,\hat{{\textbf{W}}}_c)). \end{aligned}$$

Based on the above definition, the online update law for the critic weight vector is given as

$$\begin{aligned}{} & {} \dot{\hat{{\textbf{W}}}}_c\triangleq -\frac{\alpha _{c} \varvec{\beta }}{(1+\varvec{\beta }^{\top }\varvec{\beta })^2}\delta _{B}-\alpha _{c}\gamma _{c1}\varvec{\Xi } \nonumber \\{} & {} \quad -\alpha _{c}\gamma _{c2}\frac{\varvec{\Xi }}{\Vert \varvec{\Xi }\Vert +\varepsilon _c}, \end{aligned}$$

(43)

where $\alpha _{c},\gamma _{c1},\gamma _{c2},\varepsilon _c\in {\mathbb {R}}^{+}$ are positive design gains, $\varvec{\Xi }\in {\mathbb {R}}^{{\mathcal {L}}_c}$ is defined as

$$\begin{aligned} \varvec{\Xi }\triangleq \sum _{j=1}^{N}\frac{\varvec{\beta }_j}{N(1+\varvec{\beta }_j^{\top }\varvec{\beta }_j)^2}\delta _{Bj}, \end{aligned}$$

and vector variables $\varvec{\beta },\varvec{\beta }_j\in {\mathbb {R}}^{{\mathcal {L}}_c}$ are defined as

$$\begin{aligned}&\varvec{\beta }\triangleq \nabla \varvec{\sigma }_c(\hat{{\textbf{f}}}-\lambda {\textbf{g}}\tanh (\kappa \hat{{\textbf{D}}})), \nonumber \\&\quad \varvec{\beta }_j\triangleq \nabla \varvec{\sigma }_c({\textbf{x}}_j)(\hat{{\textbf{f}}}_{s}({\textbf{x}}_j)-\lambda {\textbf{g}}({\textbf{x}}_j)\tanh (\kappa \hat{{\textbf{D}}}({\textbf{x}}_j))), \end{aligned}$$

(44)

where $\kappa \in {\mathbb {R}}^{+}$ is a positive constant. The last term in Eq. (43) resembles the last component in Eq. (34), which is a bounded control term that increases the convergence rate without employing a high-gain estimation law (see Remark 3 and Remark 4). Vector $\varvec{\beta }_j$ is obtained from the simulated experience at points ${\textbf{x}}_j$ for $j=1,\cdots ,N$, satisfying the following condition.

Assumption 3

There exists a finite set of points ${\textbf{x}}_j$ for $j=1,\cdots ,N$, such that

$$\begin{aligned} 0<c_{\beta _1}\triangleq \frac{1}{N}\left( \inf \limits _{t\in {\mathbb {R}}_{\ge t_0}}\left( \lambda _{\min }(\sum _{j=1}^{N}\frac{\varvec{\beta }_j\varvec{\beta }_j^{\top }}{(1+\varvec{\beta }_j^{\top }\varvec{\beta }_j)^2})\right) \right) . \nonumber \\ \end{aligned}$$

(45)

Assumption 3 can be satisfied when $\text {rank}(\sum _{j=1}^{N}\varvec{\beta }_j\varvec{\beta }_j^{\top })={\mathcal {L}}_c$, and it can be easily verified online. Since the vectors $\varvec{\beta }_j$ are obtained from unvisited points, a sufficient number of points can be selected to fulfill the condition (45) [10].

Now, in the following theorem, we present the stability and convergence results of the given online policy iteration algorithm.

Theorem 2

For the system of Eq. (1), consider the controller in Eq. (42), the critic weight update law in Eq. (43), and the model identifier $\hat{{\textbf{f}}}_s$ with its weight update law given in Eq. (34). Provided Assumptions (1)-(3), and the following sufficient gain conditions are satisfied:

$$\begin{aligned} \gamma _{s1}c_{\sigma _1}>\frac{\eta _1^2\varrho _1}{4}+\frac{\eta _3^2}{4}, \qquad \gamma _{c1}c_{\beta _1}>\frac{\varrho _1}{\eta _1^2}+\frac{\eta _3^2}{4}, \end{aligned}$$

(46)

where $b_{\beta }$, $\varrho _1$, $\eta _1$, $\eta _2$, and $\eta _3$ are positive constants defined subsequently in the proof, then system state ${\textbf{x}}$ and weight estimation errors $\tilde{{\textbf{W}}}_c$ and $\tilde{{\textbf{W}}}_s$ are UUB, which means UUB convergence of $\hat{{\textbf{u}}}$ to ${\textbf{u}}^{*}$.

Proof

See the proof in Appendix C. $\square$

Remark 6

Due to the existence of the fast model identifier, a similar stability analysis as presented in Appendix C can be made to show that the closed-loop system remains stable before the condition of Eq. (45) is satisfied; however, the convergence of $\hat{{\textbf{W}}}_c$ to the optimal weight cannot be guaranteed.

Remark 7

Although we addressed the effect of the estimation error of the slow model identifier as an unbounded term in the stability analysis, it can be assumed to be a priori bounded provided we use only the identifier’s outputs when the estimation error is smaller than a certain predefined value.

5 Simulation results

In this section, we present the results of simulation studies that evaluated the performance of our proposed control scheme. Since there are no known solutions to optimal control problems for bounded-input nonlinear systems, in the first two studies, to show that our proposed method converges to optimal solutions, we selected an actuator bound that is large enough to verify that the commands do not violate the bound. Input constraints were considered in the second study, where we evaluated the effectiveness of the proposed algorithm and compared the results with those of two available solutions in the literature for a bounded-input system.

5.1 Systems without actuator saturation

In this simulation study, the model of the nonlinear system of Eq. (1) was considered to be [7]

$$\begin{aligned}&{\textbf{f}}({\textbf{x}})=\begin{bmatrix} -x_1+x_2 \\ -0.5x_1-0.5x_2\left( 1-(\cos (2x_1)+2)^2\right) \end{bmatrix},\\&{\textbf{g}}({\textbf{x}})=\begin{bmatrix} 0 \\ \cos (2x_1)+2 \end{bmatrix}, \end{aligned}$$

which satisfies Assumption 1. The state vector ${\textbf{x}}=[x_1,\;x_2]^{\top }$ was initialized at ${\textbf{x}}(0)=[-1,\;-1]^{\top }$. The design parameters of the fast model identifier (21) were selected as $k_f=8$, $\alpha =1$, $\beta _1=0.2$, $\kappa _\mu =2$, $\mu _0=4$, $\mu _{\infty }=0.3$, and ${\bar{\delta }}_i=1$, and sigmoid functions were considered for the basis of the NN with ${\mathcal {L}}_f=6$. For the slow model identifier, the design parameters were selected as $\gamma _{s1}=\gamma _{s2}=3$, $\varepsilon _s=0.001$, $\varvec{\Gamma }_s(0)=3{\textbf{I}}_{{\mathcal {L}}_s}$, and $\rho _s=0.1$, and the basis was considered to be

$$\begin{aligned} \varvec{\sigma }_s=&~[x_1,\; x_2,\; \sin (x_1),\; \cos (x_1),\; \sin (x_2),\; \cos (x_2),\;\\&\sin (x_1)^2,\; \cos (x_1)^2,\; \sin (x_2)^2,\; \cos (x_2)^2,\; x_1\cos (x_2),\; \\&x_1\cos (x_2)^2,\; x_2\cos (x_1),\; x_2\cos (x_1^2)]^{\top }. \end{aligned}$$

Here, all of the initial weights were set to 0.5. We used an algorithm from a previous study [27] to record the data in the history stack for this identifier, and Assumption 2 was satisfied around $t=1.2~\text {s}$. The optimal control problem was defined by considering $Q({\textbf{x}})={\textbf{x}}^{\top }{\textbf{x}}$ and $R=1$. The design parameters were selected as $\alpha _c=200$, $\gamma _{c1}=\gamma _{c2}=1.5$, $\varepsilon _c=0.0005$, $\lambda =3$, and $\kappa =3$. The basis was selected as $\varvec{\sigma }_c=[x_1^2,\;x_1x_2,\;x_2^2]^{\top }$, the initial weights were set to 1, and the data for the simulation of the Bellman error were selected from a $5\times 5$ grid around the trajectory such that Assumption 3 was satisfied.

Based on an analytical solution, the ideal weights are ${\textbf{W}}_c=[0.5,\; 0,\; 1]^{\top }$ [7]. The estimated values in this simulation converged to $\hat{{\textbf{W}}}_c=[0.499,\; 0.00,\; 1.00]^{\top }$ after $10~\text {s}$, which shows the effectiveness of the proposed algorithm. The trajectories of the estimated weights are shown in Fig. 2. The trajectories of the norm of $\hat{{\textbf{f}}}$ estimated by the fast model identifier and its true value are shown in Fig. 3. The trajectories of the system’s states are depicted in Fig. 4. In comparison to results reported in the literature for the same nonlinear system, e.g., [7], our results show faster convergence of the estimated value function and smoother trajectories of the states. This is because these approaches require the application of an exploration input signal and forcing the system to visit many points in the state space to satisfy the PE condition; however, our approach, similar to an earlier study [11], simulates those points and gains smoother real trajectories. Also note that the design of that study [11] required an additional estimation network for the actor.

Fig. 2

Estimated value function weights

Fig. 3

Norm of unknown function ${\textbf{f}}$ estimated by fast identifier

Fig. 4

State trajectory during online learning

To demonstrate the effectiveness of the last term of the update law (Eq. 43) in increasing the convergence rate, the above simulation was repeated by removing this term from the update law. The estimated weight vector after $10~\text {s}$ was $\hat{{\textbf{W}}}_c=[0.526,\; -0.011,\; 0.782]^{\top }$, and it took about $100~\text {s}$ until the weights nearly converged to the optimal values. The time evolution of the estimated weights in this condition is shown in Fig. 5. We observed a similar level of effectiveness for the last term of the adaptation law (Eq. 34) used for the model identification.

Fig. 5

Time evolution of estimated value function weights without using last term in Eq. (43)

In another study, we considered a four-order linear dynamic system $\dot{{\textbf{x}}}={\textbf{A}}{\textbf{x}}+{\textbf{B}}{\textbf{u}}$ that describes a mechanical system consisting of a mass attached to a spring and a damper [32]. Spring constants, damping coefficients, and the mass of the system are selected to obtain the following results in the state and input matrices:

$$\begin{aligned} {\textbf{A}}=\begin{bmatrix} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} -6 &{} -1.7 &{} 0\\ 0 &{} 0 &{} 0 &{} 1\\ 0 &{} 0 &{} -3 &{} -0.2 \end{bmatrix},\qquad {\textbf{B}}=\begin{bmatrix} 0 \\ 1\\ 0\\ 0 \end{bmatrix}. \end{aligned}$$

(47)

The state vector was initialized at ${\textbf{x}}(0)=[-1,\;-1,\;-1,\;-1]^{\top }$. The design parameters for the fast model identifier were selected to be the same as those used in the previous simulation. The state vector was considered to be the basis for the slow model identifier. The parameters of this identifier were selected as $\gamma _{s1}=\gamma _{s2}=1$, and all other parameters and initial values of the weights were the same as those in the previous simulation. The design parameters for the estimation of the value function were selected as $\alpha _c=2$, $\gamma _{c1}=3$, $\gamma _{c2}=1$, $\varepsilon _c=0.001$, $\lambda =10$, and $\kappa =3$. The basis vector was $\varvec{\sigma }_c=[x_1^2,\;2x_1x_2,\;2x_1x_3,\;2x_1x_4,\;2x_2^2,\;2x_2x_3,\;2x_2x_4,\;2x_3^2,\;2x_3x_4,\;2x_4^2]^{\top }$. The initial weights were set to 1, and the data for the simulation of the Bellman error were selected from a $5\times 5\times 5\times 5$ grid around the trajectory.

For the cost function defined by ${\textbf{Q}}({\textbf{x}})={\textbf{x}}^{\top }{\textbf{x}}$ and $U({\textbf{u}})=u^2$, by solving the algebraic Riccati equation, the ideal weight vector was obtained as ${\textbf{W}}_c=[6.245,\;1.000,\;-0.203,\;-0.548,\;0.245,\;-0.054,\;-0.093,\;10.274,\;0.196,\;3.462]^{\top }$, and the estimated one after $30~\text {s}$ was $\hat{{\textbf{W}}}_c=[6.245,\;0.999,\;-0.194,\;-0.548,\;0.246,\;-0.051,\;-0.101,\;10.274,\;0.197,\;3.461]^{\top }$. These results confirm the convergence of the proposed method to the optimal control solution. The time evolution of the weights is shown in Fig. 6.

Fig. 6

Time evolution of estimated value function weights for the linear system described by Eq. (47)

5.2 Nonlinear system with actuator saturation

The nonlinear system considered in this study was defined by the following terms [13, 18]:

$$\begin{aligned} {\textbf{f}}({\textbf{x}})=\begin{bmatrix} x_1+x_2-x_1(x_1^2+x_2^2) \\ -x_1+x_2-x_2(x_1^2+x_2^2) \end{bmatrix},\qquad {\textbf{g}}({\textbf{x}})=\begin{bmatrix} 0 \\ 1 \end{bmatrix}, \end{aligned}$$

where the state vector was initialized at ${\textbf{x}}(0)=[1,\; -1]^{\top }$. The control input was assumed to be limited to $|u|\le 1$, and the nonquadratic cost function (Eq. 2) was defined by considering $Q({\textbf{x}})={\textbf{x}}^{\top }{\textbf{x}}$ and $R=1$. The design parameters of the fast model identifier were identical to those of the previous simulation example. For the slow model identifier, the design parameters were selected as $\gamma _{s1}=\gamma _{s2}=1$, $\varepsilon _s=0.1$, $\varvec{\Gamma }_s(0)=8{\textbf{I}}_{{\mathcal {L}}_s}$, and $\rho _s=0.5$, and the basis was considered to be $\varvec{\sigma }_s=[x_1,\; x_2,\; x_1x_1^2,\; x_1x_2^2,\; x_2x_1^2,\; x_2x_2^2]^{\top }$. Again, all of the initial weights were set to 0.5. Here, $\alpha _c=35$, $\gamma _{c1}=\gamma _{c2}=4.5$, $\varepsilon _c=0.001$, and $\lambda =1$ were selected as design parameters for the value function estimation. The data for the simulation of the Bellman error were selected from a $5\times 5$ grid around the trajectory, and the basis was selected as [18]

$$\begin{aligned} \varvec{\sigma }_c=&[x_1^2,\; x_2^2,\; x_1x_2,\; x_1^4,\; x_2^4,\; x_1^3x_2,\; x_1^2x_2^2,\; x_1x_2^3,\; x_1^6,\\&x_2^6,\;x_1^5x_2,\; x_1^4x_2^2,\; x_1^3x_2^3,\; x_1^2x_2^4,\; x_1x_2^5,\; x_1^8,\; x_2^8,\\&x_1^7x_2,\;x_1^6x_2^2,\; x_1^5x_2^3,\; x_1^4x_2^4,\; x_1^3x_2^5,\; x_1^2x_2^6,\; x_1x_2^7]^{\top }, \end{aligned}$$

as were the initial critic weights [18]

$$\begin{aligned} \hat{{\textbf{W}}}_c(0)=&[2.92,\; 1.84,\; 0.96,\; 1.96,\; 1.39,\; -1.07,\; -1.42, \\&-1.00,\; -1.57,\; -0.88,\; 1.14,\; 0.76,\; 3.69,\; 3.02,\\&2.66,\; -0.35,\; 1.22,\; -1.30,\; -3.35,\; 0.12,\; 2.12,\\&-0.01,\; 2.49,\; 2.13]^{\top }. \end{aligned}$$

The time evolution of the estimation of weights is shown in Fig. 7. According to the estimated values and (42), the estimated controller after $50~\text {s}$ is given by

$$\begin{aligned}&\hat{{\textbf{u}}}= -\tanh (4.5x_1 + 3.95x_2 + 12.5x_2^3 - 2.15x_1^3 \\&\qquad + 9.7x_1^2x_2+ 17.11x_1x_2^2 + 0.69x_2^5 + 0.31x1^5 + 1.1x_1^4x_2\\&\qquad + 6.69x_1^3x_2^2 + 7.86x_1^2x_2^3 + 9.07x_1x_2^4 + 6.25x_2^7 - 0.67x_1^7 \\&\qquad - 3.35x_1^6x_2 + 0.24x_1^5x_2^2 + 4.3x_1^4x_2^3 + 0.02x_1^3x_2^4\\&\qquad + 7.92x_1^2x_2^5 + 1.06x_1x_2^6). \end{aligned}$$

The trajectories of the states obtained by this estimated controller are shown in Fig. 8. The figure also shows the trajectories of the states obtained by the estimated controllers given in previous works [18] (obtained after $250~\text {s}$) and [13] (obtained offline). The evolution of the control efforts obtained by the three methods is shown in Fig. 9. The cost values measured within $20~\text {s}$ were 2.77 for our method, while those for the previous methods were 2.84 [18] and 5.46 [13]. These results demonstrate that the proposed approach yields a superior performance for an estimated optimal controller. Notably, our method achieves this result without using an exploratory signal in contrast to the earlier works [13, 18].

Fig. 7

Evolution of a small number of estimated value function weights

Fig. 8

State trajectories obtained by estimated optimal controllers

Fig. 9

Evolution of control efforts obtained by three methods

6 Conclusion

This study addressed online RL-based solutions to the optimal regulation problem of unknown continuous-time nonlinear systems. The designed method uses the simulated experience concept and incorporates actuator bounds in its control design. Two model identifiers were developed whose outputs were used to guarantee the convergence of the estimated controller to the optimal one and to keep the system stable while learning the optimal solution. The proposed estimation law for the critic network satisfies fast convergence without employing a large estimation gain. A stability analysis shows the controller’s UUB convergence to the optimal one, and the simulation results demonstrate the effectiveness of the developed technique.

7 Declarations

• This work is supported by the Innovative Science and Technology Initiative for Security, Grant Number JPJ004596, and ATLA, Japan. The study is partially based on results obtained from project JPNP20006, commissioned by the New Energy and Industrial Technology Development Organization (NEDO). This work was partially supported by JSPS KAKENHI Grant Number JP21H03527.

• The datasets generated and/or analyzed during the current study are available from the corresponding author upon reasonable request.

• The authors declare that there is no conflict of interest to disclose.

• All authors contributed to the study’s conception and design.

Appendices

Appendices

Proof of Theorem 1

Consider ${\mathcal {D}}\subseteq {\mathbb {R}}^{2n+2}$ a domain containing ${\textbf{y}}=0$, where ${\textbf{y}}\in {\mathbb {R}}^{2n+2}$ is defined as ${\textbf{y}}\triangleq [\varvec{\omega }^{\top }\;\sqrt{P}\;\sqrt{Q_f}]^{\top }$, in which $Q_f(t)\in {\mathbb {R}}^{+}$ is defined as $Q_f(t)\triangleq \frac{\alpha }{2\gamma }\text {tr}(\tilde{{\textbf{W}}}_f^{\top }\tilde{{\textbf{W}}}_f)$ with $\text {tr}(\cdot )$ denoting the trace of a matrix. Here, function $P(t)\in {\mathbb {R}}$ is given by

$$\begin{aligned}{} & {} P(t)\triangleq \beta _1\sum _{i=1}^{n}|\varsigma _i(0)|-\varvec{\varsigma }(0)^{\top }(\dot{\varvec{\epsilon }}_f(0)+{\textbf{N}}_B(0)) \nonumber \\{} & {} \quad -\int _0^t {\mathcal {K}}({\bar{t}})\text {d}{\bar{t}}, \end{aligned}$$

(48)

where function ${\mathcal {K}}(t)\in {\mathbb {R}}$ is defined as

$$\begin{aligned} {\mathcal {K}}(t)\triangleq {\textbf{e}}_{\varsigma }^{\top }\left( \dot{\varvec{\epsilon }}_0-\beta _1\text {sgn}(\varvec{\varsigma })\right) +\dot{\varvec{\varsigma }}^{\top }{\textbf{N}}_B-\beta _2\Vert \varvec{\varsigma }\Vert ^2, \end{aligned}$$

(49)

in which $\beta _2\in {\mathbb {R}}^{+}$ is a positive constant. Provided the conditions of Eqs. (30) and (31) are satisfied, it can be shown that $P(t)\ge 0$; see the proof in Appendix B. Now consider the continuously differentiable positive-definite function as follows:

$$\begin{aligned} {\mathcal {V}}=\frac{1}{2}\varvec{\varsigma }^{\top }\varvec{\varsigma }+\frac{1}{2}{\textbf{e}}_{\varsigma }^{\top }{\textbf{e}}_{\varsigma }+P+Q_f. \end{aligned}$$

(50)

It can be concluded that

$$\begin{aligned} \psi _1({\textbf{y}})\le {\mathcal {V}}({\textbf{y}})\le \psi _2({\textbf{y}}), \end{aligned}$$

(51)

where positive-definite strictly increasing functions $\psi _1,\psi _2\in {\mathbb {R}}^{+}$ are defined as $\psi _1\triangleq 0.5\Vert {\textbf{y}}\Vert ^2$ and $\psi _2\triangleq \Vert {\textbf{y}}\Vert ^2$. Using Eqs. (24), (25), and the time derivative of Eq. (48), the time derivative of ${\mathcal {V}}$ can be developed as

$$\begin{aligned} \dot{{\mathcal {V}}}=&-(\alpha -\beta _2)\varvec{\varsigma }^{\top }\varvec{\varsigma }-k_f{\textbf{e}}_{\varsigma }^{\top }{\textbf{e}}_{\varsigma }+{\textbf{e}}_{\varsigma }^{\top }\tilde{{\textbf{N}}}+{\textbf{e}}_{\varsigma }^{\top }{\textbf{N}}_B\\&-\dot{\varvec{\varsigma }}^{\top }{\textbf{N}}_B-\frac{\alpha }{\gamma }\text {tr}(\tilde{{\textbf{W}}}_f^{\top }\dot{\hat{{\textbf{W}}}}_f). \end{aligned}$$

Therefore, using Eq. (24) and the definition of ${\textbf{N}}_B$, and knowing that ${\textbf{a}}^{\top }{\textbf{b}}=\text {tr}({\textbf{b}}{\textbf{a}}^{\top })$, $\forall {\textbf{a}},{\textbf{b}}\in {\mathbb {R}}^{n}$, we can write

$$\begin{aligned} \dot{{\mathcal {V}}}=&-(\alpha -\beta _2)\varvec{\varsigma }^{\top }\varvec{\varsigma }-k_f{\textbf{e}}_{\varsigma }^{\top }{\textbf{e}}_{\varsigma }+{\textbf{e}}_{\varsigma }^{\top }\tilde{{\textbf{N}}}\\&-\frac{\alpha }{\gamma }\text {tr}(\tilde{{\textbf{W}}}_f^{\top }\dot{\hat{{\textbf{W}}}}_f-\gamma \tilde{{\textbf{W}}}_f^{\top }\dot{\varvec{\sigma }}_f\varvec{\varsigma }^{\top }\varvec{\Upsilon }_0). \end{aligned}$$

Considering the adaptation law (Eq. 29) and using the properties of the projection operator, we have

$$\begin{aligned} -\frac{\alpha }{\gamma }\text {tr}(\tilde{{\textbf{W}}}_f^{\top }\dot{\hat{{\textbf{W}}}}_f-\gamma \tilde{{\textbf{W}}}_f^{\top }\dot{\varvec{\sigma }}_f\varvec{\varsigma }^{\top }\varvec{\Upsilon }_0)\le 0. \end{aligned}$$

(52)

Therefore, using Eqs. (26) and (52), an upper bound for $\dot{{\mathcal {V}}}$ can be written as

$$\begin{aligned} \dot{{\mathcal {V}}}\le -(\alpha -\beta _2)\Vert \varvec{\varsigma }\Vert ^2-k_f\Vert {\textbf{e}}_{\varsigma }\Vert ^2+\rho (\Vert \varvec{\omega }\Vert )\Vert \varvec{\omega }\Vert \Vert {\textbf{e}}_{\varsigma }\Vert . \end{aligned}$$

By splitting $k_f$ into adjustable positive gains $k_{f1},k_{f2}\in {\mathbb {R}}^{+}$ as $k_f=k_{f1}+k_{f2}$, we can further bound $\dot{{\mathcal {V}}}$ as follows if the condition in Eq. (31) is satisfied:

$$\begin{aligned} \dot{{\mathcal {V}}}\le -\beta _3\Vert \varvec{\omega }\Vert ^2-k_{f2}\Vert {\textbf{e}}_{\varsigma }\Vert ^2+\rho (\Vert \varvec{\omega }\Vert )\Vert \varvec{\omega }\Vert \Vert {\textbf{e}}_{\varsigma }\Vert , \end{aligned}$$

(53)

where $\beta _3$ is defined as $\beta _3\triangleq \min \{(\alpha -\beta _2),k_{f1}\}$. Completing the squares for the last two terms of Eq. (53), we obtain $\dot{{\mathcal {V}}}\le -(\beta _3-\rho ^2(\Vert \varvec{\omega }\Vert )/4k_{f2})\Vert \varvec{\omega }\Vert ^2$. Therefore, we have $\dot{{\mathcal {V}}}\le c\Vert \varvec{\omega }\Vert ^2$ for some positive constant $c\in {\mathbb {R}}^{+}$ in the following domain:

$$\begin{aligned} {\mathcal {D}}\triangleq \left\{ {\textbf{y}}\in {\mathbb {R}}^{2n+2}\;|\;\Vert {\textbf{y}}\Vert \le \rho ^{-1}(2\sqrt{\beta _3 k_{f2}})\right\} , \end{aligned}$$

which, considering Eq. (51), indicates that ${\mathcal {V}}\in {\mathcal {L}}_{\infty }$ in ${\mathcal {D}}$. Therefore, from Eq. (50), we have $\varvec{\varsigma }$, ${\textbf{e}}_{\varsigma }$, P, $Q_f$, and hence $\tilde{{\textbf{W}}}_f\in {\mathcal {L}}_{\infty }$ in ${\mathcal {D}}$. Since $\varvec{\varsigma }$ is bounded, we can conclude that the prescribed performance condition is satisfied and $\tilde{{\textbf{x}}}\in {\mathcal {L}}_{\infty }$ in ${\mathcal {D}}$. To analyze the convergence of the signals, we need to show that $\varvec{\omega }$ is uniformly bounded. From Eq. (24), we can see that $\dot{\varvec{\varsigma }}\in {\mathcal {L}}_{\infty }$ in ${\mathcal {D}}$. Therefore, since $\varvec{\Upsilon }$ is bounded, from Eq. (19) we have $\dot{\tilde{{\textbf{x}}}}\in {\mathcal {L}}_{\infty }$ in ${\mathcal {D}}$. Consequently, from Eq. (22), we conclude that $\varvec{\nu }\in {\mathcal {L}}_{\infty }$ in ${\mathcal {D}}$. Since $\dot{\tilde{{\textbf{x}}}}$ is bounded, from the definition of $\varvec{\Upsilon }$, we also see that $\dot{\varvec{\Upsilon }}\in {\mathcal {L}}_{\infty }$ in ${\mathcal {D}}$. From Eq. (29), $\dot{\hat{{\textbf{W}}}}_f\in {\mathcal {L}}_{\infty }$ in ${\mathcal {D}}$, and we also have $\dot{\tilde{\varvec{\sigma }}}_f\in {\mathcal {L}}_{\infty }$. From these results and Eq. (25), we can see that $\dot{{\textbf{e}}}_{\varsigma }\in {\mathcal {L}}_{\infty }$ in ${\mathcal {D}}$. Then, since $\dot{\varvec{\varsigma }},\dot{{\textbf{e}}}_{\varsigma }\in {\mathcal {L}}_{\infty }$, we conclude that $\dot{\varvec{\omega }}\in {\mathcal {L}}_{\infty }$ in ${\mathcal {D}}$, which indicates that $\varvec{\omega }$ is uniformly continuous in ${\mathcal {D}}$.

Now consider region ${\mathcal {S}}\subset {\mathcal {D}}$ as ${\mathcal {S}}\triangleq \{{\textbf{y}}\subset {\mathcal {D}}\;|\;\psi _2({\textbf{y}})< \frac{1}{2}(\rho ^{-1}(2\sqrt{\beta _3 k_{f2}}))^2\}$. Based on the above results, Theorem 8.4 of an earlier work [33] can be used to conclude that $\Vert \varvec{\omega }\Vert \rightarrow 0$ as time goes to infinity for all ${\textbf{y}}(0)\in {\mathcal {S}}$. According to Eq. (17), $T_i\rightarrow 0$ as $\varsigma _i\rightarrow 0$, and from Eq. (14), $\Vert \tilde{{\textbf{x}}}\Vert \rightarrow 0$. Therefore, from Eqs. (19) and (24), we conclude that $\Vert \dot{\tilde{{\textbf{x}}}}\Vert \rightarrow 0$ as $t\rightarrow 0$. The convergence of $\dot{\tilde{{\textbf{x}}}}$ to zero indicates that $\hat{{\textbf{f}}}$, given by Eq. (21), converges to ${\textbf{f}}$.

Proof of $P(t)\ge 0$

Here we show that $P(t)\ge 0$. The proof follows the same steps as in a prior study [34]. Integrating both sides of Eq. (49), we have

$$\begin{aligned} \int _0^t {\mathcal {K}}({\bar{t}})\text {d}{\bar{t}}=&\int _0^t {\textbf{e}}_{\varsigma }^{\top }\left( \dot{\varvec{\epsilon }}_0-\beta _1\text {sgn}(\varvec{\varsigma })\right) \text {d}{\bar{t}}+\int _0^t \dot{\varvec{\varsigma }}^{\top }{\textbf{N}}_B\text {d}{\bar{t}}\\&-\int _0^t \beta _2\Vert \varvec{\varsigma }\Vert ^2\text {d}{\bar{t}}. \end{aligned}$$

Using Eq. (24), we have

$$\begin{aligned} \int _0^t {\mathcal {K}}({\bar{t}})\text {d}{\bar{t}}&=\int _0^t \frac{\text {d}\varvec{\varsigma }^{\top }}{\text {d}{\bar{t}}}(\dot{\varvec{\epsilon }}_0+{\textbf{N}}_B)\text {d}{\bar{t}}-\int _0^t \frac{\text {d}\varvec{\varsigma }^{\top }}{\text {d}{\bar{t}}}\beta _1\text {sgn}(\varvec{\varsigma })\text {d}{\bar{t}}\nonumber \\&+\int _0^t \alpha \varvec{\varsigma }^{\top }\left( \dot{\varvec{\epsilon }}_0-\beta _1\text {sgn}(\varvec{\varsigma })\right) \text {d}{\bar{t}}-\int _0^t \beta _2\Vert \varvec{\varsigma }\Vert ^2\text {d}{\bar{t}}. \end{aligned}$$

(54)

Integrating the first integral in Eq. (54) by parts yields

$$\begin{aligned}&\int _0^t {\mathcal {K}}({\bar{t}})\text {d}{\bar{t}} = \varvec{\varsigma }^{\top }(\dot{\varvec{\epsilon }}_0+{\textbf{N}}_B)\bigg |_0^t-\int _0^t\varvec{\varsigma }^{\top }\frac{\text {d}(\dot{\varvec{\epsilon }}_0+{\textbf{N}}_B)}{\text {d}{\bar{t}}}\text {d}{\bar{t}}\\&\quad \quad -\int _0^t \frac{\text {d}\varvec{\varsigma }^{\top }}{\text {d}{\bar{t}}}\beta _1\text {sgn}(\varvec{\varsigma })\text {d}{\bar{t}}-\int _0^t \beta _2\Vert \varvec{\varsigma }\Vert ^2\text {d}{\bar{t}}\\&\quad \quad +\int _0^t \alpha \varvec{\varsigma }^{\top }\left( \dot{\varvec{\epsilon }}_0-\beta _1\text {sgn}(\varvec{\varsigma })\right) \text {d}{\bar{t}}\\&\qquad =\varvec{\varsigma }^{\top }(\dot{\varvec{\epsilon }}_0+{\textbf{N}}_B)-\varvec{\varsigma }(0)^{\top }(\dot{\varvec{\epsilon }}_0(0)+{\textbf{N}}_B(0))\\&\qquad +\int _0^t \alpha \varvec{\varsigma }^{\top }\left( \dot{\varvec{\epsilon }}_0-\frac{1}{\alpha }\frac{\text {d}(\dot{\varvec{\epsilon }}_0+{\textbf{N}}_B)}{\text {d}{\bar{t}}}-\beta _1\text {sgn}(\varvec{\varsigma })\right) \text {d}{\bar{t}}\\&\qquad -\beta _1\sum _{i=1}^{n}|\varsigma _i|+\beta _1\sum _{i=1}^{n}|\varsigma _i(0)|-\int _0^t \beta _2\Vert \varvec{\varsigma }\Vert ^2\text {d}{\bar{t}}. \end{aligned}$$

Knowing that $\sum _{i=1}^{n}|\varsigma _i|\ge \Vert \varvec{\varsigma }\Vert$, and using Eqs. (27) and (28), we can write the following inequality:

$$\begin{aligned}&\int _0^t {\mathcal {K}}({\bar{t}})\text {d}{\bar{t}} \le (\zeta _1+\zeta _3-\beta _1)\Vert \varvec{\varsigma }\Vert +\beta _1\sum _{i=1}^{n}|\varsigma _i(0)|\\&\qquad \qquad +\int _0^t \alpha (\zeta _1+\frac{\zeta _2+\zeta _4}{\alpha }-\beta _1)\Vert \varvec{\varsigma }\Vert \text {d}{\bar{t}}\\&\qquad \quad +\int _0^t (\zeta _5-\beta _2)\Vert \varvec{\varsigma }\Vert ^2\text {d}{\bar{t}}-\varvec{\varsigma }(0)^{\top }(\dot{\varvec{\epsilon }}_0(0)+{\textbf{N}}_B(0)). \end{aligned}$$

Therefore, if the conditions in Eqs. (30) and (31) are satisfied, we have

$$\begin{aligned} \int _0^t {\mathcal {K}}({\bar{t}})\text {d}{\bar{t}} \le \beta _1\sum _{i=1}^{n}|\varsigma _i(0)|-\varvec{\varsigma }(0)^{\top }(\dot{\varvec{\epsilon }}_0(0)+{\textbf{N}}_B(0)), \end{aligned}$$

which indicates that $P(t)\ge 0$.

Proof of Theorem 2

Consider the following Lyapunov function:

$$\begin{aligned} L\triangleq V^{*}({\textbf{x}})+L_{W_c}+L_{W_s}, \end{aligned}$$

(55)

where $L_{W_s}$ is defined in Eq. (36), and $L_{W_c}\triangleq \frac{1}{2\alpha _c}\tilde{{\textbf{W}}}_c^{\top }\tilde{{\textbf{W}}}_c$, in which $\tilde{{\textbf{W}}}_c\triangleq {\textbf{W}}_c-\hat{{\textbf{W}}}_c$. Using Eqs. (1), (5), and (42), we have

$$\begin{aligned} {\dot{V}}^{*}&=\frac{\partial V^{*}}{\partial {\textbf{x}}}\dot{{\textbf{x}}} =\nabla V^{*}({\textbf{f}}+{\textbf{g}}\hat{{\textbf{u}}})\\&=\nabla V^{*}({\textbf{f}}+{\textbf{g}}{\textbf{u}}^{*})+\lambda \nabla V^{*}{\textbf{g}}(\tanh ({\textbf{D}}^{*})-\tanh (\hat{{\textbf{D}}})). \end{aligned}$$

Therefore, using Eqs. (7) and (38), ${\dot{V}}^{*}$ can be written as

$$\begin{aligned} {\dot{V}}^{*}=&-Q({\textbf{x}})-U({\textbf{u}}^{*})\nonumber \\&+\lambda ({\textbf{W}}_c^{\top }\nabla \varvec{\sigma }_c+\nabla \epsilon _c^{\top }){\textbf{g}}(\tanh ({\textbf{D}}^{*})-\tanh (\hat{{\textbf{D}}})). \end{aligned}$$

(56)

Defining $\tilde{{\textbf{u}}}\triangleq \tanh ({\textbf{D}}^{*})-\tanh (\hat{{\textbf{D}}})$, and knowing that

$$\begin{aligned}&U({\textbf{u}}^{*})>0,\\&\lambda \nabla \epsilon _c^{\top }{\textbf{g}}\tilde{{\textbf{u}}} \le \lambda \Vert \nabla \epsilon _c\Vert \Vert {\textbf{g}}\Vert \Vert \tilde{{\textbf{u}}}\Vert \le 2\lambda b_{\epsilon cx}b_g,\\&\lambda {\textbf{W}}_c^{\top }\nabla \varvec{\sigma }_c{\textbf{g}}\tilde{{\textbf{u}}} \le \lambda \Vert {\textbf{W}}_c\Vert \Vert \nabla \varvec{\sigma }_c\Vert \Vert {\textbf{g}}\Vert \Vert \tilde{{\textbf{u}}}\Vert \\&\;\;\quad \qquad \qquad \le 2\lambda \Vert {\textbf{W}}_c\Vert b_{\sigma cx}b_g, \end{aligned}$$

and $Q({\textbf{x}})>q_{\min }{\textbf{x}}^{\top }{\textbf{x}}$ for some $q_{\min }\in {\mathbb {R}}^{+}$, an upper bound can be written for ${\dot{V}}^{*}$ as

$$\begin{aligned} {\dot{V}}^{*}\le -q_{\min }\Vert {\textbf{x}}\Vert ^{2}+\kappa _1, \end{aligned}$$

(57)

where $\kappa _1\triangleq 2\lambda \Vert {\textbf{W}}_c\Vert b_{\sigma cx}b_g+2\lambda b_{\epsilon cx}b_g$.

To develop the time derivative of the second term of the right-hand side of Eq. (55), we first write the Bellman error (Eq. 10) as follows by substituting the gradient of Eq. (41) into Eq. (8):

$$\begin{aligned} \delta _B=Q({\textbf{x}})+U(\hat{{\textbf{u}}})+\hat{{\textbf{W}}}_c^{\top }\nabla \varvec{\sigma }_c\left( \hat{{\textbf{f}}}+{\textbf{g}}\hat{{\textbf{u}}}\right) . \end{aligned}$$

(58)

From Eq. (40), we have

$$\begin{aligned} Q({\textbf{x}})=-U({\textbf{u}}^{*})-{\textbf{W}}_c^{\top }\nabla \varvec{\sigma }_c\left( {\textbf{f}}+{\textbf{g}}{\textbf{u}}^{*}\right) +\epsilon _{hjb}. \end{aligned}$$

Therefore, substituting this expression into Eq. (58), we obtain

$$\begin{aligned} \delta _{B}=&~U(\hat{{\textbf{u}}})-U({\textbf{u}}^{*})-{\textbf{W}}_c^{\top }\nabla \varvec{\sigma }_c({\textbf{f}}+{\textbf{g}}{\textbf{u}}^{*})\nonumber \\&+\hat{{\textbf{W}}}_c^{\top }\nabla \varvec{\sigma }_c\left( \hat{{\textbf{f}}}+{\textbf{g}}\hat{{\textbf{u}}}\right) +\epsilon _{hjb}. \end{aligned}$$

(59)

Considering the definition of $U({\textbf{u}}^{*})$ and $U(\hat{{\textbf{u}}})$, given respectively in Eqs. (6) and (9), and knowing that $\ln ({\textbf{1}}-\tanh ^2({\textbf{D}}^{*}))=\ln ({\textbf{4}})-2{\textbf{D}}^{*}\text {sgn}({\textbf{D}}^{*})+\varvec{\epsilon }_{D^{*}}$ and $\ln ({\textbf{1}}-\tanh ^2(\hat{{\textbf{D}}}))=\ln ({\textbf{4}})-2\hat{{\textbf{D}}}\text {sgn}(\hat{{\textbf{D}}})+\varvec{\epsilon }_{D}$ for some bounded $\varvec{\epsilon }_{D^{*}}$ and $\varvec{\epsilon }_{D}$ [18], where $\text {sgn}(\cdot )$ denotes the signum function, we develop the following expression:

$$\begin{aligned} U(\hat{{\textbf{u}}})-U({\textbf{u}}^{*})=&~2\lambda ^2\bar{{\textbf{R}}}\left( {\textbf{D}}^{*}\text {sgn}({\textbf{D}}^{*})-\hat{{\textbf{D}}}\text {sgn}(\hat{{\textbf{D}}})\right) \nonumber \\&-\hat{{\textbf{W}}}_c^{\top }\nabla \varvec{\sigma }_c{\textbf{g}}\hat{{\textbf{u}}}+{\textbf{W}}_c^{\top }\nabla \varvec{\sigma }_c{\textbf{g}}{\textbf{u}}^{*}\nonumber \\&+\nabla \epsilon _c{\textbf{g}}{\textbf{u}}^{*}+\lambda ^2\bar{{\textbf{R}}}(\varvec{\epsilon }_{D}-\varvec{\epsilon }_{D^{*}}). \end{aligned}$$

(60)

The signum function can be approximated by a $\tanh$ function with the following relation quantifying the approximation error [35]:

$$\begin{aligned} 0\le x\text {sgn}(x)-x\tanh (\kappa x)\le \frac{1}{0.2785\kappa }. \end{aligned}$$

Therefore, the expression in Eq. (60) can be written as

$$\begin{aligned}&U(\hat{{\textbf{u}}})-U({\textbf{u}}^{*})=2\lambda ^2\bar{{\textbf{R}}}\left( {\textbf{D}}^{*}\tanh (\kappa {\textbf{D}}^{*})-\hat{{\textbf{D}}}\tanh (\kappa \hat{{\textbf{D}}})\right) \nonumber \\&\qquad +2\lambda ^2\bar{{\textbf{R}}}(\varvec{\kappa }_{D^{*}}-\varvec{\kappa }_{D})-\hat{{\textbf{W}}}_c^{\top }\nabla \varvec{\sigma }_c{\textbf{g}}\hat{{\textbf{u}}}+{\textbf{W}}_c^{\top }\nabla \varvec{\sigma }_c{\textbf{g}}{\textbf{u}}^{*}\nonumber \\&\qquad +\nabla \epsilon _c{\textbf{g}}{\textbf{u}}^{*}+\lambda ^2\bar{{\textbf{R}}}(\varvec{\epsilon }_{D}-\varvec{\epsilon }_{D^{*}}), \end{aligned}$$

(61)

where $\varvec{\kappa }_{D^{*}}$ and $\varvec{\kappa }_{D}$ denote the approximation errors. Then, considering the definitions of ${\textbf{D}}^{*}$ and $\hat{{\textbf{D}}}$, and adding and subtracting $\lambda {\textbf{W}}_c^{\top }\nabla \varvec{\sigma }_c{\textbf{g}}\tanh (\kappa \hat{{\textbf{D}}})$ to the right-hand side of Eq. (61), we have

$$\begin{aligned}&U(\hat{{\textbf{u}}})-U({\textbf{u}}^{*})= \lambda \tilde{{\textbf{W}}}_c^{\top }\nabla \varvec{\sigma }_c{\textbf{g}}\tanh (\kappa \hat{{\textbf{D}}})\nonumber \\&+2\lambda ^2\bar{{\textbf{R}}}(\varvec{\kappa }_{D^{*}}-\varvec{\kappa }_{D})-\hat{{\textbf{W}}}_c^{\top }\nabla \varvec{\sigma }_c{\textbf{g}}\hat{{\textbf{u}}}+{\textbf{W}}_c^{\top }\nabla \varvec{\sigma }_c{\textbf{g}}{\textbf{u}}^{*}\nonumber \\&+\nabla \epsilon _c{\textbf{g}}{\textbf{u}}^{*}+\lambda ^2\bar{{\textbf{R}}}(\varvec{\epsilon }_{D}-\varvec{\epsilon }_{D^{*}})\nonumber \\&+\lambda {\textbf{W}}_c^{\top }\nabla \varvec{\sigma }_c{\textbf{g}}\left( \tanh (\kappa {\textbf{D}}^{*})-\tanh (\kappa \hat{{\textbf{D}}})\right) . \end{aligned}$$

(62)

Substituting Eq. (62) into Eq. (59) and doing certain manipulations, we obtain

$$\begin{aligned} \delta _B=-\varvec{\beta }^{\top }\tilde{{\textbf{W}}}_c+\epsilon _{\delta }, \end{aligned}$$

(63)

where $\varvec{\beta }\in {\mathbb {R}}^{{\mathcal {L}}_c}$ is defined in Eq. (44) and $\epsilon _\delta \in {\mathbb {R}}$ is given by

$$\begin{aligned} \epsilon _{\delta }\triangleq&~2\lambda ^2\bar{{\textbf{R}}}(\varvec{\kappa }_{D^{*}}-\varvec{\kappa }_{D})+\lambda ^2\bar{{\textbf{R}}}(\varvec{\epsilon }_{D}-\varvec{\epsilon }_{D^{*}})+\nabla \epsilon _c{\textbf{g}}{\textbf{u}}^{*}\\&+\epsilon _{hjb}+\lambda {\textbf{W}}_c^{\top }\nabla \varvec{\sigma }_c{\textbf{g}}\left( \tanh (\kappa {\textbf{D}}^{*})-\tanh (\kappa \hat{{\textbf{D}}})\right) \\&-{\textbf{W}}_c^{\top }\nabla \varvec{\sigma }_c\tilde{{\textbf{f}}}, \end{aligned}$$

where all of its elements are bounded terms, and thus an upper bound can be considered for it as $|\epsilon _{\delta }|\le {\bar{\epsilon }}_{\delta }$. Also note that approximation errors $\varvec{\epsilon }_{D^{*}}$, $\varvec{\epsilon }_{D}$, $\varvec{\kappa }_{D^{*}}$, and $\varvec{\kappa }_{D}$ converge to zero as ${\textbf{x}}$ goes to zero. Following the same steps, the unmeasurable form of simulated Bellman error $\delta _{Bj}$ can be obtained as

$$\begin{aligned} \delta _{Bj}=-\varvec{\beta }_j^{\top }\tilde{{\textbf{W}}}_c-{\textbf{W}}_c^{\top }\nabla \varvec{\sigma }_{cj}\tilde{{\textbf{f}}}_{sj}+\epsilon _{\delta j}, \end{aligned}$$

(64)

where $\tilde{{\textbf{f}}}_{sj}\triangleq {\textbf{f}}_{j}-\hat{{\textbf{f}}}_{sj}={\textbf{e}}_{sj}$, subscript j indicates the jth sample of the variables, and $\epsilon _{\delta j}\triangleq 2\lambda ^2\bar{{\textbf{R}}}(\varvec{\kappa }_{D^{*}}-\varvec{\kappa }_{Dj})+\lambda ^2\bar{{\textbf{R}}}(\varvec{\epsilon }_{Dj}-\varvec{\epsilon }_{D^{*}})+\lambda {\textbf{W}}_c^{\top }\nabla \varvec{\sigma }_c{\textbf{g}}(\tanh (\kappa {\textbf{D}}^{*})-\tanh (\kappa \hat{{\textbf{D}}}({\textbf{x}}_j)))-\nabla \epsilon _c{\textbf{f}}_j$, for which an upper constant bound can be considered.

Then, using Eqs. (63) and (64) and the adaptation rule (Eq. 43), the time derivative of $L_{W_c}$ can be written as

$$\begin{aligned}&{\dot{L}}_{W_c}= -\tilde{{\textbf{W}}}_c^{\top }\bar{\varvec{\beta }}\bar{\varvec{\beta }}^{\top }\tilde{{\textbf{W}}}_c+\tilde{{\textbf{W}}}_c^{\top }\frac{\bar{\varvec{\beta }}}{m_s}\epsilon _{\delta }\\&-\frac{\gamma _{c1}}{N}\sum _{j=1}^{N}\tilde{{\textbf{W}}}_c^{\top }\bar{\varvec{\beta }}_j\bar{\varvec{\beta }}_j^{\top }\tilde{{\textbf{W}}}_c\\&-\frac{\gamma _{c1}}{N}\sum _{j=1}^{N}\tilde{{\textbf{W}}}_c^{\top }\frac{\bar{\varvec{\beta }}_j}{m_{sj}}{\textbf{W}}_c^{\top }\nabla \varvec{\sigma }_{cj}\tilde{{\textbf{f}}}_{sj}+\frac{\gamma _{c1}}{N}\sum _{j=1}^{N}\tilde{{\textbf{W}}}_c^{\top }\frac{\bar{\varvec{\beta }}_j}{m_{sj}}\epsilon _{\delta j}\\&-\frac{\gamma _{c2}\sum _{j=1}^{N}\tilde{{\textbf{W}}}_c^{\top }\bar{\varvec{\beta }}_j\bar{\varvec{\beta }}_j^{\top }\tilde{{\textbf{W}}}_c}{N(\Vert \varvec{\Xi }\Vert +\varepsilon _c)}+\frac{\gamma _{c2}\sum _{j=1}^{N}\tilde{{\textbf{W}}}_c^{\top }\bar{\varvec{\beta }}_j \epsilon _{\delta j}/m_{sj}}{N(\Vert \varvec{\Xi }\Vert +\varepsilon _c)}\\&-\frac{\gamma _{c2}\sum _{j=1}^{N}\tilde{{\textbf{W}}}_c^{\top }\bar{\varvec{\beta }}_j {\textbf{W}}_c^{\top }\nabla \varvec{\sigma }_{cj}\tilde{{\textbf{f}}}_{sj}/m_{sj}}{N(\Vert \varvec{\Xi }\Vert +\varepsilon _c)}, \end{aligned}$$

where $\bar{\varvec{\beta }}\triangleq \varvec{\beta }/(1+\varvec{\beta }^{\top }\varvec{\beta })$ and $m_s\triangleq 1+\varvec{\beta }^{\top }\varvec{\beta }$ that satisfy the following inequality:

$$\begin{aligned} \Vert \frac{\bar{\varvec{\beta }}}{m_s}\Vert \le b_{\beta }<1, \end{aligned}$$

in which $b_{\beta }$ is a positive constant. We have

$$\begin{aligned} -\frac{\gamma _{c2}\sum _{j=1}^{N}\tilde{{\textbf{W}}}_c^{\top }\bar{\varvec{\beta }}_j\bar{\varvec{\beta }}_j^{\top }\tilde{{\textbf{W}}}_c}{N(\Vert \varvec{\Xi }\Vert +\varepsilon _c)}\le -\gamma _{c2}\vartheta _c\Vert \tilde{{\textbf{W}}}_c\Vert , \end{aligned}$$

where $\vartheta _c>0$ is defined as

$$\begin{aligned} \vartheta _c\triangleq 1- \frac{(c_{\beta _2}-c_{\beta _1})\Vert \tilde{{\textbf{W}}}_c\Vert +\hbar _1+\hbar _2+\varepsilon _c}{c_{\beta _2}\Vert \tilde{{\textbf{W}}}_c\Vert +\hbar _1+\hbar _2+\varepsilon _c}, \end{aligned}$$

in which $c_{\beta _2}\triangleq \frac{1}{N}(\sup \limits _{t\in {\mathbb {R}}_{\ge t_0}}(\lambda _{\max }(\sum _{j=1}^{N}\frac{\varvec{\beta }_j\varvec{\beta }_j^{\top }}{(1+\varvec{\beta }_j^{\top }\varvec{\beta }_j)^2})))$, and $\hbar _1\triangleq {\bar{b}}_{\beta } b_{\sigma cx} b_{\sigma sx}\Vert {\varvec{W}}_c\Vert \Vert \tilde{{\textbf{W}}}_s\Vert _F$, $\hbar _2\triangleq {\bar{b}}_{\beta }b_{\sigma cx}{\bar{\epsilon }}_{sj}\Vert {\varvec{W}}_c\Vert + {\bar{b}}_{\beta }{\bar{\epsilon }}_{\delta j}$, in which ${\bar{b}}_{\beta }\triangleq \sup \limits _{j=1\cdots N}(\Vert \bar{\varvec{\beta }}_{j}/m_{sj}\Vert )$, ${\bar{\epsilon }}_{sj}\triangleq \sup \limits _{j=1\cdots N}(\Vert \varvec{\epsilon }_{sj}\Vert )$ and ${\bar{\epsilon }}_{\delta j}\triangleq \sup \limits _{j=1\cdots N}(|\epsilon _{\delta j}|)$. Also, assuming that $\varepsilon _c> \sup \limits _{j=1\cdots N}(\Vert \tilde{{\textbf{f}}}_{sj}\Vert )+{\bar{\epsilon }}_{\delta }$, the following inequality can be developed:

$$\begin{aligned}&-\frac{\gamma _{c2}\sum _{j=1}^{N}\tilde{{\textbf{W}}}_c^{\top }\bar{\varvec{\beta }}_j {\textbf{W}}_c^{\top }\nabla \varvec{\sigma }_{cj}\tilde{{\textbf{f}}}_{sj}/m_{sj}}{N(\Vert \varvec{\Xi }\Vert +\varepsilon _c)}\\&\qquad +\frac{\gamma _{c2}\sum _{j=1}^{N}\tilde{{\textbf{W}}}_c^{\top }\bar{\varvec{\beta }}_j \epsilon _{\delta j}/m_{sj}}{N(\Vert \varvec{\Xi }\Vert +\varepsilon _c)}\le \\&\qquad \gamma _{c2}{\bar{b}}_{\beta }b_{\sigma cx}\varpi _{c1}\Vert {\textbf{W}}_c\Vert \Vert \tilde{{\textbf{W}}}_c\Vert +\gamma _{c2}{\bar{b}}_{\beta }\varpi _{c2}\Vert \tilde{{\textbf{W}}}_c\Vert \end{aligned}$$

for some $\varpi _{c1},\varpi _{c2}<1$. Then, defining the following positive constants:

$$\begin{aligned}&\varrho _1\triangleq \gamma _{c1} {\bar{b}}_{\beta } b_{\sigma cx} b_{\sigma sx}\Vert {\varvec{W}}_c\Vert ,\\&\varrho _2\triangleq \gamma _{c1} {\bar{b}}_{\beta }b_{\sigma cx}{\bar{\epsilon }}_{sj}\Vert {\varvec{W}}_c\Vert +\gamma _{c2}{\bar{b}}_{\beta }b_{\sigma cx}\varpi _{c1}\Vert {\varvec{W}}_c\Vert \\&\qquad +\gamma _{c1} {\bar{b}}_{\beta }{\bar{\epsilon }}_{\delta j}+\gamma _{c2}{\bar{b}}_{\beta }\varpi _{c2}+b_{\beta }{\bar{\epsilon }}_{\delta }, \end{aligned}$$

and considering Eq. (45), the following upper bound can be written for ${\dot{L}}_{W_c}$:

$$\begin{aligned} {\dot{L}}_{W_c}\le&-\gamma _{c1}c_{\beta _1}\Vert \tilde{{\textbf{W}}}_c\Vert ^2+\varrho _1\Vert \tilde{{\textbf{W}}}_c\Vert \Vert \tilde{{\textbf{W}}}_s\Vert _F\nonumber \\&+(\varrho _2-\gamma _{c2}\vartheta _c)\Vert \tilde{{\textbf{W}}}_c\Vert . \end{aligned}$$

(65)

Therefore, using Eqs. (37), (57), and (65) and Young’s inequality, an upper bound for ${\dot{L}}$ can be written as

$$\begin{aligned} {\dot{L}}\le&-q_{\min }\Vert {\textbf{x}}\Vert ^{2}-(\gamma _{c1} c_{\beta _1}-\frac{\varrho _1}{\eta _1^2}-\frac{\eta _2^2}{4})\Vert \tilde{{\textbf{W}}}_c\Vert ^2\nonumber \\&-(\gamma _{s1}c_{\sigma _1}-\frac{\eta _1^2\varrho _1}{4}-\frac{\eta _3^2}{4})\Vert \tilde{{\textbf{W}}}_s\Vert _F^2\nonumber \\&+\kappa _1+\frac{(\varrho _2-\gamma _{c2}\vartheta _c)^2}{\eta _2^2}+\frac{\epsilon _{w}^2}{\eta _3^2}, \end{aligned}$$

(66)

where $\eta _1,\eta _2,\eta _3\in {\mathbb {R}}^{+}$ are adjustable constants. Therefore, considering Eq. (66), whenever the gain conditions in Eq. (46) are satisfied, we conclude that ${\textbf{x}}$, $\tilde{{\textbf{W}}}_c$, and $\tilde{{\textbf{W}}}_s$ are uniformly ultimately bounded.