Investigations on the nonlinear dynamic characteristics of a rotor supported by hybrid foil magnetic bearings

Abstract

Hybrid foil magnetic bearings (HFMB) are highly suitable for oil-free turbomachinery and high-speed compressors under variable conditions due to their advantages such as frictionless operation at low speeds, reliable high-speed operation and adjustable dynamic performance. By adjusting the working mode and load sharing ratio, HFMB can optimize the dynamic performance and improve the stability of the rotor system. This paper presents investigations on the rotordynamics of a rigid rotor supported by two HFMBs. The coastdown response of the rotor supported by HFMBs and gas foil bearings from 65 krpm to rest is recorded experimentally and used to validate the calculated results of the rotordynamic model. Computational methods are used to predict the effect of load sharing ratios and working modes on rotordynamics as a function of HFMB operating conditions. The effects of load and equilibrium position on the rotordynamics are also predicted. Orbit simulations, Fast Fourier Transform, Poincaré maps and bifurcation diagrams are used for the theoretical analysis. The results show that an appropriate load sharing ratio with hybrid mode can effectively improve the rotordynamic performance of the HFMBs-rotor system, while increasing the load can also significantly improve the stability of the system.

1 Introduction

The implementation of hybrid foil magnetic bearings (HFMBs) in compact, oil-free turbomachinery reduces start/stop friction and system vibration, and increases reliability and high-speed operation [1, 2]. Since the 2000s, HFMBs in side-by-side or nested configurations with different control algorithms have been implemented as high-dynamic damping bearings in oil-free (small size) rotating machines [3]. Compared to gas foil bearings (GFBs) for high speed operation, HFMBs have demonstrated superior reliability in turbomachinery [2, 4,5,6]. Swanson et al. [4] tested the load sharing capability on a test rig with a maximum speed of 36 krpm and demonstrated for the first time that HFMBs can achieve load sharing between GFBs and Active Magnetic Bearings (AMB) at different speeds and loads. Jeong and Lee [6] proposed a control algorithm applied to HFMBs to cope with sudden unbalance, and the experimental results show that the HFMB can recover to a steady state when the unbalanced mass changes abruptly. Pham and Ahn [1] applied the HFMB to a flexible rotor bearing system for the first time, and the experimental results show that the HFMB has a better vibration suppression performance compared to the GFB. Jeong et al. [2] demonstrated a turbo-blower supported by two HFMBs with PD-control. By adjusting the proportional gain, the bearing stiffness, eccentricity and dynamic performance can be changed accordingly. The successful application of HFMBs in turbo-blowers illustrates their potential value in high-speed rotating machinery applications.

The hydrodynamic pressure generated between the rotor and the top foil deforms the flexible foil structures, giving the GFB a distinct nonlinear support characteristic. Swanson [7] developed a simplified bump foil damping model in which each bump is reduced to a friction interface and a load-dependent friction element is introduced. Lee et al. [8] modelled the top foil as having relative deflection, locally varying structural stiffness and damping, taking into account the interaction between the bump foils, friction between the bump foil and other contact points. Lez et al. [9] developed a model to describe the structure of a GFB in which the bump foils have three degrees of freedom and can interact with each other, taking into account frictional forces. Feng and Kaneko [10] replaced each bump with a link spring structure and used a finite element model to resolve the deformation of the top foil. Larsen et al. [11] have developed a finite element model of the foil structures using nonlinear spring elements, taking into account the effects of the foil flexibility and friction at the contact points. The deflection of the foil structure depends on the pressure in the fluid film and the variation of the bearing gap, so the prediction of the fluid film is another point of interest for the researchers. Arakere and Nelson [12] solved the problem of compressible elastohydrodynamics of finite length GFBs by using an iterative scheme (finite difference method) to numerically solve the coupling of the nonlinear compressible Reynolds equation with the elastic equation for the deflection of the foil. Faria and San Andrés [13] have developed procedures for solving the highly nonlinear governing equations in high-speed gas lubrication for the analysis of diffusion-convection thin film gas flows. Ullah et al. [14,15,16,17] use the Levenberg–Marquardt method with artificial neural networks, an innovative convergence reliability technique, to provide numerical solutions to a wide range of fluid flow problems. The nonlinear properties of the foil structure and the fluid film result in the nonlinear behavior of the GFBs-rotor system. Bhore and Darpe [18] used time-domain orbital simulations to predict the nonlinear dynamics of the flexible rotor-GFB system. Bonello and Pham [19, 20] developed an efficient algorithm to solve the static equations simultaneously. They also applied transient nonlinear dynamic analysis and static equilibrium analysis techniques to a real turbocharger. Static stability can be promoted by increasing the length-to-radius ratio, increasing the compliance of the foil structure and reducing the undeformed radial clearance of the GFB. The nonlinear steady-state response of a rotor supported by three pad segmented GFBs was investigated numerically and experimentally by Larsen et al. [21, 22]. Xu and Kim [23] applied the measured nonlinear structural stiffness of the GFB to time-domain transient rotordynamic simulations. The results show that the dynamic coefficient is strongly influenced by the loose foil structure when the bearing load is small. Osmanski et al. [24] adopted the compliant foil structure model of Ref. [9] to predict the nonlinear time-domain rigid GFBs-rotor system. The sticking phenomenon, although prevalent in foil structures, cannot be captured by the dynamic friction model. Guan et al. [25] predicted time-domain dynamic results of a rigid rotor supported by active bump-type foil bearings (ABFBs) and compared them with experimental results.

The electromagnetic force increases rapidly as the air gap decreases, leading to instability of the AMBs at the equilibrium position. Therefore, the controller should provide a restoring force, similar to a mechanical spring, to maintain the rotor center near the equilibrium position, and a damping component to attenuate the oscillation [26,27,28,29]. The electromagnetic force is proportional to the square of the coil current and inversely proportional to the square of the air gap, which is the natural characteristic of AMBs. The saturation of the magnetic flux means that the electromagnetic force is no longer affected by changes in the coil current, which together with the natural characteristics of AMBs constitutes the nonlinearity of the electromagnetic force [30]. Chen and Lin [31] proposed a robust non-singular terminal sliding-mode control system to overcome the long convergence time, system singularity, highly nonlinear and time-varying problems of conventional terminal sliding mode control. Kandil et al. [32] and Saeed et al. [33] investigated the influence of different control parameters on the system periodic motions of a 16-pole AMB and the effect of two different control configurations on the nonlinear dynamics of a six-pole AMB, respectively. For a one-degree-of-freedom AMB, Lindlau and Knospe [34] proposed a high-performance feedback controller with μ-synthesis that can efficiently convert nonlinear systems into linear targets and also guarantee a beam compliance performance specification. Meanwhile, for the three-degree-of-freedom six-pole AMBs, some scholars have studied other control methods, including BP neural network-based active disturbance rejection control and linear/nonlinear active disturbance rejection switching control, to decouple the AMBs-rotor system [35, 36]. Zhang et al. [37] proposed a new multi-scale method to analyze the nonlinear bifurcation behavior of the AMBs-rotor system, which is strongly influenced by the nonlinear electromagnetic force and current saturation.

The nonlinear properties of GFBs and AMBs have now been thoroughly and systematically investigated. However, the mutual coupling of GFBs and AMBs in HFMBs gives rise to unique and complex nonlinear behaviors that have not been investigated. In this paper, the locus of the rotor center is tracked by simultaneously solving the equations of motion for the rigid rotor, the deformation equations for the top and bump foils, the unsteady Reynolds equation and the PID-controlled electromagnetic force equation in the time domain. The influence of the working mode and the load sharing ratio as a function of the operating conditions, as well as the load and the equilibrium position as key parameters, on the nonlinear dynamic characteristics of the rotor system is investigated.

The following study is categorized as follows: In Sect. 2, a model of an HFMB and its rotor system is presented. Section 3 describes the experimental setup of the HFMB-rotor system and compares and validates the results of the experimental tests and numerical calculations. Section 4 analyses and discusses the effects of working mode, load sharing ratio, load and equilibrium position on the nonlinear dynamic behavior of the rotor using numerical calculations. Conclusions and future work are presented in Sect. 5.

2 Theoretical model

2.1 HFMB structure

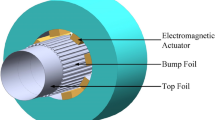
Reference [38] first proposed the nested configuration of HFMBs. In the literature, the top foil and the bump foil are nested in the gap between the rotor and the magnetic poles, as shown in Fig. 1. The space inside the AMB, which traditionally contains the coils, is used as the housing molding of the GFB with non-magnetic epoxy. As the GFB is mounted in the inner diameter of the AMB, the combination of the GFB and the AMB is realized. It is important to note that the radial thickness of the bump and top foils is part of the air gap of the AMB. Therefore, the deformation of the bump foil and the top foil does not change the air gap of the AMB, and the parameter that affects the air gap is the rotor center position. In addition, the axial length of the foil is the same as the width of the stator.

Fig. 1

Schematic description and photograph of a hybrid foil magnetic bearing

As shown in Fig. 1, the vertical down direction is defined as the positive direction of the X axis, and the horizontal right direction is defined as the positive direction of the Y axis. The upper and lower opposite poles are used to control the movement of the rotor in the X direction, and the remaining opposite poles control the movement of the rotor in the Y direction accordingly. Heshmat et al. [3] were the first to propose the operation of HFMBs. At operating speed, the AMB is fully loaded and the actual magnitude and direction of the load is calculated from the coil currents. The equilibrium position is determined based on the predetermined load sharing ratio and stored data, and then the AMB adjusts the rotor center to the new equilibrium position [4]. However, the paper does not explain what value of load sharing ratio is appropriate, i.e. how to select the load sharing ratio under steady-state operating conditions.

2.2 Theoretical model of HFMBs

The GFB in operation consists of a gas film, a top foil and a bump foil, as shown in Fig. 2. The gas is extruded from the wedge-shaped space between the rotor and the top foil to form a gas film. As the rotor moves, the circumferential pressure distribution of the gas film varies considerably, causing the GFB support to exhibit strong nonlinearity. In addition to the nonlinear characteristics of the fluid film itself, the support structure is also the main cause of the nonlinearity of the GFB support force [39,40,41,42].

Fig. 2

Calculation mode of the gas foil bearings

Hydrodynamic pressure is generated in the wedge-shaped space between the top foil and the rotor, as shown in Fig. 2. The dimensionless unsteady Reynolds equation is given by

$$ \frac{\partial }{\partial \theta }\left( {\overline{p}\overline{h}^{3} \frac{{\partial \overline{p}}}{\partial \theta }} \right) + \frac{\partial }{{\partial \overline{z}}}\left( {\overline{p}\overline{h}^{3} \frac{{\partial \overline{p}}}{{\partial \overline{z}}}} \right) = \Lambda \frac{{\partial (\overline{p}\overline{h})}}{\partial \theta }{ + 2}\Lambda \gamma \frac{{\partial (\overline{p}\overline{h})}}{{\partial \overline{t} }}. $$

(1)

The following dimensionless parameters are taken into account

$$ \overline{p} = \frac{p}{{p_{a} }}, \, \overline{h} = \frac{h}{C}, \, \overline{z} = \frac{z}{R}, \, \Lambda = \frac{6\mu \omega }{{{\text{p}}_{{\text{a}}} }}\left(\frac{R}{C}\right)^{2} , \, \overline{t} = \upsilon t, \, \gamma = \frac{\upsilon }{\omega }. $$

(2)

The gas film thickness can be determined from the initial position of the rotor and the deflection of the foil structure as shown in Fig. 2. The expression for the gas film thickness is

$$ h = C + e \cdot \cos (\theta - \theta_{0} ) + [\varepsilon ]. $$

(3)

At high speeds, film pressure is created between the rotor and the top foil, causing the flexible surface to expand radially outwards. $[\varepsilon ]$ is the deflection of the flexible surface, which consists of two parts in series, the deflection of the top foil and the deflection of the bump foil, as shown in Fig. 2. In the calculations, the top foil is modeled as a one-dimensional beam and the deflection of the foil at the bump foil is considered to be equal to the deflection of the bump foil. The foil deflection at the middle of two adjacent bump foils is considered to be the deflection of the top foil plus the deflection of the bump foil [43].

The deflection of the top foil should be [44, 45]

$$ \left\{ \begin{gathered} \varepsilon_{2i - 1,j} = \frac{2s}{{\text{E}}}\left( {\frac{{l_{0} }}{{t_{b} }}} \right)^{3} (1 - v^{2} )(p - {\text{Pa}}) \hfill \\ \varepsilon_{2i,j} = \frac{2s}{{\text{E}}}\left( {\frac{{l_{0} }}{{t_{b} }}} \right)^{3} (1 - v^{2} )(p - {\text{Pa}}) + \frac{{s^{4} \Delta z}}{{1920{\text{EI}}}}(3p_{2i + 1,j} + 3p_{2i - 1,j} - p_{2i,j} ). \hfill \\ \end{gathered} \right. $$

(4)

The boundary conditions are

$$ \left\{ \begin{gathered} p = {\text{Pa}},z = \pm L/2 \hfill \\ p = {\text{Pa}},\theta = 0,2\pi . \hfill \\ \end{gathered} \right. $$

(5)

The boundary conditions in Eq. (5) take into account the fact that the top foil does not form a complete shell and that gas flows into the lubricated film at the free end and out at the fixed end, as shown in Fig. 2. At the axial ends, the lubrication film is in direct contact with the gas [46].

Figure 3 shows the operating principle of an active electromagnetic bearing system. A closed-loop controlled electromagnetic force keeps the rotor in the specified position. The non-contact position sensors (eddy current sensors are used for the experiments) continuously measure the error between the desired position and the actual position of the rotor and feed this information to the controller. The error signal is calculated by the controller to produce a control signal that increases the coil current of one set of poles while decreasing the coil current of the opposite poles, a control method known as differential control. The electromagnetic forces in the X and Y directions under differential control can be expressed as follows.

$$ \begin{gathered} F_{mx} = F_{1} (i_{0x1} ,x_{0x1} ) - F_{2} (i_{0x2} ,x_{0x2} ) \hfill \\ + [k_{ix1} (i_{x1} - i_{0x1} ) - k_{ix2} (i_{x2} - i_{0x2} )] - [k_{xx1} (x_{x1} - x_{0x1} ) - k_{xx2} (x_{x2} - x_{0x2} )]. \hfill \\ \end{gathered} $$

(6)

$$ F_{my} = [k_{iy1} (i_{y1} - i_{0y1} ) - k_{iy2} (i_{y2} - i_{0y2} )] - [k_{xy1} (x_{y1} - x_{0y1} ) - k_{xy2} (x_{y2} - x_{0y2} )]. $$

(7)

Fig. 3

Calculation mode of the active magnetic bearing

$F_{mx}$ and $F_{my}$ are the electromagnetic forces in the X and Y directions, respectively. $F_{1}$ and $F_{2}$ denote the electromagnetic forces generated by the bias currents of the upper and lower magnetic poles, which are used to balance the load. $k_{ix1}$, $k_{ix2}$, $k_{iy1}$ and $k_{iy2}$ represent the current stiffness, and $k_{xx1}$, $k_{xx2}$, $k_{xy1}$, $k_{xy2}$ represent the displacement stiffness. The current stiffness and displacement stiffness are expressed as follows:

$$ \left\{ {\begin{array}{*{20}c} {k_{x} = \frac{{\mu_{0} A_{0} N^{2} i_{0}^{2} }}{{x_{0}^{3} }}} \\ {k_{i} = \frac{{\mu_{0} A_{0} N^{2} i_{0} }}{{x_{0}^{2} }}.} \\ \end{array} } \right. $$

(8)

Figure 4 shows the principle of the PID closed-loop control of the HFMB. It can be seen that the error e is calculated by the PID controller to produce the control signal, which is then amplified by the power amplifier to produce the coil currents. The electromagnetic force is influenced by both current and displacement variations. The current stiffness is positively related to the electromagnetic force, while the displacement stiffness is negatively related to the electromagnetic force, as described in Eqs. (6) and (7). The electromagnetic force will then act on the rotor, producing acceleration, velocity and displacement, and the displacement will be fed directly to the electromagnetic force. In addition, an eddy current displacement sensor measures the actual position of the rotor and compares it with a desired position, generating an error signal. It should be emphasized that the desired position varies according to the calculated eccentricity of the GFB and the bias current varies accordingly to balance the load.

Fig. 4

Schematic diagram of PID control loop of the HFMB system

2.3 Theoretical model of a rigid rotor

The schematic diagram of the rigid rotor supported by HFMB is shown in Fig. 5. The rotor can move freely in the spatial coordinate system, which can be decomposed into translational motion and rotational motion of the center of mass in the X/Y/Z directions. ${\hat{\text{o}}}\,{\hat{\mu }}\,{\hat{\nu }}\,{\hat{\omega }}$ is the translational coordinate system of ${\text{oxyz}}$, and ${\hat{\text{o}}}\,{\hat{\text{x}}}\,{\hat{\text{y}}}\,{\hat{\text{z}}}$ is the coordinate system that ${\hat{\text{o}}}\,{\hat{\mu }}\,{\hat{\nu }}\,{\hat{\omega }}$ rotates arbitrarily around the ${\text{X/Y/Z}}$ axes. Since the operating speed is lower than in the first bending mode, to simplify the calculation, the rotor can be modeled as four degrees of freedom (4DOF) consisting only of translations of the center of mass along the X/Y directions and rotations of the rotor around the X/Y axes [25, 47, 48].

Fig. 5

Coordinate system and rotor configuration with HFMBs

The rotor's free motion equation can be expressed as

$$ \left\{ {\begin{array}{*{20}l} {m\ddot{x} = F_{bx} + F_{ux} + mg} \\ {m\ddot{y} = F_{by} + F_{uy} } \\ {I_{T} \ddot{\theta }_{x} + I_{P} \omega \dot{\theta }_{y} = M_{xb} + M_{xu} } \\ {I_{T} \ddot{\theta }_{y} - I_{P} \omega \dot{\theta }_{x} = M_{yb} + M_{yu} } \\ \end{array} } \right\}. $$

(9)

where m is the mass of the rotor, $F_{bx}$ and $F_{by}$ are the forces generated by the HFMBs at both ends. $F_{ux}$ and $F_{uy}$ are the forces generated by the unbalanced masses. $I_{T}$ is the translational moment of inertia and $I_{P}$ is the polar moment of inertia. $\theta_{x}$ and $\theta_{y}$ are the angles of rotation about the X and Y axes. $M_{xb}$ and $M_{yb}$ are the moments of rotation generated by the bearing forces. $M_{xu}$ and $M_{yu}$ are the moments of rotation generated by the unbalanced masses.

The dynamic force of the HFMB is the sum of the hydrodynamic force of the GFB and the electromagnetic force of the AMB.

$$ \left\{ {\begin{array}{*{20}c} \begin{gathered} F_{bx} = {\text{Pa}}R^{2} \int\limits_{0}^{2\pi } {\int\limits_{0}^{L/R} {(p_{l} (\theta_{l} ,z_{l} ) - 1)\cos \theta_{l} } } d\theta_{l} dz_{l} + {\text{Pa}}R^{2} \int\limits_{0}^{2\pi } {\int\limits_{0}^{L/R} {(p_{r} (\theta_{r} ,z_{r} ) - 1)\cos \theta_{r} } } d\theta_{r} dz_{r} \hfill \\ + F_{AMBlx1} + F_{AMBrx1} - F_{AMBrlx2} - F_{AMBrx2} \hfill \\ \end{gathered} \\ \begin{gathered} F_{by} = {\text{Pa}}R^{2} \int\limits_{0}^{2\pi } {\int\limits_{0}^{L/R} {(p_{l} (\theta_{l} ,z_{l} ) - 1)\sin \theta_{l} } } d\theta_{l} dz_{l} + {\text{Pa}}R^{2} \int\limits_{0}^{2\pi } {\int\limits_{0}^{L/R} {(p_{r} (\theta_{r} ,z_{r} ) - 1)\sin \theta_{r} } } d\theta_{r} dz_{r} \hfill \\ + F_{AMBly1} + F_{AMBry1} - F_{AMBrly2} - F_{AMBry2} . \hfill \\ \end{gathered} \\ \end{array} } \right\} $$

(10)

The unbalance forces at the left and right ends are as follows:

$$ \left\{ {\begin{array}{*{20}c} {F_{ux} = m_{ul} u_{l} \omega^{2} \cos (\omega t + \phi ) + m_{ur} u_{r} \omega^{2} \cos (\omega t + \phi )} \\ {F_{uy} = m_{ul} u_{l} \omega^{2} \sin (\omega t + \phi ) + m_{ur} u_{r} \omega^{2} \sin (\omega t + \phi )} \\ \end{array} } \right\}. $$

(11)

where $m_{ul}$ and $m_{ur}$ are the unbalanced mass, $u_{l}$ and $u_{r}$ are the radius of the unbalanced mass. The torques generated by the bearing and the unbalanced mass are expressed as follows:

$$ \left\{ {\begin{array}{*{20}c} {M_{xb} = (F_{GFBly} + F_{AMBly1} - F_{AMBly2} )Z_{bl} + (F_{GFBry} + F_{AMBry1} - F_{AMBry2} )Z_{br} } \\ {M_{yb} = (F_{GFBlx} + F_{AMBlx1} - F_{AMBlx2} )Z_{bl} + (F_{GFBrx} + F_{AMBrx1} - F_{AMBrx2} )Z_{br} .} \\ \end{array} } \right. $$

(12)

$$ \left\{ {\begin{array}{*{20}c} {M_{xu} = m_{ul} u_{l} \omega^{2} \sin (\omega t + \phi )Z_{ul} + m_{ur} u_{r} \omega^{2} \sin (\omega t + \phi )Z_{ur} } \\ {M_{yu} = m_{ul} u_{l} \omega^{2} \cos (\omega t + \phi )Z_{ul} + m_{ur} u_{r} \omega^{2} \cos (\omega t + \phi )Z_{ur} .} \\ \end{array} } \right. $$

(13)

In the formula, $Z_{bl}$ and $Z_{br}$ represent the axial distance from the bearing to the center of gravity of the rotor, and $Z_{ul}$ and $Z_{ur}$ represent the axial distance from the unbalanced mass to the center of gravity of the rotor.

2.4 Orbit simulation

The effect of nonlinear hydrodynamic pressure coupled with electromagnetic forces on the rotordynamics is analyzed by orbital simulations. The locus of the rotor center is traced by simultaneously solving the rotor motion equations, the electromagnetic force equations and the Reynolds equation in the time domain during the simulation. This method can incorporate the given external forces and disturbances into the analysis, and predict the fully nonlinear behavior of the HFMBs-rotor system.

The rotor is assumed to be rigid and the dynamic parameters of the two supporting HFMBs are assumed to be different along the X/Y directions. The Wilson-θ method is introduced to calculate the equations of motion of the rotor.

$$ {\mathbf{M}}\ddot{\delta }(t) + {\mathbf{D}}\dot{\delta }(t) = {\mathbf{F}}(t). $$

(14)

M is the mass matrix, D is the damping matrix, and F is the vector force, which can be expressed as follows.

$$ {\mathbf{M}} = \left[ {\begin{array}{*{20}c} m & 0 & 0 & 0 \\ 0 & m & 0 & 0 \\ 0 & 0 & {I_{T} } & 0 \\ 0 & 0 & 0 & {I_{T} } \\ \end{array} } \right]. $$

(15)

$$ {\mathbf{D}} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {I_{P} \omega } \\ 0 & 0 & { - I_{P} \omega } & 0 \\ \end{array} } \right]. $$

(16)

$$ {\mathbf{F}} = \left[ {\begin{array}{*{20}l} {F_{ux} (t) + F_{bx} (t) - mg} \\ {F_{uy} (t) + F_{by} (t)} \\ {M_{xb} + M_{xu} } \\ {M_{yb} + M_{yu} } \\ \end{array} } \right]. $$

(17)

Suppose the acceleration changes linearly between two time nodes. The acceleration at $t_{i} + \tau$ is

$$ \ddot{\delta }(t_{i} + \tau ) = \ddot{\delta }_{i} + \frac{\tau }{1.37\Delta t}(\ddot{\delta }_{i + 1.37} - \ddot{\delta }_{i} ). $$

(18)

The following formula can be obtained by integrating Eq. (18).

$$ \left\{ {\begin{array}{*{20}c} {\ddot{\delta }_{i + 1.37} = \frac{6}{{1.37^{2} (\Delta t)^{2} }}(\delta_{i + 1.37} - \delta_{i} ) - \frac{6}{1.37\Delta t}\dot{\delta }_{i} - 2\ddot{\delta }_{i} } \\ {\dot{\delta }_{i + 1.37} = \frac{3}{1.37\Delta t}(\delta_{i + 1.37} - \delta_{i} ) - 2\dot{\delta }_{i} - \frac{1.37\Delta t}{2}\ddot{\delta }_{i} } \\ \end{array} } \right\}. $$

(19)

The force balance equation at node $i + 1.37$ is

$$ {\mathbf{M}}\ddot{\delta }_{i + 1.37} + {\mathbf{D}}\dot{\delta }_{i + 1.37} = {\mathbf{F}}_{i + 1.37} . $$

(20)

The linearized form of the vector force $F_{i + 1.37}$ is

$$ {\mathbf{F}}_{i + 1.37} = {\mathbf{F}}_{i} + 1.37({\mathbf{F}}_{i + 1} - {\mathbf{F}}_{i} ). $$

(21)

Substituting $\ddot{\delta }_{i + 1.37}$, $\dot{\delta }_{i + 1.37}$ and ${\mathbf{F}}_{i + 1.37}$ into Eq. (20) gives the iterative formula for calculating the orbit.

$$ \begin{gathered} \left[ {\frac{6}{{1.37^{2} (\Delta t)^{2} }}{\mathbf{M}} + \frac{3}{1.37\Delta t}{\mathbf{D}}} \right]\delta_{i + 1} \hfill \\ = {\mathbf{F}}_{i} + 1.37({\mathbf{F}}_{i + 1} - {\mathbf{F}}_{i} ) + \left[ {\frac{6}{{1.37^{2} (\Delta t)^{2} }}{\mathbf{M}} + \frac{3}{1.37\Delta t}{\mathbf{D}}} \right]\delta_{i} + (\frac{6}{1.37\Delta t} + 2{\mathbf{D}})\dot{\delta }_{i} + (2{\mathbf{M}} + \frac{1.37\Delta t}{2})\ddot{\delta }_{i} \hfill \\ \end{gathered} $$

(22)

3 Test rig construction and test results

3.1 Description of the test rig and hardware components

A photograph and a sectional view of the test rig are shown in Fig. 6. A rotor with a diameter of 30 mm and a length of 306.7 mm is supported by two HFMBs with an outer diameter of 100 mm and an axial length of 40 mm. A pulse turbine drives the rotor on the left and can counterbalance the weight of the thrust disc on the right. The thrust bearing at the right end is used to reduce rotor vibration in the axial direction. A series of standardized holes evenly distributed over the impulse turbine and thrust disc are used to add unbalanced mass to the rotor. The main parameters of the test rotor are given in Table 1. Since the deformation of the rotor is much smaller than the deformation of the HFMB, the rotor can be treated as rigid. Vertical and horizontal eddy current sensors are used to detect the rotor vibration at the turbine and thrust ends. Another AMB can be mounted in the middle of the rotordynamic test rig to adjust the system load. It can be mounted on the test rig through the mounting holes as it does not require a high degree of concentricity with other bearings.

Fig. 6

Photograph and cutaway view of the HFMBs-rotor test rig

Table 1 Main parameters of the rotor

Figure 7 shows the control hardware of the rotordynamic test rig of Fig. 6, which consists mainly of a controller and a power amplifier. The control flow is shown in Fig. 4. Fig. 7a shows the controller, whose chip model is TMS320FSP28377. Its main function is to collect the current position signal and compare it with the reference position, perform PID operation and output the control signal. Figure 7b shows the printed circuit board (PCB) of the switching power amplifier. A PCB controls the current to two sets of coils in a bearing for differential control. Hall current sensors are arranged in a current closed loop system to ensure accurate output current.

Fig. 7

Photography of the controller and the current amplifier of HFMBs

3.2 Model verification

Two sets of rotordynamic tests were used to validate the mathematical model. When there is no current in the coils, this is a GFBs-supported rotor system. And when there is current in the coils and the rotor position is adjusted by control, this is a HFMBs-supported rotor system.

Figure 8 compares the tested and predicted waterfall plots of the rotordynamics supported by the GFBs. It can be seen that the predicted results are in good agreement with the experimental results. Their vibrations contain three main components, 1X synchronous vibration, 1/2X subsynchronous vibration and whip. The predicted and experimental results show that the 1/2X subsynchronous vibration appears at 11 krpm and then disappears at about 15 krpm. At around 60 krpm, the whip starts to appear at a frequency of 78 Hz.

Fig. 8

Waterfall plots of rotordynamics supported by GFBs (test results and predicted results)

In fluid-lubricated bearings, self-excited, large-amplitude, sub-synchronous vibration at 1/2 the harmonic frequency can occur when partial radial friction occurs once per rotor revolution [49]. On the other hand, whip is a fluid-induced instability caused by the interaction of the rotor with the surrounding fluid [41].

Figure 9 compares the tested and predicted waterfall plots of the rotordynamics supported by the HFMBs. The vibration of the HFMB supported rotor has only two components, 1/2X subsynchronous vibration and 1X synchronous vibration. It can be seen that the 1/2X subsynchronous vibration occurs at a speed of 11 krpm. The predicted rotordynamics with the support of HFMBs agrees well with the test results. In addition, the test results show a small value of vibration around 1130 Hz at all speeds, which is considered to be caused by electromagnetic interference.

Fig. 9

Waterfall plots of rotordynamics supported by HFMBs (test results and predicted results)

Compared to the GFBs, the whip of the HFMBs disappears at high speeds. The reason for this is that the inclusion of AMBs improves the stiffness of the rotor bearing system, increases the instability threshold of the system and eliminates whip [50]. However, the 1/2X subsynchronous vibration is not significantly suppressed.

As the most important function of the operating conditions, it is necessary to discuss in detail whether it is possible to suppress the 1/2X subsynchronous vibration or whip by adjusting the working mode and the load sharing ratio. Two other important parameters, namely the load and the equilibrium position, can also have a significant influence on the subsynchronous vibrations.

4 Rotordynamic analysis: predictions results

In applications, HFMBs can adopt different working modes and load sharing ratios to achieve good dynamic performance, which may further affect the rotordynamics of the system. The working modes of HFMBs include GFB mode, AMB mode and hybrid mode. The GFB mode means that the control system is closed when the HFMB operates on the same principle as the GFB. The AMB mode can be thought of as the AMB working alone while the GFB is used as a back-up bearing. Hybrid mode is a control strategy that allows the GFB and AMB to each take a share of the load. When using the hybrid mode, the rotor dynamics can be further optimized by changing the load sharing ratio. The parameters of the HFMB are given in Table 2.

Table 2 Properties and parameters of HFMBs

4.1 Effect of working modes on rotordynamics

Figure 10 shows the dynamic orbits and FFT plots of the rotor center using different working modes at a speed of 60 krpm. It can be seen that when the GFB mode is used, the orbit of the rotor center is mainly a lot of circular rings accompanied by a slow movement of the keyphase point. The 1X synchronous vibration is 15.6 µm, while the whip vibration is 14.2 µm with a frequency of 78 Hz. The GFB model is inevitably affected by fluid swirling, which is the main cause of fluid-induced instability [49].

Fig. 10

Predicted dynamic orbits, FFT plots of the rotor center adopting different working modes at 60 krpm

When using the AMB mode, the rotor center orbit is a series of circular rings accompanied by a slow movement of the keyphase points. Since the GFB is nested within the inner diameter of the magnetic pole, even if the AMB alone is used to support the rotor, it will inevitably be affected by the fluid film. And, of course, the smaller the average eccentricity of the rotor, the smaller the effect of the fluid film. The X-direction FFT plot shows that the vibration component is mainly 16.5 µm synchronous vibration. There are very small 1/3X and 2/3X subsynchronous vibrations which result in shifts of keyphases in the rotor center orbit.

The orbit of the rotor center is a circular ring when using the hybrid mode (AMB load ratio is 0.5). The FFT plot shows a synchronous vibration of 13.4 µm, which is the best stability. The coupling of electromagnetic forces with hydrodynamic pressure gives the HFMB greater system stiffness, which increases the instability threshold for the whip and makes the rotor center orbit a circle.

Figure 11 shows the rotor center orbit and FFT plots of the HFMB using different working modes at a speed of 12 krpm. It can be seen that when the GFB mode is used, the rotor center orbit is a "rabbit ear", i.e. it contains 1X synchronous vibration and subsynchronous vibration. The keyphase points are precisely locked, indicating 1/2X subsynchronous vibration. The FFT plot shows that the GFB mode has a 1X synchronous vibration of 8.9 μm and a 1/2X subsynchronous vibration of 10 μm in the X direction.

Fig. 11

Predicted dynamic orbits, FFT plots of the rotor center adopting different working modes at 12 krpm

When using the AMB mode, the rotor center orbit is a circular ring with a synchronous vibration of 7.1 µm and optimum system stability. When using the hybrid mode (AMB load ratio is 0.5), the rotor center orbit is a "rabbit ear" with a synchronous vibration of 8.2 µm and a 1/2X subsynchronous vibration of 7 µm. Compared to the AMB mode, the hybrid mode produces 1/2X subsynchronous vibrations and the synchronous vibrations are larger. The reason is that at low speeds, the fluid radial and tangential forces are small, and the AMB mode is subjected to little fluid tangential force, so there is no subsynchronous vibration. And when the hybrid mode is used, half the load is carried by the GFB and the dynamic eccentricity increases, which increases both the fluid radial and tangential forces. The tangential forces transfer the rotational energy to the radial vibrations and 1/2X subsynchronous vibrations are generated.

The working mode is the one of the most important function of the operating conditions that allow the optimum operation of the HFMBs. The analysis shows that the hybrid mode has the best stability against high speed whip, while the AMB mode has the best stability against low speed subsynchronous vibration. The interaction of a rotor moving at high speed with the surrounding fluid causes fluid-induced instability, which is a self-excited vibration (known as whip) that causes the rotor to operate in a stable limit ring of large vibrations. The instability threshold represents the speed at which fluid-induced instability occurs and is positively related to the stiffness and natural frequency of the rotor system. As a result, when operating in GFB mode, the rotor is in a state of fluid-induced instability, whereas operating in hybrid mode increases the stiffness and natural frequency of the system, thereby increasing the instability threshold and suppressing the whip. The mechanism of low speed 1/2X subsynchronous vibration is the transfer of rotational energy from tangential friction to radial vibration. AMB mode operation avoids the generation of large tangential friction and therefore suppresses the generation of 1/2X subsynchronous vibration. Thus, a rational choice of working mode can mechanically suppress or attenuate unstable vibrations.

4.2 Effect of load sharing ratio on rotordynamics

Figure 12 shows the effect of the load sharing ratio on the static performance of HFMBs at a speed of 12 krpm. Figure 12a briefly shows the operation of an HFMB where the rotor is supported by a combination of air film pressure and electromagnetic force. The air film pressure distribution is passively formed to support the load, which is the main reason for the nonlinearity of the support force. The bias current in the X-direction is used to balance the load and therefore varies with the load ratio. The bias current and the equilibrium position together form the reference point for the linear closed-loop control of the AMB.

Fig. 12

Variation of key parameters with AMB load ratio, a schematic description of the HFMB, b predicted rotor center orbit of HFMBs, c bias-currents versus AMB load ratio, d gas film pressure versus AMB load ratio

Figure 12b shows the equilibrium position and rotor center orbit for different AMB load ratios. The equilibrium position is the predicted eccentricity of the GFB, which gradually moves from a larger eccentricity towards the center of the bearing as the AMB load ratio increases. The AMB load ratios for the three different rotor center orbit from the eccentricity to the bearing center are 0, 0.5 and 1, respectively. When the AMB load ratio is 0.5, the rotor center orbit is shown as "rabbit ears". And when the AMB load ratio is 0 and 1, the rotor center orbit is a circular ring and has better stability.

Figure 12c and d shows the predicted bias currents and gas film pressure of HFMBs. The bias current of the upper poles gradually decreases as the AMB load ratio increases, and the bias current trajectory of the lower poles is symmetrical to that of the upper poles. As the AMB load ratio increases, the bias current of the upper poles should increase and the bias current of the lower poles should decrease to balance the load. However, due to the lighter weight of the rotor (19N), the influence of the displacement stiffness is greater than the current stiffness, which determines the current downward trend of the upper poles as the AMB load ratio increases. The bias current curve of the left poles is symmetrical to that of the right poles. When the AMB load ratio is 1, the bias current of both the left and right poles reaches 0.5 A because the AMB does not carry the load in the horizontal direction.

Figure 13 shows the bifurcation diagrams of the rotor center in the vertical and horizontal directions at different AMB load ratios. Compared to Fig. 12, the bifurcation diagram shows the dynamic stability of the HFMB as the load ratio increases. It can be seen that as the AMB load ratio increases from 0 to 1, the rotor gradually moves away from the eccentricity towards to the bearing center. As the AMB load ratio changes from 0.3 to 0.8, double-dots appear and the orbit is precisely locked at 1/2X. As the AMB load ratio changes from 0.4 to 0.6, the distance between the double dots is the greatest, indicating the greatest 1/2X subsynchronous vibration and the worst stability. The bifurcation diagrams show that there is a single dot when the AMB load ratio is from 0 to 0.15 and from 0.8 to 1. This indicates that the system has good stability and that the vibration components are mainly 1X synchronous vibration. Compared with the X-direction bifurcation diagram, the Y-direction bifurcation diagram shows less 1/2X subsynchronous vibration.

Fig. 13

Bifurcation diagrams of the rotor center in the vertical and horizontal direction with different AMB load ratios at speed of 12 krpm

At high speeds, the dynamic performance of the system varies less with the AMB load ratio and is therefore not shown graphically. The system has good stability with only synchronous vibrations at any load ratio condition. This is due to the fact that in GFB mode the HFMB encounters whips, whereas in hybrid mode the AMB joins the operation and the natural frequency and instability threshold of the system increases, so that the whips disappear. Adjusting the load ratio will not reduce the instability threshold to the current operating speed, so adjusting the load ratio will not change the stability of the system.

Another important function of the operating conditions is the load sharing ratio. The load sharing ratio affects the eccentricity and fluid pressure distribution of the GFB, and therefore the bias current and equilibrium position of the AMB, and therefore the dynamic performance of the HFMB. An AMB load ratio of less than 0.25 or greater than 0.85 is beneficial to suppress 1/2X subsynchronous vibration. As the rotor approaches the edge of the bearing during a small fraction of the vibration cycle, a large tangential frictional force is generated. The tangential friction is impacting and has an effect similar to striking the rotor with a hammer, exciting the multi-order free vibration mode of the rotor (including 1/2X subsynchronous vibration). When the AMB load ratio is greater than 0.85, the dynamic eccentricity is smaller, thus avoiding greater tangential friction and 1/2X subsynchronous vibration. As the AMB load ratio decreases, the load on the GFB increases, the dynamic eccentricity increases and the rotor experiences significant tangential friction, resulting in 1/2X subsynchronous vibration. However, while subsynchronous vibration occurs, the friction itself causes an increase in the spring stiffness and natural frequency of the rotor. Therefore, as the AMB load ratio continues to decrease to 0.25, the dynamic eccentricity will increase, the natural frequency will increase and the speed of 1/2X subsynchronous vibration will increase. Increasing the AMB load ratio mechanically eliminates the 1/2X subsynchronous vibration, while decreasing the AMB load ratio increases the speed at which the 1/2X subsynchronous vibration occurs.

In fact, reducing the AMB load ratio leads to an increase in dynamic eccentricity and system stiffness, which not only increases the speed of 1/2X subsynchronous vibrations, but also increases the instability threshold of the whips. Adjusting the load sharing ratio is therefore an effective way of optimizing the stability of the system.

4.3 Effect of load on rotordynamics

The predicted dynamic orbit, FFT plots, and Poincaré maps of the rotor center at different loads are shown in Fig. 14. The loads in Fig. 14a, b and c are 9.5 N, 19 N and 38 N, respectively. The dynamic orbit plots show that the 9.5 N rotor center orbit is a circular ring with a large enclosed area. The rotor center orbit of the 19 N is a "rabbit ear". Compared to the 9.5 N, the 19 N has slightly less movement in the X-direction, but significantly less movement in the Y-direction. At 38 N, the rotor center orbit becomes a circular ring again, and the movement in both X and Y directions is minimized. The reduction in load significantly reduces the average stiffness of the system, resulting in a large radial movement of 9.5 N.

Fig. 14

Predicted dynamic orbit, FFT plots, and Poincaré maps of the rotor center for different load (rotational speed: 12 krpm, AMB load ratio: 0.5)

FFT plots in the X-direction show that the synchronous vibrations corresponding to 9.5 N, 19 N and 38 N are 23.4, 8.2 and 7.4 μm, respectively, and the synchronous vibrations decrease rapidly. At a load of 19 N, there is a large 1/2X subsynchronous vibration of 7 μm. FFT plots in the Y-direction show that the synchronous vibrations corresponding to the three loads are 29.1, 8.8 and 7.5 µm, respectively, with the same rapid decrease. Increasing the load leads to an increase in the cross-coupled stiffness and tangential force with 1/2X subsynchronous vibration at 19 N. However, after further increasing the load, the system stiffness and natural frequency increased and the speed at which 1/2X subsynchronous vibration occurred increased, so that the 1/2X subsynchronous vibration disappeared at 38 N.

The Poincaré maps show a double-dots at loads of 9.5 N and 19 N, while a single-dot is shown at 38 N. The double-dots at 9.5 N is very close, indicating the dominance of synchronous vibration with a small amount of vibration at other frequencies. And the clear double-dots at 19 N clearly show that the motion of the rotor center is a double loop.

Therefore, increasing the load at low speeds increases the stiffness and natural frequency of the system, which in turn increases the speed of 1/2X subsynchronous vibrations and suppresses the synchronous vibrations.

Figure 15 shows the dynamic orbit, the FFT plot and the Poincaré maps for a rotational speed of 60 krpm. It can be seen that the rotor center orbits of both 19 N and 38 N are circular rings, but the average dynamic eccentricity of 19 N is closer to the bearing center and the motion is greater. The FFT plots show that the synchronous vibration of 19 N is 13.4 μm in the X-direction and 13.5 μm in the Y-direction. The synchronous vibration of 38 N is 11.3 μm in the X-direction and 11 μm in the Y-direction. The Poincaré maps show single-dot with fully overlapping rotor center orbits, indicating the presence of only 1X synchronous vibration. Therefore, increasing the load at high speeds also improves the stability of the system.

Fig. 15

Predicted dynamic orbit, FFT plots, and Poincaré maps of the rotor center for different load (rotational speed: 60 krpm, AMB load ratio: 0.5)

The load is an important parameter affecting the stability of the rotor system. The analysis shows that increasing the load can effectively improve the stability of the system. The stiffness of the GFB is very sensitive to changes in load and increasing the load will greatly increase the dynamic eccentricity of the system and therefore the stiffness. Compared to the GFB, the AMB has very little change in stiffness. Increasing the load therefore increases the stiffness and natural frequency of the system, which in turn increases the speed of the 1/2X subsynchronous vibrations and the instability threshold of the whips, and to some extent weakens the amplitude of the synchronous vibrations. The additional load can therefore also be an effective means of improving system stability.

4.4 Effect of equilibrium position on rotordynamics of HFMBs

Figure 16 shows the bifurcation diagrams of the rotor center with different equilibrium positions in the vertical and horizontal directions. As shown in Fig. 16a, in the Cartesian coordinate system, the equilibrium position of the HFMB moves from (−50, 0 μm) to (50 μm, 0 μm) along the X axis. In Fig. 16b and c, the bifurcation diagram of the rotor center is divided into three parts. When the equilibrium position along the X axis changes between −20 and 15 μm (this situation is defined as A in Fig. 16), the rotor center exhibits a periodic response. As the equilibrium position increases or decreases along the X axis, i.e. the equilibrium position changes from −20 to −40 μm or from 15 to 40 μm (defined as B), the rotor motion changes from a single point to a double point. As the equilibrium position continues to increase or decrease, i.e. the equilibrium position is greater than 40 μm or less than −40 μm (defined as C), the rotor center gradually becomes unstable. The results show that equilibrium positions close to the edge of the bearing in the vertical direction lead to instability of the system.

Fig. 16

Bifurcation diagrams of the rotor center in the vertical and horizontal directions adopting different equilibrium position in the X-direction

Figure 17 shows the FFT plots of the rotor center corresponding to the three situations in Fig. 16. When the equilibrium position of the AMB is 0 μm (situation A) along the X axis, the 1X synchronous vibration is 7.71 μm. In contrast, when the equilibrium position is −30 μm (situation B), the 1X synchronous vibration is 8.03 μm and the 1/2X subsynchronous vibration is 3.96 μm. The 1X synchronous vibration of situation B is larger than that of situation A, and the 1/2X subsynchronous vibration appears. In addition, when the equilibrium position is −50 μm (situation C), the 1X synchronous vibration increases further and the frequency components of the subsynchronous vibration become chaotic.

Fig. 17

FFT plots of the rotor center for different equilibrium position along the X direction: a 0 μm, b -30 μm, c -50 μm

Figure 18 shows the bifurcation diagrams of the rotor center in the vertical and horizontal directions as the equilibrium position moves along the Y direction. The bifurcation diagram of the rotor motion can also be divided into three parts. In situation A, where the equilibrium position is between −25 and 25 μm, the movement of the rotor shows a periodic response. When the equilibrium position is in situation B (the equilibrium is between −40 and −25 μm or between 25 and 40 μm), the movement of the rotor shows quasi-periodic response. When the equilibrium position is further increased or decreased, the movement of the rotor is unexpectedly stabilizes again, which is clearly different from the change of the equilibrium position in the X-direction.

Fig. 18

Bifurcation diagrams of the rotor center in the vertical and horizontal directions adopting different equilibrium position in the Y direction

Figure 19 shows the FFT plots of the rotor center corresponding to the three situations in Fig. 18. The synchronous vibration is 8.9, 9 and 9 μm when the equilibrium position in the Y-direction is 0, −35 and −50 μm, respectively. The synchronous vibration of the rotor is almost independent of the shift of the equilibrium position in the Y direction. When the equilibrium position is −35 μm, the subsynchronous vibration is 2.2 μm with a very low frequency component. A shift in the equilibrium position in the horizontal direction therefore has little effect on the stability of the system, with larger shifts actually restoring the stability of the system.

Fig. 19

FFT plots of the rotor center for different equilibrium position in the Y direction: a 0 μm, b -35 μm, c -50 μm

The equilibrium position is a unique and important parameter for HFMBs. Normally, the equilibrium position of the AMB must to follow the eccentricity of the GFB to ensure good system operation [3]. However, the eccentricity of the GFB is difficult to predict accurately, so the equilibrium position often does not follow this eccentricity exactly [1]. The analysis shows that the stability of the rotor gradually decreases when the equilibrium position is in the vertical direction close to the bearing edge, producing a very chaotic low frequency vibration signal, while the stability of the rotor first decreases and then increases when the equilibrium position is in the horizontal direction close to the bearing edge. There are two reasons for this. Firstly, in order to achieve the adjustment of the equilibrium position, the closed-loop control system has to overcome the additional gravity in the vertical direction, which causes the AMB to have a greater nonlinear stiffness in the vertical direction than in the horizontal direction. Secondly, the dynamic behavior of the GFB is anisotropic in the X and Y directions. The predicted results show that the growth rate of damping is greater with displacement in the Y-direction than in the X-direction, resulting in greater damping in the Y-direction than in the X-direction for the same displacement. In addition, the cross-coupled stiffness is less in the Y direction than in the X direction for the same displacement. The increase in energy dissipation is accompanied by a reduction in tangential friction, which leads to an equilibrium position in the Y-direction near the edge of the bearing and can stabilize the system again.

In summary, the equilibrium position of the HFMB must be maintained within a certain range to keep the system stable. The anisotropy of the AMB and GFB means that changes in the equilibrium position in the vertical direction have a significantly greater effect on the stability of the system than in the horizontal direction.

5 Conclusion

HFMBs, which combine GFBs and AMBs, offer a number of potential performance advantages through special features that define the operating conditions. In this paper the locus of the rotor center is tracked by simultaneously solving the equations of motion for the rigid rotor, the deformation equations for the top and bump foil, the unsteady Reynolds equation and the PID-controlled electromagnetic force equation in the time domain. The accuracy of the numerical predictions is verified by comparison with the experimental results.

The working mode and load sharing ratio are two important functions of the operating conditions used to improve system stability. The AMB mode or AMB load ratio of 1 (hybrid mode) facilitates the suppression of 1/2X subsynchronous vibration at low speeds. The hybrid mode increases the instability threshold for the whip, making it easier to keep the system stable at high speeds.

Increasing the load will improve the stability of the system by increasing its stiffness and natural frequency, thereby increasing the speed of 1/2X sub synchronous vibration and the instability threshold for the whip. And the equilibrium position of HFMBs should be kept within a certain range, because the anisotropy of the dynamic characteristics of AMBs and GFBs may lead to the instability of the system.

In the future, a PID-controlled HFMBs-rotor test rig will be used to achieve optimum stability under different operating conditions by adjusting the working mode and load sharing ratio. The question of whether the equilibrium position of the AMB must accurately track the eccentricity of the GFB will be investigated more thoroughly and systematically.