1 Introduction

In a hydrogen fuel cell, the air compressor typically operates at a speed higher than 100,000 rpm, which needs to be driven by a high-speed motor, and the high-speed motor has to be supported by air foil bearings. The dynamic performance calculation of the motor rotor is extremely complex at such a high speed and has become a challenging issue in the field of high-speed motor development. Therefore, the corresponding research is required.

Xu [1] conducted the dynamic analysis of the high-speed permanent magnet synchronous motor (HSPMSM)rotor using the model module of ANSYS, and investigated the effects of the contact surface stiffness coefficient, the permanent magnet sheath material, and the inner diameter on the motor rotor’s critical speeds. Huang et al. [2] obtained the lateral bending stiffness of the silicon steel laminated structure by curve fitting, and verified the accuracy of the simplified model of the laminated structure through experiments. Huang [3] ignored system damping and used FEM method to analyze the dynamic characteristics of the motor rotor supported by static pressure air bearings. The designed motor rotor had a 25% speed variation range between the rated speed and the first critical speed. Lv [4] conducted take-off test and static and dynamic characteristics tests on bearings. Besides, the critical speeds and imbalance response of the system were calculated and analyzed by the transfer matrix method. Guang et al. [5, 6] analyzed the mechanical characteristics of active control structures and combined with an improved linkage spring model, established linear and nonlinear mechanical models for the rigid rotor system supported by active bump-type foil bearings (ABFB). Then, the coupling effect of ABFB and (bump-type thrust foil bearings)BTFB was considered, and a five degree of freedom nonlinear dynamic model for the rigid rotor was established. Compared with the four degree of freedom model, the five degree of freedom model can effectively predict the dynamic characteristics of rotors in high-speed areas. Wu [7] used the two-step QR method and finite element method to solve the critical speeds of the motor rotor, considering the unbalanced magnetic pull (UMP) caused by rotor dynamic eccentricity, and solved the rotor strains and stresses in the presence of magnetic pull and in the absence of magnetic pull, respectively. Li et al. [8] established a finite element model of the rotor dynamics of a permanent magnet motor for fuel cell air compressors, and studied the dynamic characteristics of different support methods (rigid bearing support and elastic bearing support). Dasgupta et al. [9] studied the dynamics of an eccentric flexible rotating axis with internal and external damping driven by a non-ideal source DC motor. Boroujeni et al. [10] used static functions of stator and rotor currents to calculate the UMP based on the voltage state space equations for coupled circuits in eccentric induction motors. Mohammadzadeh et al. [11] discretized the slender rotor of a centrifugal pump into an appropriate number of three-dimensional Timoshenko beam elements and studied the dynamic behavior of a nonlinear finite element model of a vertically suspended centrifugal pump slender rotor, and identified parameters that have a significant impact on the natural frequency of the rotor system. Li et al. [12] derived the value of electromagnetic force using the theory of virtual work, and established the relationship between UMP and radial displacement of the rotor, and investigated all rotor eccentricity's effects on the dynamic behavior of the motor system. Martynenko et al. [13] established a nonlinear simulation calculation model for rotor dynamics supported by magnetic levitation bearings, achieving the visualization of nonlinear dynamic phenomena of the rotor in a magnetic field. As an example of a high-speed bipolar induction generator supported by active magnetic bearings, Kim et al. [14] investigated the effect of UMP by simulation and compared the simulation results with the vibration measurement results of the testing machine. Pennacchi [15] used finite element method to model the rotor, which can accurately demonstrate the dynamic behavior of real machines. Based on a Jeffcott rotor model installed on a symmetrical positioning bearing, Dai et al. [16] studied the nonlinear dynamic behavior of the rotor dynamics model of a permanent magnet synchronous motor.

It can be seen from the literature analysis that the study on the rotordynamics of high-speed motors is still at an early stage, the impact of UMP on the motor rotor exists, but there is little study on it. Therefore, this article takes the high-speed permanent magnet synchronous motor rotor supported by air foil bearings as the study object, combines the lubrication performance of the air foil bearings supporting the rotor with the mechanical behavior of the motor rotor in the magnetic field firstly. Then a rotor dynamics theory is introduced, and the mechanical model for calculating the dynamic performance of the high-speed electric machine rotor is established. The influences of the structural parameters of the air foil bearings, the structural parameters of the motor rotor and the operating parameters on the dynamic performance of the rotor of high-speed motors are investigated in depth, which could provide theoretical references for the research and development of high-speed motors.

2 Mechanical modeling

2.1 Mechanical modeling of supporting bearings

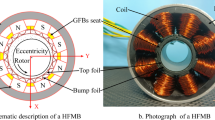
The high-speed motor for hydrogen fuel cell air compressor in this paper is horizontally placed and the support bearings are air foil journal bearings. The bearing structure is shown in Fig. 1, where RS is the inner radius of the bearing sleeve, Rj is the radius the shaft, O and O′ are the center of the bearing sleeve and shaft respectively, \(\beta\) is the bearing deflection angle, e is the eccentricity, and h is the air film thickness. The air film pressure generated by the rotation of the shaft will cause elastic deformation of the bump foil and top foil. The relationship between the gas film force and the displacement and rotational speed of the shaft is a nonlinear function. To facilitate the calculation of the stiffness and damping of the journal air foil bearing, the following assumptions are introduced:

  1. 1.

    The bump and the top foil always maintain contact, and the interaction force is located at the top of the bump.

  2. 2.

    Each bump produces the same circumferential displacement.

  3. 3.

    Each bump still maintains a circular arc after deformation, and only the curvature of the bump changes.

  4. 4.

    The bump deformation caused by force is uniformly distributed in the axial direction of the bearing.

Fig. 1
figure 1

Structural diagram of air foil bearing foil

Full size image

With the above assumptions, the deformation of the bump foil and top foil of the air foil journal bearing is shown in Fig. 2, with the bump arch flattened but still maintaining an arc. Conduct force analysis on the bumps of the bump foil located at the free end, middle area, and fixed end, respectively.

Fig. 2
figure 2

Diagram of deformation of the air foil bearing foil structure

Full size image

As shown in Fig. 3, L is the half length of a bump arch, R0 is the bump radius, 2θ is the bump angle. The free end bump is subjected to a vertical downward force of F1 from the top foil, a horizontal left frictional force as f1, a frictional force as f2 and f3 from the bearing sleeve on both ends of the bump, and a vertical upward force as F2 and F3. Additionally, the adjacent side bump exerts a horizontal force of Fle on the bump's left end. The following equations can be obtained by balancing the moment at the right end, the forces acting in the vertical and horizontal directions, and the forces acting in the horizontal direction:

$$\left\{ {\begin{array}{*{20}l} {F_{2} = \left[ {F_{1} L + f_{1} R_{0} (1 - \cos \theta )} \right]/2L} \hfill \\ {F_{3} = F_{1} - F_{2} } \hfill \\ {F_{le} = f_{1} + f_{2} + f_{3} } \hfill \\ \end{array} } \right.$$
(1)
Fig. 3
figure 3

Diagram of Stress and deformation analysis of the free end bump

Full size image

According to the friction coefficient theorem, the friction force between the bump foil, top foil, and bearing sleeve can be expressed as:

$$\left\{ {\begin{array}{*{20}l} {f_{1} = \eta_{1} F_{1} } \hfill \\ {f_{2} = \eta_{2} F_{2} } \hfill \\ {f_{3} = \eta_{2} F_{3} } \hfill \\ \end{array} } \right.$$
(2)

where η1 and η2 are the friction coefficients between the bump foil and the top foil, and between the bump foil and the bearing sleeve, respectively. According to the bending moment analysis of the cross-section m-m corresponding to any radian α, and the bending moment of section m-m can be obtained as:

$$M_{fmm} = \left( {F_{le} - f_{2} } \right)R_{0} \left[ {\cos (\theta - \alpha ) - \cos \theta } \right] - F_{2} \left[ {L - R_{0} \sin (\theta - \alpha )} \right]$$
(3)

Apply the Castigliano’s second theorem:

$$\delta_{i} = \frac{{\partial V_{\varepsilon } }}{{\partial F_{i} }} = \frac{\partial }{{\partial F_{i} }}\smallint \frac{{M^{2} (x)dx}}{2EI} = \smallint \frac{M(x)}{{EI}} \cdot \frac{\partial M(x)}{{\partial F_{i} }}dx$$
(4)

The vertical deformation at the top of the bump can be obtained:

$$W_{FV} = \smallint_{0}^{\theta } \frac{{M_{fmm} }}{EI}\frac{{\partial M_{fmm} }}{{\partial F_{1} }}R_{0} d\alpha$$
(5)

in the formula, E is the elastic modulus of the bump foil, and I is the moment of inertia of the cross section of the bump foil (which can be calculated from the bearing width L and the thickness tB of the bump foil). In order to calculate the horizontal deformation WFL of the top of the bump relative to the left end applying the Castigliano’s second theorem, a horizontal right additional force Fa is applied to the top of the bump, as shown in Fig. 2. Then, based on the force balance and moment balance, the bending moment and deformation of the section m-m corresponding to any radian α in the left half of the bump can be found out (the same for the right half). The middle area of the bump is subjected to different forces, not only from the force of the left bump, but also from the force of the right bump. The forces on the fixed end of the bump are also different, with both ends subject to forces, but the fixed end is not subjected to friction. However, fixed-end bump is similar to the free-end bump in force analysis, the vertical and horizontal deformations can also be calculated using the Castigliano’s second theorem.

Under the combined force of gas film pressure and the deformation of bump foil, the top foil undergoes corresponding deformation. Due to the much smaller displacement in the x and y directions compared to the z direction, and the fact that the displacement in the x and y directions has almost no effect on the gas film pressure, for the convenience of calculation, the displacement in the x and y directions is not considered. Based on the dimensional characteristic that the thickness of the top foil is much smaller than its length and width, which meets the conditions of using the elastic thin plate theory. Moreover, since the deformation of the top foil is less than one-fifth of its thickness, the deformation of the top foil can be analyzed using the small deflection theory [17]. The deformation analysis of the top foil is shown in Fig. 4, where tT is the thickness of the top foil, C is the flattened length of the top foil, and L is the width of the top foil. Because the top foil is rectangular after being flattened, a rectangular four node element is used to discretize the top foil along the neutral plane.

Fig. 4
figure 4

Diagram of the top foil and its thin plate unit

Full size image

According to Kirchhoff's assumption of no compressive stress, there is \(\varepsilon_{z} = \frac{\partial w}{{\partial z}} = 0\),which indicates that the deflection w is only a function of x,y, w = f(x,y). Based on the assumption of bending deformation plane section, there is \(\gamma_{zx} = \gamma_{zy} = 0\), assuming that the midplane displacement is perpendicular, the geometric Eq. (6) can be obtained:

$$\left\{ {\begin{array}{*{20}l} {\varepsilon_{x} = \frac{\partial u}{{\partial x}} = - z\frac{{\partial^{2} w}}{{\partial x^{2} }}} \hfill \\ {\varepsilon_{y} = \frac{\partial v}{{\partial y}} = - z\frac{{\partial^{2} w}}{{\partial y^{2} }}} \hfill \\ {\gamma_{xy} = \frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}} = - 2z\frac{{\partial^{2} w}}{\partial xy}} \hfill \\ \end{array} } \right.$$
(6)

Each node has 3 free degrees, namely the displacement w along the z-axis, the rotation angle around the x-axis, and the rotation angle around the y-axis. Therefore, a rectangular four node element has 12 free degrees, and the displacement field function can be expressed as:

$$\left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}c} {w(x,y) = \chi_{1} + \chi_{2} x + \chi_{3} y + \chi_{4} x^{2} + \chi_{5} xy + \chi_{6} y^{2} + \chi_{7} x^{3} } \\ { + \chi_{8} x^{2} y + \chi_{9} xy^{2} + \chi_{10} y^{3} + \chi_{11} x^{3} y + \chi_{12} xy^{3} } \\ \end{array} } \hfill \\ {\theta_{x} = \frac{\partial w}{{\partial y}} = \chi_{3} + \chi_{5} x + 2\chi_{6} y + \chi_{8} x^{2} + 2\chi_{9} xy + 3\chi_{10} y^{2} + \chi_{11} x^{3} + 3\chi_{12} xy^{2} } \hfill \\ {\theta_{y} = \frac{\partial w}{{\partial x}} = - \left( {\chi_{2} + 2\chi_{4} x + \chi_{5} y + 3\chi_{7} x^{2} + 2\chi_{8} xy + \chi_{9} y^{2} + 3\chi_{11} x^{2} y + \chi_{12} y^{3} } \right)} \hfill \\ \end{array} } \right.$$
(7)

Substituting the coordinates (x, y) of the four nodes of the rectangular element into Eq. (7), 12 equations can be obtained. By solving them together, various coefficients \(\chi_{1}\),\(\chi_{2}\),·\(\chi_{12}\) can be obtained. Then, by substituting them into Eq. (7), the following can be obtained:

$$w(x,y) = N_{i} w_{i} + N_{ix} \theta_{ix} + N_{iy} \theta_{iy} + \cdots + N_{n} w_{n} + N_{nx} \theta_{nx} + N_{ny} \theta_{ny}$$
(8)

where Ni, Nix, Niy,···Nn, Nnx, Nny are shape functions. Denote as \([N] = \left[ {\begin{array}{*{20}c} {[N]_{i} \, [N]_{j} \, [N]_{m} \, [N]_{n} } \\ \end{array} } \right]\), \([N]_{i} = \left[ {N_{i} \, N_{ix} \, N_{iy} } \right]\quad (i,j,m,n)\),then \(w(x,y)\) can be expressed as:

$$w(x,y) = [N][q]_{{\text{e}}}$$
(9)

According to Eq. (6), the strain matrix of a rectangular four node element can be obtained:

$$[{\varvec{B}}]^{e} = \left[ {\begin{array}{*{20}c} {{\varvec{B}}_{{\varvec{i}}} \user2{ B}_{{\varvec{j}}} \user2{ B}_{m} \user2{ B}_{n} } \\ \end{array} } \right] = - \left\{ {\begin{array}{*{20}c} {\frac{{\partial^{2} }}{{\partial x^{2} }}} \\ {\frac{{\partial^{2} }}{{\partial y^{2} }}} \\ {2\frac{{\partial^{2} }}{\partial x\partial y}} \\ \end{array} } \right\}[{\varvec{N}}] = - \left\{ {\begin{array}{*{20}c} {\frac{{\partial^{2} }}{{\partial x^{2} }}} \\ {\frac{{\partial^{2} }}{{\partial y^{2} }}} \\ {2\frac{{\partial^{2} }}{\partial x\partial y}} \\ \end{array} } \right\}\left[ {\begin{array}{*{20}c} {{\varvec{N}}_{{\varvec{i}}} \user2{ N}_{j} \user2{ N}_{m} \user2{ N}_{n} } \\ \end{array} } \right]$$
(10)

Based on the principle of strain energy and minimum potential energy, the stiffness matrix of the element can be derived:

$$[K]^{e} = \frac{{t^{3} }}{12}\iint\limits_{A} {[B]^{T} [D][B]dxdy = \left[ {\begin{array}{*{20}c} {[K_{ii} ]} & {[K_{ij} ]} & {[K_{im} ]} & {[K_{in} ]} \\ {[K_{ji} ]} & {[K_{jj} ]} & {[K_{jm} ]} & {[K_{jn} ]} \\ {[K_{mi} ]} & {[K_{mj} ]} & {[K_{mm} ]} & {[K_{mn} ]} \\ {[K_{ni} ]} & {[K_{nj} ]} & {[K_{nm} ]} & {[K_{nn} ]} \\ \end{array} } \right]}$$
(11)

where [D] is the element elasticity matrix, which can be obtained from the generalized Hooke's law.

From the above element stiffness matrix, the overall stiffness matrix [K] of the top foil can be obtained, and the corresponding overall load [F] can be applied according to the gas film pressure and the bump foil support force on the top foil, and [q] is denoted as the overall displacement matrix, then:

$$\left[ K \right]\left[ q \right] = [F]$$
(12)

By combining the deflection of the fixed end of the top foil and the relationship between the bump foil and the top foil with both corners being zero, the required boundary conditions can be obtained. Thus, Eq. (22) can be numerically solved to obtain the deformation of the top foil.

On the basis of the Navier Stokes equation, the continuity equation is combined with the characteristic that the thickness of the lubricating air film is substantially smaller than the length and width scales. When considering the air in the lubricating film as a Newtonian fluid and laminar flow, the following Eq. (13) is obtained. This equation is the generalized Reynolds equation that connects the air pressure distribution with a series of operating parameters.

$$\frac{\partial }{\partial x}\left( {\frac{{\rho h^{3} }}{12\mu }\frac{\partial p}{{\partial x}}} \right) + \frac{\partial }{\partial z}\left( {\frac{{\rho h^{3} }}{12\mu }\frac{\partial p}{{\partial z}}} \right) = \frac{1}{2}\frac{{\partial \left( {\rho V_{x} h} \right)}}{\partial x} + \frac{1}{2}\frac{{\partial \left( {\rho V_{z} h} \right)}}{\partial z} - \rho V_{y}$$
(13)

Spread the lubricating air film horizontally along the circumferential direction of the shaft, with the axial direction set at z, ignoring the axial motion of the air foil bearing, i.e., Vz = 0, and Vy can be represented by the thickness h of the lubricating air film to, i.e., \(V_{y} = \frac{\partial h}{{\partial t}}\), and then, by combining the ideal gas equation (without taking temperature effects into account), it can be obtained that:

$$\frac{\partial }{\partial x}\left( {ph^{3} \frac{\partial p}{{\partial x}}} \right) + \frac{\partial }{\partial z}\left( {ph^{3} \frac{\partial p}{{\partial z}}} \right) = 6\mu V_{x} \frac{\partial }{\partial x}(ph) + 12\mu \frac{\partial }{\partial t}(ph)$$
(14)

In order to improve the calculation accuracy and facilitate the promotion of application, the above formula is dimensionless. Here, the dimensionless gas film thickness \(H = \frac{h}{c}\), c is the bearing radius clearance, and the dimensionless time is \(\overline{t} = \psi t\). The dimensionless gas film pressure \(P = \frac{p}{{p_{a} }}\), pa is the atmospheric pressure; and the circumferential direction coordinates \(\varphi = \frac{x}{{R_{j} }}\), Axial coordinates \(\lambda = \frac{2z}{L}\), circumferential velocity \(V_{x} = \omega R_{j}\) (denote as U), the dimensionless form of Eq. (14) can be obtained:

$$\frac{\partial }{\partial \varphi }\left( {PH^{3} \frac{\partial P}{{\partial \varphi }}} \right) + \left( {\frac{{2R_{{\text{j}}} }}{L}} \right)^{2} \frac{\partial }{\partial \lambda }\left( {PH^{3} \frac{\partial P}{{\partial \lambda }}} \right) = {\Lambda }_{1} \frac{\partial }{\partial \varphi }(PH) + 2\gamma {\Lambda }_{1} \frac{\partial }{{\partial \overline{t}}}(PH)$$
(15)

where \(\Lambda_{1} = \frac{{6\mu UR_{j} }}{{c^{2} P_{a} }}\) is the number of bearings, μ is the aerodynamic viscosity of the lubricating air, \(\gamma = \frac{\psi }{\omega }\) is the vortex frequency ratio, \(\omega\) is the angular velocity of the shaft, \(\psi\) is the vortex angular velocity of the shaft. Adopting the perturbation method, disturbances is introduced, where P and H can be written as the sum of P0, H0 and perturbations \(P_{x}\),\(P_{{\text{y}}}\),\(P_{{x^{\prime}}}\),\(P_{{y^{\prime } }}\) in static equilibrium, i.e.:

$$\left\{ {\begin{array}{*{20}l} {P = P_{0} + P_{x} {\Delta }\overline{x} + P_{{x^{\prime}}} {\Delta }\overline{x}^{\prime } + P_{y} {\Delta }\overline{y} + P_{{y^{\prime}}} {\Delta }\overline{y}^{\prime } } \hfill \\ {H = H_{0} + H_{x} {\Delta }\overline{x} + H_{{x^{\prime}}} {\Delta }\overline{x}^{\prime } + H_{y} {\Delta }\overline{y} + H_{{y^{\prime}}} {\Delta }\overline{y}^{\prime } } \hfill \\ \end{array} } \right.$$
(16)

Substitute Eq. (16) into Eq. (15) and ignore the higher order quantities, the four equations of \(P_{x}\),\(P_{{\text{y}}}\), \(P_{{x^{\prime } }}\),\(P_{{y^{\prime } }}\) can be obtain:

$$\begin{aligned} & \frac{\partial }{\partial \varphi }\left( {P_{x} H_{0}^{3} \frac{{\partial P_{0} }}{\partial \varphi } + P_{0} H_{0}^{3} \frac{{\partial P_{x} }}{\partial \varphi } + 3P_{0} H_{0}^{2} H_{x} \frac{{\partial P_{0} }}{\partial \varphi }} \right) + \left( {\frac{{2R_{{\text{j}}} }}{L}} \right)^{2} \frac{\partial }{\partial \lambda }\left( {P_{x} H_{0}^{3} \frac{{\partial P_{0} }}{\partial \lambda } + P_{0} H_{0}^{3} \frac{{\partial P_{x} }}{\partial \lambda } + 3P_{0} H_{0}^{2} H_{x} \frac{{\partial P_{0} }}{\partial \lambda }} \right) \\ & \quad \quad = {\Lambda }_{1} \frac{\partial }{\partial \varphi }\left( {P_{0} H_{x} + P_{x} H_{0} } \right) - 2\gamma {\Lambda }_{1} \left( {P_{0} H_{{x^{\prime}}} + P_{{x^{\prime}}} H_{0} } \right) \\ \end{aligned}$$
(17)
$$\begin{aligned} & \frac{\partial }{\partial \varphi }\left( {P_{{x^{\prime}}} H_{0}^{3} \frac{{\partial P_{0} }}{\partial \varphi } + P_{0} H_{0}^{3} \frac{{\partial P_{{x^{\prime}}} }}{\partial \varphi } + 3P_{0} H_{0}^{2} H_{{x^{\prime}}} \frac{{\partial P_{0} }}{\partial \varphi }} \right) + \left( {\frac{{2R_{{\text{j}}} }}{L}} \right)^{2} \frac{\partial }{\partial \lambda }\left( {P_{{x^{\prime}}} H_{0}^{3} \frac{{\partial P_{0} }}{\partial \lambda } + P_{0} H_{0}^{3} \frac{{\partial P_{{x^{\prime}}} }}{\partial \lambda } + 3P_{0} H_{0}^{2} H_{{x^{\prime}}} \frac{{\partial P_{0} }}{\partial \lambda }} \right) \\ & \quad \quad = {\Lambda }_{1} \frac{\partial }{\partial \varphi }\left( {P_{0} H_{{x^{\prime}}} + P_{{x^{\prime}}} H_{0} } \right) + 2\gamma {\Lambda }_{1} \left( {P_{0} H_{x} + P_{x} H_{0} } \right) \\ \end{aligned}$$
(18)
$$\begin{aligned} & \frac{\partial }{\partial \varphi }\left( {P_{y} H_{0}^{3} \frac{{\partial P_{0} }}{\partial \varphi } + P_{0} H_{0}^{3} \frac{{\partial P_{y} }}{\partial \varphi } + 3P_{0} H_{0}^{2} H_{y} \frac{{\partial P_{0} }}{\partial \varphi }} \right) + \left( {\frac{{2R_{{\text{j}}} }}{L}} \right)^{2} \frac{\partial }{\partial \lambda }\left( {P_{y} H_{0}^{3} \frac{{\partial P_{0} }}{\partial \lambda } + P_{0} H_{0}^{3} \frac{{\partial P_{y} }}{\partial \lambda } + 3P_{0} H_{0}^{2} H_{y} \frac{{\partial P_{0} }}{\partial \lambda }} \right) \\ & \quad \quad = {\Lambda }_{1} \frac{\partial }{\partial \varphi }\left( {P_{0} H_{y} + P_{y} H_{0} } \right) - 2\gamma {\Lambda }_{1} \left( {P_{0} H_{{y^{\prime}}} + P_{{y^{\prime}}} H_{0} } \right) \\ \end{aligned}$$
(19)
$$\begin{aligned} & \frac{\partial }{\partial \varphi }\left( {P_{{y^{\prime}}} H_{0}^{3} \frac{{\partial P_{0} }}{\partial \varphi } + P_{0} H_{0}^{3} \frac{{\partial P_{{y^{\prime}}} }}{\partial \varphi } + 3P_{0} H_{0}^{2} H_{{y^{\prime}}} \frac{{\partial P_{0} }}{\partial \varphi }} \right) + \left( {\frac{{2R_{{\text{j}}} }}{L}} \right)^{2} \frac{\partial }{\partial \lambda }\left( {P_{{y^{\prime}}} H_{0}^{3} \frac{{\partial P_{0} }}{\partial \lambda } + P_{0} H_{0}^{3} \frac{{\partial P_{{y^{\prime}}} }}{\partial \lambda } + 3P_{0} H_{0}^{2} H_{{y^{\prime}}} \frac{{\partial P_{0} }}{\partial \lambda }} \right) \\ & \quad \quad = {\Lambda }_{1} \frac{\partial }{\partial \varphi }\left( {P_{0} H_{{y^{\prime}}} + P_{{y^{\prime}}} H_{0} } \right) + 2\gamma {\Lambda }_{1} \left( {P_{0} H_{y} + P_{y} H_{0} } \right) \\ \end{aligned}$$
(20)

Combining with Fig. 1, \(H_{x}\), \(H_{{\text{y}}}\), \(H_{{x^{\prime } }}\), \(H_{{y^{\prime } }}\) can be expressed as \(P_{x}\), \(P_{{\text{y}}}\), \(P_{{x^{\prime}}}\),\(P_{{y^{\prime } }}\) and the deformation of the foil structure. Then the finite difference method can be used in conjunction with boundary conditions to iteratively solve for \(P_{x}\), \(P_{{\text{y}}}\), \(P_{{x^{\prime } }}\), \(P_{{y^{\prime } }}\)\(.\) Finally, the four stiffness coefficients and four damping coefficients of the air foil bearing can be calculated using the following eqs. (21), (22)and the supporting model for calculating rotordynamics can be obtain.

$$\left[ {\begin{array}{*{20}c} {k_{xx} } & {k_{xy} } \\ {k_{yy} } & {k_{yx} } \\ \end{array} } \right] = \frac{{p_{{\text{a}}} R_{{\text{j}}} L}}{2c}\smallint_{ - 1}^{1} \smallint_{0}^{{\varphi_{{{\text{free}}}} }} \left[ {\begin{array}{*{20}c} { - P_{x} \sin (\beta + \varphi )} & { - P_{y} \sin (\beta + \varphi )} \\ {P_{x} \cos (\beta + \varphi )} & {P_{y} \cos (\beta + \varphi )} \\ \end{array} } \right]d\varphi d\lambda$$
(21)
$$\left[ {\begin{array}{*{20}c} {C_{xx} } & {C_{xy} } \\ {C_{yy} } & {C_{yx} } \\ \end{array} } \right] = \frac{{p_{{\text{a}}} R_{{\text{j}}} L}}{2c\psi }\smallint_{ - 1}^{1} \smallint_{0}^{{\varphi_{{{\text{free}}}} }} \left[ {\begin{array}{*{20}c} { - P_{{x^{\prime}}} \sin (\beta + \varphi )} & { - P_{{y^{\prime}}} \sin (\beta + \varphi )} \\ {P_{{x^{\prime}}} \cos (\beta + \varphi )} & {P_{{y^{\prime}}} \cos (\beta + \varphi )} \\ \end{array} } \right]d\varphi d\lambda$$
(22)

where \(\varphi_{free}\) is the angle between the free end and the fixed end of the foil structure.

2.2 Dynamic modeling of motor rotors

In this paper, the transfer matrix method is used to numerically study and analyse the rotordynamics of the motor, as shown in Figure 5. Based on the actual mass distribution of the motor and the characteristics of the impeller, the motor rotor can be simplified as an elastic damping system with a continuous distribution of 20 small segments of equal cross-sectional mass. Based on the principle of maintaining the position of the centroid constant and the moment of inertia constant, nodes are set up at the positions where there are sudden changes in the cross-section of the impeller and shaft, as well as at the supporting points of the shaft. The distributed mass is discretized into several nodes with lumped-mass, so that the shaft segments between nodes are equal cross-section shaft, finally obtaining a multi degree of freedom lumped parameter model [18], as shown in Figure 6.

Fig. 5
figure 5

Diagram of the structure of the motor rotor

Full size image
Fig. 6
figure 6

Lumped parameter model of the motor rotor

Full size image

Number the simplified nodes and shaft segments from left to right, and the disc and the shaft segment on its right form a disc shaft unit. The i-th disc shaft unit is analyzed and the state vector Zi is used to describe the state of force and deformation on the i-section without considering torsion. Zi consists of four quantities: the radial displacement xi, the deflection angle of the section θi, the cross-sectional bending moment Mi, and shear force Qi, so the state vectors on the left and right sides of the i-th lumped-mass disc are:

$$\left\{ {\begin{array}{*{20}c} {Z_{i}^{L} = [\begin{array}{*{20}c} {(X} & A & M & {Q)^{L} } \\ \end{array} ]_{i}^{T} } \\ {Z_{i}^{R} = [\begin{array}{*{20}c} {(X} & A & M & {Q)^{R} } \\ \end{array} ]_{i}^{T} } \\ \end{array} } \right.$$
(23)

Assume that the motor rotor rotates at an angular velocity \(\Omega\) and the free vortex frequency is \(\omega\). As shown in Fig. 7, the force analysis of the i-th lumped-mass disc and its adjacent axis segments shows that the mass of the disc is \({m}_{i}\). The polar moment of inertia and the diameter moment of inertia are \(J_{pi}\), \(J_{di}\), respectively; then the displacement is \(X = Ae^{iwt}\), thus \(\ddot{X} = - w^{2} X\), i.e., the inertia force of the i-th disc is \(m_{i} X_{i} w^{2}\).

Fig. 7
figure 7

Forces analysis of a disc and its adjacent axis segments

Full size image

According to the D'Alembert principle, the state vector relationship between the left and right ends of the i-th lumped-mass disc can be obtained as:

$$\left\{ {\begin{array}{*{20}l} {X_{i}^{R} = X_{i}^{L} } \hfill \\ {A_{i}^{R} = A_{i}^{L} } \hfill \\ {Q_{i}^{R} = Q_{i}^{L} + m_{i} \omega^{2} X_{i} - K_{j} X_{i} } \hfill \\ {M_{i}^{R} = M_{i}^{L} + \left( {J_{p} \Omega - J_{t} \omega } \right)_{i} \omega A_{i} } \hfill \\ \end{array} } \right.$$
(24)

Organize Eq. (24) into matrix form:

$$\left\{ {\begin{array}{*{20}l} X \hfill \\ A \hfill \\ M \hfill \\ Q \hfill \\ \end{array} } \right\}_{i}^{{\text{R}}} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & {\left( {J_{{\text{p}}} {\Omega } - J_{{\text{t}}} \omega } \right)\omega } & 1 & 0 \\ {m\omega^{2} - K_{j} } & 0 & 0 & 1 \\ \end{array} } \right]_{i} \left\{ {\begin{array}{*{20}l} X \hfill \\ A \hfill \\ M \hfill \\ Q \hfill \\ \end{array} } \right\}_{i}^{{\text{L}}}$$
(25)

Abbreviate it as the transfer relationship:

$$Z_{i}^{R} = P_{i} Z_{i}^{L}$$
(26)

As shown in Fig. 7, the state vector of the cross-section at both ends of shaft section i is:

$$Z_{i + 1}^{L} = B_{i} Z_{i}^{R}$$
(27)

Bi is the transfer matrix of the elastic shaft segment.

For the convenience of calculation, the i-th disc and its right axis segment are combined to form a disc axis unit. Since the left side of a disc axis unit is the left side of the lumped mass node, \(Z_{i + 1} = Z_{i + 1}^{L}\), also \(Z_{i + 1}^{L} = B_{i} Z_{i}^{R} = B_{i} P_{i} Z_{i}\). Then the transfer matrix Ti of the disc shaft unit can be obtained as:

$$T_{i} = B_{i} P_{i} = \left[ {\begin{array}{*{20}l} {1 + \frac{{l^{3} }}{6EI}(1 - \nu )\left( {m\omega^{2} - K_{j} } \right)} \hfill & {l + \frac{{l^{2} }}{2EI}\left( {J_{{\text{p}}} {\Omega } - J_{{\text{t}}} \omega } \right)\omega } \hfill & {\frac{{l^{2} }}{2EI}} \hfill & {\frac{{l^{3} }}{6EI}(1 - \nu )} \hfill \\ {\frac{{l^{2} }}{2EI}\left( {m\omega^{2} - K_{j} } \right)} \hfill & {1 + \frac{l}{EI}\left( {J_{{\text{p}}} {\Omega } - J_{{\text{t}}} \omega } \right)\omega } \hfill & \frac{l}{EI} \hfill & {\frac{{l^{2} }}{2EI}} \hfill \\ {l\left( {m\omega^{2} - K_{j} } \right)} \hfill & {\left( {J_{{\text{p}}} {\Omega } - J_{{\text{t}}} \omega } \right)\omega } \hfill & 1 \hfill & l \hfill \\ {\left( {m\omega^{2} - K_{j} } \right)} \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} } \right]_{i}$$
(28)

With the transfer matrix of the disc axis unit, the state variables of each disc axis unit can be calculated sequentially from the first disc shaft unit to the last one.

2.3 Calculation method for dynamics model of motor rotors

The vibration amount can be set as follows to more accurately reflect the characteristics of the vibration Time-Varying:

$$x = Xe^{\lambda t} \cos \left( {\omega t + \theta } \right)$$
(29)

In order to show that the vibration is a property within a spatial range, a sine term is added to Eq. (29) above to make it a complex number, namely:

$$x = {\text{Re}} \left. {\left\{ {Xe^{\lambda t} \cos \left( {\omega t + \theta } \right) + iXe^{\lambda t} \sin \left( {\omega t + \theta } \right)} \right.} \right\}$$
(30)

Simultaneous Euler formula:

$$e^{i\theta } = \cos \theta + i\sin \theta$$
(31)

The above Eq. (30) can be transformed to:

$$x = {\text{Re}} \left. {\left\{ {Xe^{\lambda t} e^{i(\omega t + \theta )} } \right.} \right\}$$
(32)

According to the operation rules of the index, the above Eq. (32) can be transformed into:

$$x = {\text{Re}} \left. {\left\{ {Xe^{i\theta } e^{(\lambda + \omega i)t} } \right.} \right\} = {\text{Re}} \left. {\left\{ {(X_{c} + iX_{s} )e^{(\lambda + \omega i)t} } \right.} \right\} = {\text{Re}} \left\{ {\left. {\widehat{X}e^{St} } \right\}} \right.$$
(33)

where Re represents the real part,\(\hat{X} = X_{c} + iX_{s}\) represents the complex amplitude of the vibration quantity x; \(S = \lambda + i\omega\) is the complex frequency, which includes the decay index \(\lambda\) (Unit: 1/s) and damping circular frequency (rad/s). Due to the fact that in one system, the nodes' \(\lambda\) and \(\omega\) are the same, so the Re symbol in Eq. (33) can be temporarily omitted, namely:

$$\left\{ \begin{gathered} x = \widehat{X}e^{St} \hfill \\ \dot{x} = xS \hfill \\ \end{gathered} \right.$$
(34)

Due to the characteristics of the air film of the air foil bearing, using only one direction of stiffness and damping equivalence cannot reflect its characteristics well. So the coupling of the x and y direction is considered. In order to include the supporting effect of the air film force of the air foil bearing in the calculation of the critical speed of the rotor using the transfer matrix method, the air film force of the air foil bearing can be approximated by using the supporting model shown in Fig. 8 when the shaft moves slightly around the static equilibrium position. The equations are expressed as:

$$\left\{ {\begin{array}{*{20}l} {f_{x} = f_{x0} + k_{xx} x + k_{xy} y + c_{xx} \dot{x} + c_{xy} \dot{y}} \hfill \\ {f_{y} = f_{y0} + k_{yx} x + k_{yy} y + c_{yx} \dot{x} + c_{yy} \dot{y}} \hfill \\ \end{array} } \right.$$
(35)
Fig. 8
figure 8

Air foil bearing supporting model

Full size image

Substitute the above Eq. (34) into Eq. (35) and write it in matrix form as follows:

$$\left\{ {\begin{array}{*{20}l} {f_{x} } \hfill \\ {f_{y} } \hfill \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}l} {f_{x0} } \hfill \\ {f_{y0} } \hfill \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {k_{xx} } & {k_{xy} } \\ {k_{yx} } & {k_{yy} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} x \hfill \\ y \hfill \\ \end{array} } \right\} + S\left[ {\begin{array}{*{20}c} {c_{xx} } & {c_{xy} } \\ {c_{yx} } & {c_{yy} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} x \hfill \\ y \hfill \\ \end{array} } \right\}$$
(36)

The equivalent supporting stiffness can be written as:

$$K_{T} = \left[ {\begin{array}{*{20}c} {k_{Txx} } & {k_{Txy} } \\ {k_{Tyx} } & {k_{Tyy} } \\ \end{array} } \right] + S\left[ {\begin{array}{*{20}c} {c_{xx} } & {c_{xy} } \\ {c_{yx} } & {c_{yy} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {k_{Txx} } & {k_{Txy} } \\ {k_{Tyx} } & {k_{Tyy} } \\ \end{array} } \right]$$
(37)

The support stiffness matrix and damping matrix of the air foil bearing have been obtained in eqs.(21) and (22), and the equivalent stiffness KT can be obtained by substituting them into Eq. (37).

The Riccati transfer matrix method is used to calculate the critical speeds of the motor rotor supported by air foil bearings [19]. On the basis of the vibration in a single plane shown in Fig. 6, the spatial vibration amount is represented by the complex number (Eq. 33), and the state vector of the disc-shaft unit can be expressed as:

$$Z_{i} = [\left. f \right|e]_{i}^{T} = [\left. {\begin{array}{*{20}c} {M_{x} } & {Q_{x} } & {M_{y} } & {Q_{y} } \\ \end{array} } \right|\begin{array}{*{20}c} x & A & y & B \\ \end{array} ]_{i}^{T}$$
(38)

Similarly, the transfer matrix Ti for the disc-shaft unit in the spatial domain can be obtained as:

$$T =_{i} \left[ {\begin{array}{*{20}l} 1 \hfill & l \hfill & 0 \hfill & 0 \hfill & { - l\left( {mS^{2} + K_{{{\text{Txx}}}} } \right)} \hfill & {J_{{\text{t}}} S^{2} } \hfill & { - lK_{{{\text{Txy}}}} } \hfill & {J_{{\text{p}}} {\Omega }S} \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & { - \left( {mS^{2} + K_{{{\text{Txx}}}} } \right)} \hfill & 0 \hfill & { - K_{{{\text{Txy}}}} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & l \hfill & { - lK_{{{\text{Tyx}}}} } \hfill & { - J_{{\text{p}}} {\Omega }S} \hfill & { - l\left( {mS^{2} + K_{{{\text{Tyy}}}} } \right)} \hfill & {J_{{\text{t}}} S^{2} } \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & { - K_{{{\text{Tyx}}}} } \hfill & 0 \hfill & { - \left( {mS^{2} + K_{{{\text{Tyy}}}} } \right)} \hfill & 0 \hfill \\ {\frac{{l^{2} }}{2EI}} \hfill & {\frac{{l^{2} }}{6EI}(1 - \nu )} \hfill & 0 \hfill & 0 \hfill & {1 - \frac{{l^{3} (1 - \nu )}}{6EI}\left( {mS^{2} + K_{{{\text{Txx}}}} } \right)} \hfill & {l + \frac{{l^{2} }}{2EI}J_{{\text{t}}} S^{2} } \hfill & {\frac{{l^{3} (1 - \nu )}}{6EI}K_{{{\text{Txy}}}} } \hfill & {\frac{{l^{2} }}{2EI}J_{{\text{p}}} {\Omega }S} \hfill \\ \frac{l}{EI} \hfill & {\frac{{l^{2} }}{2EI}} \hfill & 0 \hfill & 0 \hfill & { - \frac{{l^{2} }}{2EI}\left( {mS^{2} + K_{{{\text{Txx}}}} } \right)} \hfill & {1 + \frac{l}{EI}J_{{\text{t}}} S^{2} } \hfill & { - \frac{{l^{2} }}{2EI}K_{Txy} } \hfill & {\frac{{l^{2} }}{EI}J_{{\text{p}}} {\Omega }S} \hfill \\ 0 \hfill & 0 \hfill & {\frac{{l^{2} }}{2EI}} \hfill & {\frac{{l^{2} }}{6EI}(1 - \nu )} \hfill & {\frac{{l^{3} (1 - \nu )}}{6EI}K_{{{\text{Tyx}}}} } \hfill & { - \frac{{l^{2} }}{2EI}J_{{\text{p}}} {\Omega }S} \hfill & {1 - \frac{{l^{3} (1 - \nu )}}{6EI}\left( {mS^{2} + K_{{{\text{Tyy}}}} } \right)} \hfill & {l + \frac{{l^{2} }}{2EI}J_{{\text{t}}} S^{2} } \hfill \\ 0 \hfill & 0 \hfill & \frac{l}{EI} \hfill & {\frac{{l^{2} }}{2EI}} \hfill & { - \frac{{l^{2} }}{2EI}K_{Tyx} } \hfill & { - \frac{l}{EI}J_{{\text{p}}} {\Omega }S} \hfill & { - \frac{{l^{2} }}{2EI}\left( {mS^{2} + K_{{{\text{Tyy}}}} } \right)} \hfill & {1 + \frac{l}{EI}J_{{\text{t}}} S^{2} } \hfill \\ \end{array} } \right]_{i}$$
(39)

Divide the transfer matrix of the two adjacent cross-sections of the disc shaft unit into four blocks, namely:

$$[\left. f \right|e]_{i + 1}^{T} = T_{i} [\left. f \right|e]_{i}^{T} = \left[ {\begin{array}{*{20}c} {u_{11} } & {u_{12} } \\ {u_{21} } & {u_{22} } \\ \end{array} } \right]_{i} [\left. f \right|e]_{i}^{T}$$
(40)

The simultaneous Riccati transformation (Ri is referred to as the Riccati matrix of 4 × 4):

$$f_{i} = R_{i} e_{i}$$
(41)

yields:

$$\left\{ {\begin{array}{*{20}l} {e_{i} = [u_{21} R + u_{22} ]_{i}^{ - 1} e_{i + 1} } \hfill \\ {f_{i + 1} = [u_{11} R + u_{12} ]_{i} [u_{21} R + u_{22} ]_{i}^{ - 1} e_{i + 1} } \hfill \\ \end{array} } \right.$$
(42)

It is easy to observe that the Riccati matrix Ri+1 of section i + 1 is:

$$R_{i + 1} = [u_{11} R + u_{12} ]_{i} [u_{21} R + u_{22} ]_{i}^{ - 1}$$
(43)

From Eq. (43), Ri+1 can be recursively derived from Ri, so Eq. (43) is called the recursion formula for the Riccati matrix Ri. According to the boundary condition of the starting end section of the motor rotor, f1 = 0,\(e_{1} \ne 0\), with R1 = 0, and according to Eq. (43), R2, R3, R4,…, Rn+1 can be obtained sequentially. Combined with the right end section N + 1 of the motor rotor and its boundary conditions, namely:

$$\left\{ {\begin{array}{*{20}l} {f_{N + 1} = R_{N + 1} e_{N + 1} } \hfill \\ {f_{N + 1} = 0,e_{N + 1} \ne 0} \hfill \\ \end{array} } \right.$$
(44)

Obtain the frequency equation of the motor rotor in the spatial domain:

$$\det R_{N + 1} = \left| {\left. {\begin{array}{*{20}l} {S_{11} } \hfill & {S_{12} } \hfill & {S_{13} } \hfill & {S_{14} } \hfill \\ {S_{21} } \hfill & {S_{22} } \hfill & {S_{23} } \hfill & {S_{24} } \hfill \\ {S_{31} } \hfill & {S_{32} } \hfill & {S_{33} } \hfill & {S_{34} } \hfill \\ {S_{41} } \hfill & {S_{42} } \hfill & {S_{43} } \hfill & {S_{44} } \hfill \\ \end{array} } \right|} \right._{N + 1} = 0$$
(45)

The independent variable in Eq. (45) is a complex number \(S = \lambda + i\omega\), when a certain excitation speed Ω is given, the complex frequency S0 can be calculated to determine the critical speed and logarithmic decrement of each order \(\delta = - 2\pi \lambda /\omega\) (The larger the \(\delta\) value, the higher the anti-interference ability).

Due to factors such as machining errors, the motor rotor may become eccentric and the air film thickness may be uneven, resulting in the motor rotor being subjected to UMP. Assuming that the thickness of the air film remains constant along the axial direction, the eccentricity of any section of the motor rotor at any time is shown in Fig. 9, where e is the eccentricity, \(\psi\) is the angle between the connection line between the stator centroid and the rotor centroid and x-direction, \(\delta_{0}\) is the air film thickness at ideal rotation, and \(\delta\) is the air film thickness corresponding to any angle \(\theta\). The rotor with a smaller air film is subjected to greater UMP on one side.

Fig. 9
figure 9

Eccentricity geometry of the motor rotor

Full size image

From geometric analysis, it is easy to obtain the air film thickness \(\delta\) corresponding to any angle \(\theta\):

$$\delta = \delta_{0} - e\cos (\theta - \Psi )$$
(46)

where \(\delta_{0} = R - r\), R is the inner radius of the stator and r is the outer radius of the rotor.

The air film thickness corresponding to any angle \(\theta\) is different, and the magnetic flux density between the rotor and stator is different. Therefore, the air film magnetic permeability \(\Lambda\) is defined as:

$$\Lambda = \frac{{\mu_{0} S}}{\delta } = \frac{{\mu_{0} S}}{{\delta_{0} [1 - \varepsilon \cos (\theta - \Psi )]}}$$
(47)

where S is the magnetic flux area of each pole air gap,\(\varepsilon\) is the relative eccentricity(\(\varepsilon = e/\delta_{0}\)),\(\mu_{0}\) is the vacuum magnetic permeability. Write Eq. (47) as the form of Fourier series as follows:

$$\Lambda = S\sum\limits_{n = 0}^{\infty } {\Lambda_{n} } \cos (\theta - \Psi )$$
(48)

where \(\Lambda_{n}\) is the Fourier coefficient,

$${\Lambda }_{n} = \left\{ {\begin{array}{*{20}l} {\frac{{\mu_{0} }}{{\delta_{0} }}\frac{1}{{\sqrt {1 - \varepsilon^{2} } }}(n = 0)} \hfill \\ {2\frac{{\mu_{0} }}{{\delta_{0} }}\frac{1}{{\sqrt {1 - \varepsilon^{2} } }}\left( {\frac{\varepsilon }{{1 + \sqrt {1 - \varepsilon^{2} } }}} \right)^{n} \quad (n > 0)} \hfill \\ \end{array} } \right.$$
(49)

Considering only the fundamental wave of the air film, the magnetic electromotive force composes of the rotating magnetic field formed by the stator winding and the magnetic field formed by the rotor magnetic steel is [20]:

$$F(\theta ,t) = F_{s} \cos \left( {\omega_{e} t - p\theta } \right) + F_{m} \cos \left[ {\omega_{e} t - p\theta - \phi } \right]$$
(50)

where Fs is the fundamental amplitude of the stator winding magnetomotive force; Fm is the equivalent magnetic potential amplitude of the rotor magnetic steel; P is the number of magnetic poles,\(\omega_{e}\) is the electrical angular velocity, and \(\phi\) is the angle between the magnetomotive force of the stator and rotor. Also, the air film magnetic density corresponding to any angle \(\theta\) is:

$$B(\theta ,t) = \frac{F(\theta ,t)\Lambda }{S}$$
(51)

The Maxwell stress tensor method is used to calculate the UMP, and the tangential stress is:

$$\sigma = \frac{{B(\theta ,t)^{2} }}{{2\mu_{0} }}$$
(52)

Due to the small radial stress, only tangential stress is considered. Substitute Eq. (51) for Eq. (52) yields:

$$\sigma = \frac{{F^{2} (\theta ,t) \cdot [\sum\limits_{n = 0}^{\infty } {\Lambda^{n} } \cos (\theta - \Psi )]^{2} }}{{2\mu_{0} }}$$
(53)

By integrating the tangential stress along the x and y directions, the components of the UMP in the x and y directions can be obtained:

$$\left\{ {\begin{array}{*{20}l} {F_{ex} = \frac{rL}{{2\mu_{0} }}\smallint_{0}^{2\pi } F^{2} (\theta ,t)\left[ {\sum\limits_{n = 0}^{\infty } {\Lambda^{n} } \cos (\theta - \Psi )} \right]^{2} \cos \theta {\text{d}}\theta } \hfill \\ {F_{ey} = \frac{rL}{{2\mu_{0} }}\smallint_{0}^{2\pi } F^{2} (\theta ,t)\left[ {\sum\limits_{n = 0}^{\infty } {\Lambda^{n} } \cos (\theta - \Psi )} \right]^{2} \sin \theta {\text{d}}\theta } \hfill \\ \end{array} } \right.$$
(54)

where L is the length of the rotor magnetic steel. When the motor rotor rotates at an angular velocity Ω, the UMP will affect its vibration situation. Add the unbalanced force of Eq. (54) above to its position (on the 16th disc node), that is:

$$Z_{i}^{R} = P_{i} Z_{i}^{L} + F_{i}$$
(55)

And add a shaft segment to its right end to form a disc-shaft unit, then the state vector relationship at both ends is:

$$Z_{i + 1} = B_{i} (P_{i} Z_{i}^{L} + F_{i} )$$
(56)

According to the Riccati transfer matrix method, they are grouped as follows:

$$[\left. f \right|e]_{i + 1}^{T} = T_{i} [\left. f \right|e]_{i}^{T} = \left[ {\begin{array}{*{20}c} {u_{11} } & {u_{12} } \\ {u_{21} } & {u_{22} } \\ \end{array} } \right]_{i} [\left. f \right|e]_{i}^{T} + [\left. {F_{f} } \right|F_{e} ]_{i}^{T}$$
(57)

where u11, u12, u21, u22 is similar to the above without magnetic tension. Introduce Riccati transformation:

$$f_{i} = R_{i} e_{i} + N_{i}$$
(58)

Based on the boundary conditions, it can be obtained that:

$$e_{N + 1} = - R_{N + 1}^{ - 1} N_{N + 1}$$
(59)

According to the recursive formula of ei, the state vectors ei (i = N,N-1,…,2,1) of each cross-section are derived to obtain the unbalanced response of the rotor under UMP. The calculation flowchart is shown in Fig. 10.

Fig. 10
figure 10

Calculation flow chart of the motor rotor system model

Full size image

3 Example study

In order to verify the accuracy of the established model, the parameters of the rotor system model used in the literature [21] were substituted into the rotor dynamics analysis model constructed in this paper. The calculated data was compared with its experimental data, as shown in Figs. 11 and 12, and it was found that the predicted synchronous vibration amplitude of the established model could match well for two imbalance displacement \(u\) = 10.5 × 10−6 and 12 × 10−6 m, which verified the accuracy of the rotor dynamics analysis model constructed in this paper.

The parameters of the high-speed motor rotor used in this calculation are shown in Table 1.

Table 1 The motor rotor model data sheet
Full size table

The Riccati transfer matrix method is used to numerically calculate the natural frequency of the motor rotor as a function of the rotational speed, as shown in Fig. 13 (also known as the Campbell diagram).As can be seen from the figure, when the motor rotor rotates, the frequency of each mode increases with the rotational speed due to the rotational effect of the motor rotor. And there are only three intersections between the synchronous excitation line and the forward precession curve of each order within 160 krpm, indicating there are three critical speeds within the range. The first two order critical speeds are all below 15 krpm and far from the rated speed of the motor design of 120 krpm. The third order critical speed is 139.548 krpm, which is 19.548 krpm higher than the rated speed and also within the safe range. Modal analysis of the motor rotor is carried out by the finite element software called Ansys, and it is found that its third order critical speed is 158.310 krpm, which is much greater than 120 krpm. Therefore, the designed rated rotor speed is within the safe range, and the correctness of using the Riccati transfer matrix method in MATLAB numerical calculation of rotor dynamics is verified. From the obtained third-order vibration mode diagram of the motor rotor system, as shown in Fig. 14, it can be seen that the position with larger amplitude of the motor rotor appears on the both sides of the rotor, while the amplitude at the bearing position is smaller.

Fig. 11
figure 11

Synchronous vibrations for imbalance displacement \(u\) = 10.5 × 10−6 m

Full size image
Fig. 12
figure 12

Synchronous vibrations for imbalance displacement \(u\) = 12 × 10−6 m

Full size image

Based on the numerical calculation of rotor dynamics using the Riccati transfer matrix method in MATLAB, this article investigates the effects of foil thickness, bearing length, rotor radius, and aerodynamic viscosity on natural frequency and stability of the rotor. As shown in Fig. 15, the third order critical speed increases with the increase of foil thickness. From Fig. 16, it can be seen that the third order critical speed increases with the increase of bearing width. As shown in Fig. 17, the third order critical speed decreases with the increase of rotor radius. As shown in Fig. 18, the third order critical speed increases with the increase of aerodynamic viscosity. From Fig. 19, it can be seen that the logarithmic decrement of the third order natural frequency corresponding to different foil thicknesses decreases with increasing speed, and at the same speed, the logarithmic decrement increases with increasing foil thickness. From Fig. 20, it can be seen that the logarithmic decrement of the third order natural frequency points corresponding to different bearing width decreases with increasing speed, and at the same speed, the logarithmic decrement increases with increasing bearing width. From Fig. 21, it can be seen that the logarithmic decrement of the third order natural frequency points corresponding to different rotor radius decreases as the speed increases. At the same speed, the logarithmic decrement decreases as the rotor radius increases. From Fig. 22, it can be seen that the logarithmic decrement of the third order natural frequency points corresponding to different dynamic viscosities of air decreases with increasing speed, while at the same speed, the logarithmic decrement increases with increasing dynamic viscosity of air.

Fig. 13
figure 13

Campbell diagram of the motor rotor

Full size image
Fig. 14
figure 14

Third order vibration mode of the motor rotor

Full size image
Fig. 15
figure 15

The influence of foil thickness on the third order critical speed

Full size image
Fig. 16
figure 16

The influence of bearing width on the third order critical speed

Full size image
Fig. 17
figure 17

The influence of rotor radius on the third order critical speed

Full size image
Fig. 18
figure 18

The influence of dynamic viscosity of air on the third order critical speed

Full size image
Fig. 19
figure 19

The influence of foil thickness on stability

Full size image
Fig. 20
figure 20

The influence of bearing width on stability

Full size image

As shown in Figs. 23 and 24, an unbalance of 1 × 10−5 kg·m caused by uneven mass distribution is applied to the corresponding force generating disc 16, resulting in elliptical response amplitudes for both the left and right bearings. The shaft trajectory range at the left bearing is large (with a large amplitude), which is due to the large load carried by the left bearing. The maximum UMP calculated by Eq. (54) is equivalent to the unbalanced amount applied to the corresponding force generating disc 16. The shaft trajectory at the left bearing is shown in Fig. 25, and the shaft trajectory at the right bearing is shown in Fig. 26. Comparing Figs. 23, 24, 25, 26, it is easy to find that the response amplitude generated by the maximum UMP is smaller than the unbalanced amount 1 × 10−5 kg·m caused by uneven mass distribution, and the amplitude is smaller than the air film thickness 4 × 10−2 mm, which indicates that the motor can operate stably under the influence of UMP.

Fig. 21
figure 21

The influence of rotor radius on stability

Full size image
Fig. 22
figure 22

The influence of dynamic viscosity of air on stability

Full size image
Fig. 23
figure 23

The shaft trajectory of the left bearing under the influence of unbalanced mass

Full size image
Fig. 24
figure 24

The shaft trajectory of the right bearing under the influence of unbalanced mass

Full size image
Fig. 25
figure 25

The shaft trajectory of the left bearing under the influence of UMP

Full size image
Fig. 26
figure 26

The shaft trajectory of the right bearing under the influence of UMP

Full size image

4 Conclusions

  1. 1.

    A mechanical analysis is conducted on the air foil bearing, and a deformation model of the air foil bearing is constructed using the Castigliano’s second theorem, force balance equation, and small deflection elastic thin plate theory. Based on the Navier–Stokes equation and continuity equation, combined with Newtonian fluid and laminar flow conditions, the generalized Reynolds equation is derived. The perturbation method and the finite difference method are used to obtain the disturbance pressure, and the stiffness and damping of the air foil bearing are obtained by integrating the disturbance pressure, serving as the supporting model for the motor rotor. On the basis of analyzing the transfer matrix of typical disc shaft unit using the transfer matrix method, combined with the Riccati transform, the natural frequencies and the critical speeds of the motor rotor system in the spatial domain are calculated using MATLAB. The Maxwell stress tensor method is used to calculate the UMP, and the UMP is equivalent to the unbalanced mass applied to the disc it acts on. The unbalanced response is calculated, forming a theoretical model that can calculate the dynamic performance of high-speed motor rotors. A numerical calculation method for this model is established and programed using MATLAB.

  2. 2.

    Through numerical analysis, the effects of foil thickness, bearing length, rotor radius, and dynamic viscosity of air on the natural frequency and stability of the motor rotor system are studied. It is found that the third order critical speed increases with the increase of foil thickness, bearing width, and dynamic viscosity of air, while decreases with the increase of rotor radius; The logarithmic decrement of the third order natural frequency points corresponding to different foil thicknesses, bearing lengths, rotor radius, and dynamic viscosity of air decreases with increasing speed. At the same speed, the logarithmic decrement increases with increasing foil thickness, bearing length, and dynamic viscosity of air, and decreases with increasing rotor radius; The shaft trajectories of the left and right bearings under unbalanced mass and UMP are studies. It is found that the amplitude of the shaft trajectory of the left bearing with larger load is larger. However, the amplitude of the left and right bearings is smaller than the thickness of the air firm thickness, indicating that the motor rotor can operate stably under the action of unbalanced mass and UMP.