Rigid spacecraft nonlinear robust $H_\infty$ attitude controller design under actuator misalignments

Abstract

$H_\infty$ control is well-known for its robustness performance, but the spacecraft attitude $H_\infty$ controller design under actuator misalignments and disturbances remains unexplored. In addition, the heavy computational demands prevent the implementation of an $H_\infty$ controller for nonlinear systems in higher dimensions. To address these challenges, a robust $H_\infty$ controller is proposed for the rigid spacecraft attitude control problem in the presence of actuator misalignments and disturbances based on the solution of the Hamilton–Jacobi–Isaacs (HJI) partial differential equation (PDE). The $L_2$-gain of the closed-loop system is proved to be bounded by a specified disturbance attenuation level. An efficient sparse successive Chebyshev–Galerkin method is also proposed to solve the nonlinear HJI PDE, thus the implementation of the proposed controller is facilitated. It is also proved that the computational cost grows only polynomially with the system dimension. The effectiveness of the proposed robust $H_\infty$ controller is validated through numerical simulations.

1 Introduction

The rigid spacecraft attitude control system should attain its control objective under the ubiquitous disturbances and possible modeling uncertainties like actuator misalignments [1,2,3]. Robust control methods have been investigated for attitude control systems under actuator misalignments and disturbances in the literature [4]. Besides concerning with closed-loop stability, one may also want to specify and even optimize the level of disturbance attenuation for the attitude control system. In this paper, a nonlinear robust $H_\infty$ attitude controller is proposed, and the maximum level of disturbance attenuation under actuator misalignments is guaranteed. To implement the proposed controller, an efficient sparse successive Chebyshev–Galerkin method is also designed to solve the Hamilton–Jacobi–Isaacs (HJI) equation.

External disturbances have been explicitly considered in the design procedure of most attitude controllers [5,6,7,8,9,10]. In additional to disturbances, modeling uncertainties also bring non-negligible influences on the performance of the controller. Actuator uncertainties like misalignments may be introduced in the attitude control system, which are often caused by manufacturing tolerances and the deformation of the frame structure in the launching process [11]. These misalignment angles could lead to the performance degradation and even system failures for the attitude control task [12]. To calibrate the actuator misalignments, an extended Kalman filter is employed to estimate the misalignment angles in [13]. In [12] and [14], adaptive controllers are designed for attitude controller problems under misalignments. Finite-time control methods and control allocation schemes are combined in [15] to guarantee the finite-time convergence of the state under misalignments. While in [16] sliding model controller is designed to handle the attitude control problem with both actuator misalignments and faults.

Optimal control techniques have also been investigated for the attitude control problem under actuator misalignments and disturbances. In [17], a guaranteed cost controller is designed, and it is also shown that the controller converges to the optimal guaranteed cost controller during the iterations. Note also that the design of the optimal guaranteed cost controller relies on some restricted assumptions on the disturbance. In [18], an inverse optimal control-based robust controller is designed for attitude control problems with actuator misalignments. Whereas in [19] actuator misalignments and pointing constraints are considered, and an adaptive dynamic programming-based robust optimal controller is designed.

The prescribed performance control is an approach that can ensure both transient and steady-state performance of the dynamic system [20, 21]. In the context of spacecraft attitude control, prescribed performance controllers have been developed by integrating methods like backstepping and sliding mode control into the architecture [22, 23]. Furthermore, the application of prescribed performance controllers has been further extended to spacecraft with flexible appendages [24]. Compared with optimal controllers and prescribed performance controllers, the $H_\infty$ controller has preferred performance in robustness, and the $L_2$-gain of the system can also be specified [22, 25].

Linear and nonlinear $H_\infty$ control techniques have also been widely studied for spacecraft control problems. In [26], the robust attitude control problem is formulated in terms of linear matrix inequalities. Nonlinear $H_\infty$ controller design procedures usually involve solving the HJI equation, which is a nonlinear partial differential equation and generally hard to deal with. In [27], the robust $H_\infty$ controller is designed for position and attitude tracking using the $\theta -D$ method, which introduces an intermediate variable and approximately converts the HJI equations into an algebraic Riccati inequality and a sequence of Lyapunov equations. An $H_\infty$ inverse optimal controller is proposed for spacecraft attitude control problems in [28] and the solution function of the HJI equation is constructed based on a Lyapunov function, but the cost functional in the dissipation inequality cannot be pre-defined. State-dependent Riccati equation method is also employed for the $H_\infty$ control of relative motion in [29], and the spacecraft dynamics are linearized to reduce the HJI equations into Riccati equations.

The successive Galerkin approximation method is an alternative and accurate numerical scheme to solve the HJI equation raised in nonlinear $H_\infty$ control problems [30, 31]. In previous works, the multidimensional basis function set in the successive Galerkin approximation method is manually chosen, which relies heavily on design experiences and can hardly be extended to high-dimensional problems. Besides, the multidimensional integrals in the successive Galerkin approximation method are calculated using tensor-product rules and its computational cost usually grows exponentially with the dimension, which poses significant challenges for nonlinear systems in higher dimensions. Although the successive Galerkin approximation method has been used in [30, 31] to solve the HJI equation, it is generally not easy for one to properly design the multi-dimensional basis function set and quadrature rule, especially for nonlinear systems in higher dimensions.

This paper investigates the robust $H_\infty$ attitude control problem under actuator misalignment and presents the following two major contributions.

1. Development of a nonlinear robust $H_\infty$ controller: The nonlinear robust $H_\infty$ control problem for spacecraft attitude control systems subject to actuator misalignments and disturbances remains a challenging and underexplored area of research. In this paper, a robust $H_\infty$ attitude controller for attitude control systems with both actuator misalignments and disturbances is proposed by solving an HJI equation. It is proved that the closed-loop attitude control system is dissipative with respect to the prescribed supply rate.

2. Design of a sparse successive Chebyshev–Galerkin method: The conventional successive Galerkin approximation method suffers from the curse of dimensionality in dealing with nonlinear HJI equations. In this paper, a sparse successive Chebyshev-Galerkin method is proposed to efficiently obtain the nonlinear robust $H_\infty$ controller. The proposed method involves constructing a multi-dimensional basis function set and quadrature rule using the Smolyak’s sparse grid formulation. The computational cost of the sparse successive Chebyshev–Galerkin method is shown to grow only polynomially with the dimension, making it an efficient and competitive candidate for a wide range of nonlinear $H_\infty$ control problems. The robust $H_\infty$ controller can be analytically constructed using the obtained basis functions and coefficients, which helps achieve high on-line implementation efficiency.

The remainder of this paper is arranged as follows. The following section introduces the attitude control problem considered in this paper. The robust $H_\infty$ controller is designed and the dissipation analysis is given in Sect. 3. Section 4 presents a sparse successive Chebyshev–Galerkin method to efficiently implement the controller. Numerical simulations are conducted in Sect. 5 and Section 6 summarizes the paper.

2 Problem statement

Fig. 1

Misalignment angles of the attitude control system

The nonlinear robust $H_\infty$ attitude controller design problem under actuator misalignments and external disturbances is considered in this paper. Let $\varvec{\rho } =[\rho _1,\rho _2,\rho _3]^\top$, $\varvec{\omega } = [\omega _1, \omega _2, \omega _3]^\top$, and $\varvec{u} =$ $[u_1, u_2, u_3]^\top$ denote the Cayley-Rodrigues parameters, angle velocities along the principle axes, and the inputs, respectively. The attitude control system of the rigid spacecraft is described by [32]

$$\begin{aligned} \dot{\varvec{\rho }}&= H(\varvec{\rho }) \varvec{\omega } \end{aligned}$$

(1)

$$\begin{aligned} {{{J}}}\dot{\varvec{\omega }}&= S(\varvec{\omega }){{{J}}}\varvec{\omega } + \varLambda \varvec{u} + \varvec{d} \end{aligned}$$

(2)

where J is the inertia matrix and $\varvec{d} \in L_2(0,+\infty )$ is the disturbance. The matrix $\varLambda$ describes the influence of actuator misalignments. The misalignment angles could be caused by imperfection of assembling or structural deformation. The matrix $H(\varvec{\rho })$ is defined by

$$\begin{aligned} H(\varvec{\rho }) = \frac{1}{2}\left( I-S(\varvec{\rho })+\varvec{\rho }\varvec{\rho }^\top \right) \end{aligned}$$

(3)

and the skew-symmetric matrix is given by [32]

$$\begin{aligned} S(\varvec{\rho }) = \left[ \begin{matrix} 0 &{} \rho _3 &{} -\rho _2\\ -\rho _3&{} 0 &{}\rho _1 \\ \rho _2&{} -\rho _1&{} 0 \end{matrix}\right] . \end{aligned}$$

(4)

As illustrated in Fig. 1 [12], it is assumed that the three momentum wheels are orthogonally installed and aligned with the principle axes. The weighted matrix $\varLambda$ is given by [12]

$$\begin{aligned} \varLambda = \left[ \begin{matrix} \cos \Delta \alpha _1 &{} \sin \Delta \alpha _2 \sin \Delta \beta _2 &{} \sin \Delta \alpha _3 \cos \Delta \beta _3\\ \sin \Delta \alpha _1 \cos \Delta \beta _1 &{} \cos \Delta \alpha _2 &{} \sin \Delta \alpha _3 \sin \Delta \beta _3\\ \sin \Delta \alpha _1 \sin \Delta \beta _1 &{} \sin \Delta \alpha _2 \cos \Delta \beta _2 &{} \cos \Delta \alpha _3 \end{matrix} \right] \nonumber \\ \end{aligned}$$

(5)

where $\Delta \alpha _i$ and $\Delta \beta _i$ ($i=1,2,3$) are the angles of deviation from the nominal axes (see Fig. 1). Usually $\Delta \alpha _i$ is a small angle and $\Delta \beta _i \in (-\pi , \pi ]$. Specifically, the range $|\Delta \alpha _i|\le \nicefrac {\pi }{10}$ is considered in this paper since the misalignment angles of previously launched spacecraft never exceed $7^\circ$ [12].

To simplify the notation, the attitude control system of the rigid spacecraft can be rewritten into

$$\begin{aligned} \dot{\varvec{x}} = \varvec{f}(\varvec{x}) + \varvec{g}(\varvec{x})\varLambda \varvec{u} + \varvec{k}(\varvec{x}) \varvec{d} \end{aligned}$$

(6)

where

$$\begin{aligned} \varvec{f}(\varvec{x}) = \left[ \begin{array}{ll} H(\varvec{\rho }) \varvec{\omega } \\ {J}^{-1}S(\varvec{\omega }){{{J}}}\varvec{\omega } \end{array} \right] ,\ \varvec{g}(\varvec{x})= \varvec{k}(\varvec{x})= \left[ \begin{array}{ll} \varvec{0}_{3\times 3} \\ {J}^{-1} \end{array} \right] .\nonumber \\ \end{aligned}$$

(7)

The objective of this paper is to design a robust attitude controller such that the nonlinear system (6) is dissipative with respect to the supply rate

$$\begin{aligned} s(\varvec{x},\varvec{u},\varvec{d}) = -\left\| \varvec{h}(\varvec{x})\right\| ^2 - \left\| \varvec{u}\right\| _{R_\textrm{r}}^2 + \gamma ^2 \left\| \varvec{d}\right\| ^2 \end{aligned}$$

(8)

for the properly chosen positive constant $\gamma$. Here ${R_\textrm{r}}$ is a user-defined positive definite matrix. The nonlinear system (6) is said to be dissipative with respective to (8) if there exists a storage function $S\ge 0$ such that the dissipation inequality

$$\begin{aligned} S(\varvec{x}_T)+ \int _{0}^{T} (\left\| \varvec{h}(\varvec{x})\right\| ^2 + \left\| \varvec{u}(t)\right\| _{R_\textrm{r}}^2) \textrm{d}t \le \gamma ^2 S(\varvec{x}_0)\nonumber \\ +\int _{0}^{T} \left\| \varvec{d}(t)\right\| ^2 \textrm{d}t , \quad \varvec{x}_0=\varvec{x}(t=0)\nonumber \\ \end{aligned}$$

(9)

holds for all time $T\ge 0$ and all $\varvec{d}(t) \in L_2[0,T]$ [25, 33, 34], and $\varvec{h}(\varvec{x})$ is the defined cost for the states. If the storage function is continuously differentiable, take the time derivative of both side of (9), and it follows that

$$\begin{aligned} {\dot{S}} \le s(\varvec{x},\varvec{u},\varvec{d}). \end{aligned}$$

(10)

The dissipative property also implies that the $L_2$-gain of the rigid spacecraft attitude control system is less than or equal to $\gamma$ [25]. This finite-gain $L_2$ stability further suggests that ratio of energy transmission from the disturbance signal to the output signal is upper bounded by the pre-defined disturbance attenuation level. Thus, the $L_2$-gain is regarded as a measure of the robustness of a control system to various kinds of disturbances. Note that the initial state $\varvec{x}_0$ in the dissipation inequality is not necessarily at the equilibrium point.

Consider an attitude control system without actuator misalignments

$$\begin{aligned} \dot{\varvec{x}} = \varvec{f}(\varvec{x}) + \varvec{g}(\varvec{x}) \varvec{u} + \varvec{k}(\varvec{x}) \varvec{d}. \end{aligned}$$

(11)

The HJI equation for the above nonlinear system is given by

$$\begin{aligned} \frac{1}{4} V_x^\top \left[ \frac{1}{\gamma ^2} \varvec{k}(\varvec{x})\varvec{k}^\top (\varvec{x}) - \varvec{g}(\varvec{x})R^{-1}\varvec{g}^\top (\varvec{x})\right] V_x \nonumber \\ +V_x^\top \varvec{f}(\varvec{x}) + \left\| \varvec{h}(\varvec{x})\right\| ^2 = 0, \quad V(\varvec{x}=\varvec{0}) = 0 \end{aligned}$$

(12)

where $V(\varvec{x})$ is the value function of the HJI equation and $V_{\varvec{x}}=\frac{\partial V}{\partial \varvec{x}}$ is the partial derivative with respect to the state. In the remainder of this paper, V is also used as the abbreviation of $V(\varvec{x})$ for convenience.

In this paper, we set $R = \lambda I$ and I is an identity matrix and $\lambda$ is a positive number. Assume that a continuously differentiable solution exists for the HJI equation. Based on the solution $V(\varvec{x})$, the $H_\infty$ optimal controller for the nonlinear system (11) is given by

$$\begin{aligned} \varvec{u}^* = -\frac{1}{2}R^{-1}\varvec{g}^\top (\varvec{x})V_{\varvec{x}}. \end{aligned}$$

(13)

The worst disturbance $\varvec{w}^*$ that the controller $\varvec{u}^*$ is able to handle is described by

$$\begin{aligned} \varvec{w}^* = \frac{1}{2\gamma ^2}\varvec{k}^\top (\varvec{x})V_{\varvec{x}}. \end{aligned}$$

(14)

The existence condition of a continuously differentiable solution $V(\varvec{x})$ to (12) is discussed in terms of the invariant-manifold of the Hamiltonian system in [35]. Note that the solution function $V(\varvec{x})$ is also a storage function for the nonlinear system (11) with supply rate $s(\varvec{x},\varvec{u},\varvec{d}) = -\left\| \varvec{h}(\varvec{x})\right\| ^2 - \left\| \varvec{u}\right\| _{R}^2 + \gamma ^2 \left\| \varvec{d}\right\| ^2$ [33]. However, due to the uncertainty caused by actuator misalignments, the solution function of the HJI equation (with $R_\textrm{r}=R$) cannot directly solves the dissipation inequality for the nonlinear system (6). In the following sections, a nonlinear robust $H_\infty$ controller is designed such that the dissipation inequality holds for the attitude control system (6) under misalignments and disturbances.

3 Nonlinear robust $H_\infty$ attitude control method

3.1 Robust controller design

Based on the solution function $V(\varvec{x})$ of the HJI Eq. (12), the nonlinear robust $H_\infty$ controller for the attitude control system (6) is designed as

$$\begin{aligned} \varvec{u}_\textrm{r} = -R^{-1}\varvec{g}^\top (\varvec{x})V_{\varvec{x}}. \end{aligned}$$

(15)

Let $R_\textrm{r} = \nicefrac {R}{4}$, the dissipation property of the closed-loop attitude control system with actuator misalignments and disturbances is stated as follows.

Theorem 1

Assume that a continuously differentiable solution $V(\varvec{x})$ exists for the HJI Eq. (12), then the closed-loop attitude control system (6) under the controller $\varvec{u}_\textrm{r}$ is dissipative with respect to the supply rate $s(\varvec{x},\varvec{u}_\textrm{r},\varvec{d}) = -\left\| \varvec{h}(\varvec{x})\right\| ^2 - \left\| \varvec{u}_\textrm{r}\right\| _{R_\textrm{r}}^2 + \gamma ^2 \left\| \varvec{d}\right\| ^2$.

Proof

Along the trajectory of the nonlinear system (6), the time derivative of the continuously differentiable solution V is given by

$$\begin{aligned} {\dot{V}}= & {} V_{\varvec{x}}^\top \left[ \varvec{f}(\varvec{x})+\varvec{g}(\varvec{x})\varLambda \varvec{u}_\textrm{r}+\varvec{k}(\varvec{x})\varvec{d}\right] \\= & {} V_{\varvec{x}}^\top \left[ \varvec{f}(\varvec{x})+2\varvec{g}(\varvec{x})\varLambda \varvec{u}^*+\varvec{k}(\varvec{x})\varvec{d}\right] \\= & {} V_{\varvec{x}}^\top \left[ \varvec{f}(\varvec{x})+\varvec{g}(\varvec{x}) \varvec{u}^*+\varvec{k}(\varvec{x})\varvec{d}\right] + V_{\varvec{x}}^\top \varvec{g}(\varvec{x}) (2\varLambda -I) \varvec{u}^* \\= & {} V_{\varvec{x}}^\top \left[ \varvec{f}(\varvec{x})+\varvec{g}(\varvec{x}) \varvec{u}^*\right] + V_{\varvec{x}}^\top \varvec{g}(\varvec{x}) (2\varLambda -I) \varvec{u}^* \\{} & {} +V_{\varvec{x}}^\top \varvec{k}(\varvec{x})\varvec{d} \\= & {} V_{\varvec{x}}^\top \varvec{f}(\varvec{x})-\frac{1}{2} V_{\varvec{x}}^\top \varvec{g}(\varvec{x})R^{-1}\varvec{g}^\top (\varvec{x})V_x + V_{\varvec{x}}^\top \varvec{k}(\varvec{x})\varvec{d} \\{} & {} + V_{\varvec{x}}^\top \varvec{g}(\varvec{x}) (2\varLambda -I) \varvec{u}^* \\= & {} -\left\| \varvec{h}(\varvec{x})\right\| ^2 - \frac{1}{4} V_{\varvec{x}}^\top \varvec{g}(\varvec{x})R^{-1}\varvec{g}^\top (\varvec{x})V_x + V_{\varvec{x}}^\top \varvec{k}(\varvec{x})\varvec{d}\\{} & {} - \frac{1}{4\gamma ^2}V_{\varvec{x}}^\top \varvec{k}(\varvec{x})\varvec{k}^\top (\varvec{x})V_{\varvec{x}} + V_{\varvec{x}}^\top \varvec{g}(\varvec{x}) (2\varLambda -I) \varvec{u}^* \\= & {} -\left\| \varvec{h}(\varvec{x})\right\| ^2 - \frac{1}{4} V_{\varvec{x}}^\top \varvec{g}(\varvec{x})R^{-1}\varvec{g}^\top (\varvec{x})V_x + \gamma ^2 \left\| \varvec{d}\right\| ^2 \\{} & {} - \gamma ^2\left( \frac{1}{4\gamma ^4}V_{\varvec{x}}^\top \varvec{k}(\varvec{x})\varvec{k}^\top (\varvec{x})V_{\varvec{x}} -\frac{1}{\gamma ^2}V_{\varvec{x}}^\top \varvec{k}(\varvec{x})\varvec{d} + \left\| \varvec{d}\right\| ^2 \right) \\{} & {} + V_{\varvec{x}}^\top \varvec{g}(\varvec{x}) (2\varLambda -I) \varvec{u}^* \\= & {} -\left\| \varvec{h}(\varvec{x})\right\| ^2 - \frac{1}{4} V_{\varvec{x}}^\top \varvec{g}(\varvec{x})R^{-1}\varvec{g}^\top (\varvec{x})V_x + \gamma ^2 \left\| \varvec{d}\right\| ^2 \\{} & {} - \gamma ^2\left\| \frac{1}{2\gamma ^2}\varvec{k}^\top (\varvec{x})V_{\varvec{x}} -\varvec{d}\right\| ^2+ V_{\varvec{x}}^\top \varvec{g}(\varvec{x}) (2\varLambda -I) \varvec{u}^* \\= & {} -\left\| \varvec{h}(\varvec{x})\right\| ^2 - \left\| \varvec{u}^*\right\| _R^2 - \gamma ^2\left\| \frac{1}{2\gamma ^2}\varvec{k}^\top (\varvec{x})V_{\varvec{x}} -\varvec{d}\right\| ^2 \\{} & {} + \gamma ^2 \left\| \varvec{d}\right\| ^2+ V_{\varvec{x}}^\top \varvec{g}(\varvec{x}) (2\varLambda -I) \varvec{u}^* \\\le & {} -\left\| \varvec{h}(\varvec{x})\right\| ^2 - \left\| \varvec{u}^*\right\| _R^2 + \gamma ^2 \left\| \varvec{d}\right\| ^2+ V_{\varvec{x}}^\top \varvec{g}(\varvec{x}) (2\varLambda -I) \varvec{u}^* \end{aligned}$$

We firstly consider the positive definiteness of the symmetric matrix ${W} = \varLambda + \varLambda ^\top -I$. The matrix is given by 16.

The sequential principal minors of the matrix W are given as follows.

$$\begin{aligned} {W}_{1} =&2\cos \Delta \alpha _1-1 \end{aligned}$$

(15)

$$\begin{aligned} {W}_{2} =&-\left( \sin \Delta \alpha _1\cos \Delta \beta _1+\sin \Delta \alpha _2\sin \Delta \beta _2 \right) ^2 \nonumber \\ {}&+(2\cos \Delta \alpha _1 -1) (2\cos \Delta \alpha _2 -1) \nonumber \\ \ge&(2\cos \Delta \alpha _1 -1) (2\cos \Delta \alpha _2 -1) -\left( |\sin \Delta \alpha _1|\right. \nonumber \\ {}&\left. +|\sin \Delta \alpha _2|\right) ^2 \end{aligned}$$

(16)

$$\begin{aligned} {W}_{3} =&(2\cos \Delta \alpha _1-1)(2\cos \Delta \alpha _2-1)(2\cos \Delta \alpha _3-1) \nonumber \\ {}&+ 2\left( \sin \Delta \alpha _1\cos \Delta \beta _1 +\sin \Delta \alpha _2\sin \Delta \beta _2\right) \nonumber \\&\times \left( \sin \Delta \alpha _2 \sin \Delta \beta _2 + \sin \Delta \alpha _3 \sin \Delta \beta _3\right) \nonumber \\ {}&\times \left( \sin \Delta \alpha _1\sin \Delta \beta _1 + \sin \Delta \alpha _3\cos \Delta \beta _3\right) \nonumber \\ {}&-(2\cos \Delta \alpha _2-1) \left( \sin \Delta \alpha _1\sin \Delta \beta _1 \right. \nonumber \\ {}&\left. + \sin \Delta \alpha _3\cos \Delta \beta _3\right) ^2-(2\cos \Delta \alpha _1-1) \nonumber \\ {}&\times \left( \sin \Delta \alpha _2\cos \Delta \beta _2 + \sin \Delta \alpha _3\sin \Delta \beta _3\right) ^2\nonumber \\ {}&-(2\cos \Delta \alpha _3-1)\left( \sin \Delta \alpha _1\cos \Delta \beta _1 \right. \nonumber \\ {}&\left. + \sin \Delta \alpha _2\sin \Delta \beta _2\right) ^2 \nonumber \\ \ge&(2\cos \Delta \alpha _1-1)(2\cos \Delta \alpha _2-1)(2\cos \Delta \alpha _3-1) \nonumber \\ {}&- 2\left( |\sin \Delta \alpha _1|+ |\sin \Delta \alpha _2|\right) \left( |\sin \Delta \alpha _2|\right. \nonumber \\ {}&\left. + |\sin \Delta \alpha _3|\right) \left( |\sin \Delta \alpha _1|+ |\sin \Delta \alpha _3|\right) \nonumber \\ {}&-(2\cos \Delta \alpha _1-1) \left( |\sin \Delta \alpha _2|+ |\sin \Delta \alpha _3|\right) ^2\nonumber \\ {}&-(2\cos \Delta \alpha _2-1) \left( |\sin \Delta \alpha _1|+ |\sin \Delta \alpha _3|\right) ^2 \nonumber \\ {}&-(2\cos \Delta \alpha _3-1)\left( |\sin \Delta \alpha _1|+ |\sin \Delta \alpha _2|\right) ^2 \end{aligned}$$

(17)

Based on the condition $|\Delta \alpha _i|\le \nicefrac {\pi }{10}$, it is straightforward to verify that

$$\begin{aligned} {W}_{1}> 0, \quad {W}_{2}> 0, \quad {W}_{3} > 0. \end{aligned}$$

(18)

As shown above, the sequential principal minors of the symmetric matrix W are all positive, so W is positive definite. Note that

$$\begin{aligned} W = \frac{1}{2} \left( 2\varLambda -I + (2\varLambda -I)^{\top } \right) . \end{aligned}$$

(19)

By the positive definiteness of W, for any vector $\varvec{v}\in {\mathbb {R}}^{3}$ and $\varvec{v}\ne \varvec{0}$, it is straightforward to verify that $\varvec{v}^{\top }(2\varLambda -I)\varvec{v}>0$, then $2\varLambda -I$ and $(2\varLambda -I) R^{-1}$ are also positive definite. It then follows that

$$\begin{aligned} \begin{aligned} {\dot{V}} =&-\left\| \varvec{h}(\varvec{x})\right\| ^2 - \left\| \varvec{u}^*\right\| _R^2 + \gamma ^2 \left\| \varvec{d}\right\| ^2+ V_{\varvec{x}}^\top \varvec{g}(\varvec{x}) (2\varLambda -I) \varvec{u}^* \\ =&-\left\| \varvec{h}(\varvec{x})\right\| ^2 - \left\| \varvec{u}^*\right\| _R^2 + \gamma ^2 \left\| \varvec{d}\right\| ^2 \\ {}&- \frac{1}{2} V_{\varvec{x}}^\top \varvec{g}(\varvec{x}) (2\varLambda -I) R^{-1}\varvec{g}^\top (\varvec{x})V_x \\ \le&-\left\| \varvec{h}(\varvec{x})\right\| ^2 - \left\| \varvec{u}^*\right\| _R^2 + \gamma ^2 \left\| \varvec{d}\right\| ^2 \\ =&-\left\| \varvec{h}(\varvec{x})\right\| ^2 - \left\| \varvec{u}_\textrm{r}\right\| _{R_\textrm{r}}^2 + \gamma ^2 \left\| \varvec{d}\right\| ^2 \end{aligned} \end{aligned}$$

The above inequality means that the nonlinear system is dissipative with respective to the defined supply function $s(\varvec{x},\varvec{u}_\textrm{r},\varvec{d})$ [33, 35, 36]. The inequality also implies the finite-gain $L_2$ stability and internal stability of the closed-loop system [35]. $\square$

Note that the nonlinear robust $H_\infty$ controller for the attitude control system is designed based on the solution of the HJI Eq. (12). But the HJI equation is a nonlinear partial differential equation for which an analytical solution seldom exists. Numerical methods for the HJI equation also frequently suffer from heavy computational burden and even the so-called curse of dimensionality.

$$\begin{aligned} W = \left[ \begin{matrix} 2\cos \Delta \alpha _1-1 &{} \sin \Delta \alpha _2 \sin \Delta \beta _2+\sin \Delta \alpha _1 \cos \Delta \beta _1 &{} \sin \Delta \alpha _3 \cos \Delta \beta _3+\sin \Delta \alpha _1 \sin \Delta \beta _1\\ \sin \Delta \alpha _2 \sin \Delta \beta _2+\sin \Delta \alpha _1 \cos \Delta \beta _1 &{} 2\cos \Delta \alpha _2-1 &{} \sin \Delta \alpha _3 \sin \Delta \beta _3+\sin \Delta \alpha _2 \cos \Delta \beta _2\\ \sin \Delta \alpha _3 \cos \Delta \beta _3+\sin \Delta \alpha _1 \sin \Delta \beta _1 &{} \sin \Delta \alpha _3 \sin \Delta \beta _3+\sin \Delta \alpha _2 \cos \Delta \beta _2 &{} 2\cos \Delta \alpha _3-1 \end{matrix}. \right] \end{aligned}$$

(20)

3.2 Successive approximation for the nonlinear HJI equation

Compared with nonlinear PDEs, linear PDEs are more comprehensively investigated and understood. Many numerical methods have also been proposed to solve linear PDEs. Fortunately, the nonlinear HJI equation can be converted to a sequence of linear PDEs based on the successive approximation technique [30, 31, 37]. The successive approximation process is given in Algorithm 1.

Successive Approximation for the HJI Equation

The successive approximation process has a double-loop structure, namely the inner loop and the outer loop. As shown in Algorithm 1, the linear PDE

$$\begin{aligned} \left( V_x^{[i,j+1]}\right) ^\top \left[ \varvec{f}(\varvec{x}) + \varvec{g}(\varvec{x})\varvec{u}^{[i]}+ \varvec{k}(\varvec{x}) \varvec{w}^{[i,j]} \right] \nonumber \\ + \left\| \varvec{h}(\varvec{x})\right\| ^2+ \left\| \varvec{u}^{[i]}\right\| _{R}^2 - \gamma ^2 \left\| \varvec{w}^{[i,j]}\right\| ^2= 0 \end{aligned}$$

(21)

is recursively solved to update the control and disturbance strategies. These two loops of the successive approximation process can also be regarded as the strategy improvement iterations of a two-player zero-sum game [31]. In the inner loop, one player attempts to find the worst disturbance that the current controller is able to handle. Whereas in the outer loop the other player tries to optimize the performance index under the updated disturbance. The solving process continues until both strategies do not change anymore. The convergence of the successive approximation method has been investigated and proved in [30, 31, 37].

Specifically, to implement the iteration process, an initial stabilizing controller $\varvec{u}_\textrm{s}$ for the nominal spacecraft attitude control system $\dot{\varvec{x}} = \varvec{f}(\varvec{x}) + \varvec{g}(\varvec{x})\varvec{u}$ is needed. Methods like backstepping can be employed to generate a feasible controller $\varvec{u}_\textrm{s}$ for the considered nominal attitude control system.

3.3 Successive galerkin approximation for nonlinear HJI equation

The Galerkin method is an accurate approach to solve linear PDEs. It belongs to the weighted residual method and the resultant equation is in the form of

$$\begin{aligned} \int _{D} r(\varvec{x}) \ell _k(\varvec{x}) \textrm{d} \varvec{x}= 0, \quad k = 1,2,\dots ,N. \end{aligned}$$

(22)

where D is the solution domain; $\ell _k(\varvec{x})$ is the multivariate test function; $r(\varvec{x})$ is the residual of the linear PDE which is given by

$$\begin{aligned} \begin{aligned} r(\varvec{x}) =&\left( V^{[i,j]}(\varvec{x}) \right) ^\top \left[ \varvec{f}(\varvec{x}) + \varvec{g}(\varvec{x})\varvec{u}^{[i]}+ \varvec{k}(\varvec{x}) \varvec{w}^{[i,j]} \right] \\&+ \Vert \varvec{h}(\varvec{x})\Vert ^2 + \Vert \varvec{u}^{[i]}\Vert _{R}^2 - \gamma ^2 \Vert \varvec{w}^{[i,j]}\Vert ^2. \end{aligned} \end{aligned}$$

In the Galerkin method, the basis functions are identical to the test functions [38]. The solution function of the linear PDE (21) is approximated by

$$\begin{aligned} V^{[i,j]}(\varvec{x}) \approx \sum _{k=1}^{N} {c}_{k}^{[i,j]} {\ell }_k(\varvec{x}). \end{aligned}$$

(23)

Then the residual in the Galerkin method can be explicitly given by

$$\begin{aligned} \begin{aligned} r(\varvec{x}) =&\left[ \varvec{f}(\varvec{x}) + \varvec{g}(\varvec{x})\varvec{u}^{[i]}+ \varvec{k}(\varvec{x}) \varvec{\omega }^{[i,j]} \right] ^\top {\mathcal {J}}^\top (\varvec{x})\varvec{c}^{[i,j+1]}\\&+ \Vert \varvec{h}(\varvec{x})\Vert ^2 +\Vert \varvec{u}^{[i]}\Vert _{R}^2 - \gamma ^2 \Vert \varvec{\omega }^{[i,j]}\Vert ^2. \end{aligned} \end{aligned}$$

where ${\mathcal {J}}(\varvec{x})$ is the Jacobian matrix of the vector $\varvec{\ell }(\varvec{x})$, and $\varvec{c}^{[i,j]}$ and $\varvec{\ell }(\varvec{x})$ are vectors consist of ${c}_{k}^{[i,j]}$ and ${\ell }_k(\varvec{x})$, respectively. Substitute the residual $r(\varvec{x})$ into the weighted residual Eq. (22), then it follows that

$$\begin{aligned} \begin{aligned}&\int _{D} \ell _k(\varvec{x}) \left\{ \left[ \varvec{f}(\varvec{x}) + \varvec{g}(\varvec{x})\varvec{u}^{[i]}+ \varvec{k}(\varvec{x}) \varvec{w}^{[i,j]} \right] ^\top {\mathcal {J}}^\top (\varvec{x}) \right. \\&\left. \times \varvec{c}^{[i,j]}+ \Vert \varvec{h}(\varvec{x})\Vert ^2 + \Vert \varvec{u}^{[i]}\Vert _{R}^2 - \gamma ^2 \Vert \varvec{w}^{[i,j]}\Vert ^2\right\} \textrm{d} \varvec{x}= 0. \end{aligned} \end{aligned}$$

Rearrange the equation and we arrive at

$$\begin{aligned} \begin{aligned}&\int _{D} \ell _k(\varvec{x}) \left[ \varvec{f}(\varvec{x}) + \varvec{g}(\varvec{x})\varvec{u}^{[i]}+ \varvec{k}(\varvec{x}) \varvec{w}^{[i,j]} \right] ^\top {\mathcal {J}}^\top (\varvec{x}) \textrm{d} \varvec{x} \cdot \varvec{c}^{[i,j]}\\&= \int _{D} \left( - \Vert \varvec{h}(\varvec{x})\Vert ^2 - \Vert \varvec{u}^{[i]}\Vert _{R}^2 + \gamma ^2 \Vert \varvec{w}^{[i,j]}\Vert ^2\right) \ell _k(\varvec{x})\textrm{d} \varvec{x}. \end{aligned} \end{aligned}$$

The Galerkin method transforms the linearized HJI PDE into a system of linear equations, in which the unknown variable vector is $\varvec{c}^{[i,j]}$. As shown above, to implement the Galerkin method, one should choose a suitable multivariate basis function set $\{\ell _k(\varvec{x})\}$ and design a multi-dimensional quadrature rule to calculate the integration on D for both sides of the resultant equation. A successive Galerkin approximation method is designed in [30, 31], and the Galerkin method is employed to solve the linear PDE. But the multidimensional basis function set is manually chosen and the accuracy of the solution relies heavily on design experiences. Besides, multidimensional integrals in the Galerkin method are computed using tensor-product rules, which results in an exponentially growth of the computational complexity. So the successive Galerkin approximation method still suffers from heavy computational burden and even the curse of dimensionality.

3.4 Nested sparse Chebyshev basis function and Kronrod–Patterson quadrature rule

To reduce the computational cost in solving nonlinear HJI equations, nested sparse grid-based multivariate Chebyshev basis functions and Kronrod–Patterson quadrature rules are employed. The sparse grid method dates back to the Smolyak’s rule proposed in 1960 s [39], which provides a general framework for both interpolation and integration problems [40,41,42]. Given the univariate interpolation or quadrature rule $U_{i}$, a multidimensional rule can be constructed using [43]

$$\begin{aligned}{} & {} M = \sum _{q+1\le |{\varvec{i}}|\le q+d}(-1)^{q+d-|\varvec{i}|}\nonumber \\ {}{} & {} \qquad C_{q+d-|\varvec{i}|}^{d-1} U_{i_1}\otimes U_{i_2}\otimes \cdots \otimes U_{i_d}. \end{aligned}$$

(24)

where q and d are the maximum level of accuracy and the number of variables, respectively. Besides, $\varvec{i}=[i_1,i_2,\dots ,i_d]^\top$ and $|\cdot |$ represents the $l_1$ norm. The sparse grid method is able to achieve a high computational accuracy level. Instead of employing a completely tensor-product formula, the Smolyak’s rule in (24) only uses a selected and small subset of possible combinations, thus the computational cost is significantly reduced.

In this paper, the Chebyshev polynomials are chosen as the basis functions, and they are given by [44]

$$\begin{aligned}&\ell _0(x) = 1 \\&\ell _1(x) = x \\&(n+1)\ell _{n+1}(x) = (2n+1)x\ell _{n}(x) \\&- n \ell _{n-1}(x), \ n \ge 2. \end{aligned}$$

Specifically, nested sparse basis functions are used to further improve the computational efficiency. The sequence of nested univariate basis function sets are given by

$$\begin{aligned} L_i = \left\{ \ell _0(x), \ell _1(x), \ell _2(x), \dots , \ell _{2^{i}}(x)\right\} , \quad i >1 \end{aligned}$$

(25)

where $i\in {\mathbb {Z}}^+$ represents the level of accuracy, and $L_1 =\left\{ \ell _0(x)\right\}$. The nested property means that the set with lower accuracy levels are included in sets with a higher level. The nested sparse Chebyshev basis function-based approximation for a multivariate function $f(\varvec{x})$ is given by

$$\begin{aligned} {{f}}(\varvec{x})&\approx \sum _{q+1\le |{\varvec{i}}|\le q+d} (-1)^{q+d-|\varvec{i}|} C_{q+d-|\varvec{i}|}^{d-1} L_{i_1}(x_1) \nonumber \\&\quad \otimes L_{i_2}(x_2)\otimes \cdots \otimes L_{i_d}(x_d). \end{aligned}$$

(26)

The combinations of the basis functions are calculated using

$$\begin{aligned}&L_{i_1}(x_1)\otimes L_{i_2}(x_2)\otimes \cdots \otimes L_{i_d}(x_d) \nonumber \\&\quad = \sum _{i_1=1}^{N_{L_1}} \sum _{i_2=1}^{N_{L_2}} \cdots \sum _{i_d=1}^{N_{L_d}} c_{i_1i_2\dots i_d} \cdot \ell _{i_1}(x_1)\ell _{i_2}(x_2)\dots \ell _{i_d}(x_d) \end{aligned}$$

(27)

where $c_{i_1i_2\dots i_d}$ is the coefficient to be determined. Since the basis function sets are nested, a sequence of disjointed basis function sets can be defined as

$$\begin{aligned} {\hat{L}}_{i} = {L}_{i} - {L}_{i-1}, \quad i >1 \end{aligned}$$

(28)

and ${\hat{L}}_{1}={L}_{1}$. The multivariate sparse Chebyshev basis function set can also be given by [43]

$$\begin{aligned} {\mathcal {L}} = \bigcup _{d \le |\varvec{i}|\le q+d} {\hat{L}}_{i_1} (x_1)\otimes {\hat{L}}_{i_2}(x_2)\otimes \cdots \otimes {\hat{L}}_{i_d}(x_d). \end{aligned}$$

(29)

Similarly, Smolyak’s quadrature rule is used in this paper to calculate the multidimensional integrals. Specifically, a multidimensional quadrature rule is constructed using weighted combinations of the univariate rules, namely

$$\begin{aligned} I({{f}}(\varvec{x}))&= \sum _{q+1\le |{\varvec{i}}|\le q+d}(-1)^{q+d-|\varvec{i}|} C_{q+d-|\varvec{i}|}^{d-1} \nonumber \\&\quad \left[ I_{i_1}\otimes I_{i_2}\otimes \cdots \otimes I_{i_d} \right] (f). \end{aligned}$$

(30)

The combinations are further calculated using

$$\begin{aligned}&\left[ I_{i_1}\otimes I_{i_2}\otimes \cdots \otimes I_{i_d} \right] (f) \nonumber \\&\quad = \sum _{x_1\in P_{i_1}} \sum _{x_2\in P_{i_2}} \cdots \sum _{x_d \in P_{i_d}} c_{1}c_{2}\dots c_{d} \nonumber \\&\qquad \cdot f(x_1,x_2,\dots ,x_d) \end{aligned}$$

(31)

where $c_i$ is the corresponding weight for the quadrature point $x_i$.

Fig. 2

2d and 3d examples of sparse Kronrod–Patterson quadrature points

In the construction of the multidimensional rules, the Kronrod–Patterson quadrature formula is chosen as the univariate rule. The Gauss–Kronrod quadrature formula is designed by inserting Kronrod points into the Gauss quadrature nodes [45, 46]. In univariate cases, an n-point Gauss quadrature rule can reach an accuracy level of $2n-1$. It means that the n-point rule is exact for any polynomial with degree less than or equal to $2n-1$ but cannot guarantee the exactness for polynomials with degree larger than $2n-1$. Whereas in the Gauss–Kronrod quadrature formula, $n+1$ Kronrod points are generated by solving for the zeros of the Stieltjes polynomials, and then they are inserted into the n-point Gauss quadrature rule. The combination of the $2n+1$ quadrature points leads to a quadrature formula with an accuracy level of $3n+1$ [46]. The computational cost is further reduced by using a nested construction strategy, since the quadrature points at different accuracy levels are reused and less function evaluations are needed [47]. Interested readers are referred to [47] for more details of the sparse Kronrod–Patterson quadrature formula. Figure 2 illustrates 2d and 3d examples for the sparse Kronrod–Patterson quadrature points.

3.5 Sparse successive Chebyshev–Galerkin method

The approximate solution to (21) is a weighted sum of the multivariate nested sparse Chebyshev basis functions. Thus the solution function of the linear PDE (21) is approximated by

$$\begin{aligned} V^{[i,j]}(\varvec{x}) \approx \left( \varvec{c}^{[i,j]}\right) ^\top \varvec{\ell }(\varvec{x}) \end{aligned}$$

(32)

where $\varvec{c}^{[i,j+1]}$ is the weight vector to be determined and $\varvec{\ell }(\varvec{x})$ is the vector consists of the sparse Chebyshev basis functions. To simplify the notation, the weighted residual equation for the linearized PDE can be represented as

$$\begin{aligned} A^{[i,j]}\varvec{c}^{[i,j]} = \varvec{b}^{[i,j]} \end{aligned}$$

(33)

where $A^{[i,j]}$ and $\varvec{b}^{[i,j]}$ are defined by

$$\begin{aligned} A^{[k]} = \left[ \begin{matrix} \int _{D} \ell _1(\varvec{x}) \left[ \varvec{f}(\varvec{x}) + \varvec{g}(\varvec{x})\varvec{u}^{[i]}+ \varvec{k}(\varvec{x}) \varvec{\omega }^{[i,j]} \right] ^\top {\mathcal {J}}^\top (\varvec{x}) \textrm{d} \varvec{x} \\ \int _{D} \ell _2(\varvec{x}) \left[ \varvec{f}(\varvec{x}) + \varvec{g}(\varvec{x})\varvec{u}^{[i]}+ \varvec{k}(\varvec{x}) \varvec{\omega }^{[i,j]} \right] ^\top {\mathcal {J}}^\top (\varvec{x}) \textrm{d} \varvec{x} \\ \vdots \\ \int _{D} \ell _N(\varvec{x}) \left[ \varvec{f}(\varvec{x}) + \varvec{g}(\varvec{x})\varvec{u}^{[i]}+ \varvec{k}(\varvec{x}) \varvec{\omega }^{[i,j]} \right] ^\top {\mathcal {J}}^\top (\varvec{x}) \textrm{d} \varvec{x} \end{matrix} \right] \nonumber \\ \end{aligned}$$

(34)

$$\begin{aligned} \varvec{b}^{[k]} = \left[ \begin{matrix} \int _{D} \left( - \left\| \varvec{h}(\varvec{x})\right\| ^2 - \left\| \varvec{u}^{[i]}\right\| _{R}^2 + \gamma ^2 \left\| \varvec{\omega }^{[i,j]}\right\| ^2\right) \ell _1(\varvec{x})\textrm{d} \varvec{x} \\ \int _{D} \left( - \left\| \varvec{h}(\varvec{x})\right\| ^2 - \left\| \varvec{u}^{[i]}\right\| _{R}^2 + \gamma ^2 \left\| \varvec{\omega }^{[i,j]}\right\| ^2\right) \ell _2(\varvec{x})\textrm{d} \varvec{x} \\ \vdots \\ \int _{D} \left( - \left\| \varvec{h}(\varvec{x})\right\| ^2 - \left\| \varvec{u}^{[i]}\right\| _{R}^2 + \gamma ^2 \left\| \varvec{\omega }^{[i,j]}\right\| ^2\right) \ell _N(\varvec{x})\textrm{d} \varvec{x} \end{matrix} \right] .\nonumber \\ \end{aligned}$$

(35)

For the linearized PDE (21), the boundary condition at the state $\varvec{x}=\varvec{0}$ is

$$\begin{aligned} V^{[i,j]}(\varvec{x}=\varvec{0}) = 0. \end{aligned}$$

(36)

By virtue of (32), it can also be expressed as

$$\begin{aligned} \left( \varvec{c}^{[i,j]}\right) ^\top \varvec{\ell }(\varvec{0}) =0. \end{aligned}$$

(37)

Taking advantage of the designed sparse successive Chebyshev–Galerkin method, the linearized HJI PDE is now transformed into a sequence of systems of linear Eqs. (33) under the constraint (37). To efficiently find an approximated solution, the system of linear equations is converted to the constrained quadratic programming problem

$$\begin{aligned} \begin{matrix} \quad \min _{\varvec{c}^{[i,j]}} \ {} &{} \left\| A^{[i,j]}\varvec{c}^{[i,j+1]} - \varvec{b}^{[i,j]} \right\| ^2 \quad \quad \\ \mathrm {subject\ to}\ {} &{} \left( \varvec{c}^{[i,j]}\right) ^\top \varvec{\ell }(\varvec{0}) =0. \end{matrix} \end{aligned}$$

(38)

This resultant quadratic programming problem can be efficiently solved, and many off-the-shelf numerical solvers are available, such as CVX [48]. During the successive approximation process, given the coefficients the strategies in Algorithm 1 are analytically updated according to

$$\begin{aligned} \varvec{w}^{[i,j+1]}(\varvec{x})&= \frac{1}{2 \gamma ^2} \varvec{k}^\top (\varvec{x}) {\mathcal {J}}(\varvec{x}) \varvec{c}^{[i,j]}, \end{aligned}$$

(39)

$$\begin{aligned} \varvec{u}^{[i+1]}(\varvec{x})&= -\frac{1}{2}R^{-1} \varvec{g}^\top (\varvec{x}) {\mathcal {J}}(\varvec{x}) \varvec{c}^{[i,\infty ]}. \end{aligned}$$

(40)

The solving process can be terminated when the relative error between two consecutive iterations is less than a specified criterion. One can also set the maximum numbers of iterations for both the inner and outer loops. The computational time complexity of the designed sparse successive Chebyshev–Galerkin method is also analyzed.

Proposition 1

Given the maximum level of approximation q, the computational time complexity of the proposed sparse successive Chebyshev–Galerkin method grows polynomially with the dimension.

Proof

Given the maximum level of approximation q, the number of nested sparse Chebyshev basis functions is given by

$$\begin{aligned} N_{\textrm{basis}} =\,&\textrm{Card} \left\{ \bigcup _{d \le |\varvec{i}|\le q+d} {\hat{L}}_{i_1} (x_1)\otimes {\hat{L}}_{i_2}(x_2)\otimes \cdots \otimes {\hat{L}}_{i_d}(x_d) \right\} \\ \le&\max _{d \le |\varvec{i}|\le q+d} \left( \textrm{Card} \left\{ {\hat{L}}_{i_1} (x_1)\otimes {\hat{L}}_{i_2}(x_2)\otimes \cdots \otimes {\hat{L}}_{i_d}(x_d) \right\} \right) \\&\cdot \textrm{Card} \left\{ d \le |\varvec{i}|\le q+d\right\} \\ =&\max _{d \le |\varvec{i}|\le q+d} \left( \prod _{\tau =1}^{d} 2^{i_\tau -1}\right) \cdot \textrm{Card} \left\{ d \le |\varvec{i}|\le q+d\right\} \\ =&\max _{d \le |\varvec{i}|\le q+d} \left( 2^{|\varvec{i}|-d}\right) \cdot \textrm{Card} \left\{ d \le |\varvec{i}|\le q+d\right\} \\ \le&2^{q} \cdot \textrm{Card} \left\{ d \le |\varvec{i}|\le q+d\right\} \end{aligned}$$

Here the operator $\textrm{Card}\{\cdot \}$ returns the number of elements in the sets. Note that for any $i_\tau$, we have $\textrm{Card}\left\{ {\hat{L}}_{i_\tau } \right\} \le 2^{i_\tau -1}$. Based on the property of combination number $\textrm{C}_{n}^{m} = \textrm{C}_{n-1}^{m-1} + \textrm{C}_{n-1}^{m}$, the cardinality of the index set is given by

$$\begin{aligned} \begin{aligned} N_\textrm{index} = \,&\textrm{Card} \left\{ d \le |\varvec{i}|\le q+d\right\} \\ = \,&\textrm{C}_{d-1}^{d-1} + \textrm{C}_{d}^{d-1} + \textrm{C}_{d+1}^{d-1} + \cdots \\ {}&\qquad + \textrm{C}_{q+d-2}^{d-1} + \textrm{C}_{q+d-1}^{d-1} \\ = \,&\textrm{C}_{d}^{d} + \textrm{C}_{d}^{d-1} + \textrm{C}_{d+1}^{d-1} + \cdots \\ {}&\qquad + \textrm{C}_{q+d-2}^{d-1} + \textrm{C}_{q+d-1}^{d-1} \\ = \,&\textrm{C}_{d+1}^{d} + \textrm{C}_{d+1}^{d-1} + \cdots + \textrm{C}_{q+d-2}^{d-1} + \textrm{C}_{q+d-1}^{d-1} \\ = \,&\textrm{C}_{d+2}^{d} + \cdots + \textrm{C}_{q+d-2}^{d-1} + \textrm{C}_{q+d-1}^{d-1} \\ = \,&\textrm{C}_{q+d-1}^{d} + \textrm{C}_{q+d-1}^{d-1} \\ = \,&\textrm{C}_{q+d}^{d} \end{aligned} \end{aligned}$$

Then it follows that

$$\begin{aligned} N_{\textrm{basis}} \le 2^{q} \textrm{C}_{q+d}^{d}. \end{aligned}$$

(41)

Given the maximum level of approximation, the sparse grid Kronrod–Patterson quadrature formula also has a polynomially growing number of quadrature points [47]. Then it is straightforward to verify that the computational cost in the deduction of the quadratic programming problem grows polynomially with the dimension. In fact, the resultant quadratic programming problem can also be solved in polynomial time based on numerical schemes like the interior point algorithm [49]. Then it can be summarized that the computational time complexity of the designed sparse successive Chebyshev–Galerkin method grows polynomially with the system dimension. $\square$

4 Numerical simulations

Simulations are implemented on a laptop with 4.2 GHz CPU and 16 GB RAM to verify the effectiveness of the designed computational method and the proposed robust $H_\infty$ attitude controller. The inertia matrix of the rigid spacecraft is given by $J=\textrm{diag}\left( [2~\mathrm {kg/m^2}, 4~\mathrm {kg/m^2}, 2.5~\mathrm {kg/m^2}]\right)$, and the products of inertia are very small so that they can be neglected. Three different cases are considered, and the angles of deviation due to actuator misalignments are given by

$$\begin{aligned}&\textrm{case 1}: \begin{matrix} \Delta \alpha _1 = \frac{\pi }{10}, &{}\Delta \alpha _2 = \frac{-\pi }{10}, &{}\Delta \alpha _3 = \frac{\pi }{10},\\ \Delta \beta _1 = \frac{-\pi }{2}, &{}\Delta \beta _2 = \frac{\pi }{2}, &{}\Delta \beta _3 = \frac{-\pi }{2}. \end{matrix} \end{aligned}$$

(42)

$$\begin{aligned}&\textrm{case 2}: \begin{matrix} \Delta \alpha _1 = \frac{-\pi }{10}, &{}\Delta \alpha _2 = 0, &{}\Delta \alpha _3 = \frac{-\pi }{10},\\ \Delta \beta _1 = 0, &{}\Delta \beta _2 = \frac{-\pi }{2}, &{}\Delta \beta _3 = 0. \end{matrix} \end{aligned}$$

(43)

$$\begin{aligned}&\textrm{case 3}: \begin{matrix} \Delta \alpha _1 = 0, &{}\Delta \alpha _2 = \frac{\pi }{10}, &{}\Delta \alpha _3 = 0,\\ \Delta \beta _1 = \frac{\pi }{2}, &{}\Delta \beta _2 = 0, &{}\Delta \beta _3 = \frac{\pi }{2}. \end{matrix} \end{aligned}$$

(44)

4.1 Sparse successive Chebyshev–Galerkin approximation of the HJI equation

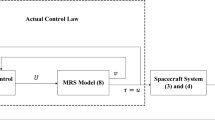
The designed sparse successive Chebyshev–Galerkin method is firstly implemented to solve nonlinear HJI Eq. (12), and the conventional successive Galerkin approximation method in [30, 31] is also incorporated for comparison. In the HJI equation, $\left\| \varvec{h}(\varvec{x})\right\| ^2=\varvec{x}^\top Q \varvec{x}$ with $Q=I$ and $R=0.5 I$. The expected disturbance attenuation level is set to $\gamma =3$. The accuracy level of the sparse basis function is chosen as $q=3$, and the accuracy level of the nested sparse Kronrod–Patterson quadrature rule is chosen as $q=7$. An initial stabilizing controller should also be chosen to initialize the solving process, and it is described by

$$\begin{aligned} \varvec{u}_\textrm{s} =\left[ \begin{array}{llllll} -2 &{} 0 &{} 0 &{} -1 &{} 0 &{} 0 \\ 0 &{} -2 &{} 0 &{} 0 &{} -1 &{} 0 \\ 0 &{} 0 &{} -2 &{} 0 &{} 0 &{} -1 \end{array}\right] \left[ \begin{array}{ll} \varvec{\rho } \\ \varvec{\omega } \end{array}\right] . \end{aligned}$$

(45)

It should be noted that, as shown in Algorithm 1, this initial controller is designed for the nominal spacecraft attitude control system. The considered solution domain is $\varvec{x} \in [-0.5,0.5]^6$. In the solving process, 7 outer loop iterations are conducted, and 7 inner loop iterations are implemented in each outer loop. After the solving process is finished, 100 points are sampled from the solution domain to evaluate the relative errors between the iterations. Specifically, the relative error between two consecutive iterations is calculated using

$$\begin{aligned} \delta _{\textrm{err}} = \frac{\sqrt{\sum _{i=1}^{N_s}\left( {\hat{V}}_\textrm{c}(\varvec{s}_i) - {\hat{V}}_\textrm{p}(\varvec{s}_i)\right) ^2}}{\sqrt{\sum _{i=1}^{N_s}\left( {\hat{V}}_\textrm{p}(\varvec{s}_i)\right) ^2}} \end{aligned}$$

(46)

where ${\hat{V}}_\textrm{c}$ and ${\hat{V}}_\textrm{p}$ are the solution functions in current and previous iterations, respectively. Besides, $\varvec{s}_i$ is the sampling points and $N_s$ is the total number of sampling points.

Fig. 3

Convergence rate, slice of the solution function, and slice of the error function

For a general nonlinear system, the conventional successive Galerkin approximation method is plagued by a significant computational burden associated with the selection of basis functions and calculation of multidimensional integrals. The manual selection of basis functions, which is commonly used, is a time-consuming process that greatly depends on design experience and can significantly impact computational results. To allow for a fair comparison, the basis functions for the conventional successive Galerkin approximation method are chosen to be the same as those used in the proposed sparse successive Chebyshev–Galerkin method.

In the simulations, 85 basis functions are employed by both methods. The same iteration process is carried out for the proposed sparse successive Chebyshev–Galerkin method and the conventional successive Galerkin approximation method, and denote the resultant solution functions for them as ${\hat{V}}^{[i,j]}$ and ${\tilde{V}}^{[i,j]}$, respectively. The proposed sparse successive Chebyshev–Galerkin method utilizes 4, 161 sparse grid quadrature points for multidimensional integration, whereas the conventional successive Galerkin approximation method requires 117, 649 tensor product Gauss-Legendre quadrature points for the same level of accuracy.

In each outer loop iteration, a sequence of disturbance update operations are implemented. The solution functions after the sequences of disturbance updates, i.e., ${\hat{V}}^{[i,7]}$ and ${\tilde{V}}^{[i,7]}$ ($i=1,2,\dots ,7$), are recorded. The relative errors between the outer loop iterations are given in Fig. 3a. It can be seen that the solution functions converge during the iterations, which is in good agreement with the theoretical analysis in [30, 37]. As illustrated in Fig. 3a, both methods exhibit a fast convergence rate and relative error levels of $10^{-8}$ are achieved after the iterations. To visualize the iterations, the $x_1-x_4$ slices of the solution functions ${\hat{V}}^{[1,7]}$ and ${\hat{V}}^{[7,7]}$ are shown in Fig. 3b. It can be observed from the figure that the solution function decreases significantly, which also demonstrates the effectiveness of the designed sparse successive Chebyshev–Galerkin method. The maximum error between the value function surfaces of ${\hat{V}}^{[7,7]}$ and ${\tilde{V}}^{[7,7]}$, as shown in Fig. 3c, is less than $7.0\times 10^{-4}$, indicating that the proposed sparse successive Chebyshev–Galerkin method achieves a performance that is very close to that of the conventional successive Galerkin approximation method.

The computational performance of the sparse successive Chebyshev–Galerkin method and the conventional successive Galerkin approximation method is also evaluated, yielding computational time durations of 50.89 seconds and 910.06 seconds, respectively. These results demonstrate the computational efficiency of the proposed numerical approach for solving the HJI equation. The superiority of the sparse successive Chebyshev–Galerkin method over the conventional successive Galerkin approximation method can be attributed to the reduced number of quadrature points utilized in the proposed method, since the proposed method employs only $3.54\%$ of the quadrature points required by the conventional successive Galerkin approximation method (4,161 vs. 117,649).

To assess the viability of the proposed approach in real-world applications, the proposed robust $H_\infty$ controller is calculated on 1,000 randomly sampled states from the solution domain and the computational time is recorded. The results indicate that, given the solution function ${\hat{V}}^{[7,7]}$, the calculation of the robust $H_\infty$ controller requires an average computational time of $3.78\times 10^{-5}$ second. These results suggest that the proposed robust $H_\infty$ controller may have potential applications in resource-constrained systems, such as nano-satellites.

4.2 Comparisons with the initial stabilizing controller

Fig. 4

Cayley-Rodrigues parameters of the robust $H_\infty$ controller and the initial controller

Fig. 5

Angular velocities of the robust $H_\infty$ controller and the initial controller

Fig. 6

Control torques of the robust $H_\infty$ controller and the initial controller

To further verify the effectiveness of the designed sparse successive Chebyshev–Galerkin method and the proposed robust $H_\infty$ controller, attitude control simulations are conducted under actuator misalignments and disturbances. Note that the solution function of the HJI Eq. (12) is solved offline, then the coefficients in (38) is obtained. The solution function and the robust controller can both analytically constructed based on the coefficients and corresponding basis functions. In the numerical experiments, the initial state is $\varvec{x}(t=0) = [0.10,-0.10,-0.05,0.05,-0.05,0.05]^\top$, and the simulation time horizon is $t\in \left[ 0 \sec , 50 \sec \right]$. The considered disturbance is given by

$$\begin{aligned} \varvec{d}(\varvec{x}) = \left[ \begin{matrix} 0.5\sqrt{\rho _1^2+\rho _2^2}\\ \frac{\sqrt{6}}{2}\cos (\rho _3)\sin (\omega _2)\\ \sqrt{\omega _1^2+\omega _2^2+\omega _3^2} \end{matrix}\right] . \end{aligned}$$

(47)

The performance of the initial stabilizing controller (45) is also evaluated and compared with the proposed controller under the 3 different configurations of misalignment angles (42,43,44), and numerical results are illustrated in Figs. 4, 5, 6.

Fig. 7

Cayley-Rodrigues parameters of the robust $H_\infty$ controller and prescribed performance controller

Fig. 8

Angular velocities of the robust $H_\infty$ controller and the prescribed performance controller

Fig. 9

Control torques of the robust $H_\infty$ controller and the prescribed performance controller

Fig. 10

States and controls of the robust $H_\infty$ controller under mixed disturbance

It is clear from the figures that the proposed robust $H_\infty$ controller successfully stabilizes the attitude control system under different settings of actuator misalignments. Whereas the states of the attitude control system diverge under the initial controller $\varvec{u}_\textrm{s}$. The robust $H_\infty$ controller is calculated based on the initial controller, but different performance is observed in the simulation, which demonstrates the effectiveness of the proposed control scheme. For the trajectories under the proposed robust $H_\infty$ controller, it is calculated that the values of $\int _{0}^{T} (\left\| \varvec{h}(t)\right\| ^2 + \left\| \varvec{u}(t)\right\| _R^2) \textrm{d}t + {\hat{V}}(\varvec{x}_T)$ in all 3 simulation cases are 0.097454, 0.100909, and 0.108900. Whereas the values of $\gamma ^2\int _{0}^{T} \left\| \varvec{w}(t)\right\| ^2 \textrm{d}t + {\hat{V}}(\varvec{x}_0)$ are 0.392765, 0.393416, and 0.402752. So the dissipation inequality (9) is satisfied with the pre-defined $L_2$-gain $\gamma =3$ for all 3 different settings. These results also verify the correctness of the obtained solution function ${\hat{V}}(\varvec{x})$. Besides, different from the initial stabilizing controller of which the trajectories differ from one another, it is observed from the figures that the robust $H_\infty$ controller achieves similar performance under different misalignment configurations, which further demonstrate the robustness of the designed controller.

4.3 Comparisons with the prescribed performance controller

The prescribed performance control (PPC) approach is widely recognized for its ability to attain superior transient performance, and thus it is also comparatively analyzed with the proposed robust $H_\infty$ controller. The prescribed performance controller is structured to ensure the transient performance of the kinematic subsystem using the backstepping technique. Numerical simulations are carried out for the attitude control systems, both with and without actuator misalignments and disturbances, the results of which are presented in Figs. 7, 8 and 9. The misalignment angles in (42) are used in the simulations.

It is observed that the attitude control system is stabilized in all simulations. For the simulations without actuator misalignments and disturbances, both the prescribed performance controller and the robust $H_\infty$ controller produce comparable performance. However, in experiments with actuator misalignments and disturbance, the state trajectories under the prescribed performance controller show increased overshot and an obviously slower convergence rate compared to the simulation without misalignments and disturbances, whereas the robust $H_\infty$ attitude controller maintains its good performance. These simulation results demonstrate the superior performance of the designed robust $H_\infty$ attitude controller.

The performance of the proposed controller is also evaluated under stochastic disturbances. The considered stochastic disturbance is a random process sampled from the multivariate uniform distribution $\varvec{d}_{\textrm{s}} \sim U(-0.1,0.1)^3$. The components of the stochastic disturbance are independent random variables with marginal distribution $U(-0.1,0.1)$. They are added to the disturbance (47) during the time period $t\in \left[ 0 \sec , 30 \sec \right]$. The rest of the settings are the same as the simulations with disturbance (47). Numerical results are given in Fig. 10. It is clear to see that the attitude control system is again successively stabilized, which shows the robustness of the proposed controller under complex disturbances. Besides, it is calculated that $\int _{0}^{T} (\left\| \varvec{h}(t)\right\| ^2 + \left\| \varvec{u}(t)\right\| _{R_\textrm{r}}^2) \textrm{d}t + {\hat{V}}(\varvec{x}_T) =0.099275$ and $\gamma ^2\int _{0}^{T} \left\| \varvec{w}(t)\right\| ^2 \textrm{d}t + {\hat{V}}(\varvec{x}_0) = 0.414893$. Then it is straightforward to verify that the disturbance attenuation level is also guaranteed to be less than the predefined value.

4.4 Comparisons of the robust $H_\infty$ attitude controller and IOC-based robust controller

Fig. 11

Cayley-Rodrigues parameters of the robust $H_\infty$ controller and IOC-based robust controller

Fig. 12

Angular velocities of the robust $H_\infty$ controller and IOC-based robust controller

Fig. 13

Control torques of the robust $H_\infty$ controller and IOC-based robust controller

An inverse optimal control (IOC)-based robust controller is designed in [18] for attitude control problems under actuator misalignments and disturbances. To further evaluate the performance of the proposed robust $H_\infty$ controller, the IOC-based robust controller in [18] is also incorporated in the numerical comparison. In this simulation, the initial state is chosen as the equilibrium point in order to compare the disturbance attenuation levels of the two controllers. The misalignment angles are also described by (42), whereas the time-varying disturbance is considered and it is given by

$$\begin{aligned} \varvec{d}(\varvec{x},t) =\frac{e^{-\frac{t}{10}}}{5} \left[ \begin{matrix} -3\sqrt{\rho _1^2+\rho _2^2}-2\sin (\rho _1)\\ \sqrt{2}\cos (\rho _3)\cos (\omega _2)+2\sin (\rho _3) \\ -\sqrt{2}\cos (\omega _1)\cos (\omega _3)+5\sin (\rho _3) \end{matrix}\right] .\nonumber \\ \end{aligned}$$

(48)

The state trajectories and controls of the two controllers are presented in Figs. 11, 12 and 13. It is observed in the figures that the attitude control system is able to reach the equilibrium point under either the proposed robust $H_\infty$ controller or the IOC-based robust controller. Based on the state trajectories and controls, it can be calculated that for the proposed robust $H_\infty$ controller $\int _{0}^{\infty } (\left\| \varvec{h}(t)\right\| ^2 + \left\| \varvec{u}(t)\right\| ^2_{R_\textrm{r}}) \textrm{d}t = 0.203085$ and $\int _{0}^{\infty } \left\| \varvec{w}(t)\right\| ^2 \textrm{d}t = 0.886121$. Whereas for the IOC-based robust controller $\int _{0}^{\infty } (\left\| \varvec{h}(t)\right\| ^2 + \left\| \varvec{u}(t)\right\| _{R_\textrm{r}}^2) \textrm{d}t = 0.667586$ and $\int _{0}^{\infty } \left\| \varvec{w}(t)\right\| ^2 \textrm{d}t = 0.903624$. The levels of disturbance attenuation for the robust $H_\infty$ controller and the IOC-based robust controller are 0.478732 and 0.859527, respectively. Though it is shown in Fig. 10 that the control torques of the robust $H_\infty$ controller are close to those of the IOC-based robust controller, the numerical results imply that the proposed method achieves better performance in dealing with the misalignment uncertainties and disturbances.

5 Conclusions

In this paper, a nonlinear robust $H_\infty$ controller is designed for rigid spacecraft attitude control systems under actuator misalignments and disturbances. The nonlinear robust $H_\infty$ controller is constructed based on the Hamilton–Jacobi–Isaacs (HJI) equation, and it is also proved that the closed-loop attitude control system can achieve the pre-defined level of disturbance attenuation. A sparse successive Chebyshev–Galerkin method is also designed to efficiently solve the HJI equation, of which the computational time complexity only grows polynomially with the dimension. Simulation results demonstrate the effectiveness of the designed numerical method and the superior performance of the proposed robust $H_\infty$ controller.