1 Introduction

Structures such as turbo machines, space manipulators and aircraft rotary wings can be regarded as rotating flexible beams in the practical engineering. It is found that the dynamics of these structures with large overall motion has an essential difference from the dynamics of that on an immobile base. Thus, the dynamic characteristic of the rotating flexible beam is a significant work and need to be researched further.

In 1987, Kane [1] investigated the dynamics of a rotating flexible cantilever beam, and proposed the concept of “Dynamic Stiffening”. Zhang and Huston [2] used Kane’s equations to capture the “Dynamic Stiffening” terms. Yoo [3] derived the motion equations of a rotating cantilever beam based on a new dynamic modeling method. And a modal formulation method was also introduced to calculate the tuned angular speed of a rotating beam where resonance occurs. Hong [4,5,6,7] presented the first-order approximation coupling (FOAC) model which was based on the theory of continuum medium mechanics and the theory of analytical dynamics. This model considers the second-order coupling term of the longitudinal displacement caused by transversal deformation, but it ignores the high-order terms of the second-order coupling term. It can be used in the cases of small deformation very well. Based on the first-order approximation coupling model, Zhang [8,9,10,11] presented the high-order approximation coupling (HOAC) model which reserves the high-order terms of the second-order coupling term. And the high-order approximation coupling model can deal with a portion of large deformation problems. Shabana [12] presented the absolute nodal coordinate formulation to solve the large deformation problems of flexible bodies. The absolute nodal coordinate formulation defines the element coordinates in the global system, and it employs the mathematical definition of the slopes instead of angles to define the orientation of the element. By using this description, not only the requirement for performing coordinate transformation can be avoided, but also a simple expression for the inertia forces is obtained conveniently. The resulting mass matrix is constant and in fact the same mass matrix that appears in the linear structural dynamics. Berzeri and Shabana [13] used the finite element absolute nodal coordinate formulation to study the centrifugal stiffening effect on rotating two-dimensional beams. A new set of coordinates and the linearization assumptions were utilized to calculate the natural frequencies and mode shapes of a rotating beam. However, in this model, the axial deformation of the beam is not considered. García-Vallejo et al. [14, 15] used the finite element absolute nodal coordinate formulation to study the geometric stiffening effect on rotating two- and three-dimensional beams. Linear and nonlinear theories of elasticity were used in their investigation. Maqueda et al. [16] studied the effect of the centrifugal forces on the eigenvalue solution obtained using two different nonlinear finite element formulations, and in this study, the effect of the axial deformation on the frequency is included. But results are not compared with the results obtained using the traditional approaches. Zhao et al. [17] studied the modal characteristics of a rotating thin plate through the use of the thin plate elements described by the absolute nodal coordinate formulation. And also the effect of the axial deformation on the frequency is considered. In fact, the difference between the results in Zhao’s work and the results obtained using conventional methods can be found. But Zhao did not indicate it. Gerstmayr and Irschik [18] developed the correct representation of bending and axial deformation in the absolute nodal coordinate formulation. The description of elastic forces can be enhanced using the material measure of curvature. Nowadays, the absolute nodal coordinate formulation has got a rapid development [19,20,21,22,23,24,25,26,27,28].

However, in practical engineering, many structures cannot be simplified as a flexible beam only. For example, when a space manipulator catches a body, usually the body is so heavy that it will have great influence on the dynamics of the manipulator. Hence, those structures should be simplified as flexible beams with an additional concentrated mass. Yang et al. [5] and Cai et al. [6] studied the characteristics of a flexible hub-beam system with a tip mass based on the first-order approximation coupling model. Simulation and comparison show that even a small tip mass may affect the dynamic characteristics and the end position of the hub-beam system greatly, which may also result in the largening of vibrating amplitude and the descending of vibrating frequency of the beam. Yoo [29] used the hybrid deformation variables to investigate the modal characteristics of a rotating cantilever beam with a concentrated mass located in an arbitrary position. It was found that the magnitude and the location of the concentrated mass had great influence on the modal characteristics of the rotating beam.

In the present work, a new dynamic model of a flexible rotating beam with a concentrated mass in arbitrary position is derived based on the absolute nodal coordinate formulation (ANCF) without any linearization assumptions. In the modeling, the longitudinal strain energy and bending strain energy of the beam are calculated by using Green-Lagrangian strain tensor and the exact expression of the flexible beam’s curvature, respectively. The analytical expressions of elastic forces and their Jacobian matrices of the flexible beam elements are derived. In order to analyze the modal characteristics of a rotating flexible beam, the linear perturbation analysis is designed to solve the nonlinear problem. Typically, in the nonlinear analysis, the Newton-Raphson procedure is used. The tangent matrix from the Newton-Raphson analysis is used in the linear perturbation analysis in order to obtain solution in the condition of deformation. Then, we can solve the above said dynamic model to obtain the natural frequency and the mode shape of the system. It needs to point out that the effect of the axial deformation on the modal characteristics is included in this model. When the flexible beam is in small deformation state, the results obtained in this paper get a good agreement with those obtained by traditional methods. Nevertheless, once the stretching of the beam is large, a big modal characteristic difference can be observed between the model proposed in this paper and the traditional models in the existing literature.

The objective of this paper is to study the modal characteristics of a rotating flexible beam with a concentrated mass at an arbitrary location based on the absolute nodal coordinate formulation. The remaining of the paper is organized as follows. In Sect. 2, a Dirac’s delta function is used to express the concentrated mass at an arbitrary location of the beam, and the dynamic equation based on ANCF is derived without any linearization assumptions. In Sect. 3, the linear perturbation analysis is designed to get the natural frequency. In Sect. 4, several numerical examples are presented to study the modal characteristics of the rotating beam, and the frequency loci veering, the mode shift and vibration nodes are also discussed. In Sect. 5, some concluding remarks are made.

2 Dynamic equations

2.1 Physical description

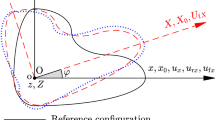
As shown in Fig. 1, the system studied here is a rotating flexible cantilever beam attached to a hub with a concentrated mass located in the arbitrary position. The radius of the rigid hub is a. The length of the beam is L. The concentrated mass k is located at an arbitrary position of the neutral axis of the beam. The distance from the concentrated mass k to O is d. The magnitude of the concentrated mass is m. The hub is rotating about the axis \(o^{*}z^{*}\) with a constant angular velocity \(\omega \). \(o^{*}{\hbox {-}x}^{*}y^{*}z^{*}\) is an inertial coordinate system. For the vibrational characteristics analysis, the rotating slender beam can be equivalently treated as a non-rotating slender beam subject to the corresponding centrifugal force. Therefore, O-XYZ originally fixed in the hub can be regarded as another inertial coordinate system which is used to describe the nodal coordinates of the cantilever beam.

Fig. 1
figure 1

System configuration

Full size image

In order to simplify the analysis, the following assumptions are made as what shown in [29]. The beam has homogeneous, elastic and isotropic material properties. It has a slender shape so that shear and rotary inertia effects are negligible. Consequently, the beam is an Euler-Bernoulli beam. The cross section of the beam is uniform along its neutral axis. The neutral and the centroidal axes of the cross section coincide, so that torsional motion due to eccentricity is not considered.

2.2 Equation derivation

As shown in Fig. 2, the beam is divided into n elements by using the finite element method. The length of the eth element is represented by \(l = L/n\). The nodal coordinates of the elements are defined in the inertial coordinate system \(O-XY\).

Fig. 2
figure 2

a Original and b current configurations of the beam in the fixed inertial coordinate system \(O-{XY}\)

Full size image
Fig. 3
figure 3

Current configuration of one element in the fixed inertial coordinate system \(O-{XY}\)

Full size image

In the finite element absolute nodal coordinate, as shown in Fig. 3, the global position vector r of an arbitrary point P on the neutral axis of a two-dimensional beam element can be defined as [20]

$$\begin{aligned} {{\varvec{r}}}=\left[ {{\begin{array}{l} {r_1 } \\ {r_2 } \\ \end{array} }} \right] =\left[ {{\begin{array}{l} {a_0 +a_1 x^{1}+a_2 x^{2}+a_3 x^{3}} \\ {b_0 +b_1 x^{1}+b_2 x^{2}+b_3 x^{3}} \\ \end{array} }} \right] ={{\varvec{Sq}}}_e \end{aligned}$$
(1)

where S is the global shape function matrix which has a complete set of rigid-body modes, x is the coordinate defined in the element coordinate system, \(a_{i}\) and \(b_{i}\) are the coefficients of the interpolating polynomial used to determine the global position and \({{\varvec{q}}}_{e}\) is the vector of element nodal coordinates

$$\begin{aligned} {{\varvec{q}}}_{{{\varvec{e}}}} =\left[ {e_1 \;e_2 \;e_3 \;e_4 \;e_5 \;e_6 \;e_7 \;e_8 } \right] ^{\mathrm{T}} \end{aligned}$$
(2)

This vector of absolute nodal coordinates includes the global position

$$\begin{aligned} e_1= & {} \left. {r_1 } \right| _{x=0} ,\quad e_2 =\left. {r_2 } \right| _{x=0} \nonumber \\ e_5= & {} \left. {r_1 } \right| _{x=l} ,\quad _6 =\left. {r_2 } \right| _{x=l} \end{aligned}$$
(3)

and the gradients of the global position vector at element nodes are defined as

$$\begin{aligned} e_3= & {} \left. {\frac{\partial r_1 }{\partial x}} \right| _{x=0} ,e_4 =\left. {\frac{\partial r_2 }{\partial x}} \right| _{x=0} \nonumber \\ e_7= & {} \left. {\frac{\partial r_1 }{\partial x}} \right| _{x=l} ,e_8 =\left. {\frac{\partial r_2 }{\partial x}} \right| _{x=l} \end{aligned}$$
(4)

in which l is the original length of the beam element (at node \(A, x=0\); while at node \(B, x=l\), as shown in Fig. 3). A cubic polynomial is employed to describe both components of the positions. Therefore, the global shape function matrix S can be written as [20]

$$\begin{aligned} {{\varvec{S}}}=\left[ {{\begin{array}{l} {{\varvec{s}}_1 } \\ {{\varvec{s}}_2 } \\ \end{array} }} \right] =\left[ {{\begin{array}{cccccccc} {s_1 }&{} 0&{} {ls_2 }&{} 0&{} {s_3 }&{} 0&{} {ls_4 }&{} 0 \\ 0&{} {s_1 }&{} 0&{} {ls_2 }&{} 0&{} {s_3 }&{} 0&{} {ls_4 } \\ \end{array} }} \right] \end{aligned}$$
(5)

in which the functions \(s_{i }=s_{i}(\xi )\) are defined as

$$\begin{aligned} \left\{ {{\begin{array}{l} {s_1 =1-3\xi ^{2}+2\xi ^{3}} \\ {s_2 =\xi -2\xi ^{2}+\xi ^{3}} \\ {s_3 =3\xi ^{2}-2\xi ^{3}} \\ {s_4 =-\xi ^{2}+\xi ^{3}} \\ \end{array} }} \right. \end{aligned}$$
(6)

and \(\xi =x/l\). It can be shown that the preceding shape function contains a complete set of rigid-body modes that can describe arbitrary rigid-body translational and rotational displacements.

The kinetic energy of element e reads

$$\begin{aligned} T_e =\frac{1}{2}\int _V {\rho \dot{{\varvec{r}}}^\mathrm{T}\dot{{\varvec{r}}} {\hbox {d}}V} =\frac{1}{2}\dot{{\varvec{ q}}}_e ^\mathrm{T}{\varvec{M}}_e \dot{{\varvec{ q}}}_e \end{aligned}$$
(7)

where \({{\varvec{M}}}_{e}\) is the eth element mass matrix, which is given by

$$\begin{aligned} {\varvec{M}}_e =\int _{ 0}^{ l} { \rho A {\varvec{S}}(x)^\mathrm{T}{\varvec{S}}(x){\hbox {d}}x} \end{aligned}$$
(8)

Where \(\rho \) is the density of the material in the reference configuration of the beam, and A is the corresponding cross-sectional area.

Let \({{{\varvec{q}}}}_{a}\) denote the global nodal coordinate vector, and \({{{\varvec{B}}}}_{e}\) denotes the element transformation matrix. \({\varvec{q}}_e ={\varvec{B}}_e \,{\varvec{q}}_a \) is obtained. Thus, the kinetic energy of the beam is given by

$$\begin{aligned} T=\sum _{e=1}^n {T_e } =\frac{1}{2}\dot{{\varvec{q}}}_a ^\mathrm{T}{\varvec{M}}_a \dot{{\varvec{q}}}_a \end{aligned}$$
(9)

where the generalized mass matrix of the beam is followed as

$$\begin{aligned} {\varvec{M}}_a =\sum _{e=1}^n {{\varvec{B}}_e ^\mathrm{T}{\varvec{M}}_e {\varvec{B}}_e } \end{aligned}$$
(10)

Based on the Euler-Bernoulli beam theory, the virtual work for elastic deformations of the eth element is modeled as

$$\begin{aligned} \delta W_{fe}= & {} -\int _V { \delta \varepsilon _x \sigma _x {\hbox {d}}V} \nonumber \\= & {} -\int _V { E\delta \varepsilon _x \varepsilon _x {\hbox {d}}V} \end{aligned}$$
(11)

where E is the elastic modulus of materials, and \(\varepsilon _x \) is the strain of point P. \(\varepsilon _x \) can be expressed as

$$\begin{aligned} \varepsilon _x =\varepsilon _{x0} -y\kappa \end{aligned}$$
(12)

where \(\varepsilon _{x0} \) and \(\kappa \) are the axial strain and the curvature along the neutral axis of the beam, respectively. Assuming that the neutral and the centroidal axes of the cross section coincide, it yields the area moments of inertia about the z-axis

$$\begin{aligned} \int _A { y{\hbox {d}}A} =0, I_z =\int _A { y^{2}{\hbox {d}}A} \end{aligned}$$
(13)

Substituting Eq. (12) and Eq. (13) into Eq. (11), the virtual work of the elastic force of the element can be formulated as

$$\begin{aligned} \delta W_{f e} =-\int _0^l {EA\delta \varepsilon _{x0} \varepsilon _{x0} {\hbox {d}}x} -\int _0^l {EI_z \frac{1}{2}\delta (|\kappa |^{2}){\hbox {d}}x} \end{aligned}$$
(14)

On the basis of the theory of the continuum mechanics, the longitudinal strain can be written as

$$\begin{aligned} \varepsilon _{x0} =\frac{1}{2}\left[ {\left( {\frac{\partial {\varvec{r}}}{\partial x}} \right) ^\mathrm{T}\left( {\frac{\partial {\varvec{r}}}{\partial x}} \right) -1} \right] \end{aligned}$$
(15)

The exact curvature of element e can be described as

$$\begin{aligned} \kappa =\left( \frac{\partial {\varvec{r}}}{\partial x}\times \frac{\partial ^{2}{\varvec{r}}}{\partial x^{2}}\right) \bigg /\left| \frac{\partial {\varvec{r}}}{\partial x}\right| ^{3}=\left( \frac{\partial {\varvec{r}}}{\partial x}\times \frac{\partial ^{2}{\varvec{r}}}{\partial x^{2}}\right) /f^{3} \end{aligned}$$
(16)

where f is defined as \(f=\left| \frac{\partial {\varvec{r}}}{\partial x}\right| =\sqrt{\left( {\frac{\partial {\varvec{r}}}{\partial x}} \right) ^\mathrm{T}\left( {\frac{\partial {\varvec{r}}}{\partial x}} \right) }\).

The elastic force of element e can be defined as

$$\begin{aligned} {\varvec{Q}}_{f e}= & {} \frac{\delta W_{f e} }{\delta {\varvec{q}}_e^\mathrm{T} } \nonumber \\= & {} -\int _0^l {EA \varepsilon _{x0} {\varvec{{S}}}^{\prime \mathrm{T}}{\varvec{{S}}}^{\prime } {\varvec{q}}_e {\hbox {d}}x} \nonumber \\&-\int _0^l {EI_z \kappa \cdot \left( {\frac{\varvec{\varGamma } }{f^{3}}-3\frac{\kappa }{f^{2}}{{\varvec{S}}}^{\prime \mathrm{T}}{{\varvec{S}}}^{\prime }} \right) {\varvec{q}}_e {\hbox {d}}x} \end{aligned}$$
(17)

where \(\varvec{\varGamma }={{\varvec{S}}}^{\prime \mathrm{T}}{\tilde{{{\varvec{I}}}}}^\mathrm{T}{ {{{\varvec{S}}}}^{\prime \prime }}+{{{{\varvec{S}}}}^{\prime \prime }}^{\mathrm{T}}{\tilde{{{\varvec{I}}}}} {{{{\varvec{S}}}}^{\prime }}\), \({\tilde{{{\varvec{I}}}}}\) represents a skew-symmetric matrix and can be written as \({\tilde{{{\varvec{I}}}}}=\left[ {{\begin{array}{cc} 0&{} {-1} \\ 1&{} 0 \\ \end{array} }} \right] \).

Then, the virtual work of the generalized elastic force can be given by

$$\begin{aligned} \delta W_f =\sum _{e=1}^n {\delta W_{f e} } =\delta {\varvec{q}}_a^\mathrm{T} {\varvec{Q}}_{f a} \end{aligned}$$
(18)

where the generalized elastic force can be written as

$$\begin{aligned} {\varvec{Q}}_{f a} =\sum _{e=1}^n {{\varvec{B}}_e ^\mathrm{T}{\varvec{Q}}_{f e} } \end{aligned}$$
(19)

In order to analyze the natural frequencies of the rotating system conveniently, the equivalent transformation of the model is introduced. The rotating slender beam is equivalently treated as a non-rotating slender beam subject to an external force. The magnitude of the external force is equal to the equivalent centrifugal force at a specific rotating velocity \(\omega \). The centrifugal force of the arbitrary point P on the neutral axis of a cantilever beam element can be expressed as

$$\begin{aligned} {\varvec{F}}_{{ ce}} =\rho A\omega ^{2}\left( \left[ {{\begin{array}{l} a \\ 0 \\ \end{array} }} \right] +{\varvec{S}}(x){\varvec{q}}_e \right) \end{aligned}$$
(20)

The virtual work of centrifugal force of the eth element is defined as

$$\begin{aligned} \begin{aligned} \delta W_{{ ce}}&=\int _0^l {\rho A\omega ^{{2}}\left( \left[ {{\begin{array}{l} a \\ 0 \\ \end{array} }} \right] +{\varvec{Sq}}_e \right) \cdot \delta ({\varvec{r}}_p ){\hbox {d}}x} \\&=\int _0^l {\rho A\omega ^{{2}}\left( \left[ {{\begin{array}{l} a \\ 0 \\ \end{array} }} \right] +{\varvec{Sq}}_e \right) \cdot \delta ({\varvec{Sq}}_e ){\hbox {d}}x} \\&=\int _0^l {\rho A\omega ^{{2}}\left( \left[ {{\begin{array}{l} a \\ 0 \\ \end{array} }} \right] ^{\mathrm{T}}+{\varvec{q}}_e^\mathrm{T} {\varvec{S}}^{\mathrm{T}}\right) {\varvec{S}}\delta {\varvec{q}}_e {\hbox {d}}x} \\&=\omega ^{{2}}\rho Aa\int _0^l {{\varvec{S}}_1 \mathrm{d}x} \delta {\varvec{q}}_e +\omega ^{{2}}{\varvec{q}}_e^\mathrm{T} M_e \delta {\varvec{q}}_e \\ \end{aligned} \end{aligned}$$
(21)

The centrifugal force of the eth element is defined as

$$\begin{aligned} {\varvec{Q}}_{{ ce}}= & {} \frac{\delta W_{{ ce}} }{\delta {\varvec{q}}_e^\mathrm{T} }=\frac{\omega ^{{2}}\rho Aa\int _0^l {{\varvec{S}}_1 \mathrm{d}x} \delta {\varvec{q}}_e }{\delta {\varvec{q}}_e^\mathrm{T} }+\frac{\omega ^{{2}}{\varvec{q}}_e^\mathrm{T} {\varvec{M}}_e \delta {\varvec{q}}_e }{\delta {\varvec{q}}_e^\mathrm{T} } \nonumber \\= & {} \omega ^{{2}}\rho Aa\int _0^l {{\varvec{S}}_1^\mathrm{T} \mathrm{d}x} +\omega ^{{2}}{\varvec{M}}_e {\varvec{q}}_e \end{aligned}$$
(22)

The virtual work of the generalized centrifugal force can be given by

$$\begin{aligned} \delta W_c =\sum _{e=1}^n {\delta W_{\hbox {ce}} } =\delta {\varvec{q}}_a^\mathrm{T} {\varvec{Q}}_{c a} \end{aligned}$$
(23)

where the generalized centrifugal force can be written as

$$\begin{aligned} {\varvec{Q}}_{c a}= & {} \sum _{e=1}^n {{\varvec{B}}_e^\mathrm{T} {\varvec{Q}}_{c e} } \nonumber \\= & {} \omega ^{{2}}a{\varvec{S}}_{x1} +\omega ^{{2}}{{\varvec{M}}}_a {\varvec{q}}_a \end{aligned}$$
(24)

in which

$$\begin{aligned} {\varvec{S}}_{x1} =\rho A\sum _{e=1}^n {{\varvec{B}}_e^\mathrm{T} } \int _0^l {{\varvec{S}}_1^\mathrm{T} \mathrm{d}x} \end{aligned}$$
(25)

Using the variation form of the D’Alembert–Lagrange’s principle (or the principle of virtual work) in dynamics, the variation motion equations of a flexible body take the form of

$$\begin{aligned} \delta W_c +\delta W_f -\delta {\varvec{q}}_a ^\mathrm{T}{\varvec{M}}_a \ddot{{\varvec{q}}}_a =0 \end{aligned}$$
(26)

Substituting Eq. (18) and Eq. (23) into Eq. (26), the motion equations of the beam can be rewritten as

$$\begin{aligned} {{\varvec{M}}}_a \ddot{{{\varvec{q}}}}_a ={\varvec{Q}}_a \end{aligned}$$
(27)

where \({\varvec{Q}}_a \) is the vector of generalized elastic force, as

$$\begin{aligned} {\varvec{Q}}_a ={\varvec{Q}}_{{ ca}} +{\varvec{Q}}_{{ fa}} \end{aligned}$$
(28)

Now, to consider the concentrated mass at an arbitrary location of the beam (as shown in Fig. 1), the mass per unit length of the beam can be expressed by using a Dirac’ s delta function as follows

$$\begin{aligned} \rho (\bar{{x}})=m\delta (\bar{{x}}-d) \end{aligned}$$
(29)

Here, \(\bar{{x}}\) is the coordinate along the axis tangent to the beam centerline without deformation. In order to find out the location of the element where the concentrated mass is, d can be rewritten as

$$\begin{aligned} d=\sum _{i=1}^{k-1} {l_i } +\Delta l, \quad k=1,2,3\ldots n \end{aligned}$$
(30)

where \(l_{i}\) is the length of the ith element \((l_{0} =0)\), \(\Delta l\) is the remainder length, and n is the total element number of the beam.

If \(0\le \Delta l<l_k \), the concentrated mass will be at the location \(\Delta l\) of the kth element of the beam.

If \(k =n\) and \(\Delta l=l_n \), the concentrated mass will be at the end of the last element of the beam. This condition is that a tip mass m is attached to the free end of the beam.

Then, the kinetic energy of the concentrated mass can be expressed as

$$\begin{aligned} T^{{*}}= & {} \frac{1}{2}\int _0^L {\rho (\bar{{x}}) \dot{{\varvec{r}}}^\mathrm{T}\dot{{\varvec{r}}} \mathrm{d}\bar{{x}}} \nonumber \\= & {} \frac{1}{2}m\dot{{\varvec{q}}}_k^\mathrm{T} {\varvec{S}}^{\mathrm{T}}(\Delta l){\varvec{S}}(\Delta l)\dot{{\varvec{q}}}_k \nonumber \\= & {} \frac{1}{2}\dot{{\varvec{q}}}_a ^\mathrm{T}{\varvec{M}}^{{*}} \dot{{\varvec{q}}}_a \end{aligned}$$
(31)

where

$$\begin{aligned} {\varvec{M}}^{{*}}=m{\varvec{B}}_k ^{\mathrm{T}}{\varvec{S}}^{\mathrm{T}}(\Delta l){\varvec{S}}(\Delta l){\varvec{B}}_k \end{aligned}$$
(32)

and \({\varvec{B}}_k \) is the element transformation matrix of the kth element. As Eq. (22), the centrifugal force of the concentrated mass can be defined as

$$\begin{aligned} {\varvec{Q}}_{c a}^{*} =\omega ^{{2}}a{\varvec{S}}_{x1}^{ *} +\omega ^{{2}}{\varvec{M}}^{*}{\varvec{q}}_a \end{aligned}$$
(33)

where

$$\begin{aligned} {\varvec{S}}_{x1}^{*} =m{\varvec{B}}_k^\mathrm{T} {\varvec{S}}_1^\mathrm{T} (\Delta l) \end{aligned}$$
(34)

Then, Eq. (27) can be rewritten as

$$\begin{aligned} {{\varvec{M}}}\ddot{{{\varvec{q}}}}_a ={\varvec{Q}} \end{aligned}$$
(35)

where

$$\begin{aligned} {{\varvec{M}}}= & {} {{\varvec{M}}}_a +{{\varvec{M}}}^{*} \end{aligned}$$
(36)
$$\begin{aligned} {\varvec{Q}}= & {} {\varvec{Q}}_{{ ca}} +{\varvec{Q}}_{{ ca}}^\mathrm{*} +{\varvec{Q}}_{{ fa}} \end{aligned}$$
(37)

The dynamic differential equation of the rotating beam, which has a concentrated mass, can be written as follows

$$\begin{aligned} {{\varvec{M}}}\ddot{{{\varvec{q}}}}_a =\omega ^{{2}}a{\varvec{S}}_x +\omega ^{{2}}{\varvec{Mq}}_a +{\varvec{Q}}_{{ fa}} \end{aligned}$$
(38)

where

$$\begin{aligned} {\varvec{S}}_x ={\varvec{S}}_{x1} +{\varvec{S}}_{x1}^\mathrm{*} \end{aligned}$$
(39)

3 Frequency analysis

The differential equation of free vibration can be rewritten as

$$\begin{aligned} {{\varvec{M}}}\ddot{{{\varvec{q}}}}_a +{\varvec{Q}}_{\mathrm{T}} =\omega ^{{2}}a{\varvec{S}}_x \end{aligned}$$
(40)

where \({\varvec{Q}}_{\mathrm{T}} =-\omega ^{{2}}{\varvec{Mq}}_a -{\varvec{Q}}_{fa} \). In the equation above, the generalized mass matrix M is constant, which is easy for nature frequency calculating. While in the high-order approximation coupling model [8], the generalized mass matrix M is a time-varying matrix. Hence, the nature frequencies are very difficult to be calculated.

In order to obtain the solution of the eigenvalue problem of the rotating beam including the effect of the centrifugal forces, the equation of motion at a particular static configuration \({\varvec{q}}_{a}\) and a prescribed angular velocity \(\omega =\dot{\Omega }\) are linearized. The perturbation form of the dynamic equations of the system in this investigation is obtained as

$$\begin{aligned} {\varvec{M}}\ddot{{\varvec{\chi }}}+{\varvec{K}}_{\mathrm{T}} ({\varvec{q}}_a ){{\varvec{\chi }} }={\varvec{0}} \end{aligned}$$
(41)

where \({\varvec{q}}_{a}\) is the current configuration in the static equilibrium. Using the Newton-Raphson algorithm, solving Eq. (40), we can obtain \({\varvec{{q}}}_{a}\) . This is the major difference from the other methods in the existing literature.

The global tangent stiffness matrix \({\varvec{{K}}}_{\mathrm{T}}\) can be obtained by differentiating the preceding equation \({\varvec{{Q}}}_{\mathrm{T}}\) with respect to the nodal coordinates \({\varvec{{q}}}_{a}\) as follows

$$\begin{aligned} {\varvec{K}}_{\mathrm{T}}= & {} \frac{\partial {\varvec{Q}}_{\mathrm{T}} }{\partial {\varvec{q}}_a } \nonumber \\= & {} -\omega ^{2}{\varvec{M}}-\frac{\partial {\varvec{Q}}_{f a} }{\partial {\varvec{q}}_a } \nonumber \\= & {} {\varvec{K}}_a -\omega ^{2}{\varvec{M}} \end{aligned}$$
(42)

\({\varvec{{K}}}_{\mathrm{T}}\) is a function of the static equilibrium configuration \({\varvec{{q}}}_{a}\). \({\varvec{{K}}}_{{a}}\) is the prestressed stiffness matrix that is computed based on the stress state of Eq. (40) by using the Newton–Raphson algorithm. This modal analysis is performed under the conditions of the centrifugal inertia force.

$$\begin{aligned} {\varvec{K}}_a =-\frac{\partial {\varvec{Q}}_{f a} }{\partial {\varvec{q}}_a }=-\sum _{e=1}^n {{\varvec{B}}_e^\mathrm{T} \frac{\partial {\varvec{Q}}_{f e} }{\partial {\varvec{q}}_e }{\varvec{B}}_e } =\sum _{e=1}^n {{\varvec{B}}_e^\mathrm{T} {\varvec{K}}_e {\varvec{B}}_e } \end{aligned}$$
(43)

Here, the eth element stiffness matrix \({\varvec{{K}}}_{e}\) can be obtained by differentiating the Eq. (17) with respect to the nodal coordinates \({\varvec{{q}}}_{e}\) as follows

Table 1 Dimensionless natural frequencies in chordwise bending vibration of the flexible beam (\(\alpha =1, \beta =1, \delta =0, \mu =70\))
Full size table
$$\begin{aligned} {\varvec{K}}_e= & {} -\frac{\partial {\varvec{Q}}_{f e} }{\partial {\varvec{q}}_e } \nonumber \\= & {} \int _0^l {EA {\varvec{{S}}}^{{\prime \mathrm{T}}}{\varvec{{S}}}^{\prime } {\varvec{q}}_e {\varvec{q}}_e^\mathrm{T} {\varvec{{S}}}^{{\prime \mathrm{T}}}{\varvec{{S}}}^{\prime } \mathrm{d}x} +\int _0^l {EA \varepsilon _{x0} {\varvec{{S}}}^{\prime \mathrm{T}}{\varvec{{S}}}^{\prime } \mathrm{d}x}\nonumber \\&+\int _0^l {EI_z \left( {\frac{\varvec{\varGamma } }{f^{3}}-3\frac{\kappa }{f^{2}}{\varvec{{S}}}^{\prime \mathrm{T}}{\varvec{{S}}}^{\prime } } \right) {\varvec{q}}_e {\varvec{q}}_e^{T} \left( {\frac{\varvec{\varGamma }^{\mathrm{T}} }{f^{3}}-3\frac{\kappa }{f^{2}}{\varvec{{S}}}^{\prime \mathrm{T}}{\varvec{{S}}}^{\prime } } \right) \mathrm{d}x} \nonumber \\&+\int _0^l {EI_z \kappa \left( {\frac{\varvec{\varGamma } }{f^{3}}-3\frac{\kappa }{f^{2}}{\varvec{{S}}}^{{\prime \mathrm{T}}}{\varvec{{S}}}^{\prime } } \right) \mathrm{d}x} \nonumber \\&+\int _0^l {EI_z \kappa \left( {-6\frac{\varvec{\varGamma } }{f^{5}}{\varvec{q}}_e {\varvec{q}}_e^\mathrm{T} {\varvec{{S}}}^{\prime \mathrm{T}}{\varvec{{S}}}^{\prime }+15\kappa \frac{1}{f^{4}}{\varvec{{S}}}^{\prime \mathrm{T}}{\varvec{{S}}}^{\prime } {{\varvec{q}}}_e {\varvec{q}}_e^\mathrm{T} {\varvec{{S}}}^{\prime \mathrm{T}}{\varvec{{S}}}^{\prime } } \right) \mathrm{d}x}\nonumber \\ \end{aligned}$$
(44)

where \({\varvec{{q}}}_{e}\) is the current configuration in the static equilibrium. And in Eq. (44) \({\varvec{{K}}}_{e}\) is strong nonlinear due to the coupling between the longitudinal deformation and the bending deformation. Thus, the effect of the axial deformation on the eigenvalue problem of the rotating beam is included.

In fact, the prestressed stiffness matrix \({\varvec{{K}}}_{{a}}\), which increases the system stiffness, has centrifugal stiffening effects. When the beam is non-rotating, it will degenerate to the structure stiffness matrix in the structural mechanics.

The chordwise bending vibration of the beam is governed by Eq. (41). To draw more general conclusions from numerical results, Eq. (41) is to be transformed into a dimensionless form. To achieve this, the following dimensionless variables and parameters are introduced

$$\begin{aligned} \tau= & {} \frac{t}{T^{*}}, \xi =\frac{x}{L}, \beta =\frac{d}{L}, \delta =\frac{a}{L}, \alpha =\frac{m}{\rho AL}, \gamma \nonumber \\= & {} T^{*}\Omega , \lambda =T^{*2}\dot{\Omega }, \mu =\sqrt{\frac{AL^{2}}{I_z }} \end{aligned}$$
(45)

where \(T^{*}\) is defined as \(T^{*}=\sqrt{\frac{\rho AL^{4}}{EI_z }}\)

Hereafter, \(\alpha , \beta \), \(\gamma \) and \(\delta \) will denote the concentrated mass ratio, concentrated mass location ratio, angular velocity ratio and hub radius ratio, respectively. The dimensionless form of the equation is finally obtained by using the dimensionless variables and parameters defined in Eq. (45). \(\mu \) is the slenderness ratio. A value of \(\mu = 70\) guarantees that the beam is slender enough for the Euler-Bernoulli beam theory to be applied.

Table 2 Dimensionless natural frequencies in chordwise bending vibration of the flexible beam (\(\alpha = 1, \beta = 1, \mu =70\))
Full size table

The dimensionless form of Eq. (41) can be obtained as follows (The details are shown in the appendix)

$$\begin{aligned} \bar{{\varvec{M}}}\frac{{\hbox {d}}^{2}\bar{\varvec{\chi }}(\tau )}{{\hbox {d}}\tau ^{2}}+\bar{{{\varvec{K}}}}_{\mathrm{T}} (\bar{{{\varvec{q}}}}_a ){\bar{\varvec{\chi }}}(\tau )={\varvec{0}} \end{aligned}$$
(46)

where \(\frac{{\hbox {d}}^{2}{\bar{\varvec{\chi }}}(\tau )}{{\hbox {d}}\tau ^{2}}\) means double differentiation of \({\bar{\varvec{\chi }}}(\tau )\) with respect to \(\tau \) (dimensionless time). The eigenvalue problem for the chordwise bending vibration of a rotating cantilever beam with a concentrated mass can be formulated by assuming that \(\bar{{\chi }}\) are harmonic functions of \(\tau \). It can be expressed as

$$\begin{aligned} \bar{{\chi }}(\tau )=e^{j\omega \tau }{{\varvec{Z}}} \end{aligned}$$
(47)

where j represents an imaginary number, \(\omega \) is the ratio of the natural frequency to the reference frequency, and Z is a constant column matrix. Substituting Eq. (47) into Eq. (46) yields

$$\begin{aligned} \omega ^{2}\bar{\varvec{{M}}}{{\varvec{Z}}}=\bar{\varvec{{K}}}_{\mathrm{T}} {{\varvec{Z}}} \end{aligned}$$
(48)

4 Numerical results

The accuracy of the ANCF method proposed in this paper is examined in Tables 1, 2, 3 and 4. In Table 1, the results of the first and the second chordwise bending natural frequencies of a rotating beam with a tip mass are given. The dimensionless parameters employed for the numerical results are \(\alpha =1, \beta =1\) and \(\delta =0\). The results obtained by using the ANCF method proposed in this paper are compared with these introduced in references [30] and [13]. As shown in the table, the two sets of results show only trivial discrepancy for values of \(\gamma \) from 0 to 10, and note that, in these cases, the beam is under small deformation. That proves the correctness of the equation derived above. Also, we can find that the natural frequencies increase as the angular velocity ratio \(\gamma \) increases.

In Table 2, the results of the first and the second chordwise bending natural frequencies of a rotating beam with a tip mass are compared between the present study and reference [13]. The dimensionless parameters employed for the numerical results are \(\alpha =1, \beta =1\) and \(\mu =70\) for (\(\delta =0\) or 1) and (\(\mu = 0, 1, 2, 3, 4, 5, 10, 20\) or 50). As shown in the table, the dimensionless natural frequencies computed by the two methods agree well with each other, when the beam is under small deformation. With the angular speed increasing, the tip axial deformation of the rotating beam becomes larger and the deviation further enlarges. It is just the difference between the dynamic model considering the axial deformation effect proposed in this paper and the dynamic model proposed in reference [13].

In Table 3, the results of the first and the second natural frequencies obtained by using the ANCF method proposed in this paper are compared with these introduced in references [29, 31] and the FOAC model, which are all based on the floating coordinate system. Since the lowest two chordwise bending natural frequencies of a rotating beam with a concentrated mass are not available in the literatures, the results of the rotating beam without a concentrated mass are compared. The dimensionless parameters employed for the numerical results are \(\alpha =0\) and \(\beta =0\) for (\(\gamma = 2, 10, 20, 30, 40 or 50\)) and (\(\delta = 0, 1\) or 5). As shown in the table, we can find that the natural frequencies increase as the angular velocity ratio \(\gamma \) increases, and the natural frequencies increase as the hub radius ratio \(\delta \) becomes larger. With the angular velocity ratio \(\gamma \) increasing, the deviation of the natural frequencies will further enlarge in the same hub radius ratio. From this table, we can find that the results of references [29, 31] and the FOAC model are nearly the same, while the results of the ANCF model proposed in this paper are different from these three. When the angular velocity ratio is small, the four results are nearly the same. In fact, from the simulation we can also find that as the angular velocity ratio \(\gamma \) and hub radius ratio \(\delta \) increase the deformation of the flexible beam will become larger, and under this condition the frequency of the ANCF model proposed in this paper will have significant differences from the other three as shown in Table 3. The reason that results in the above-mentioned differences is that the model proposed in this paper includes the axial deformation effect, whereas the other three models do not take into account the axial deformation effect.

Table 3 Comparison of the dimensionless chordwise bending natural frequencies (\(\alpha = 0, \beta = 0\))
Full size table
Table 4 Comparison of the dimensionless chordwise bending natural frequencies (\(\alpha = 0, \beta = 0\))
Full size table

In Table 4, the lowest two chordwise bending natural frequencies obtained by using the ANCF model presented in the paper are compared with the FOAC model, the nonlinear model in ANSYS and the linear model in ANSYS. The dimensionless parameters employed for the numerical results are \(\delta =1, \alpha =0, \beta =0\) and \(\gamma = 2, 10, 20, 30, 40\) or 50. Here, we can see that the results obtained using the FOAC model are nearly the same as that obtained using the linear model in ANSYS. As we know, the nonlinear model should be much more precise than the linear model when they are used in the large deformation problems. If we take the results obtained using the nonlinear model in ANSYS as the benchmark, we can conclude from the results in Table 4 that the model proposed in this paper is superior to the linear models in the analysis of large deformation cases. It is also important to mention that the results obtained using the nonlinear model in ANSYS will be divergent when \(\gamma = 40\) and 50, but the results obtained using the model presented in this paper are still convergent. This means that the ANCF model is more stable than the nonlinear model in ANSYS.

Figures 4, 5, 6 and 7 show the effect of the angular velocity ratio on the natural frequencies. The dimensionless parameters employed for the numerical results are \(\alpha =1, \delta =0\) and \(\delta = 0.3, 0.5, 0.8\) or 1. From Figs. 4, 5, 6 and 7, we can find that the frequency loci will veer, which we can call it the frequency loci veering phenomenon. When \(\beta \) is 0.5, the third frequency locus and the forth frequency locus will veer at \(\gamma \) = 9.2. When \(\beta \) is 0.8, the third frequency locus and the forth frequency locus will veer at \(\gamma = 6.6\), while the second frequency locus and the third frequency locus will also veer at \(\gamma = 17.3\). When \(\beta \) is 1.0, the third frequency locus and the forth frequency locus will veer at \(\gamma = 4.4\), while the second frequency locus and the third frequency locus will veer at \(\gamma = 16.2\). That means the location of the frequency veers will move close to the zero-point of the coordinate \(\gamma \) as the concentrated mass moves to the tip.

Fig. 4
figure 4

First five natural frequencies under the effect of dimensionless angular velocity (\(\alpha =1, \beta =0.3, \delta =0, \mu =70\))

Full size image
Fig. 5
figure 5

First five natural frequencies under the effect of dimensionless angular velocity (\(\alpha = 1, \beta = 0.5, \delta = 0, \mu =70\))

Full size image
Fig. 6
figure 6

First five natural frequencies under the effect of dimensionless angular velocity (\(\alpha =1, \beta = 0.8, \delta =0, \mu =70\))

Full size image

Figures 8, 9 and 10 show the effect of the concentrated mass ratio on the natural frequencies. The dimensionless parameters employed for the numerical results are \(\beta =1, \delta =0\) and \(\gamma = 0, 5\) or 10. Here, we can also find the frequency loci veering phenomenon. When \(\gamma \) is 0, the third frequency locus and the forth frequency locus will veer at \(\alpha = 1.59\). When \(\gamma \) is 5, the third frequency locus and the forth frequency locus will veer at \(\alpha = 0.92\). When \(\gamma \) is 10, the third frequency locus and the forth frequency locus will veer at \(\alpha \) = 0.48, while the second frequency locus and the third frequency locus will also veer at \(\alpha = 1.74\). That means the location of the frequency veers will move close to the zero-point of the coordinate \(\alpha \) as the angular velocity ratio \(\gamma \) increases.

Fig. 7
figure 7

First five natural frequencies under the effect of dimensionless angular velocity \((\alpha =1, \beta =1,\delta =0, \mu =70)\)

Full size image
Fig. 8
figure 8

First five natural frequencies under the effect of concentrated mass ratio (\(\beta =1, \gamma =0, \delta =0, \mu =70\))

Full size image

Figure 11 shows the effect of the concentrated mass location ratio on the natural frequencies. The dimensionless parameters employed for the numerical results are \(\alpha =0.5, \gamma =5\) and \(\delta =0\). From Fig. 11, we can find that the location of the concentrated mass has significantly influence on the natural frequencies. Also, frequency loci veering phenomenon exists here. When \(\gamma \) is 5, the forth frequency locus and the fifth frequency locus will veer at \(\beta = 0.09\) and 0.225.

Fig. 9
figure 9

First five natural frequencies under the effect of concentrated mass ratio (\(\beta =1, \gamma =5, \delta =0, \mu =70\))

Full size image
Fig. 10
figure 10

First five natural frequencies under the effect of concentrated mass ratio (\(\beta =1, \gamma =10, \delta =0, \mu =70\))

Full size image

Figures 12 and 13 are the first and second mode shapes when \(\beta =1, \gamma =0,\delta = 0\) and \(\mu =70\). These results indicate that the magnitude of the concentrated mass has great influence on the second mode shape.

Fig. 11
figure 11

First five natural frequencies under the effect of concentrated mass location ratio (\(\alpha =0.5, \gamma =5, \delta =0, \mu =70\))

Full size image
Fig. 12
figure 12

First mode shape (\(\beta =1, \gamma =0,\delta =0,\mu =70\))

Full size image

Figures 14 and 15 are the first five mode shapes when \(\alpha = 1\) or \(2, \beta = 1, \gamma = 0\) and \(\delta = 0\). We can see that, when \(\alpha =1\), the fourth mode shape is the stretching mode shape. But when \(\alpha = 2\), the third mode shape is the stretching mode shape. That means mode shift happens between \(\alpha = 1\) and \(\alpha = 2\). This is consistent with the frequency loci veering phenomenon in Fig. 8.

As the vibration theory describes, there exists a node, where the displacement is always zero, in the second mode shape when the beam is non-rotating. This node is called the vibration node. There exist two vibration nodes in the third mode shape, one vibration node in the second mode shape, but none in the first mode shape, as shown in Fig. 16. The vibration nodes have the following properties: when the concentrated mass is located at the position of the vibration node, no matter how the concentrated mass ratio changes the corresponding dimensionless nature frequency of the non-rotating beam will be unchanged. For example, the vibration node of the second mode shape locates at the position of \(\beta =0.78344\) in Fig. 17. Then, in Fig. 18, we can find that the corresponding second nature frequency is a constant as \(\omega _{2 }=22.0345\), no matter how the concentrated mass ratio changes. Similarly, the vibration nodes of the third mode shape locate at the positions of \(\beta = 0.50355\) and \(\beta = 0.86768\) in Fig. 16 and Fig. 19. We can also find that the corresponding third nature frequency is a constant as \(\omega _{3}= 61.6982\), no matter how the concentrated mass ratio changes.

Fig. 13
figure 13

Second mode shape (\(\beta =1, \gamma =0, \delta =0, \mu =70\))

Full size image
Fig. 14
figure 14

First five mode shapes(\(\alpha =1, \beta =1, \gamma =0,\delta =0, \mu =70\))

Full size image
Fig. 15
figure 15

First five mode shapes(\(\alpha = 2, \beta =1, \gamma =0,\delta =0, \mu =70\))

Full size image
Fig. 16
figure 16

First three natural frequencies under the effect of concentrated mass location ratio (\(\alpha =0.5, \gamma =0, \delta =0, \mu =70\))

Full size image
Fig. 17
figure 17

Second mode shape (\(\beta =1, \gamma =0,\delta =0, \mu =70\))

Full size image
Fig. 18
figure 18

First five natural frequencies under the effect of concentrated mass ratio (\(\beta = 0.78344, \gamma = 0, \delta = 0, \mu = 70\))

Full size image
Fig. 19
figure 19

Third mode shape (\(\beta = 1, \gamma = 0, \delta = 0, \mu = 70\))

Full size image

5 Conclusions

A new dynamic model of a flexible rotating beam with a concentrated mass in arbitrary position is derived based on the absolute nodal coordinate formulation (ANCF) in this paper. The longitudinal strain energy and bending strain energy of the beam are calculated by using Green-Lagrangian strain tensor and the exact expression of the flexible beam curvature, respectively. The analytical expressions of elastic forces and their Jacobian matrices of the flexible beam elements are derived. The linear perturbation analysis is used to solve the modal analysis of the rotating beam including the effect of the centrifugal forces. In order to study the natural frequencies and the mode shapes, the equation of motion is transformed into a dimensionless form by employing five dimensionless variables.

The accuracy of the ANCF model proposed in this paper is proved to be higher than the model introduced in literatures when the axial deformation of the rotating beam is large. The results show that the natural frequencies and the mode shapes are both influenced by the magnitude and the location of the concentrated mass. Furthermore, the interesting frequency veering and the associated mode shift phenomena are observed and discussed for different simulation cases. The simulation results also show that the changes in the angular velocity of the flexible beam, the magnitude and the location of the concentrated mass will give rise to the phenomena of the natural frequency loci veering and the associated mode shift. The characteristics of the vibration nodes of the non-rotating beam are also investigated.