A semi-analytic approach to study propagation and amplification of tsunami waves in mid-ocean and their run-up on shore

Abstract

The paper proposed an effective semi-analytical approach to study tsunami wave propagation along a coast line of an ocean represented by system of nonlinear partial differential equation based on shallow water assumption. An analytical solution is obtained for system of partial differential equation describing tsunami wave propagation for different ocean depth and coastal slopes. The proposed method does not require linearization, perturbation or calculation of unneeded terms; on other hand, its transforms give system of differential equation to recursive formula and provide the series solution which converges rapidly. The obtained analytical solution closely matches with the real physical phenomena of tsunami for height and velocity of tsunami wave. To show the effectiveness and reliability of the proposed method, we have compared the obtained results with exact and analytical solution available in the literature which shows excellent agreement. The impact of ocean depth and coastal slopes on tsunami run-up and wave velocity is also discussed.

1 Introduction

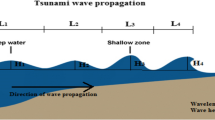
Tsunamis occur when an impulsive disturbance dislodges the water column vertically, resulting in a chain of waves in a body of water. As a result of explosions, landslides, earthquakes, volcanic eruptions, and even the effect of cosmic bodies, such as meteorites, the explosion of nuclear devices close to sea can give rise to vicious sea waves, called tsunamis [1–3]. There is no doubt that tsunamis generated by large shallow-focus earthquakes occurring near or in the ocean are among the most destructive. An earthquake’s vertical displacement can cause tsunami waves to propagate across an ocean, spreading devastation along their path as presented in Fig. 1.

Fig. 1

Tsunami wave formation

Although tsunamis originate from point sources, waves generated can cause extensive damage locally. As they travel across the ocean, their energy rapidly dissipates, which can cause property damage and death along the coastline. It is the depth of water that determines the tsunami’s speed. On approach to shore, the wave speed decreases and the wave height increases. As a tsunami develops, it goes through three stages: formation, propagation in the middle of the ocean, and breaking and running up the coastline. This paper will focus on the last two stages. There is a great deal of interest in tsunami modeling regarding the heights of tsunami run-ups at different points along a coastline. Studies have been conducted both theoretically and experimentally previously to determine how long waves run up. Some of them are referenced in this section.

Based on numerical model, Kobayashi et al. [4] predict the flow characteristics of wave trains running along a rough slope. Finite difference methods using explicit dissipative Lax–Wendroff are used to solve the finite-amplitude shallow water equations in the time domain in reference [5]. Due to the assumption that permeability is negligible, flow computations may be limited for areas on rough slopes. For irregular waves on a rough, impermeable slope of 1:3, the author in reference [6] assessed reflection and wave run-up. In order to better understand certain coastal effects of tidal waves, Kânoğlu and Synolakis [6] analyzed and experimented on piecewise linear and 2-dimensional bathymetries. In addition to comparing analytical predictions with numerical results, the authors examined data on waves run-up around an idealized conical island as well as results from Revere Beach data. A mixed Eulerian–Lagrangian optimization algorithm was presented by Maiti and Sen [7] for analyzing highly nonlinear solitary waves interacting with plane, gentle and steep slopes. In addition to wave steepness, slope of the plane is also important in finding the run-up height. The author further investigates the force and pressure exerted on impermeable walls by shallow-water solitary waves. Li and Raichlen [8] observe solitary waves running up on a uniform plane beach connected to a continuous depth ocean. In the run-up phase, wave does not break. The hodograph transformation is used to solve an analytically nonlinear shallow-water equation (NSWE) describing wave features on the beach. In a laboratory experiment, Gedik et al. [9] investigated erosion and tsunami run-up on permeable slope beaches. Using run-up height and erosion area as parameters, they developed a relationship between the two. A finite-element simulation of tsunami waves was carried out by Cai [10] using the potential flow theory, which involves solid–water interaction. In order to study the effects of different beach slopes on tsunami run-up, these researchers used a finite-element method. Based on their findings, the tsunami wave originating from a thrust fault earthquake is located above the hanging wall, and then, it splits into two waves—one above the hanging wall and the other above the foot wall-with differing amplitudes, wave forms, and velocities. Liu [11] applies the linear potential theory to analyze tsunamis prompted by underwater earthquakes, and he emphasizes on the tsunami’s initial state. Karunakar and Chakraverty [12] study the tsunami wave propagation in a crisp and interval environment using classical NSWEs. Using the line method, Mousa [13] studies how increasing sea depth and coast slope affects the height and velocity of tsunami waves. Varsoliwala and Singh [14] studies the tsunami model using the hybrid approach, namely Elzaki adomain decomposition method. For society to be protected from catastrophic destruction with minimal computing time, a model study in determining the tsunami’s travel time, amplitude, and inundation distance was proposed by Regina and Mohamed [15]. A fractional approach was used by Tandel et al. [16] to study the tsunami wave propagation model, and Liu [11] investigates tsunami waves propagation using the recently introduced notion of product-like fractal measure. Magdalena et al. [17] utilize a mathematical model to examine how submarine landslides can produce tsunami waves that are extremely damaging. Numerical solution of the NSWEs is carried out using a staggered grid finite volume method. Several attempts to obtain the exact or analytical and numerical solution of the wave equation have been made through research [18,19,20,21,22,23,24].

In this paper, an analysis of tsunami run-up is conducted by solving the classical NSWEs using reduced differential transform method. The classic NSWEs are presented as a model of tsunami run-up in this paper. Two cases are considered. The first case is the classical problem for which an analytical solution is known for a uniform sea depth and a zero beach slope. At a variable beach slope, the second case is considered. An outline of the paper is as follows: Sect. 2 describes the mathematical model of the shallow water tsunami model. The proposed semi-analytical approach is discussed in Sect. 3 with error and convergence analysis. Section 4 deals with the implementation of RDTM to the model. Section 5 deals with result and discussion followed by conclusion in Sect. 6.

2 Shallow-water tsunami model

In the same way as other waves, tsunamis have amplitudes, wavelengths, and speeds. The wavelength in waves is defined as the distance between two troughs or crests. A wave’s amplitude is determined by the height above the static water line. Tsunami waves are made up of shallow water waves, and velocity is defined as the speed of the wave. When the depth of water is smaller than the wavelength of a wave, it is considered shallow. The cross section of coast during the tsunami is shown in Fig. 2.

Fig. 2

Coast during the tsunami

The classical NSWE are given by [10, 16]:

$$\begin{aligned}{} & {} \frac{{\partial \upsilon }}{{\partial \ell }} + \upsilon \frac{{\partial \upsilon }}{{\partial \wp }} + g\frac{{\partial \omega }}{{\partial \wp }} = 0, \end{aligned}$$

(1)

$$\begin{aligned}{} & {} \frac{{\partial \omega }}{{\partial \ell }} + \frac{\partial }{{\partial \wp }} \left( {\upsilon \left( {\varphi + \omega } \right) } \right) = 0, \end{aligned}$$

(2)

where $\upsilon \left( {\wp ,\ell } \right)$,$\omega \left( {\wp ,\ell } \right)$,$\varphi \left( \wp \right)$ represent the tsunami velocity, wave amplification, varying ocean depth close to shore. Initial conditions are

$$\begin{aligned} \upsilon \left( {\wp ,0} \right)= & {} \phi \sqrt{\frac{g}{D}} {\sec ^2}h \left( {\sqrt{\frac{{3\phi }}{{4{D^3}}}} \wp } \right) , \end{aligned}$$

(3)

$$\begin{aligned} \omega \left( {\wp ,0} \right)= & {} \phi {\sec ^2}h\left( {\sqrt{\frac{{3\phi }}{{4{D^3}}}} \wp } \right) , \end{aligned}$$

(4)

where $\phi ,D,g,\wp$ represent wave amplification, ocean depth, gravitational acceleration and distance, respectively. The exact soliton solution in this stage is defined in [16] as

$$\begin{aligned}{} & {} \upsilon \left( {\wp ,\ell } \right) = \phi {\sec ^2}h\left( \sqrt{\frac{{3\phi }}{{4{D^3}}}} \nonumber \right. \\{} & {} \quad \left. \left( {\wp - \sqrt{\frac{g}{D}} \left( {1 + \frac{h}{{2d}}} \right) \ell } \right) \right) , \end{aligned}$$

(5)

$$\begin{aligned}{} & {} \omega \left( {\wp ,\ell } \right) = \upsilon \left( {\wp ,\ell } \right) \sqrt{\frac{g}{D}}. \end{aligned}$$

(6)

When $\varphi \left( \wp \right)$ is variable, there is no exact solution to the system described by Eqs. (1)–(4). Therefore, three linear functions will be solved in the form $\varphi \left( \wp \right) =m\wp +300$, where $m=0.2,0.4,0.6$, respectively. To illustrate how the slope of the coast m affects run-up heights and tsunami wave velocity at the beach, we solve this system for breaking and run-up on the beach.

3 Reduced differential transform method

Definitions and mathematical preliminaries of the proposed method for better understanding are discussed in this section. The proposed method concept has been derived from the 2-dimensional Taylor’s series expansion w.r.t to specific variable $\wp$ or $\ell$. Consider a function $\xi \left( {\wp ,\ell } \right)$ and assume that $\xi \left( {\wp ,\ell } \right) = {h_1}(\wp )\,{h_2}(\ell )$. Using the definition of the one-dimensional differential transform method (ODDTM), the function $\xi \left( {\wp ,\ell } \right)$ can be expressed as:

$$\begin{aligned} \xi \left( {\wp ,\ell } \right)&= \sum \limits _{\kappa = 0}^\infty {{H_{1,\kappa }}} {\wp ^\kappa } \sum \limits _{\eta = 0}^\infty {{H_{2,\eta }}} {\ell ^k}\nonumber \\&= \sum \limits _{\kappa = 0}^\infty {\sum \limits _{\eta = 0}^\infty {{W_{\kappa ,\eta }}} } \left( {\kappa ,\eta } \right) {\wp ^\kappa }{\ell ^\eta }, \end{aligned}$$

(7)

where ${W_{\kappa ,\eta }} = {H_{1,\kappa }}{H_{2,\eta }}$ is called the spectrum of original function. The basic concept of RDTM is as follows [24]:

Definition 1

Let $\xi \left( {\wp ,\ell } \right)$ be a continuously differentiable function, then the spectrum or transform of the form of $\xi \left( {\wp ,\ell } \right)$ w.r.t $\ell$ at is defined as:

$$\begin{aligned} {\xi _\kappa }\left( \wp \right) = \frac{1}{{\kappa !}} {\left[ {\frac{{{\partial ^\kappa }}}{{\partial {\tau ^\kappa }}}\xi \left( {\wp ,\ell } \right) } \right] _{\ell = {\ell _0}}}, \end{aligned}$$

(8)

where ${\xi _\kappa }\left( \wp \right)$ is the reduced differential transform of original function $\xi \left( {\wp ,\ell } \right)$. The inverse reduced differential transform of ${\xi _\kappa }\left( \wp \right)$ is defined as:

$$\begin{aligned}{} & {} \xi \left( {\wp ,\ell } \right) = \sum \limits _{\kappa = 0}^\infty {\xi _\kappa } \left( \wp \right) {\left( {\ell - {\ell _0}} \right) ^\kappa }. \end{aligned}$$

(8)

From Eqs. (8) and (9), we get

$$\begin{aligned}{} & {} \xi \left( {\wp ,\ell } \right) = \sum \limits _{\kappa = 0}^\infty \nonumber \\{} & {} \quad {\left[ {\frac{1}{{\kappa !}}{{\left[ {\frac{{{\partial ^\kappa }}}{{\partial {\tau ^\kappa }}}\xi \left( {\wp ,\ell } \right) } \right] }_{\tau = {\tau _0}}}} \right] } \nonumber \\{} & {} \quad {\left( {\ell - {\ell _0}} \right) ^\kappa }. \end{aligned}$$

(9)

Equation (6) can be used to derive the fundamental properties of RDTM as shown in Table 1.

Table 1 Fundamental operation of RDTM w.r.t to variable $\ell$ [10]

3.1 Implementation of RDTM

The convergence of solution obtained by RDTM is discussed in this section. For this, consider the following nonlinear PDE:

$$\begin{aligned} {\upsilon _\tau } = \upsilon \left( {\wp ,\tau ,\mu ,{\mu _\wp },{\mu _{\wp \wp }}, \ldots } \right) , \end{aligned}$$

(9)

with initial condition

$$\begin{aligned} \upsilon \left( {\wp ,0} \right) = {\upsilon _0}\left( \wp \right) . \end{aligned}$$

(10)

The fundamental operation of RDTM from Table 1 converts Eqs. (11)–(12) to recursive formula given by:

$$\begin{aligned}{} & {} \left( {\vartheta + 1} \right) {V_{_{\vartheta + 1}}}\left( \wp \right) \nonumber \\{} & {} \quad = V\left( \xi ,{v_\vartheta },\frac{{d{V_\vartheta }\left( \wp \right) }}{{d\wp }}, \frac{{{d^2}{V_\vartheta }\left( \wp \right) }}{{d{\wp ^2}}},\ldots \right) , \end{aligned}$$

(10)

and the transformed initial condition is

$$\begin{aligned} v\left( \omega \right) = {v_0}\left( \omega \right) , \end{aligned}$$

(11)

where ${V_{\vartheta + 1}}\left( \wp \right)$ and $V\left( {\xi ,{v_\vartheta },\frac{{d{V_\vartheta }\left( \wp \right) }}{{d\wp }},\frac{{{d^2}{V_\vartheta }\left( \wp \right) }}{{d{\wp ^2}}},\ldots } \right)$ are transformed form of the original function $\upsilon \left( {\wp ,\ell } \right)$ and $\upsilon \left( {\wp ,\tau ,\mu ,{\mu _\wp },{\mu _{\wp \wp }},\ldots } \right)$ obtained by applying RDTM in the $\vartheta ^{th}$ iteration. Substituting the value of ${V_\vartheta }\left( \wp \right)$ for $\vartheta =0,1,2,3,4, \ldots n$ in definition of inverse reduced differential transform, the approximate analytical series solution of Eq. (9) with initial condition Eq. (12) is given by

$$\upsilon \left( {\wp ,\ell }\right) = \sum\limits_{\kappa = 0}^\infty {{V_\kappa }\left( \wp \right)} {\left( {\ell - {\ell_0}} \right)^\kappa }$$

(12)

3.2 Convergence and error analysis of RDTM

The convergence of the series solution obtained by RDTM is discussed in reference [25]. We recall the theorems from reference [25] that assure the convergence of the series solution Eq. (15).

Theorem 1

If ${\zeta _k}\left( {\wp ,\ell } \right) = {V_k}\left( \wp \right) {\left( {\ell - {\ell _0}} \right) ^k}$, then the series solution $=\sum\limits_{\kappa = 0}^n {{\zeta _\kappa }}\left( {\wp ,\ell } \right)$ for Eq. (12), $\forall \kappa \in N \cup\left\{ 0 \right\}$ (I) is convergent if there exist $0< \eta < 1$ such that $\left\| {{\zeta _{\kappa+ 1}}} \right\| \le \eta\left\| {{\zeta _\kappa }}\right\|,$ (ii) is divergent if there exist $\eta > 1$ such that $\left\| {{\zeta _{\kappa + 1}}} \right\| \le \eta \left\| {{\zeta _\kappa }} \right\|,$ The truncation error of the series Eq. (12), which is a specific case of Banach’s fixed point theorem, is investigated in Theorem 1.

Theorem 2

Suppose $\sum\limits_{\kappa = 0}^n {{\zeta _k}\left ( {\wp ,\ell } \right)}$ is required series solution, where ${\zeta _\kappa }\left( {\wp ,\ell } \right) = {V_\kappa }\left( \wp \right){\left( {\ell - {\ell _0}} \right)^\kappa }$, converges to $\varepsilon \left( {\wp ,\ell } \right)$. If $\sum\limits_{\kappa = 0}^n {{\zeta _k}\left( {\wp ,\ell } \right)}$ is the truncated series used to approximate the solution and then estimated maximum absolute truncated error is as $\left\| {\varepsilon \left ( {\omega ,t} \right) - \sum\limits_{\kappa = 0}^n {{\zeta _\kappa } \left( {\omega,\tau } \right)} } \right\| \le \frac{1}{{1 - \eta }} {\eta ^{n + 1}}\left\| {{\zeta _0}} \right\|$. Theorems 1 & 2 can be verified in [25]. From Theorem 1 and 2, it is concluded that series solution obtained using RDTM for non-linear Eq. (12) converges to an exact solution when there exists $0< \eta < 1$ such that $\left\| {{\zeta _{\kappa + 1}}} \right\| \le \eta \left\| {{\zeta _\kappa }} \right\|, for \, \forall \,\kappa \in N \cup \left\{ 0 \right\}$. In addition, $\left\| {\varepsilon \left ( {\omega ,t} \right) - \sum\limits_{\kappa = 0}^n {{\zeta _i}\left ( {\omega ,\tau }\right)} } \right\| \le \frac{1}{{1 - \eta }} {\eta ^{n + 1}}\left\| {{\zeta _0}} \right\|$ represents the maximum estimated absolute truncated error.

4 Implementation of RDTM to tsunami wave propagation model

This section discusses the implementation of the proposed method to obtained the series solution to Eqs. (1) and (2) with initial condition Eqs. (3) and (4) with parameter value $g=9.8\,\textrm{m}/\textrm{s}^2,\phi =2$.

Case 1: Propagation of tsunami in mid-sea when- $\varphi \left( \wp \right) = D = 20$

Applying RDTM to Eqs. (1) and (2), we get the following system of recursive formula:

$$\left( {\kappa + 1} \right){\vartheta _{\kappa + 1}}\left( \wp \right) + \sum\limits_{\iota = 0}^\kappa {{\vartheta _\iota }\left( \wp \right){\vartheta _{\kappa - \iota }}\left( \wp \right)} + g\frac{{\partial {\omega _\kappa }\left( \wp \right)}}{{\partial \wp }} = 0,$$

(13)

$$\begin{aligned}& \left( {\kappa + 1} \right) {\varpi _{\kappa + 1}}\left( \wp \right) \nonumber \\&\quad + \varphi \frac{{\partial {\vartheta _\kappa }\left( \wp \right) }}{{\partial \wp }} + \sum \limits _{\iota = 0}^\kappa {{\vartheta _\iota }} \left( \wp \right) (\kappa - \iota + 1 ){\varpi _{\kappa - \iota + 1}}\left( \wp \right) \nonumber \\&\quad + \sum \limits _{\iota = 0}^\kappa {{\varpi _\iota }} \left( \wp \right) \left( {\kappa - \iota + 1} \right) \nonumber \\&\quad {\vartheta _{\kappa - \iota + 1}}\left( \wp \right) = 0, \end{aligned}$$

(14)

with initial transform condition

$$\begin{aligned}{} & {} {\vartheta _0}\left( \wp \right) = \phi \sqrt{\frac{g}{D}} {\sec ^2}h \left( {\sqrt{\frac{{3\phi }}{{4{D^3}}}} \wp } \right) , \end{aligned}$$

(15)

$$\begin{aligned}{} & {} {\varpi _0}\left( \wp \right) = \phi {\sec ^2}h \left( {\sqrt{\frac{{3\phi }}{{4{D^3}}}} \wp } \right) . \end{aligned}$$

(16)

The coefficient of series solution is obtained by substituting $\kappa = 0,1,2, \ldots ,n$ in Eqs. (13) and (14). Some of the coefficients of the series solution are mention below:

$$\begin{aligned}{} & {} {\vartheta _0}\left( \wp \right) = \frac{7}{{5\,\cosh {{\left( {\frac{{\sqrt{3} \,\sqrt{10} \, \wp }}{{400}}} \right) }^2}}}. \end{aligned}$$

(17)

$$\begin{aligned}{} & {} {\vartheta _1} = \frac{{49\,\sqrt{3} \,\sqrt{10} \,\mathrm{{sinh}}\left( {\frac{{\sqrt{3} \,\sqrt{10} \, \wp }}{{400}}} \right) }}{{500\,{\sigma _1}^3}} \nonumber \\{} & {} + \frac{{49\,\sqrt{3} \,\sqrt{10} \,\mathrm{{sinh}}\left( {\frac{{\sqrt{3} \,\sqrt{10} \, \wp }}{{400}}} \right) }}{{5000\,{\sigma _1}^5}}, \end{aligned}$$

(18)

where ${\sigma _1} = \mathrm{{cosh}}\left( {\frac{{\sqrt{3} \,\sqrt{10} \, \wp }}{{400}}} \right)$

$$\begin{aligned} \begin{array}{l} {\vartheta _2} = \frac{{3087\,\sinh {{({\sigma _4})}^2}}}{{{\sigma _2}}} + \frac{{1029\,\sinh {{({\sigma _4})}^2}}}{{20000\,\cosh {{({\sigma _4})}^6}}} - \frac{{1029}}{{{\sigma _3}}} - \frac{{1029}}{{100000\,\cosh {{({\sigma _4})}^4}}}\\ \qquad \quad + \frac{{7\,\left( {\frac{{441\,\sinh {{({\sigma _4})}^2}}}{{{\sigma _2}}} + \frac{{147\,\sinh {{({\sigma _4})}^2}}}{{40000\,\cosh {{({\sigma _4})}^6}}} - \frac{{147}}{{{\sigma _3}}} - \frac{{147}}{{200000\,\cosh {{({\sigma _4})}^4}}}} \right) }}{{10\,\cosh {{({\sigma _4})}^2}}}\\ \qquad \quad + \frac{{7\,\sqrt{3} \,\sqrt{10} \,\sinh ({\sigma _4})\,\left( {\frac{{{\sigma _1}}}{{500\,\cosh {{({\sigma _4})}^3}}} + \frac{{{\sigma _1}}}{{5000\,\cosh {{({\sigma _4})}^5}}}} \right) }}{{2000\,\cosh {{({\sigma _4})}^3}}}, \end{array} \end{aligned}$$

(19)

where ${\sigma _1} = 49\,\sqrt{3} \,\sqrt{10} \,\sinh ({\sigma _4})$, ${\sigma _2} = 20000\,\cosh {{\sigma _4})^4}$, ${\sigma _3} = 20000\,\cosh {({\sigma _4})^2}$, ${\sigma _4} = \frac{{\sqrt{3} \,\sqrt{10} \,\wp }}{{400}}.$

$$\begin{aligned} {\varpi _0}= & {} \frac{2}{{\cosh {{\left( {\frac{{\sqrt{3} \,\sqrt{10} \,\wp }}{{400}}} \right) }^2}}}. \end{aligned}$$

(20)

$$\begin{aligned} {\varpi _1}\left( x \right)= & {} \frac{{7\,\sqrt{3} \,\sqrt{10} \,\sinh \left( {\frac{{\sqrt{3} \,\sqrt{10} \,\wp }}{{400}}} \right) }}{{50\,{\sigma _1}^3}} \nonumber \\{} & {} + \frac{{7\,\sqrt{3} \,\sqrt{10} \,\sinh \left( {\frac{{\sqrt{3} \,\sqrt{10} \,\wp }}{{400}}} \right) }}{{250\,{\sigma _1}^5}}, \end{aligned}$$

(21)

where ${\sigma _1} = \mathrm{{cosh}}\left( {\frac{{\sqrt{3} \,\sqrt{10} \,\wp }}{{400}}} \right) .$

$$\begin{aligned} \begin{array}{l} {\varpi _2} = \frac{{{\sigma _3}}}{{{\sigma _6}}} + \frac{{{\sigma _4}}}{{4000\,\mathrm{{cosh}}{{({\sigma _8})}^6}}} - \frac{{147}}{{{\sigma _7}}} - \frac{{147}}{{{\sigma _5}}} \\ \qquad \quad + \frac{{7\,\left( {\frac{{63\,\mathrm{{sinh}}{{({\sigma _8})}^2}}}{{{\sigma _6}}} + \frac{{21\,\mathrm{{sinh}}{{({\sigma _8})}^2}}}{{2000\,\mathrm{{cosh}}{{({\sigma _8})}^6}}} - \frac{{21}}{{{\sigma _7}}} - \frac{{21}}{{10000\,\mathrm{{cosh}}{{({\sigma _8})}^4}}}} \right) }}{{10\,\mathrm{{cosh}}{{({\sigma _8})}^2}}} \\ \qquad \quad + \frac{{\frac{{{\sigma _3}}}{{{\sigma _5}}} + \frac{{{\sigma _4}}}{{40000\,\mathrm{{cosh}}{{({\sigma _8})}^6}}} - \frac{{147}}{{20000\,\mathrm{{cosh}}{{({\sigma _8})}^2}}} - \frac{{147}}{{200000\,\mathrm{{cosh}}{{({\sigma _8})}^4}}}}}{{\mathrm{{cosh}}{{({\sigma _8})}^2}}} \\ \qquad \quad + \frac{{7\,\sqrt{3} \,\sqrt{10} \,\mathrm{{sinh}}({\sigma _8})\,\left( {\frac{{{\sigma _2}}}{{50\,\mathrm{{cosh}}{{({\sigma _8})}^3}}} + \frac{{{\sigma _2}}}{{250\,\mathrm{{cosh}}{{({\sigma _8})}^5}}}} \right) }}{{2000\,\mathrm{{cosh}}{{({\sigma _8})}^3}}}\\ \qquad \quad + \frac{{\sqrt{3} \,\sqrt{10} \,\mathrm{{sinh}}({\sigma _8})\,\left( {\frac{{{\sigma _1}}}{{500\,\mathrm{{cosh}}{{({\sigma _8})}^3}}} + \frac{{{\sigma _1}}}{{5000\,\mathrm{{cosh}}{{({\sigma _8})}^5}}}} \right) }}{{200\,\mathrm{{cosh}}{{({\sigma _8})}^3}}}, \end{array} \end{aligned}$$

(22)

where ${\sigma _1} = 49\,\sqrt{3} \,\sqrt{10} \,\sinh ({\sigma _8}),\mathrm{{\;\;}}{\sigma _2} = 7\,\sqrt{3} \,\sqrt{10} \,\sinh ({\sigma _8}),\mathrm{{\;\;}}{\sigma _3} = 441\,\sinh {({\sigma _8})^2},\mathrm{{\;\;}}{\sigma _4} = 147\,\sinh {({\sigma _8})^2}, {\sigma _5} = 20000\,\cosh {({\sigma _8})^4},{\sigma _6} = 2000\,\cosh {{\sigma _8}^4},{\sigma _7} = 2000\,\cosh {({\sigma _8})^2},{\sigma _8} = \frac{{\sqrt{3} \,\sqrt{10} \,\wp }}{{400}}.$ The remaining coefficient of the series solution can be computed using MATLAB software package. The tsunami velocity and wave amplification (height) are given by the series as follows:

$$\begin{aligned} \upsilon \left( {\wp ,\ell } \right)&= {\vartheta _0}\left( \wp \right) \\&\quad + {\vartheta _1}\left( \wp \right) \ell + {\vartheta _2}\left( \wp \right) \,{\ell ^2} + \ldots ,\\ \omega \left( {\wp ,\ell } \right)&= {\varpi _0}\left( \wp \right) \\&\quad + {\varpi _1}\left( \wp \right) \ell + {\varpi _2}\left( \wp \right) \,{\ell ^2} + \ldots , \end{aligned}$$

where ${\vartheta _0}\left( \wp \right)$,${\vartheta _1}\left( \wp \right)$,${\vartheta _2}\left( \wp \right) ,\ldots$ and ${\varpi _0}\left( \wp \right) ,{\varpi _1}\left( \wp \right) ,{\varpi _2}\left( \wp \right) ,\ldots$ are coefficient and given by Eqs. (17)–(22).

Case II: Amplification (Breaking) and run-up of the tsunami waves on the shore Taking $\varphi \left( \wp \right) = m\wp + 300$, Eqs. (1) and (2) reduces to

$$\begin{aligned}{} & {} \frac{{\partial \upsilon }}{{\partial \ell }} + \upsilon \frac{{\partial \upsilon }}{{\partial \wp }} + g\frac{{\partial \omega }}{{\partial \wp }} = 0, \end{aligned}$$

(23)

$$\begin{aligned}{} & {} \frac{{\partial \omega }}{{\partial \ell }} + \frac{\partial }{{\partial \wp }}\left( {\upsilon \left( {m\wp + 300 + \omega } \right) } \right) = 0. \end{aligned}$$

(24)

Applying RDTM to Eqs. (23) and (24), we get following system of recursive formula:

$$\left( {\kappa + 1} \right){\vartheta _{\kappa + 1}}\left( \wp \right) + \sum\limits_{\iota = 0}^\kappa {{\vartheta _\iota }\left( \wp \right){\vartheta _{\kappa - \iota }}\left( \wp \right)} + g\frac{{\partial {\varpi _\kappa }\left( \wp \right)}}{{\partial \wp }} = 0,$$

(25)

$$\begin{aligned}{} & {} \begin{array}{l} \left( {\kappa + 1} \right) {\varpi _{\kappa + 1}}\left( \wp \right) + m{\vartheta _k}\left( \wp \right) + m\wp \frac{{\partial {\vartheta _k}\left( \wp \right) }}{{\partial \wp }} + 300\frac{{\partial {\vartheta _\kappa }\left( \wp \right) }}{{\partial \wp }} \\ + \qquad \sum \limits _{\iota = 0}^\kappa {{\vartheta _\iota }} \left( \wp \right) \left( {\kappa - \iota + 1} \right) {\varpi _{\kappa - \iota + 1}}\left( \wp \right) \\ + \qquad \sum \limits _{\iota = 0}^\kappa {{\varpi _\iota }} \left( \wp \right) \left( {\kappa - \iota + 1} \right) {\vartheta _{\kappa - \iota + 1}}\left( \wp \right) = 0. \end{array} \end{aligned}$$

(26)

The coefficient of series solution is obtained by substituting $\kappa = 0,1,2, \ldots ,n$ in Eqs. (25) and (26). Some of the coefficients of the series solution are mention below:

$$\begin{aligned}{} & {} {\vartheta _0}\left( \wp \right) \nonumber \\{} & {} \quad = \frac{7}{{5\,\cosh {{\left( {\frac{{\sqrt{3} \,\sqrt{10} \,\wp }}{{400}}} \right) }^2}}}, \end{aligned}$$

(27)

$$\begin{aligned}{} & {} {\vartheta _1} = \frac{{49\,\sqrt{3} \,\sqrt{10} \,\mathrm{{sinh}}\left( {\frac{{\sqrt{3} \,\sqrt{10} \,\wp }}{{400}}} \right) }}{{500\,{\sigma _1}^3}} \nonumber \\{} & {} \qquad \quad + \frac{{49\,\sqrt{3} \,\sqrt{10} \,\mathrm{{sinh}}\left( {\frac{{\sqrt{3} \,\sqrt{10} \,\wp }}{{400}}} \right) }}{{5000\,{\sigma _1}^5}}, \end{aligned}$$

(28)

where ${\sigma _1} = \mathrm{{cosh}}\left( {\frac{{\sqrt{3} \,\sqrt{10} \,\wp }}{{400}}} \right)$.

$$\begin{aligned}{} & {} {\varpi _0} = \frac{2}{{\cosh {{\left( {\frac{{\sqrt{3} \,\sqrt{10} \,x}}{{400}}} \right) }^2}}}. \end{aligned}$$

(29)

$$\begin{aligned}{} & {} \begin{array}{l} {\varpi _1} = \frac{{21\,\sqrt{3} \,\sqrt{10} \,\mathrm{{sinh}}\left( {\frac{{\sqrt{3} \,\sqrt{10} \,x}}{{400}}} \right) }}{{10\,{\sigma _2}^3}} + \frac{{14}}{{25{\sigma _2}^2}} \\ \qquad \quad + \frac{{7\sqrt{3} \,\sqrt{10} \,\mathrm{{sinh}}\left( {\frac{{\sqrt{3} \,\sqrt{10} \,x}}{{400}}} \right) }}{{250\,{\sigma _2}^5}} \\ \qquad \quad + \frac{{7\sqrt{3} \,\sqrt{10} \,x\,\mathrm{{sinh}}\left( {\frac{{\sqrt{3} \,\sqrt{10} \,x}}{{400}}} \right) }}{{2500\,{\sigma _2}^3}}, \end{array} \end{aligned}$$

(30)

where ${\sigma _2} = \mathrm{{cosh}}\left( {\frac{{\sqrt{3} \,\sqrt{10} \,\wp }}{{400}}} \right)$. The remaining coefficient of the series solution can be computed using MATLAB software package. The tsunami velocity and wave amplification (height) are given by the series as follows:

$$\begin{aligned}&\upsilon \left( {\wp ,\ell } \right) = {\vartheta _0}\left( \wp \right) \\&\qquad \qquad + {\vartheta _1}\left( \wp \right) \ell + {\vartheta _2}\left( \wp \right) \,{\ell ^2} + \ldots ,\\&\quad \omega \left( {\wp ,\ell } \right) = {\varpi _0}\left( \wp \right) \\&\qquad \qquad + {\varpi _1}\left( \wp \right) \ell + {\varpi _2}\left( \wp \right) \,{\ell ^2} + \ldots , \end{aligned}$$

where ${\vartheta _0}\left( \wp \right)$,${\vartheta _1}\left( \wp \right)$,${\vartheta _2}\left( \wp \right)$,...and ${\varpi _0}\left( \wp \right) ,{\varpi _1}\left( \wp \right) ,{\varpi _2}\left( \wp \right) ,\ldots$ are coefficient and given by Eqs. (27)–(30).

5 Result and discussion

The objective is to validate the solution technique, namely the reduced differential transform method for solving shallow water equations, by simulating tsunami propagation along the coastline. Two main simulation scenarios are considered: (1) mid-ocean tsunami propagation; and (2) breaking (amplification), and running-up of tsunami waves on the beach for three different coast slopes. To further clarify the results after entering the coast region, the simulation is visualized graphically in the positive portion of the computational domain.

To validate the results of RDTM, the obtain solution is compared with the exact solution for velocity and tsunami wave height in the open ocean. Figures 3 and 4 show that while propagating at a constant speed, tsunami waves maintain their shape and velocity. Nonlinear and dispersive effects in the medium cancel out to cause the tsunami wave to behave this way. Because there are no coasts where waves can break, the tsunami wave remains intact. To show the reliability and accuracy of the obtained result, comparison of exact and obtained results is shown in Figs. 4 and 5. One can check the convergence of analytical solution for particular parameter values using Theorems 1 and 2.

Fig. 3

Solution of tsunami wave velocity ($\upsilon \left( {\wp ,\ell }\right)$) and wave amplification ($\mu \left( {\wp ,\ell } \right)$) case 1, respectively

Fig. 4

Comparison of obtained result and exact solution for Case I

Fig. 5

Solution of tsunami wave velocity ($\upsilon \left( {\wp ,\ell }\right)$) and wave amplification case 1, respectively, for $m=0.2$

Tables 2 and 3 show the of tsunami velocity and wave amplification for different time and distance for Case I. Using a simulation, we have simulated the breaking behavior of the tsunami wave at three different sea depths, $\varphi \left( \wp \right) =m\wp +300$, where $m = 0.2, 0.4, 0.6$. Figures 5, 6 and 7 illustrate tsunami wave velocity and height at various time and coast slopes. For the case 2 the exact solution is not available, so to validate the obtained result by proposed method comparison is shown in Tables 4 and 5 of tsunami velocity and wave amplification for different time and distance with slope $m=0.6$. The tsunami’s wave speed and amplitude decrease as it approaches the coastline, and the wave’s amplitude grows initially before diminishing gradually as it approaches the coast. As a result of the shoaling effect, the tsunami undergoes a transformation. Due to the fact that the water becomes superficial, shoaling occurs because the waves impact the sea floor. A wave becomes sluggish as it moves over the superficial part of the water; this causes it to decelerate. Waves lose their wavelength as they decelerate, so their length decreases. Waves increase in amplitude with decreasing wavelength. It is possible to imagine that waves are compressed laterally, causing water in the waves to soar due to a very small space to occupy as wavelengths reduce. While tsunamis are relatively small in mid-ocean, they can be as big as two feet or more when they reach the coasts. In Fig. 8, the amplitude of a tsunami wave is shown to be affected by the depth of the sea near the shore and in the middle of the ocean. While sea depth affects wave width in mid-sea, it does not affect wave amplification. As the sea depth increases, the tsunami wave width increases, while the amplitude remains the same. The wavelength and amplitude of wave are both influenced by the depth when the wave is close to the shore. As sea depth increases, the width of tsunamis also increases, but their amplitudes decrease.

Table 2 Numerical value of tsunami velocity ($\upsilon \left( {\wp ,\ell }\right)$) for different time $(\ell )$ and distance ($\wp$) for Case I

Table 3 Numerical value of wave amplification ($\mu \left( {\wp ,\ell } \right)$) for different time $(\ell )$ and distance for case I

Table 4 Comparison of numerical value of tsunami velocity ($\upsilon \left( {\wp ,\ell }\right)$) for different time $(\ell )$ and distance $(\wp )$ for Case II with slope $m=0.6$

Table 5 Comparison of numerical value of wave amplification ($\mu \left( {\wp ,\ell } \right)$) for different time $(\ell )$ and distance $(\wp )$ for Case II with slope m = 0.6

Fig. 6

Tsunami wave velocity($\upsilon \left( {\wp ,\ell }\right)$) and wave amplification ($\mu \left( {\wp ,\ell } \right)$) for case II with $m=0.4$

Fig. 7

Tsunami wave velocity ($\upsilon \left( {\wp ,\ell }\right)$) and wave amplification ($\mu \left( {\wp ,\ell } \right)$) for case II with $m=0.6.$

Fig. 8

Graph of tsunami velocity ($\upsilon \left( {\wp ,\ell }\right)$) and wave amplification ($\mu \left( {\wp ,\ell } \right)$) near the coast with slope $m=0.4$ at time $\ell =1$ at different depth $D=20,25,30$

6 Conclusion

To simulate tsunami waves propagating in oceans and on ocean coasts, a robust scheme based on the Taylor’s series expansion has been presented in this paper. Numerical results indicate that the proposed scheme is highly accurate and reliable in solving such models. Using numerical simulations, we examined the effects of coast slopes and ocean depths on tsunami run-up.

The numerical simulations are based on a nonlinear shallow-water model. This study finds that tsunami wave velocity decreases as it approaches coastlines and their height increases in the first moments before decreasing over time once it enters the shoaling water. Based on previous studies and tsunami physics, the run-up height is primarily determined by the coast slope. When the coast slope becomes steep, the tsunami wave’s velocity and height decrease.