Nonlinear dynamic behavior analysis of an elastically restrained double-beam connected through a mass-spring system that is nonlinear

Abstract

Some complex engineering structures can be modeled as multiple beams connected through coupling elements. When the coupling element is elastic, it can be simplified as a mass-spring system. The existing studies mainly concentrated on the double-beam coupled through elastic connectors, where the connector is simplified as the equivalent linear stiffness element or linear mass-spring system. Furthermore, many researches ignore rotational boundary restraints in analyzing dynamic behavior of the double-beam connected through elastic connectors, limiting their engineering generality. Considering the above limitations, this study attempts to employ the cubic nonlinear stiffness in the coupling mass-spring system and study the potential application of the mass-spring system that is nonlinear on the vibration control of the double-beam system. Using the variational method and the generalized Hamiltonian method build the corresponding system’s governing functions. Applying the Galerkin truncation method (GTM) obtains the dynamic behavior of the double-beam connected through a mass-spring system that is nonlinear. According to this study, the change of the mass-spring system that is nonlinear significantly influences the dynamic behavior of the double-beam system, where the complex dynamic behavior occurs under certain parameters of the mass-spring system that is nonlinear. Suitable parameters of the mass-spring system that is nonlinear are good at the vibration suppression at the boundary of the vibration system. Furthermore, the mass-spring system that is nonlinear can change the characteristics of the double-beam system’s kinetic energy transfer. For the vibration model established in this work, a quasi-periodic vibration state can be regarded as a sign of the occurrence of the targeted energy transfer of the double-beam connected through a mass-spring system that is nonlinear.

1 Introduction

The beam structure is an important component of many complex structures in various engineering branches, including architectural engineering, aerospace engineering, marine engineering, and others. Beam structures are inevitably subjected to the unwanted vibration introduced by the working environment or energy equipment. The unwanted vibration negatively affects the stability and safety of beam structures. To suppress complex structures’ vibration, deeply understanding the vibration characteristics of beam structures is indispensable.

Vibration characteristics of beam structures have been broadly studied. Kang and Kim [1] summarized the early studies related to Euler–Bernoulli and Timoshenko beams, where the general boundary constraints were considered as boundary conditions of such beam structures. As one of the common engineering techniques, vibration characteristics of beams with elastic boundaries was obtained through the Fourier series [2]. To strengthen the convenience and applicability of the Fourier series, the improved Fourier series was proposed [3, 4], where the derivative of such a Fourier series was continuous at the boundary. Vibration characteristics of various beam structures with general boundary constraints were easily gained by employing the corresponding Fourier series [5,6,7,8,9,10]. The corresponding studies suggest that the boundary-smoothed Fourier series is accurate and correct in predicting the vibration characteristics of elastically restrained beams.

Nowadays, scholars have attempted to utilize the beneficial influence of nonlinearity to control the vibration level of elastic structures. According to the installation form, the nonlinear stiffness can be applied as nonlinear supports or nonlinear oscillators in the vibration control of beam structures. For beams with supporting nonlinearities, Özhan and Pakdemirli [11] studied three-to-one internal resonances motivated by cubic nonlinearities. Ghayesh et al. [12, 13] investigated the nonlinear vibration of beams attached with cubic nonlinear stiffness. Wang and Fang [14] and Mao et al. [15] studied the vibration of beams attached with supporting nonlinearity. Tang et al. [16] exploited the phase closure principle to predict the nonlinear characteristics of beams with nonlinear boundaries. Ding et al. [17, 18] proposed an adjustable nonlinear isolator. Considering the engineering practice, Ding and Chen [19] employed the adjustable nonlinear isolator in a slightly curved beam and studied its vibration transmissibility. Zhao and Du [20] studied the dynamic behavior of a pre-pressure beam attached with supporting nonlinearities.

For beam structures with nonlinear oscillators, Georgiades and Vakakis [21] studied the dynamic responses of a linear beam attached to a nonlinear oscillator. Such a nonlinear oscillator is defined as the nonlinear energy sink (NES). Ahmadabadi and Khadem [22, 23] and Kani et al. [24] investigated vibration control and energy harvesting of the beam by employing the NES. For beam structures with different boundaries, Parseh et al. [25] and Kani et al. [26] studied the robustness of NESs. Parseh et al. [27] stable steady-state dynamic responses of a nonlinear beam structure attached with an NES. Chen et al. [28] exploited parallel NESs to suppress the vibration of beam structures under the shock load. Then, the nonlinear forced vibration control of beam structures with an attached NES or boundary nonlinear energy sinks was studied in Refs [29, 30]. The above investigations suggest that a suitable utilization of nonlinear stiffness is good for the vibration control of beams.

On some engineering occasions, complex structures such as double-layer bridges, propulsion systems, and others can be modeled as multiple beams connected via coupling elements. When the coupling element is elastic, it can be simplified as a mass-spring system. Especially in marine engineering, ship propulsion shafting systems typically consist of multiple slender shafts. When studying the transverse vibration of such a shafting system under low rotation speed, such a slender shafting system can be simplified as beams connected through some coupling device, where the coupling device can be simplified as a mass-spring system. Furthermore, the axial motion of the shaft system is harmful to the stability of the shafting systems. Some limiters are installed on the shafting systems at both internal and boundary to limit their axial motion. For the simplified double-beam structures, Oniszczuk [31] investigated the free vibration of the double beams connected through a layer that is elastic. Gurgoze et al. [32] and Pajand and Hozhabrossadati [33] studied the bending vibration characteristics of double beams connected through a mass-spring system that was linear. Hilal [34] investigated the influence of a moving load on the dynamic responses of a double-beam system. Li and Hua [35] proposed a spectral finite element-based normal mode method to predict dynamic responses of the elastically connected double-beam. Rosa and Lippiello [36] established the vibration analysis model of the double-beam system joined by a Winkler-type soil, where free vibration of such a structure with generally restrained boundaries was studied. Zhang et al. [37], Stojanovic et al. [38], and Kozic et al. [39] investigated the vibration and buckling characteristics of a pre-pressure double-beam. Palmeri and Adhikari [40] proposed a novel state-space form to predict dynamic responses of the double-beam structure joined by an inner viscoelastic layer. Mao [41, 42] employed the Adomian modified decomposition method to study the multiple-beam structure's vibration characteristics and forced dynamic responses. Mohammadi and Nasirshoaibi [43] studied forced dynamic responses of an elastically connected pre-pressure double-beam system with a Pasternak middle layer, where the double-beam structure was simply supported. Pisarski et al. [44] employed multiple smart damping members to suppress the vibration of the double-beam system. Fei et al. [45] proposed a new method to predict the vibration characteristics of a tensioned structure. Agboola et al. [46] studied the influence of structural parameters on the vibration characteristics of the double-beam, where the double-beam is non-prismatic and simply supported. Rahman and Lee [47] proposed a new modified multi-level residue harmonic balance method to predict nonlinear dynamic responses of a double-beam structure. Lee and Wang [48] investigated the transverse vibration of a double-beam system connected through coupling elements in experiments and theory, where the external force was non-uniform. Chen et al. [49], Hao et al. [50], Zhao and Asce [51], and Li et al. [52] studied vibration characteristics of double beams with classical and generally restrained boundary conditions. Pajand et al. [53] first considered the double beams connected through a three-degree-of-freedom system. Then, natural frequencies and mode shapes were predicted through a finite element method. Guo et al. [54] established the vibration analysis model of an asymptotically reduced coupled model, which was consisting of two inclined cables and one deck beam. The dynamic responses, stability, and bifurcations of such a vibration system were systematically investigated. Stojanovic et al. [55] investigated nonlinear vibrations and vibration transmissibility of a coupled beam-arch bridge system, where the coupling devices presented nonlinear characteristics and the bridge was geometrically nonlinear. According to the above references, the existing studies mainly concentrated on the double-beam coupled through elastic connectors, where the connector is simplified as the equivalent linear stiffness element or linear mass-spring system. Many researches ignore rotational boundary restraints in analyzing dynamic behavior of the double-beam connected through elastic connectors, limiting their engineering generality.

Considering the above limitations and engineering practice, this study attempts to employ the cubic nonlinear stiffness in the coupling mass-spring system and study the potential application of the mass-spring system that is nonlinear on the transverse vibration of an elastically restrained double-beam system, where the axial motion of the double-beam system is ignored. Using the variational method and the generalized Hamiltonian method, the governing functions for a double-beam connected through a mass-spring system that is nonlinear are built. Applying the Galerkin truncation method (GTM) obtains the dynamic behavior of the double-beam connected through a mass-spring system that is nonlinear. The influence of the mass-spring system that is nonlinear on the transverse vibration of an elastically restrained double-beam system is researched.

2 Theoretical Formulations

2.1 Model Description

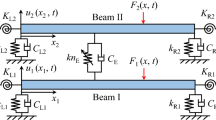
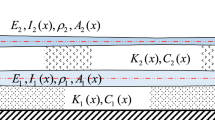
As illustrated in Fig. 1, the physical model of a double-beam connected through a mass-spring system that is nonlinear is built. Such a vibration system consists of two beams and a mass-spring system that is nonlinear. u₁(x₁,t), u₂(x₂,t), and u_E(t) are vibration displacements of each beam and the mass-spring system that is nonlinear. E₁, E₂, ρ₁, ρ₂, S₁, S₂, I₁, I₂, C_B1, and C_B2 are the elastic modulus, mass density, section area, inertia moment, and external viscous damping of each beam, respectively. To improve the generality of the vibration analysis model, this work studies the dynamic behavior of a double-beam connected through a mass-spring system that is nonlinear with general boundary conditions. Boundary translational and rotational restraining springs are introduced at the boundary of each beam, where k_L1, k_L2, k_R1, k_R2, K_L1, K_L2, K_R1, and K_R2 are stiffness coefficients of each boundary restraining spring. Different boundary conditions (clamped boundary, free boundary, simply support boundary, and elastic boundary) can be simulated by setting the stiffness coefficients of boundary restraining springs. k_E1, k_E2, kn_E1, kn_E2, C_E1, C_E2, and m_E are the linear stiffness, nonlinear stiffness, viscous damping, and concentrated mass of the mass-spring system that is nonlinear. x_E1 and x_E2 are the positions of the mass-spring system that is nonlinear, where x_E1 is the position of the system located at Beam I and x_E2 is the position of the system located at Beam II. For this study, the nonlinear stiffness of the mass-spring system that is nonlinear is regarded as cubic stiffness, which can be realized through mechanism design.

Fig. 1

The physical model of a double-beam connected through a mass-spring system that is nonlinear

In marine engineering, the shafting system under low rotation speed can be simplified as the double-beam system, where the external excitation introduced by the energy equipment typically locates on the determined position of the shafting system. In the vibration analysis, the corresponding external excitation can be approximated as a point excitation. Obviously, to ensure the service life of the energy equipment, the energy equipment is usually operated at its rated condition, which indicates that the external excitation introduced to shafting systems is typically periodic. Considering the above engineering situation, the point harmonic excitation is selected as the external excitation in this study. F₁(x₁,t) is the external force subjected to Beam I and its specific expression is defined as

$$ F_{1} \left( {x_{1} ,t} \right) = \delta \left( {x_{1} - L_{1} } \right)F_{1} \sin \left( {\omega t} \right) $$

(1)

where F₁ is the amplitude of the excitation force, δ(.) is the Dirac function, and ω is the circular frequency of the external excitation force.

Each beam in Fig. 1 is modeled as the Euler–Bernoulli beam. The potential energy and kinetic energy of the vibration system are derived as

$$ V = V_{BeamI} + V_{BeamII} + V_{BoundaryI} + V_{BoundaryII} + V_{E} $$

(2a)

and

$$ T = T_{I} + T_{II} + T_{E} $$

(2b)

V_BeamI and V_BeamII are the potential energy of each beam. V_BI and V_BII are the potential energy of boundary restraining springs belonging to each beam. V_E is the potential energy of the mass-spring system that is nonlinear. T_I, T_II, and T_E are the kinetic energy of each beam and the mass-spring system that is nonlinear.

The virtual work done by the external excitation force is derived as

$$ \delta W_{F} = \delta W_{F1} $$

(3)

δW_F1 is the virtual work done by the external excitation force on Beam I.

The virtual work done by the viscous damping is derived as

$$ \delta W_{\text{C}} = \delta W_{C1} + \delta W_{C2} + \delta W_{CE1} + \delta W_{CE2} $$

(4)

δW_C1 and δW_C2 are the virtual work done by the viscous damping of Beam I and Beam II. δW_CE1 and δW_CE2 are the virtual work done by the viscous damping of the mass-spring system that is nonlinear. The specific form of each term of Eqs. (2), (3), and (4) are listed in Appendix A.

Using the variational method and the generalized Hamiltonian method, we can find the governing functions for a double-beam connected through a mass-spring system that is nonlinear, namely,

$$ \begin{gathered} \rho_{1} S_{1} \frac{{\partial^{2} u_{1} }}{{\partial t^{2} }} + C_{B1} \frac{{\partial u_{1} }}{\partial t} + E_{1} I_{1} \frac{{\partial^{4} u_{1} }}{{\partial x_{1}^{4} }} + F_{1} \left( {x_{F1} ,t} \right) + \delta \left( {x_{1} - x_{E1} } \right) \hfill \\ \left\{ {k_{E1} \left[ {u_{1} - u_{E} \left( t \right)} \right] + kn_{E1} \left[ {u_{1} - u_{E} \left( t \right)} \right]^{3} + C_{E1} \left[ {\frac{{\partial u_{1} }}{\partial t} - \frac{{{\text{d}}u_{E} \left( t \right)}}{{{\text{d}}t}}} \right]} \right\} = 0 \hfill \\ \end{gathered} $$

(5a)

$$ \begin{gathered} \rho_{2} S_{2} \frac{{\partial^{2} u_{2} }}{{\partial t^{2} }} + C_{B2} \frac{{\partial u_{2} }}{\partial t} + E_{2} I_{2} \frac{{\partial^{4} u_{2} }}{{\partial x_{2}^{4} }} + \delta \left( {x_{2} - x_{E2} } \right) \hfill \\ \left\{ {k_{E2} \left[ {u_{2} - u_{E} \left( t \right)} \right] + kn_{E2} \left[ {u_{2} - u_{E} \left( t \right)} \right]^{3} + C_{E2} \left[ {\frac{{\partial u_{2} }}{\partial t} - \frac{{{\text{d}} u_{E} \left( t \right)}}{{{\text{d}} t}}} \right]} \right\} = 0 \hfill \\ \end{gathered} $$

(5b)

and

$$ \begin{gathered} m\frac{{{\text{d}}^{2} u_{E} }}{{{\text{d}} t^{2} }} + C_{E1} \left[ {\frac{{{\text{d}} u_{E} }}{{{\text{d}} t}} - \frac{{\partial u_{1} \left( {x_{{{\text{E}} 1}} ,t} \right)}}{\partial t}} \right] + C_{E2} \left[ {\frac{{{\text{d}} u_{E} }}{{{\text{d}} t}} - \frac{{\partial u_{2} \left( {x_{{{\text{E}} 2}} ,t} \right)}}{\partial t}} \right] \hfill \\ \begin{array}{*{20}c} {} & {} & {} \\ \end{array} + k_{E1} \left[ {u_{E} - u_{1} \left( {x_{{{\text{E}} 1}} ,t} \right)} \right] + k_{E2} \left[ {u_{E} - u_{2} \left( {x_{{{\text{E}} 2}} ,t} \right)} \right] \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} + kn_{E1} \left[ {u_{E} - u_{1} \left( {x_{{{\text{E}} 1}} ,t} \right)} \right]^{3} + kn_{E2} \left[ {u_{E} - u_{2} \left( {x_{{{\text{E}} 2}} ,t} \right)} \right]^{3} = 0 \hfill \\ \end{gathered} $$

(5c)

Boundary conditions of the double-beam system are derived as

$$ x_{1} = 0\begin{array}{*{20}c} : & {k_{{{\text{L}} 1}} u_{1} + E_{1} I_{1} \frac{{\partial^{3} u_{1} }}{{\partial x_{1}^{3} }} = 0} \\ \end{array} \begin{array}{*{20}c} , & {K_{L1} \frac{{\partial u_{1} }}{{\partial x_{1} }} - E_{1} I_{1} \frac{{\partial^{2} u_{1} }}{{\partial x_{1}^{2} }} = 0} \\ \end{array} $$

(6a)

$$ x_{1} = L_{1} \begin{array}{*{20}c} : & {k_{R1} u_{1} - E_{1} I_{1} \frac{{\partial^{3} u_{1} }}{{\partial x_{1}^{3} }} = 0} \\ \end{array} \begin{array}{*{20}c} , & {K_{R1} \frac{{\partial u_{1} }}{{\partial x_{1} }} + E_{1} I_{1} \frac{{\partial^{2} u_{1} }}{{\partial x_{1}^{2} }} = 0} \\ \end{array} . $$

(6b)

$$ x_{2} = 0\begin{array}{*{20}c} : & {k_{{{\text{L}} 2}} u_{2} + E_{2} I_{2} \frac{{\partial^{3} u_{2} }}{{\partial x_{2}^{3} }} = 0} \\ \end{array} \begin{array}{*{20}c} , & {K_{L2} \frac{{\partial u_{2} }}{{\partial x_{2} }} - E_{2} I_{2} \frac{{\partial^{2} u_{2} }}{{\partial x_{2}^{2} }} = 0} \\ \end{array} $$

(6c)

and

$$ x_{2} = L_{2} \begin{array}{*{20}c} : & {k_{R2} u_{2} - E_{2} I_{2} \frac{{\partial^{3} u_{2} }}{{\partial x_{2}^{3} }} = 0} \\ \end{array} \begin{array}{*{20}c} , & {K_{R2} \frac{{\partial u_{2} }}{{\partial x_{2} }} + E_{2} I_{2} \frac{{\partial^{2} u_{2} }}{{\partial x_{2}^{2} }} = 0} \\ \end{array} . $$

(6d)

According to Eqs. (5a) and (5b), the nonlinear restoring force introduced to Beam I and Beam II can be defined as,

$$ F_{{{\text{N}}1}} = \delta \left( {x_{1} - x_{E1} } \right)kn_{E1} \left[ {u_{1} - u_{E} \left( t \right)} \right]^{3} $$

(7a)

and

$$ F_{{{\text{N2}}}} = \delta \left( {x_{2} - x_{E2} } \right)kn_{E2} \left[ {u_{2} - u_{E} \left( t \right)} \right]^{3} $$

(7b)

where F_N1 is the nonlinear restoring force subjected to Beam I and F_N2 is the nonlinear restoring force subjected to Beam II. Furthermore, for the mass-spring system that is nonlinear, its nonlinear restoring force (F_NE) can be fined as,

$$ F_{NE} = kn_{E1} \left[ {u_{E} - u_{1} \left( {x_{{{\text{E}} 1}} ,t} \right)} \right]^{3} + kn_{E2} \left[ {u_{E} - u_{2} \left( {x_{{{\text{E}} 2}} ,t} \right)} \right]^{3} $$

(7c)

For the physical model established in this study, the corresponding terms of the generalized Hamiltonian principle are listed in Appendix B.

2.2 Solution Procedure

The governing functions of the vibration system derived in Sect. 2.1 are solved by the GTM. In this study, transverse vibration displacements of each beam are expanded as

$$ u_{1} \left( {x_{1} ,t} \right) = \sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{1} }} {\varphi_{1i} \left( {x_{1} } \right)q_{1i} \left( t \right)} $$

(8a)

and

$$ u_{2} \left( {x_{2} ,t} \right) = \sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{2} }} {\varphi_{2i} \left( {x_{2} } \right)q_{2i} \left( t \right)} $$

(8b)

where φ_1i(x₁) is the ith trial function of Beam I and φ_2i(x₂) is the ith trial function of Beam II. q_1i(t) and q_2i(t) are the i^th unknown time terms of each beam.

After substituting Eq. (8) into Eqs. (5a) and (5b), the Galerkin discretization procedure is utilized to deal with the governing functions of each beam, namely,

$$ \int_{0}^{{L_{1} }} {\left\{ \begin{gathered} \begin{array}{*{20}c} {} & {} \\ \end{array} \rho_{1} S_{1} \frac{{\partial^{2} u_{1} }}{{\partial t^{2} }} + C_{B1} \frac{{\partial u_{1} }}{\partial t} + E_{1} I_{1} \frac{{\partial^{4} u_{1} }}{{\partial x_{1}^{4} }} + F_{1} \left( {x_{1} ,t} \right) \hfill \\ + \delta \left( {x_{1} - x_{E1} } \right)\left\{ \begin{gathered} k_{E1} \left[ {u_{1} - u_{E} \left( t \right)} \right] + kn_{E1} \left[ {u_{1} - u_{E} \left( t \right)} \right]^{3} \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} + C_{E1} \left[ {\frac{{\partial u_{1} }}{\partial t} - \frac{{{\text{d}}u_{E} \left( t \right)}}{{{\text{d}}t}}} \right] \hfill \\ \end{gathered} \right\} \hfill \\ \end{gathered} \right\}\psi_{{1m_{1} }} \left( {x_{1} } \right)} {\text{d}} x_{1} = 0 $$

(9a)

and

$$ \int_{0}^{{L_{2} }} {\left\{ \begin{gathered} \begin{array}{*{20}c} {} & {} & {} \\ \end{array} \rho_{2} S_{2} \frac{{\partial^{2} u_{2} }}{{\partial t^{2} }} + C_{B2} \frac{{\partial u_{2} }}{\partial t} + E_{2} I_{2} \frac{{\partial^{4} u_{2} }}{{\partial x_{2}^{4} }} \hfill \\ + \delta \left( {x_{2} - x_{E2} } \right)\left\{ \begin{gathered} k_{E2} \left[ {u_{2} - u_{E} \left( t \right)} \right] + kn_{E2} \left[ {u_{2} - u_{E} \left( t \right)} \right]^{3} \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} + C_{E2} \left[ {\frac{{\partial u_{2} }}{\partial t} - \frac{{{\text{d}} u_{E} \left( t \right)}}{{{\text{d}} t}}} \right] \hfill \\ \end{gathered} \right\} \hfill \\ \end{gathered} \right\}\psi_{{2m_{2} }} \left( {x_{2} } \right)} {\text{d}} x_{2} = 0 $$

(9b)

where ψ_1i(x₁) is the ith weight function of Beam I and ψ_2i(x₂) is the ith weight function of Beam II. m₁ = 1, 2, …, M₁ and m₂ = 1, 2, … M₂. Equation (9a) is the m₁th residual function of Beam I, and Eq. (9b) is the m₂th residual function of Beam II.

In the GTM, a set of functions that satisfy boundary conditions can be chosen as the trail and weight functions. For the physical model established in Sect. 3.1, mode functions of the elastically restrained single beam without the mass-spring system that is nonlinear exactly satisfy the corresponding boundary conditions. Therefore, the corresponding mode functions are chosen as the trail and weight functions. Such mode functions can be accurately obtained by employing the energy principle combined with the boundary-smoothed Fourier series [8,9,10].

Equation (9) is simplified as follows,

$$ RI_{{m_{1} 1}} + RI_{{m_{1} 2}} + RI_{{m_{1} 3}} + RI_{{m_{1} 4}} + RI_{{m_{1} 5}} + RI_{{m_{1} 6}} + RI_{{m_{1} 7}} = 0 $$

(10a)

and

$$ RII_{{m_{2} 1}} + RII_{{m_{2} 2}} + RII_{{m_{2} 3}} + RII_{{m_{2} 4}} + RII_{{m_{2} 5}} + RII_{{m_{2} 6}} = 0 $$

(10b)

The specific form of each residual term in Eq. (10) is listed in Appendix C.

To establish the matrix form of Eq. (10), Eq. (10) is transformed as

$$ RI_{{m_{1} 1}} = - \left( {RI_{{m_{1} 2}} + RI_{{m_{1} 3}} + RI_{{m_{1} 4}} + RI_{{m_{1} 5}} + RI_{{m_{1} 6}} + RI_{{m_{1} 7}} } \right) $$

(11a)

and

$$ RII_{{m_{2} 1}} = - \left( {RII_{{m_{2} 2}} + RII_{{m_{2} 3}} + RII_{{m_{2} 4}} + RII_{{m_{2} 5}} + RII_{{m_{2} 6}} } \right) $$

(11b)

The specific form of $RI_{{m_{1} 1}}$ and $RII_{{m_{2} 1}}$ is expanded as

$$ RI_{{m_{1} 1}} = CI_{{m_{1} 1}} \frac{{{\text{d}}^{2} q_{11} }}{{{\text{d}} t^{2} }} + CI_{{m_{1} 2}} \frac{{{\text{d}}^{2} q_{12} }}{{{\text{d}} t^{2} }} + \ldots CI_{{m_{1} i}} \frac{{{\text{d}}^{2} q_{1i} }}{{{\text{d}} t^{2} }} \ldots + CI_{{m_{1} N_{1} }} \frac{{{\text{d}}^{2} q_{{1{\text{N}}_{1} }} }}{{{\text{d}} t^{2} }} $$

(12a)

and

$$ RII_{{m_{2} 1}} = CII_{{m_{2} 1}} \frac{{{\text{d}}^{2} q_{21} }}{{{\text{d}} t^{2} }} + CII_{{m_{2} 2}} \frac{{{\text{d}}^{2} q_{22} }}{{{\text{d}} t^{2} }} + \ldots CII_{{m_{2} i}} \frac{{{\text{d}}^{2} q_{2i} }}{{{\text{d}} t^{2} }} \ldots + CII_{{m_{2} N_{2} }} \frac{{{\text{d}}^{2} q_{{2{\text{N}}_{2} }} }}{{{\text{d}} t^{2} }} $$

(12b)

Substituting Eq. (12) into Eq. (11), the specific form of Eq. (11) is derived as

$$ CI_{{m_{1} 1}} \frac{{{\text{d}}^{2} q_{11} }}{{{\text{d}} t^{2} }} + CI_{{m_{1} 2}} \frac{{{\text{d}}^{2} q_{12} }}{{{\text{d}} t^{2} }} + \ldots CI_{{m_{1} i}} \frac{{{\text{d}}^{2} q_{1i} }}{{{\text{d}} t^{2} }} \ldots + CI_{{m_{1} N_{1} }} \frac{{{\text{d}}^{2} q_{{1{\text{N}}_{1} }} }}{{{\text{d}} t^{2} }} = - \sum\limits_{{{\text{i}} = 2}}^{7} {RI_{{m_{1} {\text{i}} }} } $$

(13a)

and

$$ CII_{{m_{2} 1}} \frac{{{\text{d}}^{2} q_{21} }}{{{\text{d}} t^{2} }} + CII_{{m_{2} 2}} \frac{{{\text{d}}^{2} q_{22} }}{{{\text{d}} t^{2} }} + \ldots CII_{{m_{2} i}} \frac{{{\text{d}}^{2} q_{2i} }}{{{\text{d}} t^{2} }} \ldots + CII_{{m_{2} N_{2} }} \frac{{{\text{d}}^{2} q_{{2{\text{N}}_{2} }} }}{{{\text{d}} t^{2} }} = - \sum\limits_{{{\text{i}} = 2}}^{6} {RII_{{m_{2} {\text{i}} }} } $$

(13b)

Then, the matrix form of the residual functions is written as

$$ \left[ {\begin{array}{*{20}c} {CI_{11} } & \ldots & {CI_{1i} } & \ldots & {CI_{{1{\text{N}}_{1} }} } \\ \ldots & \ldots & \ldots & \ldots & \ldots \\ {CI_{{{\text{m}}_{1} 1}} } & \ldots & {CI_{{{\text{m}}_{1} i}} } & \ldots & {CI_{{{\text{m}}_{1} {\text{N}}_{1} }} } \\ \ldots & \ldots & \ldots & \ldots & \ldots \\ {CI_{{{\text{M}}_{1} 1}} } & \ldots & {CI_{{{\text{M}}_{1} {\text{i}} }} } & \ldots & {CI_{{{\text{M}}_{1} {\text{N}}_{1} }} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\frac{{{\text{d}}^{2} q_{11} }}{{{\text{d}} t}}} \\ \ldots \\ {\frac{{{\text{d}}^{2} q_{{1{\text{i}} }} }}{{{\text{d}} t^{2} }}} \\ \ldots \\ {\frac{{{\text{d}}^{2} q_{{1{\text{N}}_{1} }} }}{{{\text{d}} t^{2} }}} \\ \end{array} } \right] = - \left[ {\begin{array}{*{20}c} {\sum\limits_{{{\text{i}} = 2}}^{7} {RI_{{1{\text{i}} }} } } \\ \ldots \\ {\sum\limits_{{{\text{i}} = 2}}^{7} {RI_{{m_{1} {\text{i}} }} } } \\ \ldots \\ {\sum\limits_{{{\text{i}} = 2}}^{7} {RI_{{{\text{M}}_{1} {\text{i}} }} } } \\ \end{array} } \right] $$

(14a)

and

$$ \left[ {\begin{array}{*{20}c} {CII_{11} } & \ldots & {CII_{1i} } & \ldots & {CII_{{1{\text{N}}_{2} }} } \\ \ldots & \ldots & \ldots & \ldots & \ldots \\ {CII_{{{\text{m}}_{2} 1}} } & \ldots & {CII_{{{\text{m}}_{2} i}} } & \ldots & {CII_{{{\text{m}}_{2} {\text{N}}_{2} }} } \\ \ldots & \ldots & \ldots & \ldots & \ldots \\ {CI_{{{\text{M}}_{2} 1}} } & \ldots & {CII_{{{\text{M}}_{2} {\text{i}} }} } & \ldots & {CII_{{{\text{M}}_{2} {\text{N}}_{2} }} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\frac{{{\text{d}}^{2} q_{21} }}{{{\text{d}} t^{2} }}} \\ \ldots \\ {\frac{{{\text{d}}^{2} q_{2i} }}{{{\text{d}} t^{2} }}} \\ \ldots \\ {\frac{{{\text{d}}^{2} q_{{2{\text{N}}_{2} }} }}{{{\text{d}} t^{2} }}} \\ \end{array} } \right] = - \left[ {\begin{array}{*{20}c} {\sum\limits_{{{\text{i}} = 2}}^{6} {RII_{{1{\text{i}} }} } } \\ \ldots \\ {\sum\limits_{{{\text{i}} = 2}}^{6} {RII_{{m_{2} {\text{i}} }} } } \\ \ldots \\ {\sum\limits_{{{\text{i}} = 2}}^{6} {RII_{{{\text{M}}_{2} {\text{i}} }} } } \\ \end{array} } \right]. $$

(14b)

Substituting Eq. (8) into Eq. (5c), the specific form of the governing function of the mass-spring system that is nonlinear is derived as

$$ \begin{gathered} m_{E} \frac{{{\text{d}}^{2} u_{E} }}{{{\text{d}} t^{2} }} + C_{E1} \left[ {\frac{{{\text{d}} u_{E} }}{{{\text{d}} t}} - \sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{1} }} {\varphi_{1i} \left( {x_{E1} } \right)\frac{{{\text{d}} q_{1i} \left( t \right)}}{{{\text{d}} t}}} } \right] + C_{E2} \left[ {\frac{{{\text{d}} u_{E} }}{{{\text{d}} t}} - \sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{2} }} {\varphi_{2i} \left( {x_{E2} } \right)\frac{{{\text{d}} q_{2i} \left( t \right)}}{{{\text{d}} t}}} } \right] \hfill \\ + k_{E1} \left[ {u_{E} - \sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{1} }} {\varphi_{1i} \left( {x_{E1} } \right)q_{1i} \left( t \right)} } \right] + k_{E2} \left[ {u_{E} - \sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{2} }} {\varphi_{2i} \left( {x_{E2} } \right)q_{2i} \left( t \right)} } \right] \hfill \\ + kn_{E1} \left[ {u_{E} - \sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{1} }} {\varphi_{1i} \left( {x_{E1} } \right)q_{1i} \left( t \right)} } \right]^{3} + kn_{E2} \left[ {u_{E} - \sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{2} }} {\varphi_{2i} \left( {x_{E2} } \right)q_{2i} \left( t \right)} } \right]^{3} = 0 \hfill \\ \end{gathered} $$

(15)

Equations (14a), (14b), and (15) compose the residual functions of the elastically restrained double-beam connected through a mass-spring system that is nonlinear. Such residual functions can be solved by numerical methods. By substituting the numerical results of Eqs. (14a), (14b), and (15) into Eq. (8), dynamic responses at arbitrary positions of the elastically restrained double-beam connected through a mass-spring system that is nonlinear can be gained. In the GTM, when the boundary condition changes, the dynamic behavior of the double-beam connected through a mass-spring system that is nonlinear under the changed boundary can be obtained conveniently by changing the boundary restraining springs’ stiffness coefficient. Furthermore, by introducing multiple nonlinear mass-spring systems in the double-beam system, the vibration analysis model established in this section can be extended to predict the dynamic behavior of the double-beam connected through multiple nonlinear mass-spring systems.

3 Simulation results and discussion

In this section, the correctness and stability of the GTM in solving the residual functions are studied first. Then, the influence of the mass-spring system that is nonlinear on dynamic responses of the double-beam is investigated. Furthermore, to improve the engineering acceptance of the mass-spring system that is nonlinear, in analyzing dynamic responses of the double-beam system with the variation of nonlinear mass-spring system’s parameters, synchronous change parameters of the mass-spring system that is nonlinear.

With the prosperous study of the material field, lightweight and high-strength materials are gradually employed in engineering to alternative traditional materials. Therefore, this study investigates the potential application of the mass-spring system that is nonlinear for the double-beam system which is manufactured by aluminum alloy. Table 1 shows the structural parameters of the double-beam system. Table 2 gives the parameters of the mass-spring system that is nonlinear. Figure 2 presents the relation between the nonlinear restoring force and displacement of Beam I and Beam II, where u₁, u₂, and u_E change from − 0.02 to 0.02 m. It can be seen from Fig. 2 that the nonlinear restoring force presents nonlinearity with the variation of u₁, u₂, and u_E.

Table 1 Structural parameters of beams employed in the simulation

Table 2 Parameters of the mass-spring system that is nonlinear employed in numerical simulation

Fig. 2

The relation between the nonlinear restoring force and displacement of Beam I and Beam II

3.1 Validation of the dynamic responses

This section investigates the correctness and stability of the GTM in solving the residual functions established in Sect. 2. The time-domain calculation range is selected as 0 ~ 500 T_e, in which T_e is the period of the external excitation force, namely,

$$ T_{e} = \frac{2\pi }{\omega } $$

(16)

401 ~ 500 T_e is chosen as the stable calculation results of the double-beam connected through a mass-spring system that is nonlinear. In the above time-domain region, transient dynamic responses of the vibration system have died away. The relation of the truncation number is set as N₁ = N₂ = M₁ = M₂. In plotting amplitude-frequency response curves of the double-beam connected through a mass-spring system that is nonlinear, the maximum value of the time-domain responses of the double-beam system under each excitation frequency is selected as the y coordinate while the excitation frequency is selected as the x coordinate.

Firstly, the harmonic balance method (HBM) and Lagrange method (LM) are employed to verify the correctness of the GTM in obtaining the dynamic behavior of the double-beam connected through a mass-spring system that is nonlinear, where a 4-term truncation number is applied in this part. For HBM, the time terms are set as fundamental harmonics. For LM, the matrix equation of the double-beam connected through a mass-spring system that is nonlinear is established by employing the Lagrange function combined with the energy principle. It is worth mentioning that the GTM and LM are quite different in establishing the matrix equation of the double-beam system. Furthermore, the GTM and LM calculate the dynamic behavior of the double-beam system from the time domain while the HBM calculates it from the frequency domain. Figure 3 presents amplitude-frequency curves of the double-beam system connected through a mass-spring system that is nonlinear under different methods. According to Fig. 3, amplitude-frequency curves obtained by the above three methods accurately match each other. Furthermore, in order to increase the credibility of the GTM results, Fig. 4 presents the stable time diagrams at both ends of the double-beam system predicted by the GTM, HBM, and LM, where the external excitation frequency is selected as 30 Hz. From Fig. 4, stable time diagrams predicted by the GTM, HBM, and LM match each other well. In summary, the phenomenon in Figs. 3 and 4 verifies the correctness of the GTM in predicting the dynamic behavior of the double-beam connected through a mass-spring system that is nonlinear.

Fig. 3

Amplitude-frequency curves of the double-beam connected through a mass-spring system that is nonlinear obtained through different methods

Fig. 4

Time diagrams at both ends of the double-beam connected through a mass-spring system that is nonlinear predicted by different methods (30 Hz)

Secondly, the stability of the GTM in predicting amplitude-frequency curves of the double-beam connected through a mass-spring system that is nonlinear is studied. Amplitude-frequency curves with different truncation number are graphed in Fig. 5. According to Fig. 5, amplitude-frequency curves stay stable as the truncation number is 4-term, 6-term, and 8-term. In the following study, we choose 6-term as the truncation number of GTM.

Fig. 5

Amplitude-frequency curves of the double-beam connected through a mass-spring system that is nonlinear with different truncation number

3.2 Amplitude-frequency curves influenced by the mass-spring system that is nonlinear

This section investigates the influence of mass-spring system that is nonlinear on amplitude-frequency curves. Firstly, investigate the influence of nonlinear stiffness (kn_E = kn_E1 = kn_E2) on amplitude-frequency curves. kn_E is selected as 0 N/m³, 10⁹ N/m³, 2 × 10⁹ N/m³, 3 × 10⁹ N/m³. Amplitude-frequency curves of the double-beam connected through a mass-spring system that is nonlinear under different kn_E are shown in Fig. 6. From Fig. 6, three primary resonance regions appear in amplitude-frequency curves under kn_E = 0 N/m³ while there are four primary resonance regions in amplitude-frequency curves under 10⁹ N/m³, 2 × 10⁹ N/m³, and 3 × 10⁹ N/m³. Such a phenomenon suggests that an additional resonance region is introduced in amplitude-frequency curves due to the mass-spring system that is nonlinear. Additionally, amplitude-frequency curves are no longer symmetric and peaks jump in the 2nd and 3rd resonance regions. The increase of kn_E suppresses the vibration at the 3rd primary resonance region. In the 2nd primary resonance region, the complex dynamic behavior appears with the increase of kn_E. The reason for such a phenomenon is that the nonlinear restoring force of Beam I and Beam II is proportional to the nonlinear stiffness of the mass-spring system which is nonlinear according to the definition of the nonlinear restoring force. When the other parameters of the mass-spring system that is nonlinear are determined, the nonlinear restoring force increases with the increases of the nonlinear mass-spring system’s nonlinear stiffness. Furthermore, phase diagrams are graphed in Fig. 6 to further study the complex dynamic behavior. According to subplots in Fig. 6, a closed curve is formed by Poincaré points, illustrating the state of complex dynamic behavior in Fig. 6 is quasi-periodic.

Fig. 6

Amplitude-frequency curves of the double-beam connected through a mass-spring system that is nonlinear under different kn_E

To explain the amplitude jumping phenomenon appears in the 2nd and 3rd resonance regions in Fig. 6, the max amplitude of the nonlinear restoring force acts on Beam I and Beam II with the variation of the excitation frequency is plotted in Fig. 7. From Fig. 7, the nonlinear restoring force jumps at the 2nd and 3rd resonance regions while the nonlinear restoring force keeps continuous at the 1st and 4th resonance regions. Due to the jump of the nonlinear restoring force, the amplitude jump phenomenon appears in amplitude-frequency response curves of the double-beam connected through a mass-spring system that is nonlinear, where the jumping frequency of the amplitude-frequency curves is the same as the jumping frequency in Fig. 7.

Fig. 7

The max amplitude of the nonlinear restoring force acts on Beam I and Beam II with the variation of the excitation frequency

Secondly, the influence of viscous damping (C_E = C_E1 = C_E2) on amplitude-frequency curves is studied, where C_E is selected as 5 Ns/m, 10 Ns/m, 20 Ns/m, and 40 Ns/m. kn_E is selected as 3 × 10⁹ N/m³ and other parameters of the mass-spring system that is nonlinear are the same as those in Sect. 3.1. Amplitude-frequency curves of the double-beam connected through a mass-spring system that is nonlinear under different C_E are graphed in Fig. 8. According to Fig. 8, peaks jump at the 2nd and 3rd resonance regions. The increase of C_E is good for the vibration of the double-beam system. In the 2nd primary resonance region, the complex dynamic behavior appears when C_E = 5 Ns/m. The complex dynamic behavior and amplitude-jumping phenomenon disappear with the increase of C_E. The reason for such a phenomenon is that the nonlinear restoring force acts on Beam I and Beam II is positively correlated with the relative displacement at the coupling position. The increase of C_E suppresses the peak amplitude at each primary resonance region of the double-beam system, suggesting the nonlinear restoring force at primary resonance regions decreases with the increase of C_E. The same as the analysis in Fig. 6, the vibration state of the complex dynamic behavior in Fig. 8 is quasi-periodic.

Fig. 8

Amplitude-frequency curves of the double-beam connected through a mass-spring system that is nonlinear under different C_E

Thirdly, the influence of concentrated mass (m_E) on amplitude-frequency curves is studied, where m_E is selected as 0.005, 0.01, 0.02, and 0.03 kg. kn_E is selected as 2 × 10⁹ N/m³ and other parameters of the mass-spring system that is nonlinear are shown in Table 2. Amplitude-frequency curves of the double-beam connected through a mass-spring system that is nonlinear under different m_E are graphed in Fig. 9. From Fig. 9, an amplitude-jumping phenomenon occurs at the 2nd and 3rd resonance regions. The change of m_E slightly influences the resonance regions’ peaks. In the 4th primary resonance region, the complex dynamic behavior occurs when m_E = 0.03 kg. The reason for the corresponding phenomenon is that the influence of m_E on the peak amplitude of the primary resonance regions is nonmonotonic, suggesting the nonlinear restoring force acts on Beam I and Beam II change nonmonotonic with the increase of m_E. Phase diagrams of the corresponding dynamic behavior are graphed. According to each subplot in Fig. 9, a closed curve is formed by Poincaré points, suggesting the state of complex dynamic behavior in Fig. 8 is quasi-periodic.

Fig. 9

Amplitude-frequency curves of the double-beam connected through a mass-spring system that is nonlinear under different m_E

Fourthly, the influence of coupling position (x_E = x_E1 = x_E2) on amplitude-frequency curves is studied, where x_E is selected as 0.2, 0.4, 0.6, and 0.8 m. kn_E is selected as 1.5 × 10⁹ N/m³ and other parameters of the mass-spring system that is nonlinear are shown in Table 2. Amplitude-frequency curves of the double-beam connected through a mass-spring system that is nonlinear under different x_E are graphed in Fig. 10. According to Fig. 10, an amplitude-jumping phenomenon occurs at the 2nd and 3rd primary resonance regions. A suitable parameter of x_E can beneficially suppress the vibration at the boundary of the double-beam system. Furthermore, in the 3rd primary resonance region, the complex dynamic behavior occurs when x_E = 0.4 m. The reason for the corresponding phenomenon is that the influence of x_E on the peak amplitude of the primary resonance regions is nonmonotonic, suggesting the nonlinear restoring force acts on Beam I and Beam II change nonmonotonic with the increase of x_E. Phase diagrams of the corresponding dynamic behavior are graphed. It can be seen from each subplot in Fig. 10 that a closed curve is formed by Poincaré points. The state of complex dynamic behavior in Fig. 10 is quasi-periodic.

Fig. 10

Amplitude-frequency curves of the double-beam connected through a mass-spring system that is nonlinear under different x_E

To further study the double-beam system influenced by the mass-spring system that is nonlinear, the kinetic energy of the double-beam system under the complex dynamic behavior in Figs. 6, 8, 9, and 10 are graphed in Fig. 11. Combinations of the mass-spring system that is nonlinear and excitation frequency are shown in Table 3.

Fig. 11

Kinetic energy of the double-beam connected through a mass-spring system that is nonlinear

Table 3 Combinations of the mass-spring system that is nonlinear and excitation frequency

From Fig. 11, the kinetic energy of beams is higher than the mass-spring system which is nonlinear. In the time interval T_s, the kinetic energy of Beam I targeted transfers to Beam II. For other time intervals, the kinetic energy of Beam II targeted transfers to Beam I. It should be noticed that the vibration state of the complex dynamic behavior in Figs. 6, 8, 9, and 10 is quasi-periodic, indicating that the quasi-periodic vibration state of the double-beam connected through a mass-spring system that is nonlinear can be regarded as a sign of the occurrence of the targeted energy transfer.

3.3 Single-frequency responses influenced by the mass-spring system that is nonlinear

This section investigates the influence of the mass-spring system that is nonlinear on single-frequency responses. For this section, the excitation frequency is selected as 38 Hz and the parameters of the double-beam system are shown in Table 1. In plotting dynamic responses of the double-beam system with the variation of the mass-spring system’s parameters, the maximum value of the time-domain responses of the double-beam system under the single excitation frequency is selected as the y coordinate while parameters of the mass-spring system that is nonlinear are selected as the x coordinate.

Firstly, study the influence of nonlinear stiffness (kn_E = kn_E1 = kn_E2) on single-frequency responses. Figure 12 depicts single-frequency responses of the double-beam with the change of kn_E. According to Fig. 12, as kn_E ranges from 10^8.3 to 10^9.7 N/m³, the increase of kn_E is good at vibration suppression at the boundary of Beam I. Furthermore, there are two unstable regions [10^9.7 N/m³, 10^11.1 N/m³], [10^11.8 N/m³, 10¹² N/m³] in single-frequency responses. 10^9.7 N/m³, 10^11.1 N/m³, and 10^11.8 N/m³ are defined as the converted values of kn_E. Changing kn_E around its converted values significantly changes the vibration state of the vibration system. With the continuous increase of kn_E, the variation of the complex dynamic behavior in the single-frequency responses of the double-beam system with the change of kn_E is nonmonotonic. The reason for such a phenomenon is that resonance regions of the amplitude-frequency curve shift to higher frequency regions with the increase of kn_E. In the single-frequency responses, the excitation frequency is determined as 38 Hz, which is near the 2nd and 3rd primary resonance region of the amplitude-frequency response curves. In the process of increasing kn_E, the 2nd and 3rd primary resonance regions of the amplitude-frequency response curves cross 38 Hz. In the above process, the nonlinear restoring force acting on Beam I and Beam II changes nonmonotonically, causing the nonmonotonic change of the complex dynamic behavior. Then, phase diagrams of the unstable regions are graphed. In each subplot in Fig. 12, a closed curve is formed by Poincaré points, which can be concluded that the vibration state of the unstable regions is quasi-periodic.

Fig. 12

Single-frequency responses of the double-beam connected through a mass-spring system that is nonlinear with the change of kn_E

Secondly, study the influence of viscous damping (C_E = C_E1 = C_E2) on single-frequency responses. kn_E is selected as 10¹⁰ N/m³ and other parameters of the mass-spring system that is nonlinear are the same as those in Sect. 3.1. Single-frequency responses of the double-beam with the change of C_E are graphed in Fig. 13. According to Fig. 13, when C_E in the region [13.5 Ns/m to 52 Ns/m], the increase of C_E is good at vibration suppression at the boundary of Beam II. There is an unstable region [1 Ns/m, 13.5 Ns/m] in single-frequency responses. 13.5 Ns/m is defined as the converted value of C_E. The vibration state of the double-beam changes greatly when C_E changes around its converted value. After C_E exceeds its converted value, the unstable region of the double-beam system vanishes. Furthermore, with the continuous increase of C_E, the variation of the complex dynamic behavior in the single-frequency responses of the double-beam system with the change of C_E is monotonic. The reason for such a phenomenon is that resonance regions of the amplitude-frequency curve shift to lower frequency regions with the increase of C_E under certain kn_E. In the process of increasing C_E, the 3rd primary resonance region of the amplitude-frequency response curves monotonically crosses 38 Hz. In the above process, the nonlinear restoring force acting on Beam I and Beam II changes monotonically, causing the monotonic change of the complex dynamic behavior. Phase diagrams of the unstable region are graphed. It can be seen from Fig. 13 that a closed curve is formed by Poincaré points in each subplot while phase diagrams stay stable. The above phenomenon suggests that the vibration state of the unstable region is quasi-periodic.

Fig. 13

Single-frequency responses of the double-beam connected through a mass-spring system that is nonlinear with the change of C_E

Thirdly, study the influence of concentrated mass (m_E) on single-frequency response. Single-frequency responses with the change of m_E are graphed in Fig. 14. kn_E is selected as 6 × 10⁹ N/m³ and other parameters of the mass-spring system that is nonlinear are the same as those employed in Sect. 3.1. From Fig. 14, when m_E is in the region [0.0265 kg, 0.044 kg], the increase of m_E is good at the vibration suppression at the boundary of the double-beam. There are two unstable regions [0.001 kg, 0.0265 kg], [0.044 kg, 0.05 kg] in single-frequency responses, 0.0265 kg and 0.044 kg are defined as the converted values of m_E. Changing m_E around its converted values significantly changes the state of the vibration system. The variation of the complex dynamic behavior in the single-frequency responses of the double-beam system with the increase of m_E is nonmonotonic. The reason for such a phenomenon is that the position of resonance regions of the amplitude-frequency curve is influenced by m_E, where the influence of m_E on the position of the primary resonance regions is nonmonotonic. In the increase process of increasing m_E, the 3rd primary resonance region of the amplitude-frequency response curve crosses 38 Hz multiple times. In the above process, the nonlinear restoring force acting on Beam I and Beam II changes nonmonotonically, causing the nonmonotonic change of the complex dynamic behavior. To deeply study the unstable regions’ dynamic responses, phase diagrams of the corresponding regions are graphed. The same as the analysis in Figs. 12 and 13, the state of unstable regions in Fig. 14 is quasi-periodic.

Fig. 14

Single-frequency responses of the double-beam connected through a mass-spring system that is nonlinear with the change of m_E

Fourthly, investigate the influence of coupling position (x_E = x_E1 = x_E2) on single-frequency responses. Single-frequency responses with the change of x_E are graphed in Fig. 15. kn_E is selected as 2 × 10⁹ N/m³ and other parameters of the mass-spring system that is nonlinear are the same as those employed in Sect. 3.1. According to Fig. 15, the increase of x_E is good at the vibration suppression at the boundary of the double-beam when x_E changes from 0.6 to 0.9 m. Additionally, when x_E ranges from 0.43 to 0.6 m, the vibration at the boundary of Beam II stays at a low level. An unstable region [0.37 m, 0.425 m] appears in single-frequency responses. 0.37 m and 0.425 kg are defined as the converted values of x_E. The vibration state of the double-beam changes obviously when x_E varies around its converted values. The variation of the complex dynamic behavior in the single-frequency responses of the double-beam system with the increase of x_E is nonmonotonic. The reason for such a phenomenon is that the position of resonance regions of the amplitude-frequency curve is influenced by x_E, where the influence of x_E on the position of the primary resonance regions is nonmonotonic. In the process of increasing x_E, the 3rd primary resonance region of the amplitude-frequency response curve crosses 38 Hz multiple times. In the above process, the nonlinear restoring force acting on Beam I and Beam II changes nonmonotonically, causing the nonmonotonic change of the complex dynamic behavior. Furthermore, phase diagrams of the unstable regions are graphed. The same as the analysis in Figs. 12 and 13, the unstable region’s vibration state in Fig. 15 is quasi-periodic.

Fig. 15

Single-frequency responses of the double-beam structure connected through a mass-spring system that is nonlinear with the change of x_E

To deeply study single-frequency responses influenced by the mass-spring system that is nonlinear, the kinetic energy of the double-beam under the complex dynamic behavior in Figs. 12, 13, 14, and 15 are graphed in Fig. 16. Combinations of the mass-spring system that is nonlinear are shown in Table 4.

Fig. 16

Kinetic energy of the double-beam connected through a mass-spring system that is nonlinear

Table 4 Combinations of the mass-spring system that is nonlinear

From Fig. 16, the kinetic energy of the concentrated mass is lower than that of beams. Due to the existence of the mass-spring system that is nonlinear, the kinetic energy of Beam I targeted transfers to Beam II under the time interval T_s. For other time intervals, the kinetic energy of Beam II targeted transfers to Beam I. Furthermore, according to the analysis in Figs. 12, 13, 14, and 15, the vibration state of the complex dynamic behavior is quasi-periodic. The quasi-periodic vibration state corresponds to the targeted energy transfer phenomenon between beams, suggesting the quasi-periodic vibration state of the double-beam connected through a mass-spring system that is nonlinear can be regarded as a sign of the occurrence of the targeted energy transfer.

4 Conclusion

In this study, the nonlinear dynamic behavior of an elastically restrained double-beam connected through a mass-spring system that is nonlinear is investigated. Using the variational method and the generalized Hamiltonian method build the corresponding system’s governing functions. Then, applying the Galerkin truncation method predicts the dynamic behavior of the double-beam connected through a mass-spring system that is nonlinear, where the harmonic balanced method and Lagrange method are employed to verify the correctness of the results obtained by the Galerkin truncation method. On this basis, the influence of a mass-spring system that is nonlinear on amplitude-frequency curves and single-frequency responses of an elastically restrained double-beam is investigated. For the structural parameters and boundary conditions of the double-beam system employed in this study, some conclusions are made.

• (1) The GTM has good stability and correctness in predicting dynamic responses of the double-beam connected through a mass-spring system that is nonlinear. For this study, a 4-term truncation number can keep the stability of the GTM.

• (2) Amplitude-frequency and single-frequency responses of the double-beam are both significantly influenced by changing parameters of the mass-spring system that is nonlinear. The amplitude jumping phenomenon and complex dynamic behavior of the double-beam occurs under certain parameters of the mass-spring system that is nonlinear. Around converted values of the mass-spring system that is nonlinear, the dynamic behavior of the double-beam can be easily changed.

• (3) The complex dynamic behavior of the double-beam system changes characteristics of the double-beam system’s kinetic energy transfer, where the vibration state of the double-beam system’s complex dynamic behavior is quasi-periodic. A quasi-periodic vibration state can be regarded as a sign of the occurrence of the targeted energy transfer of the double-beam connected through a mass-spring system that is nonlinear.

• (4) On the whole, changing parameters of the mass-spring system that is nonlinear can significantly influence the dynamic behavior of the double-beam while suitable parameters of the mass-spring system that is nonlinear are good at vibration suppression at the boundary of the double-beam.

Appendices

Appendix A

$$ V_{{{\text{Beam}}I}} = \int_{0}^{{L_{1} }} {\frac{1}{2}E_{1} I_{1} } \left( {\frac{{\partial^{2} u_{1} }}{{\partial x_{1}^{2} }}} \right)^{2} {\text{d}} x_{1} $$

(A1)

$$ V_{BeamII} = \int_{0}^{{L_{2} }} {\frac{1}{2}E_{2} I_{2} } \left( {\frac{{\partial^{2} u_{2} }}{{\partial x_{2}^{2} }}} \right)^{2} {\text{d}} x_{2} $$

(A2)

$$ \begin{aligned} V_{BoundaryI} = & \frac{1}{2}k_{L1} \left[ {u_{1} \left( {0,t} \right)} \right]^{2} + \frac{1}{2}k_{R1} \left[ {u_{1} \left( {L_{1} ,t} \right)} \right]^{2} \\ & + \frac{1}{2}K_{L1} \left[ {\frac{{\partial u_{1} \left( {0,t} \right)}}{{\partial x_{1} }}} \right]^{2} + \frac{1}{2}K_{R1} \left[ {\frac{{\partial u_{1} \left( {L_{1} ,t} \right)}}{{\partial x_{1} }}} \right]^{2} \\ \end{aligned} $$

(A3)

$$ \begin{aligned} V_{BoundaryII} = & \frac{1}{2}k_{{{\text{L}} 2}} \left[ {u_{2} \left( {0,t} \right)} \right]^{2} + \frac{1}{2}k_{R2} \left[ {u_{2} \left( {L_{2} ,t} \right)} \right]^{2} \\ & + \frac{1}{2}K_{L2} \left[ {\frac{{\partial u_{2} \left( {0,t} \right)}}{{\partial x_{2} }}} \right]^{2} + \frac{1}{2}K_{R2} \left[ {\frac{{\partial u_{2} \left( {L_{2} ,t} \right)}}{{\partial x_{2} }}} \right]^{2} \\ \end{aligned} $$

(A4)

$$ \begin{aligned} V_{E} = & \frac{1}{2}k_{E1} \left[ {u_{E} - u_{1} \left( {x_{E1} ,t} \right)} \right]^{2} + \frac{1}{2}k_{E2} \left[ {u_{E} - u_{2} \left( {x_{E2} ,t} \right)} \right]^{2} \\ & \frac{1}{4}kn_{E1} \left[ {u_{E} - u_{1} \left( {x_{E1} ,t} \right)} \right]^{4} + \frac{1}{4}kn_{E2} \left[ {u_{E} - u_{2} \left( {x_{E2} ,t} \right)} \right]^{4} \\ \end{aligned} $$

(A5)

$$ T_{I} = \int_{0}^{{L_{1} }} {\frac{1}{2}\rho_{1} S_{1} } \left( {\frac{{\partial u_{1} }}{\partial t}} \right)^{2} {\text{d}} t $$

(A6)

$$ T_{II} = \int_{0}^{{L_{2} }} {\frac{1}{2}\rho_{2} S_{2} } \left( {\frac{{\partial^{2} u_{2} }}{{\partial t^{2} }}} \right)^{2} {\text{d}} t $$

(A7)

$$ T_{E} = \frac{1}{2}m_{E} \left( {\frac{{{\text{d}} u_{E} }}{{{\text{d}} t}}} \right)^{2} $$

(A8)

$$ \delta W_{C1} = - \int_{0}^{{L_{1} }} {C_{B1} } \frac{{\partial u_{1} }}{\partial t}\delta u_{1} {\text{d}} x_{1} $$

(A9)

$$ \delta W_{C2} = - \int_{0}^{{L_{2} }} {C_{B2} } \frac{{\partial u_{2} }}{\partial t}\delta u_{2} {\text{d}} x_{2} $$

(A10)

$$ \delta W_{CE1} = - C_{E1} \left[ {\frac{{\partial u_{E} }}{\partial t} - \frac{{\partial u_{1} \left( {x_{E1} ,t} \right)}}{\partial t}} \right]\delta \left[ {u_{E} - u_{1} \left( {x_{E1} ,t} \right)} \right] $$

(A11)

$$ \delta W_{CE2} = - C_{E2} \left[ {\frac{{\partial u_{E} }}{\partial t} - \frac{{\partial u_{2} \left( {x_{E2} ,t} \right)}}{\partial t}} \right]\delta \left[ {u_{E} - u_{2} \left( {x_{E2} ,t} \right)} \right] $$

(A12)

$$ \delta W_{F1} = - \int_{0}^{{L_{1} }} {\delta \left( {x_{1} - L_{1} } \right)F_{1} \sin \left( {\omega t} \right)} \delta u_{1} {\text{d}} x_{1} $$

(A13)

Appendix B

$$ \begin{aligned} \int_{{t_{1} }}^{{t_{2} }} {\delta V_{{{\text{Beam}}I}} {\text{d}} t} = & \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{{L_{1} }} {E_{1} I_{1} \frac{{\partial^{4} u_{1} }}{{\partial x_{1}^{4} }}} \delta u_{1} {\text{d}} x_{1} {\text{d}} t} \\ & + \int_{{t_{1} }}^{{t_{2} }} {\left[ \begin{gathered} E_{1} I_{1} \frac{{\partial^{2} u_{1} \left( {L_{1} ,t} \right)}}{{\partial x_{1}^{2} }}\delta \left( {\frac{{\partial u_{1} }}{{\partial x_{1} }}} \right) - E_{1} I_{1} \frac{{\partial^{3} u_{1} \left( {L_{1} ,t} \right)}}{{\partial x_{1}^{3} }}\delta u_{1} \hfill \\ - E_{1} I_{1} \frac{{\partial^{2} u_{1} \left( {0,t} \right)}}{{\partial x_{1}^{2} }}\delta \left( {\frac{{\partial u_{1} }}{{\partial x_{1} }}} \right) + E_{1} I_{1} \frac{{\partial^{3} u_{1} \left( {0,t} \right)}}{{\partial x_{1}^{3} }}\delta u_{1} \hfill \\ \end{gathered} \right]} {\text{d}} t \\ \end{aligned} $$

(B1)

$$ \begin{aligned} \int_{{t_{1} }}^{{t_{2} }} {\delta V_{BeamII} {\text{d}} t} = & \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{{L_{2} }} {E_{2} I_{2} \frac{{\partial^{4} u_{2} }}{{\partial x_{2}^{4} }}} \delta u_{2} {\text{d}} x_{2} {\text{d}} t} \\ & + \int_{{t_{1} }}^{{t_{2} }} {\left[ \begin{gathered} E_{2} I_{2} \frac{{\partial^{2} u_{2} \left( {L_{2} ,t} \right)}}{{\partial x_{2}^{2} }}\delta \left( {\frac{{\partial u_{2} }}{{\partial x_{2} }}} \right) - E_{2} I_{2} \frac{{\partial^{3} u_{2} \left( {L_{2} ,t} \right)}}{{\partial x_{2}^{3} }}\delta u_{2} \hfill \\ - E_{2} I_{2} \frac{{\partial^{2} u_{2} \left( {0,t} \right)}}{{\partial x_{2}^{2} }}\delta \left( {\frac{{\partial u_{2} }}{{\partial x_{2} }}} \right) + E_{2} I_{2} \frac{{\partial^{3} u_{2} \left( {0,t} \right)}}{{\partial x_{2}^{3} }}\delta u_{2} \hfill \\ \end{gathered} \right]} {\text{d}} t \\ \end{aligned} $$

(B2)

$$ \int_{{t_{1} }}^{{t_{2} }} {\delta V_{BoundaryI} {\text{d}} t} = \int_{{t_{1} }}^{{t_{2} }} {\left[ \begin{gathered} \begin{array}{*{20}c} {} \\ \end{array} k_{L1} u_{1} \left( {0,t} \right)\delta u_{1} + K_{L1} \frac{{\partial u_{1} \left( {0,t} \right)}}{{\partial x_{1} }}\delta \left( {\frac{{\partial u_{1} }}{{\partial x_{1} }}} \right) \hfill \\ + k_{R1} u_{1} \left( {L_{1} ,t} \right)\delta u_{1} + K_{R1} \frac{{\partial u_{1} \left( {L_{1} ,t} \right)}}{{\partial x_{1} }}\delta \left( {\frac{{\partial u_{1} }}{{\partial x_{1} }}} \right) \hfill \\ \end{gathered} \right]{\text{d}} t} $$

(B3)

$$ \int_{{t_{1} }}^{{t_{2} }} {\delta V_{BoundaryII} {\text{d}} t} = \int_{{t_{1} }}^{{t_{2} }} {\left[ \begin{gathered} \begin{array}{*{20}c} {} \\ \end{array} k_{L2} u_{2} \left( {0,t} \right)\delta u_{2} + K_{L2} \frac{{\partial u_{2} \left( {0,t} \right)}}{{\partial x_{2} }}\delta \left( {\frac{{\partial u_{2} }}{{\partial x_{2} }}} \right) \hfill \\ + k_{R2} u_{2} \left( {L_{2} ,t} \right)\delta u_{2} + K_{R2} \frac{{\partial u_{2} \left( {L_{2} ,t} \right)}}{{\partial x_{2} }}\delta \left( {\frac{{\partial u_{2} }}{{\partial x_{2} }}} \right) \hfill \\ \end{gathered} \right]} {\text{d}} t $$

(B4)

$$ \int_{{t_{1} }}^{{t_{2} }} {\delta V_{E} {\text{d}} t} = \int_{{t_{1} }}^{{t_{2} }} {\left\{ \begin{gathered} \begin{array}{*{20}c} {} \\ \end{array} k_{E1} \left[ {u_{E} - u_{1} \left( {x_{E1} ,t} \right)} \right]\delta \left[ {u_{E} - u_{1} \left( {x_{E1} ,t} \right)} \right] \hfill \\ + k_{E2} \left[ {u_{E} - u_{2} \left( {x_{E2} ,t} \right)} \right]\delta \left[ {u_{E} - u_{2} \left( {x_{E2} ,t} \right)} \right] \hfill \\ + kn_{E1} \left[ {u_{E} - u_{1} \left( {x_{E1} ,t} \right)} \right]^{3} \delta \left[ {u_{E} - u_{1} \left( {x_{E1} ,t} \right)} \right] \hfill \\ + kn_{E2} \left[ {u_{E} - u_{2} \left( {x_{E2} ,t} \right)} \right]^{3} \delta \left[ {u_{E} - u_{2} \left( {x_{E2} ,t} \right)} \right] \hfill \\ \end{gathered} \right\}{\text{d}} t} $$

(B5)

$$ \int_{{t_{1} }}^{{t_{2} }} {\delta T_{I} {\text{d}} t = } - \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{{L_{1} }} {\rho_{1} S_{1} \frac{{\partial^{2} u_{1} }}{\partial t}} } \delta u_{1} {\text{d}} x_{1} {\text{d}} t $$

(B6)

$$ \int_{{t_{1} }}^{{t_{2} }} {\delta T_{II} {\text{d}} t = } - \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{{L_{2} }} {\rho_{2} S_{2} \frac{{\partial^{2} u_{2} }}{\partial t}} } \delta u_{2} {\text{d}} x_{2} {\text{d}} t $$

(B7)

$$ \int_{{t_{1} }}^{{t_{2} }} {\delta T_{E} {\text{d}} t} = - \int_{{t_{1} }}^{{t_{2} }} {m_{E} \frac{{{\text{d}}^{2} u_{\text{E}} }}{{{\text{d}} t^{2} }}\delta u_{E} } {\text{d}} t $$

(B8)

$$ \int_{{t_{1} }}^{{t_{2} }} {\delta W_{C1} {\text{d}} t} = - \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{{L_{1} }} {C_{B1} } \frac{{\partial u_{1} }}{\partial t}\delta u_{1} {\text{d}} x_{1} {\text{d}} t} $$

(B9)

$$ \int_{{t_{1} }}^{{t_{2} }} {\delta W_{C2} {\text{d}} t} = - \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{{L_{2} }} {C_{B2} } \frac{{\partial u_{2} }}{\partial t}\delta u_{2} {\text{d}} x_{2} {\text{d}} t} $$

(B10)

$$ \int_{{t_{1} }}^{{t_{2} }} {\delta W_{CE1} {\text{d}} t} = - \int_{{t_{1} }}^{{t_{2} }} {C_{E1} \left[ {\frac{{{\text{d}} u_{E} }}{{{\text{d}} t}} - \frac{{\partial u_{1} \left( {x_{E1} ,t} \right)}}{\partial t}} \right]\delta \left[ {u_{E} - u_{1} \left( {x_{E1} ,t} \right)} \right]{\text{d}} t} $$

(B11)

$$ \int_{{t_{1} }}^{{t_{2} }} {\delta W_{CE2} {\text{d}} t} = - \int_{{t_{1} }}^{{t_{2} }} {C_{E2} \left[ {\frac{{{\text{d}} u_{E} }}{{{\text{d}} t}} - \frac{{\partial u_{2} \left( {x_{E2} ,t} \right)}}{\partial t}} \right]\delta \left[ {u_{E} - u_{2} \left( {x_{E2} ,t} \right)} \right]{\text{d}} t} $$

(B12)

$$ \int_{{t_{1} }}^{{t_{2} }} {\delta W_{F1} {\text{d}} t} = - \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{{L_{1} }} {\delta \left( {x_{1} - L_{1} } \right)F_{1} \sin \left( {\omega t} \right)} \delta u_{1} {\text{d}} x_{1} {\text{d}} t} $$

(B13)

Appendix C

$$ RI_{{m_{1} 1}} = \int_{0}^{{L_{1} }} {\rho_{1} S_{1} \left[ {\sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{1} }} {\varphi_{1i} \left( {x_{1} } \right)\frac{{{\text{d}}^{2} q_{1i} \left( t \right)}}{{{\text{d}} t^{2} }}} } \right]\psi_{{1m_{1} }} \left( {x_{1} } \right){\text{d}} x_{1} } $$

(C1)

$$ RI_{{m_{1} 2}} = \int_{0}^{{L_{1} }} {C_{{{\text{B}} 1}} \left[ {\sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{1} }} {\varphi_{1i} \left( {x_{1} } \right)\frac{{{\text{d}} q_{1i} \left( t \right)}}{{{\text{d}} t}}} } \right]\psi_{{1m_{1} }} \left( {x_{1} } \right){\text{d}} x_{1} } $$

(C2)

$$ RI_{{m_{1} 3}} = \int_{0}^{{L_{1} }} {E_{1} I_{1} \left[ {\sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{1} }} {\frac{{{\text{d}}^{4} \varphi_{1i} \left( x \right)}}{{{\text{d}} x_{1}^{4} }}q_{1i} \left( t \right)} } \right]\psi_{{1m_{1} }} \left( {x_{1} } \right){\text{d}} x_{1} } $$

(C3)

$$ RI_{{m_{1} 4}} = \psi_{{1m_{1} }} \left( {x_{F1} } \right)F_{1} \sin \left( {\omega t} \right) $$

(C4)

$$ RI_{{{\text{m}}_{1} {5}}} = C_{E1} \left[ {\sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{1} }} {\varphi_{1i} \left( {x_{{{\text{E}} 1}} } \right)\frac{{{\text{d}} q_{1i} \left( t \right)}}{{{\text{d}} t}}} - u_{E} \left( t \right)} \right]\psi_{{1m_{1} }} \left( {x_{E1} } \right) $$

(C5)

$$ RI_{{{\text{m}}_{1} {6}}} = k_{E1} \left[ {\sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{1} }} {\varphi_{1i} \left( {x_{E1} } \right)q_{1i} \left( t \right)} - u_{\text{E}} \left( t \right)} \right]\psi_{{1m_{1} }} \left( {x_{E1} } \right) $$

(C6)

$$ RI_{{{\text{m}}_{1} {7}}} = kn_{E1} \left[ {\sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{1} }} {\varphi_{1i} \left( {x_{E1} } \right)q_{1i} \left( t \right)} - u_{\text{E}} \left( t \right)} \right]^{3} \psi_{{1m_{1} }} \left( {x_{E1} } \right) $$

(C7)

$$ RII_{{m_{2} 1}} = \int_{0}^{{L_{2} }} {\rho_{2} S_{2} \left[ {\sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{2} }} {\varphi_{2i} \left( {x_{2} } \right)\frac{{{\text{d}}^{2} q_{2i} \left( t \right)}}{{{\text{d}} t}}} } \right]\psi_{{2m_{2} }} \left( {x_{2} } \right){\text{d}} x_{2} } $$

(C8)

$$ RII_{{m_{2} 2}} = \int_{0}^{{L_{2} }} {C_{{{\text{B}} 2}} \left[ {\sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{2} }} {\varphi_{2i} \left( {x_{2} } \right)\frac{{{\text{d}} q_{2i} \left( t \right)}}{{{\text{d}} t}}} } \right]\psi_{{2m_{2} }} \left( {x_{2} } \right){\text{d}} x_{2} } $$

(C9)

$$ RII_{{m_{2} 3}} = \int_{0}^{{L_{2} }} {E_{2} I_{2} \left[ {\sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{2} }} {\frac{{{\text{d}}^{4} \varphi_{2i} \left( {x_{2} } \right)}}{{{\text{d}} x_{2}^{4} }}q_{2i} \left( t \right)} } \right]\psi_{{2m_{2} }} \left( {x_{2} } \right){\text{d}} x_{2} } $$

(C10)

$$ RII_{{{\text{m}}_{2} {4}}} = C_{E2} \left[ {\sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{2} }} {\varphi_{2i} \left( {x_{{{\text{E}} 2}} } \right)\frac{{{\text{d}} q_{2i} \left( t \right)}}{{{\text{d}} t}}} - u_{E} \left( t \right)} \right]\psi_{{2m_{2} }} \left( {x_{{{\text{E}} 2}} } \right) $$

(C11)

$$ RII_{{{\text{m}}_{2} 5}} = k_{E2} \left[ {\sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{2} }} {\varphi_{2i} \left( {x_{E2} } \right)q_{2i} \left( t \right)} - u_{E} \left( t \right)} \right]\psi_{{2m_{2} }} \left( {x_{E2} } \right) $$

(C12)

$$ RII_{{{\text{m}}_{2} {6}}} = kn_{E2} \left[ {\sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{2} }} {\varphi_{2i} \left( {x_{E2} } \right)q_{2i} \left( t \right)} - u_{E} \left( t \right)} \right]^{3} \psi_{{2m_{2} }} \left( {x_{E2} } \right) $$

(C13)