Influences of space perturbations on robotic assembly process of ultra-large structures

Abstract

The space assembly of two flexible beams by a dual-arm space robot is a typical assembly scenario to construct ultra-large space structure. Yet, previous studies mainly focused on the assembly of small structures, neglecting the influences of space perturbations. Two models are developed in this research to investigate the effects of space perturbations on the space assembly process of ultra-large space structures. Firstly, a theoretical modelling method is proposed based on quasi-static hypothesis and linear structural mechanics. The theoretical model can be utilized for analytically estimating the transverse and axial distributed forces of the flexible beams, structural vibrations, and the control moments of the space robot. An orbit–attitude–structure coupled simulation model is then established to validate the theoretical model and study the dynamic behaviours more accurately, using absolute nodal coordinate formulation and natural coordinate formulation. Finally, the effects of the attitude angle, orbital radius, and lengths of beams on the dynamic responses during assembly are investigated. Theoretical and simulation results show that the control moments and structural vibration amplitude increase dramatically with the length of the beams. The effects of Coriolis force and gravity gradient must be considered for ultra-large space structures during assembly, otherwise the control moments and structural vibrations would be substantially underestimated. The results are instructive to the assembly strategy design as well as modular component design of ultra-large space structures.

1 Introduction

Ultra-large size is one of the most important features for future spacecraft [1]. For instance, the diameter of the spaceport would reach more than 600 m to generate comfortable artificial gravity [2]. And the area of the solar array of the solar power satellites would reach the order of square kilometre to generate electricity for terrestrial or space use [3, 4]. Ultra-large space-based solar reflectors can reflect sunlight to the Earth, Moon, as well as Mars for solar power generation and night-time explorations [5, 6].

Space assembly is the most promising way to construct ultra-large spacecraft. It not only overcomes the mass and volume limitations of the launch vehicle, but also alleviates the effects of launch environmental loads on the whole spacecraft [7]. Compared to self-assembly or assembly by astronaut, the assembly by space robots is more appealing for ultra-large spacecraft. On the one hand, the large structural modules of the ultra-large spacecraft are usually massive and non-autonomous. Space robots are suitable for extensive and repetitive tasks with high risk and long time [8]. On the other hand, the space robots are more accurate and efficient. Moreover, they can carry out other on-orbit service and maintenance tasks after completing the assembly missions [9].

However, the studies on the dynamics and control of ultra-large space structures during space assembly are not sufficient, which is one of the key technologies for space assembly [10]. Gralla and de Weck compared the advantages of four space assembly strategies for next-generation large space structure, including self-assembly, single tug, multiple tug, and in-space refuelling [11]. They focused on the propellant requirement and orbital design for different assembly strategies. McInnes proposed a distributed orbit and attitude control law for a large space platform assembled from several rigid components [12]. The components were completely controlled by space robots like self-assembly situation. Chen et al. proposed an output consensus control method for a team of self-assembly flexible spacecraft considering collision avoidance requirement [13]. Each flexible spacecraft was modelled by a rigid hub connected with a flexible beam. Studies [12, 13] focused on the self-assembly control methods for a few components. Yet, the assembly of ultra-large space structure is a different situation: large modules should be assembled by space robots in sequence. Wang et al. studied a distributed structural vibration control method for a large space structure during assembly [14, 15]. The structure was simplified as a cantilever plate with an increasing number of modules, and the operation disturbance of the space robot was simplified as a 1-N force last for 0.1 s. Cao et al. studied the dynamic modelling and analysis of the assembly process of an orb-shaped solar array [16]. The model was established by the Tschauner–Hempel equation, finite element method, and a classical vehicle-bridge coupled model. However, the operations of the space robots were not involved in the studies [11,12,13,14,15,16].

Recent years have seen significant advancements in the study of space robot dynamics and control [17]. Studies on the assembly using space robot, however, are scarce. Boning and Dubowsky proposed a coordinate control algorithm for a cooperative space robot team to assemble large flexible space structures and conducted ground experiments [18]. Xu et al. studied the dynamic modelling, analysis, and control of a flexible-base space robot capturing a large flexible spacecraft [19]. Meng et al. investigated a vibration suppression method for a space robot with flexible appendages through the control of a manipulator theoretically and experimentally [20, 21]. The experiment demonstrated that the vibrations of flexible appendages were suppressed while the moving target was successfully captured by the space manipulator. Lu et al. studied the ground experiment of the assembly of cooperative modular components using a robot with an economic camera [22]. Ishijima et al. studied the transportation and structural control methods for the transport maneuvering of a large flexible space structure by two space robots [23]. Nevertheless, the studies [18,19,20,21,22,23] mainly concentrated on the assembly of ordinary-size structures without considering space perturbations. The influences of space perturbations increase dramatically with the size of the structure [24]. For instance, the gravity-gradient-induced deformation of a Sun-facing beam is proportional to the fifth order of its length [25].

This paper establishes two models to study the assembly process of two flexible beams by a space robot considering space perturbations. On the one hand, a quasi-static linear model (named theoretical model) is proposed and the analytical results are obtained to make quick estimations of the dynamic characteristics during assembly, including the structural vibrations of the beams and the required control moments of the space robot. On the other hand, a nonlinear and high-dimensional dynamic model (named simulation model) is constructed to study the dynamic behaviours of the assembly process accurately. The flexible beams are modelled using absolute nodal coordinate formulation (ANCF), and the space robot is modelled by natural coordinate formulation (NCF). Gravity gradient and Coriolis force are considered for the two models. Other space perturbations, such as the non-spherical gravity of the Earth, mainly produce uniform acceleration on the system and have little influence on the assembly process. Thus, they are not considered in this paper.

The rest of this paper is organized as follows. Section 2 describes the space assembly system and assembly process. Section 3 constructs a theoretical model for the structural distributed forces, structural vibrations, and control moments of the space robot. A simulation model for the assembly system is given in Sect. 4, including the trajectory planning and control methods for the space robot. Sections 5 and 6 present the comparison of the two models and the influences of system parameters. A brief discussion on the applicability of the theoretical model is presented in Sect. 7. Finally, the main conclusions are summarized in the last section.

2 Problem formulation

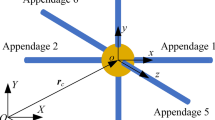
The space assembly system consists of a space robot and two flexible beams, as seen in Fig. 1. In order to reduce the complexity of the models and improve simulation efficiency, only the motions in the orbital plane are considered in this paper [26]. Although three-dimensional analyses are important to engineering applications, most structures will be in the radial, tangential, and normal directions of circular orbits during assembly to avoid the effects of gravity gradient. Furthermore, the vibrations of structures in the orbital plane will be coupled with attitude and orbital motions due to the Coriolis force, which are more complicated than the out-of-plane motions of structures. The modelling methods can be extended to more general three-dimensional cases in future works. The flexible beams have been captured tightly by the space robot and stabilized to the ideal initial conditions for the assembly process, i.e. the beams are collinear without relative motion or structural deformations.

Fig. 1

Simplified model of the space assembly system

A global inertial coordinate system ${\text{O}}XY$ is constructed, and the origin O is located at the centre of the Earth. The dual-arm space robot in this paper is similar to that in literature [27]. As there are three degrees of freedom for a planar rigid body, each arm adopts three joints in order to reach an arbitrary point in the workspace with an arbitrary attitude. The joints of the space robot are represented by B—G. Point A and Point H are end-effectors. The rigid body DE is regarded as a satellite platform of the space robot. The angles of the joints are denoted by $\theta_{1}$—$\theta_{3}$ and $\theta_{5}$—$\theta_{7}$. The attitude angle of the satellite platform is represented by $\theta_{4}$, which is approximately equal to the attitude angle of the system $\alpha$. The flexible beams are denoted by KI and MN. The space robot is considered a multi-rigid-body system because its size and flexibility are small compared to the ultra-large beams. The satellite platform and the links of the space robot are simplified as cylinders with a diameter of 0.2 m and a density of $1000{\text{ kg/m}}^{{3}}$. The lengths and masses of the rigid bodies are represented by $l_{i}$ and $m_{i}$, where $i = 1,2, \cdots ,7$ represents AB, BC, $\cdots$, and GH, respectively. The lengths of rigid bodies are $l_{2} = l_{3} = l_{5} = l_{6} = 7{\text{ m}}$ and $l_{1} = l_{4} = l_{7} = 2{\text{ m}}$.

The simplification of the grasping points has great influences on the dynamic behaviours of the assembly process. To ensure high-precision assembly, a high-stiffness grasping end-effector is requisite to restrict the movements and rotations of the assembly module. However, this study focuses on the dynamics of assembly process instead of the grasping dynamics. It is assumed that Point A and Point H are coincident with Point M and Point K, respectively, during the assembly process because the flexible beams are tightly captured. Besides, AB and GH are perpendicular to MN and KI, respectively.

In practice, ultra-large spacecraft are probably supported by slender deployable trusses due to the limitation of mass. But, the full dynamic model of a large deployable truss is not suitable for this paper because of high computational costs. Thus, a simplified Euler–Bernoulli beam model is adopted for KI and MN. The advantages of the Euler–Bernoulli beam include brief equation for the theoretical model and high efficiency for the ANCF cable element in the simulation model. The cross-sectional area, second moment of the cross section, density, and Young’s modulus of the flexible beams are denoted by $A$, $I$, $\rho$, and $E$, respectively. The lengths and masses of Beam MN and Beam KI are represented by $L_{{{\text{MN}}}} ,L_{{{\text{KI}}}} ,m_{{{\text{MN}}}} \,{\text{and}}\;m_{{{\text{KI}}}} .$

The assembly process is shown in Fig. 2. The flexible beams get close along the dashed line MK until they touch each other at point P (not necessarily the midpoint of MK), under the control of the space robot. At the same time, the attitude angle of the space robot $\theta_{4}$ remains unaltered through attitude control. The gravity, gravity gradient, and inertial forces of the assembly system are considered. The assembly system is initially in a circular orbit with a constant orbital radius $r_{0}$ and a constant orbital angular velocity $\omega_{0} = \sqrt {{\mu \mathord{\left/ {\vphantom {\mu {r_{0}^{3} }}} \right. \kern-0pt} {r_{0}^{3} }}}$, where $\mu = 3.986 \times 10^{14} {\text{ m}}^{3} \cdot {\text{s}}^{ - 2}$. The orbital angle is denoted by $\theta$ $\left( {\dot{\theta } = \omega_{0} ,\ddot{\theta } = 0} \right)$. Orbital perturbation or orbital control is not considered.

Fig. 2

Space assembly process with a constant attitude angle $\alpha$ in a circular orbit

A local coordinate system ${\text{S}}xy$ is introduced such that the $x$ axis points to Point I, and the centre of mass of the assembly system is located at $y$ axis. It should be pointed out that Point S is the centre of mass of the system on $x$ axis and is not fixed to any body, as shown in Fig. 2. The use of ${\text{S}}xy$ is convenient because Point S can be regarded as an equilibrium point of the gravitational force and inertial force.

3 Theoretical modelling method

A theoretical modelling method is proposed in this section to analyse the dynamic characteristics of the assembly process. Firstly, some assumptions are given to simplify the assembly process. Then, the transverse and axial force analyses of the flexible bodies are conducted. Finally, the analytical solutions of the vibrations of the beams and the control moments of the space robot are obtained accordingly.

3.1 Assumptions

The assembly process of ultra-large space structures is a complicated dynamic process involving not only the dynamics of the space robot and large structures, but also the control system of the space robot. In order to make quick estimations on the assembly process, a theoretical model is constructed using the quasi-static method and linear structural mechanics based on the following assumptions.

• (1) Ideal control, including the joints and the attitude, of the space robot is considered. In other words, the control errors of the joints are zero and the flexible beams get close to each other according to a planned trajectory. Based on this assumption, the coupled effects between the space robot and the flexible beams vanish.

• (2) The size, mass, and moment of inertia of the flexible beams are much larger than the space robot, because this paper concentrates on the assembly of ultra-large structures. Thus, the tedious inertial forces and moments of the links of the space robot can be neglected when calculating the joint’s control moments. This assumption can simplify the formulations of control moments because the motions of the links are much more complicated than the beams. The influences of the mass of the space robot on the control moments will be discussed in Sect. 7.

• (3) The assembly process is very slow because of the large masses of the beams. The assembly time is considerably larger than the largest structural vibration period of the beams. Thus, the dynamic effects of the system can be neglected.

• (4) Small deformation of the beams is assumed to use the linear Euler–Bernoulli beam theory so that the quasi-static deformations of the beams can be obtained.

3.2 Transverse and axial distributed forces

Based on the above assumptions of ideal control, small robot, slow assembly, and small deformation, the transverse and axial force distributions of the beams during space assembly can be derived using the infinitesimal method. The simplified model is shown in Fig. 3. The transverse and axial forces of Beam KI are firstly derived. The results are then extended to Beam MN.

Fig. 3

Simplified model of the beams

In order to use the infinitesimal method, an arbitrary point on Beam KI (Point Q) is selected. The $x$ coordinate of Point Q is denoted by $x_{{\text{Q}}}$, in which way the other points are defined. The following notation is introduced to describe the relative coordinate from Point K to Point Q

$$ x_{{{\text{KQ}}}} = x_{{\text{Q}}} - x_{{\text{K}}} $$

(1)

The relative coordinates of other points are denoted in the same way. The relative coordinate from Point S to Point Q $x_{{{\text{SQ}}}}$ can be calculated by

$$ \left\{ \begin{gathered} x_{{{\text{SQ}}}} = x_{{{\text{SP}}}} + x_{{{\text{PK}}}} + x_{{{\text{KQ}}}} \hfill \\ \dot{x}_{{{\text{SQ}}}} = \dot{x}_{{{\text{PK}}}} ,\ddot{x}_{{{\text{SQ}}}} = \ddot{x}_{{{\text{PK}}}} \hfill \\ \end{gathered} \right. $$

(2)

where $x_{{{\text{SP}}}}$ is a constant that is dependent on the parameters of the assembly system, and $x_{{{\text{PK}}}}$ is time-varying during assembly. The relative coordinate $x_{{{\text{SP}}}}$ can be calculated through the centre of mass of the system after assembly

$$ x_{{{\text{SP}}}} = \frac{{m_{{{\text{MN}}}} L_{{{\text{MN}}}} - m_{{{\text{KI}}}} L_{{{\text{KI}}}} }}{{2\left( {m_{{{\text{MN}}}} + m_{{{\text{KI}}}} + m_{{{\text{robot}}}} } \right)}} $$

(3)

where $m_{{{\text{robot}}}}$ is the mass of the space robot. It can be seen that $x_{{{\text{SP}}}} = 0$ if Beam MN has the same parameters as Beam KI. In order to calculate $x_{{{\text{PK}}}}$, the integral form of the momentum conservation law is used for the assembly process

$$ m_{{{\text{MN}}}} \left( {x_{{{\text{MK}}}} - x_{{{\text{PK}}}} } \right) + m_{{{\text{robot}}}} \left( {\frac{{x_{{{\text{MK}}}} }}{2} - x_{{{\text{PK}}}} } \right) = m_{{{\text{KI}}}} x_{{{\text{PK}}}} $$

(4)

where $x_{{{\text{MK}}}}$ is a quintic polynomial of time that will be given in the trajectory planning of the space robot. Thus, $x_{{{\text{PK}}}}$ is calculated by

$$ x_{{{\text{PK}}}} = \frac{{\left( {2m_{{{\text{MN}}}} + m_{{{\text{robot}}}} } \right)x_{{{\text{MK}}}} }}{{2\left( {m_{{{\text{MN}}}} + m_{{{\text{KI}}}} + m_{{{\text{robot}}}} } \right)}} $$

(5)

The gravitational force vector of an infinitesimal mass element ${\text{d}}m = \rho A{\text{d}}x_{{{\text{KQ}}}}$ at Point Q is calculated by

$$ {\text{d}}{\mathbf{F}}_{{{\text{gravity}}}} = - \frac{{\mu {\text{d}}m}}{{r^{3} }}{\mathbf{r}} $$

(6)

where ${\mathbf{r}} = \left[ {X_{{\text{Q}}} ,Y_{{\text{Q}}} } \right]^{{\text{T}}}$ is the global position vector of Point Q, and $r = \left\| {\mathbf{r}} \right\|$ is the orbital radius. The inertial force of ${\text{d}}m$ is

$$ {\text{d}}{\mathbf{F}}_{{{\text{inertia}}}} = - {\text{d}}m{\ddot{\mathbf{r}}} $$

(7)

The global position vector of Point Q and its derivatives are calculated by

$$ {\mathbf{r}} = \left[ \begin{gathered} X_{{\text{Q}}} \\ Y_{{\text{Q}}} \\ \end{gathered} \right] = \left[ \begin{gathered} r_{0} \cos \theta + x_{{{\text{SQ}}}} \cos \left( {\theta + \alpha } \right) \\ r_{0} \sin \theta + x_{{{\text{SQ}}}} \sin \left( {\theta + \alpha } \right) \\ \end{gathered} \right] $$

(8)

$$ {\dot{\mathbf{r}}} = \left[ \begin{gathered} \dot{X}_{{\text{Q}}} \\ \dot{Y}_{{\text{Q}}} \\ \end{gathered} \right] = \left[ \begin{gathered} - r_{0} \omega_{0} \sin \theta + \dot{x}_{{{\text{PK}}}} \cos \left( {\theta + \alpha } \right) - x_{{{\text{SQ}}}} \omega_{0} \sin \left( {\theta + \alpha } \right) \\ r_{0} \omega_{0} \cos \theta + \dot{x}_{{{\text{PK}}}} \sin \left( {\theta + \alpha } \right) + x_{{{\text{SQ}}}} \omega_{0} \cos \left( {\theta + \alpha } \right) \\ \end{gathered} \right] $$

(9)

$$ {\mathbf{\ddot{r}}} = \left[ \begin{gathered} \ddot{X}_{{\text{Q}}} \\ \ddot{Y}_{{\text{Q}}} \\ \end{gathered} \right] = \left[ \begin{gathered} - r_{0} \omega_{0}^{2} \cos \theta + \ddot{x}_{{{\text{PK}}}} \cos \left( {\theta + \alpha } \right) - 2\dot{x}_{{{\text{PK}}}} \omega_{0} \sin \left( {\theta + \alpha } \right) - x_{{{\text{SQ}}}} \omega_{0}^{2} \cos \left( {\theta + \alpha } \right) \\ - r_{0} \omega_{0}^{2} \sin \theta + \ddot{x}_{{{\text{PK}}}} \sin \left( {\theta + \alpha } \right) + 2\dot{x}_{{{\text{PK}}}} \omega_{0} \cos \left( {\theta + \alpha } \right) - x_{{{\text{SQ}}}} \omega_{0}^{2} \sin \left( {\theta + \alpha } \right) \\ \end{gathered} \right] $$

(10)

Then, the transverse and axial distributed forces of Beam KI are investigated. The transverse and axial forces of ${\text{d}}m$ are calculated by

$$ {\text{d}}F_{{\text{t}}} = \left( {{\text{d}}{\mathbf{F}}_{{{\text{gravity}}}} + {\text{d}}{\mathbf{F}}_{{{\text{inertia}}}} } \right) \cdot {\mathbf{t}} $$

(11)

$$ {\text{d}}F_{{\text{a}}} = \left( {{\text{d}}{\mathbf{F}}_{{{\text{gravity}}}} + {\text{d}}{\mathbf{F}}_{{{\text{inertia}}}} } \right) \cdot {\mathbf{a}} $$

(12)

where ${\mathbf{t}} = \left[ { - \sin \left( {\theta + \alpha } \right),\cos \left( {\theta + \alpha } \right)} \right]^{{\text{T}}}$ and ${\mathbf{a}} = \left[ {\cos \left( {\theta + \alpha } \right),\sin \left( {\theta + \alpha } \right)} \right]^{{\text{T}}}$ are the unit normal vector and unit tangent vector of the undeformed beam, respectively, and the positive transverse and axial directions are coincident with $y$ axis and $x$ axis. Thus, Eqs. (11) and (12) can be rewritten as

$$ \frac{{{\text{d}}F_{{\text{t}}} }}{{{\text{d}}m}} = - \frac{\mu }{{r^{3} }}\left[ { - X_{{\text{Q}}} \sin \left( {\theta + \alpha } \right) + Y_{{\text{Q}}} \cos \left( {\theta + \alpha } \right)} \right] + \ddot{X}_{{\text{Q}}} \sin \left( {\theta + \alpha } \right) - \ddot{Y}_{{\text{Q}}} \cos \left( {\theta + \alpha } \right) $$

(13)

$$ \frac{{{\text{d}}F_{{\text{a}}} }}{{{\text{d}}m}} = - \frac{\mu }{{r^{3} }}\left[ {X_{{\text{Q}}} \cos \left( {\theta + \alpha } \right) + Y_{{\text{Q}}} \sin \left( {\theta + \alpha } \right)} \right] - \ddot{X}_{{\text{Q}}} \cos \left( {\theta + \alpha } \right) - \ddot{Y}_{{\text{Q}}} \sin \left( {\theta + \alpha } \right) $$

(14)

Substituting Eqs. (8) and (10) into Eqs. (13) and (14) yields

$$ \frac{{{\text{d}}F_{{\text{t}}} }}{{{\text{d}}m}} = \frac{{\mu r_{0} \sin \alpha }}{{r^{3} }} - \omega_{0}^{2} r_{0} \sin \alpha - 2\omega_{0} \dot{x}_{{{\text{PK}}}} $$

(15)

$$ \frac{{{\text{d}}F_{{\text{a}}} }}{{{\text{d}}m}} = - \mu \frac{{x_{{{\text{SQ}}}} + r_{0} \cos \alpha }}{{r^{3} }} + r_{0} \omega_{0}^{2} \cos \alpha - \ddot{x}_{{{\text{PK}}}} + x_{{{\text{SQ}}}} \omega_{0}^{2} $$

(16)

In Eqs. (15) and (16), $r_{0}$, $\omega_{0}$, and $\alpha$ are constant, $x_{{{\text{PK}}}}$ is time-varying, and $r$ is determined by the cosine law

$$ r^{2} = r_{0}^{2} + x_{SQ}^{2} + 2x_{SQ} r_{0} \cos \alpha $$

(17)

The first terms of Eqs. (15) and (16) are nonlinear functions of $x_{{{\text{SQ}}}}$ because of $r$. Actually, the variation of $r$ is very small when $x_{{{\text{SQ}}}}$ varies, because the size of the flexible beam is much smaller than the orbital radius $r_{0}$. In order to obtain simple forms of the transverse and axial distributed forces, a first-order Taylor series expansion is adopted to approximate $r^{ - 3}$ around $r_{0}^{ - 3}$, which yields

$$ \begin{gathered} \frac{{{\text{d}}F_{{\text{t}}} }}{{{\text{d}}m}} = \frac{\mu }{{r_{0}^{2} }}\sin \alpha - \frac{{3\mu r_{0} \sin \alpha }}{{2r_{0}^{5} }}2x_{{{\text{SQ}}}} r_{0} \cos \alpha - \omega_{0}^{2} r_{0} \sin \alpha - 2\omega_{0} \dot{x}_{{{\text{PK}}}} \\ = - \frac{3}{2}\omega_{0}^{2} x_{{{\text{SQ}}}} \sin \left( {2\alpha } \right) - 2\omega_{0} \dot{x}_{{{\text{PK}}}} \\ \end{gathered} $$

(18)

$$ \begin{aligned} \frac{{{\text{d}}F_{{\text{a}}} }}{{{\text{d}}m}} = & - \left( {\frac{\mu }{{r_{0}^{3} }} - \frac{{3\mu x_{{{\text{SQ}}}} \cos \alpha }}{{r_{0}^{4} }}} \right)\left( {x_{{{\text{SQ}}}} + r_{0} \cos \alpha } \right) + r_{0} \omega _{0}^{2} \cos \alpha - \ddot{x}_{{{\text{PK}}}} + x_{{{\text{SQ}}}} \omega _{0}^{2} \\ & = 3\omega _{0}^{2} x_{{{\text{SQ}}}} \cos ^{2} \alpha - \ddot{x}_{{{\text{PK}}}} \\ \end{aligned} $$

(19)

The first-order Taylor series expansion is used to approximate the gravitational force because it results in linear distribution of gravitational force, so that the gravity gradient can be considered. Thus, the simplified transverse and axial distributed forces of Beam KI are obtained

$$ q_{{\text{t,KI}}} { = }\frac{{{\text{d}}F_{{\text{t}}} }}{{{\text{d}}x_{{{\text{KQ}}}} }} = - \frac{3}{2}\rho A\omega_{0}^{2} x_{{{\text{SQ}}}} \sin \left( {2\alpha } \right) - 2\rho A\omega_{0} \dot{x}_{{{\text{PK}}}} $$

(20)

$$ q_{{\text{a,KI}}} = \frac{{{\text{d}}F_{{\text{a}}} }}{{{\text{d}}x_{{{\text{KQ}}}} }} = 3\rho A\omega_{0}^{2} x_{{{\text{SQ}}}} \cos^{2} \alpha - \rho A\ddot{x}_{{{\text{PK}}}} $$

(21)

The first terms of Eqs. (20) and (21) represent the gravity gradient of Beam KI, which are dependent on the orbital radius and attitude angle. It is linearly distributed along the beam, as shown in Fig. 4. The first term of Eq. (20) is coincident with the result of literature [25]. The second term of Eq. (20) is the Coriolis force of the beam during assembly. It is proportional to the orbital angular velocity and the assembly velocity. It is distributed uniformly along the beam. The second term of Eq. (21) is the acceleration due to the assembly operation.

Fig. 4

Distributed forces of the flexible beams during assembly when $\sin \left( {2\alpha } \right) > 0$

It can be seen from Eq. (20) that the gravity-gradient term vanishes if $\alpha { = }0$ or $\alpha { = }{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}$. For the axial distributed force in Eq. (21), the gravity-gradient term reaches a maximum when $\alpha { = }0$, and becomes 0 when $\alpha { = }{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}$. Thus, $\alpha { = }{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}$ is more desirable in terms of external forces. Considering that $\dot{x}_{{{\text{PK}}}} < 0$ for the assembly process, the transverse distributed force could be reduced if $\sin \left( {2\alpha } \right) > 0$, as depicted in Fig. 4.

For Beam MN, the derivation procedure is similar, and the results of the transverse and axial distributed forces are

$$ q_{{\text{t,MN}}} = - \frac{3}{2}\rho A\omega_{0}^{2} x_{{{\text{QS}}}} \sin \left( {2\alpha } \right) - 2\rho A\omega_{0} \dot{x}_{{{\text{MP}}}} $$

(22)

$$ q_{{\text{a,MN}}} = 3\rho A\omega_{0}^{2} x_{{{\text{QS}}}} \cos^{2} \alpha - \rho A\ddot{x}_{{{\text{MP}}}} $$

(23)

where the positive transverse and axial directions of Beam MN are opposite $y$ and $x$ axes, respectively, Point Q is an arbitrary point on Beam MN, and $x_{{{\text{MP}}}} { = }x_{{{\text{MK}}}} - x_{{{\text{PK}}}}$ is also a quintic polynomial of time.

3.3 Quasi-static vibrations of the beams

Based on the transverse distributed forces of the beams, the quasi-static vibrations will be derived. The quasi-static model is justified because the external force varies much slower than structural vibrations. The joints and the attitude of the space robot are perfectly controlled, and the orbit of the assembly system is in a steady state. Moreover, the inertial forces due to overall motions have been considered in the force analyses. By using Assumption (1) in Sect. 3.1, the flexible beams can be simplified as cantilever beams, because the transformations and rotations of the captured points of the beams are ideally restricted by the space robot.

Based on Assumption (4), the quasi-static vibration of Beam KI is governed by

$$ EI\frac{{{\text{d}}^{4} v_{{{\text{KI}}}} }}{{{\text{d}}x_{{{\text{KQ}}}}^{4} }} = q_{{\text{t}}} \left( {x_{{{\text{KQ}}}} } \right) $$

(24)

The boundary conditions of the cantilever beam can be written as

$$ v_{{{\text{KI}}}} (0) = \frac{{{\text{d}}v_{{{\text{KI}}}} }}{{{\text{d}}x_{{{\text{KQ}}}} }}(0) = \frac{{{\text{d}}^{2} v_{{{\text{KI}}}} }}{{{\text{d}}x_{{{\text{KQ}}}}^{2} }}(L_{{{\text{KI}}}} ) = \frac{{{\text{d}}^{3} v_{{{\text{KI}}}} }}{{{\text{d}}x_{{{\text{KQ}}}}^{3} }}(L_{{{\text{KI}}}} ) = 0 $$

(25)

Then, the quasi-static vibration of the beam $v_{{{\text{KI}}}}$ can be obtained by integrating Eq. (24), which is shown in Appendix. Thus, the vibration of Point I is

$$ v_{{\text{I}}} = - \frac{11}{{80}}\frac{{\rho AL_{{{\text{KI}}}}^{5} }}{EI}\omega_{0}^{2} \sin \left( {2\alpha } \right) - \frac{3}{16}\frac{{\rho AL_{{{\text{KI}}}}^{4} }}{EI}\omega_{0}^{2} \left( {x_{{{\text{SP}}}} + x_{{{\text{PK}}}} } \right)\sin \left( {2\alpha } \right) - \frac{1}{4}\frac{{\rho AL_{{{\text{KI}}}}^{4} }}{EI}\omega_{0} \dot{x}_{{{\text{PK}}}} $$

(26)

According to the third term of Eq. (26), it should be emphasized that the deformation of the beam is nonzero even if the attitude angle remains 0, which is a unique characteristic of the space assembly process. The maximum deformation is at least proportional to $L_{{{\text{KI}}}}^{4}$ if $x_{{{\text{PK}}}}$ does not change with $L_{{{\text{KI}}}}$. Therefore, the vibrations of the ultra-large beam during space assembly must be considered seriously. Similarly, the vibration of Beam MN $v_{{{\text{MN}}}}$ is shown in Appendix. And the vibration of Point N is

$$ v_{{\text{N}}} = - \frac{11}{{80}}\frac{{\rho AL_{{{\text{MN}}}}^{5} }}{EI}\omega_{0}^{2} \sin \left( {2\alpha } \right) - \frac{3}{16}\frac{{\rho AL_{{{\text{MN}}}}^{4} }}{EI}\omega_{0}^{2} \left( {x_{{{\text{PS}}}} + x_{{{\text{MP}}}} } \right)\sin \left( {2\alpha } \right) - \frac{1}{4}\frac{{\rho AL_{{{\text{MN}}}}^{4} }}{EI}\omega_{0} \dot{x}_{{{\text{MP}}}} $$

(27)

3.4 Control moments of the space robot

Based on the transverse and axial distributed forces of the beams, the resultant forces and moments of the beams on the space robot are studied. These resultant forces and moments of the beams will be counteracted by the end-effectors of the space robot. Thus, they are instructive to the design of grasping end-effectors. The positive directions of the resultant forces and moments are shown in Fig. 5. They are calculated by

$$ M_{{{\text{KI}}}} = \int_{0}^{{L_{{{\text{KI}}}} }} x_{{{\text{KQ}}}} q_{{{\text{t}},{\text{KI}}}} \left( {x_{{{\text{KQ}}}} } \right){\mkern 1mu} {\text{d}}x_{{{\text{KQ}}}} $$

(28)

$$ F_{{x,{\text{KI}}}} = \int_{0}^{{L_{{{\text{KI}}}} }} q_{{{\text{a}},{\text{KI}}}} \left( {x_{{{\text{KQ}}}} } \right){\text{d}}x_{{{\text{KQ}}}} $$

(29)

$$ F_{{y,{\text{KI}}}} = \int_{0}^{{L_{{{\text{KI}}}} }} q_{{{\text{t}},{\text{KI}}}} \left( {x_{{{\text{KQ}}}} } \right){\text{d}}x_{{{\text{KQ}}}} $$

(30)

$$ M_{{{\text{MN}}}} = \int_{0}^{{L_{{{\text{MN}}}} }} x_{{{\text{QM}}}} q_{{\text{t,MN}}} \left( {x_{{{\text{QM}}}} } \right){\mkern 1mu} {\text{d}}x_{{{\text{QM}}}} $$

(31)

$$ F_{{x{\text{,MN}}}} = \int_{0}^{{L_{{{\text{MN}}}} }} q_{{\text{a,MN}}} \left( {x_{{{\text{QM}}}} } \right){\text{d}}x_{{{\text{QM}}}} $$

(32)

$$ F_{{y{\text{,MN}}}} = \int_{0}^{{L_{{{\text{MN}}}} }} q_{{\text{t,MN}}} \left( {x_{{{\text{QM}}}} } \right){\text{d}}x_{{{\text{QM}}}} $$

(33)

Fig. 5

Force analysis of the space robot

The results of Eqs. (28)–(33) are shown in the Appendix.

The joint control moments of the space robot can be estimated roughly. Based on Assumption (2), the inertial forces and moments of the links of the space robot can be neglected to simplify the control moment estimation. Thus, the resultant forces and moments of the beams are transmitted to the joints of the space robot. The control moments $M_{1}$–$M_{7}$ are defined corresponding to the joint angles $\theta_{1}$–$\theta_{7}$. The positive directions of $M_{1}$–$M_{7}$ are selected such that they increase the joint angles $\theta_{1}$–$\theta_{7}$. As seen in Fig. 5, the required control moments $M_{5}$–$M_{7}$ can be calculated by

$$ M_{7} = - M_{{{\text{KI}}}} - F_{{x,{\text{KI}}}} l_{7} $$

(34)

$$ M_{6} = M_{7} + F_{{x,{\text{KI}}}} l_{6} \cos \left( {\theta_{7} } \right) - F_{{y,{\text{KI}}}} l_{6} \sin \left( {\theta_{7} } \right) $$

(35)

$$ M_{5} = M_{6} - F_{{x,{\text{KI}}}} {\kern 1pt} l_{5} {\kern 1pt} \cos \left( {\theta_{6} + \theta_{7} } \right) + F_{{y,{\text{KI}}}} {\kern 1pt} l_{5} {\kern 1pt} \sin \left( {\theta_{6} + \theta_{7} } \right) $$

(36)

The control moments $M_{1}$–$M_{3}$ are calculated by

$$ M_{1} = M_{{{\text{MN}}}} - F_{{x{\text{,MN}}}} l_{1} $$

(37)

$$ M_{2} = M_{1} + F_{{x{\text{,MN}}}} l_{2} \cos \left( {\theta_{1} } \right) + F_{{y{\text{,MN}}}} l_{2} \sin \left( {\theta_{1} } \right) $$

(38)

$$ M_{3} = M_{2} - F_{{x{\text{,MN}}}} {\kern 1pt} l_{3} {\kern 1pt} \cos \left( {\theta_{1} + \theta_{2} } \right) - F_{{y{\text{,MN}}}} {\kern 1pt} l_{3} {\kern 1pt} \sin \left( {\theta_{1} + \theta_{2} } \right) $$

(39)

The attitude control moment of the satellite platform of the space robot can be calculated by

$$ M_{4} { = } - M_{{{\text{KI}}}} - M_{{{\text{MN}}}} - F_{{y{\text{,KI}}}} x_{{{\text{MK}}}} $$

(40)

The above control moments are useful in the controller design of the space robot.

4 Simulation modelling method

To study the space assembly process more accurately, a simulation model is built based on ANCF and NCF. The assumptions in Sect. 3.1 can be abandoned in the simulation model. Gravity gradient and Coriolis force are taken into account by adopting the second-order Taylor series expansion of the gravitational potential energy of ANCF/NCF and simulating the orbital and attitude motions. Thus, the simulation model is an orbit–attitude–structure coupled model.

4.1 Two-dimensional ANCF beam element

The flexible beams are modelled by ANCF, which is a well-known rigid-flexible coupled modelling method that is able to deal with large-deformation and large-rotation cases [28,29,30] such as soft robot [31], flexible membrane system [32], and fluid materials [33,34,35]. The two-dimensional two-node Euler–Bernoulli ANCF beam element is adopted [36]. The basic theory of this ANCF beam element is briefly introduced in this section.

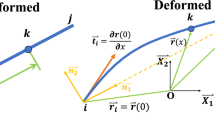
The global position vector of an arbitrary point in an element can be calculated by the following cubic interpolation

$$ {\mathbf{r}}\left( {x_{{\text{e}}} } \right) = \left[ {X,Y} \right]^{{\text{T}}} = {\mathbf{S}}\left( {x_{{\text{e}}} } \right){\mathbf{e}} $$

(41)

where $x_{{\text{e}}} \in \left[ {0,l_{{\text{e}}} } \right]$ is the local coordinate of the centreline of the element, $l_{{\text{e}}}$ is the length of the element, ${\mathbf{S}}\left( {x_{{\text{e}}} } \right)$ is a cubic shape function, and ${\mathbf{e}}$ is the generalized coordinate vector. The shape function can be found in literature [36]. The generalized coordinate vector is defined as

$$ {\mathbf{e}} = \left[ {{\mathbf{r}}^{{\text{T}}} \left( 0 \right),\frac{{\partial {\mathbf{r}}^{{\text{T}}} \left( 0 \right)}}{{\partial x_{{\text{e}}} }},{\mathbf{r}}^{{\text{T}}} \left( {l_{{\text{e}}} } \right),\frac{{\partial {\mathbf{r}}^{{\text{T}}} \left( {l_{{\text{e}}} } \right)}}{{\partial x_{{\text{e}}} }}} \right]^{{\text{T}}} $$

(42)

The dynamic equations of the element can be derived through Hamilton’s equations. To this end, the kinetic energy and potential energy are introduced. According to Eq. (41), the velocity vector of a point in an element is

$$ {\dot{\mathbf{r}}}\left( {x_{{\text{e}}} } \right){\mathbf{ = S}}\left( {x_{{\text{e}}} } \right){\dot{\mathbf{e}}} $$

(43)

Therefore, the kinetic energy of an element can be expressed as

$$ T_{{\text{e}}} = \frac{1}{2}\int_{0}^{{l_{{\text{e}}} }} {\rho A{\dot{\mathbf{r}}}^{{\text{T}}} {\dot{\mathbf{r}}}{\text{d}}x_{{\text{e}}} } = \frac{1}{2}{\dot{\mathbf{e}}}^{{\text{T}}} \int_{0}^{{l_{{\text{e}}} }} {\rho A{\mathbf{S}}^{{\text{T}}} \left( {x_{{\text{e}}} } \right){\mathbf{S}}\left( {x_{{\text{e}}} } \right){\text{d}}x_{{\text{e}}} } {\dot{\mathbf{e}}} = \frac{1}{2}{\dot{\mathbf{e}}}^{{\text{T}}} {\mathbf{M}}_{{\text{e}}} {\dot{\mathbf{e}}} $$

(44)

where ${\mathbf{M}}_{{\text{e}}}$ is the mass matrix of the element. The elastic potential energy of an element can be calculated by

$$ U_{{\text{ela,e}}} = \frac{1}{2}\int_{0}^{{l_{{\text{e}}} }} {EA\left( {\frac{\partial u}{{\partial x_{{\text{e}}} }}} \right)^{2} + EI\left( {\frac{{\partial^{2} v}}{{\partial x_{{\text{e}}}^{{2}} }}} \right)^{2} {\text{d}}x_{{\text{e}}} } $$

(45)

where $u$ and $v$ are the axial deformation and transverse deformation, respectively. By defining the axial direction, Eq. (45) can be expressed as a nonlinear function of the generalized coordinates. The detailed expression of the elastic energy is not given for simplicity, which is found in literature [36].

The key modelling procedure is to calculate the distributed gravitational force and gravity gradient on the flexible bodies. The generalized gravitational force of an element can be calculated by

$$ \left\{ \begin{gathered} {\mathbf{f}}_{{\text{gra,e}}} = - \frac{{\partial U_{{\text{gra,e}}} }}{{\partial {\mathbf{e}}}} \hfill \\ U_{{\text{gra,e}}} = - \int_{0}^{{l_{{\text{e}}} }} {\frac{\mu \rho A}{{\left( {{\mathbf{r}}^{{\text{T}}} {\mathbf{r}}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}{\text{d}}x_{{\text{e}}} } \hfill \\ \end{gathered} \right. $$

(46)

where $U_{{\text{gra,e}}}$ is the gravitational potential energy of the element. However, it is not easy to obtain the theoretical expression of ${\mathbf{f}}_{{\text{gra,e}}}$ because of the nonlinearity of the integrant. According to literature [37], the approximate expression of $U_{{\text{gra,e}}}$ is obtained by using the second-order Taylor series expansion. It should be pointed out that first-order Taylor series expansion of $U_{{\text{gra,e}}}$ only generates uniform gravitational force as it does on the ground. Thus, at least second-order Taylor series expansion should be used to consider the gravity gradient. The simplified ${\mathbf{f}}_{{\text{gra,e}}}$ becomes

$$ {\mathbf{f}}_{{\text{gra,e}}} = \frac{\mu }{{\left( {{\mathbf{r}}_{{0,{\text{e}}}}^{{\text{T}}} {\mathbf{r}}_{{0,{\text{e}}}} } \right)^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0pt} 2}}} }}\left( {{\mathbf{A}}_{{\text{e}}} {\mathbf{e}} + {\mathbf{B}}_{{\text{e}}}^{{\text{T}}} } \right) $$

(47)

where ${\mathbf{r}}_{{0,{\text{e}}}}$ is the global position vector of the centre of mass of the element. The matrixes ${\mathbf{A}}_{{\text{e}}}$ and ${\mathbf{B}}_{{\text{e}}}$ are calculated by

$$ {\mathbf{A}}_{{\text{e}}} = \frac{{\rho Al_{{\text{e}}} }}{420}\left[ {\begin{array}{*{20}c} {156{\mathbf{D}}_{{\text{e}}} } & {22l_{{\text{e}}} {\mathbf{D}}_{{\text{e}}} } & {54{\mathbf{D}}_{{\text{e}}} } & { - 13l_{{\text{e}}} {\mathbf{D}}_{{\text{e}}} } \\ {} & {4l_{{\text{e}}}^{2} {\mathbf{D}}_{{\text{e}}} } & {13l_{{\text{e}}} {\mathbf{D}}_{{\text{e}}} } & { - 3l_{{\text{e}}}^{2} {\mathbf{D}}_{{\text{e}}} } \\ {} & {} & {156{\mathbf{D}}_{{\text{e}}} } & { - 22l_{{\text{e}}} {\mathbf{D}}_{{\text{e}}} } \\ {{\text{symmetric}}} & {} & {} & {4l_{{\text{e}}}^{2} {\mathbf{D}}_{{\text{e}}} } \\ \end{array} } \right] $$

(48)

$$ {\mathbf{B}}_{{\text{e}}} = - 3\rho Al_{{\text{e}}} {\mathbf{r}}_{{0,{\text{e}}}}^{{\text{T}}} {\mathbf{r}}_{{0,{\text{e}}}} \left[ {\begin{array}{*{20}c} {\frac{1}{2}{\mathbf{r}}_{{0,{\text{e}}}}^{{\text{T}}} } & {\frac{{l_{{\text{e}}} }}{12}{\mathbf{r}}_{{0,{\text{e}}}}^{{\text{T}}} } & {\frac{1}{2}{\mathbf{r}}_{{0,{\text{e}}}}^{{\text{T}}} } & { - \frac{{l_{{\text{e}}} }}{12}{\mathbf{r}}_{{0,{\text{e}}}}^{{\text{T}}} } \\ \end{array} } \right] $$

(49)

where ${\mathbf{D}}_{{\text{e}}} = 3{\mathbf{r}}_{{0,{\text{e}}}} {\mathbf{r}}_{{0,{\text{e}}}}^{{\text{T}}} - {\mathbf{r}}_{{0,{\text{e}}}}^{{\text{T}}} {\mathbf{r}}_{{0,{\text{e}}}} {\mathbf{I}}_{2}$, and ${\mathbf{I}}_{2}$ is a 2-dimensional identity matrix. The generalized force vector of a moment is relatively complex for ANCF and NCF because they do not use rotational coordinates. In order to exert a control moment (or external moment) on the first node of an ANCF element, the following generalized force is used [38, 39]

$$ {\mathbf{f}}_{{\text{moment,e}}} = \frac{{M_{{\text{moment,e}}} }}{{e_{3}^{2} + e_{4}^{2} }}\left[ {0,0, - e_{4} ,e_{3} ,0,0,0,0} \right]^{{\text{T}}} $$

(50)

where $M_{{\text{moment,e}}}$ is the moment (the positive direction is counterclockwise), $e_{3}$ and $e_{4}$ are the third and fourth elements of ${\mathbf{e}}$.

4.2 Two-dimensional NCF

The multi-rigid-body system of the space robot is modelled by NCF. Although all rigid-body formulations lead to the same results, NCF is more suitable for complex multibody systems because all rigid bodies are described in a global Cartesian coordinate system, which is more straightforward and more convenient [40, 41]. Some difficulties of Euler angles are avoided in the NCF such as the constraint force/moment, multiple coordinate transformations, and singularity problem. The coordinates of the joints can be shared by adjacent rigid bodies to reduce the number of constraints. Furthermore, NCF has the same form of dynamic equations as ANCF and similar characteristics. It has been widely used in many dynamic studies of three-dimensional spacecraft and robotics [42,43,44]. In this section, a two-dimensional NCF is reduced from the three-dimensional NCF.

In the two-dimensional NCF, the global coordinates of two points and one vector are used to describe a rigid body. The modelling procedure of rigid body AB is taken as an example, as shown in Fig. 6. The global position vector of an arbitrary point in AB can be expressed as

$$ {\mathbf{r}} = \left[ {X,Y} \right]^{{\text{T}}} = {\mathbf{C}}\left( {x_{{1}} ,y_{1} } \right){\mathbf{e}}_{1} $$

(51)

$$ {\mathbf{e}}_{1} = \left[ {{\mathbf{r}}_{{\text{A}}} ,{\mathbf{r}}_{{\text{B}}} ,{\mathbf{v}}_{1} } \right]^{{\text{T}}} $$

(52)

where $x_{{1}}$ and $y_{1}$ are local coordinates of the rigid body, ${\mathbf{C}}\left( {x_{{1}} ,y_{1} } \right)$ is a linear shape function, ${\mathbf{e}}_{1}$ is the generalized coordinate vector, and ${\mathbf{v}}_{1}$ is a unit normal vector fixed to rigid body AB and perpendicular to AB. The expression of the shape function is

$$ {\mathbf{C}}\left( {x_{{1}} ,y_{1} } \right) = \left[ {\frac{{x_{{1}} }}{{l_{1} }}{\mathbf{I}}_{2} ,\left( {1 - \frac{{x_{{1}} }}{{l_{1} }}} \right){\mathbf{I}}_{2} ,y_{{1}} {\mathbf{I}}_{2} } \right] $$

(53)

Fig. 6

NCF description of rigid body AB

There are three degrees of freedom for a planar rigid body. However, there are six generalized coordinates in Eq. (52). Thus, they are subjected to the following three constraints that describe the length and perpendicularity of the vectors

$$ \left\{ \begin{gathered} \left( {{\mathbf{r}}_{{\text{A}}} - {\mathbf{r}}_{{\text{B}}} } \right)^{{\text{T}}} \left( {{\mathbf{r}}_{{\text{A}}} - {\mathbf{r}}_{{\text{B}}} } \right) - l_{1}^{2} = 0, \hfill \\ {\mathbf{v}}_{1}^{{\text{T}}} {\mathbf{v}}_{1} - 1 = 0, \hfill \\ \left( {{\mathbf{r}}_{{\text{A}}} - {\mathbf{r}}_{{\text{B}}} } \right)^{{\text{T}}} {\mathbf{v}}_{1} = 0 \hfill \\ \end{gathered} \right. $$

(54)

Alternatively, the vector ${\mathbf{v}}_{1}$ can be abandoned so that the generalized coordinates, constraints, and simulation time can be reduced [45]. However, it cannot be extended to three-dimensional NCF.

Similar to the ANCF, the kinetic energy of rigid body AB is calculated by

$$ T_{1} = \frac{1}{2}\int_{{V_{1} }}^{{}} {\rho {\dot{\mathbf{r}}}^{{\text{T}}} {\dot{\mathbf{r}}}{\text{d}}V_{1} } = \frac{1}{2}{\dot{\mathbf{e}}}_{1}^{{\text{T}}} \left[ {\int_{{V_{1} }}^{{}} {\rho {\mathbf{C}}^{{\text{T}}} \left( {x_{{1}} ,y_{1} } \right){\mathbf{C}}\left( {x_{{1}} ,y_{1} } \right){\text{d}}V_{1} } } \right]{\dot{\mathbf{e}}}_{1} = \frac{1}{2}{\dot{\mathbf{e}}}_{1}^{{\text{T}}} {\mathbf{M}}_{{1}} {\dot{\mathbf{e}}}_{1} $$

(55)

where $V_{1}$ and ${\mathbf{M}}_{{1}}$ are the volume and the mass matrix of rigid body AB. The generalized gravitational force of the NCF can be calculated by the same procedure as the ANCF element using the second-order Taylor series expansion of the gravitational potential energy. The final expression of the generalized gravitational force of NCF is

$$ {\mathbf{f}}_{{\text{gra,1}}} = - \frac{{\partial U_{{\text{gra,1}}} }}{{\partial {\mathbf{e}}}} = \frac{\mu }{{\left( {{\mathbf{r}}_{0,1}^{{\text{T}}} {\mathbf{r}}_{0,1} } \right)^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0pt} 2}}} }}\left( {{\mathbf{A}}_{1} {\mathbf{e}}_{1} + {\mathbf{B}}_{1}^{{\text{T}}} } \right) $$

(56)

where ${\mathbf{r}}_{{0,{\text{e}}}}$ is the global position vector of the centre of mass of rigid body AB, and $U_{{\text{gra,1}}}$ is the gravitational potential energy. The matrixes ${\mathbf{A}}_{1}$ and ${\mathbf{B}}_{1}$ are calculated by

$$ {\mathbf{A}}_{1} = \frac{1}{{l_{1}^{2} }}\left[ {\begin{array}{*{20}c} {\left( {m_{1} l_{1}^{2} + I_{x1} - 2m_{1} l_{1} x_{{{\text{G1}}}} } \right){\mathbf{D}}_{1} } & {\left( {m_{1} l_{1} x_{{{\text{G1}}}} - I_{x1} } \right){\mathbf{D}}_{1} } & {\left( {m_{1} y_{{{\text{G1}}}} l_{1}^{2} - I_{xy1} l_{1} } \right){\mathbf{D}}_{1} } \\ {} & {I_{x1} {\mathbf{D}}_{1} } & {I_{xy1} l_{1} {\mathbf{D}}_{1} } \\ {{\text{symmetric}}} & {} & {I_{y1} l_{1}^{2} {\mathbf{D}}_{1} } \\ \end{array} } \right] $$

(57)

$$ {\mathbf{B}}_{1} = - 3m_{1} {\mathbf{r}}_{0,1}^{{\text{T}}} {\mathbf{r}}_{0,1} \left[ {\begin{array}{*{20}c} {\frac{{x_{{{\text{G1}}}} }}{{l_{1} }}{\mathbf{r}}_{0,1}^{{\text{T}}} } & {\left( {1 - \frac{{x_{{{\text{G1}}}} }}{{l_{1} }}} \right){\mathbf{r}}_{0,1}^{{\text{T}}} } & {y_{{{\text{G1}}}} {\mathbf{r}}_{0,1}^{{\text{T}}} } \\ \end{array} } \right]^{{\text{T}}} $$

(58)

where $I_{x1} = \int_{{V_{1} }}^{{}} {\rho x_{1}^{2} {\text{d}}V_{1} }$, $I_{y1} = \int_{{V_{1} }}^{{}} {\rho y_{1}^{2} {\text{d}}V_{1} }$, and $I_{xy1} = \int_{{V_{1} }}^{{}} {\rho x_{1} y_{1} {\text{d}}V_{1} }$ can be calculated from the inertia matrix with respect to ${\text{A}}x_{{1}} y_{1}$ coordinate system, $x_{{{\text{G1}}}} = \int_{{V_{1} }}^{{}} {\rho x_{1} {\text{d}}V_{1} }$ and $y_{{{\text{G1}}}} = \int_{{V_{1} }}^{{}} {\rho y_{1} {\text{d}}V_{1} }$ are the centre of mass in ${\text{A}}x_{{1}} y_{1}$, and ${\mathbf{D}}_{1} = 3{\mathbf{r}}_{0,1} {\mathbf{r}}_{0,1}^{{\text{T}}} - {\mathbf{r}}_{0,1}^{{\text{T}}} {\mathbf{r}}_{0,1} {\mathbf{I}}_{2}$. Similarly, in order to exert a control moment on Rigid Body 1, the following generalized force is used

$$ {\mathbf{f}}_{{\text{moment,1}}} = \frac{{M_{{\text{moment,1}}} }}{{l_{1} }}\left[ {0,0,0,0,\left( {{\mathbf{r}}_{{\text{A}}} - {\mathbf{r}}_{{\text{B}}} } \right)^{{\text{T}}} } \right]^{{\text{T}}} $$

(59)

4.3 Dynamic modelling of the space assembly system

Based on the above ANCF and NCF, the orbit–attitude–structure coupled dynamic equations of the space assembly system are derived in this subsection, based on the constrained Hamilton’s equations.

The space robot consists of seven rigid bodies with nine degrees of freedom. According to Sect. 4.2, the space robot should contain 42 generalized coordinates and 33 constraints, including the internal constraints of each rigid body and the linear constraints between the adjacent rigid bodies. However, the global position vector of the common point of two adjacent rigid bodies appears only once in the generalized coordinate vector. Consequently, the generalized coordinate vector of the space robot is

$$ {\mathbf{q}}_{{{\text{robot}}}} = \left[ {{\mathbf{r}}_{{\text{A}}}^{{\text{T}}} ,{\mathbf{r}}_{{\text{B}}}^{{\text{T}}} ,{\mathbf{v}}_{{1}}^{{\text{T}}} ,{\mathbf{r}}_{{\text{C}}}^{{\text{T}}} ,{\mathbf{v}}_{2}^{{\text{T}}} ,{\mathbf{r}}_{{\text{D}}}^{{\text{T}}} ,{\mathbf{v}}_{3}^{{\text{T}}} ,{\mathbf{r}}_{{\text{E}}}^{{\text{T}}} ,{\mathbf{v}}_{4}^{{\text{T}}} ,{\mathbf{r}}_{{\text{F}}}^{{\text{T}}} ,{\mathbf{v}}_{5}^{{\text{T}}} ,{\mathbf{r}}_{{\text{G}}}^{{\text{T}}} ,{\mathbf{v}}_{6}^{{\text{T}}} ,{\mathbf{r}}_{{\text{H}}}^{{\text{T}}} ,{\mathbf{v}}_{7}^{{\text{T}}} } \right]^{{\text{T}}} \in {\mathbb{R}}^{30} $$

(60)

The constraints of the space robot are as follows

$$ \left\{ \begin{gathered} \left( {{\mathbf{r}}_{i1} - {\mathbf{r}}_{i2} } \right)^{{\text{T}}} \left( {{\mathbf{r}}_{i1} - {\mathbf{r}}_{i2} } \right) = l_{i}^{2} \hfill \\ {\mathbf{v}}_{i}^{{\text{T}}} {\mathbf{v}}_{i} = 1 \hfill \\ \left( {{\mathbf{r}}_{i1} - {\mathbf{r}}_{i2} } \right)^{{\text{T}}} {\mathbf{v}}_{i} = 0 \hfill \\ \end{gathered} \right.i = 1,2,...,7 $$

(61)

where ${\mathbf{r}}_{i1}$ and ${\mathbf{r}}_{i2}$ represent the global position vectors of the left and right ends of each rigid body, for instance, ${\mathbf{r}}_{11}$ and ${\mathbf{r}}_{12}$ represent ${\mathbf{r}}_{{\text{A}}}$ and ${\mathbf{r}}_{{\text{B}}}$ for $i = 1$. The constraints in Eq. (61) can also be abbreviated as

$$ {\mathbf{g}}\left( {{\mathbf{q}}_{{{\text{robot}}}} } \right) = {\mathbf{0}} \in {\mathbb{R}}^{21} $$

(62)

For the whole space assembly system, the generalized coordinate vector is

$$ {\mathbf{q}} = \left[ {{\mathbf{q}}_{{{\text{robot}}}}^{{\text{T}}} ,{\mathbf{q}}_{{{\text{MN}}}}^{{\text{T}}} ,{\mathbf{q}}_{{{\text{KI}}}}^{{\text{T}}} } \right]^{{\text{T}}} $$

(63)

where ${\mathbf{q}}_{{{\text{MN}}}}$ and ${\mathbf{q}}_{{{\text{KI}}}}$ are the generalized coordinates of Beam MN and Beam KI, respectively. The kinetic energy of the system can be expressed as

$$ T = \sum\limits_{i = 1}^{7} {T_{i} } + T_{{{\text{MN}}}} + T_{{{\text{KI}}}} = \frac{1}{2}{\dot{\mathbf{q}}}^{{\text{T}}} {\mathbf {M}} {\mathbf{\dot{q}}} $$

(64)

The mass matrix of the system ${\mathbf{M}}$ in Eq. (64) can be superposed by the mass matrices of the ANCF elements and the rigid bodies. Similarly, the potential energy of the system is

$$ U = \sum\limits_{i = 1}^{7} {U_{{{\text{gra,}}i}} } + U_{{\text{gra,MN}}} + U_{{\text{gra,KI}}} + U_{{\text{ela,MN}}} + U_{{\text{ela,KI}}} $$

(65)

The grasping relationships between the space robot and the flexible beams are equivalent to spring-damper systems for simplicity. The grasping force and moment of Point A of rigid body AB are calculated by

$$ {\mathbf{F}}_{{\text{A}}} { = }k\left( {{\mathbf{r}}_{{\text{M}}} - {\mathbf{r}}_{{\text{A}}} } \right) + c\left( {{\dot{\mathbf{r}}}_{{\text{M}}} - {\dot{\mathbf{r}}}_{{\text{A}}} } \right) $$

(66)

$$ M_{{\text{A}}} { = }k\left( {\alpha_{{{\text{AM}}}} - \frac{{\uppi }}{2}} \right) + c\dot{\alpha }_{{{\text{AM}}}} $$

(67)

where ${\mathbf{r}}_{{\text{M}}}$ is the first two generalized coordinates of ${\mathbf{q}}_{{{\text{MN}}}}$, and $\alpha_{{{\text{AM}}}}$ is the angle between AB and MN. The coefficients $k = 10^{6}$ and $c = 10^{4}$ are selected for displacements, while $k = 2 \times 10^{7}$ and $c = 2 \times 10^{4}$ are used for rotations. They are selected by the try-and-error method such that the grasping displacements and rotations are small enough and has little influence on the dynamics during assembly, because this paper is focused on the dynamics of the assembly process. The angle $\alpha_{{{\text{AM}}}}$ can be calculated by the following expression because it is approximately ${\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}$

$$ \alpha = \arccos \left( {{\mathbf{v}}_{{{\text{MN}}}}^{{\text{T}}} \frac{{{\mathbf{r}}_{{\text{B}}} - {\mathbf{r}}_{{\text{A}}} }}{{l_{1} }}} \right) $$

(68)

where ${\mathbf{v}}_{{\text{NM}}}$ represents the unit tangent vector of the beam MN at point M obtained by the 3^rd and 4^th generalized coordinates of ${\mathbf{q}}_{{{\text{MN}}}}$. The expressions of grasping forces and moments of GH, MN, and KI can be obtained similarly.

Based on the kinetic energy and potential energy, the dynamic equations of the space assembly system are derived by using the constrained Hamiltonian principle to obtain the following first-order differential–algebraic equations

$$ \left\{ \begin{gathered} {\dot{\mathbf{q}}} = {\mathbf{M}}^{ - 1} {\mathbf{p}}, \hfill \\ {\dot{\mathbf{p}}} = - \frac{{\partial U\left( {\mathbf{q}} \right)}}{{\partial {\mathbf{q}}}} - \frac{{\partial {\mathbf{g}}^{{\text{T}}} \left( {\mathbf{q}} \right)}}{{\partial {\mathbf{q}}}}{{\varvec{\uplambda}}} + {\mathbf{Q}}, \hfill \\ {\mathbf{g}}\left( {\mathbf{q}} \right) = {\mathbf{0}} \hfill \\ \end{gathered} \right. $$

(69)

where ${\mathbf{p}}$ is termed the generalized momentum vector of the system, ${{\varvec{\uplambda}}}$ is a vector of Lagrangian multiplier, ${\mathbf{Q}}$ is a generalized external force vector obtained by the principle virtual work. The gravitational force and gravity gradient of the space assembly system are considered in Eq. (69) by using the second-order Taylor series expansion of gravitational potential energy. The initial orbital and attitude conditions $r_{0} ,\dot{r}_{0} = 0,\theta_{0} = 0,\dot{\theta }_{0} = \sqrt {{\mu \mathord{\left/ {\vphantom {\mu {r_{0}^{3} }}} \right. \kern-0pt} {r_{0}^{3} }}} ,\alpha_{0} \;{\text{and}}\;\dot{\alpha }_{0} = 0$ are used to simulate the orbit and attitude of the system. The inertial forces of the system, including the transverse distributed Coriolis forces and axial distributed inertia forces of the beams, are automatically taken into account. Thus, Eq. (69) is an orbit–attitude–structure coupled dynamic model.

The differential–algebraic equation set (69) is solved by the energy- and constraint-conserving algorithm in literature [46], which is briefly introduced as follows. Firstly, Eq. (69) can be rewritten as

$$ \left\{ \begin{aligned} & {\mathbf{\dot{x} = f}}\left( {{\mathbf{x,\lambda }}} \right) \hfill \\ & {\mathbf{g}}\left( {\mathbf{x}} \right){\mathbf{ = 0}} \hfill \\ \end{aligned} \right. $$

(70)

where ${\mathbf{x}}{ = }\left[ {{\mathbf{q}}^{{\text{T}}} ,{\mathbf{p}}^{{\text{T}}} } \right]^{{\text{T}}}$. The two-stage fourth-order Runge–Kutta method is used to discretize the differential equations, and the Lagrangian multiplier ${{\varvec{\uplambda}}}$ is assumed unchanged in one time step. Thus, Eq. (69) becomes

$$ {\mathbf{x}}_{n + 1} = {\mathbf{x}}_{n} + \frac{1}{2}{\text{d}}t\left( {{\mathbf{k}}_{1} + {\mathbf{k}}_{2} } \right) $$

(71)

and

$$ \left\{ \begin{gathered} {\mathbf{k}}_{1} = {\mathbf{f}}\left( {{\mathbf{x}}_{n} + a_{11} {\text{d}}t{\mathbf{k}}_{1} + a_{12} {\text{d}}t{\mathbf{k}}_{2} ,{{\varvec{\uplambda}}}_{n + 1} } \right) \hfill \\ {\mathbf{k}}_{2} = {\mathbf{f}}\left( {{\mathbf{x}}_{n} + a_{21} {\text{d}}t{\mathbf{k}}_{1} + a_{22} {\text{d}}t{\mathbf{k}}_{2} ,{{\varvec{\uplambda}}}_{n + 1} } \right) \hfill \\ {\mathbf{g}}\left( {{\mathbf{x}}_{n} + {{{\text{d}}t\left( {{\mathbf{k}}_{1} + {\mathbf{k}}_{2} } \right)} \mathord{\left/ {\vphantom {{{\text{d}}t\left( {{\mathbf{k}}_{1} + {\mathbf{k}}_{2} } \right)} 2}} \right. \kern-0pt} 2}} \right) = {\mathbf{0}} \hfill \\ \end{gathered} \right. $$

(72)

The nonlinear equation set (72) is solved by the Newton–Raphson iteration method

$$ {\mathbf{y}}_{k + 1} = {\mathbf{y}}_{k} - {\mathbf{J}}^{ - 1} \left( {{\mathbf{y}}_{k} } \right){\mathbf{h}}\left( {{\mathbf{y}}_{k} } \right) $$

(73)

where ${\mathbf{y}} = \left[ {{\mathbf{k}}_{1}^{{\text{T}}} ,{\mathbf{k}}_{2}^{{\text{T}}} ,{{\varvec{\uplambda}}}_{n + 1}^{{\text{T}}} } \right]^{{\text{T}}}$, ${\mathbf{h}}\left( {\mathbf{y}} \right)$ is the abbreviation of Eq. (72), and ${\mathbf{J}}\left( {\mathbf{y}} \right)$ is Jacobian matrix of ${\mathbf{h}}\left( {\mathbf{y}} \right)$.

4.4 Trajectory planning and control

Trajectory planning and trajectory tracking control of the space robot are not the focus of this paper. However, they should be considered in order to accomplish the assembly process. Under the control of the space robot, the flexible beams should get close to each other smoothly. Besides, the motions of the flexible beams should be strictly along $x$ axis to avoid exciting the vibrations of the beams to the maximum extent. This requirement can be satisfied by the ingenious cooperative trajectory planning and control of the joints such that the $y$ coordinate of the centre of mass of the space robot is unaltered during assembly.

The trajectories are firstly planned in the ${\text{S}}xy$ coordinate system, and then transferred into the joint space through nonlinear geometric relationships. The quintic polynomial is used to plan the relative coordinate from Point M to Point K

$$ x_{{{\text{MK}}}} \left( t \right) = a_{0} + a_{1} t + a_{2} t^{2} + a_{3} t^{3} + a_{4} t^{4} + a_{5} t^{5} $$

(74)

with the following conditions

$$ \left\{ \begin{gathered} x_{{{\text{MK}}}} \left( 0 \right) = x_{{{\text{MK}}0}} ,\dot{x}_{{{\text{MK}}}} \left( 0 \right) = 0,\ddot{x}_{{{\text{MK}}}} \left( 0 \right) = 0, \hfill \\ x_{{{\text{MK}}}} \left( {t_{{{\text{end}}}} } \right) = 0,\dot{x}_{{{\text{MK}}}} \left( {t_{{{\text{end}}}} } \right) = 0,\ddot{x}_{{{\text{MK}}}} \left( {t_{{{\text{end}}}} } \right) = 0 \hfill \\ \end{gathered} \right. $$

(75)

where $t_{{{\text{end}}}}$ is the assembly duration, $x_{{{\text{MK0}}}} = 18{\text{ m}}$ is the initial assembly distance used in this paper, and $a_{i}$ can be determined by the initial and terminal conditions. Then, the space robot keeps a symmetrical configuration during the assembly process. Links AB and GH are perpendicular to the flexible beams. Thus, the following relationships can be obtained

$$ \left\{ \begin{gathered} \theta_{7} { = }\theta_{1} ,\theta_{6} { = }\theta_{2} ,\theta_{5} { = }\theta_{3} , \hfill \\ \theta_{1} { + }\theta_{2} { + }\theta_{3} { = }\frac{5\pi }{2} \hfill \\ \end{gathered} \right. $$

(76)

The two unknowns in Eq. (76) are $\theta_{1}$ and $\theta_{2}$, which can be obtained through geometric relationships. In addition, $\theta_{4} = \alpha$ is the given attitude angle in the simulations. The relative coordinate from Point M to Point K can also be calculated by the joint angles

$$ x_{{{\text{MK}}}} = l_{4} + 2l_{2} \sin \theta_{1} - 2l_{3} \sin \left( {\theta_{1} { + }\theta_{2} } \right) $$

(77)

In order to maintain the $y$ coordinates of Point M and Point K $y_{{\text{M}}} = y_{{\text{K}}} = 0$, the centre of mass of the space robot should be unchanged in the simulation, which is calculated by

$$ y_{{\text{cm,robot}}} = l_{1} + \frac{{ - \left( {m_{2} l_{2} + 2m_{3} l_{2} + m_{4} l_{2} } \right)\cos \theta_{1} + \left( {m_{3} l_{3} + m_{4} l_{3} } \right)\cos \left( {\theta_{1} + \theta_{2} } \right)}}{{2m_{2} + 2m_{3} + m_{4} }} $$

(78)

In this paper, $y_{{\text{cm,robot}}} = 6{\text{ m}}$ is adopted. It should be pointed out that the trajectory planning methods of space robots with a floating base, such as the virtual arm method [47], are not used because relative trajectories are required for the assembly process, instead of absolute trajectories in [47]. By solving nonlinear Eqs. (77) and (78), $\theta_{1}$ and $\theta_{2}$ can be obtained. The other joint angles can be calculated through Eq. (76). The planned trajectories of the joint angles are shown in Fig. 7.

Fig. 7

Trajectory planning results of joints

The simple feedforward–feedback control method is used to track the planned trajectories of the joints of the space robot. The control moments are calculated by

$$ M_{i} { = }K_{{{\text{FF}}}} M_{{{\text{theory,}}i}} + K_{{{\text{p}}i}} e_{i} + K_{{{\text{d}}i}} \dot{e}_{i} $$

(79)

where $i = 1,2, \cdots ,7$ ($i = 4$ is the attitude control of the space robot, and other values are joint control), $M_{{{\text{theory,}}i}}$ denote the control moments of the theoretical model given in Eqs. (34)–(40), $K_{{{\text{FF}}}}$ is a switch parameter for the feedforward control moment, $e_{i}$ are the control errors of $\theta_{i}$, $K_{{{\text{p}}i}}$ and $K_{{{\text{d}}i}}$ are the proportional and derivative gains, respectively. The parameter $K_{{{\text{FF}}}} = 1$ means that the controller is a feedforward–feedback controller, while $K_{{{\text{FF}}}} = 0$ represents a pure feedback controller. The errors are defined as

$$ e_{i} { = }\theta_{{i,{\text{planned}}}} - \theta_{i} $$

(80)

where $\theta_{{i,{\text{planned}}}}$ represent the planned results, and $\theta_{i}$ can be calculated by the generalized coordinates in numerical simulations. The following proportional and derivative gains are adopted for simplicity

$$ \left\{ \begin{gathered} K_{{{\text{p}}i}} = 1.0 \times 10^{6} ,i = 1,2, \cdots ,7 \hfill \\ K_{{{\text{d}}i}} = 2.0 \times 10^{4} ,i = 1,2, \cdots ,7 \hfill \\ \end{gathered} \right. $$

(81)

5 Numerical validation and simulations

This section compares the numerical results of the theoretical model and the simulation model to show the validation of the two modelling methods. The flexible beams KI and MN are composed of $n_{{{\text{KI}}}}$ and $n_{{{\text{MN}}}}$ structural modules. The parameters of a structural module are shown in Table 1. The lengths of the flexible beams are calculated by

$$ L_{{{\text{KI}}}} = n_{{{\text{KI}}}} L_{{{\text{module}}}} ,L_{{{\text{MN}}}} = n_{{{\text{MN}}}} L_{{{\text{module}}}} $$

(82)

Table 1 Parameters of a structural module

The parameters of nine typical cases are given in Table 2. Case 1 is a typical case that other cases are based on Case 1. Case 2 adopts a pure feedback controller. Case 3 studies the effects of the attitude angle $\alpha$. Case 4 and Case 5 investigate the influences of the numbers of structural modules for the flexible beams. Case 6–Case 9 further study the effects of the Coriolis force and gravity gradient. The LEO in Table 2 represents low Earth orbit that $r_{0} = 7136636{\text{ m}}$ and $\omega_{0} = \left( {{{2\pi } \mathord{\left/ {\vphantom {{2\pi } {6000}}} \right. \kern-0pt} {6000}}} \right) \, {{{\text{rad}}} \mathord{\left/ {\vphantom {{{\text{rad}}} {\text{s}}}} \right. \kern-0pt} {\text{s}}}$. The time step in simulations is 0.001 s, the assembly duration is $t_{{{\text{end}}}} = 300{\text{ s}}$, and the simulation time is 500 s. The space robot implements the assembly task in the first 300 s, and remains stationary in the following 200 s. As a simple comparison, the CPU time of the simulation model is about 13,327 s, while it takes less than 0.01 s to obtain the theoretical results. The simulation results are shown in Figs. 8, 9, 10, 11, 12, 13, 14, 15, and 16.

Table 2 Nine cases in the simulations

Fig. 8

Grasping errors of displacements and rotations in Case 1

Fig. 9

Control errors in Case 1

Fig. 10

Control errors in Case 2

Fig. 11

Control moments in Case 1

Fig. 12

Control moments in Case 2

Fig. 13

Control results in $x$ axis

Fig. 14

Control results in $y$ axis

Fig. 15

Structural vibrations of Point I

Fig. 16

Structural vibrations of Point N

The grasping errors of displacements and rotations for Case 1 are shown in Fig. 8. It can be seen that the grasping errors remain very small in the simulation. Thus, the influences of the grasping errors on the simulation results are negligible.

The control errors of the space robot in Case 1 and Case 2 are depicted in Fig. 9 and Fig. 10, respectively. It can be seen that the control errors for Case 1 are smaller than $10^{ - 4} {\text{ deg}}$, which reveals the high accuracy of the feedforward–feedback controller. The control errors for Case 2 are about 20 times larger than those of Case 1. In addition, the errors of the stationary stage (the last 200 s) in the simulation are comparatively smaller than the assembly stage (the first 300 s) for both cases. The control moments of the theoretical model and the simulation model in Case 1 and Case 2 are given in Fig. 11 and Fig. 12. The maximum control moments are a little less than 40 N·m. It is worth noting that the control moments of the stationary stage are nonzero because of the axial gravity-gradient distributed forces of the beams. The control moments of the theoretical model for Case 1 are consistent with the simulation model. This phenomenon indicates the validation of the two models. Besides, there is an obvious fluctuation in the control moments of the simulation model for Case 2. It can be concluded that the feedforward control moments improve the control accuracies greatly. Thus, the feedforward–feedback controller is adopted in the following simulations.

The control results in the ${\text{S}}xy$ coordinate system are presented in Fig. 13 and Fig. 14. It can be found that the control results in the simulations can track the planned results precisely. Particularly, the displacement in $y$ axis is very small such that the flexible beams move in the $x$ direction strictly. It means that the operation of the space robot is well planned and controlled to avoid the transverse displacements as well as structural vibrations of the flexible beams. This technique is useful for space robots assembling ultra-large space structures. Besides, the motions of flexible beams in $x$ direction satisfy the quintic polynomial to accomplish smooth assembly. The control errors in both $x$ axis and $y$ axis can also be reduced greatly by using the feedforward control moments.

The structural vibrations of Beam KI and Beam MN are illustrated in Figs. 15 and  16. The maximum deformations are less than 1 mm for the two cases. The vibrations of Beam KI are similar to Beam MN because they have the same parameters. In these two cases, the theoretical structural vibrations are induced by the Coriolis force during assembly, because the attitude angle $\alpha = 0$ and the transverse gravity-gradient forces vanish, as seen in Eqs. (26) and (27).

The structural vibrations for Case 1 match the theoretical model, while the vibrations of Case 2 are superposed by a small-amplitude vibration. The difference is due to the controller of the space robot. As can be seen in Figs. 11 and  12, the theoretical control moments at $t = 0$ are nonzero due to the axial distributed gravity-gradient force, as shown in Eqs. (29), (32), and (34)–(39). The nonzero control moments at the beginning can be provided by the feedforward control moments for Case 1, which leads to the high control accuracies. On the contrary, these control moments need to be provided by the control errors for the feedback controller in Case 2.

It should be mentioned that the period of the additional vibrations for Case 2 (about 22 s) is larger than the free vibration period of the flexible beams with cantilever boundary (about 10 s), because the vibrations of the beams are coupled with the control of the space robot. However, the assembly duration is much larger than the vibration period in simulation, and Assumption (3) is satisfied.

The above simulation results show the validity of the proposed theoretical modelling method because the results of the two models are consistent with each other. By using the control moments of the theoretical model as feedforward control moments, the control accuracies are improved by 20 times, the structural vibration amplitudes are reduced, while the control moments become smoother.

6 Dynamic characteristics for different parameters

The dynamic characteristics of the system during assembly process are analysed for different parameters in this section, including the effects of the attitude angle, orbital radius, and lengths of the flexible beams.

6.1 Effects of the attitude angle

In order to study the effects of the attitude angle, the assembly process is performed with an attitude angle of $\alpha = {\text{80 deg}}$ (Case 3 of Table 2). The simulation results are depicted in Figs. 17, 18, and 19. It can be seen that the control of the space robot is very accurate in Case 3 although the control errors are slightly larger than Case 1. In terms of control moments, it is interesting that the trends and the variation amplitudes of the control moments in Case 3 are similar to those in Case 1, except that the maximum absolute value of the control moments in Case 3 is considerably smaller than Case 1. The same phenomenon can also be clearly seen in the structural vibrations in Case 3 in Fig. 19. By using the attitude angle $\alpha = {\text{80 deg}}$, the vibration curve of Case 1 in Fig. 15 is reduced as a whole.

Fig. 17

Control errors in Case 3

Fig. 18

Control moments in Case 3

Fig. 19

Structural vibrations of Point I in Case 3

This phenomenon can be explained by the transverse distributed force of Beam KI (Eq. (20) and Fig. 4). The structural vibrations of Case 1 are mainly induced by the distributed Coriolis force because $\alpha = 0$. In Case 3, the transverse gravity-gradient force is in the opposite direction of the Coriolis forces by using a suitable attitude angle, i.e. the external forces of the flexible beams are counteracted each other. Besides, the distributed Coriolis force depends on time, while the transverse gravity-gradient force depends on attitude angle. That is the reason for the similarities between Case 1 and Case 3 in terms of control moments and structural vibrations.

In addition, it should also be pointed out that the differences between the theoretical model and the simulation model in Case 3 are larger than Case 1. The reason is that the initial deformation of the beam in the theoretical model is nonzero due to the transverse distributed force for nonzero attitude angle. However, the beams of the simulation model are undeformed according to Sect. 2. In other words, the differences between the two models in Case 3 can be attributed to the different initial conditions of the two models. The differences would increase greatly with the lengths of the beams, as will be shown in the following simulations. This problem can be addressed by further considering the effects of the initial conditions in the theoretical model or by giving appropriate initial deformations of the beams in the simulation model.

Based on the parameters of Case 3, the dynamic characteristics during space assembly are studied by changing the attitude angle from $- 90{\text{ deg}}$ to $90{\text{ deg}}$. The theoretical and simulation results are shown in Fig. 20, 21, and 22. The vibrations of Point N coincide with Point I, which are not shown for simplicity.

Fig. 20

Maximum absolute value of control moments for different attitude angles based on Case 3

Fig. 21

Control moments at the end of the assembly for different attitude angles based on Case 3

Fig. 22

Maximum absolute value of $v_{{\text{I}}}$ for different attitude angles based on Case 3

The maximum control moments depend largely on the attitude angle because of the influences of the gravity gradient. The control moments reach the minimum values when the attitude angle is around $\alpha = 10{\text{ deg}}$ or $\alpha = 80{\text{ deg}}$, because the gravity gradient and the Coriolis force counteract each other to the maximum extent. The maximum control moments appear at $\alpha = - {\text{45 deg}}$ when the gravity gradient reaches a maximum value with the same direction of the Coriolis force.

The control moments at the end of the assembly process reflect the influence of the gravity gradient on the system, which are shown in Fig. 21 for different attitude angles. It can be seen that the control moments at the end of the assembly process become 0 when $\alpha = \pm 90{\text{ deg}}$, which is an unstable equilibrium point of the gravity gradient. For the stable equilibrium attitude angle $\alpha = 0{\text{ deg}}$, the axial distributed gravity-gradient force is nonzero and thus the control moments are also nonzero.

In terms of the maximum structural vibrations of the flexible beams, the variation trends are similar to the maximum control moments, with minimum values at $\alpha = 13{\text{ deg}}$ or $\alpha = 77{\text{ deg}}$. In addition, most of the simulation results agree well with the theoretical results in Figs. 20, 21, and 22. However, there are noticeable errors in the maximum structural vibrations from $\alpha = 20{\text{ deg}}$ to $\alpha = 80{\text{ deg}}$ in Fig. 22. Actually, the maximum absolute value of $v_{{\text{I}}}$ from $\alpha = 20{\text{ deg}}$ to $\alpha = 80{\text{ deg}}$ is the minimum value of $v_{{\text{I}}}$. Otherwise, it is the maximum value of $v_{{\text{I}}}$. The reason for the noticeable errors in Fig. 22 from $\alpha = 20{\text{ deg}}$ to $\alpha = 80{\text{ deg}}$ is the differences of initial conditions of the two models, as explained in Fig. 19.

6.2 Effects of structural parameters

In this subsection, the effects of structural parameters on the dynamic characteristics of the assembly system are analysed. Particularly, the flexibility of a beam is sensitive to its length. Besides, the lengths of the beams would change when the beams are composed of different numbers of structural modules. Thus, the dynamic responses are studied for different numbers of structural modules $n_{{{\text{KI}}}}$ and $n_{{{\text{MN}}}}$.

The dynamic responses of Case 4 when $n_{{{\text{MN}}}} { = }1$ and $n_{{{\text{KI}}}} { = }5$ are shown in Figs. 23, 24, and 25. It can be seen that the maximum values of $M_{4}$–$M_{7}$ are increased to about five times of the maximum control moments in Fig. 11, while the growths of $M_{1}$–$M_{3}$ are unobvious. Besides, in the last 200 s of the simulation, the control moments $M_{4}$–$M_{7}$ are not settled under the influence of structural vibrations of Point I, as seen in Fig. 24. The structural vibration amplitude of Beam KI is much larger than that of Beam MN.

Fig. 23

Control moments in Case 4

Fig. 24

Structural vibrations of Point I in Case 4

Fig. 25

Structural vibrations of Point N in Case 4

The results of the two models are coincident in terms of the control moments $M_{1}$–$M_{3}$ and the structural vibrations of Point N, while the errors between the two models are obvious for $M_{4}$–$M_{7}$ and $v_{{\text{I}}}$, especially for the last 200 s.

The dynamic response of Case 5 when $n_{{{\text{MN}}}} { = }n_{{{\text{KI}}}} { = }5$ is illustrated in Fig. 26 and Fig. 27. In this case, the errors of all control moments between the two models are apparent. All control moments are increased greatly compared to Fig. 11. The control moments $M_{4}$–$M_{7}$ are much larger than those of Case 4, although they have the same lengths of Beam KI. The structural vibrations of Point I are also increased to about three times of Case 4. The reason is that the centre of mass of the system $x_{{{\text{SP}}}}$ and the assembly distance of Beam KI $x_{{{\text{PK}}}}$ are altered greatly when $n_{{{\text{MN}}}}$ increases from 1 to 5, according to Eq. (3) and Eq. (5). The vibrations of Point N are consistent with Point I.

Fig. 26

Control moments in Case 5

Fig. 27

Structural vibrations of Point I in Case 5

Based on Case 4 and Case 5, the dynamic behaviours during assembly are studied for different value of $n_{{{\text{KI}}}}$, which are depicted in Figs. 28, 29, 30, 31, and 32. It can be seen from Figs. 28, 29, and 30 that the maximum control moments increase linearly with $n_{{{\text{KI}}}}$. The maximum absolute value of $v_{{\text{I}}}$ increases rapidly with $n_{{{\text{KI}}}}$, and the increasing rate becomes larger for large $n_{{{\text{KI}}}}$. On the other hand, the growth of the maximum absolute value of $v_{{\text{N}}}$ is much slower, and it tends to converge to a small value.

Fig. 28

Maximum absolute value of control moments for different $n_{{{\text{KI}}}}$ when $n_{{{\text{MN}}}} { = }1$

Fig. 29

Maximum absolute value of $v_{{\text{I}}}$ for different $n_{{{\text{KI}}}}$ when $n_{{{\text{MN}}}} { = }1$

Fig. 30

Maximum absolute value of $v_{{\text{N}}}$ for different $n_{{{\text{KI}}}}$ when $n_{{{\text{MN}}}} { = }1$

Fig. 31

Maximum absolute value of control moments for different $n_{{{\text{KI}}}}$ when $n_{{{\text{MN}}}} { = }n_{{{\text{KI}}}}$

Fig. 32

Maximum absolute value of $v_{{\text{I}}}$ for different $n_{{{\text{KI}}}}$ when $n_{{{\text{MN}}}} { = }n_{{{\text{KI}}}}$

The dynamic characteristics are also studied when both $n_{{{\text{KI}}}}$ and $n_{{{\text{MN}}}}$ increase, as shown in Figs. 31 and 32. The growths of the control moments and the structural vibrations are much more severe than Figs. 28 and 29. The control moments in Fig. 31 are approximately eight times of the moments in Fig. 28. And the vibrations in Fig. 32 are about four times larger than Fig. 29. The results indicate that the control of the space robot would become more and more difficult during the whole assembly process of an ultra-large beam, because the control moments and structural vibrations increase rapidly. However, the problems of large control moments and structural vibrations can be released considerably if the structural modules are assembled one by one. The simulation results are meaningful to the assembly strategy design as well as modular component design of ultra-large space structures.

It can also be seen in Figs. 28, 29, 30, 31, and 32 that the errors between the theoretical model and the simulation model increase remarkably when $n_{{{\text{KI}}}} > 5$. The reason is that the flexibilities of the flexible beams increase with the length. When $n_{{{\text{KI}}}} { = }5$, the vibration period of Beam KI (assumed cantilever boundary conditions) becomes 250 s, which approaches the assembly duration (300 s) in the simulation. Thus, Assumption (3) in Sect. 3.1 is no longer satisfied. The distributed forces of the beams cannot be considered as quasi-static. Thus, a more complicated dynamic model should be constructed for the fast assembly operations. Increasing the assembly duration can reduce the control moments, structural vibrations, as well as the errors between the two models.

6.3 Effects of the Coriolis force

This subsection aims to compare the maximum control moments between the assembly considering space perturbations and the assembly without space perturbations, because space perturbations were not considered in many previous studies of the assembly dynamics and control [13, 48]. The assembly without space perturbation can be obtained by setting $r_{0} = \infty$ and $\omega_{0} = 0$. Theoretical and simulation results of the control moments in Case 6 and Case 7 are shown in Fig. 33 and Fig. 34. Structural vibrations are not induced ideally in Case 6 and Case 7, and the structural vibration amplitudes of the simulation model are less than 3 mm.

Fig. 33

Maximum absolute value of control moments in Case 6 ($n_{{{\text{MN}}}} { = }1$)

Fig. 34

Maximum absolute value of control moments in Case 7 ($n_{{{\text{MN}}}} { = }n_{{{\text{KI}}}}$)

It is seen that the maximum control moments of Case 6 increase very slowly compared to those in Fig. 28. The control moments of Fig. 28 are about six times larger than Fig. 33. The results in Fig. 28 are mainly influenced by the Coriolis force, because the attitude angle $\alpha = 0{\text{ deg}}$. However, the effects of Coriolis force or gravity gradient are not considered in Fig. 33. Similarly, the maximum control moments of Case 7 increase linearly with $n_{{{\text{KI}}}}$, which are much lower than those in Fig. 31. Thus, it can be concluded that the control moments of the space robot would be underestimated greatly if the Coriolis force is not considered during the assembly process, which would lead to failures of the assembly mission.

6.4 Effects of the orbital radius

Finally, the effects of orbital radius are studied by comparing the results of Case 8 and Case 9. The orbital conditions of GEO are $r_{0} = 42164142{\text{ m}}$ and $\omega_{0} = 7.292124 \times 10^{ - 5}$. The theoretical and simulation results are presented in Figs. 35, 36, 37, and  38. It can be seen that the maximum control moments are about 1200 Nm in LEO, while they become less than 50 Nm in GEO, i.e. the maximum value is reduced by more than 24 times. Moreover, the control moments in GEO are less influenced by the attitude angle (and the gravity gradient). In high-Earth orbit, the effects of Coriolis force should also be considered because the effects of the Coriolis force are only decreased with $\omega_{0}$, while the effects of the gravity gradient decrease with $\omega_{0}^{2}$. Similarly, the structural vibration amplitudes of Point I in GEO are reduced by about 100 times, and are less influenced by the attitude angle. The errors of the control moments and structural vibrations between the two models are mainly due to the difference of initial structural deformations as discussed in Sect. 5. It can be concluded that the assembly of ultra-large beams in high orbits is more desirable because of low gravity gradient and Coriolis force.

Fig. 35

Control moments of Case 8

Fig. 36

Structural vibrations of Point I of Case 8

Fig. 37

Control moments of Case 9

Fig. 38

Structural vibrations of Point I of Case 9

7 Discussion on the applicability of the theoretical model

It can be seen in the above analyses that the theoretical model is accurate and high efficient in many cases. It is essential to further study the applicability of the theoretical model for engineering applications. Nevertheless, the applicability is affected by numerous factors, such as the mass and size of the space robot, assembly time, control gains of the joints, number of modules, orbital radius, and attitude angle. It is not realistic to compare the theoretical model and simulation model for all factors. Thus, the influences of the robot’s density and assembly time on the errors between the two models are briefly studied based on the parameters of Case 1.

The root mean square (RMS) error of $v_{{\text{I}}}$ is studied for different robot’s density and assembly time, which are defined as

$$ \Delta_{{{\text{RMS}}}} { = }\frac{1}{{v_{{\text{I,theory,max}}} - v_{{\text{I,theory,min}}} }}\sqrt {\frac{{\sum {\left( {v_{{\text{I,theory}}} - v_{{\text{I,simulation}}} } \right)^{2} } }}{n}} $$

(83)

where $n$ is the number of $v_{{\text{I,theory}}}$. The RMS errors of the control moments are defined in the same way. The results are shown in Figs. 39, 40, 41, and 42.

Fig. 39

RMS error of structural vibrations for different robot’s density based on Case 1

Fig. 40

RMS error of control moments for different robot’s density based on Case 1

Fig. 41

RMS error of structural vibrations for different assembly time based on Case 1

Fig. 42

RMS error of control moments for different assembly time based on Case 1

It can be seen that the RMS errors of the structural vibrations and control moments are increased with the robot’s density. However, the RMS error of $v_{{\text{I}}}$ is less than 2% even if the robot’s density is ${\text{5000 kg/m}}^{{3}}$. The RMS errors of control moments are more sensitive to the robot’s density than the structural vibrations, because the inertial forces of the links are not considered in the theoretical control moments of the joints. When the assembly time varies from 100 to 1000 s, the RMS errors of structural vibrations and control moments remain very small. In general, the RMS errors decrease as the assembly time increases. When the assembly time is larger than 400 s, the RMS errors of $v_{{\text{I}}}$ and $M_{1}$ increase slightly because of the decreases of $\left( {v_{{\text{I,theory,max}}} - v_{{\text{I,theory,min}}} } \right)$ and $\left( {M_{{\text{1,theory,max}}} - M_{{\text{1,theory,min}}} } \right)$. The accuracy of the theoretical model in Figs. 39, 40, 41, and 42 reveals the reasonability of Assumptions (2) and (3).

8 Conclusions

This paper studies the dynamics and control of the assembly process of two large flexible beams by a space robot considering the gravity gradient and Coriolis force. A theoretical modelling method is proposed to estimate the dynamic characteristics of the assembly process quickly. A theoretical model and a simulation model are built. The effects of space perturbations and system parameters on the control moments of the space robot and the structural vibrations of the beams are studied. The following conclusions can be drawn according to theoretical and simulation results.

• (1) The dynamic responses of the theoretical model and simulation model agree well with each other under the premise of ideal control, small robot, slow assembly, and small deformation. The theoretical control moments can be used as feedforward control moments for the space robot to greatly improve control accuracy.

• (2) When the numbers of structural modules of both flexible beams increase synchronously, the control moments and structural vibrations increase dramatically. And the increasing rate becomes faster and faster as the numbers rise. When the number of structural modules of one beam increases while the other beam contains only one structural module, the above problem can be relieved significantly. Thus, the structural modules should be assembled one by one to reduce control moments and structural vibrations.

• (3) If the effects of Coriolis force and gravity gradient were not considered, the control moments and structural vibrations during space assembly would be underestimated substantially.

• (4) By adjusting the attitude angle in the assembly process, the effects of the Coriolis force and gravity gradient can be countered each other to some extent. A positive pitch attitude angle is more preferable than a negative value, because the effects of the Coriolis force and the gravity gradient would be superposed for a negative value.

• (5) The gravity gradient is proportional to $\omega_{0}^{2}$ while the Coriolis force is proportional to $\omega_{0}$. Thus, both the control moments and structural vibrations can be reduced greatly in GEO compared to LEO.

Appendix

The quasi-static vibration of Beam KI $v_{{{\text{KI}}}}$ is obtained by integrating Eq. (24) with the boundary conditions in Eq. (25)

$$ \begin{gathered} v_{{{\text{KI}}}} = - \frac{3}{2}\frac{\rho A}{{EI}}\omega_{0}^{2} \left( {\frac{1}{120}x_{{{\text{KQ}}}}^{5} - \frac{{L_{{{\text{KI}}}}^{2} }}{12}x_{{{\text{KQ}}}}^{3} + \frac{{L_{{{\text{KI}}}}^{3} }}{6}x_{{{\text{KQ}}}}^{2} } \right)\sin \left( {2\alpha } \right) \\ - \frac{3}{2}\frac{\rho A}{{EI}}\omega_{0}^{2} \left( {\frac{1}{24}x_{{{\text{KQ}}}}^{4} - \frac{{L_{{{\text{KI}}}} }}{6}x_{{{\text{KQ}}}}^{3} + \frac{{L_{{{\text{KI}}}}^{2} }}{4}x_{{{\text{KQ}}}}^{2} } \right)\left( {x_{{{\text{SP}}}} + x_{{{\text{PK}}}} } \right)\sin \left( {2\alpha } \right) \\ - 2\frac{\rho A}{{EI}}\omega_{0} \dot{x}_{{{\text{PK}}}} \left( {\frac{1}{24}x_{{{\text{KQ}}}}^{4} - \frac{{L_{{{\text{KI}}}} }}{6}x_{{{\text{KQ}}}}^{3} + \frac{{L_{{{\text{KI}}}}^{2} }}{4}x_{{{\text{KQ}}}}^{2} } \right) \\ \end{gathered} $$

(A1)

Similarly, the quasi-static vibration of Beam MN $v_{{{\text{MN}}}}$ is

$$ \begin{gathered} v_{{{\text{MN}}}} = - \frac{3}{2}\frac{\rho A}{{EI}}\omega_{0}^{2} \left( {\frac{1}{120}x_{{{\text{QM}}}}^{5} - \frac{{L_{{{\text{MN}}}}^{2} }}{12}x_{{{\text{QM}}}}^{3} + \frac{{L_{{{\text{MN}}}}^{3} }}{6}x_{{{\text{QM}}}}^{2} } \right)\sin \left( {2\alpha } \right) \\ - \frac{3}{2}\frac{\rho A}{{EI}}\omega_{0}^{2} \left( {\frac{1}{24}x_{{{\text{QM}}}}^{4} - \frac{{L_{{{\text{MN}}}} }}{6}x_{{{\text{QM}}}}^{3} + \frac{{L_{{{\text{MN}}}}^{2} }}{4}x_{{{\text{QM}}}}^{2} } \right)\left( {x_{{{\text{PS}}}} + x_{{{\text{MP}}}} } \right)\sin \left( {2\alpha } \right) \\ - 2\frac{\rho A}{{EI}}\omega_{0} \dot{x}_{{{\text{MP}}}} \left( {\frac{1}{24}x_{{{\text{QM}}}}^{4} - \frac{{L_{{{\text{MN}}}} }}{6}x_{{{\text{QM}}}}^{3} + \frac{{L_{{{\text{MN}}}}^{2} }}{4}x_{{{\text{QM}}}}^{2} } \right) \\ \end{gathered} $$

(A2)

The results of Eqs. (28)–(33) are

$$ M_{{{\text{KI}}}} = - L_{{{\text{KI}}}}^{2} \rho A\omega_{0} {\kern 1pt} \left[ {\dot{x}_{{{\text{PK}}}} + \frac{1}{2}L_{{{\text{KI}}}} \omega_{0} \sin \left( {2{\kern 1pt} \alpha } \right) + \frac{{3{\kern 1pt} }}{4}\omega_{0} \left( {x_{{{\text{SP}}}} + x_{{{\text{PK}}}} } \right)\sin \left( {2{\kern 1pt} \alpha } \right)} \right] $$

(A3)

$$ F_{{x,{\text{KI}}}} = \frac{{\rho AL_{{{\text{KI}}}} }}{2}\left[ {3{\kern 1pt} L_{{{\text{KI}}}} \omega_{0}^{2} \cos^{2} \left( \alpha \right) + 6{\kern 1pt} \omega_{0}^{2} \left( {x_{{{\text{SP}}}} + x_{{{\text{PK}}}} } \right)\cos^{2} \left( \alpha \right) - 2{\kern 1pt} \ddot{x}_{{{\text{PK}}}} } \right] $$

(A4)

$$ F_{{y,{\text{KI}}}} = - \frac{{\rho AL_{{{\text{KI}}}} \omega_{0} }}{4}\left[ {8\dot{x}_{{{\text{PK}}}} + 3{\kern 1pt} L_{{{\text{KI}}}} \omega_{0} \sin \left( {2{\kern 1pt} \alpha } \right) + 6\omega_{0} \left( {x_{{{\text{SP}}}} + x_{{{\text{PK}}}} } \right)\sin \left( {2{\kern 1pt} \alpha } \right)} \right] $$

(A5)

$$ M_{{{\text{MN}}}} = - L_{{{\text{MN}}}}^{2} \rho A\omega_{0} {\kern 1pt} \left[ {\dot{x}_{{{\text{MP}}}} + \frac{1}{2}L_{{{\text{MN}}}} \omega_{0} \sin \left( {2{\kern 1pt} \alpha } \right) + \frac{{3{\kern 1pt} }}{4}\omega_{0} \left( {x_{{{\text{MP}}}} + x_{{{\text{PS}}}} } \right)\sin \left( {2{\kern 1pt} \alpha } \right)} \right] $$

(A6)

$$ F_{{x{\text{,MN}}}} = \frac{{\rho AL_{{{\text{MN}}}} }}{2}\left[ {3{\kern 1pt} L_{{{\text{MN}}}} \omega_{0}^{2} \cos^{2} \left( \alpha \right) + 6{\kern 1pt} \omega_{0}^{2} \left( {x_{{{\text{MP}}}} + x_{{{\text{PS}}}} } \right)\cos^{2} \left( \alpha \right) - 2{\kern 1pt} \ddot{x}_{{{\text{MP}}}} } \right] $$

(A7)

$$ F_{{y{\text{,MN}}}} = - \frac{{\rho AL_{{{\text{MN}}}} \omega_{0} }}{4}\left[ {8\dot{x}_{{{\text{MP}}}} + 3{\kern 1pt} L_{{{\text{MN}}}} \omega_{0} \sin \left( {2{\kern 1pt} \alpha } \right) + 6\omega_{0} \left( {x_{{{\text{MP}}}} + x_{{{\text{PS}}}} } \right)\sin \left( {2{\kern 1pt} \alpha } \right)} \right] $$

(A8)