Two-dimensional composite multi-scale time–frequency reverse dispersion entropy-based fault diagnosis for rolling bearing

Abstract

Multi-scale dispersion entropy (MDE_1D) is an effective nonlinear dynamic tool to characterize the complexity of time series and has been extensively applied to mechanical fault diagnosis. However, with the increase of scale factor, the values of MDE_1D often fluctuate largely, resulting in poor stability. Besides, it only extracts the complexity information from the time domain of vibration signal, while the complexity information in the frequency domain is ignored. To enhance the stability of MDE_1D and extract the complexity characteristics from the time–frequency domain of vibration signal, this paper first develops a two-dimensional multi-scale reverse dispersion entropy (MRDE_2D), inspired by the MDE_1D and two-dimensional multi-scale dispersion entropy (MDE_2D) through introducing the “distance information from white noise”. Then a two-dimensional multi-scale time–frequency reverse dispersion entropy (MTFRDE_2D) combined with time–frequency analysis is proposed. After that, considering that the length of the coarse-grained sequence used in the multi-scale coarse-grained process of MTFRDE_2D will become shorter and shorter with the increase of scale factor, resulting in a loss of potentially useful information, the two-dimensional composite multi-scale time–frequency reverse dispersion entropy (CMTFRDE_2D) is proposed through using the composite coarse-grained process. The effectiveness and advantages of CMTFRDE_2D algorithm are demonstrated by analyzing different kinds of noise signals. Following that, a new rolling bearing fault diagnosis method is proposed based on the CMTFRDE_2D for feature extraction and gravitational search algorithm optimized support vector machine for mode identification. The proposed fault diagnosis method is employed on two rolling bearing test data sets and also compared with the existing MTFRDE_2D,- MRDE_2D,- MDE_2D,- and MDE_1D-based fault diagnosis methods. The analysis results reveal that the proposed fault diagnosis method can successfully extract the fault information from rolling bearing vibration signals in time–frequency domain and can accurately identify different fault locations and severities of rolling bearings with certain advantages.

1 Introduction

Thanks to the advantages of low friction resistance and high mechanical efficiency, rolling bearing performs an essential role in a range of industry applications. However, rolling bearing usually operates under harsh working environment, which makes it prone to failure. Hence, it is important significance to study the condition monitoring and early fault diagnosis approaches of rolling bearing [1].

As rolling bearing often presents non-stationary and nonlinear characteristics of vibration signal when local failure occurs in operation [2, 3], the traditional linear analysis methods inevitably have certain limitations. Therefore, the effective extraction of fault feature information hidden in the non-stationary and nonlinear signals becomes critical to rolling bearing fault diagnosis and prognosis.

Entropy index, including approximate entropy (ApEn_1D) [4], sample entropy (SampEn_1D) [5, 6], fuzzy entropy (FE_1D) [7], and permutation entropy (PE_1D) [8,9,10], has been recognized as a commonly-used nonlinear analysis tool which is widely used in feature extraction for rolling bearing, because of their stable and robust merits for relatively short data. PE_1D is a nonlinear dynamic analysis to detect random changes in time series, which has the advantages of fast calculation speed and strong anti-noise ability. But the PE_1D does not consider the relationship between the amplitudes of the original signal in the calculation process. Dispersion Entropy (DE_1D) has recently been proposed by Azami et al. [11, 12] for the measurement of complexity in time series to address the shortcomings of PE_1D. However, the stability of DE_1D is poor and is easily affected by relevant parameters. Subsequently, the reverse dispersion entropy (RDE_1D) was proposed to improve the stability of DE_1D by Li et al. [13], which is defined as “distance to white noise” and its better stability relative to DE_1D was verified by the simulation tests and ship signals.

The above methods are all single-scale analysis tools based on entropy index, while the vibration signals usually contain different fault information in different scale ranges, thus the single-scale analysis tool still has some constraints to deal with these kinds of signals. The multi-scale dispersion entropy (MDE_1D) was proposed [14] to characterize the time series complexity on multiple time scales and applied to the field of biomedical signal analysis. However, MDE_1D is defined on the one-dimensional time series and cannot be used to characterize the complexity characteristics of two-dimensional images. Recently, two-dimensional multi-scale dispersion entropy (MDE_2D) was proposed by Furlong et al. [15, 16] to characterize the complex characteristics of images in different scales.

MDE_1D can only extract the time-domain characteristics of vibration signal, resulting in a loss and waste of the frequency domain information. MDE_2D can effectively represent the complex characteristics of image, but the entropy value of MDE_2D has poor stability and cannot provide stable and reliable analysis results. In this paper, first, the two-dimensional multi-scale reverse dispersion entropy (MRDE_2D) is proposed for solving the problem of MDE_2D entropy values with poor stability. After that, the two-dimensional multi-scale time–frequency reverse dispersion entropy (MTFRDE_2D) is proposed by introducing time–frequency analysis [17, 18] for measuring the complexity of the time–frequency distribution of vibration signals. However, as the coarse-grained sequence used in the multi-scale coarse-grained process of MTFRDE_2D will become shorter in length with increasing scale factor, it will lose much potentially useful information. Then the two-dimensional composite multi-scale time–frequency reverse dispersion entropy (CMTFRDE_2D) is proposed to fully use the time–frequency distribution information of vibration signals on different scales. Finally, the effectiveness and superiority of CMTFRDE_2D are verified by simulation signal analysis.

In general, the vibration signal of normal bearing, similar to white noise, is random with a high degree of irregularity. The vibration signal will become regular and periodic, impacted by the complexity change when the rolling bearing works with partial failures. In addition, the information of time–frequency distribution will also change with the increasing failure severity for the vibration signals usually contain different fault information in different scale ranges. Therefore, the proposed CMTFRDE_2D method can be utilized to extract the time–frequency distribution information in different scales from the vibration signal of rolling bearings. After that, the gravitational search algorithm optimized support vector machine (GSA-SVM) is used for pattern recognition of fault features to achieve intelligent diagnosis of rolling bearing. According to the above analysis, a rolling bearing fault diagnosis method is proposed based on the CMTFRDE_2D and GSA-SVM. The validity and advantages of the proposed fault diagnosis method are illustrated through two groups of rolling bearing test data under different operating conditions.

The major contributions of this paper are as follows:

• (1) CMTFRDE_2D is proposed to extract the fault features of the time–frequency distribution of vibration signals, which overcomes the defect that traditional entropy only extracts the time-domain features.

• (2) In CMTFRDE_2D, the information utilization of the original signal is effectively improved by using the coarse-grained process of the moving average of adjacent elements.

• (3) A rolling bearing fault diagnosis method is proposed based on the CMTFRDE_2D and GSA-SVM, and the validity and superiority of the proposed method are verified by two sets of measured data.

This paper is structured as follows. In Sect. 2, the algorithms of RDE_2D and MRDE_2D are reviewed firstly and then the CMTFRDE_2D algorithm is introduced, as well as the parameters selection of RDE_2D and the performance of CMTFRDE_2D are investigated. In Sect. 3, a new rolling bearing fault diagnosis method is proposed based on CMTFRDE_2D and GSA-SVM. In Sect. 4, the effectiveness of the proposed fault diagnosis methods is verified by two sets of rolling bearing test data with different operating conditions. Finally, the discussion of conclusions is presented in Sect. 5.

2 CMTFRDE_2D and its related algorithms

2.1 RDE_2D algorithm

DE_2D is a nonlinear analysis tool that can effectively characterize the complexity of images, but it has poor stability. In this paper, RDE_2D is proposed by introducing “distance information from white noise” to improve the stability of DE_2D, and its steps can be described as follows:

• (1) For a given image signal U with pixel size $h \times w$, its discrete form is denoted as the matrix $U = \{ u_{i,j} \}_{i = 1,2, \cdots ,h}^{j = 1,2, \cdots ,w}$. First, U is mapped to $Y = \{ y_{i,j} \}_{i = 1,2, \cdots ,h}^{j = 1,2, \cdots ,w}$ by utilizing the normal cumulative distribution function, namely

  $$ y_{i,j} = \frac{1}{{\sigma \sqrt {2\pi } }}\int_{ - \infty }^{{u_{i,j} }} {\frac{e^{ - (t - \mu )^{2} }}{{2\sigma^{2} }}\;} dt $$

  (1)

  where $\sigma$ and $\mu$ are the standard deviation and mean value of U, respectively. The range of $y_{i,j}$ is [0,1].

• (2) A linear operation is used to map $y_{i,j}$ to the symbol sequence $z_{i,j}^{c}$, that is

  $$ z_{i,j}^{c} = {\text{int}} (c \times y_{i,j} + \, 0.5) $$

  (2)

  where int(·) indicates the rounding process, and c is a positive integer, indicating the number of classes. $z_{i,j}^{c}$ stands for the class sequence of i-th row and j-th column elements mapped from the element $u_{i,j}^{{}}$ of image U.

• (3) Based on the embedding theory, the embedding matrix is reconstructed as:

  $$ z^{m} = \left\{ {z_{d,r}^{m,c} } \right\} = \left[ {\begin{array}{*{20}c} {z_{d,r}^{c} } & {z_{d,r + 1}^{c} } & \cdots & {z_{{d,r + (m_{w} - 1)}}^{c} } \\ {z_{d + 1,r}^{c} } & {z_{d + 1,r + 1}^{c} } & \cdots & {z_{{d + 1,r + (m_{w} - 1)}}^{c} } \\ \vdots & \vdots & \vdots & \vdots \\ {z_{{d + (m_{h} - 1),r}}^{c} } & {z_{{d + (m_{h} - 1),r + 1}}^{c} } & \cdots & {z_{{d + (m_{h} - 1),r + (m_{w - 1} )}}^{c} } \\ \end{array} } \right] $$

  (3)

  where m is embedding dimension, $1 \le d \le h - (m_{h} - 1)$ and $1 \le r \le w - (m_{w} - 1)$. For each element in $z^{m}$ is mapped to a dispersion pattern ${\varvec{\pi}} = \pi_{{x_{0} x_{1} \cdots x_{{m_{h} \times m_{w - 1} }} }}$, where $z_{d,r}^{c} = x_{0}$, $z_{d,r + 1}^{c} = x_{1}$,$...$, $z_{{d + (m_{h} - 1),r + (m_{w} - 1)}}^{c} = x_{{m_{h} \times m_{w} - 1}}$. Since there are $m_{h} \times m_{w}$ elements in the matrix, and each element is mapped between 1 and c, there are total ${\varvec{q}} = c^{{m_{h} \times m_{w} }}$ possible dispersion patterns corresponding to $z^{m}$.

• (4) The probability $p({\varvec{\pi}})$ of each potential dispersion pattern in all possible dispersion patterns q can be computed by:

  $$ p({\varvec{\pi}}) = \frac{{{\text{number}}\left\{ {z_{d,r}^{m,c} {\text{ has type }}{\varvec{\pi}}} \right\}}}{{\left( {h - \left( {m_{h} - 1} \right)} \right)\left( {w - \left( {m_{w} - 1} \right)} \right)}} $$

  (4)

  where number{·} indicates the number of $z_{d,r}^{m,c}$ mapped to dispersion pattern $\pi$. In fact, $p({\varvec{\pi}})$ is equal to the ratio of the number of $z_{d,r}^{m,c}$ mapped to the dispersion pattern ${\varvec{\pi}}$ to the total number $(h - (m_{h} - 1))(w - (m_{w} - 1))$ of all embedded vectors in $z^{m}$.

• (5) RDE_2D is defined as the distance to white noise by combining distance information as:

  $$ {\text{RDE}}_{{{\text{2D}}}} {(}U,m,c) = \sum\limits_{\pi = 1}^{{\varvec{q}}} {\left( {p{{(\varvec{\pi}}) - \frac{1}{{\varvec{q}}}} } \right)^{2} } = \sum\limits_{\pi = 1}^{{\varvec{q}}} {p \, ({\varvec{\pi}})^{2} } - \frac{1}{{\varvec{q}}} $$

  (5)

There are two key parameters in RDE_2D that are required to be set in advance, i.e., embedding dimension m and class c. In the literature [15], it is suggested that m is set from 1 to 5, and c is set from 3 to 8. Generally, the larger m is, the subtle changes cannot be accurately reflected in the joint probability dynamic reconstruction of the sequence, and the computation time is longer. To balance the accuracy and computation efficiency, m = 2 is chosen in this paper.

In the following, a MIX_2D(n) function composed of periodic signals and random signals regulated by different probabilities n ($0 \le n \le 1$) was defined to verify the performance of RDE_2D in detecting the degree of image irregularity and investigate the effect of c on RDE_2D, where the MIX_2D(n) is defined as below [19]

$$ {\text{MIX}}_{{{\text{2D}}}} (n)_{i,j} = (1 - N_{i,j} )X_{i,j} + N_{i,j} Y_{i,j} $$

(6)

where the sinusoidal image $X_{i,j} = \sin (\frac{2\pi i}{{12}}) + \sin (\frac{2\pi j}{{12}})$, random image $Y_{i,j}$ consists of uniform white noise in the range $[ - \sqrt 3 ,\sqrt 3 ]$. When the random variable $N_{i,j} = 1$, the probability is n, while when $N_{i,j} = 0$ the probability is $1 - n$. In fact, when the probability n takes any value in the range, the MIX_2D(n) generates an image that presents a specific spatial regularity. For example, when n = 0, MIX_2D(n) generates regular periodic images. With the increase of probability n ($0 \le n \le 1$), the irregularity of the image generated by MIX_2D(n) gradually increases, and a completely random and highly irregular image is generated when n = 1.

For different probability n, the MIX_2D(n) randomly generates synthetic images with different regularity (as shown in Fig. 1), and its RDE_2D value is computed and the entropy value curve is displayed in Fig. 2. As seen in Fig. 2, with the increasing of n value, the irregularity of the image generated by MIX_2D(n) will become higher and higher. Since the reverse dispersion entropy (or RDE_2D) is defined as the distance to white noise (or random image), the RDE_2D values will become smaller with the increase of the image irregularity. Therefore, the trend of RDE_2D is in line with the expected effect and corresponds to the image shown in Fig. 1, which further verifies the effectiveness of RDE_2D in measuring the degree of image irregularity. In addition, Fig. 2 indicates that the value of entropy tends to decrease with the increase of c, and the entropy difference between different n becomes smaller and smaller, which is not conducive to classification. It also can be observed from Fig. 2 that when c = 3, the difference of RDE_2D value for different noises is the largest, and thus we set c = 3.

Fig. 1

Composite image generated by MIX_2D(n) for different n values

Fig. 2

RDE_2D for different n values

2.2 MRDE _2D algorithm

Since the fault information is usually distributed on different time scales, accordingly, the complexity of image will change on different scales. In this part, MRDE_2D is proposed to reflect the complexity information of image on different scales, with its steps being described as follows.

• (1) For image U with size $h \times w$ and given scale factor of $\tau$, the size of the resulting coarse-grained image is $\left\lfloor {h/\tau } \right\rfloor \times \left\lfloor {w/\tau } \right\rfloor$, where $\left\lfloor \cdot \right\rfloor$ denotes rounding. The two-dimensional coarse-grained process of image is described by:

  $$ y_{i,j}^{(\tau )} = \frac{1}{{\tau^{2} }}\sum\limits_{\begin{subarray}{l} e = (i - 1)\tau + 1 \\ f = (j - 1)\tau + 1 \end{subarray} }^{\begin{subarray}{l} e = i\tau \\ f = j\tau \end{subarray} } {x_{e,f} } ,\;1 \le i \le \left\lfloor {h/\tau } \right\rfloor ,\;1 \le j \le \left\lfloor {w/\tau } \right\rfloor $$

  (7)

• (2) For the coarse-grained image $y^{(\tau )} = \left\{ {y_{i,j}^{(\tau )} } \right\}$ with different scale factors $\tau$, MRDE_2D is defined by:

  $$ {\text{MRDE}}_{{{\text{2D}}}} \left( {U,\tau ,m,c} \right)={\text{RDE}}_{{{\text{2D}}}} \left( {y^{(\tau )} ,m,c} \right) $$

  (8)

MRDE_2D overcomes the problem that RDE_2D can only extract the complexity of single scale time series. It extends the traditional coarse-grained method to a two-dimensional coarse-grained way which is applicable to image processing, and multi-scale image analysis has been developed to characterize the degree of irregularity of images for different scales. The schematic diagram of the two-dimensional coarse-grained for scale factor $\tau = 2$ is displayed in Fig. 3.

Fig. 3

Schematic diagram of two-dimensional coarse-grained for $\tau = 2$

Although MRDE_2D overcomes the shortcomings of RDE_2D cannot perform multi-scale analysis of images, the coarse-grained process of MRDE_2D for images is relatively complex and computationally expensive. In addition, MDE_1D cannot comprehensively utilize the information in the time–frequency domain of vibration signals. Therefore, the MTFRDE_2D method is proposed, which combines the advantages of MRDE_2D and MDE_1D to extract the time–frequency distribution information of vibration signals. However, as the length of the coarse-grained sequence utilized in the multi-scale coarse-grained process of MTFRDE_2D will become shorter with the increase of scale factor, which inevitably leads to the loss of much potentially useful information. To address this issue, the CMTFRDE_2D method is proposed for solving the problem of information loss caused by MTFRDE_2D.

2.3 Introduction of CMTFRDE_2D algorithm

The steps of the CMTFRDE_2D algorithm are given as follows.

• (1) For a given scale factor $\tau$, the n-th ($1 \le n \le \tau$) coarse-grained sequence $y_{n}^{(\tau )} = \{ y_{n,1}^{(\tau )} ,y_{n,2}^{(\tau )} , \cdots \}$ of the original time series $\{ x(s),s = 1,2, \cdots ,S\}$ is defined as:

  $$ y_{n,j}^{(\tau )} = \frac{1}{\tau }\sum\limits_{s = n + (j - 1)\tau }^{j\tau + n - 1} {x_{s} } ,\;1 \le j \le {S \mathord{\left/ {\vphantom {S \tau }} \right. \kern-0pt} \tau },\;1 \le n \le \tau $$

  (9)

• (2) For each coarse-grained sequence $y_{n}^{(\tau )}$ obtained when the scale factor is $\tau$, its time–frequency distribution $U_{n}^{(\tau )}$ is calculated through continuous wavelet transform, namely:

  $$ U(a,b) = \int_{ - \infty }^{ + \infty } {y_{j}^{(\tau )} \psi_{a,b}^{*} {\text{ d}}s = \frac{1}{\sqrt a }\int_{ - \infty }^{ + \infty } {y_{j}^{(\tau )} \psi^{*} \left( {\frac{s - b}{a}} \right){\text{ d}}s} } $$

  (10)

  where $a$ is the scale and $a > 0$, $b$ represents the translation factor, $\frac{1}{\sqrt a }$ is the normalization factor in ensuring that $a$ and $b$ having the same energy, and $U(a,b)$ is the continuous wavelet transform of the coarse-grained time series $y_{j}^{(\tau )}$.

• (3) For the time–frequency distribution $U_{n}^{(\tau )}$ of all coarse-grained sequences with scale factor $\tau$, its CMTFRDE_2D can be calculated by:

  $$ {\text{CMTFRDE}}_{{{\text{2D}}}} {(}U,\tau ,m,c) = \frac{1}{\tau }\sum\limits_{n = 1}^{\tau } {{\text{RDE}}_{{{\text{2D}}}} (U_{n}^{(\tau )} ,m,c)} $$

  (11)

The CMTFRDE_2D method reduces the fluctuation of entropy value with increasing scale factor by averaging RDE_2D values of $\tau$ coarse-grained sequence time–frequency images. Also, it can reduce the information loss caused by the coarse-grained process used in MTFRDE_2D. Since CMTFRDE_2D is to calculate the RDE_2D values of the time–frequency distribution of composite coarse-grained time series, and thus the parameters settings are the same as RDE_2D, i.e., m = 2 and c = 3 are set. The comparison of the computation process between MRDE_2D and CMTFRDE_2D is displayed in Fig. 4.

Fig. 4

The flowcharts of MRDE_2D and CMTFRDE_2D

In the following, four kinds of noises, including pink noise, blue noise, purple noise, and red noise with a length of 1024, are selected as the research objects [20,21,22] to verify the effectiveness of CMTFRDE_2D in the complexity measurement of image and their waveforms in time-domain are exhibited in Fig. 5. The CMTFRDE_2D, MTFRDE_2D, MRDE_2D and MDE_2D values of the above noise signals with a maximum scale of $\tau_{\max } = 20$ were calculated [23], and the mean–variance diagram is displayed in Fig. 6. As seen in Fig. 5, the waveforms of pink noise and red noise are quite different that can be distinguished obviously, while the blue noise and purple noise waveforms are very similar and difficult to distinguish. The four different colored noises in the mean–variance diagram shown in Fig. 6 can be distinguished by the CMTFRDE_2D method, where the pink and red noises are more clearly distinguished from the other two noises, corresponding to the waveforms shown in Fig. 5, and thus the validity of the proposed method for feature extraction is confirmed. The standard deviation of the CMTFRDE_2D method is the smallest among the four processing methods for different noise vibration signals, and this indicates that the CMTFRDE_2D method has better stability and robustness in nonlinear dynamic feature reflection.

Fig. 5

The colored noise waveform of (a) blue noise, (b) pink noise, (c) red noise, and (d) purple noise

Fig. 6

The mean standard deviation diagram of colored noise (a) CMTFRDE_2D, (b) MTFRDE_2D, (c) MRDE_2D and (d) MDE_2D

3 The proposed fault diagnosis method

The mentioned analysis demonstrates that CMTFRDE_2D is an efficient method for vibration signals complexity analysis, which is used for feature extraction of rolling bearing vibration signals in this paper. However, it is essential to select an appropriate classifier to realize an intelligent fault classification of rolling bearing. Support vector machine (SVM) [24, 25] is a pattern recognition tool that is suitable for small sample classification, and its performance depends significantly on the selection of kernel parameter g and penalty factor c. In general, c is used to achieve a compromise between minimizing the number of misclassified samples and maximizing the classification interval. When the value of c is small, the phenomenon of under-fitting occurs, which leads to lower training accuracy and poorer generalization performance. On the contrary, there will be an over-fitting phenomenon. And g mainly affects the distribution of sample data in high-dimensional space, which also has a significant impact on the classification performance of SVM. However, the c and g value in SVM cannot be changed once determined. Therefore, the parameters of SVM need to be optimized to improve the classification efficiency. Particle swarm optimization (PSO) [26], chicken swarm optimization (CSO) [27] and gravitational search algorithm (GSA) [28, 29] are commonly used optimization algorithms. GSA is a cluster intelligence optimization algorithm with high robustness and easy implementation. The algorithm simulates the universal gravitational in physics, and the particles scattered in space move each other according to the gravitational interaction, and finally calculates the optimal position to realize position optimization. Therefore, the gravitational search algorithm is selected to optimize the relevant parameters of SVM in this paper.

3.1 Principle of gravitational search algorithm

GSA is a heuristic algorithm based on the law of universal gravitation. It can optimize the position of objects by simulating the interaction between objects with arbitrary mass to achieve the effect of parameter optimization. GSA needs to set parameters such as allowable range for search space, the maximum number of iterations and the number of agents in advance, and randomly initialize the positions of particles. Then the velocity, acceleration and position of the particle are updated according to formulas (12)–(15), and the iteration is stopped after the termination condition is satisfied, and the optimal parameters are output. The specific steps of GSA algorithm are described in the literature [30].

$$ F_{ij}^{l} (t) = G(t)\frac{{M_{pi} (t) \times M_{dj} (t)}}{{R_{ij} (t) + \xi }}(x_{j}^{l} (t) - x_{i}^{l} (t)) $$

(12)

$$ a_{i}^{l} (t) = \frac{{\sum\limits_{j = 1,j \ne i}^{N} {rand_{j} F_{ij}^{l} (t)} }}{{M_{i} (t)}} $$

(13)

$$ v_{i}^{l} (t + 1) = rand_{i} \times v_{i}^{l} (t) + a_{i}^{l} (t) $$

(14)

$$ x_{i}^{l} (t + 1) = x_{i}^{l} (t) + v_{i}^{l} (t + 1) $$

(15)

where $G(t)$ is the gravitational constant at time t, $M_{pi} (t)$ and $M_{dj} (t)$ are the gravitational masses of particles i and j respectively, $\xi$ is a small constant, $R_{ij} (t)$ is the Euclidean distance between particles i and j, and $F_{ij}^{l} (t)$ is the resultant force of interaction between particles i and j. $a_{i}^{l} (t)$ is the acceleration of particle i in the l-th dimension, $M_{i} (t)$ is the inertial masses of particles i. $rand_{j}$ is a random variable between [0,1], $v_{i}^{l} (t)$ and $x_{i}^{l} (t)$ are the velocity and position of particle i at the t-th iterations.

3.2 GSA-SVM optimization process

The penalty factor c and the kernel parameter g in the SVM are optimized using the GSA algorithm, and the specific steps are as follows:

• (1) The parameters of GSA-SVM are initialized, i.e., the number of agents equals 20, the maximum number of iterations is 30, the allowable range for search space is from 0.01 to 100, and randomly initialize position of particle.

• (2) The minimum value of the objective function is used as the optimization target, and the fitness value of particle is calculated. It is worth noting that GSA-SVM takes the error rate between the actual output and the theoretical output of the test set as the fitness function, that is, the error rate of the classification prediction is used as the fitness value [31].

• (3) The mass of each particle and the resultant force of interaction between particles are calculated.

• (4) The velocity, acceleration and position of particle are updated, that is, the kernel parameter g and penalty factor c of SVM are updated.

• (5) Repeat steps (2) ~ (4) until the maximum number of iterations is achieved, and the iteration is terminated to output the optimal parameters.

3.3 The proposed method

Based on the advantages of CMTFRDE_2D and GSA-SVM mentioned above, a new rolling bearing fault diagnosis model is proposed, and the detailed procedures are described as below.

• (1) The vibration signals of rolling bearing are collected in M different statues and each state contains N samples with the same length. The CMTFRDE_2D values for the time–frequency distribution of each state vibration signal with the maximum scale of $\tau_{\max }$ are calculated and used being the sets of sample feature vectors.

• (2) The sample feature vectors for each state vibration signal are divided randomly for I training samples and J testing samples, where N = I + J.

• (3) The selected training samples are input to the GSA-SVM based classifier for training, in which GSA-SVM dynamically updates penalty factor c and kernel parameter g according to the different input training samples to obtain the optimal parameters.

• (4) The testing samples are input into the GSA-SVM for classification prediction, and the fault locations and severities are judged according to the output results of classifier to achieve fault diagnosis of rolling bearing.

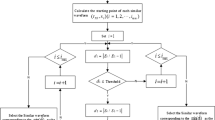
The process of the proposed fault diagnosis method is illustrated in Fig. 7.

Fig. 7

Flowchart of the proposed method

4 Experimental data analysis

4.1 Experiment 1

The rolling bearing data of Case Western Reserve University¹ are employed to verify the validity of the proposed diagnosis method. The test bearing model used in the experiment is the 6205-2RSJEM SKF with a single point of failure assigned to the rolling bearing by EDM technology [32]. The test stand is displayed in Fig. 8. The vibration acceleration signals of rolling bearing with 12 different states were collected, respectively, under operating conditions with a sampling frequency of 12 kHz and a speed of 1730 r/min, including normal bearing (denoted as Norm) and ball element fault, outer race fault and inner race fault bearings with fault diameters of 0.1778 mm, 0.3556 mm and 0.5334 mm, respectively, as well as ball element fault (BE4) and inner race fault (IR4) with fault diameter of 0.7112 mm. Among which ball element fault, outer race fault, and inner race fault with fault diameter of 0.1778 mm are denoted as BE1, OR1 and IR1, respectively. The bearings with fault diameter of 0.3556 mm are denoted as BE2, OR2 and IR2, and the bearings with fault diameter of 0.5334 mm are denoted as BE3, OR3 and IR3. The waveforms of vibration signals in time domain are shown in Fig. 9.

Fig. 8

Case Western Reserve University bearing test bench

Fig. 9

The time-domain waveforms of rolling bearing vibration signals

According to the proposed method, first, there are 30 samples with a length of 1024 collected from each of the above 12 states of rolling bearing vibration signal, and the CMTFRDE_2D value for time–frequency distribution with the maximum scale $\tau_{\max } = 20$ of the collected data is calculated and the corresponding mean–variance diagram is present in Fig. 10a. According to Fig. 10a, the CMTFRDE_2D of rolling bearing vibration signals in 12 states decreases as the scale factor increases and can be effectively distinguished. In addition, the normal condition bearing has the smallest value of CMTFRDE_2D. This is because the resulting vibrations in rolling bearing during normal operation are random, the complexity of the signal is relatively large, and the corresponding entropy value is also large. The vibration generated will be accompanied by a certain periodic shock when the rolling bearing operates with local failure, resulting in the entropy being smaller than the normal state. However, reverse dispersion entropy is defined as the “distance from white noise” and thus the CMTFRDE_2D is smallest when rolling bearings in normal conditions. The CMTFRDE_2D value is larger for the vibration signal that has a periodic shock when the rolling bearing operates with local failure. In conclusion, CMTFRDE_2D can effectively characterize the fault features of rolling bearing vibration signals.

Fig. 10

The mean standard deviation diagram of different processing methods (a) CMTFRDE_2D, (b) MTFRDE_2D, (c) MRDE_2D, (d) MDE_2D and (e) MDE_1D

Next, in order to demonstrate the advantages of CMTFRDE_2D method, it is compared with MTFRDE_2D, MRDE_2D, MDE_2D and MDE_1D methods, respectively. The MTFRDE_2D, MDE_2D, MRDE_2D and MDE_1D values are calculated for the rolling bearing vibration signals (to make the test results not affected by the parameter settings, the parameter settings of MTFRDE_2D, MRDE_2D, MDE_2D and MDE_1D methods are the same as CMTFRDE_2D), and the mean standard deviation diagrams are shown in Fig. 10(b–e). Compared with Fig. 10(c and d), the MRDE_2D and MDE_2D curves show opposite trends, i.e., the MDE_2D value for the vibration signal of rolling bearing gradually increases, while the MRDE_2D value progressively decreases as the scale factor increases. The vibration signals of rolling bearings can be distinguished in different states by both methods. Besides, the standard deviation of the processing results of the MRDE_2D method is smaller compared to the MDE_2D method, which indicates that the MRDE_2D method has stronger stability and robustness. As shown in Fig. 10(a and b), the two methods have similar trends, and the corresponding entropy values decrease gradually as the scale factor increases. The standard deviations of the CMTFRDE_2D and MTFRDE_2D are both smaller than those of the MRDE_2D method, and the standard deviations of CMTFRDE_2D values are smaller compared to those of MTFRDE_2D as the scale factor increases. It reveals that the CMTFRDE_2D method has better stability and reflects the advantages of composite multi-scale. In addition, the MDE_1D curve of the bearing vibration signal in the normal state is clearly distinguished from that of the vibration signal in the faulty state, but when the scale factor is large, the MDE_1D curve is not easy to differentiate for the faulty state rolling bearing vibration signal overlaps with each other. Moreover, the standard deviation of the MDE_1D value is relatively large, and the stability is lower than the proposed method. In conclusion, the proposed CMTFRDE_2D method can extract the time–frequency distribution information of rolling bearing vibration signal on different scales and has better stability.

To demonstrate the superiority of the proposed method in recognition accuracy, 10 samples are randomly chosen from the sample feature set of vibration signals in each state for training samples, and other 20 samples as testing sample sets and corresponding class labels are created. The classification labels are shown in Table 1. After that, the training samples are input into GSA-SVM to train, and the best kernel parameters and penalty factor obtained after training are 5.2282 and 34.8106, respectively. The testing samples are input into the trained multi-fault classifier to perform classification and the results are displayed in Fig. 11. By observing Fig. 11, it is found that the actual output result is exactly the same as the predicted result, with a recognition accuracy of 100%. Hence, the proposed CMTFRDE_2D method can effectively extract the complex features for the time–frequency distribution of vibration signals, and the proposed fault diagnosis method can precisely recognize the different fault locations and severities of rolling bearings.

Table 1 Rolling bearing test data classification label

Fig. 11

CMTFRDE_2D classification results

Further, the obtained MTFRDE_2D, MRDE_2D, MDE_2D, and MDE_1D sample feature sets are input into GSA-SVM to train and test, with the test results being displayed in Fig. 12 and Table 2. By observing Fig. 12a–c, it is found that the diagnosis performance based on the MRDE_2D method (5 samples are wrongly classified) is higher than that based on the MDE_2D method (8 samples are wrongly classified), and the recognition accuracy is 97.92% and 96.67%, respectively. Besides, the two samples in IR2 and one sample in OR2 are misjudged as BE1 and BE3 by the MTFRDE_2D method, respectively. The identification accuracy is 98.75% which is higher than that of the MRDE_2D method. From Fig. 12, it is found that the MDE_1D-based fault diagnosis method has the lowest recognition accuracy of 95.42%, with 11 samples being misjudged in total, which is lower than other two-dimensional entropy-based fault recognition methods, indicating that the two-dimensional entropy-based fault diagnosis method is better than the one-dimensional entropy method. In addition, these four methods of fault diagnosis all have different degrees of misjudgment, and their recognition accuracy is lower than that of the proposed method. Hence, the CMTFRDE_2D-based fault diagnosis method has certain superiority.

Fig. 12

Classification results of different methods (a) MTFRDE_2D (b) MRDE_2D (c) MDE_2D (d) MDE_1D

Table 2 Optimal parameters and recognition rate of five methods

It is compared with PSO-SVM and CSO-SVM to verify the advantages of GSA-SVM in rolling bearing fault features pattern recognition. Without loss of generality, the same numbers of training samples and testing samples is used as above, and the corresponding classification results are listed in Table 2. From Table 2, it is found that PSO-SVM based on parameter optimization has the lowest identification rate for each feature set among the three parameters optimized classifiers. In contrast, the GSA-SVM has the highest recognition rate for each feature set, indicating that the GSA method can effectively avoid the local optimization situation and get relatively better parameter optimization results. Therefore, GSA-SVM has certain superiority in fault classification of rolling bearings.

Finally, the influence of input features number on the diagnosis results is investigated. Without loss of generality, the same number of training and testing samples are applied as in the above experiments. The first 15 sample features are sequentially input into GSA-SVM to train, and the recognition precision of the five methods is shown in Fig. 13. By observing Fig. 13, it is found that the identification accuracy of the MDE_1D-based method is always lower than the other four methods when the number of input samples is greater than 5, which is because the MDE_1D method can only extract fault information in the time-domain with the incomplete fault information leading to the lowest recognition accuracy. In addition, the CMTFRDE_2D method can always obtain the highest recognition accuracy compared with the other four methods regardless of the number of input features. Therefore, the proposed fault diagnosis method can also obtain higher recognition accuracy and has better robustness and stability when the number of input features is small.

Fig. 13

The recognition rate of five methods when inputting different feature numbers

In conclusion, the CMTFRDE_2D method can effectively extract the fault characteristics from the time–frequency distribution of rolling bearings, and has better stability compared with the existing methods. The CMTFRDE_2D and GSA-SVM-based fault diagnosis method can accurately identify the different health states of rolling bearings. In addition, the proposed method can obtain the highest recognition accuracy when the number of input sample features is small, which indicates that it is more suitable for small sample classification. Overall, the advantages of the proposed fault diagnosis methods mainly come from the fact that CMTFRDE_2D can effectively improve the information utilization of the original signal, and the extracted features contain more fault information. Meanwhile, GSA-SVM can avoid the occurrence of local optimization in parameter optimization, thus improving the fault recognition rate of the diagnostic model.

4.2 Experiment 2

The test data obtained from the self-made rolling bearing simulation test rig is used for analyzing to further verify the superiority of the proposed method, and the simulation test rig as shown in Fig. 14. The test bearing type is SKF 6206-2Z, and the ball element fault (BE), outer race fault (OR), and inner race fault (IR) are arranged on the bearing utilizing wire cutting technology, respectively. The rolling bearing vibration acceleration signals of seven different fault depths were collected under the operating condition with a sampling frequency of 10.24 kHz, a motor speed of 1500 r/min, and a load of 7 kN. The specific description is shown in Table 3. Thirty samples with a length of 1024 are selected from each state rolling bearing vibration signal. The waveforms of the vibration signals in time-domain are shown in Fig. 15.

Fig. 14

Self-made rolling bearing simulation test bench

Table 3 Rolling bearing test data classification label

Fig. 15

The time-domain waveform of rolling bearing vibration signals

Firstly, the CMTFRDE_2D, MTFRDE_2D, MRDE_2D, MDE_2D, and MDE_1D values of the above vibration signal with the maximum scale $\tau_{\max } = 20$ are calculated, respectively, and other parameters settings are the same as those in Experiment 1. The mean standard deviation diagram of the corresponding entropy values is displayed in Fig. 16. As seen in Fig. 16, the overall change trends of MRDE_2D and MDE_2D are opposite as the scale factor increases, but the standard deviation of the MRDE_2D processing results is smaller and has more excellent stability. Compared with the MTFRDE_2D, the CMTFRDE_2D method has stronger stability and robustness, although the processing results of the two methods have similar trends.

Fig. 16

The mean standard deviation diagram of different processing methods (a) CMTFRDE_2D, (b) MTFRDE_2D, (c) MRDE_2D, (d) MDE_2D and (e) MDE_1D

A GSA-SVM multi-fault classifier is constructed to further demonstrate the advantages of the proposed fault diagnosis method in recognition accuracy. Without losing generality, the same number of training and testing samples as in Experiment 1, and the specific description is shown in Table 3. After that, the training and testing samples are input into GSA-SVM to perform prediction and classification, and the corresponding optimization parameters and output results are listed in Fig. 17 and Table 4, respectively. By observing Fig. 17 and Table 4, it is found that the proposed method correctly classifies the vibration signals of rolling bearings with different fault locations and severities, and the recognition accuracy is 100%. The MTFRDE_2D-based fault diagnosis method divides two samples of BE1 into BE2 by mistake with a recognition accuracy of 98.57%, which indicates that the MTFRDE_2D method can accurately identify different fault locations, but the ability to distinguish different fault degrees of the same locations is lower than the proposed method. The fault diagnosis methods based on MRDE_2D, MDE_2D, and MDE_1D all have different degrees of misjudgment, and the recognition accuracy is MRDE_2D, MDE_2D, and MDE_1D in descending order. To sum up, the proposed CMTFRDE_2D-based fault diagnosis method has the highest recognition accuracy among the five different fault diagnosis methods and has certain advantages.

Fig. 17

Classification results of different methods (a) CMTFRDE_2D, (b) MTFRDE_2D, (c) MRDE_2D, (d) MDE_2D and (e) MDE_1D

Table 4 Optimal parameters and recognition rate of five methods

Next, compared with PSO-SVM and CSO-SVM to illustrate the advantage of the GSA-SVM classifier, the results are listed in Table 4. As demonstrated in Table 4, the GSA-SVM can achieve the highest recognition accuracy no matter which feature set is input among the three classifiers that optimized parameters based on different algorithms, which further verifies the superiority of the GSA-SVM in fault pattern identification.

Finally, the influence of the input features number on the classification results is investigated. The 30 samples of rolling bearing vibration signals in each state are divided randomly into 10 samples to train and the other 20 samples to test. The recognition accuracy obtained according to the different number of input features is displayed in Fig. 18. As demonstrated in Fig. 18, when the number of input features is small, the other four methods have poor classification results. While the recognition precision of the CMTFRDE_2D method is higher than the other four methods regardless of the number of input features. In addition, when the number of input features is greater than 10, the recognition rate of the CMTFRDE_2D method reaches and stabilizes at 100%. Combined with the analysis results of Experiment 1, it can be seen that better classification results can be obtained with the number of input features greater than 11. Therefore, the method of fault diagnosis based on CMTFRDE_2D has more advantages in small sample classification.

Fig. 18

The recognition rate of five methods when inputting different feature numbers

5 Conclusion

In this paper, firstly, based on the definition of MDE_2D, the two-dimensional multi-scale reverse dispersion entropy (MRDE_2D) is proposed by introducing “distance information from white noise”, and then the two-dimensional multi-scale time–frequency reverse dispersion entropy (MTFRDE_2D) is developed to quantify the complexity of time–frequency distribution information for vibration signal of rolling bearing. Based on that, the two-dimensional composite multi-scale time–frequency reverse dispersion entropy (CMTFRDE_2D) is proposed to reduce the information loss caused by conventional coarse-grained used in MTFRDE_2D, and to alleviate the phenomenon that the entropy value fluctuation of MTFRDE_2D as the scale factor increases. The effectiveness and stability of the CMTFRDE_2D for signal complexity measurement are verified through four kinds of colored noise analysis. After that, an intelligent diagnosis method of rolling bearing based on CMTFRDE_2D and GSA-SVM is proposed, which is subsequently employed on rolling bearing test data under two different working conditions. The results reveal that the proposed method can accurately identify different locations and severities of faults in rolling bearings with greater robustness and stability than the MTFRDE_2D, MRDE_2D, MDE_2D, and MDE_1D methods. In addition, the effect of the number of input features upon the classification results also is investigated. The results indicate that the proposed method still has high recognition precision with less input features, and it is found that a higher recognition rate can be achieved with a number of input features greater than 11. Finally, the superiority of GSA-SVM in fault pattern recognition is demonstrated by comparing it with several other most commonly employed optimization algorithms. In summary, the CMTFRDE_2D and GSA-SVM-based rolling bearing fault diagnosis method can effectively extract the fault information of vibration signal and has a certain superiority over the compared methods in fault identification. However, the parameter selection of CMTFRDE_2D still requires to be studied in future work.

In fact, due to the influence of background noise and complex environment in practical engineering applications, it is not easy to effectively diagnose mechanical equipment in different health conditions without the given known knowledge. We want to say that this paper verifies the validity and superiority of the proposed method through the test data of rolling bearings under two different working conditions, which provides a new way for the fault diagnosis of mechanical equipment. In addition, we will apply the proposed method to the fault diagnosis of planetary gears and rotors in the future work to further study the application area of this method.