1 Introduction

For the requirement of traffic safety and convenience, intelligent vehicles have been widely concerned all over the world in recent years [1, 25, 33]. With the development of electronic information technology, control theory, artificial intelligence, and communication technology, the intelligent vehicle has reached the L4 level of driverless technology. Lane-keeping control technology is basic for an intelligent vehicle. Many researchers have proposed some achievements in recent years [11, 30]. For example, Netto et al. applied the self-tuning regulator to solve the vehicle lateral control problem for the vehicle lane-keeping in [26]. Amditis et al. presented a situation-adaptive lane-keeping support system that has three layers: the perception layer, decision, and action layers in [2]. Marino et al. designed a nested PID steering controller for the lane-keeping system in [21]. In [38], Xu et al. used control barrier functions to design a modular correct-by-construction control method. In [6], Chen et al. designed a lane-keeping system using adaptive model-predictive control with a time-variant prediction model. In [32], Suh et al. proposed a stochastic model-predictive control method to obtain the desired steering angle and longitudinal acceleration for the lane-keeping system. Hu et al. studied the lane-keeping control of AGV which considered rollover prevention and input saturation and proposed a state observer-based sliding mode control method in [16]. Dai and Koutsoukos used multi-modal port-Hamiltonian systems to design an approach for safety analysis of the lane-keeping system in [10]. Choi et al. proposed a robust lane tracking control method to compensate winding disturbance in [9]. An et al. proposed a dual-layer-oriented strategy for the lane-keeping system which includes an inner controller and an outer cooperative copilot controller in [3]. An AGV lane-keeping system based on a linear parameter varying model is proposed by Salt Ducaju et al. in [31]. Chen et al. designed a feedforward-feedback controller based on a deep convolutional fuzzy system in [8]. Meng et al. proposed a lane-keeping control method based on non-smooth finite-time for an electric vehicle to improve the output response and robustness of the controller in [24]. Hu and Wang built a quantitative trust dynamic model of the driver for adaptive cruise control to describe the human-vehicle relationship in [15]. An adaptive-weight predictive controller based on a square-root cubature Kalman filter-based vehicle sideslip angle observer was designed by Wang et al. in [35]. In [42], Zhang et al. proposed a stacking-based ensemble learning method for the recognition of the vehicle lane-changing maneuver to improve recognition accuracy.

These aforementioned achievements show their effectiveness in theory and practice. But because of the nonlinear and unknown disturbances in the lane-keeping dynamic model, the existing methods sometimes cannot acquire the desired effect on robustness, response speed, and control accuracy. To solve these problems, the new lane-keeping control methods should be studied via modern control theory. In recent years, some researchers proposed a kind of homogeneous domination control method via the homogeneous principle. The homogeneous domination control method has specific advantages for robustness and nonlinearity. Now the researchers mainly study the homogeneous domination control method in theory. Qian proposed a homogeneous domination approach for the global output-feedback stabilization of nonlinear systems firstly in paper [27]. He and his followers developed the homogeneous domination control method for many nonlinear systems [4, 5, 12, 18, 22, 29, 40, 43]. This novel method also attracts other researchers. Xie and Liu designed a state feedback controller based on a homogeneous domination approach for stochastic high-order nonlinear systems with time-varying delay in [37]. Then, Xie and Li studied the finite-time output-feedback stabilization of a class of high-order nonholonomic systems under weaker conditions in [36]. In [41], Zhang et al. proposed a homogeneous domination feedback technology for a class of disturbed higher-order nonlinear systems. Yang et al. discussed the state feedback stabilization problem for a class of high-order uncertain nonlinear systems with multiple time delays in [39]. Sun and Wang proposed a control strategy based on a double-domination approach to attenuate disturbance for a system whose output function is not precisely unknown in [34]. Chen et al. renovated the adding a power integrator technique based on the constructed fraction-type asymmetric barrier Lyapunov function and distinctive non-smooth state observer in [7]. In [20], an adaptive homogeneous domination method was designed for a time-varying system with a complicated polynomial growing condition. The aforementioned studies show the advantages of the homogeneous domination method in theory. But almost no one applied this method to engineering. We studied the homogeneous domination theory and proposed the homogeneous domination-based control methods for vehicle active suspension in [22, 23]. The applications in engineering show the advantages of the homogeneous domination methods. Inspired by [22, 23], we propose a homogeneous domination control method for the vehicle lane-keeping system to improve the robustness, response speed, and control accuracy in this paper. The contributions of this paper are as follows.

  • A two-degree-of-freedom (2DOF) vehicle lane-keeping trajectory tracking error model is built which is obtained via a lateral dynamic model. Thus, this model considers lateral stability as well as lane-keeping.

  • Combining the lane-keeping system with the homogeneous domination method, the proposed lane-keeping control method doesn’t require the nonlinear terms of the control system to meet the strict linear growth condition for global asymptotical stabilization which is required for most of the existing control methods.

  • A homogeneous domination-based lane-keeping controller is designed which has stronger robustness, faster response, and lower energy output than a normal sliding mode controller.

The rest of this paper is organized as follows. The 2DOF lane-keeping trajectory tracking error model is constructed in Sect. 2. Then, the lane-keeping control method based on homogeneous domination is proposed in Sect. 3. Numerical simulation and hardware-in-the-loop test are carried out to verify the effectiveness of the proposed method in Sect. 4. Finally, the conclusion is given in Sect. 5.

2 Construction of lane-keeping model

To reduce the difficulty of developing lane-keeping control method for an intelligent vehicle, we ignore the roll and pitch motions and built a 2DOF model for the lane-keeping system as shown in Fig. 1.

Fig. 1
figure 1

The two-degree-of-freedom lane-keeping model

Full size image

To obtain the lane-keeping dynamic equations, the force condition of the 2DOF model is analyzed. A vehicle should keep lateral stability when it runs along the desired lane. Thus the forces along the Y-axis should keep balance firstly, i.e.,

$$\begin{aligned} m{\dot{v}}_y+mv_x{\dot{\varphi }}-F_{xf}\sin \left( \delta _f\right) -F_{yf}\cos \left( \delta _f\right) -F_{yr}=0. \end{aligned}$$
(1)

Secondly, the moments around the centroid also should keep balance, i.e.,

$$\begin{aligned} I_z\ddot{\varphi }-l_f\left[ F_{xy}\sin \left( \delta _f\right) +F_{yf}\cos \left( \delta _f\right) \right] +l_rF_{yr}=0. \end{aligned}$$
(2)

Therefore, the lane-keeping dynamic equations of the 2DOF model are

$$\begin{aligned} \begin{aligned}&m\left( {\dot{v}}_y+{v}_x{\dot{\varphi }}\right) =F_{xf}\sin \left( \delta _f\right) +F_{yf}\cos \left( \delta _f\right) +F_{yr}\\&\quad I_z\ddot{\varphi }=l_f\left[ F_{xy}\sin \left( \delta _f\right) +F_{yf}\cos \left( \delta _f\right) \right] -l_rF_{yr},\\ \end{aligned}\nonumber \\ \end{aligned}$$
(3)

where \(\delta _f\) is the front wheel angle, \(\varphi \) is the yaw angle, \(F_{xf} \) and \(F_{xr} \) are the front wheel longitudinal force and rear wheel longitudinal force, respectively, \(F_{yf} \) and \(F_{yr} \) are the front wheel lateral force and rear wheel lateral force, respectively, \(v_x \) and \(v_y \) are the longitudinal velocity and lateral velocity, respectively, m and \(I_z \) are the vehicle mass and moment of inertia, respectively, \(l_f \) and \(l_r \) are the distances between the front wheel axis and centroid, and the rear wheel axis and centroid, respectively.

Because \(\varphi \) is small, \(\cos \varphi \approx 1,\sin \varphi \approx 0,\tan \varphi \approx \varphi \). Ignoring the influence of front wheel driving force for vehicle lateral motion, and setting the longitudinal velocity as constant, a 2DOF lateral motion dynamic equations are obtained as

$$\begin{aligned} \begin{aligned} {\dot{v}}_y&=-{\dot{\varphi }}{v}_x+\frac{1}{m}\left[ F_{yf}\cos \left( \delta _f\right) +F_{yr}\right] \\ \ddot{\varphi }&=\frac{1}{I_z}\left[ l_fF_{yf}\cos \left( \delta _f\right) -l_rF_{yr}\right] .\\ \end{aligned} \end{aligned}$$
(4)

The slip angles of front and real wheels are calculated as

$$\begin{aligned} \begin{aligned} \alpha _f&=\arctan \left( \frac{v_y+l_f\varphi }{v_x}\right) -\delta _f\approx \frac{v_y+l_f{\dot{\varphi }}}{v_x}-\delta _f\\ \alpha _r&=\arctan \left( \frac{v_y-l_r\varphi }{v_x}\right) \approx \frac{v_y-l_r{\dot{\varphi }}}{v_x}.\\ \end{aligned} \end{aligned}$$
(5)

When a vehicle runs under lane-keeping condition, the tire lateral elasticity can be considered to be linear. Then, the tire lateral forces are obtained by using the following linear functions

$$\begin{aligned} \begin{aligned} F_{yf}={\overline{C}}_{\alpha _f}\alpha _f\\ F_{yr}={\overline{C}}_{\alpha _r}\alpha _r. \end{aligned} \end{aligned}$$
(6)

Substituting Eq. (5) into Eq. (6), Eq. (6) can be rewritten as

$$\begin{aligned} \begin{aligned} F_{yf}&={\overline{C}}_{\alpha _f}\left( \frac{v_y+l_f{\dot{\varphi }}}{v_x}-\delta _{f}\right) \\ F_{yr}&={\overline{C}}_{\alpha _r}\frac{v_y-l_r{\dot{\varphi }}}{v_x}. \end{aligned} \end{aligned}$$
(7)

Substituting Eq. (7) into Eq. (4), Eq. (4) can be rewritten as

$$\begin{aligned} \begin{aligned} {\dot{v}}_y&=\frac{{\overline{C}}_{\alpha _f}+{\overline{C}}_{\alpha _r}}{mv_x}v_y+\left( \frac{{\overline{C}}_{\alpha _f}l_f-{\overline{C}}_{\alpha _r}l_r}{mv_x}-v_x \right) {\dot{\varphi }}-\frac{{\overline{C}}_{\alpha _f}}{m}\delta _f\\ \ddot{\varphi }&=\frac{l_f{\overline{C}}_{\alpha _f}-l_r{\overline{C}}_{\alpha _r}}{I_zv_x}v_y+\frac{{l_f}^2{\overline{C}}_{\alpha _f}+{l_r}^2{\overline{C}}_{\alpha _r}}{I_zv_x}{\dot{\varphi }}-\frac{l_f{\overline{C}}_{\alpha _f}}{I_z}\delta _f. \end{aligned}\nonumber \\ \end{aligned}$$
(8)

Generally speaking, in the lane-keeping control system, the lateral deviation, i.e., the error between the reference value and practical value, is controller input. We define the lateral offset error and the yaw angle error as \({\widetilde{y}}\) and \(\widetilde{\varphi }\), respectively. Then,

$$\begin{aligned} \begin{aligned} {\widetilde{y}}&=y-y_{\text {ref}}\\ \dot{{\widetilde{y}}}&={\dot{y}}+v_x\widetilde{\varphi }\\ \widetilde{\varphi }&=\varphi -\varphi _{\text {ref}}\\ \dot{\widetilde{\varphi }}&={\dot{\varphi }}-{\dot{\varphi }}_{\text {ref}}.\\ \end{aligned} \end{aligned}$$
(9)

Therefore, the 2DOF dynamic equations can be described as

$$\begin{aligned} \begin{aligned} \ddot{{\widetilde{y}}}&=\ddot{y}+v_x\left( {\dot{\varphi }}-{\dot{\varphi }}_{\text {ref}}\right) \\&=\frac{{\overline{C}}_{\alpha _f}+{\overline{C}}_{\alpha _r}}{mv_x}{\dot{y}}+\left( \frac{{l_f}{\overline{C}}_{\alpha _f}-{l_r}{\overline{C}}_{\alpha _r}}{mv_x}-v_x \right) {\dot{\varphi }} \\&\quad +v_x\left( {\dot{\varphi }}-{\dot{\varphi }}_{\text {ref}}\right) \\&=\frac{{\overline{C}}_{\alpha _f}+{\overline{C}}_{\alpha _r}}{mv_x}\dot{{\widetilde{y}}}-\frac{{\overline{C}}_{\alpha _f}+{\overline{C}}_{\alpha _r}}{m} \widetilde{\varphi }+\frac{{l_f}{\overline{C}}_{\alpha _f}-{l_r}{\overline{C}}_{\alpha _r}}{mv_x}\dot{\widetilde{\varphi }}\\&~~~~~-\frac{{\overline{C}}_{\alpha _f}}{m}\delta _f+\left( \frac{{l_f}{\overline{C}}_{\alpha _f}-{l_r}{\overline{C}}_{\alpha _r}}{mv_x}-v_x \right) {\dot{\varphi }}_{\text {ref}}\\ \ddot{\widetilde{\varphi }}&=\ddot{\varphi }-\ddot{\varphi }_{ref}=\frac{l_f{\overline{C}}_{\alpha _f}-l_r{\overline{C}}_{\alpha _r}}{I_zv_x}{\dot{y}}+\frac{{l_f}^2{\overline{C}}_{\alpha _f}+{l_r}^2{\overline{C}}_{\alpha _r}}{I_zv_x}{\dot{\varphi }}\\&~~~~~-\frac{l_f{\overline{C}}_{\alpha _f}}{I_z}\delta _f-\ddot{\varphi }_{\text {ref}}\\&=\frac{l_f{\overline{C}}_{\alpha _f}-l_r{\overline{C}}_{\alpha _r}}{I_zv_x}\dot{{\widetilde{y}}}-\frac{l_f{\overline{C}}_{\alpha _f}-l_r{\overline{C}}_{\alpha _r}}{I_z}\widetilde{\varphi }\\&\quad +\frac{{l_f}^2{\overline{C}}_{\alpha _f}+{l_r}^2{\overline{C}}_{\alpha _r}}{I_zv_x}\dot{\widetilde{\varphi }}\\&~~~~~~-\frac{l_f{\overline{C}}_{\alpha _f}}{I_z}\delta _f+\frac{{l_f}^2{\overline{C}}_{\alpha _f}+{l_r}^2{\overline{C}}_{\alpha _r}}{I_zv_x}{\dot{\varphi }}_{\text {ref}}-\ddot{\varphi }_{\text {ref}}. \end{aligned}\nonumber \\ \end{aligned}$$
(10)

Then, the dynamic equations can be described as

$$\begin{aligned} {\dot{X}}={\widetilde{A}}X+{\widetilde{B}}U+\Phi , \end{aligned}$$
(11)

where \(X=\left[ {\widetilde{y}} \quad \dot{{\widetilde{y}}} \quad \widetilde{\varphi } \quad \dot{\widetilde{\varphi }}\right] ^T\), \(U=\delta _f\),

$$\begin{aligned} \begin{aligned} {\widetilde{A}}=\begin{bmatrix} 0 &{} 1 &{}0 &{}0\\ 0&{} \frac{{\overline{C}}_{\alpha _f}+{\overline{C}}_{\alpha _r}}{mv_x}&{} \frac{{\overline{C}}_{\alpha _f}+{\overline{C}}_{\alpha _r}}{m} &{} \frac{l_f{\overline{C}}_{\alpha _f}-l_r{\overline{C}}_{\alpha _r}}{mv_x}\\ 0&{} 0&{}0&{}1\\ 0&{} \frac{l_f{\overline{C}}_{\alpha _f}-l_r{\overline{C}}_{\alpha _r}}{I_zv_x} &{} -\frac{l_f{\overline{C}}_{\alpha _f}-l_r{\overline{C}}_{\alpha _r}}{I_z} &{} \frac{{l_f}^2{\overline{C}}_{\alpha _f}+{l_r}^2{\overline{C}}_{\alpha _r}}{I_zv_x} \end{bmatrix}, \end{aligned} \end{aligned}$$
$$\begin{aligned}&{\widetilde{B}}=\begin{bmatrix} 0\\ -\frac{{\overline{C}}_{\alpha _f}}{m}\\ 0\\ -\frac{l_f{\overline{C}}_{\alpha _f}}{I_z} \end{bmatrix},&\Phi =\begin{bmatrix} 0\\ \left( \frac{{l_f}{\overline{C}}_{\alpha _f}-{l_r}{\overline{C}}_{\alpha _r}}{mv_x}-v_x\right) {\dot{\varphi }}_{ref}\\ 0\\ \frac{{l_f}^2{\overline{C}}_{\alpha _f}+{l_r}^2{\overline{C}}_{\alpha _r}}{I_zv_x}{\dot{\varphi }}_{ref}-\ddot{\varphi }_{ref} \end{bmatrix} . \end{aligned}$$

Remark 1

A vehicle has thousands of parts. It is a highly nonlinear system that is very difficult to analyze. If too many factors are considered, the lane-keeping system may be uncontrollable. In this manuscript, we ignore the influence of front wheel driving force on vehicle lateral motion and set the longitudinal velocity as constant. Otherwise, some nonlinear terms will be generated in the dynamic equations and state equations that will cause control difficulty of the lane-keeping control system.

3 Homogeneous domination-based lane-keeping control method

For analysis convenience, we define \(x_1={\widetilde{y}},x_2=\dot{{\widetilde{y}}}, x_3=\widetilde{\varphi },x_4=\dot{\widetilde{\varphi }},{\tilde{u}}(x)=\delta _f\). Eq. (11) can be transferred to the state equations as

$$\begin{aligned} \begin{aligned}&{\dot{x}}_1=x_2 \\&{\dot{x}}_2=a_1x_3+\Psi _1(x)\\&{\dot{x}}_3=x_4 \\&{\dot{x}}_4=a_2{\tilde{u}}(x)+\Psi _2(x)\\&y=x_1,\\ \end{aligned} \end{aligned}$$
(12)

where \(a_1=\frac{{\overline{C}}_{\alpha _f}+{\overline{C}}_{\alpha _r}}{m}\), \(a_2=-\frac{l_f{\overline{C}}_{\alpha _f}}{I_z} \),

$$\begin{aligned} \begin{aligned}&\Psi _1(x)=\frac{{\overline{C}}_{\alpha _f}+{\overline{C}}_{\alpha _r}}{m v_x}x_2+\frac{l_f{\overline{C}}_{\alpha _f}-l_r{\overline{C}}_{\alpha _r}}{mv_x}x_4\\&~~~~~~~~~~~~~~~~-\frac{{\overline{C}}_{\alpha _f}}{m}{\tilde{u}}(x),\\&\Psi _2(x)=\frac{l_f{\overline{C}}_{\alpha _f}-l_r{\overline{C}}_{\alpha _r}}{I_zv_x} x_2-\frac{l_f{\overline{C}}_{\alpha _f}-l_r{\overline{C}}_{\alpha _r}}{I_z} x_3\\&~~~~~~~~~~~~~~~~+\frac{{l_f}^2{\overline{C}}_{\alpha _f}+{l_r}^2{\overline{C}}_{\alpha _r}}{I_zv_x}x_4. \end{aligned} \end{aligned}$$

Furtherly, we define

$$\begin{aligned}&z_1=x_1,z_2=x_2,z_3=a_1x_3,z_4=a_1x_4,\nonumber \\&v=a_1a_2{\tilde{u}},\omega _{2}=\Psi _1,\omega _4=a_1\Psi _2,\omega _1=\omega _3=0. \end{aligned}$$
(13)

System (12) is transferred to

$$\begin{aligned} \begin{aligned}&{\dot{z}}_i=z_{i+1}+\omega _i, i=1,\cdots ,4 \\&y=z_1,\\ \end{aligned} \end{aligned}$$
(14)

where \(v:=z_5 \in {\mathbb {R}}\).

3.1 Homogeneous domination approach and useful lemmas

To easily understand the proposed homogeneous domination approach for lane-keeping, we introduce some useful definitions and lemmas firstly.

Definition 1

[17] Weighted Homogeneity: For a selected coordinates \((x_1,x_2,\cdots , x_n) \in {\mathbb {R}}^n\) and real numbers \(r_1,r_2,\cdots ,r_n\), where \(r_i >0\),

  • Dilation \(\Delta _\varepsilon (x)\) is defined as \(\Delta _\varepsilon (x)=\left( \varepsilon ^{r_1}x_1,\varepsilon ^{r_2}x_2,\right. \left. \cdots , \varepsilon ^{r_n}x_n\right) \), \(\forall \varepsilon >0\), where \(r_i\) are called as the weights of the coordinations.

  • A function \(V \in C\left( {\mathbb {R}}^n, {\mathbb {R}}\right) \) is considered to be homogeneous of degree \(\tau \) if there exists a \(\tau \in {\mathbb {R}}\), then \(\forall x \in {\mathbb {R}}^n \setminus {0}, \varepsilon >0, V\left( \Delta _{\varepsilon }(x)\right) =\varepsilon ^\tau V\left( x_1, x_2, \cdots , x_n\right) \).

  • A vector field \(f \in C\left( {\mathbb {R}}^n, {\mathbb {R}}^n\right) \) is considered to be homogeneous of degree \(\tau \) if there exists a \(\tau \in {\mathbb {R}}\), then \(\forall x \in {\mathbb {R}}^n \setminus {0}, \varepsilon >0, f_i\left( \Delta _{\varepsilon }(x)\right) =\varepsilon ^{\tau +r_i} f_i(x)\).

  • A homogeneous p-norm is defined as

    $$\begin{aligned} \Vert x\Vert _{\Delta _{\varepsilon },p}=\left( \sum _{i=1}^n|x_i|^{\frac{p}{r_i}}\right) ^{\frac{1}{p}},\forall x \in {\mathbb {R}}^n, \end{aligned}$$
    (15)

    where p is a constant and \(p \ge 1\).

Based on Definition 1, researchers proposed some useful properties of homogeneous function as follows.

Lemma 1

[14] Given a dilation weight \(\Delta =\left( r_1,r_2,\cdots ,r_n\right) \), if \(V_1\) and \(V_2\) are homogeneous functions of degree \(\tau _1\) and \(\tau _2\) with respect to a same dilation weight, respectively, the homogeneous degree of \(V_1\cdot V_2\) is \(\tau _1+\tau _2\) with respect to the same dilation weight.

Lemma 2

[14] Suppose that \(V_1\) and \(V_2\) are homogeneous functions of degree \(\tau _1\) and \(\tau _2\) with respect to a same dilation weight, respectively. Then, \(V_1\cdot V_2\) is also homogeneous with respect to the same dilation weight and the homogeneous degree is \(\tau _1+\tau _2\).

Lemma 3

[14] Suppose \(V: {\mathbb {R}}^n \longrightarrow {\mathbb {R}}\) is a homogeneous function of degree \(\tau \) with respect to a given dilation weight \(\Delta =\left( r_1,\cdots ,r_n\right) \). Then, the following items hold.

  • \(\partial V / \partial x_i\) is homogeneous of degree \(\tau -r_i\) with respect to the dilation weight \(\Delta \).

  • There is a positive constant \(w_1\) to ensure \(V(x) \le w_1 \Vert x\Vert ^\tau _\Delta \).

  • If V(x) is positive definite, there is a positive constant \(w_2\) to ensure \(w_2\Vert x\Vert ^\tau _\Delta \le V(x)\).

On the other hand, for designing a homogeneous domination controller for vehicle lane-keeping, we give some other necessary lemmas.

Lemma 4

[19] When \(x \in {\mathbb {R}}, y \in {\mathbb {R}}, p \ge 1\), the following inequalities hold,

$$\begin{aligned}&|x+y|^p \le 2^{p-1}\left| x^p+y^p\right| , \end{aligned}$$
(16)
$$\begin{aligned}&\left( |x|+|y|\right) ^{1/p} \le |x|^{1/p}+|y|^{1/p}\nonumber \\&\qquad \qquad \qquad \qquad \le 2^{\frac{p-1}{p}}\left( |x|+|y|\right) ^{1/p}. \end{aligned}$$
(17)

If \(p \ge 1\) is odd, then

$$\begin{aligned} |x-y|^p \le 2^{p-1}\left| x^p-y^p\right| . \end{aligned}$$
(18)

Lemma 5

[28] When c, d are positive constants, the following inequality holds,

$$\begin{aligned} |x|^c|y|^d \le \frac{c}{c+d} \gamma |x|^{c+d}+\frac{d}{c+d}\gamma ^{-c/d}|y|^{c+d}. \end{aligned}$$
(19)

Lemma 6

[19] For a positive odd integer \(p \ge 1\), the following inequality holds,

$$\begin{aligned} |x^p-y^p| \le p|x-y|\left( |x|^{p-1}+|y|^{p-1}\right) . \end{aligned}$$
(20)

Lemma 7

[13] For any \(x_i \in {\mathbb {R}},i = 1,\cdots ,n\) and a real number \(p \ge 1\), the following inequalities hold,

$$\begin{aligned}&\left( |x_1|+\cdots +|x_n|\right) ^p \le n^{p-1}\left( |x_1|^p+\cdots +|x_n|^p\right) ,\end{aligned}$$
(21)
$$\begin{aligned}&\left( |x_1|+\cdots +|x_n|\right) ^{1/p} \le |x_1|^{1/p}+\cdots +|x_n|^{1/p}. \end{aligned}$$
(22)

Next, a homogeneous domination controller will be designed based on the following Definition 2 and Assumption 1.

Definition 2

Denote \(\tau =q/p\), where q is even and p is odd, then

$$\begin{aligned} l_i=(i-1)\tau +1, i=1,2,3,4. \end{aligned}$$
(23)

Assumption 1

There are constants \(\tau \ge 0\) and \(c \ge 0\) leading to

$$\begin{aligned} |\omega _i| \le c\left( |x_1|^{i\tau +1}+\cdots +|x_i|^{p_m}\right) ,i=1,2,3,4, \end{aligned}$$
(24)

where \(p_m=\frac{i\tau +1}{(i-1)\tau +1}\).

3.2 Design of the homogeneous domination controller for lane-keeping

We present a theorem to describe the main contribution of this paper.

Theorem 1

Based on Assumption 1, the lane-keeping system (14) can be globally asymptotically stabilized by a homogeneous domination-based state feedback controller (25) to enable the vehicle running along the desired lane.

$$\begin{aligned} u(x)\!=\!-\gamma _4\left( z_4\!+\!\left( z_3+\!\left( z_2+z_1^{h_1}\gamma _1\right) ^{h_2}\gamma _2\right) ^{h_3}\gamma _3\right) ^{h_4}\!, \nonumber \\ \end{aligned}$$
(25)

where \( h_1=l_2/l_1, h_2=l_3/l_2, h_3=l_4/l_3, h_4=(l_4+\tau )/l_4 \), \(\gamma _i\) and \(l_i\) are constants. \(\gamma _i\) are the coefficients of Hurwitz polynomial.

The general procedure of the homogeneous domination-based lane-keeping control method is shown in Fig. 2.

Fig. 2
figure 2

Homogeneous domination-based control method for lane-keeping system

Full size image

Next we will prove Theorem 1

Proof

We select a function as

$$\begin{aligned} V_1(z_1)=\frac{l_1}{2l_4-\tau } {z_1}^{\frac{2l_4-\tau }{l_1}}. \end{aligned}$$
(26)

The derivative of Eq. (26) along the trajectory of (14) is

$$\begin{aligned} \begin{aligned} \begin{aligned} {\dot{V}}_1&={z_1}^{\frac{2l_4-\tau }{l_1}-1} z_2 \le {z_1}^{\frac{2l_4-\tau }{l_1}-1}\left( z_2+c{x_1}^{\frac{l2}{l1}}\right) \\&\le {z_1}^{\frac{2l_4-\tau }{l_1}-1}\left( z_2-{z_2}^{*}+{z_2}^{*}+c{z_1}^{\frac{l2}{l1}}\right) . \end{aligned} \end{aligned} \end{aligned}$$
(27)

Define \( {z_2}^{*}=-\gamma _1{z_1}^{l2/l1}, \gamma _1=4+c \), Eq. (27) is rewritten as

$$\begin{aligned} {\dot{V}}_1 \le -4{z_1}^{\frac{2l_4}{l_1}}+{z_1}^{\frac{2l_4-\tau }{l_1}-1}\left( {z_2}-{z_2}^{*}\right) . \end{aligned}$$
(28)

Suppose that there is a positive definite and homogeneous \(C^1\) Lyapunov function \(V_{k-1}:{\mathbb {R}}^{n-1} \rightarrow {\mathbb {R}} \) at step \(k-1, k=2,3,4\) with respect to Definition 2. The respective virtual controllers \(z_1^*, z_2^*, z_3^*, z_4^*\) are defined as

$$\begin{aligned} \begin{aligned}&{z_1}^{*}=0,\quad \quad \quad \quad \quad \quad \quad \xi _1={z_1}-{z_1}^{*},\\&{z_j}^{*}=-\gamma _{j-1} \xi _{j-1}^{\frac{l_j}{l_{j-1}}} , \quad \quad \quad \xi _j={z_j}-{z_j}^{*}, j=2, 3, 4, \end{aligned} \end{aligned}$$
(29)

where \(\gamma _{j-1}>0\). \(V_2\) and \(V_3\) are selected as

$$\begin{aligned} V_2=V_1+\frac{l_2}{2l_2-\tau }\xi _2^{\frac{2l_4-\tau }{l_2}}, \end{aligned}$$
$$\begin{aligned} V_3=V_2+\frac{l_3}{2l_3-\tau }\xi _3^{\frac{2l_4-\tau }{l_3}}. \end{aligned}$$

Then,

$$\begin{aligned} {\dot{V}}_{2} \le -3\sum _{j=1}^{2} \xi _{j}^\frac{2l_4}{l_{j}} + \xi _2^{\frac{2l_4 - \tau }{l_{2}} -1} \left( {z_3}-{z_3}^{*}\right) , \end{aligned}$$
(30)
$$\begin{aligned} {\dot{V}}_{3} \le -2\sum _{j=1}^{3} \xi _{j}^\frac{2l_4}{l_{j}} + \xi _3^{\frac{2l_4 - \tau }{l_{3}} -1} \left( {z_4}-{z_4}^{*}\right) . \end{aligned}$$
(31)

Therefore, \({\dot{V}}_4\) should also hold as the forms of (30) and (31). \(V_4\) is constructed as

$$\begin{aligned} V_4\left( z_1, z_2,z_3, z_4\right) =V_{3}+\frac{l_4}{2l_4-\tau } \xi _4^{\frac{2l_4-\tau }{l_4}}. \end{aligned}$$
(32)

The derivative of \(V_4\) is

$$\begin{aligned} \begin{aligned} {\dot{V}}_4(z_1,z_2, z_3, z_4)&\le -2\sum _{j=1}^{3} \xi _j^\frac{2l_4}{l_j}+ \xi _{3}^{\frac{2l_4-\tau }{l_{3}}-1} \xi _{4}\\&+\xi _{4}^{\frac{2l_4-\tau }{l_4}-1} \left( z_{5}+\omega _4(z)-\sum _{i=1}^{3} \frac{\partial {z_4}^{*}}{\partial z_i} {\dot{z}}_i \right) . \end{aligned} \end{aligned}$$
(33)

Next we will deal with each term in the right hand side of Eq. (33). Via Young Inequality there exists

$$\begin{aligned} \begin{aligned} {\xi _{3}}^{\frac{2l_4-\tau }{l_3}-1} {\xi _{4}}&=\left( \xi _{3}^\frac{1}{l_{3}}\right) ^{2l_4-\tau -l_{3}} \left( \xi _{4}^\frac{1}{l_{4}}\right) ^{l_4}\\&\le \frac{c}{2l_4}\beta \xi _{3}^{\frac{2l_4}{l_{3}}}+\frac{d}{2l_4} \beta ^{-\frac{c}{d}} \xi _{3}^{\frac{2l_4}{l_{4}}}\\&=\frac{1}{2} \xi _{3}^{\frac{2l_4}{l_{3}}}+c_4 \xi _{4}^{\frac{2l_4}{l_{4}}}, \end{aligned} \end{aligned}$$
(34)

where \( c_4=\frac{d}{2l_4} \beta ^{-\frac{c}{d}} \).

As aforementioned information, one obtains

$$\begin{aligned} \begin{aligned} \frac{l_4+\tau }{l_j}=\frac{4 \tau +1}{(j-1)\tau +1} =\frac{4q+p}{(j-1)q+p}\ge 1. \end{aligned} \end{aligned}$$
(35)

By Lemma 4 and Assumption 1, there are

$$\begin{aligned} \begin{aligned} |z_j|^{\frac{n \tau +1}{(j-1)\tau +1}}&=|\xi _j-\xi _{j-1}^{\frac{l_j}{l_{j-1}}} \gamma _{j-1}|\\&\le 2^{\frac{4 \tau +1}{l_j}-1}\left| \xi _j^{\frac{l_4+\tau }{l_j}}-\gamma _{j-1}^{\frac{l_4+\tau }{l_j}} \xi _{j-1}^{\frac{l_j}{l_{j-1}} \frac{l_4+\tau }{l_j}}\right| \\&\le 2^{\frac{4 \tau +1}{l_j}-1}\left( \left| {\xi _j}^{\frac{l_4+\tau }{l_j}}\right| +\gamma _{j-1}^{\frac{l_4+\tau }{l_j}} \left| \xi _{j-1}^{\frac{l_4+\tau }{l_{j-1}}}\right| \right) \end{aligned} \end{aligned}$$
(36)

and

$$\begin{aligned} \begin{aligned} |\omega _4 (z)|&\le c \sum _{j=1}^{4} \left| \xi _j-{\xi _{j-1}}^{\frac{l_j}{l_{j-1}}} \gamma _{j-1}\right| \\&\le c \sum _{j=1}^{4} 2^{\frac{4 \tau +1}{l_j}-1}\left( \left| \xi _j^{\frac{l_4+\tau }{l_j}}\right| +\gamma _{j-1}^{\frac{l_4+\tau }{l_j}} \left| \xi _{j-1}^{\frac{l_4+\tau }{l_{j-1}}}\right| \right) \\&={\bar{c}}_4 \sum _{j=1}^{4} \left| {\xi _j}\right| ^{\frac{l_4+\tau }{l_j}} \end{aligned}\nonumber \\ \end{aligned}$$
(37)

for a constant \({\bar{c}}_4\).

The last term of the right hand side of Eq. (33) is estimated according to reference [27] as

$$\begin{aligned} \left| \sum _{i=1}^{3} \frac{\partial {z_4}^{*}}{\partial z_i} {\dot{z}}_i\right| \le {\tilde{c}}_4\left( |\xi _1|^{\frac{l_4+\tau }{l_1}}+\cdots +|\xi _4|^{\frac{l_4+\tau }{l_4}}\right) . \end{aligned}$$
(38)

Combining Eq. (37) with Eq. (38) generates

$$\begin{aligned} \begin{aligned}&\xi _{4}^{\frac{2l_4-\tau }{l_4}-1} \left( \omega _4(z)-\sum _{i=1}^{3} \frac{\partial {z_4}^{*}}{\partial z_i} {\dot{z}}_i \right) \\ {}&\quad \le z_{4}^{\frac{2l_4-\tau }{l_4}-1} ({\bar{c}}_4+{\tilde{c}}_4) \sum _{i=1}^{4} |\xi _i|^{\frac{l_4+\tau }{l_i}}\\&\quad \le ({\bar{c}}_4+{\tilde{c}}_4) \sum _{i=1}^{3} \left( \frac{c}{c+d}\beta \left| \xi _{4}^{\frac{l_i}{l_4}}\right| ^{\frac{2l_4}{l_i}} \right. \\&\qquad \left. +\frac{d}{c+d}\beta ^{-\frac{c}{d}} |\xi _i|^{\frac{2l_4}{l_i}}\right) \\&\quad + ({\bar{c}}_4+{\tilde{c}}_4) \xi _4^{\frac{2l_4}{l_4}} \le \frac{1}{2} \sum _{i=1}^{3} \xi _i^{\frac{2l_4}{l_i}}+{\hat{c}}_4 \xi _4^{\frac{2l_4}{l_4}}, \end{aligned} \end{aligned}$$
(39)

where \(c={\frac{l_4-\tau }{l_4}}, d=\frac{l_4+\tau }{l_4}, \frac{d}{c+d}\beta ^{-\frac{c}{d}} ({\bar{c}}_4+{\tilde{c}}_4)= \frac{1}{2}\), \( {\hat{c}}_4 \) is a constant.

Table 1 The parameters of a vehicle
Full size table
Table 2 The parameters of the homogeneous controller
Full size table

Substituting Eq. (34) and Eq. (39 )into Eq. (32) obtains

$$\begin{aligned} \begin{aligned} {\dot{V}}_4&\le -2 \sum _{j=1}^{3} \xi _j^{\frac{2l_4}{l_j}}+\frac{1}{2}\xi _{3}^{\frac{2l_4}{l_{3}}} +c_4\xi _3^{\frac{2l_4}{l_4}}+\xi _4^{\frac{2l_4-\tau }{l_4}-1}z_{5}\\&\quad ~~~~+\frac{1}{2} \sum _{l=1}^{3} \xi _l^{\frac{2l_4}{l_l}}+{\hat{c}}_4 \xi _4^{\frac{2l_4}{l_4}}\\&\le -2 \sum _{j=1}^{3} \xi _j^{\frac{2l_4}{l_j}}+\sum _{i=1}^{3} \xi _i^{\frac{2l_4}{l_i}}+\xi _4^{\frac{2l_4-\tau }{l_4}-1}z_{5}\\&\quad ~~~~+(c_n+{\hat{c}}_4) \xi _4^{\frac{2l_4-\tau }{l_4}-1} \xi _4^{\frac{2l_4+\tau }{l_4}}\\&\quad =-\sum _{j=1}^{3} \xi _j^{\frac{2l_4}{l_j}}+\xi _4^{\frac{2l_4-\tau }{l_4}-1} \left( z_{5}+(c_4+{\hat{c}}_4) \xi _4^{\frac{l_5}{l_4}}\right) . \end{aligned} \end{aligned}$$
(40)

According to the aforementioned virtual controllers, there exists

$$\begin{aligned} z_{5}^{*}=-\gamma _4 \xi _4^{\frac{l_5}{l_4}}=-\left( 1+c_4+{\hat{c}}_4\right) \xi _4^{\frac{l_5}{l_4}}. \end{aligned}$$
(41)

Then,

$$\begin{aligned} \begin{aligned} {\dot{V}}_4&\le - \sum _{j=1}^{3} \xi _j^{\frac{2l_4}{l_j}}+\xi _4^{\frac{2l_4-\tau }{l_4}-1} \left( z_{5}- z_{5}^{*}- \xi _4^{\frac{l_5}{l_4}}\right) \\&\quad = - \sum _{j=1}^{3} \xi _j^{\frac{2l_4}{l_j}}+\xi _4^{\frac{2l_4-\tau }{l_4}-1} \left( z_{5}- z_{5}^{*}\right) \\&\qquad - \xi _4^{\frac{2l_4-\tau }{l_4}-1} - \xi _4^{\frac{l_5}{l_4}}\\&\quad =- \sum _{j=1}^{4} \xi _j^{\frac{2l_4}{l_j}}+\xi _4^{\frac{2l_4-\tau }{l_4}-1} \left( z_{5}- z_{5}^{*}\right) . \end{aligned} \end{aligned}$$
(42)

Therefore, Lyapunov function \(V_4\) holds at step 4.

We design the state feedback controller as

$$\begin{aligned} u=z_5^{*}=-\gamma _4 \xi _4^{\frac{l_4+\tau }{l_4}}. \end{aligned}$$
(43)

It is obvious that

$$\begin{aligned} {\dot{V}}_4 \le -\sum _{j=1}^{4} \xi _j^\frac{2l_4}{l_j} <0 \end{aligned}$$
(44)

with this designed controller, i.e., system (14) can be globally asymptotically stabilized by the controller (25) or (43).

Proof ends.

4 Simulation and HIL test analysis

4.1 Numerical simulation

In this section, the designed controller is simulated compared with a sliding mode controller for verifying effectiveness. In the numerical simulation, two kinds of disturbances, a constant lateral offset 1 m and \(\sin (2\pi t)/\left( 1+t^3\right) \) m, are applied to the system separately. Two vehicle speeds, 40 km/h and 80 km/h are selected for the simulation. The vehicle parameters are shown in Table 1. The parameters used in the designed homogeneous controller are shown in Table 2. Next, we analyze the simulation results as two groups according to two kinds of disturbances.

Fig. 3
figure 3

The yaw rate with different controllers suffering 1m lateral offset disturbance under 40 km/h

Full size image
Fig. 4
figure 4

The yaw rate with different controllers suffering 1m lateral offset disturbance under 80 km/h

Full size image

(1) Suffering 1m lateral offset disturbance under different vehicle speeds

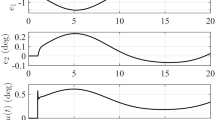
Figures 3 and 4 are the yaw rates under 40 km/h and 80 km/h with two controllers, respectively. Figures 5 and 6 are the lateral offsets under 40 km/h and 80 km/h with two controllers, respectively. And Figs. 7 and 8 are the controller outputs under 40 km/h and 80 km/h, respectively. From which one obtains that the designed homogeneous controller has better effectiveness than the sliding mode controller for yaw rate and lateral offset with smaller controller output. In detail, Figs. 3 and 4 show that the designed homogeneous controller and sliding mode controller can both stabilize the yaw rate within 2 sec. But the homogeneous controller has smaller oscillations than the sliding mode controller. Figures 5 and 6 especially show that the homogeneous controller has advantage for lateral offset compared with the sliding mode controller. The lateral offset is stabilized to zero within 1.5 sec and has very small oscillations with the homogeneous controller. But the lateral offset is stabilized to zero within 2.5 sec and has a dramatic change which is dangerous for a vehicle with the sliding mode controller. As shown in Figs. 7 and 8, the homogeneous controller has a smoother output and stronger robustness than the sliding mode controller.

Fig. 5
figure 5

The lateral offset with different controllers suffering 1m lateral offset disturbance under 40 km/h

Full size image
Fig. 6
figure 6

The lateral offset with different controllers suffering 1m lateral offset disturbance under 80 km/h

Full size image
Fig. 7
figure 7

The outputs of different controllers suffering 1m lateral offset disturbance under 40 km/h

Full size image
Fig. 8
figure 8

The outputs of different controllers suffering 1m lateral offset disturbance under 80 km/h

Full size image

(2) Suffering \(\sin (2\pi t)/\left( 1+t^3\right) \) m lateral offset disturbance under different vehicle speeds

Figures 9 and 10 are the yaw rates under 40 km/h and 80 km/h with two controllers, respectively. Figures 11 and 12 are the lateral offsets under 40 km/h and 80 km/h with two controllers, respectively. And Figs. 13 and 14 are the controller outputs under 40 km/h and 80 km/h, respectively. From which one obtains that the simulation results are similar to the results under the constant lateral offset. The designed homogeneous controller still shows its advantage compared with the sliding mode controller for the yaw rate and lateral offset under different vehicle speeds. Further speaking, Figs. 9 and 10 show that the designed homogeneous controller stabilizes the yaw rate to zero within 2 sec under different vehicle speeds, and the sliding mode controller needs about 3 sec to stabilize the yaw rate to zero. Figures 11 and 12 show that the lateral offset is attenuated rapidly to zero within 2 sec with the homogeneous controller. But the lateral offset has a violent oscillation with the sliding mode controller and tends to zero after 3 sec. Figures 13 and 14 show that the designed homogeneous controller still has stronger robustness than the sliding mode controller and just outputs a smaller steering wheel angle to keep the vehicle running along the desired lane.

Fig. 9
figure 9

The yaw rate with different controllers suffering \(\sin (2\pi t)/\left( 1+t^3\right) \) m lateral offset disturbance under 40 km/h

Full size image
Fig. 10
figure 10

The yaw rate with different controllers suffering \(\sin (2\pi t)/\left( 1+t^3\right) \) m lateral offset disturbance under 80 km/h

Full size image
Fig. 11
figure 11

The lateral offset with different controllers suffering \(\sin (2\pi t)/\left( 1+t^3\right) \) m lateral offset disturbance under 40 km/h

Full size image
Fig. 12
figure 12

The lateral offset with different controllers suffering \(\sin (2\pi t)/\left( 1+t^3\right) \) m lateral offset disturbance under 80 km/h

Full size image
Fig. 13
figure 13

The outputs of different controllers suffering \(\sin (2\pi t)/\left( 1+t^3\right) \) m lateral offset disturbance under 40 km/h

Full size image
Fig. 14
figure 14

The outputs of different controllers suffering \(\sin (2\pi t)/\left( 1+t^3\right) \) m lateral offset disturbance under 80 km/h

Full size image
Fig. 15
figure 15

The hardware-in-loop test system

Full size image
Fig. 16
figure 16

The lateral offset with different controllers under 40 km/h

Full size image
Fig. 17
figure 17

The yaw rate with different controllers under 40 km/h

Full size image

4.2 Hardware-in-the-loop test

To further verify the effectiveness of the designed homogeneous domination control method for practical engineering, the hardware-in-the-loop (HIL) test is carried out. The HIL simulation system is composed of a driversell car designed by ourselves, MicroAutoBox, Lenovo Legion laptop (CPU Intel i7-11800H, GPU NVIDIA RTX3060, RAM DDR4 2666), and Autoware software. We still compare the designed homogeneous domination controller with the sliding mode controller. In the HIL test, the driverless car shown in Fig. 15a runs along a straight line lane. MicroAutoBox shown in Fig. 15b acquires the necessary signals from the driverless car and outputs control orders to the steering motor and four in-wheel motors according to the designed control algorithm. The interface of the HIL test is shown in Fig. 15c. Figures 16, 17, and 18 are the test results under 40 km/h. From Fig. 16, one obtains that the homogeneous controller responds when the lateral offset is up to 0.05 m at 2.3 sec. The lateral offset is corrected to −0.02 m by the homogeneous controller, then tends to zero after 6.4 sec. The sliding mode controller responds when the lateral offset is up to 0.08 m at 2.4 sec. The lateral offset is corrected to −0.035m by the sliding mode controller, then tends to zero after 6.8 sec. Figure 17 shows that the yaw rate is limited to −0.1 rad/s at 2.3 sec and corrected to the desired value rapidly by the homogeneous controller, then tends to zero after 4.7 sec. But the yaw rate just is limited to −0.15 rad/s at 2.4 second corrected to a max of 0.04 rad/s by the sliding mode controller which deviates from the desired value larger than the homogeneous controller. Figure 18 shows the steering wheel angles under two controllers. We can find that the steering wheel angle is smaller under the homogeneous controller than the sliding mode controller, i.e., the homogeneous controller can improve the handling stability and need less energy costs. Figures 19, 20, and 21 are the test results under 80 km/h. These results are similar to the results under 40 km/h. These test results verify that the homogeneous domination controller method has better effectiveness than the sliding mode control method for practical engineering.

Remark 2

The HIL test results show that the lane-keeping performance with the proposed method meets the requirement of China National Standards GB/T 39323-2020 Performance Requirement and Testing Method for Lane Keeping Assist(LKA) System of Passenger Cars, in which the lateral offset should be within 0.4 m, and the lateral acceleration should be within 3 \(\mathrm{{m/s^2}}\). We use the lateral offset and yaw rate to evaluate the proposed method. The relationship between lateral acceleration and yaw rate is \(\ddot{\varphi }=v_x\cdot {\dot{\varphi }}\).

Fig. 18
figure 18

The steering wheel angle with different controllers under 40 km/h

Full size image
Fig. 19
figure 19

The lateral offset with different controllers under 80 km/h

Full size image
Fig. 20
figure 20

The yaw rate with different controllers under 80 km/h

Full size image
Fig. 21
figure 21

The steering wheel angle with different controllers under 80 km/h

Full size image

5 Conclusion

In this paper, a 2DOF lane-keeping trajectory tracking error model is first built. Then, the state equations of the lane-keeping control system are obtained based on the dynamic model. A lane-keeping control method is proposed based on the homogeneous domination control theory. In the method, a homogeneous domination state feedback controller is designed. By the Lyapunov method, the designed controller is proved that it can globally asymptotically stabilize the system. The homogeneous domination method does not require the nonlinear terms of the control system to meet the strict linear growth condition which is the common assumption in the most of existing control methods. Numerical simulation results show that the homogeneous controller is better than the sliding mode controller on lateral offset, yaw rate, and controller output. HIL test is also carried out to verify the effectiveness of the designed homogeneous state feedback controller in practical engineering. The results also show that the homogeneous domination method has strong robustness, fast response, and low energy costs. These features are more suitable for the lane-keeping system.