Stochastic investigation of the input uncertainty effects on the dynamic responses of constrained pipelines conveying fluids

Abstract

The dynamic response of a cantilevered pipe conveying fluid is investigated when several input parameters of the system are introduced to uncertainty. After the nonlinear equations of motions are derived, five input parameters are subject to a $\pm \,5\%$ uncertainty with a uniform distribution. First, a parametric study is performed by varying each parameter individually. Then, the Pearson correlation coefficients are calculated and discussed before a full Monte Carlo simulation is performed, and the histograms of results are investigated. It is evident that the outer diameter of the pipe has the largest effect on the maximum displacement of the pipe in the post-flutter regime. Chaotic behavior is exhibited when motion-limiting constraints are present in the system, so the system is tested with motion-limiting constraints as well. Monte Carlo simulation is performed, and bivariate diagrams are plotted to investigate how uncertainty affects the maximum displacement and periodicity of the oscillations together. Again, the outer diameter of the pipe is seen to be the most sensitive parameter to uncertainty when motion-limiting constraints are present. However, the parameters besides the outer diameter exhibit more sensitivity at high flow speeds. The results indicate that it is necessary to control the uncertainty introduced in the outer diameter to achieve expected dynamical responses at low flow speeds, but the uncertainty in all parameters must be controlled at higher flow speeds when motion-limiting constraints are present to achieve the expected behavior and chaotic responses.

1 Introduction

Complete understanding of the dynamic response is imperative to the design and lifetime of every engineered system. If the dynamic response is not properly characterized, the resulting behavior of the system may behave unexpectedly and damage the system. This is particularly true when the dynamics of the system exhibit nonlinear behavior. Therefore, nonlinear dynamics have been studied for decades and is still heavily researched today [1,2,3,4,5,6,7,8,9,10,11]. The research of nonlinear dynamics is true for all applications including cylindrical structures with internal flow. Ashley and Haviland [12] were the first to spark interest in pipeline conveying fluid systems in 1950. They studied the effects of external forcing from crosswinds on aboveground simply supported pipelines and found that the internal fluid flow caused damping of the system which led to a constant pipe frequency over time. Niordson and Housner [13, 14] were able to derive the equations of motion of the simply supported pipeline and found that buckling could occur at sufficiently high internal flow speeds. Although Long [15] did not test the cantilevered pipeline system at sufficient flow speeds to prove the loss of stability, it was proven that the internal fluid flow induced damping in the system that reduced the frequency of the pipe over time, unlike the simply supported systems.

The most influential researchers on the subject are Paidoussis and his collaborators [2,3,4, 16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]. Gregory and Paidoussis [16] were the first to analytically and experimentally prove that cantilevered pipeline conveying fluid systems lose stability via Hopf bifurcation at critical flow speeds. Interestingly, chaotic oscillations were found in several experiments and calculations when motion-limiting devices were implemented to the system [2, 4, 19, 34,35,36]. A trilinear spring was used to model the motion-limiting constraints in a study performed by Paidoussis and Semler [4]. Several bifurcations were observed in these experiments including chaotic oscillations. Installation error or wear from extended use could cause the constraints to be asymmetrical. Therefore, Wang et al. [35] used the same trilinear spring model as Paidoussis and Semler [4], but the motion-limiting constraints were not placed symmetrically around the pipe. They found that the constraint gap size, stiffness, and symmetric offset have great effects on the behavior of the system. For example, chaos and other nonlinear responses may disappear at very small constraint stiffnesses and gaps.

Like Wang et al. [35] noted that systems in real-world applications are slightly different from their design. This can be due to wear and tear from extended use, fabrication or installation error, or even slight changes in material properties. Therefore, the use of uncertainty quantification methods is necessary in the design process. There have been numerous mathematical models developed to quantify the uncertainty in a system’s performance. Ceballes and Abdelkefi [37] discussed many of the uncertainty quantification methods used in this work and applied them to the uncertainty quantification of carbon nanotubes. Generally, uncertainty quantification analysis is performed by changing the nominal value of several input or environment parameters and comparing the output of the system to the nominal output. It comes as no surprise that a specific output of the system is needed to be calculated. The chosen output of the system is commonly referred to as the quantity of interest (QOI). There can be multiple QOIs for a single uncertainty quantification analysis and can be the displacement of the system, stress induced in the system, or temperature for example.

In the large number of studies performed regarding pipeline conveying fluid systems, there is a distinct few uncertainty quantification studies on the system. Guo et al. [38] used an artificial neural network to investigate the uncertainty of the natural frequencies of a pipe conveying fluid system with a functionally graded material when the diameter of the functionally graded material pipe is varied. An uncertainty quantification analysis was performed by Ritto et al. [39] on the simply supported pipeline conveying fluid system proposed by Paidoussis and Issid [17]. Ritto et al. [39] tested how the uncertainties of the assumptions made in the system could affect the flutter for different flow speeds. The study showed that the system exhibited random responses to different levels of uncertainty and investigated the reliability of the system for different flow speeds. To the authors’ best knowledge, there have not been many uncertainty quantification and sensitivity analysis studies regarding the cantilevered pipe conveying fluid systems.

A recent study from Alvis et al. [40] performed uncertainty quantification analyses on the cantilevered pipeline conveying fluid system. The QOI of this study was the flow speed at which stability is lost—also referred to as the flow speed at the onset of instability. It was found that the flow speed at the onset of instability was most affected by uncertainty introduced into the outer diameter of the pipe. The density of the pipe showed sensitivity to uncertainty, but the effect on the onset of bifurcation was negligible when the value of the outer diameter was away from the nominal value. This study expands on the previous work and focuses on the dynamical responses under input uncertainty. A cantilevered pipeline conveying fluid system is investigated both with and without motion-limiting constraints. Therefore, the QOI in this study is the maximum displacement of the system when motion-limiting constraints are not present. There are two QOIs for the second part of the study when motion-limiting constraints are present, namely the maximum displacement of the system and the presence of chaos in the system.

The full nonlinear equations of motion and the parameters of the nominal system are defined in Sect. 2. Then, Sect. 3 establishes the uncertainty quantification and sensitivity analysis methods used in this study and describes procedure of each method in detail. The maximum displacement of the cantilevered pipeline conveying fluid without the addition of motion-limiting constraints is investigated and discussed in Sect. 4. First, the parametric study is performed over the entire flow speed range to show the entire behavior of the pipeline conveying fluid system. Then, five flow speeds are selected and studied more in depth by performing the parametric study with more points of uncertainty calculated. The Monte Carlo simulation [41] is then carried out after ensuring that the number of iterations is high enough to reach an accurate solution. The Pearson correlation coefficients [42] are calculated, and the histograms of the simulation are investigated. Section 5 discusses the displacement and stability of the pipeline under uncertainty when the motion-limiting constraints are included in the system. Many of the same uncertainty quantification methods are employed including the parametric study of the entire flow speed. The results from Monte Carlo simulation are presented in bivariate diagrams so that the effects of the uncertainty on the displacement and stability of the system can be investigated together. The motion-limiting constraints are then introduced into uncertainty compared to the results from the pipe parameters in Sect. 6. Finally, summary and conclusions are presented in Sect. 7.

2 Modeling and problem formulation of the pipeline conveying fluid

2.1 Equation of motion derivation and discretization

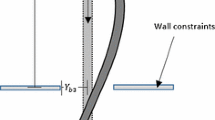
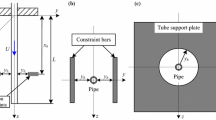
The system under investigation is a cantilevered pipeline hanging vertically with length $L$, outer diameter ${d}_{\mathrm{o}}$, and inner diameter ${d}_{\mathrm{i}}$. The system will lose stability and begin to oscillate once the velocity of the fluid conveyed inside the pipe, $U$, reaches a critical flow speed. To prevent these oscillations from reaching a large amplitude, motion-limiting constraints are implemented into the system, as indicated in the schematic of the pipeline system shown in Fig. 1. In this schematic, $S$ depicts the coordinate along the centerline of the pipe, ${S}_{\mathrm{c}}$ represents the location of the motion-limiting constraints down the $X$-axis. The constraints are set a symmetric distance away from the pipe, ${Y}_{\mathrm{c}}$; and the pipe oscillates solely in the $Y$-direction.

Fig. 1

Schematic of the pipeline conveying fluid under consideration

The modeling of this system has been extensively investigated and compared to experimental results [2]. Due to this, the modeling in this investigation will only be briefly explained. Following the work of Semler et al. [34], the equation of motion is derived as seen in equation (1) where ${Y}^{\prime}$ represents the derivative with respect to the position of the beam’s centerline X and $\dot{Y}$ represents the derivative with respect to time, t. Also, $EI$ is the structural rigidity of the pipe, $M$ represents the mass per unit length of the fluid, η denotes the Kelvin–Voigt damping coefficient, and $g$ is the gravitational constant.

$$ \begin{aligned} & EI\left( {Y^{{{\text{iv}}}} + \eta \dot{Y}^{{{\text{iv}}}} } \right) + \left( {m + M} \right)gY^{\prime } + 2MU\dot{Y}^{\prime } + MU^{2} Y^{\prime \prime } - \left( {m + M} \right)g\left( {L - S} \right)Y^{\prime \prime } \\ & \quad + \left( {m + M} \right)\ddot{Y} + 2MU\dot{Y}^{\prime } Y^{\prime 2} + Y^{\prime \prime } Y^{\prime 2} \left[ {MU^{2} - \frac{3}{2}\left( {m + M} \right)g\left( {L - S} \right)} \right] + \frac{1}{2}g\left( {m + M} \right)Y^{\prime 3} \\ & \quad + EI\left( {Y^{{{\text{iv}}}} Y^{\prime 2} + 4Y^{\prime\prime\prime}Y^{\prime \prime } Y^{\prime } + Y^{\prime \prime 3} } \right) - Y^{\prime\prime}\left[ {\int_{s}^{L} {2MUY^{\prime } \dot{Y}^{\prime } + MU^{2} Y^{\prime } Y^{\prime \prime } + \int_{0}^{s} {\left( {m + M} \right)\left( {\dot{Y}^{\prime 2} + Y^{\prime } \ddot{Y}^{\prime } } \right){\text{d}}S} \;{\text{d}}S} } \right] \\ & \quad + Y^{\prime } \int_{0}^{s} {\left( {m + M} \right)\left( {\dot{Y}^{\prime 2} + Y^{\prime } \ddot{Y}^{\prime } } \right){\text{d}}S} + F\left( S \right)\left( {S - S_{{\text{c}}} } \right) = 0 \\ \end{aligned} $$

(1)

In Eq. (1), $F$ represents the force imparted on the system from the motion-limiting constraints. The representation of the forcing chosen by Paidoussis and Semler [4] followed a modified trilinear spring model and can be expressed as:

$$ F\left( Y \right) = k_{3} \left\{ {Y - 0.5\left( {\left| {Y + Y_{{\text{c}}} } \right| - \left| {Y - Y_{{\text{c}}} } \right|} \right)} \right\}^{3} $$

(2)

Semler and his collaborators nondimensionalized the equation of motion after deriving the nonlinear equations of motion [34]. This allows for more straightforward calculations of the complex equations of motion, but because this study investigates the uncertainty of the input parameters, it is best to keep the equation of motion in its dimensional form. If the results are analyzed while nondimensionalized, the results would be skewed by the nondimensionalization of the system and need to be converted back to the dimensional values.

To solve the system, the equation of motion is discretized using the Galerkin method by assuming $Y\left(S,t\right)$ is equal to the infinite sum of the cantilevered beam eigenfunction ${\phi }_{i}\left(S\right)$ multiplied by the general coordinate ${q}_{i}\left(t\right)$, as shown in Eq. (3) where $N$ represents the number of modes of the cantilever beam eigenfunction.

$$ Y\left( {S,t} \right) = \sum\limits_{i = 1}^{N} {\phi_{i} \left( S \right)q_{i} \left( t \right)} $$

(3)

Equation (3) is substituted into Eq. (1) and multiplied by ${\phi }_{i}\left(S\right)$ and integrated from $0$ to $L$. Following the work of Taylor et al. [36], the nonlinear reduced-order model is expressed so that each constant can be related to a physical meaning as seen in Eq. (4) where all coefficients are defined in the Appendix.

$$ \begin{aligned} & \ddot{q}_{j} + \left[ {C_{ij} + U\left( {Cu} \right)_{ij} } \right]\dot{q}_{j} + \left[ {K_{ij} + U^{2} \left( {Ku} \right)_{ij} } \right]q_{j} + \left[ {M_{ijkl} } \right]\dot{q}_{j} \dot{q}_{k} q_{l} \\ & \quad + \left[ {U\left( N \right)_{ijkl} } \right]\dot{q}_{j} q_{k} q_{l} + \left[ {P_{ijkl} + U^{2} \left( {Pu} \right)_{ijkl} } \right]q_{j} q_{k} q_{l} + F\left( {\sum\limits_{z = 1}^{N} {\phi_{z} \left( {S_{c} } \right)q_{z} \left( t \right)} } \right)\phi_{i} \left( {S_{{\text{c}}} } \right) = 0 \\ \end{aligned} $$

(4)

2.2 Nominal system parameter definitions and modeling verification

After determining the governing equation of motion of the system, the nominal system’s parameters can be defined. Uncertainty is introduced into the following five pipe parameters, namely the length of the pipe $L$, the outer diameter ${d}_{\mathrm{o}}$, inner diameter ${d}_{\mathrm{i}}$, modulus of elasticity $E$, and density $\rho$. The nominal configuration follows the experimental system of Paidoussis and Moon and has been validated many times [2]. The pipeline itself is made of a casted elastomer that allows the system to lose stability at a lower flow speed. The pipeline parameters are listed in Table 1.

Table 1 Nominal pipeline parameters

To solve the nonlinear reduced-order model, it is first necessary to find the number of necessary modes of the cantilevered beam eigenfunction used in the Galerkin discretization. Using a linear eigenvalue analysis, Paidoussis et al. [20] found four modes in the Galerkin discretization to be necessary to yield an accurate result. Therefore, four modes are used in the estimation of the displacement of the pipeline’s dynamics. Like the previous uncertainty quantification study performed by Alvis et al. [40], the mass of the internal fluid is assumed to be constant. As the internal diameter is varied, the volume of the fluid per unit length would change as well which could potentially change the physics of the system. However, it is assumed that this small variation would not have profound effects on the output of the system. This is especially possible if there are any uncertainty introduced into the density of the fluid. This uncertainty in the density of the fluid could offset any change in the system output from the variance of the mass of the fluid by changing the internal diameter of the pipe, so for simplicity, the mass of the internal fluid is held constant and only structural parameters are affected in this study. The location, gap size, and stiffness of the constraints are again chosen from the work of Paidoussis and Semler [4] and are listed in Table 2.

Table 2 Constraint parameters

When the system is analyzed with the defined parameters, the peaks from the time histories at each flow speed can be plotted into a bifurcation diagram which shows the behavior and motion of the system. Bifurcation diagrams plot the peak-to-peak values of the time histories at each flow speed. Therefore, if only one point is plotted, the system is stable at its equilibrium, and if multiple points are plotted the pipe is oscillating. Two points plotted signify a 1-period oscillation, and many points signify an aperiodic movement.

The bifurcation diagram for the nominal design with and without motion-limiting constraints is plotted in Fig. 2. The pipeline system loses stability and begins to oscillate at $7.43\,\mathrm{m}/\mathrm{s}$. In the case without constraints, in Fig. 2a, the pipeline system oscillates periodically for all flow speeds. However, in Fig. 2b, when motion-limiting constraints are present, the displacement of the pipe is limited, and multiple aperiodic responses can be observed. Eventually, the pipe sticks in the constraint and no longer oscillates at a certain flow speed. The behavior of this system is characterized at the point of contact where Paidoussis and Semler characterized the system at the tip of the pipe [4]. However, Taylor et al. [36] suggested that characterizing the system at the point of contact yields more accurate observations. This model has been validated with results from several research studies [35, 36]. As mentioned, the purpose of this work is to investigate the dynamic response of the system when uncertainty is introduced into the system. Therefore, the maximum pipe displacement is investigated in the system without constraints, and the maximum pipe displacement and the presence of aperiodic behaviors are studied in the system with constraints present.

Fig. 2

Bifurcation diagrams when system: a does not include motion-limiting constraints and b does include motion-limiting constraints

3 Uncertainty quantification and sensitivity analysis methods

This study employs the parametric study, Monte Carlo simulations, and Pearson correlation coefficients. The parametric study is useful for researchers to identify which parameter in a given system is the most influential to uncertainty. In this method, each parameter in the system is varied over the selected uncertainty range individually which allows for a smaller number of iterations when compared to the stochastic model where all parameters are varied at the same time. However, because the parametric study investigates the parameters individually, the effects of the parameters interacting with each other cannot be investigated. In the parametric study, the output of the system will be plotted against the change of each parameter due to uncertainty. A slope of zero indicates that a parameter is insensitive to the added uncertainty, whereas a more sensitive parameter will have a higher slope. It can be assumed that the parameters that show very low sensitivity to uncertainty will have a negligible effect on the system when all parameters are varied together. By neglecting insensitive parameters, a great deal of time can be saved in the full stochastic simulation.

The Monte Carlo simulation is employed by randomly selecting a value for each parameter in a given uncertainty range within a selected uncertainty distribution. Then, the dynamic response of the system is calculated, and the entire process is iterated several times. This study focuses on a uniform distribution, but many distributions can be implemented as shown in the study performed in [37]. The shape of the distribution can have significant impacts on the performance of the system. A Gaussian or normal distribution centered around the nominal case should obviously yield the most results centered around the nominal case, but distributions that have a broader input uncertainty range like the uniform distribution, or distributions that are not centered around the nominal case like the beta distribution may not yield results centered around the nominal case. The uniform distribution is chosen in this case because it shows how a broad uncertainty range affects the output of the system.

The number of iterations selected in stochastic models like the Monte Carlo simulation is very important to the solution’s accuracy. The law of large numbers first proved by Bernoulli and further explained by Poisson states that if an experiment is performed a large number of times, the average of all results will amount to the expected result [43]. If too few samples are selected, the behavior of the system may be mischaracterized. However, using too many iterations will yield an accurate result, but will have an immense computational cost and will only be a fraction, if any, more accurate than a solution yielded with fewer points. In this manner, a convergence analysis is needed to find the most accurate output while yielding a reasonable computational effort.

After the ideal number of iterations has been determined and the Monte Carlo simulation is performed, more analysis of the system can begin. One such analysis is the Pearson correlation coefficient which helps to determine the parameter sensitivity. The Pearson correlation coefficient is calculated by dividing the covariance of a pair of variables by the product of that pair’s standard deviation, as seen in Eq. (5), where ${r}_{xy}$ is the Pearson correlation coefficient between any independent and dependent variables $x$ and $y$, respectively [42]. The number of variables in the data set (which in this case is equal to the number of iterations chosen from the convergence analysis) is defined as $n$, and finally, $\overline{x }$ and $\overline{y }$ refer to the mean value of each data set.

$$ r_{xy} = \frac{{\sum\nolimits_{i = 1}^{n} {\left( {x_{i} - \overline{x}} \right)\left( {y_{i} - \overline{y}} \right)} }}{{\sqrt {\sum\nolimits_{i = 1}^{n} {\left( {x_{i} - \overline{x}} \right)^{2} } \sqrt {\sum\nolimits_{i = 1}^{n} {\left( {y_{i} - \overline{y}} \right)^{2} } } } }} $$

(5)

The value of $r$ ranges between $+\,1$ and $-\,1$ which indicates a complete correlation between the independent and dependent variables. The positive or negative sign of the Pearson correlation coefficient signifies the trend of the parameter under uncertainty. To clarify, a positive Pearson correlation coefficient indicates that as the value of a given parameter increases due to added uncertainty, the output of the system will also increase, whereas a negative slope indicates that as the value of a given parameter increases the output will decrease. There is no correlation between an input parameter and the output if the Pearson correlation coefficient is equal to $0$.

It is important to note that if the relationship between input and output is nonmonotonic, or does not strictly increase or decrease, cancellation effects can be present and decrease the value of $r$. Therefore, data that show nonlinear trends can falsely cause a parameter to appear insensitive according to the Pearson correlation coefficient. A way to visually check the correlation of an input parameter is to plot a scatter plot of the input parameter against the output of the system when all parameters are being varied. A more sensitive parameter will have the output results closely gathered, usually following the trends from the parametric study where the parameters are varied individually. An insensitive parameter will not follow the trends of the parametric study and will have a wide range of seemingly randomly placed points on the scatter plot [37].

Another important aspect of characterizing the results of the Monte Carlo study involves plotting a histogram of the QOI. The preferred distribution of the output histogram is where the majority of the results are closely gathered around the nominal output. This ensures that the system will behave as expected when uncertainties are introduced into the system. If the histogram shows the most likely outcome is away from the nominal designed case, the engineers designing the system can investigate how to decrease the input uncertainty to ensure that the system behaves as expected. In this study, an uncertainty range of $\pm \,5\%$ is used with a uniform distribution. This broad uncertainty range and distribution allows for a more complete understanding of how the system will behave when introduced to input uncertainty.

4 Dynamic response of pipeline conveying fluid without motion-limiting constraints under uncertainty

Understanding the dynamics of the system without external forcing/constraint will help to better understand the impacts the motion-limiting constraints impart on the system. Therefore, the system without motion-limiting constraints is analyzed first. The parameters are individually analyzed first. This gives insight into how sensitive the parameters are to input uncertainty regarding the onset of bifurcation as well as the dynamic response in the post-flutter regime. Then, all parameters are influenced by uncertainty simultaneously in a Monte Carlo simulation. The parameters’ correlation is investigated using scatter plots and Pearson correlation coefficients, and the output of the system is analyzed using histograms. Therefore, the dynamic response of the system under input uncertainty is investigated when the change in parameters interacts with each other, and the most sensitive parameter is identified.

4.1 Uncertainty analysis of individual parameters

First, the system is analyzed over the entire flow speed range when each parameter is varied individually, and the bifurcation diagrams are plotted. This way an understanding of how the input parameter affects the entire system’s response can be investigated. It would be impossible to perform an analysis over the entire flow speed range for the full Monte Carlo simulation due to the incredible computational time and memory needed for the high number of iterations needed. In the previous study performed by Alvis et al. [40], a range of flow speeds where the pipeline system loses stability is found from $6.76$ to $7.81\,\mathrm{m}/\mathrm{s}$. The bifurcation diagrams from the parametric study are shown in Fig. 3 where the bifurcation diagrams plotted in color represent the dynamics of the system when a parameter is introduced to uncertainty, and the bifurcation diagrams plotted in black represent the dynamics of the system at the maximum and minimum bifurcation points found in the previous study when all parameters are varied together [40].

Fig. 3

Bifurcation diagrams from the parametric study when varying: a ${d}_{o}$, b ${d}_{i}$, c $L$, d $E$, and e $\rho$

Interesting dynamical behaviors are immediately evident in Fig. 3. Two aspects of the bifurcation diagrams that bring insight into how uncertainty is affecting the system are the flow speed at which the system loses stability and the behavior of the displacement of the system in the post-flutter regime. Focusing on the flow speed at the onset of instability, it is clear that ${d}_{o}$ is the most sensitive parameter, followed by $\rho$, ${d}_{\mathrm{i}}$, and finally $L$ and $E$, which shows very little sensitivity to uncertainty. This can be seen from the range of the flow speeds at the onset of instability where a wider range indicates a more sensitive parameter, and a small range indicates an insensitive parameter. The onset of instability occurs in all plots of Fig. 3 between the maximum and minimum cases from the previous study [40]. This indicates that there must be an interaction between the parameters because the flow speed range at the onset of instability increases when all parameters are varied together. It is interesting that the ${d}_{\mathrm{o}}$ and $L$ parameters in Fig. 3a, c, respectively, are exhibiting nonmonotonic parameters. As the uncertainty introduced into the parameter is increased from $-\,5$ to $5\%$, the ${d}_{\mathrm{i}}$, $E$, and $\rho$ parameters show the flow speed at the onset of instability is either strictly increasing, in the case of ${d}_{\mathrm{i}}$ and $E$ in Fig. 3b, d, respectively, or strictly decreasing in the case of $\rho$ in Fig. 3e. This is not the case regarding ${d}_{\mathrm{o}}$ and $L$. When the value of ${d}_{\mathrm{o}}$ expands away from the nominal value, the flow speed at the onset of instability decreases compared to the nominal case. As the uncertainty increases in $L$ from $-\,5$ to $1.67\%$, the flow speed at the onset of instability increases. However, as the uncertainty increases further to $3.33\%$ the flow speed at the onset of instability begins to decrease. When the input uncertainty is increased to $+\,5\%$, the flow speed at the onset of instability is below that of the nominal case.

It is also interesting that a given parameter’s sensitivity to uncertainty for the onset of instability does not necessarily correlate with a sensitivity with the dynamic response of the system. For example, the onset of instability changes by a large margin when uncertainty is introduced into $\rho$, but the dynamical response hardly changes at higher flow speeds. This can be seen in Fig. 3e where the onset of instability ranges from $7.2$ to $7.8\,\mathrm{m}/\mathrm{s}$, but the displacements of the pipe quickly converge together as the flow speed increases. The dynamic response is also not affected much by the inclusion of uncertainty in ${d}_{\mathrm{i}}$ in Fig. 3d where again the displacements converge at higher flow velocities. This is in stark contrast to ${d}_{\mathrm{o}}$ in Fig. 3a where the flow speed at the onset of instability ranges from $7.11$ to $7.44\,\mathrm{m}/\mathrm{s}$, but the behavior of the displacement changes drastically from the different amount of uncertainty introduced into the system. The displacement for the higher input uncertainty of $3.33\%$ and $5\%$ extends past the displacement of the minimum case when all parameters are being varied together and eventually curves back down. The onset of bifurcation is almost equal for the input uncertainty of $-\,1.67\%$ and $0\%$, but the dynamic response is very different. For $-1.67\%$ input uncertainty, the displacement of the pipe increases very sharply once the system becomes unstable, whereas the displacement increases at a slower rate for the nominal case. This indicates that the response of the system can vary greatly depending on the system’s parameters even if the onset of instability occurs at the same flow speed.

The displacement of the pipeline system in Fig. 3c when uncertainty is introduced into $L$ also does not converge at higher flow speeds. At the final plotted flow speed of $9\,\mathrm{m}/\mathrm{s}$, the largest displacement is the case when $L$ is at $-\,5\%$ of the nominal critical flow speed. As the input uncertainty increases to $+\,5\%$, the displacement at a flow speed of $9\,\mathrm{m}/\mathrm{s}$ steadily decreases where the lowest displacement is for the case when $L$ is at $5\%$ of the nominal critical flow speed. This would make logical sense if the onset of instability was monotonic. The case that loses stability first would have the highest amplitude, and the case that loses stability last would have the lowest amplitude. However, this is clearly not the case in this instance. From this preliminary study, it can be assumed that the dynamical response of the system is most sensitive to change in the ${d}_{\mathrm{o}}$. The next sensitive parameter is $L$, but the change in displacement is not very large. The displacements of these two parameters in Fig. 3a, c change the most throughout the uncertainty range, whereas the other parameters seem to converge as the flow speed increases.

As previously mentioned, it is not possible to complete the Monte Carlo simulation over the entire flow speed range due to the high number of samples to reach an accurate result and the large computational memory and time needed to solve the response at each flow speed. Therefore, five flow speeds over a wide range have been selected to be investigated and can be seen in Table 3. For clarity, the selected flow speeds will be referred to as the percent difference from the onset of bifurcation at the nominal case. The flow speeds have been chosen over a wide range to give a good representation of how the system is behaving throughout the flow speed range. In the case of $-\,5\%$ of the nominal critical flow speed when the parameters are varying individually, the system has not reached the onset of instability when uncertainty is present which can be seen in Fig. 3. In the case of $-\,3\%$ of the nominal critical flow speed, the only parameter that has reached the onset of instability is ${d}_{\mathrm{o}}$. These flow speeds will be important to investigate when all parameters vary together because it will show how parameter interaction will further decrease the onset of instability. At $3\%$, $5\%$, and $10\%$ of the nominal critical flow speed, all parameters have resulted in an unstable system. By investigating these flow speeds, an understanding of how uncertainty affects the system at higher flow speeds can be achieved.

Table 3 Investigated flow speeds and the corresponding percent difference from the nominal onset of instability

The parametric studies at the selected flow speeds are plotted in Fig. 4. It is clear that the system is stable for all parameters under the entire uncertainty range at a flow speed of $-\,5\%$, as presented in Fig. 4a. The change in displacement is negligible and is essentially zero. When increasing to a flow speed of $-\,3\%$, the only parameter that causes the system to become unstable is ${d}_{\mathrm{o}}$, and the level of uncertainty must be quite high to cause this instability. This indicates that ${d}_{\mathrm{o}}$ is the most sensitive parameter to the onset of instability. The parametric studies for the flow speeds of $3\%$, $5\%$, and $10\%$ in Fig. 4c–e are very similar in shape. In each graph, the maximum displacement of the system is most sensitive to uncertainty in ${d}_{\mathrm{o}}$. This can be seen clearly because the displacement changes the most from the nominal case and has the steepest slope in ${d}_{\mathrm{o}}$. It is difficult to judge which parameter is the most sensitive to uncertainty after ${d}_{\mathrm{o}}$. $\rho$ appears to have the biggest slope of the remaining parameters, but it is close to that of ${d}_{\mathrm{i}}$ and $E$. More investigations will be needed to find which parameters are more sensitive, particularly when the parameters are varying together.

Fig. 4

Parametric study at the flow speeds of: a $-\,5\%$, b $-\,3\%$, c 3 $\%$, d 5%, and e 10 $\%$ of the nominal critical flow speed

It is interesting to note that many of the parameters are not exhibiting linear behavior. This indicates that each parameter’s sensitivity to uncertainty is changing over time, and the effects of uncertainty on the pipeline conveying fluid are very complicated. The nonlinear curves in the parametric study make it difficult for engineers to estimate how the system will behave at higher uncertainties. The behavior is similar in the three cases above the nominal critical flow speed. Continuing to investigate Fig. 4c–e, the displacement of the pipe increases as uncertainty in ${d}_{\mathrm{o}}$ and $L$ increases. It is clear that the displacement when ${d}_{\mathrm{o}}$ is influenced by uncertainty is much higher than that of $L$, but this nonlinear behavior is present in both parameters and could lead to interesting interacting effects. This could make the average output of the system under uncertainty be much higher than that of the nominal case, which is unwanted in design. It is interesting to note, however, that the nonlinear behavior lessens as the flow speed increases. The nonlinear effects are clearly present at a flow speed of 3% of the nominal critical flow speed in Fig. 4c, but the change in slope is less at the flow speed of 5% of the nominal critical flow speed in Fig. 4d. This trend continues and most of the slopes are constant at a flow speed of 10% except that ${d}_{\mathrm{o}}$ has a large change of direction at around $0.5\%$ uncertainty, but the slope at higher uncertainty levels is much more constant than at the previous flow speeds.

The sensitivity in each parameter is also decreasing as the flow speed increases. This can be seen in the relative change in displacement. At the flow speed of $3\%$ in Fig. 4c, the nominal displacement is $0.022\,\mathrm{m}$, and the maximum displacement for ${d}_{\mathrm{o}}$ is $0.042\,\mathrm{m}$ for a difference of $0.02\,\mathrm{m}$. At the flow speed of $10\%$ in Fig. 4e, the nominal displacement is $0.037\,\mathrm{m}$, and the maximum displacement is $0.051\,\mathrm{m}$ for a difference of $0.014\,\mathrm{m}$. When investigating $\rho$ specifically, the minimum displacement at a flow speed of $3\%$ is $0.012\,\mathrm{m}$ and the maximum displacement is $0.029\,\mathrm{m}$ for a difference of $0.017\,\mathrm{m}$. At the flow speed of $10\%$, the minimum and maximum displacement values for $\rho$ are $0.035\,\mathrm{m}$ and $0.38\,\mathrm{m}$. This is only a difference of $0.003\,\mathrm{m}$. This indicates that as the flow speed increases after becoming unstable the displacement of the system begins to converge, and the introduction of uncertainty into the system will not affect the dynamic response as much as earlier in the system.

After understanding how input uncertainty affects the parameters on their own, analysis of the system where each parameter varies at the same time can be investigated. As mentioned earlier, the range of input uncertainty will be $\pm \,5\%$ with a uniform distribution. The value for each parameter will be randomly picked within this range with a uniform probability distribution. It is necessary to analyze the system with as many randomly selected values as needed to reach an accurate result. To find this necessary number of iterations, the simulation is run multiple times where each subsequent run has more iterations than the last. The number of iterations needed is assumed to be accurate once the average result converges to a single value. Figure 5 shows the results of the convergence analysis where Fig. 5a shows all analyses together and Fig. 5b shows just the convergence analysis of $3\%$ for clarification. Inspecting this figure, it is clear that convergence is reached relatively quickly for all cases. However, by inspecting the zoomed-in analysis for $3\%$, it is clear that 10,012 iterations are necessary to reach an accurate result at a reasonable computation time.

Fig. 5

Convergence analysis for the system without constraints where a shows all convergence analysis studies and b shows a close up of $3\%$ nominal flow speed

4.2 Correlation of parameters uncertainty response to total output

Once the analysis is performed with 10,012 randomly selected at each flow speed, the output of the system can be plotted against the value of an individual parameter in a scatter plot. These scatter plots can help determine which parameters are most sensitive, and the Pearson correlation coefficients can be calculated. To reiterate, a scatter plot that has most of the points closely plotted together signifies a parameter that is sensitive to the uncertainty introduced into the system. On the other hand, a scatter plot with a wide range of randomly plotted points indicates a parameter that is not sensitive, and uncertainty introduced into these parameters does not influence the output of the system. Because each parameter is varied individually in the parametric study, the effects of the parameters interacting with each other cannot be known, but the effects of the parameters interacting with each other can better be seen in the scatter plots when the parametric study results are plotted over the results of the Monte Carlo study. A parameter is highly sensitive to uncertainty if the scatter plots follow the same trend as the parametric study and are centered around the parametric study results. However, if the results do not follow the trend of the parametric study or are not centered around the parametric study results, the parameter could be either not sensitive to uncertainty or overpowered by the effects of other parameters. The scatter plots of pipe displacement against parameter input uncertainty are shown in Fig. 6 where the black lines represent the results from the parametric study. Each subfigure represents the results of a single parameter, and the different colors represent the results at different flow speeds.

Fig. 6

Pipe displacement against the percent of input uncertainty where the black line represents the results from the parametric study for a ${d}_{o}$, b ${d}_{i}$, c $L$, d $E$, and e $\rho$

The majority of the results for the first flow speed at $-\,5\%$ of the nominal critical flow speed across all parameters are at a displacement of zero. This indicates that at the lesser flow speeds, most of the cases have not yet reached an internal flow speed that would cause the system to lose stability which is expected. When the uncertainty in ${d}_{\mathrm{o}}$ is very low, as depicted in Fig. 6a, all cases are stable, and some cases begin to become unstable as the value of ${d}_{\mathrm{o}}$ diverges farther away from the nominal value. The output distribution of ${d}_{\mathrm{o}}$ has a very similar shape to the parametric study at $-\,3\%$ of the nominal flow speed. This indicates that interaction between the parameters is causing the system to become unstable earlier than when the parameters are being varied on their own.

As the flow speed increases to $-\,3\%$, more of the results are unstable, but many of the results are still at a displacement of zero. The trend in ${d}_{\mathrm{o}}$ continues at this flow speed where there are less unstable cases around the nominal parameter value and more unstable cases when there is more uncertainty introduced into the system. The other parameters have a mostly uniform distribution throughout the entire parameter range which indicates that ${d}_{\mathrm{o}}$ is the most sensitive parameter out of all other parameters. This is further proven by investigating ${d}_{\mathrm{o}}$ at a flow speed of $3\%$ the nominal critical flow speed. At this flow speed, it is clear that the trend of data is following the results from the parametric study as shown in the black line in Figs. 6a and 4c. The results are closely gathered together at negative uncertainty values which indicate high uncertainty and should indicate a high Pearson correlation coefficient. However, because the trend of the displacement is not monotonic, the result of the Pearson correlation coefficient cannot be fully trusted for ${d}_{\mathrm{o}}$. It is interesting to note that the sensitivity of ${d}_{\mathrm{o}}$ decreases as the input uncertainty becomes positive and grows to 5%. This is shown by the results closely gathered together at an uncertainty value of $-\,5\%$ but is more spread out as the uncertainty grows to 5%. This is especially evident at the flow speed of $10\%$ the nominal critical value in Fig. 6a.

Another indication that ${d}_{\mathrm{o}}$ is the most sensitive parameter is that the results of the scatter plot in Fig. 6a are centered around the results from the parametric study, and the results from all the other parameters are not centered around the results from the parametric study. It is clear in Fig. 6b–e that the displacement from the parametric study is much less than the average displacement of the Monte Carlo study. This indicates that ${d}_{\mathrm{o}}$ is so sensitive to uncertainty change that the change in the system from input uncertainty overpowers the change from the other parameters. As discussed earlier, the displacement increases as the value of ${d}_{\mathrm{o}}$ diverges farther away from the nominal value, so the increase in average displacement of the other parameters makes sense. It is difficult to determine which parameter is the second most sensitive without first calculating the Pearson correlation coefficients, but $L$ appears to be the next most sensitive, especially at a flow speed of $10\%$ of the nominal critical value in Fig. 6c. The results are closely gathered around 5% parameter uncertainty, although much less so than that of ${d}_{\mathrm{o}}$ at $-\,5\%$ parameter uncertainty.

The Pearson correlation coefficients follow the trends that are laid out from the parametric study and are presented in Table 4. As shown in Fig. 4, the sensitivity of each parameter decreases as the flow speed increases. This trend is present in the Pearson correlation coefficients for all parameters except for ${d}_{\mathrm{o}}$ and $L$ which can be explained due to the cancellation effects from the nonlinear behavior in these parameters. Excluding ${d}_{\mathrm{o}}$ and $L$, $E$ is the most sensitive parameter followed by ${d}_{\mathrm{i}}$ and then $\rho$. This does not fully agree with the results from the parametric study. In the parametric study, $\rho$ appears to be the second most influential parameter, but it is the least influential parameter according to the Pearson correlation coefficient. This indicates that the interaction occurring between $\rho$ and the other parameters is causing $\rho$ to be less influential to the system output.

Table 4 Pearson correlation coefficients for the pipe displacement for each parameter at the selected flow speeds

4.3 Analysis of Monte Carlo simulations using histograms of output

Another valuable method of characterizing the results is to investigate histograms of the system output. The distribution of the histograms can clearly indicate whether the average system output is occurring around the nominal output or not. It is preferable to have most of the outputs around the nominal case because this is the expected behavior. If the majority of the outputs are away from the nominal output, the designed system will not behave as expected, and could potentially be operating in a way that could harm the system. Also, the system can be analyzed while keeping certain parameters held constant. The change in, or lack thereof, can help indicate which parameters are most sensitive, and which parameters should be held as close to the nominal value as possible to have the preferred outcome occur more often. An example of this is shown in Fig. 7 where the histograms are plotted when all system’s parameters are varying together and when ${d}_{\mathrm{o}}$ is held at its nominal value while the other parameters are varied. The black dashed line in Fig. 7 represents the displacement of the system at its nominal configuration. It is immediately evident that at all flow speeds that when ${d}_{\mathrm{o}}$ is held constant that the distribution shifts more toward the nominal value. This confirms that ${d}_{\mathrm{o}}$ is very sensitive to uncertainty and that the best results will occur when the amount of uncertainty introduced into ${d}_{\mathrm{o}}$ is limited.

Fig. 7

Output histogram of system’s displacement where all parameters are varying together and when ${d}_{o}$ is held at its nominal value for flow speeds of: a $-\,5\%$, b $-\,3\%$, c $3\%$, d 5%, and e $10\%$ the nominal critical flow speed

It would be beneficial to investigate the histograms when the other parameters are held constant, but the figures would become illegible if each histogram was overlaid on the same plot. To avoid this, the histograms are plotted in 3D space where the Z-axis represents the percent of occurrences, and the graphs are viewed looking down onto the XY-plane. The percent of occurrences is represented from a color bar where little occurrences appear navy blue, and many occurrences appear as a dark red. A color of pure white is used when no data are present in the specified displacement range. Figure 8a depicts the output histograms at a flow speed of −$\,5\%$ of the nominal critical flow speed. At this point, $94.54\%$ of the cases have not reached instability, and when ${d}_{\mathrm{o}}$ is held constant the number of stable cases rises to $99.89\%$. The next most sensitive parameter is $L$ which is evident by the histogram shifting to the left toward the nominal displacement, and $\rho$ is the least sensitive parameter at that flow speed. Increasing to $-\,3\%$ the nominal critical flow speed in Fig. 8b, it is again clear that ${d}_{\mathrm{o}}$ is the most sensitive parameter. The percent of occurrences at a displacement of zero for ${d}_{\mathrm{o}}$ is close to 90% of all occurrences for ${d}_{\mathrm{o}}$, but the other parameters have the percent of occurrences around 70%. At these low flow speeds, the majority of the cases are stable, and the uncertainty introduced into the system has little effect on the overall system performance.

Fig. 8

Histograms for pipe displacement where certain parameters are held at their nominal values at a flow speed of: a $-\,5\%$, b $-\,3\%$, c $3\%$, d 5%, e $10\%$ the nominal critical value

Uncertainty plays a bigger role at higher flow speeds like at $3\%$ the nominal flow speed, as depicted in Fig. 8c. At lower flow speeds, the maximum percent of occurrences is between 88.36 and 99.89% in a single displacement range. The percent of occurrences in a single displacement range is drastically decreased at $3\%$ the nominal critical flow speed to 7.82%. The maximum number and percent of occurrences for each investigated flow speed are presented in Table 5. This indicates that the results are much more spread out, and the odds of having the result behave like the designed case decrease. The average result under uncertainty is $0.0303\,\mathrm{m}$, whereas the nominal displacement is at $0.0221\,\mathrm{m}$. When ${d}_{\mathrm{o}}$ is held constant at its nominal value, the average displacement is $0.0239\,\mathrm{m}$, and the range of displacements has gone down. It is interesting to note, however, that more cases are still stable when ${d}_{\mathrm{o}}$ is held constant than when all of the parameters vary together. Similar to the $-\,3\%$ nominal critical flow speed case, there is not much change in the system when the other parameters are held constant. This again indicates that the sensitivity of ${d}_{\mathrm{o}}$ is so high that the uncertainty in other parameters does not have a large impact on the system when ${d}_{\mathrm{o}}$itself is under uncertainty.

Table 5 Maximum number of occurrences for each analyzed flow speed

This trend continues at a flow speed of 5% of the nominal critical flow speed. Again, the results that most closely match the nominal case is when ${d}_{\mathrm{o}}$ is held constant. In this case, the nominal displacement is $0.0281\,\mathrm{m}$, and the average displacement when ${d}_{\mathrm{o}}$ is held at its nominal value is $0.0295\,\mathrm{m}$, whereas the average displacement when all parameters are varying together is $0.0347\,\mathrm{m}$. The average displacement in the other parameters does not change which is again caused by the overpowering of ${d}_{\mathrm{o}}$, but at this flow speed, the range in $\rho$ is reduced particularly at the lower displacements. The average displacements for all parameters at each flow speed are listed in Table 6. This indicates that the majority of the lower displacements are caused by $\rho$, which makes sense when compared to Fig. 3e. The parametric study shows that the system loses stability at the highest flow speed when $\rho$ is much less than its nominal value. This late loss of stability causes the displacement to be very low which does not occur if $\rho$ is not affected by uncertainty. Although the average number of results is close to the nominal output when ${d}_{\mathrm{o}}$ is held constant, it is still not centered around the nominal output as preferred. This means that the uncertainty in the other parameters is still affecting the system greatly.

Table 6 Nominal and average displacements of when all parameters are varied and when certain parameters are held constant for each investigated flow speed

This is not the case at the highest flow speed of $10\%$ the nominal critical flow speed. When ${d}_{\mathrm{o}}$ is held at its nominal value at this flow speed, the average result is clearly centered around the nominal displacement. The nominal displacement at this flow speed is $0.0366\,\mathrm{m}$, and the average displacement when ${d}_{\mathrm{o}}$ is excluded is $0.0369\,\mathrm{m}$. This is in stark contrast to the average displacement of $0.0404\,\mathrm{m}$ when all parameters are varied at the same time. The average displacement again is not greatly affected when the other parameters are held constant, but ${d}_{\mathrm{o}}$ is centered around the nominal output. This shows that the sensitivity in the parameters is decreasing as the flow speed increases. At this point, ${d}_{\mathrm{o}}$ is still very influential to the output of the system, but the other parameters are converging to the same displacement as the flow speed increases regardless of uncertainty in the system. Therefore, the uncertainty introduced into the system has a much more profound effect at lower flow speeds than it does at higher flow speeds, and ${d}_{\mathrm{o}}$ is by far the most sensitive parameter.

5 Dynamic response of pipeline conveying fluid with motion-limiting constraints under uncertainty

After determining how the pipeline conveying fluid system behaves under uncertainty without constraints, the system can be analyzed while implementing the motion-limiting constraints. The uncertainty analysis process is almost identical to when the system did not have constraints except there is a presence of aperiodic responses and chaos for certain flow speeds. Therefore, there are two QOI’s for this uncertainty analysis, namely displacement and whether the system is aperiodic/chaotic or not. As mentioned earlier, the bifurcation diagram plots the peak-to-peak values of the time history which represents where the pipe changes direction. Only two points would be plotted if the pipe was oscillating periodically, and many points would be plotted if it were oscillating chaotically. Counting the number of points in the bifurcation diagram is an easy way to determine whether the system is oscillating periodically or aperiodically/chaotically.

The process of finding the maximum displacement for the aperiodic system is outlined and plotted in Fig. 9. When deciding how to characterize the dynamic response of the system, it is decided to compare the maximum displacement to the minimum displacement of the same constraint. To this end, the maximum and minimum points with a positive displacement are collected, and the negative displacements are neglected as the system is mostly symmetrical. The segments of the bifurcation diagram that are not symmetrical will not greatly affect the output of the uncertainty quantification analysis because of the system’s high dependency on initial conditions. Depending on the initial conditions, the behavior of the system can change drastically, and certain segments of the bifurcation diagram can be flipped from positive to negative. By performing the analysis over many different iterations, the unsymmetrical segments will average out so that the system will be correctly characterized.

Fig. 9

Process of finding maximum and minimum displacements for Monte Carlo study where: a represents the whole bifurcation diagram, b represents the positive displacements used to calculate the maximum and minimum displacements, c the maximum and minimum displacements, and d the maximum and minimum displacements overlaid the positive displacements of the bifurcation diagram

If the difference of the maximum and minimum displacements is greater than zero, the system is oscillating aperiodically/chaotically, and a difference equal to zero would indicate that the system is stable or oscillating periodically. This falls apart, however, when the system regains its periodicity as shown in Fig. 9 at $8.1\,\mathrm{m}/\mathrm{s}$. Because the system is oscillating periodically with multiple peaks, taking the difference of maximum and minimum displacements, in this case, would be greater than zero and would lead to the mischaracterization of chaotic behavior. Also, investigating the maximum displacement gives a better understanding of the dynamical response than investigating the difference between the maximum and minimum displacements. Therefore, only the maximum positive displacements are used, and the number of peak-to-peak points is used to characterize chaotic behavior. One problem with the proposed method, however, is when the pipe sticks in the constraint on the negative side. When this happens, there are no displacements on the positive side during sticking, so the maximum displacement at these points is set to $0\,\mathrm{m}$.

5.1 Uncertainty analysis of individual parameters with motion-limiting constraints

The parametric study is first performed over the entire flow speed range by varying the same five parameters individually. The results from the parametric study are shown in Fig. 10, and it is immediately apparent that ${d}_{\mathrm{o}}$ is again a very sensitive parameter. Unlike the case without motion-limiting constraints, $L$ also has a profound effect on the chaotic response of the system. On the other hand, the effects of uncertainty are negligible in $\rho$. This is particularly interesting because $\rho$ is very sensitive to the onset of instability, but even though the critical flow speed has a wide range, the chaotic response is occurring at effectively the same flow speed range and amplitudes regardless of the amount of uncertainty introduced into the parameter. This is in contrast with $E$ which is not affected by uncertainty at the onset of instability but shows a larger sensitivity in the dynamical response, as shown in Fig. 10d. The first case to exhibit chaotic behavior is when $E$ is at $-\,5\%$ of its nominal value, which makes sense because that same case is the first to lose stability. As the value of $E$ increases, the flow speed at the onset of instability increases and so does the flow speed at which chaotic behavior begins. The shape of the chaotic regions does not change as the uncertainty increases but is shifted to the right as the uncertainty increases. The shape of the chaos regions does not change much either when ${d}_{\mathrm{i}}$ is varied individually, as shown in Fig. 10b. The onset of instability varies much more than the onset of instability when $E$ varies individually, but the changes in the chaos region are much less than that of $E$. Additionally, it is interesting to note that the first case to become chaotic is when ${d}_{\mathrm{i}}$ is at 5% its nominal value which is also the case that loses stability last. As ${d}_{\mathrm{i}}$ decreases, the chaos region begins at a slightly later flow speed. This indicates that the chaotic response does not strictly depend on when the system loses stability.

Fig. 10

Parametric study with motion-limiting constraints for a ${d}_{o}$, b ${d}_{i}$, c $L$, d $E$, and e $\rho$

Unlike the system without motion-limiting constraints, the dynamic response of the system is very dependent on $L$, as shown in Fig. 10c. When $L$ is low, the system takes a long time to start oscillating chaotically, and the region of double centering is small where the pipe does not oscillate fully around each constraint. As the uncertainty in $L$ increases, the onset of chaos occurs at lower flow speeds, and the pipe begins to oscillate more fully around the constraints. Also, as the uncertainty increases, the range of chaos that is occurring around the entire center is widening. This is exemplified when $L$ is 5% of its nominal value where the full chaos region has grown to cover a large range of flow speeds. This massive range of chaos could cause fatal failure to the system, especially because a chaos region that large would not be expected to occur under normal operating conditions. It should be mentioned that the location of the constraints is kept constant which implies the strong relationship between the length of the pipe, the constraint’s location, and the presence of the chaotic responses.

Figure 10a represents the parametric study of ${d}_{\mathrm{o}}$, where the chaotic response varies wildly depending on the level of uncertainty introduced into the parameter. When ${d}_{\mathrm{o}}$ is set to $-\,5\%$ of its nominal value, the onset of stability is very low, and the pitchfork bifurcation and first-period doubling occur almost immediately after contacting the motion-limiting constraints and shortly after begins to oscillate chaotically. As the value of ${d}_{\mathrm{o}}$ increases, so does the onset of chaotic double centering. The chaotic double centering first appears when input uncertainty is $-1.67\%$, and this region grows larger as the uncertainty increases until the value of ${d}_{\mathrm{o}}$ is 5% the nominal value where the chaotic double centering region covers a large flow speed range. The sticking phenomenon occurs at the earliest and latest flow speed when ${d}_{\mathrm{o}}$is changed due to uncertainty compared to any other parameter. This high range of chaotic responses makes the expected response of the system hard to predict when uncertainty is allowed to be introduced in this parameter. When ${d}_{\mathrm{i}}$, $E$, and $\rho$ parameters are changed due to uncertainty, the range of chaotic responses is not changed much. Therefore, if uncertainty is allowed to be introduced into these parameters, the regions of chaos will not be vastly different than it was expected to be, but uncertainty introduced into ${d}_{\mathrm{o}}$ and $L$ will cause the system to behave very differently than what it was designed to. These are the most sensitive parameters when being varied on their own, but it is possible that the interaction of the parameters will cause the system to behave differently. To this end, the full Monte Carlo simulation is needed to be calculated to gain a full understanding of the system.

5.2 Convergences analysis and investigation of Monte Carlo simulation output using bivariate diagrams

To avoid memory and computation issues like previously, several flow speeds of interest are selected to be analyzed. When motion-limiting constraints were not implemented, the flow speeds were selected to gain an understanding of how the system would behave across a wide flow speed range. In this instance, the selected flow speeds are selected to understand how the specific chaotic regions present in the nominal system change under uncertainty. The selected flow speeds to investigate are shown in Fig. 11. Although six flow speeds are investigated, only three flow speeds are shown in this work due to brevity. The selected flow speeds are given in Table 7.

Fig. 11

Bifurcation diagram of the nominal system with selected flow speeds for uncertainty quantification analysis for: a the entire response and b the displacements taken in study

Table 7 Selected flow speeds for investigation

Again, before the full Monte Carlo simulation can be performed, it is first necessary to find the number of iterations needed to reach an accurate solution. To this effect, a convergence analysis is carried out and plotted in Fig. 12. Similar to the case without motion-limiting constraints, convergence is reached relatively early and 10,012 iterations are chosen to reach an accurate solution at a reasonable computational time. The convergence analysis for the average maximum displacement is shown Fig. 12a and appears to have not reached convergence. This is not necessarily the case, however. The difference between the displacements is very small, and the average displacement for each flow speed is close to each other, so the differences between each iteration appear to be much larger. For example, for the case at $7.96\,\mathrm{m}/\mathrm{s}$, the average displacement is $0.0215\,\mathrm{m}$ at 10,012 iterations and the displacement at 20,000 iterations is $0.02145\,\mathrm{m}$. This is only a percent difference of $0.23\%$. The maximum percent difference between 10,012 iterations and any case after it is $0.33\%$. This small percent difference does not have a large impact on the system, so 10,012 iterations will be used for the following Monte Carlo simulation.

Fig. 12

Convergence analysis for the system with motion-limiting constraints for: a the average maximum displacement and b the average number of peak-to-peak values from time histories

After determining the needed iterations for the convergence, the full Monte Carlos simulation can begin. The histograms for both maximum displacement and number of points are shown in Fig. 13 when the flow speed is considered 7.96 m/s and where the black dashed lines represent the nominal value for the respective graph. The effects of uncertainty are clearly seen by investigating the trends. Figure 13a represents the maximum displacement of the pipe and shows a large cluster of points around the nominal value. This is preferred, but there is also almost 7% of the total cases that are either stable or sticking at the negative constraint. The number of peak-to-peak points is shown in Fig. 13b, but the majority of results are around zero. This indicates that the pipeline is stable or oscillating periodically. The problem with viewing the histograms of the maximum displacement and number of points separately is that the correlation between the two is impossible to comprehend.

Fig. 13

Histograms where the black dashed lines represent the nominal value at $7.96\,\mathrm{m}/\mathrm{s}$ for: a the maximum pipe displacement and b the number of peak-to-peak time history values

To gain an understanding of the coupling between the two QOI’s, bivariate diagrams are plotted. A bivariate diagram is plotted by counting the number of occurrences at the maximum displacement at a specific peak-to-peak value. Much like the 3D histograms plotted in Fig. 8, a bivariate diagram is viewed at the XY-plane where the Z-axis represents the number of occurrences. This is shown by a color bar where pure white again indicates that there are no results occurring at the given maximum displacement and number of points ranges. The X-axis again represents the maximum displacement, but the Y-axis represents the number of points. The XY-plane is cut into a grid where each slice of boxes represents the histogram at the selected number of points or maximum displacement. For example, to view the histogram of the maximum displacements at $400$ peak-to-peak points, find $400$ points on the Y-axis and trace across the X-axis. Alternatively, to investigate how the number of points changes at a specific flow speed, find the flow speed of interest on the X-axis and trace upward along the Y-axis. This gives a better understanding of how the system behaves.

The bivariate diagrams for the selected flow speeds are shown in Fig. 14 where the yellow dashed lines represent the nominal number of peak-to-peak points and maximum displacement depending on the direction of each line. The intersection of the nominal lines shows the nominal output of the system. When all parameters are influenced by uncertainty, the overall shape of the results is very similar, but the peak occurrence locations change slightly. At a flow speed of $7.96\,\mathrm{m}/\mathrm{s}$, Fig. 14a shows that the majority of results are not around the nominal values. All peak locations occur when there are very little number of peak-to-peak points. The grid point at $\left(\mathrm{0,0}\right)$ indicates that the system is stable, or the sticking phenomena have occurred at a negative displacement. When there are results that have around zero number of points but have a maximum amplitude higher than zero, the system is oscillating periodically, or sticking has occurred at a positive displacement. There is no way to distinguish between sticking and periodic motion in this method. The maximum number of occurrences at a flow speed of $7.96\,\mathrm{m}/\mathrm{s}$ is around $17\%$ at a displacement of around $0.022\,\mathrm{m}$. There is a small grouping of results near the nominal output at around $300$ points and $0.025\,\mathrm{m}$. Each grid in this grouping has only around $2\%$ of the total occurrences. The uncertainty introduced into the system is causing the majority of the results to be pulled away from the nominal result, and the majority of cases can occur around the nominal result by limiting the uncertainty in certain parameters.

Fig. 14

Results from Monte Carlo simulation plotted in bivariate diagrams for a flow speed of a $7.96\,\mathrm{m}/\mathrm{s}$, b $8.13\,\mathrm{m}/\mathrm{s}$, and c $8.35\,\mathrm{m}/\mathrm{s}$

Similar results are seen at the flow speed of $8.13\,\mathrm{m}/\mathrm{s}$ in Fig. 14b. Again, the majority of cases are when the system is periodic or stable, but this time much more of the cases are at the $\left(\mathrm{0,0}\right)$ grid location. The percentage of occurrences at this grid location is around $12\%$ which is compared to $7\%$ at the first flow speed. The majority of maximum amplitudes has also increased to around $0.026\,\mathrm{m}$ at around $12\%$ of the total occurrences. The grouping around $300$ peak-to-peak points and $0.025\,\mathrm{m}$ has increased its total occurrences at 5%. This grouping has not changed location when the flow speed was at $7.96\,\mathrm{m}/\mathrm{s}$, but at this flow speed, it is much closer to the nominal value. This indicates that the behavior of the system is shifting due to uncertainty, and many of the same results are happening at multiple flow speeds.

The same trends persist when the flow speed is increased to $8.35\,\mathrm{m}/\mathrm{s}$. The three highest locations of results are in the same spot: the grid location at $\left(\mathrm{0,0}\right)$, the stable or periodic response at $0.026\,\mathrm{m}$, and the grouping of results around $300$ peak-to-peak points and a displacement of $0.025\,\mathrm{m}$. The shape of output is very similar to the previous flow speeds, but the maximum total percent of occurrences has increased to $23\%$. This peak of occurrences occurs at a maximum displacement of $0.026\,\mathrm{m}$, and the percent of occurrences around $\left(\mathrm{0,0}\right)$ has increased to $19\%$. The grouping of results around $300$ peak-to-peak points is at the same location and has increased to almost 6% of the total number of occurrences. This increase in occurrences is indicating that higher flow speeds are less affected by the uncertainty introduced into the system. Also, none of the areas that show a high value of occurrences are around the nominal output, but there is a grouping of results that show a very low percentage of occurrences around the nominal value. At all flow speeds, most of the results are occurring away from the nominal value. It is necessary to find which parameters are most sensitive and limit the uncertainty in these parameters to have the majority of outputs occur around the nominal result.

The Monte Carlo study is repeated while holding certain parameters at their nominal values, and the results are shown in Figs. 15, 16, and 17 for $7.96\,\mathrm{m}/\mathrm{s}$, $8.13\,\mathrm{m}/\mathrm{s}$, and $8.35\,\mathrm{m}/\mathrm{s}$, respectively. Figure 15b, d, e shows the results while ${d}_{\mathrm{i}}$, $E$, and $\rho$ are held constant, respectively. When these parameters are held constant, there is very little difference from the case when all parameters vary together which indicates that the parameters are insensitive to uncertainty. When $L$ is held at its nominal value, the occurrences at high values of peak-to-peak points and maximum displacements decrease toward the nominal value, but the shape is still similar to the original Monte Carlo study. Therefore, $L$ is slightly sensitive to uncertainty, but the uncertainty in the other parameters still causes the system to behave away from the nominal values. The most sensitive parameter by far is again ${d}_{\mathrm{o}}$, as depicted in Fig. 15a. The range of displacements and count of peak-to-peak points have greatly reduced to values around the nominal case. This is very close to the desired result, but the peak of the total occurrences of $24\%$ is exhibiting periodic or stable behavior. In an attempt to bring the majority of results closer to the nominal value, the two most sensitive parameters, ${d}_{\mathrm{o}}$ and $L$, are held constant at their nominal value, as shown in Fig. 15f. When these two parameters are held constant, it is immediately evident that the range of results has again reduced around the nominal output. The largest peak of results is still stable or periodic with $23\%$ of total occurrences around $0.022\,\mathrm{m}$, but the grouping of results at $300$ peak-to-peak points and $0.025\,\mathrm{m}$ has increased to around $11\%$ of the total occurrences. This value is not exactly equal to the nominal result, but it is very close and there are not any results far away from the nominal output. With these parameters held constant at this flow speed, the system should behave close to as it is expected to.

Fig. 15

Bivariate diagrams at $7.96\,\mathrm{m}/\mathrm{s}$ where the parameters held constant are: a ${d}_{o}$, b ${d}_{i}$, c $L$, d $E$, e $\rho$, and f ${d}_{o}$ and $L$

Fig. 16

Bivariate diagrams at $8.13\,\mathrm{m}/\mathrm{s}$ where the parameters held constant are: a ${d}_{o}$, b ${d}_{i}$, c $L$, d $E$, e $\rho$, and f ${d}_{o}$ and $L$

Fig. 17

Bivariate diagrams at $8.35\,\mathrm{m}/\mathrm{s}$ where the parameters held constant are: a ${d}_{o}$, b ${d}_{i}$, c $L$, d $E$, e $\rho$, and f ${d}_{o}$ and $L$

When the flow speed is increased to $8.13\,\mathrm{m}/\mathrm{s}$, many of the trends are repeated from the flow speed of $7.96\,\mathrm{m}/\mathrm{s}$, as shown in Fig. 16. The system output is hardly affected when ${d}_{i}$, $E$, and $\rho$ are held at their nominal values which is evident from comparing Fig. 14 to Fig. 16b, d, e for ${d}_{i}$, $E$, and $\rho$, respectively. Again, it is evident that ${d}_{\mathrm{o}}$ is very sensitive to the introduction of uncertainty as the range of results has decreased around the nominal value, although remarkably less so than the previous flow speed which is shown in Fig. 16a. Figure 16c shows that $L$ is just about as sensitive as ${d}_{\mathrm{o}}$ at this flow speed because the bivariate diagrams when ${d}_{\mathrm{o}}$ and $L$ are very similar to each other. The major differences between the two diagrams are that many cases are stable with no displacement when $L$ is constant. About $16\%$ of the total occurrences are present at this flow speed, while there are no stable or periodic cases at that displacement when ${d}_{\mathrm{o}}$ is held constant. Instead, the periodic cases are occurring more at varied displacements, and the number of results at the grouping at $300$ peak-to-peak points and $0.025\,\mathrm{m}$ has increased to $7\%$ of the total occurrences. Additionally, the Monte Carlo study is run again where ${d}_{\mathrm{o}}$ and $L$ are held at their nominal values, and the desired output of the system is close to being achieved, as shown in Fig. 16f. The range of the results has decreased by a sufficient amount to be around the nominal output. The highest number of total occurrences is around $11\%$ which is located at a periodic displacement of $0.027\,\mathrm{m}$. This peak is around the nominal displacement, but the nominal number of peak-to-peak points is around $300$. Also, there is a group of results around the nominal value with a peak of occurrences around $11\%$. This is a reasonable result which again shows the importance of minimizing the uncertainty introduced into the ${d}_{\mathrm{o}}$ and $L$ parameters.

Investigating the bivariate histograms at a flow speed of $8.35\,\mathrm{m}/\mathrm{s}$ in Fig. 17 shows no good distributions are found where the majority of results are around the nominal output. The distribution of the results is broadly spread out when ${d}_{o}$ is held constant, as shown in Fig. 17a. There are groupings of results around $0.03\,\mathrm{m}$ and $400$ peak-to-peak points which have not been seen yet. When the other parameters are held constant, the maximum percent of total occurrences at a single grid location is around $23\%$, but when ${d}_{\mathrm{o}}$ is held constant, the maximum percent of total occurrences is just under $10\%$. This indicates uncertainty is affecting the other parameters at higher flow speeds more than they had at lower flow speeds, but ${d}_{\mathrm{o}}$ is so sensitive that any uncertainty introduced into the parameter will overpower the other parameters and be the main influence on the behavior of the system. Figure 17c depicts the results when $L$ is held constant at its nominal value and clearly shows that $L$ is less sensitive to uncertainty than it was at other flow speeds. The number of peak-to-peak points has decreased toward the nominal value besides the results around the displacement of $0.03\,\mathrm{m}$ which is affected less than the other displacements. However, the high-density regions are about the same as when all parameters are varying at the same time. Therefore, keeping $L$ constant does not greatly affect the output at this flow speed.

The results are unchanged again when ${d}_{\mathrm{i}}$, $E$, and $\rho$ are held at their nominal values, as observed in Fig. 17b, d, e, respectively. The important difference between these parameters at this flow speed compared to lower flow speeds is the broad range of results when ${d}_{o}$ is held constant compared to the earlier flow speeds where there is a much smaller range of results. Therefore, ${d}_{\mathrm{i}}$. $E$, and $\rho$ are showing more sensitivity at higher flow speeds but are being overpowered by ${d}_{\mathrm{o}}$ when it is introduced to uncertainty. If the desired internal flow speed of the system is around $8.35\,\mathrm{m}/\mathrm{s}$ or more, then the uncertainty is needed to be greatly controlled in all parameters, but if the desired flow speed is lower, then controlling the uncertainty introduced into the ${d}_{\mathrm{o}}$ and $L$ may be proficient enough to each good results. Again, the Monte Carlo study is run where both ${d}_{\mathrm{o}}$ and $L$ are held at their nominal values, and the results can be seen in Fig. 17f. There are more results closer to the nominal output, but there are still many high-density peaks that are far from the nominal result which again indicates that the other parameters are being more influenced by the system.

6 Uncertainty in parameters of motion-limiting constraints

This study has so far focused on the introduction of uncertainty into the parameters of the pipeline itself. However, the configuration of the motion-limiting constraints could have large impacts on the dynamic response of the system. Therefore, an uncertainty quantification analysis is performed on the motion-limiting constraints. The constraint parameters introduced to a $\pm \,5\%$ input uncertainty are the location of the constraints along the length of the pipe, ${S}_{c}$; the gap size, ${Y}_{\mathrm{c}}$; and the stiffness of the constraints, ${k}_{3}$.

First, a parametric study is conducted over the entire flow speed for the three constraint parameters. The bifurcation diagrams for each parameter are shown in Fig. 18 where the different colors illustrate how the parameter is varied by the input uncertainty. It should be first noted that the focus of this analysis is the dynamic response of the system after the loss of stability. Because only the constraint parameters are being varied in this analysis, the flow speed at the onset of instability does not change with uncertainty. Figure 18a shows the bifurcation diagrams for ${S}_{\mathrm{c}}$ which is highly sensitive to uncertainty.

Fig. 18

Parametric study with motion-limiting constraints for a ${S}_{c}$, b ${Y}_{c}$, and c ${k}_{3}$

As ${S}_{\mathrm{c}}$ decreases along the length of the pipe, the flow speed at which sticking occurs increases. At an uncertainty of $-\,5\%$, the pipeline oscillates chaotically or aperiodically for a wide flow speed range. This wide aperiodic region is similar to the case when the length is at 5% uncertainty in Fig. 10c. Additionally, the flow speed at which this aperiodic region begins is at a greater flow speed than any other uncertainty levels for this parameter. As ${S}_{\mathrm{c}}$ increases, the flow speed where the aperiodic region oscillates around both constraints decreases, and the range of flow speeds that this region covers decreases as well to the point where this aperiodic region at an uncertainty of 5% covers a very small flow speed range. The opposite trend appears for the first aperiodic response. When the uncertainty of ${S}_{\mathrm{c}}$ is at 5%, two chaotic/aperiodic regions can be seen around the constraints at a flow speed of $8\,\mathrm{m}/\mathrm{s}$ where the pipeline is oscillating around the center. As the location of ${S}_{\mathrm{c}}$ decreases along the length of the pipe, the displacement range that this aperiodic region covers around each constraint decreases to the point that the pipeline does not seem to be oscillating aperiodically or chaotically.

The other constraint parameters do not show much sensitivity to the input uncertainty range analyzed. There is essentially no variation in the bifurcation diagrams for ${k}_{3}$ in Fig. 18c. There is a small variation with regards to ${Y}_{\mathrm{c}}$, however. The flow speed at which all critical behavior changes occur, including sticking, increase as ${Y}_{\mathrm{c}}$ increases. Additionally, the maximum displacement of the pipe increases at larger ${Y}_{\mathrm{c}}$ values. This finding is consistent with the work of Wang et. al. [35]. However, Wang et al. [35] studied a much larger variation in gap sizes and found a larger disparity in the behavior of the pipeline. At the relatively small variance of $\pm \,5\%$, the behavior of the pipe remains comparable.

The Monte Carlo Simulation is again employed to investigate the effects of uncertainty on the motion-limiting constraint parameters. Bivariate diagrams are used to visualize the response and can be seen in Fig. 19, where the yellow dashed lines represent the output from the nominal configuration. The flow speed of $7.96\,\mathrm{m}/\mathrm{s}$ is plotted in Fig. 19a, and the majority of the results are occurring around the nominal displacement. The maximum percent of occurrences can be seen where the pipeline is stable around a displacement of $0.0237\,\mathrm{m}$ which is close to the nominal value of $0.0243\,\mathrm{m}$. Another grouping of responses is above the nominal number of points at around 285. This is similar to the pipeline parameter results when ${d}_{\mathrm{o}}$ and $L$ are held constant in Fig. 15f. However, one important distinction is the difference between the total amount of occurrences. The maximum percentage of occurrences in one flow speed and number of peak-to-peak range when ${d}_{\mathrm{o}}$ and $L$ are held constant is 23%. However, the maximum percentage of occurrences for the constraint parameters is 19%. This indicates that the constraint parameters are more sensitive to the effects of input uncertainty than ${d}_{\mathrm{i}}$, $E$, and $\rho .$ However, the majority of results are closer to the displacement of the nominal system at this flow speed than when ${d}_{\mathrm{o}}$ and $L$ are affected by input uncertainty. This agrees with the results from the parametric study in Fig. 18 where the behavior of the pipe at lower flow speeds is very similar to the nominal case.

Fig. 19

Bivariate diagrams of motion-limiting constraint parameters for a flow speed of a $7.96\,\mathrm{m}/\mathrm{s}$, b $8.13\,\mathrm{m}/\mathrm{s}$, and c $8.35\,\mathrm{m}/\mathrm{s}$

The bivariate diagram for the flow speed of $8.13\,\mathrm{m}$ is plotted in Fig. 19b. The results are again similar to the pipeline parameter analysis where ${d}_{\mathrm{o}}$ and $L$ are held constant in Fig. 16f. The maximum percent of occurrences for the constraint parameters is almost $14\%$ at a stable or periodic oscillations and a displacement of $0.026\,\mathrm{m}$. This peak of occurrences is around the same location as the pipe parameter case, but the maximum percent of occurrences in this case is 19%. Also, there are two regions of high occurrences in the constraint parameter case, whereas there is only one region in the pipe parameter case. Indeed, the results of this analysis are spread out more throughout the bivariate diagram compared to the pipe parameter case which can be easily seen when comparing the results along the results around $0$ peak-to-peak time history values. This again shows that the constraint parameters are more sensitive to uncertainty than ${d}_{\mathrm{i}}$, $E$, and $\rho$. Finally, the flow speed of $8.35\,\mathrm{m}/\mathrm{s}$ is analyzed when uncertainty is introduced into all constraint parameters simultaneously. The bivariate diagram is shown in Fig. 19c, and the output has a thin grouping of results around a displacement of $0.03\,\mathrm{m}/\mathrm{s}$ from the number of peak-to-peak time history values ranging from $0$ to about $450$. This is similar to the pipe parameter case seen in Fig. 17f when ${d}_{\mathrm{o}}$ and $L$ are held constant. For the pipe parameter case, however, there is a large grouping of results in the displacement range of $0.0025$ and $0.025\,\mathrm{m}/\mathrm{s}$ and between $0$ and $350$ peak-to-peak time history values. This contrasts with the constraint parameter case where there are very few results in this same range other than the cases that are periodic or stable.

It is interesting to note that at this flow speed the constraint parameters are less sensitive to uncertainty than the pipe parameters when ${d}_{\mathrm{o}}$ and $L$ are held constant. This is proven from the maximum percent occurrences at around 17% for the constraint case, and the maximum percent of occurrences for the pipe parameter case is only $12.\,5\%$. Investigating the parameter study of the constraint parameters gives insight into why this is taking place. Figure 18a shows a periodic response at $8.35\,\mathrm{m}/\mathrm{s}$ when ${S}_{\mathrm{c}}$ decreases, and the pipeline is sticking when ${S}_{\mathrm{c}}$ is moved $3.33\%$ and 5% from its nominal location. Each of these responses produces a number of peak-to-peak time history values in the bivariate diagram. Additionally, the response of the pipe is periodic at $8.35\,\mathrm{m}/\mathrm{s}$ as ${k}_{3}$ increases, as shown in Fig. 18b. Therefore, many of the responses of the pipeline system at this flow speed are either periodic or stable even when the parameters interact with each other.

To investigate how the most sensitive constraint parameter interacts with the most sensitive pipe parameter, parametric studies are performed on ${S}_{\mathrm{c}}$ when ${d}_{\mathrm{o}}$ is introduced to $-\,5\%$ and 5% uncertainty individually as shown in Fig. 20. It can be seen that the behavior of these parameters does not cancel each other out but instead compound with each other. Figure 20a shows the parametric study of ${S}_{\mathrm{c}}$ when ${d}_{\mathrm{o}}$ is set to $-\,5\%$, and the trends of ${S}_{\mathrm{c}}$ continue from the previous parametric study. When the input uncertainty of ${S}_{\mathrm{c}}$ is $-\,5\%$, a large region of chaotic/aperiodic is present, and as ${S}_{\mathrm{c}}$ increases, the flow speed at which behavior changes occur decreases. At 5% input uncertainty, the flow speed of sticking is lower than when only ${d}_{\mathrm{o}}$ is affected by uncertainty.

Fig. 20

Parametric study of ${S}_{c}$ when a ${d}_{o}=-\,5\%$ and b ${d}_{o}=\,5\%$

This trend is again seen when the input uncertainty of ${d}_{\mathrm{o}}$ is 5% in Fig. 20b. The behavior of the pipe when ${d}_{\mathrm{o}}$ at this uncertainty is drastically different than the nominal configuration. When the uncertainty of ${S}_{\mathrm{c}}$ is 5%, sticking and other behavior changes occur at lower flow speeds than when only ${d}_{\mathrm{o}}$ is affected by uncertainty. Additionally, the behavior of the pipe changes as ${S}_{\mathrm{c}}$ increases. The sticking behavior is visible when the uncertainty of ${S}_{\mathrm{c}}$ is $-1.66\%$, but the sticking behavior is no longer seen at uncertainty of $-3.33\%$. Instead, period-4 oscillations exist after the aperiodic/chaotic region that covers the entire displacement range around 9.7 m/s. Then, additional bifurcations can be seen around 9.9 m/s. The behavior changes again when the uncertainty of ${S}_{\mathrm{c}}$ is $-\,5\%$ where the large chaotic/aperiodic region is no longer present. Alternatively, a bifurcation can be seen after the periodic oscillations of the pipe, and the pipeline then exhibits period-4 oscillations. This behavior is drastically different than the nominal configuration of the pipeline and would likely perform outside of the designed specifications. Uncertainty would have to be limited in these parameters to ensure the system would behave as expected.

7 Conclusions

The goal of this study was to analyze the dynamical response of the pipeline conveying fluid in the post-flutter regime when input uncertainty is introduced into the system. This input uncertainty can be from many diverse sources including tolerances in manufacturing, material sourcing, environmental conditions, and fatigue. The modeling of the system was discussed, and two pipeline configurations were defined. The first configuration was the pipeline system without any motion-limiting constraints which gave a good understanding of how the system behaves naturally under uncertainty. The QOI for this configuration is the maximum displacement of the pipe. The five parameters that were introduced to a uniform 5% uncertainty were ${d}_{\mathrm{o}}$, ${d}_{\mathrm{i}}$, $L$, $E$, and $\rho$, and the three uncertainty methods performed were extended parametric study, Monte Carlo simulation, and Pearson correlation coefficients. It was determined from all analyses that ${d}_{\mathrm{o}}$ was by far the most sensitive parameter. The other parameters were affected by uncertainty at flow speeds around the nominal onset of instability, but the majority of results were close to the nominal output when ${d}_{\mathrm{o}}$ is held at its nominal value. It is important to reduce uncertainty in all parameters, but it is necessary that ${d}_{\mathrm{o}}$ is as close to its designed dimension as possible to have a chance at behaving as expected. Also, the parameters become less sensitive to uncertainty as the flow speed increases.

The second configuration was the pipeline system with motion-limiting constraints which induce chaotic behavior. Two QOIs were used to characterize the behavior of the chaotic responses, namely the maximum displacement of the pipe and the number of peak-to-peak points from the time history at the specific flow speed. The parametric study and the Monte Carlo simulation methods were examined to understand the response of the system. Again, ${d}_{\mathrm{o}}$ was determined to be the most sensitive parameter except $L$ is also quite sensitive. At low flow speeds, the system exhibited behaviors similar to the nominal system when ${d}_{\mathrm{o}}$ is held at its nominal value. When the flow speed is increased slightly, however, the uncertainty is needed to be controlled in both ${d}_{\mathrm{o}}$ and $L$ to achieve nominal results. Although ${d}_{\mathrm{o}}$ is the most sensitive parameter at high flow speeds, the other parameters are more sensitive to uncertainty. Therefore, the uncertainty needs to be minimized in all parameters if the system is designed to operate at higher flow speeds.

Finally, the parameters pertaining to the motion-limiting constraints were analyzed. The parameter that was most sensitive to input uncertainty was ${S}_{\mathrm{c}}$, and ${Y}_{\mathrm{c}}$ and ${k}_{3}$ showed little sensitivity to uncertainty. A Monte Carlo analysis found that the three constraint parameters produced results similar to when ${d}_{\mathrm{i}}$, $E$, and $\rho$ were influenced by a $\pm \,5\%$ uncertainty. However, drastic behavior changes were observed when ${S}_{\mathrm{c}}$ and ${d}_{\mathrm{o}}$ were both influenced by input uncertainty simultaneously. Indeed, even small amounts of uncertainty introduced into these parameters concurrently could cause the designed system to behave radically different than the nominal case. Uncertainty is needed to be limited in ${S}_{\mathrm{c}}$ when motion-limiting constraints are present to ensure precise behavior of the designed system.

Appendix

$$ \beta = \sqrt[4]{{\frac{m + M}{{EI}}\omega^{2} }} $$

(A1)

$$ C_{ij} = EI\eta \int_{0}^{L} {\beta^{4} \phi_{j} \phi_{i} {\text{d}}S = } \delta_{ij} \eta \omega^{2} $$

(A2)

$$ \left( {Cu} \right)_{ij} = 2M\int_{0}^{L} {\phi^{\prime}_{j} \phi_{i} } $$

(A3)

$$ K_{ij} = \int_{0}^{L} {\left[ {EI\beta^{4} \phi_{j} - \left( {m + M} \right)g\left( {L - S} \right)\phi^{\prime\prime}_{j} + \left( {m + M} \right)\phi^{\prime}_{j} } \right]\phi_{i} {\text{d}}S} $$

(A4)

$$ \left( {Ku} \right)_{ij} = M\int\limits_{0}^{1} {\phi^{\prime\prime}_{j} \phi_{i} {\text{d}}s} $$

(A5)

$$ M_{ijkl} = \int_{0}^{L} {\left( {\phi^{\prime}_{l} \int_{0}^{s} {\left( {m + M} \right)\phi^{\prime}_{k} \phi^{\prime}_{j} ds} - \phi^{\prime\prime}_{l} \int_{s}^{L} {\int_{0}^{s} {\left( {m + M} \right)\phi^{\prime}_{k} \phi^{\prime}_{j} {\text{d}}s} {\text{d}}s} } \right)\phi_{i} {\text{d}}s} $$

(A6)

$$ N_{ijkl} = 2M\int_{0}^{L} {\left( {\phi^{\prime}_{l} \phi^{\prime}_{k} \phi^{\prime}_{j} + \phi^{\prime}_{l} \int_{0}^{s} {\phi^{\prime\prime}_{k} \phi^{\prime}_{j} {\text{d}}s} - \phi^{\prime\prime}_{l} \int_{s}^{L} {\left( {\phi^{\prime\prime}_{k} \phi^{\prime}_{j} {\text{d}}s - \int_{0}^{s} {\phi^{\prime\prime}_{k} \phi^{\prime}_{j} {\text{d}}s} } \right){\text{d}}s} } \right)\phi_{i} {\text{d}}s} $$

(A7)

$$ \begin{aligned} P_{ijkl} & = \int_{0}^{L} {\left[ { - \frac{3}{2}\left( {m + M} \right)g\left( {L - s} \right)\phi^{\prime\prime}_{l} \phi^{\prime}_{k} \phi^{\prime}_{j} - \frac{1}{2}\left( {m + M} \right)g\phi^{\prime}_{l} \phi^{\prime}_{k} \phi^{\prime}_{j} + 3EI\phi^{\prime\prime\prime}_{l} \phi^{\prime\prime}_{k} \phi^{\prime}_{j} + EI\phi^{\prime\prime}\phi^{\prime\prime}\phi^{\prime\prime}} \right.} \\ & \quad + \phi^{\prime}_{l} \int_{0}^{s} {\left( {\left( {m + M} \right)g\left( {L - s} \right)\phi^{\prime\prime\prime}_{k} \phi^{\prime}_{j} + EI\phi^{\prime\prime\prime}_{k} \phi^{\prime\prime}_{j} } \right){\text{d}}s} - \phi^{\prime\prime}_{l} \int_{s}^{L} {\left( {\left( { - \left( {m + M} \right)g\phi^{\prime}_{k} \phi^{\prime}_{j} + EI\phi_{k}^{iv} \phi^{\prime\prime}_{j} } \right){\text{d}}s} \right.} \\ & \quad \left. {\left. { + \int_{0}^{s} {\left( {\left( {m + M} \right)g\left( {L - s} \right)\phi^{\prime\prime\prime}_{k} \phi^{\prime}_{j} + EI\phi_{k}^{iv} \phi^{\prime\prime}_{j} } \right)_{j} {\text{d}}s} } \right){\text{d}}s} \right]\phi_{i} {\text{d}}s \\ \end{aligned} $$

(A8)

$$ \left( {Pu} \right)_{ijkl} = M\int_{0}^{L} {\left( {\phi^{\prime\prime}_{l} \phi^{\prime}_{k} \phi^{\prime}_{j} - \phi^{\prime}_{l} \int_{0}^{s} {\phi^{\prime\prime\prime}_{k} \phi^{\prime}_{j} {\text{d}}s} - \phi^{\prime\prime}_{l} \int_{s}^{L} {\left( {\phi^{\prime\prime}_{k} \phi^{\prime}_{j} {\text{d}}s - \int_{0}^{s} {\phi^{\prime\prime\prime}_{k} \phi^{\prime}_{j} {\text{d}}s} } \right){\text{d}}s} } \right)\phi_{i} {\text{d}}s} $$

(A9)