1 Introduction

Research in the field of discontinuous nonlinear dynamical systems has received a lot of attention in the last few decades [1,2,3,4,5,6,7]. Because of their interesting linear and nonlinear dynamic behaviors, cantilevered pipes conveying fluid have become a great topic of research. Since the early 1950s, many researchers have studied variations of the seemingly straightforward application through modifying and introducing several new parameters to the system, such as motion-limiting constraints. As such, this topic has remained of interest in an extensive list of applications in which proper characterization of the stability of the system holds great importance. Applications of cantilevered pipes conveying fluid can include micro-/nano-fluid devices, which hold as promising candidates in drug delivery [8,9,10,11], oil pipelines, whose constraints are present at a larger scale [12, 13], mechanical pumps [14], components in reactor systems [15], and more. In each of these systems, a full understanding of the dynamic stability should be considered.

Variations of the cantilevered pipe systems have been considered to include both linear and nonlinear springs [16,17,18], an additional tip-mass [19], and the impacting force in which nonlinear aspects were considered, most notably in [20,21,22,23,24,25]. In these works, significant contributions and variations were made to the original system, leading to contributions in nonlinear dynamics. In studying cantilevered pipes, both 2-D (planar) and 3-D vibrations have been considered by researchers.

For both 2-D and 3-D analyses of cantilevered pipes, Païdoussis and his collaborators are known to have made the most extensive contributions [10, 16, 18,19,20,21,22,23,24,25,26,27,28,29,30,31]. Other contributions were made by Tang and Dowell [32], in which they studied the buckling of a cantilevered pipe and its nonlinear response. The system composed of a pipe with an inset steel strip and equispaced magnets on either side. It was shown that once the flow velocity exceeded a threshold of fluttering at its buckled state, chaotic motions could arise. In the work of Païdoussis, variations were made to involve motion-limiting constraints. It was shown that for sufficiently high flow velocities, chaotic oscillations occur, both theoretically and experimentally. To validate theoretical models with experiments, a cubic spring, or trilinear model was utilized to represent the wall force in conjunction with the full nonlinear equations of motion. In a 3-D analysis of the cantilevered pipe, Païdoussis et al. [17], the 3-D nonlinear dynamics of the previously mentioned pipe were investigated. The cantilevered pipe was additionally constrained by arrays of two of four linear springs or a single spring at an arbitrary point along the length. In theoretical and experimental studies, it was shown that the system can lose stability by planar flutter or divergence. In addition, 2-D or 3-D periodic, quasiperiodic, or chaotic oscillations could occur.

In different studies, various types of bifurcations were shown to occur. In this analysis, it is particularly interesting to consider grazing bifurcations. The grazing bifurcations of limit cycles is common discontinuity-induced bifurcations which takes place when a periodic orbit reaches a boundary tangentially with zero speed [33]. Noting that analysis is being done at the point of contact, it is expected that grazing will occur between the wall and the pipe. In general, grazing bifurcation has been found in cantilever beams [34,35,36,37,38,39,40], spring-mass systems [41,42,43,44,45], mechanical structures such as the bump-stop in a wheel suspension system of a vehicle [46], and tapping force atomic microscopy [47]. In addition, possible grazing bifurcations can exist in aeroelastic systems with a freeplay nonlinearity in the flap or pitch degree of freedom [48,49,50,51,52,53,54]. When impact problems are present, grazing-sliding bifurcations are most commonly considered in which abrupt changes in stability are found [55, 56]. In this work, the sliding bifurcation, though often found in impact problems, is not considered because of the finite stiffness in the force representation. However, greater detail on sliding bifurcations can be found in [55]. It should be mentioned that the generalization of the grazing bifurcations in dynamic systems with sliding motion in the boundary is the grazing-sliding bifurcation [57]. In an effort to understand whether or not grazing bifurcations should be considered in this work, the work of researchers investigating the presence of grazing-sliding bifurcations in forced oscillators with dry friction were reviewed [58,59,60,61,62,63,64].

The purpose of this work is to demonstrate the importance of studying a cantilevered pipe conveying flow with symmetric constraints at the point of contact rather than at the tip. In doing so, a nonlinear analysis is performed using bifurcation diagrams, time histories, phase portraits, power spectra, and Poincaré sections. Emphasis is placed on determining key flow speeds using the bifurcation diagram at the point of contact and making comparisons with the same flow speeds at the tip in order to study the inherent differences between the two. In Sect. 2, the nonlinear equations of motion are presented and discretized using the Galerkin method. In Sect. 3, validation with previous works is shown, along with the selection of the key flow speeds. In Sect. 4, progressions of phase portraits are presented at the point of contact to show the onset of grazing bifurcations in the system. In the remaining sections, comparisons are made between the tip and point of contact and final conclusions are drawn.

2 Nonlinear equations of motion and discretization of a constrained cantilevered pipe conveying fluid

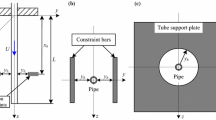
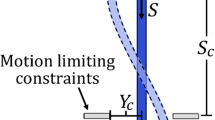
As shown in Fig. 1, the system under consideration is composed of a tubular beam of length L, cross-sectional area A, mass per unit length \(m_{t}\), flexural rigidity EI, and Kelvin-Voight damping \(\eta \). In addition to the properties of the beam, the conveyed fluid has mass per unit length \(m_{f}\) and flows with constant axial velocity V. At its resting state, it is assumed that gravity acts in the positive X-axis and when in motion is constrained to the (X, Y) plane. When the considered pipe is in motion, it is constrained by motion-limiting constraints at \(Y=S_{b}\) with a symmetric gap of \(Y_{b3}\).

Fig. 1
figure 1

A schematic representation of a cantilevered pipe conveying fluid with symmetric constraints

Full size image

Following the work of Semler et al. [20], in which the equation of motion for the cantilevered pipe was first derived, later to include the presence of the symmetric constraints [23], the nonlinear equation of motion of the cantilevered beam with symmetric constraints is written as [25]:

$$\begin{aligned}&{} { EI}(Y^{{ iv}}+\eta \dot{Y}^{{ iv}})+2m_f V{\dot{Y}}'+m_f V^{2}{Y}''\nonumber \\&\quad -\,(m_t +m_f )g(L-S){Y}''+(m_t+m_f )\ddot{Y} \nonumber \\&\quad +\,2m_f V{\dot{Y}}'{Y}'^{2}\left[ {m_f V^{2}-\frac{3}{2}(m_t +m_f )g(L-S)} \right] \nonumber \\&\quad +\,\frac{1}{2}(m{ }_t+m_f )g{Y}'^{3}{+}{} { EI}(Y^{{ iv}}{Y}'^{2}{+}4{Y}'''{Y}''{Y}'{+}{Y}''^{3}) \nonumber \\&\quad -\,{Y}''\left[ {\mathop {\int }\limits _S^L} \left( 2m_f V{\dot{Y}}'{Y}'+m_f V^{2}{Y}''{Y}'\right. \right. \nonumber \\&\quad \left. \left. +\,{\mathop {\int }\limits _0^\rho } {(m_t +m_f )({\dot{Y}}'^{2}+{Y}'{\ddot{Y}}')d\varepsilon } \right) d\rho \right] \nonumber \\&\quad +\,{Y}'{\mathop {\int }\limits _0^S} {(m_t +m_f )({\dot{Y}}'^{2}+{Y}'{\ddot{Y}}')d\rho }\nonumber \\&\quad +\,F(Y)\delta (S-S_b )=0 \end{aligned}$$
(1)

where \(\rho \) and \(\varepsilon \) are dummy variables for S in integration. \((\dot{Y})\) and \(({Y}')\) denote differentiation with respect to time, t, and position along the beam’s centerline, X, respectively. In addition, as presented in Eq. (1), F(Y) is a representation of the force created from the motion-limiting constraints and \(\delta (S-S_{b})\) denotes the Dirac delta function. The following relationships are defined for nondimensional analysis as:

$$\begin{aligned}&s=\frac{S}{L},\,\,y=\frac{Y}{L},\,\,\tau =\left( {\frac{{ EI}}{m_t +m_f }} \right) ^{\frac{1}{2}}\frac{t}{L^{2}},\nonumber \\&\xi = \left( {\frac{{ EI}}{m_t +m_f }} \right) ^{\frac{1}{2}}\frac{\eta }{L^{2}}, \nonumber \\&u=\left( {\frac{m_f }{{ EI}}} \right) ^{\frac{1}{2}}{it VL},\,\,\gamma =\frac{m_t +m_f }{{ EI}}L^{3}g, \nonumber \\&m_r =\frac{m_f }{m_t +m_f },\,\,f(y)=\frac{F(Y)L^{3}}{{ EI}} \end{aligned}$$
(2)

In the nondimensional form, \((\dot{Y})\) and \(({Y}')\) denote differentiation with respect to \(\tau \) and s. Note that nonlinear terms are present in Eq. (1) and are removed by perturbation technique [20]. Substituting the nondimensional terms from Eq. (2) and removing the nonlinear terms by perturbation technique in Eq. (1), the following equation is obtained as:

$$\begin{aligned}&\ddot{y}+\xi \dot{y}^{{ iv}}+2u\sqrt{m_r }{\dot{y}}'+y^{{ iv}}+{y}''\left[ {u^{2}-\gamma (1-s)} \right] \nonumber \\&\quad +\,\gamma {y}'+2u\sqrt{m_r }{\dot{y}}'{y}'^{2} \nonumber \\&\quad +\,{y}''{y}'^{2}\left[ {u^{2}-\frac{3}{2}\gamma (1-s)} \right] \nonumber \\&\quad +\,\left( {-\frac{1}{2}{y}'^{3}+3{y}'''{y}''{y}'+{y}''^{3}} \right) \nonumber \\&\quad -\,{y}''\left[ {\mathop {\int }\limits _s^1} \left( -\gamma y{\prime }^{2}+2u\sqrt{m_r }{\dot{y}}'{y}'\right. \right. \nonumber \\&\quad \left. \left. +\,u^{2}{y}''{y}'+{y}'''{y}'' \right) d\rho \right] \nonumber \\&\quad -\,{y}''\left[ {\mathop {\int }\limits _s^1} {\mathop {\int }\limits _0^\rho } {({\dot{y}}'^{2}-2u\sqrt{m_r }{\dot{y}}''{y}'} \right. \nonumber \\&\quad \left. -\,{y}'''{y}'\left[ {u^{2}-\gamma (1-\varepsilon )} \right] +y^{{ iv}}{y}'')d\varepsilon d\rho \right] \nonumber \\&\quad +\,{y}'{\mathop {\int }\limits _0^s} \left( {\dot{y}}'^{2}-2u\sqrt{m_r }{\dot{y}}''{y}'-{y}'''{y}'\left[ {u^{2}-\gamma (1-\rho )} \right] \right. \nonumber \\&\quad \left. +\,y^{{ iv}}{y}'' \right) d\rho +f(y)\delta (s-s_b )=0 \end{aligned}$$
(3)

To approximate Eq. (3) as an infinite set of ordinary differential equations, thereby discretizing the system, the Galerkin method is employed. Therefore, utilizing the cantilever beam eigenfunctions \(\phi _{i}(s)\) and the generalized coordinates \(q_{i}(\tau )\), \(y(s,\tau )\) can be approximated by:

$$\begin{aligned} y(s,\tau )={\mathop {\sum }\limits _{i=1}^N} {\phi _i (s)q_i (\tau )} \end{aligned}$$
(4)

When substituting Eq. (4) back into equation (3), multiplying by \(\phi _{i}(s)\), and integrating from 0 to 1, one reaches the form:

$$\begin{aligned}&\ddot{q}_i +\left[ {C_{{ ij}} +u\sqrt{m_r}({ Cu})_{{ ij}} } \right] \dot{q}_j\nonumber \\&\quad +\left[ {K_{{ ij}} +u^{2}({ Ku})_{{ ij}} +\gamma ({ Kg})_{{ ij}} } \right] q_j \nonumber \\&\quad +\left[ {M{ }_{{ ijkl}}} \right] \dot{q}_j \dot{q}_k q_l +\left[ {u\sqrt{m_r }(N_{{ ijkl}} )} \right] \dot{q}_j \dot{q}_k q_l\nonumber \\&\quad +\left[ {P_{{ ijkl}} +u^{2}({ Pu})_{{ ijkl}} +\gamma ({ Pg})_{{ ijkl}} } \right] q_j q_k q_l\nonumber \\&\quad +f\left( {\mathop {\sum }\limits _{z=1}^N} {\phi _z (s_b )q_z (\tau )} \right) \phi _i (s_b )=0 \end{aligned}$$
(5)

In this study, the mass ratio \(m_{r}\) and the gravitational relationship remain constant, so Eq. (5) is rewritten as:

$$\begin{aligned}&\ddot{q}_i +\left[ {C_{{ ij}} +u(Cu^{*})_{{ ij}} } \right] \dot{q}_j +\left[ {K_{{ ij}}^*+u^{2}(Ku)_{{ ij}} } \right] q_j \nonumber \\&\quad +\left[ {M_{{ ijkl}} } \right] \dot{q}_j \dot{q}_k q_l +\left[ {u(N_{{ ijkl}}^*)} \right] \dot{q}_j q_k q_l \nonumber \\&\quad +\left[ {P_{{ ijkl}}^*+u^{2}({ Pu})_{{ ijkl}} } \right] q_j q_k q_l \nonumber \\&\quad +f\left( {\mathop {\sum }\limits _{z=1}^N} {\phi _z (s_b )q_z (\tau )} \right) \phi _i (s_b )=0 \end{aligned}$$
(6)

Referring to Eq. (6), all constants are provided as:

$$\begin{aligned}&C_{{ ij}} ={\mathop {\int }\limits _0^1} {\xi _j \lambda _j^4 \phi _j \phi _i} \hbox {d}{} { s}=\delta _{{ ij}} \xi _i \lambda _i^4 \end{aligned}$$
(7)
$$\begin{aligned}&K_{{ ij}}^{*}={\mathop {\int }\limits _0^1} {\left( {\lambda _j ^{4}\phi _j +\gamma \left( {(s-1){\phi }''_j +{\phi }'_j } \right) } \right) } \phi _i \hbox {d}{} { s} \end{aligned}$$
(8)
$$\begin{aligned}&({ Cu}^{*})_{{ ij}} =2\sqrt{m_r }{\mathop {\int }\limits _0^1} {\phi }'_j \phi _i \hbox {d}{} { s} \end{aligned}$$
(9)
$$\begin{aligned}&({ Ku})_{{ ij}} ={\mathop {\int }\limits _0^1} {{\phi }''_j } \phi _i \hbox {d}{} { s}\end{aligned}$$
(10)
$$\begin{aligned}&M_{{ ijkl}} ={\mathop {\int }\limits _0^1} {\left( {{\phi }'_l {\mathop {\int }\limits _0^s} {{\phi }'_k {\phi }'_j d\rho -{\phi }''_l } {\mathop {\int }\limits _s^1} {\mathop {\int }\limits _0^\rho } {{\phi }'_k } } {\phi }''_j d\varepsilon d\rho \right) } \phi _i \hbox {d}{} { s}\nonumber \\ \end{aligned}$$
(11)
$$\begin{aligned} N_{{ ijkl}}^*= & {} 2\sqrt{m_r }{\mathop {\int }\limits _0^1} \left[ {\phi }'_l \left( {{\phi }'_k {\phi }'_j -{\mathop {\int }\limits _0^s} {{\phi }'_k {\phi }''_j d\rho } } \right) \right. \nonumber \\&\quad \left. -{\phi }''_l {\mathop {\int }\limits _s^1} {\left( {{\phi }'_k {\phi }'_j -{\mathop {\int }\limits _0^\rho } {{\phi }'_k {\phi }''_j d\varepsilon } } \right) d\rho } \right] \phi _i \hbox {d}{} { s} \nonumber \\ \end{aligned}$$
(12)
$$\begin{aligned}&P_{{ ijkl}}^*=\displaystyle {\mathop {\int }\limits _0^1} \nonumber \\&\quad \times {\left\{ {\begin{array}{l} {\phi }'_l \left[ {\phi }''_k \left( {3{\phi }'''_j +\,{\phi }'_j \left\{ {\frac{3}{2}\gamma \left[ {s-1} \right] } \right\} } \right) \right. \\ \left. -\frac{1}{2}{\phi }'_k {\phi }'_j +{\mathop {\int }\limits _0^s} {\left( {{\phi }'_k {\phi }'''_j \left\{ {\gamma \left[ {1-\rho } \right] } \right\} +\lambda _k^4 \phi _k {\phi }''_j } \right) d\rho } \right] \\ +\,{\phi }''_l \left[ {\phi }''_k {\phi }''_j -{\mathop {\int }\limits _s^1} \left( {\phi }''_k \left\{ {{\phi }'''_j -\gamma {\phi }''_j } \right\} \right. \right. \\ \left. \left. +\,{\mathop {\int }\limits _0^\rho } {\left\{ {{\phi }'_k {\phi }'''_j \left[ {\gamma (1-\varepsilon )} \right] +\lambda _k^4 \phi _k {\phi }''} \right\} } d\varepsilon \right) d\rho \right] \\ \end{array}} \right\} } \phi _i \hbox {d}{} { s}\nonumber \\ \end{aligned}$$
(13)
$$\begin{aligned} ({ Pu})_{{ ijkl}}= & {} {\mathop {\int }\limits _0^1} \left\{ -{\phi }'_l {\mathop {\int }\limits _0^s} {\phi }'_k {\phi }'''_j d\rho +\,{\phi }''_l \left[ {\phi }'_k {\phi }'_j \right. \right. \nonumber \\&\quad \left. \left. -\,{\mathop {\int }\limits _s^1} {\left( {{\phi }'_k {\phi }'_j -{\mathop {\int }\limits _0^\rho } {{\phi }'_k {\phi }'''_j d\varepsilon } } \right) d\rho } \right] \right\} \phi _i \hbox {d}{} { s} \end{aligned}$$
(14)

The reason for presenting Eq. (6) and its constants in Eqs. (7–14) as shown is to allow for the predetermination of all coefficients, such that each coefficient may have a physical meaning in the analysis of the system. Note that the provided form of the constants differs from the work of Païdoussis and Semler [25]. In doing so, the system only depends on the value of u for all other fixed parameters, thereby saving significant computation time. The model is then rewritten in state space form as:

$$\begin{aligned} \left\{ {{\begin{array}{l} {\dot{p}} \\ {\dot{q}} \\ \end{array} }} \right\} =\left[ {-{\mathop {\sum }\limits _{I}} C -{\mathop {\sum }\limits _{0}} K } \right] \left\{ {{\begin{array}{l} p \\ q \\ \end{array} }} \right\} +\{{ NL}(p,q)\} \end{aligned}$$
(15)
Fig. 2
figure 2

Forcing function that represents the symmetric wall constraints with \(\kappa _{{3}}={5.6}\times {10}^{{6}}\) and \(y_{{ b3}}={0.044}\)

Full size image
Fig. 3
figure 3

Bifurcation diagrams of the cantilevered pipe conveying flow at with symmetric constraints at a the tip and b the point of contact with \(\kappa _{{3}}={5.6}\times {10}^{{6}}\), \(y_{{ b3}}={0.044}\), and \(s_{b}={0.65}\)

Full size image

where

$$\begin{aligned}&\sum C =C+u({ Cu}^{*}) \hbox { and } \nonumber \\&\quad \sum {K=K+u^{2}(Ku)+\gamma ({ Kg})} \end{aligned}$$
(16)

The position and velocity are then expressed as:

$$\begin{aligned} y(s,\tau )={\mathop {\sum }\limits _{i=1}^N} {\phi _i (s)q_i (\tau )},\,\, \dot{y}(s,\tau )={\mathop {\sum }\limits _{i=1}^N} {\phi _i (s)p_i (\tau )} \end{aligned}$$
(17)

Referring again to the work of Païdoussis et al. [24] for the experimentally derived damping forces, the logarithmic decrements for the first 4 modes are \(\delta _{{1}}={0.0028}, \delta _{{2}}={0.0081}, \delta _{{3}}={0.144}\), and \(\delta _{{4}}={0.144}\). The damping is then determined using \(\xi _i =\frac{\delta _i \lambda _i^2 }{\pi }\), where \(\lambda _{i}\) are the eigenvalues for the different modes of the beam.

Finally, considering the nonlinear force, again presented by Païdoussis and Semler [25], a modified trilinear spring model for the wall is considered as:

$$\begin{aligned} f(y)=\kappa _3 \left\{ {y-\frac{1}{2}\left( {\left| {y+y_{b3} } \right| -\left| {y-y_{b3} } \right| } \right) } \right\} ^{3} \end{aligned}$$
(18)

Figure 2 gives a representation of the forcing function with \(\kappa _{{3}}={5.6}\times {10}^{{6}}\) and \(y_{{ b3}}={0.044}\).

3 Validation and point of contact bifurcation region selection

Proper characterization of this system arises from selecting the most appropriate point of observation, such that more accurate results may be obtained. While using the tip as the observation point is practical experimentally, it may not be the best way to characterize the overall stability of the cantilevered pipe. This is concluded because the observed instabilities, bifurcations, or chaos can originate at the point of contact rather than the tip.

Table 1 Selection of critical flow speeds when studying the point of contact and their apparent region identification
Full size table

The validation with the work of Païdoussis and Semler [25] is shown in Fig. 3a, in which the obtained results yield full agreement at the tip. Parameters used that are separate from the forcing function include \(m_{r}={0.213}, s_{b}={0.65}\), and \(\gamma ={26.75}\). The initial value of \(u={8.2}\) is used with the initial condition \(q_{{1}}{(0)}={0.002}\), and all other initial conditions equal to zero. After that, the value of u is increased and the previous final condition is used as the next initial condition. This is done again to reduce computation time and more accurately represent the experimental setup. In Fig. 3b, the bifurcation diagram is presented at the point of contact for the same previously listed parameters. It can easily be seen that discontinuities and jumps that were not present in the tip model have become apparent at the point of contact. In addition, better trends are found regarding the interaction between the pipe and the symmetric constraining wall.

Fig. 4
figure 4

Phase portraits of the transition after the period doubling bifurcation becomes chaotic at the point of contact with a flow speed of a \(u={9.125}\) and b \(u={9.126}\)

Full size image

After validating results through the bifurcation diagram, relevant flow speeds are selected at which the system is changing behavior or bifurcation are occurring. The point in which the pipe first touches the wall is neglected because the nonlinearity in the wall does not result in an additional effect from the first grazing, other than decreasing the rate of the limit cycle amplitude increase. Each of the remaining regions are then selected with their apparent identification and are presented in Table 1. It is immediately apparent that there are several regions that would be overlooked this system were studied at the tip instead of the point of contact. Each region will be explained in greater detail in later sections.

Fig. 5
figure 5

Phase portraits of the transition after going from two centers at a \(u={9.312}\) to one at b \(u={9.313}\)

Full size image
Fig. 6
figure 6

Phase portraits of the wall grazing at a \(u={9.582}\) and b \(u={9.583}\)

Full size image

4 Progressions of the bifurcations at the point of contact using phase portraits

Before making the direct comparisons between the point of contact and the tip, progressions of several regions’ phase portraits are provided to better understand the system as the flow speed increases. Results shown in this section are only for the point of contact. While performing nonlinear analysis and characterization at the point of contact using time histories, power spectra, phase portraits, and Poincaré sections is possible, phase portraits have been presented to qualitatively characterize the systems, particularly in regions in which grazing is present. For example, the third region is selected after the system apparently loses the effect of the pitchfork bifurcation at \(u={9.125}\). The fourth region is immediately after the chaotic region where the system transitions back to the period halving region at \(u={9.313}\). The seventh region is selected at \(u={9.582}\) right at the system begins to fully make contact with both walls. Finally, the last region is selected to further characterize the grazing bifurcation.

As shown in Fig. 4, there is a transition occurring right after the period doubling bifurcation in which the system becomes chaotic. Before this region, the system oscillates about only one center, at which \(u={9.125}\). Then, when \(u={9.126}\), the system alternates between the two centers. This is due to the grazing bifurcation that is observable on the interior of the phase portrait in Fig. 4a. When the system is no longer impacting the wall, it loses its identity and can then change center. This does not always happen due to the chaotic nature of the system, but before this critical grazing point takes place, this change does not occur at all.

In Fig. 5, the bifurcation presented is the counterpart to the double-center bifurcation in which it changes behavior from two centers back to a single center. This is likely due to a crossing over of the maximum value of the low impact side with the minimum value of the high impact side. This bounding of the opposite center leads to a more predictable trajectory that is selected from initial conditions. As the centers move further away from each other, this further reinforces the period halving bifurcations.

Fig. 7
figure 7

Phase portraits of the sticking phenomenon at a \(u={9.656}\) and b \(u={9.657}\)

Full size image

The next bifurcation of interest is after the system begins to become excited enough to again graze against the wall, shown in Fig. 6. When this occurs, the system again loses its predictable trajectory and begins to fully impact both walls in a broadband chaotic motion. This broadband motion is just a chaotic oscillation between the two established orbits. Since the depth of the impact into the wall is variable, the presence of grazing again does not indicate an immediate shift but rather an eventual one given enough time. The higher the flow velocity is increased, the deeper the impact and thus an increased chance of switching centers will occur.

Eventually, the center transition to a point in which they are deep into the wall. This will lead to the sticking phenomena and change of behavior, as shown in Fig. 7. Looking at the tip, the system would seem to exhibit random behavior, but studying the point of contact clearly shows the system is trying to converge.

5 Comparisons of the bifurcations at the tip and point of contact

After qualitatively studying the phase portraits of several key regions, a more detailed analysis is performed to include time histories, power spectra, phase portraits, and Poincaré sections. It should be noted that each region has been named from the initial identifications from the bifurcation diagrams. The results will show the significant differences between system characterization and analysis at the tip versus the point of contact.

5.1 Pitchfork bifurcation

In the first selected region at the flow velocity at which the pitchfork bifurcation occurs, there is little qualitative difference between the phase portraits and time histories, as shown in the plotted curves in Fig. 8. This is due to the motion being dominated by a single mode. Since there is only one mode being expressed, the tip is just a scaled representation of the impact point. Using a trilinear wall, the drift does not occur until much later after the initial contact. Note that the results shown in Fig. 8 correspond the apparent pitchfork bifurcation occurring at \(u={9.004}\).

Fig. 8
figure 8

Nonlinear dynamic analysis showing region 1 pitchfork bifurcation at \(u={9.004}\) with \(f={4.0687}\) for the a point of contact time history and point of contact power spectrum, b point of contact phase portrait, c point of contact Poincaré section, d tip time history and tip power spectrum, e tip phase portrait, and f tip Poincaré section

Full size image

5.2 1st Period doubling

At period doubling critical flow speed, shown in Fig. 9, there is the appearance of the period two superharmonic frequency. On the low impact side, the initial value where the bifurcation occurs stays the mean value though the entire period doubling process. It only starts to change once the system loses the enforced single center. This could mean that the system is staying periodic but with very high periodicity and the grazing being the catalyst for chaotic motion. Again, the power spectra, phase portraits, and Poincaré maps all have very similar appearances when scaled but this changes as the period doubling occurs. This means that it is occurring in a different mode shape resulting in the differences between the tip and point of contact.

Fig. 9
figure 9

Nonlinear dynamic analysis showing region 2 first period doubling bifurcation at \(u={9.068}\) with \(f={4.2341}\) for the a point of contact time history and point of contact power spectrum, b point of contact phase portrait, c point of contact Poincaré section, d tip time history and tip power spectrum, e tip phase portrait, and f tip Poincaré section

Full size image
Fig. 10
figure 10

Nonlinear dynamic analysis showing region 3 chaotic section with double center at \(u={9.125}\) with \(f={4.3948}\) for the a point of contact time history and point of contact power spectrum, b point of contact phase portrait, c point of contact Poincaré section, d tip time history and tip power spectrum, e tip phase portrait, and f tip Poincaré section

Full size image

5.3 Chaotic double centering

For the double-center bifurcation critical flow speed, it can be clearly seen that grazing occurs, as shown in Fig. 10. Once there is a trajectory that has a zero velocity and does not make contact with the wall, the system loses the wall influenced center. It will then take a trajectory similar to the unconstrained until it reestablishes contact with a wall. This means that with trajectories very close to the wall it is more likely to keep the same center rather than switch. Another note is the phase portraits are beginning to change relative to each other as a result of the other modes gaining amplitude. This is seen as in minor changes in the power spectra and phase portraits, but it is most evident in the Poincaré section. The difference can be described from the larger amplitude of the doubled mode being expressed in the tip more.

5.4 Single center separation

At this bifurcation, the system reestablishes a single center. This is due to the maximum of the low impact trajectory not reaching the minimum of the high impact trajectory. Looking at the tip, an overlap in the phase portraits that is not present at the point of contact is seen, as depicted in Fig. 11.

Fig. 11
figure 11

Nonlinear dynamic analysis showing region 4 single center separation at \(u={9.331}\) with \(f={5.1641}\) for the a point of contact time history and point of contact power spectrum, b point of contact phase portrait, c point of contact Poincaré section, d tip time history and tip power spectrum, e tip phase portrait, and f tip Poincaré section

Full size image

5.5 Quasi periodic expansion

While the system is undergoing this bifurcation, it is noted that at the trajectories clearly separating while away from the wall and are compact inside the wall, which can be seen in Fig. 12. This expansion is likely from the addition of a new frequency from a secondary Hopf bifurcation. Initially, it has no common factors with the primary frequency leading to the quasiperiodic nature. As the amplitude of the second frequency increases, it changes until it becomes factorable by the frequency of the primary oscillation. When this occurs, it changes from quasiperiodic to period-n, in this case period-5.

Fig. 12
figure 12

Nonlinear dynamic analysis showing region 5 quasi periodic expansion at \(u={9.553}\) with \(f={6.7070}\) for the a point of contact time history and point of contact power spectrum, b point of contact phase portrait, c point of contact Poincaré section with, d tip time history and tip power spectrum, e tip phase portrait, and f tip Poincaré section

Full size image
Fig. 13
figure 13

Nonlinear dynamic analysis showing region 6 chaotic breakdown at \(u={9.574}\) with \(f={6.6972}\) for the a point of contact time history and point of contact power spectrum, b point of contact phase portrait, c point of contact Poincaré section, d tip time history and tip power spectrum, e tip phase portrait, and f tip Poincaré section

Full size image
Fig. 14
figure 14

Nonlinear dynamic analysis showing region 7 chaotic double centering at \(u={9.582}\) with \(f={6.7232}\) for the a point of contact time history and point of contact power spectrum, b point of contact phase portrait, c point of contact Poincaré section with, d tip time history and tip power spectrum, e tip phase portrait, and f tip Poincaré section with \(f={6.7232}\)

Full size image
Fig. 15
figure 15

Nonlinear dynamic analysis showing region 8 sticking at \(u={9.657}\) with \(f={8.0074}\) for a point of contact time history and point of contact power spectrum, b point of contact phase portrait, c point of contact Poincaré section, d tip time history and tip power spectrum, e tip phase portrait, and f tip Poincaré section

Full size image

5.6 Chaotic breakdown

In this section, the chaotic breakdown occurs right after the second, secondary period doubling. This appears to happen because on the rebound side two trajectories overlap along the zero velocity axis. The overlapping of the trajectories, while at a zero velocity causes a breakdown of periodicity of the system resulting in jumps between known periodic orbits. The intersection of trajectories occurs before but never along the zero axis. At the tip, the corresponding trajectories from the period doubling cross each other along a different axis rather than the zero velocity axis. The onset of breakdown is therefore easier to predict while observing the point of contact rather than the tip. This is demonstrated in Fig. 13.

5.7 Chaotic double centering

Again, it can be observed that a double-center bifurcation occurs as a result of grazing. For the time history, it is extended further than shown in the earlier comparison because a grazing bifurcation does occur later in the history, as shown in Fig. 14. This shows that the initial grazing causes a trajectory change that then results in a deeper impact on the grazed wall which then leads to the change of center. As before, the grazing only indicates that a change of center can occur and as the flow velocity further increases the change becomes more frequent. This bifurcation is very obvious when making observations at the point of contact, whereas at the tip the centers are so close to each other that it is less obvious as to the source of the phenomena.

5.8 Sticking

As the center moves inside the wall, the point of contact converges toward its associated center within the wall, as presented in Fig. 15. It will then bounce out and make contact with the opposing wall. As soon as the rebound out does not have enough velocity to make contact with the opposite wall, then the system will stick. This motion is essentially impossible to observe at the tip as the sticking for this case has the tip actually near the resting location and continues to move for higher values of u, as seen in Fig. 3a. Another benefit toward looking at the point of contact is the fairly obvious location of the centers. In Fig. 15d, it can be seen that the tip converges to a point and then drift upwards in a non-oscillatory manner, while in the impact location it does not change when the sticking occurs.

6 Conclusions

In this work, it was shown that the sources of bifurcations in a cantilevered pipe conveying fluid with symmetric constraints are more accurately identified when analyzed at the point of contact versus the tip. When the tip is studied rather than the point of contact, key behaviors at critical flow speeds that give a lot of information about the stability of the system cannot be properly characterized. For this reason, the system should be studied at the point of contact. After validating the model at the tip with previous works, key flow speeds were selected using the bifurcation diagram at the tip. Progressions of key bifurcations at the point of contact were shown qualitatively with phase portraits, in which grazing bifurcations were identified. Once studying these regions qualitatively, further comparisons were made between the tip and the point of contact using modern methods of nonlinear dynamics such as time history, power spectra, phase portraits, and Poincaré maps. The results further emphasized the importance of studying the point of contact for continuous beam systems with motion-limiting constraints.