Flexible multibody dynamic analysis of shells with an edge center-based strain smoothing MITC method

Abstract

In this study, a dynamic analysis method for flexible multibody systems using Reissner–Mindlin shells was developed, and an edge center-based strain smoothing mixed interpolation of tensorial components (MITC) method that described the deformation of flexible shells was presented. Three primary achievements were completed. First, a new dynamics equation for Reissner–Mindlin shells based on the floating frame of reference formulation was modeled, in which the coupling of the bending and membrane deformations with rigid motion was considered comprehensively. Second, an edge center-based strain smoothing (ECSS) method that effectively improved the membrane and bending behavior for MITC3 elements was proposed. Third, the ECSS method was designed to construct a linear strain field within an element to ensure the strain consistency at the junction center of the element, resulting in a smoother stress field. The superior performance of the proposed method was verified by convergence analyses, and its advantages for flexible multibody dynamics analyses were also highlighted numerically.

1 Introduction

Thin-walled structures such as plates and shells are often designed and applied in engineering practice because of their remarkable performance. The structural characteristics of plates and shells have been widely investigated by researchers, and a series of classical plate and shell theoretical models have been proposed, such as Kirchhoff Love theory and Reissner–Mindlin theory [1,2,3,4,5]. The structural characteristics of plates and shells have been paid much attention by researchers, and a series of analytical and numerical methods have been proposed to investigate them [6,7,8,9,10]. Nevertheless, many multibody dynamic systems composed of plates and shells exist in mechanical and aerospace engineering fields [11, 12]. It is worth noting that because deformation in thin-walled structures is common, it is more reasonable to regard a structure as a flexible multibody system consisting of plates and shells.

The dynamic theory of flexible multibody system reveals the dynamic characteristics of a system when it experiences a large range of spatial motion. Because of the complexity of the governing equations, which are usually solved numerically, there are two key points, one is the interaction, or coupling, between the spatial motion of the flexible body and its structural deformation, and the other is the discretization of structural deformation. In particular, for thin-walled structures, discretization through 3D solid elements is computationally costly. Therefore, it is very important to establish the dynamic model of thin-walled structure based on shell theory and adopt appropriate numerical method for discretization.

Many scholars have made important contributions to flexible multibody system modeling, which can be traced back to the kineto-elastodynamics (KED) method proposed by Winfry [13, 14] for flexible beam dynamics in mechanical systems. The KED method is a unidirectional coupling analysis of rigid dynamics and structural dynamics, and it ignores the influence of structural deformation on rigid motion. The KDE method has exposed problems in the analysis of modern lightweight mechanical systems with high flexibility, and this method has difficulty in meeting the needs of engineering practice. Many scholars, represented by Shabana et al., subsequently developed theoretical modeling methods for flexible multibody systems, such as the floating frame of reference formulation (FFRF) [15, 16], the geometrically exact formulation (GEF) [17,18,19], and the absolute node coordinate formulation (ANCF) [20,21,22]. The GEF is primarily used to study beams, and is only seldom used for plate and shell structures [23, 24]. Updating the algorithm for rotation parameters and handling the singularity are two problems involved in the GEF. The ANCF avoids the problem of describing the complex rotation of a flexible body using a slope vector, and Wang et al. applied ANCF to study the dynamics of thin shells [25,26,27]. However, a large number of degrees of freedom (DOFs) make the simulation process inefficient, and the convergence is poor due to Poisson's ratio and shear locking problems. Both GEF and ANCF are more suitable analyzing multibody systems with large deformation, while FFRF is a powerful tool widely adopted in engineering systems with common elastic deformation. The FFRF couples the rigid motion and elastic deformation of a flexible body by establishing a floating reference coordinate system and representing the flexible deformation in this coordinate system. At present, the FFRF is primarily used to study the dynamics of solid structures [28,29,30,31], but the research regarding using FFRF modeling for shell structures is limited.

One characteristic of the FFRF is that it can flexibly select the deformation discretization method for a flexible body, such as the finite segment method, the assumed modal method, the finite element method (FEM), and the meshfree method. The FEM is undoubtedly the most recognized method for the analysis of plate and shell structures. Among them, the Reissner–Mindlin shell element, which takes the transverse shear strains into consideration and only requires a C0-continuous shape function for displacement discretization, has attracted the attention of most researchers. C0-continuous shell elements inherently have two kinds of locking problems: shear locking and membrane locking. Scholars have conducted many in-depth studies regarding the shear locking problem. They have proposed several correction schemes to handle the shear strain in a shell element, such as the reducing integration scheme [32], the assumed natural strain (ANS) method [33, 34], the discrete shear gap (DSG) method [35,36,37]. The mixed interpolation of tensorial components (MITC) method proposed by Bathe et al. [38] has a simple formula. Besides, the element stiffness matrix is not affected by node numbering. Because the three-node MITC (MITC3) element has attractive advantages mentioned above, many of its enhancements have been further developed [39, 40]. The strain smoothing theory [41] has recently been introduced into the conventional FEM to improve its performance, and it can essentially be regarded as an optimal treatment for membrane deformation. The so-called smoothed finite element methods (SFEMs), such as the node-based SFEM (NSFEM) and the edge-based SFEM (ESFEM) proposed by Liu et al. [42,43,44,45], are effective means of improving accuracy without adding DOFs. These methods can also be conveniently combined with other methods that can overcome shear locking, such as the MITC and DSG methods, to study plate and shell structures [46,47,48]. Lee et al. [49,50,51] proposed a new strain smoothing element (SSE) to further improve the performance and applied it to linear and nonlinear analyses of shells, thereby significantly improving the membrane behavior. A breakthrough is that the SSE constructs linear strain within an element based on a low-order element through a strain smoothing operation and a linear combination of strains. More recently, Tang et al. [52, 53] presented an edge center-based strain smoothing (ECSS) element, which not only constructs an element-linear strain field but also accounts for strain consistency at the element junction center, thus significantly improving the stress smoothness.

In this paper, we extend the FFRF to study the dynamics of thin-walled structures, and a flexible multibody system dynamics modeling method of Reissner–Mindlin shell is proposed. To efficiently and accurately characterize the elastic deformation of Reissner–Mindlin shell, an edge center-based strain smoothing mixed interpolation of tensorial components (ECSS-MITC) method is presented, which can optimally improve the membrane, bending, and shear behavior of shell element, as well as dramatically improve the stress field smoothness without additional post-processing.

The organization of the paper is described as follows. In Sect. 2, the kinematic equation for a Reissner–Mindlin shell is discussed within FFRF framework. In Sect. 3, the proposed ECSS-MITC discretization scheme is introduced in detail. Based on the information in Sects. 2 and 3, the construction of a dynamics equation for a flexible multibody system with shells is described in Sect. 4. The key matrix integral formula involved in the dynamics equation and the reduced order method for solving the equation based on modal synthesis are given in “Appendix A” and “Appendix B”, respectively. Section 5 discusses the performance testing of the ECSS-MITC scheme using two benchmark structure analyses. Section 6 presents three numerical examples of flexible multibody dynamics. Finally, a summary and further propositions for the entire work are provided in Sect. 7.

2 Kinematic description of Reissner–Mindlin shell

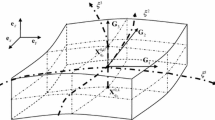
A spatial flexible shell $I$ is shown in Fig. 1, where $O - xyz$ is the inertial coordinate system. $\overline{O}^{I} - \overline{x}^{I} \overline{y}^{I} \overline{z}^{I}$ is the floating coordinate system and is rigidly linked to the shell. In the figure, a point $P$ in the shell space is deformed to a point $P_{f}$ during movement. The spatial position ${\mathbf{r}}_{{P_{f} }}$ of $P_{f}$ can be expressed by Eq. (1):

$$ {\mathbf{r}}_{{P_{f} }} = {\mathbf{R}}^{I} + {\mathbf{r}}_{{\overline{O}^{I} P_{f} }} = {\mathbf{R}}^{I} + {\mathbf{A}}^{I} {\overline{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }} = {\mathbf{R}}^{I} + {\mathbf{A}}^{I} \left( {{\overline{\mathbf{r}}}_{{\overline{O}^{I} P}}^{0} + {\overline{\mathbf{u}}}_{f} } \right) $$

(1)

Fig. 1

Kinematic representation of a shell

In Eq. (1), ${\mathbf{R}}^{I} = \left[ {\begin{array}{*{20}l} {R_{x}^{I} } & {R_{y}^{I} } & {R_{z}^{I} } \\ \end{array} } \right]^{{\text{T}}}$ is described in the inertial coordinate system and represents the translational displacement of $\overline{O}^{I} - \overline{x}^{I} \overline{y}^{I} \overline{z}^{I}$ with respect to $O - xyz$. ${\mathbf{r}}_{{\overline{O}^{I} P_{f} }}$ is the position vector of point $P_{f}$ relative to the origin $\overline{O}^{I}$ of the floating coordinate system, and its vector in the floating coordinate system $\overline{O}^{I} - \overline{x}^{I} \overline{y}^{I} \overline{z}^{I}$ is denoted as ${\overline{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}$. ${\overline{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }} = {\overline{\mathbf{r}}}_{{\overline{O}^{I} P}}^{0} + {\overline{\mathbf{u}}}_{f}$ consists of two parts, namely the position ${\overline{\mathbf{r}}}_{{\overline{O}^{I} P}}^{0}$ of point $P$ without deformation and the displacement ${\overline{\mathbf{u}}}_{f}$ caused by the deformation. Both are described in $\overline{O}^{I} - \overline{x}^{I} \overline{y}^{I} \overline{z}^{I}$. ${\mathbf{A}}^{I}$ is the coordinate transformation matrix between two coordinate systems, consisting of the rotational displacement ${{\varvec{\uptheta}}}^{I} = \left[ {\begin{array}{*{20}l} {\theta_{x}^{I} } & {\theta_{y}^{I} } & {\theta_{z}^{I} } \\ \end{array} } \right]^{{\text{T}}}$ of the floating coordinate system with respect to the inertial coordinate system.

For plate and shell problems, the middle plane is generally extracted to represent the entire motion. As shown in Fig. 1, the middle surface of the shell structure is a spatial curved surface, which is regarded as a splicing of several planes. A local coordinate system $e - \hat{x}\hat{y}\hat{z}$, can be constructed, where the coordinate plane $e - \hat{x}\hat{y}$ is located in the original plane and the $e\hat{z}$ axis is perpendicular to $e - \hat{x}\hat{y}$. According to the Reissner–Mindlin plate theory, the displacement ${\overline{\mathbf{u}}}_{f} \left( {\overline{x},\overline{y},\overline{z}} \right)$ caused by deformation can be firstly expressed in $e - \hat{x}\hat{y}\hat{z}$ by Eq. (2):

$$ {\hat{\mathbf{u}}}_{f} \left( {\hat{x},\hat{y},\hat{z}} \right) = \left[ {\begin{array}{*{20}l} {\hat{u}_{o} \left( {\hat{x},\hat{y}} \right) + \hat{z}\hat{\theta }_{oy} \left( {\hat{x},\hat{y}} \right)} \\ {\hat{v}_{o} \left( {\hat{x},\hat{y}} \right) - \hat{z}\hat{\theta }_{ox} \left( {\hat{x},\hat{y}} \right)} \\ {\hat{w}_{o} \left( {\hat{x},\hat{y}} \right)} \\ \end{array} } \right] $$

(2)

Equation (2) shows that the displacement vector in the plate space is represented by three translational DOFs ($\hat{u}_{0}$, $\hat{v}_{0}$, and $\hat{w}_{0}$) and two rotational DOFs ($\hat{\theta }_{ox}$ and $\hat{\theta }_{oy}$) in the middle plane of the plate. Since the different plates spliced into shells are in different local coordinate systems, to facilitate subsequent transformation into a unified coordinate system, a rotational DOF $\hat{\theta }_{oz}$ along $e\hat{z}$ is introduced here. The deformation can be expressed discretely by Eqs. (3)–(6):

$$ {\hat{\mathbf{u}}}_{o} = \sum\limits_{i} {{\mathbf{N}}_{i} {\hat{\mathbf{u}}}_{i} } $$

(3)

$$ {\hat{\mathbf{u}}}_{0} = \left\{ {\begin{array}{*{20}l} {\hat{u}_{0} } & {\hat{v}_{0} } & {\hat{w}_{0} } & {\hat{\theta }_{ox} } & {\hat{\theta }_{oy} } & {\hat{\theta }_{oz} } \\ \end{array} } \right\}^{{\text{T}}} $$

(4)

$$ {\hat{\mathbf{u}}}_{i} = \left\{ {\begin{array}{*{20}l} {\hat{u}_{i} } & {\hat{v}_{i} } & {\hat{w}_{i} } & {\hat{\theta }_{xi} } & {\hat{\theta }_{yi} } & {\hat{\theta }_{zi} } \\ \end{array} } \right\}^{{\text{T}}} $$

(5)

$$ {\mathbf{N}}_{i} = {\text{diag}}\left\{ {\begin{array}{*{20}l} {N_{i} } & {N_{i} } & {N_{i} } & {N_{i} } & {N_{i} } & {N_{i} } \\ \end{array} } \right\} $$

(6)

In Eqs. (3)–(6), $N_{i}$ represents the interpolation function and ${\hat{\mathbf{u}}}_{i}$ represents the generalized displacement array of discrete nodes.

Accordingly, ${\hat{\mathbf{u}}}_{f}$ is expressed by Eqs. (7)–(10):

$$ {\hat{\mathbf{u}}}_{f} = \sum\limits_{i} {{\hat{\mathbf{S}}}_{i} {\hat{\mathbf{u}}}_{i} } $$

(7)

$$ {\hat{\mathbf{S}}}_{i} = {\hat{\mathbf{S}}}_{im} + \hat{z}{\hat{\mathbf{S}}}_{ib} $$

(8)

$$ {\hat{\mathbf{S}}}_{im} = \left[ {\begin{array}{*{20}l} {N_{i} } & 0 & 0 & 0 & 0 & 0 \\ 0 & {N_{i} } & 0 & 0 & 0 & 0 \\ 0 & 0 & {N_{i} } & 0 & 0 & 0 \\ \end{array} } \right] $$

(9)

$$ {\hat{\mathbf{S}}}_{ib} = \left[ {\begin{array}{*{20}l} 0 & 0 & 0 & 0 & {N_{i} } & 0 \\ 0 & 0 & 0 & { - N_{i} } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right] $$

(10)

The general form of Eq. (7) is obtained through matrix assembly:

$$ {\mathbf{\hat{u}}}_{f} = \hat{\mathbf{S}}\hat{\mathbf{q}}_{f}^{I} $$

(11)

$$ {\hat{\mathbf{S}}} = {\hat{\mathbf{S}}}_{m} + \hat{z}{\hat{\mathbf{S}}}_{b} $$

(12)

where ${\hat{\mathbf{q}}}_{f}^{I} = \left[ {\begin{array}{*{20}l} {{\hat{\mathbf{u}}}_{1}^{{\text{T}}} } & {{\hat{\mathbf{u}}}_{2}^{{\text{T}}} } & \cdots & {{\hat{\mathbf{u}}}_{n}^{{\text{T}}} } \\ \end{array} } \right]^{{\text{T}}}$ represents the global DOFs of the deformed body $I$, and $n$ is the total number of nodes.

The deformation displacements ${\overline{\mathbf{u}}}_{f}$ and ${\hat{\mathbf{u}}}_{f}$ are the same vectors represented in different coordinate systems, and Eq. (13) represents the transformation relationship between them:

$$ {\overline{\mathbf{u}}}_{f} = {{\varvec{\uplambda}}}^{e} {\hat{\mathbf{u}}}_{f} $$

(13)

In Eq. (13), ${{\varvec{\uplambda}}}^{e}$ is the transformation matrix between coordinate systems $\overline{O}^{I} - \overline{x}^{I} \overline{y}^{I} \overline{z}^{I}$ and $e - \hat{x}\hat{y}\hat{z}$. Similarly, there is also a transformation relationship between the nodal displacements:

$$ {\overline{\mathbf{q}}}_{f}^{I} = {\mathbf{T\hat{q}}}_{f}^{I} $$

(14)

where ${\mathbf{T}}$ is assembled from the transformation matrix ${{\varvec{\uplambda}}}^{e}$ corresponding to each local coordinate system. Equations (15) and (16) can be obtained by substituting Eqs. (11) and (14) into Eq. (13):

$$ {\overline{\mathbf{u}}}_{f} = {{\varvec{\uplambda}}}^{e} \hat{\mathbf{S}}\hat{\mathbf{q}}_{f}^{I} = {{\varvec{\uplambda}}}^{e} {\hat{\mathbf{S}}\mathbf{T}}^{{\text{T}}} {\overline{\mathbf{q}}}_{f}^{I} = {{\varvec{\uplambda}}}^{e} {\overline{\mathbf{S}\overline{q}}}_{f}^{I} $$

(15)

$$ {\overline{\mathbf{S}}} = {\hat{\mathbf{S}}\mathbf{T}}^{{\text{T}}} = {\overline{\mathbf{S}}}_{m} + \hat{z}{\overline{\mathbf{S}}}_{b} $$

(16)

Substituting Eq. (15) into (1) yields Eq. (17):

$$ {\mathbf{r}}_{{P_{f} }} = {\mathbf{R}}^{I} + {\mathbf{A}}^{I} {\overline{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }} = {\mathbf{R}}^{I} + {\mathbf{A}}^{I} \left( {{\overline{\mathbf{r}}}_{{\overline{O}^{I} P}}^{0} + {{\varvec{\uplambda}}}^{e} {\overline{\mathbf{S}\overline{q}}}_{f}^{I} } \right) $$

(17)

By taking the derivative of Eq. (17) with respect to time and considering ${\dot{\overline{\mathbf{r}}}}_{{\overline{O}^{I} P}}^{0}$, Eqs. (18) and (19) are obtained:

$$ {\dot{\mathbf{r}}}_{{P_{f} }} = {\dot{\mathbf{R}}}^{I} + {\mathbf{A}}^{I} {\dot{\overline{\mathbf{r}}}}_{{\overline{O}^{I} P_{f} }} + {{\varvec{\upomega}}}^{I} \times {\mathbf{r}}_{{\overline{O}^{I} P_{f} }} $$

(18)

$$ {\dot{\overline{\mathbf{r}}}}_{{\overline{O}^{I} P_{f} }} = {{\varvec{\uplambda}}}^{e} {\overline{\mathbf{S}\dot{\overline{q}}}}_{f}^{I} $$

(19)

In a similar way, taking the second derivative of Eq. (17) with respect to time yields Eqs. (20) and (21):

$$ {\ddot{\mathbf{r}}}_{{P_{f} }} = {\ddot{\mathbf{R}}}^{I} + {\mathbf{A}}^{I} {\ddot{\overline{\mathbf{r}}}}_{{\overline{O}^{I} P_{f} }} + 2{{\varvec{\upomega}}}^{I} \times {\dot{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }} + {{\varvec{\upvarepsilon}}}^{I} \times {\mathbf{r}}_{{\overline{O}^{I} P_{f} }} + {{\varvec{\upomega}}}^{I} \times \left( {{{\varvec{\upomega}}}^{I} \times {\mathbf{r}}_{{\overline{O}^{I} P_{f} }} } \right) $$

(20)

$$ {\ddot{\overline{\mathbf{r}}}}_{{\overline{O}^{I} P_{f} }} = {{\varvec{\uplambda}}}^{e} {\overline{\mathbf{S}\ddot{\overline{q}}}}_{f}^{I} $$

(21)

Rewriting Eqs. (18) and (20) produces Eqs. (22) and (23):

$$ {\dot{\mathbf{r}}}_{{P_{f} }} = \left[ {\begin{array}{*{20}l} {\mathbf{I}} & { - {\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }} } & {{\mathbf{A}}^{I} {{\varvec{\uplambda}}}^{e} {\overline{\mathbf{S}}}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {{\dot{\mathbf{R}}}^{I} } \\ {{{\varvec{\upomega}}}^{I} } \\ {{\dot{\overline{\mathbf{q}}}}_{f}^{I} } \\ \end{array} } \right] = {\mathbf{L}}^{I} {\dot{\mathbf{X}}}^{I} $$

(22)

$$ {\ddot{\mathbf{r}}}_{{P_{f} }} = \left[ {\begin{array}{*{20}l} {\mathbf{I}} & { - {\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }} } & {{\mathbf{A}}^{I} {{\varvec{\uplambda}}}^{e} {\overline{\mathbf{S}}}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {{\ddot{\mathbf{R}}}^{I} } \\ {{{\varvec{\upvarepsilon}}}^{I} } \\ {{\ddot{\overline{\mathbf{q}}}}_{f}^{I} } \\ \end{array} } \right] + 2{\tilde{\mathbf{\omega }}}^{I} {\mathbf{A}}^{I} {{\varvec{\uplambda}}}^{e} {\overline{\mathbf{S}\dot{\overline{q}}}}_{f}^{I} + {\tilde{\mathbf{\omega }}}^{I} {\tilde{\mathbf{\omega }}}^{I} {\mathbf{r}}_{{\overline{O}^{i} P_{f} }} = {\mathbf{L}}^{I} {\ddot{\mathbf{X}}}^{I} + {\mathbf{a}}_{v}^{I} $$

(23)

where ${\mathbf{L}}^{I} = \left[ {\begin{array}{*{20}l} {\mathbf{I}} & { - {\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }} } & {{\mathbf{A}}^{I} {{\varvec{\uplambda}}}^{e} {\overline{\mathbf{S}}}} \\ \end{array} } \right]$, ${\dot{\mathbf{X}}}^{I} = \left[ {\begin{array}{*{20}l} {{\dot{\mathbf{R}}}^{I} } \\ {{{\varvec{\upomega}}}^{I} } \\ {{\dot{\overline{\mathbf{q}}}}_{f}^{I} } \\ \end{array} } \right]$, ${\ddot{\mathbf{X}}}^{I} = \left[ {\begin{array}{*{20}l} {{\ddot{\mathbf{R}}}^{I} } \\ {{{\varvec{\upvarepsilon}}}^{I} } \\ {{\ddot{\overline{\mathbf{q}}}}_{f}^{I} } \\ \end{array} } \right]$ and ${\mathbf{a}}_{v}^{I} = 2{\tilde{\mathbf{\omega }}}^{I} {\mathbf{A}}^{I} {{\varvec{\uplambda}}}^{e} {\overline{\mathbf{S}\dot{\overline{q}}}}_{f}^{I} + {\tilde{\mathbf{\omega }}}^{I} {\tilde{\mathbf{\omega }}}^{I} {\mathbf{r}}_{{\overline{O}^{I} P_{f} }}$. ${\tilde{\mathbf{\omega }}}^{I}$ and ${\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}$ are the antisymmetric matrices corresponding to the vectors ${{\varvec{\upomega}}}^{I}$ and ${\mathbf{r}}_{{\overline{O}^{I} P_{f} }}$ respectively.

Considering Eq. (16), ${\mathbf{r}}_{{\overline{O}^{I} P_{f} }}$ and ${\mathbf{a}}_{v}^{I}$ can be decomposed into three parts:

$$ {\mathbf{r}}_{{\overline{O}^{I} P_{f} }} = {\mathbf{r}}_{{\overline{O}^{I} P_{f} }}^{0} + {\mathbf{r}}_{{\overline{O}^{I} P_{f} }}^{m} + \hat{z}{\mathbf{r}}_{{\overline{O}^{I} P_{f} }}^{b} $$

(24)

$$ {\mathbf{a}}_{v}^{I} = {\mathbf{a}}_{v}^{I0} + {\mathbf{a}}_{v}^{Im} + \hat{z}{\mathbf{a}}_{v}^{Ib} $$

(25)

where:

$$ \left\{ \begin{gathered} {\mathbf{r}}_{{\overline{O}^{I} P_{f} }}^{0} = {\mathbf{A}}^{I} {\overline{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}^{0} \hfill \\ {\mathbf{r}}_{{\overline{O}^{I} P_{f} }}^{m} = {\mathbf{A}}^{I} {{\varvec{\uplambda}}}^{e} {\overline{\mathbf{S}}}_{m} {\overline{\mathbf{q}}}_{f}^{I} \hfill \\ {\mathbf{r}}_{{\overline{O}^{I} P_{f} }}^{b} = {\mathbf{A}}^{I} {{\varvec{\uplambda}}}^{e} {\overline{\mathbf{S}}}_{b} {\overline{\mathbf{q}}}_{f}^{I} \hfill \\ \end{gathered} \right. $$

(26)

$$ \left\{ \begin{gathered} {\mathbf{a}}_{v}^{I0} = {\tilde{\mathbf{\omega }}}^{I} {\tilde{\mathbf{\omega }}}^{I} {\mathbf{r}}_{{\overline{O}^{I} P_{f} }}^{0} \hfill \\ {\mathbf{a}}_{v}^{Im} = 2{\tilde{\mathbf{\omega }}}^{I} {\mathbf{A}}^{I} {{\varvec{\uplambda}}}^{e} {\overline{\mathbf{S}}}_{m} {\dot{\overline{\mathbf{q}}}}_{f}^{I} + {\tilde{\mathbf{\omega }}}^{I} {\tilde{\mathbf{\omega }}}^{I} {\mathbf{r}}_{{\overline{O}^{I} P_{f} }}^{m} \hfill \\ {\mathbf{a}}_{v}^{Ib} = 2{\tilde{\mathbf{\omega }}}^{I} {\mathbf{A}}^{I} {{\varvec{\uplambda}}}^{e} {\overline{\mathbf{S}}}_{b} {\dot{\overline{\mathbf{q}}}}_{f}^{I} + {\tilde{\mathbf{\omega }}}^{I} {\tilde{\mathbf{\omega }}}^{I} {\mathbf{r}}_{{\overline{O}^{I} P_{f} }}^{b} \hfill \\ \end{gathered} \right. $$

(27)

Remark 1

${\mathbf{r}}_{{\overline{O}^{I} P_{f} }}^{m}$ and ${\mathbf{a}}_{v}^{Im}$ represent the motion caused by the membrane deformation of the shell. ${\mathbf{r}}_{{\overline{O}^{I} P_{f} }}^{b}$ and ${\mathbf{a}}_{v}^{Ib}$ denote the motion caused by the bending behavior of the shell, which is a characteristic of shell structures rather than solid structures due to the rotational DOFs introduced previously. Both the membrane and bending deformations are coupled to the dynamic equation and affect the dynamic characteristics of the system.

3 Deformation discretization based on the ECSS-MITC method

3.1 MITC3 Reissner–Mindlin shell element

According to the finite element strategy, curved shells were discretized into spatial triangular elements in this study. The node numbers in the spatial triangular shell element are denoted in the counterclockwise direction as i, j, and k. To analyze a triangular Reissner–Mindlin plate element e, a local coordinate system $e - \hat{x}\hat{y}\hat{z}$ is established for the element. Node i is employed as the origin, and the coordinate axis $i\hat{x}$ is located in the element edge $ij$, as shown in Fig. 2. Based on Eq. (3), the element displacement can be expressed in the matrix form presented in Eqs. (28)–(31):

$$ {\hat{\mathbf{u}}}_{o}^{e} = {\hat{\mathbf{N}}}^{e} {\hat{\mathbf{q}}}_{f}^{e} $$

(28)

$$ {\hat{\mathbf{N}}}^{e} = \left[ {\begin{array}{*{20}l} {{\mathbf{N}}_{i} } & {{\mathbf{N}}_{j} } & {{\mathbf{N}}_{k} } \\ \end{array} } \right] $$

(29)

$$ {\hat{\mathbf{q}}}_{f}^{e} = \left[ {\begin{array}{*{20}l} {{\hat{\mathbf{q}}}_{fi}^{{\text{T}}} } & {{\hat{\mathbf{q}}}_{fj}^{{\text{T}}} } & {{\hat{\mathbf{q}}}_{fk}^{{\text{T}}} } \\ \end{array} } \right]^{{\text{T}}} $$

(30)

$$ {\hat{\mathbf{q}}}_{fl} = \left[ {\begin{array}{*{20}l} {\hat{u}_{l} } & {\hat{v}_{l} } & {\hat{w}_{l} } & {\hat{\theta }_{{l\hat{x}}} } & {\hat{\theta }_{{l\hat{y}}} } & {\hat{\theta }_{{l\hat{z}}} } \\ \end{array} } \right]^{{\text{T}}} \, \left( {l = i,j,k} \right) $$

(31)

Fig. 2

Spatial triangular shell element

In Eqs. (28)–(31), ${\hat{\mathbf{q}}}_{f}^{e}$ is the local nodal displacement, and ${\mathbf{N}}_{l}$ denotes the matrix of shape function for node l. The shape function of a three-node triangular element is expressed as Eqs. (32) and (33):

$$ N_{l} = \frac{1}{{2A^{e} }}\left( {a_{l} + b_{l} \hat{x} + c_{l} \hat{y}} \right)\left( {l = i,j,k} \right) $$

(32)

$$ \left\{ \begin{gathered} a_{i} = \hat{x}_{j} \hat{y}_{k} - \hat{x}_{k} \hat{y}_{j} \hfill \\ a_{j} = \hat{x}_{k} \hat{y}_{i} - \hat{x}_{i} \hat{y}_{k} \hfill \\ a_{k} = \hat{x}_{i} \hat{y}_{j} - \hat{x}_{j} \hat{y}_{i} \hfill \\ \end{gathered} \right.,\quad \left\{ \begin{gathered} b_{i} = \hat{y}_{j} - \hat{y}_{k} \hfill \\ b_{j} = \hat{y}_{k} - \hat{y}_{i} \hfill \\ b_{k} = \hat{y}_{i} - \hat{y}_{j} \hfill \\ \end{gathered} \right.,\quad \left\{ \begin{gathered} c_{i} = - \hat{x}_{j} + \hat{x}_{k} \hfill \\ c_{j} = - \hat{x}_{k} + \hat{x}_{i} \hfill \\ c_{k} = - \hat{x}_{i} + \hat{x}_{j} \hfill \\ \end{gathered} \right. $$

(33)

In Eqs. (32) and (33), $A^{e}$ is the area of the element, and $\left( {\hat{x}_{l} ,\hat{y}_{l} } \right)$ are node coordinates in the local coordinate system as shown in Fig. 2.

Equations (34)–(37) can be obtained using Eq. (14):

$$ {\hat{\mathbf{q}}}_{f}^{e} = \left( {{\mathbf{T}}^{e} } \right)^{{\text{T}}} {\overline{\mathbf{q}}}_{f}^{e} $$

(34)

$$ {\overline{\mathbf{q}}}_{f}^{e} = \left[ {\begin{array}{*{20}l} {{\overline{\mathbf{q}}}_{fi}^{{\text{T}}} } & {{\overline{\mathbf{q}}}_{fj}^{{\text{T}}} } & {{\overline{\mathbf{q}}}_{fk}^{{\text{T}}} } \\ \end{array} } \right]^{{\text{T}}} $$

(35)

$$ {\mathbf{T}}^{e} = {\text{diag}}\left\{ {\begin{array}{*{20}l} {{\mathbf{H}}^{e} } & {{\mathbf{H}}^{e} } & {{\mathbf{H}}^{e} } \\ \end{array} } \right\} $$

(36)

$$ {\mathbf{H}}^{e} = \left[ {\begin{array}{*{20}l} {{{\varvec{\uplambda}}}^{e} } & {\mathbf{0}} \\ {\mathbf{0}} & {{{\varvec{\uplambda}}}^{e} } \\ \end{array} } \right] $$

(37)

Substituting Eq. (34) into (28) yields Eq. (38):

$$ {\hat{\mathbf{u}}}_{o}^{e} = {\hat{\mathbf{N}}}^{e} \left( {{\mathbf{T}}^{e} } \right)^{{\text{T}}} {\overline{\mathbf{q}}}_{f}^{e} $$

(38)

Assembling Eq. (38) into a global form to facilitate final calculations produces Eqs. (39) and (40):

$$ {\hat{\mathbf{u}}}_{o}^{e} = {\mathbf{N}}^{e} {\overline{\mathbf{q}}}_{f} $$

(39)

$$ {\mathbf{N}}^{e} = \left[ {\begin{array}{*{20}l} \cdots & {{\mathbf{N}}_{i} \left( {{\mathbf{T}}^{e} } \right)^{{\text{T}}} } & \cdots & {{\mathbf{N}}_{j} \left( {{\mathbf{T}}^{e} } \right)^{{\text{T}}} } & \cdots & {{\mathbf{N}}_{k} \left( {{\mathbf{T}}^{e} } \right)^{{\text{T}}} } & \cdots \\ \end{array} } \right] $$

(40)

In Eqs. (39) and (40), ${\overline{\mathbf{q}}}_{f} = \left[ {\begin{array}{*{20}l} {{\overline{\mathbf{q}}}_{f1}^{{\text{T}}} } & {{\overline{\mathbf{q}}}_{f2}^{{\text{T}}} } & \cdots & {{\overline{\mathbf{q}}}_{fN}^{{\text{T}}} } \\ \end{array} } \right]^{{\text{T}}}$ represents the global nodal displacement vector, and N is the number of nodes. The size of matrix ${\mathbf{N}}^{e}$ is ${6} \times {6}N$, where the position corresponding to node serial number $l$ ($l = i,j,k$) is $\underbrace {{{\mathbf{N}}_{l} \left( {{\mathbf{T}}^{e} } \right)^{{\text{T}}} }}_{6 \times 6}$ and the other positions are $\mathop {\mathbf{0}}\limits_{6 \times 6}$.

For cases of small deformation, the strain components of the Reissner–Mindlin plate can be expressed by Eqs. (41) and (42):

$$ {{\varvec{\upvarepsilon}}} = \left[ {\begin{array}{*{20}l} {{{\varvec{\upvarepsilon}}}_{{\text{m}}} } \\ {\mathbf{0}} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}l} {\hat{z}{{\varvec{\upvarepsilon}}}_{{\text{b}}} } \\ {\mathbf{0}} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}l} {\mathbf{0}} \\ {{{\varvec{\upvarepsilon}}}_{{\text{s}}} } \\ \end{array} } \right] $$

(41)

$$ {{\varvec{\upvarepsilon}}}_{{\text{m}}} = \left[ {\begin{array}{*{20}l} {\frac{{\partial \hat{u}_{o} }}{{\partial \hat{x}}}} \\ {\frac{{\partial \hat{v}_{o} }}{{\partial \hat{y}}}} \\ {\frac{{\partial \hat{u}_{o} }}{{\partial \hat{y}}} + \frac{{\partial \hat{v}_{o} }}{{\partial \hat{x}}}} \\ \end{array} } \right],\quad {{\varvec{\upvarepsilon}}}_{{\text{b}}} = \left[ {\begin{array}{*{20}l} {\frac{{\partial \hat{\theta }_{oy} }}{{\partial \hat{x}}}} \\ { - \frac{{\partial \hat{\theta }_{ox} }}{{\partial \hat{y}}}} \\ {\frac{{\partial \hat{\theta }_{oy} }}{{\partial \hat{y}}} - \frac{{\partial \hat{\theta }_{ox} }}{{\partial \hat{x}}}} \\ \end{array} } \right],\quad {{\varvec{\upvarepsilon}}}_{{\text{s}}} = \left[ {\begin{array}{*{20}l} {\frac{{\partial \hat{w}}}{\partial x} + \hat{\theta }_{y} } \\ {\frac{{\partial \hat{w}}}{\partial y} - \hat{\theta }_{x} } \\ \end{array} } \right] $$

(42)

where ${{\varvec{\upvarepsilon}}}_{{\text{m}}}$, ${{\varvec{\upvarepsilon}}}_{{\text{b}}}$ and ${{\varvec{\upvarepsilon}}}_{{\text{s}}}$ correspond to the membrane, bending, and shear strains, respectively. In an MITC3 element, the membrane and bending strain components are obtained using Eq. (42):

$$ {{\varvec{\upvarepsilon}}}_{{\text{m}}}^{e} = {\mathbf{B}}_{{\text{m}}}^{e} {\overline{\mathbf{q}}}_{f} $$

(43)

$$ {{\varvec{\upvarepsilon}}}_{{\text{b}}}^{e} = {\mathbf{B}}_{{\text{b}}}^{e} {\overline{\mathbf{q}}}_{f} $$

(44)

$$ {\mathbf{B}}_{{\text{m}}}^{e} = \left[ {\begin{array}{*{20}l} \cdots & {{\mathbf{B}}_{{{\text{m}}i}} \left( {{\mathbf{T}}^{e} } \right)^{{\text{T}}} } & \cdots & {{\mathbf{B}}_{{{\text{m}}j}} \left( {{\mathbf{T}}^{e} } \right)^{{\text{T}}} } & \cdots & {{\mathbf{B}}_{{{\text{m}}k}} \left( {{\mathbf{T}}^{e} } \right)^{{\text{T}}} } & \cdots \\ \end{array} } \right] $$

(45)

$$ {\mathbf{B}}_{{\text{b}}}^{e} = \left[ {\begin{array}{*{20}l} \cdots & {{\mathbf{B}}_{{{\text{b}}i}} \left( {{\mathbf{T}}^{e} } \right)^{{\text{T}}} } & \cdots & {{\mathbf{B}}_{{{\text{b}}j}} \left( {{\mathbf{T}}^{e} } \right)^{{\text{T}}} } & \cdots & {{\mathbf{B}}_{{{\text{b}}k}} \left( {{\mathbf{T}}^{e} } \right)^{{\text{T}}} } & \cdots \\ \end{array} } \right] $$

(46)

where

$$ {\mathbf{B}}_{{{\text{m}}l}} = \frac{1}{{2A^{e} }}\left[ {\begin{array}{*{20}l} {b_{l} } & 0 & 0 & 0 & 0 & 0 \\ 0 & {c_{l} } & 0 & 0 & 0 & 0 \\ {c_{l} } & {b_{l} } & 0 & 0 & 0 & 0 \\ \end{array} } \right]\quad \quad \left( {l = i,j,k} \right) $$

(47)

$$ {\mathbf{B}}_{{{\text{b}}l}} = \frac{1}{{2A^{e} }}\left[ {\begin{array}{*{20}l} 0 & 0 & 0 & 0 & {b_{l} } & 0 \\ 0 & 0 & 0 & { - c_{l} } & 0 & 0 \\ 0 & 0 & 0 & { - b_{l} } & {c_{l} } & 0 \\ \end{array} } \right]\quad \quad \, \left( {l = i,j,k} \right) $$

(48)

To handle the shear locking problem, an MITC3 element assumes a constant covariant transverse shear strain condition along its edge [38]

Reference [48], thus, the shear strain component can be expressed by Eqs. (49)–(50).

$$ {{\varvec{\upvarepsilon}}}_{{\text{s}}}^{e} = {\mathbf{B}}_{{\text{s}}}^{e} {\overline{\mathbf{q}}}_{f} $$

(49)

$$ {\mathbf{B}}_{{\text{s}}}^{e} = \left[ {\begin{array}{*{20}l} \cdots & {{\mathbf{B}}_{{{\text{s}}i}} \left( {{\mathbf{T}}^{e} } \right)^{{\text{T}}} } & \cdots & {{\mathbf{B}}_{{{\text{s}}j}} \left( {{\mathbf{T}}^{e} } \right)^{{\text{T}}} } & \cdots & {{\mathbf{B}}_{{{\text{s}}k}} \left( {{\mathbf{T}}^{e} } \right)^{{\text{T}}} } & \cdots \\ \end{array} } \right] $$

(50)

$$ {\mathbf{B}}_{{{\text{s}}i}} { = }{\mathbf{J}}^{ - 1} \left[ {\begin{array}{*{20}l} 0 & 0 & { - 1} & {\frac{{c_{k} }}{3} - \frac{{c_{j} }}{6}} & { - \frac{{b_{k} }}{3} + \frac{{b_{j} }}{6}} & 0 \\ 0 & 0 & { - 1} & { - \frac{{c_{j} }}{3} + \frac{{c_{k} }}{6}} & {\frac{{b_{j} }}{3} - \frac{{b_{k} }}{6}} & 0 \\ \end{array} } \right] $$

(51)

$$ {\mathbf{B}}_{{{\text{s}}j}} { = }{\mathbf{J}}^{ - 1} \left[ {\begin{array}{*{20}l} 0 & 0 & 1 & {\frac{{c_{k} }}{2} + \frac{{c_{j} }}{6}} & { - \frac{{b_{k} }}{2} - \frac{{b_{j} }}{6}} & 0 \\ 0 & 0 & 0 & { - \frac{{c_{j} }}{6}} & {\frac{{b_{j} }}{6}} & 0 \\ \end{array} } \right] $$

(52)

$$ {\mathbf{B}}_{{{\text{s}}m}} { = }{\mathbf{J}}^{ - 1} \left[ {\begin{array}{*{20}l} 0 & 0 & 0 & {\frac{{c_{k} }}{6}} & { - \frac{{b_{k} }}{6}} & 0 \\ 0 & 0 & 1 & { - \frac{{c_{j} }}{2} - \frac{{c_{k} }}{6}} & {\frac{{b_{j} }}{2} + \frac{{b_{k} }}{6}} & 0 \\ \end{array} } \right] $$

(53)

In Eqs. (51)–(53), ${\mathbf{J}}^{ - 1} = \frac{1}{{2A^{e} }}\left[ {\begin{array}{*{20}l} {b_{j} } & {b_{k} } \\ {c_{j} } & {c_{k} } \\ \end{array} } \right]$.

3.2 Edge center-based strain smoothing method

Equation (42) indicates that ${{\varvec{\upvarepsilon}}}_{{\text{m}}}$ and ${{\varvec{\upvarepsilon}}}_{{\text{b}}}$ are constant matrices in an MITC3 element, resulting in discontinuity of the strain field obtained by numerical analysis. To improve the smoothness of the strain field, a linear strain field construction method using edge centers is first proposed. Then, the strain smoothing operation performed through adjacent elements is further developed to update the strain values of the edge centers of linear elements.

Referring to the concept of linear displacement field construction, the gradient of a physical quantity $\psi^{\left( P \right)}$ at point P in an element can be constructed in linear form, as shown in Eq. (54):

$$ \psi^{\left( P \right)} = \sum\limits_{l} {N_{l}^{\left( P \right)} \psi_{l} } $$

(54)

where $N_{l}^{\left( P \right)}$ denotes the shape function value at point P and $\psi_{l}$ indicates nodal gradient.

Generally, the values of three points that are not collinear can construct a linear field in a two-dimensional plane. In this study, the three edge centers of the triangular element were employed to construct a corresponding linear gradient field. As shown in Fig. 3, the gradient values of the edge centers can be measured by nodal gradient interpolation.

$$ \left[ {\begin{array}{*{20}l} {\psi^{{\left( {E_{1} } \right)}} } \\ {\psi^{{\left( {E_{2} } \right)}} } \\ {\psi^{{\left( {E_{3} } \right)}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {N_{i}^{{\left( {E_{1} } \right)}} } & {N_{j}^{{\left( {E_{1} } \right)}} } & {N_{k}^{{\left( {E_{1} } \right)}} } \\ {N_{i}^{{\left( {E_{2} } \right)}} } & {N_{j}^{{\left( {E_{2} } \right)}} } & {N_{k}^{{\left( {E_{2} } \right)}} } \\ {N_{i}^{{\left( {E_{3} } \right)}} } & {N_{j}^{{\left( {E_{3} } \right)}} } & {N_{k}^{{\left( {E_{3} } \right)}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {\psi_{i} } \\ {\psi_{j} } \\ {\psi_{k} } \\ \end{array} } \right] = {\mathbf{J}}_{{{\text{EC}}}} \left[ {\begin{array}{*{20}l} {\psi_{i} } \\ {\psi_{j} } \\ {\psi_{k} } \\ \end{array} } \right] $$

(55)

where ${\mathbf{J}}_{{{\text{EC}}}}$ is the matrix of the shape function values:

$$ {\mathbf{J}}_{{{\text{EC}}}} = \frac{1}{2}\left[ {\begin{array}{*{20}l} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 1 & 0 & 1 \\ \end{array} } \right] $$

(56)

Fig. 3

Edge centers of the triangular element

By inverting Eq. (55), the nodal gradients expressed by the edge centers or face centers can be obtained; then the gradient field in the element can be calculated using Eq. (54).

$$ \left[ {\begin{array}{*{20}l} {\psi_{i} } \\ {\psi_{j} } \\ {\psi_{k} } \\ \end{array} } \right] = {\mathbf{J}}_{{{\text{EC}}}}^{ - 1} \left[ {\begin{array}{*{20}l} {\psi^{{\left( {E_{1} } \right)}} } \\ {\psi^{{\left( {E_{2} } \right)}} } \\ {\psi^{{\left( {E_{3} } \right)}} } \\ \end{array} } \right] $$

(57)

The strain is constant inside conventional linear elements, so it is useless to apply Eq. (57) directly. Therefore, a strain smoothing method based on the edge centers was developed during this study. The edge center strains are updated by smoothing the strains of adjacent elements, which makes Eq. (57) meaningful.

Since the strain tensor of a shell element is defined in the corresponding local coordinate system, the strain smoothing strategies in different coordinate systems are given by Eq. (58):

$$ {{\varvec{\tilde \varepsilon }}}^{1} = \frac{1}{{A_{1} + A_{2} }}\left( {A_{1} {{\varvec{\upvarepsilon}}}_{1}^{1} + A_{2} {\mathbf{R}}^{{\text{T}}} {{\varvec{\upvarepsilon}}}_{2}^{2} {\mathbf{R}}} \right) $$

(58)

In Eq. (58), $A_{i}$ is the element area of $e_{i}$, and ${{\varvec{\upvarepsilon}}}_{i}^{j}$ ($i,j = 1,2$) denotes the matrix form of the element strain tensor of $e_{i}$ in coordinate system $O_{j}$. The transformation relation between the two coordinate systems is given by the orthogonal matrix ${\mathbf{R}}$.

In a target element, such as the red element shown in Fig. 4, the smoothed strains on its three edge centers are obtained by a smoothing operation with adjacent elements, such as the blue elements shown in Fig. 4. Equation (58) can be expanded to obtain smoothed forms of the membrane and bending strain components:

$$ {{\varvec{\tilde \varepsilon }}}_{{\text{m}}}^{{E_{k} }} = \frac{1}{{A^{e} + A^{{e_{k} }} }}\left( {A^{e} {{\varvec{\upvarepsilon}}}_{{\text{m}}}^{e} + A^{{e_{k} }} {{\varvec{\upvarepsilon}}}_{{\text{m}}}^{{e_{k} \to e}} } \right){ = }{\tilde{\mathbf{B}}}_{{\text{m}}}^{{E_{k} }} {\overline{\mathbf{q}}}_{f} \quad \quad \left( {k = 1,2,3} \right) $$

(59)

$$ {{\varvec{\tilde \varepsilon }}}_{{\text{b}}}^{{E_{k} }} = \frac{1}{{A^{e} + A^{{e_{k} }} }}\left( {A^{e} {{\varvec{\upvarepsilon}}}_{{\text{b}}}^{e} + A^{{e_{k} }} {{\varvec{\upvarepsilon}}}_{{\text{b}}}^{{e_{k} \to e}} } \right){ = }{\tilde{\mathbf{B}}}_{{\text{b}}}^{{E_{k} }} {\overline{\mathbf{q}}}_{f} \quad \quad \left( {k = 1,2,3} \right) $$

(60)

$$ {{\varvec{\upvarepsilon}}}_{{\text{m}}}^{{e_{k} \to e}} = {\mathbf{R}}_{{\text{m}}}^{{}} {\mathbf{R}}_{{{\text{m}}_{k} }}^{{}} {{\varvec{\upvarepsilon}}}_{{\text{m}}}^{{e_{k} }} = {\mathbf{R}}_{{\text{m}}}^{{}} {\mathbf{R}}_{{{\text{m}}_{k} }}^{{}} {\mathbf{B}}_{{\text{m}}}^{{e_{k} }} {\overline{\mathbf{q}}}_{f} = {\mathbf{B}}_{{\text{m}}}^{{e_{k} \to e}} {\overline{\mathbf{q}}}_{f} $$

(61)

$$ {{\varvec{\upvarepsilon}}}_{b}^{{e_{k} \to e}} = {\mathbf{R}}_{{\text{b}}}^{{}} {\mathbf{R}}_{{{\text{b}}_{k} }}^{{}} {{\varvec{\upvarepsilon}}}_{{\text{b}}}^{{e_{k} }} = {\mathbf{R}}_{{\text{b}}}^{{}} {\mathbf{R}}_{{{\text{b}}_{k} }}^{{}} {\mathbf{B}}_{{\text{b}}}^{{e_{k} }} {\overline{\mathbf{q}}}_{f} = {\mathbf{B}}_{{\text{b}}}^{{e_{k} \to e}} {\overline{\mathbf{q}}}_{f} $$

(62)

$$ {\tilde{\mathbf{B}}}_{{\text{m}}}^{{E_{k} }} = \frac{1}{{A^{e} + A^{{e_{k} }} }}\left( {A^{e} {\mathbf{B}}_{{\text{m}}}^{e} + A^{{e_{k} }} {\mathbf{B}}_{{\text{m}}}^{{e_{k} \to e}} } \right) $$

(63)

$$ {\tilde{\mathbf{B}}}_{{\text{b}}}^{{E_{k} }} = \frac{1}{{A^{e} + A^{{e_{k} }} }}\left( {A^{e} {\mathbf{B}}_{{\text{b}}}^{e} + A^{{e_{k} }} {\mathbf{B}}_{{\text{b}}}^{{e_{k} \to e}} } \right) $$

(64)

Fig. 4

Target element and adjacent elements

In Eqs. (59)–(64), ${{\varvec{\upvarepsilon}}}_{{\text{m}}}^{e}$ and ${{\varvec{\upvarepsilon}}}_{{\text{b}}}^{e}$ represent the membrane and bending strains, respectively, of the target element $e$ in its own local coordinate system. ${{\varvec{\upvarepsilon}}}_{{\text{m}}}^{{e_{k} }}$ and ${{\varvec{\upvarepsilon}}}_{{\text{b}}}^{{e_{k} }}$ are the strains of the adjacent elements $e_{k}$ in their own local coordinate system, and they are denoted as ${{\varvec{\upvarepsilon}}}_{{\text{m}}}^{{e_{k} \to e}}$ and ${{\varvec{\upvarepsilon}}}_{{\text{b}}}^{{e_{k} \to e}}$ after a conversion to the coordinate system of element $e$ using Eqs. (61) and (62). In these equations, the transformation matrixes ${\mathbf{R}}_{{\text{m}}}^{{}}$, ${\mathbf{R}}_{{\text{b}}}^{{}}$, ${\mathbf{R}}_{{{\text{m}}_{k} }}^{{}}$ and ${\mathbf{R}}_{{{\text{b}}_{k} }}^{{}}$ are given by Eqs. (65) and (66):

$$ \left( {{\mathbf{R}}_{{\text{m}}}^{{}} } \right)^{{\text{T}}} = \left( {{\mathbf{R}}_{{\text{b}}}^{{}} } \right)^{{\text{T}}} = \left[ {\begin{array}{*{20}l} {n_{{\hat{x}^{e} \overline{x}}}^{2} } & {n_{{\hat{y}^{e} \overline{x}}}^{2} } & {2n_{{\hat{x}^{e} \overline{x}}} n_{{\hat{y}^{e} \overline{x}}} } \\ {n_{{\hat{x}^{e} \overline{y}}}^{2} } & {n_{{\hat{y}^{e} \overline{y}}}^{2} } & {2n_{{\hat{x}^{e} \overline{y}}} n_{{\hat{y}^{e} \overline{y}}} } \\ {n_{{\hat{x}^{e} \overline{z}}}^{2} } & {n_{{\hat{y}^{e} \overline{z}}}^{2} } & {2n_{{\hat{x}^{e} \overline{z}}} n_{{\hat{y}^{e} \overline{z}}} } \\ {n_{{\hat{x}^{e} \overline{x}}} n_{{\hat{x}^{e} \overline{y}}} } & {n_{{\hat{y}^{e} \overline{x}}} n_{{\hat{y}^{e} \overline{y}}} } & {n_{{\hat{x}^{e} \overline{x}}} n_{{\hat{y}^{e} \overline{y}}} + n_{{\hat{y}^{e} \overline{x}}} n_{{\hat{x}^{e} \overline{y}}} } \\ {n_{{\hat{x}^{e} \overline{y}}} n_{{\hat{x}^{e} \overline{z}}} } & {n_{{\hat{y}^{e} \overline{y}}} n_{{\hat{y}^{e} \overline{z}}} } & {n_{{\hat{x}^{e} \overline{z}}} n_{{\hat{y}^{e} \overline{y}}} + n_{{\hat{y}^{e} \overline{z}}} n_{{\hat{x}^{e} \overline{y}}} } \\ {n_{{\hat{x}^{e} \overline{x}}} n_{{\hat{x}^{e} \overline{z}}} } & {n_{{\hat{y}^{e} \overline{x}}} n_{{\hat{y}^{e} \overline{z}}} } & {n_{{\hat{x}^{e} \overline{x}}} n_{{\hat{y}^{e} \overline{z}}} + n_{{\hat{y}^{e} \overline{x}}} n_{{\hat{x}^{e} \overline{z}}} } \\ \end{array} } \right] $$

(65)

$$ {\mathbf{R}}_{{{\text{m}}_{k} }}^{{}} = {\mathbf{R}}_{{{\text{b}}_{k} }}^{{}} = \left[ {\begin{array}{*{20}l} {n_{{\hat{x}^{{e_{k} }} \overline{x}}}^{2} } & {n_{{\hat{y}^{{e_{k} }} \overline{x}}}^{2} } & {n_{{\hat{x}^{{e_{k} }} \overline{x}}} n_{{\hat{y}^{{e_{k} }} \overline{x}}} } \\ {n_{{\hat{x}^{{e_{k} }} \overline{y}}}^{2} } & {n_{{\hat{y}^{{e_{k} }} \overline{y}}}^{2} } & {n_{{\hat{x}^{{e_{k} }} \overline{y}}} n_{{\hat{y}^{{e_{k} }} \overline{y}}} } \\ {n_{{\hat{x}^{{e_{k} }} \overline{z}}}^{2} } & {n_{{\hat{y}^{{e_{k} }} \overline{z}}}^{2} } & {n_{{\hat{x}^{{e_{k} }} \overline{z}}} n_{{\hat{y}^{{e_{k} }} \overline{z}}} } \\ {2n_{{\hat{x}^{{e_{k} }} \overline{x}}} n_{{\hat{x}^{{e_{k} }} \overline{y}}} } & {2n_{{\hat{y}^{{e_{k} }} \overline{x}}} n_{{\hat{y}^{{e_{k} }} \overline{y}}} } & {n_{{\hat{x}^{{e_{k} }} \overline{x}}} n_{{\hat{y}^{{e_{k} }} \overline{y}}} + n_{{\hat{y}^{{e_{k} }} \overline{x}}} n_{{\hat{x}^{{e_{k} }} \overline{y}}} } \\ {2n_{{\hat{x}^{{e_{k} }} \overline{y}}} n_{{\hat{x}^{{e_{k} }} \overline{z}}} } & {2n_{{\hat{y}^{{e_{k} }} \overline{y}}} n_{{\hat{y}^{{e_{k} }} \overline{z}}} } & {n_{{\hat{x}^{{e_{k} }} \overline{z}}} n_{{\hat{y}^{{e_{k} }} \overline{y}}} + n_{{\hat{y}^{{e_{k} }} \overline{z}}} n_{{\hat{x}^{{e_{k} }} \overline{y}}} } \\ {2n_{{\hat{x}^{{e_{k} }} \overline{x}}} n_{{\hat{x}^{{e_{k} }} \overline{z}}} } & {2n_{{\hat{y}^{{e_{k} }} \overline{x}}} n_{{\hat{y}^{{e_{k} }} \overline{z}}} } & {n_{{\hat{x}^{{e_{k} }} \overline{x}}} n_{{\hat{y}^{{e_{k} }} \overline{z}}} + n_{{\hat{y}^{{e_{k} }} \overline{x}}} n_{{\hat{x}^{{e_{k} }} \overline{z}}} } \\ \end{array} } \right] $$

(66)

It should be noted that if there is no adjacent element on an edge of the target element, the target element itself is used as the adjacent element during the smoothing operation. Substituting the updated smoothed strains of edge centers obtained using Eqs. (59) and (60) into Eq. (57), and expanding it yields Eqs. (67)–(70):

$$ \left\{ \begin{array}{*{20}l} {{\varvec{\tilde \varepsilon }}}_{{\text{m}}}^{i} = {{\varvec{\tilde \varepsilon }}}_{{\text{m}}}^{{E_{1} }} - {{\varvec{\tilde \varepsilon }}}_{{\text{m}}}^{{E_{2} }} + {{\varvec{\tilde \varepsilon }}}_{{\text{m}}}^{{E_{3} }} = {\tilde{\mathbf{B}}}_{{\text{m}}}^{i} {\overline{\mathbf{q}}}_{f} \hfill \\ {{\varvec{\tilde \varepsilon }}}_{{\text{m}}}^{j} = {{\varvec{\tilde \varepsilon }}}_{{\text{m}}}^{{E_{1} }} + {{ \varvec{\tilde \varepsilon }}}_{{\text{m}}}^{{E_{2} }} - {{\varvec{\tilde \varepsilon }}}_{{\text{m}}}^{{E_{3} }} = {\tilde{\mathbf{B}}}_{{\text{m}}}^{j} {\overline{\mathbf{q}}}_{f} \hfill \\ {{\varvec{\tilde \varepsilon }}}_{{\text{m}}}^{k} = - {{\varvec{\tilde \varepsilon }}}_{{\text{m}}}^{{E_{1} }} + {{\varvec{\tilde\varepsilon }}}_{{\text{m}}}^{{E_{2} }} + {{\varvec{\tilde \varepsilon }}}_{{\text{m}}}^{{E_{3} }} = {\tilde{\mathbf{B}}}_{{\text{m}}}^{k} {\overline{\mathbf{q}}}_{f} \hfill \\ \end{array} \right. $$

(67)

$$ \left\{ \begin{array}{*{20}l} {{ \varvec{\tilde \varepsilon }}}_{{\text{b}}}^{i} = {{\varvec{\tilde\varepsilon }}}_{{\text{b}}}^{{E_{1} }} - {{\varvec{\tilde \varepsilon }}}_{{\text{b}}}^{{E_{2} }} + {{\varvec{\tilde \varepsilon }}}_{{\text{b}}}^{{E_{3} }} = {\tilde{\mathbf{B}}}_{{\text{b}}}^{i} {\overline{\mathbf{q}}}_{f} \hfill \\ {{\varvec{\tilde \varepsilon }}}_{{\text{b}}}^{j} = {{\varvec{\tilde\varepsilon }}}_{{\text{b}}}^{{E_{1} }} + {{\varvec{\tilde \varepsilon }}}_{{\text{b}}}^{{E_{2} }} - {{\varvec{\tilde\varepsilon }}}_{{\text{b}}}^{{E_{3} }} = {\tilde{\mathbf{B}}}_{{\text{b}}}^{j} {\overline{\mathbf{q}}}_{f} \hfill \\ {{\varvec{\tilde\varepsilon }}}_{{\text{b}}}^{k} = - {{\varvec{\tilde \varepsilon }}}_{{\text{b}}}^{{E_{1} }} + {{\varvec{\tilde \varepsilon }}}_{{\text{b}}}^{{E_{2} }} + {{\varvec{\tilde \varepsilon }}}_{{\text{b}}}^{{E_{3} }} = {\tilde{\mathbf{B}}}_{{\text{b}}}^{k} {\overline{\mathbf{q}}}_{f} \hfill \\ \end{array} \right. $$

(68)

$$ \left\{ \begin{array}{*{20}l} {\tilde{\mathbf{B}}}_{{\text{m}}}^{i} = {\tilde{\mathbf{B}}}_{{\text{m}}}^{{E_{1} }} - {\tilde{\mathbf{B}}}_{{\text{m}}}^{{E_{2} }} + {\tilde{\mathbf{B}}}_{{\text{m}}}^{{E_{3} }} \hfill \\ {\tilde{\mathbf{B}}}_{{\text{m}}}^{j} = {\tilde{\mathbf{B}}}_{{\text{m}}}^{{E_{1} }} + {\tilde{\mathbf{B}}}_{{\text{m}}}^{{E_{2} }} - {\tilde{\mathbf{B}}}_{{\text{m}}}^{{E_{3} }} \hfill \\ {\tilde{\mathbf{B}}}_{{\text{m}}}^{k} = - {\tilde{\mathbf{B}}}_{{\text{m}}}^{{E_{1} }} + {\tilde{\mathbf{B}}}_{{\text{m}}}^{{E_{2} }} + {\tilde{\mathbf{B}}}_{{\text{m}}}^{{E_{3} }} \hfill \\ \end{array} \right. $$

(69)

$$ \left\{ \begin{array}{*{20}l} {\tilde{\mathbf{B}}}_{{\text{b}}}^{i} = {\tilde{\mathbf{B}}}_{{\text{b}}}^{{E_{1} }} - {\tilde{\mathbf{B}}}_{{\text{b}}}^{{E_{2} }} + {\tilde{\mathbf{B}}}_{{\text{b}}}^{{E_{3} }} \hfill \\ {\tilde{\mathbf{B}}}_{{\text{b}}}^{j} = {\tilde{\mathbf{B}}}_{{\text{b}}}^{{E_{1} }} + {\tilde{\mathbf{B}}}_{{\text{b}}}^{{E_{2} }} - {\tilde{\mathbf{B}}}_{{\text{b}}}^{{E_{3} }} \hfill \\ {\tilde{\mathbf{B}}}_{{\text{b}}}^{k} = - {\tilde{\mathbf{B}}}_{{\text{b}}}^{{E_{1} }} + {\tilde{\mathbf{B}}}_{{\text{b}}}^{{E_{2} }} + {\tilde{\mathbf{B}}}_{{\text{b}}}^{{E_{3} }} \hfill \\ \end{array} \right. $$

(70)

Accordingly, the element-linear strain field can be expressed by Eqs. (71)–(74):

$$ {{\varvec{\tilde\varepsilon }}}_{{\text{m}}}^{e} = N_{i} {{\varvec{\tilde \varepsilon }}}_{{\text{m}}}^{i} + N_{j} {{\varvec{\tilde \varepsilon }}}_{{\text{m}}}^{j} + N_{k} {{\varvec{\tilde \varepsilon }}}_{{\text{m}}}^{k} = {\tilde{\mathbf{B}}}_{{\text{m}}}^{e} {\mathbf{d}} $$

(71)

$$ {{\varvec{\tilde \varepsilon }}}_{{\text{b}}}^{e} = N_{i} {{\varvec{\tilde \varepsilon }}}_{{\text{b}}}^{i} + N_{j} {{\varvec{\tilde \varepsilon }}}_{{\text{b}}}^{j} + N_{k} {{\varvec{\tilde \varepsilon }}}_{{\text{b}}}^{k} = {\tilde{\mathbf{B}}}_{{\text{b}}}^{e} {\mathbf{d}} $$

(72)

$$ {\tilde{\mathbf{B}}}_{{\text{m}}}^{e} = N_{i} {\tilde{\mathbf{B}}}_{{\text{m}}}^{i} + N_{j} {\tilde{\mathbf{B}}}_{{\text{m}}}^{j} + N_{k} {\tilde{\mathbf{B}}}_{{\text{m}}}^{k} $$

(73)

$$ {\tilde{\mathbf{B}}}_{{\text{b}}}^{e} = N_{i} {\tilde{\mathbf{B}}}_{{\text{b}}}^{i} + N_{j} {\tilde{\mathbf{B}}}_{{\text{b}}}^{j} + N_{k} {\tilde{\mathbf{B}}}_{{\text{b}}}^{k} $$

(74)

Remark 2

According to the smoothing strategy in Eqs. (59) and (60), consistency of the membrane and bending strains at the element junction center can be ensured.

Proof.

Adjacent shell elements are shown in Fig. 5. If $e_{1}$ is selected as the target element, then the smoothed strain ${\tilde{\mathbf{\varepsilon }}}^{1}$ can be expressed by Eq. (75):

$$ {{\varvec{\tilde \varepsilon }}}^{1} = \frac{1}{{A_{1} + A_{2} }}\left( {A_{1} {{\varvec{\upvarepsilon}}}_{1}^{1} + A_{2} {\mathbf{R}}^{{\text{T}}} {{\varvec{\upvarepsilon}}}_{2}^{2} {\mathbf{R}}} \right) $$

(75)

Fig. 5

Shell elements and their local coordinate systems

If $e_{2}$ is selected as the target element, then the smoothed strain ${\tilde{\mathbf{\varepsilon }}}^{2}$ is expressed by Eq. (76):

$$ {{\varvec{\tilde \varepsilon }}}^{2} = \frac{1}{{A_{1} + A_{2} }}\left( {A_{1} {\mathbf{R {\varvec \varepsilon }}}_{1}^{1} {\mathbf{R}}^{{\text{T}}} + A_{2} {{\varvec{\upvarepsilon}}}_{2}^{2} } \right) $$

(76)

Equation (77) necessarily follows:

$$ {{\varvec{\tilde \varepsilon }}}^{1} = {\mathbf{R}}^{{\text{T}}} {{\tilde{ \varvec \varepsilon }}}^{2} {\mathbf{R}},\quad {{\tilde{\varvec \varepsilon }}}^{2} = {\mathbf{R\tilde{ \varvec \varepsilon }}}^{1} {\mathbf{R}}^{{\text{T}}} $$

(77)

Equation (77) indicates that ${\tilde{\varvec{\varepsilon }}}^{1}$ and ${\tilde{\varvec{\varepsilon }}}^{2}$ are the same strain tensors represented in different coordinate systems. Therefore, the strain smoothing method proposed in this study ensures that the membrane and bending strains at the element junction are consistent, thereby improving the smoothness of the global stresses and strains from those of linear elements with discontinuous strains.

4 Dynamic equations for a flexible multibody system based on the ECSS-MITC method

4.1 Principle of virtual power

The virtual work caused by the elastic force of shell $I$ can be expressed by Eq. (78):

$$ \begin{aligned} {\delta }W_{f}^{I} & = - \left( {\int_{{\Omega^{I} }} {{\delta }{{\varvec{\upvarepsilon}}}_{{\text{m}}}^{{\text{T}}} {\mathbf{D}}_{{\text{m}}} {{\varvec{\upvarepsilon}}}_{{\text{m}}} } {\text{d}}\Omega^{I} + \int_{{\Omega^{I} }} {{\delta }{{\varvec{\upvarepsilon}}}_{{\text{b}}}^{{\text{T}}} {\mathbf{D}}_{{\text{b}}} {{\varvec{\upvarepsilon}}}_{{\text{b}}} } {\text{d}}\Omega^{I} + \int_{{\Omega^{I} }} {{\delta }{{\varvec{\upvarepsilon}}}_{{\text{s}}}^{{\text{T}}} {\mathbf{D}}_{{\text{s}}} {{\varvec{\upvarepsilon}}}_{{\text{s}}} } {\text{d}}\Omega^{I} } \right) \\ {\mathbf{D}}_{{\text{m}}} & = t{\mathbf{D}}_{0} ,\quad {\mathbf{D}}_{{\text{b}}} = \frac{{t^{3} }}{12}{\mathbf{D}}_{0} ,\quad {\mathbf{D}}_{{\text{s}}} = \kappa tG\left[ {\begin{array}{*{20}l} 1 & 0 \\ 0 & 1 \\ \end{array} } \right] \\ {\mathbf{D}}_{0} & = \frac{E}{{1 - v^{2} }}\left[ {\begin{array}{*{20}l} 1 & v & 0 \\ v & 1 & 0 \\ 0 & 0 & {{{\left( {1 - v} \right)} \mathord{\left/ {\vphantom {{\left( {1 - v} \right)} 2}} \right. \kern-\nulldelimiterspace} 2}} \\ \end{array} } \right] \\ \end{aligned} $$

(78)

where $G$ denotes the shear modulus, $\kappa = {5 \mathord{\left/ {\vphantom {5 6}} \right. \kern-\nulldelimiterspace} 6}$ represents the shear correction coefficient, and $E$ and $v$ are the Young's modulus and Poisson's ratio, respectively.

The geometry of the flexible body is approximated by discrete elements, and then Eqs. (49), (71) and (72) are substituted into Eq. (78) to obtain Eq. (79):

$$ \begin{aligned} {\delta }W_{f}^{I} & = - {\delta }\left( {{\overline{\mathbf{q}}}_{f}^{I} } \right)^{{\text{T}}} {\mathbf{K}}_{ff}^{I} {\overline{\mathbf{q}}}_{f}^{I} \\ {\mathbf{K}}_{ff}^{I} & = {\mathbf{K}}_{{\text{m}}}^{I} + {\mathbf{K}}_{{\text{b}}}^{I} + {\mathbf{K}}_{{\text{s}}}^{I} \\ & \left\{ \begin{gathered} {\mathbf{K}}_{{\text{m}}}^{I} = \sum\limits_{e} {\int_{{\Omega_{e}^{I} }} {\left( {{\tilde{\mathbf{B}}}_{{\text{m}}}^{e} } \right)^{{\text{T}}} {\mathbf{D}}_{{\text{m}}} {\tilde{\mathbf{B}}}_{{\text{m}}}^{e} } {\text{d}}\Omega^{I} } \hfill \\ {\mathbf{K}}_{{\text{b}}}^{e} = \sum\limits_{e} {\int_{{\Omega_{e}^{I} }} {\left( {{\tilde{\mathbf{B}}}_{{\text{b}}}^{e} } \right)^{{\text{T}}} {\mathbf{D}}_{{\text{b}}} {\tilde{\mathbf{B}}}_{{\text{b}}}^{e} } {\text{d}}\Omega^{I} } \hfill \\ {\mathbf{K}}_{{\text{s}}}^{e} = \sum\limits_{e} {\int_{{\Omega_{e}^{I} }} {\left( {{\mathbf{B}}_{{\text{s}}}^{e} } \right)^{{\text{T}}} {\mathbf{D}}_{{\text{s}}} {\mathbf{B}}_{{\text{s}}}^{e} } {\text{d}}\Omega^{I} } \hfill \\ \end{gathered} \right. \\ \end{aligned} $$

(79)

Equation (79) is then extended to include rigid displacement:

$$ \begin{aligned} {\delta }W_{f}^{I} & = - \left( {{\mathbf{X}}^{I} } \right)^{{\text{T}}} {\mathbf{K}}^{I} {\delta }{\mathbf{X}}^{I} = \left( {{\mathbf{Q}}_{f}^{I} } \right)^{{\text{T}}} {\delta }{\mathbf{X}}^{I} \\ {\mathbf{K}}^{I} & = \left[ {\begin{array}{*{20}l} {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {{\mathbf{K}}_{ff}^{I} } \\ \end{array} } \right] \\ \end{aligned} $$

(80)

In Eq. (80), ${\mathbf{Q}}_{f}^{I} = - \left( {{\mathbf{K}}^{I} } \right)^{{\text{T}}} {\mathbf{X}}^{I}$ denotes the generalized elastic force.

The external force acting on the shell is represented by ${\mathbf{F}}_{l}^{I}$. The virtual work caused by ${\mathbf{F}}_{l}^{I}$ given by Eq. (81):

$$ {\delta }W_{l}^{I} = \left( {{\mathbf{F}}_{l}^{I} } \right)^{{\text{T}}} {\delta }{\mathbf{r}}_{{P_{f} }} $$

(81)

Considering:

$$ {\delta }{\mathbf{r}}_{{P_{f} }} = \frac{{\partial {\mathbf{r}}_{{P_{f} }} }}{{\partial {\mathbf{X}}^{I} }}{\delta }{\mathbf{X}}^{I} = \frac{{\partial {\dot{\mathbf{r}}}_{{P_{f} }} }}{{\partial {\dot{\mathbf{X}}}^{I} }}{\delta }{\mathbf{X}}^{I} = {\mathbf{L}}^{I} {\delta }{\mathbf{X}}^{I} $$

(82)

Hence:

$$ {\delta }W_{l}^{i} = \left( {{\mathbf{F}}_{l}^{i} } \right)^{{\text{T}}} {\mathbf{L}}^{i} {\delta }{\mathbf{X}}^{i} = \left( {{\mathbf{Q}}_{\mathrm{l}}^{i} } \right)^{{\text{T}}} {\delta }{\mathbf{X}}^{i} $$

(83)

In Eq. (83), ${\mathbf{Q}}_{{\text{l}}}^{I} = \left( {{\mathbf{L}}^{I} } \right)^{{\text{T}}} {\mathbf{F}}_{l}^{I}$ denotes the generalized external force.

Based on this analysis, the generalized force can be expressed by Eq. (84):

$$ {\mathbf{Q}}^{I} = {\mathbf{Q}}_{f}^{I} + {\mathbf{Q}}_{\mathrm{l}}^{I} $$

(84)

Equation (85) is obtained from the virtual power principle:

$$ \int_{{\Omega^{I} }} {\rho^{I} {\delta }\left( {{\dot{\mathbf{r}}}_{{P_{f} }}^{I} } \right)^{{\text{T}}} {\ddot{\mathbf{r}}}_{{P_{f} }}^{I} {\text{d}}\Omega^{I} } - {\delta }\left( {{\dot{\mathbf{X}}}^{I} } \right)^{{\text{T}}} {\mathbf{Q}}^{I} = 0 $$

(85)

where $\rho^{I}$ denotes the density of shell $I$. Substituting Eqs. (22) and (23) into Eq. (85) yields Eq. (86):

$$ {\delta }\left( {{\dot{\mathbf{X}}}^{I} } \right)^{{\text{T}}} \int_{{\Omega^{I} }} {\rho^{I} \left( {{\mathbf{L}}^{I} } \right)^{{\text{T}}} \left( {{\mathbf{L}}^{I} {\ddot{\mathbf{X}}}^{I} + {\mathbf{a}}_{v}^{I} } \right){\text{d}}\Omega^{I} {{ + \delta }}\left( {{\dot{\mathbf{X}}}^{I} } \right)^{{\text{T}}} {\mathbf{K}}^{I} {\mathbf{X}}^{I} - {\delta }\left( {{\dot{\mathbf{X}}}^{I} } \right)^{{\text{T}}} {\mathbf{Q}}_{\mathrm{l}}^{I} = 0} $$

(86)

Equation (87) is obtained by further rearranging Eq. (86) and accounting for the arbitrariness of ${\delta }\left( {{\dot{\mathbf{X}}}^{i} } \right)^{{\text{T}}}$:

$$ \begin{aligned} & {\mathbf{M}}^{I} {\ddot{\mathbf{X}}}^{I} + {\mathbf{K}}^{I} {\mathbf{X}}^{I} = {\mathbf{Q}}_{\mathrm{l}}^{I} - {\mathbf{Q}}_{\mathrm{v}}^{I} \\ & {\mathbf{M}}^{I} = \int_{{\Omega^{I} }} {\rho^{I} \left( {{\mathbf{L}}^{I} } \right)^{{\text{T}}} {\mathbf{L}}^{I} {\text{d}}\Omega^{I} } ,\quad {\mathbf{Q}}_{\mathrm{v}}^{I} = \int_{{\Omega^{I} }} {\rho^{I} \left( {{\mathbf{L}}^{I} } \right)^{{\text{T}}} {\mathbf{a}}_{v}^{I} {\text{d}}\Omega^{I} } \\ \end{aligned} $$

(87)

Equation (87) is the dynamic equation for the shell in an unconstrained state. Detailed forms of the mass matrix ${\mathbf{M}}^{I}$ and the velocity coupling vector ${\mathbf{Q}}_{\mathrm{v}}^{I}$ are discussed in “Appendix A”.

4.2 Governing equations with constraints

For a dynamic system with $N$ multiflexible bodies in a free state, the system dynamics equation can be expressed by Eq. (88):

$$ \begin{aligned} & {\mathbf{M}}\ddot{\mathbf{X}} + {\mathbf{KX}} = {\mathbf{Q}}_{\mathrm{l}} - {\mathbf{Q}}_{\mathrm{v}} \\ & {\mathbf{M}} = {\text{diag}}\left\{ {\begin{array}{*{20}l} {{\mathbf{M}}^{1} } & \cdots & {{\mathbf{M}}^{I} } & \cdots & {{\mathbf{M}}^{N} } \\ \end{array} } \right\} \\ & {\mathbf{K}} = {\text{diag}}\left\{ {\begin{array}{*{20}l} {{\mathbf{K}}^{1} } & \cdots & {{\mathbf{K}}^{I} } & \cdots & {{\mathbf{K}}^{N} } \\ \end{array} } \right\} \\ & {\mathbf{X}} = \left[ {\begin{array}{*{20}l} {\left( {{\mathbf{X}}^{1} } \right)^{{\text{T}}} } & \cdots & {\left( {{\mathbf{X}}^{I} } \right)^{{\text{T}}} } & \cdots & {\left( {{\mathbf{X}}^{N} } \right)^{{\text{T}}} } \\ \end{array} } \right]^{{\text{T}}} \\ & {\mathbf{Q}}_{{\text{l}}} = \left[ {\begin{array}{*{20}l} {\left( {{\mathbf{Q}}_{{\text{l}}}^{1} } \right)^{{\text{T}}} } & \cdots & {\left( {{\mathbf{Q}}_{{\text{l}}}^{I} } \right)^{{\text{T}}} } & \cdots & {\left( {{\mathbf{Q}}_{{\text{l}}}^{N} } \right)^{{\text{T}}} } \\ \end{array} } \right]^{{\text{T}}} \\ & {\mathbf{Q}}_{{\text{v}}} = \left[ {\begin{array}{*{20}l} {\left( {{\mathbf{Q}}_{{\text{v}}}^{1} } \right)^{{\text{T}}} } & \cdots & {\left( {{\mathbf{Q}}_{{\text{v}}}^{I} } \right)^{{\text{T}}} } & \cdots & {\left( {{\mathbf{Q}}_{{\text{v}}}^{N} } \right)^{{\text{T}}} } \\ \end{array} } \right]^{{\text{T}}} \\ \end{aligned} $$

(88)

Considering kinematic constraints in a multibody system, the vector equation in Eq. (89) is satisfied:

$$ {\mathbf{C}}\left( {{\mathbf{X}},t} \right) = {\mathbf{0}} $$

(89)

By introducing a Lagrange multiplier ${{\varvec{\upalpha}}}$, the following differential equations are obtained:

$$ {\mathbf{M}}\ddot{\mathbf{X}} + {\mathbf{KX}} + {\mathbf{C}}_{{\mathbf{X}}}^{{\text{T}}} {{\varvec{\upalpha}}} = {\mathbf{Q}}_{\mathrm{l}} - {\mathbf{Q}}_{\mathrm{v}} $$

(90)

where ${\mathbf{C}}_{{\mathbf{X}}}$ is the Jacobian of the constraint function ${\mathbf{C}}\left( {{\mathbf{X}},t} \right)$.

The acceleration constraint equation is obtained by taking the second derivative of the constraint equation with respect to time

$$ \begin{aligned} {\ddot{\mathbf{C}}} & = {\mathbf{C}}_{{\mathbf{X}}} {\ddot{\mathbf{X}}} + {\mathbf{Q}}_{c} \\ {\mathbf{Q}}_{c} & = - {\mathbf{C}}_{tt} - 2{\mathbf{C}}_{{{\mathbf{X}}t}} {\dot{\mathbf{X}}} - \left( {{\mathbf{C}}_{{\mathbf{X}}} {\dot{\mathbf{X}}}} \right)_{{\mathbf{X}}} {\dot{\mathbf{X}}} \\ \end{aligned} $$

(91)

The governing equation with kinematic constraints is obtained by combining Eqs. (88) and  (91):

$$ \left[ {\begin{array}{*{20}l} {\mathbf{M}} & {{\mathbf{C}}_{{\mathbf{X}}}^{{\text{T}}} } \\ {{\mathbf{C}}_{{\mathbf{X}}} } & {\mathbf{0}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {{\ddot{\mathbf{X}}}} \\ {{\varvec{\upalpha}}} \\ \end{array} } \right]{ = }\left[ {\begin{array}{*{20}l} {{\mathbf{Q}}_{\mathrm{l}} - {\mathbf{Q}}_{\mathrm{v}} - {\mathbf{KX}}} \\ {{\mathbf{Q}}_{c} } \\ \end{array} } \right] $$

(92)

5 Convergence tests

For this section, two typical structural analyses were conducted to verify the performance of the proposed ECSS-MITC method. To quantitatively measure the accuracy of the numerical method, the strain energy error norm $e_{e}$ was defined as shown in Eq. (93):

$$ e_{e} = \sqrt {\frac{{\left| {E^{{{\text{num}}}} - E^{{{\text{Ref}}}} } \right|}}{{E^{{{\text{Ref}}}} }}} $$

(93)

where $E^{{{\text{num}}}}$ and $E^{{{\text{Ref}}}}$ represent the numerical and reference strain energy results, respectively.

5.1 Hyperboloid shell

First, a hyperboloid shell problem was used as a benchmark to conduct a comprehensive performance test of the proposed ECSS-MITC method. As shown in Fig. 6, the thickness is represented by $t$ and the middle surface of the hyperboloid shell satisfies the geometric equation: $x^{2} + y^{2} = 1 + z^{2}$, where $y \in \left[ { - 1,1} \right]$. The inner wall of the shell was subjected to a harmonic pressure distribution of $p = p_{0} {\text{cos}}\left( {{2}\theta } \right)$, where $p_{0} = 1000$. When the upper and lower ends of the shell are clamped, the shell is in a state dominated by membrane deformation. This was the situation of focus during this test. Considering the symmetry of the problem, one-eighth of the original problem was selected for analysis. Meshes were assigned as shown in Fig. 6, in which $N$ meshes were uniformly arranged along the $y$ axis. Regular meshes were uniformly arranged along the circumferential direction, while there were distorted for distortion meshes. The mesh size was defined as $h = {1 \mathord{\left/ {\vphantom {1 N}} \right. \kern-\nulldelimiterspace} N}$.

Fig. 6

Geometry and mesh of the hyperboloid shell

Figure 7 shows the strain energy error convergence curves for the four numerical methods at different thicknesses. In the figure, $R$ represents the linear fitting slope corresponding to the curve. The smaller ${\text{log}}\left( {e_{e} } \right)$ or ${\text{log}}\left( h \right)$ respectively represent the smaller error or the finer mesh, and a larger $R$ value indicates a greater error convergence rate. It can be seen from the overall trend of the curves in the figure that the error of the ECSS-MITC method is smaller than that of the other three methods, and the error converges faster with the increase of the number of meshes. In addition, as the thickness decreases, these methods are affected by shear locking, while the ECSS-MITC method is relatively less affected. It can be concluded that the ECSS-MITC method proposed in this study possesses advantages over other methods in terms of the error convergence rate and accuracy, and can satisfactorily overcome the shear locking problem.

Fig. 7

Convergence curves for the strain energy error norm with different thicknesses: a $t = 0.01$, and b $t = 0.001$. (Color figure online)

Figures 8 and 9 show Von Mises equivalent stress distributions obtained from different numerical methods with $N = 16$ (without other post-processing). Although it has been proven above that the ECSS scheme proposed in this paper can guarantee strain consistency at the element edge junctions, this advantage is more intuitively highlighted in these figures. The results of the MITC3, DSG and NSFEM methods all have obvious stress discontinuities between elements or between smoothed domains, while the ECSS-MITC results are relatively smoother. Additionally, the smoothness of the ECSS-MITC results is weak at the boundary with a large stress gradient. This occurs primarily because of the lack of elements involved in the smoothing operation at the boundary. Managing this problem will also be the focus of subsequent research.

Fig. 8

Von Mises equivalent stress distributions in the top surface with thickness $t = 0.01$ using different methods: a DSG, b MITC3, c NSFEM, d ECSS-MITC, and e Abaqus. (Color figure online)

Fig. 9

Von Mises equivalent stress distributions in the top surface with thickness $t = 0.001$ using different methods: a DSG, b MITC3, c NSFEM, d ECSS-MITC, and e Abaqus. (Color figure online)

Subsequently, the sensitivity to mesh distortion and the computational efficiency of the ECSS-MITC method were tested, and the results are shown in Figs. 10 and 11, respectively. The results in Fig. 10 indicate that the error convergence curve for the ECSS-MITC method is not seriously affected by the distorted mesh. For the computational efficiency study, we present a curve analyzing the error versus the CPU runtime ($t_{{{\text{CPU}}}}$), and all methods were programmed into the same hardware environment (CPU: Intel Core i7-10510U; Memory: 16 GB). Compared with the other methods tested, the ECSS-MITC has certain advantages in computational efficiency.

Fig. 10

Strain energy convergence curves using distorted mesh with thickness of $t = 0.001$. (Color figure online)

Fig. 11

Computational efficiency curves with thickness of $t = 0.001$. (Color figure online)

5.2 Cylindrical shell

Next, a cylindrical shell with length $L = 1$, radius $R = 1$ and thickness $t$ as shown in Fig. 12, was employed as another benchmark problem for convergence tests. Two cylindrical shell states are discussed. They are clamped and free at both ends of the shell ($z = \pm L$), corresponding to membrane-dominated and bending-dominated problems, respectively. The inner wall of the shell was subjected to a distributed load equal to that in the hyperboloid shell analysis: $p\left( \theta \right) = p_{0} {\text{cos}}\left( {2\theta } \right)$, where $p_{0} = 1000$. The material parameters were also the same as for the hyperboloid shell. Considering symmetry, one-eighth of the original model was selected for analysis. The strategy of arranging $N$ meshes along the axis was adopted as shown in Fig. 6, and the mesh size was defined as $h = {L \mathord{\left/ {\vphantom {L N}} \right. \kern-\nulldelimiterspace} N}$. The reference results were obtained by simulating in Abaqus (15,958 nodes and 15,700 quadratic quadrilateral elements).

Fig. 12

Cylindrical shell

Figure 13 shows the convergence curves for the four numerical methods at different thicknesses for the analysis of the membrane-dominant problem, and Fig. 14 shows the results for the bending-dominant problem. In this verification process, we can find that membrane locking and bending locking have a greater impact on the NSFEM and DSG methods. Although the MITC3 method has certain advantages in overcoming membrane locking and bending locking, the effect of the ECSS-MITC method is more obvious. Similarly, the ECSS-MITC method is less sensitive to shear locking effects as the thickness decreases.

Fig. 13

Strain energy error convergence results for the membrane problem: a ${t \mathord{\left/ {\vphantom {t L}} \right. \kern-\nulldelimiterspace} L} = 0.01$, and b ${t \mathord{\left/ {\vphantom {t L}} \right. \kern-\nulldelimiterspace} L} = 0.001$. (Color figure online)

Fig. 14

Strain energy error convergence results for the bending problem: a ${t \mathord{\left/ {\vphantom {t L}} \right. \kern-\nulldelimiterspace} L} = 0.01$, and b ${t \mathord{\left/ {\vphantom {t L}} \right. \kern-\nulldelimiterspace} L} = 0.001$. (Color figure online)

Based on the analysis results of the above two benchmark examples, it can be concluded that: firstly, the ECSS-MITC method has obvious effect in overcoming membrane locking and shear locking, and thus exhibits high accuracy and high error convergence rate in the analysis. Secondly, the ECSS-MITC method is less sensitive to mesh distortion and has high computational efficiency. Finally, the ECSS-MITC can obtain a smoother stress field without additional post-processing.

6 Numerical tests of dynamic problems

6.1 In-plane single pendulum

A two-dimensional pendulum dynamics problem was first considered to illustrate the advantages of using the proposed ECSS method for flexible dynamics analyses. As shown in Fig. 15, a beam rotated about axis $Oz$ under the drive of moment $M = 100{\text{ N}}\,{\text{mm}}$. The beam was assumed to be in a state of plane stress and had a unit thickness. Reference results were obtained in Abaqus using four-node quadrilateral elements, and the total number of nodes and elements were 15,175 and 14,869, respectively.

Fig. 15

Geometry, materials and mesh for the single pendulum model. (Color figure online)

Figures 16, 17, 18 and 19 show the rotation angle, rotational angular velocity, displacement, and strain energy results, respectively, obtained from the ECSS method, as well as error comparisons with two other numerical methods. These figures show that the results obtained from the ECSS method are highly consistent with the Abaqus simulation results. In addition, by analyzing the accuracy of the three methods, it is not difficult to observe that the accuracy of the ECSS method is higher than that of the FEM or the NSFEM for this dynamic analysis.

Fig. 16

Rotation curves for the beam: a angle, and b absolute error. (Color figure online)

Fig. 17

Angular velocity of the beam: a velocity, and b absolute error. (Color figure online)

Fig. 18

Displacement curve at point $\left( {50,10} \right)$: a displacement in the y direction, and b absolute error. (Color figure online)

Fig. 19

Strain energy of the beam, a strain energy, and b absolute error. (Color figure online)

6.2 Double pendulum problem for shell structures

Next, a double pendulum system composed of thin-walled structures was investigated. As shown in Fig. 20, a flexible shell was fixed to the ground by a revolute joint, and a rigid plate was connected to one end of the shell by another revolute joint. The shell was a quarter of a cylindrical shell with a radius of $R = {\text{500 mm}}$, a width of $W_{{1}} = {\text{200 mm}}$ and a thickness of $t_{1} = 10{\text{ mm}}$. The plate had a width of $W_{2} = {\text{200 mm}}$, a length of $L = 5{\text{00 mm}}$ and a thickness of $t_{2} = 10{\text{ mm}}$. The flexible shell was subjected to a moment $M = M_{0} {\text{sin}}\left( {8\pi t} \right)$ along the $Oz$ axis, where $M_{{0}} = - {\text{200 N}}\,{\text{m}}$ and the minus sign indicates the negative direction along the $Oz$ axis. Under the revolute joint constraints, the shell rotated around the $Oz$ axis and drove the plate to move with the shell, while the plate rotated around the edge CD. In this analysis, a modal synthesis method was adopted to further reduce the order of the system. A supplemental description of the modal synthesis theory is provided in “Appendix B”. Reference results were obtained in Abaqus using four-node quadrilateral elements, and the total number of nodes and elements were 10,047 and 9800, respectively.

Fig. 20

Double pendulum system with a thin-walled structure, and the mesh for the flexible shell

First, the influence of the number of modes on the results is discussed. Figure 21 shows the strain energy curves for the flexible shell obtained by selecting the first 2, 5, and 10 modes. The figure shows that when only the first two modes are selected, the strain energy error obtained is significantly larger. When the first 5 and 10 modes are selected, there is no obvious difference between the results. Therefore, to reduce the computational burden, the first five modes were used for subsequent analysis.

Fig. 21

Strain energy response of the flexible shell, a strain energy, and b absolute error (Color figure online)

Figures 22 and 23 show the rigid rotational angular displacement and the angular velocity of the double pendulum system respectively. Figure 24 shows the displacement curve of point B in the rotation process. These results indicate that the method presented in this study can obtain satisfactory results for the analysis of multibody problems. Furthermore, Fig. 25 shows the stress distribution in the flexible shell for different numerical discretization schemes. It is apparent that the ECSS-MITC method still possesses the advantage of obtaining a highly smooth stress field for this example.

Fig. 22

Rotation curves for the multibody systems: a flexible shell, and b rigid plate. (Color figure online)

Fig. 23

Angular velocity of the multibody systems: a flexible shell, and b rigid plate (Color figure online)

Fig. 24

Displacement curve at point B: a in the x direction, and b in the y direction. (Color figure online)

Fig. 25

Von Mises equivalent stresses in flexible shell at $t = 0.2{\text{ s}}$, a DSG, b MITC3, c NSFEM, d ECSS-MITC, and d Abaqus. (Color figure online)

Furthermore, we compare the running time of the two methods. Table 1 lists the discretization strategy of the flexible body and the CPU time of the running process. It can be seen that the computational efficiency of ECSS-MITC is satisfactory. In addition, it should be noted that there is still room for optimization of our program code to further improve the computational efficiency.

Table 1 Comparison of discretization strategy and computation time between the two methods

6.3 Dynamics analysis of an engineering manipulator

Finally, the proposed method was applied to the dynamic analysis of an engineering manipulator. Figure 26 shows the 3D geometric model for the whole manipulator system. A motor drove the manipulator to rotate around the shaft after passing through a reducer. The load was fixed at one end of the manipulator and moved to a corresponding position with the manipulator to complete the work process. The manipulator was welded with steel plates and shells with a thickness of 4 mm, while the load, with a total mass of about 80 kg, was regarded as a rigid body during the motion process. The output driving torque curve for the motor after the reducer is shown in Fig. 27. Reference results were obtained by simulation in Abaqus, and pre-processing used a mixed triangle and quadrilateral mesh. The numbers of triangular and quadrilateral meshes were 491 and 31,631, respectively, and the total number of nodes was 31,937. In the ECSS-MITC numerical analysis, a total of 2494 triangular elements and 1296 nodes were used. The modal synthesis method was again employed to select the first five modes for analysis.

Fig. 26

Manipulator system

Fig. 27

Torque curve

Figure 28 shows the rotation angle and angular velocity curves for the manipulator during its motion. Figure 29 shows the displacement curve of the barycenter of the load. In addition, in the analysis of this problem, ECSS-MITC uses a small number of meshes to get a good agreement with the reference, and its running time is about 50 min. Abaqus, as a reference, uses a large number of meshes and runs for a total of about 14 h. It is apparent that the method proposed in this study is highly accurate and efficient when solving complicated models, which indicates that it has considerable engineering application value.

Fig. 28

Manipulator rotation results: a angle, and b angular velocity. (Color figure online)

Fig. 29

Displacement results for the barycenter of the load: a in the x direction, and b in the y direction. (Color figure online)

Synthesis of the above three dynamic problems. We sum up two key points, one is that the ESS-MITC method still maintains its own advantages in the analysis of flexible multibody dynamics. The other is that the multibody dynamics method of shell structure proposed in this paper can well analyze the dynamic characteristics of various thin-walled structures and has a wide range of applications.

7 Conclusions

The main purpose of this paper is to study the dynamics of multibody systems with thin-walled structures. To solve this problem, we propose a dynamic modeling method for flexible multibody system based on the Reissner–Mindlin shell in the FFRF framework. In addition, an ECSS-MITC method is proposed for the numerical discretization of shell structures. In this paper, we give a rigorous mathematical derivation of our work. On this basis, a series of numerical examples are given to verify our work.

The ECSS-MITC method proposed in this study processes the membrane and bending strains by strain smoothing with an MITC3 element. A linear strain field is constructed within the element and the strain consistency is ensured at the element junction center. Therefore, the ECSS-MITC method not only improves the membrane behavior, but also produces a smoother stress field without additional post-processing. Through the analysis of two benchmark examples, the ECSS-MITC method shows excellent performance in analysis of shell problem, such as high precision, high error convergence, less sensitive to mesh distortion and high efficiency. In particular, it can obtain a smoother stress field without additional post-processing.

In the light of the deformation characteristics of the Reissner–Mindlin plates, in addition to the membrane behavior, the bending behavior is also coupled with the rigid motion in the dynamics equation, which is different from the behavior of the solid flexible multibody model. By combining with the ECSS-MITC method, we have achieved satisfactory results in the analysis of the flexible multibody systems. The results of dynamic response are in good agreement with the reference results under a small number of meshes.

The model presented in this paper can be regarded as a general dynamics model for flexible multibody analyses of Reissner–Mindlin shells. Importantly, they can be conveniently and efficiently applied to engineering problems. Although the work in this paper focuses on the problem of large rotation and small deformation, we intend to further explore the problem of nonlinear deformation and the coupling of multiple physical fields.

Appendices

Appendix A

1.1 Integral of the element mass matrix

After the structure is discretized, the symmetrical mass matrix can be expressed as follows:

$$ {\mathbf{M}}^{I} = \sum\limits_{e} {\int_{{\Omega_{e}^{I} }} {\rho^{I} \left( {{\mathbf{L}}^{I} } \right)^{{\text{T}}} {\mathbf{L}}^{I} {\text{d}}\Omega^{I} } } = \sum\limits_{e} {{\mathbf{M}}_{\mathrm{e}}^{I} } $$

where ${\mathbf{M}}_{\mathrm{e}}^{I}$ represents the element mass matrix, which is symmetric. It can be decomposed into the following block matrices, which represent the rigid translation, rigid rotation, flexible deformation and the coupling among them, respectively.

$$ {\mathbf{M}}_{\mathrm{e}}^{I} = \sum\limits_{e} {\int_{{\Omega_{e}^{I} }} {\rho^{I} \left( {{\mathbf{L}}^{I} } \right)^{{\text{T}}} {\mathbf{L}}^{I} {\text{d}}\Omega^{I} } } = \left[ {\begin{array}{*{20}l} {{\mathbf{M}}_{\mathrm{e}RR}^{I} } & {{\mathbf{M}}_{\mathrm{e}R\theta }^{I} } & {{\mathbf{M}}_{\mathrm{e}Rf}^{I} } \\ {\left( {{\mathbf{M}}_{\mathrm{e}R\theta }^{I} } \right)^{{\text{T}}} } & {{\mathbf{M}}_{\mathrm{e}\theta \theta }^{I} } & {{\mathbf{M}}_{\mathrm{e}\theta f}^{I} } \\ {\left( {{\mathbf{M}}_{\mathrm{e}Rf}^{I} } \right)^{{\text{T}}} } & {\left( {{\mathbf{M}}_{\mathrm{e}\theta f}^{I} } \right)^{{\text{T}}} } & {{\mathbf{M}}_{\mathrm{eff}}^{I} } \\ \end{array} } \right] $$

Based on the formula of ${\mathbf{L}}^{I} = \left[ {\begin{array}{*{20}l} {\mathbf{I}} & { - {\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }} } & {{\mathbf{A}}^{I} {{\varvec{\uplambda}}}^{e} {\overline{\mathbf{S}}}} \\ \end{array} } \right]$ derived in Sect. 2, the formula of each block matrix in ${\mathbf{M}}_{\mathrm{e}}^{I}$ is presented in detail below.

(1) ${\mathbf{M}}_{\mathrm{e}RR}^{I} = \int_{{\Omega_{e}^{I} }} {\rho^{I} {\mathbf{I}}{\text{d}}\Omega^{I} } = m_{\mathrm{e}}^{I} {\mathbf{I}}$where $m_{\mathrm{e}}^{I} = \int_{{\Omega_{e}^{I} }} {\rho^{I} {\text{d}}\Omega^{I} }$ denotes the element mass.

(2) ${\mathbf{M}}_{\mathrm{e}R\theta }^{I} = - \int_{{\Omega_{e}^{I} }} {\rho^{I} {\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }} {\text{d}}\Omega^{I} }$.

Considering Eq. (24):

$$ \begin{aligned} {\mathbf{M}}_{\mathrm{e}R\theta }^{I} &= - \int_{{\Omega_{e}^{I} }} {\rho^{I} \left( {{\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}^{0} + {\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}^{m} + \hat{z}{\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}^{b} } \right){\text{d}}\Omega^{I} } \\ & = - \int_{{A_{e} }} {\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\rho^{I} \left( {{\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}^{0} + {\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}^{m} + \hat{z}{\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}^{b} } \right)} {\text{d}}\hat{z}{\text{d}}A} \\ & = - \rho^{I} h^{I} \int_{{A_{e} }} {\left( {{\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}^{0} + {\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}^{m} } \right){\text{d}}A} \end{aligned} $$

where $h^{I}$ is the element thickness.

(3) ${\mathbf{M}}_{\mathrm{e}Rf}^{I} = - \int_{{\Omega_{e}^{I} }} {\rho^{I} {\mathbf{A}}^{I} {{\varvec{\uplambda}}}^{e} {\overline{\mathbf{S}}}{\text{d}}\Omega^{I} }$.

Considering Eq. (16):

$$ \begin{aligned} {\mathbf{M}}_{\mathrm{e}Rf}^{I} &= - \rho^{I} {\mathbf{A}}^{I} {{\varvec{\uplambda}}}^{e} \int_{{\Omega_{e}^{I} }} {{\overline{\mathbf{S}}}{\text{d}}\Omega^{I} } \\ & = - \rho^{I} {\mathbf{A}}^{I} {{\varvec{\uplambda}}}^{e} \int_{{A_{e} }} {\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\left( {{\overline{\mathbf{S}}}_{m} + \hat{z}{\overline{\mathbf{S}}}_{b} } \right){\text{d}}\hat{z}} {\text{d}}A} \\ & = - \rho^{I} h^{I} {\mathbf{A}}^{I} {{\varvec{\uplambda}}}^{e} \int_{{A_{e} }} {{\overline{\mathbf{S}}}_{m} {\text{d}}A} \\ \end{aligned} $$

(4) ${\mathbf{M}}_{\mathrm{e}\theta \theta }^{I} = \int_{{\Omega_{e}^{I} }} {\rho^{I} {\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}^{T} {\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }} {\text{d}}\Omega^{I} } = - \int_{{\Omega_{e}^{I} }} {\rho^{I} {\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }} {\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }} {\text{d}}\Omega^{I} }$.

Considering Eq. (24):

$$ {\mathbf{M}}_{\mathrm{e}\theta \theta }^{I} = \left\{ \begin{gathered} - \rho^{I} h^{I} \int_{{A_{e} }} {\left( {{\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}^{0} + {\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}^{m} } \right)\left( {{\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}^{0} + {\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}^{m} } \right){\text{d}}A} \hfill \\ - \rho^{I} \frac{{\left( {h^{I} } \right)^{3} }}{12}\int_{{A_{e} }} {{\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}^{b} {\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}^{b} {\text{d}}A} \hfill \\ \end{gathered} \right\} $$

(5) ${\mathbf{M}}_{\mathrm{e}\theta f}^{I} = - \int_{{\Omega_{e}^{I} }} {\rho^{I} {\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}^{{\text{T}}} {\mathbf{A}}^{I} {{\varvec{\uplambda}}}^{e} {\overline{\mathbf{S}}}{\text{d}}} \Omega^{I} = \int_{{\Omega_{e}^{I} }} {\rho^{I} {\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }} {\mathbf{A}}^{I} {{\varvec{\uplambda}}}^{e} {\overline{\mathbf{S}}}{\text{d}}\Omega^{I} }$.

Similarly:

$$ \begin{aligned} {\mathbf{M}}_{\mathrm{e}\theta f}^{I} &= \int_{{A_{e} }} {\int_{{ - \frac{{h^{I} }}{2}}}^{{\frac{{h^{I} }}{2}}} {\rho^{I} \left( {{\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}^{0} + {\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}^{m} + \hat{z}{\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}^{b} } \right){\mathbf{A}}^{I} {{\varvec{\uplambda}}}^{e} \left( {{\overline{\mathbf{S}}}_{m} + \hat{z}{\overline{\mathbf{S}}}_{b} } \right){\text{d}}\hat{z}{\text{d}}A} } \hfill \\ & = \left\{ \begin{gathered} \rho^{I} h^{I} \int_{{A_{e} }} {\left( {{\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}^{0} + {\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}^{m} } \right){\mathbf{A}}^{I} {{\varvec{\uplambda}}}^{I} {\overline{\mathbf{S}}}_{m} {\text{d}}A} \hfill \\ + \rho^{I} \frac{{\left( {h^{I} } \right)^{3} }}{12}\int_{{\Omega^{e} }} {{\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}^{b} {\mathbf{A}}^{I} {{\varvec{\uplambda}}}^{e} {\overline{\mathbf{S}}}_{b} {\text{d}}\Omega^{e} } \hfill \\ \end{gathered} \right\} \\ \end{aligned} $$

(6) ${\mathbf{M}}_{\mathrm{eff}}^{I} = \int_{{\Omega_{e}^{I} }} {\rho^{I} \left( {{\mathbf{A}}^{I} {{\varvec{\uplambda}}}^{e} {\overline{\mathbf{S}}}} \right)^{{\text{T}}} \left( {{\mathbf{A}}^{I} {{\varvec{\uplambda}}}^{e} {\overline{\mathbf{S}}}} \right){\text{d}}\Omega^{I} }$.

Since $\left( {{\mathbf{A}}^{I} } \right)^{{\text{T}}} {\mathbf{A}}^{I} = \left( {{{\varvec{\uplambda}}}^{e} } \right)^{{\text{T}}} {{\varvec{\uplambda}}}^{e} = {\mathbf{I}}$:

$$ \begin{aligned} {\mathbf{M}}_{\mathrm{eff}}^{I} &= \int_{{\Omega_{e}^{I} }} {\rho^{I} {\overline{\mathbf{S}}}^{{\text{T}}} {\overline{\mathbf{S}}}{\text{d}}\Omega^{I} } \\ & = \int_{{A_{e} }} {\int_{{ - \frac{{h^{I} }}{2}}}^{{\frac{{h^{I} }}{2}}} {\rho^{I} \left( {{\overline{\mathbf{S}}}_{m} + \hat{z}{\overline{\mathbf{S}}}_{b} } \right)^{{\text{T}}} \left( {{\overline{\mathbf{S}}}_{m} + \hat{z}{\overline{\mathbf{S}}}_{b} } \right){\text{d}}\hat{z}{\text{d}}A} } \hfill \\ &= \rho^{I} h^{I} \int_{{A_{e} }} {{\overline{\mathbf{S}}}_{m}^{{\text{T}}} {\overline{\mathbf{S}}}_{m} {\text{d}}A} + \rho^{I} \frac{{\left( {h^{I} } \right)^{3} }}{12}\int_{{A_{e} }} {{\overline{\mathbf{S}}}_{b}^{{\text{T}}} {\overline{\mathbf{S}}}_{b} {\text{d}}A} \\ \end{aligned} $$

1.2 Integral of the element velocity coupling vector

The specific expression for ${\mathbf{Q}}_{\mathrm{v}}^{I}$ can be similarly decomposed:

$$ {\mathbf{Q}}_{\mathrm{v}}^{I} = \sum\limits_{e} {\int_{{\Omega_{e}^{I} }} {\rho^{I} \left( {{\mathbf{L}}^{I} } \right)^{{\text{T}}} {\mathbf{a}}_{v}^{I} {\text{d}}\Omega^{I} } } = \sum\limits_{e} {\left[ {\begin{array}{*{20}l} {{\mathbf{Q}}_{evR}^{I} } \\ {{\mathbf{Q}}_{ev\theta }^{I} } \\ {{\mathbf{Q}}_{evf}^{I} } \\ \end{array} } \right]} $$

Similarly, consider Eqs. (16), (24) and (25) to integrate the above vectors:

$$ \begin{aligned} {\mathbf{Q}}_{evR}^{I} &= \int_{{\Omega_{e}^{I} }} {\rho^{I} {\mathbf{a}}_{v}^{I} {\text{d}}\Omega^{I} } \\ & = \rho^{I} h^{I} \int_{{A_{e} }} {{\mathbf{a}}_{v}^{I0} + {\mathbf{a}}_{v}^{Im} {\text{d}}A} \\ \end{aligned} $$

$$ \begin{aligned} {\mathbf{Q}}_{ev\theta }^{I} &= - \int_{{\Omega_{e}^{I} }} {\rho^{I} {\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}^{{\text{T}}} {\mathbf{a}}_{v}^{I} {\text{d}}\Omega^{I} } \\ & = \int_{{\Omega_{e}^{I} }} {\rho^{I} {\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }} {\mathbf{a}}_{v}^{I} {\text{d}}\Omega^{I} } \\ & = \left\{ \begin{gathered} \rho^{I} h^{I} \int_{{A_{e} }} {\left( {{\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}^{0} + {\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}^{m} } \right)\left( {{\mathbf{a}}_{v}^{I0} + {\mathbf{a}}_{v}^{Im} } \right){\text{d}}A} \hfill \\ + \rho^{I} \frac{{\left( {h^{I} } \right)^{3} }}{12}\int_{{A_{e} }} {{\tilde{\mathbf{r}}}_{{\overline{O}^{I} P_{f} }}^{b} {\mathbf{a}}_{v}^{Ib} {\text{d}}A} \hfill \\ \end{gathered} \right\} \\ \end{aligned} $$

$$ \begin{aligned} {\mathbf{Q}}_{evf}^{I} &= \int_{{\Omega_{e}^{I} }} {\rho^{I} \left( {{\mathbf{A}}^{I} {{\varvec{\uplambda}}}^{e} {\overline{\mathbf{S}}}} \right)^{{\text{T}}} {\mathbf{a}}_{v}^{I} {\text{d}}\Omega^{I} } \\ & = \left\{ \begin{gathered} \rho^{I} h^{I} \int_{{A_{e} }} {\left[ {{\mathbf{A}}^{I} {{\varvec{\uplambda}}}^{e} \left( {{\overline{\mathbf{S}}}_{0} + {\overline{\mathbf{S}}}_{m} } \right)} \right]^{{\text{T}}} \left( {{\mathbf{a}}_{v}^{I0} + {\mathbf{a}}_{v}^{Im} } \right){\text{d}}A} \hfill \\ + \rho^{I} \frac{{\left( {h^{I} } \right)^{3} }}{12}\int_{{A_{e} }} {\left( {{\mathbf{A}}^{I} {{\varvec{\uplambda}}}^{e} {\overline{\mathbf{S}}}_{b} } \right)^{{\text{T}}} {\mathbf{a}}_{v}^{Ib} {\text{d}}A} \hfill \\ \end{gathered} \right\} \\ \end{aligned} $$

Appendix B

By solving the generalized eigenvalue equation $\omega^{2} {\mathbf{M}}_{ff}^{I} {\mathbf{\varphi }}^{I} = {\mathbf{K}}_{ff}^{I} {\mathbf{\varphi }}^{I}$, the modal shape ${\mathbf{\varphi }}_{j}^{I}$ corresponding to the $j{{{\text{th}}}}$ natural frequency of flexible body $I$ can be obtained. The physical coordinates ${\overline{\mathbf{q}}}_{f}^{I}$ can be converted to the modal space by selecting the first M-order modes:

$$ {\overline{\mathbf{q}}}_{f}^{I} = {\mathbf{V}}_{M} {\mathbf{p}}^{I} $$

where ${\mathbf{p}}^{I}$ indicates the modal coordinates, and ${\mathbf{V}}_{M} = \left[ {\begin{array}{*{20}l} {{\mathbf{\varphi }}_{1}^{I} } & {{\mathbf{\varphi }}_{2}^{I} } & \cdots & {{\mathbf{\varphi }}_{M}^{I} } \\ \end{array} } \right]$ consists of the first M-order modes.

In general, the employed modal order M is far less than the DOFs of the discrete flexible body. Therefore, the original governing equation Eq. (87) can be reduced to the following equation:

$$ \left[ {\begin{array}{*{20}l} {{\mathbf{M}}_{RR}^{I} } & {{\mathbf{M}}_{R\theta }^{I} } & {{\tilde{\mathbf{M}}}_{Rf}^{I} } \\ {\left( {{\mathbf{M}}_{R\theta }^{I} } \right)^{{\text{T}}} } & {{\mathbf{M}}_{\theta \theta }^{I} } & {{\tilde{\mathbf{M}}}_{\theta f}^{I} } \\ {\left( {{\tilde{\mathbf{M}}}_{Rf}^{I} } \right)^{{\text{T}}} } & {\left( {{\tilde{\mathbf{M}}}_{\theta f}^{I} } \right)^{{\text{T}}} } & {{\tilde{\mathbf{M}}}_{ff}^{I} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {{\ddot{\mathbf{R}}}^{I} } \\ {{{\varvec{\upvarepsilon}}}^{I} } \\ {{\ddot{\mathbf{p}}}^{I} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}l} {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {{\tilde{\mathbf{K}}}_{ff}^{I} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {{\mathbf{R}}^{I} } \\ {{{\varvec{\uptheta}}}^{I} } \\ {{\mathbf{p}}^{I} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {{\mathbf{Q}}_{R}^{I} } \\ {{\mathbf{Q}}_{\theta }^{I} } \\ {{\tilde{\mathbf{Q}}}_{f}^{I} } \\ \end{array} } \right] $$

where ${\tilde{\mathbf{M}}}_{Rf}^{I} = {\mathbf{M}}_{Rf}^{I} {\mathbf{V}}_{M}$, ${\tilde{\mathbf{M}}}_{\theta f}^{I} = {\mathbf{M}}_{\theta f}^{I} {\mathbf{V}}_{M}$, ${\tilde{\mathbf{M}}}_{ff}^{I} = {\mathbf{V}}_{M}^{{\text{T}}} {\mathbf{M}}_{ff}^{I} {\mathbf{V}}_{M}$, ${\tilde{\mathbf{K}}}_{ff}^{I} = {\mathbf{V}}_{M}^{{\text{T}}} {\mathbf{K}}_{ff}^{I} {\mathbf{V}}_{M}$, ${\tilde{\mathbf{Q}}}_{f}^{I} = {\mathbf{V}}_{M}^{{\text{T}}} {\mathbf{Q}}_{f}^{I}$.