1 Introduction

The recent advancements in networking and communication technologies raises the demand to store and transmit data over the network which requires improvement in the application areas concerning cryptography, cybersecurity, etc. [72]. The data transmitted and stored using open network are prone to information leakage. With the increase in volume, velocity, and veracity of the multimedia data, it becomes necessary to enhance the security, confidentiality, and privacy of the information [38, 57]. The requirement of confidentiality and authenticity of the information being downloaded, uploaded, and stored is one of the major issues in cloud data storage and encryption related applications. Thus, the need for securing the information from illegal and unlicensed access becomes a necessity [8]. Cryptography is a vital technique which guarantees the privacy of secret data by converting it to an unrecognizable form. Both images and text are converted to an unreadable form using the process of encryption [53].

Images play a significant role as an essential multimedia resource in the modern big data era which constitutes a large amount of information [30, 70]. Henceforth, the maintenance of integrity and security of images have become a major concern in many fields such as military, internet communication, multimedia systems, telemedicine, e-commerce, e-learning, banking, etc. [13, 56, 60]. The modern cryptographic applications offer a workable solution to the persisting issues of sharing images through internet.

In general, the image encryption model is divided into two parts: confusion and diffusion [17, 23]. The randomness in the pixels of plain image is introduced in the confusion process, whereas the pixel values of the image are altered in the diffusion process by using various methods [19].

Frequently, mathematics plays a vital role in various cryptographic models for enhancing the level of security [40, 44, 63, 67]. The researchers have utilized different techniques such as chaotic maps, matrix theory, wavelet theory, numerical techniques, magic cubes, transformation theory, elliptic curves, DNA encoding, etc., for encrypting images [10, 43, 50, 52, 64]. The matrix theory fulfills the requirement by using singular value decomposition, permutation, inverse of matrices, etc., in cryptographic models [43, 45, 68]. Most commonly, the special type of matrices named as magic squares raise the level of randomness in the encryption models to a higher extent [41]. In addition to matrix theory, the chaos maps have been widely used by the experimenters in the image encryption algorithms because of its unpredictability and sensitivity of initial state [25, 49]. The shuffling and altering of image pixels have been performed in the confusion and diffusion phases, respectively, of the encryption algorithms by using different chaotic maps [32, 37]. Despite this the sensitivity of chaotic maps to parameter initialization disturbs the stability of image encryption algorithms. Thus, the chaotic maps are required to be used in combination with other components to achieve the optimum extent of stability. Moreover, it is also necessary to introduce the new methods for construction of magic squares which are capable of raising the level of randomness in the image encryption models in comparison to the existing models.

In this work, a new approach for the generation of magic square has been instigated. The flexible structural features as well as complex arrangement of the elements of a novel magic square along with chaotic map and differential encoding enlighten the way toward the field of image encryption. The proposed model has been implemented on both color as well as grayscale images. The alteration in pixel values has been performed by taking advantage of elements and properties of newly constructed magic square which enhances the reliability and feasibility of the proposed model.

The rest of paper is outlined as under: The related work is outlined in Sect. 2. The motivation behind this work is elaborated in Sect. 3. The detailed description of all the phases of the proposed encryption and decryption model along with the construction of novel magic square is given in Sect. 4. The anatomization and detailed discussions of the proposed model are presented in Sect. 5. The conclusions procured from the work are delineated in Sect. 6.

2 Related work

A square matrix of order n, in which the elements alongside each row, each column, and each of the two main diagonals are sum up to a fixed constant is known as magic square [34]. The algebraic properties of magic squares enlighten the way toward different application areas illustrated as image processing, cryptography, game theory, graph theory, and appreciably more.

The researchers represented several methods for the construction of magic squares having fabulous mathematical characteristics. Li et al. showed the construction of pandiagonal magic squares of doubly even order using magic rectangles [29]. Lee et al. gave the necessary and sufficient condition for the non-singularity of regular magic squares by virtue of centro-skew matrices [28]. Chan et al. gave the method for the construction of singular and non-singular regular classical magic squares of odd order [6]. Liu et al. proved the non-singularity of the odd-order classical regular magic square generated using the centro-skew S-circulant matrix [31]. Miranda et al. gave a method for the generation of doubly even-order magic square along with the generalization of Durer\(^{\prime }\)s magic square [33]. The growing need of randomness in cryptographic models motivated the researchers to introduce reliable method for the construction of magic squares.

The various types of chaotic maps are used in combination with other components for the improvement in security of image encryption models in case of both grayscale and color images by the researchers. Shuangyuan et al. instigated the image encryption technique based on matrix transformation by locating the possible changed region [48]. Pappachan and Baby proposed image encryption model using combination of magic square and Tinkerbell maps [36]. Zhong et al. came forward with the concept of Good Lattice Point (GLP) for image encryption algorithms by modifying the pixel values using magic square operations [69]. Sowmiya et al. utilized the elements of pandiagonal magic squares in the model generated to encrypt images [51]. Farhan et al. [9] generated the keys using magic square for color image encryption. Rageed and Sadiq [39] introduced the composition of magic square along with 3D-chaotic map to encrypt and decrypt color images. Hua et al. [21] propounded a color image encryption algorithm using orthogonal Latin squares and 2D chaotic map. Wang and Liu [55] performed the image encryption by associating the octree diffusing and magic square scrambling with chaotic maps. Senthilnayaki et al. propounded a medical image encryption model based on magic square and particle swarm optimization (PSO) [47].

From the earlier work, it has been concluded that the erstwhile image encryption models lack in efficiency due to tight correlation, high redundancy, and big data stream. Also, it is necessary to introduce more mathematically rigorous method for the construction of large order magic squares. Moreover, the image encryption models based on single component along with either chaotic map or magic square are resilient in spite of the models based on combination of more than two components. Henceforth, in this paper the mathematically strong method for the generation of large order magic squares is formulated. Furthermore, this novel magic square is used in association with chaotic maps and differential encoding technique for encryption of both color as well as grayscale images. The differential encoding is utilized for the first time in encryption model to enhance the bit-level security and complexity.

3 Motivation

It has been observed from the literature that the mathematical approaches are capable of generating a more secure encryption models in comparison to any other techniques. Also, the less frequent availability of mathematically rigorous methods for the construction of large order magic squares has been noticed by us. Moreover, the magic squares are capable of generating a more secure encryption algorithm on combining with other components such as chaotic maps, scrambling techniques, DNA encoding, wavelet algorithms, etc. In addition, with growing demands it is necessary to pay attention to some techniques which are not explored yet. The differential encoding is one such technique which has not been utilized widely in spite of its great ability to provide the bit-level privacy to the encrypted data. Hence, these limitations of the benchmark models motivate us to propose an image encryption model by combining the concepts of magic square and differential encoding technique with the chaotic maps. The instigation of a novel magic square raises the level of complexity and security by making use of its elements. Also, the differential encoding technique is used to enhance the bit-level security of the proposed encryption model. Thus, the integration of chaotic map with the magic square and differential encoding in the propounded encryption model efficiently neglects all the major shortcomings of the image encryption models.

4 Proposed encryption/decryption model

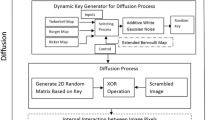
The proposed model for encryption and decryption of grayscale and color images has been instigated in this paper. Figure 1 shows the block diagram of the proposed encryption model. In the proposed model the encryption process comprises of two phases: confusion and diffusion. The scrambling technique has been used in the confusion phase to randomize the image pixels. Further, the diffusion phase has been accomplished using components: magic square, differential encoding technique, and chaotic map are explained in the following subsections.

Fig. 1
figure 1

Block diagram of proposed encryption model

Full size image

4.1 Encryption model

All the phases of the encryption model have been explained in this subsection. The proposed model has been implemented on both grayscale and color images of different sizes. The systematic arrangement of all the components of the propounded image encryption model is shown in Fig. 1.

4.1.1 Confusion phase

In this phase, the initial locations of the pixels in the plain image are changed to any other random location to increase the haphazardness at the starting point of the encryption process [17]. In the proposed encryption model the scrambling has been performed by implementing 2D Arnold map given in Algorithm 1.

figure a

4.1.2 Diffusion phase

The diffusion phase of encryption model is essential to alter the pixel values of the plain image for generating an encrypted image. The propounded model contains components in the diffusion phase: magic square, differential encoding technique, and chaotic map are explained as follows:

4.1.0.1 Magic square

The \(n\times n\)-array of \(n^{2}\) numbers in which the sum of elements of each row, each column, main diagonal, and anti-diagonal is equal to a fixed constant is called as magic square and the fixed constant is termed as magic constant [42]. Mathematically, if \([a_{ij}] \) is a magic square of order n, then

$$\begin{aligned}&\sum _{j=1}^{n} a_{ij}=k \;\; \hbox {and}\;\; \sum _{j=1}^{n} a_{ji}=k \;\;\;\;\forall \;\;i=1,2,3,\ldots \end{aligned}$$
(1)
$$\begin{aligned}&\sum _{i=1}^{n} a_{ii}=k\;\; \hbox {and} \;\; \sum _{i=1}^{n} a_{i,n-i+1}=k. \end{aligned}$$
(2)

The utilization of magic squares in the encryption model raises the level of complexity and security of the encrypted image. Moreover, the level of security in the proposed encryption model has been escalated by combining the concept of magic square with other components. The elements of magic squares have been used to change the pixel values of the plain image in the proposed model. The doubly even-order magic square of order sixteen has been harnessed in the propounded model generated by using following novel approach:

Let us consider two sets \(P=\{ p_{k} \;|\; \forall \; 1\le k\le \frac{n}{2}\}\) and \(Q=\{ q_{l}\; | \;\forall \; 1 \le l \le \frac{n}{2} \}\), where

$$\begin{aligned}{} & {} p_{k}={\left\{ \begin{array}{ll} 4s+1 &{} \text {if}\;\; k \;\;\text {is odd} \\ 4s+4 &{} \text {if}\;\; k\;\; \text {is even} \end{array}\right. } \;\;\;\hbox {and}\nonumber \\{} & {} q_{l}={\left\{ \begin{array}{ll} 4s+2 &{} \text {if}\;\; l \;\;\text {is odd} \\ 4s+3 &{} \text {if}\;\; l \;\; \text {is even}\\ \end{array}\right. } \end{aligned}$$
(3)

for all \(0 \le s \le \frac{n}{4}-1.\) Thus, the elements of first row of \(A=[a_{ij}]_{n\times n}\) are given by

$$\begin{aligned} a_{1j}={\left\{ \begin{array}{ll} j &{} \text {if}\;\; j\in P \\ n^{2}+1-j &{} \text {if}\;\; j\in Q \end{array}\right. }. \end{aligned}$$
(4)

Now, define

$$\begin{aligned}{} & {} \delta _{r}={\left\{ \begin{array}{ll} n(n-r)+1-a_{1j} &{} \text {if}\;\; j\in P \\ n(n+r)+1-a_{1j} &{} \text {if}\;\; j\in Q \end{array}\right. } \nonumber \\{} & {} \qquad \text {for all}\;\; 1\le r\le \frac{n}{2}-1. \end{aligned}$$
(5)

The filling of remaining first \(\frac{n}{2}-1\) number of rows of A, starting from second row, is performed by using the following procedure:

Let \(s_{1}=\{ 1,2,5,6,\ldots \}=\{ x_{f}\; \vert \;\forall \;1 \le f \le \frac{n}{4} \}\) and \(s_{2}=\{ 3,4,7,8,\ldots \}=\{ y_{g}\; \vert \;\forall \;1 \le g \le \frac{n}{4}-1 \}\) be any two sets, where

$$\begin{aligned}{} & {} x_{f}={\left\{ \begin{array}{ll} 4h+1 &{} \text {if}\;\; f\;\; \text {is odd} \\ 4h+2 &{} \text {if}\;\; f\;\; \text {is even} \end{array}\right. } \;\; \hbox {and} \nonumber \\{} & {} y_{g}={\left\{ \begin{array}{ll} 4h+3 &{} \text {if}\;\; g\;\; \text {is odd} \\ 4h+4 &{} \text {if}\;\; g\;\; \text {is even} \end{array}\right. } \end{aligned}$$
(6)

for \(0\le h \le \Big \lfloor \frac{n}{8}-\frac{1}{2}\Big \rfloor \).

Therefore, the elements of all the remaining rows starting from the second row and up to \(\left( \frac{n}{2} \right) ^{th}\) row are given by

$$\begin{aligned} a_{r+1,j}={\left\{ \begin{array}{ll} \delta _{r} &{} \text {if}\;\; r \in s_{1} \\ n^{2}+1-\delta _{r} &{} \text {if}\;\; r \in s_{2} \end{array}\right. }. \end{aligned}$$
(7)

The elements of the lower half portion of matrix A, i.e., from \(\left( \frac{n}{2} +1 \right) ^{th}\) row to \(n^{th}\) row, are calculated by using the following expression

$$\begin{aligned} a_{n-i+1,j}=n^{2}+1-a_{i,n-j+1}, \;\; \text {for}\;\; 1\le j\le n. \end{aligned}$$
(8)

Therefore, the sum of elements of the first row (i.e. for \(i=1\)) is

$$\begin{aligned} \sum _{j=1}^{n} a_{1j}= & {} \sum _{j \in P} j+\sum _{j\in Q} (n^{2}+1-j)\nonumber \\= & {} \sum _{j\in P} j+\sum _{j\in Q} (n^{2}+1)-\sum _{j\in Q} j \nonumber \\= & {} \sum _{j\in Q} (n^{2}+1) \qquad \Big \{ \because \sum p_{k} =\sum q_{l} \Big \} \nonumber \\= & {} \frac{n(n^{2}+1)}{2}. \end{aligned}$$
(9)

The sum of elements of the \(i^{th}\) row, for \(2 \le i \le \frac{n}{2}\), evaluated by considering two cases is given by

Case-I: when \(r\in s_{1}\) then the row sum is

$$\begin{aligned} \sum _{j=1}^{n} a_{ij}= & {} \sum _{j=1}^{n} a_{r+1,j}\nonumber \\= & {} \sum _{j=1}^{n} \delta _{r} =\sum _{j\in P} \{ n(n-r)+1-a_{1j} \} \nonumber \\{} & {} + \sum _{j\in Q} \{ n(n+r)+1-a_{1j} \} = (n^{2}+1)\nonumber \\{} & {} \sum _{j\in P} (1)+(n^{2}+1)\sum _{j\in Q} (1) \nonumber \\{} & {} - nr\sum _{j\in P} (1)+nr \sum _{j\in Q} (1)\nonumber \\{} & {} -\left( \sum _{j\in P} a_{1j}+\sum _{j\in Q}a_{1j} \right) \nonumber \\= & {} (n^{2}+1)\left( \frac{n}{2}\right) +(n^{2}+1)\left( \frac{n}{2}\right) \nonumber \\{} & {} -nr\left( \frac{n}{2}\right) +nr\left( \frac{n}{2}\right) \nonumber \\{} & {} - \left( \sum _{j\in P} j+\sum _{j\in Q} (n^{2}+1-j) \right) \quad \{\hbox {from}~(9)\} \nonumber \\= & {} \frac{n(n^{2}+1)}{2}. \end{aligned}$$
(10)

Case-II: when \(r\in s_{2}\) then the row sum is

$$\begin{aligned} \sum _{j=1}^{n} a_{ij}= & {} \sum _{j=1}^{n} a_{r+1,j}=\sum _{j=1}^{n} \left( n^{2}+1-\delta _{r} \right) \nonumber \\= & {} \sum _{j\in P} \{ n^{2}+1-n^{2}+nr-1+a_{1j}\}\nonumber \\{} & {} +\sum _{j\in Q} \{ n^{2}+1-n^{2}-nr-1+a_{1j} \}\nonumber \\= & {} \sum _{j\in P} nr-\sum _{j\in Q} nr+\left( \sum _{j\in P} a_{1j} +\sum _{j\in Q} a_{1j} \right) \nonumber \\= & {} nr\sum _{j\in P} (1)-nr\sum _{j\in Q} (1)\nonumber \\{} & {} +\frac{n(n^{2}+1)}{2} \quad \{ \hbox {from}\,\,(9)\} \nonumber \\= & {} nr\left( \frac{n}{2} \right) -nr\left( \frac{n}{2} \right) \nonumber \\{} & {} +\frac{n(n^{2}+1)}{2} =\frac{n(n^{2}+1)}{2}. \end{aligned}$$
(11)

Next, the sum of elements of each \(i^{th}\) row, for \(\frac{n}{2}+1 \le i \le n\), is

$$\begin{aligned} \sum _{j=1}^{n}a_{ij}= & {} \sum _{j=1}^{n} a_{n-i+1,j} =\sum _{j=1}^{n} \{ n^{2}+1-a_{i,n-j+1} \} \nonumber \\= & {} (n^{2}+1)\sum _{j=1}^{n} (1) -\frac{n(n^{2}+1)}{2}\nonumber \\{} & {} \left\{ \because \sum _{j=1}^{n} a_{i,n-j+1}=\sum _{j=1}^{n} a_{ij},\right. \nonumber \\{} & {} \left. \qquad \text {for}\quad 1\le i\le \frac{n}{2} \right\} \nonumber \\= & {} \frac{n(n^{2}+1)}{2}. \end{aligned}$$
(12)

The main diagonal elements of the matrix A are defined by

$$\begin{aligned} a_{ii}=(n+1)(i-1)+1, \;\; \text {for}\;\; 1\le i\le n, \end{aligned}$$
(13)

and their sum is evaluated by

$$\begin{aligned} \sum _{i=1}^{n} a_{ii}= & {} \sum _{i=1}^{n} \{ (n+1)(i-1)+1\}\nonumber \\= & {} (n+1)\sum _{i=1}^{n}(i-1)+\sum _{i=1}^{n}(1) \nonumber \\= & {} (n+1)\left( \frac{n(n+1)}{2}-n \right) +n\nonumber \\= & {} \frac{n(n^{2}+1)}{2}. \end{aligned}$$
(14)

Similarly, the anti-diagonal elements of the matrix A are defined by

$$\begin{aligned} a_{i,n-i+1}= (n-1)i+1, \;\; \text {for}\;\; 1\le i\le n \end{aligned}$$
(15)

and their sum is

$$\begin{aligned} \sum _{i=1}^{n} a_{i,n-i+1}= & {} \sum _{i=1}^{n}\{ (n-1)i+1\}\nonumber \\= & {} (n-1)\frac{n(n+1)}{2}+n \nonumber \\= & {} \frac{n(n^{2}+1)}{2}. \end{aligned}$$
(16)

The column-wise definition of the above-constructed matrix \(A=[a_{ij}]_{n\times n}\) is given below:

For \(j=1,\) the elements of matrix A are given by

$$\begin{aligned} a_{i1}={\left\{ \begin{array}{ll} n(i-1)+1 &{} \text {if}\;\; i \in P \\ n(n+1-i) &{} \text {if}\;\; i \in Q \end{array}\right. } \end{aligned}$$
(17)

and their sum is

$$\begin{aligned} \sum _{i=1}^{n} a_{i1}= & {} \sum _{i\in P} \{ n(i-1)+1 \}\nonumber \\{} & {} +\sum _{i\in Q} \{ (n^{2}+1)-n(i-1)-1 \} \nonumber \\= & {} n\sum _{i\in P}(i-1)+\sum _{i\in P}(1)+(n^{2}+1)\nonumber \\{} & {} \sum _{i\in Q}(1) -n\sum _{i\in Q} (i-1)-\sum _{i\in Q} (1) \nonumber \\= & {} n\left( \frac{n(n+1)}{4}-\frac{n}{2} \right) +\frac{n}{2} +\frac{n(n^{2}+1)}{2}\nonumber \\{} & {} -n\left( \frac{n(n+1)}{4}-\frac{n}{2} \right) -\frac{n}{2} \nonumber \\= & {} \frac{n(n^{2}+1)}{2}. \end{aligned}$$
(18)

For \(2\le j \le \frac{n}{2}\), the elements of the matrix A are defined by

$$\begin{aligned}&a_{ij}=a_{i,r+1}={\left\{ \begin{array}{ll} n^{2}+1-\delta _{r}^{\prime } &{} \text {if}\;\; r \in s_{1} \\ \delta _{r}^{\prime } &{} \text {if}\;\; r \in s_{2} \end{array}\right. } \end{aligned}$$
(19)
$$\begin{aligned}&\text {where},\;\; \delta _{r}^{\prime }={\left\{ \begin{array}{ll} a_{i1}+r &{} \text {if}\;\; i \in P \\ a_{i1}-r &{} \text {if}\;\; i \in Q \end{array}\right. } \end{aligned}$$
(20)

and \(s_{1},s_{2},P,Q,r\) are same as defined previously and their sum is evaluated as below:

Fig. 2
figure 2

Block diagram of differential encoding technique

Full size image

Case-I: when \(r\in s_{1}\) then the sum of elements of each column is

$$\begin{aligned} \sum _{i=1}^{n} a_{ij}= & {} \sum _{i=1}^{n} a_{i,r+1} =\sum _{i=1}^{n} \{ (n^{2}+1)-\delta _{r}^{\prime } \} \nonumber \\= & {} (n^{2}+1)\sum _{i=1}^{n} (1)-\sum _{i\in P} (a_{i1}+r)\nonumber \\{} & {} -\sum _{i\in Q} (a_{i1}-r) \nonumber \\= & {} n(n^{2}+1)-\frac{n(n^{2}+1)}{2}-r\left( \frac{n}{2}\right) \nonumber \\{} & {} +r\left( \frac{n}{2} \right) =\frac{n(n^{2}+1)}{2}. \end{aligned}$$
(21)

Case-II: when \(r\in s_{2}\) then the sum of elements of each column is

$$\begin{aligned} \sum _{i=1}^{n} a_{ij}= & {} \sum _{i=1}^{n} a_{i,r+1}= \sum _{i=1}^{n} \delta _{r}^{\prime } \nonumber \\= & {} \sum _{i\in P} (a_{i1}+r) +\sum _{i\in Q} (a_{i1}-r) \nonumber \\= & {} \left( \sum _{i\in P} a_{i1}+\sum _{i \in Q} a_{i1} \right) +\sum _{i \in P}r-\sum _{i\in Q} r \nonumber \\= & {} \frac{n(n^{2}+1)}{2}+r \left( \frac{n}{2} \right) \nonumber \\{} & {} -r \left( \frac{n}{2} \right) =\frac{n(n^{2}+1)}{2}. \end{aligned}$$
(22)

Now, for \(\frac{n}{2}+1\le j \le n\), the elements of the above-generated matrix A are given by

$$\begin{aligned} a_{i,n-j+1}=(n^{2}+1)-a_{n-i+1,j}\;,\text {for}\;\; 1\le i \le n \end{aligned}$$
(23)

and their sum is

$$\begin{aligned} \sum _{i=1}^{n} a_{ij}= & {} \sum _{i=1}^{n} a_{i,n-j+1} =\sum _{i=1}^{n} \{ (n^{2}+1)-a_{n-i+1,j} \} \nonumber \\{} & {} \left\{ \because \sum _{i=1}^{n} a_{n-i+1,j} =\frac{n(n^{2}+1)}{2},\right. \nonumber \\{} & {} \left. \quad \quad \text {for} \;\; 1\le j \le \frac{n}{2} \right\} \nonumber \\= & {} (n^{2}+1)n- \frac{n(n^{2}+1)}{2}= \frac{n(n^{2}+1)}{2}. \end{aligned}$$
(24)

Hence, the matrix A constructed above is a magic square with magic sum \(\frac{n(n^{2}+1)}{2}.\)

Algorithm 2 for the construction of above-introduced new class of doubly even-ordered magic square is as under:

figure b

4.1.0.2 Differential encoding technique

The differential encoding technique is implemented to impart unambiguous signal reception. In this technique, the previous reference bit is XOR with next bit in the sequence to hide the bit information of the plain image [73]. In this paper, it has been applied to encode the elements of the magic square which raises the level of security and complexity of the encrypted image. The encoding and decoding formulas used in implementation of this technique have been given below:

$$\begin{aligned}{} & {} e_{n}=d_{n}\oplus e_{n-1} \end{aligned}$$
(25)
$$\begin{aligned}{} & {} \tilde{d_{n}}=\tilde{e_{n}}\oplus \tilde{e}_{n-1} \end{aligned}$$
(26)

where \(d_{n},e_{n},\tilde{d_{n}}\) and \(\tilde{e_{n}}\) are the input, encoded, receiver and decoded sequences.

The block diagram of the differential encoding technique is depicted in Fig. 2. The examples of the sequence employed in the encryption and decryption model generated by this technique are demonstrated in Figs. 3 and 4.

Fig. 3
figure 3

Illustration of differential encoding technique used in encryption model

Full size image

4.1.0.3 Chaotic map

The random behavior, vulnerability, and susceptibility features of the chaotic maps increase their demand in the image encryption models [11]. The sequences generated using Piece-wise Linear Chaotic Map (PWLCM) alter the pixel values of the plain image to a high extent. Moreover, the chaotic maps generate different sequences each time for the same image which makes it hard for the intruders to fetch any information related to the plain image from the encrypted image. Two secret keys \(n_{0}\) (control parameters) and \(x_{0}\) (initial value) are used for the generation of chaotic sequences.

The complete utilization of the above components in the encryption model is outlined in Algorithm 3 as under:

figure c
Fig. 4
figure 4

Illustration of differential encoding technique used in decryption model

Full size image
Fig. 5
figure 5

Encrypted and Decrypted test images

Full size image

4.2 Decryption model

The decryption has been accomplished by applying the encryption algorithm in reverse order. Starting with the conversion of 2D encrypted image to 1D array, the reverse circular shift and XOR operation have been applied to fetch the encoded magic square values using chaotic maps in binary form. The reverse differential encoding technique is used to extract the actual selected entries of the magic square which are further used to fetch the pixel values of the plain image. The reverse scrambling algorithm has been used to restore the original positions of the pixels in the plain image from the encrypted image. The reverse of the scrambling process is depicted with the help of Algorithm 4 as below:

figure d

5 Results and discussions

In this paper, the proposed encryption and decryption model based on the integration of magic square and differential encoding with chaotic maps has been analyzed. The model has been investigated in MATLAB 2021a platform, on Windows 10 Pro operating system with Intel\(\circledR \) Xenon\(\circledR \) CPU E5-2650 v3 (2.30 GHz) and 8GB of RAM. The 20 grayscale and 10 color images have been investigated using the proposed image encryption model while the results of only 17 images have been shown in the paper. The images available in USC-SIPI database have been utilized for the attestation of the propounded model [59]. The security, visual and statistical examination of the proposed model has been performed to confirm the resistance ability of the model against differential, entropy, visual, statistical, and cropping attacks. The grayscale and color images of resolution \(256\times 256\) pixels, \(512 \times 512\) pixels, and \(1024 \times 1024\) pixels have been considered for experimentation of the proposed model.

Fig. 6
figure 6

Histograms of color test images

Full size image
Fig. 7
figure 7

Histograms of grayscale test images

Full size image

5.1 Visual analysis

The visual analysis is used to check the dissimilarity and similarity of the plain image with encrypted and decrypted image respectively. Figure 5 depicts the plain, encrypted, and decrypted grayscale and color images of different sizes using the proposed model. In case of color images, the component-wise encryption has been carried out using the proposed model. The encrypted images constitute the smooth distribution of the RGB and grayscale components. The visual inspection of the encrypted images shows that no information about structural outline of the plain image has been revealed. Also, a high visual similarity has been observed between decrypted and plain images.

5.2 Histogram analysis

The histograms invaded the demographic dissimilarity between the pixel values of the plain and encrypted images. The effectiveness of the resistance against statistical attacks of the encryption model is guaranteed by the even and smooth distribution plots [2].

In Figs. 6 and 7, the histograms of original and encrypted color and grayscale images are represented. The uneven distribution in the histogram of the plain images convey the useful information about the pixel values. The histograms of the encrypted images are uniformly distributed in the case of grayscale as well as color images which guarantee the strength of the proposed model to resist statistical attacks. The uniformity in the histograms is justified by using the chi-square test [17, 23, 35] to obtain the numerical results instead of visual spoofing and its values are calculated by the following formula:

$$\begin{aligned} \chi ^{2}=\sum _{i=1}^{N} \frac{(P_{i}-E_{i})^{2}}{E_{i}} \end{aligned}$$

where \(E_{i}=\frac{MN}{256}\) and \(P_{i}\) represents the expected and observed frequencies of each level in the image and \(i=1,2,3,\ldots ,255.\) Generally, for the different levels of significance the chi-square values are \(\chi ^{2}_{0.05}(255) =293.2478,\chi ^{2}_{0.01}(255)=310.4574\) and \(\chi ^{2}_{0.1}(255) =284.3359\).

In Table 1, the chi-square values of the encrypted image are less than the chi-square values of the plain image which proves the uniformity of histograms of encrypted images.

Table 1 Chi-square test values of color and grayscale test images
Full size table

5.3 Key space analysis

The security of an image encryption model from the brute-force attacks is assured by the enough large size of key space. The required size of the key space must be greater than \(2^{128}\) to resist the brute-force attacks effectively [39, 46]. In the proposed image encryption model the key \(k=(k_{1},k_{2},k_{3},k_{4})\) is used for the decryption process at the receiver end. Here, the sub-keys \(k_{1},k_{2},k_{3},k_{4}\) represent the size of key of the 2D Arnold map used as scrambling technique, the size of key generated by magic square, the size of key produced by reference bits, and the size of key consisting of the parameters \(n_{0}=(n_{1},n_{2},n_{3})\) as well as initial values \(x_{0}=(x_{1},x_{2},x_{3})\) of the PWLCM map respectively. Further, if the size of each element of the magic square of order m is \(2^{b}\) bits then the size of the sub-key \(k_{2}\) is \((2^{b})^{m^{2}}\). Also, if the computer precision is \(10^{-15}\) then the size of key generated by each parameter and initial value in PWLCM is \(10^{15}\) which means the size of sub-key \(k_{4}\) is \((10^{15})^{3} \times (10^{15})^{3} \approx 2^{299}.\) Hence, the total size of the key space is calculated as

$$\begin{aligned}{} & {} k_{1}\times (2^{b})^{m^{2}} \times k_{3} \times (10^{15})^{3} \times (10^{15})^{3} \\{} & {} \quad \approx k_{1}\times (2^{b})^{m^{2}} \times k_{3} \times 2^{299} \\{} & {} \quad = k_{1}\times k_{3}\times (2^{b m^{2}+299}) \end{aligned}$$

which is much larger than \(2^{128}\). This infers that the proposed model is capable of resisting brute-force attacks.

5.4 Key sensitivity analysis

The high sensitivity of the key in the encryption model guarantee the infeasibility of the brute force attack to decrypt the encrypted image. It means that the slightest changes made in the key used for decryption purpose do not allow the images to be get decrypted [4, 65]. In the proposed model, the change in only a single parameter of the key \(k=(k_{1},k_{2},k_{3},k_{4})\) do not allow the encrypted image to reveal any information related to the plain image. For instance, in case of RGB image if change the initial value \(x_{0}=(x_{1},x_{2},x_{3})\) of the PWLCM from \(x_{1}=0.157613081677548, x_{2}=0.970592781760616, x_{3}=0.957166948242946\) to \(x_{1}=0.157613081977548, x_{2}=0.970592781960616, x_{3}=0.957166948942946\) then this modified key do not generate the original plain image. Similarly, the intruder will never be able to obtain the original plain image if two or more parameters of the key are changed. The results of the decrypted images after changing one, two and three parameters in the key of the image 4.1.04 (RGB image) and 5.1.12 (gray image) are shown in Fig. 8 which ensures that the proposed model efficiently resists the brute force attacks.

Fig. 8
figure 8

a, e plain images \(^{\backprime \backprime }\)4.1.04\(^{\prime \prime }\) and \(^{\backprime \backprime }\)5.1.12\(^{\prime \prime }\); b, f decrypted form of images with one key changed; c, g decrypted form of images with two keys changed; d, h decrypted form of images with three keys changed

Full size image

5.5 Speed analysis

The time taken for the execution of an algorithm is also a significant factor, with respect to enhanced security level. The times taken by the encryption and decryption algorithms of the proposed model are given in Table 2, in case of both grayscale and color test images. The average times taken for the encryption of grayscale images of sizes \(256\times 256\), \(512\times 512\) and \(1024\times 1024\) pixels are 2.3 s, 9.5 s and 38.5 s respectively. In the same way, the encryption times of \(256\times 256\) and \(512\times 512\) pixels color images are 6.75 s and 27.7 s, respectively. Also, their corresponding average decryption times in case of both grayscale as well as color images are 3.66 s, 14.95 s, 60.31 s, 11.07 s and 45.23 s. It has been concluded that the proposed model is faster in comparison to some erstwhile models [3, 5, 16, 24, 54, 58, 66]. Also, the proposed image encryption model is slower in comparison to the other state-of-the-art models [22, 26, 62, 64]. The main reason is that in order to improve the encryption security of this encryption method the image is scrambled with complex chaotic map, and the alteration of image pixel values using the elements of proposed magic square, which greatly increases the encryption speed.

Table 2 Speed analysis of color and grayscale test images
Full size table

The comparative analysis of the average values of time taken for encryption and decryption of \(256 \times 256\) grayscale images is represented in Table 3. The bold values indicate that the proposed model has better speed efficiency in comparison to erstwhile image encryption models. The data used for comparison of the algorithms introduced by Hu et al. [16], Wang and Liu [58], Zhan et al. [65], Chai et al. [5] has been taken from Yan et al. [62].

Table 3 A comparative analysis of average encryption and decryption speeds
Full size table
Fig. 9
figure 9

Correlation between two adjacent pixels of plain and encrypted color test images

Full size image
Fig. 10
figure 10

Correlation between two adjacent pixels of plain and encrypted grayscale test images

Full size image

5.6 Correlation coefficient analysis

The relation between the neighboring pixels of the plain and encrypted images is revealed by evaluating the correlation coefficients [12] horizontally, vertically and diagonally using the formula given below:

$$\begin{aligned} r(u,v)=\frac{\sum _{i=1}^{N} \left( \left( u_{i}-\frac{1}{N} \sum _{i=1}^{n}u_{i} \right) \left( v_{i}-\frac{1}{N} \sum _{i=1}^{N}v_{i} \right) \right) }{\sqrt{\sum _{i=1}^{N} \left( u_{i}-\frac{1}{N} \sum _{i=1}^{N}u_{i} \right) ^{2}}\; \sqrt{\sum _{i=1}^{N} \left( v_{i}-\frac{1}{N} \sum _{i=1}^{N}v_{i} \right) ^{2}}} \end{aligned}$$
(27)

where N is the size of the image and u, v are adjacent pixel values of the grayscale image or RGB components.

The average horizontal, vertical and diagonal correlation coefficients have been evaluated for both plain and encrypted images in this work. The correlation between neighboring pixels of the plain and encrypted images has been performed by randomly choosing 3000 pairs of neighboring pixels in opposite directions. The pixels value \((x+1,y)\) with respect to the variable position (x, y) is considered for horizontal correlation. In the same way, the neighboring pixels \((x,y+1)\) and \((x+1,y+1)\) have been used for vertical and diagonal correlation respectively over the value (x, y).

In Fig. 9, the average horizontal, vertical, and diagonal correlation scatter plot of the color images have been depicted. The linear relationship has been followed in the plots of plain image which infers the strong correlation between the neighboring pixel values. On the other hand, the weak correlation between the neighboring pixel values of the encrypted image in the figure shows that the statistical attacks get weaker against the proposed model.

Figure 10 represents the correlation coefficient scatter plots of the grayscale images. The plots of plain images show that the points are closely placed along the diagonal line which implies high correlation between the neighboring pixels. While the symmetrically distributed points in the plots of encrypted images depict the low correlational among the neighboring pixels. Thus, the proposed model greatly minimizes the correlation between the neighboring pixels of the encrypted image which enhances the resisting power of the proposed model against statistical attack.

Table 4 Correlation coefficients of color and grayscale test images
Full size table

The average values of correlation coefficients of the plain and encrypted images are indicated in Table 4. The negative values of the correlation coefficient of the encrypted images obtained by using the proposed model depicts the weak relationship among the neighboring pixels. This implies that the proposed model is highly resistant to statistical-based attacks.

5.7 Information entropy analysis

The distribution and randomness in the pixels of an image is measured by entropy parameter and is calculated using the formula shown as follows:

$$\begin{aligned} H(t)=\sum _{i=0}^{255} p(t_{i})\;\hbox {log}_{a} \left( \frac{1}{p(t_{i})} \right) \end{aligned}$$
(28)

where \(t_{i}\) is the pixel value and \(p(t_{i})\) is its probability of occurrence in the image.

Table 5 contains the entropy values of color and grayscale images. It has been delineated that the entropy values of the encrypted images procured using the proposed model lies between 7.9970 and 7.9999 which is near to 8. Hence, in the proposed model there are very less chances of information leakage. This implies that the proposed model is less prone to statistical and entropy attacks.

The comparison of the proposed model with the erstwhile models for the entropy values is shown in Table 6. The bold values indicate the better score obtained by the proposed model which proves that the proposed model is more secure to the entropy and statistical attacks as compared to the existing models.

Table 5 Entropy values of color and grayscale test images
Full size table
Table 6 A comparison of entropy values
Full size table

5.8 Differential attack

The information transmitted through open network in the form of images is prone to the differential attacks. The performance of the model against differential attack is ensured by using the two widely used parameters: NPCR and UACI. The extent of percentage of distinct pixels in the two encrypted images is measured by using NPCR (number of pixels change rate). On the other hand, UACI metric (unified averaged changed intensity) depicts the average dissimilarity between the two encrypted images. The formulas used for finding the NPCR and UACI values are as follows:

$$\begin{aligned} \hbox {NPCR}(C_{1},C_{2})&=\frac{\sum _{i=1}^{M} \sum _{j=1}^{N} c(i,j)}{w\times h} \end{aligned}$$
(29)
$$\begin{aligned} \hbox {UACI}(C_{1},C_{2})&= \frac{1}{w \times h}\nonumber \\&\quad \left( \sum _{i=1}^{M} \sum _{j=1}^{N} \frac{|C_{1}(i,j)-C_{2}(i,j)| }{255}\right) \end{aligned}$$
(30)

where M and N represent the width and height of the plain image, \(C_{1}\) and \(C_{2}\) are two encrypted images encrypted before and after one pixel change, c is the difference between the corresponding pixel values of the encrypted images \(C_{1}\) and \(C_{2}\), and \(w\times h\) is the number of pixels in the plain image.

Table 7 The NPCR and UACI results of color and grayscale images (significance level \(\alpha =0.05\))
Full size table

The NPCR and UACI values of the encrypted images using the proposed model are shown in Table 7. The values of NPCR and UACI have been analyzed for significance value at \(\alpha =0.05\). The proposed model pass the test results for all the images corresponding to the theoretical NPCR and UACI critical values which shows the resistance against the differential attacks.

In Table 8, juxtaposition of the proposed model with existing models is presented. The bold values of NPCR and UACI indicates the failure of the encryption models. It has been observed that the proposed model pass all the NPCR and UACI test results for the significant level at \(\alpha =0.05\). However, the existing encryption models proposed by [2, 27] and [18] do not give a test result of \(100\%\) which implies that these models can be prone to the differential attack than the rest of the models. However, the proposed scheme exhibits excellent performance by comparison, which proves the progress of this work.

Table 8 A comparison of NPCR and UACI values
Full size table
Fig. 11
figure 11

Cropping attack analysis results for (1/3)rd and (1/4)th data loss

Full size image
Table 9 SSIM values of color and grayscale test images
Full size table

5.9 Cropping attack

The anti-shearing aptness of the encryption model is verified by trimming some portions of the encrypted image. The trimming can spread the subtle changes in the plain image to the whole encrypted image in the encryption process. It also, tells about the effect of data loss in an encrypted image before decryption process [19].

The cropping attack has been applied on all the test images, but the results of only one grayscale and one color image are represented in Fig. 11. It has been observed that decryption process of the proposed model can still recover the plain image even after the loss of (1/3)rd and (1/4)th amount of data in the encrypted image [17]. The most of the information of the recovered images are easily recognizable even with addition of some noise. Therefore, when the encrypted image encounters cropping attack in the transmission, the proposed model has better security and can effectively resist the cropping attack.

5.10 SSIM

Structural Similarity Index Metric (SSIM) qualifies the degree of structural invariance between the two images [7]. It ranges from 0 to 1. The SSIM value 1 instigates that the images are completely indistinguishable, while its 0 value represents the characteristic dissimilarity between two images [14].

From Table 9 it has been analyzed that the plain versus decrypted images got the SSIM value equal to 1 which depicts the complete structural similarity between the plain and decrypted images. The SSIM values of the plain versus encrypted images ranges from 0.0043 to 0.0107 which means that the two images are completely distinct with respect to the image pixel values. Hence, the proposed image encryption model is effective and feasible against statistical attacks which implies that there are very few chances of information loss.

The experimental and statistical analysis conveys that the proposed image encryption and decryption model has better performance as compared to the existing models. The experimental results show that the proposed model resist statistical, entropy, differential, and cropping attacks in an efficient way.

6 Conclusion

This work propounds an image encryption and decryption model based on the scrambling algorithm, a novel magic square and differential encoding technique along with chaotic maps to enhance the level of security and privacy. The propounded model comprises two phases: confusion and diffusion. In the proposed model, the coordinate positions of the image pixels have been randomized by employing the scrambling algorithm which intensifies the degree of intricacy in the encrypted image before altering the pixel values. The elements of the magic square are utilized to change the image pixel values which reduce the plain image information hidden in the encrypted image. Further, the bit-level security of the proposed model has been improved by virtue of the implementation of the differential encoding technique on the magic square values. The XOR operation has been performed on the encoded and chaotic map values before applying the circular shift. Next, the complexity of the magic square values has been increased by using differential encoding and chaotic map. The in-depth security, structural, visual, and robustness anatomization of the propounded model have been performed to check the validity of the model against entropy, statistical, cropping, and differential attacks. The comparative inspection of the proposed model with the existing models reveals that the proposed model is more secure against different types of attacks. Henceforth, the proposed model is feasible and efficient for cryptographic application areas. In future, the researchers may work on the combination of algebraic properties of the magic square propounded in this paper along with wavelet transformations, numerical methods, DNA encoding technique, etc. These combinations might be able to generate the image encryption model with more enhanced level of security and complexity. Also, the proposed model will be tested for video and audio data encryption.