Analysis of zig-zag scan based modified feedback convolution algorithm against differential attacks and its application to image encryption

Abstract

In this paper, a novel zig-zag scan-based feedback convolution algorithm for image encryption against differential attacks is proposed. The two measures Number of Pixel Change Rate (NPCR) and Unified Average Changed Intensity (UACI) are commonly utilized for analyzing the differential attacks. From the study of the existing papers, even though high Number of Pixel Change Rate and Unified Average Changed Intensity values are obtained, a few values lie in the critical range of α-level significance which in turn increase the possibility of differential attacks. To overcome differential attacks, two aspects of scanning with different test cases are analyzed and from these analyses, it is concluded that zig-zag scan based feedback convolution in forward and reverse direction achieves good Number of Pixel Change Rate and Unified Average Changed Intensity without critical values. Zig-zag scan based feedback convolution in forward and reverse direction is enforced for key sequence generation and applied in diffusion process to achieve high level of security. Moreover, plain image related initial seed is also generated to overcome the chosen/known plain text attacks. Both numerical and theoretical analyses are performed to prove that the proposed encryption method is resistant to differential attacks. General security measures are carried out for the proposed method to validate its security level. From the simulations, it is shown that the proposed methodology has good keyspace, high key sensitivity, good randomness, and uniform distribution of cipher image pixels.

1 Introduction

Due to the incredible development of information technology, numerous information/data is being transferred via telecommunication networks like internet, computer networks, telephone networks, TCP/IP networks, etc. The information may be a text or multimedia information like image, audio, video, etc. In today’s world, the security of information/data is questionable because of the development of network technologies. Particularly, image security is essential for many domains and at the same time conventional cryptographic algorithms like RSA, AES, and DES are not pertinent because of certain aspects of the image such as huge data size, high correlation, etc. Over the last two decades, chaotic system is utilized for image encryption due to the extrinsic features like ergodicity, high randomness and high sensitivity to initial conditions/parameters. As a result of the fabulous features of chaos, many researchers have been developing chaos-based image cryptosystem for the past few years [9, 11, 16, 29, 30, 32, 40]. The security of the cryptosystem is proved theoretically by analyzing the cryptosystem against computational uncertainty for which the system gives high randomness. But in the practical level of cryptography, security is analyzed by checking its resistance to various kinds of attacks such as differential attacks, brute force attacks, pattern attacks, etc. [6, 18, 19, 27, 31]. Jakimoski and Kocarev [14], proposed a new block cipher using one-dimensional chaotic map which is analyzed against two necessary attacks i) differential analysis (chosen/known-plaintext attacks) ii) linear cryptanalysis (use of linear expressions used in the cryptosystem to reveal the weakness in the cipher image). Of these possible attacks, the most vulnerable is the differential attack, since the attackers target on plain image related attacks and any encryption algorithm should resist this kind of attack.

The differential attack is analyzed with the help of two measures - NPCR (Number of Pixels Change Rate) and UACI (Unified Average Changing Intensity) [2, 5, 9, 11, 28, 29, 32, 38, 40]. Yue et al. [36] have formulated a mathematical design for Number of Pixel Change Rate and Unified Average Changed Intensity and used these values to regulate the statistical belief of Number of Pixel Change Rate and Unified Average Changed Intensity. From this statistical hypothesis, few values are identified as critical values with three α-level significance values 0.01, 0.05, and 0.001. However, all the existing encryption algorithms skip the observations on “differential attacks.” The researchers focus on encryption algorithms with less computational complexity and fewer encryption times forget about the protection against differential attacks. Among the many attacks possible in image encryption the most vulnerable attack is differential attacks. Also, the security of any encryption scheme highly depends on diffusion process as it is easy to cryptanalyse permutation only process. The main aim of this paper is to provide good encryption from diffusion effect itself by analyzing good Number of Pixel Change Rate and Unified Average Changed Intensity values as it can be concluded that the overall encryption system is enough to withstand differential attacks if the diffusion effect itself achieves good Number of Pixel Change Rate and Unified Average Changed Intensity.

The main contributions of the present work are,

• (i) A novel zig-zag scan based chaotic feedback convolution model is constructed, and this model is investigated for its feasibility against differential attacks by learning the Number of Pixel Change Rate and Unified Average Changed Intensity values.

• (ii) Various scanning methodologies for chaotic feedback convolution model are analyzed for finding the best model.

• (iii) Inspired by the constructed chaotic forward and reverse zigzag scan convolution with feedback given in middle as the best model , this model is integrated into the key generation process of encryption in order to overcome differential attacks.

• (iv) Non-critical Number of Pixel Change Rate and Unified Average Changed Intensity values are obtained from the diffusion effect itself.

• (v) Further, to overcome plain image related attacks, the initial seed of logistic map is generated from plain image. Also, realization of one-time pad technique is also utilized for highly secure applications.

The rest of this paper is organized as follows: Section 2 gives a detailed explanation of the existing encryption algorithms. Section 3 explains the preliminary concepts used in the proposed method, the construction of proposed framework along with its investigation and the integration of the proposed framework into the encryption procedures. Security analysis of the proposed method and theoretical proof for perfect secrecy are given in Section 4 and the findings are summarized in Section 5.

2 Related work

Due to rapid growth in multimedia and internet technology, multimedia information such as images, videos, etc are shared online. So, the confidentiality of information i.e., information security has become more important. For this purpose, different techniques are approached. Rasul et al. [8], have designed image encryption based on DNA sequence and the NPCR and UACI values of different sample images are indeed theoretically critical in the null hypothesis test at 0.05 level suggested in [36]. Teng et al. [34] implemented self-adaptive chaotic image encryption for bit-level encryption and decryption for which the NPCR value is 93.6768% and UACI value is 33.3364%. These values intuitively show that the cryptosystem is vulnerable to differential attack. In [24, 35, 39], some of the NPCR and UACI values are theoretical critical values. In these schemes, even though the keystream is strongly correlated with the plain image, they are vulnerable to differential attacks due to ineffective diffusion effect. In Shannon’s theory [33], it is described that good mixing of transformations is needed for achieving perfect secrecy of the cryptosystem and one-time pad technique is observed to be highly secure as the key is changed for every encryption. Based on this, one-time keys are generated and applied in encryption scenarios [3, 7, 10, 17, 21, 22]. Liu et al. [23] have proposed a coupled chaotic network model for image encryption which does not have critical values but involves one-time pad for secure encryption. Chang’e Dong [7] has proposed an image encryption technique based on a coupled chaotic system with one time keys and the average Number of Pixel Change Rate and Unified Average Changed Intensity values are 99.61233%, 33.45033%, and it shows that all Number of Pixel Change Rate and Unified Average Changed Intensity values are non-critical because of one-time keys. Liu et al. [22] have proposed image encryption for color images and the one-time initial values are generated from environmental noise and the average of non-critical Number of Pixel Change Rate and Unified Average Changed Intensity values are 99.6097% and 33.4819% respectively. Moreover, Cao et al. [3] proposed an encryption scheme at bit-level with initial seeds of chaotic map updated in real-time based on the acquired ciphertext. Gao, H and Gao, T [10] implemented an encryption scheme that possesses double verification and one-time pad is used for achieving high level of security. The disadvantage of one-time keys is, if they are not random for every encryption then there will be a possibility to attacks. In the work proposed by Li et al. [20], image encryption is formulated in which the key sequence is related with the plain image and the pixels are permuted in two stages; pixel level and bit level. Brindha and Ammasai [28], proposed a plain image related strong diffusion for images without critical values but computational load is high in the diffusion phase. Also, the keys with same size as that of the plain image need to be sent for decryption.

Hua et al. [12] proposed a high-efficiency scrambling by newly designed cosine transform related chaotic systems and the diffusion process achieves high Number of Pixel Change Rate and Unified Average Changed Intensity without the knowledge of plain image. Similarly, a novel cyclic group-based sequence is produced for image encryption in [15, 26], and in these schemes the keys are not correlated with plain image and there is no strong diffusion. Hence, in both schemes there is a possibility to plain image related attacks. Moreover, in Luo et al. [26] scheme, the histogram plots are not uniform and the entropy value is 7.9974 which is less compared with recent encryption techniques and this may induce statistical attacks. Chai et al. [4] have suggested plain image related chaotic encryption using DNA encode rules with no theoretical values in Number of Pixel Change Rate and Unified Average Changed Intensity but DNA operations are time-consuming which in turn increase cost. To overcome the limitation in [4], optical XOR operation is implemented by Huo et al. [13] but this scheme does not show the resistance against differential attacks and does not pass the randomness test. But the advantage is its fastest implementation in encryption process. Yavuz [37] proposed a content-sensitive dynamic switching function with good security and without any critical values, but the keys used in the encryption process is not dynamic.

From the study of the existing literature, it is found that even though Number of Pixel Change Rate and Unified Average Changed Intensity values are good enough to resist the differential attack, these values are yet to be analyzed for finding further security leakages based on critical values as suggested by Wu et al. [36]. Also some of the plain image related encryption schemes [5, 28] are having same size key as the input which leads to high transmission load. Moreover, few encryption schemes [7, 17, 21,22,23, 38] fully rely on one-time keys without strong diffusion to overcome the differential attacks. If the one-time keys are not completely random for every encryption then it may lead to differential attack.

Different from previous research, this paper thoroughly studies the effects of non-critical Number of Pixel Change Rate and Unified Average Changed Intensity values to differential attacks. Meanwhile, to overcome the differential attacks, a new image encryption scheme is proposed in the present work to achieve non-critical Number of Pixel Change Rate and Unified Average Changed Intensity values only from the diffusion effect using chaos-based zig-zag feedback convolution. One-time key is also presented but it is an optional add-on security for highly secure applications. Thus, the proposed work can make significant contributions to the chaotic image encryption research area.

3 Proposed framework

In this section, the basics behind the proposed framework along with clear explanation about the proposed work is explained.

3.1 Fundamental knowledge

The fundamental concepts behind the proposed image encryption are described as follows:

3.1.1 Chaos theory

Due to intrinsic properties of Chaos, it is useful in many applications like image encryption, pseudo-random number generation, hash functions, etc. In the key generation of the proposed encryption process, random numbers are generated from the chaotic map, and for simplicity, one-dimensional chaotic map such as a logistic map is used. The logistic map is defined as:

$$ x_{q+1} = \mu x_{q}\left( 1-x_{q}\right) $$

(1)

where the initial seed x₀ varies from 0 to 1 and the parameter μ has the range $\left [3.5 4.0\right ]$.

3.1.2 Convolution function

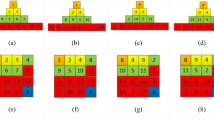
Ahmad and Sundararajan [1] proposed a two-dimensional convolution with discrete space for processing the image in spatial domains. Spatial information of an image is utilized for filters and are applied in edge detection, smoothening, enhancing and sharpening of images. Ludwig [25] explains that, each pixel of the image is processed by chosen kernel matrix values. Figure 1 clearly shows the convolution applied for a sample matrix and the shaded boxes represent the matrix padded with zeros. The steps involved in general convolution are:

• i) The kernel matrix is shifted horizontally and vertically using the raster scan method in each element of the matrix A(i,j) to perform convolution.

• ii) The kernel matrix is multiplied with the neighbouring pixel values of A(i,j) and finally the multiplied values are added to get $A^{\prime }(i, j)$ and are stored in the same position.

Fig. 1

General Framework of convolution

3.2 Overview of the proposed framework

The convolution function describes the spatial information of an image and this is an approach used for ideal filtering. The same function is used to construct the chaotic convolution function and relevant analyses are carried out for this model for analysing non-critical Number of Pixel Change Rate and Unified Average Changed Intensity values with different test cases. According to the Number of Pixel Change Rate and Unified Average Changed Intensity values, the proposed zig-zag scan based chaotic feedback convolution model is proved to be good enough to describe the key sequence of an image encryption process. From the analyses, it is also proved that the proposed zig-zag scan based model is good in terms of withstanding differential attacks from diffusion effect itself and shows its adaptability to image encryption. Moreover, a simple method is provided for the initial seed generation of Logistic map to withstand the chosen/known plain text attacks. In view of this, the proposed model has greater ability to withstand differential attacks than other existing models. In the following sections, the procedure for constructing the chaotic convolution function and the investigation for finding the best model to overcome the differential attacks are explained. The constructed chaotic convolution function is embedded into the key generation function of encryption system. Followed by this, the encryption and decryption procedures are explained. Then, the relevant security analyses and theoretical proof for perfect secrecy of the model are presented. The overview of the proposed framework is illustrated in Fig. 2. It clearly explains the proposed framework with its investigations against differential attacks. Followed by this, the best method is integrated into encryption process and then security analysis for the proposed encryption process is also performed.

Fig. 2

Overview of the proposed framework

3.3 Construction of chaotic convolution function

A chaotic feedback based convolution is used for the key generation process of proposed image encryption. The general convolution function given in (2) is modified and applied in the key generation process of image encryption. The random matrix $A \left (i, j\right )$ is filled with arbitrary numbers where 1 ≤ i ≤ m, 1 ≤ j ≤ n and m& n are the number of rows and columns in the random matrix generated, $H\left (x, y\right )$ denotes the kernel or mask matrix values applied for each element of the random matrix where $-\infty \leq x \leq \infty$, $-\infty \leq y \leq \infty$.

The general convolution formula applied in any discrete two-dimensional space is given as

$$ \begin{array}{@{}rcl@{}} A^{\prime}\left( i, j\right) &=& \sum\limits^{\infty}_{y = -\infty}\sum\limits^{\infty}_{x = -\infty} A\left( i-x, j-y\right).H\left( x, y\right) 1\\ &\leq& k \leq m\times n \end{array} $$

(2)

In the general framework, same kernel H(x,y) is selected for image processing depending on the applications like smoothing, filtering, blurring, etc. Kernel/mask varies for each element of random matrix used in the key generation process which is generated by the pseudo-random generator like logistic map.

For the key generation process, a separate kernel matrix is applied for each element of random matrix, so the convolution operation for each element in the random matrix is described as,

$$ \begin{array}{@{}rcl@{}} A^{\prime}\left( i, j\right) &=& \sum\limits^{\infty}_{y = -\infty}\sum\limits^{\infty}_{x = -\infty} A\left( i-x, j-y\right).H_{k}\left( x, y\right) 1\\ &\leq& k \leq m\times n \end{array} $$

(3)

where $H_{k}\left (x,y\right )$ is described as the separate kernel for each element in the random matrix and this matrix is generated from the logistic map. Equation (3) is used for the generation of keys in the image encryption process.

3.4 Investigation of chaotic convolution function against differential attacks

In this section, the effectiveness of combining chaotic convolution in 10 different models is investigated. The models are basically designed by two scanning methods, feedback position in kernel matrix. The main objective of this investigation is to learn Number of Pixel Change Rate and Unified Average Changed Intensity values for designed test models as those are the measures to evaluate the differential attacks. Among the differently designed models, the effective model which gives good Number of Pixel Change Rate and Unified Average Changed Intensity to overcome the differential attacks is found out and is applied for encryption. Basically, the two measures NPCR and UACI are used to analyze the differences of ciphered images with a tiny change given in the input image. These two measures are defined as,

$$ NPCR =\frac{ {\sum}_{p =1}^{m}{\sum}_{q =1}^{n} \delta \left( p, q \right)}{mn} \times 100\% $$

(4)

where $\delta \left (p,q\right ) = \left \{\begin {array}{rcl} 1, & \text {if}\ c_{1}\left (p,q\right ) \neq c_{2}\left (p,q\right )\\ 0, & \text {otherwise} \end {array}\right .$

$$ UACI = \frac{1}{mn} \sum\limits_{p = 1}^{m} \sum\limits_{q = 1}^{n} \left( \frac{\left|c_{1}\left( p,q\right)-c_{2}\left( p,q\right)\right|}{255}\right) \times 100 \% $$

(5)

where m and n are the number of rows and columns in the image and c₁ and c₂ are the two cipher images. To analyze the proposed model of key generation, a logistic map with initial seeds x₀ = 3.4 and x₀ = 3.5 are used and iterated for generating random values in MATLAB and these values are changed into a matrix with a size equivalent to the plain image. The theoretical critical values for NPCR and UACI are given in Table 1 for various levels which is noted in [36]. Using these reference values in Table 1, the NPCR and UACI values computed for formulated test cases are checked whether it is theoretically critical or not.

Table 1 Theoretically NPCR & UACI critical values with three α-level significance

For formulating various models/test cases, two strategies are considered (i) Feedback (ii) Scanning methodology. Feedback is analysed because independent element operation is also a factor of attacks in the resultant matrix. The dependency on the previously computed value reduces attacks and also increases the number of pixel change rate.The feedback is given to one of the elements in the mask matrix. The size of the mask matrix is 3 × 3 having 3 rows and 3 columns and a total of 9 entries. Hence there is a need to analyze which entry is suitable for giving the feedback to get high change rate and changing intensity. For analyzing this, the representation of random matrix is given in Fig. 3a and further, the kernel mask is analyzed for giving feedback in middle or neighbouring 8 entries. The neighbouring entries of mask matrix are specified as dotted entries and the middle entry is represented by X as shown in Fig. 3b. Moreover, each and every element of the random matrix are read and convolution operation is performed. For scanning the elements, two scanning techniques are considered: i) snake scan as illustrated in Fig. 3c ii) zigzag scan which is illustrated in Fig. 8 and the test cases are analyzed for these types of scanning.

Fig. 3

a Random matrix representation with padded zeros (b) kernel matrix (c) Snake scan

Using these strategies, the 10 test cases are analyzed with examples. The first 5 test cases read the elements of the random matrix to perform convolution operation using snake scan in forward and reverse directions. The remaining 5 test cases employ a zigzag scan method in forward and reverse directions. The cases are i) without feedback ii) forward feedback given in one of the neighbouring entries in mask matrix iii) forward feedback given in middle entry of mask matrix iv) forward and reverse feedback given in one of the neighbouring entries of mask matrix v) forward and reverse feedback given in middle entry of mask matrix. The numerical analysis for all cases is performed in a random matrix of size 8 × 8 as shown in Fig. 4a. The one bit changed matrix at position (1, 8) is illustrated in Fig. 4b. Similarly, 16 locations are chosen such that $\left (1, 1 \right )$, $\left (88, 150\right )$, $\left (193, 66\right )$, $\left (179, 229\right )$, $\left (141, 36\right )$, $\left (66,216\right )$, $\left (209, 63\right )$, $\left (158, 122\right )$, $\left (213, 150\right )$, $\left (235, 74\right )$, $\left (193, 98\right )$, $\left (246, 168\right )$, $\left (10, 218\right )$, $\left (1, 8\right )$, $\left (128, 128\right )$, $\left (256, 256\right )$ positions are tested against all cases to find out the number of elements change rate and changed intensity values.

Fig. 4

a Random matrix of the size of 8 × 8 (b) Same random matrix of entry (1, 8) with one bit changed

3.4.1 Reading each element using snake scan

• Case 1: Forward Snake scan without feedback

For the random matrix, the convolution operation is applied to each element with the individual mask without feedback. The resultant matrix named as c₁ got from random matrix is compared against the resultant matrix c₂ generated from one (one bit) change in the random matrix. After analyzing these two resultant matrices it is found that the change in one element affects only the neighbouring elements of the changed element and it is shown in Fig. 5a. The Number of Pixel Change Rate and Unified Average Changed Intensity value is also very less.

Fig. 5

The resultant matrices C₁ and C₂ for cases (1)-(5): Top row is the resultant matrix of a random matrix, bottom row is the resultant matrix of random matrix with one-bit change

• Case 2: Forward snake scan convolution with feedback given in one of the neighbouring entries of mask matrix

For each value of random matrix, the convolution operation is applied together with feedback given in one of the neighbouring 8 entries in the forward direction as shown in Fig. 3b. The resultant matrices c₁ and c₂ are obtained from same input matrix with one-bit difference in singe element/entry. By analyzing these two matrices, it is found that the convolution effect starts from changed bit position. Consider a change in location entry (1, 1) which is expected to produce all entry changes in resultant matrix c₂ but due to edge and corner entries, the effect of feedback is not taken for computation. From Fig. 5b, it is inferred that the change starts from one-bit change in the random matrix and the change rate of resultant matrix c₂ is $\frac {1}{4}^{th}$ of resultant matrix c₁ which leads to less Number of Pixel Change Rate and Unified Average Changed Intensity values.

• Case 3: Forward snake scan convolution with feedback given in middle entry of mask matrix

This case is the same as the previous case, but the feedback is given in the middle of the mask value to overcome the issues of edge and corner entries. Analysis of resultant matrices shows that the change starts from one-bit change entry and this is illustrated in Fig. 5c from which it can be observed that 50% of the entries remain same for both resultant matrices which results in less Number of Pixel Change Rate and Unified Average Changed Intensity values.

• Case 4: Forward and reverse snake scan convolution with feedback given in one of the neighbouring entries of mask matrix

The feedback is given similar to case 2 and the resultant Number of Pixel Change Rate and Unified Average Changed Intensity values are little bit high compared to that of case 2 because of the convolution operation done in both directions. In this case, many of the entries are changed as given in Fig. 5d but few of the entries remain same because of less impact of feedback on edge and corner entries which leads to less intensity change.

• Case 5: Forward and Reverse snake scan convolution with feedback given in the middle entry of mask matrix

The feedback given in the mask matrix is the same as case 3, but the convolution is performed in both directions (forward and reverse). Analysis of this case shows high Number of Pixel Change Rate and Unified Average Changed Intensity for first and last entry of the input matrix because one-bit change starts from the first element onwards, which in turn induces changes in all elements in the random matrix. Figure 5e illustrates that only five entries are same in the resultant matrices.

3.4.2 Reading each element using the Zigzag scan

• Case 6: Forward zigzag convolution without feedback

Similar to case 1, the convolution operation is applied to the random matrix without feedback but it reads each element using zigzag scan. Here also the neighbouring elements get affected as illustrated in Fig. 6a and it has less Number of Pixel Change Rate and Unified Average Changed Intensity values.

Fig. 6

The resultant matrices C₁ and C₂ for cases (6)-(10): Top row is the resultant matrix of a random matrix, bottom row is the resultant matrix of random matrix with one-bit change

• Case 7: Forward zigzag convolution with feedback given in any one of the neighbouring entries

For each element of the random matrix, the convolution operation is applied together with feedback given in any one of the neighbouring entries in forwarding direction as shown in Fig. 3b. For one-bit change in any one element of random matrix, the changes between two resultant matrices start from the neighbouring elements, and after that, all the remaining elements are changed. But the major drawback of this case is explained by the following examples: i) if the value in entry (1, 8) at random matrix is changed then in the resultant matrix c₂, all pixels are not changed because the change starts from that chosen entry and sometimes less intensity change leads to less Number of Pixel Change Rate and this is demonstrated in Fig. 6b. If the feedback is given to edge or corner entries it does not give much effect due to which there is a less intensity change. ii) if the value at entry (8, 8) of random matrix is changed, then in the resultant matrix c₂, only 5 elements/entries are changed as it is a corner element. So the Number of Pixel Change Rate decreases as in this case feedback is given in the forward direction neighbouring pixels only.

• Case 8: Forward zigzag convolution with feedback given in middle entry of mask

This case is same as the previous case but the feedback is given in the middle of the mask values to overcome the issues of edge and corner pixels. Analysis of this case shows that input matrix and one-bit change in one element of input matrix produces two different resultant matrices, but the effect is only for the first entry and the last entry. For all the remaining entries, the change starts from that changed entry and a few of the intensity changes produce the same intensity value again in the resultant matrix c₁. For example, if the entry in (1, 8) is changed for one-bit then the resultant matrix c₂ changes starting from that neighbourhood elements only as shown in Fig. 6c. From this analysis, it is evident that all entries do not give full effect for one-bit change so Number of Pixel Change Rate and Unified Average Changed Intensity values are very less which may further lead to attacks.

• Case 9: Forward and reverse zigzag convolution with feedback given in any one of the neighbouring entries

From the analysis of the above cases, the values of Number of Pixel Change Rate and Unified Average Changed Intensity are very less, so the zigzag convolution is applied reversely, i.e., from the last element to first element of random matrix. In this case also, similar to case 7, very less Number of Pixel Change Rate and Unified Average Changed Intensity values are obtained at edge and corner elements as the feedback effect are not taken. For change in location (1, 8), the resultant matrices c₁ and c₂ have 17 same entries because of edge and corner entries and is illustrated in Fig. 6d.

• Case 10: Zigzag forward and reverse convolution with feedback given in middle pixel

The above case 9, achieves good Number of Pixel Change Rate and Unified Average Changed Intensity values for the changed entries (1, 1) and (256, 256) of a random matrix. The remaining entries depend on the change of intensity in the elements. Figure 6e shows the resultant matrices for this case and it shows that all element values are modified for one-bit change in any one element of random matrix. So, the zigzag scan convolution operation applied in forward and reverse directions and the middle of the mask replaced by the previously computed value play an important role in achieving the good Number of Pixel Change Rate and Unified Average Changed Intensity values without any theoretical critical values for resisting differential attack.

3.4.3 Observations made from the investigations

Using MATLAB, all the above investigated test cases are simulated for a random matrix of size 256 × 256 in which the random values are generated from a Logistic map. The generated random matrix and its variant (i.e., one-bit changed similar random matrix) are given as input to the all 10 test cases to generate two cipher matrices C₁ and C₂. Then, the Number of Pixel Change Rate and Unified Average Changed Intensity results are obtained from analysing the cipher images for all test cases are listed in Tables 2 and 3. From Tables 2 and 3, after analyzing the test cases, the feedback convolution model, i.e. using zigzag scan and feedback applied in the middle of the mask for changing the value in forward and reverse directions is proved to give better security. The Number of Pixel Change Rate and Unified Average Changed Intensity values given in Tables 2 and 3 are plotted in Fig. 7 and it is inferred that cases 5, 8, and 10 give better Number of Pixel Change Rate and Unified Average Changed Intensity values because of the feedback given in middle entry. Also it is noted that change rate of each element fully depends on the changed intensity. Further, it can be observed that the variation of Number of Pixel Change Rate and Unified Average Changed Intensity values is exactly similar and proportionate i.e., the changed intensity is $\frac {1}{3}^{rd}$ of the change rate of elements, which is an added advantage of the proposed algorithm. Hence, it is concluded that feedback given in middle entry gives much more effect compared to feedback given in neighbouring entries. And at the same time, to overcome the differential attacks, the key generation process is finally correlated with the plain image, i.e. the seed taken for the pseudo-random generator is computed from the plain image. If the attacker use the same plain image to reveal the secret key in such cases, one-time key is also proposed for the encryption scheme.

Table 2 NPCR values for various test cases

Table 3 UACI values for various test cases

Fig. 7

The NPCR and UACI values plotted for all test cases

3.5 Integration of zig-zag scan based chaotic convolution into the key generation process

Any encryption scheme will provide better security if it has a good diffusion effect. Permutation of the plain image does not give better effect as it can be easily broken by cryptanalysis. So, in order to improve the effect of diffusion and to overcome differential attacks, two aspects of scanning with different test cases are analyzed using NPCR and UACI measures for the key generation of the proposed encryption scheme. From the investigations, the zig-zag scan based chaotic convolution operation with feedback given in middle is integrated into the generation of keys applied in the image encryption process i.e., diffusion phase. Further, the clear explanation about the key generation process is explained here which is done in two directions.

• i) Forward direction

• ii) Reverse direction

3.5.1 Forward direction

For the key generation, the random values are generated from the pseudo-random generator (logistic map), and these values are stored in an array

$$ arr_{m\times n} = \left\{a_{1},a_{2},...,a_{m\times n}\right\} $$

(6)

and this array is reshaped into a matrix described as

$$ A\left( i,j\right) = \left( \begin{array}{ccc} a_{11} & {\cdots} & a_{1m} \\ {\cdots} & {\ddots} & {\vdots} \\ a_{n1} & {\cdots} & a_{mn} \end{array} \right) $$

(7)

This random matrix is used as the input for the convolution operation. Using the same pseudo-random generator (logistic map) another set of random values is generated for the kernel matrix which is to be applied for each element in the matrix $A \left (i, j\right )$ and these values are stored into an array

$$ arr1_{m\times n} = \left\{kr_{1},kr_{2},...,kr_{m\times n \times 3 \times 3}\right\} $$

(8)

These values are reshaped into a matrix described as

$$ Kr = \left( \begin{array}{ccc} kr_{11} & {\cdots} & kr_{19} \\ {\cdots} & {\ddots} & {\vdots} \\ kr_{\left( m\times n\right)1} & {\cdots} & kr_{\left( m\times n\right)9} \end{array} \right) $$

(9)

Each row of this matrix is extracted and reshaped into a mask size of 3 × 3, and is applied to each element in the matrix $A \left (i, j\right )$, to get the intermediate output described as

$$ O_{1} = \left( \begin{array}{ccc} o_{11} & {\cdots} & o_{1m} \\ {\cdots} & {\ddots} & {\vdots} \\ o_{n1} & {\cdots} & o_{mn} \end{array} \right) $$

(10)

For instance, for the first element in $A \left (i, j\right )$ which is represented as a₁₁, the needed kernel matrix is extracted from the first row of matrix Kr and is represented as

$$ Kr_{1} = \left\{kr_{11},kr_{12},...,kr_{19}\right\} $$

(11)

This is reshaped into a 3 × 3 matrix represented as

$$ H_{1} = \left( \begin{array}{ccc} kr_{11} & kr_{14} & kr_{17} \\ kr_{12} & kr_{15} & kr_{18} \\ kr_{13} & kr_{16} & kr_{19} \end{array} \right) $$

(12)

After applying the values of H₁ to a₁₁, the computed value is stored in the intermediate output o₁₁.For the second element, the kernel matrix is represented as

$$ H_{2} = \left( \begin{array}{ccc} kr_{21} & kr_{24} & kr_{27} \\ kr_{22} & kr_{25} & kr_{28} \\ kr_{23} & kr_{26} & kr_{29} \end{array} \right) $$

(13)

This middle value of the matrix is replaced by the previously computed value of the intermediate matrix O₁ and the kernel matrix for the second element is modified to get the feedback from the previous output

$$ H_{2} = \left( \begin{array}{ccc} kr_{21} & kr_{24} & kr_{27} \\ kr_{22} & o_{11} & kr_{28} \\ kr_{23} & kr_{26} & kr_{29} \end{array} \right) $$

(14)

This feedback based convolution is applied for all the elements in $A \left (i, j\right )$ and for the last element in the matrix, the kernel matrix is described as

$$ H_{m\times n} = \left( \begin{array}{ccc} kr_{\left( m\times n \right)1} & kr_{\left( m\times n \right)4} & kr_{\left( m\times n \right)7} \\ kr_{\left( m\times n \right)2} & o_{\left( m-1 \right)\left( n\right)} & kr_{\left( m\times n \right)8} \\ kr_{\left( m\times n \right)3} & kr_{\left( m\times n \right)6} & kr_{\left( m\times n \right)9} \end{array} \right) $$

(15)

The convolution applied for the matrix $A \left (i, j\right )$ for each element using zigzag scan method in two directions is shown in Fig. 8. After computing the intermediate value in the forward direction from the first element to the last element using random values generated from the chaotic map, the convolution is applied in the reverse direction for different kernel values generated from same chaotic map with different initial seed from the last element to the first element. The reverse process also follows zigzag scan from the last element to the first element and is explained in the next section.

Fig. 8

Zigzag scan process for reading pixels in the image

3.5.2 Reverse direction

The intermediate output O₁ is given as the input to this process. Using the chaotic map, the random numbers are generated and these values are stored in an array as

$$ arr_{2} = \left\{krr_{1},krr_{2},...,krr_{m\times n \times 3 \times 3}\right\} $$

(16)

This array is reshaped into a matrix, represented as

$$ krr = \left( \begin{array}{ccc} krr_{11} & {\cdots} & krr_{19} \\ {\cdots} & {\ddots} & {\vdots} \\ krr_{\left( m\times n\right)1} & {\cdots} & krr_{\left( m \times n\right)9} \end{array} \right) $$

(17)

Each row of the matrix krr is used as kernel value and is applied to the matrix O₁ to get final output matrix

$$ O_{2} = \left( \begin{array}{ccc} o_{11} & {\cdots} & o_{1m} \\ {\cdots} & {\ddots} & {\vdots} \\ o_{n1} & {\cdots} & o_{mn} \end{array} \right) $$

(18)

Here the last element o_mn is read and changed using the kernel matrix described as

$$ krr_{1} = \left\{krr_{11},krr_{12},...,krr_{19}\right\} $$

(19)

These array values are reshaped into a 3 × 3 matrix, represented as

$$ H_{1} = \left( \begin{array}{ccc} krr_{11} & krr_{14} & krr_{17} \\ krr_{12} & krr_{15} & krr_{18} \\ krr_{13} & krr_{16} & krr_{19} \end{array} \right) $$

(20)

For the last element o_mn, the value of the first element o₁₁ in the intermediate matrix O₁ is given as the feedback in the middle of the mask matrix H₁ and is represented as

$$ H_{1} = \left( \begin{array}{ccc} krr_{11} & krr_{14} & krr_{17} \\ krr_{12} & o_{11} & krr_{18} \\ krr_{13} & krr_{16} & krr_{19} \end{array} \right) $$

(21)

Using this kernel matrix, the value of the last element is changed and for $o_{\left (m-1\right )\left (n-1 \right )}$ element of the intermediate matrix, the kernel matrix is represented as

$$ H_{2} = \left( \begin{array}{ccc} krr_{21} & krr_{24} & krr_{27} \\ krr_{22} & krr_{25} & krr_{28} \\ krr_{23} & krr_{26} & krr_{29} \end{array} \right) $$

(22)

Now the middle value of the mask is replaced by the previous computed value of the output matrix, and this is represented as

$$ H_{m\times n} = \left( \begin{array}{ccc} krr_{\left( m\times n \right)1} & krr_{\left( m\times n \right)4} & krr_{\left( m\times n \right)7} \\ krr_{\left( m\times n \right)2} & o_{\left( m \right)\left( n+1\right)} & krr_{\left( m\times n \right)8} \\ krr_{\left( m\times n \right)3} & krr_{\left( m\times n \right)6} & krr_{\left( m\times n \right)9} \end{array} \right) $$

(23)

After applying the reverse convolution operation, each element is modified and made dependent on the previously computed value. This zig-zag scan based feedback convolution method is used in the diffusion process of the proposed encryption process and it is found to be very effective against differential attacks.

3.6 Proposed encryption and decryption process

From the proper investigations, the zig-zag scan based feedback convolution is utilized for the proposed encryption process as it is proved to be effective to withstand differential attacks. The block diagram for the encryption/decryption process is given in Fig. 9. Permutation and Diffusion phases are involved in the encryption of images. The initial seed generated from the plain image is accorded to the chaos generator to generate random values. The same random values are utilized to get index order sequences applied in permutation process. The key matrix obtained from proposed chaotic convolution model is XORed with permuted image to get the cipher image. The initial value of logistic map is generated from the plain image to overcome the differential attacks and the one time key is also applied in the generation of initial value to overcome plain image related attacks.

Fig. 9

Block diagram of the proposed encryption scheme

3.6.1 Initial seed generation

The generation of initial seed used in the Logistic map is explained here. The following steps are performed in the seed generation process.

• Step 1: The count of each pixel level in the plain image and the probability of each pixel level is calculated.

• Step 2: 100 random pixel levels are chosen and, the sum of the probabilities of chosen pixel levels are given as initial seed for the logistic map.

  $$ \begin{array}{llll} sum_{R_{\left( 1-100\right)}} & = {\sum}_{1}^{100} r_{1},r_{2},r_{3},...,r_{100}\\ & = 0.003781+0.003766+,...,+0.0036\\ & = 0.390305 \end{array} $$

  (24)

  This initial seed is given for the proposed key generation process and it acts as the one-time key. If same 100 random pixels are used then the key depends only on plain image.

3.6.2 Permutation phase

• Step 1: A plain image of the size I = m × n is taken and is converted into a one dimensional array $P = \left \{p_{1},p_{2},...,p_{\left (m \times n\right )}\right \}$, where m and n are the height and width of the plain image, respectively.

• Step 2: The initial value x₀ of the logistic map is obtained from the initial seed generation and iterated for m × n times, to generate the sequence $X = \left \{x_{1},x_{2},...,x_{m \times n}\right \}$. The sequence X is sorted in ascending order to get the index order sequence $F_{X} = \left \{F_{x_{1}},F_{x_{2}},...,F_{x_{m \times n}}\right \}$.

• Step 3: From the index order sequence, the plain image is shuffled and the shuffled values are stored in an array $S = \left \{s_{1},s_{2},...,s_{m\times n}\right \}$ and the array is reshaped into a matrix $S = \left (\begin {array}{ccc} s_{11} & {\cdots } & s_{1m} \\ {\cdots } & {\ddots } & {\vdots } \\ s_{n1} & {\cdots } & s_{mn} \end {array} \right )$ to get the shuffled/permuted image.

3.6.3 Diffusion phase

The chaotic map given in (1), is used to generate the chaos sequence $x_{i}\left (q\right )$ by utilizing the initial seed generated from probability of pixels and the key sequence is generated from zigzag convolution method in (3), and is given by

$$ k_{i}\left( q\right) = o_{2} mod \left( m\right) $$

(25)

where o₂ is the final output matrix of the modified convolution process and m is the positive number described by the quantization level of plain image $p_{i}\left (q \right )$. The shuffled image $s_{i}\left (q\right )$ and the key matrix $k_{i}\left (q\right )$ are given to encryption function (XOR) and the cipher image $c_{i}\left (q\right )$ is obtained. This encryption function is described as

$$ c_{i}\left( q\right) = E\left( s_{i}\left( q\right),k_{i}\left( q\right)\right) = s_{i}\left( q\right) \oplus k_{i}\left( q\right) $$

(26)

where $E\left (s,k \right )$ is the bit-wise XOR function. The cipher image is transmitted to the corresponding receiver through a proper channel. The results for the proposed encryption method with different stages are illustrated in Fig. 10. In this, the standard test image of size 256 × 256 from SIPI-USC database is given as input and this is given Fig. 10a–d. The results obtained for permutation, diffusion phases are shown in Fig. 10e–h and i–l respectively. The obtained permuted and encrypted images totally disrupt the plain image pixels i.e., none of the information is revealed to the attackers.

Fig. 10

Results obtained for different stages of proposed encryption process using different test images (a–d) Input image (e–h) Permuted image (i–l) Encrypted image (Lena, Peppers, Cameraman, Baboon)

3.6.4 Decryption

For decrypting the cipher image, the initial value for the logistic map is sent to the receiver. Now, the receiver will have the knowledge of the secret key, cipher image and the defined encryption process. Using this, the same convolution process is applied for generating the key sequence given in (27). The decryption function is described as

$$ p_{i}\left( q\right) = D\left( c_{i}\left( q\right),k_{i}\left( q\right)\right) = c_{i}\left( q\right) \oplus k_{i}\left( q\right) $$

(27)

where i = 1,2,...,m × n.

$$ \text{That is,} s_{i}\left( q\right) = c_{i}\left( q\right) \oplus k_{i}\left( q\right) $$

(28)

From (28), the shuffled values are converted into a plain image.

4 Security analysis

This section gives the possible cryptographic attacks for breaking confidentiality. The performance of the proposed method is evaluated using different security measures to overcome the cryptographic attacks such as statistical, and differential attacks. For the sake of that, different standard security measures are simulated against certain amount of sample images with different sizes from the USC-SIPI image database, and they are described in the following subsections.

4.1 Key sensitivity analysis

In this analysis, a trivial change in encryption and decryption key is analyzed for three different cases: i) the encryption/decryption key is changed from x₀ to x₀ + 1 or x₀ − 1 ii) the magnitude of the key is changed from 10¹⁵ to 10⁷ iii) the parameter value μ is changed to μ + 1 or μ − 1. The sample image Lena of size 256 × 256 is given in Fig. 11a and the encrypted and decrypted images using the correct key are given in Fig. 11b–c. For these above mentioned three cases, the simulation is done and shown in Fig. 11d–f. In this, the encryption key is incremented or decremented by single bit and then the decrypted image is given Fig. 11d is obtained. Similarly, the magnitude of the key x₀ and parameter value is changed and the decrypted image given in Fig. 11e–f is obtained. From these results, it is shown that, the proposed image encryption is sensitive to the secret keys which further shows its resistance to attacks.

Fig. 11

Key sensitivity analysis (a) Plain image (b) Encrypted image using correct secret key (c) Decrypted image using correct secret key (d) Decrypted image with single bit changed (e) Decrypted image for change in magnitude of the key x₀ (f) Decrypted image for change in magnitude of the parameter

4.2 Correlation among adjacent pixels

In the plain image, the adjacent pixel correlation is very high. In order to hide the statistical behaviour of the image, the correlation of adjacent pixels should be nearer to zero so that the intruder does not get any information about the image. For various images, simulation is done for analyzing the correlation of the adjacent vertical, diagonal and horizontal pixels, for w = 6000 pairs of random samples. The following formulas are used for computing the correlation among adjacent pixels.

$$ R_{ij} = \frac{\left|cov\left( i,j\right)\right|}{\sqrt D\left( i \right) \times \sqrt D\left( j\right)} $$

(29)

in which

$$ cov\left( i, j\right) = \frac{1}{w} \sum\limits_{t = 1}^{w} \left( i_{t} - E\left( i\right)\right)\left( j_{t}-E\left( j\right)\right) $$

(30)

$$ E\left( i\right) = \frac{1}{w} \sum\limits_{t = 1}^{w} i_{t} $$

(31)

$$ D\left( i\right) = \frac{1}{w} \sum\limits_{t = 1}^{w} \left( i_{t}-E\left( i\right)\right)^{2} $$

(32)

where i_t and j_t are the chosen t^th pair of adjacent pixel grey values. E(i) and D(i) are the expectation and variance of the pixels. The correlation between the adjacent pixels of the plain and encrypted image is given in Table 4. From the numerical results noted in Table 4, it is shown that there is very less correlation among adjacent pixels of encrypted image. In other words, the correlation among adjacent pixels in all three directions is less than 0.01. For, Fig. 11a and b, the correlation analysis is performed and Fig. 12 represents the original image and cipher image correlation in horizontal, vertical, and diagonal directions of three planes. From the Fig. 12a, c, e, it is clearly observed that the plain image is having high correlation compared to the cipher image correlation given in Fig. 12b, d, f. The cipher image correlation is close to zero to resist the statistical attack.

Fig. 12

Correlation between adjacent pixels in horizontal, vertical, and diagonal directions

Table 4 Correlation values of all three planes for different images

4.3 Histogram analysis

The statistical property is revealed from histograms, as in an image if the Grey values are not uniformly distributed, then the attackers can easily retrieve the information from histogram analysis. If the encryption algorithm is good, then the Grey values in the image are uniformly distributed which means that all pixel values have equal probability. The histograms of plain and enciphered images are illustrated in Fig. 13 and it proves that it is difficult to get the original image from histogram analysis.

Fig. 13

Histogram analysis (a) Plain image (b) cipher image (c) Histogram of plain image (d) Histogram of cipher image

Figure 13a and b are the original and encrypted images where as c and d are the histogram plots of original and encrypted images respectively. Here, Fig. 13c reveals some pattern (non-uniform distributions) in their histogram plots for all the test images. But for all test images, the proposed cryptosystem makes the ciphered image to be uniformly distributed as given in Fig. 13d which confirms that proposed scheme withstands statistical attack.

4.4 Entropy analysis

The entropy is computed by,

$$ H(d) = \sum\limits^{2^{n}-1}_{q=0} P\left( d_{i} \right) \times \log_{2} \left( P\left( d_{i} \right)\right) $$

(33)

where $P\left (d_{i} \right )$ represents the probability of each pixel level. According to (33), the ideal value for H(d) is equal to 8. Using (33), the entropy is calculated for various enciphered images and they are listed in Table 5. From the simulation results, the maximum value achieved for entropy of the proposed algorithm is found to be 7.9994. It shows that the proposed system generates encrypted images with very high entropy, and it is also nearer to the ideal entropy value. Moreover, it indicates that the cryptosystem has high randomness.

Table 5 NPCR, UACI for different images using three cases and Entropy value for different cipher images

4.5 Differential analysis

The differential attack will frame a relationship among the differences in plain and ciphered image to predict the original image. Number of Pixel Change Rate and Unified Average Changed Intensity are the two good measures for analyzing differential attacks.

In [36], the randomness tests are carried out for both Number of Pixel Change Rate and Unified Average Changed Intensity. From this, the Theoretical Critical Values(TCV) for NPCR and UACI with different size of images are given in Table 1. Three different α-level significance are α = 0.05,α = 0.01,α = 0.001, and the Number of Pixel Change Rate and Unified Average Changed Intensity score to meet the requirements are given in Table 1. If the Number of Pixel Change Rate value is less than the critical values then the cipher images are not random-like in a particular α level significance. Similarly, if the Unified Average Changed Intensity values does not fall into the expected intervals given in the table, then the cipher pair is not a random one in the α-level significance. In order to analyse this, randomly selected test images with one-bit(arbitrarily) modified image variants are used and the analyses is made for three cases (i) diffusion only (ii) plain image related (iii) One-time key. The obtained values are recorded in Table 5. From this evaluation, it is shown that the proposed method has high Number of Pixel Change Rate and good Unified Average Changed Intensity in order to withstand differential attacks. The values of Number of Pixel Change Rate and Unified Average Changed Intensity for different images of the proposed algorithm with one-time key added method is added only for the additional level of security as diffusion itself gives high level of security in the key generation method.

4.6 Speed analysis

In general, for any algorithm, the encryption time and computational load are to be analyzed. The algorithm runs on Windows 10, 64 Bit, Matlab R2018a, Intel Pentium N3540, CPU @2.16 GHz processor, with RAM of 8.00 GB memory. The basic operations of the proposed model are addition, multiplication, modulo and XOR. Due to the multiplication operation in key generation process of the proposed model, the proposed method has high computational load. The execution time of the proposed algorithm is 10.44 seconds which is somewhat high compared to other existing algorithms. The assured level of security from the diffusion effect itself, may compensate the speed limitations of the proposed method as it can be overcome by making use of high end processors.

Table 6 Comparison of the proposed method with respect to properties

4.7 Discussion and evaluation of the proposed scheme against existing methods

In this section, the superiority of the proposed method against other existing schemes is discussed in two different ways. The superiority is evaluated (i) Using properties behind a good encryption scheme (ii) Using standard security measures.

4.7.1 Performance comparison with respect to properties behind a good encryption scheme

From the review of existing encryption techniques, all encryption schemes rely on the following properties to achieve high level of security. The security features are given as (i) Null Theoretical Critical Values(TCV) of Number of Pixel Change Rate & Unified Average Changed Intensity specified in [36] (ii) Incorporate plain image in key generation (Plain Image Related-PIR) (iii) One-time key (OTK) (iv) Strong Diffusion (SD). Along with these features Decryption Complexity (DC) is also analyzed against different schemes.

Using these features, the proposed scheme is compared with different encryption schemes and are listed in Table 6. From Table 6, it is inferred that few schemes [3, 24, 30, 38] are having theoretical critical values of Number of Pixel Change Rate and Unified Average Changed Intensity. Even though, the schemes [38] & [3] are related to plain image or/and one-time key they provide critical values of Number of Pixel Change Rate & Unified Average Changed Intensity. Using the second feature, i.e., generation of keys related to plain image the schemes [2, 4, 28, 37] are proposed without critical values. But [2, 28] are having high transmission load and [4] takes high computation time. Similarly, [10, 13] impose PIR encryption and PIR+OTK based encryption respectively and produces good Number of Pixel Change Rate and Unified Average Changed Intensity but [13] impose a possibility to statistical attacks and [10] depends on OTK to get non critical Number of Pixel Change Rate and Unified Average Changed Intensity values. The third feature OTK is solely utilized to achieve good encryption in a few schemes [3, 17, 22] but if one-time key is not completely random-like then there is a potential to attacks. Further, the schemes [12, 15] have strong diffusion property without relating to plain image for withstanding differential attacks but these schemes are vulnerable to the chosen/known plain text attacks. The encryption scheme given in [26] achieves good Number of Pixel Change Rate and Unified Average Changed Intensity without any critical values and without any specified feature listed above, but this scheme is vulnerable to statistical attacks and plain image related attacks.

Finally, [5, 7] are having similar features of the proposed method (i.e., plain image related, strong diffusion, and one-time key) with good Number of Pixel Change Rate and Unified Average Changed Intensity values. But [5] needs to send key matrix with the same size of input image to the receiver end whereas [7] needs to send the plain image itself for generating keys which are not feasible in real time.

From the analysis of the existing schemes using various properties, the proposed method is highly superior to other encryption methods. In the next section, security metrics are compared with the other existing methods.

4.7.2 Performance comparison with respect to security metrics

In this section, the proposed encryption method is compared with the existing literature using general security measures utilized for evaluating the encryption scheme. For this, Lena image of size 256 × 256 is taken and the entropy, correlation values are noted in Table 7. From Table 7, it is inferred that in a few schemes [4, 5, 15, 28, 37], the entropy value is closer to the proposed scheme but these schemes do not achieve all the quality features whereas in the remaining schemes, entropy is lesser than the proposed scheme. From this, it is shown that the randomness of the existing system is less compared with that of the proposed one. Moreover, the adjacent pixel correlation values also indicate that the proposed scheme is superior to the other methods. The algorithm presented in [22] obtains a high Number of Pixel Change Rate of 99.66653 % which is closer to the proposed work but this algorithm relies fully on one-time key. Similarly, [15] has Number of Pixel Change Rate of 99.6944 but this scheme does not relate with plain image leading to plain image related attacks. From the above three security measures, it is shown that our scheme is better than other existing methods.

Table 7 Comparison of the proposed method with respect to security metrics

4.8 Chosen/known plain text attacks

A cryptanalyst literally knows about the design and work flow of the cryptosystem by its study. Realizing the secrets about key is hard compared to realizing the intermediate parameters of the cryptosystem. Generally, the attackers focus to reveal the intermediate parameters. From (26), if the attacker realizes the key matrix k_i(q), the permuted matrix s_i(q) can be revealed simply and, after that using shuffled image the plain image can be easily retrieved from the analysis. For extracting the key matrix k_i(q), the attacker chooses the plain pixels P_i = p₁p₂p₃... = 000... and the permuted plain image s_i(q) = 0 is obtained for the pixels p_i = 0 where 1 ≤ i ≤ m × n. It looks that, the key matrix k_i(q) can be retrieved by (34).

$$ c_{i}(q) = k_{i}(q) $$

(34)

But in the proposed scheme, as the plain image is correlated with the generation of initial value used in the logistic map, different key matrix is generated for every plain image and also during every time of encryption. Hence the proposed method is ineffective to the chosen/known plain text attacks. Similar to realizing k_i(q), for extracting the shuffled matrix s_i(q), the attacker chooses an input image P of size m × n with all rows of the 1^st column represented as 1, all rows of the 2^nd column represented as 2 and so on, until all rows of the last column are represented as n and then tries to reveal the order of the shuffled transformations. But the shuffled vector is also changed every time in the proposed scheme because of initial seed generation of logistic map. So the attacker will not be able to get the shuffled vector also. It shows that the chosen/known plain text attack is infeasible for our proposed scheme in the confusion stage itself.

4.9 Theoretical proof

The proposed convolution method is analyzed theoretically for Shannon’s perfect secrecy in this section.

4.9.1 Perfect secrecy

The proposed image encryption algorithm needs to satisfy the unconditional security (perfect secrecy) which specifies the cipher image’s security against all attacks ignoring the attacker’s ability. For analyzing such unconditional security, the following two assumptions are made:

• (i) The attacker has only cipher image and does not have the key matrix and plain image.

• (ii) The key used in the proposed algorithm is used only once because of one-time encryption.

The proposed encryption scheme is defined as

$$ \begin{array}{@{}rcl@{}} C\left( j\right) &=& Enc\left( K\left( x\right), A\left( i\right)\right)\\ &=& a \oplus k, for a \in A, k \in K, \end{array} $$

(35)

$$ \begin{array}{@{}rcl@{}} A\left( j\right) &=& Dec\left( K\left( x\right), C\left( i\right)\right)\\ &=& c \oplus k, for a \in A, k \in K, \end{array} $$

(36)

An encryption system achieves perfect secrecy if it meets the requirements for all pixels a₁,a₂,...,a_n in the space A for all cipher pixels c₁,c₂,...,c_n, such that

$$ \begin{array}{llll} prob\left[enc\left( k,a_{1}\right) = c \right] = prob\left[enc\left( k,a_{2}\right) = c \right] = ... \\ = prob\left[enc\left( k,a_{n}\right) = c \right] \end{array} $$

(37)

According to (37), if the probability distributions of cipher image are equal, then perfect secrecy is achieved.

4.9.2 Theorem

Let an image encryption algorithm have |A| = |K| = |C|, then the perfect secrecy is allowed if and only if,

• i) the key matrix has an equal probability of each pixel $1/\left |K\right |$ and ∀i ∈ P,∀j ∈ C and there exists a unique key for each encryption such that $e_{k}\left (i \right ) = j$.

• ii) if the proposed cryptosystem has perfect secrecy then $prob\left [C = c\right ] = prob\left [A = a \right ]$

Proof

• i) $prob\left [C = c|A = a\right ] = prob\left [k = \left (c \oplus k\right )\bmod 256\right ]$

  $$ prob\left[C = c|A = a\right] = \frac{1}{m \times n} $$

  (38)

  i.e., the generated key has a uniform distribution with equal probability in the proposed work

• ii) $prob\left [C = c\right ] = \sum prob\left [ C = c|A = a^{\prime }].prob[a \right .$ $\left .= d_{k}\left (c\right )\right ]$

  by using (35), $prob\left [a = d_{k}\left (c\right )\right ] = prob\left [m^{\prime }\right .$$\left .= c \oplus k \right ]$

  $$= {\sum}^{}_{} prob\left[k = m^{\prime} \oplus c\right]. prob\left[m^{\prime} = c \oplus k\right]$$
  $$= {\sum}^{}_{} \frac{1}{m \times n}. prob\left[m^{\prime} = c \oplus k\right]$$
  $$= {\sum}^{}_{} \frac{1}{m\times n}.1 $$

Therefore $prob\left [m^{\prime } = c \oplus k\right ] = 1$ (sum of the probabilities of plain pixels is one)

$$prob\left[k = m^{\prime} \oplus c\right] =\frac{1}{m\times n}$$

$$ prob \left[C = c\right] = {\sum}_{}^{} \frac{1}{m\times n} $$

(39)

Using Bayes theorem,

$$prob\left[A = a|C = c\right] = \frac{prob\left[C = c | A = a\right].prob\left[A = a\right]}{prob\left[C =c\right]}$$

From (38) and (39),

$$ prob\left[A = a|C = c\right] = prob\left[A = a\right] $$

(40)

From (40), the proposed method is said to achieve perfect secrecy and this can be proved from the distributions of pixel values in the ciphered image. □

5 Conclusion

In this paper, an efficient zig-zag scan based feedback convolution in forward and reverse direction is proposed, which is used for describing the key sequence in image encryption. The chaotic convolution framework is constructed from traditional convolution function, and then this model is investigated using different test cases on two aspects (i) scanning the pixels (ii) feedback applied in middle or neighbour pixels. From the proper investigations, it is found that the effect of the proposed chaotic convolution is superior at zig-zag scan with feedback given at middle position in both directions. In other words, from the analyses, the established model is concluded to provide good diffusion effect to withstand differential attacks without any critical Number of Pixel Change Rate and Unified Average Changed Intensity values. The effect of the proposed model is integrated into key generation process of the image encryption. Meanwhile, to overcome the plain image related attacks, (chosen/known plain text attacks) the initial seed is generated from the plain image. High Number of Pixel Change Rate and Unified Average Changed Intensity are obtained from the proposed key generation with less correlation and uniform distribution of cipher image. The proposed methodology achieves better randomness and keys exhibit high sensitivity. Numerical results are analyzed and it is shown that the proposed work is efficient for generating dynamic keys. The Shannon’s perfect secrecy is also proved theoretically for the proposed encryption system. In future, hardware implementation of the proposed model will be realized to integrate it with real time applications such as surveillance camera.