Some new kink type solutions for the new (3+1)-dimensional Boiti–Leon–Manna–Pempinelli equation

Abstract

Exact solutions of higher-dimensional nonlinear equations takes a major place in the study of nonlinear phenomena observed in nature. In this article, some new kink type solutions are investigated for the new (3+1)-dimensional Boiti-Leon-Manna-Pempinelli(BLMP) equation. Firstly, a variety of solutions are obtained by Hirota’s bilinear form, which include kink type wave solution, periodic solitary wave solutions and singular solitary wave solutions using extended homoclinic test approach. Secondly, solutions with three wave form are obtained by generalized three wave method. The extended homoclinic test approach is also used to construct solutions with a tail which explain some physical phenomenon. Moreover, some figures of the solutions are shown behind.

1 Introduction

Nonlinear science is a vital discovery in the area of natural science since the 20th century, and its rapid development has made it one of the popular topics in mathematical physics. In recent decades, researches on soliton solutions [1],rogue waves solutions [2], periodic wave solutions [3], interaction solutions [4] and lump solutions [5] of nonlinear partial differential equations (NLPDEs) have received increasing attention from experts and scholars.

Recently, nonlinear evolution equations (NLEEs) has wide application in various fields. Various methods have been proposed to explore nonlinear phenomena. For example, three-wave method [6, 7], tanh method [8], Bäcklund transformation [9], Darboux transformation [10], Exp-function method [11], Hirota bilinear method [12], homogeneous balance method [13], the generally projective F-expansions [14], (G’/G)-expansion method [15], auxiliary equation method [16], Riccati equation method [17], simplest equation method [18, 19], etc.

Wazwaz proposed a new (3+1)-dimensional Boiti-Leon-Manna-Pempinelli (BLMP) equation which has time dependent coefficients. It’s written as the form [20]

$$\begin{aligned}&F(t) (u_x+u_y+u_z)_t+G(t)(u_x+u_y+u_z)_{xxx}\nonumber \\&\quad +H(t)(u_x(u_x+u_y+u_z))_x=0. \end{aligned}$$

(1.1)

It comes from one of the most typical NLEEs, which is the (3+1)-dimensional BLMP equation

$$\begin{aligned} (u_y+u_z)_t+(u_y+u_z)_{xxx}+(u_x(u_y+u_z))_x=0, \nonumber \\ \end{aligned}$$

(1.2)

which includes three expressions which consist the derivatives $u_y + u_z$. The Eq. (1.1) has the additional derivative $u_x$ to every expressions.

Let $F(t)=1, G(t)=1, H(t)=1$, Eq.(1.1) reduces to the a equation mainly discussed in this paper with constant coefficients

$$\begin{aligned}&(u_x+u_y+u_z)_t+(u_x+u_y+u_z)_{xxx}\nonumber \\&\quad +(u_x(u_x+u_y+u_z))_x=0. \end{aligned}$$

(1.3)

These equations describe a kind of physical phenomenon in the natural world, that is, the propagation of waves in incompressible fluid. To confirm its integrability, the Painlév analysis is used by Wazwaz to obtain the compatibility condition. By the simplified Hirota’s method and the complex Hirota’s criteria, the multiple soliton solutions and multiple complex soliton solutions are determined. [20]

Based on the new (3+1)-dimensional BLMP equation given by Wazwaz, scholars have obtained many new research achievements. Liu and Wazwaz further get breather wave solutions, lump type solutions of equation (1.3) in Ref. [21]. Yuan presented more kinds of the interaction solutions, including lump and N-soliton solutions. The breather-wave solution is studied in Ref. [22]. Han and Bao investigated the equation (1.1) with time-dependent coefficients on the basis of the Hirota bilinear method, and obtained the mixed high-order lump N-soliton solutions and the hybrid solutions in Ref. [23]. To construct test functions, Qiao, Zhang and Yue used a specific bilinear neural network framework. Three kinds of periodic-type solutions of Eq. (1.3) are given in Ref. [24].

The paper is structured as follows, Sect. 2 obtains kink-shaped solitary wave solutions, singular solitary wave solutions, periodic wave solutions and periodic kink wave solutions by using the extended homoclinic test approach. In Sect. 3 a three-wave method is used to find three-wave solutions. We get periodic kink wave solutions, periodic cross kink wave solutions and periodic wave solutions. Section 4 obtains kink-shaped solitary wave solutions with tails, by using the extended homoclinic test approach. Section 5 is dedicated to giving the conclusion.

2 Extended homoclinic test approach

The new (3+1)-dimensional BLMP equation with constant coefficients has been written as

$$\begin{aligned}&(u_x+u_y+u_z)_t+(u_x+u_y+u_z)_{xxx}\nonumber \\&\quad +(u_x(u_x+u_y+u_z))_x=0. \end{aligned}$$

(2.1)

According to the function transformation

$$\begin{aligned} u(x,y,z,t)=6[\ln {f(x,y,z,t)}]_x \ , \end{aligned}$$

(2.2)

the Hirota bilinear form of Eq. (2.1) is

$$\begin{aligned}&[D_x^4+D_yD_x^3+D_zD_x^3+D_tD_x+D_tD_y\nonumber \\&\quad +D_tD_z]f\cdot f=0. \end{aligned}$$

(2.3)

Then Eq. (2.1) becomes

$$\begin{aligned}&{3f_{xx}}^2+3f_{xz}f_{xx}+3f_{xy} f_{xx}-f_t f_z-f_t f_y-f_t f_x\nonumber \\&\quad -3f_x f_{xxz}-3f_x f_{xxy}-f_z f_{xxx}\nonumber \\&\quad -f_y f_{xxx}-4f_xf_{xxx}+f(f_{zt}+f_{yt}+f_{xt}\nonumber \\&\quad +f_{xxxz}+f_{xxxy}+f_{xxxx} )=0. \end{aligned}$$

(2.4)

Let f take the form

$$\begin{aligned} f = k_1\cos ({\xi _1})+k_2\exp ({\xi _{2}})+\exp ({-\xi _{2} }), \end{aligned}$$

(2.5)

where $\xi _i=a_i x+b_i y+c_i z+d_i t, k_i\in {\mathbb {R}}, a_i,b_i,c_i,d_i\in {\mathbb {C}}( i=1,2)$are undetermined constants.

Substituting Eq. (2.5) into (2.3) and setting coefficients of

$$\begin{aligned}&\cos ({\xi _1}) \exp {(-\xi _2)}, \cos {(\xi _1)}\exp {(\xi _2)},\\&\sin {(\xi _1)}\exp {(-\xi _2)}, \sin {(\xi _1)}\exp {(\xi _2)} \end{aligned}$$

and the constant term to zero, we obtain a set of algebraic equations (2.6) with respect to $k_i$ and $a_i,b_i,c_i,d_i, (i=1,2).$

$$\begin{aligned} \left\{ \begin{aligned}&k_1(-a_1^4-(b_1+c_1)a_1^3+3a_2(c_2+2a_2+b_2)a_1^2\\&\quad +[(3b_1+3c_1)a_2^2+d_1]a_1 \\&-a_2^4+(-c_2-b_2)a_2^3-a_2d_2+(b_1+c_1)d_1\\&\quad -d_2(c_2+b_2))=0,\\&k_1 ((-c_2-4a_2-b_2 ) a_1^3-3a_2 (b_1+c_1 ) a_1^2\\&\quad +[4a_2^3+(3c_2+3b_2 ) a_2^2+d_2 ] a_1\\&+(b_1+c_1 ) a_2^3+d_1 a_2+(c_2+b_2 ) d_1+d_2 (b_1+c_1 ))=0,\\&k_1k_2(a_1^4+(b_1+c_1)a_1^3-3a_2(c_2+2a_2+b_2)a_1^2\\&\quad -[(3b_1+3c_1)a_2^2+d_1]a_1 \\&a_2^4+(c_2+b_2)a_2^3+a_2d_2+(-b_1-c_1)d_1+d_2(c_2+b_2))=0,\\&k_1 k_2((-c_2-4a_2-b_2 ) a_1^3-3a_2 (b_1+c_1 ) a_1^2\\&\quad +[4a_2^3+(3c_2+3b_2 ) a_2^2+d_2 ] a_1\\&+(b_1+c_1 ) a_2^3+d_1 a_2+(c_2+b_2 ) d_1+d_2 (b_1+c_1 ))=0,\\&-(a_1+b_1+c_1 )(-4a_1^3+d_1 ) k_1^2+(a_2+b_2+c_2 )(4a_2^3+d_2 )4k_2=0. \end{aligned} \right. \end{aligned}$$

(2.6)

Solving Eq. (2.6), we have following conclusion.

2.1 Solution in the situation $k_1 = 0$

If $k_1=0$, we have some cases.

Case 1

I.

$$\begin{aligned} k_1 = 0, \ a_2 =-c_2 - b_2, \end{aligned}$$

(2.7)

where $a_1, b_1, b_2, c_1, c_2, d_1, d_2,$ and $k_2$ are free parameters.

II.

$$\begin{aligned} k_1 = 0, \ d_2 =-4a_2^3, \end{aligned}$$

(2.8)

where $a_1, a_2, b_1, b_2, c_1, c_2, d_1$ and $k_2$ are free parameters.

Fig. 1

The singular solitary wave solution $u_3$ at $a_1=1, c_1=1, a_2=1, b_2=1, k_1=1, z=0, {\textbf {a}} t=$-$1, {\textbf {b}} t=0, {\textbf {c}} t=1$

Fig. 2

The singular solitary wave solution $u_5$ at $a_2=1, b_1=1, b_2=1, k_1=1, x=0, {\textbf {a}} t=-5, {\textbf {b}} t=0 ,{\textbf {c}} t=5$

Substituting Eq. (2.7–2.8) into Eq. (2.5) and Eq. (2.2), we obtain the solutions in the case of $i=1$ and $i=2$. The corresponding solutions are given by

$$\begin{aligned} u=C_i \frac{ {k_2} {\mathrm e}^{\zeta _i}- {\mathrm e}^{-\zeta _i}}{{k_2} \,{\mathrm e}^{\zeta _i}+{\mathrm e}^{-\zeta _i}},\quad i=1,2, \end{aligned}$$

(2.9)

where

$$\begin{aligned}&\zeta _1={\left( -{c_2} -{b_2} \right) x +{b_2} y +{c_2} z +{d_2} t},\\&\zeta _2={-a_2 x -{b_2} y -{c_2} z + 4a_2^3t}, \ C_1=-6\left( {c_2}\right. \\&\left. +{b_2} \right) , \ C_2=6{a_2}. \end{aligned}$$

In particular, solutions Eq. (2.9) can be expressed as

$$\begin{aligned} u_1= & {} C_i\tanh \left( {\zeta _i +\frac{1}{2}\ln {k_2}}\right) ,\quad k_2>0,i=1,2,\nonumber \\ \end{aligned}$$

(2.10)

$$\begin{aligned} u_2= & {} C_i\coth \left( {\zeta _i+\frac{1}{2}\ln {\left( -k_2\right) }}\right) ,\quad k_2<0,i=1,2, \nonumber \\ \end{aligned}$$

(2.11)

where

$$\begin{aligned} \begin{aligned}&\zeta _1={\left( -{c_2} -{b_2} \right) x +{b_2} y +{c_2} z +{d_2} t},\\&\zeta _2={-a_2 x -{b_2} y -{c_2} z + 4a_2^3t},\\&\ C_1=-6\left( {c_2} +{b_2} \right) , \ C_2=6{a_2}. \end{aligned} \end{aligned}$$

It is easy to know that $u_1$, $u_2$ are kink-shaped solitary wave solutions.

To simplify the results, the sign of $k_2$ will not be discussed in each case later.

2.2 Solution in the situation $k_2=0$

If $k_2=0$, we have

Case 2

$$\begin{aligned} b_1= & {} -a_1-c_1, \ d_1 = a_1^3-3a_1a_2^2, \ d_2 \nonumber \\&=3a_1^2a_2-a_2^3,\ k_2 = 0, \end{aligned}$$

(2.12)

where $a_1, a_2, b_2, c_1, c_2,$ and $k_1$ are free parameters.

Substituting Eq. (2.12) into Eq. (2.2) and Eq. (2.5), the solutions are yielded that

$$\begin{aligned} u=6\frac{- {k_1}{a_1} \sin {\left( \zeta _1\right) }-{a_2} \,{\mathrm e}^{\zeta _2}}{{k_1} \cos { \left( \zeta _1\right) }+{\mathrm e}^{\zeta _2}}, \end{aligned}$$

(2.13)

where $\zeta _1=\left( {a_1} x +\left( -{a_1} -{c_1} \right) y +{c_1} z +\left( {a_1}^{3}-3 {a_1} \right. \right. \left. \left. {a_2}^{2}\right) t \right)$, $\zeta _2=-{a_2} x -{b_2} y -{c_2} z -\left( 3{a_1}^{2} {a_2} -{a_2}^{3}\right) t$.

In particular, solution Eq. (2.13) can be expressed as

$$\begin{aligned} u_3=6\frac{- {k_1}{a_1} \sin {\left( \zeta _1\right) }-{a_2} \left( \cosh {\zeta _2}+\sinh {\zeta _2}\right) }{{k_1} \cos { \left( \zeta _1\right) }+\cosh {\zeta _2}+\sinh {\zeta _2}}, \end{aligned}$$

(2.14)

where $\zeta _1=\left( {a_1} x +\left( -{a_1} -{c_1} \right) y +{c_1} z +\left( {a_1}^{3}-3 {a_1} \right. \right. \left. \left. {a_2}^{2}\right) t \right)$, $\zeta _2=-{a_2} x -{b_2} y -{c_2} z -\left( 3{a_1}^{2} {a_2} -{a_2}^{3}\right) t$.

Case 3

The case of complex solutions.

I.

$$\begin{aligned} b_2= & {} -\frac{1}{{3 {a_1} ({a_1}^{2}+{a_2}^{2})}}(b_{2a} +b_{2b}+b_{2c} + b_{2d}),\nonumber \\ d_1= & {} 4a_1^3,d_2=\pm \left( 3 \,\mathrm {i}{a_1}^{3}+3 \,\mathrm {i} {a_1}{a_2}^{2}\right) +3{a_2}{a_1}^{2}\nonumber \\&-{a_2}^{3}, k_2=0, \end{aligned}$$

(2.15)

where $a_1, a_2, b_1, c_1, c_2,$ and $k_1$ are free parameters. and

$$\begin{aligned} b_{2a}= & {} 3 {a_1}^{3} {c_2} -3 {a_2} \,{a_1}^{2} {b_1} -3 {a_2} \,{a_1}^{2}{c_1} +4 {a_1} \,{a_2}^{3}\\&+3 {a_1} \,{a_2}^{2} {c_2}+{a_2}^{3} {b_1}+{a_2}^{3}{c_1},\\ b_{2b}= & {} ({a_1}(\pm (3 \,\mathrm {i} {a_1}^{3}+3 \,\mathrm {i}{a_1} \,{a_2}^{2})+3 {a_2} \,{a_1}^{2}-{a_2}^{3}),\\ b_{2c}= & {} (\pm (3 \,\mathrm {i}{a_1}^{3}+3 \,\mathrm {i} {a_1} \,{a_2}^{2})+3{a_2} \,{a_1}^{2}-{a_2}^{3}) {b_1},\\ b_{2d}= & {} {\left( \pm \left( 3 \,\mathrm {i} {a_1}^{3}+3 \,\mathrm {i} {a_1} \,{a_2}^{2}\right) +3 {a_2} \,{a_1}^{2}-{a_2}^{3}\right) {c_1}}),\\ \end{aligned}$$

II.

$$\begin{aligned} a_1= & {} \pm \text {i}a_2 , \ b_1 =\mp \mathrm{i}a_2-c_1 , \nonumber \\ d_1 = \mp 4\text {i} a_2^3, \ b_2= & {} -a_2-c_2, \ k_2 = 0, \end{aligned}$$

(2.16)

where $a_2, c_1, c_2, d_2$ and $k_1$ are free parameters.

Substituting Eq. (2.15–2.16) into Eq. (2.5) and Eq. (2.2), we obtain $a^*=a_1$, $i=1$ and $a^*=\pm \text {i}a_2$, $i=2$, respectively. The corresponding solutions are given by

$$\begin{aligned} u=-6\frac{ {k_1}{a^*} \sin {\left( \zeta _i\right) }+{a_2} \,{\mathrm e}^{\eta _i}}{{k_1} \cos { \left( \zeta _i\right) }+{\mathrm e}^{\eta _i}},\ i=1,2, \end{aligned}$$

(2.17)

where $\zeta _1= {a_1} x +{b_1} y +{c_1} z+4 {a_1}^{3} t,$ $\eta _1=-{a_2} x -b_2y-{c_2} z -(\pm \left( 3 \,\mathrm {i}{a_1}^{3}+3 \,\mathrm {i} {a_1}{a_2}^{2}\right) +3{a_2}{a_1}^{2}-{a_2}^{3})t,$ $\zeta _{2}=\left( \pm \mathrm {i}\right) {a_2} x +\left( \left( \mp \mathrm {i}\right) {a_2} -{c_1} \right) y +{c_1} z +4 \left( \mp \mathrm {i}\right) a_2^{3} t ,$ $\eta _{2}=-{a_2} x -\left( -{a_2} -{c_2} \right) y -{c_2} z -{d_2} t.$

Here, the form of $b_2$ is shown in Eq. (2.15). In particular, solution Eq. (2.17) can be expressed as

$$\begin{aligned} u_4= & {} -6\frac{ {k_1} {a^*} \sin \! \left( \zeta _{i}\right) +{a_2}\left( \cosh {\eta _i}+\sinh {\eta _i}\right) }{{k_1} \cos \! \left( \zeta _{i}\right) +\cosh {\eta _i}+\sinh {\eta _i}},\ i\nonumber \\= & {} 1,2, \end{aligned}$$

(2.18)

where $\zeta _1= {a_1} x +{b_1} y +{c_1} z+4 {a_1}^{3} t,$ $\eta _1=-{a_2} x -b_2y-{c_2} z -(\pm \left( 3 \,\mathrm {i}{a_1}^{3}+3 \,\mathrm {i} {a_1}{a_2}^{2}\right) +3{a_2}{a_1}^{2}-{a_2}^{3})t,$ $\zeta _{2}=\left( \pm \mathrm {i}\right) {a_2} x +\left( \left( \mp \mathrm {i}\right) {a_2} -{c_1} \right) y +{c_1} z +4 \left( \mp \mathrm {i}\right) a_2^{3} t ,$ $\eta _{2}=-{a_2} x -\left( -{a_2} -{c_2} \right) y -{c_2} z -{d_2} t.$

Case 4

$$\begin{aligned} a_1 = 0, \ d_1 = 0, \ d_2 =-a_2^3, \ k_2 = 0, \end{aligned}$$

(2.19)

where $a_2, b_1, b_2, c_1, c_2,$ and $k_1$ are free parameters.

Substituting Eq. (2.19) into Eq. (2.2) and Eq. (2.5), the solutions are yielded that

$$\begin{aligned} u=-\frac{6{a_2} \,{\mathrm e}^{\zeta _1}}{{k_1} \cos \! \left( {b_1} y +{c_1} z \right) +{\mathrm e}^{\zeta _1}}, \end{aligned}$$

(2.20)

where $\zeta _1={a_2}^{3} t -{a_2} x -{b_2} y -{c_2} z$. In particular, solution Eq. (2.20) can be expressed as

$$\begin{aligned} u_5=-6{a_2}\frac{ \cosh {\zeta _1}+\sinh {\zeta _1}}{{k_1} \cos { \left( {b_1} y +{c_1} z\right) }+\cosh {\zeta _1}+\sinh {\zeta _1}},\nonumber \\ \end{aligned}$$

(2.21)

where $\zeta _1={a_2}^{3} t -{a_2} x -{b_2} y -{c_2} z$.

2.3 Solution in the situation $k_1\ne 0$ and $k_2\ne 0$

If $k_1\ne 0$ and $k_2\ne 0$, we have following conclusion.

Case 5

$$\begin{aligned} a_1=0, \ d_1 = 0, \ b_2 =-a_2-c_2, \ d_2 =-a_2^3, \end{aligned}$$

(2.22)

where $a_2, b_1, c_1, c_2, k_1$ and $k_2$ are free parameters.

Substituting Eq. (2.22) into Eq. (2.2) and Eq. (2.5), the solutions are yielded that

$$\begin{aligned} u=6{a_2}\frac{{k_2} {\mathrm e}^{\zeta _{1}}- {\mathrm e}^{-\zeta _{1}}}{{k_1} \cos \! \left( \zeta _{2} \right) +{k_2} \,{\mathrm e}^{\zeta _{1}}+{\mathrm e}^{-\zeta _{1}}}, \end{aligned}$$

(2.23)

where $\zeta _{1}={a_2} x +\left( -{a_2} -{c_2} \right) y +{c_2} z -{a_2}^{3} t$, $\zeta _{2}={b_1} y +{c_1} z$.

In particular, the solution Eq. (2.23) can be expressed as

$$\begin{aligned} u_6=12\sqrt{k_2}{a_2}\frac{\sinh \left( {\zeta _{1} +\frac{1}{2}\ln {k_2}}\right) }{{k_1} \cos \! \left( \zeta _{2}\right) +2\sqrt{k_2}\cosh \left( {\zeta _{1} +\frac{1}{2}\ln {k_2}}\right) }\nonumber \\, \end{aligned}$$

(2.24)

where $\zeta _{1}={a_2} x +\left( -{a_2} -{c_2} \right) y +{c_2} z -{a_2}^{3} t$,$\zeta _{2}={b_1} y +{c_1} z$.

Fig. 3

The periodic kink wave solution $u_6$ at $a_2=1, b_1=1, c_1=1, c_2=1, k_1=1, k_2=1, x=0, {\textbf {a}}t=-5 , {\textbf {b}} t=0 , {\textbf {c}} t=5$

Fig. 4

The periodic solitary wave solution $u_7$ at $a_1=1,b_2=1, c_1=1, c_2=1, k_1=1, k_2=1, {\textbf {a}} z=0,t=0, {\textbf {b}} x=0, t=0$

Fig. 5

The periodic kink wave solution $u_8$ at $i=1, a_2=2, b_1=1, c_1=1, c_2=2, d_2=2, k_1=1, k_2=2, z=0, \mathrm{at}=-5, \mathrm{bt}=0, \mathrm{ct}=5$

Case 6

$$\begin{aligned} b_1 =-a_1-c_1 ,\ d_1 = a_1^3, \ a_2 = 0, \ d_2 =0, \end{aligned}$$

(2.25)

where $a_1, b_2, c_1, c_2, k_1$ and $k_2$ are free parameters.

Substituting Eq. (2.25) into Eq. (2.2) and Eq. (2.5), we obtain the solution

$$\begin{aligned} u=-6 {k_1} {a_1}\frac{ \sin \! \left( \zeta _{1} \right) }{{k_1} \cos \! \left( \zeta _{1}\right) +{k_2} \,{\mathrm e}^{\zeta _{2}}+{\mathrm e}^{-\zeta _{2}}}, \end{aligned}$$

(2.26)

where $\zeta _{1}={a_1} x +\left( -{a_1} -{c_1} \right) y +{c_1} z +a_1^{3} t$, $\zeta _{2}=b_2y +{c_2} z$.

In particular, the solution Eq. (2.26)can be expressed as

$$\begin{aligned} u_7=-6 {k_1} {a_1}\frac{ \sin \! \left( \zeta _{1} \right) }{{k_1} \cos \! \left( \zeta _{1}\right) +2\sqrt{k_2}\cosh \left( {\zeta _{2} +\frac{1}{2}\ln {k_2}}\right) }\nonumber \\, \end{aligned}$$

(2.27)

where $\zeta _{1}={a_1} x +\left( -{a_1} -{c_1} \right) y +{c_1} z +a_1^{3} t$, $\zeta _{2}=b_2y +{c_2} z$.

Case 7

$$\begin{aligned} b_1 =-a_1-c_1 , \ a_2 = -c_2-b_2, \end{aligned}$$

(2.28)

where $a_1, b_2, c_1, c_2, d_1, d_2, k_1$ and $k_2$ are free parameters.

Substituting Eq. (2.28) into Eq. (2.5) and Eq. (2.2), we obtain

$$\begin{aligned} u=6\frac{- {k_1} a_1 \sin \! \left( \zeta _1 \right) +\left( -{c_2} -{b_2} \right) ({k_2}\,{\mathrm e}^{\zeta _{2}}- \,{\mathrm e}^{-\zeta _{2}})}{{k_1} \cos \! \left( \zeta _1\right) +{k_2} \,{\mathrm e}^{\zeta _{2}}+{\mathrm e}^{-\zeta _{2}}}, \end{aligned}$$

(2.29)

where $\zeta _{1}={a_1} x +\left( -{a_1} -{c_1} \right) y +{c_1} z +{d_1} t$, $\zeta _{2}=\left( -{c_2} -{b_2} \right) x +{b_2} y +{c_2} z +{d_2} t$.

In particular, the solution Eq. (2.29) can be expressed as

$$\begin{aligned} u_8=6\frac{- {k_1} a_1 \sin \! \left( \zeta _1 \right) +\left( -{c_2} -{b_2} \right) \left( 2\sqrt{k_2}\sinh \left( {\zeta _{2} +\frac{1}{2}\ln {k_2}}\right) \right) }{{k_1} \cos \! \left( \zeta _1\right) +2\sqrt{k_2}\cosh \left( {\zeta _{2} +\frac{1}{2}\ln {k_2}}\right) },\nonumber \\ \end{aligned}$$

(2.30)

where $\zeta _{1}={a_1} x +\left( -{a_1} -{c_1} \right) y +{c_1} z +{d_1} t$, $\zeta _{2}=\left( -{c_2} -{b_2} \right) x +{b_2} y +{c_2} z +{d_2} t$.

Case 8

Compared with the case7, the solution obtained is complex solutions.

$$\begin{aligned} a_1=\pm \text {i} a_2, \ d_1 = \mp 4\text {i}a_2^3 , \ d_2 =- 4a_2^3, \end{aligned}$$

(2.31)

where $a_2, b_1, b_2, c_1, c_2, k_1$ and $k_2$ are free parameters.

Substituting Eq. (2.31) into Eq. (2.2) and Eq. (2.5), we obtain

$$\begin{aligned} u=6\frac{ \mp \mathrm {i}{a_2}{k_1}\sin \! \left( \zeta _{1}\right) +{a_2}({k_2} \,{\mathrm e}^{\zeta _{2}}- \,{\mathrm e}^{-\zeta _{2}})}{{k_1} \cos \! \left( \zeta _{1}\right) +{k_2} \,{\mathrm e}^{\zeta _{2}}+{\mathrm e}^{-\zeta _{2}}}, \end{aligned}$$

(2.32)

where $\zeta _{1}=\pm \mathrm {i} {a_2} x +{b_1} y +{c_1} z \mp 4\mathrm {i}{a_2}^{3} t$, $\zeta _{2}=-4 {a_2}^{3} t +{a_2} x +{b_2} y +{c_2} z$.

In particular, the solution Eq. (2.32) can be expressed as

$$\begin{aligned} u_9=6\frac{ \mp \mathrm {i}{a_2}{k_1} \sin \! \left( \zeta _1 \right) +{a_2} \left( 2\sqrt{k_2}\sinh \left( {\zeta _{2} +\frac{1}{2}\ln {k_2}}\right) \right) }{{k_1} \cos \! \left( \zeta _1\right) +2\sqrt{k_2}\cosh \left( {\zeta _{2} +\frac{1}{2}\ln {k_2}}\right) }, \end{aligned}$$

(2.33)

where $\zeta _{1}=\pm \mathrm {i} {a_2} x +{b_1} y +{c_1} z \mp 4\mathrm {i}{a_2}^{3} t$, $\zeta _{2}=-4 {a_2}^{3} t +{a_2} x +{b_2} y +{c_2} z$.

3 Three wave method

Now, the equation (1.3) is considered by three wave method. We assume it has three wave solutions, which takes the form

$$\begin{aligned} f(x,y,z,t)= & {} \exp \left( \xi _1 \right) + \delta _1 \cos \left( \xi _2 \right) + \delta _2 \cosh \left( \xi _3 \right) \nonumber \\&+ \delta _3\exp \left( -\xi _1 \right) , \end{aligned}$$

(3.1)

where

$$\begin{aligned} \xi _i= & {} P_i x+Q_i y+R_i z\\&+w_i t; \delta _i\in {\mathbb {R}}; R_i,Q_i,R_i,w_i\in {\mathbb {R}}(i=1,2,3) \end{aligned}$$

are undetermined constants.

Substituting Eq. (3.1) into Eq. (2.5) and setting coefficients of

$$\begin{aligned}&\cosh {(\xi _3)} \exp {(\pm \xi _1)}, \cos {(\xi _2)}\exp {( \pm \xi _1)}, \sinh {(\xi _3)}\exp {( \pm \xi _1)}, \\&\sin {(\xi _2)}\exp {( \pm \xi _1)},\cos {(\xi _2)} \cosh {(\xi _3)}, \sin {(\xi _2)}\sinh {(\xi _3)}, \end{aligned}$$

and the constant term to zero, a set of nonlinear algebraic equations Eq. (3.2).

$$\begin{aligned} \left\{ \begin{aligned}&\delta _2\delta _3[P_1^4+\left( R_1+Q_1\right) P_1^3+3P_3\left( R_3+Q_3+2P_3\right) P_1^2\\&\quad +\left( \left( 3R_1+3Q_1\right) P_3^2+w_1\right) P_1\\&+P_3^4+\left( Q_3+R_3\right) P_3^3+w_3P_3 +\left( R_1+Q_1 \right) w_1\\&\quad +w_3\left( Q_3+R_3 \right) ]=0,\\&\delta _1\delta _3[P_1^4+\left( R_1+Q_1\right) P_1^3-3P_2\left( R_2+Q_2+2P_2\right) P_1^2\\&\quad +\left( \left( -3R_1-3Q_1\right) P_2^2+w_1\right) P_1 \\&+P_2^4+\left( Q_2+R_2\right) P_2^3-w_2P_2 +\left( R_1+Q_1 \right) w_1\\&\quad +w_2\left( R_2+Q_2 \right) ]=0,\\&\delta _2\delta _3[\left( R_3+Q_3+4P_3\right) P_1^3+3P_3\left( R_1+Q_1\right) P_1^2\\&\quad +\left( 4P_3^3+\left( 3R_3+3Q_3\right) P_3^2+w_3\right) P_1 \\&+\left( R_1+Q_1\right) P_3^3+w_1P_3 +\left( R_3+Q_3 \right) w_1\\&\quad +w_3\left( R_1+Q_1 \right) ]=0,\\&\delta _1\delta _3[\left( R_2+Q_2+4P_2\right) P_1^3+3P_2\left( R_1+Q_1\right) P_1^2\\&\quad +\left( -4P_2^3+\left( -3R_2-3Q_2\right) P_2^2+w_2\right) P_1 \\&+ \left( -R_1-Q_1\right) P_2^3+w_1P_2 +\left( R_2+Q_2 \right) w_1\\&\quad +w_2\left( R_1+Q_1 \right) ]=0,\\&\delta _2[P_1^4+\left( R_1+Q_1\right) P_1^3+3P_3\left( R_3+Q_3+2P_3\right) P_1^2\\&\quad +\left( \left( 3R_1+3Q_1\right) P_3^2+w_1\right) P_1 \\&+P_3^4+\left( Q_3+R_3\right) P_3^3+w_3P_3 +\left( R_1+Q_1 \right) w_1\\&\quad +w_3\left( Q_3+R_3 \right) ]=0,\\&\delta _1[P_1^4+\left( R_1+Q_1\right) P_1^3-3P_2\left( R_2+Q_2+2P_2\right) P_1^2\\&\quad +\left( \left( -3R_1-3Q_1\right) P_2^2+w_1\right) P_1 \\&+P_2^4+\left( Q_2+R_2\right) P_2^3-w_2P_2 +\left( R_1+Q_1 \right) w_1\\&\quad +w_2\left( R_2+Q_2 \right) ]=0,\\&\delta _2(\left( R_3+Q_3+4P_3\right) P_1^3+3P_3\left( R_1+Q_1\right) P_1^2\\&\quad +\left( 4P_3^3+\left( 3R_3+3Q_3\right) P_3^2+w_3\right) P_1 \\&\left( R_1+Q_1\right) P_3^3+w_1P_3 +\left( R_3+Q_3 \right) w_1\\&\quad +w_3\left( R_1+Q_1 \right) )=0,\\&\delta _1(\left( R_2+Q_2+4P_2\right) P_1^3+3P_2\left( R_1+Q_1\right) P_1^2\\&\quad +\left( 4P_2^3+\left( -3R_2-3Q_2\right) P_2^2+w_2\right) P_1 \\&\left( -R_1-Q_1\right) P_2^3+w_1P_2 +\left( R_2+Q_2 \right) w_1\\&\quad +w_2\left( R_1+Q_1 \right) )=0,\\&\delta _1\delta _2(P_2^4+\left( R_2+Q_2\right) P_2^3-3P_3\left( R_3+Q_3+2P_3\right) P_3^2\\&\quad +\left( \left( -3R_2-3Q_2\right) P_3^2-w_2\right) P_2 \\&+P_3^4+\left( Q_3+R_3\right) P_3^3-w_3P_3 +\left( -R_2-Q_2 \right) w_2\\&\quad +w_3\left( R_3+Q_3 \right) )=0,\\&\delta _1\delta _2(\left( -R_3-Q_3-4P_3\right) P_2^3-3P_3\left( R_2+Q_2\right) P_2^2\\&\quad +\left( 4P_3^3+\left( 3R_3+3Q_3\right) P_3^2+w_3\right) P_2 \\&+ \left( R_2+Q_2\right) P_3^3+w_2P_3 +\left( R_3+Q_3 \right) w_2\\&\quad +w_3\left( R_2+Q_2 \right) )=0,\\&(-4P_2^3+w_2)\cdot (R_2+P_2+Q_2)=0,\\&(4P_3^3+w_3)\cdot (R_3+P_3+Q_3)=0,\\&(4P_1^3+w_1)\cdot (R_1+P_1+Q_1)=0. \end{aligned} \right. \end{aligned}$$

(3.2)

Solve Eq. (3.2), we have following conclusion.

In general, we only consider the case where the free parameters are real numbers, and let $\delta _1 \ne 0,\delta _2 \ne 0$ and $\delta _3\ne 0$.

In addition, if $\delta _2 = 0$, Eq. (3.1) has the same form as Eq. (2.5).

Case 1

$$\begin{aligned} R_1= & {} -P_1-Q_1,\ R_2=-Q_2-P_2, \ R_3\nonumber \\= & {} -Q_3-P_3, \end{aligned}$$

(3.3)

where $Q_1, Q_2, Q_3, P_1, P_2, P_3, w_1, w_2$ and $w_3$ are free parameters.

Substituting Eq. (3.3) into Eq. (2.2) and Eq. (3.1), we obtain the solution

$$\begin{aligned} u=6 \frac{{P_1} \,{\mathrm e}^{\eta _1}- \delta _1 {P_2} \sin \! \left( \eta _2 \right) + \delta _2 {P_3} \sinh \! \left( \eta _3 \right) - \delta _3 {P_1} \,{\mathrm e}^{-\eta _1}}{{\mathrm e}^{\eta _1}+\delta _1 \cos \! \left( \eta _2 \right) +\delta _2 \cosh \! \left( \eta _3 \right) +\delta _3 \,{\mathrm e}^{-\eta _1}} \end{aligned}$$

(3.4)

where $\eta _1={P_1} x +{Q_1} y +\left( -{Q_1} -{P_1} \right) z +{w_1} t.$ $\eta _2={P_2} x +{Q_2} y +\left( -{Q_2} -{P_2} \right) z +{w_2} t .$ $\eta _3={P_3} x +{Q_3} y +\left( -{Q_3} -{P_3} \right) z +{w_3} t .$

In particular, solution Eq. (3.4) can be expressed as

$$\begin{aligned} u_1=6 \frac{- \delta _1 {P_2} \sin \! \left( \eta _2 \right) + \delta _2 {P_3} \sinh \! \left( \eta _3 \right) +2P_1\sqrt{\delta _3}\sinh {\left( \eta _1+\frac{1}{2}\ln {\frac{1}{\delta _3}}\right) }}{\delta _1 \cos \! \left( \eta _2 \right) +\delta _2 \cosh \! \left( \eta _3 \right) +2\sqrt{\delta _3}\cosh {\left( \eta _1+\frac{1}{2}\ln {\frac{1}{\delta _3}}\right) }} , \nonumber \\ \end{aligned}$$

(3.5)

where $\eta _1={P_1} x +{Q_1} y +\left( -{Q_1} -{P_1} \right) z +{w_1} t.$ $\eta _2={P_2} x +{Q_2} y +\left( -{Q_2} -{P_2} \right) z +{w_2} t .$ $\eta _3={P_3} x +{Q_3} y +\left( -{Q_3} -{P_3} \right) z +{w_3} t .$

Fig. 6

The periodic kink wave solution $u_1$ at $\delta _1=1, \delta _2=1, \delta _3=1, Q_1=1, Q_2=1, Q_3=1, P_1=1, P_2=1, P_3=1, w_1=2, w_2=2, w_3=2, z=0, {\textbf {a}} t=-5, {\textbf {b}} t=0, {\textbf {c}} t=5$

Case 2

$$\begin{aligned} P_1= & {} -\root 3 \of {w_1},\ R_1=-Q_1+\root 3 \of {w_1}, \ P_2=\root 3 \of {w_2}, \nonumber \\ R_2= & {} -Q_2-\root 3 \of {w_2}, \ P_3=0, \ w_3=0, \end{aligned}$$

(3.6)

where $Q_1, Q_2, Q_3, R_3, w_1$ and $w_2$ are free parameters.

Substituting Eq. (3.5) into Eq. (2.2) and Eq. (3.1), we obtain the solution

$$\begin{aligned} u=6\frac{- \root 3 \of {w_1} {\mathrm e}^{\eta _1}- \delta _1\root 3 \of {w_2}\sin \! \left( \eta _2\right) + \delta _3 \root 3 \of {w_1} {\mathrm e}^{-\eta _1}}{{\mathrm e}^{\eta _1}+\delta _1 \cos \! \left( \eta _2 \right) +\delta _2 \cosh \! \left( \eta _3 \right) +\delta _3 \,{\mathrm e}^{-\eta _1}},\nonumber \\ \end{aligned}$$

(3.7)

where $\eta _1=-\root 3 \of {w_1} x +{Q_1} y +\left( -{Q_1} +\root 3 \of {w_1}\right) z +{w_1} t$, $\eta _2=\root 3 \of {w_2} x +{Q_2} y +\left( -{Q_2} -\root 3 \of {w_2}\right) z +{w_2} t$, $\eta _3={Q_3} y +{R_3} z$.

In particular, solution Eq. (3.7) can be expressed as

$$\begin{aligned} u_2=6\frac{- \delta _1\root 3 \of {w_2}\sin \! \left( \eta _2\right) -2\root 3 \of {w_1}\sqrt{\delta _3}\sinh {\left( \eta _1+\frac{1}{2}\ln {\frac{1}{\delta _3}}\right) }}{\delta _1 \cos \! \left( \eta _2 \right) +\delta _2 \cosh \! \left( \eta _3\right) +2\sqrt{\delta _3}\cosh {\left( \eta _1+\frac{1}{2}\ln {\frac{1}{\delta _3}}\right) }} , \nonumber \\ \end{aligned}$$

(3.8)

where $\eta _1=-\root 3 \of {w_1} x +{Q_1} y +\left( -{Q_1} +\root 3 \of {w_1}\right) z +{w_1} t$, $\eta _2=\root 3 \of {w_2} x +{Q_2} y +\left( -{Q_2} -\root 3 \of {w_2}\right) z +{w_2} t$, $\eta _3={Q_3} y +{R_3} z$.

Fig. 7

The periodic cross kink wave solution $u_2$ at $\delta _1=1, \delta _2=1, \delta _3=1, Q_1=2, Q_2=1, Q_3=1, R_3=1, w_1=1, w_2=1, z=0, {\textbf {a}} t=-5, {\textbf {b}} t=0, {\textbf {c}} t=5$

Case 3

$$\begin{aligned} P_1= & {} -\root 3 \of {w_1}, \ R_1=-Q_1+\root 3 \of {w_1}, \ P_2=0, \ w_2 =0, \nonumber \\ P_3= & {} -\root 3 \of {w_3}, \ R_3=-Q_3+\root 3 \of {w_3}, \end{aligned}$$

(3.9)

where $Q_1, Q_2, Q_3, R_2, w_1$ and $w_3$ are free parameters.

Substituting Eq. (3.9) into Eq. (2.2) and Eq. (3.1), we obtain the solution

$$\begin{aligned} u=6\frac{-{\root 3 \of {w}_1} {\mathrm e}^{\eta _1}- \delta _2 \root 3 \of {w_3}\sinh \! \left( \eta _2\right) +\delta _3 \,\root 3 \of {w_1} {\mathrm e}^{-\eta _1}}{{\mathrm e}^{\eta _1}+\delta _1 \cos \! \left( \eta _3 \right) +\delta _2 \cosh \! \left( \eta _2\right) +\delta _3 \,{\mathrm e}^{-\eta _1}},\nonumber \\ \end{aligned}$$

(3.10)

where $\eta _1=-\root 3 \of {w_1} x +{Q_1} y +{R_1} z +{w_1} t$, $\eta _2=-\root 3 \of {w_3} x +{Q_3} y +\left( -{Q_3} +\root 3 \of {w_3}\right) z +{w_3}t$, $\eta _3={Q_2} y +{R_2} z$.

In particular, solution Eq. (3.10) can be expressed as

$$\begin{aligned} u_3=6\frac{- \delta _2 \root 3 \of {w_3}\sinh \! \left( \eta _2\right) -2\root 3 \of {w_1}\sqrt{\delta _3}\sinh {\left( \eta _1+\frac{1}{2}\ln {\frac{1}{\delta _3}}\right) }}{\delta _1 \cos \! \left( \eta _3 \right) +\delta _2 \cosh \! \left( \eta _2\right) +2\sqrt{\delta _3}\cosh {\left( \eta _1+\frac{1}{2}\ln {\frac{1}{\delta _3}}\right) }},\nonumber \\ \end{aligned}$$

(3.11)

where $\eta _1=-\root 3 \of {w_1} x +{Q_1} y +{R_1} z +{w_1} t$, $\eta _2=-\root 3 \of {w_3} x +{Q_3} y +\left( -{Q_3} +\root 3 \of {w_3}\right) z +{w_3}t$, $\eta _3={Q_2} y +{R_2} z$.

Fig. 8

The periodic kink wave solution $u_3$ at $\delta _1=1, \delta _2=1, \delta _3=1, Q_1=1, Q_2=1, Q_3=3, R_1=1, R_2=1, w_1=1, w_2=1, w_3=1, x=0, {\textbf {a}} t=-5, {\textbf {b}} t=0, {\textbf {c}} t=5$

Case 4

$$\begin{aligned} P_1= & {} -\root 3 \of {w_1}, \ R_1=-Q_1+\root 3 \of {w_1}, \ P_2=0, \ w_2 =0, \nonumber \\ P_3= & {} 0,\ w_3=0, \end{aligned}$$

(3.12)

where $Q_1, Q_2, Q_3, R_2, R_3,$ and $w_1$ are free parameters.

Substituting Eq. (3.12) into Eq. (2.2) and Eq. (3.1), we obtain the solution

$$\begin{aligned} u=-6\frac{ \root 3 \of {w_1}({\mathrm e}^{\eta _1}-\delta _3{\mathrm e}^{-\eta _1})}{{\mathrm e}^{\eta _1}+\delta _1 \cos \! \left( \eta _2 \right) +\delta _2 \cosh \! \left( \eta _3\right) +\delta _3 \,{\mathrm e}^{-\eta _1}}, \end{aligned}$$

(3.13)

where $\eta _1=-\root 3 \of {w_1} x +{Q_1} y +\left( -{Q_1} +\root 3 \of {w_1}\right) z +{w_1} t$, $\eta _2={Q_2} y +{R_2} z$, $\eta _3={Q_3} y +{R_3} z$.

In particular, solution Eq. (3.13) can be expressed as

$$\begin{aligned} u_4=-6\frac{ 2\sqrt{\delta _3}\root 3 \of {w_1}\sinh {\left( \eta _1+\frac{1}{2}\ln {\frac{1}{\delta _3}}\right) }}{\delta _1 \cos \! \left( \eta _2 \right) +\delta _2 \cosh \! \left( \eta _3\right) +2\sqrt{\delta _3}\cosh {\left( \eta _1+\frac{1}{2}\ln {\frac{1}{\delta _3}}\right) }},\nonumber \\ \end{aligned}$$

(3.14)

where $\eta _1=-\root 3 \of {w_1} x +{Q_1} y +\left( -{Q_1} +\root 3 \of {w_1}\right) z +{w_1} t$, $\eta _2={Q_2} y +{R_2} z$, $\eta _3={Q_3} y +{R_3} z$.

Fig. 9

The periodic cross kink wave solution $u_4$ at $\delta _1=1, \delta _2=1, \delta _3=1, Q_1=2, Q_2=1, Q_3=1, R_2=1, R_3=1, w_1=1, x=0, {\textbf {a}} t=-5, {\textbf {b}} t=0, {\textbf {c}} t=5$

Case 5

$$\begin{aligned} P_1= & {} 0, \ w_1 =0, \ P_2=\root 3 \of {w_2}, \ R_2=-Q_2-\root 3 \of {w_2}, \nonumber \\ P_3= & {} -\root 3 \of {w_3}, \ R_3=-Q_3+\root 3 \of {w_3}, \end{aligned}$$

(3.15)

where $Q_1, Q_2, Q_3, R_1, w_2$ and $w_3$ are free parameters.

Substituting Eq. (3.15) into (2.2) and Eq. (3.1), we obtain the solution

$$\begin{aligned} u=-6\frac{ \delta _1 \root 3 \of {w_2} \sin \! \left( \eta _1 \right) + \delta _2 \,\root 3 \of {w_3} \sinh \! \left( \eta _{2}\right) }{{\mathrm e}^{\eta _{3}}+\delta _1 \cos \! \left( \eta _1 \right) +\delta _2 \cosh \! \left( \eta _{2} \right) +\delta _3 \,{\mathrm e}^{-\eta _{3}}},\nonumber \\ \end{aligned}$$

(3.16)

where $\eta _1=\root 3 \of {w_2} x +{Q_2} y +\left( -{Q_2} -\root 3 \of {w_2}\right) z +{w_2} t$ , $\eta _2=-\root 3 \of {w_3} x +{Q_3} y +\left( -{Q_3} +\root 3 \of {w_3}\right) z +{w_3} t$, $\eta _{3}={Q_1} y +{R_1} z$.

In particular, solution Eq. (3.16) can be expressed as

$$\begin{aligned} u_5=-6\frac{ \delta _1 \root 3 \of {w_2} \sin \! \left( \eta _1 \right) + \delta _2 \,\root 3 \of {w_3} \sinh \! \left( \eta _{2}\right) }{\delta _1 \cos \! \left( \eta _1 \right) +\delta _2 \cosh \! \left( \eta _{2} \right) +2\sqrt{\delta _3}\cosh {\left( \eta _3+\frac{1}{2}\ln {\frac{1}{\delta _3}}\right) }},\nonumber \\ \end{aligned}$$

(3.17)

where $\eta _1=\root 3 \of {w_2} x +{Q_2} y +\left( -{Q_2} -\root 3 \of {w_2}\right) z +{w_2} t$ , $\eta _{2}=-\root 3 \of {w_3} x +{Q_3} y +\left( -{Q_3} +\root 3 \of {w_3}\right) z +{w_3} t$, $\eta _{3}={Q_1} y +{R_1} z$.

Fig. 10

The periodic cross kink wave solution $u_5$ at $\delta _1=1, \delta _2=1, \delta _3=1, Q_1=1, Q_2=1, Q_3=2, R_1=1, w_2=1, w_3=1, x=0, {\textbf {a}} t=-5, {\textbf {b}} t=0, {\textbf {c}} t=5$

Case 6

$$\begin{aligned} P_1= & {} 0, \ w_1 =0, \ P_2=\root 3 \of {w_2}, \ R_2=-Q_2-\root 3 \of {w_2},\nonumber \\ P_3= & {} 0, \ w_3=0, \end{aligned}$$

(3.18)

where $Q_1, Q_2, Q_3, R_1, R_3$ and $w_2$ are free parameters.

Substituting Eq. (3.18) into Eq. (2.2) and Eq. (3.1), we obtain the solution

$$\begin{aligned} u=-6\frac{ \delta _1\root 3 \of {w_2} \sin \! \left( \eta _{1} \right) }{{\mathrm e}^{\eta _{2}}+\delta _1 \cos \! \left( \eta _{1} \right) +\delta _2 \cosh \! \left( \eta _{3}\right) +\delta _3 \,{\mathrm e}^{-\eta _{2}}}, \nonumber \\ \end{aligned}$$

(3.19)

where $\eta _{1}=\root 3 \of {w_2} x +{Q_2} y +\left( -{Q_2} -\root 3 \of {w_2}\right) z +{w_2} t$, $\eta _{2}={Q_1} y +{R_1} z$, $\eta _{3}={Q_3} y +{R_3} z$.

In particular, solution Eq. (3.19) can be expressed as

$$\begin{aligned} u_6=-6\frac{ \delta _1\root 3 \of {w_2} \sin \! \left( \eta _{1} \right) }{\delta _1 \cos \! \left( \eta _{1} \right) +\delta _2 \cosh \! \left( \eta _{3}\right) +2\sqrt{\delta _3}\cosh {\left( \eta _2+\frac{1}{2}\ln {\frac{1}{\delta _3}}\right) }},\nonumber \\ \end{aligned}$$

(3.20)

where $\eta _{1}=\root 3 \of {w_2} x +{Q_2} y +\left( -{Q_2} -\root 3 \of {w_2}\right) z +{w_2} t$, $\eta _{2}={Q_1} y +{R_1} z$, $\eta _{3}={Q_3} y +{R_3} z$.

Fig. 11

The periodic wave solution $u_6$ at $\delta _1=1, \delta _2=1, \delta _3=1, Q_1=1, Q_2=1, Q_3=1, R_1=1, R_3=1, w_2=1, {\textbf {a}} z=0,t=0, {\textbf {b}} x=0, t=0$

Case 7

$$\begin{aligned} P_1= & {} 0, \ w_1 =0, \ P_2=0, \ w_2 =0, \ P_3=-\root 3 \of {w_3}, \nonumber \\ R_3= & {} -Q_3+\root 3 \of {w_3}, \end{aligned}$$

(3.21)

where $Q_1, Q_2, Q_3, R_1, R_2$ and $w_3$ are free parameters.

Substituting Eq. (3.21) into Eq. (3.1) and Eq. (2.2), we obtain the solution

$$\begin{aligned} u=-6\frac{\delta _2 \root 3 \of {w_3} \sinh \! \left( \eta _{1} \right) }{{\mathrm e}^{\eta _{2}}+\delta _1 \cos \! \left( \eta _{3} \right) +\delta _2 \cosh \! \left( \eta _{1} \right) +\delta _3 \,{\mathrm e}^{-\eta _{2}}},\nonumber \\ \end{aligned}$$

(3.22)

where $\eta _{1}=-\root 3 \of {w_3} x +{Q_3} y +\left( -{Q_3} +\root 3 \of {w_3}\right) z +{w_3} t$, $\eta _{2}={Q_1} y +{R_1} z$, $\eta _{3}={Q_2} y +{R_2} z$.

In particular, solution Eq. (3.22) can be expressed as

$$\begin{aligned} u_7=-6\frac{\delta _2 \root 3 \of {w_3} \sinh \! \left( \eta _{1} \right) }{\delta _1 \cos \! \left( \eta _{3} \right) +\delta _2 \cosh \! \left( \eta _{1} \right) +2\sqrt{\delta _3}\cosh {\left( \eta _2+\frac{1}{2}\ln {\frac{1}{\delta _3}}\right) }},\nonumber \\ \end{aligned}$$

(3.23)

where $\eta _{1}=-\root 3 \of {w_3} x +{Q_3} y +\left( -{Q_3} +\root 3 \of {w_3}\right) z +{w_3} t$, $\eta _{2}={Q_1} y +{R_1} z$, $\eta _{3}={Q_2} y +{R_2} z$.

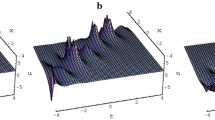
The figure of $u_7$ is similar to the figure of $u_4$, and it is a periodic cross kink wave solution.

4 Non-traveling wave solutions

In this section, we use the extended homoclinic test approach in Ref. [25] to get non-traveling wave solutions, which in form

$$\begin{aligned} u(x,y,z,t)=\varphi \left( \xi ,t\right) +q(z) , \end{aligned}$$

(4.1)

where $\xi =x+my+nt+\theta (z)$, m, n are two nonzero constants, $\varphi (\xi ,t), q(z)$ and $\theta (z)$ are three functions undetermined. Substituting Eq. (4.1) into (2.1), we obtain

$$\begin{aligned}&\left( 1+m+\theta '{ (z)}\right) \varphi _{\xi \xi \xi \xi }+\left( n+mn+n\theta '{ (z)}\right. \nonumber \\&\quad \left. +q' (z)\right) \varphi _{\xi \xi }\nonumber \\&+\left( 2+2m+2\theta ' {(z)}\right) \varphi _{\xi } \varphi _{\xi \xi }+\left( 1+m+\theta ' {(z)}\right) \nonumber \\&\quad \varphi _{\xi t}=0. \end{aligned}$$

(4.2)

To simplify Eq. (4.2), we let

$$\begin{aligned} n+mn+n\theta ' (z)+q' (z)=0. \end{aligned}$$

(4.3)

From Eq. (4.3), we get

$$\begin{aligned} \begin{aligned} q(z)&=-\int [(n+mn+n\theta '(z))\mathrm {d}z]+c \\&=-n\theta (z)-(nm+n)z+c. \end{aligned} \end{aligned}$$

(4.4)

where c is the integral constant. Therefore, in the condition of $(1+m+\theta ' (z))\ne 0$, Eq. (4.2) reduces to

$$\begin{aligned} \varphi _{\xi \xi \xi \xi }+2\varphi _{\xi }\varphi _{\xi \xi }+\varphi _{\xi t}=0. \end{aligned}$$

(4.5)

Integrating Eq. (4.5) once with respect to $\xi$. Let constant $c=0$, we get

$$\begin{aligned} \varphi _{\xi \xi \xi }+(\varphi _\xi )^2+\varphi _t=0. \end{aligned}$$

(4.6)

Let

$$\begin{aligned} \psi (\xi ,t)=-\frac{1}{3}\varphi ({\xi ,t}). \end{aligned}$$

(4.7)

Substituting Eq. (4.7) into (4.6), one gets

$$\begin{aligned} \psi _{\xi \xi \xi }-3\psi _\xi ^2+\psi _t=0. \end{aligned}$$

(4.8)

In order to solving Eq. (4.8), a nonlinear function transformation of dependent variable are used

$$\begin{aligned} \psi =-2(\ln \phi )_\xi , \end{aligned}$$

(4.9)

where $\phi (\xi ,t)$ will be determined later. Substituting Eq. (4.9) into Eq. (4.8), one can get a bilinear equation

$$\begin{aligned} \left( D_\xi D_t+D_\xi ^4\right) \phi \cdot \phi =0. \end{aligned}$$

(4.10)

Let the solution in the form

$$\begin{aligned} \phi =k_1\cos (\zeta _1)+k_2\exp (\zeta _2)+\exp (-\zeta _2), \end{aligned}$$

(4.11)

where $\zeta _i=a_i \xi +b_i t, k_i\in {\mathbb {R}}; a_i,b_i\in {\mathbb {C}}(i=1,2)$ are undetermined constants.

Fig. 12

The exact kink-like solution with tail $u_1$ at $x=y=0,a_2=1, k_2=1,n=3,m=1,c=0, {\textbf {a}} \theta (z)=z, {\textbf {b}} \theta (z)=z^2, {\textbf {c}} \theta (z)=z^3$

Substituting Eq. (4.11) into (4.10) and setting coefficients of $\cos ^2(\zeta _1)$, $\cos (\zeta _1) \exp (\zeta _2)$, $\cos (\zeta _1) \exp (-\zeta _2)$,$\sin ^2(\zeta _1)$, $\sin (\zeta _1) \exp (\zeta _2)$, $\sin (\zeta _1) \exp (-\zeta _2)$ and the constant term to zero, a set of nonlinear algebraic equations with respect to $a_i, b_i$ and $k_i,(i = 1, 2)$ are given

$$\begin{aligned} \left\{ \begin{aligned}&k_1^2(4a_1^4-a_1b_1)=0,\\&k_1k_2(a_1^4+a_2^4-6a_1^2a_2^2+a_2b_2-a_1b_1)=0,\\&k_1(a_1^4+a_2^4-6a_1^2a_2^2+a_2b_2-a_1b_1)=0,\\&k_2(16a_2^4+4a_2b_2)=0,\\&k_1k_2(4a_1a_2^3-4a_1^3a_2+a_1b_2+a_2b_1)=0,\\&k_1(-4a_1a_2^3+4a_1^3a_2-a_1b_2-a_2b_1)=0. \end{aligned} \right. \end{aligned}$$

(4.12)

Solving Eq. (4.12), we have the following results.

Case1

$$\begin{aligned} k_1 = 0, \ b_2 =-4a_2^3, \end{aligned}$$

(4.13)

where $a_1, a_2 , b_1$ and $k_2$ are free parameters.

Collecting Eq. (4.1), (4.4), (4.7), (4.9), (4.11), (4.13), we obtain the solution

$$\begin{aligned} u=6 a_2 \frac{ {k_2} {\mathrm e}^{\lambda _1}- { \mathrm e}^{-\lambda _1}}{{k_2}{\mathrm e}^{\lambda _1}+{\mathrm e}^{-\lambda _1}}-n\theta (z)-(nm+n)z+c . \nonumber \\ \end{aligned}$$

(4.14)

where$\lambda _1=a_2 \left( x+my+ \left( n-4a_2^2 \right) t+\theta (z) \right) .$

In particular, solution Eq. (4.14) can be expressed as

$$\begin{aligned} u_1= & {} 6a_2 \tanh \left( {\lambda _1 +\frac{1}{2}\ln {k_2}}\right) \nonumber \\&-n\theta (z)-(nm+n)z+c, \quad k_2>0 \end{aligned}$$

(4.15)

$$\begin{aligned} u_2= & {} 6a_2 \coth \left( {\lambda _1 +\frac{1}{2}\ln {(-k_2)}}\right) \nonumber \\&-n\theta (z)-(nm+n)z+c, \quad k_2<0 \end{aligned}$$

(4.16)

where$\lambda _1=a_2 \left( x+my+ \left( n-4a_2^2 \right) t+\theta (z) \right) .$

Case 2

$$\begin{aligned} a_1= & {} \frac{3^{3/4}\sqrt{2}}{6}((\pm \text {i}) \pm 1)a_2, \ b_1\nonumber \\= & {} \frac{2\cdot 3^{3/4}\sqrt{2}}{3}((\pm \text {i}) \pm 1)a_2^3, \nonumber \\ b_2= & {} -4a_2^3, \ k_2 = 0, \end{aligned}$$

(4.17)

where $a_2$ and $k_1$ are free parameters.

Collecting Eq. (4.1), (4.4), (4.7), (4.9), (4.11), (4.17), we obtain the solution

$$\begin{aligned} u=-{a_2}\frac{ 3^{\frac{3}{4}} \sqrt{2}\, \left( \left( \pm \text {i}\right) \pm 1\right) {k_1} \sin \lambda _2 +6 \,{ e}^{-{a_2} \lambda _3 }}{{k_1} \cos \lambda _2 +{ e}^{-{a_2} \lambda _3 }},\nonumber \\ \end{aligned}$$

(4.18)

where $\lambda _2=\frac{3^{\frac{3}{4}} \sqrt{2}}{6}\, \left( \left( \pm \text {i}\right) \pm 1\right) {a_2} \big (4 {a_2}^{2} t +m y +n t +\theta (z)+x \big )$and $\lambda _3=-4 {a_2}^{2} t +m y +n t +\theta \left( z \right) +x$.

In particular, solution Eq. (4.18) can be expressed as

$$\begin{aligned} u_3=-{a_2}\frac{ 3^{\frac{3}{4}} \sqrt{2}\, \left( \left( \pm \text {i}\right) \pm 1\right) {k_1} \sin \lambda _2 +6 \,\left( \cosh {(-{a_2} \lambda _3) }+\sinh {(-{a_2} \lambda _3 )}\right) }{{k_1} \cos \lambda _2 +\cosh {(-{a_2} \lambda _3) }+\sinh {(-{a_2} \lambda _3 )}},\nonumber \\ \end{aligned}$$

(4.19)

where $\lambda _2=\frac{3^{\frac{3}{4}} \sqrt{2}}{6}\, \left( \left( \pm \text {i}\right) \pm 1\right) {a_2} \big (4 {a_2}^{2} t +m y +n t +\theta \left( z \right) +x \big )$ and $\lambda _3=-4 {a_2}^{2} t +m y +n t +\theta \left( z \right) +x$.

Case 3

$$\begin{aligned} a_1 = 0, \ b_1 =0, \ b_2 =-a_2^3, \ k_2 = 0, \end{aligned}$$

(4.20)

where $a_2$ and $k_1$ are free parameters.

Collecting Eqs. (4.20, 4.11, 4.9, 4.7, 4.4) with Eq. (4.1), we obtain the solution

$$\begin{aligned} u=-6a_2\frac{{\mathrm e}^{-\lambda _4}}{{k_1} +{\mathrm e}^{-\lambda _4}}-n\theta (z)-(nm+n)z+c, \nonumber \\ \end{aligned}$$

(4.21)

where $\lambda _4=a_2\left( x+my+\left( n-a_2^2\right) t+\theta (z) \right)$.

In particular, solution Eq. (4.21) can be expressed as

$$\begin{aligned} u_4= & {} -6a_2\frac{\left( \cosh {(-\lambda _4)}+\sinh {(-\lambda _4)}\right) }{{k_1} +\left( \cosh {(-\lambda _4)}+\sinh {(-\lambda _4)}\right) }\nonumber \\&-n\theta (z)-(nm+n)z+c, \end{aligned}$$

(4.22)

The figure of $u_4$ is similar to the figure of $u_1$, and it is a kink-like solution with tail.

5 Discussion and conclusions

In this work, we mainly investigate the new (3+1)-dimensional BLMP equation, which is firstly proposed by Wazwaz. In Sect. 2, it is devoted to use the extended homoclinic test approach to construct solutions. If $k_1=0$, a kink-shaped solitary wave solution is obtained, if $k_2=0$, different kinds of singualr solitary wave solutions are obtained; if $k_1\ne 0$ and $k_2 \ne 0$, we get 2 kinds of periodic kink wave solutions and periodic solitary wave solution. In Sect. 3, we use the three wave method to construct three wave solutions. It is obviously that, if $\delta _2 = 0$, the form of the solution constructed is the same as extended homoclinic test approach. In this section, we let the free parameters are real numbers and let $\delta _1 \ne 0, \delta _2 \ne 0,$ and $\delta _3 \ne 0.$ And the periodic kink wave solutions, periodic cross kink wave solutions and periodic wave solutions are obtained. In Sect. 4, we also use the extended homoclinic test approach to construct kink-shaped solitary wave solutions, what is different from the second part is that these solutions have a tail. These results reflect that the methods used in this paper are effective for seeking solutions of higher dimensional NLEEs.