1 Introduction

Many significant phenomena and dynamic processes in physics, chemistry, biology and mechanics can be represented by nonlinear partial differential equations (NLPDEs). When we want to understand the mechanism of phenomena in nature which have described by NLPDEs, we have to obtain the exact solutions of the NLPDEs. Searching for exact solutions of NLPDEs has long been an important work for both mathematicians and physicists. In recent years, quite a few methods have been proposed to solve solutions of NLPDEs, such as the tanh-function method [1], the sech-function method [2], the homogeneous balance method [3], the inverse scattering transformation approach [4], the Bäcklund transformation (BT) [5], the Darboux transformation [6], the bilinear method [7], Painlevé analysis [8], the Wronskian technique [9] and the exp-function method [10, 11], and so on. It is well known that the study of soliton generating NLPDEs are of great interest not only in (1+1)-dimensional systems, but also in (2+1)- and (3+1)-dimensional systems. Recently, Dai et al. [12] constructed the extended homoclinic test approach (EHTA) to seek solitary-wave solution of high dimensional nonlinear wave system. Some exact solutions including breather type soliton, periodic type of soliton and two soliton solutions are obtained [12–17]. In this letter, we solve the (2+1)- and (3+1)-dimensional BLMP equation by using the extended homoclinic test approach (EHTA) and study the strangely mechanical features of these wave solutions.

This paper is organized as follow: in Sect. 2, a direct formulation of the procedure for the extended homoclinic test approach (EHTA) is made. In Sect. 3, we solve the (2+1)-dimensional BLMP equation by using EHTA. In Sect. 4, we apply EHTA to the (3+1)-dimensional BLMP equation. We conclude the paper in the final section.

2 The extended homoclinic test approach

To explain these fundamental steps of the extended homoclinic test approach, we consider a general form of a (3+1)-dimensional nonlinear partial differential equation as

$$\begin{aligned} F(u,u_t ,u_x ,u_y ,u_z ,u_{xx} ,u_{yy} ,u_{zz},\ldots )=0, \end{aligned}$$
(1)

where \(u=u(x,y,z,t)\) and \(F\) is a polynomial of \(u\) and its derivatives.

The basic steps of the EHTA can be expressed in the following form, (for more details see [12]).

Step 1 We make a transformation as

$$\begin{aligned} u=T(f), \end{aligned}$$
(2)

where \(f\) is a new unknown function. By substituting Eq. (2) into Eq. (1), we can obtain the Hirota’s bilinear form

$$\begin{aligned} G(D_t ,D_x ,D_y ,D_z ; f,f)=0, \end{aligned}$$
(3)

where \(D_t,\,D_x ,\,D_y \) and \(D_z\) are Hirota’s bilinear operators [18] which is defined by

$$\begin{aligned}&D_x^{m}D_y^{k}D_z^{p}D_t^{n}f(x,y,z,t)\cdot g(x,y,z,t) \\&\quad =\Big (\frac{\partial }{\partial x_1}-\frac{\partial }{\partial x_2}\Big )^{m}\Big (\frac{\partial }{\partial y_1}-\frac{\partial }{\partial y_2}\Big )^{k}\Big (\frac{\partial }{\partial z_1}-\frac{\partial }{\partial z_2}\Big )^{p} \\&\qquad \times \, \Big (\frac{\partial }{\partial t_1}-\frac{\partial }{\partial t_2}\Big )^{n}\Big [f\Big (x_1 ,y_1 ,z_1 ,t_1\Big )\\&\qquad \qquad g(x_2 ,y_2 ,z_2 ,t_2 )\Big ], \end{aligned}$$

where the right-hand side is computed in

$$\begin{aligned} x_1 =x_2 =x,\, y_1 =y_2 =y,\, z_1 =z_2 =z,\, t_1 =t_2 =t. \end{aligned}$$

Step 2 To obtain the exact solutions of Eq. (3), we suppose the standard ansatz in EHTA as

$$\begin{aligned} f(x,y,z,t)=e^{-\xi _1 }+\delta _1 \cos (\xi _2 )+\delta _2 e^{\xi _1}, \end{aligned}$$
(4)

where \(\xi _i =a_i x+b_i y+c_i z+d_i t,\,a_i ,b_i ,c_i ,d_i \) and \(\delta _i,\, (i=1,2)\) are unknown constants to be determined later. Substituting Eq. (4) into (3), and collecting the coefficients of \(\sin (\xi _2),\,\cos (\xi _2)\) and \(e^{j\xi _1},\,j=-1,0,1\),then equating coefficients of these terms to zero, we obtain a set of algebraic equations.

Step 3 Solving the set of algebraic equation defined by step 4 with the help of

Maple, we can find solutions of \(a_i ,b_i ,c_i ,d_i \) and \(\delta _i \, (i=1,2)\). Substituting the identified values of \(a_i ,b_i ,c_i ,d_i\) and \(\delta _i \,(i=1,2)\) into Eq. (4) and then Eq. (2), we can obtain abundant exact solution of Eq. (1).

3 Application to the (2+1)-dimensional BLMP equation

We study the (2+1)-dimensional Boiti–Leon–Manna–Pempinelli (BLMP) equation as

$$\begin{aligned} u_{yt} +u_{xxxy} -3u_{xx} u_y -3u_x u_{xy} =0, \end{aligned}$$
(5)

which was derived by Gilson et al. [19] and recently investigated by Luo [20]. This equation was used to describe the (2+1)-dimensional interaction of the Riemann wave propagated along the \(y\)-axis with a long wave propagated along the \(x\)-axis. Based on the binary Bell polynomials, the bilinear form for the BLMP equation is obtained in [20]. The variable separable solutions and some novel localized excitations for the (2+1)-dimensional BLMP were obtained in [21]. New solutions of (2+1)-dimensional BLMP equation from Wronskian formalism and the Hirota method are obtained in [22, 23].

Under the dependent variable transformation \(u=-2(\ln f)_x\), the Eq. (5) is transformed into the Hirota’s bilinear form

$$\begin{aligned} (D_y D_t +D_y D_x^{3})f\cdot f=0, \end{aligned}$$
(6)

Now we assume the solution of Eq. (6) as

$$\begin{aligned} f(x,y,z,t)=e^{-\xi _1 }+\delta _1 \cos (\xi _2 )+\delta _2 e^{\xi _1}, \end{aligned}$$
(7)

where \(\xi _i =a_i x+b_i y+c_i z+d_i t,\,a_i ,b_i ,c_i ,d_i \) and \(\delta _i ,\, (i=1,2)\) are some constants to be determined later. Now substituting Eq. (7) into Eq. (6) and equating all the coefficients of \(\sin (\xi _2),\,\cos (\xi _2 )\) and \(e^{j\xi _1},\,j=-1,0,1\) to zero, we can obtain the following set of algebraic equation for \(a_i ,b_i ,c_i ,d_i\) and \(\delta _i,\, (i=1,2)\)

$$\begin{aligned} \left\{ {\begin{array}{l} a_1^{3}b_1 + a_2^{3}b_2 -b_2 d_2 +b_1 d_2 -3a_1^{2}a_2 b_2 -3a_1 a_2^{2}b_1 =0, \\ -a_2^{3}b_1 + b_1 d_2 +b_2 d_1 -3a_1 a_2^{2}b_2 +3a_1^{2}a_2 b_1 +a_1^{3}b_2 =0, \\ 16a_1^{3}b_1 \delta _2 +4a_2^{3}b_2 \delta _1^{2}-b_2 d_2 \delta _1^{2}+4b_1 d_1 \delta _2 =0. \\ \end{array}} \right. \nonumber \\ \end{aligned}$$
(8)

Solving the system of Eq. (8) with the help of Maple, we obtain the following cases:

Case 1

$$\begin{aligned} a_2&= -\frac{4a_1 b_1 \delta _2}{b_2 \delta _1^{2}},\quad d_1 =\frac{a_1^{3}\left( -\delta _1^{4}b_2^{2}+48\delta _2^{2}b_1^{2}\right) }{\delta _1^{4}b_2^{2}}, \nonumber \\ d_2&= -\frac{4\delta _2 a_1^{3}b_1 \left( -3\delta _1^{4}b_2^{2}+16\delta _2^{2}b_1^{2}\right) }{\delta _1^{6}b_2^{3}} \end{aligned}$$
(9)

where \(a_1 ,b_1 ,b_2 ,\delta _1\) and \(\delta _2\) are some free real constants. Substituting Eq. (9) into \(u=-2(\ln f)_x\) with Eq. (7), we obtain the solution

$$\begin{aligned} u(x,y,z,t)=\frac{-2\left( -a_1 e^{-\xi _1 }-\delta _1 \sin (\xi _2 )a_2 +\delta _2 a_1 e^{\xi _1 }\right) }{e^{-\xi _1 }+\delta _1 \cos (\xi _2)+\delta _2 e^{\xi _1 }}. \end{aligned}$$
(10)

If \(\delta _2 >0\), then we obtain the exact solution as

$$\begin{aligned} u(x,y,z,t)=\frac{-2(2a_1 \sqrt{\delta _2 }\sinh (\xi _1 -\theta )-\delta _1 \sin (\xi _2 )a_2 )}{2\sqrt{\delta _2 }\cosh (\xi _1 -\theta )+\delta _1 \cos (\xi _2 )}, \end{aligned}$$

for \(\theta =\frac{1}{2}\ln (\delta _2 )\).

If \(\delta _2 <0\), then we obtain the exact solution as

$$\begin{aligned}u(x,y,z,t)=\frac{-2(2a_1 \sqrt{-\delta _2 }\cosh (\xi _1 \!-\!\theta )\!-\!\delta _1 \sin (\xi _2 )a_2 )}{2\sqrt{-\delta _2 }\sinh (\xi _1 \!-\!\theta )+\delta _1 \cos (\xi _2 )}, \end{aligned}$$

for \(\theta =\frac{1}{2}\ln (-\delta _2 )\), where

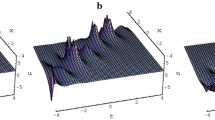
$$\begin{aligned} \xi _1&= a_1 x+b_1 y+\frac{a_1^{3}\left( -\delta _1^{4}b_2^{2}+48\delta _2^{2}b_1^{2}\right) }{\delta _1^{4}b_2^{2}}t,\\ \xi _2&= -\frac{4a_1 b_1 \delta _2 }{b_2 \delta _1^{2}}x+b_2 y-\frac{4\delta _2 a_1^{3}b_1 \left( -3\delta _1^{4}b_2^{2}+16\delta _2 ^{2}b_1^{2}\right) }{\delta _1^{6}b_2^{3}}t. \end{aligned}$$

Obviously, the Eq. (10) is a periodic solitary-wave solution that is to say it is a periodic wave with period \(2\pi \) with \(X=\xi _2 \), and meanwhile is also solitary wave with \(Y=\xi _1 -\theta \).

Figure 1 shows the periodic solitary-wave solutions for some special values of the solution parameters in cases 1.

Fig. 1
figure 1

Kinky periodic-wave solution for case 1 as \(a_1 =0.5,b_1 =1,b_2 =1,\delta _1 =1,\delta _2 =1\) and \(t=0\)

Full size image

Case 2

$$\begin{aligned} b_2 =0,\quad d_1 =3a_1 a_2^{2}-a_1^{3},\quad d_2 =-3a_2 a_1^{2}+a_2^{3},\quad \delta _2 =0 \end{aligned}$$
(11)

where \(a_1 ,a_2 ,b_1\) and \(\delta _1 \) are some free real constants. Substituting Eq. (11) into \(u=-2(\ln f)_x\) with Eq. (7), we obtain the solution

$$\begin{aligned} u(x,y,z,t)=\frac{-2\left( -a_1 e^{-\xi _1 }-\delta _1 \sin (\xi _2 )a_2\right) }{e^{-\xi _1 }+\delta _1 \cos (\xi _2 )}, \end{aligned}$$
(12)

for

$$\begin{aligned} \xi _1&= a_1 x+b_1 y+(3a_1 a_2^{2}-a_1^{3})t,\\ \xi _2&= a_2 x+\left( -3a_2 a_1^{2}+a_2^{3}\right) t. \end{aligned}$$

Figure 2 shows the periodic solitary-wave solutions for some special values of the solution parameters in cases 2.

Fig. 2
figure 2

Kinky periodic-wave solution for case 2 as \(a_1 =2,a_2 =0.5,b_1 =2,\delta _1 =1\) and \(t=0\)

Full size image

Case 3

$$\begin{aligned} d_1 =-4a_1^{3},\, \delta _1 =0 \end{aligned}$$
(13)

where \(a_1 ,a_2 ,b_1 ,b_2 ,d_2\) and \(\delta _2\) are some free real constants. Substituting Eq. (13) into \(u=-2(\ln f)_x\) with Eq. (7), we obtain the solution

$$\begin{aligned} u(x,y,z,t)=\frac{-2\left( -a_1 e^{-\xi _1 }+\delta _2 a_1 e^{\xi _1}\right) }{e^{-\xi _1}+\delta _2 e^{\xi _1 }}, \end{aligned}$$
(14)

If \(\delta _2 >0\), then we obtain the exact solution as

$$\begin{aligned} u(x,y,z,t)=\frac{-4a_1 \sqrt{\delta _2 }\sinh (\xi _1 -\theta )}{2\sqrt{\delta _2 }\cosh (\xi _1 -\theta )}, \end{aligned}$$

for \(\theta =\frac{1}{2}\ln (\delta _2)\).

If \(\delta _2 <0\), then we obtain the exact solution as

$$\begin{aligned} u(x,y,z,t)=\frac{-4a_1 \sqrt{-\delta _2 }\cosh (\xi _1 -\theta )}{2\sqrt{-\delta _2}\sinh (\xi _1 -\theta )}, \end{aligned}$$

for \(\theta =\frac{1}{2}\ln (-\delta _2 )\), where

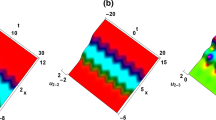
$$\begin{aligned} \xi _1 =a_1 x+b_1 y-4a_1^{3}t,\qquad \xi _2 =a_2 x+b_2 y+d_2 t. \end{aligned}$$

Obviously, the Eq. (14) is an exact kink solution.

Figure 3 shows the exact kink solutions for some special values of the solution parameters in cases 3.

Fig. 3
figure 3

Exact kink solution for case3 as \(a_1 =1,a_2 =3,b_1 =1,b_2 =2,d_2 =1,\delta _1 =1\) and \(t=0\)

Full size image

4 Application to the (3+1)-dimensional BLMP equation

In this section, we extend our analysis to construct the exact solutions to the (3+1)-dimensional Boiti–Leon–Manna–Pempinelli (BLMP) equation as

$$\begin{aligned}&u_{yt} +u_{zt} +u_{xxxy} +u_{xxxz}-3u_x (u_{xy} +u_{xz} ) \nonumber \\&\quad -3u_{xx} (u_y +u_z )=0. \end{aligned}$$
(15)

This equation was introduced in [24]. Based on the multiple exp-function method, the single-wave, double-wave and multi-wave solutions for the (3+1)-dimensional BLMP equation are obtained in [24], by means of the Wronskian technique, some exact solutions including rational solutions, soliton solutions, positons and negatons are obtained in [25].

By using the transformation \(u=-2(\ln f)_x\), Eq. (15) can be converted into the following Hirota’s bilinear form

$$\begin{aligned} (D_y D_t +D_z D_t +D_y D_x^{3}+D_z D_x^{3})f\cdot f=0. \end{aligned}$$
(16)

Similarly, we assume the solution of Eq. (16) as

$$\begin{aligned} f(x,y,z,t)=e^{-\xi _1 }+\delta _1 \cos (\xi _2 )+\delta _2 e^{\xi _1 }, \end{aligned}$$
(17)

where \(\xi _i =a_i x+b_i y+c_i z+d_i t,\,a_i ,b_i ,c_i ,d_i\) and \(\delta _i,\,(i=1,2)\) are some constants to be determined later. Now substituting Eq. (17) into Eq. (16) and equating all the coefficients of \(\sin (\xi _2),\cos (\xi _2)\) and \(e^{j\xi _1},j=-1,0,1\) to zero, we can obtain the following set of algebraic equation for \(a_i ,b_i ,c_i ,d_i\) and \(\delta _i,\, (i=1,2)\)

$$\begin{aligned} \left\{ {\begin{array}{l} -3a_1 a_2^{2}c_1 \!-\!3a_1^{2}a_2 c_2 \!+a_1^{3}b_1 \!+\!a_2^{3}b_2 -b_2 d_2+b_1 d_2 \\ -3a_1^{2}a_2 b_2 -3a_1 a_2^{2}b_1 + c_1 d_1 -c_2 d_2 +a_1^{3}c_1 +a_2^{3}c_2 =0, \\ -a_2^{3}b_1 +b_1 d_2 +b_2 d_1 -3a_1 a_2^{2}c_2 -3a_1 a_2^{2}b_2 +c_1 d_2\\ +c_2 d_1 +3a_1^{2}a_2 b_1 + a_1^{3}b_2 -a_2^{3}c_1 +3a_1^{2}a_2 c_1 +a_1^{3}c_2 =0, \\ 4a_2^{3}c_2 \delta _1^{2}+16a_1^{3}b_1 \delta _2 +4a_2^{3}b_2 \delta _1^{2}-b_2 d_2 \delta _1^{2}+16a_1^{3}c_1 \delta _2 \\ +4b_1 d_1 \delta _2 + 4c_1 d_1 \delta _2 -c_2 d_2 \delta _1^{2}=0. \\ \end{array}} \right. \nonumber \\ \end{aligned}$$
(18)

Solving the set of algebraic equation with the aid of Maple, yields the following cases:

Case 1

$$\begin{aligned} b_1&= -\frac{1}{4}\frac{4a_1 c_1 \delta _2 +\delta _1^{2}a_2 b_2 +\delta _1^{2}a_2 c_2}{a_1 \delta _2 }, \nonumber \\ d_1&= -a_1 \left( -3a_2^{2}+a_1^{2}\right) , d_2 =-3a_2 a_1^{2}+a_2^{3} \end{aligned}$$
(19)

where \(a_1 ,a_2 ,b_2 ,c_1 ,c_2 ,\delta _1\) and \(\delta _2\) are some free real constants. Substituting Eq. (19) into \(u=-2(\ln f)_x\) with Eq. (17), we obtain the solution

$$\begin{aligned} u(x,y,z,t)=\frac{-2\left( -a_1 e^{-\xi _1 }-\delta _1 \sin (\xi _2 )a_2 +\delta _2 a_1 e^{\xi _1 }\right) }{e^{-\xi _1 }+\delta _1 \cos (\xi _2)+\delta _2 e^{\xi _1 }}, \end{aligned}$$
(20)

If \(\delta _2 >0\), then we obtain the exact solution as

$$\begin{aligned} u(x,y,z,t)=\frac{-2(2a_1 \sqrt{\delta _2 }\sinh (\xi _1 -\theta )-\delta _1 \sin (\xi _2 )a_2 )}{2\sqrt{\delta _2 }\cosh (\xi _1 -\theta )+\delta _1 \cos (\xi _2 )}, \end{aligned}$$

for \(\theta =\frac{1}{2}\ln (\delta _2 )\).

If \(\delta _2 <0\), then we obtain the exact solution as

$$\begin{aligned} u(x,y,z,t)=\frac{-2(2a_1 \sqrt{-\delta _2 }\cosh (\xi _1 -\theta )-\delta _1 \sin (\xi _2 )a_2 )}{2\sqrt{-\delta _2 }\sinh (\xi _1 -\theta )+\delta _1 \cos (\xi _2 )}, \end{aligned}$$

for \(\theta =\frac{1}{2}\ln (-\delta _2)\), where

$$\begin{aligned} \xi _1&= a_1 x-\frac{1}{4}\frac{4a_1 c_1 \delta _2 +\delta _1^{2}a_2 b_2 +\delta _1^{2}a_2 c_2 }{a_1 \delta _2}y+c_1 z \\&\qquad -\,a_1 \left( -3a_2^{2}+a_1^{2}\right) t,\\ \xi _2&= a_2 x+b_2 y+c_2 z+\left( -3a_2 a_1^{2}+a_2^{3}\right) t. \end{aligned}$$

Obviously, the Eq. (20) is a periodic solitary-wave solution that is to say it is a periodic wave with period \(2\pi \) with \(X=\xi _2 \), and meanwhile is also solitary wave with \(Y=\xi _1 -\theta \).

Figure 4 shows the periodic solitary-wave solutions for some special values of the solution parameters in cases 1.

Fig. 4
figure 4

Kinky periodic-wave solution for case 1 as \(a_1 =0.5\), \(a_2 =1\), \(b_2 =1\), \(c_1 =1\), \(c_2 =1\), \(\delta _1 =1\), \(\delta _2 =1\), \(t=1\) and \(z=1\)

Full size image

Case 2

$$\begin{aligned} a_1 =0,b_2 =-c_2 ,d_1 =0,d_2 =a_2^{3} \end{aligned}$$
(21)

where \(a_2 ,b_1 ,c_1 ,c_2 ,\delta _1\) and \(\delta _2\) are some free real constants. Substituting Eq. (21) into \(u=-2(\ln f)_x\) with Eq. (17), we obtain the solution

$$\begin{aligned} u(x,y,z,t)=\frac{2\delta _1 \sin (\xi _2 )a_2 }{e^{-\xi _1 }+\delta _1 \cos (\xi _2 )+\delta _2 e^{\xi _1 }}, \end{aligned}$$
(22)

for

$$\begin{aligned} \xi _1 =b_1 y+c_1 z,\quad \xi _2 =a_2 x-c_2 y+c_2 z+a_2^{3}t. \end{aligned}$$

If \(\delta _2 >0\), then we obtain the exact solution as

$$\begin{aligned} u(x,y,z,t)=\frac{2\delta _1 \sin (\xi _2 )a_2 }{2\sqrt{\delta _2 }\cosh (\xi _1 -\theta )+\delta _1 \cos (\xi _2 )}, \end{aligned}$$

for \(\theta =\frac{1}{2}\ln (\delta _2)\).

If \(\delta _2 <0\), then we obtain the exact solution as

$$\begin{aligned} u(x,y,z,t)=\frac{2\delta _1 \sin (\xi _2 )a_2 }{2\sqrt{-\delta _2 }\sinh (\xi _1 -\theta )+\delta _1 \cos (\xi _2 )}, \end{aligned}$$

for \(\theta =\frac{1}{2}\ln (-\delta _2 )\).

Apparently, the Eq. (22) is a periodic soliton that is to say it is a periodic solution with period \(2\pi \) with \(X=\xi _2 \), and meanwhile is solitary wave with \(Y=\xi _1 -\theta \).

Figure 5 shows the periodic soliton solutions for some special values of the solution parameters in cases 2.

Fig. 5
figure 5

Periodic soliton solution for case 2 as \(a_2 =1.5,b_1 =1,c_1 =1,c_2 =1,\delta _1 =1,\delta _2 =1,t=1\) and \(z=-1\)

Full size image

Case 3

$$\begin{aligned} a_2 =0, d_1 =-a_1^{3}, d_2 =0, \delta _2 =0 \end{aligned}$$
(23)

where \(a_1 ,b_1 ,b_2 ,c_1 ,c_2\) and \(\delta _1\) are some free real constants. Substituting Eq. (23) into \(u=-2(\ln f)_x\) with Eq. (17), we obtain the solution

$$\begin{aligned} u(x,y,z,t)=\frac{2a_1 e^{-\xi _1 }}{e^{-\xi _1 }+\delta _1 \cos (\xi _2)}, \end{aligned}$$
(24)

for \(\xi _1 =a_1 x+b_1 y+c_1 z-a_1^{3}t,\, \xi _2 =b_2 y+c_2 z\).

Figure 6 shows the periodic solitary-wave solutions for some special values of the solution parameters in cases 3.

Fig. 6
figure 6

Kinky periodic-wave solution for case 3 as \(a_1 =1,b_1 =1,b_2 =1.6,c_1 =1,c_2 =2,\delta _1 =1,t=0\) and \(z=0\)

Full size image

5 Conclusion

In conclusion, we solve the (2+1)- and (3+1)-dimensional Boiti–Leon–Manna–Pempinelli (BLMP) equations by using the extended homoclinic approach, new exact solutions including kinky periodic solitary-wave solutions, periodic soliton solutions and kink solutions are obtained in this paper. To our knowledge, these solutions are novel. In addition, the differently mechanical features of these exact solutions are studied. These results show that EHTA combined with the bilinear form is a simple and powerful method to seek exact solutions of nonlinear partial differential equations. whether there are similar results to other equations is still an open problem.