Abstract
In this paper, planar forced oscillations of a particle connected to the support via two nonlinear springs linked in series and two viscous dampers are investigated. The constitutive relationships for elastic forces of both springs are postulated in the form of the third-order power law. The geometric nonlinearity caused by the transverse motion of the pendulum is approximated by three terms of the Taylor series, which limits the range of applicability of the obtained results to swings with maximum amplitudes of about 0.6 rad. The system has two degrees of freedom, but its motion is described by two differential equations and one algebraic equation which have been derived using the Lagrange equations of the second kind. The classical multiple scales method (MSM) in the time domain was employed. However, the MSM variant with three scales of the time variable has been modified by developing new and dedicated algorithms to adapt the technique to solving problems described by the differential and algebraic equations (DAEs). The paper investigates the cases of forced and damped oscillation in non-resonant conditions, three cases of external resonances, and the internal 1: 2 resonance in the system. Moreover, the analysis of the stationary periodic states with external resonances was carried out, and investigations into the system’s stability were concluded in each case. Two methods of assessing asymptotic solutions have been proposed. The first is based on the determination of the error satisfying the equations of the mathematical model. The second one is a relative measure in the sense of the \({L}^{2}\)-norm, which compares the asymptotic solution with the numerical one determined using the NDSolve procedure of Mathematica software. These measures show that the applied MSM solves the system to a high degree of accuracy and exposes the key dynamical features of the system. It was observed that the system exhibits jump phenomena at some points in the resonance cases, with stable and unstable periodic orbits. This feature predicts chaotic vibration in the system and defines the regions for its applications.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Nowadays, numerous computational techniques and algorithms are developed and offered for applied scientists and engineers to study various mathematical models governed by nonlinear PDEs and ODEs. However, direct use of the finite element method, finite-difference method, the Bubnov–Galerkin method, etc., reduces the problem described by the nonlinear PDEs to that of a set of a large number of coupled second-order nonlinear ODEs sometimes linked with algebraic equation (AE) either linear or nonlinear.
It may happen that in the case of coupled nonlinear ODEs and AEs, mainly when it involves time-dependent and discontinuous coefficients, a direct numerical analysis does not allow for proper conclusions of the obtained results (digits) though performed with the help of illustrative 2D/3D figures. In many instances, some key nonlinear features are hidden and sometimes omitted while carrying out direct numerical studies.
On the other hand, it was observed that the traditional approach based on analytical/semi-analytical techniques might reveal many exciting features like the prediction of various types of resonances and stationary/nonstationary processes based on the reduced amplitude-phase ODEs. Moreover, other phenomena such as jump and hysteresis with simultaneous quantifying bifurcation diagrams and stability of the periodic solutions can be observed.
There is also an observed attempt to the second step of reducing the problems to a few degrees of freedom systems governed by second-order ODEs based on some introduced assumptions and hypotheses.
As it is well-recognized [1], the asymptotic method (AM) combined with the multiple scale method (MSM) allows one to shed light and give a physical interpretation to the usually disordered and sometimes abundant numerically obtained data.
It occurs that the mentioned analytical approaches are not limited to weak nonlinearity, and they are nowadays strongly supported by algebraic manipulators of various technical computing environments being widely available and extensively employed by scientists and engineers. Additionally, there are situations where direct numerical simulation may lead to difficulties in getting reliable and validated solutions but can be overcome by appropriate use of the AM combined with MSM.
The combination of AM and MSM stands for the effective tool in the range of limiting values of the nonlinear dynamics of the carried out processes where the use of the computational schemes is problematic. It should be emphasized that in many cases, those solutions can be successfully used beyond their nominal range of application. They can even be understood as first approximations of some asymptotic approaches, which allows for constructing subsegment approximations that refine the corresponding solutions.
We briefly describe a few works related to our study in what follows.
Rand and Holmes [2] studied a pair of weakly coupled van der Pol oscillators, emphasizing phase-locked periodic motions. The problem was reduced to the study of three algebraic equations.
Benedettini and Rega [3] employed a high-order perturbation analysis for the primary resonance while analyzing the nonlinear dynamics of an elastic cable under planar excitation. Multivaluedness of the response curves were illustrated.
Luongo and Polone [4] carried out the multiple time-scale investigation for divergence-Hopf bifurcation of imperfect symmetric systems. The method was validated through the analysis of a 2DoF rigid bar system (Augustin’s model) and transversal flow.
Rega et al. [5] used two analytical approaches to construct asymptotic models for the nonlinear 3D responses of an elastic suspended shallow cable under harmonic excitation. Primary resonances of the in-plane and out-of-plane symmetric/antisymmetric modes were investigated based on the multiple scales method. Frequency response curves were obtained and discussed.
Belhaq and Houssini [6] proposed a novel method for the construction of an asymptotic expansion of the quasi-periodic solution based on the KBM (Krylov–Bogolubov–Mitropolskiy) method combined with the multiple scale method. The authors also considered features of chaos and its suppression based on 1DoF nonlinear oscillator parametrically and externally driven.
Leamy and Gottlieb [7] studied internal resonances in whirling strings with an account of longitudinal dynamics and material nonlinearities. Direct application of the multiple scales method on the three governing PDEs was addressed, and periodic, quasi-periodic, and aperiodic motions were detected and discussed.
Belhaq and Lakrad [8] extended the classical multiple scales method by employing the Jacobian elliptic functions. The advantages of the proposed method were outlined.
Belhaq et al. [9] found asymptotic solutions of damped nonlinear quasi-periodic Mathieu equations using a double multiple scales method. Explicit analytical approximations were reported and then compared with the numerical integration of the original governing ODE.
Lacarbonara et al. [10] employed two analytical methods, i.e., the full-basis Galerkin discretization approach and the direct treatment, both based on the multiple scales technique. Closed-form conditions for nonlinear orthogonality of the modes were discussed, among others.
Abdulle and Weinan [11] developed a numerical method called the finite-difference heterogeneous MSM for solving multi-scale parabolic systems. The novel approach was supplemented by a few illustrative examples.
Luongo et al. [12] adopted the multiple scale method to study 1:1 resonant multiple Hopf bifurcations of discrete autonomous dynamical systems. They used fractional power expansion of a perturbation parameter, and they obtained m-order differential bifurcation equation in the complex amplitude of the unique critical vector. In order to illustrate the algorithm, mechanical systems subjected to aerodynamic forces triggering 1:1 resonant double Hopf bifurcations were presented.
Warmiński [13] studied oscillations of parametrically and self-excited 2DoF system with a Duffing nonlinearity. Using the multiple scales method, he detected synchronization phenomena near the principal resonances, i.e., in the neighborhood of the natural frequencies; the first p1, the second p2, and near the combination (p1 + p2)/2.
Abouhazim et al. [14] investigated three-period quasi-periodic oscillators in the vicinity of 2:2:1 resonance in a self-excited quasi-periodic Mathieu equation using the method of multiple scales. The efficiency of the method was validated.
Luongo and Di Egidio [15] employed the multiple scale method to a 1D continuous model to derive equations governing the system’s asymptotic dynamics around a bifurcation point. Nonlinear, integro-differential equations of motion were derived and expanded up to cubic terms. Divergence, Hopf, and double-zero bifurcations were revealed. They employed multiple scales analysis to study the three bifurcations, and the relevant bifurcation equations were derived in their normal form.
Abouhazim et al. [16] investigated the damped cubic nonlinear quasi-periodic Mathieu equation in the vicinity of the principal 2:2:1 resonance. In particular, the effects of damping and nonlinearity on the resonant quasi-periodic motions were reported.
Srinil et al. [17] investigated resonant multimodal dynamics due to 2:1 internal resonances in the finite-amplitude free oscillations of horizontal/inclined cables. A second-order asymptotic analysis under planar 2:1 resonance was analyzed with the help of multiple scales. Approximate horizontal/inclined cable models were validated numerically.
Kramer et al. [18] addressed the problems dealing with applications of MSM to three or more time scales.
Gottlieb and Cohen [19] studied the self-excited oscillations of a string on an elastic foundation under a nonlinear feed-forward force. The employed asymptotic multiple scale method yielded slowly varying evolution equations. The derived bifurcation structure included various regions of both stable and unstable coexisting periodic solutions defined by primary and secondary Hopf stability thresholds. They found the existence of quasi-periodic, combination-tone solutions and complex nonstationary solutions that emerged in a range of the asymptotically predicted unstable regions.
Suchorsky et al. [20] employed a two-variable expansion perturbation method to study the oscillations of a van der Pol-type system with delayed feedback. The resulting amplitude-delay relation predicted two Hopf bifurcation curves, such that in the region between these curves, oscillations were quenched.
Zulli and Luongo [21] considered a 2DoF nonlinear system modeling dynamics of two towers exposed to turbulent window flow and linked by a nonlinear viscous device. Periodic and quasi-periodic solutions were revealed and studied by using a perturbation technique. In particular, the effects of viscous damping on the dynamics of the structure were illustrated, including mitigating the oscillations of the two independent towers.
Cacan et al. [22] developed an enriched multiple scales method and studied periodic solutions of the classical forced Duffing and van der Pol oscillators. Analytical investigations were validated by numerical simulations.
Settimi et al. [23] employed multiple scale asymptotics to carry out an external feedback control in a nonlinear continuum formulation of a noncontact AFM model. The investigation included controllable periodic dynamics and additional periodic and distinct quasi-periodic solutions beyond the asymptotic stability thresholds.
Mora and Gottlieb [24] analyzed the oscillations of a parametrically excited microbeam-string affected by nonlinear damping. Both principal parametric resonance and 3:1 internal resonance were studied using the asymptotic multiple scales method. A bifurcation structure, including the coexisting in-plane and out-of-phase solutions, Hopf bifurcations, and conditions for the loss of orbital stability combined with nonstationary quasi-periodic solutions and strange chaotic attractors were reported.
Wilbanks et al. [25] used the multiple scales technique to analyze a two-scale command shaping feed-forward control method to reduce undesirable residual oscillations of traditional and non-traditional Duffing systems.
Kovaleva et al. [26] analyzed the parametric pendulum’s stationary and nonstationary oscillatory dynamics using the limiting phase trajectory concept. A reduced-order model was proposed, allowing the prediction of highly modulated regimes outside the traditionally considered range of initial conditions.
Guo and Rega [27] formulated solvability conditions while carrying out multi-scale dynamic analysis of 1D structures with non-homogeneous boundaries. The formulation allowed one to study four typical continuous structures, i.e., strings, cables, beams, and arches.
Kovaleva et al. [26] studied low- and high-amplitude oscillators of three nonlinear coupled pendula (trimer) beyond the quasi-linear approximation. The reduction in the system dimension via the asymptotic procedure allowed for revealing energy exchange and nonstationary energy localization. The beating-like periodic and quasi-periodic recurrent energy exchange between the pendula was addressed.
Fronk and Leamy [28] revealed angle- and amplitude-dependent invariant waveforms, and plane-wave stability in 2D periodic media by higher-order multiple scales analysis. Simultaneous analysis of nonlinear shear lattices confirmed that the inclusion of higher-order terms in the injected waveforms significantly reduced the growth of higher harmonics. Implications for encryptions strategies and damage detection using weakly nonlinear lattices were suggested.
Rand et al. [29] employed the perturbation technique combined with the multiple scale method to derive and analyze a simplified third-order model capturing the key features of the dynamics of microscale oscillators with thermos-optical feedback. In addition, the bifurcation diagram of the system was presented.
Clementi et al. [30] addressed the internal resonance of a 2DoF mechanical system with quadratic and cubic nonlinearities using the multiple scale method. The authors highlighted a few unexpected but relevant features and hinted at exploiting the obtained results.
Guo and Rega [31] showed that the full-spectrum forced solutions at lower-order and the high-order cross-interactions with the structural modes were captured by the direct perturbation technique matched with the multiple scales method, but not by the discretized perturbation. Two different correction schemes were utilized to remove the occurred errors. The obtained results can be employed to analyze structures with initial curvature.
Warmiński [32] studied regular and chaotic oscillations of a nonlinear structure under the self-, parametric, and external excitations. Approximate analytical solutions were derived based on the multiple scale method. The similarities and differences between the van der Pol and Rayleigh models were demonstrated for periodic, quasi-periodic, and chaotic oscillations.
Lenci et al. [33] studied the internal resonances between the longitudinal and transversal oscillations of forces on Timoshenko beam with an axial end spring by means of the multiple scale method. The results were reliability discussed. Effects of jumping phenomena from hardening to softening by crossing the exact internal resonance value were illustrated.
On the other hand, mechanical systems containing parallel or serially connected springs are widely investigated in the field of theoretical and applied mechanics. Such systems are applied in mechanical and civil engineering, mechatronics, and micro-electro-mechanical systems (MEMS). Various spatial configurations and connections between the springs could exhibit rich dynamical behavior, especially in the case of nonlinear elastic characteristics. An interesting way of observing the behavior of such systems could be in the case of various resonances. For example, Andrzejewski and Awrejcewicz [34] and Suciu et al. [35] tested the serial and parallel massless springs in the structure of a car suspension. The authors showed that the proper connections significantly influenced oscillation damping.
The one-dimensional oscillator consisting of two springs, one of which has a nonlinear characteristic, was investigated by Telli and Kopmaz in [36]. The differential–algebraic system that governs the motion was tested in two ways. At first, the initial value problem was solved numerically. The second approach consisted of deriving one approximate differential equation for the internal motion for which the approximate analytical method was employed. The used procedure yielded the appropriate properties of the springs.
The system of the spring in various configurations was described by Weggel et al. in [37]. The authors showed how to find the effective stiffness of a system of linear springs connected in various ways. The approximate analytical method of nonlinear normal modes was applied to qualitatively analyze the strongly nonlinear spring-body system dynamics of two degrees of freedom (DOF).
Manevich and Musienko [38] presented the asymptotic analysis of the one and two DOF systems. The authors contributed an effective method of qualitative research of non-damped free oscillations.
Two systems of one and two DOF with the springs connected in series governed by ODEs and ALs analyzed by Starosta et al. in [39] are of differential and algebraic types. The suitably modified multiple scale method (MSM) was applied to solve the dynamical problem of free non-damped oscillation. The nonlinear damping in a one-dimensional oscillator was examined by Awrejcewicz et al. [40].
In the linear case, the superposition principle applies, and the connections of springs in series create no difficulties. Depending on the degree of complexity of the connections, the equivalent spring constant can be introduced, or one may retain the algebraic equations that result in a positive semi-definite mass matrix in the model [41]. Hence, it is easy to eliminate one coordinate of the coordinates. However, in nonlinear systems, the principle of superposition does not work, which is a source of model-related and computational difficulties. It is not possible to introduce the equivalent stiffness in the form of a close relationship. Therefore, it becomes necessary to solve problems described by differential–algebraic equations (DAEs).
This paper investigates the forced planar motion of the small body connected to the support via two nonlinear springs coupled in series and two viscous dampers. An in-depth analysis of the behavior of the system is based on the asymptotic approach with the use of MSM in the time domain. Although the multi-scale method is a proven and widely used tool in nonlinear dynamics for solving problems described by differential equations, only a few papers are directed to problems involving DAEs. The MSM method based on the operator of the harmonic oscillator causes that the means used to solve the algebraic equation cannot be too advanced. They cannot violate the linear character of the operator. Nevertheless, this approach occurred to be effective for analyzing quite simple mechanical systems considered in our earlier papers [39, 40]. Therefore, the purpose of the present paper is to examine this approach in planar system with two degrees of freedom and physical and geometrical nonlinearities.
Besides the issue of developing an algorithm for employing the method, the main problem with the application of MSM is whether a usually small number of asymptotic series approximating the solution will satisfy the algebraic equations with sufficient accuracy. Therefore, the paper proposes two ways of assessing asymptotic solutions. One of them, an absolute error nature, is based on the determination of the error satisfying individual equations of the whole model. The second one is a relative measure in the sense of the \({L}^{2}\)-norm that compares the asymptotic solution with the numerical one determined using the NDSolve procedure of Mathematica software.
The study of the vibrational motion of the spring pendulum with two springs in series presented in the paper is quite broad. It includes the cases of forced and damped oscillation in non-resonant conditions, three separately considered types of external resonances, and the internal 1: 2 resonance. Moreover, as part of the examination of external resonances, an analysis of the stationary periodic states is also carried out.
It should be noted that coupled spring (elastic) pendula are rarely investigated based on analytical approaches due to the problems of constructing the solutions validated for both stationary and nonstationary dynamics.
Our work not only gives hints to solving similar problems, but also exhibits its interdisciplinary aspects, including the multi-level quantum systems by unifying nonstationary classical and quantum problems.
Though the mathematical model is derived based on the classical mechanics’ example, it can be used to study other physical systems like paraffin crystals, ferromagnetic chains, and other organic molecules, including DNA [42, 43].
The above-mentioned development of algorithms for the application of the MSM method to solve five separate cases of motion of the spring pendulum described by DAEs that are characterized by both physical and geometric nonlinearities stands for a novelty of the paper. In addition, we propose two types of measures for quantitatively examining the accuracy of the asymptotic solutions. The evaluation of the error using a set of six quantities, assigned to individual equations and unknowns, gave one the answer to the doubt as to whether the accuracy of the solutions satisfies that of the algebraic equation or not. It turned out that in each of the considered cases, the accuracy of its satisfying is the highest.
The rest of the paper is organized as follows. The aspects connected with modeling, deriving the governing equations based on the Lagrangian approach, and dimensionless formulation are outlined in Sect. 2. A brief introduction to MSM and the assumptions determining the applicability of the asymptotic solutions stand for the subject of Sect. 3. A detailed description of the way of deriving the asymptotic solution for non-resonant oscillation of the pendulum and a discussion of results are presented in Sect. 4. Asymptotic solutions for three cases of external resonances are derived and discussed in Sect. 5. The determination of stationary periodic oscillations for the external resonances together with the stability analysis is described in Sect. 6. The asymptotic solution for 1: 2 internal resonance is presented in Sect. 7. Finally, conclusions and remarks are reported in Sect. 8.
2 Mathematical model
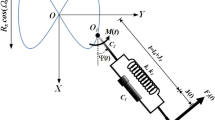
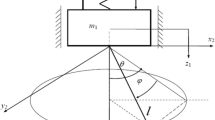
Let us consider two small particles of mass m and \({m}_{0}\) sliding on a bar. The system shown in Fig. 1 is constrained to the motion on the vertical plane. The bar can turn about the pin at the immovable point O, while the particles are coupled via a spring. The second spring connects one of the balls with point O. In their natural state, the springs have the lengths \({L}_{01}\) and \({L}_{02},\) respectively. The relationship between the elastic force and the elongation for each spring can be written as follows:
Spring pendulum with two material points
where \({k}_{i}, {\Lambda }_{i}\) are the elastic coefficients of the i-th spring, and \({\Delta }_{i}\) its total elongation.
The nonlinear contributions to the whole elastic force are assumed to be small. There are two viscous dampers with coefficients \({C}_{1}\) and \({C}_{2}\) in the system. Both springs, the bar, and the dampers are assumed to be massless. The size of the force \(\overrightarrow{F}\), acting on the ball of mass \(m\) along the bar, changes harmonically according to the formula \(F\left(t\right)={F}_{0} \mathrm{cos}\left({\Omega }_{1} t\right)\), whereas the bar is loaded by the given torque of magnitude \(M\left(t\right)={M}_{0} \mathrm{cos}\left({\Omega }_{2} t\right).\)
The system has three degrees of freedom. We introduce the generalized coordinates: \({X}_{1}\left(t\right)\) and \({X}_{2}\left(t\right)\), which define the position of the balls, and the angle \(\Phi \left(t\right).\) The kinetic energy relative to the inertial system, assumed at point O, has the following form:
The potential energy of the conservative forces, expressed in terms of the generalized coordinates, is as follows:
where \(g\) is the Earth’s gravitational acceleration.
The harmonic forcing and the forces contributing to damping are introduced into consideration as the generalized forces:
The Lagrange equations of the second kind yield the governing equations of motion:
From Eqs. (5)–(7), one can derive equations governing the spring pendulum with two nonlinear springs connected in series. Such a system, shown in Fig. 2, stands for the subject of the paper. The point connecting the springs is marked with the symbol S, and it can be treated as the massless counterpart of the particle, the mass tending to zero. Therefore, the point keeps the possibility of movement along the bar. Formally, the systems shown in Figs. 1 and 2 differ only in the presence of the ball of mass \({m}_{0}.\) This means that assuming that \({m}_{0}=0\) in Eqs. (5)–(7), we get
Pendulum with two springs connected serially
where \({L}_{0}={L}_{01}+{L}_{02}.\)
Equation (8) is algebraic and describes the equilibrium condition for the forces of both springs. The mathematical model, given by Eqs. (8)–(10), belongs to the class of dynamical systems governed by the differential–algebraic equations (DAEs). Elimination, in the strict sense, of the \(X_{1}\) coordinate is not a good option for computational reasons, so both coordinates are necessary to define the state of the system unambiguously. Assuming that Eq. (8) depicts constraints, the \(X_{1}\) coordinate can be regarded as complementary one, but not independent. As a result, the system shown in Fig. 2 has two degrees of freedom.
Bishop et al. [41] discussed the special cases of linear mechanical systems leading to the formulation with positively semi-definite matrices of mass or stiffness. The case with the positively semi-definite matrix of mass is characterized by the fact that at least one of the Lagrange equations becomes an algebraic equation.
The initial conditions of the form:
where \({X}_{0}, {V}_{0},{\Phi }_{0}, {\Omega }_{0}\) are known quantities, and are necessary for an unambiguous solving of Eqs. (8)–(10).
The pendulum reaches the stable static equilibrium position when
where
The problem of vibration of the pendulum is described by seventeen physical quantities (four variables and thirteen parameters). Among them, there are three independent fundamental physical dimensions, namely mass, time, and length. According to the Buckingham π theorem [44], the problem can be rewritten in terms of fourteen (i.e., 17–3) dimensionless quantities, including ten parameters. In order to transform Eqs. (8)–(10) into their counterpart dimensionless form, we propose to introduce the reference system with the analogous structure as the considered one, but with the springs whose elastic properties are linear, i.e., with \({\Lambda }_{1}=0\) and \({\Lambda }_{2}=0.\) The effective stiffness of the reference system is
The eigenfrequency of the reference system
is used for defining the dimensionless time
Assuming the natural length \({L}_{0}\) of both springs increased by \({X}_{2e}\) as the reference length, i.e., \(L={L}_{0}+{X}_{2e},\) we define the dimensionless coordinates
Observe that both coordinates \({x}_{1}\) and \({x}_{2}\) are functions of the dimensionless time \(\tau \). We also substitute the original generalized coordinate \(\Phi (t)\) with the function \(\varphi \left(\tau \right)\) of dimensionless time.
The other dimensionless parameters describing the properties of the system and the harmonic forces are defined as follows:
Dimensionless quantity \({\alpha }_{i}\) stands for the ratio of the nonlinear to the linear contribution of the entire spring force. Parameters \({c}_{1}\) and \({c}_{2}\) make sense of dimensionless viscous damping coefficients. The parameter w expresses the ratio of the frequency of small isochronous oscillations of a mathematical pendulum of mass \(m\) and length \(L\) to the frequency \(\omega \) of the reference system. The dimensionless coefficient \({f}_{1}\) can be interpreted as the ratio of the amplitude of the exciting force \(\overrightarrow{F}\) to the magnitude of a force causing the spring to be elongated twice. Indirectly, a similar interpretation may be applied to the coefficient \({f}_{2}\) when we assume that \({M}_{0}/L\) stands for a force.
Making use of definitions (13)–(17), one can write the equations of the mathematical model in the following dimensionless form:
where the quantities \({x}_{1e}\) and \({x}_{2e}\) satisfy the following equilibrium conditions
The initial conditions (11) in the dimensionless form are
where \({x}_{0}=\frac{{X}_{0}}{L}, {v}_{0}=\frac{{V}_{0}}{L\omega }.\)
3 Method of finding solution: general remarks
The approximate analytical solution in the asymptotic sense to the problem given by (18)–(22) is obtained using the multiple scales method in the time domain (MSM). Following MSM, we introduce the small parameter \(\varepsilon \) that is a number satisfying a priori the inequalities \(0<\varepsilon \ll 1.\) Instead of the dimensionless time τ, n variables describe the evolution of the pendulum over time. We decide to choose the variant of the MSM with three variables: \({\tau }_{0}, {\tau }_{1}, {\tau }_{2}\) that are related to the time \(\tau \) as follows:
The unknown generalized coordinates and the auxiliary function \({x}_{1}(\tau )\) are approximated by the following asymptotic expansions
where functions \({\xi }_{1k}\left({\tau }_{0}, {\tau }_{1}, {\tau }_{2}\right), {\xi }_{2k}\left({\tau }_{0}, {\tau }_{1}, {\tau }_{2}\right), {\phi }_{k}\left({\tau }_{0}, {\tau }_{1}, {\tau }_{2}\right)\) for \(k=1, \dots , 3\) are sght.
The asymptotic expansions (24)–(26) are uniformly valid on some finite interval \(\langle 0,{\tau }_{M}),\) where \({\tau }_{M}\) is of order \(\mathrm{O}\left({\upvarepsilon }^{-n}\right).\) The size of the interval is important in the context of an intended steady-state study. The use of three scales, not two, is exactly motivated by the observation, which is mentioned in the latter part of the work.
The differential operators relating to the time \(\tau \) are replaced by operators with partial derivatives. According to the chain rule, we can write
Limiting the considering only to a weakly nonlinear system, we assume that some parameters describing the pendulum and its loading are small. We express the assumptions about the smallness as follows:
The coefficients \({\widehat{\alpha }}_{1}, {\widehat{\alpha }}_{2}, {\widehat{c}}_{1}, {\widehat{c}}_{2}, {\widehat{f}}_{1} , {\widehat{f}}_{2}\) are finite when\(\varepsilon \to 0\).
In order to ensure the linearity of the differential operators of approximate equations within the framework of MSM, one needs to approximate the trigonometric functions of the angle \(\varphi \). By expanding the functions in the Taylor series around zero and taking only the first three terms, we get an approximation that satisfies these expectations.
Due to the occurrence of differential and algebraic equations, some modifications in the standard MSM approach are needed to solve the problem satisfactorily.
4 Non-resonant oscillations
Inserting Eqs. (23)–(26) and (29)–(30) and then calculating all the necessary derivatives according to (27)–(28) yields equations with a small parameter in a few different powers. Each of the three equations should be satisfied for any value of \(\varepsilon \). After ordering the terms of the equations according to the powers of the small parameter, omitting all terms of the order \(O\left({\varepsilon }^{4}\right)\) and higher, one can realize the requirement by the method of undetermined coefficients. In this way, we obtain the set of nine equations with unknown functions \({\xi }_{1k}\left({\tau }_{0}, {\tau }_{1}, {\tau }_{2}\right),\) \({\xi }_{2k}\left({\tau }_{0}, {\tau }_{1}, {\tau }_{2}\right),\) \({\phi }_{k}\left({\tau }_{0}, {\tau }_{1}, {\tau }_{2}\right),\) where \(k=\mathrm{1,2},3.\) The equations are divided into three groups. The following equations, accompanied by \({\varepsilon }^{1}\), belong to the first group
Equations (31)–(33) are called equations of the first-order approximation. The terms standing at \({\varepsilon }^{2}\) create the following equations of the second-order approximation
The coefficients that are accompanied by \({\varepsilon }^{3}\) form the equations of the third-order approximation
Contrary to the systems governed by only differential equations, there is one algebraic equation at each level of the asymptotic approximation. The way of the approximate solving these equations strongly depends on the linear nature of the differential operator which occurs in the other equations. This requirement makes that the relationship between \(\xi {}_{1k}\) and \({\xi }_{2k}\), for k = 1,..,3, is linear. Such a rough linearization is justified by assumptions (29).
The system of Eqs. (31)–(39) is solved recursively. In estimating the solution, we always start with the algebraic equation. The algebraic equations enable one to express the functions \({\xi }_{1k}\left({\tau }_{0}, {\tau }_{1}, {\tau }_{2}\right)\) in terms of the functions \({\xi }_{2k}\left({\tau }_{0}, {\tau }_{1}, {\tau }_{2}\right)\), where \(k=\mathrm{0,1},2.\)
From Eqs. (31) and (34), we get
Substituting Eq. (40), for \({\xi }_{11}\), into Eq. (32) yields
The general solution to this linear homogenous equation is
where i denotes the imaginary unit, \({B}_{1}\) and its complex conjugate \({\overline{B} }_{1}\) are unknown complex-valued functions of both slower time scales. Taking into account Eqs. (40) and (42), we can write
The general solution to Eq. (32), which also is linear and homogenous, reads
where \({\overline{B} }_{2}\) is the complex conjugate to \({B}_{2}.\)
We start the solution of the second-order approximation equations from Eq. (35). After substituting relationship (40) and then solutions (42) and (44), we obtain
The secular terms, which for Eq. (45) are periodic functions with period 2π, violate the postulate about the uniform validity of the series (24)–(26). Thus, they must be removed by satisfying the following conditions:
Taking into account (46), we get
Due to the same form of differential operators of Eqs. (41) and (47), we omit the general solution to the homogeneous equation corresponding to Eq. (47). The particular solution has the following form:
Making use of relationship (40), we determine the function \({\xi }_{12}\left({\tau }_{0}, {\tau }_{1}, {\tau }_{2}\right)\), i.e., we have
Substituting solutions (42) and (44) into Eq. (36) yields
The periodic functions with period \(2w\pi \) are the secular terms for Eq. (50). The following solvability conditions provide the elimination of the secular
The particular solution to the equation, derived from Eq. (50) taking into account conditions (51), is as follows:
Beginning with the solution of the third-order approximation equations, we determine the function \({\xi }_{13}\left({\tau }_{0}, {\tau }_{1}, {\tau }_{2}\right)\) in terms of \({\xi }_{23}\left({\tau }_{0}, {\tau }_{1}, {\tau }_{2}\right).\) Employing Eqs. (37) and (42)–(43), we obtain
Substituting solutions (42)–(44), (48), and (52) to Eq. (38) generates the appearance of the secular terms, i.e., the periodic functions with the period of \(2\pi \). The necessity to eliminate them leads to the following solvability conditions:
Taking into account solvability conditions (54)–(55) makes it possible to obtain a uniformly valid solution to Eq. (38) which has the following form:
The detailed form of Eq. (38), after elimination of the secular terms (54)–(55), is quoted in Appendix as Eq. (A1). In Appendix, there is also the new form of Eq. (53), in which solution (56) is regarded (Eq. (A2)).
We insert solutions (42), (44), (48), and (52) into Eq. (39). The following conditions
provide elimination of the secular terms, i.e., the periodic functions with the period of \(2w\pi \). The detailed form of Eq. (39), after elimination of the secular terms (57)–(58), can be found in Appendix under number (A3). The particular solution to Eq. (A3) is as follows:
The unknown functions \({B}_{1}\left({\tau }_{1},{\tau }_{2}\right)\) and \({B}_{2}\left({\tau }_{1}, {\tau }_{2}\right)\) together with their complex conjugates are restricted by solvability conditions (46), (51), (54)–(55), and (57)–(58). We conclude from Eqs. (46) and (51) that all these functions do not depend on the variable \({\tau }_{1}\). Taking into account this circumstance, we depict the functions in the exponential form as follows:
where functions \({b}_{j}\left({\tau }_{2}\right)\) and\({\psi }_{j}\left({\tau }_{2}\right)\), for \(j=\mathrm{1,2},\) are real-valued. Inserting relationships (60) into solvability conditions (54)–(55) and (57)–(58) yields the following set of four partial differential equations with unknown functions \({b}_{j}\left({\tau }_{2}\right)\) and \({\psi }_{j}\left({\tau }_{2}\right)\), for\(j=\mathrm{1,2}\),
Solving Eqs. (61)–(64) with respect to the derivatives, one can obtain
Equations (65)–(68) describe the variability of the functions \({b}_{j}\left({\tau }_{2}\right)\) and \({\psi }_{j}\left({\tau }_{2}\right)\), for \(j=\mathrm{1,2}\), in the slowest scale of the time. According to definition (27), the following identity is valid for any function only of the variable \({\tau }_{2}\)
Let us introduce the functions \({a}_{1}({\tau }_{2})\) and \({a}_{2}\left({\tau }_{2}\right)\) such that
Multiplying Eqs. (65)–(66) by \({\varepsilon }^{3}\), while Eqs. (67)–(68) by \({\varepsilon }^{2}\) and taking into account identity (69) and relationships (29), we obtain
The following initial conditions
provide the unambiguous determination of the functions \({a}_{1}, {a}_{2}, {\psi }_{1}, {\psi }_{2}.\) The initial values \({a}_{10}, {a}_{20}, {\psi }_{10}\), and \({\psi }_{20}\) are related to the initial values \({x}_{0}, {v}_{0}, {\varphi }_{0}\) and \({\omega }_{0}\).
The exact solution to the initial value problem given by Eqs. (71)–(75) has the following form:
Assembling, accordingly to expansions (24)–(26), the solutions obtained using the recursive procedure, we obtain the following form of the asymptotic solution
where the functions \({\tilde{x }}_{1}\left(\tau \right), {\tilde{x }}_{2}\left(\tau \right),\) and \({\tilde{x }}_{2}\left(\tau \right)\) are defined in Appendix.
The functions \({a}_{1}\left(\tau \right),{a}_{2}\left(\tau \right), {\psi }_{1}\left(\tau \right),\) and \({\psi }_{2}\left(\tau \right)\) are defined by Eqs. (76)–(79). The functions \({a}_{1}\left(\tau \right)\) and \({\psi }_{1}\left(\tau \right)\) depict the amplitude and the phase of the function \({a}_{1}\left(\tau \right)\mathrm{cos}\left(\tau +{\psi }_{1}\left(\tau \right)\right)\) corresponding to the first term of the asymptotic expansion (24). Similarly, the functions \({a}_{2}\left(\tau \right)\) and \({\psi }_{2}\left(\tau \right)\) are the amplitude and the phase of the function \({a}_{2}\left(\tau \right)\mathrm{cos}\left(\tau +{\psi }_{2}\left(\tau \right)\right)\) which corresponds to the first term of the asymptotic expansion (25). In the context of this interpretation, we say that Eqs. (71)–(74) are the equations of amplitude and phase modulation.
Asymptotic solutions (80)–(82) fail when any of the denominators’ terms equals zero or close to zero, which implies the occurrence of resonant oscillations. Equations (80)–(82) describe the pendulum’s oscillation and the variability of strains of both springs, excluding the resonant cases.
Let us assume the following values of the dimensionless parameters describing the mechanical features of the pendulum:
The parameters characterizing the forces and the initial values are as follows:
Requiring that the asymptotic solution satisfy initial conditions (22), we get a set of algebraic equations with unknown \({a}_{10}, {a}_{20}, {\psi }_{10},\) and \({\psi }_{20}.\) For the data considered, solving these equations gives the following results:
The time histories of the longitudinal and swing oscillation are shown in Figs. 3, 4, 5 and 6. The first two of them show the transient situation. The effect of slow attenuation of both vibrations is observed here. The next two figures depict the transition from the state of transient oscillations to the steady ones. In the case of the longitudinal vibrations, it takes more time to pass to the stationary regime. To verify the correctness and accuracy of the asymptotic solution, each figure also shows graphs of the solution obtained by numerically integrating the governing Eqs. (18)–(20) with initial conditions (22). For this purpose, we employ the NDSolve procedure of the Mathematica 12.0 software. The index of DAEs (18)–(20), understood as the minimum number of differentiations necessary to solve the equations for the first derivatives of variables, is equal to two. NDSolve converts the system into so-called residual form and then the built-in solver reduces the index to one. The converted residual form is solved using the IDA (i.e., Implicit Differential–Algebraic solver). The methods of IDA are based on backward differentiation formulas BDF. The calculations were carried out with standard machine precision, i.e., around sixteen digits. The approximate asymptotic solution is drawn using a solid line, whereas a dotted line depicts the numerical solution.
Transient longitudinal oscillation; solid line—asymptotic solution, dotted line—numerical solution
Transient swing oscillation; solid line—asymptotic solution, dotted line—numerical solution
Transition from the transient oscillation to the steady one for \({x}_{2}\left(\tau \right)\); solid line—asymptotic solution, dotted line—numerical solution
Transition from the transient oscillation to steady one for \(\varphi \left(\tau \right)\); solid line—asymptotic solution, dotted line—numerical solution
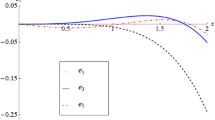
The time-varying dimensionless deformations of both springs for the transient and stationary vibrations are shown in Figs. 7 and 8, respectively. The dimensionless elongation \({\Delta }_{1}\) of the spring with one end immovable is equal to the coordinate \({x}_{1}\left(\tau \right),\) while the strain \({\Delta }_{2}\) of the intermediate spring is understood as the difference \({x}_{2}\left(\tau \right)-{x}_{1}\left(\tau \right).\) The deformations determined on the ground of the asymptotic approximation are drawn by solid lines, whereas the dotted lines depict the deformations calculated numerically. One can note the high compatibility of the curves presenting the numerical and asymptotic solutions in each of Figs. 3, 4, 5, 6, 7 and 8.
Strain of both springs for transient oscillation; solid line—asymptotic solution, dotted line—numerical solution
Strain of both springs for stationary oscillation; solid line—asymptotic solution, dotted line—numerical solution
The quantitative evaluation of the accuracy of approximate solutions (80)—(82) is established based on the following measures:
where \({H}_{1}, {H}_{2},\) and \({H}_{3}\) stand for, in order, the differential operators, i.e., the left sides of Eqs. (18)–(20), \({x}_{1n}\left(\tau \right), {x}_{2n}\left(\tau \right), {\varphi }_{n}\left(\tau \right)\) are the approximate solutions to Eqs. (18)–(20) obtained numerically using the procedure NDSolve included in Mathematica 12.0, and \({\tau }_{s}\) and \({\tau }_{e}\) denote the instants chosen from the interval of simulation.
When the exact solution is unknown, any attempts to introduce the relative error are problematic. Assuming the numerical solution as the sufficiently accurate approximation, one can assess the accuracy of the approximate asymptotic solution using the relative error \({\delta }_{i}, i=\mathrm{1,2},3,\) in the sense of \({L}^{2}\) norm. The measures defined by Eq. (83) evaluate the error of the satisfying governing equations and, hence, it has the nature of the absolute error. Both measures of error are based on the metric of the space of square-integrable functions induced by the inner product. They can serve as a good estimation of the distance between functions on the whole interval. In light of such an interpretation, formula (83) allows for the assessment of the error in meeting individual governing equations in the considered interval. Formula (84) gives the distance between the numerical and asymptotic solutions on the interval.
Estimating the accuracy of the asymptotic solution shown in Figs. 3, 4, 5, 6, 7 and 8, we assumed \({\tau }_{s}=0\) and \({\tau }_{e}=1200\). The values of both measures of error are collected in Table 1. Except for the function \({x}_{2}\left(\tau \right),\) the asymptotic solutions are almost one order of magnitude less accurate than numerical ones on the assumed interval. However, the small values of both measures of error confirm that the results obtained using the MSM can be considered reliable for the range of parameters consistent with assumptions (29).
5 External resonance cases
Approximate solution (80)–(82) allows one to recognize the following resonant cases:
-
(i)
primary external resonances, when \({p}_{1}\approx 1, {p}_{2}\approx w ;\)
-
(ii)
internal resonance, when \(2w\approx 1.\)
The resonant cases require a separate approach based on additionally formulated assumptions, and we provide solutions for all detected external resonance cases. However, to avoid unnecessary repetitions, the solution procedure will be described in detail only for the external resonance \({p}_{1}\approx 1\). Then, the resonant phenomena are expected in a neighborhood of the natural frequency, which in dimensionless formulation equals 1. Following the MSM, we introduce the detuning parameter \({\sigma }_{1}\), as follows:
Assuming that the detuning parameter is of the order \(O\left(\varepsilon \right),\) we write
and the coefficient \({\widehat{\sigma }}_{1}\) is finite when \(\varepsilon \to 0\).
While maintaining assumptions (29), inserting relations (23)–(28) and approximations (30) into governing Eqs. (18)–(20), and taking into account resonance condition (85), we get three equations containing the small parameter \(\varepsilon \) in various powers. These equations need to be rearranged according to the powers of the small parameter. The requirement that each of these equations should be satisfied for any value of \(\varepsilon \) yields a system of DAEs. Omitting all terms of the order \(O\left({\varepsilon }^{4}\right)\), we get nine equations that are organized into three groups, as follows:
-
(i)
equations of the first-order approximation
$$ \lambda \xi_{21} - \left( {1 + \lambda } \right)\xi_{11} = 0, $$(87)$$ \frac{{\partial^{2} \xi_{21} }}{{\partial \tau_{0}^{2} }} + \left( {1 + \lambda } \right)\left( {\xi_{21} - \xi_{11} } \right) = 0, $$(88)$$ \frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{0}^{2} }} + w^{2} \phi_{1} = 0; $$(89) -
(ii)
equations of the second-order approximation
$$ \lambda \xi_{22} - \left( {1 + \lambda } \right)\xi_{12} = 0, $$(90)$$ \frac{{\partial^{2} \xi_{22} }}{{\partial \tau_{0}^{2} }} + \left( {1 + \lambda } \right)\left( {\xi_{22} - \xi_{12} } \right) = - 2\frac{{\partial^{2} \xi_{21} }}{{\partial \tau_{0} \partial \tau_{1} }} + \left( {\frac{{\partial \phi_{1} }}{{\partial \tau_{0} }}} \right)^{2} - \frac{{w^{2} }}{2}\phi_{1}^{2} , $$(91)$$ \frac{{\partial^{2} \phi_{2} }}{{\partial \tau_{0}^{2} }} + w^{2} \phi_{2} = - 2\xi_{21} \frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{0}^{2} }} - 2\frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} - 2 \frac{{\partial \xi_{21} }}{{\partial \tau_{0} }}\frac{{\partial \phi_{1} }}{{\partial \tau_{0} }} - w^{2} \xi_{21} \phi_{1} ; $$(92) -
(iii)
equations of the third-order approximation
$$ \lambda \xi_{23} - \left( {1 + \lambda } \right)\xi_{13} = 3 \hat{\alpha }_{1} x_{1e}^{2} \xi_{11} - 3\lambda \tilde{\alpha }_{2} \left( {x_{2e} - x_{1e} } \right)^{2} \left( {\xi_{21} - \xi_{11} } \right), $$(93)$$ \begin{aligned} \frac{{\partial^{2} \xi_{23} }}{{\partial \tau_{0}^{2} }} + \left( {1 + \lambda } \right)\left( {\xi_{23} - \xi_{13} } \right) = \hat{f}_{1} \sin \left( {\left( {1 + \varepsilon \hat{\sigma }_{1} } \right)\tau_{0} } \right) - \hat{c}_{1} \frac{{\partial \xi_{21} }}{{\partial \tau_{0} }} \hfill \\ - 3\left( {1 + \lambda } \right)\hat{\alpha }_{2} \left( {x_{2e} - x_{1e} } \right)^{2} \left( {\xi_{21} - \xi_{11} } \right) - w^{2} \phi_{1} \phi_{2} - \frac{{\partial^{2} \xi_{21} }}{{\partial \tau_{1}^{2} }} - 2\frac{{\partial^{2} \xi_{21} }}{{\partial \tau_{0} \partial \tau_{2} }} - 2\frac{{\partial^{2} \xi_{22} }}{{\partial \tau_{0} \partial \tau_{1} }} \hfill \\ + \xi_{21} \left( { \frac{{\partial \phi_{1} }}{{\partial \tau_{0} }}} \right)^{2} + 2\frac{{\partial \phi_{1} }}{{\partial \tau_{0} }}\left( { \frac{{\partial \phi_{1} }}{{\partial \tau_{1} }} + \frac{{\partial \phi_{2} }}{{\partial \tau_{0} }}} \right), \hfill \\ \end{aligned} $$(94)$$ \begin{aligned} \frac{{\partial^{2} \phi_{3} }}{{\partial \tau_{0}^{2} }} + w^{2} \phi_{3} & = \hat{f}_{2} \sin \left( {p_{2} \tau_{0} } \right) - \hat{c}_{2} \frac{{\partial \phi_{1} }}{{\partial \tau_{0} }} - \frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{1}^{2} }} - 2\frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{0} \partial \tau_{2} }} - 2\frac{{\partial^{2} \phi_{2} }}{{\partial \tau_{0} \partial \tau_{1} }} + \frac{{w^{2} }}{6}\phi_{1}^{3} \\ & - w^{2} \left( {\xi_{22} \phi_{1} + \xi_{21} \phi_{2} } \right) - \frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{0}^{2} }}\left( {\xi_{21}^{2} + 2\xi_{22} } \right) - 2\frac{{\partial \phi_{1} }}{{\partial \tau_{0} }}\left( {\frac{{\partial \xi_{21} }}{{\partial \tau_{1} }} + \xi_{21} \frac{{\partial \xi_{21} }}{{\partial \tau_{0} }} + \frac{{\partial \xi_{22} }}{{\partial \tau_{0} }}} \right) \\ & - 2\xi_{21} \left( {2\frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} + \frac{{\partial^{2} \phi_{2} }}{{\partial \tau_{0}^{2} }}} \right) - 2\frac{{\partial \xi_{21} }}{{\partial \tau_{0} }}\left( {\frac{{\partial \phi_{1} }}{{\partial \tau_{1} }} + \frac{{\partial \phi_{2} }}{{\partial \tau_{0} }}} \right). \\ \end{aligned} $$(95)
The functions \({\xi }_{1k}\left({\tau }_{0},{\tau }_{1}, {\tau }_{2}\right), {\xi }_{2k}\left({\tau }_{0},{\tau }_{1}, {\tau }_{2}\right), {\phi }_{k},\) where \(k=\mathrm{0,1},2,\) are to be determined. From Eq. (87), it follows that
We substitute dependence (96) into Eq. (88) which becomes the following homogeneous differential equation
The general solution to Eq. (97) reads
where \({B}_{1}\) and its complex conjugate \({\overline{B} }_{1}\) are unknown complex-valued functions of both slower time scales. Taking into account Eqs. (96) and (98), we write
The general solution to homogenous Eq. (89) has the form
where \({\overline{B} }_{2}\) is the complex conjugate to \({B}_{2}.\)
Making use of Eq. (90), substituting solution (98) for \({\xi }_{21}\) and solution (100) for \({\phi }_{1}\), and eliminating the secular terms according to
the following form of Eqs. (91)–(92) is obtained
The particular solutions to Eqs. (103)–(104) take the following form:
Equations (90) and (106) yield
Using Eq. (93), we derive the following relationship:
After substituting solutions (98)–(102), (105)–(106), and (108) into Eqs. (94)–(95), it is necessary to eliminate the secular terms from them. Consequently, the following solvability conditions should be satisfied:
The form of Eqs. (94)–(95) which was derived after the elimination of the secular terms (109)–(112) is quoted in Appendix as Eqs. (A7)–(A8). The particular solutions to Eqs. (A7)–(A8) are given by
Substituting solutions (98)–(99) and (113) into Eq. (108), we obtain
Solvability conditions (101)–(102) imply no dependence of the unknown functions \({B}_{1}\) and \({B}_{2}\) on the variable \({\tau }_{1}.\) Presenting the functions in the exponential form according to (60), taking into account smallness assumptions (29) and (70), and relation (69) between derivatives, we obtain the following form of the modulation equations:
The initial conditions to Eqs. (116)–(119) have the same form as conditions (75). The second equation of this system is not coupled with the others, which enables solving it separately. The exact solution to Eq. (117) is as follows:
Substituting Eq. (120) for \({a}_{2}\left(\tau \right)\) into Eqs. (116) and (118)–(119), we get the initial value problem which should be solved numerically.
The combination of the solutions, obtained in the recursive procedure, according to Eqs. (24)–(26) leads to an approximate asymptotic solution in the form
The auxiliary function \({x}_{1}\left(\tau \right)\) is defined as follows:
The functions \({a}_{1}\left(\tau \right),{a}_{2}\left(\tau \right), {\psi }_{1}\left(\tau \right),\) and \({\psi }_{2}\left(\tau \right)\) are the solutions to modulation problem (116)–(119) and \({\tilde{x }}_{2}\left(\tau \right),\stackrel{\sim }{\varphi }\left(\tau \right), {\tilde{x }}_{1}(\tau )\) are defined by Eqs. (A4)–(A5) and (A6), respectively. The approximate solution, given by Eqs. (121)–(123) together with modulation Eqs. (116)–(119), is applicable for the external resonance \({p}_{1}\approx 1\).
The asymptotic solution for the main resonance \({p}_{2}=w+{\sigma }_{2},\) where \({\sigma }_{2}\) as the detuning parameter is of the order \(\varepsilon \), is as follows:
The amplitudes \({a}_{1}\left(\tau \right),{a}_{2}\left(\tau \right)\) and the phases \({\psi }_{1}\left(\tau \right),\) \({\psi }_{2}\left(\tau \right)\) satisfy the following modulation equations:
that are supplemented by initial conditions (75). Equation (127) has the exact solution of the form:
When the resonance is caused by both excitations simultaneously, i.e., \({p}_{1}=1+{\sigma }_{1}\) and \({p}_{2}=w+{\sigma }_{2}\), the asymptotic solution takes the following form:
The modulation equations corresponding to the case of two simultaneously occurring main resonance have the form:
and are supplemented by initial conditions (75). Now, the modulation problem can be solved numerically.
Let the pendulum with the same parameters as specified in Sect. 4 serve as an example in numerical simulations for the external resonance. Thus, we take the following values:
The values assumed for initial conditions (22) are
The external load is defined by the following values:
We take the following initial values for the modulation problem (135)–(138)
The relationship between initial values (140) and (141) has been determined using the analytical form of solution (121)–(123).
Figure 9 shows the time history of transient vibrations in the longitudinal direction with a clear tendency to increase the amplitude. Due to the presence of damping in the system, the resonant oscillations settle themselves at the amplitude value of about 0.04. The effect of slow but clear damping of the pendulum oscillations in the transverse direction is observed in Fig. 11 concerning the transitional state. The graphs of the dimensionless deformations of both springs in the steady state are shown in Fig. 12.
Transient longitudinal oscillations in the main resonance \({p}_{1}\approx 1\); solid line—asymptotic solution, dotted line—numerical solution
When \(\lambda >1\), the distal spring connected directly to the immovable point O is more flexible and therefore subject to greater deformations. In each of Figs. 9, 10, 11, 12 and 13, the functions resulting from the asymptotic solution (121)–(123) are drawn with solid lines. On the other hand, the corresponding functions that are obtained numerically by solving Eqs. (18)–(20) are depicted as dotted lines. The difference between asymptotic and numerical solutions is imperceptible in the graphs. Using measures (83)–(84), both the error of satisfying the governing equations by the asymptotic solution and the relative error related to the numerical solution was assessed. Their values are as follows:
Stationary longitudinal oscillations in the main resonance \({p}_{1}\approx 1\); solid line—asymptotic solution, dotted line—numerical solution
Transient swing oscillations in the main resonance \({p}_{1}\approx 1\); solid line—asymptotic solution, dotted line—numerical solution
Strain of both springs versus time for the stationary vibration in the main resonance \({p}_{1}\approx 1\); solid line—asymptotic solution, dotted line—numerical solution
Transient swing oscillations in the main resonance \({p}_{2}\approx w\); solid line—asymptotic solution, dotted line—numerical solution
The definite integrals in formulas (83)–(84) have been calculated on the interval \(\langle \mathrm{0,1500}\rangle .\) The error of approximation (30) contributes to the greater value of the error \({\delta }_{3}\). The small values of the error measures of both types confirm the usefulness of the asymptotic solution for the description of vibration under the external resonance \(p\approx 1\).
We present the approximate solutions adequate for the external resonance \({p}_{2}\approx w\) assuming the following values of the parameters describing the harmonic load
The values of the parameters expressing mechanical properties of the pendulum and the initial values are defined by Eqs. (139)–(140), respectively. The following values of amplitudes and phases correspond to these initial values:
The error measures according to formulas (83)–(84) employed to the solution shown in Figs. 13, 14, 15 and 16 and computed on the interval \(\langle \mathrm{0,1500}\rangle \) take values
Stationary swing oscillations in the main resonance \({p}_{2}\approx w\); solid line—asymptotic solution, dotted line—numerical solution
Longitudinal oscillations for large values of the time variable; solid line—asymptotic solution, dotted line—numerical solution
Strain of both springs versus time for large values of the time variable; solid line—asymptotic solution, dotted line—numerical solution
Figures 13 and 14 show how the swing oscillations change from the transient state to steady-state oscillation in the external resonance \({p}_{2}\approx w\). The amplitude of the oscillations reaches relatively large values. However, they still fall within the range to which the approximate formula (30) can be applied. There is a slight, but noticeable in the figures, difference in the course of asymptotic and numerical solutions. It is also reflected in higher values of the relative error (84). While the transverse vibration stabilized fairly quickly, the longitudinal vibration remains transient on the whole interval \(\langle \mathrm{0,1500}\rangle \), as shown in Fig. 15. The distal spring connected to the immovable point O is subject to greater deformation for large values of the time variable which is shown in Fig. 16. The same convention of presenting the results holds as previously in Figs. 13, 14, 15 and 16. The approximate numerical solutions obtained with the use of the NDSolve procedure are drawn with dotted lines, while the solid line was assigned to asymptotic solutions (124)–(126).
The asymptotic solution (132)–(134) that is valid in the case of double external resonance is presented in the graphs for the values of the parameters listed in Eqs. (139)–(140). We supplement the set of data with the following values concerning the forces
Calculating, the initial values for the modulation problem, we obtain
Figures 17and18 show how the longitudinal oscillations change from the transient state to almost steady-state oscillation. The variability of the pendulum oscillation in the transverse direction on the whole interval \(\langle \mathrm{0,1500}\rangle \) is shown in Fig. 19. In the steady state, the amplitude \({a}_{2}(\tau )\) stabilizes at a level slightly exceeding the value of 0.2, i.e., within the range when approximation (30) is valid. The differences in the course of the numerical solutions depicted with a dotted line and the asymptotic solutions drawn with a solid line are practically invisible on the graphs. This conclusion is confirmed by the values of the relative error of the asymptotic solution related to the numerical solution which are as follows:
Transition of longitudinal oscillations from transient to steady state for the double external resonance; solid line—asymptotic solution, dotted line—numerical solution
Almost stationary longitudinal oscillations in the double external resonance; solid line—asymptotic solution, dotted line—numerical solution
Transient and stationary swing oscillations for the double external resonance; solid line—asymptotic solution, dotted line—numerical solution
The measures of the satisfying of the governing equations take the following values:
The error of both types have been calculated on the interval \(\langle \mathrm{0,1500}\rangle \). Figure 20 shows graphs of distal and intermediate spring deformations as a function of time for stationary oscillation. Also, in this case, one can observe a high agreement of the results obtained by the asymptotic and numerical methods. Observe that the amplitudes of the deformations of the distal spring are larger.
Strain of springs versus time for the stationary vibration in the double resonance; solid line—asymptotic solution, dotted line—numerical solution
6 Steady states at external resonances
We start the section devoted to the steady-state oscillation of the pendulum under the conditions of external resonance with a discussion of the case of two simultaneously occurring resonances, i.e., \({p}_{1}\approx 1\) and \({p}_{2}\approx w\). Following the approach of MSM to the steady-state analysis, we define the modified phases
Introducing these definitions into Eqs. (135)–(138) enables to transform them onto an autonomous dynamical system governed by the following amplitude and phase ODEs:
According to the assumptions about the nonstationary vibration, we postulate that the time derivatives of the amplitude and the modified phase become equal to zero. This requirement allows one to write the following equations
that govern the steady-state oscillation at the double external resonance. The amplitudes and modified phases that satisfy system (147)–(150) are constant quantities representing the fixed point of the dynamical system (143)–(146).
Employing the Pythagorean identity, the modified phases can be eliminated from Eqs. (147)–(150), which allows one to express the direct dependence between the amplitudes and the parameters of the harmonic forces in the form of the following algebraic equations:
The real solutions of system (151)–(152), with given values of the amplitudes \({f}_{1}\) and \({f}_{2}\) as well the detuning parameters \({\sigma }_{1}\) and \({\sigma }_{2}\), are the values of the amplitudes at the steady oscillation. By changing the values of the detuning parameters, one can determine the curves of the resonance responses. However, the study of the stability of the fixed points requires also knowing the values of the modified phases. Therefore, it is necessary to solve the system of four Eqs. (147)–(150). The substitutions
where
allow one to transform Eqs. (147)–(150) into a more convenient, fully algebraic form. Namely, we get
Let \({(a}_{1s},{a}_{2s},{\theta }_{1s}, {\theta }_{2s})\) be any fixed point of the dynamical system (143)–(146). To examine the stability of this point in the sense of Lyapunov, we introduce the functions \({\tilde{a }}_{i}\left(\tau \right)\) and \({\stackrel{\sim }{\theta }}_{i}\left(\tau \right), i=\mathrm{1,2},\) that can be treated as small perturbations of the fixed point, i.e.,
Inserting functions (158) into Eqs. (143)–(146) yields
The right-hand sides of Eqs. (159)–(162) can be treated as functions of the small perturbations. We expand the functions into the Taylor series around zero that corresponds to the fixed point \({(a}_{1s},{a}_{2s},{\theta }_{1s}, {\theta }_{2s}).\) Then, ignoring the terms of the order higher than one, we get the following linearized form of Eqs. (159)–(162):
Equations (163)–(166) take into account that the fixed point satisfies the steady-state Eqs. (154)–(157). The general solution to Eqs. (163)–(166) can be presented in the form of the linear combination of the exponential functions
where \({r}_{j} , j=\mathrm{1,4},\) are the roots of the characteristic equation
The symbol I denotes the identity matrix of dimension \(4\times 4\), and B is the \(4\times 4\)-matrix whose entries are as follows:
The roots of Eq. (168) are the eigenvalues of matrix B. If the real parts of all eigenvalues of the matrix B are negative, then the fixed point \({(a}_{1s},{a}_{2s},{\theta }_{1s}, {\theta }_{2s})\) is asymptotically stable in the sense of Lyapunov.
System of Eqs. (154)–(157) is solved numerically using the procedure NSolve of the Mathematica. Determining the real roots in the iterative procedure enables the drawing of the resonance response curves, and now it is also possible to visualize the relationship between the modified phases and the detuning parameters. The study of stability of the resonance response curves is based on the eigenvalues of the matrix B, which are determined using the standard procedure Eigenvalues of the Mathematica.
Let us assume the following values of the dimensionless parameters describing the mechanical features of the pendulum:
The magnitudes of the dimensionless amplitudes of harmonic forces are assumed to be \({f}_{1}={f}_{2}=0.008.\)
In order to illustrate the influence of the detuning parameter \({\sigma }_{1}\) on the course of the double resonance, we change its values from −0.005 to 0.005 with the step of size \(2\cdot {10}^{-5}.\) The detuning parameter \({\sigma }_{2}=-0.004\) ensures that the frequency of the force \({f}_{2}\) is close to \(w.\) In Figs. 21, 22 and 23, the resonance responses curves of the spring pendulum are presented. The relationship between the amplitudes \({a}_{1}\) and \({a}_{2}\) and the detuning parameter \({\sigma }_{1}\) as well as the relationship between both modified phases and the detuning parameter \({\sigma }_{1}\) are depicted. All the points that make up the resonance response curves presented in Figs. 21–24 are stable. The amplitude \({a}_{1}\) reaches its maximum value for \({\sigma }_{1}\) slightly greater than zero. As the parameter \({\sigma }_{1}\) increases, the modified phase \({\theta }_{1}\) changes from 0 to \(\pi \). Both the amplitude \({a}_{2}\) and the phase \({\theta }_{2}\) change their values to a small extent, and both of these quantities reach their minima for \({\sigma }_{1}\) slightly greater than zero.
Amplitude \({a}_{1}\) versus the detuning parameter \(\sigma {}_{1}\) at the double external resonance; \({\sigma }_{2}=-0.004\)
Amplitude \({a}_{2}\) versus the detuning parameter \(\sigma {}_{1}\) at the double external resonance; \({\sigma }_{2}=-0.004\)
Modified phase \({\theta }_{1}\) versus the detuning parameter \(\sigma {}_{1}\) at the double external resonance for \({\sigma }_{2}=-0.004\)
Modified phase \({\theta }_{2}\) versus the detuning parameter \(\sigma {}_{1}\) at the double external resonances for \({\sigma }_{2}=-0.004.\)
In turn, the curves, drawn in Figs. 25, 26, 27 and 28, show how the parameter \({\sigma }_{2}\) influences the course of the double resonance. The parameter \({\sigma }_{2}\) varies from -0.005 to 0.005 with the step of size \(2\cdot {10}^{-5}\), and the detuning parameter \({\sigma }_{1}\) is equal to 0.01 which guarantees that the frequency of the force \({f}_{1}\) is close to 1. Branches made of unstable fixed points appeared on the graphs of the curves depicting the influence of the parameter \({\sigma }_{2}\). The stable branches of the curves have been drawn using points of larger size, so they are darker. The curve \({a}_{2}\) versus \({\sigma }_{2}\) has a shape typical for systems with the nonlinearity of the cubic type and the soft characteristic. The amplitude reaches large values which are close to the limit of the range of the applicability of the approximation given by formula (30). The modified phase \({\theta }_{2}\) passes from 0 to \(\pi \) in the narrow range of negative values of the parameter \({\sigma }_{2}\). In the same interval, the modified phase \({\theta }_{1}\) decreases slightly, and the amplitude \({a}_{1}\) increases by almost twice.
Amplitude \({a}_{1}\) versus the detuning parameter \(\sigma {}_{2}\) at the double external resonance for \({\sigma }_{1}=0.01;\) stable branches are darker
Amplitude \({a}_{2}\) versus the detuning parameter \(\sigma {}_{2}\) at the double external resonance for \({\sigma }_{1}=0.01;\) stable branches are darker
Modified phase \({\theta }_{1}\) versus the detuning parameter \(\sigma {}_{2}\) at the double external resonance for \({\sigma }_{1}=0.01\); stable branches are darker
Modified phase \({\theta }_{2}\) versus the detuning parameter \({\sigma }_{2}\) at the double external resonance for \({\sigma }_{1}=0.01\); stable branches are darker
Due to the occurrence of the unstable fixed points in the range between about -0.004 and -0.002, the jump phenomena are possible with slight fluctuations in the frequency of the torque that forces the transverse oscillation. The shape of the resonance response curves in the double resonance can change dramatically. For example, a small change in the value of the parameter \({\sigma }_{1}\) from 0.01 to 0.004, without changing any other parameter, leads to the results shown in Figs. 29, 30, 31 and 32.
Amplitude \({a}_{1}\) versus the detuning parameter \(\sigma {}_{2}\) at the double external resonance for \({\sigma }_{1}=0.004;\) stable branches are darker
Amplitude \({a}_{2}\) versus the detuning parameter \(\sigma {}_{2}\) at the double external resonance for \({\sigma }_{1}=0.004;\) stable branches are darker
Modified phase \({\theta }_{1}\) versus the detuning parameter \(\sigma {}_{2}\) at the double external resonance for \({\sigma }_{1}=0.004\); stable branches are darker
Modified phase \({\theta }_{2}\) versus the detuning parameter \({\sigma }_{2}\) at the double external resonance for \({\sigma }_{1}=0.01\); stable branches are darker
Equations (116)–(119) describe the slow evolution of the amplitudes and phases for the conditions of the external resonance \({p}_{1}\approx 1\). According to Eq. (120), the amplitude \({a}_{2}(\tau )\) tends asymptotically to zero. Taking into account Eq. (A5), one can conclude that the function \(\stackrel{\sim }{\varphi }(\tau )\) also vanishes asymptotically, and the steady resonant solution for \(\varphi (\tau )\) becomes pure harmonic, owing to (122). Such behavior of the spring pendulum is a consequence of the assumption of weak coupling between the longitudinal and transverse motion. The phase \({\psi }_{2}(\tau )\) is related to the other variables of the modulation problem, but due to the disappearance of the function \(\stackrel{\sim }{\varphi }(\tau )\) with time, the variability of the phase \({\psi }_{2}(\tau )\) is not important. In other words, we can write the modulation problem for the external resonance \({p}_{1}\approx 1\) as follows:
After introducing the modified phase \({\theta }_{1}(\tau )\), according to definition (142), we can formulate the following equations governing the amplitude and phase of the steady-state oscillation
The exact solution to Eqs. (171)–(172) can be found. Namely, by eliminating the modified phase \({\theta }_{1}\), we obtain the direct dependence between the amplitude \(a{}_{1}\) and the parameter \({\sigma }_{1}\)
Solving Eq. (173) for the square of \({a}_{1}\) yields
The solution for the variable \({\theta }_{1}\) is
Equation (174) shows that the amplitude of steady oscillations reaches its maximum \({a}_{1max}=\left|{f}_{1}/{c}_{1}\right|\) when the detuning parameter takes the value
At the same value \({\sigma }_{1}^{*}\), the modified phase passes through zero. It means that both the nonlinear properties of the springs and their individual contribution to the whole stiffness (via the parameter \(\lambda \)) affect the resonance \({p}_{1}\approx 1.\)
The matrix necessary to test the stability of the fixed point \(\left({a}_{1s},{\theta }_{1s}\right)\) has the following form:
Inserting Eq. (177) into Eq. (176) yields
Taking into account Eq. (171), we can write Eq. (178) in the form:
It results from Eq. (179) that both its roots have negative real parts. Thus, all points of the resonance response curves, shown in Figs. 33 and 34, are stable. The following data was adopted to draw the figures:
Amplitude \({a}_{1}\) versus the detuning parameter \({\sigma }_{1}\) at the resonance \({p}_{1}\approx 1\)
Modified phase \({\theta }_{1}\) versus the detuning parameter \({\sigma }_{1}\) at the resonance \({p}_{1}\approx 1\)
We start the study of the resonance \({p}_{2}\approx w\) with modulation Eqs. (127)–(130). According to Eq. (131), the amplitude \({a}_{1}\left(\tau \right)\) asymptotically tends to zero. For sufficiently large values of the variable \(\tau\), the influence of amplitude \({a}_{1}\left(\tau \right)\) becomes insignificant. Therefore, the solution to Eq. (129) is also irrelevant. Contrary to the resonance \({p}_{1}\approx 1\), the coupling between the transverse and longitudinal movement is maintained even for large values of time \(\tau \). The coupling is caused by the second term of the solution \({\tilde{x }}_{1}(\tau )\) (see Eq. (A4)). Thus, we can write the modulation problem for stationary states in the external resonance \({p}_{2}\approx w\) as follows:
After introducing the modified phase \({\theta }_{2}(\tau )\), according to definition (142), we formulate the following equations governing the amplitude and phase of the stationary vibration
By eliminating the modified phase \({\theta }_{2}\), we obtain the direct dependence between the amplitude \({a}_{2}\) and the parameter \({\sigma }_{2}\)
We test the stability of the fixed points that are the roots of Eqs. (182)–(183) in the same way as in the case of double resonance \(p_{1} \approx 1 \) and \(p_{2} \approx w\). The matrix necessary to test the stability of the fixed point \(\left({a}_{2s},{\theta }_{2s}\right)\) has the form
The following parameters are fixed: \(w=0.13, {c}_{2}=0.0015, {f}_{2}=0.0001.\)
The resonance response curves with two separable stable branches (points of which are drawn with larger dots) and an unstable branch are presented in Figs. 35 and 36.
Amplitude \({a}_{2}\) versus the detuning parameter \({\sigma }_{2}\) at the resonance \({p}_{2}\approx w\); stable branches are darker
Modified phase \({\theta }_{2}\) versus the detuning parameter \({\sigma }_{2}\) at the resonance \({p}_{2}\approx w\); stable branches are darker
7 Internal resonance
When the pendulum is constructed in such a way that the relation 2w ≈ 1 between the frequencies holds, then its oscillation shows the strong effects of coupling between the motion in the longitudinal and transverse directions. To express the closeness of the frequencies, we introduce the detuning parameter \(\sigma_{3}\) in the following manner
As previously, we employ MSM to investigate this case of resonance. Assumptions (29) about the smallness of some parameters of the mathematical model remain valid. Following the same procedure as in Sects. 4 and 5, we obtain the approximate asymptotic solution, which is valid for the internal resonance, of the following form:
The auxiliary function \({x}_{1}\left(\tau \right)\) is as follows:
The functions \({a}_{1}\left(\tau \right),{a}_{2}\left(\tau \right), {\psi }_{1}\left(\tau \right),\) and \({\psi }_{2}\left(\tau \right)\) are solutions to the modulation ODEs of the following form:
ODEs (190)–(193) are supplemented by initial conditions (75), and the modulation problem is solved numerically.
The following parameters are fixed during numerical calculations:
The external load parameters are fixed:
The initial values for the equations of motion are as follows:
The calculated initial values of the amplitudes and phases that are consistent with the values of \({x}_{0}, {v}_{0},\)
\({\varphi }_{0}\) and \({\omega }_{0}\) are:
The relationship between the initial values has been determined using the analytical form of solution (194)–(195).
In Figs. 37 and 38, the time history of the pendulum oscillations in the longitudinal and transverse direction is shown, respectively. Figure 39 reports how the deformations of the springs change with dimensionless time \(\tau\). The same method of presentation is maintained, in which the solution obtained numerically using NDSolve is drawn with a dotted line and the asymptotic solution (solid line). One can observe high compliance between both solutions, which is now worth underlying when the internal resonance affects the pendulum motion besides the forces. The following values of the measures (83)–(84)
Longitudinal oscillations in the internal resonance; solid line—asymptotic solution, dotted line—numerical solution
Swing oscillations in the internal resonance; solid line—asymptotic solution, dotted line—numerical solution
Deformations of the spring versus time in the internal resonance; solid line—asymptotic solution, dotted line—numerical solution
confirm the usefulness of the asymptotic solution (187)–(188). The error values were calculated on the interval \(\langle \mathrm{0,1000}\rangle \).
In each of Figs. 37, 38, and 39, one can notice the alternating changes in the amplitude of oscillations in the transverse and longitudinal directions, characteristic of internal resonance. This trend is weakened by damping and disrupted by external forces. Thus, the amplitudes \({a}_{1}\left(\tau \right)\) and \({a}_{2}\left(\tau \right)\) describing the slow variation tendency (but only of the first terms of the solutions), drawn with a solid black line in Figs. 37 and 38, do not exactly pass through the local maxima and minima. The effects of internal resonance in its pure form can be observed in Figs. 40 and 41. These graphs show the asymptotic solutions that were obtained, assuming that \(c_{1} = c_{2} = 0 \) and \(f_{1} = f_{2} = 0 \) and without changing the values of the other parameters of the model. In this conservative system, the oscillations are realized with the fixed modulation of slowly changing amplitudes caused by internal resonance. The figures also show the numerical solutions (drawn with the dotted line).
Longitudinal oscillations in the internal resonance for \({c}_{1}={c}_{2}=0\) and \({f}_{1}={f}_{2}=0.\)
Swing oscillations in the internal resonance for \({c}_{1}={c}_{2}=0\) and \({f}_{1}={f}_{2}=0;\) solid line—asymptotic solution, dotted line—numerical solution
The latter case proves that asymptotic solutions are universal and that on their basis, various special cases can be discussed without the need to construct new solutions.
8 Conclusions
Harmonically forced and viscously damped planar oscillations of the spring pendulum with two serially connected nonlinear springs have been analyzed. We derived the equations of motion from the Lagrange formalism, taking as a starting point an analogous one-dimensional oscillator with two degrees of freedom, i.e., a pendulum with two particles. The mathematical model of the spring pendulum includes two second-order ODEs and one algebraic equation (AE).
The governing equations concerning both non-resonant and resonant oscillations are solved using the MSM, which has been appropriately modified to solve the differential–algebraic equations. The variant of the MSM with three variables in the time domain has been employed. The accuracy of the obtained solutions has been estimated using two measures. The first assesses the error satisfying the equations of the mathematical model. The second one stands for a relative measure in the sense of the \({L}^{2}\)-norm and compares the asymptotic solution with the numerical one determined using the NDSolve procedure of Mathematica software. These errors serve as measurable criteria for identifying the accuracy of the solution methods.
The asymptotic solution, valid for non-resonant motion, enabled the prediction of three resonance cases: two external resonances and the 1:2 internal resonance. Asymptotic solutions for the two single external resonances and the case of two simultaneously occurring resonances \(p_{1} \approx 1\) and \(p_{2} \approx w\) have been derived. The approximate asymptotic solutions for each of the resonance cases are based on different assumptions, so they must be constructed independently. Although asymptotic solutions were obtained from the constituted sequence limited only to three terms, the formulas representing them are complex. The comparison of the forms of the asymptotic solutions for non-resonant oscillation and external resonances made it possible to find common terms that depend only on the structure, geometry, and mechanical properties of the pendulum. Writing the solutions in this more compact form enables a more straightforward analysis of the influence of individual parameters on the pendulum’s motion.
Within the procedure of solving the problem corresponding to a given resonance case, the modulation equations of the amplitudes and phases are derived. The modulation equations obtained for external resonances are the basis for the steady-state analysis. Studies of the periodic stationary solutions, supplemented with the analysis of the stability in the Lyapunov sense, have been carried out for each of the considered external resonance. The resonance response curves have been depicted in the form of the dependencies: the amplitude versus the detuning parameter and the modified phase versus the detuning parameter. The shape of the resonance response curves of the pendulum at the double resonance strongly depends on the forcing parameters. Slight changes with regard to the frequency or the amplitude of the force dramatically change the form of the response curves. Taking into account the jump phenomenon between stable branches, one should predict the chaotic behavior in this regime. For the case of \(p_{1} \approx 1\) resonance, the analytical form of the dependencies between the amplitude and the detuning parameter as well as between the modified phase and the detuning parameter has been derived. It was also proved that all fixed points are stable.
The occurrence of internal resonances depends on the fulfillment of certain design conditions. For the spring pendulum, it appears when there is the 1: 2 relationship between the dimensionless frequencies characteristic for the longitudinal and transverse oscillations. Taking into account both the measures satisfying the governing equations and compliance with the numerical solution, one can conclude that the asymptotic solution works well both in the presence and absence of the damping and external forces. The presented possibility of obtaining a solution for a specific case from a more general solution proves the advantages of approximate analytical methods based on our approach.
Sypniewska-Kamińska et al. in [45] pointed the impact of the error of approximation of the trigonometric functions by the Taylor series on the accuracy of asymptotic solutions. Therefore, the solutions were rejected for which the oscillation amplitude values in the transverse direction exceed the approximation applicability range (i.e., about 0.6 rad). This observation also holds for resonance cases.
Mechanical systems consisting of elastic elements connected in series have great potential for technical applications. For example, in vehicle’s suspension or passive damping systems. The study of such systems with an analytical approach can bring many benefits. It is obvious that the analytical results, even approximate, allow for a much broader analysis of the behavior of the system than the numerical solutions.
References
Awrejcewicz, J., Starosta, R., Sypniewska-Kamińska, G.: Asymptotic Multiple Scale Method in Time Domain. Multi-Degree-of-Freedom Stationary and Nonstationary Dynamics. CRC Press, London (2022)
Rand, R.H., Holmes, P.J.: Bifurcation of periodic motions in two weakly coupled van der Pol oscillators. Int. J. Non-Lin. Mech. 15, 387–399 (1980)
Benedettini, F., Rega, G.: Non-linear dynamics of an elastic cable under planar excitation. Int. J. Non-Lin. Mech. 22(6), 497–509 (1987)
Luongo, A., Polone, A.: Multiple scale analysis for divergence-Hopf bifurcation of imperfect symmetric systems. J. Sound Vib. 218(3), 527–539 (1998)
Rega, G., Lacarbonara, W., Nayfeh, A.H., Chin, C.M.: Multiple resonances in suspended cables: direct versus reduced-order models. Int. J. Non-Lin. Mech. 34, 901–924 (1999)
Belhaq, M., Houssini, M.: Quasi-periodic oscillations, chaos and suppression of chaos in a nonlinear oscillator driven by parametric and external excitations. Nonlin. Dyn. 18, 1–24 (1999)
Leamy, M.J., Gottlieb, O.: Internal resonances in whirling strings involving longitudinal dynamics and material non-linearities. J. Sound Vib. 236(4), 683–703 (2000)
Belhaq, M., Lakrad, F.: The elliptic multiple scales method for a class of autonomous strongly non-linear oscillators. J. Sound Vib. 234(3), 547–553 (2000)
Belhaq, M., Guennoun, K., Houssini, M.: Asymptotic solutions for a damped non-linear quasi-periodic Mathieu equation. Int. J. Non-Lin. Mech. 37, 445–460 (2002)
Lacarbonara, W., Rega, G., Nayfeh, A.H.: Resonant non-linear normal modes. Part I: analytical treatment for structural one-dimensional systems. Int. J. Non-Lin. Mech. 38, 851–872 (2003)
Abdulle, A., Weinan, E.: Finite difference heterogeneous multi-scale method for homogenization problems. J. Comput. Phys. 191, 18–39 (2003)
Luongo, A., Di Egidio, A., Paolone, A.: Multiscale analysis of defective multiple-Hopf bifurcations. Comp. Struct. 82, 2705–2722 (2004)
Warmiński, J.: Regular and chaotic vibrations of a parametrically and self-excited system under internal resonance condition. Meccanica 40, 181–202 (2005)
Abouhazim, N., Belhaq, M., Lakrad, F.: Three-period quasi-periodic solutions in the self-excited quasi-periodic Mathieu oscillator. Nonlin. Dyn. 39, 395–409 (2005)
Luongo, A., Di Egidio, A.: Divergence, Hopf and double-zero bifurcations of a nonlinear planar beam. Comp. Struct. 84, 1596–1605 (2006)
Abouhazim, N., Rand, R.H., Belhaq, M.: The damped nonlinear quasiperiodic Mathieu equation near 2:2:1 resonance. Nonlin. Dyn. 45, 237–247 (2006)
Srinil, N., Rega, G., Chucheepsakul, S.: Two-to-one resonant multi-modal dynamics of horizontal/inclined cables. Part I: theoretical formulation and model validation. Nonlin. Dyn. 48, 23–252 (2007)
Kramer, P., Khan, A., Stathos, P., Lee de Ville, R.E.: Method of multiple scales with three time scales. In s. (2007)
Gottlieb, O., Cohen, A.: Self-excited oscillations of a string on an elastic foundation subject to a nonlinear feed-forward force. Int. J. Mech. Sci. 52, 1535–1545 (2010)
Suchorsky, M.K., Sah, S.M., Rand, R.H.: Using delay to quench undesirable vibrations. Nonlin. Dyn. 62, 407–416 (2010)
Zulli, D., Luongo, A.: Bifurcation and stability of a two-tower system under wind-induced parametric, external and self-excitation. J. Sound Vib. 331, 365–383 (2012)
Cacan, M.R., Leadenham, S., Leamy, M.J.: An enriched multiple scales method for harmonically forced nonlinear systems. Nonlin. Dyn. 78, 1205–1220 (2014)
Settimi, V., Gottlieb, O., Rega, G.: Asymptotic analysis of a noncontact AFM microcantilever sensor with external feedback control. Nonlin. Dyn. 79, 2675–2698 (2015)
Mora, K., Gottlieb, O.: Parametric excitation of a microbeam-string with asymmetric electrodes: multimode dynamics and the effect of nonlinear damping. J. Vib. Acoust. 139, 040903 (2017)
Wilbanks, J.J., Adams, Ch.J., Leamy, M.J.: Two-scale command shaping for feedforward control of nonlinear systems. Nonlin. Dyn. 92, 885–903 (2018)
Kovaleva, M., Manevitch, L., Romeo, F.: Stationary and non-stationary oscillatory dynamics of the parametric pendulum. Comm. Nonlin. Sci. Num. Simul. 76, 1–11 (2019)
Guo, T., Rega, G.: Solvability conditions in multi-scale dynamic analysis of one-dimensional structures with non-homogeneous boundaries: a general operator formulation. Int. J. Non-Lin. Mech. 115, 68–75 (2019)
Fronk, M.D., Leamy, M.J.: Direction-dependent invariant waveforms and stability in two-dimensional, weakly nonlinear lattices. J. Sound Vib. 447, 37–154 (2019)
Rand, R.H., Zehnder, A.T., Shayak, B., Bhaskar, A.: Simplified model and analysis of a pair of coupled thermo-optical MEMS oscillators. Nonlin. Dyn. 99, 73–83 (2020)
Clementi, F., Lenci, S., Rega, G.: 1:1 internal resonance in a two d.o.f. complete system: a comprehensive analysis and its possible exploitation for design. Meccanica 55, 1309–1332 (2020)
Guo, T., Rega, G.: Direct and discretized perturbations revisited: a new error source interpretation, with application to moving boundary problem. Eur. J. Mech. Sol. 81, 103936 (2020)
Warmiński, J.: Nonlinear dynamics of self-, parametric, and externally excited oscillator with time delay: van der Pol versus Rayleigh models. Nonlin. Dyn. 99, 35–56 (2020)
Lenci, S., Clementi, F., Kloda, L., Warmiński, J., Rega, G.: Longitudinal-transversal internal resonances in Timoshenko beams with an axial elastic boundary condition. Nonlin. Dyn. 103, 3489–3513 (2021)
Andrzejewski, R., Awrejcewicz, J.: Nonlinear Dynamics of a Wheeled Vehicle. Springer, Berlin (2005)
Suciu, C.V., Tobiishi, T., Mouri, R.: Modeling and simulation of a vehicle suspension with variable damping versus the excitation frequency. J. Telecom. Inf. Technol. 1(2012), 83–89 (2012)
Telli, S., Kopmaz, O.: Free vibrations of a mass grounded by linear and nonlinear springs in series. J. Sound Vib. 289, 689–710 (2006)
Weggel, D.C., Boyajian, D.M., Chen, S.E.: Modelling structures as systems of springs. World Trans. Eng. Technol. Educ. 6(1), 169–172 (2007)
Manevitch, L.I., Musienko, A.I.: Limiting phase trajectories and energy exchange between anharmonic oscillator and external force. Nonlin. Dyn. 58, 633–642 (2009)
Starosta, R., Awrejcewicz, J., Sypniewska-Kamińska, G.: Quantifying non-linear dynamics of mass-springs in series oscillators via asymptotic approach. Mech. Sys. Sig. Proc. 89, 149–158 (2017)
Awrejcewicz, J., Starosta, R., Sypniewska-Kamińska, G.: Nonlinear vibration of a lumped system with springs-in-series. Meccanica 56, 753–767 (2021)
Bishop, R.E.D., Gladwell, G.M.L., Michaelson, S.: The Matrix Analysis of Vibration. Cambridge University Press, Cambridge (2008)
Takeno, Sh., Honmma, S.: A sine-lattice (sine-form) discrete sine-Gordon) equation-one- and two-kink solutions and physical models. J. Phys. Soc. Jpn. 55, 65 (1986)
Yomosa, S.: Soliton excitations in deoxyribonucleic acid (DNA) double helices. Phys. Rev. A 27, 2120 (1983)
Duckworth, R.A.: Mechanics of Fluids. Longman Group Limited, London (1997)
Sypniewska-Kamińska, G., Awrejcewicz, J., Kamiński, H., Salamon, R.: s. Meccanica 56, 963–980 (2021)
Acknowledgements
This paper was financially supported by the grant of the Ministry of Science and Higher Education 0612/SBAD/3588 and the grant of Polish National Science Centre OPUS 18 No. 2019/35/B/ST8/00980.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflicts of interest to report regarding the present study.
Data Availability Statement
Data will be available on reasonable request.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
The detailed form of Eq. (38) after substitution Eqs. (42)–(44), (48), (52) and elimination of the secular terms (54)–(55) follows
Equation (53) with inserted solution (56) instead of the function \({\xi }_{23}({\tau }_{0},{\tau }_{1}, {\tau }_{2})\) reads:
The detailed form of Eq. (39) after substitution Eqs. (42)–(44), (48), (52) and elimination of the secular terms (57)–(58) is as follows:
Functions \({\tilde{x }}_{1}\left(\tau \right), {\tilde{x }}_{2}\left(\tau \right),\) and \(\stackrel{\sim }{\varphi }\left(\tau \right)\) in Eqs. (83)–(85), and (7) have the following form:
The detailed form of Eqs. (94)–(95) after elimination of the secular terms (109)–(112) reads
Rights and permissions
About this article
Cite this article
Sypniewska-Kamińska, G., Starosta, R. & Awrejcewicz, J. Quantifying nonlinear dynamics of a spring pendulum with two springs in series: an analytical approach. Nonlinear Dyn 110, 1–36 (2022). https://doi.org/10.1007/s11071-022-07612-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-022-07612-2